Twierdzenie Czebyszewa o funkcji π(n): Różnice pomiędzy wersjami
| Linia 1059: | Linia 1059: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie | + | <span style="font-size: 110%; font-weight: bold;">Zadanie A38</span><br/> |
| + | Niech <math>x \in \mathbb{R}_+</math>. Pokazać, że dla dowolnego <math>n \in \mathbb{Z}_+</math> istnieje takie <math>x_0</math>, że dla każdego <math>x > x_0</math> jest <math>\log x < x^{1 / n}</math>. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | <span style="border-bottom-style: double;">Pierwszy sposób</span><br/> | ||
| + | Rozważmy ciąg nierówności | ||
| + | |||
| + | ::<math>\log x < 2 n \cdot x^{1 / 2 n} < x^{1 / n}</math> | ||
| + | |||
| + | Z twierdzenia A37 wiemy, że pierwsza nierówność jest prawdziwa dla dowolnych <math>x \in \mathbb{R}_+</math> i <math>n \in \mathbb{Z}_+</math>. Podnosząc strony drugiej nierówności do potęgi <math>2 n</math> otrzymujemy <math>(2 n)^{2 n} \cdot x < x^2</math>, czyli nierówność ta jest prawdziwa dla <math>x > (2 n)^{2 n}</math>. Wynika stąd, że wystarczy przyjąć <math>x_0 = (2 n)^{2 n}</math>. | ||
| + | |||
| + | |||
| + | <span style="border-bottom-style: double;">Drugi sposób</span><br/> | ||
| + | Nierówność <math>\log x < x^{1 / n}</math> możemy równoważnie zapisać w postaci <math>x < \exp (x^{1 / n})</math>. Jeżeli położymy <math>x = t^n</math>, to otrzymamy nierówność <math>t^n {< e^t} </math>. Ponieważ<ref name="exp1"/> | ||
| + | |||
| + | ::<math>e^t = \sum_{k = 0}^{\infty} \frac{t^k}{k!} = 1 + t + \frac{t^2}{2} + \frac{t^3}{6} + \frac{t^4}{24} + \frac{t^5}{120} + \ldots</math> | ||
| + | |||
| + | to | ||
| + | |||
| + | ::<math>e^t > \frac{t^{n + 1}}{(n + 1) !} > t^n</math> | ||
| + | |||
| + | Pierwsza nierówność jest prawdziwa dla <math>t > 0</math>, bo pomijamy wyrazy dodatnie, a druga dla <math>t > (n + 1) !</math> Wystarczy zatem przyjąć <math>x_0 = [(n + 1) !]^n</math>. Ponieważ <math>[(n + 1) !]^n > (2 n)^{2 n}</math> dla <math>n \geqslant 4</math>, to jest to gorsze oszacowanie wartości <math>x_0</math>.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span style="font-size: 110%; font-weight: bold;">Twierdzenie A39</span><br/> | ||
Dla funkcji <math>p_n</math> i <math>\pi (n)</math> prawdziwe są następujące oszacowania: | Dla funkcji <math>p_n</math> i <math>\pi (n)</math> prawdziwe są następujące oszacowania: | ||
| Linia 1118: | Linia 1145: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie | + | <span style="font-size: 110%; font-weight: bold;">Twierdzenie A40</span><br/> |
Dla <math>n \geqslant 1</math> prawdziwe jest oszacowanie | Dla <math>n \geqslant 1</math> prawdziwe jest oszacowanie | ||
| Linia 1144: | Linia 1171: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Zadanie | + | <span style="font-size: 110%; font-weight: bold;">Zadanie A41</span><br/> |
| − | Korzystając z twierdzenia | + | Korzystając z twierdzenia A40 pokazać, że |
:* <math>p_1 p_2 \cdot \ldots \cdot p_n > (p_{n + 1})^2 \qquad \qquad \text{dla } \; n \geqslant 4</math> | :* <math>p_1 p_2 \cdot \ldots \cdot p_n > (p_{n + 1})^2 \qquad \qquad \text{dla } \; n \geqslant 4</math> | ||
| Linia 1172: | Linia 1199: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie | + | <span style="font-size: 110%; font-weight: bold;">Twierdzenie A42</span><br/> |
Każda liczba pierwsza <math>p</math>, taka że <math>p \in \left( \frac{n}{2}, n \right]</math> występuje w rozwinięciu <math>n!</math> na czynniki pierwsze z wykładnikiem równym jeden. | Każda liczba pierwsza <math>p</math>, taka że <math>p \in \left( \frac{n}{2}, n \right]</math> występuje w rozwinięciu <math>n!</math> na czynniki pierwsze z wykładnikiem równym jeden. | ||
| Linia 1188: | Linia 1215: | ||
| − | Rezultat uzyskany w twierdzeniu A25 zainspirował nas do postawienia pytania: jakie warunki musi spełniać liczba pierwsza <math>p</math>, aby występowała w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem równym jeden lub równym zero? Twierdzenia | + | Rezultat uzyskany w twierdzeniu A25 zainspirował nas do postawienia pytania: jakie warunki musi spełniać liczba pierwsza <math>p</math>, aby występowała w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem równym jeden lub równym zero? Twierdzenia A43 i A45 udzielają na to pytanie precyzyjnej odpowiedzi. Przykłady A44 i A46 to tylko twierdzenia A43 i A45 dla wybranych wartości liczby <math>k</math>. Jeśli Czytelnik nie miał problemów ze zrozumieniem dowodów twierdzeń A43 i A45, to może je pominąć. |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie | + | <span style="font-size: 110%; font-weight: bold;">Twierdzenie A43</span><br/> |
Niech <math>k</math> będzie dowolną ustaloną liczbą naturalną. Jeżeli <math>n \geqslant 2 (k + 1) \left( k + \tfrac{1}{2} \right)</math> i liczba pierwsza <math>p \in \left( {\small\frac{n}{k + 1}}, {\small\frac{n}{k + \tfrac{1}{2}}} \right]</math>, to <math>p</math> występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem równym jeden. | Niech <math>k</math> będzie dowolną ustaloną liczbą naturalną. Jeżeli <math>n \geqslant 2 (k + 1) \left( k + \tfrac{1}{2} \right)</math> i liczba pierwsza <math>p \in \left( {\small\frac{n}{k + 1}}, {\small\frac{n}{k + \tfrac{1}{2}}} \right]</math>, to <math>p</math> występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem równym jeden. | ||
| Linia 1286: | Linia 1313: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Przykład | + | <span style="font-size: 110%; font-weight: bold;">Przykład A44</span><br/> |
Jeżeli <math>n \geqslant 6</math> i liczba pierwsza <math>p \in \left( \frac{n}{2}, \frac{2 n}{3} \right]</math>, to <math>p</math> występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem równym jeden. | Jeżeli <math>n \geqslant 6</math> i liczba pierwsza <math>p \in \left( \frac{n}{2}, \frac{2 n}{3} \right]</math>, to <math>p</math> występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem równym jeden. | ||
| Linia 1349: | Linia 1376: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie | + | <span style="font-size: 110%; font-weight: bold;">Twierdzenie A45</span><br/> |
Niech <math>k</math> będzie dowolną ustaloną liczbą całkowitą dodatnią. Jeżeli liczba pierwsza <math>p \in \left( \frac{n}{k + \tfrac{1}{2}}, \frac{n}{k} \right]</math>, to dla <math>n \geqslant 2 k (k + \tfrac{1}{2})</math> liczba <math>p</math> nie występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze. | Niech <math>k</math> będzie dowolną ustaloną liczbą całkowitą dodatnią. Jeżeli liczba pierwsza <math>p \in \left( \frac{n}{k + \tfrac{1}{2}}, \frac{n}{k} \right]</math>, to dla <math>n \geqslant 2 k (k + \tfrac{1}{2})</math> liczba <math>p</math> nie występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze. | ||
| Linia 1426: | Linia 1453: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Przykład | + | <span style="font-size: 110%; font-weight: bold;">Przykład A46</span><br/> |
Jeżeli <math>n \geqslant 8</math> i liczba pierwsza <math>p \in \left( \frac{2 n}{5}, \frac{n}{2} \right]</math>, to <math>p</math> nie występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze. | Jeżeli <math>n \geqslant 8</math> i liczba pierwsza <math>p \in \left( \frac{2 n}{5}, \frac{n}{2} \right]</math>, to <math>p</math> nie występuje w rozwinięciu liczby <math>\binom{2 n}{n}</math> na czynniki pierwsze. | ||
| Linia 1491: | Linia 1518: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Uwaga | + | <span style="font-size: 110%; font-weight: bold;">Uwaga A47</span><br/> |
| − | Z przykładu | + | Z przykładu A44 nie wynika, że w przedziale <math>\left( \frac{n}{2}, \frac{2 n}{3} \right]</math> znajduje się choćby jedna liczba pierwsza <math>p</math>. Analogiczna uwaga jest prawdziwa w przypadku przykładu A46 oraz twierdzeń A43 i A45. Istnienie liczby pierwszej w określonym przedziale będzie tematem kolejnego artykułu. |
| − | <span style="font-size: 110%; font-weight: bold;">Przykład | + | <span style="font-size: 110%; font-weight: bold;">Przykład A48</span><br/> |
| − | Pokazujemy i omawiamy wynik zastosowania twierdzeń | + | Pokazujemy i omawiamy wynik zastosowania twierdzeń A43 i A45 do współczynnika dwumianowego <math>\binom{2 \cdot 3284}{3284}</math>. Można udowodnić, że granicę stosowalności obu twierdzeń bardzo dokładnie opisuje warunek <math>p > \sqrt{2 n}</math>, co w naszym przypadku daje <math>p > \sqrt{2 \cdot 3284} \approx 81.04</math>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż przykład|Hide=Ukryj przykład}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż przykład|Hide=Ukryj przykład}} | ||
Wybraliśmy współczynnik dwumianowy <math>\binom{2 \cdot 3284}{3284}</math> dlatego, że w rozkładzie tego współczynnika na czynniki pierwsze występują wszystkie liczby pierwsze <math>p \leqslant 107</math>, co ułatwia analizowanie występowania liczb pierwszych. Tylko sześć liczb pierwszych: 2, 3, 59, 61, 73, 79 występuje z wykładnikiem większym niż jeden. Ponieważ <math>\sqrt{2 \cdot 3284} \approx 81.043</math>, zatem liczba 79 jest ostatnią liczbą pierwszą, która mogłaby wystąpić z wykładnikiem większym niż jeden i tak właśnie jest.<br/> | Wybraliśmy współczynnik dwumianowy <math>\binom{2 \cdot 3284}{3284}</math> dlatego, że w rozkładzie tego współczynnika na czynniki pierwsze występują wszystkie liczby pierwsze <math>p \leqslant 107</math>, co ułatwia analizowanie występowania liczb pierwszych. Tylko sześć liczb pierwszych: 2, 3, 59, 61, 73, 79 występuje z wykładnikiem większym niż jeden. Ponieważ <math>\sqrt{2 \cdot 3284} \approx 81.043</math>, zatem liczba 79 jest ostatnią liczbą pierwszą, która mogłaby wystąpić z wykładnikiem większym niż jeden i tak właśnie jest.<br/> | ||
| − | Poniżej wypisaliśmy wszystkie liczby pierwsze <math>p \leqslant 3284</math>, które występują w rozwinięciu współczynnika dwumianowego <math>\binom{2 \cdot 3284}{3284}</math> na czynniki pierwsze. Pogrubienie oznacza, że dana liczba rozpoczyna nowy wiersz w tabeli. Ostatnią pogrubioną i dodatkowo podkreśloną liczbą jest liczba 107, bo wszystkie liczby pierwsze mniejsze od 107 powinny pojawić się w tabeli – oczywiście tak się nie stanie, bo twierdzeń | + | Poniżej wypisaliśmy wszystkie liczby pierwsze <math>p \leqslant 3284</math>, które występują w rozwinięciu współczynnika dwumianowego <math>\binom{2 \cdot 3284}{3284}</math> na czynniki pierwsze. Pogrubienie oznacza, że dana liczba rozpoczyna nowy wiersz w tabeli. Ostatnią pogrubioną i dodatkowo podkreśloną liczbą jest liczba 107, bo wszystkie liczby pierwsze mniejsze od 107 powinny pojawić się w tabeli – oczywiście tak się nie stanie, bo twierdzeń A43 i A45 nie można stosować bez ograniczeń dla coraz większych liczb <math>k</math>. |
| Linia 1511: | Linia 1538: | ||
Liczba 821 została pogrubiona (w tabeli), bo jest liczbą pierwszą i wyznacza początek przedziału otwartego, konsekwentnie liczba 821 nie występuje w rozkładzie współczynnika dwumianowego <math>\binom{2 \cdot 3284}{3284}</math> na czynniki pierwsze.<br/> | Liczba 821 została pogrubiona (w tabeli), bo jest liczbą pierwszą i wyznacza początek przedziału otwartego, konsekwentnie liczba 821 nie występuje w rozkładzie współczynnika dwumianowego <math>\binom{2 \cdot 3284}{3284}</math> na czynniki pierwsze.<br/> | ||
| − | Czytelnik łatwo sprawdzi, że największą wartością liczby <math>k</math>, dla jakiej można jeszcze stosować twierdzenie | + | Czytelnik łatwo sprawdzi, że największą wartością liczby <math>k</math>, dla jakiej można jeszcze stosować twierdzenie A43, jest <math>k = 39</math>. Podobnie największą wartością liczby <math>k</math>, dla jakiej można jeszcze stosować twierdzenie A45, jest <math>k = 40</math>. Wartości te i odpowiadające im przedziały zostały pogrubione, aby uwidocznić granicę stosowania tych twierdzeń. Łatwo odczytujemy, że twierdzenia A43 i A45 można stosować dla liczb pierwszych <math>p</math> spełniających warunek <math>p > 81.09</math>. Co bardzo dokładnie pokrywa się z warunkiem <math>p > \sqrt{2 \cdot 3284} \approx 81.04</math><br/> |
Liczba 73 jest ostatnią poprawnie pokazaną liczbą pierwszą. Po niej nie pojawiają się liczby pierwsze 71 i 67, które występują w rozwinięciu współczynnika dwumianowego <math>\binom{2 \cdot 3284}{3284}</math> na czynniki pierwsze.<br/> | Liczba 73 jest ostatnią poprawnie pokazaną liczbą pierwszą. Po niej nie pojawiają się liczby pierwsze 71 i 67, które występują w rozwinięciu współczynnika dwumianowego <math>\binom{2 \cdot 3284}{3284}</math> na czynniki pierwsze.<br/> | ||
Wersja z 17:24, 17 maj 2024
Oznaczenia
Będziemy stosowali następujące oznaczenia:
- [math]\displaystyle{ \mathbb{Z} }[/math] — zbiór liczb całkowitych
- [math]\displaystyle{ \mathbb{Z}_+ }[/math] — zbiór liczb całkowitych dodatnich
- [math]\displaystyle{ \mathbb{N} }[/math] — zbiór liczb naturalnych [math]\displaystyle{ \mathbb{N} = \mathbb{Z}_{+}\cup \left \{ 0 \right \} }[/math]
- [math]\displaystyle{ \mathbb{R} }[/math] — zbiór liczb rzeczywistych
- [math]\displaystyle{ d \mid n }[/math] — czytaj: d dzieli n ([math]\displaystyle{ d }[/math] jest dzielnikiem liczby [math]\displaystyle{ n }[/math])
- [math]\displaystyle{ d \nmid n }[/math] — czytaj: d nie dzieli n ([math]\displaystyle{ d }[/math] nie jest dzielnikiem liczby [math]\displaystyle{ n }[/math])
- [math]\displaystyle{ p_n }[/math] — [math]\displaystyle{ n }[/math]-ta liczba pierwsza
- [math]\displaystyle{ \pi (n) }[/math] — ilość liczb pierwszych nie większych od [math]\displaystyle{ n }[/math]
- [math]\displaystyle{ P(n) }[/math] — iloczyn liczb pierwszych nie większych od [math]\displaystyle{ n }[/math]
- [math]\displaystyle{ \lfloor x \rfloor }[/math] — największa liczba całkowita nie większa od [math]\displaystyle{ x }[/math]
- [math]\displaystyle{ \binom{n}{m} }[/math] — współczynnik dwumianowy (symbol Newtona), [math]\displaystyle{ \binom{n}{m} = \frac{n!}{m! \cdot (n - m) !} }[/math]
- [math]\displaystyle{ \log (x) }[/math] — logarytm naturalny liczby [math]\displaystyle{ x \gt 0 }[/math]
- [math]\displaystyle{ W_p (n) }[/math] — wykładnik z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze liczby [math]\displaystyle{ n }[/math]
- [math]\displaystyle{ n }[/math] — oznacza zawsze liczbę naturalną
- [math]\displaystyle{ p }[/math] — oznacza zawsze liczbę pierwszą
- [math]\displaystyle{ \mathbb{Z} }[/math] — zbiór liczb całkowitych
Przykładowe wartości niektórych wypisanych wyżej funkcji:
- [math]\displaystyle{ p_2 = 3 }[/math], [math]\displaystyle{ p_{10} = 29 }[/math], [math]\displaystyle{ p_{100} = 541 }[/math]
- [math]\displaystyle{ \pi (10) = 4 }[/math], [math]\displaystyle{ \pi (100) = 25 }[/math], [math]\displaystyle{ \pi (541) = 100 }[/math]
- [math]\displaystyle{ P(5) = 30 }[/math], [math]\displaystyle{ P(10) = 210 }[/math], [math]\displaystyle{ P(50) = 614889782588491410 }[/math]
- [math]\displaystyle{ \lfloor 1.2 \rfloor = 1 }[/math], [math]\displaystyle{ \lfloor 2.8 \rfloor = 2 }[/math], [math]\displaystyle{ \lfloor - 1.5 \rfloor = - 2 }[/math]
- [math]\displaystyle{ \binom{5}{2} = 10 }[/math], [math]\displaystyle{ \binom{10}{5} = 252 }[/math], [math]\displaystyle{ \binom{9}{3} = 84 }[/math]
- [math]\displaystyle{ W_2 (8) = 3 }[/math], [math]\displaystyle{ W_3 (18) = 2 }[/math], [math]\displaystyle{ W_7 (28) = 1 }[/math]
- [math]\displaystyle{ p_2 = 3 }[/math], [math]\displaystyle{ p_{10} = 29 }[/math], [math]\displaystyle{ p_{100} = 541 }[/math]
Funkcje te są zaimplementowane w PARI/GP[1]
- [math]\displaystyle{ p_n }[/math] = prime(n)
- [math]\displaystyle{ \pi (n) }[/math] = primepi(n)
- [math]\displaystyle{ P(n) }[/math] = prodeuler(p=2, n, p)
- [math]\displaystyle{ \lfloor x \rfloor }[/math] = floor(x)
- [math]\displaystyle{ \binom{n}{m} }[/math] = binomial(n, m)
- [math]\displaystyle{ W_p (n) }[/math] = valuation(n, p)
- [math]\displaystyle{ p_n }[/math] = prime(n)
Twierdzenie Czebyszewa
W 1852 roku rosyjski matematyk Czebyszew[2][3] udowodnił, że dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ a \cdot \frac{n}{\log n} \: \underset{n \geqslant 11}{\lt } \: \pi (n) \: \underset{n \geqslant 96098}{\lt } \: b \cdot \frac{n}{\log n} }[/math]
gdzie
- [math]\displaystyle{ a = \log (2^{1 / 2} \cdot 3^{1 / 3} \cdot 5^{1 / 5} \cdot 30^{- 1 / 30}) = 0.921292022 \qquad \quad b = \tfrac{6}{5} a = 1.105550428 }[/math]
Dziwnym zrządzeniem losu rezultat ten określany jest jako nierówności Czebyszewa (których nie należy mylić z nierównościami udowodnionymi przez Czebyszewa w teorii prawdopodobieństwa), a twierdzeniem Czebyszewa nazywany jest łatwy wniosek z tych nierówności. Stąd tytuł tego artykułu: „Twierdzenie Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math]”
Twierdzenie Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math] nabrało nowego życia, gdy w 1936 Erdos[4] zelementaryzował jego dowód. Elementarny dowód daje mniej dokładne oszacowania, ale pozwala zapoznać się z tym pięknym twierdzeniem nawet uczniom szkoły podstawowej.
Czytelnik powinien mieć świadomość, że rezultat ten ma już jedynie znaczenie historyczne – dzisiaj dysponujemy znacznie lepszymi oszacowaniami[5][6][7][8] funkcji [math]\displaystyle{ \pi (n) }[/math] oraz [math]\displaystyle{ p_n }[/math]
- [math]\displaystyle{ \frac{n}{\log n} \left( 1 + \frac{1}{\log n} \right) \underset{n \geqslant 599}{\lt } \pi (n) \underset{n \geqslant 2}{\lt } \frac{n}{\log n} \left( 1 + \frac{1.28}{\log n} \right) }[/math]
- [math]\displaystyle{ n (\log n + \log \log n - 1) \underset{n \geqslant 2}{\lt } p_n \underset{n \geqslant 6}{\lt } n (\log n + \log \log n) }[/math]
Przedstawimy tutaj elementarny dowód twierdzenia Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math] oraz analogiczne oszacowanie dla funkcji [math]\displaystyle{ p_n }[/math].
Twierdzenie A1
Prawdziwe są następujące oszacowania:
- [math]\displaystyle{ 0.72 \cdot n \log n \underset{n \geqslant 1}{\lt } p_n \underset{n \geqslant 3}{\lt } 2n \log n }[/math]
- [math]\displaystyle{ \frac{2}{3} \cdot \frac{n}{\log n} \underset{n \geqslant 3}{\lt } \pi (n) \underset{n \geqslant 2}{\lt } \frac{2 n}{\log n} }[/math]
Dowód powyższego twierdzenia jest łatwy, ale wymaga udowodnienia kolejno wielu, przeważnie bardzo prostych, twierdzeń pomocniczych.
Oszacowanie [math]\displaystyle{ p_n }[/math] od dołu i [math]\displaystyle{ \pi (n) }[/math] od góry
Rozpoczniemy od oszacowania liczby [math]\displaystyle{ \binom{2n}{n} }[/math]. Badanie właściwości tego współczynnika dwumianowego jest kluczowe dla naszego dowodu.
Twierdzenie A2
Niech [math]\displaystyle{ n, k \in \mathbb{N} }[/math]. Współczynnik dwumianowy [math]\displaystyle{ \binom{n}{k} }[/math] jest zawsze liczbą całkowitą dodatnią.
Indukcja matematyczna. Ponieważ
- [math]\displaystyle{ \binom{0}{0} = \binom{1}{0} = \binom{1}{1} = 1 }[/math]
to twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math]. Zakładając prawdziwość twierdzenia dla wszystkich liczb całkowitych należących do przedziału [math]\displaystyle{ [1, n] }[/math] mamy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ \binom{n + 1}{0} = \binom{n + 1}{n + 1} = 1 }[/math]
Dla [math]\displaystyle{ k }[/math] spełniającego warunek [math]\displaystyle{ 1 \leqslant k \leqslant n }[/math], jest
- [math]\displaystyle{ \binom{n + 1}{k} = \binom{n}{k} + \binom{n}{k - 1} }[/math]
Na podstawie założenia indukcyjnego liczby po prawej stronie są liczbami całkowitymi dodatnimi, zatem [math]\displaystyle{ \binom{n + 1}{k} }[/math] dla wszystkich wartości [math]\displaystyle{ k }[/math] jest liczbą całkowitą dodatnią. Co należało pokazać.
□
Twierdzenie A3
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] jest liczbą parzystą.
Łatwo zauważamy, że
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{n! \cdot n!} = \frac{2 n \cdot (2 n - 1)!}{n \cdot (n - 1) ! \cdot n!} = 2 \cdot \binom{2 n - 1}{n - 1} }[/math]
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{n! \cdot n!} = \frac{2 n \cdot (2 n - 1)!}{n \cdot (n - 1) ! \cdot n!} = 2 \cdot \binom{2 n - 1}{n - 1} }[/math]
□
Twierdzenie A4
Prawdziwe są następujące oszacowania współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math]
- [math]\displaystyle{ 3.8^{n + 1} \underset{n \geqslant 80}{\lt } \binom{2 n}{n} \underset{n \geqslant 5}{\lt } 4^{n - 1} }[/math]
Indukcja matematyczna. W przypadku lewej nierówności łatwo sprawdzamy, że [math]\displaystyle{ 3.8^{81} \lt \binom{160}{80} }[/math]. Zakładając prawdziwość nierówności dla [math]\displaystyle{ n \geqslant 80 }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ \binom{2 (n + 1)}{n + 1} = \binom{2 n}{n} \cdot \frac{(2 n + 2) (2 n + 1)}{(n + 1) (n + 1)} \gt 3.8^{n + 1} \cdot 2 \cdot \left( 2 - \frac{1}{n + 1} \right) \geqslant 3.8^{n + 1} \cdot 2 \cdot \left( 2 - \frac{1}{80 + 1} \right) \gt 3.8^{n + 1} \cdot 3.9753 \gt 3.8^{n + 2} }[/math]
Prawa nierówność jest prawdziwa dla [math]\displaystyle{ n = 5 }[/math]. Zakładając prawdziwość nierówności dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]:
- [math]\displaystyle{ \binom{2 (n + 1)}{n + 1} = \binom{2 n}{n} \cdot \frac{(2 n + 2) (2 n + 1)}{(n + 1) (n + 1)} \lt 4^{n -1} \cdot 2 \cdot \left( 2 - \frac{1}{n + 1} \right) \lt 4^n }[/math]
□
Twierdzenie A5
Dla [math]\displaystyle{ n \geqslant 12 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \gt 3 n }[/math].
Indukcja matematyczna. Dowód oprzemy na spostrzeżeniu, że wśród kolejnych sześciu liczb naturalnych [math]\displaystyle{ 6 k, 6 k + 1, 6 k + 2, 6 k + 3, 6 k + 4, 6 k + 5 }[/math] jedynie dwie: [math]\displaystyle{ 6 k + 1 }[/math] i [math]\displaystyle{ 6 k + 5 }[/math] mogą być pierwsze. Wynika stąd, że [math]\displaystyle{ p_{n + 2} \geqslant p_n + 6 }[/math] dla [math]\displaystyle{ n \geqslant 4 }[/math]. Dowód indukcyjny przeprowadzimy, stosując krok równy [math]\displaystyle{ 2 }[/math]. Twierdzenie jest oczywiście prawdziwe dla [math]\displaystyle{ n = 12 }[/math], bowiem [math]\displaystyle{ p_{12} = 37 \gt 3 \cdot 12 = 36 }[/math], podobnie [math]\displaystyle{ p_{13} = 41 \gt 3 \cdot 13 = 39 }[/math]. Zakładając prawdziwość twierdzenia dla wszystkich liczb naturalnych [math]\displaystyle{ k \in [12, n] }[/math], otrzymujemy dla [math]\displaystyle{ n + 2 }[/math]:
- [math]\displaystyle{ p_{n + 2} \geqslant p_n + 6 \gt 3 n + 6 = 3 \cdot (n + 2) }[/math]
Uwaga: inaczej mówiąc, dowodzimy twierdzenie osobno dla [math]\displaystyle{ n }[/math] parzystych [math]\displaystyle{ (n \geqslant 12) }[/math] i osobno dla [math]\displaystyle{ n }[/math] nieparzystych [math]\displaystyle{ (n \geqslant 13) }[/math].
□
Twierdzenie A6
Ciąg [math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n }[/math] jest rosnący i ograniczony. Dla wyrazów ciągu [math]\displaystyle{ (a_n) }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ 2 \leqslant a_n \lt 3 }[/math].
W artykule, w którym pojęcie współczynnika dwumianowego odgrywa główną rolę, nie mogło zabraknąć dowodu odwołującego się do wzoru dwumianowego
- [math]\displaystyle{ \left ( x + y \right )^{n} = \sum_{k=0}^{n} \binom{n}{k} x^{n-k}y^{k} = \binom{n}{0} x^{n} + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^{2} + \ldots + \binom{n}{n}y^{n} }[/math]
gdzie [math]\displaystyle{ \binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} }[/math].
Dowód opiera się na spostrzeżeniu, że [math]\displaystyle{ e = \sum_{k=0}^{\infty} \frac{1}{k!} = 2.718281828 \ldots }[/math], a wykorzystanie wzoru dwumianowego pozwala przekształcić wyrażenie [math]\displaystyle{ \left( 1 + \frac{1}{n} \right)^n }[/math] do postaci sumy z wyraźnie wydzielonym czynnikiem [math]\displaystyle{ \frac{1}{k!} }[/math]. Stosując wzór dwumianowy, możemy zapisać [math]\displaystyle{ n }[/math]-ty wyraz ciągu [math]\displaystyle{ (a_n) }[/math] w postaci
- [math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n = }[/math]
- [math]\displaystyle{ \quad \; = \sum_{k=0}^{n} \binom{n}{k} \frac{1}{n^k} = }[/math]
- [math]\displaystyle{ \quad \; = 2 + \sum_{k=2}^{n} \frac{n!}{k! \cdot (n - k)!} \cdot \frac{1}{n^k} = }[/math]
- [math]\displaystyle{ \quad \; = 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \frac{n \cdot (n - 1) \cdot \ldots \cdot (n - (k - 1))}{n^k} = }[/math]
- [math]\displaystyle{ \quad \; = 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n} \right) }[/math]
Odpowiednio dla wyrazu [math]\displaystyle{ a_{n + 1} }[/math] mamy
- [math]\displaystyle{ a_{n + 1} = \left( 1 + \frac{1}{n + 1} \right)^{n + 1} = }[/math]
- [math]\displaystyle{ \qquad \: = 2 + \sum_{k=2}^{n + 1} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n + 1} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n + 1} \right) \gt }[/math]
- [math]\displaystyle{ \qquad \: \gt 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n + 1} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n + 1} \right) \gt }[/math]
- [math]\displaystyle{ \qquad \: \gt 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n} \right) = }[/math]
- [math]\displaystyle{ \qquad \: = a_n }[/math]
Ostatnia nierówność jest prawdziwa, bo dla dowolnej liczby [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] jest [math]\displaystyle{ 1 - \frac{x}{n + 1} \gt 1 - \frac{x}{n} }[/math]
Zatem ciąg [math]\displaystyle{ (a_n) }[/math] jest rosnący. Musimy jeszcze wykazać, że jest ograniczony od góry. Pokazaliśmy wyżej, że wyraz [math]\displaystyle{ a_n }[/math] może być zapisany w postaci
- [math]\displaystyle{ a_n = 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n} \right) }[/math]
Ponieważ czynniki w nawiasach są dodatnie i mniejsze od jedności, to
- [math]\displaystyle{ a_n \leqslant 2 + \sum_{k=2}^{n} \frac{1}{k!} = }[/math]
- [math]\displaystyle{ \quad \; \leqslant 1 + 1 + \sum_{k=2}^{n} \frac{1}{2^{k-1}} = }[/math]
- [math]\displaystyle{ \quad \; = 1 + \left ( 1 + \frac{1}{2} + \frac{1}{2^2} + \ldots + \frac{1}{2^{n-1}}\right ) = }[/math]
- [math]\displaystyle{ \quad \; = 1 + \frac{1 - \left ( \frac{1}{2} \right )^{n}}{1 - \frac{1}{2}} = }[/math]
- [math]\displaystyle{ \quad \; = 1 + 2 - \frac{1}{2^{n-1}} \lt }[/math]
- [math]\displaystyle{ \quad \; \lt 3 }[/math]
Druga nierówność (nieostra) jest prawdziwa, bo dla [math]\displaystyle{ k \geqslant 2 }[/math] zachodzi oczywista nierówność [math]\displaystyle{ k! \geqslant 2^{k - 1} }[/math]. Do sumy ujętej w nawiasy zastosowaliśmy wzór na sumę częściową szeregu geometrycznego.
Ponieważ [math]\displaystyle{ a_1 = 2 }[/math], to prawdziwe jest oszacowanie [math]\displaystyle{ 2 \leqslant a_n \lt 3 }[/math]. Zauważmy jeszcze (już bez dowodu), że ciąg [math]\displaystyle{ (a_n) }[/math], jako rosnący i ograniczony od góry[9], jest zbieżny. Granicą ciągu [math]\displaystyle{ (a_n) }[/math] jest liczba niewymierna [math]\displaystyle{ e = 2.718281828 \ldots }[/math], która jest podstawą logarytmu naturalnego.
□
Twierdzenie A7
Prawdziwe są następujące oszacowania:
- [math]\displaystyle{ n^n \underset{n \geqslant 13}{\lt } p_1 p_2 \cdot \ldots \cdot p_n \underset{n \geqslant 3}{\lt } (n \log n)^n }[/math]
Indukcja matematyczna. Udowodnimy tylko oszacowanie od dołu. Dowód oszacowania od góry przedstawimy po zakończeniu dowodu twierdzenia A1. Łatwo sprawdzamy, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 13 }[/math]. Zakładając prawdziwość twierdzenia dla liczb naturalnych [math]\displaystyle{ k \in [13, n] }[/math] mamy dla [math]\displaystyle{ n + 1 }[/math]:
- [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n p_{n + 1} \gt n^n \cdot p_{n + 1} \gt n^n \cdot 3 (n + 1) \gt n^n \cdot \left( 1 + \frac{1}{n} \right)^n \cdot (n + 1) = (n + 1)^{n + 1} }[/math]
Gdzie skorzystaliśmy z faktu, że [math]\displaystyle{ p_n \gt 3 n }[/math] dla [math]\displaystyle{ n \geqslant 12 }[/math] oraz z właściwości rosnącego ciągu [math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n \lt e = 2.718281828 \ldots \lt 3 }[/math] (zobacz twierdzenie A6).
□
Twierdzenie A8
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \frac{P (2 n)}{P (n)} \lt 4^{n - 1} }[/math], gdzie [math]\displaystyle{ P (n) }[/math] oznacza iloczyn wszystkich liczb pierwszych nie większych od [math]\displaystyle{ n }[/math].
Rozważmy współczynnik dwumianowy
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{n! \cdot n!} = \frac{2 n \cdot (2 n - 1) \cdot \ldots \cdot (n + 1)}{n!} }[/math]
Każda liczba pierwsza należąca do przedziału [math]\displaystyle{ [n + 1, 2 n] }[/math] występuje w liczniku wypisanego wyżej ułamka i nie występuje w mianowniku. Wynika stąd oszacowanie
- [math]\displaystyle{ \binom{2 n}{n} = C \cdot \underset{n + 1 \leqslant p_k \leqslant 2 n}{\prod p_k} \gt \underset{n + 1 \leqslant p_k \leqslant 2 n}{\prod p_k} = \frac{P (2 n)}{P (n)} }[/math]
Zauważmy, że wypisany w powyższej nierówności iloczyn liczb pierwszych jest liczbą nieparzystą. Ponieważ współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] jest dodatnią liczbą całkowitą parzystą, zatem również czynnik [math]\displaystyle{ C \geqslant 2 }[/math] musi być dodatnią liczbą całkowitą parzystą. Łącząc uzyskaną nierówność z oszacowaniem z twierdzenia A4, otrzymujemy natychmiast:
- [math]\displaystyle{ \frac{P (2 n)}{P (n)} \lt \binom{2 n}{n} \lt 4^{n - 1} }[/math]
Dla [math]\displaystyle{ n = 2, 3, 4 }[/math] sprawdzamy uzyskany rezultat bezpośrednio.
□
Twierdzenie A9
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ P(n) \lt 4^n }[/math]
Indukcja matematyczna. Oszacowanie [math]\displaystyle{ P(n) \lt 4^n }[/math] jest prawdziwe dla [math]\displaystyle{ n = 1, 2 }[/math]. Zakładając prawdziwość oszacowania dla wszystkich liczb całkowitych nie większych od [math]\displaystyle{ n }[/math], dla [math]\displaystyle{ n + 1 }[/math] rozpatrzymy dwa przypadki. Jeżeli [math]\displaystyle{ n + 1 = 2 k + 1 }[/math] jest liczbą nieparzystą większą lub równą [math]\displaystyle{ 3 }[/math], to mamy
- [math]\displaystyle{ P(n + 1) = P (2 k + 1) = P (2 k + 2) = P (k + 1) \cdot \frac{P (2 k + 2)}{P (k + 1)} \lt 4^{k + 1} \cdot 4^k = 4^{2 k + 1} = 4^{n + 1} }[/math]
gdzie skorzystaliśmy z założenia indukcyjnego i oszacowania z twierdzenia A8.
Jeżeli [math]\displaystyle{ n + 1 = 2 k }[/math] jest liczbą parzystą większą lub równą [math]\displaystyle{ 4 }[/math], to mamy
- [math]\displaystyle{ P(n + 1) = P (2 k) = P (k) \cdot \frac{P (2 k)}{P (k)} \lt 4^k \cdot 4^{k - 1} = 4^{2 k - 1} \lt 4^{2 k} = 4^{n + 1} }[/math]
gdzie ponownie skorzystaliśmy z założenia indukcyjnego i oszacowania z twierdzenia A8.
□
Twierdzenie A10
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \gt \frac{1}{2 \log 2} \cdot n \log n }[/math].
Ponieważ z definicji [math]\displaystyle{ P(p_n) = p_1 p_2 \cdot \ldots \cdot p_n }[/math], to korzystając z oszacowań uzyskanych w twierdzeniach A7 i A9 dostajemy dla [math]\displaystyle{ n \geqslant 13 }[/math]
- [math]\displaystyle{ n^n \lt p_1 p_2 \cdot \ldots \cdot p_n = P (p_n) \lt 4^{p_n} }[/math]
Logarytmując obie strony nierówności, mamy
- [math]\displaystyle{ n \log n \lt p_n \cdot \log 4 }[/math]
Skąd natychmiast wynika dowodzone oszacowanie
- [math]\displaystyle{ p_n \gt \frac{1}{2 \log 2} \cdot n \log n \gt 0.72 \cdot n \log n }[/math]
Prawdziwość powyższej nierówności dla [math]\displaystyle{ n \leqslant 12 }[/math] sprawdzamy bezpośrednio.
□
Twierdzenie A11
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (2 n) - \pi (n) \lt 2 \log 2 \cdot \frac{n}{\log n} }[/math].
Każda liczba pierwsza należąca do przedziału [math]\displaystyle{ [n + 1, 2 n] }[/math] jest dzielnikiem współczynnika dwumianowego
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{n! \cdot n!} = \frac{2 n \cdot (2 n - 1) \cdot \ldots \cdot (n + 1)}{n!} }[/math]
bowiem dzieli licznik i nie dzieli mianownika. Ponieważ dla każdej z tych liczb jest [math]\displaystyle{ p \gt n }[/math], to
- [math]\displaystyle{ n^{\pi (2 n) - \pi (n)} \lt \prod_{n \lt p_i \leqslant 2 n} p_i \lt \binom{2 n}{n} \lt 4^n }[/math]
Ostatnia nierówność wynika z twierdzenia A4. Logarytmując, dostajemy
- [math]\displaystyle{ [\pi (2 n) - \pi (n)] \cdot \log n \lt 2 n \cdot \log 2 }[/math]
Czyli
- [math]\displaystyle{ \pi (2 n) - \pi (n) \lt 2 \log 2 \cdot \frac{n}{\log n} }[/math]
□
Twierdzenie A12
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (n) \lt 2 \cdot \frac{n}{\log n} }[/math].
Indukcja matematyczna. Oszacowanie [math]\displaystyle{ \pi (n) \lt 2 \cdot \frac{n}{\log n} }[/math] jest prawdziwe dla [math]\displaystyle{ 2 \leqslant n \leqslant 62 }[/math], co łatwo sprawdzamy przez bezpośrednie wyliczenie. W programie GP/PARI wystarczy wpisać polecenie:
for(n = 2, 62, if( primepi(n) >= 2 * n/log(n), print(n) ))
Zakładając prawdziwość wzoru dla wszystkich liczb naturalnych należących do przedziału [math]\displaystyle{ [2, n] }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
a) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą parzystą, to:
- [math]\displaystyle{ \pi (n + 1) = \pi (n) = 2 \cdot \frac{n}{\log n} \lt 2 \cdot \frac{n + 1}{\log (n + 1)} }[/math]
Ostatnia nierówność wynika ze spostrzeżenia, że funkcja [math]\displaystyle{ \frac{x}{\log x} }[/math] jest funkcją rosnącą dla [math]\displaystyle{ x \gt e \approx 2.71828 }[/math]. Można też wykorzystać oszacowanie [math]\displaystyle{ \log(1 + x) \lt x }[/math] prawdziwe dla [math]\displaystyle{ x \gt 0 }[/math].
b) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą nieparzystą, to możemy położyć [math]\displaystyle{ n + 1 = 2 k + 1 }[/math] i otrzymujemy:
- [math]\displaystyle{ \pi (n + 1) = \pi (2 k + 1) }[/math]
- [math]\displaystyle{ \quad = \pi (2 k + 2) }[/math]
- [math]\displaystyle{ \quad = \pi (k + 1) + [\pi (2 k + 2) - \pi (k + 1)] }[/math]
- [math]\displaystyle{ \quad \lt 2 \cdot \frac{k + 1}{\log (k + 1)} + 2 \log 2 \cdot \frac{k + 1}{\log (k + 1)} }[/math]
- [math]\displaystyle{ \quad = (1 + \log 2) \cdot \frac{2 k + 2}{\log (k + 1)} }[/math]
- [math]\displaystyle{ \quad \lt \left[ 1.7 \cdot \frac{2 k + 2}{\log (k + 1)} \cdot \frac{\log (2 k + 1)}{2 k + 1} \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]
- [math]\displaystyle{ \quad = \left[ 1.7 \cdot \frac{2 k + 2}{2 k + 1} \cdot \frac{\log (2 k + 2)}{\log (k + 1)} \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]
- [math]\displaystyle{ \quad = \left[ 1.7 \cdot \left( 1 + \frac{1}{2 k + 1} \right) \cdot \frac{\log (k + 1) + \log 2}{\log (k + 1)} \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]
- [math]\displaystyle{ \quad = \left[ 1.7 \cdot \left( 1 + \frac{1}{2 k + 1} \right) \cdot \left( 1 + \frac{\log 2}{\log (k + 1)} \right) \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]
- [math]\displaystyle{ \quad \lt 2 \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]
- [math]\displaystyle{ \quad = 2 \cdot \frac{n + 1}{\log (n + 1)} }[/math]
Ostatnia nierówność wynika z faktu, że czynnik w nawiasie kwadratowym maleje wraz ze wzrostem [math]\displaystyle{ k }[/math] i dla [math]\displaystyle{ k = 63 }[/math] osiąga wartość [math]\displaystyle{ 1.9989 \ldots }[/math]
□
Wykładnik z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w [math]\displaystyle{ n! }[/math]
Uzyskanie kolejnych oszacowań wymaga znalezienia wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} }[/math].
Definicja A13
Funkcję [math]\displaystyle{ \lfloor x \rfloor }[/math] (czytaj: całość z [math]\displaystyle{ x }[/math]) definiujemy jako największą liczbę całkowitą nie większą od [math]\displaystyle{ x }[/math]. Operacyjnie możemy ją zdefiniować następująco: niech liczby [math]\displaystyle{ x, \varepsilon \in \mathbb{R} }[/math], liczba [math]\displaystyle{ k \in \mathbb{Z} }[/math] oraz [math]\displaystyle{ 0 \leqslant \varepsilon \lt 1 }[/math], jeżeli [math]\displaystyle{ x = k + \varepsilon }[/math], to [math]\displaystyle{ \lfloor x \rfloor = \lfloor k + \varepsilon \rfloor = k }[/math].
Twierdzenie A14
Dla [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math], [math]\displaystyle{ x \in \mathbb{R} }[/math] jest [math]\displaystyle{ \left \lfloor \frac{x}{n} \right\rfloor = \left \lfloor \frac{\left \lfloor x \right \rfloor}{n} \right \rfloor }[/math].
Korzystając z definicji A13, przedstawmy liczbę w postaci [math]\displaystyle{ x = k + \varepsilon }[/math], gdzie [math]\displaystyle{ 0 \leqslant \varepsilon \lt 1 }[/math].
Z twierdzenia o dzieleniu z resztą liczbę [math]\displaystyle{ k }[/math] możemy zapisać w postaci [math]\displaystyle{ k = q n + r }[/math], gdzie [math]\displaystyle{ 0 \leqslant r \leqslant n - 1 }[/math], mamy zatem [math]\displaystyle{ x = q n + r + \varepsilon }[/math]. Ponieważ [math]\displaystyle{ 0 \leqslant r + \varepsilon \lt n }[/math], to po podzieleniu przez [math]\displaystyle{ n }[/math] dostajemy
- [math]\displaystyle{ 0 \leqslant \frac{r + \varepsilon}{n} \lt 1 }[/math]
czyli
- [math]\displaystyle{ \left \lfloor \frac{x}{n} \right \rfloor = \left \lfloor \frac{qn + r + \varepsilon }{n} \right \rfloor = \left \lfloor q + \frac{r + \varepsilon }{n} \right \rfloor = q }[/math]
Podobnie, ponieważ [math]\displaystyle{ 0 \leqslant r \lt n }[/math], to [math]\displaystyle{ 0 \leqslant \frac{r}{n} \lt 1 }[/math] i otrzymujemy
- [math]\displaystyle{ \left\lfloor \frac{\left \lfloor x \right\rfloor}{n} \right\rfloor = \left \lfloor \frac{\left \lfloor qn + r + \varepsilon \right \rfloor}{n} \right \rfloor = \left \lfloor \frac{qn + r}{n} \right \rfloor = \left \lfloor q + \frac{r}{n} \right \rfloor = q }[/math]
□
Twierdzenie A15
Niech [math]\displaystyle{ x \in \mathbb{R} }[/math]. Liczba [math]\displaystyle{ \lfloor 2 x \rfloor - 2 \lfloor x \rfloor }[/math] przyjmuje wartości [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math].
Niech [math]\displaystyle{ x = k + \varepsilon }[/math], gdzie [math]\displaystyle{ 0 \leqslant \varepsilon \lt 1 }[/math]. Mamy
- [math]\displaystyle{ \lfloor 2 x \rfloor - 2 \lfloor x \rfloor = \lfloor 2 k + 2 \varepsilon \rfloor - 2 \lfloor k + \varepsilon \rfloor = 2 k + \lfloor 2 \varepsilon \rfloor - 2 k -2 \lfloor \varepsilon \rfloor = \lfloor 2 \varepsilon \rfloor }[/math]
Ponieważ [math]\displaystyle{ 0 \leqslant 2 \varepsilon \lt 2 }[/math], zatem [math]\displaystyle{ \lfloor 2 \varepsilon \rfloor = 0 }[/math] lub [math]\displaystyle{ \lfloor 2 \varepsilon \rfloor = 1 }[/math].
□
Bardzo istotnym rezultatem (z punktu widzenia przyszłych obliczeń) będzie znalezienie wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w iloczynie [math]\displaystyle{ 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n = n! }[/math]
Definicja A16
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą, zaś [math]\displaystyle{ a }[/math] dowolną liczbą naturalną. Jeżeli liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia liczby naturalnej [math]\displaystyle{ n \geqslant 2 }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ a }[/math], to powiemy, że funkcja [math]\displaystyle{ W_p (n) }[/math] przyjmuje wartość [math]\displaystyle{ a }[/math]. Fakt ten możemy zapisać następująco
- [math]\displaystyle{ W_p (n) = a \qquad\qquad \iff \qquad\qquad p^{a} \mid n \qquad \text{i} \qquad p^{a + 1} \nmid n }[/math]
Przykład A17
[math]\displaystyle{ W_5 (100) = 2 }[/math], [math]\displaystyle{ W_7 (42) = 1 }[/math], ponieważ [math]\displaystyle{ 11! = 2^8 \cdot 3^4 \cdot 5^2 \cdot 7 \cdot 11 }[/math], to [math]\displaystyle{ W_3 (11!) = 4 }[/math]
Wprost z definicji funkcji [math]\displaystyle{ W_p (n) }[/math] wynikają następujące właściwości:
Twierdzenie A18
Podstawowe własności funkcji [math]\displaystyle{ W_p (n) }[/math]
- [math]\displaystyle{ \;\; W_p (n \cdot m) = W_p (n) + W_p (m) }[/math]
- [math]\displaystyle{ \;\; W_p (n \cdot p^a) = a + W_p (n) }[/math]
- [math]\displaystyle{ \;\; W_{p}\left ( \frac{n}{m} \right ) = W_{p}\left ( n \right ) - W_{p}\left ( m \right ) \quad \text{o ile} \quad \frac{n}{m}\in \mathbb{Z}_{+} }[/math]
- [math]\displaystyle{ \;\; p \nmid n \quad\quad \iff \quad\quad W_p (n) = 0 }[/math]
Twierdzenie A19
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą. Ilość liczb podzielnych przez [math]\displaystyle{ p }[/math] i występujących w ciągu [math]\displaystyle{ 1, 2, 3, \ldots, n }[/math] wynosi [math]\displaystyle{ r = \left\lfloor \frac{n}{p} \right\rfloor }[/math].
Wśród liczb naturalnych [math]\displaystyle{ 1, 2, 3, \ldots, n }[/math] istnieje pewna ilość liczb podzielnych przez [math]\displaystyle{ p }[/math]. Liczby te możemy z łatwością wypisać, będą nimi
- [math]\displaystyle{ 1 \cdot p, 2 \cdot p, 3 \cdot p, \ldots, r \cdot p }[/math]
Gdzie [math]\displaystyle{ r }[/math] jest największą liczbą całkowitą nie większą niż [math]\displaystyle{ \frac{n}{p} }[/math], czyli [math]\displaystyle{ r = \left\lfloor \frac{n}{p} \right\rfloor }[/math].
□
Przykład A20
Ilość liczb całkowitych dodatnich podzielnych przez [math]\displaystyle{ 5 }[/math] i nie większych od [math]\displaystyle{ 63 }[/math] wynosi [math]\displaystyle{ \left\lfloor \frac{63}{5} \right\rfloor = 12 }[/math]. Liczby te to [math]\displaystyle{ 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 }[/math].
Twierdzenie A19 umożliwi nam określenie wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w [math]\displaystyle{ n! }[/math]
Twierdzenie A21
Liczba pierwsza [math]\displaystyle{ p }[/math] występuje w iloczynie [math]\displaystyle{ n! }[/math] z wykładnikiem [math]\displaystyle{ W_p (n!) = \sum_{k = 1}^{\infty} \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]
Dowód sprowadza się do znalezienia wartości funkcji [math]\displaystyle{ W_p (n!) }[/math].
- [math]\displaystyle{ W_p (n!) = W_p (1 \cdot 2 \cdot 3 \cdot \ldots \cdot n) = W_p \left( p \cdot 2 p \cdot 3 p \cdot \ldots \cdot \left\lfloor \frac{n}{p} \right\rfloor \cdot p \right) }[/math]
Pozostawiliśmy jedynie czynniki podzielne przez [math]\displaystyle{ p }[/math] (czynniki niepodzielne przez [math]\displaystyle{ p }[/math] nie dają wkładu do wykładnika, z jakim [math]\displaystyle{ p }[/math] występuje w [math]\displaystyle{ n! }[/math]), wyłączając czynnik [math]\displaystyle{ p }[/math] z każdej z liczb [math]\displaystyle{ p, 2 p, 3 p, \ldots, \left\lfloor \frac{n}{p} \right\rfloor \cdot p }[/math] mamy
- [math]\displaystyle{ W_p (n!) = W_p \left( p^{\lfloor n / p \rfloor} \cdot 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p} \right\rfloor \right) = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p} \right\rfloor \right) }[/math]
Otrzymane wyrażenie przekształcamy analogicznie jak wyżej
- [math]\displaystyle{ W_p (n!) = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( p \cdot 2 p \cdot 3 p \cdot \ldots \cdot \left\lfloor \frac{\lfloor n / p \rfloor}{p} \right\rfloor \cdot p \right) }[/math]
Z twierdzenia A14 wiemy, że dla [math]\displaystyle{ x \in \mathbb{R} }[/math] i [math]\displaystyle{ n \in \mathbb{Z}_{+} }[/math] jest:
- [math]\displaystyle{ \left\lfloor \frac{\lfloor x \rfloor}{n} \right\rfloor = \left \lfloor \frac{x}{n} \right \rfloor }[/math]
zatem
- [math]\displaystyle{ W_p (n!) = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( p \cdot 2 p \cdot 3 p \cdot \ldots \cdot \left\lfloor \frac{n}{p^2} \right\rfloor \cdot p \right) = }[/math]
- [math]\displaystyle{ \;\, = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( p^{\lfloor n / p^2 \rfloor} \cdot 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p^2} \right\rfloor \right) = }[/math]
- [math]\displaystyle{ \;\, = \left\lfloor \frac{n}{p} \right\rfloor + \left\lfloor \frac{n}{p^2} \right\rfloor + W_p \left( 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p^2} \right\rfloor \right) }[/math]
Oczywiście opisaną wyżej procedurę możemy powtarzać wielokrotnie. Zakończenie następuje wtedy, gdy wykładnik liczby pierwszej [math]\displaystyle{ p }[/math] osiągnie wartość tak dużą, że [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math]. Ponieważ nie wiemy, jaka to wartość (choć możemy ją oszacować), to stosujemy zapis
- [math]\displaystyle{ W_p (n!) = \sum_{k = 1}^{\infty} \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]
zdając sobie sprawę z tego, że w rzeczywistości sumowanie obejmuje jedynie skończoną liczbę składników.
□
Uwaga A22
Należy zauważyć, że liczba sumowań jest skończona, bowiem bardziej precyzyjnie możemy powyższy wzór zapisać w postaci
- [math]\displaystyle{ W_p (n!) = \sum_{k = 1}^B \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]
gdzie [math]\displaystyle{ B = \lfloor \log_2 (n) \rfloor }[/math]. Jest tak dlatego, że jeżeli [math]\displaystyle{ k }[/math] przekroczy [math]\displaystyle{ \lfloor \log_2 (n) \rfloor }[/math], to dla liczby pierwszej [math]\displaystyle{ p = 2 }[/math], jak również dla wszystkich innych liczb pierwszych mamy
- [math]\displaystyle{ \frac{n}{p^k} \lt 1 }[/math]
czyli dla [math]\displaystyle{ k \gt B }[/math] sumujemy same zera.
Przykład A23
Niech [math]\displaystyle{ n = 30 }[/math], [math]\displaystyle{ p = 3 }[/math]
- [math]\displaystyle{ W_3 (30!) = W_3 (1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 30) = }[/math]
- [math]\displaystyle{ \quad = W_3 (3\cdot 6 \cdot 9 \cdot 12 \cdot 15 \cdot 18 \cdot 21 \cdot 24 \cdot 27 \cdot 30) = }[/math]
- [math]\displaystyle{ \quad = W_3 (3^{10} \cdot 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10) = }[/math]
- [math]\displaystyle{ \quad = 10 + W_3 (1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10) = }[/math]
- [math]\displaystyle{ \quad = 10 + W_3 (3 \cdot 6 \cdot 9) = }[/math]
- [math]\displaystyle{ \quad = 10 + W_3 (3^3 \cdot 1 \cdot 2 \cdot 3) = }[/math]
- [math]\displaystyle{ \quad = 10 + 3 + W_3 (1 \cdot 2 \cdot 3) = }[/math]
- [math]\displaystyle{ \quad = 10 + 3 + W_3 (3) = }[/math]
- [math]\displaystyle{ \quad = 10 + 3 + 1 = }[/math]
- [math]\displaystyle{ \quad = 14 }[/math]
Co jest zgodne ze wzorem:
- [math]\displaystyle{ W_3 (30!) = \left\lfloor \frac{30}{3} \right\rfloor + \left\lfloor \frac{30}{3^2} \right\rfloor + \left\lfloor \frac{30}{3^3} \right\rfloor = 10 + 3 + 1 = 14 }[/math]
Podobnie jak w poprzednim podrozdziale będziemy badali współczynnik dwumianowy postaci [math]\displaystyle{ \binom{2 n}{n} }[/math]. Teraz już łatwo możemy policzyć wykładnik, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze tego współczynnika dwumianowego.
Twierdzenie A24
Liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] z wykładnikiem
- [math]\displaystyle{ u = \sum^{\infty}_{k = 1} \left( \left \lfloor \frac{2n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right) }[/math]
Ponieważ [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} }[/math], to liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] z wykładnikiem:
- [math]\displaystyle{ W_p \left( \binom{2 n}{n} \right) = W_p ((2 n) !) - 2 W_p (n!) = \sum^{\infty}_{k = 1} \left \lfloor \frac{2n}{p^{k}} \right \rfloor - 2 \sum^{\infty}_{k = 1} \left \lfloor \frac{n}{p^{k}} \right \rfloor = \sum^{\infty}_{k = 1} \left( \left \lfloor \frac{2n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right) }[/math]
□
Twierdzenie A25
Liczby pierwsze spełniające warunek [math]\displaystyle{ p \gt \sqrt{2 n} }[/math] występują w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u = 1 }[/math] lub [math]\displaystyle{ u = 0 }[/math].
Jeżeli [math]\displaystyle{ p \gt \sqrt{2 n} }[/math], to dla [math]\displaystyle{ k \geqslant 2 }[/math] mamy [math]\displaystyle{ p^k \geqslant p^2 \gt 2 n \gt n }[/math]. Zatem dla [math]\displaystyle{ k \geqslant 2 }[/math] jest [math]\displaystyle{ \left\lfloor \frac{2 n}{p^k} \right\rfloor = \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math] i otrzymujemy
- [math]\displaystyle{ u = \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) = \left \lfloor \frac{2 n}{p} \right \rfloor - 2 \left \lfloor \frac{n}{p} \right \rfloor }[/math]
Na mocy twierdzenia A15 (dla [math]\displaystyle{ x = \tfrac{n}{p} }[/math]), dostajemy natychmiast, że [math]\displaystyle{ u = 1 }[/math] lub [math]\displaystyle{ u = 0 }[/math].
□
Twierdzenie A26
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą. Jeżeli [math]\displaystyle{ p^a \biggr\rvert \binom{2 n}{n} }[/math], to [math]\displaystyle{ p^a \leqslant 2 n }[/math].
Niech [math]\displaystyle{ u }[/math] oznacza wykładnik, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze. Mamy
- [math]\displaystyle{ u = \sum_{k = 1}^{\infty} \left( \left\lfloor \frac{2 n}{p^k} \right\rfloor - 2 \left\lfloor \frac{n}{p^k} \right\rfloor \right) }[/math]
gdzie sumowanie przebiega w rzeczywistości od [math]\displaystyle{ k = 1 }[/math] do [math]\displaystyle{ k = s }[/math], a wartość liczby [math]\displaystyle{ s }[/math] wynika z warunku [math]\displaystyle{ p^s \leqslant 2 n \lt p^{s + 1} }[/math]. Ponieważ sumowane wyrazy są równe [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy natychmiast oszacowanie [math]\displaystyle{ u \leqslant s }[/math], skąd wynika następujący ciąg nierówności
- [math]\displaystyle{ p^a \leqslant p^u \leqslant p^s \leqslant 2 n }[/math]
□
Oszacowanie [math]\displaystyle{ p_n }[/math] od góry i [math]\displaystyle{ \pi (n) }[/math] od dołu
Z twierdzenia A26 wynika natychmiast
Twierdzenie A27
Niech [math]\displaystyle{ \binom{2 n}{n} = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s }[/math] będzie rozkładem współczynnika dwumianowego na czynniki pierwsze. Dla każdej liczby pierwszej [math]\displaystyle{ q_i }[/math], [math]\displaystyle{ i = 1, \ldots, s }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ q^{\alpha_i}_i \leqslant 2 n }[/math].
Uwaga: w powyższym twierdzeniu [math]\displaystyle{ q_i }[/math] nie oznacza [math]\displaystyle{ i }[/math]-tej liczby pierwszej, a pewną liczbą pierwszą o indeksie [math]\displaystyle{ i }[/math] ze zboru liczb pierwszych [math]\displaystyle{ q_1, \ldots q_s }[/math], które wchodzą do rozkładu współczynnika dwumianowego na czynniki pierwsze z wykładnikiem większym od zera.
Twierdzenie A28
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest następujące oszacowanie współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math]
- [math]\displaystyle{ \binom{2 n}{n} \leqslant (2 n)^{\pi (2 n)} \lt (2 n + 1)^{\pi (2 n + 1)} }[/math]
Dowód wynika natychmiast z twierdzenia A27, bowiem
- [math]\displaystyle{ \binom{2 n}{n} = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s \leqslant (2 n)^s \leqslant (2 n)^{\pi (2 n)} \lt (2 n + 1)^{\pi (2 n + 1)} }[/math]
□
Twierdzenie A29
Dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]
W twierdzeniu A4 oszacowaliśmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math]. Przepiszemy, to twierdzenie w postaci bardziej czytelnej dla potrzeb tego dowodu
- [math]\displaystyle{ \left( \sqrt{3.8} \right)^{2 n} \lt \left( \sqrt{3.8} \right)^{2 n + 1} \lt \left( \sqrt{3.8} \right)^{2 n + 2} = 3.8^{n + 1} \lt \binom{2 n}{n} }[/math]
Nierówności te są prawdziwe dla [math]\displaystyle{ n \geqslant 80 }[/math]. Z twierdzenia A28 mamy
- [math]\displaystyle{ \left( \sqrt{3.8} \right)^{2 n} \lt \left( \sqrt{3.8} \right)^{2 n + 1} \lt \binom{2 n}{n} \leqslant (2 n)^{\pi (2 n)} \lt (2 n + 1)^{\pi (2 n + 1)} }[/math]
Łącząc odpowiednie oszacowania współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] od góry z odpowiednimi oszacowaniami od dołu, dostajemy
- [math]\displaystyle{ (2 n + 1)^{\pi (2 n + 1)} \gt \left( \sqrt{3.8} \right)^{2 n + 1} }[/math]
- [math]\displaystyle{ (2 n)^{\pi (2 n)} \gt \left( \sqrt{3.8} \right)^{2 n} }[/math]
Zatem zarówno dla parzystych, jak i nieparzystych liczb [math]\displaystyle{ m \geqslant 160 }[/math] jest
- [math]\displaystyle{ m^{\pi (m)} \gt \left( \sqrt{3.8} \right)^m }[/math]
- [math]\displaystyle{ \pi (m) \cdot \log m \gt m \cdot \log \left( \sqrt{3.8} \right) }[/math]
Czyli
- [math]\displaystyle{ \pi (m) \gt \frac{1}{2} \cdot \log \left ( 3.8 \right ) \cdot \frac{m}{\log m} \gt 0.6675 \cdot \frac{m}{\log m} \gt \frac{2}{3} \cdot \frac{m}{\log m} }[/math]
Dla [math]\displaystyle{ m = 3, 4, \ldots, 159 }[/math] prawdziwość nierówności sprawdzamy przez bezpośrednie wyliczenie. W programie GP/PARI wystarczy wykonać polecenie
for(n = 2, 200, if( primepi(n) <= 2/3 * n/log(n), print(n) ))
□
Twierdzenie A30
Niech [math]\displaystyle{ n \geqslant 3 }[/math]. Dla [math]\displaystyle{ n }[/math]-tej liczby pierwszej [math]\displaystyle{ p_n }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \lt 2 n \log n }[/math]
Rozpoczniemy od pokazania, że dla [math]\displaystyle{ x \gt 83499.14 }[/math] prawdziwe jest następujące oszacowanie funkcji [math]\displaystyle{ \log x }[/math] od góry
- [math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 4} }[/math]
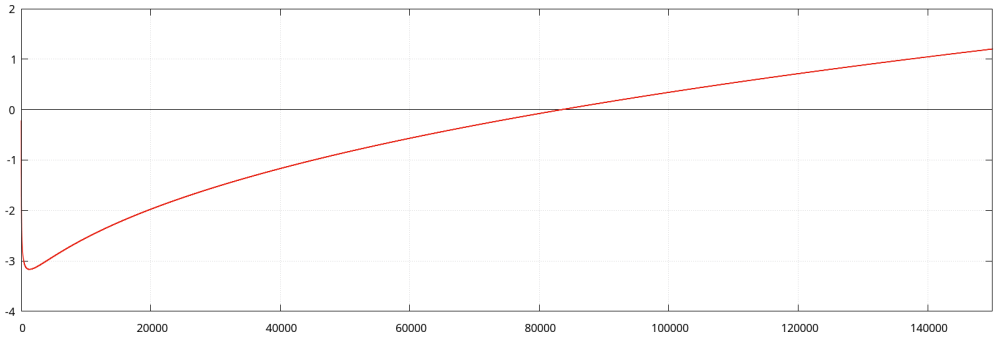
Wiemy, że dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] istnieje takie [math]\displaystyle{ x_0 }[/math], że dla [math]\displaystyle{ x \gt x_0 }[/math] jest [math]\displaystyle{ \log x \lt x^{1 / n} }[/math]. Zatem dla odpowiednio dużych [math]\displaystyle{ x }[/math] z pewnością będzie [math]\displaystyle{ \tfrac{2}{3} \cdot x^{1 / 4} \gt \log x \, }[/math][a]. Zamieszczony niżej obrazek przedstawia wykres funkcji [math]\displaystyle{ f( x ) = \tfrac{2}{3} \cdot x^{1 / 4} - \log x }[/math].
Wpisując w PARI/GP polecenie
solve(x = 80000, 10^5, 2/3 * x^(1/4) - log(x))
wyliczamy, że funkcja [math]\displaystyle{ f( x ) }[/math] przecina oś [math]\displaystyle{ O X }[/math] w punkcie [math]\displaystyle{ x = 83499.136 \ldots }[/math] Wynika stąd, że dla [math]\displaystyle{ x \gt 83499.14 }[/math] prawdziwa jest nierówność
- [math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 4} }[/math]
Z twierdzenia A29 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]. Kładąc [math]\displaystyle{ n = p_k }[/math], otrzymujemy dla [math]\displaystyle{ k \geqslant 2 }[/math]
- [math]\displaystyle{ k = \pi (p_k) \gt \frac{2}{3} \cdot \frac{p_k}{\log p_k} }[/math]
Zatem
- [math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \log p_k \qquad \qquad (1) }[/math]
Korzystając z wcześniej pokazanego oszacowania, otrzymujemy nierówność prawdziwą dla [math]\displaystyle{ p_k \gt 83499 }[/math]
- [math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{2}{3} \cdot (p_k)^{1 / 4} }[/math]
czyli
- [math]\displaystyle{ (p_k)^{3 / 4} \lt k }[/math]
- [math]\displaystyle{ p_k \lt k^{4 / 3} }[/math]
Wstawiając to oszacowanie ponownie do [math]\displaystyle{ (1) }[/math], dostajemy
- [math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{4}{3} \cdot \log k = 2 k \log k }[/math]
Wpisując w PARI/GP polecenie
for(k = 1, 10^5, p = prime(k); if( p > 83499, print("end"); break() ); if( p >= 2 * k * log(k), print(k) ))
łatwo sprawdzamy, że oszacowanie [math]\displaystyle{ p_k \lt 2 k \log k }[/math] jest prawdziwe dla [math]\displaystyle{ k \geqslant 3 }[/math].
[a] Bardziej precyzyjnie: pochodna funkcji [math]\displaystyle{ f(x) = \tfrac{2}{3} \cdot x^{1 / 4} - \log x }[/math] jest równa [math]\displaystyle{ \frac{1}{6 x^{3 / 4}} - \frac{1}{x} }[/math] (zobacz WolframAlpha). Łatwo sprawdzamy, że pochodna jest ujemna w przedziale [math]\displaystyle{ (0, 1296) }[/math] i dodatnia w przedziale [math]\displaystyle{ (1296, \infty) }[/math]. Wynika stąd, że funkcja [math]\displaystyle{ f( x ) }[/math] jest funkcją malejącą dla [math]\displaystyle{ x \lt 1296 }[/math] i rosnącą dla [math]\displaystyle{ x \gt 1296 }[/math].
□
Dowód twierdzenia A30 kończy dowód całego twierdzenia A1. Możemy teraz dokończyć dowód twierdzenia A7 i pokazać, że dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest oszacowanie:
- [math]\displaystyle{ p_1 \cdot \ldots \cdot p_n \lt (n \log n)^n }[/math]
Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 3 }[/math]. Zakładając prawdziwość twierdzenia dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]:
- [math]\displaystyle{ p_1 \cdot \ldots \cdot p_n p_{n + 1} \lt (n \log n)^n \cdot p_{n + 1} \lt }[/math]
- [math]\displaystyle{ \quad \lt n^n \cdot (\log n)^n \cdot 2 (n + 1) \log (n + 1) \leqslant }[/math]
- [math]\displaystyle{ \quad \leqslant n^n \cdot \left( 1 + \frac{1}{n} \right)^n \cdot (n + 1) \cdot (\log n)^n \cdot \log (n + 1) \lt }[/math]
- [math]\displaystyle{ \quad \lt (n + 1)^{n + 1} \cdot [\log (n + 1)]^n \cdot \log (n + 1) = }[/math]
- [math]\displaystyle{ \quad = [(n + 1) \cdot \log (n + 1)]^{n + 1} }[/math]
Gdzie skorzystaliśmy z twierdzenia A30 oraz z faktu, że ciąg [math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n }[/math] jest ciągiem ograniczonym [math]\displaystyle{ 2 \leqslant a_n \lt 3 }[/math] (zobacz twierdzenie A6).
□
Uwagi do dowodu
Wydłużając znacząco czas obliczeń, moglibyśmy nieco poprawić uzyskane wyżej oszacowanie i udowodnić
Twierdzenie A31
Niech [math]\displaystyle{ n \geqslant 3 }[/math]. Dla [math]\displaystyle{ n }[/math]-tej liczby pierwszej [math]\displaystyle{ p_n }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \lt 1.875 \cdot n \log n }[/math]
Rozpoczniemy od pokazania, że dla [math]\displaystyle{ x \gt 7572437.23 }[/math] prawdziwe jest następujące oszacowanie funkcji [math]\displaystyle{ \log x }[/math] od góry
- [math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 5} }[/math]
Wiemy, że dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] istnieje takie [math]\displaystyle{ x_0 }[/math], że dla [math]\displaystyle{ x \gt x_0 }[/math] jest [math]\displaystyle{ \log x \lt x^{1 / n} }[/math]. Zatem dla odpowiednio dużych [math]\displaystyle{ x }[/math] z pewnością będzie [math]\displaystyle{ \tfrac{2}{3} \cdot x^{1 / 5} \gt \log x \, }[/math][a]. Wpisując w PARI/GP polecenie
solve(x = 10^6, 10^7, 2/3 * x^(1/5) - log(x))
wyliczamy, że funkcja [math]\displaystyle{ f(x) = \tfrac{2}{3} \cdot x^{1 / 5} - \log x }[/math] przecina oś [math]\displaystyle{ O X }[/math] w punkcie [math]\displaystyle{ x = 7572437.223 \ldots }[/math] Wynika stąd, że dla [math]\displaystyle{ x \gt 7572437.23 }[/math] prawdziwa jest nierówność
- [math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 5} }[/math]
Z twierdzenia A29 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]. Kładąc [math]\displaystyle{ n = p_k }[/math], otrzymujemy dla [math]\displaystyle{ k \geqslant 2 }[/math]
- [math]\displaystyle{ k = \pi (p_k) \gt \frac{2}{3} \cdot \frac{p_k}{\log p_k} }[/math]
Zatem
- [math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \log p_k \qquad \qquad (1) }[/math]
Korzystając z wcześniej pokazanego oszacowania, otrzymujemy nierówność prawdziwą dla [math]\displaystyle{ p_k \gt 7572437 }[/math]
- [math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{2}{3} \cdot (p_k)^{1 / 5} }[/math]
czyli
- [math]\displaystyle{ (p_k)^{4 / 5} \lt k }[/math]
- [math]\displaystyle{ p_k \lt k^{5 / 4} }[/math]
Wstawiając to oszacowanie ponownie do [math]\displaystyle{ (1) }[/math], dostajemy
- [math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{5}{4} \cdot \log k = 1.875 \cdot k \log k }[/math]
Wpisując w PARI/GP polecenie
for(k = 1, 10^7, p = prime(k); if( p > 7572437, print("end"); break() ); if( p >= 2 * k * log(k), print(k) ))
łatwo sprawdzamy, że oszacowanie [math]\displaystyle{ p_k \lt 1.875 \cdot k \log k }[/math] jest prawdziwe dla [math]\displaystyle{ k \geqslant 3 }[/math].
[a] Bardziej precyzyjnie: pochodna funkcji [math]\displaystyle{ f(x) = \tfrac{2}{3} \cdot x^{1 / 5} - \log x }[/math] jest równa [math]\displaystyle{ \frac{2}{15 x^{4 / 5}} - \frac{1}{x} }[/math] (zobacz WolframAlpha). Łatwo sprawdzamy, że pochodna jest ujemna w przedziale [math]\displaystyle{ (0, 23730.46875) }[/math] i dodatnia w przedziale [math]\displaystyle{ (23730.46875, \infty) }[/math]. Wynika stąd, że funkcja [math]\displaystyle{ f( x ) }[/math] jest funkcją malejącą dla [math]\displaystyle{ x \lt 23730.46875 }[/math] i rosnącą dla [math]\displaystyle{ x \gt 23730.46875 }[/math].
□
Twierdzenie A32
Niech [math]\displaystyle{ n \geqslant 2 }[/math]. Dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ \pi (n) \lt 1.733 \cdot \frac{n}{\log n} }[/math]
Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] jest
- [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} \gt n^{4 / 5} }[/math]
Ostatnia nierówność wynika z faktu, że dla [math]\displaystyle{ x \gt 7572437.223 \ldots }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ \frac{2}{3} \cdot \frac{x}{\log x} \gt x^{4 / 5} }[/math]
Korzystając z twierdzenia A9 możemy napisać ciąg nierówności
- [math]\displaystyle{ 4^n \gt P (n) = p_1 p_2 \cdot \ldots \cdot p_{\pi (n)} \gt \pi (n)^{\pi (n)} \gt (n^{4 / 5})^{\pi (n)} = n^{4 \pi (n) / 5} }[/math]
skąd otrzymujemy, że dla [math]\displaystyle{ n \geqslant 7572438 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ \pi (n) \lt 1.733 \cdot \frac{n}{\log n} }[/math]
W GP/PARI sprawdzamy, że otrzymana nierówność jest prawdziwa dla [math]\displaystyle{ n \geqslant 2 }[/math]
for(n = 2, 8*10^6, if( primepi(n) >= 1.733 * n/log(n), print(n) ))
□
Uwaga A33
Dowód twierdzenia A31 wymagał wykorzystania polecenia PARI/GP, w którym wielokrotnie była wywoływana funkcja prime(n). Analogiczna sytuacja miała miejsce w przypadku twierdzenia A32 – tam musieliśmy wielokrotnie wywoływać funkcję primepi(n). Znacznie lepiej w takim przypadku jest napisać krótki program, który zamiast wielokrotnie wywoływać te funkcje, będzie je obliczał w sposób ciągły w całym testowanym przedziale wartości. Taka zmiana znacząco skraca czas obliczeń. Podane niżej programy Test1(n) i Test2(n) wywołane z parametrami n = 520000 i odpowiednio n = 8*10^6 odpowiadają poleceniom
for(s = 1, 520000, if( prime(s) >= s^(5/4), print(s) ))
for(n = 2, 8 * 10^6, if( primepi(n) >= 1.733 * n / log(n), print(n) ))
ale wykonywane są znacznie szybciej.
Test1(n) =
\\ test oszacowania: prime(k) >= k^(5/4) dla 1 <= k <= n
\\ bez bezpośredniego odwoływania się do funkcji prime(k)
{
local(p, k);
k = 1;
p = 2;
while( k <= n,
if( p >= k^(5/4), print(k) );
k = k + 1;
p = nextprime(p + 1); \\ liczba p ma wartość prime(k)
);
}
Test2(n) =
\\ test oszacowania: primepi(k) < 1.733*k/log(k) dla 2 <= k <= n
\\ bez bezpośredniego odwoływania się do funkcji primepi(k)
{
local(s, k);
s = 1;
k = 2;
while( k <= n,
if( s >= 1.733 * k / log(k), print(k) );
k = k + 1;
s = s + isprime(k); \\ dla kolejnych k liczba s ma wartość primepi(k)
);
}
Uwaga A34
Czytelnik nie powinien mieć złudzeń, że postępując podobnie, uzyskamy istotne polepszenie oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math] lub [math]\displaystyle{ p_n }[/math]. Już osiągnięcie tą drogą oszacowania [math]\displaystyle{ p_n \lt 1.6 \cdot n \log n }[/math] przekracza możliwości obliczeniowe współczesnych komputerów. Wystarczy zauważyć, że nierówność
- [math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 16} }[/math]
jest prawdziwa dla [math]\displaystyle{ x \gt 7.671 \cdot 10^{32} }[/math].
Zastosowania
Ciekawy rezultat wynika z twierdzenia A7, ale wcześniej musimy udowodnić twierdzenie o średniej arytmetycznej i geometrycznej.
Twierdzenie A35
Dla dowolnych liczb dodatnich [math]\displaystyle{ a_1, a_2, \ldots, a_n }[/math] średnia arytmetyczna jest nie mniejsza od średniej geometrycznej
- [math]\displaystyle{ \frac{a_1 + a_2 + \ldots + a_n}{n} \geqslant \sqrt[n]{a_1 a_2 \cdot \ldots \cdot a_n} }[/math]
Twierdzenie jest w sposób oczywisty prawdziwe dla [math]\displaystyle{ n = 1 }[/math]. Równie łatwo stwierdzamy prawdziwość nierówności dla [math]\displaystyle{ n = 2 }[/math]
- [math]\displaystyle{ (a_1 - a_2)^2 \geqslant 0 }[/math]
- [math]\displaystyle{ a^2_1 - 2 a_1 a_2 + a^2_2 \geqslant 0 }[/math]
- [math]\displaystyle{ a^2_1 + 2 a_1 a_2 + a^2_2 \geqslant 4 a_1 a_2 }[/math]
- [math]\displaystyle{ (a_1 + a_2)^2 \geqslant 4 a_1 a_2 }[/math]
- [math]\displaystyle{ \frac{a_1 + a_2}{2} \geqslant \sqrt{a_1 a_2} }[/math]
Dla potrzeb dowodu zapiszemy dowodzoną nierówność w postaci
- [math]\displaystyle{ \left( \frac{a_1 + a_2 + \ldots + a_n}{n} \right)^n \geqslant a_1 a_2 \cdot \ldots \cdot a_n }[/math]
Zakładając, że twierdzenie jest prawdziwe dla wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ n }[/math] dla [math]\displaystyle{ n + 1 }[/math] mamy
a) w przypadku gdy [math]\displaystyle{ n + 1 = 2 k }[/math] jest liczbą parzystą
- [math]\displaystyle{ \left( \frac{a_1 + a_2 + \ldots + a_{n + 1}}{n + 1} \right)^{n + 1} = \left( \frac{a_1 + a_2 + \ldots + a_{2 k}}{2 k} \right)^{2 k} = }[/math]
- [math]\displaystyle{ \quad = \left[ \left( \frac{\frac{a_1 + a_2}{2} + \frac{a_3 + a_4}{2} + \ldots + \frac{a_{2 k - 1} + a_{2 k}}{2}}{k} \right)^k \right]^2 \geqslant }[/math]
- [math]\displaystyle{ \quad \geqslant \left( \frac{a_1 + a_2}{2} \cdot \frac{a_3 + a_4}{2} \cdot \ldots \cdot \frac{a_{2 k - 1} + a_{2 k}}{2} \right)^2 \geqslant }[/math]
- [math]\displaystyle{ \quad \geqslant \left( \sqrt{a_1 a_2} \cdot \sqrt{a_3 a_4} \cdot \ldots \cdot \sqrt{a_{2 k - 1} a_{2 k}} \right)^2 = }[/math]
- [math]\displaystyle{ \quad = a_1 a_2 \cdot \ldots \cdot a_{2 k} = }[/math]
- [math]\displaystyle{ \quad = a_1 a_2 \cdot \ldots \cdot a_{n + 1} }[/math]
Gdzie skorzystaliśmy z założenia indukcyjnego i prawdziwości dowodzonego twierdzenia dla [math]\displaystyle{ n = 2 }[/math].
b) w przypadku gdy [math]\displaystyle{ n + 1 = 2 k - 1 }[/math] jest liczbą nieparzystą, możemy skorzystać z udowodnionego wyżej punktu a) dla parzystej ilości liczb
- [math]\displaystyle{ a_1, a_2, \ldots, a_{2 k - 1}, S }[/math]
gdzie przez [math]\displaystyle{ S }[/math] oznaczyliśmy średnią arytmetyczną liczb [math]\displaystyle{ a_1, a_2, \ldots, a_{2 k - 1} }[/math]
- [math]\displaystyle{ S = \frac{a_1 + a_2 + \ldots + a_{2 k - 1}}{2 k - 1} }[/math]
Na mocy punktu a) prawdziwa jest nierówność
- [math]\displaystyle{ \left( \frac{a_1 + a_2 + \ldots + a_{2 k - 1} + S}{2 k} \right)^{2 k} = \left( \frac{(2 k - 1) S + S}{2 k} \right)^{2 k} \geqslant a_1 a_2 \cdot \ldots \cdot a_{2 k - 1} \cdot S }[/math]
Skąd otrzymujemy
- [math]\displaystyle{ S^{2 k} \geqslant a_1 a_2 \cdot \ldots \cdot a_{2 k - 1} \cdot S }[/math]
- [math]\displaystyle{ S^{2 k - 1} \geqslant a_1 a_2 \cdot \ldots \cdot a_{2 k - 1} }[/math]
Co należało pokazać.
□
Twierdzenie A36
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwa jest nierówność [math]\displaystyle{ p_1 + p_2 + \ldots + p_n \gt n^2 }[/math].
Korzystając z twierdzeń A7 i A35 możemy napisać następujący ciąg nierówności dla [math]\displaystyle{ n }[/math] kolejnych liczb pierwszych
- [math]\displaystyle{ \frac{p_1 + p_2 + \ldots + p_n}{n} \geqslant \sqrt[n]{p_1 \cdot p_2 \cdot \ldots \cdot p_n} \gt \sqrt[n]{n^n} = n }[/math]
Stąd otrzymujemy natychmiast tezę twierdzenia, którą sprawdzamy dla [math]\displaystyle{ n \lt 13 }[/math]. Do sprawdzenia można wykorzystać proste polecenie w PARI/GP
for(n = 1, 20, s = 0; for(k = 1, n, s = s + prime(k)); if( s <= n^2, print(n) ))
□
Twierdzenie A1 pozwala nam udowodnić różne oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math] i [math]\displaystyle{ p_n }[/math], które byłyby trudne do uzyskania inną drogą. Wykorzystujemy do tego znany fakt, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ n_0 }[/math], że dla każdego [math]\displaystyle{ n \gt n_0 }[/math] prawdziwa jest nierówność [math]\displaystyle{ \log x \lt x^{\varepsilon} }[/math]. Inaczej mówiąc, funkcja [math]\displaystyle{ \log x }[/math] rośnie wolniej niż najwolniej rosnąca funkcja potęgowa. Nim przejdziemy do dowodu takich przykładowych oszacowań, udowodnimy pomocnicze twierdzenie, które wykorzystamy przy szacowaniu.
Twierdzenie A37
Prawdziwe są następujące nierówności:
- 1. [math]\displaystyle{ e^x \gt x \qquad \qquad \qquad \quad \:\, }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R} }[/math]
- 2. [math]\displaystyle{ e^x \gt 2 x \qquad \qquad \qquad \;\;\,\, }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R} }[/math]
- 3. [math]\displaystyle{ \log x \lt n \cdot x^{1 / n} \qquad \quad \;\;\: }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] i dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]
- 4. [math]\displaystyle{ \log x \leqslant n (x^{1 / n} - 1) \qquad }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] i dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]
Punkt 1. i punkt 2.
Ponieważ funkcję [math]\displaystyle{ \exp (x) }[/math] możemy zdefiniować w sposób równoważny wzorem[10]
- [math]\displaystyle{ e^x = \sum_{k = 0}^{\infty} \frac{x^k}{k!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} + \ldots }[/math]
to funkcja [math]\displaystyle{ e^x }[/math] jest funkcją dodatnią, bo dla [math]\displaystyle{ x \gt 0 }[/math] sumujemy tylko wyrazy dodatnie, dla [math]\displaystyle{ x = 0 }[/math] mamy [math]\displaystyle{ e^0 = 1 }[/math], a dla [math]\displaystyle{ x \lt 0 }[/math] możemy napisać [math]\displaystyle{ e^x = \frac{1}{e^{| x |}} \gt 0 }[/math].
Ponieważ funkcje [math]\displaystyle{ x \, }[/math] i [math]\displaystyle{ \, 2 x }[/math] są ujemne lub równe zero dla [math]\displaystyle{ x \leqslant 0 }[/math], to pozostaje rozważyć jedynie przypadek, gdy [math]\displaystyle{ x \gt 0 }[/math]. Łatwo zauważmy, że
- [math]\displaystyle{ e^x - x = \sum_{k = 0}^{\infty} \frac{x^k}{k!} - x = 1 + \sum^{\infty}_{k = 2} \frac{x^k}{k!} \gt 0 }[/math]
- [math]\displaystyle{ e^x - 2 x = \sum_{k = 0}^{\infty} \frac{x^k}{k!} - 2 x = 1 - x + \frac{x^2}{2} + \sum_{k = 3}^{\infty} \frac{x^k}{k!} = \frac{1}{2} + \frac{(x - 1)^2}{2} + \sum_{k = 3}^{\infty} \frac{x^k}{k!} \gt 0 }[/math]
Punkt 3.
W rozpatrywanej nierówności połóżmy zmienną pomocniczą [math]\displaystyle{ x = e^y }[/math], gdzie [math]\displaystyle{ y \in \mathbb{R} }[/math]. Otrzymujemy
- [math]\displaystyle{ y \lt n \cdot (e^y)^{1 / n} }[/math]
Czyli
- [math]\displaystyle{ \frac{y}{n} \lt e^{y / n} }[/math]
Otrzymana nierówność jest prawdziwa dla dowolnego [math]\displaystyle{ \frac{y}{n} \in \mathbb{R} }[/math] na mocy punktu 1. tego twierdzenia.
Punkt 4.
Rozważmy funkcję
- [math]\displaystyle{ f(x) = n \cdot x^{1 / n} - \log x }[/math]
Pochodna tej funkcji jest równa
- [math]\displaystyle{ f' (x) = \frac{x^{1 / n} - 1}{x} }[/math]
Pochodna jest równa zero dla [math]\displaystyle{ x = 1 }[/math]. Dla [math]\displaystyle{ 0 \lt x \lt 1 }[/math] pochodna jest ujemna, a dla [math]\displaystyle{ x \gt 1 }[/math] jest dodatnia, zatem w punkcie [math]\displaystyle{ x = 1 }[/math] funkcja [math]\displaystyle{ f(x) }[/math] ma minimum i [math]\displaystyle{ f(1) = n }[/math]. Wynika stąd oszacowanie
- [math]\displaystyle{ f(x) = n \cdot x^{1 / n} - \log x \geqslant n }[/math]
Skąd otrzymujemy
- [math]\displaystyle{ \log x \leqslant n (x^{1 / n} - 1) }[/math]
- [math]\displaystyle{ \log x \leqslant n (x^{1 / n} - 1) }[/math]
□
Zadanie A38
Niech [math]\displaystyle{ x \in \mathbb{R}_+ }[/math]. Pokazać, że dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] istnieje takie [math]\displaystyle{ x_0 }[/math], że dla każdego [math]\displaystyle{ x \gt x_0 }[/math] jest [math]\displaystyle{ \log x \lt x^{1 / n} }[/math].
Pierwszy sposób
Rozważmy ciąg nierówności
- [math]\displaystyle{ \log x \lt 2 n \cdot x^{1 / 2 n} \lt x^{1 / n} }[/math]
Z twierdzenia A37 wiemy, że pierwsza nierówność jest prawdziwa dla dowolnych [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] i [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Podnosząc strony drugiej nierówności do potęgi [math]\displaystyle{ 2 n }[/math] otrzymujemy [math]\displaystyle{ (2 n)^{2 n} \cdot x \lt x^2 }[/math], czyli nierówność ta jest prawdziwa dla [math]\displaystyle{ x \gt (2 n)^{2 n} }[/math]. Wynika stąd, że wystarczy przyjąć [math]\displaystyle{ x_0 = (2 n)^{2 n} }[/math].
Drugi sposób
Nierówność [math]\displaystyle{ \log x \lt x^{1 / n} }[/math] możemy równoważnie zapisać w postaci [math]\displaystyle{ x \lt \exp (x^{1 / n}) }[/math]. Jeżeli położymy [math]\displaystyle{ x = t^n }[/math], to otrzymamy nierówność [math]\displaystyle{ t^n {\lt e^t} }[/math]. Ponieważ[10]
- [math]\displaystyle{ e^t = \sum_{k = 0}^{\infty} \frac{t^k}{k!} = 1 + t + \frac{t^2}{2} + \frac{t^3}{6} + \frac{t^4}{24} + \frac{t^5}{120} + \ldots }[/math]
to
- [math]\displaystyle{ e^t \gt \frac{t^{n + 1}}{(n + 1) !} \gt t^n }[/math]
Pierwsza nierówność jest prawdziwa dla [math]\displaystyle{ t \gt 0 }[/math], bo pomijamy wyrazy dodatnie, a druga dla [math]\displaystyle{ t \gt (n + 1) ! }[/math] Wystarczy zatem przyjąć [math]\displaystyle{ x_0 = [(n + 1) !]^n }[/math]. Ponieważ [math]\displaystyle{ [(n + 1) !]^n \gt (2 n)^{2 n} }[/math] dla [math]\displaystyle{ n \geqslant 4 }[/math], to jest to gorsze oszacowanie wartości [math]\displaystyle{ x_0 }[/math].
□
Twierdzenie A39
Dla funkcji [math]\displaystyle{ p_n }[/math] i [math]\displaystyle{ \pi (n) }[/math] prawdziwe są następujące oszacowania:
- [math]\displaystyle{ 10 n \underset{n \geqslant 6473}{\lt } p_n \underset{n \geqslant 2}{\lt } n^2 }[/math]
- [math]\displaystyle{ \sqrt{n} \underset{n \geqslant 5}{\lt } \pi (n) \underset{n \geqslant 64721}{\lt } \frac{n}{10} }[/math]
Lewa górna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 1 }[/math] jest [math]\displaystyle{ p_n \gt 0.72 \cdot n \log n }[/math]. Wystarczy rozwiązać nierówność:
- [math]\displaystyle{ 0.72 \cdot \log n \gt 10 }[/math]
czyli [math]\displaystyle{ n \gt \exp \left( \frac{10}{0.72} \right) = 1076137.5 }[/math]
W PARI/GP wpisujemy polecenie:
- for(n=1, 11*10^5, if( prime(n) <= 10*n, print(n) ))
Prawa górna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] jest [math]\displaystyle{ p_n \lt 2 n \log n }[/math]. Zatem wystarczy pokazać, że [math]\displaystyle{ 2 n \log n \lt n^2 }[/math]. Korzystając z twierdzenia A37, łatwo zauważmy, że dla [math]\displaystyle{ n \gt 16 }[/math] jest:
- [math]\displaystyle{ n - 2 \log n \gt n - 2 \cdot 2 \cdot n^{1 / 2} = \sqrt{n} \left( \sqrt{n} - 4 \right) \gt 0 }[/math]
Przypadki [math]\displaystyle{ n \leqslant 16 }[/math] sprawdzamy bezpośrednio.
Lewa dolna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] jest [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]. Zatem wystarczy pokazać, że [math]\displaystyle{ \frac{2}{3} \cdot \frac{n}{\log n} \gt \sqrt{n} }[/math]. Korzystając z twierdzenia A37, łatwo zauważmy, że dla [math]\displaystyle{ n \gt 6^4 = 1296 }[/math] jest:
- [math]\displaystyle{ \frac{2}{3} \cdot \frac{n}{\log n} - \sqrt{n} \gt \frac{2}{3} \cdot \frac{n}{4 \cdot n^{1 / 4}} - \sqrt{n} = \frac{1}{6} \cdot n^{3 / 4} - \sqrt{n} = \frac{1}{6} \sqrt{n} (n^{1 / 4} - 6) \gt 0 }[/math]
Sprawdzenie przypadków [math]\displaystyle{ n \leqslant 1296 }[/math] sprowadza się do wpisania w PARI/GP polecenia:
- for(n=1, 2000, if( primepi(n) <= sqrt(n), print(n) ))
Prawa dolna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] jest [math]\displaystyle{ \pi (n) \lt \frac{2 n}{\log n} }[/math]. Zatem wystarczy pokazać, że [math]\displaystyle{ \frac{2 n}{\log n} \lt \frac{n}{10} }[/math]. Nierówność ta jest prawdziwa dla [math]\displaystyle{ \log n \gt 20 }[/math], czyli dla
- [math]\displaystyle{ n \gt e^{20} \gt 485165195.4 }[/math]
Sprawdzenie przypadków dla [math]\displaystyle{ n \leqslant 490 \cdot 10^6 }[/math] będzie wymagało napisania w PARI/GP krótkiego programu i wywołania go z parametrem n = 490*10^6
Test3(n) =
\\ test oszacowania: primepi(k) < k/10 dla 2 <= k <= n
\\ bez bezpośredniego odwoływania się do funkcji primepi(k)
{
local(s, k);
s = 1;
k = 2;
while( k <= n,
if( s >= k/10, print(k) );
k = k + 1;
s = s + isprime(k); \\ dla kolejnych k liczba s ma wartość primepi(k)
);
}
□
Twierdzenie A40
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n^2})^{n / 3} }[/math]
Korzystając kolejno z twierdzeń A30, A37 i A7, łatwo otrzymujemy
- [math]\displaystyle{ (p_{n^2})^{n / 3} \lt (2 \cdot n^2 \cdot \log n^2)^{n / 3} }[/math]
- [math]\displaystyle{ \;\; = (4 \cdot n^2 \cdot \log n)^{n / 3} }[/math]
- [math]\displaystyle{ \;\; \lt (8 \cdot n^{5 / 2})^{n / 3} }[/math]
- [math]\displaystyle{ \;\; = (2 \cdot n^{5 / 6})^n }[/math]
- [math]\displaystyle{ \;\; \lt n^n }[/math]
- [math]\displaystyle{ \;\; \lt p_1 p_2 \cdot \ldots \cdot p_n }[/math]
Zauważmy, że nierówność [math]\displaystyle{ 2 \cdot n^{5 / 6} \lt n }[/math] jest prawdziwa dla [math]\displaystyle{ n \gt 2^6 }[/math]. Sprawdzając bezpośrednio dla [math]\displaystyle{ n \leqslant 64 }[/math] stwierdzamy, że dowodzona nierówność jest prawdziwa dla [math]\displaystyle{ n \geqslant 1 }[/math].
□
Zadanie A41
Korzystając z twierdzenia A40 pokazać, że
- [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n + 1})^2 \qquad \qquad \text{dla } \; n \geqslant 4 }[/math]
- [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{2 n})^3 \qquad \qquad \;\; \text{dla } \; n \geqslant 7 }[/math]
Punkt 1.
Ponieważ [math]\displaystyle{ n^2 \gt n + 1 }[/math] dla [math]\displaystyle{ n \geqslant 2 }[/math] oraz [math]\displaystyle{ {\small\frac{n}{3}} \gt 2 }[/math] dla [math]\displaystyle{ n \gt 6 }[/math], to dla [math]\displaystyle{ n \gt 6 }[/math] jest
- [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n^2})^{n / 3} \gt (p_{n + 1})^2 }[/math]
Sprawdzając bezpośrednio dla [math]\displaystyle{ n \leqslant 6 }[/math], łatwo stwierdzamy prawdziwość oszacowania dla [math]\displaystyle{ n \geqslant 4 }[/math].
Punkt 2.
Ponieważ [math]\displaystyle{ n^2 \gt 2 n }[/math] dla [math]\displaystyle{ n \gt 2 }[/math] oraz [math]\displaystyle{ {\small\frac{n}{3}} \gt 3 }[/math] dla [math]\displaystyle{ n \gt 9 }[/math], to dla [math]\displaystyle{ n \gt 9 }[/math] jest
- [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n^2})^{n / 3} \gt (p_{2 n})^3 }[/math]
Sprawdzając bezpośrednio dla [math]\displaystyle{ n \leqslant 9 }[/math], łatwo stwierdzamy prawdziwość oszacowania dla [math]\displaystyle{ n \geqslant 7 }[/math].
□
Twierdzenie A42
Każda liczba pierwsza [math]\displaystyle{ p }[/math], taka że [math]\displaystyle{ p \in \left( \frac{n}{2}, n \right] }[/math] występuje w rozwinięciu [math]\displaystyle{ n! }[/math] na czynniki pierwsze z wykładnikiem równym jeden.
Z twierdzenia A21 wiemy, że każda liczba pierwsza [math]\displaystyle{ p }[/math] występuje w iloczynie [math]\displaystyle{ n! }[/math] z wykładnikiem [math]\displaystyle{ W_p (n!) = \sum_{k = 1}^{\infty} \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]
Z założenia [math]\displaystyle{ p \leqslant n }[/math] i [math]\displaystyle{ 2 p \gt n }[/math], zatem:
- 1. [math]\displaystyle{ \frac{n}{p} \geqslant 1 }[/math] oraz [math]\displaystyle{ \frac{n}{p} \lt 2 }[/math], czyli [math]\displaystyle{ \left\lfloor \frac{n}{p} \right\rfloor = 1 }[/math]
- 2. [math]\displaystyle{ \frac{n}{p^2} \lt \frac{2}{p} \leqslant 1 }[/math], czyli [math]\displaystyle{ \left\lfloor \frac{n}{p^2} \right\rfloor = 0 }[/math] i tym bardziej [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math] dla [math]\displaystyle{ k \geqslant 3 }[/math]
- 2. [math]\displaystyle{ \frac{n}{p^2} \lt \frac{2}{p} \leqslant 1 }[/math], czyli [math]\displaystyle{ \left\lfloor \frac{n}{p^2} \right\rfloor = 0 }[/math] i tym bardziej [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math] dla [math]\displaystyle{ k \geqslant 3 }[/math]
□
Rezultat uzyskany w twierdzeniu A25 zainspirował nas do postawienia pytania: jakie warunki musi spełniać liczba pierwsza [math]\displaystyle{ p }[/math], aby występowała w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden lub równym zero? Twierdzenia A43 i A45 udzielają na to pytanie precyzyjnej odpowiedzi. Przykłady A44 i A46 to tylko twierdzenia A43 i A45 dla wybranych wartości liczby [math]\displaystyle{ k }[/math]. Jeśli Czytelnik nie miał problemów ze zrozumieniem dowodów twierdzeń A43 i A45, to może je pominąć.
Twierdzenie A43
Niech [math]\displaystyle{ k }[/math] będzie dowolną ustaloną liczbą naturalną. Jeżeli [math]\displaystyle{ n \geqslant 2 (k + 1) \left( k + \tfrac{1}{2} \right) }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left( {\small\frac{n}{k + 1}}, {\small\frac{n}{k + \tfrac{1}{2}}} \right] }[/math], to [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden.
Najpierw udowodnimy przypadek [math]\displaystyle{ k = 0 }[/math].
Zauważmy, że każda liczba pierwsza [math]\displaystyle{ p \in (n, 2 n] }[/math] występuje dokładnie jeden raz w liczniku ułamka
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
i nie występuje w mianowniku. Zatem w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze wystąpi z wykładnikiem równym [math]\displaystyle{ 1 }[/math].
Co kończy dowód twierdzenia w przypadku, gdy [math]\displaystyle{ k = 0 }[/math].
Możemy teraz przejść do dowodu dla wszystkich [math]\displaystyle{ k \geqslant 1 }[/math].
Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]
Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Rozważmy dowolną liczbę pierwszą występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:
- [math]\displaystyle{ k p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k }[/math] razy w mianowniku
- [math]\displaystyle{ (k + 1) p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku (jako [math]\displaystyle{ p, 2 p, \ldots, k p }[/math])
- [math]\displaystyle{ (2 k + 1) p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ (k + 1) p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k + 1 }[/math] razy w liczniku
- [math]\displaystyle{ (2 k + 2) p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ (2 k + 1) p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k + 1 }[/math] razy w liczniku (jako [math]\displaystyle{ (k + 1) p, (k + 2) p, \ldots, (2 k + 1) p }[/math])
Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left(\frac{n}{k + 1}, \frac{n}{k + \frac{1}{2}} \right] }[/math] pojawia się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku i dokładnie [math]\displaystyle{ k + 1 }[/math] razy w liczniku ułamka
- [math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Zatem występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem jeden.
Niech [math]\displaystyle{ q }[/math] będzie największą liczbą pierwszą nie większą od ustalonej liczby [math]\displaystyle{ 2 k + 1 }[/math]. Rozpatrywane przez nas wielokrotności liczby zwiększają wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ r_i \in \{ 2, 3, \ldots, q \} }[/math]. Dlatego twierdzenie nie może dotyczyć tych liczb i musimy nałożyć warunek
- [math]\displaystyle{ r_i \notin \left( \frac{n}{k + 1}, \frac{n}{k + \frac{1}{2}} \right] }[/math]
Warunek ten będzie z pewnością spełniony, gdy
- [math]\displaystyle{ q \leqslant 2 k + 1 \leqslant \frac{n}{k + 1} }[/math]
czyli dla [math]\displaystyle{ n }[/math] spełniających nierówność [math]\displaystyle{ n \geqslant (k + 1) (2 k + 1) }[/math].
Oczywiście nie wyklucza to możliwości, że istnieją liczby [math]\displaystyle{ n \lt 2 (k + 1) (k + \tfrac{1}{2}) }[/math], dla których twierdzenie jest prawdziwe. Pozostaje (przy ustalonej wartości liczby [math]\displaystyle{ k }[/math]) bezpośrednio sprawdzić prawdziwość twierdzenia dla [math]\displaystyle{ n \lt 2 (k + 1) (k + \tfrac{1}{2}) }[/math].
Dowód na podstawie twierdzenia A24
Rozważmy najpierw pierwszy składnik sumy
- [math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) }[/math]
Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 1 }[/math], to będziemy szukali oszacowania od dołu. Z założenia mamy
1) [math]\displaystyle{ p \gt \frac{n}{k + 1} \quad\ \implies \quad \frac{n}{p} \lt k + 1 \quad\ \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \leqslant k }[/math]
2) [math]\displaystyle{ p \leqslant \frac{n}{k + \tfrac{1}{2}} \quad\ \implies \quad \frac{2 n}{p} \geqslant 2 k + 1 \quad\ \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \geqslant 2 k + 1 }[/math]
Zatem
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \geqslant 2 k + 1 - 2 k = 1 }[/math]
Ponieważ każdy ze składników sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 1 }[/math]
Założenie, że [math]\displaystyle{ n \geqslant 2 (k + 1)^2 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy
- [math]\displaystyle{ p \gt \frac{n}{k + 1} \quad \implies \quad \frac{2 n}{p} \lt 2 k + 2 \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{(2 n)^s}{p^s} \lt (2 k + 2)^s \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 2)^2}{2 n} \cdot \left( \frac{2 k + 2}{2 n} \right)^{s - 2} \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 2)^2}{2 n} \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{2 n}{p^s} \lt 1 \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math]
Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^s} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 2 (k + 1)^2 }[/math] jest
- [math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) = 1 }[/math]
Pozostaje bezpośrednio sprawdzić, dla jakich wartości [math]\displaystyle{ n \lt 2 (k + 1)^2 }[/math] twierdzenie pozostaje prawdziwe.
Ponieważ analiza krotności pojawiania się liczby pierwszej [math]\displaystyle{ p }[/math] jest bardziej precyzyjna, to podajemy, że twierdzenie jest z pewnością prawdziwe dla [math]\displaystyle{ n \geqslant 2 (k + 1) (k + \tfrac{1}{2}) }[/math]
□
Przykład A44
Jeżeli [math]\displaystyle{ n \geqslant 6 }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left( \frac{n}{2}, \frac{2 n}{3} \right] }[/math], to [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden.
Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]
Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Rozważmy dowolną liczbę pierwszą występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:
- [math]\displaystyle{ p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej jeden raz w mianowniku
- [math]\displaystyle{ 2 p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie jeden raz w mianowniku (jako [math]\displaystyle{ p }[/math])
- [math]\displaystyle{ 3 p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej dwa razy w liczniku
- [math]\displaystyle{ 4 p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 3 p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie dwa razy w liczniku (jako [math]\displaystyle{ 2 p }[/math] i [math]\displaystyle{ 3 p }[/math])
Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math] pojawia się dokładnie jeden raz w mianowniku i dokładnie dwa razy w liczniku ułamka
- [math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Zatem występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem jeden.
Wielokrotności liczby [math]\displaystyle{ p }[/math] podnoszą wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ p = 2, 3 }[/math]. Dlatego zakładamy, że [math]\displaystyle{ n \geqslant 6 }[/math], bo dla [math]\displaystyle{ n \geqslant 6 }[/math] liczby pierwsze [math]\displaystyle{ p = 2, 3 }[/math] nie spełniają warunku [math]\displaystyle{ p \in \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math].
Bezpośrednio sprawdzamy, że twierdzenie nie jest prawdziwe dla [math]\displaystyle{ n = 5 }[/math] i liczba [math]\displaystyle{ 3^2 }[/math] dzieli liczbę [math]\displaystyle{ \binom{10}{5} = 252 = 9 \cdot 28 }[/math]
Dowód na podstawie twierdzenia A24
Rozważmy najpierw pierwszy składnik sumy
- [math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) }[/math]
Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 1 }[/math], to będziemy szukali oszacowania od dołu. Z założenia mamy
- 1) [math]\displaystyle{ p \gt \frac{n}{2} \quad \implies \quad \frac{n}{p} \lt 2 \quad \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \leqslant 1 }[/math]
- 2) [math]\displaystyle{ p \leqslant \frac{2 n}{3} \quad \implies \quad \frac{2 n}{p} \geqslant 3 \quad \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \geqslant 3 }[/math]
Zatem
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \geqslant 3 - 2 = 1 }[/math]
Ponieważ każdy ze składników sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 1 }[/math]
Założenie, że [math]\displaystyle{ n \geqslant 9 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy
- [math]\displaystyle{ p \gt \frac{n}{2} \quad \implies \quad \frac{(2 n)^k}{p^k} \lt 4^k \quad \implies \quad \frac{2 n}{p^k} \lt \frac{16}{2 n} \cdot \left( \frac{4}{2 n} \right)^{k - 2} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{16}{2 n} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{16}{18} \quad \implies \quad \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math]
Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 9 }[/math] jest
- [math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) = 1 }[/math]
Dla [math]\displaystyle{ n = 6, 7 }[/math] żadna liczba pierwsza nie należy do [math]\displaystyle{ \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math]. Dla [math]\displaystyle{ n = 8 }[/math] łatwo sprawdzamy, że liczba [math]\displaystyle{ 5 }[/math] wchodzi do rozkładu liczby [math]\displaystyle{ \binom{16}{8} = 12870 }[/math] na czynniki pierwsze z wykładnikiem równym jeden.
Zatem dla [math]\displaystyle{ n \geqslant 6 }[/math] liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math] wchodzi do rozkładu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden.
□
Twierdzenie A45
Niech [math]\displaystyle{ k }[/math] będzie dowolną ustaloną liczbą całkowitą dodatnią. Jeżeli liczba pierwsza [math]\displaystyle{ p \in \left( \frac{n}{k + \tfrac{1}{2}}, \frac{n}{k} \right] }[/math], to dla [math]\displaystyle{ n \geqslant 2 k (k + \tfrac{1}{2}) }[/math] liczba [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.
Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]
Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Rozważmy dowolną liczbę pierwszą [math]\displaystyle{ p }[/math] występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:
- [math]\displaystyle{ k p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k }[/math] razy w mianowniku
- [math]\displaystyle{ (k + 1) p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku (jako [math]\displaystyle{ p, 2 p, \ldots, k p }[/math])
- [math]\displaystyle{ 2 k p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ (k + 1) p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k }[/math] razy w liczniku
- [math]\displaystyle{ (2 k + 1) p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 k p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k }[/math] razy w liczniku (jako [math]\displaystyle{ (k + 1) p, (k + 2) p, \ldots, 2 k p }[/math])
Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left( \frac{n}{k + \frac{1}{2}}, \frac{n}{k} \right] }[/math] pojawia się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku i dokładnie [math]\displaystyle{ k }[/math] razy w liczniku ułamka
- [math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Co oznacza, że [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.
Niech [math]\displaystyle{ q }[/math] będzie największą liczbą pierwszą nie większą od ustalonej liczby [math]\displaystyle{ 2 k }[/math]. Rozpatrywane przez nas wielokrotności liczby [math]\displaystyle{ p }[/math] zwiększają wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ r_i \in \{ 2, 3, \ldots, q \} }[/math]. Dlatego twierdzenie nie może dotyczyć tych liczb i musimy nałożyć warunek
- [math]\displaystyle{ r_i \notin \left( \frac{n}{k + \frac{1}{2}}, \frac{n}{k} \right] }[/math]
Warunek ten będzie z pewnością spełniony, gdy
- [math]\displaystyle{ q \leqslant 2 k \leqslant \frac{n}{k + \frac{1}{2}} }[/math]
czyli dla [math]\displaystyle{ n }[/math] spełniających nierówność [math]\displaystyle{ n \geqslant 2 k (k + \tfrac{1}{2}) }[/math]. Oczywiście nie wyklucza to możliwości, że istnieją liczby [math]\displaystyle{ n \lt 2 k (k + \tfrac{1}{2}) }[/math], dla których twierdzenie jest prawdziwe. Pozostaje (przy ustalonej wartości liczby [math]\displaystyle{ k }[/math]) bezpośrednio sprawdzić prawdziwość twierdzenia dla [math]\displaystyle{ n \lt 2 k (k + \tfrac{1}{2}) }[/math].
Dowód na podstawie twierdzenia A24
Rozważmy najpierw pierwszy składnik sumy
- [math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) }[/math]
Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 0 }[/math], to będziemy szukali oszacowania od góry. Z założenia mamy
1) [math]\displaystyle{ p \gt \frac{n}{k + \frac{1}{2}} \quad\ \implies \quad \frac{2 n}{p} \lt 2 k + 1 \quad\ \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \leqslant 2 k }[/math]
2) [math]\displaystyle{ p \leqslant \frac{n}{k} \quad\ \implies \quad \frac{n}{p} \geqslant k \quad\ \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \geqslant k }[/math]
Zatem
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \leqslant 2 k - 2 k = 0 }[/math]
Ponieważ każdy ze składników sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 0 }[/math]
Założenie, że [math]\displaystyle{ 2 n \geqslant (2 k + 1)^2 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy
- [math]\displaystyle{ p \gt \frac{2 n}{2 k + 1} \quad \implies \quad \frac{(2 n)^s}{p^s} \lt (2 k + 1)^s \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 1)^2}{2 n} \cdot \left( \frac{2 k + 1}{2 n} \right)^{s - 2} \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 1)^2}{2 n} \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \frac{2 n}{p^s} \lt 1 \quad \implies }[/math]
- [math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math]
Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^s} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ 2 n \geqslant (2 k + 1)^2 }[/math] jest
- [math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) = 0 }[/math]
Pozostaje bezpośrednio sprawdzić, dla jakich wartości [math]\displaystyle{ n \lt \frac{1}{2} (2 k + 1)^2 }[/math] twierdzenie pozostaje prawdziwe.
Ponieważ analiza krotności pojawiania się liczby pierwszej [math]\displaystyle{ p }[/math] jest bardziej precyzyjna, to podajemy, że twierdzenie jest z pewnością prawdziwe dla [math]\displaystyle{ n \geqslant 2 k (k + \tfrac{1}{2}) }[/math].
□
Przykład A46
Jeżeli [math]\displaystyle{ n \geqslant 8 }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left( \frac{2 n}{5}, \frac{n}{2} \right] }[/math], to [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.
Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]
Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka
- [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Rozważmy dowolną liczbę pierwszą [math]\displaystyle{ p }[/math] występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:
- [math]\displaystyle{ 2 p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej dwa razy w mianowniku
- [math]\displaystyle{ 3 p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie dwa razy w mianowniku (jako [math]\displaystyle{ p }[/math] i [math]\displaystyle{ 2 p }[/math])
- [math]\displaystyle{ 4 p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 3 p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej dwa razy w liczniku
- [math]\displaystyle{ 5 p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 4 p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie dwa razy w liczniku (jako [math]\displaystyle{ 3 p }[/math] i [math]\displaystyle{ 4 p }[/math])
Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math] pojawia się dokładnie dwa razy w mianowniku i dokładnie dwa razy w liczniku ułamka
- [math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]
Zatem nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.
Wielokrotności liczby [math]\displaystyle{ p }[/math] podnoszą wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ 2 }[/math] i [math]\displaystyle{ 3 }[/math]. Dlatego zakładamy, że [math]\displaystyle{ n \geqslant 8 }[/math], bo dla [math]\displaystyle{ n \geqslant 8 }[/math] liczby pierwsze [math]\displaystyle{ 2, 3 }[/math] nie spełniają warunku [math]\displaystyle{ p \in \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math].
Bezpośrednio sprawdzamy, że twierdzenie nie jest prawdziwe dla [math]\displaystyle{ n = 7 }[/math] i liczba [math]\displaystyle{ 3 }[/math] dzieli liczbę [math]\displaystyle{ \binom{14}{7} = 3432 }[/math]
Dowód na podstawie twierdzenia A24
Rozważmy najpierw pierwszy składnik sumy
- [math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) }[/math]
Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 0 }[/math], to będziemy szukali oszacowania od góry. Z założenia mamy
- 1) [math]\displaystyle{ p \gt \frac{2 n}{5} \quad \implies \quad \frac{2 n}{p} \lt 5 \quad \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \leqslant 4 }[/math]
- 2) [math]\displaystyle{ p \leqslant \frac{n}{2} \quad \implies \quad \frac{n}{p} \geqslant 2 \quad \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \geqslant 2 }[/math]
Zatem
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \leqslant 4 - 4 = 0 }[/math]
Ponieważ każdy ze składników szukanej sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy
- [math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 0 }[/math]
Założenie, że [math]\displaystyle{ n \geqslant 13 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy
- [math]\displaystyle{ p \gt \frac{2 n}{5} \quad \implies \quad \frac{(2 n)^k}{p^k} \lt 5^k \quad \implies \quad \frac{2 n}{p^k} \lt \frac{25}{2 n} \cdot \left( \frac{5}{2 n} \right)^{k - 2} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{25}{2 n} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{25}{26} \quad \implies \quad \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math]
Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 13 }[/math] jest
- [math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) = 0 }[/math]
Dla [math]\displaystyle{ n = 8, 9 }[/math] żadna liczba pierwsza nie należy do [math]\displaystyle{ \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math].
Dla [math]\displaystyle{ n = 10, 11, 12 }[/math] łatwo sprawdzamy, że liczba [math]\displaystyle{ 5 }[/math] nie dzieli liczb [math]\displaystyle{ \binom{20}{10} = 184756 }[/math], [math]\displaystyle{ \binom{22}{11} = 705432 }[/math] oraz [math]\displaystyle{ \binom{24}{12} = 2704156 }[/math].
Zatem dla [math]\displaystyle{ n \geqslant 8 }[/math] liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math] nie dzieli liczby [math]\displaystyle{ \binom{2 n}{n} }[/math].
□
Uwaga A47
Z przykładu A44 nie wynika, że w przedziale [math]\displaystyle{ \left( \frac{n}{2}, \frac{2 n}{3} \right] }[/math] znajduje się choćby jedna liczba pierwsza [math]\displaystyle{ p }[/math]. Analogiczna uwaga jest prawdziwa w przypadku przykładu A46 oraz twierdzeń A43 i A45. Istnienie liczby pierwszej w określonym przedziale będzie tematem kolejnego artykułu.
Przykład A48
Pokazujemy i omawiamy wynik zastosowania twierdzeń A43 i A45 do współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math]. Można udowodnić, że granicę stosowalności obu twierdzeń bardzo dokładnie opisuje warunek [math]\displaystyle{ p \gt \sqrt{2 n} }[/math], co w naszym przypadku daje [math]\displaystyle{ p \gt \sqrt{2 \cdot 3284} \approx 81.04 }[/math].
Wybraliśmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] dlatego, że w rozkładzie tego współczynnika na czynniki pierwsze występują wszystkie liczby pierwsze [math]\displaystyle{ p \leqslant 107 }[/math], co ułatwia analizowanie występowania liczb pierwszych. Tylko sześć liczb pierwszych: 2, 3, 59, 61, 73, 79 występuje z wykładnikiem większym niż jeden. Ponieważ [math]\displaystyle{ \sqrt{2 \cdot 3284} \approx 81.043 }[/math], zatem liczba 79 jest ostatnią liczbą pierwszą, która mogłaby wystąpić z wykładnikiem większym niż jeden i tak właśnie jest.
Poniżej wypisaliśmy wszystkie liczby pierwsze [math]\displaystyle{ p \leqslant 3284 }[/math], które występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] na czynniki pierwsze. Pogrubienie oznacza, że dana liczba rozpoczyna nowy wiersz w tabeli. Ostatnią pogrubioną i dodatkowo podkreśloną liczbą jest liczba 107, bo wszystkie liczby pierwsze mniejsze od 107 powinny pojawić się w tabeli – oczywiście tak się nie stanie, bo twierdzeń A43 i A45 nie można stosować bez ograniczeń dla coraz większych liczb [math]\displaystyle{ k }[/math].
26, 38, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 592, 612, 67, 71, 732, 792, 83, 89, 97, 101, 103, 107, 127, 137, 139, 151, 157, 167, 173, 197, 199, 211, 223, 239, 241, 257, 277, 281, 283, 307, 311, 331, 337, 367, 373, 379, 383, 419, 421, 431, 433, 479, 487, 491, 499, 503, 557, 563, 569, 571, 577, 587, 593, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179
Liczba 821 została pogrubiona (w tabeli), bo jest liczbą pierwszą i wyznacza początek przedziału otwartego, konsekwentnie liczba 821 nie występuje w rozkładzie współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] na czynniki pierwsze.
Czytelnik łatwo sprawdzi, że największą wartością liczby [math]\displaystyle{ k }[/math], dla jakiej można jeszcze stosować twierdzenie A43, jest [math]\displaystyle{ k = 39 }[/math]. Podobnie największą wartością liczby [math]\displaystyle{ k }[/math], dla jakiej można jeszcze stosować twierdzenie A45, jest [math]\displaystyle{ k = 40 }[/math]. Wartości te i odpowiadające im przedziały zostały pogrubione, aby uwidocznić granicę stosowania tych twierdzeń. Łatwo odczytujemy, że twierdzenia A43 i A45 można stosować dla liczb pierwszych [math]\displaystyle{ p }[/math] spełniających warunek [math]\displaystyle{ p \gt 81.09 }[/math]. Co bardzo dokładnie pokrywa się z warunkiem [math]\displaystyle{ p \gt \sqrt{2 \cdot 3284} \approx 81.04 }[/math]
Liczba 73 jest ostatnią poprawnie pokazaną liczbą pierwszą. Po niej nie pojawiają się liczby pierwsze 71 i 67, które występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] na czynniki pierwsze.
| [math]\displaystyle{ k }[/math] | [math]\displaystyle{ \frac{3284}{k+1} }[/math] | [math]\displaystyle{ p \in \left ( \frac{3284}{k + 1}, \frac{3284}{k + \tfrac{1}{2}} \right ] }[/math] | [math]\displaystyle{ \frac{3284}{k+\tfrac{1}{2}} }[/math] | [math]\displaystyle{ \frac{3284}{k} }[/math] |
|---|---|---|---|---|
| 0 | 3284 | {3299, 3301, ..., 6553, 6563} | 6568 | |
| 1 | 1642 | {1657, 1663, ..., 2161, 2179} | 2189,33 | 3284 |
| 2 | 1094,67 | {1097, 1103, ..., 1303, 1307} | 1313,60 | 1642 |
| 3 | 821 | {823, 827, ..., 929, 937} | 938,29 | 1094,67 |
| 4 | 656,80 | {659, 661, 673, 677, 683, 691, 701, 709, 719, 727} | 729,78 | 821 |
| 5 | 547,33 | {557, 563, 569, 571, 577, 587, 593} | 597,09 | 656,80 |
| 6 | 469,14 | {479, 487, 491, 499, 503} | 505,23 | 547,33 |
| 7 | 410,50 | {419, 421, 431, 433} | 437,87 | 469,14 |
| 8 | 364,89 | {367, 373, 379, 383} | 386,35 | 410,50 |
| 9 | 328,40 | {331, 337} | 345,68 | 364,89 |
| 10 | 298,55 | {307, 311} | 312,76 | 328,40 |
| 11 | 273,67 | {277, 281, 283} | 285,57 | 298,55 |
| 12 | 252,62 | {257} | 262,72 | 273,67 |
| 13 | 234,57 | {239, 241} | 243,26 | 252,62 |
| 14 | 218,93 | {223} | 226,48 | 234,57 |
| 15 | 205,25 | {211} | 211,87 | 218,93 |
| 16 | 193,18 | {197, 199} | 199,03 | 205,25 |
| 17 | 182,44 | {} | 187,66 | 193,18 |
| 18 | 172,84 | {173} | 177,51 | 182,44 |
| 19 | 164,20 | {167} | 168,41 | 172,84 |
| 20 | 156,38 | {157} | 160,20 | 164,20 |
| 21 | 149,27 | {151} | 152,74 | 156,38 |
| 22 | 142,78 | {} | 145,96 | 149,27 |
| 23 | 136,83 | {137, 139} | 139,74 | 142,78 |
| 24 | 131,36 | {} | 134,04 | 136,83 |
| 25 | 126,31 | {127} | 128,78 | 131,36 |
| 26 | 121,63 | {} | 123,92 | 126,31 |
| 27 | 117,29 | {} | 119,42 | 121,63 |
| 28 | 113,24 | {} | 115,23 | 117,29 |
| 29 | 109,47 | {} | 111,32 | 113,24 |
| 30 | 105,94 | {107} | 107,67 | 109,47 |
| 31 | 102,63 | {103} | 104,25 | 105,94 |
| 32 | 99,52 | {101} | 101,05 | 102,63 |
| 33 | 96,59 | {97} | 98,03 | 99,52 |
| 34 | 93,83 | {} | 95,19 | 96,59 |
| 35 | 91,22 | {} | 92,51 | 93,83 |
| 36 | 88,76 | {89} | 89,97 | 91,22 |
| 37 | 86,42 | {} | 87,57 | 88,76 |
| 38 | 84,21 | {} | 85,30 | 86,42 |
| 39 | 82,10 | {83} | 83,14 | 84,21 |
| 40 | 80,10 | {} | 81,09 | 82,10 |
| 41 | 78,19 | {79} | 79,13 | 80,10 |
| 42 | 76,37 | {} | 77,27 | 78,19 |
| 43 | 74,64 | {} | 75,49 | 76,37 |
| 44 | 72,98 | {73} | 73,80 | 74,64 |
| 45 | 71,39 | {} | 72,18 | 72,98 |
| 46 | 69,87 | {} | 70,62 | 71,39 |
| 47 | 68,42 | {} | 69,14 | 69,87 |
| 48 | 67,02 | {} | 67,71 | 68,42 |
| 49 | 65,68 | {} | 66,34 | 67,02 |
| 50 | 64,39 | {} | 65,03 | 65,68 |
| 51 | 63,15 | {} | 63,77 | 64,39 |
| 52 | 61,96 | {} | 62,55 | 63,15 |
| 53 | 60,81 | {61} | 61,38 | 61,96 |
| 54 | 59,71 | {} | 60,26 | 60,81 |
| 55 | 58,64 | {59} | 59,17 | 59,71 |
| 56 | 57,61 | {} | 58,12 | 58,64 |
| 57 | 56,62 | {} | 57,11 | 57,61 |
| 58 | 55,66 | {} | 56,14 | 56,62 |
| 59 | 54,73 | {} | 55,19 | 55,66 |
| 60 | 53,84 | {} | 54,28 | 54,73 |
| 61 | 52,97 | {53} | 53,40 | 53,84 |
| 62 | 52,13 | {} | 52,54 | 52,97 |
| 63 | 51,31 | {} | 51,72 | 52,13 |
| 64 | 50,52 | {} | 50,91 | 51,31 |
| 65 | 49,76 | {} | 50,14 | 50,52 |
| 66 | 49,01 | {} | 49,38 | 49,76 |
| 67 | 48,29 | {} | 48,65 | 49,01 |
| 68 | 47,59 | {} | 47,94 | 48,29 |
| 69 | 46,91 | {47} | 47,25 | 47,59 |
| 70 | 46,25 | {} | 46,58 | 46,91 |
□
Przypisy
- ↑ Wikipedia, PARI/GP, (Wiki-en)
- ↑ Wikipedia, Pafnuty Czebyszew (1821 - 1893), (Wiki-pl), (Wiki-ru)
- ↑ P. L. Chebyshev, Mémoire sur les nombres premiers, J. de Math. Pures Appl. (1) 17 (1852), 366-390, (LINK)
- ↑ P. Erdos, Beweis eines Satzes von Tschebyschef, Acta Litt. Sci. Szeged 5 (1932), 194-198, (LINK1), (LINK2)
- ↑ P. Dusart, The [math]\displaystyle{ k^{th} }[/math] prime is greater than [math]\displaystyle{ k (\ln k + \ln \ln k - 1) }[/math] for [math]\displaystyle{ k \geqslant 2 }[/math], Math. Of Computation, Vol. 68, Number 225 (January 1999), pp. 411-415.
- ↑ P. Dusart, Sharper bounds for [math]\displaystyle{ \psi }[/math], [math]\displaystyle{ \theta }[/math], [math]\displaystyle{ \pi }[/math], [math]\displaystyle{ p_k }[/math], Rapport de recherche no. 1998-06, Université de Limoges
- ↑ P. Dusart, Estimates of some functions over primes without R.H., (2010), (LINK)
- ↑ P. Dusart, Explicit estimates of some functions over primes, Ramanujan Journal. 45 (1) (January 2018) pp. 225-234.
- ↑ Wikipedia, Twierdzenie o zbieżności ciągu monotonicznego, (LINK)
- ↑ 10,0 10,1 Wikipedia, Characterizations of the exponential function, (Wiki-en)