Szeregi liczbowe: Różnice pomiędzy wersjami
| (Nie pokazano 29 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 201: | Linia 201: | ||
| − | <span id="D11" style="font-size: 110%; font-weight: bold;">Twierdzenie | + | <span id="D11" style="font-size: 110%; font-weight: bold;">Definicja D11</span><br/> |
| + | Powiemy, że szereg <math>\sum_{n = 0}^{\infty} a_n</math> jest '''bezwzględnie zbieżny''', jeżeli szereg <math>\sum_{n = 0}^{\infty} | a_n |</math> jest zbieżny. | ||
| + | |||
| + | Powiemy, że szereg <math>\sum_{n = 0}^{\infty} a_n</math> jest '''warunkowo zbieżny''', jeżeli szereg <math>\sum_{n = 0}^{\infty} a_n</math> jest zbieżny, ale szereg <math>\sum_{n = 0}^{\infty} | a_n |</math> jest rozbieżny. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D12" style="font-size: 110%; font-weight: bold;">Twierdzenie D12</span><br/> | ||
Niech <math>n \in \mathbb{Z}_+</math>. Jeżeli wyrazy ciągu <math>(a_n)</math> można zapisać w jednej z postaci | Niech <math>n \in \mathbb{Z}_+</math>. Jeżeli wyrazy ciągu <math>(a_n)</math> można zapisać w jednej z postaci | ||
| Linia 239: | Linia 246: | ||
| − | <span id=" | + | <span id="D13" style="font-size: 110%; font-weight: bold;">Twierdzenie D13</span><br/> |
Następujące szeregi są zbieżne | Następujące szeregi są zbieżne | ||
| Linia 290: | Linia 297: | ||
| − | <span id=" | + | <span id="D14" style="font-size: 110%; font-weight: bold;">Twierdzenie D14</span><br/> |
Następujące szeregi są zbieżne | Następujące szeregi są zbieżne | ||
| Linia 395: | Linia 402: | ||
| − | Rezultat ten wykorzystamy w pełni w przykładzie [[# | + | Rezultat ten wykorzystamy w pełni w przykładzie [[#D15|D15]], a do pokazania zbieżności szeregu wystarczy nam prawa nierówność. Mamy |
::<math>\sum_{k = 3}^{n} {\small\frac{1}{k \cdot \log^2 \! k}} < \sum_{k = 3}^{n} \left[ {\small\frac{1}{\log (k - 1)}} - {\small\frac{1}{\log (k)}} \right]</math> | ::<math>\sum_{k = 3}^{n} {\small\frac{1}{k \cdot \log^2 \! k}} < \sum_{k = 3}^{n} \left[ {\small\frac{1}{\log (k - 1)}} - {\small\frac{1}{\log (k)}} \right]</math> | ||
| Linia 409: | Linia 416: | ||
| − | <span id=" | + | <span id="D15" style="font-size: 110%; font-weight: bold;">Przykład D15</span><br/> |
Na przykładzie szeregu <math>\sum_{k = 3}^{\infty} {\small\frac{1}{k \cdot \log^2 k}}</math> pokażemy, jak należy obliczać przybliżoną wartość sumy szeregu. | Na przykładzie szeregu <math>\sum_{k = 3}^{\infty} {\small\frac{1}{k \cdot \log^2 k}}</math> pokażemy, jak należy obliczać przybliżoną wartość sumy szeregu. | ||
| Linia 419: | Linia 426: | ||
Wartość pierwszej części możemy policzyć bezpośrednio, a dla drugiej części powinniśmy znaleźć jak najlepsze oszacowanie. | Wartość pierwszej części możemy policzyć bezpośrednio, a dla drugiej części powinniśmy znaleźć jak najlepsze oszacowanie. | ||
| − | Dowodząc twierdzenie [[# | + | Dowodząc twierdzenie [[#D14|D14]], w punkcie 4. pokazaliśmy, że prawdziwy jest ciąg nierówności |
::<math>{\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} < {\small\frac{1}{k \cdot \log^2 k}} < {\small\frac{1}{\log (k - 1)}} - {\small\frac{1}{\log (k)}}</math> | ::<math>{\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} < {\small\frac{1}{k \cdot \log^2 k}} < {\small\frac{1}{\log (k - 1)}} - {\small\frac{1}{\log (k)}}</math> | ||
| Linia 446: | Linia 453: | ||
Poniżej przedstawiamy wartości oszacowania sumy szeregu znalezione przy pomocy programu PARI/GP dla kolejnych wartości <math>m</math>. Wystarczy proste polecenie | Poniżej przedstawiamy wartości oszacowania sumy szeregu znalezione przy pomocy programu PARI/GP dla kolejnych wartości <math>m</math>. Wystarczy proste polecenie | ||
| − | for(n=1, 8, s = sum( k = 3, 10^n, 1/k/(log(k))^2 ); print("n= ", n, " a= ", s+1/log(10^n+1), " b= ", s+1/log(10^n) )) | + | <span style="font-size: 90%; color:black;">'''for'''(n = 1, 8, s = '''sum'''( k = 3, 10^n, 1/k/('''log'''(k))^2 ); '''print'''( "n= ", n, " a= ", s + 1/'''log'''(10^n+1), " b= ", s + 1/'''log'''(10^n) ))</span> |
::{| class="wikitable plainlinks" style="font-size: 100%; text-align: center; margin-right: auto;" | ::{| class="wikitable plainlinks" style="font-size: 100%; text-align: center; margin-right: auto;" | ||
| Linia 483: | Linia 490: | ||
== Szeregi nieskończone i całka oznaczona == | == Szeregi nieskończone i całka oznaczona == | ||
| − | <span id=" | + | <span id="D16" style="font-size: 110%; font-weight: bold;">Twierdzenie D16</span><br/> |
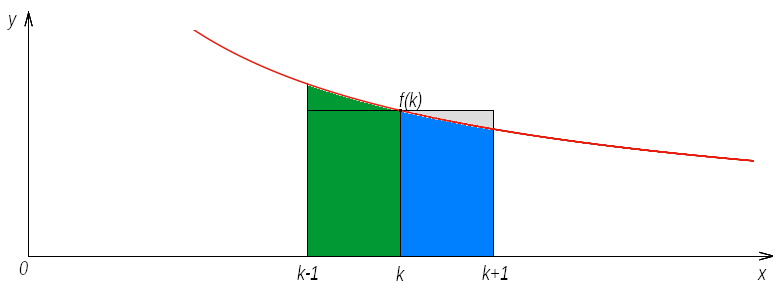
Jeżeli funkcja <math>f(x)</math> jest ciągła, dodatnia i malejąca w przedziale <math>[m, n + 1]</math>, to prawdziwy jest następujący ciąg nierówności | Jeżeli funkcja <math>f(x)</math> jest ciągła, dodatnia i malejąca w przedziale <math>[m, n + 1]</math>, to prawdziwy jest następujący ciąg nierówności | ||
| Linia 518: | Linia 525: | ||
| − | <span id=" | + | <span id="D17" style="font-size: 110%; font-weight: bold;">Przykład D17</span><br/> |
Rozważmy szereg <math>\sum_{k = 1}^{\infty} {\small\frac{1}{k}}</math>. | Rozważmy szereg <math>\sum_{k = 1}^{\infty} {\small\frac{1}{k}}</math>. | ||
| Linia 542: | Linia 549: | ||
| − | <span id=" | + | <span id="D18" style="font-size: 110%; font-weight: bold;">Twierdzenie D18 (kryterium całkowe zbieżności szeregów)</span><br/> |
Załóżmy, że funkcja <math>f(x)</math> jest ciągła, dodatnia i malejąca w przedziale <math>[m, + \infty)</math>. Szereg <math>\sum_{k = m}^{\infty} f(k)</math> jest zbieżny lub rozbieżny w zależności od tego, czy funkcja pierwotna <math>F(x) = \int f (x) d x</math> ma dla <math>x \rightarrow \infty</math> granicę skończoną, czy nie. | Załóżmy, że funkcja <math>f(x)</math> jest ciągła, dodatnia i malejąca w przedziale <math>[m, + \infty)</math>. Szereg <math>\sum_{k = m}^{\infty} f(k)</math> jest zbieżny lub rozbieżny w zależności od tego, czy funkcja pierwotna <math>F(x) = \int f (x) d x</math> ma dla <math>x \rightarrow \infty</math> granicę skończoną, czy nie. | ||
| Linia 555: | Linia 562: | ||
| − | Po tych uwagach dotyczących założeń możemy przejść do właściwego dowodu. Korzystając ze wzoru udowodnionego w twierdzeniu [[# | + | Po tych uwagach dotyczących założeń możemy przejść do właściwego dowodu. Korzystając ze wzoru udowodnionego w twierdzeniu [[#D16|D16]] i przechodząc z <math>n</math> do nieskończoności, dostajemy |
::<math>0 \leqslant \int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f (m) + \int_{m}^{\infty} f(x) d x</math> | ::<math>0 \leqslant \int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f (m) + \int_{m}^{\infty} f(x) d x</math> | ||
| Linia 570: | Linia 577: | ||
| − | <span id=" | + | <span id="D19" style="font-size: 110%; font-weight: bold;">Przykład D19</span><br/> |
Przykłady zebraliśmy w tabeli. Przy obliczaniu całek nieoznaczonych Czytelnik może skorzystać ze strony [https://www.wolframalpha.com/input?i=integral+1%2Fsqrt%28x%29 WolframAlpha]. | Przykłady zebraliśmy w tabeli. Przy obliczaniu całek nieoznaczonych Czytelnik może skorzystać ze strony [https://www.wolframalpha.com/input?i=integral+1%2Fsqrt%28x%29 WolframAlpha]. | ||
| Linia 603: | Linia 610: | ||
| − | <span id=" | + | <span id="D20" style="font-size: 110%; font-weight: bold;">Twierdzenie D20</span><br/> |
Jeżeli funkcja <math>f(x)</math> jest ciągła, dodatnia i malejąca w przedziale <math>[m, \infty)</math> oraz | Jeżeli funkcja <math>f(x)</math> jest ciągła, dodatnia i malejąca w przedziale <math>[m, \infty)</math> oraz | ||
| Linia 615: | Linia 622: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Korzystając ze wzoru udowodnionego w twierdzeniu [[# | + | Korzystając ze wzoru udowodnionego w twierdzeniu [[#D16|D16]] i przechodząc z <math>n</math> do nieskończoności, dostajemy |
::<math>\int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f(m) + \int_{m}^{\infty} f(x) d x</math> | ::<math>\int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f(m) + \int_{m}^{\infty} f(x) d x</math> | ||
| Linia 633: | Linia 640: | ||
| − | <span id=" | + | <span id="D21" style="font-size: 110%; font-weight: bold;">Przykład D21</span><br/> |
| − | Twierdzenie [[# | + | Twierdzenie [[#D20|D20]] umożliwia określenie, z jaką dokładnością została wyznaczona suma szeregu. Wyznaczmy sumę szeregu <math>\sum_{k = 1}^{\infty} {\small\frac{1}{(k + 1) \sqrt{k}}}</math>. Mamy |
::<math>S(m) = \sum_{k = 1}^{m} {\small\frac{1}{(k + 1) \sqrt{k}}}</math> | ::<math>S(m) = \sum_{k = 1}^{m} {\small\frac{1}{(k + 1) \sqrt{k}}}</math> | ||
| Linia 676: | Linia 683: | ||
W programie PARI/GP wystarczy napisać: | W programie PARI/GP wystarczy napisać: | ||
| − | f(k) = 1.0/(k+1)/sqrt(k) | + | <span style="font-size: 90%; color:black;">f(k) = 1.0 / (k+1) / '''sqrt'''(k)</span> |
| − | S(m) = sum( k = 1, m, f(k) ) | + | <span style="font-size: 90%; color:black;">S(m) = '''sum'''( k = 1, m, f(k) )</span> |
| − | R(m) = Pi - 2*atan( sqrt(m) ) | + | <span style="font-size: 90%; color:black;">R(m) = '''Pi''' - 2*'''atan'''( '''sqrt'''(m) )</span> |
| − | for(j=1, 9, m=10^j; suma=S(m); reszta=R(m); print( "j= ", j, " a= ", suma + reszta - f(m), " b= ", suma + reszta )) | + | <span style="font-size: 90%; color:black;">'''for'''(j = 1, 9, m = 10^j; suma = S(m); reszta = R(m); '''print'''( "j= ", j, " a= ", suma + reszta - f(m), " b= ", suma + reszta ))</span> |
| − | Prostym wnioskiem z twierdzenia [[# | + | Prostym wnioskiem z twierdzenia [[#D16|D16]] jest następujące<br/> |
| − | <span id=" | + | <span id="D22" style="font-size: 110%; font-weight: bold;">Twierdzenie D22</span><br/> |
Niech <math>f(x)</math> będzie funkcją ciągłą, dodatnią i malejącą w przedziale <math>[m, + \infty)</math>. Jeżeli przy wyliczaniu sumy szeregu nieskończonego <math>\sum_{k = a}^{\infty} f (k)</math> (gdzie <math>a < m</math>) zastąpimy sumę <math>\sum_{k = m}^{\infty} f (k)</math> całką <math>\int_{m}^{\infty} f (x) d x</math>, to błąd wyznaczenia sumy szeregu nie przekroczy <math>f(m)</math>. | Niech <math>f(x)</math> będzie funkcją ciągłą, dodatnią i malejącą w przedziale <math>[m, + \infty)</math>. Jeżeli przy wyliczaniu sumy szeregu nieskończonego <math>\sum_{k = a}^{\infty} f (k)</math> (gdzie <math>a < m</math>) zastąpimy sumę <math>\sum_{k = m}^{\infty} f (k)</math> całką <math>\int_{m}^{\infty} f (x) d x</math>, to błąd wyznaczenia sumy szeregu nie przekroczy <math>f(m)</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Korzystając ze wzoru z twierdzenia [[# | + | Korzystając ze wzoru z twierdzenia [[#D16|D16]] i przechodząc z <math>n</math> do nieskończoności, otrzymujemy |
::<math>\int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f(m) + \int_{m}^{\infty} f(x) d x</math> | ::<math>\int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f(m) + \int_{m}^{\infty} f(x) d x</math> | ||
| Linia 711: | Linia 718: | ||
| − | <span id=" | + | <span id="D23" style="font-size: 110%; font-weight: bold;">Twierdzenie D23</span><br/> |
Niech <math>f(x)</math> będzie funkcją ciągłą, dodatnią i malejącą w przedziale <math>[m, + \infty)</math>. Jeżeli szereg <math>\sum_{k = m}^{\infty} f (k)</math> jest zbieżny, to dla każdego <math>n \geqslant m</math> prawdziwe jest następujące oszacowanie sumy częściowej szeregu <math>S(n)</math> | Niech <math>f(x)</math> będzie funkcją ciągłą, dodatnią i malejącą w przedziale <math>[m, + \infty)</math>. Jeżeli szereg <math>\sum_{k = m}^{\infty} f (k)</math> jest zbieżny, to dla każdego <math>n \geqslant m</math> prawdziwe jest następujące oszacowanie sumy częściowej szeregu <math>S(n)</math> | ||
| Linia 723: | Linia 730: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia [[# | + | Z twierdzenia [[#D16|D16]] mamy |
::<math>S(n) = \sum_{k = m}^{n} f (k) \leqslant f (m) + \int_{m}^{n} f (x) d x</math> | ::<math>S(n) = \sum_{k = m}^{n} f (k) \leqslant f (m) + \int_{m}^{n} f (x) d x</math> | ||
| Linia 743: | Linia 750: | ||
| − | <span id=" | + | <span id="D24" style="font-size: 110%; font-weight: bold;">Uwaga D24</span><br/> |
Niech <math>f(x)</math> będzie funkcją ciągłą, dodatnią i malejącą w przedziale <math>[m, \infty)</math>. Rozważmy szereg <math>\sum_{k = m}^{\infty} f (k)</math>. Zauważmy, że: | Niech <math>f(x)</math> będzie funkcją ciągłą, dodatnią i malejącą w przedziale <math>[m, \infty)</math>. Rozważmy szereg <math>\sum_{k = m}^{\infty} f (k)</math>. Zauważmy, że: | ||
* korzystając z całkowego kryterium zbieżności, możemy łatwo zbadać, czy szereg <math>\sum_{k = m}^{\infty} f (k)</math> jest zbieżny | * korzystając z całkowego kryterium zbieżności, możemy łatwo zbadać, czy szereg <math>\sum_{k = m}^{\infty} f (k)</math> jest zbieżny | ||
| − | * jeżeli szereg jest zbieżny, to ponownie wykorzystując całki (twierdzenie [[# | + | * jeżeli szereg jest zbieżny, to ponownie wykorzystując całki (twierdzenie [[#D23|D23]]), możemy znaleźć oszacowanie sumy częściowej szeregu <math>S(n) = \sum_{k = m}^{n} f(k)</math> |
Jednak dysponując już oszacowaniem sumy częściowej szeregu <math>S(n) = \sum_{k = m}^{n} f(k)</math>, możemy udowodnić jego poprawność przy pomocy indukcji matematycznej, a stąd łatwo pokazać zbieżność szeregu <math>\sum_{k = m}^{\infty} f(k)</math>. Zauważmy, że wybór większego <math>B</math> ułatwia dowód indukcyjny. Stałą <math>C</math> najlepiej zaokrąglić w górę do wygodnej dla nas wartości. | Jednak dysponując już oszacowaniem sumy częściowej szeregu <math>S(n) = \sum_{k = m}^{n} f(k)</math>, możemy udowodnić jego poprawność przy pomocy indukcji matematycznej, a stąd łatwo pokazać zbieżność szeregu <math>\sum_{k = m}^{\infty} f(k)</math>. Zauważmy, że wybór większego <math>B</math> ułatwia dowód indukcyjny. Stałą <math>C</math> najlepiej zaokrąglić w górę do wygodnej dla nas wartości. | ||
| Linia 754: | Linia 761: | ||
Czasami potrzebujemy takiego uproszczenia problemu, aby udowodnić zbieżność szeregów bez odwoływania się do całek. Zauważmy, że Czytelnik nawet nie musi znać całek – wystarczy, że policzy je przy pomocy programów, które potrafią to robić (np. WolframAlpha). Kiedy już znajdziemy oszacowanie sumy częściowej szeregu, nie musimy wyjaśniać, w jaki sposób je znaleźliśmy – wystarczy udowodnić, że jest ono poprawne, a do tego wystarczy indukcja matematyczna. | Czasami potrzebujemy takiego uproszczenia problemu, aby udowodnić zbieżność szeregów bez odwoływania się do całek. Zauważmy, że Czytelnik nawet nie musi znać całek – wystarczy, że policzy je przy pomocy programów, które potrafią to robić (np. WolframAlpha). Kiedy już znajdziemy oszacowanie sumy częściowej szeregu, nie musimy wyjaśniać, w jaki sposób je znaleźliśmy – wystarczy udowodnić, że jest ono poprawne, a do tego wystarczy indukcja matematyczna. | ||
| − | Zamieszczonej niżej zadania pokazują, jak wykorzystać w tym celu twierdzenie [[# | + | Zamieszczonej niżej zadania pokazują, jak wykorzystać w tym celu twierdzenie [[#D23|D23]]. |
| − | <span id=" | + | <span id="D25" style="font-size: 110%; font-weight: bold;">Zadanie D25</span><br/> |
| − | Korzystając z twierdzenia [[# | + | Korzystając z twierdzenia [[#D23|D23]], znaleźć oszacowania sumy częściowej szeregów |
::<math>\sum_{k = 1}^{\infty} {\small\frac{1}{k^2}} \qquad</math> oraz <math>\qquad \sum_{k = 2}^{\infty} {\small\frac{1}{k (\log k)^2}}</math> | ::<math>\sum_{k = 1}^{\infty} {\small\frac{1}{k^2}} \qquad</math> oraz <math>\qquad \sum_{k = 2}^{\infty} {\small\frac{1}{k (\log k)^2}}</math> | ||
| Linia 789: | Linia 796: | ||
| − | <span id=" | + | <span id="D26" style="font-size: 110%; font-weight: bold;">Zadanie D26</span><br/> |
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania <math>\sum_{k = 1}^{n} {\small\frac{1}{k^2}} \leqslant 2 - {\small\frac{1}{n}}</math> i udowodnić, że szereg <math>\sum_{k = 1}^{\infty} {\small\frac{1}{k^2}}</math> jest zbieżny. | Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania <math>\sum_{k = 1}^{n} {\small\frac{1}{k^2}} \leqslant 2 - {\small\frac{1}{n}}</math> i udowodnić, że szereg <math>\sum_{k = 1}^{\infty} {\small\frac{1}{k^2}}</math> jest zbieżny. | ||
| Linia 815: | Linia 822: | ||
| − | <span id=" | + | <span id="D27" style="font-size: 110%; font-weight: bold;">Zadanie D27</span><br/> |
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania <math>\sum_{k = 2}^{n} {\small\frac{1}{k (\log k)^2}} < 2.5 - {\small\frac{1}{\log n}}</math> i udowodnić, że szereg <math>\sum_{k = 2}^{\infty} {\small\frac{1}{k (\log k)^2}}</math> jest zbieżny. | Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania <math>\sum_{k = 2}^{n} {\small\frac{1}{k (\log k)^2}} < 2.5 - {\small\frac{1}{\log n}}</math> i udowodnić, że szereg <math>\sum_{k = 2}^{\infty} {\small\frac{1}{k (\log k)^2}}</math> jest zbieżny. | ||
| Linia 855: | Linia 862: | ||
== Szeregi nieskończone i liczby pierwsze == | == Szeregi nieskończone i liczby pierwsze == | ||
| − | <span id=" | + | <span id="D28" style="font-size: 110%; font-weight: bold;">Twierdzenie D28</span><br/> |
Następujące szeregi są zbieżne | Następujące szeregi są zbieżne | ||
| Linia 896: | Linia 903: | ||
| − | <span id=" | + | <span id="D29" style="font-size: 110%; font-weight: bold;">Twierdzenie D29</span><br/> |
Następujące szeregi są zbieżne | Następujące szeregi są zbieżne | ||
| Linia 940: | Linia 947: | ||
::<math>0 < {\small\frac{1}{p_k \log p_k}} < {\small\frac{1}{a \cdot k \cdot (\log k)^2}}</math> | ::<math>0 < {\small\frac{1}{p_k \log p_k}} < {\small\frac{1}{a \cdot k \cdot (\log k)^2}}</math> | ||
| − | Zatem na mocy kryterium porównawczego ze zbieżności szeregu <math>\sum_{k = 2}^{\infty} {\small\frac{1}{k \cdot (\log k)^2}}</math> (zobacz twierdzenie [[# | + | Zatem na mocy kryterium porównawczego ze zbieżności szeregu <math>\sum_{k = 2}^{\infty} {\small\frac{1}{k \cdot (\log k)^2}}</math> (zobacz twierdzenie [[#D14|D14]] p. 4 lub przykład [[#D19|D19]] p. 5) wynika zbieżność szeregu <math>\sum_{k = 2}^{\infty} {\small\frac{1}{p_k \log p_k}}</math> |
'''Punkt 2.'''<br/> | '''Punkt 2.'''<br/> | ||
| Linia 961: | Linia 968: | ||
| − | <span id=" | + | <span id="D30" style="font-size: 110%; font-weight: bold;">Twierdzenie D30</span><br/> |
Szereg <math>\sum_{p \geqslant 2} {\small\frac{\log p}{p}}</math> jest rozbieżny. | Szereg <math>\sum_{p \geqslant 2} {\small\frac{\log p}{p}}</math> jest rozbieżny. | ||
| Linia 979: | Linia 986: | ||
| − | <span id=" | + | <span id="D31" style="font-size: 110%; font-weight: bold;">Uwaga D31</span><br/> |
Moglibyśmy oszacować rozbieżność szeregu <math>\sum_{p \geqslant 2} {\small\frac{\log p}{p}}</math> podobnie, jak to uczyniliśmy w przypadku twierdzenia [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B37|B37]], ale tym razem zastosujemy inną metodę, która pozwoli nam uzyskać bardziej precyzyjny rezultat. | Moglibyśmy oszacować rozbieżność szeregu <math>\sum_{p \geqslant 2} {\small\frac{\log p}{p}}</math> podobnie, jak to uczyniliśmy w przypadku twierdzenia [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B37|B37]], ale tym razem zastosujemy inną metodę, która pozwoli nam uzyskać bardziej precyzyjny rezultat. | ||
| − | <span id=" | + | <span id="D32" style="font-size: 110%; font-weight: bold;">Twierdzenie D32</span><br/> |
Niech <math>n \in \mathbb{Z}_+</math>. Prawdziwe są następujące nierówności | Niech <math>n \in \mathbb{Z}_+</math>. Prawdziwe są następujące nierówności | ||
| Linia 1036: | Linia 1043: | ||
| − | <span id=" | + | <span id="D33" style="font-size: 110%; font-weight: bold;">Twierdzenie D33</span><br/> |
Niech <math>n \in \mathbb{Z}_+</math>. Dla wykładnika, z jakim liczba pierwsza <math>p</math> występuje w rozwinięciu liczby <math>n!</math> na czynniki pierwsze, prawdziwe są oszacowania | Niech <math>n \in \mathbb{Z}_+</math>. Dla wykładnika, z jakim liczba pierwsza <math>p</math> występuje w rozwinięciu liczby <math>n!</math> na czynniki pierwsze, prawdziwe są oszacowania | ||
| Linia 1085: | Linia 1092: | ||
| − | <span id=" | + | <span id="D34" style="font-size: 110%; font-weight: bold;">Twierdzenie D34</span><br/> |
Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | ||
| Linia 1095: | Linia 1102: | ||
::<math>n! < \prod_{p \leqslant n} p^{n / (p - 1)}</math> | ::<math>n! < \prod_{p \leqslant n} p^{n / (p - 1)}</math> | ||
| − | Ponieważ dla <math>n \geqslant 1</math> jest <math>n! > n^n e^{- n}</math> (zobacz punkt 1. twierdzenia [[# | + | Ponieważ dla <math>n \geqslant 1</math> jest <math>n! > n^n e^{- n}</math> (zobacz punkt 1. twierdzenia [[#D32|D32]]), to |
::<math>n^n e^{- n} < \prod_{p \leqslant n} p^{n / (p - 1)}</math> | ::<math>n^n e^{- n} < \prod_{p \leqslant n} p^{n / (p - 1)}</math> | ||
| Linia 1109: | Linia 1116: | ||
| − | <span id=" | + | <span id="D35" style="font-size: 110%; font-weight: bold;">Twierdzenie D35 (pierwsze twierdzenie Mertensa</span><ref name="Mertens1"/><ref name="Mertens2"/><span style="font-size: 110%; font-weight: bold;">, 1874)</span><br/> |
Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | ||
| Linia 1120: | Linia 1127: | ||
| − | to z twierdzenia [[# | + | to z twierdzenia [[#D34|D34]] dostajemy |
::<math>\sum_{p \leqslant n} {\small\frac{\log p}{p}} + \sum_{p \leqslant n} {\small\frac{\log p}{p (p - 1)}} - \log n > - 1</math> | ::<math>\sum_{p \leqslant n} {\small\frac{\log p}{p}} + \sum_{p \leqslant n} {\small\frac{\log p}{p (p - 1)}} - \log n > - 1</math> | ||
| Linia 1134: | Linia 1141: | ||
::::::<math>\quad \;\: > - 1.755367</math> | ::::::<math>\quad \;\: > - 1.755367</math> | ||
| − | Gdzie wykorzystaliśmy zbieżność szeregu <math>\sum_{p \geqslant 2} {\small\frac{\log p}{p (p - 1)}}</math> (twierdzenie [[# | + | Gdzie wykorzystaliśmy zbieżność szeregu <math>\sum_{p \geqslant 2} {\small\frac{\log p}{p (p - 1)}}</math> (twierdzenie [[#D29|D29]] p. 3).<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 1140: | Linia 1147: | ||
| − | <span id=" | + | <span id="D36" style="font-size: 110%; font-weight: bold;">Twierdzenie D36 (pierwsze twierdzenie Mertensa</span><ref name="Mertens1"/><ref name="Mertens2"/><span style="font-size: 110%; font-weight: bold;">, 1874)</span><br/> |
Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | ||
| Linia 1185: | Linia 1192: | ||
| − | <span id=" | + | <span id="D37" style="font-size: 110%; font-weight: bold;">Twierdzenie D37</span><br/> |
Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | Dla dowolnego <math>n \in \mathbb{Z}_+</math> prawdziwe jest następujące oszacowanie | ||
| Linia 1195: | Linia 1202: | ||
::<math>{\small\frac{1}{p}} = {\small\frac{1}{p - 1}} - {\small\frac{1}{p (p - 1)}}</math> | ::<math>{\small\frac{1}{p}} = {\small\frac{1}{p - 1}} - {\small\frac{1}{p (p - 1)}}</math> | ||
| − | to z twierdzenia [[# | + | to z twierdzenia [[#D36|D36]] dostajemy |
::<math>\sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \sum_{p \leqslant n} {\small\frac{\log p}{p (p - 1)}} - \log n < \log 4 - 1</math> | ::<math>\sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \sum_{p \leqslant n} {\small\frac{\log p}{p (p - 1)}} - \log n < \log 4 - 1</math> | ||
| Linia 1213: | Linia 1220: | ||
| − | <span id=" | + | <span id="D38" style="font-size: 110%; font-weight: bold;">Uwaga D38</span><br/> |
{| class="wikitable" | {| class="wikitable" | ||
| | | | ||
| Linia 1230: | Linia 1237: | ||
| − | <span id=" | + | <span id="D39" style="font-size: 110%; font-weight: bold;">Uwaga D39</span><br/> |
{| class="wikitable" | {| class="wikitable" | ||
| | | | ||
| Linia 1247: | Linia 1254: | ||
| − | <span id=" | + | <span id="D40" style="font-size: 110%; font-weight: bold;">Uwaga D40</span><br/> |
Dla <math>n \leqslant 10^{10}</math> wartości wyrażeń | Dla <math>n \leqslant 10^{10}</math> wartości wyrażeń | ||
| Linia 1258: | Linia 1265: | ||
| − | <span id=" | + | <span id="D41" style="font-size: 110%; font-weight: bold;">Twierdzenie D41</span><br/> |
Prawdziwy jest następujący związek | Prawdziwy jest następujący związek | ||
| Linia 1299: | Linia 1306: | ||
| − | <span id=" | + | <span id="D42" style="font-size: 110%; font-weight: bold;">Twierdzenie D42</span><br/> |
Dla <math>n \geqslant 318</math> prawdziwe jest oszacowanie | Dla <math>n \geqslant 318</math> prawdziwe jest oszacowanie | ||
| Linia 1336: | Linia 1343: | ||
| − | Z twierdzenia [[# | + | Z twierdzenia [[#D41|D41]] wiemy, że |
::<math>\sum_{p \geqslant 2} {\small\frac{\log p}{p (p - 1)}} - E = - \gamma</math> | ::<math>\sum_{p \geqslant 2} {\small\frac{\log p}{p (p - 1)}} - E = - \gamma</math> | ||
| Linia 1377: | Linia 1384: | ||
| − | Korzystając kolejno z twierdzeń [[# | + | Korzystając kolejno z twierdzeń [[#D16|D16]] i [[Ciągi liczbowe#C18|C18]], dostajemy |
::<math>\sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \log n > - \gamma - {\small\frac{0.3}{\log n}} - \int_{n}^{\infty} {\small\frac{\log x}{(x - 1)^2}} d x</math> | ::<math>\sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \log n > - \gamma - {\small\frac{0.3}{\log n}} - \int_{n}^{\infty} {\small\frac{\log x}{(x - 1)^2}} d x</math> | ||
| Linia 1400: | Linia 1407: | ||
| − | <span id=" | + | <span id="D43" style="font-size: 110%; font-weight: bold;">Zadanie D43</span><br/> |
Niech <math>r = 1 - \log (2) \approx 0.30685281944</math>. Pokazać, że z nierówności prawdziwej dla <math>x \geqslant 32</math> | Niech <math>r = 1 - \log (2) \approx 0.30685281944</math>. Pokazać, że z nierówności prawdziwej dla <math>x \geqslant 32</math> | ||
| Linia 1408: | Linia 1415: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| − | Z twierdzenia [[# | + | Z twierdzenia [[#D42|D42]] wiemy, że dla <math>x \geqslant 318</math> jest |
::<math>\sum_{p \leqslant x} {\small\frac{\log p}{p - 1}} - \log x < - \gamma + {\small\frac{1}{2\log x}} \leqslant - \gamma + {\small\frac{1}{2 \log (318)}} = - 0.490441 \ldots < - 0.306852 \ldots = - r</math> | ::<math>\sum_{p \leqslant x} {\small\frac{\log p}{p - 1}} - \log x < - \gamma + {\small\frac{1}{2\log x}} \leqslant - \gamma + {\small\frac{1}{2 \log (318)}} = - 0.490441 \ldots < - 0.306852 \ldots = - r</math> | ||
| Linia 1419: | Linia 1426: | ||
| − | Niech <math>a \in \mathbb{Z}</math> i <math>a \geqslant 32</math>. Korzystając z twierdzenia [[# | + | Niech <math>a \in \mathbb{Z}</math> i <math>a \geqslant 32</math>. Korzystając z twierdzenia [[#D33|D33]], łatwo znajdujemy oszacowanie |
::<math>a! = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_n}_n</math> | ::<math>a! = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_n}_n</math> | ||
| Linia 1449: | Linia 1456: | ||
| − | Jednocześnie z twierdzenia [[# | + | Jednocześnie z twierdzenia [[#D32|D32]] wiemy, że prawdziwa jest nierówność <math>b! > b^b e^{- b}</math>, zatem |
::<math>b^b e^{- b} < b! < {\normalsize\frac{(a \cdot e^{- r})^b}{a \cdot e^{-r}}}</math> | ::<math>b^b e^{- b} < b! < {\normalsize\frac{(a \cdot e^{- r})^b}{a \cdot e^{-r}}}</math> | ||
| Linia 1496: | Linia 1503: | ||
| − | <span id=" | + | <span id="D44" style="font-size: 110%; font-weight: bold;">Definicja D44</span><br/> |
Powiemy, że liczby pierwsze <math>p, q</math> są liczbami bliźniaczymi (tworzą parę liczb bliźniaczych), jeżeli <math>\left | p - q \right | = 2</math> | Powiemy, że liczby pierwsze <math>p, q</math> są liczbami bliźniaczymi (tworzą parę liczb bliźniaczych), jeżeli <math>\left | p - q \right | = 2</math> | ||
| − | <span id=" | + | <span id="D45" style="font-size: 110%; font-weight: bold;">Twierdzenie D45* (Viggo Brun, 1919)</span><br/> |
Suma odwrotności par liczb pierwszych <math>p</math> i <math>p + 2</math>, takich że liczba <math>p + 2</math> jest również pierwsza, jest skończona | Suma odwrotności par liczb pierwszych <math>p</math> i <math>p + 2</math>, takich że liczba <math>p + 2</math> jest również pierwsza, jest skończona | ||
| Linia 1511: | Linia 1518: | ||
| − | <span id=" | + | <span id="D46" style="font-size: 110%; font-weight: bold;">Zadanie D46</span><br/> |
Pokazać, że istnieje nieskończenie wiele liczb pierwszych nietworzących par liczb bliźniaczych. | Pokazać, że istnieje nieskończenie wiele liczb pierwszych nietworzących par liczb bliźniaczych. | ||
| Linia 1537: | Linia 1544: | ||
| − | == Dowód z Księgi. Rozbieżność sumy <math>\textstyle \sum | + | == Dowód z Księgi. Rozbieżność sumy <math>\textstyle \sum {\small\frac{1}{p}}</math> == |
| − | <span id=" | + | <span id="D47" style="font-size: 110%; font-weight: bold;">Twierdzenie D47</span><br/> |
Suma odwrotności liczb pierwszych jest rozbieżna. | Suma odwrotności liczb pierwszych jest rozbieżna. | ||
| Linia 1596: | Linia 1603: | ||
== Sumowanie przez części == | == Sumowanie przez części == | ||
| − | <span id=" | + | <span id="D48" style="font-size: 110%; font-weight: bold;">Uwaga D48</span><br/> |
Omawianie metody sumowania przez części<ref name="sumowanie1"/> rozpoczniemy od udowodnienia prostego twierdzenia, które dobrze ilustruje tę metodę i ułatwi zrozumienie uogólnienia. Potrzebna nam będzie następująca funkcja | Omawianie metody sumowania przez części<ref name="sumowanie1"/> rozpoczniemy od udowodnienia prostego twierdzenia, które dobrze ilustruje tę metodę i ułatwi zrozumienie uogólnienia. Potrzebna nam będzie następująca funkcja | ||
| Linia 1618: | Linia 1625: | ||
| − | <span id=" | + | <span id="D49" style="font-size: 110%; font-weight: bold;">Twierdzenie D49</span><br/> |
Niech <math>n \in \mathbb{Z}_+</math> i niech <math>\sum_{p \leqslant n} {\small\frac{1}{p}}</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>n</math>. Prawdziwy jest następujący związek | Niech <math>n \in \mathbb{Z}_+</math> i niech <math>\sum_{p \leqslant n} {\small\frac{1}{p}}</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>n</math>. Prawdziwy jest następujący związek | ||
| Linia 1652: | Linia 1659: | ||
| − | <span id=" | + | <span id="D50" style="font-size: 110%; font-weight: bold;">Zadanie D50</span><br/> |
Pokazać, że dla <math>n \geqslant 1</math> prawdziwe jest oszacowanie <math>\sum_{p \leqslant n} {\small\frac{1}{p}} > {\small\frac{2}{3}} \cdot \log \log (n + 1)</math>. | Pokazać, że dla <math>n \geqslant 1</math> prawdziwe jest oszacowanie <math>\sum_{p \leqslant n} {\small\frac{1}{p}} > {\small\frac{2}{3}} \cdot \log \log (n + 1)</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| − | Z twierdzenia [[# | + | Z twierdzenia [[#D49|D49]] wiemy, że dla <math>n \geqslant 1</math> prawdziwy jest wzór |
::<math>\sum_{p \leqslant n} {\small\frac{1}{p}} = {\small\frac{\pi (n)}{n}} + \sum_{k = 2}^{n - 1} {\small\frac{\pi (k)}{k (k + 1)}}</math> | ::<math>\sum_{p \leqslant n} {\small\frac{1}{p}} = {\small\frac{\pi (n)}{n}} + \sum_{k = 2}^{n - 1} {\small\frac{\pi (k)}{k (k + 1)}}</math> | ||
| Linia 1674: | Linia 1681: | ||
:::<math>\quad \; = {\small\frac{1}{3}} + {\small\frac{2}{3}} \cdot \sum_{j = 5}^n {\small\frac{1}{j \log j}}</math> | :::<math>\quad \; = {\small\frac{1}{3}} + {\small\frac{2}{3}} \cdot \sum_{j = 5}^n {\small\frac{1}{j \log j}}</math> | ||
| − | Korzystając z twierdzenia [[# | + | Korzystając z twierdzenia [[#D16|D16]], otrzymujemy |
::<math>\sum_{p \leqslant n} {\small\frac{1}{p}} \geqslant {\small\frac{1}{3}} + {\small\frac{2}{3}} \cdot \int_{5}^{n + 1} {\small\frac{d x}{x \log x}}</math> | ::<math>\sum_{p \leqslant n} {\small\frac{1}{p}} \geqslant {\small\frac{1}{3}} + {\small\frac{2}{3}} \cdot \int_{5}^{n + 1} {\small\frac{d x}{x \log x}}</math> | ||
| Linia 1690: | Linia 1697: | ||
| − | <span id=" | + | <span id="D51" style="font-size: 110%; font-weight: bold;">Zadanie D51</span><br/> |
Pokazać, że oszacowanie <math>\pi (n) < n^{1 - \varepsilon}</math>, gdzie <math>\varepsilon \in (0, 1)</math>, nie może być prawdziwe dla prawie wszystkich liczb naturalnych. | Pokazać, że oszacowanie <math>\pi (n) < n^{1 - \varepsilon}</math>, gdzie <math>\varepsilon \in (0, 1)</math>, nie może być prawdziwe dla prawie wszystkich liczb naturalnych. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| − | Przypuśćmy, że dla prawie wszystkich liczb naturalnych jest <math>\pi (n) < n^{1 - \varepsilon}</math>. Zatem istnieje taka liczba <math>n_0</math>, że dla wszystkich <math>n \geqslant n_0</math> jest <math>\pi (n) < n^{1 - \varepsilon}</math>. Korzystając ze wzoru (zobacz [[# | + | Przypuśćmy, że dla prawie wszystkich liczb naturalnych jest <math>\pi (n) < n^{1 - \varepsilon}</math>. Zatem istnieje taka liczba <math>n_0</math>, że dla wszystkich <math>n \geqslant n_0</math> jest <math>\pi (n) < n^{1 - \varepsilon}</math>. Korzystając ze wzoru (zobacz [[#D49|D49]]) |
::<math>\sum_{p \leqslant n} {\small\frac{1}{p}} = {\small\frac{\pi (n)}{n}} + \sum_{k = 2}^{n - 1} {\small\frac{\pi (k)}{k (k + 1)}}</math> | ::<math>\sum_{p \leqslant n} {\small\frac{1}{p}} = {\small\frac{\pi (n)}{n}} + \sum_{k = 2}^{n - 1} {\small\frac{\pi (k)}{k (k + 1)}}</math> | ||
| Linia 1716: | Linia 1723: | ||
:::<math>\quad \; = C_3</math> | :::<math>\quad \; = C_3</math> | ||
| − | Co jest niemożliwe, bo lewa strona rośnie nieograniczenie wraz ze wzrostem <math>n</math> (zobacz [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B37|B37]], [[# | + | Co jest niemożliwe, bo lewa strona rośnie nieograniczenie wraz ze wzrostem <math>n</math> (zobacz [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B37|B37]], [[#D47|D47]], [[#D50|D50]]).<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 1722: | Linia 1729: | ||
| − | <span id=" | + | <span id="D52" style="font-size: 110%; font-weight: bold;">Twierdzenie D52 (sumowanie przez części)</span><br/> |
Niech <math>a_j</math>, <math>b_j</math> będą ciągami określonymi przynajmniej dla <math>s \leqslant j \leqslant n</math>. Prawdziwy jest następujący wzór | Niech <math>a_j</math>, <math>b_j</math> będą ciągami określonymi przynajmniej dla <math>s \leqslant j \leqslant n</math>. Prawdziwy jest następujący wzór | ||
| Linia 1769: | Linia 1776: | ||
| − | <span id=" | + | <span id="D53" style="font-size: 110%; font-weight: bold;">Zadanie D53</span><br/> |
| − | Pokazać, że <math>\sum_{k = 1}^{n} k | + | Niech <math>r \neq 1</math>. Pokazać, że <math>\sum_{k = 1}^{n} k r^k = \frac{n r^{n + 2} - (n + 1) r^{n + 1} + r}{(r - 1)^2}</math>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| − | + | Korzystając ze wzoru na sumowanie przez części, połóżmy <math>s = 0</math>, <math>a_k = k \;</math> i <math>\; b_k = r^k</math>. Zauważmy, że sumowanie od <math>k = 0</math> nic nie zmienia, a nieco upraszcza przekształcenia, bo możemy korzystać wprost ze wzoru na sumę częściową szeregu geometrycznego. Otrzymujemy | |
| − | ::<math>\sum_{k = 0}^{n} k | + | ::<math>\sum_{k = 0}^{n} k r^k = n \cdot B (n) - \sum_{k = 0}^{n - 1} (k + 1 - k) B (k)</math> |
gdzie | gdzie | ||
| − | ::<math>B(k) = \sum_{j = 0}^{k} | + | ::<math>B(k) = \sum_{j = 0}^{k} r^j = {\small\frac{r^{k + 1} - 1}{r - 1}}</math> |
Zatem | Zatem | ||
| − | ::<math>\sum_{k = 0}^{n} k | + | ::<math>\sum_{k = 0}^{n} k r^k = n \cdot {\small\frac{r^{n + 1} - 1}{r - 1}} - \sum_{k = 0}^{n - 1} {\small\frac{r^{k + 1} - 1}{r - 1}}</math> |
| + | |||
| + | ::::<math>\;\, = {\small\frac{1}{r - 1}} \left( n r^{n + 1} - n - \sum_{k = 0}^{n - 1} r^{k + 1} + \sum_{k = 0}^{n - 1} 1 \right)</math> | ||
| − | ::::<math>\;\ | + | ::::<math>\;\, = {\small\frac{1}{r - 1}} \left( n r^{n + 1} - n - r \sum_{k = 0}^{n - 1} r^k + n \right)</math> |
| − | ::::<math>\;\ | + | ::::<math>\;\, = {\small\frac{1}{r - 1}} \left( n r^{n + 1} - r \cdot {\small\frac{r^n - 1}{r - 1}} \right)</math> |
<div style="margin-top: 1em; margin-bottom: 1em;"> | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| − | ::::<math>\;\ | + | ::::<math>\;\, = {\small\frac{1}{(r - 1)^2}} (n r^{n + 2} - n r^{n + 1} - r^{n + 1} + r)</math> |
</div> | </div> | ||
| − | <div style="margin-top: | + | <div style="margin-top: 1em; margin-bottom: 1em;"> |
| − | ::::<math>\;\ | + | ::::<math>\;\, = \frac{n r^{n + 2} - (n + 1) r^{n + 1} + r}{(r - 1)^2}</math> |
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
| Linia 1807: | Linia 1812: | ||
| − | <span id=" | + | <span id="D54" style="font-size: 110%; font-weight: bold;">Twierdzenie D54 (kryterium Dirichleta)</span><br/> |
Niech <math>(a_k) \;</math> i <math>\; (b_k)</math> będą ciągami liczb rzeczywistych. Jeżeli | Niech <math>(a_k) \;</math> i <math>\; (b_k)</math> będą ciągami liczb rzeczywistych. Jeżeli | ||
| Linia 1837: | Linia 1842: | ||
::::::::<math>\;\;\; = M (a_1 - a_n)</math> | ::::::::<math>\;\;\; = M (a_1 - a_n)</math> | ||
| − | (zobacz [[# | + | (zobacz [[#D12|D12]]). Jeżeli ciąg <math>(a_k)</math> jest rosnący, to |
::<math>\sum_{k = 1}^{n - 1} | (a_k - a_{k + 1}) B (k) | \leqslant \sum_{k = 1}^{n - 1} M (a_{k + 1} - a_k)</math> | ::<math>\sum_{k = 1}^{n - 1} | (a_k - a_{k + 1}) B (k) | \leqslant \sum_{k = 1}^{n - 1} M (a_{k + 1} - a_k)</math> | ||
| Linia 1845: | Linia 1850: | ||
::::::::<math>\;\;\; = - M (a_1 - a_n)</math> | ::::::::<math>\;\;\; = - M (a_1 - a_n)</math> | ||
| − | Łącząc uzyskane rezultaty możemy napisać | + | Łącząc uzyskane rezultaty oraz uwzględniając fakt, że ciąg <math>(a_n)</math> jest ograniczony, bo jest zbieżny (zobacz [[Ciągi liczbowe#C9|C9]]), możemy napisać |
| − | ::<math>\sum_{k = 1}^{n - 1} | (a_k - a_{k + 1}) B (k) | \leqslant M | a_1 - a_n | \leqslant M (| a_1 | + | a_n |) \leqslant 2 M | + | ::<math>\sum_{k = 1}^{n - 1} | (a_k - a_{k + 1}) B (k) | \leqslant M | a_1 - a_n | \leqslant M (| a_1 | + | a_n |) \leqslant 2 M U</math> |
| − | + | Ponieważ sumy częściowe szeregu <math>\sum_{k = 1}^{\infty} | (a_k - a_{k + 1}) B (k) |</math> tworzą ciąg rosnący i ograniczony od góry, to szereg ten jest zbieżny (zobacz [[Ciągi liczbowe#C10|C10]]). Wynika stąd zbieżność szeregu <math>\sum_{k = 1}^{\infty} (a_k - a_{k + 1}) B (k)</math> (zobacz [[#D10|D10]]). Zatem szereg <math>\sum_{k = 1}^{\infty} a_k b_k</math> musi być zbieżny. Co należało pokazać.<br/> | |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 1855: | Linia 1860: | ||
| − | <span id=" | + | <span id="D55" style="font-size: 110%; font-weight: bold;">Zadanie D55</span><br/> |
Udowodnić następujące wzory | Udowodnić następujące wzory | ||
| Linia 1923: | Linia 1928: | ||
| − | <span id=" | + | <span id="D56" style="font-size: 110%; font-weight: bold;">Zadanie D56</span><br/> |
Pokazać, że szereg <math>\sum_{k = 1}^{\infty} {\small\frac{\sin k}{k}}</math> jest zbieżny. | Pokazać, że szereg <math>\sum_{k = 1}^{\infty} {\small\frac{\sin k}{k}}</math> jest zbieżny. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| − | W zadaniu [[# | + | W zadaniu [[#D55|D55]] p.1 pokazaliśmy, że prawdziwy jest wzór |
::<math>\sum_{j = 1}^{k} \sin j = | ::<math>\sum_{j = 1}^{k} \sin j = | ||
| Linia 1951: | Linia 1956: | ||
| − | <span id=" | + | <span id="D57" style="font-size: 110%; font-weight: bold;">Zadanie D57</span><br/> |
Pokazać, że szereg <math>\sum_{k = 2}^{\infty} {\small\frac{\sin k}{\log k}}</math> jest zbieżny, a suma tego szeregu jest w przybliżeniu równa <math>0.6839137864 \ldots</math> | Pokazać, że szereg <math>\sum_{k = 2}^{\infty} {\small\frac{\sin k}{\log k}}</math> jest zbieżny, a suma tego szeregu jest w przybliżeniu równa <math>0.6839137864 \ldots</math> | ||
| Linia 1959: | Linia 1964: | ||
::<math>S_{10^6} = 0.609189 \qquad S_{10^7} = 0.748477 \qquad S_{10^8} = 0.727256 \qquad S_{10^9} = 0.660078</math> | ::<math>S_{10^6} = 0.609189 \qquad S_{10^7} = 0.748477 \qquad S_{10^8} = 0.727256 \qquad S_{10^9} = 0.660078</math> | ||
| − | Okazuje się, że tutaj też będzie pomocne sumowanie przez części. We wzorze na sumowanie przez części połóżmy <math>s = 2</math>, <math>a_k = {\small\frac{1}{\log k}}</math> i <math>b_k = \sin k</math>. Korzystając ze wzoru pokazanego w zadaniu [[# | + | Okazuje się, że tutaj też będzie pomocne sumowanie przez części. We wzorze na sumowanie przez części połóżmy <math>s = 2</math>, <math>a_k = {\small\frac{1}{\log k}}</math> i <math>b_k = \sin k</math>. Korzystając ze wzoru pokazanego w zadaniu [[#D55|D55]] p.1, otrzymujemy |
::<math>B(k) = \sum_{j = 2}^{k} \sin j = {\small\frac{\cos \left( \tfrac{1}{2} \right) - \cos \left( k + \tfrac{1}{2} \right)}{2 \sin \left( \tfrac{1}{2} \right)}} - \sin (1) = C_1 + C_2 \cos \left( k + \tfrac{1}{2} \right)</math> | ::<math>B(k) = \sum_{j = 2}^{k} \sin j = {\small\frac{\cos \left( \tfrac{1}{2} \right) - \cos \left( k + \tfrac{1}{2} \right)}{2 \sin \left( \tfrac{1}{2} \right)}} - \sin (1) = C_1 + C_2 \cos \left( k + \tfrac{1}{2} \right)</math> | ||
| Linia 1981: | Linia 1986: | ||
::<math>\sum_{k = 2}^{\infty} {\small\frac{\sin k}{\log k}} = {\small\frac{C_1}{\log 2}} + C_2 \sum_{k = 2}^{\infty} \left( {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \right) \cos \left( k + \tfrac{1}{2} \right)</math> | ::<math>\sum_{k = 2}^{\infty} {\small\frac{\sin k}{\log k}} = {\small\frac{C_1}{\log 2}} + C_2 \sum_{k = 2}^{\infty} \left( {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \right) \cos \left( k + \tfrac{1}{2} \right)</math> | ||
| − | Zauważmy, że szereg po prawej stronie jest zbieżny nawet bez uzbieżniającego czynnika <math>\cos \left( k + \tfrac{1}{2} \right)</math>, bo bez tego czynnika mielibyśmy szereg teleskopowy (zobacz [[# | + | Zauważmy, że szereg po prawej stronie jest zbieżny nawet bez uzbieżniającego czynnika <math>\cos \left( k + \tfrac{1}{2} \right)</math>, bo bez tego czynnika mielibyśmy szereg teleskopowy (zobacz [[#D12|D12]]). Pozwala to oczekiwać, że sumy częściowe szeregu po prawej stronie będą znacznie szybciej zbiegały do sumy szeregu. Rzeczywiście, tym razem dla sum |
::<math>S_n = {\small\frac{C_1}{\log 2}} + C_2 \sum_{k = 2}^{n} \left( {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \right) \cos \left( k + \tfrac{1}{2} \right)</math> | ::<math>S_n = {\small\frac{C_1}{\log 2}} + C_2 \sum_{k = 2}^{n} \left( {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \right) \cos \left( k + \tfrac{1}{2} \right)</math> | ||
| Linia 1998: | Linia 2003: | ||
::<math>\sum_{k = 2}^{\infty} \left( {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \right) \cos \left( k + \tfrac{1}{2} \right)</math> | ::<math>\sum_{k = 2}^{\infty} \left( {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \right) \cos \left( k + \tfrac{1}{2} \right)</math> | ||
| − | We wzorze na sumowanie przez części połóżmy <math>s = 2</math>, <math>a_k = {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \;</math> i <math>\; b_k = \cos \left( k + \tfrac{1}{2} \right)</math>. Korzystając ze wzoru pokazanego w zadaniu [[# | + | We wzorze na sumowanie przez części połóżmy <math>s = 2</math>, <math>a_k = {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \;</math> i <math>\; b_k = \cos \left( k + \tfrac{1}{2} \right)</math>. Korzystając ze wzoru pokazanego w zadaniu [[#D55|D55]] p.2, otrzymujemy |
::<math>B(k) = \sum_{j = 2}^{k} b_j = \sum_{j = 2}^{k} \cos \left( j + \tfrac{1}{2} \right) = {\small\frac{\sin (k + 1) - \sin (1)}{2 \sin \left( \tfrac{1}{2} \right)}} - \cos \left( \tfrac{3}{2} \right) = C_3 + C_4 \cdot \sin (k + 1)</math> | ::<math>B(k) = \sum_{j = 2}^{k} b_j = \sum_{j = 2}^{k} \cos \left( j + \tfrac{1}{2} \right) = {\small\frac{\sin (k + 1) - \sin (1)}{2 \sin \left( \tfrac{1}{2} \right)}} - \cos \left( \tfrac{3}{2} \right) = C_3 + C_4 \cdot \sin (k + 1)</math> | ||
| Linia 2073: | Linia 2078: | ||
::<math>{\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} > {\small\frac{1}{\log (k + 1)}} - {\small\frac{1}{\log (k + 2)}}</math> | ::<math>{\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} > {\small\frac{1}{\log (k + 1)}} - {\small\frac{1}{\log (k + 2)}}</math> | ||
| − | Ciągi <math>(a_k)_{k = 1}^n</math> liczb rzeczywistych takie, że <math>2 a_k \leqslant a_{k - 1} + a_{k + 1}</math> dla <math>k = 2, \ldots, n - 1</math> nazywamy ciągami wypukłymi<ref name="convexseq1"/>. Wprost z definicji funkcji wypukłej wynika, że jeżeli <math>f(x)</math> jest funkcją wypukłą i <math>a_k = f (k)</math>, to ciąg <math>(a_k)</math> jest ciągiem wypukłym.<br/> | + | Ciągi <math>(a_k)_{k = 1}^n</math> liczb rzeczywistych takie, że <math>2 a_k \leqslant a_{k - 1} + a_{k + 1}</math> dla <math>k = 2, \ldots, n - 1</math> nazywamy ciągami wypukłymi<ref name="convexseq1"/>. Wprost z definicji funkcji wypukłej wynika, że jeżeli <math>f(x)</math> jest funkcją wypukłą i <math>a_k = f (k)</math>, to ciąg <math>(a_k)</math> jest ciągiem wypukłym.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 2079: | Linia 2084: | ||
| − | <span id=" | + | <span id="D58" style="font-size: 110%; font-weight: bold;">Zadanie D58</span><br/> |
Niech <math>\theta (n) = \sum_{p \leqslant n} \log p</math>. Pokazać, że | Niech <math>\theta (n) = \sum_{p \leqslant n} \log p</math>. Pokazać, że | ||
| Linia 2105: | Linia 2110: | ||
| − | <span id=" | + | <span id="D59" style="font-size: 110%; font-weight: bold;">Twierdzenie D59</span><br/> |
Niech <math>\theta (n) = \sum_{p \leqslant n} \log p</math>. Jeżeli prawdziwe jest oszacowanie <math>{\small\frac{A \cdot n}{\log n}} < \pi (n) < {\small\frac{B \cdot n}{\log n}}</math>, gdzie <math>A, B \in \mathbb{R}_+</math>, to istnieje granica | Niech <math>\theta (n) = \sum_{p \leqslant n} \log p</math>. Jeżeli prawdziwe jest oszacowanie <math>{\small\frac{A \cdot n}{\log n}} < \pi (n) < {\small\frac{B \cdot n}{\log n}}</math>, gdzie <math>A, B \in \mathbb{R}_+</math>, to istnieje granica | ||
| Linia 2123: | Linia 2128: | ||
::<math>\theta (n) = \log n \cdot \pi (n) - \sum_{k = 2}^{n - 1} \log \left( 1 + {\small\frac{1}{k}} \right) \pi (k)</math> | ::<math>\theta (n) = \log n \cdot \pi (n) - \sum_{k = 2}^{n - 1} \log \left( 1 + {\small\frac{1}{k}} \right) \pi (k)</math> | ||
| − | (zobacz [[# | + | (zobacz [[#D58|D58]]) otrzymujemy |
::<math>{\small\frac{\theta (n)}{\log n \cdot \pi (n)}} = 1 - {\small\frac{1}{\log n \cdot \pi (n)}} \cdot \sum_{k = 2}^{n - 1} \log \left( 1 + {\small\frac{1}{k}} \right) \pi (k)</math> | ::<math>{\small\frac{\theta (n)}{\log n \cdot \pi (n)}} = 1 - {\small\frac{1}{\log n \cdot \pi (n)}} \cdot \sum_{k = 2}^{n - 1} \log \left( 1 + {\small\frac{1}{k}} \right) \pi (k)</math> | ||
| Linia 2173: | Linia 2178: | ||
| − | <span id=" | + | <span id="D60" style="font-size: 110%; font-weight: bold;">Uwaga D60</span><br/> |
Funkcja <math>\theta (n)</math> jest ściśle związana z dobrze nam znaną funkcją <math>P (n)</math>. Ponieważ <math>P(n) = \prod_{p \leqslant n} p</math>, to | Funkcja <math>\theta (n)</math> jest ściśle związana z dobrze nam znaną funkcją <math>P (n)</math>. Ponieważ <math>P(n) = \prod_{p \leqslant n} p</math>, to | ||
::<math>\log P (n) = \log \left( \prod_{p \leqslant n} p \right) = \sum_{p \leqslant n} \log p = \theta (n)</math>. | ::<math>\log P (n) = \log \left( \prod_{p \leqslant n} p \right) = \sum_{p \leqslant n} \log p = \theta (n)</math>. | ||
| − | Z twierdzenia [[# | + | Z twierdzenia [[#D59|D59]] wynika, że jeżeli istnieje granica <math>{\small\frac{\theta (n)}{n}}</math>, to będzie istniała granica dla <math>{\small\frac{\pi (n) \cdot \log n}{n}}</math>. Jeżeli istnieje granica <math>{\small\frac{\pi (n) \cdot \log n}{n}}</math>, to będzie istniała granica dla <math>{\small\frac{\theta (n)}{n}}</math> (zobacz [[Ciągi liczbowe#C12|C12]] p.3). |
Wiemy, że dla funkcji <math>\theta (n)</math>, gdzie <math>n \geqslant 2</math>, prawdziwe jest oszacowanie<ref name="Dusart18"/> | Wiemy, że dla funkcji <math>\theta (n)</math>, gdzie <math>n \geqslant 2</math>, prawdziwe jest oszacowanie<ref name="Dusart18"/> | ||
| Linia 2186: | Linia 2191: | ||
| − | <span id=" | + | <span id="D61" style="font-size: 110%; font-weight: bold;">Zadanie D61</span><br/> |
Niech <math>\theta (n) = \sum_{p \leqslant n} \log p</math>. Pokazać, że | Niech <math>\theta (n) = \sum_{p \leqslant n} \log p</math>. Pokazać, że | ||
| Linia 2192: | Linia 2197: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| − | Kładąc we wzorze na sumowanie przez części (zobacz [[# | + | Kładąc we wzorze na sumowanie przez części (zobacz [[#D52|D52]]) <math>s = 2</math>, <math>a_k = {\small\frac{1}{\log k}}</math> i <math>b_k = D (k) \cdot \log k</math>. Otrzymujemy |
::<math>\sum_{k = 2}^{n} D (k) = {\small\frac{1}{\log n}} \cdot B (n) - \sum_{k = 2}^{n - 1} \left( {\small\frac{1}{\log (k + 1)}} - {\small\frac{1}{\log k}} \right) B (k)</math> | ::<math>\sum_{k = 2}^{n} D (k) = {\small\frac{1}{\log n}} \cdot B (n) - \sum_{k = 2}^{n - 1} \left( {\small\frac{1}{\log (k + 1)}} - {\small\frac{1}{\log k}} \right) B (k)</math> | ||
| Linia 2218: | Linia 2223: | ||
| + | == Iloczyn Cauchy'ego szeregów == | ||
| + | <span id="D62" style="font-size: 110%; font-weight: bold;">Twierdzenie D62 (kryterium d'Alemberta)</span><br/> | ||
| + | Niech <math>(a_n)</math> będzie ciągiem liczb rzeczywistych i istnieje granica | ||
| + | ::<math>g = \lim_{n \rightarrow \infty} \left| {\small\frac{a_{n + 1}}{a_n}} \right|</math> | ||
| + | Jeżeli | ||
| + | :* <math>g < 1</math>, to szereg <math>\sum_{n = 0}^{\infty} a_n</math> jest bezwzględnie zbieżny | ||
| + | :* <math>g > 1</math>, to szereg <math>\sum_{n = 0}^{\infty} a_n</math> jest rozbieżny | ||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Rozważmy najpierw przypadek, gdy <math>g = \lim_{n \rightarrow \infty} \left| {\small\frac{a_{n + 1}}{a_n}} \right| < 1</math>. Niech <math>r</math> będzie dowolną liczbą rzeczywistą taką, że <math>g < r < 1</math> i przyjmijmy <math>\varepsilon = r - g</math>. Z definicji granicy ciągu wiemy, że prawie wszystkie wyrazy ciągu <math>\left( \left| {\small\frac{a_{n + 1}}{a_n}} \right| \right)</math> spełniają warunek | ||
| + | |||
| + | ::<math>- \varepsilon < \left| {\small\frac{a_{n + 1}}{a_n}} \right| - g < \varepsilon</math> | ||
| + | |||
| + | Możemy przyjąć, że są to wszystkie wyrazy, poczynając od <math>N</math>. Z prawej nierówności otrzymujemy, że dla <math>n \geqslant N</math> jest | ||
| + | |||
| + | ::<math>\left| {\small\frac{a_{n + 1}}{a_n}} \right| < r</math> | ||
| + | ::<math>| a_{n + 1} | < r | a_n |</math> | ||
| + | ::<math>| a_{n + k} | < r^k | a_n |</math> | ||
| + | Ostatnią nierówność można łatwo udowodnić metodą indukcji matematycznej względem <math>k</math>. Korzystając ze wzoru na sumę szeregu geometrycznego<ref name="GeometricSeries1"/>, otrzymujemy | ||
| + | ::<math>\sum_{k = N + 1}^{\infty} | a_k | = \sum_{k = 1}^{\infty} | a_{N + k} | < \sum_{k = 1}^{\infty} r^k | a_n | = r | a_n | \sum_{k = 1}^{\infty} r^{k - 1} = | a_n | \cdot {\small\frac{r}{1 - r}}</math> | ||
| + | Zatem szereg <math>\sum_{i = 0}^{\infty} a_i</math> jest bezwzględnie zbieżny. | ||
| − | == | + | W przypadku, gdy <math>g = \lim_{n \rightarrow \infty} \left| {\small\frac{a_{n + 1}}{a_n}} \right| > 1</math> wybieramy liczbę <math>r</math> tak, aby spełniała warunek <math>1 < r < g</math> i przyjmujemy <math>\varepsilon = g - r</math>. Z definicji granicy ciągu wiemy, że prawie wszystkie wyrazy ciągu <math>\left( \left| {\small\frac{a_{n + 1}}{a_n}} \right| \right)</math> spełniają warunek |
| − | < | ||
| − | < | + | ::<math>- \varepsilon < \left| {\small\frac{a_{n + 1}}{a_n}} \right| - g < \varepsilon</math> |
| − | < | + | Przyjmując, że są to wszystkie wyrazy, poczynając od <math>N</math>, z lewej nierówności otrzymujemy dla <math>n \geqslant N</math> |
| − | < | + | ::<math>\left| {\small\frac{a_{n + 1}}{a_n}} \right| > r > 1</math> |
| − | < | + | Czyli <math>| a_{n + 1} | > | a_n |</math>, zatem dla wszystkich <math>k > N</math> jest <math>| a_k | > | a_N | > 0</math> i nie może być spełniony podstawowy warunek zbieżności szeregu (zobacz [[#D4|D4]]). Zatem szereg jest rozbieżny. Co kończy dowód.<br/> |
| + | □ | ||
| + | {{\Spoiler}} | ||
| − | |||
| − | |||
| − | < | + | <span id="C62" style="font-size: 110%; font-weight: bold;">Uwaga C62</span><br/> |
| + | W przypadku, gdy <math>\lim_{n \rightarrow \infty} \left| {\small\frac{a_{n + 1}}{a_n}} \right| = 1</math> kryterium d'Alemberta nie rozstrzyga o zbieżności lub rozbieżności szeregu <math>\sum_{n = 0}^{\infty} a_n</math>. Czytelnikowi zostawiamy zastosowanie tego kryterium do szeregów | ||
| − | < | + | ::<math>\sum_{n = 1}^{\infty} 1 \qquad \qquad \sum_{n = 1}^{\infty} {\small\frac{1}{n}} \qquad \qquad \sum_{n = 1}^{\infty} {\small\frac{(- 1)^{n + 1}}{n}} \qquad \qquad \sum_{n = 1}^{\infty} {\small\frac{1}{n^2}}</math> |
| − | |||
| − | |||
| − | < | + | <span id="D64" style="font-size: 110%; font-weight: bold;">Przykład D64</span><br/> |
| + | Niech <math>x \in \mathbb{R}</math>. Zbadamy zbieżność szeregu | ||
| − | < | + | ::<math>e^x = \sum_{n = 0}^{\infty} {\small\frac{x^n}{n!}} = 1 + x + {\small\frac{x^2}{2}} + {\small\frac{x^3}{6}} + {\small\frac{x^4}{24}} + {\small\frac{x^5}{120}} + \ldots</math> |
| − | + | Ponieważ | |
| − | < | + | ::<math>\lim_{n \rightarrow \infty} \left| {\small\frac{x^{n + 1}}{(n + 1) !}} \cdot {\small\frac{n!}{x^n}} \right| = \lim_{n \rightarrow \infty} {\small\frac{| x |}{n + 1}} = 0</math> |
| − | + | to z kryterium d'Alemberta wynika, że szereg jest bezwzględnie zbieżny. | |
| − | |||
| − | <ref name="convexseq1">ciąg wypukły (ang. ''convex sequence'')</ref> | + | |
| + | <span id="D65" style="font-size: 110%; font-weight: bold;">Zadanie D65</span><br/> | ||
| + | Pokazać, że szereg <math>\sum_{n = 0}^{\infty} {\small\frac{n^n}{n!}}</math> jest rozbieżny. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Łatwo znajdujemy, że | ||
| + | |||
| + | ::<math>\left| {\small\frac{a_{n + 1}}{a_n}} \right| = {\small\frac{(n + 1)^{n + 1}}{(n + 1) !}} \cdot {\small\frac{n!}{n^n}} = {\small\frac{(n + 1) (n + 1)^n}{(n + 1) n!}} \cdot {\small\frac{n!}{n^n}} = \left( 1 + {\small\frac{1}{n}} \right)^n \xrightarrow{\; n \rightarrow \infty \;} e > 1</math> | ||
| + | |||
| + | Z kryterium d'Alemberta wynika, że szereg jest rozbieżny.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D66" style="font-size: 110%; font-weight: bold;">Uwaga D66</span><br/> | ||
| + | W twierdzeniu [[Twierdzenie Czebyszewa o funkcji π(n)#A37|A37]], korzystając z następującej definicji funkcji <math>e^x</math> | ||
| + | |||
| + | ::<math>e^x = \sum_{k = 0}^{\infty} {\small\frac{x^k}{k!}} = 1 + x + {\small\frac{x^2}{2}} + {\small\frac{x^3}{6}} + {\small\frac{x^4}{24}} + {\small\frac{x^5}{120}} + \ldots</math> | ||
| + | |||
| + | pominęliśmy dowód własności <math>e^x e^{- x} = 1</math>. Spróbujemy teraz pokazać, że <math>e^x e^y = e^{x + y}</math>. | ||
| + | |||
| + | ::<math>e^x e^y = \left( \sum_{i = 0}^{\infty} {\small\frac{x^i}{i!}} \right) \left( \sum_{j = 0}^{\infty} {\small\frac{y^j}{j!}} \right) = \sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} {\small\frac{x^i y^j}{i! \cdot j!}}</math> | ||
| + | |||
| + | Oznaczmy <math>a_i = {\small\frac{x^i}{i!}}</math> oraz <math>b_j = {\small\frac{y^j}{j!}}</math> i przyjrzyjmy się sumowaniu po <math>i, j</math>. W podwójnej sumie po prawej stronie <math>\sum^{\infty}_{i = 0} \sum_{j = 0}^{\infty} a_i b_j</math> sumujemy po kolejnych liniach poziomych tak, jak to zostało pokazane na rysunku | ||
| + | |||
| + | ::{| class="wikitable" style="text-align:center;" | ||
| + | |- style="background-color: LightGray" | ||
| + | | <math> a_6 b_0 </math> || <math> </math> || <math> </math> || <math> </math> || <math> </math> || <math> </math> || <math> \cdots </math> | ||
| + | |- style="background-color: Violet" | ||
| + | | <math> a_5 b_0 </math> || <math> a_5 b_1 </math> || <math> a_5 b_2 </math> || <math> a_5 b_3 </math> || <math> a_5 b_4 </math> || <math> a_5 b_5 </math> || <math> \cdots </math> | ||
| + | |- style="background-color: Cyan" | ||
| + | | <math> a_4 b_0 </math> || <math> a_4 b_1 </math> || <math> a_4 b_2 </math> || <math> a_4 b_3 </math> || <math> a_4 b_4 </math> || <math> a_4 b_5 </math> || <math> \cdots </math> | ||
| + | |- style="background-color: Green" | ||
| + | | <math> a_3 b_0 </math> || <math> a_3 b_1 </math> || <math> a_3 b_2 </math> || <math> a_3 b_3 </math> || <math> a_3 b_4 </math> || <math> a_3 b_5 </math> || <math> \cdots </math> | ||
| + | |- style="background-color: Yellow" | ||
| + | | <math> a_2 b_0 </math> || <math> a_2 b_1 </math> || <math> a_2 b_2 </math> || <math> a_2 b_3 </math> || <math> a_2 b_4 </math> || <math> a_2 b_5 </math> || <math> \cdots </math> | ||
| + | |- style="background-color: Orange" | ||
| + | | <math> a_1 b_0 </math> || <math> a_1 b_1 </math> || <math> a_1 b_2 </math> || <math> a_1 b_3 </math> || <math> a_1 b_4 </math> || <math> a_1 b_5 </math> || <math> \cdots </math> | ||
| + | |- style="background-color: Red" | ||
| + | | <math> a_0 b_0 </math> || <math> a_0 b_1 </math> || <math> a_0 b_2 </math> || <math> a_0 b_3 </math> || <math> a_0 b_4 </math> || <math> a_0 b_5 </math> || <math> \; \cdots \; </math> | ||
| + | |} | ||
| + | |||
| + | Zastępując sumowanie po kolejnych liniach poziomych sumowaniem po kolejnych przekątnych, otrzymamy taki rysunek | ||
| + | |||
| + | ::{| class="wikitable" style="text-align:center;" | ||
| + | |- | ||
| + | | bgcolor="LightGray" | <math> a_6 b_0 </math> || <math> </math> || || || || || | ||
| + | |- | ||
| + | | bgcolor="Violet" | <math> a_5 b_0 </math> || bgcolor="LightGray" | <math> </math> || || || || || | ||
| + | |- | ||
| + | | bgcolor="Cyan" | <math> a_4 b_0 </math> || bgcolor="Violet" | <math> a_4 b_1 </math> || bgcolor="LightGray" | <math> </math> || || || || | ||
| + | |- | ||
| + | | bgcolor="Green" | <math> a_3 b_0 </math> || bgcolor="Cyan" | <math> a_3 b_1 </math> || bgcolor="Violet" | <math> a_3 b_2 </math> || bgcolor="LightGray" | <math> </math> || || || | ||
| + | |- | ||
| + | | bgcolor="Yellow" | <math> a_2 b_0 </math> || bgcolor="Green" | <math> a_2 b_1 </math> || bgcolor="Cyan" | <math> a_2 b_2 </math> || bgcolor="Violet" | <math> a_2 b_3 </math> || bgcolor="LightGray" | <math> </math> || || | ||
| + | |- | ||
| + | | bgcolor="Orange" | <math> a_1 b_0 </math> || bgcolor="Yellow" | <math> a_1 b_1 </math> || bgcolor="Green" | <math> a_1 b_2 </math> || bgcolor="Cyan" | <math> a_1 b_3 </math> || bgcolor="Violet" | <math> a_1 b_4 </math> || bgcolor="LightGray" | <math> </math> || | ||
| + | |- | ||
| + | | bgcolor="Red" | <math> a_0 b_0 </math> || bgcolor="Orange" | <math> a_0 b_1 </math> || bgcolor="Yellow" | <math> a_0 b_2 </math> || bgcolor="Green" | <math> a_0 b_3 </math> || bgcolor="Cyan" | <math> a_0 b_4 </math> || bgcolor="Violet" | <math> a_0 b_5 </math> || bgcolor="LightGray" | <math> a_0 b_6 </math> | ||
| + | |} | ||
| + | |||
| + | Co odpowiada sumie <math>\sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {a_k} b_{n - k}</math>, gdzie <math>n</math> numeruje kolejne przekątne. Taka zmiana sposobu sumowania powoduje następujące przekształcenie wzoru | ||
| + | |||
| + | ::<math>e^x e^y = \sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} {\small\frac{x^i y^j}{i! \cdot j!}} = \sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {\small\frac{x^k y^{n - k}}{k! \cdot (n - k) !}}</math> | ||
| + | |||
| + | Ponieważ | ||
| + | |||
| + | ::<math>{\small\frac{1}{k! \cdot (n - k) !}} = {\small\frac{1}{n!}} \cdot {\small\frac{n!}{k! \cdot (n - k)!}} = {\small\frac{1}{n!}} \cdot {\small\binom{n}{k}}</math> | ||
| + | |||
| + | to otrzymujemy | ||
| + | |||
| + | ::<math>e^x e^y = \sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} {\small\frac{x^i y^j}{i! \cdot j!}} | ||
| + | = \sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {\small\frac{x^k y^{n - k}}{k! \cdot (n - k) !}} | ||
| + | = \sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {\small\frac{1}{n!}} \cdot {\small\binom{n}{k}} \cdot x^k y^{n - k} | ||
| + | = \sum_{n = 0}^{\infty} {\small\frac{1}{n!}} \sum_{k = 0}^{n} {\small\binom{n}{k}} \cdot x^k y^{n - k} | ||
| + | = \sum_{n = 0}^{\infty} {\small\frac{1}{n!}} (x + y)^n = e^{x + y}</math> | ||
| + | |||
| + | Pokazaliśmy tym samym, że z definicji | ||
| + | |||
| + | ::<math>e^x = \sum_{k = 0}^{\infty} {\small\frac{x^k}{k!}} = 1 + x + {\small\frac{x^2}{2}} + {\small\frac{x^3}{6}} + {\small\frac{x^4}{24}} + {\small\frac{x^5}{120}} + \ldots</math> | ||
| + | |||
| + | wynika podstawowa własność funkcji wykładniczej <math>e^x e^y = e^{x + y}</math>. | ||
| + | |||
| + | Mamy świadomość, że dokonana przez nas zmiana sposobu sumowania była nieformalna i w związku z tym nie wiemy, czy była poprawna. Zatem musimy precyzyjnie zdefiniować takie sumowanie i zbadać, kiedy jest dopuszczalne. Dopiero wtedy będziemy mogli być pewni, że policzony rezultat jest poprawny. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D67" style="font-size: 110%; font-weight: bold;">Definicja D67</span><br/> | ||
| + | Iloczynem Cauchy'ego szeregów <math>\sum_{i = 0}^{\infty} a_i</math> oraz <math>\sum_{j = 0}^{\infty} b_j</math> nazywamy szereg <math>\sum_{n = 0}^{\infty} c_n</math>, gdzie | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} a_k b_{n - k} = a_0 b_n + a_1 b_{n - 1} + \ldots + a_{n - 1} b_1 + a_n b_0</math> | ||
| + | |||
| + | W przypadku szeregów, których wyrazy są numerowane od liczby <math>1</math>, iloczynem Cauchy'ego szeregów <math>\sum_{i = 1}^{\infty} a_i</math> oraz <math>\sum_{j = 1}^{\infty} b_j</math> nazywamy szereg <math>\sum_{n = 1}^{\infty} c_n</math>, gdzie | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 1}^{n} a_k b_{n - k + 1} = a_1 b_n + a_2 b_{n - 1} + \ldots + a_{n - 1} b_2 + a_n b_1</math> | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D68" style="font-size: 110%; font-weight: bold;">Zadanie D68</span><br/> | ||
| + | Niech <math>c_n = \sum_{k = 0}^{n} a_k b_{n - k}</math>. Pokazać, że | ||
| + | |||
| + | :* jeżeli <math>(a_n) = (1, 0, 0, 0, 0, \ldots)</math>, <math>\; (b_n)</math> jest dowolnym ciągiem, to <math>c_n = b_n</math> | ||
| + | |||
| + | :* jeżeli <math>(a_n) = (1, 1, 1, 1, 1, \ldots)</math>, <math>\; (b_n)</math> jest dowolnym ciągiem, to <math>c_n = \sum_{k = 0}^{n} b_k = B_n</math> | ||
| + | |||
| + | :* jeżeli <math>a_n = b_n = {\small\frac{r^n}{n!}}</math>, to <math>c_n = {\small\frac{(2 r)^n}{n!}}</math> | ||
| + | |||
| + | :* jeżeli <math>(a_n) = (a, r, r^2, r^3, \ldots)</math>, <math>\; (b_n) = (b, r, r^2, r^3, \ldots)</math>, to <math>c_n = | ||
| + | \begin{cases} | ||
| + | \qquad \qquad \qquad \; a b & \text{gdy } \; n = 0 \\ | ||
| + | (a + b + n - 1) r^n & \text{gdy } \; n \geqslant 1 \\ | ||
| + | \end{cases}</math> | ||
| + | |||
| + | :* jeżeli <math>(a_n) = (a, q, q^2, q^3, \ldots)</math>, <math>\; (b_n) = (b, r, r^2, r^3, \ldots)</math>, gdzie <math>q \neq r</math>, to <math>c_n = | ||
| + | \begin{cases} | ||
| + | \qquad \qquad \qquad \qquad \qquad \qquad \, a b & \text{gdy } \; n = 0 \\ | ||
| + | q^n \left( b + {\large\frac{r}{q - r}} \right) + r^n \left( a - {\large\frac{q}{q - r}} \right) & \text{gdy } \; n \geqslant 1 \\ | ||
| + | \end{cases}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | |||
| + | '''Punkt 1.''' | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} a_k b_{n - k} = a_0 b_n = b_n</math> | ||
| + | |||
| + | '''Punkt 2.''' | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} a_k b_{n - k} = \sum_{k = 0}^{n} b_{n - k} = \sum^n_{j = 0} b_j = B_n</math> | ||
| + | |||
| + | '''Punkt 3.''' | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} a_k b_{n - k} = \sum_{k = 0}^{n} {\small\frac{r^k r^{n - k}}{k!(n - k) !}} = {\small\frac{r^n}{n!}} \sum_{k = 0}^{n} {\small\frac{n!}{k! (n - k) !}} = {\small\frac{r^n}{n!}} \sum_{k = 0}^{n} {\small\binom{n}{k}} = {\small\frac{(2 r)^n}{n!}}</math> | ||
| + | |||
| + | '''Punkt 4.''' | ||
| + | |||
| + | Dla <math>n = 0</math> mamy <math>c_0 = a_0 b_0 = a b</math> | ||
| + | |||
| + | Dla <math>n = 1</math> mamy <math>c_1 = a_0 b_1 + a_1 b_0 = a \cdot r + r \cdot b = (a + b) r</math> | ||
| + | |||
| + | Dla <math>n \geqslant 2</math> jest | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} a_k b_{n - k}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = a_0 b_n + a_n b_0 + \sum_{k = 1}^{n - 1} a_k b_{n - k}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = a \cdot r^n + r^n \cdot b + \sum_{k = 1}^{n - 1} r^k r^{n - k}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = (a + b) r^n + \sum_{k = 1}^{n - 1} r^n</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = (a + b + n - 1) r^n</math> | ||
| + | |||
| + | Zbierając, otrzymujemy | ||
| + | |||
| + | ::<math>c_n = | ||
| + | \begin{cases} | ||
| + | \qquad \qquad \qquad \; a b & \text{gdy } \; n = 0 \\ | ||
| + | (a + b + n - 1) r^n & \text{gdy } \; n \geqslant 1 \\ | ||
| + | \end{cases}</math> | ||
| + | |||
| + | '''Punkt 5.''' | ||
| + | |||
| + | Dla <math>n = 0</math> mamy <math>c_0 = a_0 b_0 = a b</math> | ||
| + | |||
| + | Dla <math>n = 1</math> mamy <math>c_1 = a_0 b_1 + a_1 b_0 = a r + b q</math> | ||
| + | |||
| + | Dla <math>n \geqslant 2</math> jest | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} a_k b_{n - k}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = a_0 b_n + a_n b_0 + \sum_{k = 1}^{n - 1} a_k b_{n - k}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = a r^n + b q^n + \sum_{k = 1}^{n - 1} q^k r^{n - k}</math> | ||
| + | |||
| + | Jeżeli <math>r = 0</math>, to <math>\sum_{k = 1}^{n - 1} q^k r^{n - k} = 0</math>. Jeżeli <math>r \neq 0</math>, to | ||
| + | |||
| + | ::<math>\sum_{k = 1}^{n - 1} q^k r^{n - k} = r^n \sum_{k = 1}^{n - 1} \left( {\small\frac{q}{r}} \right)^k = r^n \cdot {\small\frac{\left( {\normalsize\frac{q}{r}} \right)^n - {\normalsize\frac{q}{r}}}{{\normalsize\frac{q}{r}} - 1}} = {\small\frac{r q^n - q r^n}{q - r}}</math> | ||
| + | |||
| + | Zauważmy, że znaleziony wzór obejmuje również przypadek <math>r = 0</math>. Zatem | ||
| + | |||
| + | ::<math>c_n = a r^n + b q^n + {\small\frac{r q^n - q r^n}{q - r}}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = q^n \left( b + {\small\frac{r}{q - r}} \right) + r^n \left( a - {\small\frac{q}{q - r}} \right)</math> | ||
| + | |||
| + | Zbierając, otrzymujemy | ||
| + | |||
| + | ::<math>c_n = | ||
| + | \begin{cases} | ||
| + | \qquad \qquad \qquad \qquad \qquad \qquad \, a b & \text{gdy } \; n = 0 \\ | ||
| + | q^n \left( b + {\large\frac{r}{q - r}} \right) + r^n \left( a - {\large\frac{q}{q - r}} \right) & \text{gdy } \; n \geqslant 1 \\ | ||
| + | \end{cases}</math><br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D69" style="font-size: 110%; font-weight: bold;">Przykład D69</span><br/> | ||
| + | Ostatni punkt zadania [[#D68|D68]] pozwala stworzyć wiele przykładowych szeregów i ich iloczynów Cauchy'ego. Przypomnijmy, że | ||
| + | |||
| + | ::<math>(a_n) = (a, q, q^2, q^3, \ldots)</math>, <math>\quad (b_n) = (b, r, r^2, r^3, \ldots)</math>, gdzie <math>\, q \neq r</math> | ||
| + | |||
| + | ::<math>c_n = | ||
| + | \begin{cases} | ||
| + | \qquad \qquad \qquad \qquad \qquad \qquad \, a b & \text{gdy } \; n = 0 \\ | ||
| + | q^n \left( b + {\large\frac{r}{q - r}} \right) + r^n \left( a - {\large\frac{q}{q - r}} \right) & \text{gdy } \; n \geqslant 1 \\ | ||
| + | \end{cases}</math> | ||
| + | |||
| + | |||
| + | Przykłady zebraliśmy w tabeli. | ||
| + | |||
| + | ::{| class="wikitable plainlinks" style="font-size: 90%; text-align: center; margin-right: auto;" | ||
| + | |- | ||
| + | ! <math>\boldsymbol{a}</math> || <math>\boldsymbol{q}</math> || <math>\boldsymbol{b}</math> || <math>\boldsymbol{r}</math> || <math>\boldsymbol{(c_n)}</math> || <math>\boldsymbol{\sum_{n=0}^{\infty} a_n}</math> || <math>\boldsymbol{\sum_{n=0}^{\infty} b_n}</math> || <math>\boldsymbol{\sum_{n=0}^{\infty} c_n}</math> | ||
| + | |- | ||
| + | |<math>3</math> || <math>{\small\frac{1}{2}}</math> || <math>-2</math>|| <math>{\small\frac{1}{3}}</math> || <math>(-6,0,0,0,0,0,…)</math> || zbieżny || zbieżny || zbieżny | ||
| + | |- | ||
| + | |<math>-2</math> || <math>2</math> || <math>3</math> || <math>3</math> || <math>(-6,0,0,0,0,0,…)</math> || rozbieżny || rozbieżny || zbieżny | ||
| + | |- | ||
| + | | <math>{\small\frac{r - 2q}{r - q}}</math> || <math>q</math> || <math>{\small\frac{r}{r - q}}</math> || <math>r</math> || <math>\left( {\small\frac{r ( r - 2q )}{(r - q)^2}}, r, r^2, r^3, r^4, r^5, \ldots \right)</math> || zbieżny / rozbieżny || zbieżny / rozbieżny || zbieżny / rozbieżny | ||
| + | |- | ||
| + | | <math>4</math> || <math>{\small\frac{1}{2}}</math> || <math>-2</math> || <math>{\small\frac{1}{3}}</math> || <math>\left( -8,{\small\frac{1}{3}}, {\small\frac{1}{3^2}}, {\small\frac{1}{3^3}}, {\small\frac{1}{3^4}}, {\small\frac{1}{3^5}}, \ldots \right)</math> || zbieżny || zbieżny || zbieżny | ||
| + | |- | ||
| + | | <math>{\small\frac{7}{3}}</math> || <math>2</math> || <math>- {\small\frac{1}{3}}</math> || <math>{\small\frac{1}{2}}</math> || <math>\left( - {\small\frac{7}{9}}, {\small\frac{1}{2}}, {\small\frac{1}{2^2}}, {\small\frac{1}{2^3}}, {\small\frac{1}{2^4}}, {\small\frac{1}{2^5}}, \ldots \right)</math> || rozbieżny || zbieżny || zbieżny | ||
| + | |- | ||
| + | | <math>-1</math> || <math>2</math> || <math>3</math> || <math>3</math> || <math>(-3,3,3^2,3^3,3^4,3^5,…)</math> || rozbieżny || rozbieżny || rozbieżny | ||
| + | |- | ||
| + | | <math>{\small\frac{1}{2}}</math> || <math>1</math> || <math>{\small\frac{1}{2}}</math> || <math>-1</math> || <math>\left( {\small\frac{1}{4}}, 0, 0, 0, 0, 0, \ldots \right)</math> || rozbieżny || rozbieżny || zbieżny | ||
| + | |- | ||
| + | | <math>-1</math> || <math>1</math> || <math>2</math> || <math>2</math> || <math>(-2, 0, 0, 0, 0, 0, \ldots )</math> || rozbieżny || rozbieżny || zbieżny | ||
| + | |- | ||
| + | | <math>-1</math> || <math>1</math> || <math>3</math> || <math>2</math> || <math>(-3, 1, 1, 1, 1, 1,\ldots )</math> || rozbieżny || rozbieżny || rozbieżny | ||
| + | |- | ||
| + | | <math>2</math> || <math>1</math> || <math>-1</math> || <math>{\small\frac{1}{2}}</math> || <math>(-2,0,0,0,0,0,…)</math> || rozbieżny || zbieżny || zbieżny | ||
| + | |- | ||
| + | | <math>2</math> || <math>1</math> || <math>0</math> || <math>{\small\frac{1}{2}}</math> || <math>(0, 1, 1, 1, 1, 1, \ldots )</math> || rozbieżny || zbieżny || rozbieżny | ||
| + | |- | ||
| + | | <math>{\small\frac{r - 2}{r - 1}}</math> || <math>1</math> || <math>{\small\frac{r}{r - 1}}</math> || <math>r</math> || <math>\left( {\small\frac{r ( r - 2 )}{(r - 1)^2}}, r, r^2, r^3, r^4, r^5, \ldots \right)</math> || rozbieżny || zbieżny / rozbieżny || zbieżny / rozbieżny | ||
| + | |- | ||
| + | | <math>0</math> || <math>1</math> || <math>2</math> || <math>2</math> || <math>(0, 2, 2^2, 2^3, 2^4, 2^5, \ldots )</math> || rozbieżny || rozbieżny || rozbieżny | ||
| + | |- | ||
| + | | <math>3</math> || <math>1</math> || <math>-1</math> || <math>{\small\frac{1}{2}}</math> || <math>\left( - 3, {\small\frac{1}{2}}, {\small\frac{1}{2^2}}, {\small\frac{1}{2^3}}, {\small\frac{1}{2^4}}, {\small\frac{1}{2^5}}, \ldots \right)</math> || rozbieżny || zbieżny || zbieżny | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D70" style="font-size: 110%; font-weight: bold;">Przykład D70</span><br/> | ||
| + | Podamy przykład szeregów zbieżnych, których iloczyn Cauchy'ego jest rozbieżny. Rozważmy zbieżny szereg (zobacz [[#D5|D5]]) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{\infty} {\small\frac{(- 1)^k}{\sqrt{k + 1}}} = 0.604898643 \ldots \qquad \qquad</math> ([https://www.wolframalpha.com/input?i=Sum%5B+%28-1%29%5Ek%2Fsqrt%28k%2B1%29%2C+%7Bk%2C+0%2C+infinity%7D+%5D WolframAlpha]) | ||
| + | |||
| + | Mnożąc powyższy szereg przez siebie według reguły Cauchy'ego, otrzymujemy | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} {\small\frac{(- 1)^k}{\sqrt{k + 1}}} \cdot {\small\frac{(- 1)^{n - k}}{\sqrt{n - k + 1}}} | ||
| + | = (- 1)^n \cdot \sum_{k = 0}^{n} {\small\frac{1}{\sqrt{(k + 1) (n - k + 1)}}}</math> | ||
| + | |||
| + | Ale <math>k \leqslant n \;</math> i <math>\; n - k \leqslant n</math>, zatem | ||
| + | |||
| + | ::<math>{\small\frac{1}{\sqrt{(k + 1) (n - k + 1)}}} \geqslant {\small\frac{1}{\sqrt{(n + 1) (n + 1)}}} = {\small\frac{1}{n + 1}}</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>| c_n | \geqslant \sum_{k = 0}^{n} {\small\frac{1}{n + 1}} = 1</math> | ||
| + | |||
| + | Ponieważ <math>\lim_{n \rightarrow \infty} c_n \neq 0</math>, to iloczyn Cauchy'ego jest rozbieżny (zobacz [[#D4|D4]]). | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D71" style="font-size: 110%; font-weight: bold;">Zadanie D71</span><br/> | ||
| + | Pokazać, że jeżeli <math>a_n = b_n = r^n \;</math> i <math>\; c_n = (n + 1) r^n</math> (zobacz [[#D68|D68]] p.3), to szeregi <math>\sum_{n = 0}^{\infty} a_n</math> oraz <math>\sum_{n = 0}^{\infty} c_n</math> są jednocześnie zbieżne lub jednocześnie rozbieżne. Sprawdzić, że w przypadku, gdy szeregi te są zbieżne, prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\left( \sum_{i = 0}^{\infty} a_i \right) \cdot \left( \sum_{j = 0}^{\infty} b_j \right) = \sum_{n = 0}^{\infty} \left( \sum_{k = 0}^{n} a_k b_{n - k} \right)</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Zbieżność szeregu <math>\sum_{n = 0}^{\infty} (n + 1) r^n</math> łatwo zbadamy, stosując kryterium d'Alemberta. | ||
| + | |||
| + | ::<math>\left| {\small\frac{c_{n + 1}}{c_n}} \right| = \left| {\small\frac{(n + 2) r^{n + 1}}{(n + 1) r^n}} \right| = {\small\frac{n + 2}{n + 1}} \cdot | r | \xrightarrow{\; n \rightarrow \infty \;} | r |</math> | ||
| + | |||
| + | Zatem szereg <math>\sum_{n = 0}^{\infty} (n + 1) r^n</math> jest zbieżny, gdy <math>| r | < 1</math> i rozbieżny, gdy <math>| r | > 1</math>, tak samo, jak szereg <math>\sum_{n = 0}^{\infty} r^n</math>. W przypadku, gdy <math>r = \pm 1</math> szereg <math>\sum_{n = 0}^{\infty} r^n</math> jest rozbieżny, a odpowiednie sumy częściowe szeregu <math>\sum_{n = 0}^{\infty} (n + 1) r^n</math> są równe | ||
| + | |||
| + | :* gdy <math>r = 1</math>, <math>c_n = n + 1</math>, <math>\quad C_L = \sum_{n = 0}^{L} (n + 1) = {\small\frac{(L + 1) (L + 2)}{2}} \xrightarrow{\; L \rightarrow \infty \;} \infty \qquad \qquad</math> (zobacz <span style="color: Green">[a]</span>, [https://www.wolframalpha.com/input?i=Sum%5B+n%2B1%2C+%7Bn%2C+0%2C+L%7D+%5D WolframAlpha]) | ||
| + | |||
| + | :* gdy <math>r = - 1</math>, <math>c_n = (n + 1) (- 1)^n</math>, <math>\quad C_L = \sum_{n = 0}^{L} (n + 1) (- 1)^n = (- 1)^L \cdot {\small\frac{2 L + 3}{4}} + {\small\frac{1}{4}} \xrightarrow{\; L \rightarrow \infty \;} \pm \infty \qquad \qquad</math> (zobacz [[#D53|D53]], [https://www.wolframalpha.com/input?i=Sum%5B+%28n%2B1%29*%28-1%29%5En%2C+%7Bn%2C+0%2C+L%7D+%5D WolframAlpha]) | ||
| + | |||
| + | W przypadku, gdy <math>| r | < 1</math> wiemy<ref name="GeometricSeries1"/>, że <math>\sum_{n = 0}^{\infty} r^n = {\small\frac{1}{1 - r}}</math>. Korzystając z zadania [[#D53|D53]], otrzymujemy | ||
| + | |||
| + | ::<math>\sum_{n = 0}^{L} (n + 1) r^n = \sum_{n = 0}^{L} n r^n + \sum_{n = 0}^{L} r^n = {\small\frac{L r^{L + 2} - (L + 1) r^{L + 1} + r}{(r - 1)^2}} + {\small\frac{r^{L + 1} - 1}{r - 1}} = {\small\frac{(L + 1) r^{L + 2} - (L + 2) r^{L + 1} + 1}{(r - 1)^2}} \xrightarrow{\; L \rightarrow \infty \;} {\small\frac{1}{(r - 1)^2}}</math> | ||
| + | |||
| + | |||
| + | Ponieważ szereg <math>\sum_{n = 0}^{\infty} (n + 1) r^n</math> jest zbieżny, gdy <math>| r | < 1</math>, to musi być <math>\lim_{n \rightarrow \infty} (n + 1) r^n = 0</math> (zobacz [[#D4|D4]]). Pokazaliśmy, że w rozważanym przypadku iloczyn sum szeregów jest równy sumie iloczynu Cauchy'ego tych szeregów. | ||
| + | |||
| + | |||
| + | <hr style="width: 25%; height: 2px; " /> | ||
| + | <span style="color: Green">[a]</span> Zauważmy, że | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k = {\small\frac{1}{2}} \left( \sum_{k = 0}^{n} k + \sum_{k = 0}^{n} k \right) = {\small\frac{1}{2}} \left[ \sum_{k = 0}^{n} k + \sum_{j = 0}^{n} (n - j) \right] = {\small\frac{1}{2}} \left[ \sum_{k = 0}^{n} k + \sum_{k = 0}^{n} (n - k) \right] = {\small\frac{1}{2}} \sum_{k = 0}^{n} (k + n - k) = {\small\frac{n}{2}} \sum_{k = 0}^{n} 1 = {\small\frac{n (n + 1)}{2}}</math><br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D72" style="font-size: 110%; font-weight: bold;">Uwaga D72</span><br/> | ||
| + | Przykłady [[#D69|D69]] i [[#D70|D70]] pokazują, że w ogólności nie jest prawdziwy wzór | ||
| + | |||
| + | ::<math>\left( \sum_{i = 0}^{\infty} a_i \right) \cdot \left( \sum_{j = 0}^{\infty} b_j \right) = \sum_{n = 0}^{\infty} \left( \sum_{k = 0}^{n} a_k b_{n - k} \right)</math> | ||
| + | |||
| + | Skoro iloczyn sum szeregów nie zawsze jest równy sumie iloczynu Cauchy'ego tych szeregów, to musimy ustalić, jakie warunki muszą być spełnione, aby tak było. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D73" style="font-size: 110%; font-weight: bold;">Uwaga D73</span><br/> | ||
| + | Nim przejdziemy do dowodu twierdzenia Mertensa, zauważmy, że od sumowania po <math>m + 1</math> kolejnych przekątnych | ||
| + | |||
| + | ::<math>\sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k}</math> | ||
| + | |||
| + | możemy łatwo przejść do sumowania po liniach poziomych lub po liniach pionowych. Rysunek przedstawia sytuację, gdy <math>m = 5</math>. | ||
| + | |||
| + | ::{| class="wikitable" style="text-align:center;" | ||
| + | |- | ||
| + | | bgcolor="LightGray" | <math> a_6 b_0 </math> || <math> </math> || || || || || | ||
| + | |- | ||
| + | | bgcolor="Violet" | <math> a_5 b_0 </math> || bgcolor="LightGray" | <math> </math> || || || || || | ||
| + | |- | ||
| + | | bgcolor="Cyan" | <math> a_4 b_0 </math> || bgcolor="Violet" | <math> a_4 b_1 </math> || bgcolor="LightGray" | <math> </math> || || || || | ||
| + | |- | ||
| + | | bgcolor="Green" | <math> a_3 b_0 </math> || bgcolor="Cyan" | <math> a_3 b_1 </math> || bgcolor="Violet" | <math> a_3 b_2 </math> || bgcolor="LightGray" | <math> </math> || || || | ||
| + | |- | ||
| + | | bgcolor="Yellow" | <math> a_2 b_0 </math> || bgcolor="Green" | <math> a_2 b_1 </math> || bgcolor="Cyan" | <math> a_2 b_2 </math> || bgcolor="Violet" | <math> a_2 b_3 </math> || bgcolor="LightGray" | <math> </math> || || | ||
| + | |- | ||
| + | | bgcolor="Orange" | <math> a_1 b_0 </math> || bgcolor="Yellow" | <math> a_1 b_1 </math> || bgcolor="Green" | <math> a_1 b_2 </math> || bgcolor="Cyan" | <math> a_1 b_3 </math> || bgcolor="Violet" | <math> a_1 b_4 </math> || bgcolor="LightGray" | <math> </math> || | ||
| + | |- | ||
| + | | bgcolor="Red" | <math> a_0 b_0 </math> || bgcolor="Orange" | <math> a_0 b_1 </math> || bgcolor="Yellow" | <math> a_0 b_2 </math> || bgcolor="Green" | <math> a_0 b_3 </math> || bgcolor="Cyan" | <math> a_0 b_4 </math> || bgcolor="Violet" | <math> a_0 b_5 </math> || bgcolor="LightGray" | <math> a_0 b_6 </math> | ||
| + | |} | ||
| + | |||
| + | Przejście do sumowania po liniach poziomych | ||
| + | |||
| + | ::<math>\sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k} = \sum_{i = 0}^{m} \sum_{j = 0}^{m - i} a_i b_j</math> | ||
| + | |||
| + | Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach poziomych, a druga po kolejnych elementach w <math>i</math>-tej linii poziomej. | ||
| + | |||
| + | |||
| + | Przejście do sumowania po liniach pionowych | ||
| + | |||
| + | ::<math>\sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k} = \sum_{i = 0}^{m} \sum_{j = 0}^{m - i} a_j b_i</math> | ||
| + | |||
| + | Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach pionowych, a druga po kolejnych elementach w <math>i</math>-tej linii pionowej. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D74" style="font-size: 110%; font-weight: bold;">Twierdzenie D74 (Franciszek Mertens)</span><br/> | ||
| + | Jeżeli szereg <math>\sum_{i = 0}^{\infty} a_i = A</math> jest zbieżny bezwzględnie, szereg <math>\sum_{j = 0}^{\infty} b_j = B</math> jest zbieżny, to ich iloczyn Cauchy'ego <math>\sum_{n = 0}^{\infty} c_n</math>, gdzie <math>c_n = \sum_{k = 0}^{n} a_k b_{n - k}</math>, jest zbieżny i <math>\sum_{n = 0}^{\infty} c_n = A B</math>. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Z założenia szereg <math>\sum_{i = 0}^{\infty} a_i</math> jest zbieżny bezwzględnie, oznaczmy <math>\sum_{i = 0}^{\infty} | a_i | = A'</math>. Niech | ||
| + | |||
| + | ::<math>A_n = \sum_{i = 0}^{n} a_i \qquad \qquad B_n = \sum_{j = 0}^{n} b_j \qquad \qquad C_n = \sum_{k = 0}^{n} c_k \qquad \qquad \beta_n = B_n - B</math> | ||
| + | |||
| + | Przekształcając sumę <math>C_m</math>, otrzymujemy | ||
| + | |||
| + | ::<math>C_m = \sum_{n = 0}^{m} c_n</math> | ||
| + | |||
| + | :::<math>\; = \sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k}</math> | ||
| + | |||
| + | Przechodzimy od sumowania po <math>m + 1</math> kolejnych przekątnych do sumowania po <math>m + 1</math> kolejnych liniach poziomych (zobacz [[#D73|D73]]). | ||
| + | |||
| + | ::<math>C_m = \sum_{i = 0}^{m} \sum_{j = 0}^{m - i} a_i b_j</math> | ||
| + | |||
| + | :::<math>\; = \sum_{i = 0}^{m} a_i \sum_{j = 0}^{m - i} b_j</math> | ||
| + | |||
| + | :::<math>\; = \sum_{i = 0}^{m} a_i B_{m - i}</math> | ||
| + | |||
| + | :::<math>\; = \sum_{i = 0}^{m} a_i \left( {B + \beta_{m - i}} \right)</math> | ||
| + | |||
| + | :::<math>\; = \sum_{i = 0}^{m} a_i B + \sum_{i = 0}^{m} a_i \beta_{m - i}</math> | ||
| + | |||
| + | :::<math>\; = B \sum_{i = 0}^{m} a_i + \sum_{i = 0}^{m} a_i \beta_{m - i}</math> | ||
| + | |||
| + | :::<math>\; = A_m B + \sum_{k = 0}^{m} \beta_k a_{m - k}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>C_m - A_m B = \sum_{k = 0}^{m} \beta_k a_{m - k}</math> | ||
| + | |||
| + | Niech | ||
| + | |||
| + | ::<math>\delta_m = \sum_{k = 0}^{m} \beta_k a_{m - k}</math> | ||
| + | |||
| + | Oczywiście chcemy pokazać, że <math>C_m \longrightarrow A B</math>. Ponieważ <math>A_m B \longrightarrow A B</math>, to wystarczy pokazać, że <math>\delta_m \longrightarrow 0</math>. | ||
| + | |||
| + | Z założenia <math>B_m \longrightarrow B</math>, zatem <math>\beta_m \longrightarrow 0</math>. Ze zbieżności ciągu <math>(\beta_k)</math> wynika, że | ||
| + | |||
| + | :* ciąg <math>(\beta_k)</math> jest ograniczony, czyli istnieje taka liczba <math>U > 0</math>, że dla każdego <math>k \geqslant 0</math> jest <math>| \beta_k | \leqslant U</math> (zobacz [[Ciągi liczbowe#C9|C9]]) | ||
| + | |||
| + | :* dla dowolnego <math>\varepsilon_1 > 0</math> prawie wszystkie wyrazy ciągu <math>(\beta_k)</math> spełniają warunek <math>| \beta_k | < \varepsilon_1</math> (zobacz [[Ciągi liczbowe#C4|C4]], [[Ciągi liczbowe#C6|C6]]) | ||
| + | |||
| + | Możemy przyjąć, że warunek <math>| \beta_k | < \varepsilon_1</math> spełniają wszystkie wyrazy, poczynając od <math>M = M (\varepsilon_1)</math>. Zatem dla <math>m > M</math> dostajemy | ||
| + | |||
| + | ::<math>| \delta_m | \leqslant \sum_{k = 0}^{M} | \beta_k | | a_{m - k} | + \sum_{k = M + 1}^{m} | \beta_k | | a_{m - k} |</math> | ||
| + | |||
| + | :::<math>\;\; < U (| a_m | + \ldots + | a_{m - M} |) + \varepsilon_1 \sum_{k = M + 1}^{m} | a_{m - k} |</math> | ||
| + | |||
| + | :::<math>\;\; < U (| a_{m - M} | + \ldots + | a_m |) + \varepsilon_1 A'</math> | ||
| + | |||
| + | Z założenia szereg <math>\sum_{i = 0}^{\infty} a_i</math> jest zbieżny, zatem musi być <math>\lim_{m \rightarrow \infty} a_m = 0</math> (zobacz [[#D4|D4]]). Czyli dla dowolnego <math>\varepsilon_2 > 0</math> prawie wszystkie wyrazy ciągu <math>(a_k)</math> spełniają warunek <math>| a_k | < \varepsilon_2</math>. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od <math>N = N (\varepsilon_2)</math>. Zatem dla <math>m > M + N</math> otrzymujemy | ||
| + | |||
| + | ::<math>| \delta_m | < U (| a_{m - M} | + \ldots + | a_m |) + \varepsilon_1 A'</math> | ||
| + | |||
| + | :::<math>\;\; < \varepsilon_2 (M + 1) U + \varepsilon_1 A'</math> | ||
| + | |||
| + | |||
| + | Prawa strona nierówności jest dowolnie mała. Przykładowo dla dowolnego <math>\varepsilon > 0</math> wystarczy wybrać <math>\varepsilon_1 = {\small\frac{\varepsilon / 2}{A'}}</math> i <math>\varepsilon_2 = {\small\frac{\varepsilon / 2}{(M + 1) U}}</math>, aby otrzymać <math>| \delta_m | < \varepsilon</math> dla wszystkich <math>m > M + N</math>. Ponieważ prawie wszystkie wyrazy ciągu <math>\delta_m</math> spełniają warunek <math>| \delta_m | < \varepsilon</math>, to <math>\lim_{m \rightarrow \infty} \delta_m = 0</math>. Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D75" style="font-size: 110%; font-weight: bold;">Zadanie D75</span><br/> | ||
| + | Pokazać, że iloczyn Cauchy'ego dwóch szeregów bezwzględnie zbieżnych jest bezwzględnie zbieżny. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Z założenia szeregi <math>\sum_{i = 0}^{\infty} a_i</math> oraz <math>\sum_{j = 0}^{\infty} b_j</math> są bezwzględnie zbieżne, zatem możemy napisać | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{\infty} | a_i | = A' \qquad \qquad \sum^{\infty}_{j = 0} | b_j | = B'</math> | ||
| + | |||
| + | Zauważmy, że suma <math>\sum_{n = 0}^{m} \sum_{k = 0}^{n} | a_k | | b_{n - k} |</math> obejmuje <math>m + 1</math> przekątnych. Łatwo możemy przejść od sumowania po kolejnych przekątnych do sumowana po <math>m + 1</math> kolejnych liniach poziomych (zobacz [[#D73|D73]]). | ||
| + | |||
| + | ::<math>C'_m = \sum_{n = 0}^{m} | c_n |</math> | ||
| + | |||
| + | :::<math>\; = \sum_{n = 0}^{m} \left| \sum_{k = 0}^{n} a_k b_{n - k} \right|</math> | ||
| + | |||
| + | :::<math>\; \leqslant \sum_{n = 0}^{m} \sum_{k = 0}^{n} | a_k b_{n - k} |</math> | ||
| + | |||
| + | :::<math>\; = \sum_{n = 0}^{m} \sum_{k = 0}^{n} | a_k | | b_{n - k} |</math> | ||
| + | |||
| + | :::<math>\; = \sum_{i = 0}^{m} \sum_{j = 0}^{m - i} | a_i | | b_j | \qquad \qquad</math> (zmieniliśmy sposób sumowania) | ||
| + | |||
| + | :::<math>\; = \sum_{i = 0}^{m} | a_i | \sum_{j = 0}^{m - i} | b_j |</math> | ||
| + | |||
| + | :::<math>\; \leqslant A' B'</math> | ||
| + | |||
| + | Ponieważ ciąg sum częściowych <math>C'_m</math> jest rosnący (bo sumujemy wartości nieujemne) i ograniczony od góry, to jest zbieżny.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D76" style="font-size: 110%; font-weight: bold;">Zadanie D76</span><br/> | ||
| + | Podać przykład szeregów zbieżnych, z których tylko jeden jest bezwzględnie zbieżny i których iloczyn Cauchy'ego jest warunkowo zbieżny. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Zauważmy, że szereg <math>\sum_{i = 0}^{\infty} {\small\frac{(- 1)^i}{2^i}} = {\small\frac{2}{3}}</math> jest bezwzględnie zbieżny, bo <math>\sum_{i = 0}^{\infty} {\small\frac{1}{2^i}} = 2</math> jest zbieżny. Szereg <math>\sum_{j = 0}^{\infty} {\small\frac{(- 1)^j}{j + 1}} = \log 2</math> jest zbieżny na mocy kryterium Leibniza (zobacz [[#D5|D5]]), ale nie jest bezwzględnie zbieżny (zobacz [[#D17|D17]], [[#D19|D19]] p.1, [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B34|B34]]). | ||
| + | |||
| + | Zatem na podstawie twierdzenia Mertensa iloczyn Cauchy'ego tych szeregów <math>\sum_{n = 0}^{\infty} c_n</math>, gdzie | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} {\small\frac{(- 1)^k}{2^k}} \cdot {\small\frac{(- 1)^{n - k}}{n - k + 1}}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = (- 1)^n \sum_{k = 0}^{n} {\small\frac{1}{2^k (n - k + 1)}}</math> | ||
| + | |||
| + | jest zbieżny. Łatwo widzimy, że | ||
| + | |||
| + | ::<math>| c_n | = \sum_{k = 0}^{n} {\small\frac{1}{2^k (n - k + 1)}}</math> | ||
| + | |||
| + | :::<math>\; = {\small\frac{1}{n + 1}} + \sum_{k = 1}^{n} {\small\frac{1}{2^k (n - k + 1)}}</math> | ||
| + | |||
| + | :::<math>\; \geqslant {\small\frac{1}{n + 1}}</math> | ||
| + | |||
| + | Ponieważ szereg <math>\sum_{n = 0}^{\infty} {\small\frac{1}{n + 1}}</math> jest rozbieżny i | ||
| + | |||
| + | ::<math>0 \leqslant {\small\frac{1}{n + 1}} \leqslant | c_n |</math> | ||
| + | |||
| + | to na mocy kryterium porównawczego (zobacz [[#D9|D9]]) szereg <math>\sum_{n = 0}^{\infty} | c_n |</math> jest rozbieżny. Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D77" style="font-size: 110%; font-weight: bold;">Zadanie D77</span><br/> | ||
| + | Podać przykład szeregów warunkowo zbieżnych, których iloczyn Cauchy'ego jest warunkowo zbieżny. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Szereg <math>\sum_{j = 0}^{\infty} {\small\frac{(- 1)^j}{j + 1}} = \log 2</math> jest warunkowo zbieżny (zobacz [[#D5|D5]], [[#D17|D17]], [[#D19|D19]] p.1, [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B34|B34]]). Iloczyn Cauchy'ego dwóch takich szeregów jest równy <math>\sum_{n = 0}^{\infty} c_n</math>, gdzie | ||
| + | |||
| + | ::<math>c_n = \sum_{k = 0}^{n} {\small\frac{(- 1)^k}{k + 1}} \cdot {\small\frac{(- 1)^{n - k}}{n - k + 1}}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = (- 1)^n \sum_{k = 0}^{n} {\small\frac{1}{(k + 1) (n - k + 1)}}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = {\small\frac{(- 1)^n}{n + 2}} \sum_{k = 0}^{n} {\small\frac{(n - k + 1) + (k + 1)}{(k + 1) (n - k + 1)}}</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = {\small\frac{(- 1)^n}{n + 2}} \sum_{k = 0}^{n} \left( {\small\frac{1}{k + 1}} + {\small\frac{1}{n - k + 1}} \right)</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = {\small\frac{(- 1)^n}{n + 2}} \left( \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} + \sum_{j = 0}^{n} {\small\frac{1}{j + 1}} \right)</math> | ||
| + | |||
| + | ::<math>\;\;\;\:\, = {\small\frac{2 (- 1)^n}{n + 2}} \sum_{k = 0}^{n} {\small\frac{1}{k + 1}}</math> | ||
| + | |||
| + | |||
| + | Ponieważ (zobacz [[#D17|D17]]) | ||
| + | |||
| + | ::<math>\log (n + 1) < \sum_{k = 1}^{n} {\small\frac{1}{k}} < 1 + \log n</math> | ||
| + | |||
| + | to | ||
| + | |||
| + | ::<math>{\small\frac{2}{n + 2}} \cdot \log (n + 2) < | c_n | < {\small\frac{2}{n + 2}} \cdot (1 + \log (n + 1))</math> | ||
| + | |||
| + | Z twierdzenia o trzech ciągach wynika natychmiast, że <math>\lim_{n \rightarrow \infty} | c_n | = 0</math>. Pokażemy teraz, że ciąg <math>(| c_n |)</math> jest ciągiem malejącym. | ||
| + | |||
| + | ::<math>| c_n | - | c_{n - 1} | = {\small\frac{2}{n + 2}} \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} - {\small\frac{2}{n + 1}} \sum_{k = 0}^{n - 1} {\small\frac{1}{k + 1}}</math> | ||
| + | |||
| + | :::::<math>\;\;\;\; = {\small\frac{2}{n + 2}} \cdot {\small\frac{1}{n + 1}} + {\small\frac{2}{n + 2}} \sum_{k = 0}^{n - 1} {\small\frac{1}{k + 1}} - {\small\frac{2}{n + 1}} \sum_{k = 0}^{n - 1} {\small\frac{1}{k + 1}}</math> | ||
| + | |||
| + | :::::<math>\;\;\;\; = {\small\frac{2}{(n + 2) (n + 1)}} + \left( {\small\frac{2}{n + 2}} - {\small\frac{2}{n + 1}} \right) \sum_{k = 0}^{n - 1} {\small\frac{1}{k + 1}}</math> | ||
| + | |||
| + | :::::<math>\;\;\;\; = {\small\frac{2}{(n + 2) (n + 1)}} - {\small\frac{2}{(n + 2) (n + 1)}} \sum_{k = 0}^{n - 1} {\small\frac{1}{k + 1}}</math> | ||
| + | |||
| + | :::::<math>\;\;\;\; \leqslant 0</math> | ||
| + | |||
| + | Bo <math>\; \sum_{k = 0}^{n - 1} {\small\frac{1}{k + 1}} \geqslant 1</math>. Ponieważ ciąg <math>(| c_n |)</math> jest malejący i zbieżny do zera, to z kryterium Leibniza (zobacz [[#D5|D5]]) szereg <math>\sum_{n = 0}^{\infty} (- 1)^n | c_n |</math> jest zbieżny. Zauważmy jeszcze, że dla <math>n \geqslant 1</math> mamy | ||
| + | |||
| + | ::<math>0 \leqslant {\small\frac{1}{n + 1}} \leqslant {\small\frac{2 \log (n + 2)}{n + 2}} < | c_n |</math> | ||
| + | |||
| + | Zatem na podstawie kryterium porównawczego (zobacz [[#D9|D9]]) szereg <math>\sum_{n = 0}^{\infty} | c_n |</math> jest rozbieżny.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D78" style="font-size: 110%; font-weight: bold;">Uwaga D78</span><br/> | ||
| + | Nim przejdziemy do dowodu twierdzenia Abela, musimy udowodnić trzy twierdzenia dotyczące pewnych granic. Warto zauważyć, że twierdzenie [[#D80|D80]] pozwala przypisać wartość sumy do szeregów, których suma w zwykłym sensie nie istnieje. Uogólnienie to nazywamy sumowalnością w sensie Cesàro<ref name="CesaroSum1"/>. Nie będziemy zajmowali się tym tematem, ale podamy ciekawy przykład. | ||
| + | |||
| + | Rozważmy szereg <math>\sum_{i = 0}^{\infty} (- 1)^i</math>. Sumy częściowe tego szeregu wynoszą <math>S_k = {\small\frac{1 + (- 1)^k}{2}}</math> i tworzą ciąg rozbieżny, ale ciąg kolejnych średnich arytmetycznych dla ciągu <math>(S_k)</math> jest równy | ||
| + | |||
| + | ::<math>x_n = {\small\frac{S_0 + \ldots + S_n}{n + 1}} | ||
| + | = {\small\frac{1}{n + 1}} \cdot \sum_{k = 0}^{n} {\small\frac{1 + (- 1)^k}{2}} | ||
| + | = {\small\frac{1}{2}} + {\small\frac{1 + (- 1)^n}{4 (n + 1)}} \xrightarrow{\; n \rightarrow \infty \;} {\small\frac{1}{2}} \qquad \qquad</math> ([https://www.wolframalpha.com/input?i=1%2F%28n%2B1%29+*+Sum%5B+%281+%2B+%28-1%29%5Ek+%29%2F2%2C+%7Bk%2C+0%2C+n%7D+%5D WolframAlfa]) | ||
| + | |||
| + | Zatem szereg <math>\sum_{i = 0}^{\infty} (- 1)^i</math> jest sumowalny w sensie Cesàro i jego suma jest równa <math>{\small\frac{1}{2}}</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D79" style="font-size: 110%; font-weight: bold;">Twierdzenie D79</span><br/> | ||
| + | Jeżeli <math>\lim_{n \rightarrow \infty} a_n = 0</math>, to <math>\lim_{n \rightarrow \infty} {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} | a_k | = 0</math>. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Z założenia <math>\lim_{n \rightarrow \infty} a_n = 0</math>. Ze zbieżności ciągu <math>(a_k)</math> wynika, że | ||
| + | |||
| + | :* ciąg <math>(a_k)</math> jest ograniczony, czyli istnieje taka liczba <math>U > 0</math>, że dla każdego <math>k \geqslant 0</math> jest <math>| a_k | \leqslant U</math> (zobacz [[Ciągi liczbowe#C9|C9]]) | ||
| + | |||
| + | :* dla dowolnego <math>\varepsilon > 0</math> prawie wszystkie wyrazy ciągu <math>(a_k)</math> spełniają warunek <math>| a_k | < \varepsilon</math> (zobacz [[Ciągi liczbowe#C4|C4]], [[Ciągi liczbowe#C6|C6]]) | ||
| + | |||
| + | Możemy przyjąć, że warunek <math>| a_k | < \varepsilon</math> spełniają wszystkie wyrazy, poczynając od <math>N = N (\varepsilon)</math>. Zatem dla <math>n > N</math> możemy napisać | ||
| + | |||
| + | ::<math>{\small\frac{1}{n + 1}} \sum_{k = 0}^{n} | a_k | = {\small\frac{| a_0 | + \ldots + | a_N | + |a_{N + 1} | + \ldots + | a_n |}{n + 1}}</math> | ||
| + | |||
| + | ::::::<math>\,\, < {\small\frac{U (N + 1)}{n + 1}} + {\small\frac{\varepsilon (n - N)}{n + 1}}</math> | ||
| + | |||
| + | ::::::<math>\,\, < {\small\frac{U (N + 1)}{n + 1}} + \varepsilon</math> | ||
| + | |||
| + | Ponieważ liczba <math>n</math> może być dowolnie duża, to wyrażenie <math>{\small\frac{U (N + 1)}{n + 1}}</math> może być dowolnie małe. W szczególności warunek | ||
| + | |||
| + | ::<math>{\small\frac{U (N + 1)}{n + 1}} < \varepsilon</math> | ||
| + | |||
| + | jest spełniony dla <math>n > {\small\frac{U (N + 1)}{\varepsilon}} - 1</math> i otrzymujemy, że | ||
| + | |||
| + | ::<math>{\small\frac{1}{n + 1}} \sum_{k = 0}^{n} | a_k | < 2 \varepsilon</math> | ||
| + | |||
| + | dla wszystkich <math>n > \max \left( N, {\small\frac{U (N + 1)}{\varepsilon}} - 1 \right)</math>. Zatem <math>\lim_{n \rightarrow \infty} {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} | a_k | = 0</math>. Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D80" style="font-size: 110%; font-weight: bold;">Twierdzenie D80</span><br/> | ||
| + | Jeżeli ciąg <math>(a_k)</math> jest zbieżny, to ciąg kolejnych średnich arytmetycznych <math>x_n = {\small\frac{a_0 + \ldots + a_n}{n + 1}}</math> jest zbieżny do tej samej granicy. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Z założenia ciąg <math>(a_k)</math> jest zbieżny, zatem możemy napisać | ||
| + | |||
| + | ::<math>\lim_{k \rightarrow \infty} a_k = g</math> | ||
| + | |||
| + | Z definicji ciągu <math>(x_n)</math> dostajemy | ||
| + | |||
| + | ::<math>x_n - g = {\small\frac{a_0 + \ldots + a_n}{n + 1}} - g | ||
| + | = {\small\frac{a_0 + \ldots + a_n - (n + 1) g}{n + 1}} | ||
| + | = {\small\frac{(a_0 - g) + \ldots + (a_n - g)}{n + 1}} | ||
| + | = {\small\frac{a_0 - g}{n + 1}} + \ldots + {\small\frac{a_n - g}{n + 1}}</math> | ||
| + | |||
| + | Wynika stąd, że | ||
| + | |||
| + | ::<math>0 \leqslant | x_n - g | \leqslant {\small\frac{| a_0 - g |}{n + 1}} + \ldots + {\small\frac{| a_n - g |}{n + 1}} = {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} | a_k - g |</math> | ||
| + | |||
| + | W granicy, gdy <math>n \rightarrow \infty</math>, z twierdzenia [[#D79|D79]] i twierdzenia o trzech ciągach (zobacz [[Ciągi liczbowe#C10|C10]]) otrzymujemy | ||
| + | |||
| + | ::<math>\lim_{n \rightarrow \infty} | x_n - g | = 0</math> | ||
| + | |||
| + | Czyli <math>\lim_{n \rightarrow \infty} x_n = g</math> (zobacz [[Ciągi liczbowe#C8|C8]] p.2). Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D81" style="font-size: 110%; font-weight: bold;">Twierdzenie D81</span><br/> | ||
| + | Niech <math>(a_n)</math> i <math>(b_n)</math> będą zbieżnymi ciągami liczb rzeczywistych. Jeżeli <math>\lim_{n \rightarrow \infty} a_n = a</math> i <math>\lim_{n \rightarrow \infty} b_n = b</math>, to <math>\lim_{n \rightarrow \infty} {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a_k b_{n - k} = a b</math>. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | |||
| + | '''1. Przypadek, gdy''' <math>\boldsymbol{\lim_{n \rightarrow \infty} a_n = 0}</math> | ||
| + | |||
| + | Ponieważ ciąg <math>(b_n)</math> jest zbieżny, to jest ograniczony (zobacz [[Ciągi liczbowe#C9|C9]]), czyli istnieje taka liczba <math>U > 0</math>, że dla każdego <math>k \geqslant 0</math> jest <math>| b_k | \leqslant U</math>. Zatem | ||
| + | |||
| + | ::<math>0 \leqslant \left| {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a_k b_{n - k} \right| \leqslant {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} | a_k | | b_{n - k} | \leqslant {\small\frac{U}{n + 1}} \sum_{k = 0}^{n} | a_k |</math> | ||
| + | |||
| + | W granicy, gdy <math>n \rightarrow \infty</math>, z twierdzenia [[#D79|D79]] i twierdzenia o trzech ciągach (zobacz [[Ciągi liczbowe#C10|C10]]) otrzymujemy | ||
| + | |||
| + | ::<math>\lim_{n \rightarrow \infty} \left| {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a_k b_{n - k} \right| = 0</math> | ||
| + | |||
| + | Czyli <math>\lim_{n \rightarrow \infty} \left( {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a_k b_{n - k} \right) = 0</math> (zobacz [[Ciągi liczbowe#C8|C8]] p.2). | ||
| + | |||
| + | |||
| + | '''2. Przypadek, gdy''' <math>\boldsymbol{\lim_{n \rightarrow \infty} a_n \neq 0}</math> | ||
| + | |||
| + | Niech <math>x_n = a_n - a</math>. Oczywiście <math>\lim_{n \rightarrow \infty} x_n = 0</math>. Podstawiając, otrzymujemy | ||
| + | |||
| + | ::<math>{\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a_k b_{n - k} = {\small\frac{1}{n + 1}} \sum^n_{k = 0} (a + x_k) b_{n - k}</math> | ||
| + | |||
| + | :::::::<math>\, = {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a b_{n - k} + {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} x_k b_{n - k}</math> | ||
| + | |||
| + | :::::::<math>\, = a \cdot {\small\frac{1}{n + 1}} \sum_{j = 0}^{n} b_j + {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} x_k b_{n - k}</math> | ||
| + | |||
| + | W granicy, gdy <math>n \longrightarrow \infty</math>, z twierdzenia [[#D80|D80]] i udowodnionego wyżej przypadku, gdy <math>\lim_{n \rightarrow \infty} a_n = 0</math>, dostajemy | ||
| + | |||
| + | ::<math>\lim_{n \rightarrow \infty} {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a_k b_{n - k} = a b</math> | ||
| + | |||
| + | Co kończy dowód.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <span id="D82" style="font-size: 110%; font-weight: bold;">Twierdzenie D82 (Niels Henrik Abel)</span><br/> | ||
| + | Jeżeli szeregi <math>\sum_{i = 0}^{\infty} a_i = A</math> oraz <math>\sum_{j = 0}^{\infty} b_j = B</math> są zbieżne i ich iloczyn Cauchy'ego <math>\sum_{n = 0}^{\infty} c_n</math>, gdzie <math>c_n = \sum_{k = 0}^{n} a_k b_{n - k}</math>, jest zbieżny, to <math>\sum_{n = 0}^{\infty} c_n = A B</math>. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Będziemy stosowali następujące oznaczenia | ||
| + | |||
| + | ::<math>A_n = \sum_{i = 0}^{n} a_i \qquad \qquad \;\, B_n = \sum_{i = 0}^{n} b_i \qquad \qquad \;\; C_n = \sum_{i = 0}^{n} c_i</math> | ||
| + | |||
| + | Z założenia szeregi są zbieżne, zatem możemy napisać | ||
| + | |||
| + | ::<math>\lim_{n \rightarrow \infty} A_n = A \qquad \qquad \lim_{n \rightarrow \infty} B_n = B \qquad \qquad \lim_{n \rightarrow \infty} C_n = C</math> | ||
| + | |||
| + | Rozważmy sumę | ||
| + | |||
| + | ::<math>\sum_{m = 0}^{L} C_m = \sum_{m = 0}^{L} \sum_{n = 0}^{m} c_n</math> | ||
| + | |||
| + | ::::<math>\;\; = \sum_{m = 0}^{L} \sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k}</math> | ||
| + | |||
| + | Od sumowania wyrazów <math>a_k b_{n - k}</math> po <math>m + 1</math> kolejnych przekątnych przechodzimy do sumowania po <math>m + 1</math> kolejnych liniach poziomych (zobacz [[#D73|D73]]). | ||
| + | |||
| + | ::<math>\sum_{m = 0}^{L} C_m = \sum_{m = 0}^{L} \sum_{i = 0}^{m} \sum_{j = 0}^{m - i} a_i b_j</math> | ||
| + | |||
| + | ::::<math>\;\; = \sum_{m = 0}^{L} \sum_{i = 0}^{m} a_i \sum^{m - i}_{j = 0} b_j</math> | ||
| + | |||
| + | ::::<math>\;\; = \sum_{m = 0}^{L} \sum_{i = 0}^{m} a_i B_{m - i}</math> | ||
| + | |||
| + | ::::<math>\;\; = \sum_{m = 0}^{L} \sum_{k = 0}^{m} a_k B_{m - k}</math> | ||
| + | |||
| + | Od sumowania wyrazów <math>a_k B_{m - k}</math> po <math>L + 1</math> kolejnych przekątnych przechodzimy do sumowania po <math>L + 1</math> kolejnych liniach pionowych (zobacz [[#D73|D73]]). | ||
| + | |||
| + | ::<math>\sum_{m = 0}^{L} C_m = \sum_{i = 0}^{L} \sum_{j = 0}^{L - i} a_j B_i</math> | ||
| + | |||
| + | ::::<math>\;\; = \sum_{i = 0}^{L} B_i \sum_{j = 0}^{L - i} a_j</math> | ||
| + | |||
| + | ::::<math>\;\; = \sum_{i = 0}^{L} B_i A_{L - i}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>{\small\frac{1}{L + 1}} \sum_{m = 0}^{L} C_m = {\small\frac{1}{L + 1}} \sum_{i = 0}^{L} B_i A_{L - i}</math> | ||
| + | |||
| + | W granicy, gdy <math>L \longrightarrow \infty</math>, z twierdzeń [[#D80|D80]] i [[#D81|D81]] otrzymujemy <math>C = A B</math>. Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Liczby Catalana == | ||
| + | |||
| + | <span id="D83" style="font-size: 110%; font-weight: bold;">Definicja D83</span><br/> | ||
| + | Liczby Catalana <math>C_n</math> definiujemy wzorem | ||
| + | |||
| + | ::<math>C_n = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | gdzie <math>n \geqslant 0</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D84" style="font-size: 110%; font-weight: bold;">Twierdzenie D84</span><br/> | ||
| + | Liczby Catalana <math>C_n</math> mają następujące własności | ||
| + | |||
| + | :* <math>C_n</math> są liczbami całkowitymi dodatnimi | ||
| + | |||
| + | <div style="margin-top: 1.5em; margin-bottom: 1em;"> | ||
| + | :* <math>C_n = {\small\frac{1}{2 n + 1}} {\small\binom{2 n + 1}{n}} = {\small\frac{1}{n}} {\small\binom{2 n}{n - 1}}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>C_{n + 1} = {\small\frac{2 (2 n + 1)}{n + 2}} C_n</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>C_{n + 1} = \sum_{k = 0}^{n} C_k C_{n - k}</math> | ||
| + | </div> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | |||
| + | '''Punkt 1.''' | ||
| + | |||
| + | Twierdzenie jest prawdziwe dla początkowych wartości <math>n \geqslant 0</math>, bo <math>(C_n) = (1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, \ldots)</math>. W ogólności wystarczy zauważyć, że dla <math>n \geqslant 0</math> mamy | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>{\small\binom{2 n}{n + 1}} = {\small\frac{(2 n) !}{(n + 1) ! (n - 1) !}} = {\small\frac{n}{n + 1}} \cdot {\small\frac{(2 n) !}{n!n!}} = {\small\frac{n}{n + 1}} {\small\binom{2 n}{n}} < {\small\binom{2 n}{n}}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>{\small\binom{2 n}{n}} - {\small\binom{2 n}{n + 1}} = {\small\binom{2 n}{n}} - {\small\frac{n}{n + 1}} {\small\binom{2 n}{n}} = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}} = C_n</math> | ||
| + | </div> | ||
| + | |||
| + | Zatem <math>C_n</math> jest liczbą całkowitą większą od zera. | ||
| + | |||
| + | '''Punkt 2.''' | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>{\small\frac{1}{2 n + 1}} {\small\binom{2 n + 1}{n}} = {\small\frac{1}{2 n + 1}} \cdot {\small\frac{(2 n + 1) !}{n! (n + 1) !}} = {\small\frac{1}{2 n + 1}} \cdot {\small\frac{2 n + 1}{n + 1}} \cdot {\small\frac{(2 n) !}{n!n!}} = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}} = C_n</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>{\small\frac{1}{n}} {\small\binom{2 n}{n - 1}} = {\small\frac{1}{n}} \cdot {\small\frac{(2 n) !}{(n - 1) ! (n + 1) !}} = {\small\frac{1}{n + 1}} \cdot {\small\frac{(2 n) !}{n!n!}} = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}} = C_n</math> | ||
| + | </div> | ||
| + | |||
| + | '''Punkt 3.''' | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>{\small\frac{C_{n + 1}}{C_n}} = {\small\frac{1}{n + 2}} \cdot {\small\frac{(2 n + 2) !}{(n + 1) ! (n + 1) !}} \cdot (n + 1) \cdot {\small\frac{n!n!}{(2 n) !}}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::<math>\;\;\;\: = {\small\frac{1}{n + 2}} \cdot {\small\frac{(2 n + 2) (2 n + 1)}{(n + 1)^2}} \cdot {\small\frac{(2 n) !}{n!n!}} \cdot (n + 1) \cdot {\small\frac{n!n!}{(2 n) !}} =</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::<math>\;\;\;\: = {\small\frac{2 (2 n + 1)}{n + 2}}</math> | ||
| + | </div> | ||
| + | |||
| + | '''Punkt 4.''' | ||
| + | |||
| + | Dowód tego punktu został umieszczony w Uzupełnieniu (zobacz [[#D109|D109]]).<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D85" style="font-size: 110%; font-weight: bold;">Zadanie D85</span><br/> | ||
| + | Niech <math>C_n</math> oznacza <math>n</math>-tą liczbę Catalana i niech <math>\sum_{n = 0}^{\infty} x_n</math> oznacza szereg, który otrzymujemy, mnożąc szereg <math>\sum_{n = 0}^{\infty} a_n</math> przez siebie według reguły Cauchy'ego. Pokazać, że | ||
| + | |||
| + | :* jeżeli <math>a_n = C_n</math>, to <math>x_n = C_{n + 1}</math> | ||
| + | |||
| + | :* jeżeli <math>a_0 = \alpha \;</math> i <math>\; a_n = r^{n - 1} C_{n - 1}</math> dla <math>n \geqslant 1</math>, to <math>x_0 = \alpha^2</math>, <math>\; x_1 = 2 \alpha C_0 \;</math> i <math>\; x_n = (1 + 2 \alpha r) r^{n - 2} C_{n - 1}</math> dla <math>n \geqslant 2</math> | ||
| + | |||
| + | Dla jakich wartości <math>\alpha, r</math> szereg <math>\sum_{n = 0}^{\infty} x_n</math> jest zbieżny? | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | |||
| + | '''Punkt 2.''' | ||
| + | |||
| + | Dla <math>n = 0</math> mamy <math>x_0 = a_0 a_0 = \alpha^2</math> | ||
| + | |||
| + | Dla <math>n = 1</math> mamy <math>x_1 = a_0 a_1 + a_1 a_0 = 2 a_0 a_1 = 2 \alpha C_0</math> | ||
| + | |||
| + | Dla <math>n \geqslant 2</math> jest | ||
| + | |||
| + | ::<math>x_n = \sum_{k = 0}^{n} a_k a_{n - k}</math> | ||
| + | |||
| + | ::<math>\;\;\;\;\: = a_0 a_n + a_n a_0 + \sum_{k = 1}^{n - 1} a_k a_{n - k}</math> | ||
| + | |||
| + | ::<math>\;\;\;\;\: = 2 a_0 a_n + \sum_{k = 1}^{n - 1} r^{k - 1} C_{k - 1} \cdot r^{n - k - 1} C_{n - k - 1}</math> | ||
| + | |||
| + | ::<math>\;\;\;\;\: = 2 \alpha r^{n - 1} C_{n - 1} + r^{n - 2} \sum_{k = 1}^{n - 1} C_{k - 1} C_{n - k - 1}</math> | ||
| + | |||
| + | ::<math>\;\;\;\;\: = 2 \alpha r^{n - 1} C_{n - 1} + r^{n - 2} \sum_{j = 0}^{n - 2} C_j C_{n - 2 - j}</math> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>\;\;\;\;\: = 2 \alpha r^{n - 1} C_{n - 1} + r^{n - 2} C_{n - 1}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 2em; margin-bottom: 1em;"> | ||
| + | ::<math>\;\;\;\;\: = r^{n - 2} C_{n - 1} (1 + 2 \alpha r)</math> | ||
| + | </div> | ||
| + | |||
| + | Zauważmy, że | ||
| + | |||
| + | ::<math>{\small\frac{C_n}{C_{n - 1}}} = \frac{{\normalsize\frac{1}{n + 1}} {\normalsize\binom{2 n}{n}}}{{\normalsize\frac{1}{n}} {\normalsize\binom{2 n - 2}{n - 1}}} | ||
| + | = {\small\frac{n}{n + 1}} \cdot {\small\frac{2 n (2 n - 1) (2 n - 2) !}{n^2 [(n - 1) !]^2}} \cdot {\small\frac{[(n - 1) !]^2}{(2 n - 2) !}} | ||
| + | = {\small\frac{n}{n + 1}} \cdot {\small\frac{2 n (2 n - 1)}{n^2}} | ||
| + | = {\small\frac{2 (2 n - 1)}{n + 1}}</math> | ||
| + | |||
| + | Z kryterium d'Alemberta dla szeregu <math>\sum_{n = 0}^{\infty} a_n</math> i szeregu <math>\sum_{n = 0}^{\infty} x_n</math> otrzymujemy | ||
| + | |||
| + | ::<math>\left| {\small\frac{a_{n + 1}}{a_n}} \right| = \left| {\small\frac{r^n C_n}{r^{n - 1} C_{n - 1}}} \right| = | r | \cdot {\small\frac{C_n}{C_{n - 1}}} = | r | \cdot {\small\frac{2 (2 n - 1)}{n + 1}} \xrightarrow{\; n \rightarrow \infty \;} 4 | r |</math> | ||
| + | |||
| + | |||
| + | ::<math>\left| {\small\frac{x_{n + 1}}{x_n}} \right| = \left| {\small\frac{r^{n - 1} C_n (1 + 2 \alpha r)}{r^{n - 2} C_{n - 1} (1 + 2 \alpha r)}} \right| = | r | \cdot {\small\frac{C_n}{C_{n - 1}}} \xrightarrow{\; n \rightarrow \infty \;} 4 | r |</math> | ||
| + | |||
| + | Zatem szeregi te są bezwzględnie zbieżne w przypadku, gdy <math>| r | < {\small\frac{1}{4}}</math>. W szczególności dla <math>\alpha = - {\small\frac{1}{2 r}}</math> szereg <math>\sum_{n = 0}^{\infty} x_n</math> zawsze będzie zbieżny, bo od trzeciego wyrazu będzie się składał z samych zer. Wiemy, że w przypadku, gdy <math>r = {\small\frac{1}{4}}</math> szereg <math>\sum_{n = 0}^{\infty} {\small\frac{C_n}{4^n}} = 2</math> jest zbieżny.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Sumy współczynników dwumianowych == | ||
| + | |||
| + | <span id="D86" style="font-size: 110%; font-weight: bold;">Twierdzenie D86</span><br/> | ||
| + | Dla <math>n \geqslant 0 \;</math> i <math>\; r \in \mathbb{R}</math> prawdziwe są wzory | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} r^k {\small\binom{n}{k}} = (r + 1)^n</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\frac{r^{k + 1}}{k + 1}} {\small\binom{n}{k}} = {\small\frac{(r + 1)^{n + 1} - 1}{n + 1}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k {\small\binom{n}{k}} = n 2^{n - 1}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} = n (n + 1) 2^{n - 2}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | |||
| + | '''Punkt 1.''' | ||
| + | |||
| + | Ze wzoru dwumianowego natychmiast otrzymujemy | ||
| + | |||
| + | ::<math>(1 + r)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} r^k</math> | ||
| + | |||
| + | '''Punkt 2.''' | ||
| + | |||
| + | Całkując obie strony wzoru dwumianowego | ||
| + | |||
| + | ::<math>(1 + x)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} x^k</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>\int^r_0 (1 + x)^n d x = \sum_{k = 0}^{n} {\small\binom{n}{k}} \int^r_0 x^k d x</math> | ||
| + | |||
| + | ::<math>{\small\frac{(r + 1)^{n + 1} - 1}{n + 1}} = \sum_{k = 0}^{n} {\small\frac{r^{k + 1}}{k + 1}} {\small\binom{n}{k}}</math> | ||
| + | |||
| + | '''Punkt 3.''' | ||
| + | |||
| + | Obliczając pochodną każdej ze stron wzoru dwumianowego | ||
| + | |||
| + | ::<math>(1 + x)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} x^k</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>n (1 + x)^{n - 1} = \sum_{k = 0}^{n} {\small\binom{n}{k}} k x^{k - 1}</math> | ||
| + | |||
| + | Kładąc <math>x = 1</math>, dostajemy dowodzony wzór. | ||
| + | |||
| + | '''Punkt 4.''' | ||
| + | |||
| + | Obliczając drugą pochodną każdej ze stron wzoru dwumianowego | ||
| + | |||
| + | ::<math>(1 + x)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} x^k</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>n(n - 1) (1 + x)^{n - 2} = \sum_{k = 0}^{n} {\small\binom{n}{k}} k (k - 1) x^{k - 1}</math> | ||
| + | |||
| + | Kładąc <math>x = 1</math>, dostajemy | ||
| + | |||
| + | ::<math>n(n - 1) 2^{n - 2} = \sum_{k = 0}^{n} {\small\binom{n}{k}} k (k - 1) = \sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} - \sum_{k = 0}^{n} k {\small\binom{n}{k}} = \sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} - n 2^{n - 1}</math> | ||
| + | |||
| + | Skąd natychmiast wynika dowodzony wzór.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D87" style="font-size: 110%; font-weight: bold;">Twierdzenie D87</span><br/> | ||
| + | Dla <math>n, m \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{m} {\small\binom{n + k}{n}} = {\small\binom{n + m + 1}{n}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Ze wzoru Pascala | ||
| + | |||
| + | ::<math>{\small\binom{a}{k}} = {\small\binom{a - 1}{k}} + {\small\binom{a - 1}{k - 1}}</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>{\small\binom{a - 1}{k}} = {\small\binom{a}{k}} - {\small\binom{a - 1}{k - 1}}</math> | ||
| + | |||
| + | Kładąc <math>a = n + k + 1</math>, mamy | ||
| + | |||
| + | ::<math>{\small\binom{n + k}{k}} = {\small\binom{n + k + 1}{k}} - {\small\binom{n + k}{k - 1}}</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>{\small\binom{n + k}{n}} = {\small\binom{n + k + 1}{n + 1}} - {\small\binom{n + k}{n + 1}}</math> | ||
| + | |||
| + | Wykorzystując powyższy wzór, łatwo pokazujemy, że (zobacz [[#D12|D12]]) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{m} {\small\binom{n + k}{n}} = 1 + \sum_{k = 1}^{m} {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = 1 + \sum_{k = 1}^{m} \left[ {\small\binom{n + k + 1}{n + 1}} - {\small\binom{n + k}{n + 1}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = 1 - \sum_{k = 1}^{m} \left[ {\small\binom{n + k}{n + 1}} - {\small\binom{n + k + 1}{n + 1}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = 1 - \left[ 1 - {\small\binom{n + m + 1}{n + 1}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = {\small\binom{n + m + 1}{n}}</math> | ||
| + | |||
| + | Co kończy dowód.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | === <span style="border-bottom:2px solid #000;">Suma nieoznaczona</span> === | ||
| + | |||
| + | <span id="D88" style="font-size: 110%; font-weight: bold;">Uwaga D88</span><br/> | ||
| + | Sumą nieoznaczoną<ref name="IndefiniteSum1"/> (lub antyróżnicą) funkcji <math>f(k)</math>, będziemy nazywali dowolną funkcję <math>F(k)</math> taką, że | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>F(k + 1) - F (k) = f (k)</math> | ||
| + | </div> | ||
| + | |||
| + | Łatwo zauważamy, że istnieje cała rodzina funkcji <math>F(k)</math>, bo jeżeli <math>F (k)</math> jest sumą nieoznaczoną, to <math>F (k) + C</math>, gdzie <math>C</math> jest stałą, również jest sumą nieoznaczoną. W szczególności | ||
| + | |||
| + | ::<math>\sum_{k = a}^{b} f (k) = \sum_{k = a}^{b} (F (k + 1) - F (k))</math> | ||
| + | |||
| + | ::::<math>\;\;\;\: = - \sum_{k = a}^{b} (F (k) - F (k + 1))</math> | ||
| + | |||
| + | <div style="margin-top: 1.1em; margin-bottom: 1em;"> | ||
| + | ::::<math>\;\;\;\: = - ( F (a) - F (b + 1) )</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1.5em; margin-bottom: 1em;"> | ||
| + | ::::<math>\;\;\;\: = F (b + 1) - F (a)</math> | ||
| + | </div> | ||
| + | |||
| + | Co przez analogię do całki nieoznaczonej możemy zapisać jako | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>\sum_{k = a}^{b} f (k) = F (k) \biggr\rvert_{a}^{b + 1} \qquad \qquad \qquad ( 1 )</math> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | Należy podkreślić różnicę między sumą oznaczoną <math>S(n)</math> a sumą nieoznaczoną <math>F(k)</math>. Niech <math>f(k) = k^2</math>. Oczywiście | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} k^2 = {\small\frac{1}{6}} n (n + 1) (2 n + 1)</math> | ||
| + | |||
| + | ::<math>F(k) = {\small\frac{1}{6}} (k - 1) k (2 k - 1)</math> | ||
| + | |||
| + | Ponieważ dla sumy <math>S(n)</math> prawdziwy jest związek <math>S(n + 1) - S (n) = f (n + 1)</math>, to otrzymujemy <math>F(k) = S (k - 1)</math>. Weźmy kolejny przykład, niech <math>f(k) = r^k</math>, gdzie <math>r</math> jest stałą. Mamy | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} r^k = {\small\frac{r^{n + 1} - 1}{r - 1}}</math> | ||
| + | |||
| + | ale | ||
| + | |||
| + | ::<math>F(k) = {\small\frac{r^k}{r - 1}}</math> | ||
| + | |||
| + | i nie jest prawdą, że <math>F(k) = S (k - 1)</math>, bo pominięty został wyraz <math>{\small\frac{- 1}{r - 1}}</math>, który jest stałą, ale jest to zrozumiałe. | ||
| + | |||
| + | Niech teraz <math>f(n, k) = {\small\binom{n + k}{n}}</math>. Wiemy, że (zobacz [[#D87|D87]]) | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | ::<math>F(n, k) = {\small\frac{k}{n + 1}} {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | Tym razem otrzymujemy zupełnie inne wyniki: suma <math>S(n)</math> nie zależy od dwóch zmiennych, bo jest to niemożliwe, a suma nieoznaczona nadal zależy od <math>k</math>, bo dla <math>F(n, k)</math> musi być prawdziwy wzór <math>(1)</math>. Łatwo widzimy, że | ||
| + | |||
| + | ::<math>S (n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1}</math> | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D89" style="font-size: 110%; font-weight: bold;">Uwaga D89</span><br/> | ||
| + | Powiedzmy, że dysponujemy wzorem <math>S(b) = \sum_{k = a}^{b} f (k)</math> i chcemy udowodnić jego poprawność. W prostych przypadkach możemy wykorzystać indukcję matematyczną: wystarczy pokazać, że | ||
| + | |||
| + | ::<math>S(k + 1) = S (k) + f (k + 1)</math> | ||
| + | |||
| + | Jeżeli już udało nam się pokazać związek <math>f(k) = S (k) - S (k - 1)</math>, to równie dobrze możemy zamienić sumę na sumę teleskopową (zobacz [[#D12|D12]]), aby otrzymać, że | ||
| + | |||
| + | ::<math>\sum_{k = a + 1}^{b} f (k) = \sum_{k = a + 1}^{b} ( S (k) - S (k - 1) )</math> | ||
| + | |||
| + | :::::<math>\;\, = - \sum_{k = a + 1}^{b} ( S (k - 1) - S (k) )</math> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::::<math>\;\, = - ( S (a) - S (b) )</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 2em; margin-bottom: 1em;"> | ||
| + | :::::<math>\;\, = S (b) - S (a)</math> | ||
| + | </div> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>S(b) = \sum_{k = a + 1}^{b} f (k) + S (a) = \sum_{k = a}^{b} f (k)</math> | ||
| + | |||
| + | bo <math>S(a) = f (a)</math>. | ||
| + | |||
| + | |||
| + | W przypadkach bardziej skomplikowanych nie możemy tak postąpić. W poprzedniej uwadze rozważaliśmy sumę | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | ale | ||
| + | |||
| + | ::<math>S(n) - S (n - 1) = {\small\frac{3 n + 1}{2 (n + 1)}} {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | I nie da się pokazać związku <math>S(k) - S (k - 1) = f (n, k)</math>, bo różnica <math>S(k) - S (k - 1)</math> nie zależy od <math>n</math>. | ||
| + | |||
| + | Tutaj z pomocą przychodzi nam suma nieoznaczona. W programie Maxima możemy ją policzyć, wpisując polecenia | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">'''load''' ("zeilberger"); | ||
| + | '''AntiDifference'''('''binomial'''(n+k, n), k);</span> | ||
| + | |||
| + | Otrzymujemy | ||
| + | |||
| + | ::<math>F(n, k) = {\small\frac{k}{n + 1}} {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | Oczywiście | ||
| + | |||
| + | ::<math>F(n, k + 1) - F (n, k) = {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | i | ||
| + | |||
| + | ::<math>S(n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | Podsumujmy. Jakkolwiek znalezienie ogólnego wzoru na sumę <math>S (n) = \sum_{k = 0}^{n} f (k)</math> może być bardzo trudne, to udowodnienie poprawności tego wzoru może być znacznie łatwiejsze (metodą indukcji matematycznej lub obliczając sumę teleskopową). Podobnie jest w bardziej skomplikowanym przypadku, gdy szukamy ogólnego wzoru na sumę <math>S(n) = \sum_{k = 0}^{n} f (n, k)</math>. Tutaj wymienionych przed chwilą metod zastosować nie można, a znalezienie wzoru na sumę nieoznaczoną <math>F(n, k)</math> może być jeszcze trudniejsze, ale gdy już taki wzór mamy, to sprawdzenie jego poprawności, czyli związku <math>F(n, k + 1) - F (n, k) = f (n, k)</math>, może być bardzo łatwe, a wtedy otrzymujemy natychmiast | ||
| + | |||
| + | ::<math>S(n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1}</math> | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D90" style="font-size: 110%; font-weight: bold;">Zadanie D90</span><br/> | ||
| + | Korzystając z programu Maxima znaleźć sumę nieoznaczoną <math>F(n, k)</math> dla funkcji | ||
| + | |||
| + | ::<math>f(n, k) = {\small\frac{1}{(k + 1) (n - k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | i pokazać, że prawdziwy jest wzór <math>C_{n + 1} = \sum_{k = 0}^{n} C_k C_{n - k}</math>, gdzie <math>C_n</math> są liczbami Catalana. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Wpisując w programie Maxima polecenia | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">'''load''' ("zeilberger"); | ||
| + | '''AntiDifference'''( 1/(k+1) * 1/(n-k+1) * '''binomial'''(2*k, k) * '''binomial'''(2*n-2*k, n-k), k);</span> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>F(n, k) = - {\small\frac{(n - 2 k + 1) (2 n - 2 k + 1)}{(n + 1) (n + 2) (n - k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 (n - k)}{n - k}}</math> | ||
| + | |||
| + | Czytelnik bez trudu pokaże, że | ||
| + | |||
| + | ::<math>F(n, k + 1) = - {\small\frac{(2 k + 1) (n - 2 k - 1)}{(n + 1) (n + 2) (k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | oraz łatwo sprawdzi związek <math>F(n, k + 1) - F (n, k) = f (n, k)</math> i wyliczy sumę oznaczoną. | ||
| + | |||
| + | Chcemy zwrócić uwagę na występującą tutaj trudność. Oczywiście | ||
| + | |||
| + | ::<math>S (n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1}</math> | ||
| + | |||
| + | ale funkcja <math>F(n, k)</math> nie jest określona dla <math>k = n + 1</math>. Żeby ominąć ten problem, możemy przekształcić funkcję <math>F(n, k)</math> tak, aby możliwe było obliczenie jej wartości dla <math>k = n + 1</math> | ||
| + | |||
| + | ::<math>F(n, k) = - {\small\frac{n - 2 k + 1}{2 (n + 1) (n + 2)}} {\small\binom{2 k}{k}} {\small\binom{2 (n - k + 1)}{n - k + 1}}</math> | ||
| + | |||
| + | lub zapisać sumę w postaci | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n, k) = \sum_{k = 0}^{n - 1} f (n, k) + f (n, n) = F (n, k) \biggr\rvert_{k = 0}^{k = n} + f (n, n)</math><br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | === <span style="border-bottom:2px solid #000;">Znajdowanie równania rekurencyjnego dla sumy <math>\boldsymbol{S(n)}</math></span> === | ||
| + | |||
| + | <span id="D91" style="font-size: 110%; font-weight: bold;">Uwaga D91</span><br/> | ||
| + | Rozważmy sumę | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} f (n, k)</math> | ||
| + | |||
| + | W twierdzeniach [[#D107|D107]] i [[#D108|D108]] wyliczyliśmy <math>S(n)</math>, znajdując najpierw równanie rekurencyjne dla sumy. Możemy przypuszczać, że równanie rekurencyjne dla sumy <math>S(n)</math> wynika z istnienia odpowiedniego równania rekurencyjnego dla składników sumy <math>f(n, k)</math>. Zagadnieniem tym zajmowała się siostra Mary Celine Fasenmyer, która podała algorytm postępowania<ref name="Fasenmyer1"/><ref name="Fasenmyer2"/>. Prace Zeilbergera oraz Wilfa i Zeilbergera uogólniły ten algorytm<ref name="Zeilberger1"/><ref name="WilfZeilberger1"/>. My przedstawimy jedynie kilka prostych przypadków, które zilustrujemy przykładami. Szersze omówienie tematu Czytelnik znajdzie w książce Petkovšeka, Wilfa i Zeilbergera<ref name="PetkovsekWilfZeilberger1"/>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D92" style="font-size: 110%; font-weight: bold;">Twierdzenie D92</span><br/> | ||
| + | Niech <math>S(n) = \sum_{k = 0}^{n} f (n, k)</math>. Jeżeli składniki sumy <math>f(n, k)</math> spełniają równanie rekurencyjne | ||
| + | |||
| + | ::<math>a \cdot f (n + 1, k + 1) + b \cdot f (n + 1, k) + c \cdot f (n, k + 1) + d \cdot f (n, k) = 0</math> | ||
| + | |||
| + | gdzie współczynniki <math>a, b, c, d</math> są funkcjami tylko <math>n</math>, to suma <math>S (n)</math> spełnia równanie rekurencyjne | ||
| + | |||
| + | ::<math>(a + b) S (n + 1) + (c + d) S (n) - a \cdot f (n + 1, 0) - b \cdot f (n + 1, n + 1) - c [f (n, 0) - f (n, n + 1)] = 0</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Łatwo zauważamy, że | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n + 1, k + 1) = \sum_{j = 1}^{n + 1} f (n + 1, j)</math> | ||
| + | |||
| + | :::::::<math>\;\;\;\,\, = - f (n + 1, 0) + \sum^{n + 1}_{j = 0} f (n + 1, j)</math> | ||
| + | |||
| + | :::::::<math>\;\;\;\,\, = - f (n + 1, 0) + S (n + 1)</math> | ||
| + | |||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n + 1, k) = - f (n + 1, n + 1) + \sum_{k = 0}^{n + 1} f (n + 1, k) =</math> | ||
| + | |||
| + | ::::::<math>\;\;\; = - f (n + 1, n + 1) + S (n + 1)</math> | ||
| + | |||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n, k + 1) = \sum_{j = 1}^{n + 1} f (n, j)</math> | ||
| + | |||
| + | ::::::<math>\;\;\; = - f (n, 0) + f (n, n + 1) + \sum_{j = 0}^{n} f (n, j)</math> | ||
| + | |||
| + | ::::::<math>\;\;\; = - f (n, 0) + f (n, n + 1) + S (n)</math> | ||
| + | |||
| + | |||
| + | Zatem sumując założone równanie rekurencyjne | ||
| + | |||
| + | ::<math>a \cdot f (n + 1, k + 1) + b \cdot f (n + 1, k) + c \cdot f (n, k + 1) + d \cdot f (n, k) = 0</math> | ||
| + | |||
| + | po <math>k</math> od <math>k = 0</math> do <math>k = n</math>, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot [- f (n + 1, 0) + S (n + 1)] + b \cdot [- f (n + 1, n + 1) + S (n + 1)] + c \cdot [- f (n, 0) + f (n, n + 1) + S (n)] + d \cdot S (n) = 0</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>(a + b) S (n + 1) + (c + d) S (n) - a \cdot f (n + 1, 0) - b \cdot f (n + 1, n + 1) - c [f (n, 0) - f (n, n + 1)] = 0</math> | ||
| + | |||
| + | Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D93" style="font-size: 110%; font-weight: bold;">Uwaga D93</span><br/> | ||
| + | Nie ma sensu stosowanie opisanej powyżej metody do prostych sum postaci <math>\sum_{k = 0}^{n} f (k)</math>, bo równanie rekurencyjne otrzymujemy w takim przypadku natychmiast: <math>S(n + 1) - S (n) = f (n + 1)</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D94" style="font-size: 110%; font-weight: bold;">Zadanie D94</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D87|D87]]) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | W tym przypadku nie otrzymamy równania rekurencyjnego, ale od razu wzór ogólny na sumę <math>S(n)</math>. | ||
| + | |||
| + | Oczywiście <math>f(n, k) = {\small\binom{n + k}{n}}</math>. Po podstawieniu do równania (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{f (n + 1, k + 1)}{f (n, k)}} + b \cdot {\small\frac{f (n + 1, k)}{f (n, k)}} + c \cdot {\small\frac{f (n, k + 1)}{f (n, k)}} + d = 0</math> | ||
| + | |||
| + | i zredukowaniu silni, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{(n + k + 1) (n + k + 2)}{(k + 1) (n + 1)}} + b \cdot {\small\frac{n + k + 1}{n + 1}} + c \cdot {\small\frac{n + k + 1}{k + 1}} + d = 0</math> | ||
| + | |||
| + | Sprowadzając do wspólnego mianownika, mamy | ||
| + | |||
| + | ::<math>(a + b) k^2 + ((2 a + b + c + d) n + 3 a + 2 b + c + d) k + (a + c) n^2 + (3 a + b + 2 c + d) n + 2 a + b + c + d = 0</math> | ||
| + | |||
| + | Ponieważ powyższe równanie musi być prawdziwe dla każdego <math>k</math>, to współczynniki przy potęgach <math>k</math> muszą być równe zero. Zatem dostajemy układ równań | ||
| + | |||
| + | ::<math> | ||
| + | \begin{cases} | ||
| + | a + b = 0 \\ | ||
| + | (2 a + b + c + d) n + 3 a + 2 b + c + d = 0 \\ | ||
| + | (a + c) n^2 + (3 a + b + 2 c + d) n + 2 a + b + c + d = 0 \\ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Łatwo znajdujemy rozwiązania: <math>b = - a</math>, <math>c = - a</math>, <math>d = 0</math>. Skąd wynika związek dla <math>S(n)</math> (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>- a S (n) = a - a {\small\binom{2 n + 2}{n + 1}} - a \left( 1 - {\small\binom{2 n + 1}{n}} \right)</math> | ||
| + | |||
| + | ::::<math>\;\;\: = - a \left[ {\small\binom{2 n + 2}{n + 1}} - {\small\binom{2 n + 1}{n}} \right]</math> | ||
| + | |||
| + | ::::<math>\;\;\: = - a {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | I otrzymaliśmy dowodzony wzór. | ||
| + | |||
| + | |||
| + | Do obliczeń wykorzystaliśmy oprogramowanie Maxima. Poniżej podajemy kod procedury.<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \\ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum1() := | ||
| + | ( | ||
| + | f(n, k):= '''binomial'''(n+k, n), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n,k) ), | ||
| + | F1: a * f(n+1,k+1)/f(n,k) + b * f(n+1,k)/f(n,k) + c * f(n,k+1)/f(n,k) + d, /* równanie rekurencyjne dla składników sumy f(n, k) */<!--\\--> | ||
| + | S1: (a+b) * S[n+1] + (c+d) * S[n] - a * f(n+1, 0) - b * f(n+1, n+1) - c * ( f(n, 0) - f(n, n+1) ), /* równanie rekurencyjne dla sumy S(n) */<!--\\--> | ||
| + | /* przekształcamy F1, S1 */<!--\\--> | ||
| + | F2: '''minfactorial'''( '''makefact'''(F1) ), /* zamień na silnie i uprość silnie */<!--\\--> | ||
| + | '''print'''("równanie: ", F2),<!--\\--> | ||
| + | F3: '''num'''( '''factor'''(F2) ), /* faktoryzuj i weź licznik */<!--\\--> | ||
| + | '''print'''("licznik = ", '''rat'''(F3, k)),<!--\\--> | ||
| + | deg: '''hipow'''(F3, k),<!--\\--> | ||
| + | '''print'''("stopień = ", deg), | ||
| + | /* stopień wielomianu F3 jest równy deg i mamy deg+1 równań */<!--\\--> | ||
| + | LE: ['''subst'''(0, k, F3) = 0],<!--\\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F3, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\\--> | ||
| + | '''print'''("lista równań: ", LE), | ||
| + | sol: '''solve'''( LE, [a, b, c, d] ), /* lista rozwiązań */ | ||
| + | '''print'''("rozwiązanie: ", sol), | ||
| + | S2: '''minfactorial'''( '''makefact'''(S1) ), /* zamień na silnie i uprość silnie */<!--\\--> | ||
| + | S3: '''subst'''( sol[1], S2 ), /* pierwszy element listy sol */<!--\\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\\--> | ||
| + | '''solve'''( S4 = 0, S[n] )<!--\\--> | ||
| + | /* S[n] = (2*n+1)! / (n! * (n+1)!) */ | ||
| + | )$</span> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D95" style="font-size: 110%; font-weight: bold;">Zadanie D95</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D86|D86]] p.1) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} r^k {\small\binom{n}{k}} = (r + 1)^n</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Oczywiście <math>f(n, k) = r^k {\small\binom{n}{k}}</math>. Po podstawieniu do równania (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{f (n + 1, k + 1)}{f (n, k)}} + b \cdot {\small\frac{f (n + 1, k)}{f (n, k)}} + c \cdot {\small\frac{f (n, k + 1)}{f (n, k)}} + d = 0</math> | ||
| + | |||
| + | i zredukowaniu silni, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{(n + 1) r}{k + 1}} + b \cdot {\small\frac{n + 1}{n - k + 1}} + c \cdot {\small\frac{(n - k) r}{k + 1}} + d = 0</math> | ||
| + | |||
| + | Sprowadzając do wspólnego mianownika, mamy | ||
| + | |||
| + | ::<math>(c r - d) k^2 + (- ((a + 2 c) n + a + c) r + (b + d) n + b) k + ((a + c) n^2 + (2 a + c) n + a) r + (b + d) n + b + d = 0</math> | ||
| + | |||
| + | Ponieważ powyższe równanie musi być prawdziwe dla każdego <math>k</math>, to współczynniki przy potęgach <math>k</math> muszą być równe zero. Zatem dostajemy układ równań | ||
| + | |||
| + | ::<math> | ||
| + | \begin{cases} | ||
| + | c r - d = 0 \\ | ||
| + | - ((a + 2 c) n + a + c) r + (b + d) n + b = 0 \\ | ||
| + | ((a + c) n^2 + (2 a + c) n + a) r + (b + d) n + b + d = 0 \\ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Łatwo znajdujemy rozwiązania: <math>b = 0</math>, <math>c = - a</math>, <math>d = - a \cdot r</math>. Skąd wynika związek dla <math>S(n)</math> (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>S(n + 1) = (r + 1) S (n)</math> | ||
| + | |||
| + | Metodą indukcji matematycznej dowodzimy, że <math>S(n) = (r + 1)^n</math>. | ||
| + | |||
| + | |||
| + | Do obliczeń wykorzystaliśmy oprogramowanie Maxima. Poniżej podajemy kod procedury.<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \\ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum2() := | ||
| + | ( | ||
| + | f(n, k):= r^k * '''binomial'''(n, k), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n,k) ), | ||
| + | F1: a * f(n+1,k+1)/f(n,k) + b * f(n+1,k)/f(n,k) + c * f(n,k+1)/f(n,k) + d, /* równanie rekurencyjne dla składników sumy f(n, k) */<!--\\--> | ||
| + | S1: (a+b) * S[n+1] + (c+d) * S[n] - a * f(n+1, 0) - b * f(n+1, n+1) - c * ( f(n, 0) - f(n, n+1) ), /* równanie rekurencyjne dla sumy S(n) */<!--\\--> | ||
| + | /* przekształcamy F1, S1 */<!--\\--> | ||
| + | F2: '''minfactorial'''( '''makefact'''(F1) ), /* zamień na silnie i uprość silnie */<!--\\--> | ||
| + | '''print'''("równanie: ", F2),<!--\\--> | ||
| + | F3: '''num'''( '''factor'''(F2) ), /* faktoryzuj i weź licznik */<!--\\--> | ||
| + | '''print'''("licznik = ", '''rat'''(F3, k)),<!--\\--> | ||
| + | deg: '''hipow'''(F3, k),<!--\\--> | ||
| + | '''print'''("stopień = ", deg), | ||
| + | /* stopień wielomianu F3 jest równy deg i mamy deg+1 równań */<!--\\--> | ||
| + | LE: ['''subst'''(0, k, F3) = 0],<!--\\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F3, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\\--> | ||
| + | '''print'''("lista równań: ", LE), | ||
| + | sol: '''solve'''( LE, [a, b, c, d] ), /* lista rozwiązań */ | ||
| + | '''print'''("rozwiązanie: ", sol), | ||
| + | S2: '''minfactorial'''( '''makefact'''(S1) ), /* zamień na silnie i uprość silnie */<!--\\--> | ||
| + | S3: '''subst'''( sol[1], S2), /* pierwszy element listy sol */<!--\\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\\--> | ||
| + | /* S[n+1] = (r+1)*S[n] */ | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S4 = 0, S[n] ) /* S[n] = C*(r+1)^n */<!--\\--> | ||
| + | )$</span> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D96" style="font-size: 110%; font-weight: bold;">Zadanie D96</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D86|D86]] p.2) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{n}{k}} = {\small\frac{2^{n + 1} - 1}{n + 1}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Oczywiście <math>f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math>. Po podstawieniu do równania (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{f (n + 1, k + 1)}{f (n, k)}} + b \cdot {\small\frac{f (n + 1, k)}{f (n, k)}} + c \cdot {\small\frac{f (n, k + 1)}{f (n, k)}} + d = 0</math> | ||
| + | |||
| + | i zredukowaniu silni, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{n + 1}{k + 2}} + b \cdot {\small\frac{n + 1}{n - k + 1}} + c \cdot {\small\frac{n - k}{k + 2}} + d = 0</math> | ||
| + | |||
| + | Sprowadzając do wspólnego mianownika, mamy | ||
| + | |||
| + | ::<math>(c - d) k^2 + ((- a + b - 2 c + d) n - a + b - c - d) k + (a + c) n^2 + (2 a + 2 b + c + 2 d) n + a + 2 b + 2 d = 0</math> | ||
| + | |||
| + | Ponieważ powyższe równanie musi być prawdziwe dla każdego <math>k</math>, to współczynniki przy potęgach <math>k</math> muszą być równe zero. Zatem dostajemy układ równań | ||
| + | |||
| + | ::<math> | ||
| + | \begin{cases} | ||
| + | c - d = 0 \\ | ||
| + | (- a + b - 2 c + d) n - a + b - c - d = 0 \\ | ||
| + | (a + c) n^2 + (2 a + 2 b + c + 2 d) n + a + 2 b + 2 d = 0 \\ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Łatwo znajdujemy rozwiązania: <math>b = 0</math>, <math>c = - a \cdot {\small\frac{n + 1}{n + 2}}</math>, <math>d = - a \cdot {\small\frac{n + 1}{n + 2}}</math>. Skąd wynika związek dla <math>S(n)</math> (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>(n + 2) S (n + 1) = 2 (n + 1) S (n) + 1</math> | ||
| + | |||
| + | Metodą indukcji matematycznej łatwo dowodzimy, że <math>S(n) = {\small\frac{2^{n + 1} - 1}{n + 1}}</math>. | ||
| + | |||
| + | |||
| + | Do obliczeń wykorzystaliśmy oprogramowanie Maxima. Poniżej podajemy kod procedury.<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \\ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum3() := | ||
| + | ( | ||
| + | f(n, k):= 1/(k+1) * '''binomial'''(n, k), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n,k) ), | ||
| + | F1: a * f(n+1,k+1)/f(n,k) + b * f(n+1,k)/f(n,k) + c * f(n,k+1)/f(n,k) + d, /* równanie rekurencyjne dla składników sumy f(n, k) */<!--\\--> | ||
| + | S1: (a+b) * S[n+1] + (c+d) * S[n] - a * f(n+1, 0) - b * f(n+1, n+1) - c * ( f(n, 0) - f(n, n+1) ), /* równanie rekurencyjne dla sumy S(n) */<!--\\--> | ||
| + | /* przekształcamy F1, S1 */<!--\\--> | ||
| + | F2: '''minfactorial'''( '''makefact'''(F1) ), /* zamień na silnie i uprość silnie */<!--\\--> | ||
| + | '''print'''("równanie: ", F2),<!--\\--> | ||
| + | F3: '''num'''( '''factor'''(F2) ), /* faktoryzuj i weź licznik */<!--\\--> | ||
| + | '''print'''("licznik = ", '''rat'''(F3, k)),<!--\\--> | ||
| + | deg: '''hipow'''(F3, k),<!--\\--> | ||
| + | '''print'''("stopień = ", deg), | ||
| + | /* stopień wielomianu F3 jest równy deg i mamy deg+1 równań */<!--\\--> | ||
| + | LE: ['''subst'''(0, k, F3) = 0],<!--\\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F3, k^i)=0, LE), /* kolejne równania wpisujemy do listy LE */<!--\\--> | ||
| + | '''print'''("lista równań: ", LE), | ||
| + | sol: '''solve'''( LE, [a, b, c, d] ), /* lista rozwiązań */ | ||
| + | '''print'''("rozwiązanie: ", sol), | ||
| + | S2: '''minfactorial'''( '''makefact'''(S1) ), /* zamień na silnie i uprość silnie */<!--\\--> | ||
| + | S3: '''subst'''( sol[1], S2), /* pierwszy element listy sol */<!--\\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\\--> | ||
| + | /* (n+2)*S[n+1] = 2*(n+1)*S[n] + 1 */ | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S4 = 0, S[n] ) /* S[n] = ( (C+1) * 2^n - 1 )/(n + 1) */<!--\\--> | ||
| + | )$</span> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D97" style="font-size: 110%; font-weight: bold;">Zadanie D97</span><br/> | ||
| + | Niech <math>n \in \mathbb{N}_0 \;</math> i <math>\; k \in \mathbb{Z}</math>. Uzasadnić, dlaczego przyjmujemy, że <math>{\small\binom{n}{k}} = 0</math>, gdy <math>k < 0 \;</math> lub <math>\; k > n</math>. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Jeżeli zapiszmy <math>{\small\binom{n}{k}}</math> w postaci | ||
| + | |||
| + | ::<math>{\small\binom{n}{k}} = {\small\frac{n!}{k! (n - k) !}} = {\small\frac{n \cdot (n - 1) \cdot \ldots \cdot (n - k + 1)}{k!}}</math> | ||
| + | |||
| + | to natychmiast widzimy, że prawa strona musi być równa zero dla <math>k > n</math>. | ||
| + | |||
| + | Jeżeli we wzorze Pascala | ||
| + | |||
| + | ::<math>{\small\binom{n}{k}} = {\small\binom{n - 1}{k}} + {\small\binom{n - 1}{k - 1}}</math> | ||
| + | |||
| + | położymy <math>n = m + 1 \;</math> i <math>\; k = 0</math>, to otrzymamy | ||
| + | |||
| + | ::<math>1 = 1 + {\small\binom{m}{- 1}}</math> | ||
| + | |||
| + | czyli <math>{\small\binom{m}{- 1}} = 0</math> | ||
| + | |||
| + | I tak samo dla wszystkich <math>k < 0</math>. | ||
| + | |||
| + | |||
| + | Znacznie mocniejszego uzasadnienia dostarczy nam funkcja gamma (zobacz [[#D110|D110]]), która jest uogólnieniem silni na liczby rzeczywiste. Rozważmy funkcję | ||
| + | |||
| + | ::<math>g(n, x) = {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1) \Gamma (n - x + 1)}}</math> | ||
| + | |||
| + | Jeżeli <math>k \in \mathbb{Z} \;</math> i <math>\; 0 \leqslant k \leqslant n</math>, to funkcja <math>g(n, k)</math> jest równa współczynnikowi dwumianowemu <math>{\small\binom{n}{k}}</math>. | ||
| + | |||
| + | ::<math>g(n, k) = {\small\frac{\Gamma (n + 1)}{\Gamma (k + 1) \Gamma (n - k + 1)}} = {\small\frac{n!}{k! (n - k) !}} = {\small\binom{n}{k}}</math> | ||
| + | |||
| + | |||
| + | W przypadku, gdy <math>k < 0</math>, mamy | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow k} g (n, x) = \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1) \Gamma (n - x + 1)}} = \lim_{x \rightarrow k} {\small\frac{1}{\Gamma (x + 1)}} \cdot \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (n - x + 1)}} = 0 \cdot {\small\frac{\Gamma (n + 1)}{\Gamma (n - k + 1)}} = 0</math> | ||
| + | |||
| + | |||
| + | W przypadku, gdy <math>k > n</math>, dostajemy | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow k} g (n, x) = \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1) \Gamma (n - x + 1)}} = \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1)}} \cdot \lim_{x \rightarrow k} {\small\frac{1}{\Gamma (n - x + 1)}} = {\small\frac{\Gamma (n + 1)}{\Gamma (k + 1)}} \cdot 0 = 0</math> | ||
| + | |||
| + | |||
| + | Co najlepiej wyjaśnia, dlaczego przyjmujemy, że <math>{\small\binom{n}{k}} = 0</math>, gdy <math>k < 0 \;</math> lub <math>\; k > n</math>.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D98" style="font-size: 110%; font-weight: bold;">Twierdzenie D98</span><br/> | ||
| + | Niech <math>n, I, J \in \mathbb{N}_0 \;</math> i <math>\; k \in \mathbb{Z}</math>. Jeżeli <math>f(n, k) = 0</math> | ||
| + | dla <math>k \notin [0, n] \,</math> i składniki sumy <math>f(n, k)</math> spełniają równanie rekurencyjne | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = 0</math> | ||
| + | |||
| + | gdzie współczynniki <math>a_{i j}</math> są funkcjami tylko <math>n</math>, to suma | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} f (n, k)</math> | ||
| + | |||
| + | spełnia następujące równanie rekurencyjne | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} S (n + i) \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Z założenia <math>f(n, k) = 0</math> dla <math>k \notin [0, n]</math>, zatem sumę <math>S(n)</math> możemy zapisać w postaci | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} f (n, k) = \sum_{k = - \infty}^{+ \infty} f (n, k)</math> | ||
| + | |||
| + | Niech <math>0 \leqslant i \leqslant I</math> oraz <math>0 \leqslant j \leqslant J</math>. Rozważmy sumę | ||
| + | |||
| + | ::<math>\sum_{k = - J}^{n + I} f (n + i, k + j)</math> | ||
| + | |||
| + | Zauważmy, że <math>f(n + i, k + j) = 0</math> dla <math>k \notin [- J, n + I]</math>, bo | ||
| + | |||
| + | :* dla <math>k < - J</math> mamy <math>k + j < - J + j \leqslant 0</math> | ||
| + | :* dla <math>k > n + I</math> mamy <math>k + j > n + I + j \geqslant n + I \geqslant n + i</math> | ||
| + | |||
| + | Wynika stąd, że rozszerzając rozpatrywaną sumę na cały zbiór liczb całkowitych, nie zmienimy wartości sumy. Czyli, że | ||
| + | |||
| + | ::<math>\sum_{k = - J}^{n + I} f (n + i, k + j) = \sum_{k = - \infty}^{+ \infty} f (n + i, k + j)</math> | ||
| + | |||
| + | |||
| + | Teraz już łatwo otrzymujemy równanie rekurencyjne dla sumy <math>S(n)</math> | ||
| + | |||
| + | ::<math>0 = \sum_{k = - J}^{n + I} \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{k = - J}^{n + I} f (n + i, k + j) \,</math><span style="color: Green"><sup>[a]</sup></span> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{k = - \infty}^{+ \infty} f (n + i, k + j)</math> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum^{+ \infty}_{l = - \infty} f (n + i, l)</math> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot S (n + i)</math> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} S (n + i) \left[ \sum_{j = 0}^{J} a_{i j} \right]</math> | ||
| + | |||
| + | Co należało pokazać. | ||
| + | |||
| + | |||
| + | <hr style="width: 25%; height: 2px; " /> | ||
| + | <span style="color: Green">[a]</span> W przypadku wielokrotnych sum skończonych możemy dowolnie zmieniać ich kolejność ze względu na łączność dodawania.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D99" style="font-size: 110%; font-weight: bold;">Uwaga D99</span><br/> | ||
| + | Z zadania [[#D97|D97]] wynika, że jeżeli funkcja <math>f(n, k)</math> zawiera czynnik <math>{\small\binom{n}{k}}</math>, to może spełniać warunek <math>f(n, k) = 0</math> dla <math>k \notin [0, n]</math>. Oczywiście nie jest to warunek wystarczający, bo funkcja <math>f (n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math> jest różna od zera dla <math>k = - 1</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D100" style="font-size: 110%; font-weight: bold;">Zadanie D100</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D86|D86]] p.3) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k {\small\binom{n}{k}} = n 2^{n - 1}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Oczywiście <math>f(n, k) = k {\small\binom{n}{k}}</math>. Do rozwiązania problemu wykorzystamy oprogramowanie Maxima i procedurę<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \\ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum5(I, J) := | ||
| + | ( | ||
| + | '''read'''("podaj definicję f(n, k)"), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n, k) ), | ||
| + | F1: '''sum'''( '''sum'''( a[i,j] * f(n+i, k+j), i, 0, I), j, 0, J) / f(n, k),<!--\\--> | ||
| + | F2: '''num'''( '''factor'''( '''minfactorial'''( '''makefact'''( '''expand'''( F1 ) ) ) ) ),<!--\\--> | ||
| + | deg: '''hipow'''(F2, k),<!--\\--> | ||
| + | LE: ['''subst'''(0, k, F2) = 0],<!--\\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F2, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\\--> | ||
| + | LV: '''create_list'''(a[i, j], i, 0, I , j, 0, J), /* lista zmiennych */ | ||
| + | sol: '''solve'''( LE, LV ), /* lista rozwiązań */ | ||
| + | S1: '''sum'''( S[n+i] * '''sum'''(a[i,j], j, 0, J), i, 0, I),<!--\\--> | ||
| + | S2: '''subst'''( sol[1], S1 ), /* pierwszy element listy sol */<!--\\--> | ||
| + | S3: '''num'''( '''factor'''( '''expand'''( S2 ) ) ),<!--\\--> | ||
| + | '''print'''("rekurencja: ", S3 = 0),<!--\\--> | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S3 = 0, S[n] )<!--\\--> | ||
| + | )$</span> | ||
| + | |||
| + | |||
| + | Wywołujemy procedurę <span style="font-size: 90%; color:black;"><code>sum5(1, 2)</code></span> i wpisujemy funkcję | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">f(n, k):= k * '''binomial'''(n, k)</span> | ||
| + | |||
| + | W wyniku otrzymujemy równanie rekurencyjne | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">n * S[n+1] = 2 * (n+1) * S[n]</span> | ||
| + | |||
| + | którego rozwiązanie jest postaci | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">S[n] = C * n * 2^(n-1)</span> | ||
| + | |||
| + | Łatwo sprawdzamy, że <span style="font-size: 90%; color:black;"><code>C = 1</code></span>. Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D101" style="font-size: 110%; font-weight: bold;">Zadanie D101</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwe są wzory | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} = n (n + 1) 2^{n - 2}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^3 {\small\binom{n}{k}} = n^2 (n + 3) 2^{n - 3}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\binom{n}{k}}^2 = {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k {\small\binom{n}{k}}^2 = {\small\frac{1}{2}} n {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^2 {\small\binom{n}{k}}^2 = n^2 {\small\binom{2 n - 2}{n - 1}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^3 {\small\binom{n}{k}}^2 = {\small\frac{1}{2}} n^2 (n + 1) {\small\binom{2 n - 2}{n - 1}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Wskazówki: | ||
| + | |||
| + | Korzystamy z procedury <span style="font-size: 90%; color:black;"><code>sum5()</code></span>, której kod został podany w zadaniu [[#D100|D100]]. | ||
| + | |||
| + | Zawsze próbujemy znaleźć rozwiązanie dla najmniejszych wartości parametrów <span style="font-size: 90%; color:black;"><code>I, J</code></span>. | ||
| + | |||
| + | ::<math>\Gamma \left( n + {\small\frac{1}{2}} \right) = 2^{- 2 n} \sqrt{\pi} \cdot {\small\frac{(2 n) !}{n!}} = 2^{- 2 n} \sqrt{\pi} \cdot n! \cdot {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | '''Punkt 1.''' <span style="font-size: 90%; color:black;"><code>sum5(1, 2)</code></span>, zobacz też <span style="font-size: 90%; color:black;"><code>sum5(2, 1)</code></span> | ||
| + | |||
| + | '''Punkt 2.''' <span style="font-size: 90%; color:black;"><code>sum5(1, 3)</code></span>, zobacz też <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 3.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 4.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 5.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 6.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 3)</code></span>, zobacz też <span style="font-size: 90%; color:black;"><code>sum5(3, 2)</code></span><br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D102" style="font-size: 110%; font-weight: bold;">Uwaga D102</span><br/> | ||
| + | Niech <math>S(n) = \sum_{k = 0}^{n} f (n, k)</math>. Wiemy (zobacz [[#D98|D98]]), że jeżeli dla dowolnego <math>n</math> wartość funkcji <math>f(n, k)</math> jest określona dla wszystkich <math>k \in \mathbb{Z} \;</math> i <math>\; f(n, k) = 0</math> dla <math>k \notin [0, n]</math>, to sumę <math>S(n)</math> możemy zapisać w równoważnej postaci | ||
| + | <math>S(n) = \sum_{k = 0}^{n} f (n, k) = \sum_{k \in \mathbb{Z}} f (n, k)</math> | ||
| + | |||
| + | |||
| + | Rozważmy teraz funkcję <math>f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math>, która powyższego warunku nie spełnia, bo jest różna od zera dla <math>k = - 1</math>. Jeżeli zapiszemy <math>f(n, k)</math> w postaci | ||
| + | |||
| + | ::<math>f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}} = {\small\frac{1}{k + 1}} \cdot {\small\frac{n!}{k! (n - k) !}} = {\small\frac{n!}{(k + 1) ! (n - k) !}}</math> | ||
| + | |||
| + | to natychmiast widzimy, że | ||
| + | |||
| + | ::<math>f(n, - 1) = {\small\frac{n!}{0! (n + 1) !}} = {\small\frac{1}{n + 1}}</math> | ||
| + | |||
| + | Zatem w przypadku tej funkcji mamy | ||
| + | |||
| + | ::<math>\sum_{k \in \mathbb{Z}} f (n, k) = \sum_{k = 0}^{n} f (n, k) + f (n, - 1) = S (n) + {\small\frac{1}{n + 1}}</math> | ||
| + | |||
| + | |||
| + | '''Zakładając''', że spełnione jest równanie | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = 0</math> | ||
| + | |||
| + | otrzymujemy następujące równanie rekurencyjne dla sumy <math>S(n) = \sum_{k \in \mathbb{Z}} f (n, k)</math> | ||
| + | |||
| + | ::<math>\sum_{k \in \mathbb{Z}} \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{k \in \mathbb{Z}} f (n + i, k + j)</math> | ||
| + | |||
| + | :::::::::::<math>\;\;\;\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{l \in \mathbb{Z}} f (n + i, l)</math> | ||
| + | |||
| + | :::::::::::<math>\;\;\;\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \left[ S (n + i) + {\small\frac{1}{n + i + 1}} \right]</math> | ||
| + | |||
| + | :::::::::::<math>\;\;\;\, = \sum_{i = 0}^{I} \left[ S (n + i) + {\small\frac{1}{n + i + 1}} \right] \cdot \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0</math> | ||
| + | |||
| + | |||
| + | Jeżeli mamy skończoną liczbę punktów <math>k_r \notin [0, n]</math>, w których funkcja <math>f(n, k)</math> jest określona i różna od zera, to możemy zdefiniować funkcję | ||
| + | |||
| + | ::<math>T(n) = f (n, k_1) + f (n, k_2) + f (n, k_3) + \ldots = \sum_r f (n, k_r)</math> | ||
| + | |||
| + | W takim przypadku otrzymamy następujące równanie rekurencyjne dla sumy <math>S (n) = \sum_{k = 0}^{n} f (n, k)</math> | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} [S (n + i) + T (n + i)] \cdot \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0</math> | ||
| + | |||
| + | |||
| + | Wystarczy drobna modyfikacja procedury <span style="font-size: 90%; color:black;"><code>sum5()</code></span>, aby obejmowała ona również takie przypadki<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \\ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum6(I, J):= | ||
| + | ( | ||
| + | '''read'''("podaj definicję f(n, k)"), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n, k) ), | ||
| + | '''read'''("podaj definicję T(n)"), /* suma skończonych wartości funkcji f(n, k), gdzie k<0 lub k>n */ | ||
| + | '''print'''("T(n) = ", T(n) ), | ||
| + | F1: '''sum'''( '''sum'''( a[i,j] * f(n+i, k+j), i, 0, I), j, 0, J) / f(n, k),<!--\\--> | ||
| + | F2: '''num'''( '''factor'''( '''minfactorial'''( '''makefact'''( '''expand'''( F1 ) ) ) ) ),<!--\\--> | ||
| + | deg: '''hipow'''(F2, k),<!--\\--> | ||
| + | LE: ['''subst'''(0, k, F2) = 0],<!--\\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F2, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\\--> | ||
| + | LV: '''create_list'''(a[i, j], i, 0, I , j, 0, J), /* lista zmiennych */ | ||
| + | sol: '''solve'''( LE, LV ), /* lista rozwiązań */ | ||
| + | S1: '''sum'''( ( S[n+i] + T(n+i) ) * '''sum'''( a[i,j], j, 0, J ), i, 0, I ),<!--\\--> | ||
| + | S2: '''num'''( '''factor'''( '''minfactorial'''( '''makefact'''( '''expand'''( S1 ) ) ) ) ),<!--\\--> | ||
| + | S3: '''subst'''( sol[1], S2 ), /* pierwszy element listy sol */<!--\\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\\--> | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S4 = 0, S[n] )<!--\\--> | ||
| + | )$</span> | ||
| + | |||
| + | |||
| + | Korzystając z powyższej procedury, Czytelnik może łatwo policzyć wypisane poniżej sumy. | ||
| + | |||
| + | ::{| class="wikitable plainlinks" style="font-size: 90%; text-align: center; margin-right: auto;" | ||
| + | |- | ||
| + | ! <math>\boldsymbol{f(n,k)}</math> || <math>\boldsymbol{f(n,-1)}</math> || <math>\boldsymbol{f(n,-2)}</math> || <math>\boldsymbol{\sum_{k = 0}^n f(n,k)}</math> || WolframAlpha | ||
| + | |- | ||
| + | | <math>{\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math> || <math>{\small\frac{1}{n + 1}}</math> || <math>0</math> || <math>{\small\frac{2^{n + 1} - 1}{n + 1}}</math> || [https://www.wolframalpha.com/input?i=Sum%5B1%2F%28k%2B1%29+*+binomial%28n%2Ck%29%2C+%7Bk%2C+0%2C+n%7D%5D LINK1] | ||
| + | |- | ||
| + | | <math>{\small\frac{1}{k + 2}} {\small\binom{n}{k}}</math> || <math>0</math> || <math>- {\small\frac{1}{(n + 1) (n + 2)}}</math> || <math>{\small\frac{n 2^{n + 1} + 1}{(n + 1) (n + 2)}}</math> || [https://www.wolframalpha.com/input?i=Sum%5B1%2F%28k%2B2%29+*+binomial%28n%2C+k%29%2C+%7Bk%2C+0%2C+n%7D%5D LINK2] | ||
| + | |- | ||
| + | | <math>{\small\frac{1}{(k + 1) (k + 2)}} {\small\binom{n}{k}}</math> || <math>{\small\frac{1}{n + 1}}</math> || <math>{\small\frac{1}{(n + 1) (n + 2)}}</math> || <math>{\small\frac{2^{n + 2} - n - 3}{(n + 1) (n + 2)}}</math> || [https://www.wolframalpha.com/input?i=Sum%5B1%2F%28k%2B1%29+*+1%2F%28k%2B2%29+*+binomial%28n%2C+k%29%2C+%7Bk%2C+0%2C+n%7D%5D LINK3] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D103" style="font-size: 110%; font-weight: bold;">Zadanie D103</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = 4^n</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Zauważmy, że składniki sumy są równe zero dla <math>k \notin [0, n]</math> (zobacz zadanie [[#D115|D115]]). Zatem korzystając z procedury <span style="font-size: 90%; color:black;"><code>sum6(2, 1)</code></span>, otrzymujemy równanie rekurencyjne | ||
| + | |||
| + | ::<math>(n + 2) S (n + 2) - 4 (2 n + 3) S (n + 1) + 16 (n + 1) S (n) = 0</math> | ||
| + | |||
| + | i rozwiązanie | ||
| + | |||
| + | ::<math>S(n) = C \cdot 4^n</math> | ||
| + | |||
| + | Łatwo sprawdzamy, że <math>C = 1</math>.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D104" style="font-size: 110%; font-weight: bold;">Zadanie D104</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Zauważmy, że składniki sumy są równe zero dla <math>k \notin [0, n]</math> (zobacz [[#D115|D115]]) poza punktem <math>k = - 1</math>. Wiemy, że (zobacz [[#D116|D116]]) | ||
| + | |||
| + | ::<math>\lim_{k \rightarrow - 1} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} = - {\small\frac{1}{2}}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>\lim_{k \rightarrow - 1} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = - {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>f(n, - 1) = - {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | |||
| + | Korzystając z procedury <span style="font-size: 90%; color:black;"><code>sum6(2, 1)</code></span>, otrzymujemy równanie rekurencyjne | ||
| + | |||
| + | ::<math>(n^2 + 5 n + 6) S (n + 2) - 8 (n^2 + 4 n + 4) S (n + 1) + 16 (n^2 + 3 n + 2) S (n) + 2 \cdot {\small\frac{(2 n + 2) !}{[(n + 1) !]^2}} = 0</math> | ||
| + | |||
| + | ::<math>(n + 2) (n + 3) S (n + 2) - 8 (n + 2)^2 S (n + 1) + 16 (n + 1) (n + 2) S (n) + 2 \cdot {\small\frac{(2 n + 2) !}{[(n + 1) !]^2}} = 0</math> | ||
| + | |||
| + | ::<math>(n + 3) S (n + 2) - 8 (n + 2) S (n + 1) + 16 (n + 1) S (n) + 2 \cdot {\small\frac{(2 n + 2) !}{(n + 1) ! (n + 2) !}} = 0</math> | ||
| + | |||
| + | Maxima nie potrafi rozwiązać tego równania rekurencyjnego, ale można sprawdzić, że <math>S(n) = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> jest jego rozwiązaniem.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Uzupełnienie == | ||
| + | |||
| + | | ||
| + | |||
| + | === <span style="border-bottom:2px solid #000; padding-bottom: 0.2em">Dowód własności liczb Catalana <math>{\small C_{n + 1} = \textstyle\sum_{k = 0}^{n} C_k C_{n - k}}</math></span> === | ||
| + | |||
| + | <span id="D105" style="font-size: 110%; font-weight: bold;">Uwaga D105</span><br/> | ||
| + | Przedstawiony poniżej dowód czwartego punktu twierdzenia [[#D84|D84]] został oparty na pracy Jovana Mikicia<ref name="JovanMikic1"/>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D106" style="font-size: 110%; font-weight: bold;">Twierdzenie D106</span><br/> | ||
| + | Jeżeli funkcja <math>f(k)</math> nie zależy od <math>n</math> i dane są sumy | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} f (k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | ::<math>T(n) = \sum_{k = 0}^{n} (n - k) f (k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | to | ||
| + | |||
| + | ::<math>T(n) = 4 T (n - 1) + 2 S (n - 1)</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Z definicji sumy <math>T(n)</math> ostatni wyraz tej sumy jest równy zero, zatem dla <math>n \geqslant 1</math> mamy | ||
| + | |||
| + | ::<math>T(n) = \sum_{k = 0}^{n - 1} (n - k) f (k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = \sum_{k = 0}^{n - 1} (n - k) f (k) \cdot {\small\frac{(2 n - 2 k) (2 n - 2 k - 1)}{(n - k)^2}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k - 2}{n - k - 1}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = \sum_{k = 0}^{n - 1} 2 (2 n - 2 k - 1) f (k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k - 2}{n - k - 1}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = \sum_{k = 0}^{n - 1} [4 (n - 1 - k) + 2] f (k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k - 2}{n - k - 1}}</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>T(n) = 4 T (n - 1) + 2 S (n - 1)</math> | ||
| + | |||
| + | Co kończy dowód.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D107" style="font-size: 110%; font-weight: bold;">Twierdzenie D107</span><br/> | ||
| + | Dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = 4^n</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Niech | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | ::<math>T(n) = \sum_{k = 0}^{n} (n - k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | Zauważmy, że | ||
| + | |||
| + | ::<math>T(n) = \sum_{k = 0}^{n} (n - k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = {\small\frac{1}{2}} \left[ \sum_{k = 0}^{n} (n - k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} + \sum_{k = 0}^{n} (n - k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} \right]</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = {\small\frac{1}{2}} \left[ \sum_{k = 0}^{n} (n - k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} + \sum_{j = 0}^{n} j {\small\binom{2 n - 2 j}{n - j}} {\small\binom{2 j}{j}} \right]</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = {\small\frac{1}{2}} \left[ \sum_{k = 0}^{n} (n - k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} + \sum_{k = 0}^{n} k {\small\binom{2 n - 2 k}{n - k}} {\small\binom{2 k}{k}} \right]</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = {\small\frac{1}{2}} \sum_{k = 0}^{n} (n - k + k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = {\small\frac{n}{2}} \sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = {\small\frac{n S (n)}{2}}</math> | ||
| + | |||
| + | Ponieważ <math>T(n) = {\small\frac{n S (n)}{2}} \;</math> i <math>\; T(n) = 4 T (n - 1) + 2 S (n - 1)</math> (zobacz [[#D106|D106]]), to otrzymujemy | ||
| + | |||
| + | ::<math>{\small\frac{n S (n)}{2}} = 4 \cdot {\small\frac{(n - 1) S (n - 1)}{2}} + 2 S (n - 1)</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>n S (n) = 4 n S (n - 1) - 4 S (n - 1) + 4 S (n - 1)</math> | ||
| + | |||
| + | ::<math>S(n) = 4 S (n - 1)</math> | ||
| + | |||
| + | Metodą indukcji matematycznej łatwo dowodzimy, że <math>S(n) = 4^n</math>. Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D108" style="font-size: 110%; font-weight: bold;">Twierdzenie D108</span><br/> | ||
| + | Dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Oznaczmy | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | ::<math>T(n) = \sum_{k = 0}^{n} {\small\frac{n - k}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | Zauważmy, że | ||
| + | |||
| + | ::<math>T(n) = \sum_{k = 0}^{n} {\small\frac{n - k}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = \sum_{k = 0}^{n} {\small\frac{n + 1 - (k + 1)}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::<math>\;\;\:\, = (n + 1) \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} - \sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::<math>\;\;\:\, = (n + 1) S (n) - 4^n</math> | ||
| + | </div> | ||
| + | |||
| + | Ponieważ <math>T(n) = (n + 1) S (n) - 4^n \;</math> i <math>\; T(n) = 4 T (n - 1) + 2 S (n - 1)</math> (zobacz [[#D106|D106]]), to otrzymujemy | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>(n + 1) S (n) - 4^n = 4 \cdot (n S (n - 1) - 4^{n - 1}) + 2 S (n - 1)</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>(n + 1) S (n) - 4^n = 4 n S (n - 1) - 4^n + 2 S (n - 1)</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>S(n) = {\small\frac{2 (2 n + 1)}{n + 1}} S (n - 1)</math> | ||
| + | </div> | ||
| + | |||
| + | Metodą indukcji matematycznej dowodzimy, że <math>S(n) = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math>. Dla <math>n = 0</math> mamy <math>S(0) = 1 \;</math> i <math>\; {\small\frac{1}{2}} {\small\binom{2}{1}} = 1</math>. Zatem wzór jest prawdziwy dla <math>n = 0</math>. Zakładając, że wzór jest prawdziwy dla <math>n - 1</math>, otrzymujemy dla <math>n</math> | ||
| + | |||
| + | ::<math>{\small\frac{2 (2 n + 1)}{n + 1}} S (n - 1) = {\small\frac{2 n + 1}{n + 1}} \cdot {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | :::::::<math>\;\;\; = {\small\frac{2 n + 1}{n + 1}} \cdot {\small\frac{(n + 1)^2}{(2 n + 1) (2 n + 2)}} \cdot {\small\frac{(2 n + 1) (2 n + 2)}{(n + 1)^2}} \cdot {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | :::::::<math>\;\;\; = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | :::::::<math>\;\;\; = S (n)</math> | ||
| + | |||
| + | Co kończy dowód.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D109" style="font-size: 110%; font-weight: bold;">Twierdzenie D109</span><br/> | ||
| + | Jeżeli <math>C_n</math> są liczbami Catalana, to | ||
| + | |||
| + | ::<math>C_{n + 1} = \sum_{k = 0}^{n} C_k C_{n - k}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Zauważmy, że | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} C_k C_{n - k} = \sum_{k = 0}^{n} {\small\frac{1}{(k + 1) (n - k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::::<math>\;\;\:\, = {\small\frac{1}{n + 2}} \sum_{k = 0}^{n} \left( {\small\frac{1}{k + 1}} + {\small\frac{1}{n - k + 1}} \right) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::::<math>\;\;\:\, = {\small\frac{1}{n + 2}} \left[ \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} + \sum_{k = 0}^{n} {\small\frac{1}{n - k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\:\, = {\small\frac{1}{n + 2}} \left[ \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} + \sum_{j = 0}^{n} {\small\frac{1}{j + 1}} {\small\binom{2 n - 2 j}{n - j}} {\small\binom{2 j}{j}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\:\, = {\small\frac{2}{n + 2}} \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | :::::<math>\;\;\:\, = {\small\frac{2}{n + 2}} \cdot {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | :::::<math>\;\;\:\, = {\small\frac{1}{n + 2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | :::::<math>\;\;\:\, = C_{n + 1}</math> | ||
| + | |||
| + | Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | === <span style="border-bottom:2px solid #000;">Funkcja gamma</span> === | ||
| + | |||
| + | | ||
| + | |||
| + | <span id="D110" style="font-size: 110%; font-weight: bold;">Definicja D110</span><br/> | ||
| + | Funkcja <math>\Gamma (z)</math><ref name="gamma1"/> jest zdefiniowana równoważnymi wzorami | ||
| + | |||
| + | ::<math>\Gamma (z) = \int_{0}^{\infty} t^{z - 1} e^{- t} \, d t \qquad \operatorname{Re}(z) > 0 \qquad \qquad</math> (definicja całkowa Eulera) | ||
| + | |||
| + | ::<math>\Gamma (z) = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \qquad z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad</math> (definicja Gaussa) | ||
| + | |||
| + | ::<math>\Gamma (z) = {\small\frac{1}{z}} \prod_{n = 1}^{\infty} \left( 1 + {\small\frac{1}{n}} \right)^z \left( 1 + {\small\frac{z}{n}} \right)^{- 1} \qquad z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad</math> (definicja iloczynowa Eulera) | ||
| + | |||
| + | ::<math>\Gamma (z) = {\small\frac{e^{- \gamma z}}{z}} \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{z}{n}} \right)^{- 1} e^{\tfrac{z}{n}} \qquad z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad</math> (definicja iloczynowa Weierstrassa) | ||
| + | |||
| + | Trzy ostatnie wzory możemy wykorzystać do zdefiniowania funkcji <math>{\small\frac{1}{\Gamma (z)}}</math>, która jest określona dla dowolnych <math>z \in \mathbb{C}</math> | ||
| + | |||
| + | ::<math>{\small\frac{1}{\Gamma (z)}} = \lim_{n \rightarrow \infty} {\small\frac{z (z + 1) \cdot \ldots \cdot (z + n)}{n^z n!}}</math> | ||
| + | |||
| + | ::<math>{\small\frac{1}{\Gamma (z)}} = z \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{1}{n}} \right)^{- z} \left( 1 + {\small\frac{z}{n}} \right)</math> | ||
| + | |||
| + | ::<math>{\small\frac{1}{\Gamma (z)}} = z e^{\gamma z} \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{z}{n}} \right) e^{- \tfrac{z}{n}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż wykres|Hide=Ukryj wykres}} | ||
| + | |||
| + | Poniżej przedstawiamy wykresy funkcji <math>\Gamma (x)</math> (kolor niebieski) i <math>\, {\small\frac{1}{\Gamma (x)}}</math> (kolor czerwony). | ||
| + | |||
| + | ::[[File: gamma1.png|700px|none]] | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż równoważność definicji|Hide=Ukryj równoważność definicji}} | ||
| + | |||
| + | '''Równoważność definicji Gaussa i definicji całkowej Eulera''' | ||
| + | |||
| + | Niech <math>n \in \mathbb{Z}_+ \,</math> i <math>\; \operatorname{Re}(z) > 0</math>. Rozważmy całki | ||
| + | |||
| + | ::<math>I_k = \int^n_0 t^{z - 1 + k} \left( 1 - {\small\frac{t}{n}} \right)^{n - k} d t</math> | ||
| + | |||
| + | gdzie <math>k = 0, \ldots, n</math>. Całkując przez części | ||
| + | |||
| + | ::<math>d u = t^{z - 1 + k} \, d t \qquad \qquad \qquad v = \left( 1 - {\small\frac{t}{n}} \right)^{n - k}</math> | ||
| + | |||
| + | ::<math>u = {\small\frac{t^{z + k}}{z + k}} \qquad \qquad \qquad \quad \; d v = - {\small\frac{n - k}{n}} \cdot \left( 1 - {\small\frac{t}{n}} \right)^{n - k - 1} d t</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>I_k = {\small\frac{t^{z + k}}{z + k}} \cdot \left( 1 - {\small\frac{t}{n}} \right)^{n - k} \, \biggr\rvert_{0}^{n} \; + \; {\small\frac{n - k}{n (z + k)}} \int^n_0 t^{z + k} \left( 1 - {\small\frac{t}{n}} \right)^{n - k - 1} d t</math> | ||
| + | |||
| + | ::<math>\;\;\;\,\, = {\small\frac{n - k}{n (z + k)}} \cdot I_{k + 1}</math> | ||
| + | |||
| + | Zatem całkując <math>n</math>-krotnie przez części, mamy | ||
| + | |||
| + | ::<math>I_0 = {\small\frac{n}{n z}} \cdot I_1</math> | ||
| + | |||
| + | ::<math>\;\;\;\,\, = {\small\frac{n}{n z}} \cdot {\small\frac{n - 1}{n (z + 1)}} \cdot I_2</math> | ||
| + | |||
| + | ::<math>\;\;\;\,\, = {\small\frac{n}{n z}} \cdot {\small\frac{n - 1}{n (z + 1)}} \cdot {\small\frac{n - 2}{n (z + 2)}} \cdot I_3</math> | ||
| + | |||
| + | ::<math>\;\;\;\,\, = {\small\frac{n}{n z}} \cdot {\small\frac{n - 1}{n (z + 1)}} \cdot {\small\frac{n - 2}{n (z + 2)}} \cdot \ldots \cdot {\small\frac{1}{n (z + n - 1)}} \cdot I_n</math> | ||
| + | |||
| + | Ponieważ | ||
| + | |||
| + | ::<math>I_n = \int^n_0 t^{z + n - 1} \, d t = {\small\frac{n^{z + n}}{z + n}}</math> | ||
| + | |||
| + | to | ||
| + | |||
| + | ::<math>I_0 = \int^n_0 t^{z - 1} \left( 1 - {\small\frac{t}{n}} \right)^n d t = {\small\frac{n}{n z}} \cdot {\small\frac{n - 1}{n (z + 1)}} \cdot {\small\frac{n - 2}{n (z + 2)}} \cdot \ldots \cdot {\small\frac{1}{n (z + n - 1)}} \cdot {\small\frac{n^{z + n}}{z + n}}</math> | ||
| + | |||
| + | :::::::::<math>\;\;\;\; = {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| + | |||
| + | Przechodząc z <math>n</math> do nieskończoności, dostajemy | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>\lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} = \lim_{n \rightarrow \infty} \int^n_0 t^{z - 1} \left( 1 - {\small\frac{t}{n}} \right)^n d t = \int_{0}^{\infty} t^{z - 1} e^{- t} \, d t</math> | ||
| + | </div> | ||
| + | |||
| + | Co należało pokazać. | ||
| + | |||
| + | |||
| + | '''Równoważność definicji iloczynowej Eulera i definicji Gaussa''' | ||
| + | |||
| + | ::<math>{\small\frac{1}{z}} \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{1}{n}} \right)^z \left( 1 + {\small\frac{z}{n}} \right)^{- 1} = {\small\frac{1}{z}} \cdot \lim_{n \rightarrow \infty} \prod^n_{k = 1} \left( 1 + {\small\frac{1}{k}} \right)^z \left( 1 + {\small\frac{z}{k}} \right)^{- 1}</math> | ||
| + | |||
| + | ::::::::::<math>\:\, = {\small\frac{1}{z}} \cdot \lim_{n \rightarrow \infty} \prod^n_{k = 1} \frac{\left( 1 + {\small\frac{1}{k}} \right)^z}{1 + {\small\frac{z}{k}}}</math> | ||
| + | |||
| + | ::::::::::<math>\:\, = {\small\frac{1}{z}} \cdot \lim_{n \rightarrow \infty} \prod^n_{k = 1} {\small\frac{k (k + 1)^z}{(k + z) k^z}}</math> | ||
| + | |||
| + | ::::::::::<math>\:\, = \lim_{n \rightarrow \infty} {\small\frac{n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \cdot \left( {\small\frac{(n + 1) !}{n!}} \right)^z</math> | ||
| + | |||
| + | ::::::::::<math>\:\, = \lim_{n \rightarrow \infty} {\small\frac{(n + 1)^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| + | |||
| + | ::::::::::<math>\:\, = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \cdot \left( 1 + {\small\frac{1}{n}} \right)^z</math> | ||
| + | |||
| + | ::::::::::<math>\:\, = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| + | |||
| + | Co należało pokazać. | ||
| + | |||
| + | |||
| + | '''Równoważność definicji iloczynowej Weierstrassa i definicji Gaussa''' | ||
| + | |||
| + | Stała <math>\gamma</math> jest równa | ||
| + | |||
| + | ::<math>\gamma = \lim_{n \rightarrow \infty} \left( - \log n + \sum_{k = 1}^{n} {\small\frac{1}{k}} \right)</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>{\small\frac{e^{- \gamma z}}{z}} \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{z}{n}} \right)^{- 1} e^{\tfrac{z}{n}} = z^{- 1} \cdot e^{- \gamma z} \cdot \left( \lim_{n \rightarrow \infty} \prod^n_{k = 1} \frac{e^{\tfrac{z}{k}}}{1 + \tfrac{z}{k}} \right)</math> | ||
| + | |||
| + | :::::::::<math>\, = z^{- 1} \cdot \left( \lim_{n \rightarrow \infty} e^{\left( \log n - 1 - \tfrac{1}{2} - \ldots - \tfrac{1}{n} \right) z} \right) \cdot \left( \lim_{n \rightarrow \infty} \prod^n_{k = 1} \frac{k e^{\tfrac{z}{k}}}{z + k} \right)</math> | ||
| + | |||
| + | :::::::::<math>\, = \left( \lim_{n \rightarrow \infty} e^{\left( \log n - 1 - \tfrac{1}{2} - \ldots - \tfrac{1}{n} \right) z} \right) \cdot \left( \lim_{n \rightarrow \infty} {\small\frac{n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \cdot e^{\left( 1 + \tfrac{1}{2} + \ldots + \tfrac{1}{n} \right) z} \right)</math> | ||
| + | |||
| + | :::::::::<math>\, = \lim_{n \rightarrow \infty} e^{z \log n} \cdot {\small\frac{n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| + | |||
| + | :::::::::<math>\, = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| + | |||
| + | Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D111" style="font-size: 110%; font-weight: bold;">Twierdzenie D111</span><br/> | ||
| + | Dla funkcji <math>\Gamma (z)</math> prawdziwe są następujące wzory | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>\Gamma (1) = 1</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1.5em; margin-bottom: 1em;"> | ||
| + | :* <math>z \Gamma (z) = \Gamma (z + 1) \qquad z \notin \mathbb{Z}_- \cup \{ 0 \}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1.5em; margin-bottom: 1em;"> | ||
| + | :* <math>\Gamma (z) \Gamma (- z + 1) = {\small\frac{\pi}{\sin (\pi z)}} \qquad z \notin \mathbb{Z}</math> | ||
| + | </div> | ||
| + | |||
| + | :* <math>\Gamma (2 z) = {\small\frac{2^{2 z - 1}}{\sqrt{\pi}}} \cdot \Gamma (z) \Gamma \left( z + {\small\frac{1}{2}} \right) \qquad 2 z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad </math> (wzór Legendre'a o podwajaniu) | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | |||
| + | '''Punkt 1.''' | ||
| + | |||
| + | ::<math>\Gamma (1) = \int_{0}^{\infty} t^{1 - 1} e^{- t} d t = \int_{0}^{\infty} e^{- t} d t = - e^{- t} \biggr\rvert_{0}^{\infty} = 0 - (- 1) = 1</math> | ||
| + | |||
| + | '''Punkt 2.''' | ||
| + | |||
| + | Z definicji Gaussa funkcji <math>\Gamma (z)</math> otrzymujemy | ||
| + | |||
| + | ::<math>\Gamma (z) = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| + | |||
| + | ::<math>\Gamma (z + 1) = \lim_{n \rightarrow \infty} {\small\frac{n^{z + 1} n!}{(z + 1) (z + 2) \cdot \ldots \cdot (z + n + 1)}}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>z \Gamma (z) = z \cdot \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| + | |||
| + | :::<math>\;\;\;\;\, = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{(z + 1) \cdot \ldots \cdot (z + n)}} \cdot {\small\frac{n}{z + n + 1}} \cdot {\small\frac{z + n + 1}{n}}</math> | ||
| + | |||
| + | :::<math>\;\;\;\;\, = \lim_{n \rightarrow \infty} {\small\frac{n^{z + 1} n!}{(z + 1) \cdot \ldots \cdot (z + n) (z + n + 1)}} \cdot \left( 1 + {\small\frac{z + 1}{n}} \right)</math> | ||
| + | |||
| + | :::<math>\;\;\;\;\, = \lim_{n \rightarrow \infty} {\small\frac{n^{z + 1} n!}{(z + 1) \cdot \ldots \cdot (z + n) (z + n + 1)}} \cdot \lim_{n \rightarrow \infty} \left( 1 + {\small\frac{z + 1}{n}} \right)</math> | ||
| + | |||
| + | :::<math>\;\;\;\;\, = \Gamma (z + 1)</math> | ||
| + | |||
| + | '''Punkt 3.''' | ||
| + | |||
| + | Z definicji iloczynowej Eulera mamy | ||
| + | |||
| + | ::<math>\Gamma (z) = {\small\frac{1}{z}} \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{1}{n}} \right)^z \left( 1 + {\small\frac{z}{n}} \right)^{- 1}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>{\small\frac{1}{\Gamma (z) \Gamma (- z + 1)}} = {\small\frac{1}{- z \Gamma (z) \Gamma (- z)}}</math> | ||
| + | |||
| + | ::::::<math>\; = {\small\frac{z \cdot (- z)}{- z}} \cdot \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{1}{n}} \right)^{- z} \left( 1 + {\small\frac{z}{n}} \right) \left( 1 + {\small\frac{1}{n}} \right)^z \left( 1 - {\small\frac{z}{n}} \right)</math> | ||
| + | |||
| + | ::::::<math>\; = z \cdot \prod^{\infty}_{n = 1} \left( 1 - {\small\frac{z^2}{n^2}} \right)</math> | ||
| + | |||
| + | ::::::<math>\; = {\small\frac{\sin (\pi z)}{\pi}}</math> | ||
| + | |||
| + | gdzie wykorzystaliśmy wzór Eulera | ||
| + | |||
| + | ::<math>\prod^{\infty}_{n = 1} \left( 1 - {\small\frac{z^2}{n^2}} \right) = {\small\frac{\sin (\pi z)}{\pi z}}</math> | ||
| + | |||
| + | Dowód wzoru Eulera jest trudny. Elegancki dowód, ale tylko dla liczb rzeczywistych, Czytelnik znajdzie na stronie [https://proofwiki.org/wiki/Euler_Formula_for_Sine_Function/Real_Numbers#Proof_1 ProofWiki]. | ||
| + | |||
| + | |||
| + | '''Punkt 4.''' | ||
| + | |||
| + | Z definicji Gaussa funkcji gamma mamy | ||
| + | |||
| + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{n^{2 z} n!}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + n)}}</math> | ||
| + | |||
| + | Jeżeli w powyższym równaniu położymy <math>2 n</math> zamiast <math>n</math>, to dostaniemy | ||
| + | |||
| + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n)}}</math> | ||
| + | |||
| + | |||
| + | Zauważmy teraz, że | ||
| + | |||
| + | ::<math>2^{2 n + 2} [z (z + 1) \cdot \ldots \cdot (z + n)] \cdot \left[ \left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right) \right] = [2 z (2 z + 2) \cdot \ldots \cdot (2 z + 2 n)] \cdot [(2 z + 1) (2 z + 3) \cdot \ldots \cdot (2 z + 2 n + 1)]</math> | ||
| + | |||
| + | ::::::::::::::::::::::<math>\;\;\;\,\, = 2 z (2 z + 1) (2 z + 2) (2 z + 3) \cdot \ldots \cdot (2 z + 2 n) (2 z + 2 n + 1)</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n)}}</math> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::<math>\;\;\;\:\, = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n) (2 z + 2 n + 1)}} \cdot (2 z + 2 n + 1)</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::<math>\;\;\;\:\, = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2^{2 n + 2} [z (z + 1) \cdot \ldots \cdot (z + n)] \cdot \left[ \left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right) \right]}} \cdot 2 n \left( 1 + {\small\frac{2 z + 1}{2 n}} \right)</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::<math>\;\;\;\:\, = 2^{2 z} \cdot \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \cdot {\small\frac{n^{z + (1 / 2)} n!}{\left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right)}} \cdot {\small\frac{(2 n) !}{(n!)^2}} \cdot {\small\frac{\sqrt{n}}{2^{2 n + 1}}} \cdot \left( 1 + {\small\frac{2 z + 1}{2 n}} \right)</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::<math>\;\;\;\:\, = 2^{2 z} \cdot \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \cdot \lim_{n \rightarrow \infty}{\small\frac{n^{z + (1 / 2)} n!}{\left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right)}} \cdot \lim_{n \rightarrow \infty} {\small\frac{(2 n) !}{(n!)^2}} \cdot {\small\frac{\sqrt{n}}{2^{2 n + 1}}} \cdot \lim_{n \rightarrow \infty} \left( 1 + {\small\frac{2 z + 1}{2 n}} \right)</math> | ||
| + | </div> | ||
| + | |||
| + | :::<math>\;\;\;\:\, = 2^{2 z} \cdot \Gamma (z) \cdot \Gamma \left( z + {\small\frac{1}{2}} \right) \cdot C \cdot 1</math> | ||
| + | |||
| + | |||
| + | Ponieważ wyrażenie | ||
| + | |||
| + | ::<math>\lim_{n \rightarrow \infty} {\small\frac{(2 n) !}{(n!)^2}} \cdot {\small\frac{\sqrt{n}}{2^{2 n + 1}}}</math> | ||
| + | |||
| + | nie zależy od <math>z</math>, a wartości funkcji <math>\Gamma (2 z)</math>, <math>\Gamma (z)</math> i <math>\Gamma \left( z + {\small\frac{1}{2}} \right)</math> są określone dla <math>2 z \notin \mathbb{Z}_- \cup \{ 0 \}</math>, to powyższa granica musi być pewną stałą. Jeżeli po lewej stronie położymy <math>z = {\small\frac{1}{2}}</math>, to otrzymamy | ||
| + | |||
| + | ::<math>\Gamma (1) = 2 \cdot \Gamma \left( {\small\frac{1}{2}} \right) \Gamma (1) \cdot C</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>C = {\small\frac{1}{2 \sqrt{\pi}}}</math> | ||
| + | |||
| + | I ostatecznie dostajemy | ||
| + | |||
| + | ::<math>\Gamma (2 z) = {\small\frac{2^{2 z - 1}}{\sqrt{\pi}}} \cdot \Gamma (z) \Gamma \left( z + {\small\frac{1}{2}} \right)</math> | ||
| + | |||
| + | |||
| + | Przy okazji pokazaliśmy asymptotykę: <math>{\small\binom{2 n}{n}} \sim {\small\frac{2^{2 n}}{\sqrt{\pi \, n}}}</math> | ||
| + | |||
| + | |||
| + | Zauważmy jeszcze, że gdy położymy <math>2 n + 1</math> zamiast <math>n</math>, to otrzymamy taki sam rezultat, bo | ||
| + | |||
| + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{(2 n + 1)^{2 z} (2 n + 1) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n + 1)}} = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n)}} \cdot \left( 1 + {\small\frac{1}{2 n}} \right)^{\! 2 z} \cdot \left( {\small\frac{1}{1 + {\normalsize\frac{2 z}{2 n + 1}}}} \right)</math><br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | Ze wzorów podanych w twierdzeniu [[#D111|D111]] otrzymujemy<br/> | ||
| + | <span id="D112" style="font-size: 110%; font-weight: bold;">Twierdzenie D112</span><br/> | ||
| + | Niech <math>k \in \mathbb{Z} \;</math> i <math>\; n \in \mathbb{N}_0</math> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1.5em;"> | ||
| + | :* <math>\Gamma \left( {\small\frac{1}{2}} \right) = \sqrt{\pi}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1.5em;"> | ||
| + | :* <math>\Gamma (n + 1) = n!</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>\Gamma \left( z + {\small\frac{1}{2}} \right) \Gamma \left( - z + {\small\frac{1}{2}} \right) = {\small\frac{\pi}{\cos (\pi z)}} \qquad z \neq k + {\small\frac{1}{2}}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>\Gamma \left( n + {\small\frac{1}{2}} \right) \Gamma \left( - n + {\small\frac{1}{2}} \right) = \pi \cdot (- 1)^n</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>\Gamma \left( n + {\small\frac{1}{2}} \right) = 2^{- 2 n} \sqrt{\pi} \cdot {\small\frac{(2 n) !}{n!}}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>\Gamma \left( - n + {\small\frac{1}{2}} \right) = (- 1)^n \cdot 2^{2 n} \sqrt{\pi} \cdot {\small\frac{n!}{(2 n) !}}</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :* <math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (2 z)}{\Gamma (z)}} = (- 1)^n \cdot {\small\frac{1}{2}} \cdot {\small\frac{n!}{(2 n) !}}</math> | ||
| + | </div> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | |||
| + | '''Punkt 1.''' | ||
| + | |||
| + | Wystarczy położyć <math>z = {\small\frac{1}{2}}</math> we wzorze 3. twierdzenia [[#D111|D111]] | ||
| + | |||
| + | '''Punkt 2.''' | ||
| + | |||
| + | Indukcja matematyczna. Wzór jest prawdziwy dla <math>n = 0</math>. Zakładając, że jest prawdziwy dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | ||
| + | |||
| + | ::<math>\Gamma (n + 2) = (n + 1) \Gamma (n + 1) = (n + 1) n! = (n + 1) !</math> | ||
| + | |||
| + | Zauważmy, że funkcja <math>\Gamma (z)</math> jest rozszerzeniem pojęcia silni na zbiór liczb rzeczywistych / zespolonych. | ||
| + | |||
| + | '''Punkt 3.''' | ||
| + | |||
| + | Wystarczy położyć <math>z = z' + {\small\frac{1}{2}}</math> we wzorze 3. twierdzenia [[#D111|D111]] | ||
| + | |||
| + | '''Punkt 4.''' | ||
| + | |||
| + | Wystarczy położyć <math>z = n</math> we wzorze 3. tego twierdzenia | ||
| + | |||
| + | '''Punkt 5.''' | ||
| + | |||
| + | Indukcja matematyczna. Wzór jest prawdziwy dla <math>n = 0</math>. Zakładając, że jest prawdziwy dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | ||
| + | |||
| + | ::<math>\Gamma \left( n + 1 + {\small\frac{1}{2}} \right) = \left( n + {\small\frac{1}{2}} \right) \Gamma \left( n + {\small\frac{1}{2}} \right)</math> | ||
| + | |||
| + | ::::::<math>\;\;\:\, = \left( n + {\small\frac{1}{2}} \right) \cdot 2^{- 2 n} \sqrt{\pi} \cdot {\small\frac{(2 n) !}{n!}}</math> | ||
| + | |||
| + | ::::::<math>\;\;\:\, = \left( n + {\small\frac{1}{2}} \right) \cdot {\small\frac{4 (n + 1)}{(2 n + 2) (2 n + 1)}} \cdot 2^{- 2 n - 2} \sqrt{\pi} \cdot {\small\frac{(2 n + 2) !}{(n + 1) !}}</math> | ||
| + | |||
| + | ::::::<math>\;\;\:\, = 2^{- 2 n - 2} \sqrt{\pi} \cdot {\small\frac{(2 n + 2) !}{(n + 1) !}}</math> | ||
| + | |||
| + | bo | ||
| + | |||
| + | ::<math>\left( n + {\small\frac{1}{2}} \right) \cdot {\small\frac{4 (n + 1)}{(2 n + 2) (2 n + 1)}} = 1</math> | ||
| + | |||
| + | '''Punkt 6.''' | ||
| + | |||
| + | Ze wzoru 3. i 4. tego twierdzenia dostajemy | ||
| + | |||
| + | ::<math>\Gamma \left( - n + {\small\frac{1}{2}} \right) = \frac{\pi \cdot (- 1)^n}{\Gamma \left( n + {\small\frac{1}{2}} \right)} = \frac{\pi \cdot (- 1)^n \cdot n!}{2^{- 2 n} \sqrt{\pi} \cdot (2 n) !} = (- 1)^n \cdot 2^{2 n} \sqrt{\pi} \cdot {\small\frac{n!}{(2 n) !}}</math> | ||
| + | |||
| + | '''Punkt 7.''' | ||
| + | |||
| + | Ze wzoru Legendre'a o podwajaniu otrzymujemy | ||
| + | |||
| + | ::<math>{\small\frac{\Gamma (2 z)}{\Gamma (z)}} = {\small\frac{2^{2 z - 1}}{\sqrt{\pi}}} \cdot \Gamma \left( z + {\small\frac{1}{2}} \right)</math> | ||
| + | |||
| + | gdzie <math>z \notin \mathbb{Z}_- \cup \{ 0 \}</math> | ||
| + | |||
| + | Dla <math>z = - n</math> po lewej stronie mamy symbol nieoznaczony <math>{\small\frac{\infty}{\infty}}</math>, ale w punktach <math>z = - n</math> istnieje granica funkcji <math>{\small\frac{\Gamma (2 z)}{\Gamma (z)}}</math> | ||
| + | |||
| + | ::<math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (2 z)}{\Gamma (z)}} = {\small\frac{2^{- 2 n - 1}}{\sqrt{\pi}}} \cdot \Gamma \left( - n + {\small\frac{1}{2}} \right) = {\small\frac{2^{- 2 n - 1}}{\sqrt{\pi}}} \cdot (- 1)^n \cdot 2^{2 n} \sqrt{\pi} \cdot {\small\frac{n!}{(2 n) !}} = (- 1)^n \cdot {\small\frac{1}{2}} \cdot {\small\frac{n!}{(2 n) !}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż wykres|Hide=Ukryj wykres}} | ||
| + | |||
| + | Poniżej przedstawiamy wykres funkcji <math>{\small\frac{\Gamma (2 x)}{\Gamma (x)}} \cdot 10^{| x |}</math>. Uwaga: wykres funkcji <math>{\small\frac{\Gamma (2 x)}{\Gamma (x)}}</math> został celowo zniekształcony przez dodanie czynnika <math>10^{| x |}</math>, aby dało się zauważyć, że wartości granic <math>\lim_{x \rightarrow - n} {\small\frac{\Gamma (2 x)}{\Gamma (x)}}</math> są różne od zera dla <math>n \in \mathbb{N}_0</math>. | ||
| + | |||
| + | ::[[File: gamma2.png|700px|none]] | ||
| + | □ | ||
| + | {{\Spoiler}}<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D113" style="font-size: 110%; font-weight: bold;">Twierdzenie D113</span><br/> | ||
| + | Jeżeli <math>n \in \mathbb{N}_0 \,</math> i <math>\; a \in \mathbb{Z}_+</math>, to | ||
| + | |||
| + | ::<math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (a z)}{\Gamma (z)}} = (- 1)^{(a - 1) n} \cdot {\small\frac{1}{a}} \cdot {\small\frac{n!}{(a n) !}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Wiemy, że jeżeli <math>z</math> nie jest liczbą całkowitą, to prawdziwy jest wzór (zobacz [[#D111|D111]] p.3) | ||
| + | |||
| + | ::<math>\Gamma (z) \Gamma (- z + 1) = {\small\frac{\pi}{\sin (\pi z)}}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>\Gamma (a z) \Gamma (- a z + 1) = {\small\frac{\pi}{\sin (\pi a z)}}</math> | ||
| + | |||
| + | Dzieląc powyższe równania przez siebie, otrzymujemy | ||
| + | |||
| + | ::<math>{\small\frac{\Gamma (a z) \Gamma (- a z + 1)}{\Gamma (z) \Gamma (- z + 1)}} = {\small\frac{\pi}{\sin (\pi a z)}} \cdot {\small\frac{\sin (\pi z)}{\pi}} = {\small\frac{\sin (\pi z)}{\sin (\pi a z)}}</math> | ||
| + | |||
| + | Skąd dostajemy | ||
| + | |||
| + | ::<math>{\small\frac{\Gamma (a z)}{\Gamma (z)}} = {\small\frac{\Gamma (- z + 1)}{\Gamma (- a z + 1)}} \cdot {\small\frac{\sin (\pi z)}{\sin (\pi a z)}}</math> | ||
| + | |||
| + | Niech <math>k</math> oznacza dowolną liczbę całkowitą. W granicy, gdy <math>z \rightarrow k</math>, mamy | ||
| + | |||
| + | ::<math>\lim_{z \rightarrow k} {\small\frac{\sin (\pi z)}{\sin (\pi a z)}} = {\small\frac{\pi \cdot \cos (\pi k)}{a \pi \cdot \cos (\pi a k)}} = {\small\frac{1}{a}} \cdot {\small\frac{(- 1)^k}{(- 1)^{a k}}} = {\small\frac{1}{a}} \cdot (- 1)^{(a - 1) k}</math> | ||
| + | |||
| + | gdzie skorzystaliśmy z reguły de l'Hospitala. Wynika stąd, że | ||
| + | |||
| + | ::<math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (a z)}{\Gamma (z)}} = {\small\frac{\Gamma (n + 1)}{\Gamma (a n + 1)}} \cdot {\small\frac{1}{a}} \cdot (- 1)^{(a - 1) n} = (- 1)^{(a - 1) n} \cdot {\small\frac{1}{a}} \cdot {\small\frac{n!}{(a n) !}}</math> | ||
| + | |||
| + | Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D114" style="font-size: 110%; font-weight: bold;">Twierdzenie D114</span><br/> | ||
| + | Jeżeli <math>n \in \mathbb{N}_0 \,</math> i <math>\; a \in \mathbb{Z}_+</math>, to | ||
| + | |||
| + | ::<math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (a z + 1)}{\Gamma (b z + 1)}} = (- 1)^{(a - b) n} \cdot {\small\frac{(b n) !}{(a n) !}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Z twierdzenia [[#D111|D111]] p.2 wynika, że | ||
| + | |||
| + | ::<math>\Gamma (a z + a n + 1) = \Gamma (a z + 1) \cdot \prod^{a n}_{j = 1} (a z + j)</math> | ||
| + | |||
| + | ::<math>\Gamma (b z + b n + 1) = \Gamma (b z + 1) \cdot \prod^{b n}_{j = 1} (b z + j)</math> | ||
| + | |||
| + | Dzieląc równania przez siebie, otrzymujemy | ||
| + | |||
| + | ::<math>{\small\frac{\Gamma (a z + 1)}{\Gamma (b z + 1)}} = {\small\frac{\Gamma (a z + a n + 1)}{\Gamma (b z + b n + 1)}} \cdot \frac{\displaystyle\prod^{b n}_{j = 1} (b z + j)}{\displaystyle\prod^{a n}_{j = 1} (a z + j)} = {\small\frac{\Gamma (a z + a n + 1)}{\Gamma (z + n + 1)}} \cdot \frac{\displaystyle\prod^{b n - 1}_{j = 1} (b z + j)}{\displaystyle\prod^{a n - 1}_{j = 1} (a z + j)} \cdot {\small\frac{b}{a}}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (a z + 1)}{\Gamma (b z + 1)}} = | ||
| + | {\small\frac{b}{a}} \cdot \frac{\displaystyle\prod^{b n - 1}_{j = 1} (- b n + j)}{\displaystyle\prod^{a n - 1}_{j = 1} (- a n + j)} \cdot {\small\frac{\Gamma (1)}{\Gamma (1)}} = | ||
| + | {\small\frac{b}{a}} \cdot \frac{(- 1)^{b n - 1} \cdot \displaystyle\prod^{b n - 1}_{j = 1} (b n - j)}{(- 1)^{a n - 1} \cdot \displaystyle\prod^{a n - 1}_{j = 1} (a n - j)} = | ||
| + | {\small\frac{b}{a}} \cdot (- 1)^{(a - b) n} \cdot {\small\frac{(b n - 1) !}{(a n - 1) !}} = | ||
| + | (- 1)^{(a - b) n} \cdot {\small\frac{(b n) !}{(a n) !}}</math> | ||
| + | |||
| + | Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D115" style="font-size: 110%; font-weight: bold;">Zadanie D115</span><br/> | ||
| + | Niech <math>n \in \mathbb{Z}_+ \,</math> i <math>\; g(n) = {\small\binom{2 n}{n}}</math>. Pokazać, że | ||
| + | |||
| + | :* rozszerzając funkcję <math>g(n)</math> na zbiór liczb rzeczywistych, otrzymujemy <math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)^2}}</math> | ||
| + | |||
| + | :* <math>\lim_{x \rightarrow - n} g (x) = 0</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Zapiszmy funkcję <math>g(n) = {\small\binom{2 n}{n}}</math> w postaci | ||
| + | |||
| + | ::<math>g(n) = {\small\binom{2 n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{\Gamma (2 n + 1)}{\Gamma (n + 1)^2}}</math> | ||
| + | |||
| + | Możemy teraz przejść do zmiennej rzeczywistej | ||
| + | |||
| + | ::<math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)^2}}</math> | ||
| + | |||
| + | bo funkcja <math>\Gamma (x)</math> jest rozszerzeniem pojęcia silni na zbiór liczb rzeczywistych. | ||
| + | |||
| + | Korzystając z twierdzenia [[#D114|D114]], otrzymujemy | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow - n} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)}} = (- 1)^n \cdot {\small\frac{n!}{(2 n) !}}</math> | ||
| + | |||
| + | Ale wiemy, że (zobacz [[#D110|D110]]) | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow - n} {\small\frac{1}{\Gamma (x + 1)}} = 0</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow - n} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)^2}} = 0</math> | ||
| + | |||
| + | Co należało pokazać i co jest dobrze widoczne na wykresie funkcji <math>{\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)^2}}</math> | ||
| + | |||
| + | ::[[File: gamma3.png|600px|none]] | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D116" style="font-size: 110%; font-weight: bold;">Zadanie D116</span><br/> | ||
| + | Niech <math>n \in \mathbb{N}_0 \,</math> i <math>\; g(n) = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}}</math>. Pokazać, że | ||
| + | |||
| + | :* rozszerzając funkcję <math>g(n)</math> na zbiór liczb rzeczywistych, otrzymujemy <math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 2) \Gamma (x + 1)}}</math> | ||
| + | |||
| + | :* <math>\lim_{x \rightarrow - 1} g (x) = - {\small\frac{1}{2}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Oczywiście funkcja <math>g(k)</math> nie jest określona w punkcie <math>k = - 1</math> | ||
| + | |||
| + | ::<math>g(k) = {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} = {\small\frac{1}{k + 1}} \cdot {\small\frac{(2 k) !}{(k!)^2}} = {\small\frac{(2 k) !}{(k + 1) !k!}} = {\small\frac{\Gamma (2 k + 1)}{\Gamma (k + 2) \Gamma (k + 1)}}</math> | ||
| + | |||
| + | Jeżeli przejdziemy do zmiennej rzeczywistej | ||
| + | |||
| + | ::<math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 2) \Gamma (x + 1)}}</math> | ||
| + | |||
| + | to łatwo pokażemy, że granica funkcji <math>g(x)</math> w punkcje <math>x = - 1</math> istnieje i jest równa <math>- {\small\frac{1}{2}}</math>. | ||
| + | |||
| + | Z twierdzenia [[#D114|D114]] dostajemy | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow - 1} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)}} = (- 1) \cdot {\small\frac{1}{2}} = - {\small\frac{1}{2}}</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow - 1} g (x) = \lim_{x \rightarrow - 1} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 2) \Gamma (x + 1)}} = - {\small\frac{1}{2}} \cdot {\small\frac{1}{\Gamma (1)}} = - {\small\frac{1}{2}}</math> | ||
| + | |||
| + | |||
| + | Co dobrze widać na wykresie funkcji <math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 2) \Gamma (x + 1)}}</math> | ||
| + | |||
| + | ::[[File: gamma4.png|600px|none]] | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Przypisy == | ||
| + | <references> | ||
| + | |||
| + | <ref name="DirichletEta">Wikipedia, ''Funkcja η'', ([https://pl.wikipedia.org/wiki/Funkcja_%CE%B7 Wiki-pl]), ([https://en.wikipedia.org/wiki/Dirichlet_eta_function Wiki-en])</ref> | ||
| + | |||
| + | <ref name="RiemannZeta">Wikipedia, ''Funkcja dzeta Riemanna'', ([https://pl.wikipedia.org/wiki/Funkcja_dzeta_Riemanna Wiki-pl]), ([https://en.wikipedia.org/wiki/Riemann_zeta_function Wiki-en])</ref> | ||
| + | |||
| + | <ref name="calkowalnosc1">Twierdzenie: funkcja ciągła w przedziale domkniętym jest całkowalna w tym przedziale.</ref> | ||
| + | |||
| + | <ref name="calkowalnosc2">W szczególności: funkcja ograniczona i mająca skończoną liczbę punktów nieciągłości w przedziale domkniętym jest w tym przedziale całkowalna.</ref> | ||
| + | |||
| + | <ref name="Mertens1">Wikipedia, ''Twierdzenia Mertensa'', ([https://pl.wikipedia.org/wiki/Twierdzenia_Mertensa Wiki-pl]), ([https://en.wikipedia.org/wiki/Mertens%27_theorems Wiki-en])</ref> | ||
| + | |||
| + | <ref name="Mertens2">Wikipedia, ''Franciszek Mertens'', ([https://pl.wikipedia.org/wiki/Franciszek_Mertens Wiki-pl])</ref> | ||
| + | |||
| + | <ref name="Rosser1">J. B. Rosser and L. Schoenfeld, ''Approximate formulas for some functions of prime numbers'', Illinois J. Math. 6 (1962), 64-94, ([https://projecteuclid.org/journals/illinois-journal-of-mathematics/volume-6/issue-1/Approximate-formulas-for-some-functions-of-prime-numbers/10.1215/ijm/1255631807.full LINK])</ref> | ||
| + | |||
| + | <ref name="twierdzenie">Zobacz twierdzenie [[#D42|D42]].</ref> | ||
| + | |||
| + | <ref name="A001620">The On-Line Encyclopedia of Integer Sequences, ''A001620 - Decimal expansion of Euler's constant'', ([https://oeis.org/A001620 A001620])</ref> | ||
| + | |||
| + | <ref name="A083343">The On-Line Encyclopedia of Integer Sequences, ''A083343 - Decimal expansion of constant B3 (or B_3) related to the Mertens constant'', ([https://oeis.org/A083343 A083343])</ref> | ||
| + | |||
| + | <ref name="A138312">The On-Line Encyclopedia of Integer Sequences, ''A138312 - Decimal expansion of Mertens's constant minus Euler's constant'', ([https://oeis.org/A138312 A138312])</ref> | ||
| + | |||
| + | <ref name="Dusart10">Pierre Dusart, ''Estimates of Some Functions Over Primes without R.H.'', 2010, ([https://arxiv.org/abs/1002.0442 LINK])</ref> | ||
| + | |||
| + | <ref name="Wiki1">Wikipedia, ''Stałe Bruna'', ([https://pl.wikipedia.org/wiki/Sta%C5%82e_Bruna Wiki-pl]), ([https://en.wikipedia.org/wiki/Brun%27s_theorem Wiki-en])</ref> | ||
| + | |||
| + | <ref name="A065421">The On-Line Encyclopedia of Integer Sequences, ''A065421 - Decimal expansion of Viggo Brun's constant B'', ([https://oeis.org/A065421 A065421])</ref> | ||
| + | |||
| + | <ref name="Erdos1">Paul Erdős, ''Über die Reihe'' <math>\textstyle \sum {\small\frac{1}{p}}</math>, Mathematica, Zutphen B 7, 1938, 1-2.</ref> | ||
| + | |||
| + | <ref name="sumowanie1">sumowanie przez części (ang. ''summation by parts'')</ref> | ||
| + | |||
| + | <ref name="convexseq1">ciąg wypukły (ang. ''convex sequence'')</ref> | ||
<ref name="Dusart18">Pierre Dusart, ''Explicit estimates of some functions over primes'', The Ramanujan Journal, vol. 45(1), 2018, 227-251.</ref> | <ref name="Dusart18">Pierre Dusart, ''Explicit estimates of some functions over primes'', The Ramanujan Journal, vol. 45(1), 2018, 227-251.</ref> | ||
| + | |||
| + | <ref name="GeometricSeries1">Wikipedia, ''Szereg geometryczny'', ([https://pl.wikipedia.org/wiki/Szereg_geometryczny Wiki-pl]), ([https://en.wikipedia.org/wiki/Geometric_series Wiki-en])</ref> | ||
| + | |||
| + | <ref name="CesaroSum1">Wikipedia, ''Sumowalność metodą Cesàro'', ([https://pl.wikipedia.org/wiki/Sumowalno%C5%9B%C4%87_metod%C4%85_Ces%C3%A0ro Wiki-pl]), ([https://en.wikipedia.org/wiki/Ces%C3%A0ro_summation Wiki-en])</ref> | ||
| + | |||
| + | <ref name="IndefiniteSum1">Wikipedia, ''Indefinite sum'', ([https://en.wikipedia.org/wiki/Indefinite_sum Wiki-en])</ref> | ||
| + | |||
| + | <ref name="Fasenmyer1">Sister Mary Celine Fasenmyer, ''Some Generalized Hypergeometric Polynomials'', Bull. Amer. Math. Soc. 53 (1947), 806-812</ref> | ||
| + | |||
| + | <ref name="Fasenmyer2">Sister Mary Celine Fasenmyer, ''A Note on Pure Recurrence Relations'', Amer. Math. Monthly 56 (1949), 14-17</ref> | ||
| + | |||
| + | <ref name="Zeilberger1">Doron Zeilberger, ''Sister Celine's technique and its generalizations'', Journal of Mathematical Analysis and Applications, 85 (1982), 114-145</ref> | ||
| + | |||
| + | <ref name="WilfZeilberger1">Herbert Wilf and Doron Zeilberger, ''Rational Functions Certify Combinatorial Identities'', J. Amer. Math. Soc. 3 (1990), 147-158</ref> | ||
| + | |||
| + | <ref name="PetkovsekWilfZeilberger1">Marko Petkovšek, Herbert Wilf and Doron Zeilberger, ''A = B'', AK Peters, Ltd., 1996</ref> | ||
| + | |||
| + | <ref name="JovanMikic1">Jovan Mikić, ''A Proof of a Famous Identity Concerning the Convolution of the Central Binomial Coefficients'', Journal of Integer Sequences, Vol. 19, No. 6 (2016), pp. 1 - 10, ([https://cs.uwaterloo.ca/journals/JIS/VOL19/Mikic2/mikic15.html LINK])</ref> | ||
| + | |||
| + | <ref name="gamma1">Wikipedia, ''Funkcja Γ'', ([https://pl.wikipedia.org/wiki/Funkcja_%CE%93 Wiki-pl]), ([https://en.wikipedia.org/wiki/Gamma_function Wiki-en])</ref> | ||
</references> | </references> | ||
Aktualna wersja na dzień 11:37, 28 sty 2025
Szeregi nieskończone
Definicja D1
Sumę wszystkich wyrazów ciągu nieskończonego [math]\displaystyle{ (a_n) }[/math]
- [math]\displaystyle{ a_1 + a_2 + a_3 + \ldots + a_n + \ldots = \sum_{k = 1}^{\infty} a_k }[/math]
nazywamy szeregiem nieskończonym o wyrazach [math]\displaystyle{ a_n }[/math].
Definicja D2
Ciąg [math]\displaystyle{ S_n = \sum_{k = 1}^{n} a_k }[/math] nazywamy ciągiem sum częściowych szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math].
Definicja D3
Szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] będziemy nazywali zbieżnym, jeżeli ciąg sum częściowych [math]\displaystyle{ \left ( S_n \right ) }[/math] jest zbieżny.
Twierdzenie D4 (warunek konieczny zbieżności szeregu)
Jeżeli szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] jest zbieżny, to [math]\displaystyle{ \lim_{n \to \infty} a_n = 0 }[/math].
Okazuje się, że bardzo łatwo podać przykład szeregów, dla których warunek [math]\displaystyle{ \lim_{n \to \infty} a_n = 0 }[/math] jest warunkiem wystarczającym. Opisany w poniższym twierdzeniu rodzaj szeregów nazywamy szeregami naprzemiennymi.
Twierdzenie D5 (kryterium Leibniza)
Niech ciąg [math]\displaystyle{ (a_n) }[/math] będzie ciągiem malejącym o wyrazach nieujemnych. Jeżeli
- [math]\displaystyle{ \underset{n \rightarrow \infty}{\lim} a_n = 0 }[/math]
to szereg [math]\displaystyle{ \underset{k = 1}{\overset{\infty}{\sum}} (- 1)^{k + 1} \cdot a_k }[/math] jest zbieżny.
Twierdzenie D6
Dla [math]\displaystyle{ s \gt 1 }[/math] prawdziwy jest następujący związek
- [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{(- 1)^{k + 1}}{k^s}} = (1 - 2^{1 - s}) \sum_{k = 1}^{\infty} {\small\frac{1}{k^s}} }[/math]
Przykład D7
Szeregi niekończone często definiują ważne funkcje. Dobrym przykładem może być funkcja eta Dirichleta[1], którą definiuje szereg naprzemienny
- [math]\displaystyle{ \eta (s) = \sum_{k = 1}^{\infty} {\small\frac{(- 1)^{k + 1}}{k^s}} }[/math]
lub funkcja dzeta Riemanna[2], którą definiuje inny szereg
- [math]\displaystyle{ \zeta (s) = \sum_{k = 1}^{\infty} {\small\frac{1}{k^s}} }[/math]
Na podstawie twierdzenia D6 funkcje te są związane wzorem
- [math]\displaystyle{ \eta (s) = (1 - 2^{1 - s}) \zeta (s) }[/math]
Dla [math]\displaystyle{ s \in \mathbb{R}_+ }[/math] funkcja eta Dirichleta jest zbieżna. Możemy ją wykorzystać do znajdowania sumy szeregu naprzemiennego [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{(- 1)^{k + 1}}{k^s}} }[/math].
[math]\displaystyle{ s = {\small\frac{1}{2}} }[/math] [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{(- 1)^{k + 1}}{\sqrt{k}}} = 0.604898643421 \ldots }[/math] WolframAlpha [math]\displaystyle{ s = 1 }[/math] [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{(- 1)^{k + 1}}{k}} = \log 2 = 0.693147180559 \ldots }[/math] WolframAlpha [math]\displaystyle{ s = 2 }[/math] [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{(- 1)^{k + 1}}{k^2}} = {\small\frac{\pi^2}{12}} = 0.822467033424 \ldots }[/math] WolframAlpha
Twierdzenie D8
Niech [math]\displaystyle{ N \in \mathbb{Z}_+ }[/math]. Szeregi [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] oraz [math]\displaystyle{ \sum_{k = N}^{\infty} a_k }[/math] są jednocześnie zbieżne lub jednocześnie rozbieżne. W przypadku zbieżności zachodzi związek
- [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k = \left ( a_1 + a_2 + \ldots + a_{N - 1} \right ) + \sum_{k = N}^{\infty} a_k }[/math]
Twierdzenie D9 (kryterium porównawcze)
Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ k \gt N_0 }[/math] jest spełniony warunek
- [math]\displaystyle{ 0 \leqslant a_k \leqslant b_k }[/math]
to
- zbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} b_k }[/math] pociąga za sobą zbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math]
- rozbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] pociąga za sobą rozbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} b_k }[/math]
Twierdzenie D10
Jeżeli szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \left | a_k \right | }[/math] jest zbieżny, to szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] jest również zbieżny.
Definicja D11
Powiemy, że szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math] jest bezwzględnie zbieżny, jeżeli szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} | a_n | }[/math] jest zbieżny.
Powiemy, że szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math] jest warunkowo zbieżny, jeżeli szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math] jest zbieżny, ale szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} | a_n | }[/math] jest rozbieżny.
Twierdzenie D12
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Jeżeli wyrazy ciągu [math]\displaystyle{ (a_n) }[/math] można zapisać w jednej z postaci
- [math]\displaystyle{ \quad a_k = f_k - f_{k + 1} }[/math]
- [math]\displaystyle{ \quad a_k = f_{k - 1} - f_k }[/math]
to odpowiadający temu ciągowi szereg nazywamy szeregiem teleskopowym. Suma częściowa szeregu teleskopowego jest odpowiednio równa
- [math]\displaystyle{ \quad \sum_{k = m}^{n} a_k = f_m - f_{n + 1} }[/math]
- [math]\displaystyle{ \quad \sum_{k = m}^{n} a_k = f_{m - 1} - f_n }[/math]
Twierdzenie D13
Następujące szeregi są zbieżne
1. [math]\displaystyle{ \quad \sum^{\infty}_{k = 1} {\small\frac{1}{k (k + 1)}} = 1 }[/math] 2. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} {\small\frac{1}{k (k - 1)}} = 1 }[/math] 3. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} {\small\frac{1}{k^2 - 1}} = {\small\frac{3}{4}} }[/math] 4. [math]\displaystyle{ \quad \sum^{\infty}_{k = 1} {\small\frac{1}{k^2}} = {\small\frac{\pi^2}{6}} = 1.644934066848 \ldots }[/math] A013661, WolframAlpha
Twierdzenie D14
Następujące szeregi są zbieżne
1. [math]\displaystyle{ \quad \sum_{k = 1}^{\infty} {\small\frac{1}{(k + 1) \sqrt{k}}} = 1.860025079221 \ldots }[/math] 2. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} {\small\frac{\log k}{k (k + 1)}} = 0.788530565911 \ldots }[/math] A085361 3. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} {\small\frac{\log k}{k (k - 1)}} = 1.257746886944 \ldots }[/math] A131688 4. [math]\displaystyle{ \quad \sum^{\infty}_{k = 3} {\small\frac{1}{k \cdot \log^2 \! k}} = 1.069058310734 \ldots }[/math] A115563
Przykład D15
Na przykładzie szeregu [math]\displaystyle{ \sum_{k = 3}^{\infty} {\small\frac{1}{k \cdot \log^2 k}} }[/math] pokażemy, jak należy obliczać przybliżoną wartość sumy szeregu.
Ponieważ nie jesteśmy w stanie zsumować nieskończenie wielu wyrazów, zatem najlepiej będzie podzielić szereg na dwie części
- [math]\displaystyle{ \sum_{k = 3}^{\infty} {\small\frac{1}{k \cdot \log^2 k}} = \sum_{k = 3}^{m} {\small\frac{1}{k \cdot \log^2 k}} + \sum_{k = m + 1}^{\infty} {\small\frac{1}{k \cdot \log^2 k}} }[/math]
Wartość pierwszej części możemy policzyć bezpośrednio, a dla drugiej części powinniśmy znaleźć jak najlepsze oszacowanie.
Dowodząc twierdzenie D14, w punkcie 4. pokazaliśmy, że prawdziwy jest ciąg nierówności
- [math]\displaystyle{ {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \lt {\small\frac{1}{k \cdot \log^2 k}} \lt {\small\frac{1}{\log (k - 1)}} - {\small\frac{1}{\log (k)}} }[/math]
Wykorzystamy powyższy wzór do znalezienia potrzebnego nam oszacowania. Sumując strony nierówności, dostajemy
- [math]\displaystyle{ \sum_{k = m + 1}^{n} \left( {\small\frac{1}{\log (k)}} - {\small\frac{1}{\log (k + 1)}} \right) \lt \sum_{k = m + 1}^{n} {\small\frac{1}{k \cdot \log^2 k}} \lt \sum_{k = m + 1}^{n} \left( {\small\frac{1}{\log (k - 1)}} - {\small\frac{1}{\log (k)}} \right) }[/math]
Ponieważ szeregi po lewej i po prawej stronie są szeregami teleskopowymi, to łatwo znajdujemy, że
- [math]\displaystyle{ {\small\frac{1}{\log (m + 1)}} - {\small\frac{1}{\log (n + 1)}} \lt \sum_{k = m + 1}^{n} {\small\frac{1}{k \cdot \log^2 k}} \lt {\small\frac{1}{\log m}} - {\small\frac{1}{\log n}} }[/math]
Przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, otrzymujemy oszacowanie
- [math]\displaystyle{ {\small\frac{1}{\log (m + 1)}} \lt \sum_{k = m + 1}^{\infty} {\small\frac{1}{k \cdot \log^2 k}} \lt {\small\frac{1}{\log m}} }[/math]
Teraz pozostaje dodać sumę wyrazów szeregu od [math]\displaystyle{ k = 3 }[/math] do [math]\displaystyle{ k = m }[/math]
- [math]\displaystyle{ {\small\frac{1}{\log (m + 1)}} + \sum_{k = 3}^{m} {\small\frac{1}{k \cdot \log^2 k}} \lt \sum_{k = 3}^{\infty} {\small\frac{1}{k \cdot \log^2 k}} \lt {\small\frac{1}{\log m}} + \sum_{k = 3}^{m} {\small\frac{1}{k \cdot \log^2 k}} }[/math]
Poniżej przedstawiamy wartości oszacowania sumy szeregu znalezione przy pomocy programu PARI/GP dla kolejnych wartości [math]\displaystyle{ m }[/math]. Wystarczy proste polecenie
for(n = 1, 8, s = sum( k = 3, 10^n, 1/k/(log(k))^2 ); print( "n= ", n, " a= ", s + 1/log(10^n+1), " b= ", s + 1/log(10^n) ))
[math]\displaystyle{ m = 10^1 }[/math] [math]\displaystyle{ 1.06 }[/math] [math]\displaystyle{ 1.07 }[/math] [math]\displaystyle{ m = 10^2 }[/math] [math]\displaystyle{ 1.068 }[/math] [math]\displaystyle{ 1.069 }[/math] [math]\displaystyle{ m = 10^3 }[/math] [math]\displaystyle{ 1.06904 }[/math] [math]\displaystyle{ 1.06906 }[/math] [math]\displaystyle{ m = 10^4 }[/math] [math]\displaystyle{ 1.069057 }[/math] [math]\displaystyle{ 1.069058 }[/math] [math]\displaystyle{ m = 10^5 }[/math] [math]\displaystyle{ 1.0690582 }[/math] [math]\displaystyle{ 1.0690583 }[/math] [math]\displaystyle{ m = 10^6 }[/math] [math]\displaystyle{ 1.06905830 }[/math] [math]\displaystyle{ 1.06905831 }[/math] [math]\displaystyle{ m = 10^7 }[/math] [math]\displaystyle{ 1.0690583105 }[/math] [math]\displaystyle{ 1.0690583109 }[/math] [math]\displaystyle{ m = 10^8 }[/math] [math]\displaystyle{ 1.06905831071 }[/math] [math]\displaystyle{ 1.06905831074 }[/math]
Dysponując oszacowaniem reszty szeregu, znaleźliśmy wartość sumy szeregu z dokładnością 10 miejsc po przecinku.
Natomiast samo zsumowanie [math]\displaystyle{ 10^8 }[/math] wyrazów szeregu daje wynik
- [math]\displaystyle{ \sum_{k = 3}^{10^8} {\small\frac{1}{k \cdot \log^2 k}} = 1.014 771 500 510 916 \ldots }[/math]
Zatem mimo zsumowania stu milionów(!) wyrazów szeregu otrzymaliśmy rezultat z dokładnością jednego(!) miejsca po przecinku. Co więcej, nie wiemy, jaka jest dokładność uzyskanego rezultatu. Znając oszacowanie od dołu i od góry, dokładność jednego miejsca po przecinku uzyskaliśmy po zsumowaniu dziesięciu(!) wyrazów szeregu.
Rozpatrywana wyżej sytuacja pokazuje, że w przypadku znajdowania przybliżonej wartości sumy szeregu ważniejsze od sumowania ogromnej ilości wyrazów jest posiadanie oszacowania nieskończonej reszty szeregu. Ponieważ wyznaczenie tego oszacowania na ogół nie jest proste, pokażemy jak ten problem rozwiązać przy pomocy całki oznaczonej.
Szeregi nieskończone i całka oznaczona
Twierdzenie D16
Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] jest ciągła, dodatnia i malejąca w przedziale [math]\displaystyle{ [m, n + 1] }[/math], to prawdziwy jest następujący ciąg nierówności
- [math]\displaystyle{ 0 \leqslant \int_{m}^{n + 1} f(x) d x \leqslant \sum_{k = m}^{n} f(k) \leqslant f (m) + \int_{m}^{n} f(x) d x }[/math]
Przykład D17
Rozważmy szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k}} }[/math].
Funkcja [math]\displaystyle{ f(x) = {\small\frac{1}{x}} }[/math] jest ciągła, dodatnia i silnie malejąca w przedziale [math]\displaystyle{ (0, + \infty) }[/math], zatem dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ \int_{1}^{n + 1} {\small\frac{d x}{x}} \lt \sum_{k = 1}^{n} {\small\frac{1}{k}} \lt 1 + \int_{1}^{n} {\small\frac{d x}{x}} }[/math]
Przy obliczaniu całek oznaczonych Czytelnik może skorzystać ze strony WolframAlpha.
- [math]\displaystyle{ \log (n + 1) \lt \sum_{k = 1}^{n} {\small\frac{1}{k}} \lt 1 + \log n }[/math]
Ponieważ
- [math]\displaystyle{ \log (n + 1) = \log \left( n \left( 1 + {\small\frac{1}{n}} \right) \right) = \log n + \log \left( 1 + {\small\frac{1}{n}} \right) \gt \log n + {\small\frac{1}{n + 1}} }[/math]
to dostajemy
- [math]\displaystyle{ {\small\frac{1}{n + 1}} \lt \sum_{k = 1}^{n} {\small\frac{1}{k}} - \log n \lt 1 }[/math]
Zauważmy: nie tylko wiemy, że szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k}} }[/math] jest rozbieżny, ale jeszcze potrafimy określić, jaka funkcja tę rozbieżność opisuje! Mamy zatem podstawy, by przypuszczać, że całki umożliwią opracowanie metody, która pozwoli rozstrzygać o zbieżności szeregów.
Twierdzenie D18 (kryterium całkowe zbieżności szeregów)
Załóżmy, że funkcja [math]\displaystyle{ f(x) }[/math] jest ciągła, dodatnia i malejąca w przedziale [math]\displaystyle{ [m, + \infty) }[/math]. Szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f(k) }[/math] jest zbieżny lub rozbieżny w zależności od tego, czy funkcja pierwotna [math]\displaystyle{ F(x) = \int f (x) d x }[/math] ma dla [math]\displaystyle{ x \rightarrow \infty }[/math] granicę skończoną, czy nie.
Przykład D19
Przykłady zebraliśmy w tabeli. Przy obliczaniu całek nieoznaczonych Czytelnik może skorzystać ze strony WolframAlpha.
szereg [math]\displaystyle{ \sum_{k = m}^{\infty} a_k }[/math] funkcja [math]\displaystyle{ f(x) }[/math] całka [math]\displaystyle{ F(x) = \int f(x) d x }[/math] granica [math]\displaystyle{ \lim_{x \to \infty} F(x) }[/math] wynik 1. [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k}} }[/math] [math]\displaystyle{ {\small\frac{1}{x}} }[/math] [math]\displaystyle{ \log x }[/math] [math]\displaystyle{ \infty }[/math] szereg rozbieżny 2. [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{\sqrt{k}}} }[/math] [math]\displaystyle{ {\small\frac{1}{\sqrt{x}}} }[/math] [math]\displaystyle{ 2 \sqrt{x} }[/math] [math]\displaystyle{ \infty }[/math] szereg rozbieżny 3. [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k^2}} }[/math] [math]\displaystyle{ {\small\frac{1}{x^2}} }[/math] [math]\displaystyle{ - {\small\frac{1}{x}} }[/math] [math]\displaystyle{ 0 }[/math] szereg zbieżny 4. [math]\displaystyle{ \sum_{k = 2}^{\infty} {\small\frac{1}{k \log k}} }[/math] [math]\displaystyle{ {\small\frac{1}{x \log x}} }[/math] [math]\displaystyle{ \log \log x }[/math] [math]\displaystyle{ \infty }[/math] szereg rozbieżny 5. [math]\displaystyle{ \sum_{k = 2}^{\infty} {\small\frac{1}{k \log^2 \! k}} }[/math] [math]\displaystyle{ {\small\frac{1}{x \log^2 \! x}} }[/math] [math]\displaystyle{ - {\small\frac{1}{\log x}} }[/math] [math]\displaystyle{ 0 }[/math] szereg zbieżny
Stosując kryterium całkowe, można łatwo pokazać, że szeregi
- [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k^s}} }[/math]
- [math]\displaystyle{ \sum_{k = 2}^{\infty} {\small\frac{1}{k \log^s \! k}} }[/math]
są zbieżne dla [math]\displaystyle{ s \gt 1 }[/math] i rozbieżne dla [math]\displaystyle{ s \leqslant 1 }[/math].
Twierdzenie D20
Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] jest ciągła, dodatnia i malejąca w przedziale [math]\displaystyle{ [m, \infty) }[/math] oraz
- [math]\displaystyle{ R(m) = \int_{m}^{\infty} f(x) d x }[/math]
- [math]\displaystyle{ S(m) = \sum_{k = a}^{m} f(k) }[/math]
gdzie [math]\displaystyle{ a \lt m }[/math], to prawdziwe jest następujące oszacowanie sumy szeregu nieskończonego [math]\displaystyle{ \sum_{k = a}^{\infty} f (k) }[/math]
- [math]\displaystyle{ S(m) + R(m) - f(m) \leqslant \sum_{k = a}^{\infty} f(k) \leqslant S(m) + R(m) }[/math]
Przykład D21
Twierdzenie D20 umożliwia określenie, z jaką dokładnością została wyznaczona suma szeregu. Wyznaczmy sumę szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{(k + 1) \sqrt{k}}} }[/math]. Mamy
- [math]\displaystyle{ S(m) = \sum_{k = 1}^{m} {\small\frac{1}{(k + 1) \sqrt{k}}} }[/math]
- [math]\displaystyle{ \int {\small\frac{d x}{(x + 1) \sqrt{x}}} = 2 \text{arctg} \left( \sqrt{x} \right) }[/math]
- [math]\displaystyle{ R(m) = \int_{m}^{\infty} {\small\frac{d x}{(x + 1) \sqrt{x}}} = \pi - 2 \text{arctg} \left( \sqrt{m} \right) }[/math]
Zatem
- [math]\displaystyle{ S(m) + R (m) - f (m) \leqslant \sum_{k = 1}^{\infty} {\small\frac{1}{(k + 1) \sqrt{k}}} \leqslant S (m) + R (m) }[/math]
Dla kolejnych wartości [math]\displaystyle{ m }[/math] otrzymujemy
[math]\displaystyle{ m }[/math] [math]\displaystyle{ S(m) + R(m) - f(m) }[/math] [math]\displaystyle{ S(m) + R(m) }[/math] [math]\displaystyle{ 10^1 }[/math] [math]\displaystyle{ 1.84 }[/math] [math]\displaystyle{ 1.87 }[/math] [math]\displaystyle{ 10^2 }[/math] [math]\displaystyle{ 1.85 }[/math] [math]\displaystyle{ 1.86 }[/math] [math]\displaystyle{ 10^3 }[/math] [math]\displaystyle{ 1.86000 }[/math] [math]\displaystyle{ 1.86004 }[/math] [math]\displaystyle{ 10^4 }[/math] [math]\displaystyle{ 1.860024 }[/math] [math]\displaystyle{ 1.860025 }[/math] [math]\displaystyle{ 10^5 }[/math] [math]\displaystyle{ 1.86002506 }[/math] [math]\displaystyle{ 1.86002509 }[/math] [math]\displaystyle{ 10^6 }[/math] [math]\displaystyle{ 1.860025078 }[/math] [math]\displaystyle{ 1.860025079 }[/math] [math]\displaystyle{ 10^7 }[/math] [math]\displaystyle{ 1.86002507920 }[/math] [math]\displaystyle{ 1.86002507923 }[/math] [math]\displaystyle{ 10^8 }[/math] [math]\displaystyle{ 1.860025079220 }[/math] [math]\displaystyle{ 1.860025079221 }[/math] [math]\displaystyle{ 10^9 }[/math] [math]\displaystyle{ 1.8600250792211 }[/math] [math]\displaystyle{ 1.8600250792212 }[/math]
W programie PARI/GP wystarczy napisać:
f(k) = 1.0 / (k+1) / sqrt(k) S(m) = sum( k = 1, m, f(k) ) R(m) = Pi - 2*atan( sqrt(m) ) for(j = 1, 9, m = 10^j; suma = S(m); reszta = R(m); print( "j= ", j, " a= ", suma + reszta - f(m), " b= ", suma + reszta ))
Prostym wnioskiem z twierdzenia D16 jest następujące
Twierdzenie D22
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ [m, + \infty) }[/math]. Jeżeli przy wyliczaniu sumy szeregu nieskończonego [math]\displaystyle{ \sum_{k = a}^{\infty} f (k) }[/math] (gdzie [math]\displaystyle{ a \lt m }[/math]) zastąpimy sumę [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math] całką [math]\displaystyle{ \int_{m}^{\infty} f (x) d x }[/math], to błąd wyznaczenia sumy szeregu nie przekroczy [math]\displaystyle{ f(m) }[/math].
Twierdzenie D23
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ [m, + \infty) }[/math]. Jeżeli szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math] jest zbieżny, to dla każdego [math]\displaystyle{ n \geqslant m }[/math] prawdziwe jest następujące oszacowanie sumy częściowej szeregu [math]\displaystyle{ S(n) }[/math]
- [math]\displaystyle{ S(n) = \sum_{k = m}^{n} f (k) \leqslant C - B \int_{n}^{\infty} f (x) d x }[/math]
gdzie [math]\displaystyle{ B }[/math] oraz [math]\displaystyle{ C }[/math] są dowolnymi stałymi spełniającymi nierówności
- [math]\displaystyle{ B \geqslant 1 }[/math]
- [math]\displaystyle{ C \geqslant f (m) + B \int_{m}^{\infty} f (x) d x }[/math]
Uwaga D24
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ [m, \infty) }[/math]. Rozważmy szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math]. Zauważmy, że:
- korzystając z całkowego kryterium zbieżności, możemy łatwo zbadać, czy szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math] jest zbieżny
- jeżeli szereg jest zbieżny, to ponownie wykorzystując całki (twierdzenie D23), możemy znaleźć oszacowanie sumy częściowej szeregu [math]\displaystyle{ S(n) = \sum_{k = m}^{n} f(k) }[/math]
Jednak dysponując już oszacowaniem sumy częściowej szeregu [math]\displaystyle{ S(n) = \sum_{k = m}^{n} f(k) }[/math], możemy udowodnić jego poprawność przy pomocy indukcji matematycznej, a stąd łatwo pokazać zbieżność szeregu [math]\displaystyle{ \sum_{k = m}^{\infty} f(k) }[/math]. Zauważmy, że wybór większego [math]\displaystyle{ B }[/math] ułatwia dowód indukcyjny. Stałą [math]\displaystyle{ C }[/math] najlepiej zaokrąglić w górę do wygodnej dla nas wartości.
Czasami potrzebujemy takiego uproszczenia problemu, aby udowodnić zbieżność szeregów bez odwoływania się do całek. Zauważmy, że Czytelnik nawet nie musi znać całek – wystarczy, że policzy je przy pomocy programów, które potrafią to robić (np. WolframAlpha). Kiedy już znajdziemy oszacowanie sumy częściowej szeregu, nie musimy wyjaśniać, w jaki sposób je znaleźliśmy – wystarczy udowodnić, że jest ono poprawne, a do tego wystarczy indukcja matematyczna.
Zamieszczonej niżej zadania pokazują, jak wykorzystać w tym celu twierdzenie D23.
Zadanie D25
Korzystając z twierdzenia D23, znaleźć oszacowania sumy częściowej szeregów
- [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k^2}} \qquad }[/math] oraz [math]\displaystyle{ \qquad \sum_{k = 2}^{\infty} {\small\frac{1}{k (\log k)^2}} }[/math]
Zadanie D26
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k^2}} \leqslant 2 - {\small\frac{1}{n}} }[/math] i udowodnić, że szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k^2}} }[/math] jest zbieżny.
Zadanie D27
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania [math]\displaystyle{ \sum_{k = 2}^{n} {\small\frac{1}{k (\log k)^2}} \lt 2.5 - {\small\frac{1}{\log n}} }[/math] i udowodnić, że szereg [math]\displaystyle{ \sum_{k = 2}^{\infty} {\small\frac{1}{k (\log k)^2}} }[/math] jest zbieżny.
Szeregi nieskończone i liczby pierwsze
Twierdzenie D28
Następujące szeregi są zbieżne
1. [math]\displaystyle{ \quad \sum_{k = 1}^{\infty} {\small\frac{(- 1)^{k + 1}}{p_k}} = 0.269605966 \ldots }[/math] 2. [math]\displaystyle{ \quad \sum_{p \geqslant 2} {\small\frac{1}{p^2}} = 0.452247420041 \ldots }[/math] A085548 3. [math]\displaystyle{ \quad \sum_{p \geqslant 2} {\small\frac{1}{(p - 1)^2}} = 1.375064994748 \ldots }[/math] A086242 4. [math]\displaystyle{ \quad \sum_{p \geqslant 2} {\small\frac{1}{p (p - 1)}} = 0.773156669049 \ldots }[/math] A136141
Twierdzenie D29
Następujące szeregi są zbieżne
1. [math]\displaystyle{ \quad \sum_{p \geqslant 2} {\small\frac{1}{p \log p}} = 1.636616323351 \ldots }[/math] A137245 2. [math]\displaystyle{ \quad \sum_{p \geqslant 2} {\small\frac{1}{p^2 \log p}} = 0.507782187859 \ldots }[/math] A221711 3. [math]\displaystyle{ \quad \sum_{p \geqslant 2} {\small\frac{\log p}{p (p - 1)}} = 0.755366610831 \ldots }[/math] A138312 4. [math]\displaystyle{ \quad \sum_{p \geqslant 2} {\small\frac{\log p}{p^2}} = 0.493091109368 \ldots }[/math] A136271
Twierdzenie D30
Szereg [math]\displaystyle{ \sum_{p \geqslant 2} {\small\frac{\log p}{p}} }[/math] jest rozbieżny.
Uwaga D31
Moglibyśmy oszacować rozbieżność szeregu [math]\displaystyle{ \sum_{p \geqslant 2} {\small\frac{\log p}{p}} }[/math] podobnie, jak to uczyniliśmy w przypadku twierdzenia B37, ale tym razem zastosujemy inną metodę, która pozwoli nam uzyskać bardziej precyzyjny rezultat.
Twierdzenie D32
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Prawdziwe są następujące nierówności
[math]\displaystyle{ \quad 1. \quad }[/math] [math]\displaystyle{ n! \gt n^n e^{- n} }[/math] [math]\displaystyle{ \text{dla} \;\; n \geqslant 1 }[/math] [math]\displaystyle{ \quad 2. \quad }[/math] [math]\displaystyle{ n! \lt n^{n + 1} e^{- n} }[/math] [math]\displaystyle{ \text{dla} \;\; n \geqslant 7 }[/math]
Twierdzenie D33
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Dla wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ n! }[/math] na czynniki pierwsze, prawdziwe są oszacowania
[math]\displaystyle{ \quad 1. \quad }[/math] [math]\displaystyle{ {\small\frac{n}{p}} - 1 \lt W_p (n!) \lt {\small\frac{n}{p - 1}} }[/math] [math]\displaystyle{ \quad 2. \quad }[/math] [math]\displaystyle{ {\small\frac{n + 1}{p}} - 1 \leqslant W_p (n!) \leqslant {\small\frac{n - 1}{p - 1}} }[/math]
Twierdzenie D34
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \log n \gt - 1 }[/math]
Twierdzenie D35 (pierwsze twierdzenie Mertensa[5][6], 1874)
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p}} - \log n \gt - 1.755367 }[/math]
Twierdzenie D36 (pierwsze twierdzenie Mertensa[5][6], 1874)
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p}} - \log n \lt 0.386295 }[/math]
Twierdzenie D37
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \log n \lt 1.141661 }[/math]
Uwaga D38
|
Dokładniejsze oszacowanie sumy [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p}} }[/math] jest dane wzorem
gdzie [math]\displaystyle{ E = 1.332582275733 \ldots }[/math] Dla [math]\displaystyle{ n \geqslant 319 }[/math] mamy też[7]
|
Uwaga D39
|
Dokładniejsze oszacowanie sumy [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} }[/math] jest dane wzorem
gdzie [math]\displaystyle{ \gamma = 0.5772156649 \ldots }[/math] jest stałą Eulera. Dla [math]\displaystyle{ n \geqslant 318 }[/math] prawdziwe jest oszacowanie[8]
|
Uwaga D40
Dla [math]\displaystyle{ n \leqslant 10^{10} }[/math] wartości wyrażeń
- [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p}} - \log n + E }[/math]
- [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \log n + \gamma }[/math]
są liczbami dodatnimi.
Twierdzenie D41
Prawdziwy jest następujący związek
- [math]\displaystyle{ \sum_{p \geqslant 2} {\small\frac{\log p}{p (p - 1)}} = \sum_{n = 2}^{\infty} \left( \sum_{p \geqslant 2} {\small\frac{\log p}{p^n}} \right) = E - \gamma }[/math]
gdzie
- [math]\displaystyle{ \quad \gamma = 0.577215664901532 \ldots }[/math] jest stałą Eulera[9]
- [math]\displaystyle{ \quad E = 1.332582275733220 \ldots }[/math][10]
- [math]\displaystyle{ \quad E - \gamma = 0.755366610831688 \ldots }[/math][11]
Twierdzenie D42
Dla [math]\displaystyle{ n \geqslant 318 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ \left| \sum_{p \leqslant n} {\small\frac{\log p}{p - 1}} - \log n + \gamma \right| \lt {\small\frac{1}{2 \log n}} }[/math]
Zadanie D43
Niech [math]\displaystyle{ r = 1 - \log (2) \approx 0.30685281944 }[/math]. Pokazać, że z nierówności prawdziwej dla [math]\displaystyle{ x \geqslant 32 }[/math]
- [math]\displaystyle{ \sum_{p \leqslant x} {\small\frac{\log p}{p - 1}} \lt \log x - r }[/math]
wynika twierdzenie Czebyszewa.
Definicja D44
Powiemy, że liczby pierwsze [math]\displaystyle{ p, q }[/math] są liczbami bliźniaczymi (tworzą parę liczb bliźniaczych), jeżeli [math]\displaystyle{ \left | p - q \right | = 2 }[/math]
Twierdzenie D45* (Viggo Brun, 1919)
Suma odwrotności par liczb pierwszych [math]\displaystyle{ p }[/math] i [math]\displaystyle{ p + 2 }[/math], takich że liczba [math]\displaystyle{ p + 2 }[/math] jest również pierwsza, jest skończona
- [math]\displaystyle{ \underset{p + 2 \in \mathbb{P}}{\sum_{p \geqslant 2}} \left( {\small\frac{1}{p}} + {\small\frac{1}{p + 2}} \right) = \left( {\small\frac{1}{3}} + {\small\frac{1}{5}} \right) + \left( {\small\frac{1}{5}} + {\small\frac{1}{7}} \right) + \left( {\small\frac{1}{11}} + {\small\frac{1}{13}} \right) + \left( {\small\frac{1}{17}} + {\small\frac{1}{19}} \right) + \ldots = B_2 }[/math]
gdzie [math]\displaystyle{ B_2 = 1.90216058 \ldots }[/math] jest stałą Bruna[13][14].
Zadanie D46
Pokazać, że istnieje nieskończenie wiele liczb pierwszych nietworzących par liczb bliźniaczych.
Dowód z Księgi. Rozbieżność sumy [math]\displaystyle{ \textstyle \sum {\small\frac{1}{p}} }[/math]
Twierdzenie D47
Suma odwrotności liczb pierwszych jest rozbieżna.
Sumowanie przez części
Uwaga D48
Omawianie metody sumowania przez części[16] rozpoczniemy od udowodnienia prostego twierdzenia, które dobrze ilustruje tę metodę i ułatwi zrozumienie uogólnienia. Potrzebna nam będzie następująca funkcja
- [math]\displaystyle{ D(k) = \begin{cases} 1 & \text{gdy } k \, \text{ jest liczbą pierwszą} \\ 0 & \text{gdy } k \, \text{ nie jest liczbą pierwszą} \\ \end{cases} }[/math]
Łatwo znajdujemy związek funkcji [math]\displaystyle{ D(k) }[/math] z funkcją [math]\displaystyle{ \pi (k) }[/math]
- [math]\displaystyle{ \pi (k) - \pi (k - 1) = \sum_{p \leqslant k} 1 - \sum_{p \leqslant k - 1} 1 }[/math]
- [math]\displaystyle{ \; = \sum_{i = 1}^{k} D (i) - \sum_{i = 1}^{k - 1} D (i) }[/math]
- [math]\displaystyle{ \; = D (k) + \sum_{i = 1}^{k - 1} D (i) - \sum_{i = 1}^{k - 1} D (i) }[/math]
- [math]\displaystyle{ \; = D (k) }[/math]
Twierdzenie D49
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] i niech [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{1}{p}} }[/math] oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ n }[/math]. Prawdziwy jest następujący związek
- [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{1}{p}} = {\small\frac{\pi (n)}{n}} + \sum_{k = 2}^{n - 1} {\small\frac{\pi (k)}{k (k + 1)}} }[/math]
Zadanie D50
Pokazać, że dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \sum_{p \leqslant n} {\small\frac{1}{p}} \gt {\small\frac{2}{3}} \cdot \log \log (n + 1) }[/math].
Zadanie D51
Pokazać, że oszacowanie [math]\displaystyle{ \pi (n) \lt n^{1 - \varepsilon} }[/math], gdzie [math]\displaystyle{ \varepsilon \in (0, 1) }[/math], nie może być prawdziwe dla prawie wszystkich liczb naturalnych.
Twierdzenie D52 (sumowanie przez części)
Niech [math]\displaystyle{ a_j }[/math], [math]\displaystyle{ b_j }[/math] będą ciągami określonymi przynajmniej dla [math]\displaystyle{ s \leqslant j \leqslant n }[/math]. Prawdziwy jest następujący wzór
- [math]\displaystyle{ \sum_{k = s}^{n} a_k b_k = a_n \cdot B (n) - \sum_{k = s}^{n - 1} (a_{k + 1} - a_k) B (k) }[/math]
gdzie [math]\displaystyle{ B(k) = \sum_{j = s}^{k} b_j }[/math]. Wzór ten nazywamy wzorem na sumowanie przez części.
Zadanie D53
Niech [math]\displaystyle{ r \neq 1 }[/math]. Pokazać, że [math]\displaystyle{ \sum_{k = 1}^{n} k r^k = \frac{n r^{n + 2} - (n + 1) r^{n + 1} + r}{(r - 1)^2} }[/math].
Twierdzenie D54 (kryterium Dirichleta)
Niech [math]\displaystyle{ (a_k) \; }[/math] i [math]\displaystyle{ \; (b_k) }[/math] będą ciągami liczb rzeczywistych. Jeżeli
- ciąg [math]\displaystyle{ (a_k) }[/math] jest monotoniczny
- ciąg [math]\displaystyle{ (a_k) }[/math] jest monotoniczny
- [math]\displaystyle{ \lim_{k \rightarrow \infty} a_k = 0 }[/math]
- istnieje taka stała [math]\displaystyle{ M }[/math], że [math]\displaystyle{ \left| \sum_{j = 1}^{k} b_j \right| \leqslant M }[/math] dla dowolnej liczby [math]\displaystyle{ k }[/math]
to szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k b_k }[/math] jest zbieżny.
Zadanie D55
Udowodnić następujące wzory
[math]\displaystyle{ \quad \sum_{j = 1}^{k} \sin j = {\small\frac{\cos \left( \tfrac{1}{2} \right) - \cos \left( k + \tfrac{1}{2} \right)}{2 \sin \left( \tfrac{1}{2} \right)}} = {\small\frac{\sin \left( {\normalsize\frac{k}{2}} \right) \cdot \sin \left( {\normalsize\frac{k + 1}{2}} \right)}{\sin \left( \tfrac{1}{2} \right)}} \quad }[/math]
[math]\displaystyle{ \quad \sum_{j = 1}^{k} \cos \left( j + \tfrac{1}{2} \right) = {\small\frac{\sin (k + 1) - \sin (1)}{2 \sin \left( \tfrac{1}{2} \right)}} = {\small\frac{\sin \left( {\normalsize\frac{k}{2}} \right) \cos \left( {\normalsize\frac{k}{2}} + 1 \right)}{\sin \left( \tfrac{1}{2} \right)}} \quad }[/math]
Zadanie D56
Pokazać, że szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{\sin k}{k}} }[/math] jest zbieżny.
Zadanie D57
Pokazać, że szereg [math]\displaystyle{ \sum_{k = 2}^{\infty} {\small\frac{\sin k}{\log k}} }[/math] jest zbieżny, a suma tego szeregu jest w przybliżeniu równa [math]\displaystyle{ 0.6839137864 \ldots }[/math]
Zadanie D58
Niech [math]\displaystyle{ \theta (n) = \sum_{p \leqslant n} \log p }[/math]. Pokazać, że
- [math]\displaystyle{ \theta (n) = \log n \cdot \pi (n) - \sum_{k = 2}^{n - 1} \log \left( 1 + {\small\frac{1}{k}} \right) \pi (k) }[/math]
Twierdzenie D59
Niech [math]\displaystyle{ \theta (n) = \sum_{p \leqslant n} \log p }[/math]. Jeżeli prawdziwe jest oszacowanie [math]\displaystyle{ {\small\frac{A \cdot n}{\log n}} \lt \pi (n) \lt {\small\frac{B \cdot n}{\log n}} }[/math], gdzie [math]\displaystyle{ A, B \in \mathbb{R}_+ }[/math], to istnieje granica
- [math]\displaystyle{ \lim_{n \to \infty} {\small\frac{\theta (n)}{\pi (n) \cdot \log n}} = 1 }[/math]
Uwaga D60
Funkcja [math]\displaystyle{ \theta (n) }[/math] jest ściśle związana z dobrze nam znaną funkcją [math]\displaystyle{ P (n) }[/math]. Ponieważ [math]\displaystyle{ P(n) = \prod_{p \leqslant n} p }[/math], to
- [math]\displaystyle{ \log P (n) = \log \left( \prod_{p \leqslant n} p \right) = \sum_{p \leqslant n} \log p = \theta (n) }[/math].
Z twierdzenia D59 wynika, że jeżeli istnieje granica [math]\displaystyle{ {\small\frac{\theta (n)}{n}} }[/math], to będzie istniała granica dla [math]\displaystyle{ {\small\frac{\pi (n) \cdot \log n}{n}} }[/math]. Jeżeli istnieje granica [math]\displaystyle{ {\small\frac{\pi (n) \cdot \log n}{n}} }[/math], to będzie istniała granica dla [math]\displaystyle{ {\small\frac{\theta (n)}{n}} }[/math] (zobacz C12 p.3).
Wiemy, że dla funkcji [math]\displaystyle{ \theta (n) }[/math], gdzie [math]\displaystyle{ n \geqslant 2 }[/math], prawdziwe jest oszacowanie[18]
- [math]\displaystyle{ \left| {\small\frac{\theta (n)}{n}} - 1 \right| \leqslant {\small\frac{151.3}{\log^4 n}} }[/math]
Zadanie D61
Niech [math]\displaystyle{ \theta (n) = \sum_{p \leqslant n} \log p }[/math]. Pokazać, że
- [math]\displaystyle{ \pi (n) = {\small\frac{\theta (n)}{\log n}} + \sum_{k = 2}^{n - 1} {\small\frac{\log \left( 1 + {\normalsize\frac{1}{k}} \right)}{\log k \cdot \log (k + 1)}} \cdot \theta (k) }[/math]
Iloczyn Cauchy'ego szeregów
Twierdzenie D62 (kryterium d'Alemberta)
Niech [math]\displaystyle{ (a_n) }[/math] będzie ciągiem liczb rzeczywistych i istnieje granica
- [math]\displaystyle{ g = \lim_{n \rightarrow \infty} \left| {\small\frac{a_{n + 1}}{a_n}} \right| }[/math]
Jeżeli
- [math]\displaystyle{ g \lt 1 }[/math], to szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math] jest bezwzględnie zbieżny
- [math]\displaystyle{ g \gt 1 }[/math], to szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math] jest rozbieżny
Uwaga C62
W przypadku, gdy [math]\displaystyle{ \lim_{n \rightarrow \infty} \left| {\small\frac{a_{n + 1}}{a_n}} \right| = 1 }[/math] kryterium d'Alemberta nie rozstrzyga o zbieżności lub rozbieżności szeregu [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math]. Czytelnikowi zostawiamy zastosowanie tego kryterium do szeregów
- [math]\displaystyle{ \sum_{n = 1}^{\infty} 1 \qquad \qquad \sum_{n = 1}^{\infty} {\small\frac{1}{n}} \qquad \qquad \sum_{n = 1}^{\infty} {\small\frac{(- 1)^{n + 1}}{n}} \qquad \qquad \sum_{n = 1}^{\infty} {\small\frac{1}{n^2}} }[/math]
Przykład D64
Niech [math]\displaystyle{ x \in \mathbb{R} }[/math]. Zbadamy zbieżność szeregu
- [math]\displaystyle{ e^x = \sum_{n = 0}^{\infty} {\small\frac{x^n}{n!}} = 1 + x + {\small\frac{x^2}{2}} + {\small\frac{x^3}{6}} + {\small\frac{x^4}{24}} + {\small\frac{x^5}{120}} + \ldots }[/math]
Ponieważ
- [math]\displaystyle{ \lim_{n \rightarrow \infty} \left| {\small\frac{x^{n + 1}}{(n + 1) !}} \cdot {\small\frac{n!}{x^n}} \right| = \lim_{n \rightarrow \infty} {\small\frac{| x |}{n + 1}} = 0 }[/math]
to z kryterium d'Alemberta wynika, że szereg jest bezwzględnie zbieżny.
Zadanie D65
Pokazać, że szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} {\small\frac{n^n}{n!}} }[/math] jest rozbieżny.
Uwaga D66
W twierdzeniu A37, korzystając z następującej definicji funkcji [math]\displaystyle{ e^x }[/math]
- [math]\displaystyle{ e^x = \sum_{k = 0}^{\infty} {\small\frac{x^k}{k!}} = 1 + x + {\small\frac{x^2}{2}} + {\small\frac{x^3}{6}} + {\small\frac{x^4}{24}} + {\small\frac{x^5}{120}} + \ldots }[/math]
pominęliśmy dowód własności [math]\displaystyle{ e^x e^{- x} = 1 }[/math]. Spróbujemy teraz pokazać, że [math]\displaystyle{ e^x e^y = e^{x + y} }[/math].
- [math]\displaystyle{ e^x e^y = \left( \sum_{i = 0}^{\infty} {\small\frac{x^i}{i!}} \right) \left( \sum_{j = 0}^{\infty} {\small\frac{y^j}{j!}} \right) = \sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} {\small\frac{x^i y^j}{i! \cdot j!}} }[/math]
Oznaczmy [math]\displaystyle{ a_i = {\small\frac{x^i}{i!}} }[/math] oraz [math]\displaystyle{ b_j = {\small\frac{y^j}{j!}} }[/math] i przyjrzyjmy się sumowaniu po [math]\displaystyle{ i, j }[/math]. W podwójnej sumie po prawej stronie [math]\displaystyle{ \sum^{\infty}_{i = 0} \sum_{j = 0}^{\infty} a_i b_j }[/math] sumujemy po kolejnych liniach poziomych tak, jak to zostało pokazane na rysunku
[math]\displaystyle{ a_6 b_0 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ \cdots }[/math] [math]\displaystyle{ a_5 b_0 }[/math] [math]\displaystyle{ a_5 b_1 }[/math] [math]\displaystyle{ a_5 b_2 }[/math] [math]\displaystyle{ a_5 b_3 }[/math] [math]\displaystyle{ a_5 b_4 }[/math] [math]\displaystyle{ a_5 b_5 }[/math] [math]\displaystyle{ \cdots }[/math] [math]\displaystyle{ a_4 b_0 }[/math] [math]\displaystyle{ a_4 b_1 }[/math] [math]\displaystyle{ a_4 b_2 }[/math] [math]\displaystyle{ a_4 b_3 }[/math] [math]\displaystyle{ a_4 b_4 }[/math] [math]\displaystyle{ a_4 b_5 }[/math] [math]\displaystyle{ \cdots }[/math] [math]\displaystyle{ a_3 b_0 }[/math] [math]\displaystyle{ a_3 b_1 }[/math] [math]\displaystyle{ a_3 b_2 }[/math] [math]\displaystyle{ a_3 b_3 }[/math] [math]\displaystyle{ a_3 b_4 }[/math] [math]\displaystyle{ a_3 b_5 }[/math] [math]\displaystyle{ \cdots }[/math] [math]\displaystyle{ a_2 b_0 }[/math] [math]\displaystyle{ a_2 b_1 }[/math] [math]\displaystyle{ a_2 b_2 }[/math] [math]\displaystyle{ a_2 b_3 }[/math] [math]\displaystyle{ a_2 b_4 }[/math] [math]\displaystyle{ a_2 b_5 }[/math] [math]\displaystyle{ \cdots }[/math] [math]\displaystyle{ a_1 b_0 }[/math] [math]\displaystyle{ a_1 b_1 }[/math] [math]\displaystyle{ a_1 b_2 }[/math] [math]\displaystyle{ a_1 b_3 }[/math] [math]\displaystyle{ a_1 b_4 }[/math] [math]\displaystyle{ a_1 b_5 }[/math] [math]\displaystyle{ \cdots }[/math] [math]\displaystyle{ a_0 b_0 }[/math] [math]\displaystyle{ a_0 b_1 }[/math] [math]\displaystyle{ a_0 b_2 }[/math] [math]\displaystyle{ a_0 b_3 }[/math] [math]\displaystyle{ a_0 b_4 }[/math] [math]\displaystyle{ a_0 b_5 }[/math] [math]\displaystyle{ \; \cdots \; }[/math]
Zastępując sumowanie po kolejnych liniach poziomych sumowaniem po kolejnych przekątnych, otrzymamy taki rysunek
[math]\displaystyle{ a_6 b_0 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_5 b_0 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_4 b_0 }[/math] [math]\displaystyle{ a_4 b_1 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_3 b_0 }[/math] [math]\displaystyle{ a_3 b_1 }[/math] [math]\displaystyle{ a_3 b_2 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_2 b_0 }[/math] [math]\displaystyle{ a_2 b_1 }[/math] [math]\displaystyle{ a_2 b_2 }[/math] [math]\displaystyle{ a_2 b_3 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_1 b_0 }[/math] [math]\displaystyle{ a_1 b_1 }[/math] [math]\displaystyle{ a_1 b_2 }[/math] [math]\displaystyle{ a_1 b_3 }[/math] [math]\displaystyle{ a_1 b_4 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_0 b_0 }[/math] [math]\displaystyle{ a_0 b_1 }[/math] [math]\displaystyle{ a_0 b_2 }[/math] [math]\displaystyle{ a_0 b_3 }[/math] [math]\displaystyle{ a_0 b_4 }[/math] [math]\displaystyle{ a_0 b_5 }[/math] [math]\displaystyle{ a_0 b_6 }[/math]
Co odpowiada sumie [math]\displaystyle{ \sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {a_k} b_{n - k} }[/math], gdzie [math]\displaystyle{ n }[/math] numeruje kolejne przekątne. Taka zmiana sposobu sumowania powoduje następujące przekształcenie wzoru
- [math]\displaystyle{ e^x e^y = \sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} {\small\frac{x^i y^j}{i! \cdot j!}} = \sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {\small\frac{x^k y^{n - k}}{k! \cdot (n - k) !}} }[/math]
Ponieważ
- [math]\displaystyle{ {\small\frac{1}{k! \cdot (n - k) !}} = {\small\frac{1}{n!}} \cdot {\small\frac{n!}{k! \cdot (n - k)!}} = {\small\frac{1}{n!}} \cdot {\small\binom{n}{k}} }[/math]
to otrzymujemy
- [math]\displaystyle{ e^x e^y = \sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} {\small\frac{x^i y^j}{i! \cdot j!}} = \sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {\small\frac{x^k y^{n - k}}{k! \cdot (n - k) !}} = \sum_{n = 0}^{\infty} \sum_{k = 0}^{n} {\small\frac{1}{n!}} \cdot {\small\binom{n}{k}} \cdot x^k y^{n - k} = \sum_{n = 0}^{\infty} {\small\frac{1}{n!}} \sum_{k = 0}^{n} {\small\binom{n}{k}} \cdot x^k y^{n - k} = \sum_{n = 0}^{\infty} {\small\frac{1}{n!}} (x + y)^n = e^{x + y} }[/math]
Pokazaliśmy tym samym, że z definicji
- [math]\displaystyle{ e^x = \sum_{k = 0}^{\infty} {\small\frac{x^k}{k!}} = 1 + x + {\small\frac{x^2}{2}} + {\small\frac{x^3}{6}} + {\small\frac{x^4}{24}} + {\small\frac{x^5}{120}} + \ldots }[/math]
wynika podstawowa własność funkcji wykładniczej [math]\displaystyle{ e^x e^y = e^{x + y} }[/math].
Mamy świadomość, że dokonana przez nas zmiana sposobu sumowania była nieformalna i w związku z tym nie wiemy, czy była poprawna. Zatem musimy precyzyjnie zdefiniować takie sumowanie i zbadać, kiedy jest dopuszczalne. Dopiero wtedy będziemy mogli być pewni, że policzony rezultat jest poprawny.
Definicja D67
Iloczynem Cauchy'ego szeregów [math]\displaystyle{ \sum_{i = 0}^{\infty} a_i }[/math] oraz [math]\displaystyle{ \sum_{j = 0}^{\infty} b_j }[/math] nazywamy szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} c_n }[/math], gdzie
- [math]\displaystyle{ c_n = \sum_{k = 0}^{n} a_k b_{n - k} = a_0 b_n + a_1 b_{n - 1} + \ldots + a_{n - 1} b_1 + a_n b_0 }[/math]
W przypadku szeregów, których wyrazy są numerowane od liczby [math]\displaystyle{ 1 }[/math], iloczynem Cauchy'ego szeregów [math]\displaystyle{ \sum_{i = 1}^{\infty} a_i }[/math] oraz [math]\displaystyle{ \sum_{j = 1}^{\infty} b_j }[/math] nazywamy szereg [math]\displaystyle{ \sum_{n = 1}^{\infty} c_n }[/math], gdzie
- [math]\displaystyle{ c_n = \sum_{k = 1}^{n} a_k b_{n - k + 1} = a_1 b_n + a_2 b_{n - 1} + \ldots + a_{n - 1} b_2 + a_n b_1 }[/math]
Zadanie D68
Niech [math]\displaystyle{ c_n = \sum_{k = 0}^{n} a_k b_{n - k} }[/math]. Pokazać, że
- jeżeli [math]\displaystyle{ (a_n) = (1, 0, 0, 0, 0, \ldots) }[/math], [math]\displaystyle{ \; (b_n) }[/math] jest dowolnym ciągiem, to [math]\displaystyle{ c_n = b_n }[/math]
- jeżeli [math]\displaystyle{ (a_n) = (1, 1, 1, 1, 1, \ldots) }[/math], [math]\displaystyle{ \; (b_n) }[/math] jest dowolnym ciągiem, to [math]\displaystyle{ c_n = \sum_{k = 0}^{n} b_k = B_n }[/math]
- jeżeli [math]\displaystyle{ a_n = b_n = {\small\frac{r^n}{n!}} }[/math], to [math]\displaystyle{ c_n = {\small\frac{(2 r)^n}{n!}} }[/math]
- jeżeli [math]\displaystyle{ (a_n) = (a, r, r^2, r^3, \ldots) }[/math], [math]\displaystyle{ \; (b_n) = (b, r, r^2, r^3, \ldots) }[/math], to [math]\displaystyle{ c_n = \begin{cases} \qquad \qquad \qquad \; a b & \text{gdy } \; n = 0 \\ (a + b + n - 1) r^n & \text{gdy } \; n \geqslant 1 \\ \end{cases} }[/math]
- jeżeli [math]\displaystyle{ (a_n) = (a, q, q^2, q^3, \ldots) }[/math], [math]\displaystyle{ \; (b_n) = (b, r, r^2, r^3, \ldots) }[/math], gdzie [math]\displaystyle{ q \neq r }[/math], to [math]\displaystyle{ c_n = \begin{cases} \qquad \qquad \qquad \qquad \qquad \qquad \, a b & \text{gdy } \; n = 0 \\ q^n \left( b + {\large\frac{r}{q - r}} \right) + r^n \left( a - {\large\frac{q}{q - r}} \right) & \text{gdy } \; n \geqslant 1 \\ \end{cases} }[/math]
Przykład D69
Ostatni punkt zadania D68 pozwala stworzyć wiele przykładowych szeregów i ich iloczynów Cauchy'ego. Przypomnijmy, że
- [math]\displaystyle{ (a_n) = (a, q, q^2, q^3, \ldots) }[/math], [math]\displaystyle{ \quad (b_n) = (b, r, r^2, r^3, \ldots) }[/math], gdzie [math]\displaystyle{ \, q \neq r }[/math]
- [math]\displaystyle{ c_n = \begin{cases} \qquad \qquad \qquad \qquad \qquad \qquad \, a b & \text{gdy } \; n = 0 \\ q^n \left( b + {\large\frac{r}{q - r}} \right) + r^n \left( a - {\large\frac{q}{q - r}} \right) & \text{gdy } \; n \geqslant 1 \\ \end{cases} }[/math]
Przykłady zebraliśmy w tabeli.
[math]\displaystyle{ \boldsymbol{a} }[/math] [math]\displaystyle{ \boldsymbol{q} }[/math] [math]\displaystyle{ \boldsymbol{b} }[/math] [math]\displaystyle{ \boldsymbol{r} }[/math] [math]\displaystyle{ \boldsymbol{(c_n)} }[/math] [math]\displaystyle{ \boldsymbol{\sum_{n=0}^{\infty} a_n} }[/math] [math]\displaystyle{ \boldsymbol{\sum_{n=0}^{\infty} b_n} }[/math] [math]\displaystyle{ \boldsymbol{\sum_{n=0}^{\infty} c_n} }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ -2 }[/math] [math]\displaystyle{ {\small\frac{1}{3}} }[/math] [math]\displaystyle{ (-6,0,0,0,0,0,…) }[/math] zbieżny zbieżny zbieżny [math]\displaystyle{ -2 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ (-6,0,0,0,0,0,…) }[/math] rozbieżny rozbieżny zbieżny [math]\displaystyle{ {\small\frac{r - 2q}{r - q}} }[/math] [math]\displaystyle{ q }[/math] [math]\displaystyle{ {\small\frac{r}{r - q}} }[/math] [math]\displaystyle{ r }[/math] [math]\displaystyle{ \left( {\small\frac{r ( r - 2q )}{(r - q)^2}}, r, r^2, r^3, r^4, r^5, \ldots \right) }[/math] zbieżny / rozbieżny zbieżny / rozbieżny zbieżny / rozbieżny [math]\displaystyle{ 4 }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ -2 }[/math] [math]\displaystyle{ {\small\frac{1}{3}} }[/math] [math]\displaystyle{ \left( -8,{\small\frac{1}{3}}, {\small\frac{1}{3^2}}, {\small\frac{1}{3^3}}, {\small\frac{1}{3^4}}, {\small\frac{1}{3^5}}, \ldots \right) }[/math] zbieżny zbieżny zbieżny [math]\displaystyle{ {\small\frac{7}{3}} }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ - {\small\frac{1}{3}} }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ \left( - {\small\frac{7}{9}}, {\small\frac{1}{2}}, {\small\frac{1}{2^2}}, {\small\frac{1}{2^3}}, {\small\frac{1}{2^4}}, {\small\frac{1}{2^5}}, \ldots \right) }[/math] rozbieżny zbieżny zbieżny [math]\displaystyle{ -1 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ (-3,3,3^2,3^3,3^4,3^5,…) }[/math] rozbieżny rozbieżny rozbieżny [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ -1 }[/math] [math]\displaystyle{ \left( {\small\frac{1}{4}}, 0, 0, 0, 0, 0, \ldots \right) }[/math] rozbieżny rozbieżny zbieżny [math]\displaystyle{ -1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ (-2, 0, 0, 0, 0, 0, \ldots ) }[/math] rozbieżny rozbieżny zbieżny [math]\displaystyle{ -1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ (-3, 1, 1, 1, 1, 1,\ldots ) }[/math] rozbieżny rozbieżny rozbieżny [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ -1 }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ (-2,0,0,0,0,0,…) }[/math] rozbieżny zbieżny zbieżny [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ (0, 1, 1, 1, 1, 1, \ldots ) }[/math] rozbieżny zbieżny rozbieżny [math]\displaystyle{ {\small\frac{r - 2}{r - 1}} }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ {\small\frac{r}{r - 1}} }[/math] [math]\displaystyle{ r }[/math] [math]\displaystyle{ \left( {\small\frac{r ( r - 2 )}{(r - 1)^2}}, r, r^2, r^3, r^4, r^5, \ldots \right) }[/math] rozbieżny zbieżny / rozbieżny zbieżny / rozbieżny [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ (0, 2, 2^2, 2^3, 2^4, 2^5, \ldots ) }[/math] rozbieżny rozbieżny rozbieżny [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ -1 }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ \left( - 3, {\small\frac{1}{2}}, {\small\frac{1}{2^2}}, {\small\frac{1}{2^3}}, {\small\frac{1}{2^4}}, {\small\frac{1}{2^5}}, \ldots \right) }[/math] rozbieżny zbieżny zbieżny
Przykład D70
Podamy przykład szeregów zbieżnych, których iloczyn Cauchy'ego jest rozbieżny. Rozważmy zbieżny szereg (zobacz D5)
- [math]\displaystyle{ \sum_{k = 0}^{\infty} {\small\frac{(- 1)^k}{\sqrt{k + 1}}} = 0.604898643 \ldots \qquad \qquad }[/math] (WolframAlpha)
Mnożąc powyższy szereg przez siebie według reguły Cauchy'ego, otrzymujemy
- [math]\displaystyle{ c_n = \sum_{k = 0}^{n} {\small\frac{(- 1)^k}{\sqrt{k + 1}}} \cdot {\small\frac{(- 1)^{n - k}}{\sqrt{n - k + 1}}} = (- 1)^n \cdot \sum_{k = 0}^{n} {\small\frac{1}{\sqrt{(k + 1) (n - k + 1)}}} }[/math]
Ale [math]\displaystyle{ k \leqslant n \; }[/math] i [math]\displaystyle{ \; n - k \leqslant n }[/math], zatem
- [math]\displaystyle{ {\small\frac{1}{\sqrt{(k + 1) (n - k + 1)}}} \geqslant {\small\frac{1}{\sqrt{(n + 1) (n + 1)}}} = {\small\frac{1}{n + 1}} }[/math]
Czyli
- [math]\displaystyle{ | c_n | \geqslant \sum_{k = 0}^{n} {\small\frac{1}{n + 1}} = 1 }[/math]
Ponieważ [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n \neq 0 }[/math], to iloczyn Cauchy'ego jest rozbieżny (zobacz D4).
Zadanie D71
Pokazać, że jeżeli [math]\displaystyle{ a_n = b_n = r^n \; }[/math] i [math]\displaystyle{ \; c_n = (n + 1) r^n }[/math] (zobacz D68 p.3), to szeregi [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math] oraz [math]\displaystyle{ \sum_{n = 0}^{\infty} c_n }[/math] są jednocześnie zbieżne lub jednocześnie rozbieżne. Sprawdzić, że w przypadku, gdy szeregi te są zbieżne, prawdziwy jest wzór
- [math]\displaystyle{ \left( \sum_{i = 0}^{\infty} a_i \right) \cdot \left( \sum_{j = 0}^{\infty} b_j \right) = \sum_{n = 0}^{\infty} \left( \sum_{k = 0}^{n} a_k b_{n - k} \right) }[/math]
Uwaga D72
Przykłady D69 i D70 pokazują, że w ogólności nie jest prawdziwy wzór
- [math]\displaystyle{ \left( \sum_{i = 0}^{\infty} a_i \right) \cdot \left( \sum_{j = 0}^{\infty} b_j \right) = \sum_{n = 0}^{\infty} \left( \sum_{k = 0}^{n} a_k b_{n - k} \right) }[/math]
Skoro iloczyn sum szeregów nie zawsze jest równy sumie iloczynu Cauchy'ego tych szeregów, to musimy ustalić, jakie warunki muszą być spełnione, aby tak było.
Uwaga D73
Nim przejdziemy do dowodu twierdzenia Mertensa, zauważmy, że od sumowania po [math]\displaystyle{ m + 1 }[/math] kolejnych przekątnych
- [math]\displaystyle{ \sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k} }[/math]
możemy łatwo przejść do sumowania po liniach poziomych lub po liniach pionowych. Rysunek przedstawia sytuację, gdy [math]\displaystyle{ m = 5 }[/math].
[math]\displaystyle{ a_6 b_0 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_5 b_0 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_4 b_0 }[/math] [math]\displaystyle{ a_4 b_1 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_3 b_0 }[/math] [math]\displaystyle{ a_3 b_1 }[/math] [math]\displaystyle{ a_3 b_2 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_2 b_0 }[/math] [math]\displaystyle{ a_2 b_1 }[/math] [math]\displaystyle{ a_2 b_2 }[/math] [math]\displaystyle{ a_2 b_3 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_1 b_0 }[/math] [math]\displaystyle{ a_1 b_1 }[/math] [math]\displaystyle{ a_1 b_2 }[/math] [math]\displaystyle{ a_1 b_3 }[/math] [math]\displaystyle{ a_1 b_4 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ a_0 b_0 }[/math] [math]\displaystyle{ a_0 b_1 }[/math] [math]\displaystyle{ a_0 b_2 }[/math] [math]\displaystyle{ a_0 b_3 }[/math] [math]\displaystyle{ a_0 b_4 }[/math] [math]\displaystyle{ a_0 b_5 }[/math] [math]\displaystyle{ a_0 b_6 }[/math]
Przejście do sumowania po liniach poziomych
- [math]\displaystyle{ \sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k} = \sum_{i = 0}^{m} \sum_{j = 0}^{m - i} a_i b_j }[/math]
Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach poziomych, a druga po kolejnych elementach w [math]\displaystyle{ i }[/math]-tej linii poziomej.
Przejście do sumowania po liniach pionowych
- [math]\displaystyle{ \sum_{n = 0}^{m} \sum_{k = 0}^{n} a_k b_{n - k} = \sum_{i = 0}^{m} \sum_{j = 0}^{m - i} a_j b_i }[/math]
Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach pionowych, a druga po kolejnych elementach w [math]\displaystyle{ i }[/math]-tej linii pionowej.
Twierdzenie D74 (Franciszek Mertens)
Jeżeli szereg [math]\displaystyle{ \sum_{i = 0}^{\infty} a_i = A }[/math] jest zbieżny bezwzględnie, szereg [math]\displaystyle{ \sum_{j = 0}^{\infty} b_j = B }[/math] jest zbieżny, to ich iloczyn Cauchy'ego [math]\displaystyle{ \sum_{n = 0}^{\infty} c_n }[/math], gdzie [math]\displaystyle{ c_n = \sum_{k = 0}^{n} a_k b_{n - k} }[/math], jest zbieżny i [math]\displaystyle{ \sum_{n = 0}^{\infty} c_n = A B }[/math].
Zadanie D75
Pokazać, że iloczyn Cauchy'ego dwóch szeregów bezwzględnie zbieżnych jest bezwzględnie zbieżny.
Zadanie D76
Podać przykład szeregów zbieżnych, z których tylko jeden jest bezwzględnie zbieżny i których iloczyn Cauchy'ego jest warunkowo zbieżny.
Zadanie D77
Podać przykład szeregów warunkowo zbieżnych, których iloczyn Cauchy'ego jest warunkowo zbieżny.
Uwaga D78
Nim przejdziemy do dowodu twierdzenia Abela, musimy udowodnić trzy twierdzenia dotyczące pewnych granic. Warto zauważyć, że twierdzenie D80 pozwala przypisać wartość sumy do szeregów, których suma w zwykłym sensie nie istnieje. Uogólnienie to nazywamy sumowalnością w sensie Cesàro[20]. Nie będziemy zajmowali się tym tematem, ale podamy ciekawy przykład.
Rozważmy szereg [math]\displaystyle{ \sum_{i = 0}^{\infty} (- 1)^i }[/math]. Sumy częściowe tego szeregu wynoszą [math]\displaystyle{ S_k = {\small\frac{1 + (- 1)^k}{2}} }[/math] i tworzą ciąg rozbieżny, ale ciąg kolejnych średnich arytmetycznych dla ciągu [math]\displaystyle{ (S_k) }[/math] jest równy
- [math]\displaystyle{ x_n = {\small\frac{S_0 + \ldots + S_n}{n + 1}} = {\small\frac{1}{n + 1}} \cdot \sum_{k = 0}^{n} {\small\frac{1 + (- 1)^k}{2}} = {\small\frac{1}{2}} + {\small\frac{1 + (- 1)^n}{4 (n + 1)}} \xrightarrow{\; n \rightarrow \infty \;} {\small\frac{1}{2}} \qquad \qquad }[/math] (WolframAlfa)
Zatem szereg [math]\displaystyle{ \sum_{i = 0}^{\infty} (- 1)^i }[/math] jest sumowalny w sensie Cesàro i jego suma jest równa [math]\displaystyle{ {\small\frac{1}{2}} }[/math].
Twierdzenie D79
Jeżeli [math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = 0 }[/math], to [math]\displaystyle{ \lim_{n \rightarrow \infty} {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} | a_k | = 0 }[/math].
Twierdzenie D80
Jeżeli ciąg [math]\displaystyle{ (a_k) }[/math] jest zbieżny, to ciąg kolejnych średnich arytmetycznych [math]\displaystyle{ x_n = {\small\frac{a_0 + \ldots + a_n}{n + 1}} }[/math] jest zbieżny do tej samej granicy.
Twierdzenie D81
Niech [math]\displaystyle{ (a_n) }[/math] i [math]\displaystyle{ (b_n) }[/math] będą zbieżnymi ciągami liczb rzeczywistych. Jeżeli [math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = a }[/math] i [math]\displaystyle{ \lim_{n \rightarrow \infty} b_n = b }[/math], to [math]\displaystyle{ \lim_{n \rightarrow \infty} {\small\frac{1}{n + 1}} \sum_{k = 0}^{n} a_k b_{n - k} = a b }[/math].
Twierdzenie D82 (Niels Henrik Abel)
Jeżeli szeregi [math]\displaystyle{ \sum_{i = 0}^{\infty} a_i = A }[/math] oraz [math]\displaystyle{ \sum_{j = 0}^{\infty} b_j = B }[/math] są zbieżne i ich iloczyn Cauchy'ego [math]\displaystyle{ \sum_{n = 0}^{\infty} c_n }[/math], gdzie [math]\displaystyle{ c_n = \sum_{k = 0}^{n} a_k b_{n - k} }[/math], jest zbieżny, to [math]\displaystyle{ \sum_{n = 0}^{\infty} c_n = A B }[/math].
Liczby Catalana
Definicja D83
Liczby Catalana [math]\displaystyle{ C_n }[/math] definiujemy wzorem
- [math]\displaystyle{ C_n = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}} }[/math]
gdzie [math]\displaystyle{ n \geqslant 0 }[/math].
Twierdzenie D84
Liczby Catalana [math]\displaystyle{ C_n }[/math] mają następujące własności
- [math]\displaystyle{ C_n }[/math] są liczbami całkowitymi dodatnimi
- [math]\displaystyle{ C_n = {\small\frac{1}{2 n + 1}} {\small\binom{2 n + 1}{n}} = {\small\frac{1}{n}} {\small\binom{2 n}{n - 1}} }[/math]
- [math]\displaystyle{ C_{n + 1} = {\small\frac{2 (2 n + 1)}{n + 2}} C_n }[/math]
- [math]\displaystyle{ C_{n + 1} = \sum_{k = 0}^{n} C_k C_{n - k} }[/math]
Zadanie D85
Niech [math]\displaystyle{ C_n }[/math] oznacza [math]\displaystyle{ n }[/math]-tą liczbę Catalana i niech [math]\displaystyle{ \sum_{n = 0}^{\infty} x_n }[/math] oznacza szereg, który otrzymujemy, mnożąc szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} a_n }[/math] przez siebie według reguły Cauchy'ego. Pokazać, że
- jeżeli [math]\displaystyle{ a_n = C_n }[/math], to [math]\displaystyle{ x_n = C_{n + 1} }[/math]
- jeżeli [math]\displaystyle{ a_0 = \alpha \; }[/math] i [math]\displaystyle{ \; a_n = r^{n - 1} C_{n - 1} }[/math] dla [math]\displaystyle{ n \geqslant 1 }[/math], to [math]\displaystyle{ x_0 = \alpha^2 }[/math], [math]\displaystyle{ \; x_1 = 2 \alpha C_0 \; }[/math] i [math]\displaystyle{ \; x_n = (1 + 2 \alpha r) r^{n - 2} C_{n - 1} }[/math] dla [math]\displaystyle{ n \geqslant 2 }[/math]
Dla jakich wartości [math]\displaystyle{ \alpha, r }[/math] szereg [math]\displaystyle{ \sum_{n = 0}^{\infty} x_n }[/math] jest zbieżny?
Sumy współczynników dwumianowych
Twierdzenie D86
Dla [math]\displaystyle{ n \geqslant 0 \; }[/math] i [math]\displaystyle{ \; r \in \mathbb{R} }[/math] prawdziwe są wzory
- [math]\displaystyle{ \sum_{k = 0}^{n} r^k {\small\binom{n}{k}} = (r + 1)^n }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\frac{r^{k + 1}}{k + 1}} {\small\binom{n}{k}} = {\small\frac{(r + 1)^{n + 1} - 1}{n + 1}} }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} k {\small\binom{n}{k}} = n 2^{n - 1} }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} = n (n + 1) 2^{n - 2} }[/math]
Twierdzenie D87
Dla [math]\displaystyle{ n, m \geqslant 0 }[/math] prawdziwy jest wzór
- [math]\displaystyle{ \sum_{k = 0}^{m} {\small\binom{n + k}{n}} = {\small\binom{n + m + 1}{n}} }[/math]
Suma nieoznaczona
Uwaga D88
Sumą nieoznaczoną[21] (lub antyróżnicą) funkcji [math]\displaystyle{ f(k) }[/math], będziemy nazywali dowolną funkcję [math]\displaystyle{ F(k) }[/math] taką, że
- [math]\displaystyle{ F(k + 1) - F (k) = f (k) }[/math]
Łatwo zauważamy, że istnieje cała rodzina funkcji [math]\displaystyle{ F(k) }[/math], bo jeżeli [math]\displaystyle{ F (k) }[/math] jest sumą nieoznaczoną, to [math]\displaystyle{ F (k) + C }[/math], gdzie [math]\displaystyle{ C }[/math] jest stałą, również jest sumą nieoznaczoną. W szczególności
- [math]\displaystyle{ \sum_{k = a}^{b} f (k) = \sum_{k = a}^{b} (F (k + 1) - F (k)) }[/math]
- [math]\displaystyle{ \;\;\;\: = - \sum_{k = a}^{b} (F (k) - F (k + 1)) }[/math]
- [math]\displaystyle{ \;\;\;\: = - ( F (a) - F (b + 1) ) }[/math]
- [math]\displaystyle{ \;\;\;\: = F (b + 1) - F (a) }[/math]
Co przez analogię do całki nieoznaczonej możemy zapisać jako
- [math]\displaystyle{ \sum_{k = a}^{b} f (k) = F (k) \biggr\rvert_{a}^{b + 1} \qquad \qquad \qquad ( 1 ) }[/math]
Należy podkreślić różnicę między sumą oznaczoną [math]\displaystyle{ S(n) }[/math] a sumą nieoznaczoną [math]\displaystyle{ F(k) }[/math]. Niech [math]\displaystyle{ f(k) = k^2 }[/math]. Oczywiście
- [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} k^2 = {\small\frac{1}{6}} n (n + 1) (2 n + 1) }[/math]
- [math]\displaystyle{ F(k) = {\small\frac{1}{6}} (k - 1) k (2 k - 1) }[/math]
Ponieważ dla sumy [math]\displaystyle{ S(n) }[/math] prawdziwy jest związek [math]\displaystyle{ S(n + 1) - S (n) = f (n + 1) }[/math], to otrzymujemy [math]\displaystyle{ F(k) = S (k - 1) }[/math]. Weźmy kolejny przykład, niech [math]\displaystyle{ f(k) = r^k }[/math], gdzie [math]\displaystyle{ r }[/math] jest stałą. Mamy
- [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} r^k = {\small\frac{r^{n + 1} - 1}{r - 1}} }[/math]
ale
- [math]\displaystyle{ F(k) = {\small\frac{r^k}{r - 1}} }[/math]
i nie jest prawdą, że [math]\displaystyle{ F(k) = S (k - 1) }[/math], bo pominięty został wyraz [math]\displaystyle{ {\small\frac{- 1}{r - 1}} }[/math], który jest stałą, ale jest to zrozumiałe.
Niech teraz [math]\displaystyle{ f(n, k) = {\small\binom{n + k}{n}} }[/math]. Wiemy, że (zobacz D87)
- [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}} }[/math]
- [math]\displaystyle{ F(n, k) = {\small\frac{k}{n + 1}} {\small\binom{n + k}{n}} }[/math]
Tym razem otrzymujemy zupełnie inne wyniki: suma [math]\displaystyle{ S(n) }[/math] nie zależy od dwóch zmiennych, bo jest to niemożliwe, a suma nieoznaczona nadal zależy od [math]\displaystyle{ k }[/math], bo dla [math]\displaystyle{ F(n, k) }[/math] musi być prawdziwy wzór [math]\displaystyle{ (1) }[/math]. Łatwo widzimy, że
- [math]\displaystyle{ S (n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1} }[/math]
Uwaga D89
Powiedzmy, że dysponujemy wzorem [math]\displaystyle{ S(b) = \sum_{k = a}^{b} f (k) }[/math] i chcemy udowodnić jego poprawność. W prostych przypadkach możemy wykorzystać indukcję matematyczną: wystarczy pokazać, że
- [math]\displaystyle{ S(k + 1) = S (k) + f (k + 1) }[/math]
Jeżeli już udało nam się pokazać związek [math]\displaystyle{ f(k) = S (k) - S (k - 1) }[/math], to równie dobrze możemy zamienić sumę na sumę teleskopową (zobacz D12), aby otrzymać, że
- [math]\displaystyle{ \sum_{k = a + 1}^{b} f (k) = \sum_{k = a + 1}^{b} ( S (k) - S (k - 1) ) }[/math]
- [math]\displaystyle{ \;\, = - \sum_{k = a + 1}^{b} ( S (k - 1) - S (k) ) }[/math]
- [math]\displaystyle{ \;\, = - ( S (a) - S (b) ) }[/math]
- [math]\displaystyle{ \;\, = S (b) - S (a) }[/math]
Czyli
- [math]\displaystyle{ S(b) = \sum_{k = a + 1}^{b} f (k) + S (a) = \sum_{k = a}^{b} f (k) }[/math]
bo [math]\displaystyle{ S(a) = f (a) }[/math].
W przypadkach bardziej skomplikowanych nie możemy tak postąpić. W poprzedniej uwadze rozważaliśmy sumę
- [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}} }[/math]
ale
- [math]\displaystyle{ S(n) - S (n - 1) = {\small\frac{3 n + 1}{2 (n + 1)}} {\small\binom{2 n}{n}} }[/math]
I nie da się pokazać związku [math]\displaystyle{ S(k) - S (k - 1) = f (n, k) }[/math], bo różnica [math]\displaystyle{ S(k) - S (k - 1) }[/math] nie zależy od [math]\displaystyle{ n }[/math].
Tutaj z pomocą przychodzi nam suma nieoznaczona. W programie Maxima możemy ją policzyć, wpisując polecenia
load ("zeilberger");
AntiDifference(binomial(n+k, n), k);
Otrzymujemy
- [math]\displaystyle{ F(n, k) = {\small\frac{k}{n + 1}} {\small\binom{n + k}{n}} }[/math]
Oczywiście
- [math]\displaystyle{ F(n, k + 1) - F (n, k) = {\small\binom{n + k}{n}} }[/math]
i
- [math]\displaystyle{ S(n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1} = {\small\binom{2 n + 1}{n}} }[/math]
Podsumujmy. Jakkolwiek znalezienie ogólnego wzoru na sumę [math]\displaystyle{ S (n) = \sum_{k = 0}^{n} f (k) }[/math] może być bardzo trudne, to udowodnienie poprawności tego wzoru może być znacznie łatwiejsze (metodą indukcji matematycznej lub obliczając sumę teleskopową). Podobnie jest w bardziej skomplikowanym przypadku, gdy szukamy ogólnego wzoru na sumę [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} f (n, k) }[/math]. Tutaj wymienionych przed chwilą metod zastosować nie można, a znalezienie wzoru na sumę nieoznaczoną [math]\displaystyle{ F(n, k) }[/math] może być jeszcze trudniejsze, ale gdy już taki wzór mamy, to sprawdzenie jego poprawności, czyli związku [math]\displaystyle{ F(n, k + 1) - F (n, k) = f (n, k) }[/math], może być bardzo łatwe, a wtedy otrzymujemy natychmiast
- [math]\displaystyle{ S(n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1} }[/math]
Zadanie D90
Korzystając z programu Maxima znaleźć sumę nieoznaczoną [math]\displaystyle{ F(n, k) }[/math] dla funkcji
- [math]\displaystyle{ f(n, k) = {\small\frac{1}{(k + 1) (n - k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} }[/math]
i pokazać, że prawdziwy jest wzór [math]\displaystyle{ C_{n + 1} = \sum_{k = 0}^{n} C_k C_{n - k} }[/math], gdzie [math]\displaystyle{ C_n }[/math] są liczbami Catalana.
Znajdowanie równania rekurencyjnego dla sumy [math]\displaystyle{ \boldsymbol{S(n)} }[/math]
Uwaga D91
Rozważmy sumę
- [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} f (n, k) }[/math]
W twierdzeniach D107 i D108 wyliczyliśmy [math]\displaystyle{ S(n) }[/math], znajdując najpierw równanie rekurencyjne dla sumy. Możemy przypuszczać, że równanie rekurencyjne dla sumy [math]\displaystyle{ S(n) }[/math] wynika z istnienia odpowiedniego równania rekurencyjnego dla składników sumy [math]\displaystyle{ f(n, k) }[/math]. Zagadnieniem tym zajmowała się siostra Mary Celine Fasenmyer, która podała algorytm postępowania[22][23]. Prace Zeilbergera oraz Wilfa i Zeilbergera uogólniły ten algorytm[24][25]. My przedstawimy jedynie kilka prostych przypadków, które zilustrujemy przykładami. Szersze omówienie tematu Czytelnik znajdzie w książce Petkovšeka, Wilfa i Zeilbergera[26].
Twierdzenie D92
Niech [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} f (n, k) }[/math]. Jeżeli składniki sumy [math]\displaystyle{ f(n, k) }[/math] spełniają równanie rekurencyjne
- [math]\displaystyle{ a \cdot f (n + 1, k + 1) + b \cdot f (n + 1, k) + c \cdot f (n, k + 1) + d \cdot f (n, k) = 0 }[/math]
gdzie współczynniki [math]\displaystyle{ a, b, c, d }[/math] są funkcjami tylko [math]\displaystyle{ n }[/math], to suma [math]\displaystyle{ S (n) }[/math] spełnia równanie rekurencyjne
- [math]\displaystyle{ (a + b) S (n + 1) + (c + d) S (n) - a \cdot f (n + 1, 0) - b \cdot f (n + 1, n + 1) - c [f (n, 0) - f (n, n + 1)] = 0 }[/math]
Uwaga D93
Nie ma sensu stosowanie opisanej powyżej metody do prostych sum postaci [math]\displaystyle{ \sum_{k = 0}^{n} f (k) }[/math], bo równanie rekurencyjne otrzymujemy w takim przypadku natychmiast: [math]\displaystyle{ S(n + 1) - S (n) = f (n + 1) }[/math].
Zadanie D94
Pokazać, że dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór (zobacz D87)
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}} }[/math]
Zadanie D95
Pokazać, że dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór (zobacz D86 p.1)
- [math]\displaystyle{ \sum_{k = 0}^{n} r^k {\small\binom{n}{k}} = (r + 1)^n }[/math]
Zadanie D96
Pokazać, że dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór (zobacz D86 p.2)
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{n}{k}} = {\small\frac{2^{n + 1} - 1}{n + 1}} }[/math]
Zadanie D97
Niech [math]\displaystyle{ n \in \mathbb{N}_0 \; }[/math] i [math]\displaystyle{ \; k \in \mathbb{Z} }[/math]. Uzasadnić, dlaczego przyjmujemy, że [math]\displaystyle{ {\small\binom{n}{k}} = 0 }[/math], gdy [math]\displaystyle{ k \lt 0 \; }[/math] lub [math]\displaystyle{ \; k \gt n }[/math].
Twierdzenie D98
Niech [math]\displaystyle{ n, I, J \in \mathbb{N}_0 \; }[/math] i [math]\displaystyle{ \; k \in \mathbb{Z} }[/math]. Jeżeli [math]\displaystyle{ f(n, k) = 0 }[/math]
dla [math]\displaystyle{ k \notin [0, n] \, }[/math] i składniki sumy [math]\displaystyle{ f(n, k) }[/math] spełniają równanie rekurencyjne
- [math]\displaystyle{ \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = 0 }[/math]
gdzie współczynniki [math]\displaystyle{ a_{i j} }[/math] są funkcjami tylko [math]\displaystyle{ n }[/math], to suma
- [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} f (n, k) }[/math]
spełnia następujące równanie rekurencyjne
- [math]\displaystyle{ \sum_{i = 0}^{I} S (n + i) \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0 }[/math]
Uwaga D99
Z zadania D97 wynika, że jeżeli funkcja [math]\displaystyle{ f(n, k) }[/math] zawiera czynnik [math]\displaystyle{ {\small\binom{n}{k}} }[/math], to może spełniać warunek [math]\displaystyle{ f(n, k) = 0 }[/math] dla [math]\displaystyle{ k \notin [0, n] }[/math]. Oczywiście nie jest to warunek wystarczający, bo funkcja [math]\displaystyle{ f (n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}} }[/math] jest różna od zera dla [math]\displaystyle{ k = - 1 }[/math].
Zadanie D100
Pokazać, że dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór (zobacz D86 p.3)
- [math]\displaystyle{ \sum_{k = 0}^{n} k {\small\binom{n}{k}} = n 2^{n - 1} }[/math]
Zadanie D101
Pokazać, że dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwe są wzory
- [math]\displaystyle{ \sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} = n (n + 1) 2^{n - 2} }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} k^3 {\small\binom{n}{k}} = n^2 (n + 3) 2^{n - 3} }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\binom{n}{k}}^2 = {\small\binom{2 n}{n}} }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} k {\small\binom{n}{k}}^2 = {\small\frac{1}{2}} n {\small\binom{2 n}{n}} }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} k^2 {\small\binom{n}{k}}^2 = n^2 {\small\binom{2 n - 2}{n - 1}} }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} k^3 {\small\binom{n}{k}}^2 = {\small\frac{1}{2}} n^2 (n + 1) {\small\binom{2 n - 2}{n - 1}} }[/math]
Uwaga D102
Niech [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} f (n, k) }[/math]. Wiemy (zobacz D98), że jeżeli dla dowolnego [math]\displaystyle{ n }[/math] wartość funkcji [math]\displaystyle{ f(n, k) }[/math] jest określona dla wszystkich [math]\displaystyle{ k \in \mathbb{Z} \; }[/math] i [math]\displaystyle{ \; f(n, k) = 0 }[/math] dla [math]\displaystyle{ k \notin [0, n] }[/math], to sumę [math]\displaystyle{ S(n) }[/math] możemy zapisać w równoważnej postaci
[math]\displaystyle{ S(n) = \sum_{k = 0}^{n} f (n, k) = \sum_{k \in \mathbb{Z}} f (n, k) }[/math]
Rozważmy teraz funkcję [math]\displaystyle{ f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}} }[/math], która powyższego warunku nie spełnia, bo jest różna od zera dla [math]\displaystyle{ k = - 1 }[/math]. Jeżeli zapiszemy [math]\displaystyle{ f(n, k) }[/math] w postaci
- [math]\displaystyle{ f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}} = {\small\frac{1}{k + 1}} \cdot {\small\frac{n!}{k! (n - k) !}} = {\small\frac{n!}{(k + 1) ! (n - k) !}} }[/math]
to natychmiast widzimy, że
- [math]\displaystyle{ f(n, - 1) = {\small\frac{n!}{0! (n + 1) !}} = {\small\frac{1}{n + 1}} }[/math]
Zatem w przypadku tej funkcji mamy
- [math]\displaystyle{ \sum_{k \in \mathbb{Z}} f (n, k) = \sum_{k = 0}^{n} f (n, k) + f (n, - 1) = S (n) + {\small\frac{1}{n + 1}} }[/math]
Zakładając, że spełnione jest równanie
- [math]\displaystyle{ \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = 0 }[/math]
otrzymujemy następujące równanie rekurencyjne dla sumy [math]\displaystyle{ S(n) = \sum_{k \in \mathbb{Z}} f (n, k) }[/math]
- [math]\displaystyle{ \sum_{k \in \mathbb{Z}} \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{k \in \mathbb{Z}} f (n + i, k + j) }[/math]
- [math]\displaystyle{ \;\;\;\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{l \in \mathbb{Z}} f (n + i, l) }[/math]
- [math]\displaystyle{ \;\;\;\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \left[ S (n + i) + {\small\frac{1}{n + i + 1}} \right] }[/math]
- [math]\displaystyle{ \;\;\;\, = \sum_{i = 0}^{I} \left[ S (n + i) + {\small\frac{1}{n + i + 1}} \right] \cdot \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0 }[/math]
Jeżeli mamy skończoną liczbę punktów [math]\displaystyle{ k_r \notin [0, n] }[/math], w których funkcja [math]\displaystyle{ f(n, k) }[/math] jest określona i różna od zera, to możemy zdefiniować funkcję
- [math]\displaystyle{ T(n) = f (n, k_1) + f (n, k_2) + f (n, k_3) + \ldots = \sum_r f (n, k_r) }[/math]
W takim przypadku otrzymamy następujące równanie rekurencyjne dla sumy [math]\displaystyle{ S (n) = \sum_{k = 0}^{n} f (n, k) }[/math]
- [math]\displaystyle{ \sum_{i = 0}^{I} [S (n + i) + T (n + i)] \cdot \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0 }[/math]
Wystarczy drobna modyfikacja procedury sum5(), aby obejmowała ona również takie przypadki
sum6(I, J):=
(
read("podaj definicję f(n, k)"), /* składnik sumy */
print("f(n, k) = ", f(n, k) ),
read("podaj definicję T(n)"), /* suma skończonych wartości funkcji f(n, k), gdzie k<0 lub k>n */
print("T(n) = ", T(n) ),
F1: sum( sum( a[i,j] * f(n+i, k+j), i, 0, I), j, 0, J) / f(n, k),
F2: num( factor( minfactorial( makefact( expand( F1 ) ) ) ) ),
deg: hipow(F2, k),
LE: [subst(0, k, F2) = 0],
for i: 1 thru deg do push(coeff(F2, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */
LV: create_list(a[i, j], i, 0, I , j, 0, J), /* lista zmiennych */
sol: solve( LE, LV ), /* lista rozwiązań */
S1: sum( ( S[n+i] + T(n+i) ) * sum( a[i,j], j, 0, J ), i, 0, I ),
S2: num( factor( minfactorial( makefact( expand( S1 ) ) ) ) ),
S3: subst( sol[1], S2 ), /* pierwszy element listy sol */
S4: num( factor( expand( S3 ) ) ),
print("rekurencja: ", S4 = 0),
load("solve_rec"),
solve_rec( S4 = 0, S[n] )
)$
Korzystając z powyższej procedury, Czytelnik może łatwo policzyć wypisane poniżej sumy.
[math]\displaystyle{ \boldsymbol{f(n,k)} }[/math] [math]\displaystyle{ \boldsymbol{f(n,-1)} }[/math] [math]\displaystyle{ \boldsymbol{f(n,-2)} }[/math] [math]\displaystyle{ \boldsymbol{\sum_{k = 0}^n f(n,k)} }[/math] WolframAlpha [math]\displaystyle{ {\small\frac{1}{k + 1}} {\small\binom{n}{k}} }[/math] [math]\displaystyle{ {\small\frac{1}{n + 1}} }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ {\small\frac{2^{n + 1} - 1}{n + 1}} }[/math] LINK1 [math]\displaystyle{ {\small\frac{1}{k + 2}} {\small\binom{n}{k}} }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - {\small\frac{1}{(n + 1) (n + 2)}} }[/math] [math]\displaystyle{ {\small\frac{n 2^{n + 1} + 1}{(n + 1) (n + 2)}} }[/math] LINK2 [math]\displaystyle{ {\small\frac{1}{(k + 1) (k + 2)}} {\small\binom{n}{k}} }[/math] [math]\displaystyle{ {\small\frac{1}{n + 1}} }[/math] [math]\displaystyle{ {\small\frac{1}{(n + 1) (n + 2)}} }[/math] [math]\displaystyle{ {\small\frac{2^{n + 2} - n - 3}{(n + 1) (n + 2)}} }[/math] LINK3
Zadanie D103
Pokazać, że dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = 4^n }[/math]
Zadanie D104
Pokazać, że dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}} }[/math]
Uzupełnienie
Dowód własności liczb Catalana [math]\displaystyle{ {\small C_{n + 1} = \textstyle\sum_{k = 0}^{n} C_k C_{n - k}} }[/math]
Uwaga D105
Przedstawiony poniżej dowód czwartego punktu twierdzenia D84 został oparty na pracy Jovana Mikicia[27].
Twierdzenie D106
Jeżeli funkcja [math]\displaystyle{ f(k) }[/math] nie zależy od [math]\displaystyle{ n }[/math] i dane są sumy
- [math]\displaystyle{ S(n) = \sum_{k = 0}^{n} f (k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} }[/math]
- [math]\displaystyle{ T(n) = \sum_{k = 0}^{n} (n - k) f (k) {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} }[/math]
to
- [math]\displaystyle{ T(n) = 4 T (n - 1) + 2 S (n - 1) }[/math]
Twierdzenie D107
Dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = 4^n }[/math]
Twierdzenie D108
Dla [math]\displaystyle{ n \geqslant 0 }[/math] prawdziwy jest wzór
- [math]\displaystyle{ \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}} }[/math]
Twierdzenie D109
Jeżeli [math]\displaystyle{ C_n }[/math] są liczbami Catalana, to
- [math]\displaystyle{ C_{n + 1} = \sum_{k = 0}^{n} C_k C_{n - k} }[/math]
Funkcja gamma
Definicja D110
Funkcja [math]\displaystyle{ \Gamma (z) }[/math][28] jest zdefiniowana równoważnymi wzorami
- [math]\displaystyle{ \Gamma (z) = \int_{0}^{\infty} t^{z - 1} e^{- t} \, d t \qquad \operatorname{Re}(z) \gt 0 \qquad \qquad }[/math] (definicja całkowa Eulera)
- [math]\displaystyle{ \Gamma (z) = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \qquad z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad }[/math] (definicja Gaussa)
- [math]\displaystyle{ \Gamma (z) = {\small\frac{1}{z}} \prod_{n = 1}^{\infty} \left( 1 + {\small\frac{1}{n}} \right)^z \left( 1 + {\small\frac{z}{n}} \right)^{- 1} \qquad z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad }[/math] (definicja iloczynowa Eulera)
- [math]\displaystyle{ \Gamma (z) = {\small\frac{e^{- \gamma z}}{z}} \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{z}{n}} \right)^{- 1} e^{\tfrac{z}{n}} \qquad z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad }[/math] (definicja iloczynowa Weierstrassa)
Trzy ostatnie wzory możemy wykorzystać do zdefiniowania funkcji [math]\displaystyle{ {\small\frac{1}{\Gamma (z)}} }[/math], która jest określona dla dowolnych [math]\displaystyle{ z \in \mathbb{C} }[/math]
- [math]\displaystyle{ {\small\frac{1}{\Gamma (z)}} = \lim_{n \rightarrow \infty} {\small\frac{z (z + 1) \cdot \ldots \cdot (z + n)}{n^z n!}} }[/math]
- [math]\displaystyle{ {\small\frac{1}{\Gamma (z)}} = z \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{1}{n}} \right)^{- z} \left( 1 + {\small\frac{z}{n}} \right) }[/math]
- [math]\displaystyle{ {\small\frac{1}{\Gamma (z)}} = z e^{\gamma z} \prod^{\infty}_{n = 1} \left( 1 + {\small\frac{z}{n}} \right) e^{- \tfrac{z}{n}} }[/math]
Twierdzenie D111
Dla funkcji [math]\displaystyle{ \Gamma (z) }[/math] prawdziwe są następujące wzory
- [math]\displaystyle{ \Gamma (1) = 1 }[/math]
- [math]\displaystyle{ z \Gamma (z) = \Gamma (z + 1) \qquad z \notin \mathbb{Z}_- \cup \{ 0 \} }[/math]
- [math]\displaystyle{ \Gamma (z) \Gamma (- z + 1) = {\small\frac{\pi}{\sin (\pi z)}} \qquad z \notin \mathbb{Z} }[/math]
- [math]\displaystyle{ \Gamma (2 z) = {\small\frac{2^{2 z - 1}}{\sqrt{\pi}}} \cdot \Gamma (z) \Gamma \left( z + {\small\frac{1}{2}} \right) \qquad 2 z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad }[/math] (wzór Legendre'a o podwajaniu)
Ze wzorów podanych w twierdzeniu D111 otrzymujemy
Twierdzenie D112
Niech [math]\displaystyle{ k \in \mathbb{Z} \; }[/math] i [math]\displaystyle{ \; n \in \mathbb{N}_0 }[/math]
- [math]\displaystyle{ \Gamma \left( {\small\frac{1}{2}} \right) = \sqrt{\pi} }[/math]
- [math]\displaystyle{ \Gamma (n + 1) = n! }[/math]
- [math]\displaystyle{ \Gamma \left( z + {\small\frac{1}{2}} \right) \Gamma \left( - z + {\small\frac{1}{2}} \right) = {\small\frac{\pi}{\cos (\pi z)}} \qquad z \neq k + {\small\frac{1}{2}} }[/math]
- [math]\displaystyle{ \Gamma \left( n + {\small\frac{1}{2}} \right) \Gamma \left( - n + {\small\frac{1}{2}} \right) = \pi \cdot (- 1)^n }[/math]
- [math]\displaystyle{ \Gamma \left( n + {\small\frac{1}{2}} \right) = 2^{- 2 n} \sqrt{\pi} \cdot {\small\frac{(2 n) !}{n!}} }[/math]
- [math]\displaystyle{ \Gamma \left( - n + {\small\frac{1}{2}} \right) = (- 1)^n \cdot 2^{2 n} \sqrt{\pi} \cdot {\small\frac{n!}{(2 n) !}} }[/math]
- [math]\displaystyle{ \lim_{z \rightarrow - n} {\small\frac{\Gamma (2 z)}{\Gamma (z)}} = (- 1)^n \cdot {\small\frac{1}{2}} \cdot {\small\frac{n!}{(2 n) !}} }[/math]
Twierdzenie D113
Jeżeli [math]\displaystyle{ n \in \mathbb{N}_0 \, }[/math] i [math]\displaystyle{ \; a \in \mathbb{Z}_+ }[/math], to
- [math]\displaystyle{ \lim_{z \rightarrow - n} {\small\frac{\Gamma (a z)}{\Gamma (z)}} = (- 1)^{(a - 1) n} \cdot {\small\frac{1}{a}} \cdot {\small\frac{n!}{(a n) !}} }[/math]
Twierdzenie D114
Jeżeli [math]\displaystyle{ n \in \mathbb{N}_0 \, }[/math] i [math]\displaystyle{ \; a \in \mathbb{Z}_+ }[/math], to
- [math]\displaystyle{ \lim_{z \rightarrow - n} {\small\frac{\Gamma (a z + 1)}{\Gamma (b z + 1)}} = (- 1)^{(a - b) n} \cdot {\small\frac{(b n) !}{(a n) !}} }[/math]
Zadanie D115
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ \, }[/math] i [math]\displaystyle{ \; g(n) = {\small\binom{2 n}{n}} }[/math]. Pokazać, że
- rozszerzając funkcję [math]\displaystyle{ g(n) }[/math] na zbiór liczb rzeczywistych, otrzymujemy [math]\displaystyle{ g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)^2}} }[/math]
- [math]\displaystyle{ \lim_{x \rightarrow - n} g (x) = 0 }[/math]
Zadanie D116
Niech [math]\displaystyle{ n \in \mathbb{N}_0 \, }[/math] i [math]\displaystyle{ \; g(n) = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}} }[/math]. Pokazać, że
- rozszerzając funkcję [math]\displaystyle{ g(n) }[/math] na zbiór liczb rzeczywistych, otrzymujemy [math]\displaystyle{ g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 2) \Gamma (x + 1)}} }[/math]
- [math]\displaystyle{ \lim_{x \rightarrow - 1} g (x) = - {\small\frac{1}{2}} }[/math]
Przypisy
- ↑ Wikipedia, Funkcja η, (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Funkcja dzeta Riemanna, (Wiki-pl), (Wiki-en)
- ↑ Twierdzenie: funkcja ciągła w przedziale domkniętym jest całkowalna w tym przedziale.
- ↑ W szczególności: funkcja ograniczona i mająca skończoną liczbę punktów nieciągłości w przedziale domkniętym jest w tym przedziale całkowalna.
- ↑ Skocz do: 5,0 5,1 Wikipedia, Twierdzenia Mertensa, (Wiki-pl), (Wiki-en)
- ↑ Skocz do: 6,0 6,1 Wikipedia, Franciszek Mertens, (Wiki-pl)
- ↑ J. B. Rosser and L. Schoenfeld, Approximate formulas for some functions of prime numbers, Illinois J. Math. 6 (1962), 64-94, (LINK)
- ↑ Zobacz twierdzenie D42.
- ↑ The On-Line Encyclopedia of Integer Sequences, A001620 - Decimal expansion of Euler's constant, (A001620)
- ↑ The On-Line Encyclopedia of Integer Sequences, A083343 - Decimal expansion of constant B3 (or B_3) related to the Mertens constant, (A083343)
- ↑ The On-Line Encyclopedia of Integer Sequences, A138312 - Decimal expansion of Mertens's constant minus Euler's constant, (A138312)
- ↑ Pierre Dusart, Estimates of Some Functions Over Primes without R.H., 2010, (LINK)
- ↑ Wikipedia, Stałe Bruna, (Wiki-pl), (Wiki-en)
- ↑ The On-Line Encyclopedia of Integer Sequences, A065421 - Decimal expansion of Viggo Brun's constant B, (A065421)
- ↑ Paul Erdős, Über die Reihe [math]\displaystyle{ \textstyle \sum {\small\frac{1}{p}} }[/math], Mathematica, Zutphen B 7, 1938, 1-2.
- ↑ sumowanie przez części (ang. summation by parts)
- ↑ ciąg wypukły (ang. convex sequence)
- ↑ Pierre Dusart, Explicit estimates of some functions over primes, The Ramanujan Journal, vol. 45(1), 2018, 227-251.
- ↑ Skocz do: 19,0 19,1 Wikipedia, Szereg geometryczny, (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Sumowalność metodą Cesàro, (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Indefinite sum, (Wiki-en)
- ↑ Sister Mary Celine Fasenmyer, Some Generalized Hypergeometric Polynomials, Bull. Amer. Math. Soc. 53 (1947), 806-812
- ↑ Sister Mary Celine Fasenmyer, A Note on Pure Recurrence Relations, Amer. Math. Monthly 56 (1949), 14-17
- ↑ Doron Zeilberger, Sister Celine's technique and its generalizations, Journal of Mathematical Analysis and Applications, 85 (1982), 114-145
- ↑ Herbert Wilf and Doron Zeilberger, Rational Functions Certify Combinatorial Identities, J. Amer. Math. Soc. 3 (1990), 147-158
- ↑ Marko Petkovšek, Herbert Wilf and Doron Zeilberger, A = B, AK Peters, Ltd., 1996
- ↑ Jovan Mikić, A Proof of a Famous Identity Concerning the Convolution of the Central Binomial Coefficients, Journal of Integer Sequences, Vol. 19, No. 6 (2016), pp. 1 - 10, (LINK)
- ↑ Wikipedia, Funkcja Γ, (Wiki-pl), (Wiki-en)