Ciągi liczbowe: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| (Nie pokazano 18 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 7: | Linia 7: | ||
== Ciągi nieskończone == | == Ciągi nieskończone == | ||
<span style="font-size: 110%; font-weight: bold;">Definicja C1</span><br/> | <span id="C1" style="font-size: 110%; font-weight: bold;">Definicja C1</span><br/> | ||
Niech <math>n \in \mathbb{Z}_+</math>. Jeżeli każdej liczbie <math>n</math> przypiszemy pewną liczbę rzeczywistą <math>a_n</math>, to powiemy, że liczby <math>a_1, a_2, \ldots, a_n, \ldots</math> tworzą ciąg nieskończony. | Niech <math>n \in \mathbb{Z}_+</math>. Jeżeli każdej liczbie <math>n</math> przypiszemy pewną liczbę rzeczywistą <math>a_n</math>, to powiemy, że liczby <math>a_1, a_2, \ldots, a_n, \ldots</math> tworzą ciąg nieskończony. | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga C2</span><br/> | <span id="C2" style="font-size: 110%; font-weight: bold;">Uwaga C2</span><br/> | ||
Ciąg nieskończony <math>a_1, a_2, \ldots, a_n, \ldots</math> będziemy oznaczać <math>(a_n)</math>. Często, o ile nie będzie prowadziło to do nieporozumień, ciąg nieskończony będziemy nazywać po prostu ciągiem. | Ciąg nieskończony <math>a_1, a_2, \ldots, a_n, \ldots</math> będziemy oznaczać <math>(a_n)</math>. Często, o ile nie będzie prowadziło to do nieporozumień, ciąg nieskończony będziemy nazywać po prostu ciągiem. | ||
<span style="font-size: 110%; font-weight: bold;">Definicja C3</span><br/> | <span id="C3" style="font-size: 110%; font-weight: bold;">Definicja C3</span><br/> | ||
Niech <math>n \in \mathbb{Z}_+</math>. Ciąg <math>(a_n)</math> będziemy nazywali | Niech <math>n \in \mathbb{Z}_+</math>. Ciąg <math>(a_n)</math> będziemy nazywali | ||
::* ciągiem rosnącym, jeżeli dla każdego <math>n</math> jest <math>a_{n + 1} \geqslant a_n</math> | ::* ciągiem rosnącym, jeżeli dla każdego <math>n</math> jest <math>a_{n + 1} \geqslant a_n</math> | ||
| Linia 32: | Linia 32: | ||
<span style="font-size: 110%; font-weight: bold;">Definicja | <span id="C4" style="font-size: 110%; font-weight: bold;">Zadanie C4</span><br/> | ||
Niech <math>a \in \mathbb{R}_+</math>, <math>\, b \in \mathbb{R} \,</math> i <math>\, n \in \mathbb{Z}_+</math>. Pokazać, że jeżeli ciąg <math>(u_n)</math> jest ciągiem silnie rosnącym dla <math>n > n_0</math>, to ciąg <math>v_n = a u_n + b</math> też jest ciągiem silnie rosnącym dla <math>n > n_0</math>. Pokazać, że analogiczne stwierdzenie jest prawdziwe dla ciągów słabo rosnących, słabo malejących i silnie malejących. | |||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | |||
Niech <math>n > n_0</math>, mamy | |||
::<math>v_{n + 1} - v_n = (a u_{n + 1} + b) - (a u_n + b) = a (u_{n + 1} - u_n) > 0</math> | |||
Co należało pokazać.<br/> | |||
□ | |||
{{\Spoiler}} | |||
<span id="C5" style="font-size: 110%; font-weight: bold;">Definicja C5</span><br/> | |||
Niech <math>\varepsilon \in \mathbb{R}_+</math>. Liczbę <math>a</math> będziemy nazywali granicą ciągu <math>(a_n)</math>, jeżeli dla dowolnego <math>\varepsilon</math> w przedziale <math>(a - \varepsilon, a + \varepsilon)</math> znajdują się '''prawie wszystkie wyrazy ciągu''' <math>(a_n)</math> (to znaczy wszystkie poza co najwyżej skończoną ilością). | Niech <math>\varepsilon \in \mathbb{R}_+</math>. Liczbę <math>a</math> będziemy nazywali granicą ciągu <math>(a_n)</math>, jeżeli dla dowolnego <math>\varepsilon</math> w przedziale <math>(a - \varepsilon, a + \varepsilon)</math> znajdują się '''prawie wszystkie wyrazy ciągu''' <math>(a_n)</math> (to znaczy wszystkie poza co najwyżej skończoną ilością). | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C6" style="font-size: 110%; font-weight: bold;">Uwaga C6</span><br/> | ||
1) sens definicji jest taki: jeżeli liczba <math>a</math> jest granicą ciągu <math>(a_n)</math>, to dla dowolnie małego <math>\varepsilon > 0</math>, poza przedziałem <math>(a - \varepsilon, a + \varepsilon)</math> może się znaleźć co najwyżej skończona ilość wyrazów ciągu <math>(a_n)</math> | 1) sens definicji jest taki: jeżeli liczba <math>a</math> jest granicą ciągu <math>(a_n)</math>, to dla dowolnie małego <math>\varepsilon > 0</math>, poza przedziałem <math>(a - \varepsilon, a + \varepsilon)</math> może się znaleźć co najwyżej skończona ilość wyrazów ciągu <math>(a_n)</math> | ||
2) słabsze żądanie, aby w przedziale <math>(a - \varepsilon, a + \varepsilon)</math> znajdowała się nieskończona ilość wyrazów ciągu nie prowadzi do poprawnej definicji granicy. Przykładowo, w przedziale <math>(1 - \varepsilon, 1 + \varepsilon)</math> znajduje się nieskończenie wiele wyrazów ciągu <math>a_n = (-1)^n</math>, ale ani liczba <math>1</math>, ani liczba <math>- 1</math> nie są granicami tego ciągu. O ciągu <math>a_n = (- 1)^n</math> mówimy, że nie ma granicy. | 2) słabsze żądanie, aby w przedziale <math>(a - \varepsilon, a + \varepsilon)</math> znajdowała się nieskończona ilość wyrazów ciągu, nie prowadzi do poprawnej definicji granicy. Przykładowo, w przedziale <math>(1 - \varepsilon, 1 + \varepsilon)</math> znajduje się nieskończenie wiele wyrazów ciągu <math>a_n = (-1)^n</math>, ale ani liczba <math>1</math>, ani liczba <math>- 1</math> nie są granicami tego ciągu. O ciągu <math>a_n = (- 1)^n</math> mówimy, że nie ma granicy. | ||
3) ze względu na równoważność warunków | 3) ze względu na równoważność warunków | ||
| Linia 49: | Linia 63: | ||
::* <math>\quad | a_n - a | < \varepsilon</math> | ::* <math>\quad | a_n - a | < \varepsilon</math> | ||
definicja | definicja [[#C5|C5]] może być wypowiedziana następująco | ||
<span style="font-size: 110%; font-weight: bold;">Definicja | <span id="C7" style="font-size: 110%; font-weight: bold;">Definicja C7</span><br/> | ||
Liczbę <math>a</math> będziemy nazywali granicą ciągu <math>(a_n)</math>, jeżeli dla dowolnego <math>\varepsilon > 0</math> '''prawie wszystkie wyrazy ciągu''' <math>(a_n)</math> spełniają warunek <math>|a_n - a| < \varepsilon</math>. | Liczbę <math>a</math> będziemy nazywali granicą ciągu <math>(a_n)</math>, jeżeli dla dowolnego <math>\varepsilon > 0</math> '''prawie wszystkie wyrazy ciągu''' <math>(a_n)</math> spełniają warunek <math>|a_n - a| < \varepsilon</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Definicja | <span id="C8" style="font-size: 110%; font-weight: bold;">Definicja C8</span><br/> | ||
Ciąg <math>(a_n)</math> mający granicę (w rozumieniu definicji | Ciąg <math>(a_n)</math> mający granicę (w rozumieniu definicji [[#C5|C5]] lub [[#C7|C7]]) będziemy nazywali ciągiem zbieżnym, a fakt ten zapisujemy symbolicznie następująco | ||
::<math>\lim_{n \to \infty} a_n = a</math> lub <math>a_n \longrightarrow a</math> | ::<math>\lim_{n \to \infty} a_n = a</math> lub <math>a_n \longrightarrow a</math> | ||
| Linia 68: | Linia 82: | ||
Zauważmy jeszcze, że wprost z definicji granicy wynika</br> | Zauważmy jeszcze, że wprost z definicji granicy wynika</br> | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C9" style="font-size: 110%; font-weight: bold;">Twierdzenie C9</span><br/> | ||
:: | ::1. <math>\quad \lim_{n \to \infty} a_n = a \qquad \iff \qquad \lim_{n \to \infty} (a_n - a) = 0 \qquad \iff \qquad \lim_{n \to \infty} | a_n - a | = 0</math> | ||
::3. <math>\quad \lim_{n \to \infty} a_n = a \ | ::2. <math>\quad \lim_{n \to \infty} a_n = 0 \qquad \iff \qquad \lim_{n \to \infty} | a_n | = 0</math> | ||
::3. <math>\quad \lim_{n \to \infty} a_n = a \qquad \implies \qquad \lim_{n \to \infty} | a_n | = | a |</math> | |||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| Linia 79: | Linia 94: | ||
Prawdziwość twierdzenia wynika ze względu na identyczność warunków, które muszą spełniać prawie wszystkie wyrazy ciągu | Prawdziwość twierdzenia wynika ze względu na identyczność warunków, które muszą spełniać prawie wszystkie wyrazy ciągu | ||
::<math>| a_n - a | < \varepsilon \ | ::<math>| a_n - a | < \varepsilon \qquad \iff \qquad | (a_n - a) - 0 | < \varepsilon \qquad \iff \qquad \big|| a_n - a | - 0 \big| < \varepsilon</math> | ||
'''Punkt 2.'''<br/> | '''Punkt 2.'''<br/> | ||
| Linia 95: | Linia 110: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C10" style="font-size: 110%; font-weight: bold;">Twierdzenie C10</span><br/> | ||
Jeżeli ciąg <math>(a_n)</math> jest zbieżny, to jest ograniczony. | |||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | |||
Z założenia ciąg <math>(a_n)</math> jest zbieżny, zatem możemy napisać, że <math>\lim_{n \rightarrow \infty} a_n = a</math>. Z definicji granicy (zobacz [[#C5|C5]], [[#C7|C7]]) dla dowolnego <math>\varepsilon > 0</math> prawie wszystkie wyrazy ciągu <math>(a_n)</math> spełniają warunek <math>| a_n - a | < \varepsilon</math>. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od pewnego <math>N = N (\varepsilon)</math>. Zatem dla <math>n > N</math> jest | |||
::<math>a - \varepsilon < a_n < a + \varepsilon</math> | |||
Wynika stąd, że dla każdego <math>n \geqslant 1</math> jest | |||
::<math>m \leqslant a_n \leqslant M</math> | |||
gdzie | |||
::<math>M = \max (a_1, \ldots, a_N, a + \varepsilon)</math> | |||
::<math>m = \min (a_1, \ldots, a_N, a - \varepsilon)</math> | |||
Ponieważ <math>- | m | \leqslant m \;</math> i <math>\; M \leqslant | M |</math>, to | |||
::<math>- | m | \leqslant a_n \leqslant | M |</math> | |||
Jeżeli oznaczymy <math>U = \max (| m |, | M |)</math>, to możemy napisać | |||
::<math>- U \leqslant a_n \leqslant U</math> | |||
Czyli dla każdego <math>n \geqslant 1</math> jest <math>| a_n | \leqslant U</math>. Co kończy dowód.<br/> | |||
□ | |||
{{\Spoiler}} | |||
<span id="C11" style="font-size: 110%; font-weight: bold;">Twierdzenie C11 (twierdzenie o trzech ciągach)</span><br/> | |||
Jeżeli istnieje taka liczba całkowita <math>N_0</math>, że dla każdego <math>n > N_0</math> jest spełniony warunek | Jeżeli istnieje taka liczba całkowita <math>N_0</math>, że dla każdego <math>n > N_0</math> jest spełniony warunek | ||
| Linia 107: | Linia 154: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Niech <math>\varepsilon</math> będzie dowolną, ustaloną liczbą większą od <math>0</math>. Z założenia prawie wszystkie wyrazy ciągu <math>(a_n)</math> spełniają warunek <math>|a_n - g| < \varepsilon</math>. Możemy | Niech <math>\varepsilon</math> będzie dowolną, ustaloną liczbą większą od <math>0</math>. Z założenia prawie wszystkie wyrazy ciągu <math>(a_n)</math> spełniają warunek <math>|a_n - g| < \varepsilon</math>. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od wyrazu <math>N_a</math>. Podobnie prawie wszystkie wyrazy ciągu <math>(b_n)</math> spełniają warunek <math>|b_n - g| < \varepsilon</math> i podobnie możemy przyjąć, że są to wszystkie wyrazy, poczynając od wyrazu <math>N_b</math> | ||
Nierówność <math>a_n \leqslant x_n \leqslant b_n</math> jest spełniona dla wszystkich wyrazów, poczynając od <math>N_0</math>, zatem oznaczając przez <math>M</math> największą z liczb <math>N_a</math>, <math>N_b</math>, <math>N_0</math>, możemy napisać, że o ile <math>n > M</math>, to spełnione są jednocześnie nierówności | Nierówność <math>a_n \leqslant x_n \leqslant b_n</math> jest spełniona dla wszystkich wyrazów, poczynając od <math>N_0</math>, zatem oznaczając przez <math>M</math> największą z liczb <math>N_a</math>, <math>N_b</math>, <math>N_0</math>, możemy napisać, że o ile <math>n > M</math>, to spełnione są jednocześnie nierówności | ||
| Linia 130: | Linia 177: | ||
Bez dowodu podamy kilka ważnych twierdzeń.<br> | Bez dowodu podamy kilka ważnych twierdzeń.<br> | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C12" style="font-size: 110%; font-weight: bold;">Twierdzenie C12*</span><br/> | ||
Jeżeli istnieje taka liczba całkowita <math>n</math> i rzeczywista <math>M</math>, że dla każdego <math>k > n</math> jest | Jeżeli istnieje taka liczba całkowita <math>n</math> i rzeczywista <math>M</math>, że dla każdego <math>k > n</math> jest | ||
| Linia 140: | Linia 187: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C13" style="font-size: 110%; font-weight: bold;">Twierdzenie C13*</span><br/> | ||
Jeżeli istnieje taka liczba całkowita <math>n</math> i rzeczywista <math>M</math>, że dla każdego <math>k > n</math> jest | Jeżeli istnieje taka liczba całkowita <math>n</math> i rzeczywista <math>M</math>, że dla każdego <math>k > n</math> jest | ||
| Linia 150: | Linia 197: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C14" style="font-size: 110%; font-weight: bold;">Twierdzenie C14*</span><br/> | ||
Jeżeli <math>\lim_{n \to \infty} a_n = a</math> oraz <math>\lim_{n \to \infty} b_n = b</math>, gdzie <math>a, b</math> są dowolnymi liczbami rzeczywistymi, to | Jeżeli <math>\lim_{n \to \infty} a_n = a</math> oraz <math>\lim_{n \to \infty} b_n = b</math>, gdzie <math>a, b</math> są dowolnymi liczbami rzeczywistymi, to | ||
| Linia 158: | Linia 205: | ||
Jeżeli dodatkowo dla każdego <math>n</math> jest <math>b_n \neq 0</math> i <math>b \neq 0</math>, to | Jeżeli dodatkowo dla każdego <math>n</math> jest <math>b_n \neq 0</math> i <math>b \neq 0</math>, to | ||
: 3. <math>\quad \lim_{n \to \infty} \frac{a_n}{b_n} = \frac{a}{b}</math> | : 3. <math>\quad \lim_{n \to \infty} {\small\frac{a_n}{b_n}} = {\small\frac{a}{b}}</math> | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C15" style="font-size: 110%; font-weight: bold;">Twierdzenie C15</span><br/> | ||
Jeżeli <math>\lim_{n \to \infty} a_n = 0</math>, zaś ciąg <math>(x_n)</math> jest ograniczony, czyli istnieje taka liczba <math>M > 0</math>, że dla każdej wartości <math>n</math> prawdziwa jest nierówność <math>| x_n | < M</math>, to | Jeżeli <math>\lim_{n \to \infty} a_n = 0</math>, zaś ciąg <math>(x_n)</math> jest ograniczony, czyli istnieje taka liczba <math>M > 0</math>, że dla każdej wartości <math>n</math> prawdziwa jest nierówność <math>| x_n | < M</math>, to | ||
| Linia 168: | Linia 215: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Wystarczy pokazać, że (zobacz twierdzenie | Wystarczy pokazać, że (zobacz twierdzenie [[#C9|C9]] p.2) | ||
::<math>\lim_{n \to \infty} |x_n \cdot a_n| = 0</math> | ::<math>\lim_{n \to \infty} |x_n \cdot a_n| = 0</math> | ||
| Linia 176: | Linia 223: | ||
::<math>0 \leqslant |x_n \cdot a_n| \leqslant |a_n| \cdot M</math> | ::<math>0 \leqslant |x_n \cdot a_n| \leqslant |a_n| \cdot M</math> | ||
Zatem z twierdzenia o trzech ciągach otrzymujemy natychmiast, że | Zatem z twierdzenia o trzech ciągach otrzymujemy natychmiast, że | ||
::<math>\lim_{n \to \infty} |x_n \cdot a_n| = 0</math> | ::<math>\lim_{n \to \infty} |x_n \cdot a_n| = 0</math> | ||
| Linia 186: | Linia 233: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C16" style="font-size: 110%; font-weight: bold;">Twierdzenie C16</span><br/> | ||
Dla <math>a \geqslant 0</math> i <math>n \geqslant 1</math> prawdziwa jest nierówność | Dla <math>a \geqslant 0</math> i <math>n \geqslant 1</math> prawdziwa jest nierówność | ||
::<math>(1 + a)^{1 / n} \leqslant 1 + \frac{a}{n}</math> | ::<math>(1 + a)^{1 / n} \leqslant 1 + {\small\frac{a}{n}}</math> | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Wzór jest prawdziwy dla <math>a = 0</math>. Zakładając, że <math>a > 0</math> i korzystając ze wzoru dwumianowego, mamy dla <math>n \geqslant 1</math> | Wzór jest prawdziwy dla <math>a = 0</math>. Zakładając, że <math>a > 0</math> i korzystając ze wzoru dwumianowego, mamy dla <math>n \geqslant 1</math> | ||
::<math>\left( 1 + \frac{a}{n} \right)^n = \sum_{k=0}^{n}\left [\binom{n}{k} \cdot \left ( \frac{a}{n} \right )^k \right ] \geqslant</math> | ::<math>\left( 1 + {\small\frac{a}{n}} \right)^n = \sum_{k=0}^{n} \left [ {\small\binom{n}{k}} \cdot \left ( {\small\frac{a}{n}} \right )^k \right ] \geqslant</math> | ||
:::::<math>\;\; \geqslant \sum_{k=0}^{1}\left [\binom{n}{k} \cdot \left ( \frac{a}{n} \right )^k \right ] =</math> | :::::<math>\;\; \geqslant \sum_{k=0}^{1} \left [ {\small\binom{n}{k}} \cdot \left ( {\small\frac{a}{n}} \right )^k \right ] =</math> | ||
:::::<math>\;\; = 1 + n \cdot \frac{a}{n} =</math> | :::::<math>\;\; = 1 + n \cdot {\small\frac{a}{n}} =</math> | ||
:::::<math>\;\; = 1 + a</math> | :::::<math>\;\; = 1 + a</math> | ||
| Linia 205: | Linia 252: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C17" style="font-size: 110%; font-weight: bold;">Twierdzenie C17</span><br/> | ||
Jeżeli <math>A > 0</math>, to <math>\lim_{n \to \infty} \sqrt[n]{A} = 1</math>. | Jeżeli <math>A > 0</math>, to <math>\lim_{n \to \infty} \sqrt[n]{A} = 1</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Dla <math>A > 1</math> możemy napisać <math>A = 1 + a</math>, gdzie <math>a > 0</math>, wtedy z twierdzenia | Dla <math>A > 1</math> możemy napisać <math>A = 1 + a</math>, gdzie <math>a > 0</math>, wtedy z twierdzenia [[#C16|C16]] otrzymujemy | ||
::<math>1 < \sqrt[n]{A} = (1 + a)^{1 / n} \leqslant 1 + \frac{a}{n}</math> | ::<math>1 < \sqrt[n]{A} = (1 + a)^{1 / n} \leqslant 1 + {\small\frac{a}{n}}</math> | ||
Z twierdzenia o trzech ciągach dostajemy natychmiast (dla <math>A > 1</math>) | Z twierdzenia o trzech ciągach dostajemy natychmiast (dla <math>A > 1</math>) | ||
| Linia 217: | Linia 264: | ||
::<math>\lim_{n \to \infty} \sqrt[n]{A} = 1</math> | ::<math>\lim_{n \to \infty} \sqrt[n]{A} = 1</math> | ||
W przypadku gdy <math>0 < A < 1</math>, możemy napisać <math>A = \frac{1}{B}</math>, gdzie <math>B > 1</math>, wtedy ze względu na udowodniony wyżej rezultat <math>\lim_{n \to \infty} \sqrt[n]{B} = 1</math> | W przypadku gdy <math>0 < A < 1</math>, możemy napisać <math>A = {\small\frac{1}{B}}</math>, gdzie <math>B > 1</math>, wtedy ze względu na udowodniony wyżej rezultat <math>\lim_{n \to \infty} \sqrt[n]{B} = 1</math> | ||
::<math>\lim_{n \to \infty} \sqrt[n]{A} = \lim_{n \to \infty} \frac{1}{\sqrt[n]{B}} = \frac{1}{\underset{n \rightarrow \infty}{\lim} \sqrt[n]{B}} = 1</math> | ::<math>\lim_{n \to \infty} \sqrt[n]{A} = \lim_{n \to \infty} {\small\frac{1}{\sqrt[n]{B}}} = \frac{1}{\underset{n \rightarrow \infty}{\lim} \sqrt[n]{B}} = 1</math> | ||
Jeżeli <math>A = 1</math>, to <math>\sqrt[n]{A} = 1</math> dla każdego <math>n \geqslant 1</math>. Co kończy dowód.<br/> | Jeżeli <math>A = 1</math>, to <math>\sqrt[n]{A} = 1</math> dla każdego <math>n \geqslant 1</math>. Co kończy dowód.<br/> | ||
| Linia 227: | Linia 274: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C18" style="font-size: 110%; font-weight: bold;">Twierdzenie C18</span><br/> | ||
Jeżeli prawie wszystkie wyrazy | Jeżeli prawie wszystkie wyrazy ciągu <math>(a_n)</math> spełniają warunek <math>0 < m < a_n < M</math>, to <math>\lim_{n \to \infty} \sqrt[n]{a_n} = 1</math> | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| Linia 239: | Linia 286: | ||
::<math>\sqrt[n]{m} \leqslant \sqrt[n]{a_n} \leqslant \sqrt[n]{M}</math> | ::<math>\sqrt[n]{m} \leqslant \sqrt[n]{a_n} \leqslant \sqrt[n]{M}</math> | ||
Z twierdzenia | Z twierdzenia [[#C17|C17]] wiemy, że <math>\lim_{n \to \infty} \sqrt[n]{m} = \lim_{n \to \infty} \sqrt[n]{M} = 1</math>, zatem na podstawie twierdzenia o trzech ciągach otrzymujemy natychmiast <math>\lim_{n \to \infty} \sqrt[n]{a_n} = 1</math><br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 245: | Linia 292: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C19" style="font-size: 110%; font-weight: bold;">Twierdzenie C19</span><br/> | ||
Następujące ciągi są silnie rosnące i zbieżne | Następujące ciągi są silnie rosnące i zbieżne | ||
::{| class="wikitable plainlinks" style="font-size: 100%; text-align: center; margin-right: auto;" | ::{| class="wikitable plainlinks" style="font-size: 100%; text-align: center; margin-right: auto;" | ||
|- style=height:4em | |- style=height:4em | ||
| <math>\quad 1. \quad</math> || <math>\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n = e = 2.718281828 \ldots</math> | | <math>\quad 1. \quad</math> || <math>\lim_{n \to \infty} \left( 1 + {\small\frac{1}{n}} \right)^n = e = 2.718281828 \ldots</math> | ||
|- style=height:4em | |- style=height:4em | ||
| <math>\quad 2. \quad</math> || <math>\lim_{n \to \infty} \left( 1 - \frac{1}{n} \right)^n = \frac{1}{e} = 0.367879441 \ldots</math> | | <math>\quad 2. \quad</math> || <math>\lim_{n \to \infty} \left( 1 - {\small\frac{1}{n}} \right)^n = {\small\frac{1}{e}} = 0.367879441 \ldots</math> | ||
|} | |} | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
'''Punkt 1'''<br/> | '''Punkt 1'''<br/> | ||
W twierdzeniu A6 pokazaliśmy, że ciąg | W twierdzeniu [[Twierdzenie Czebyszewa o funkcji π(n)#A6|A6]] pokazaliśmy, że ciąg | ||
::<math>a_n = \left( 1 + \frac{1}{n} \right)^n</math> | ::<math>a_n = \left( 1 + {\small\frac{1}{n}} \right)^n</math> | ||
jest silnie rosnący i ograniczony od góry. Zatem z twierdzenia | jest silnie rosnący i ograniczony od góry. Zatem z twierdzenia [[#C12|C12]] wynika, że jest zbieżny. Liczbę będącą granicą tego ciągu oznaczamy literą <math>e</math>, jest ona podstawą logarytmu naturalnego. | ||
'''Punkt 2'''<br/> | '''Punkt 2'''<br/> | ||
Pokażemy najpierw, że ciąg <math>\left( 1 - \frac{1}{n} \right)^n</math> jest silnie rosnący. Musimy pokazać, że prawdziwa jest nierówność | Pokażemy najpierw, że ciąg <math>\left( 1 - {\small\frac{1}{n}} \right)^n</math> jest silnie rosnący. Musimy pokazać, że prawdziwa jest nierówność | ||
::<math>\left( 1 - \frac{1}{n + 1} \right)^{n + 1} > \left( 1 - \frac{1}{n} \right)^n</math> | ::<math>\left( 1 - {\small\frac{1}{n + 1}} \right)^{n + 1} > \left( 1 - {\small\frac{1}{n}} \right)^n</math> | ||
Łatwo sprawdzamy prawdziwość nierówności dla <math>n = 1</math>. Załóżmy teraz, że <math>n \geqslant 2</math>. Przekształcając, | Łatwo sprawdzamy prawdziwość nierówności dla <math>n = 1</math>. Załóżmy teraz, że <math>n \geqslant 2</math>. Przekształcając, | ||
::<math>\left( \frac{n}{n + 1} \right)^{n + 1} > \left( \frac{n - 1}{n} \right)^n</math> | ::<math>\left( {\small\frac{n}{n + 1}} \right)^{n + 1} > \left( {\small\frac{n - 1}{n}} \right)^n</math> | ||
::<math>\frac{n}{n + 1} \cdot \left( \frac{n}{n + 1} \right)^n \cdot \left( \frac{n}{n - 1} \right)^n > 1</math> | ::<math>{\small\frac{n}{n + 1}} \cdot \left( {\small\frac{n}{n + 1}} \right)^n \cdot \left( {\small\frac{n}{n - 1}} \right)^n > 1</math> | ||
::<math>\left( \frac{n^2}{n^2 - 1} \right)^n > \frac{n + 1}{n}</math> | ::<math>\left( {\small\frac{n^2}{n^2 - 1}} \right)^n > {\small\frac{n + 1}{n}}</math> | ||
otrzymujemy nierówność równoważną, | otrzymujemy nierówność równoważną, | ||
::<math>\left( 1 + \frac{1}{n^2 - 1} \right)^n > 1 + \frac{1}{n}</math> | ::<math>\left( 1 + {\small\frac{1}{n^2 - 1}} \right)^n > 1 + {\small\frac{1}{n}}</math> | ||
którą już łatwo udowodnić, bo | którą już łatwo udowodnić, bo | ||
::<math>\left( 1 + \frac{1}{n^2 - 1} \right)^n > \left( 1 + \frac{1}{n^2} \right)^n = \sum_{k = 0}^{n} \binom{n}{k} \cdot \left( \frac{1}{n^2} \right)^k > \sum_{k = 0}^{1} \binom{n}{k} \cdot \frac{1}{n^{2k}} = 1 + \frac{1}{n}</math> | ::<math>\left( 1 + {\small\frac{1}{n^2 - 1}} \right)^n > \left( 1 + {\small\frac{1}{n^2}} \right)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} \cdot \left( {\small\frac{1}{n^2}} \right)^k > \sum_{k = 0}^{1} {\small\binom{n}{k}} \cdot {\small\frac{1}{n^{2k}}} = 1 + {\small\frac{1}{n}}</math> | ||
Ponieważ dla każdego <math>n \geqslant 1</math> jest <math>\left( 1 - \frac{1}{n} \right)^n \leqslant 1</math> (bo iloczyn liczb mniejszych od <math>1</math> nie może być liczbą większą do jedności), to z twierdzenia | Ponieważ dla każdego <math>n \geqslant 1</math> jest <math>\left( 1 - {\small\frac{1}{n}} \right)^n \leqslant 1</math> (bo iloczyn liczb mniejszych od <math>1</math> nie może być liczbą większą do jedności), to z twierdzenia [[#C12|C12]] wynika, że ciąg ten jest zbieżny. Zatem możemy napisać | ||
::<math>\underset{n \rightarrow \infty}{\lim} \left( 1 - \frac{1}{n} \right)^n = g</math> | ::<math>\underset{n \rightarrow \infty}{\lim} \left( 1 - {\small\frac{1}{n}} \right)^n = g</math> | ||
Rozważmy teraz iloczyn wypisanych w twierdzeniu ciągów | Rozważmy teraz iloczyn wypisanych w twierdzeniu ciągów | ||
::<math>\left( 1 + \frac{1}{n} \right)^n \cdot \left( 1 - \frac{1}{n} \right)^n = \left( 1 - \frac{1}{n^2} \right)^n = \left[ \left( 1 - \frac{1}{n^2} \right)^{n^2} \right]^{1 / n}</math> | ::<math>\left( 1 + {\small\frac{1}{n}} \right)^n \cdot \left( 1 - {\small\frac{1}{n}} \right)^n = \left( 1 - {\small\frac{1}{n^2}} \right)^n = \left[ \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \right]^{1 / n}</math> | ||
Łatwo widzimy, że ciąg <math>\left( 1 - \frac{1}{n^2} \right)^{n^2}</math> jest podciągiem ciągu <math>\left( 1 - \frac{1}{n} \right)^n</math>, zatem jest ograniczony i dla <math>n \geqslant 2</math> spełniony jest układ nierówności | Łatwo widzimy, że ciąg <math>\left( 1 - {\small\frac{1}{n^2}} \right)^{n^2}</math> jest podciągiem ciągu <math>\left( 1 - {\small\frac{1}{n}} \right)^n</math>, zatem jest ograniczony i dla <math>n \geqslant 2</math> spełniony jest układ nierówności | ||
::<math>0 < \left( \frac{3}{4} \right)^4 \leqslant \left( 1 - \frac{1}{n^2} \right)^{n^2} \leqslant 1</math> | ::<math>0 < \left( {\small\frac{3}{4}} \right)^4 \leqslant \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \leqslant 1</math> | ||
Z twierdzenia | Z twierdzenia [[#C18|C18]] dostajemy | ||
::<math>\lim_{n \to \infty} \left[ \left( 1 - \frac{1}{n^2} \right)^{n^2} \right]^{1 / n} = 1</math> | ::<math>\lim_{n \to \infty} \left[ \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \right]^{1 / n} = 1</math> | ||
Z twierdzenia | Z twierdzenia [[#C14|C14]] p. 2 wynika natychmiast, że | ||
::<math>e \cdot g = \lim_{n \to \infty} \left[ \left( 1 + \frac{1}{n} \right)^n \cdot \left( 1 - \frac{1}{n} \right)^n \right] = \lim_{n \to \infty} \left[ \left( 1 - \frac{1}{n^2} \right)^{n^2} \right]^{1 / n} = 1</math> | ::<math>e \cdot g = \lim_{n \to \infty} \left[ \left( 1 + {\small\frac{1}{n}} \right)^n \cdot \left( 1 - {\small\frac{1}{n}} \right)^n \right] = \lim_{n \to \infty} \left[ \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \right]^{1 / n} = 1</math> | ||
Zatem <math>g = \frac{1}{e}</math>.<br/> | Zatem <math>g = {\small\frac{1}{e}}</math>.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 310: | Linia 357: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C20" style="font-size: 110%; font-weight: bold;">Twierdzenie C20</span><br/> | ||
Dla <math>n \geqslant 2</math> prawdziwe są następujące nierówności | Dla <math>n \geqslant 2</math> prawdziwe są następujące nierówności | ||
::{| class="wikitable plainlinks" style="font-size: 100%; text-align: center; margin-right: auto;" | ::{| class="wikitable plainlinks" style="font-size: 100%; text-align: center; margin-right: auto;" | ||
|- style=height:4em | |- style=height:4em | ||
| <math>\quad 1. \quad</math> || <math> \frac{1}{n + 1} < \log \left( 1 + \frac{1}{n} \right) < \frac{1}{n}</math> | | <math>\quad 1. \quad</math> || <math> {\small\frac{1}{n + 1}} < \log \left( 1 + {\small\frac{1}{n}} \right) < {\small\frac{1}{n}}</math> | ||
|- style=height:4em | |- style=height:4em | ||
| <math>\quad 2. \quad</math> || <math>- \frac{1}{n - 1} < \log \left( 1 - \frac{1}{n} \right) < - \frac{1}{n}</math> | | <math>\quad 2. \quad</math> || <math>- {\small\frac{1}{n - 1}} < \log \left( 1 - {\small\frac{1}{n}} \right) < - {\small\frac{1}{n}}</math> | ||
|} | |} | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Ponieważ ciąg <math>\left( 1 + \frac{1}{n} \right)^n</math> jest silnie rosnący, to | Ponieważ ciąg <math>\left( 1 + {\small\frac{1}{n}} \right)^n</math> jest silnie rosnący, to | ||
::<math>\left( 1 + \frac{1}{n} \right)^n < e</math> | ::<math>\left( 1 + {\small\frac{1}{n}} \right)^n < e</math> | ||
Logarytmując powyższą nierówność, mamy | Logarytmując powyższą nierówność, mamy | ||
::<math>n \cdot \log \left( 1 + \frac{1}{n} \right) < 1</math> | ::<math>n \cdot \log \left( 1 + {\small\frac{1}{n}} \right) < 1</math> | ||
Stąd wynika natychmiast, że | Stąd wynika natychmiast, że | ||
::<math>\log \left( 1 + \frac{1}{n} \right) < \frac{1}{n}</math> | ::<math>\log \left( 1 + {\small\frac{1}{n}} \right) < {\small\frac{1}{n}}</math> | ||
Ponieważ ciąg <math>\left( 1 - \frac{1}{n} \right)^n</math> również jest silnie rosnący, to postępując analogicznie, dostajemy | Ponieważ ciąg <math>\left( 1 - {\small\frac{1}{n}} \right)^n</math> również jest silnie rosnący, to postępując analogicznie, dostajemy | ||
::<math>\left( 1 - \frac{1}{n} \right)^n < \frac{1}{e}</math> | ::<math>\left( 1 - {\small\frac{1}{n}} \right)^n < {\small\frac{1}{e}}</math> | ||
::<math>n \cdot \log \left( 1 - \frac{1}{n} \right) < - 1</math> | ::<math>n \cdot \log \left( 1 - {\small\frac{1}{n}} \right) < - 1</math> | ||
::<math>\log \left( 1 - \frac{1}{n} \right) < - \frac{1}{n}</math> | ::<math>\log \left( 1 - {\small\frac{1}{n}} \right) < - {\small\frac{1}{n}}</math> | ||
Przekształcając otrzymane wzory, otrzymujemy | Przekształcając otrzymane wzory, otrzymujemy | ||
::<math>- \log \left( 1 + \frac{1}{n} \right) = - \log \left( \frac{n + 1}{n} \right) = \log \left( \frac{n}{n + 1} \right) = \log \left( 1 - \frac{1}{n + 1} \right) < - \frac{1}{n + 1}</math> | ::<math>- \log \left( 1 + {\small\frac{1}{n}} \right) = - \log \left( {\small\frac{n + 1}{n}} \right) = \log \left( {\small\frac{n}{n + 1}} \right) = \log \left( 1 - {\small\frac{1}{n + 1}} \right) < - {\small\frac{1}{n + 1}}</math> | ||
oraz | oraz | ||
::<math>- \log \left( 1 - \frac{1}{n} \right) = - \log \left( \frac{n - 1}{n} \right) = \log \left( \frac{n}{n - 1} \right) = \log \left( 1 + \frac{1}{n - 1} \right) < \frac{1}{n - 1}</math><br/> | ::<math>- \log \left( 1 - {\small\frac{1}{n}} \right) = - \log \left( {\small\frac{n - 1}{n}} \right) = \log \left( {\small\frac{n}{n - 1}} \right) = \log \left( 1 + {\small\frac{1}{n - 1}} \right) < {\small\frac{1}{n - 1}}</math><br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 359: | Linia 406: | ||
== Liczby pierwsze w ciągach arytmetycznych == | == Liczby pierwsze w ciągach arytmetycznych == | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C21" style="font-size: 110%; font-weight: bold;">Twierdzenie C21</span><br/> | ||
Każda liczba naturalna <math>n \geqslant 2</math> jest liczbą pierwszą lub iloczynem liczb pierwszych. | Każda liczba naturalna <math>n \geqslant 2</math> jest liczbą pierwszą lub iloczynem liczb pierwszych. | ||
| Linia 384: | Linia 431: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C22" style="font-size: 110%; font-weight: bold;">Twierdzenie C22 (Euklides, IV w. p.n.e.)</span><br/> | ||
Istnieje nieskończenie wiele liczb pierwszych. | Istnieje nieskończenie wiele liczb pierwszych. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Przypuśćmy, że istnieje jedynie skończona ilość liczb pierwszych <math>p_1, p_2, \ldots, p_n</math> . Wtedy liczba <math>a = p_1 \cdot p_2 \cdot \ldots \cdot p_n + 1</math> jest większa od jedności i z twierdzenia | Przypuśćmy, że istnieje jedynie skończona ilość liczb pierwszych <math>p_1, p_2, \ldots, p_n</math> . Wtedy liczba <math>a = p_1 \cdot p_2 \cdot \ldots \cdot p_n + 1</math> jest większa od jedności i z twierdzenia [[#C21|C21]] wynika, że posiada dzielnik będący liczbą pierwszą, ale jak łatwo zauważyć żadna z liczb pierwszych <math>p_1, p_2, \ldots, p_n</math> nie jest dzielnikiem liczby <math>a</math>. Zatem istnieje liczba pierwsza <math>p</math> będąca dzielnikiem pierwszym liczby <math>a</math> i różna od każdej z liczb <math>p_1, p_2, \ldots, p_n</math>. Co kończy dowód.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 394: | Linia 441: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C23" style="font-size: 110%; font-weight: bold;">Twierdzenie C23</span><br/> | ||
Jeżeli liczba naturalna <math>n</math> jest postaci <math>4 k + 3</math><ref name="LiczbaJestPostaci"/>, to ma dzielnik postaci <math>4 k + 3</math> będący liczbą pierwszą. | Jeżeli liczba naturalna <math>n</math> jest postaci <math>4 k + 3</math><ref name="LiczbaJestPostaci"/>, to ma dzielnik postaci <math>4 k + 3</math> będący liczbą pierwszą. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Jeżeli <math>n</math> jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy zatem sytuację gdy <math>n</math> jest liczbą złożoną. Z założenia <math>n</math> jest liczbą nieparzystą, zatem możliwe są trzy typy iloczynów | Jeżeli <math>n</math> jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy zatem sytuację, gdy <math>n</math> jest liczbą złożoną. Z założenia <math>n</math> jest liczbą nieparzystą, zatem możliwe są trzy typy iloczynów | ||
::<math>(4 a + 1) (4 b + 1) = 16 a b + 4 a + 4 b + 1 = 4 (4 a b + a + b) + 1</math> | ::<math>(4 a + 1) (4 b + 1) = 16 a b + 4 a + 4 b + 1 = 4 (4 a b + a + b) + 1</math> | ||
| Linia 412: | Linia 459: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C24" style="font-size: 110%; font-weight: bold;">Twierdzenie C24</span><br/> | ||
Istnieje nieskończenie wiele liczb pierwszych postaci <math>4 k + 3</math>. | Istnieje nieskończenie wiele liczb pierwszych postaci <math>4 k + 3</math>. | ||
| Linia 420: | Linia 467: | ||
::<math>M = 4 p_1 \cdot \ldots \cdot p_s - 1 = 4 (p_1 \cdot \ldots \cdot p_s - 1) + 3</math> | ::<math>M = 4 p_1 \cdot \ldots \cdot p_s - 1 = 4 (p_1 \cdot \ldots \cdot p_s - 1) + 3</math> | ||
jest postaci <math>4 k + 3</math> i jak wiemy z twierdzenia | jest postaci <math>4 k + 3</math> i jak wiemy z twierdzenia [[#C23|C23]], ma dzielnik pierwszy <math>q</math> postaci <math>4 k + 3</math>. Ale jak łatwo zauważyć, żadna z liczb <math>p_1, \ldots, p_s</math> nie dzieli liczby <math>M</math>. Zatem istnieje liczba pierwsza <math>q</math> postaci <math>4 k + 3</math> różna od każdej z liczb <math>p_1, p_2, \ldots, p_s</math>. Otrzymana sprzeczność kończy dowód.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 426: | Linia 473: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C25" style="font-size: 110%; font-weight: bold;">Twierdzenie C25</span><br/> | ||
Jeżeli liczba naturalna <math>n</math> jest postaci <math>6 k + 5</math>, to ma dzielnik postaci <math>6 k + 5</math> będący liczbą pierwszą. | Jeżeli liczba naturalna <math>n</math> jest postaci <math>6 k + 5</math>, to ma dzielnik postaci <math>6 k + 5</math> będący liczbą pierwszą. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Jeżeli <math>n</math> jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy sytuację gdy <math>n</math> jest liczbą złożoną. Z twierdzenia | Jeżeli <math>n</math> jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy sytuację, gdy <math>n</math> jest liczbą złożoną. Z twierdzenia [[#C21|C21]] wiemy, że w tym przypadku liczba <math>n</math> będzie iloczynem liczb pierwszych. Zauważmy, że nieparzyste liczby pierwsze mogą być jedynie postaci <math>6 k + 1</math> lub <math>6 k + 5</math> (liczba <math>6 k + 3</math> jest liczbą złożoną). Ponieważ iloczyn liczb postaci <math>6 k + 1</math> | ||
::<math>(6 a + 1) (6 b + 1) = 36 a b + 6 a + 6 b + 1 = 6 (6 a b + a + b) + 1</math> | ::<math>(6 a + 1) (6 b + 1) = 36 a b + 6 a + 6 b + 1 = 6 (6 a b + a + b) + 1</math> | ||
| Linia 440: | Linia 487: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C26" style="font-size: 110%; font-weight: bold;">Twierdzenie C26</span><br/> | ||
Istnieje nieskończenie wiele liczb pierwszych postaci <math>6 k + 5</math>. | Istnieje nieskończenie wiele liczb pierwszych postaci <math>6 k + 5</math>. | ||
| Linia 448: | Linia 495: | ||
::<math>M = 6 p_1 \cdot \ldots \cdot p_s - 1 = 6 (p_1 \cdot \ldots \cdot p_s - 1) + 5</math> | ::<math>M = 6 p_1 \cdot \ldots \cdot p_s - 1 = 6 (p_1 \cdot \ldots \cdot p_s - 1) + 5</math> | ||
jest postaci <math>6 k + 5</math> i | jest postaci <math>6 k + 5</math> i ma dzielnik pierwszy <math>q</math> postaci <math>6 k + 5</math> (zobacz [[#C25|C25]]). Ale jak łatwo zauważyć żadna z liczb <math>p_1, \ldots, p_s</math> nie dzieli liczby <math>M</math>. Zatem istnieje liczba pierwsza <math>q</math> postaci <math>6 k + 5</math> różna od każdej z liczb <math>p_1, p_2, \ldots, p_s</math>. Otrzymana sprzeczność kończy dowód.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 454: | Linia 501: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C27" style="font-size: 110%; font-weight: bold;">Twierdzenie C27</span><br/> | ||
Istnieje nieskończenie wiele liczb pierwszych postaci <math>3 k + 2</math>. | Istnieje nieskończenie wiele liczb pierwszych postaci <math>3 k + 2</math>. | ||
| Linia 468: | Linia 515: | ||
::<math>3 k + 2 = 3 (2 j + 1) + 2 = 6 j + 5</math> | ::<math>3 k + 2 = 3 (2 j + 1) + 2 = 6 j + 5</math> | ||
o którym wiemy, że zawiera nieskończenie wiele liczb pierwszych (zobacz twierdzenie | o którym wiemy, że zawiera nieskończenie wiele liczb pierwszych (zobacz twierdzenie [[#C26|C26]]). Zatem w ciągu arytmetycznym postaci <math>3 k + 2</math> występuje nieskończenie wiele liczb pierwszych.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 474: | Linia 521: | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C28" style="font-size: 110%; font-weight: bold;">Uwaga C28</span><br/> | ||
Zauważmy, że liczby postaci <math>2 k + 1</math> to wszystkie liczby nieparzyste dodatnie. Ponieważ wszystkie liczby pierwsze (poza liczbą <math>2</math>) są liczbami nieparzystymi, to wśród liczb postaci <math>2 k + 1</math> występuje nieskończenie wiele liczb pierwszych. | Zauważmy, że liczby postaci <math>2 k + 1</math> to wszystkie liczby nieparzyste dodatnie. Ponieważ wszystkie liczby pierwsze (poza liczbą <math>2</math>) są liczbami nieparzystymi, to wśród liczb postaci <math>2 k + 1</math> występuje nieskończenie wiele liczb pierwszych. | ||
| Linia 481: | Linia 528: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C29" style="font-size: 110%; font-weight: bold;">Twierdzenie C29* (Peter Gustav Lejeune Dirichlet, 1837)</span><br/> | ||
Niech <math>a \in \mathbb{Z}_+</math> i <math>b \in \mathbb{Z}</math>. Jeżeli liczby <math>a</math> i <math>b</math> są względnie pierwsze, to w ciągu arytmetycznym <math>a k + b</math> występuje nieskończenie wiele liczb pierwszych. | Niech <math>a \in \mathbb{Z}_+</math> i <math>b \in \mathbb{Z}</math>. Jeżeli liczby <math>a</math> i <math>b</math> są względnie pierwsze, to w ciągu arytmetycznym <math>a k + b</math> występuje nieskończenie wiele liczb pierwszych. | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C30" style="font-size: 110%; font-weight: bold;">Uwaga C30</span><br/> | ||
Dowód twierdzenia Dirichleta jest bardzo trudny. Natomiast bardzo łatwo można pokazać, że dowolny ciąg arytmetyczny <math>a k + b</math> zawiera nieskończenie wiele liczb złożonych. Istotnie, jeżeli liczby <math>a, b</math> nie są względnie pierwsze, to wszystkie wyrazy ciągu są liczbami złożonymi. Jeżeli <math>a, b</math> są względnie pierwsze i <math>b > 1 ,</math> to wystarczy przyjąć <math>k = b t</math>. Jeżeli są względnie pierwsze i <math>b = 1</math>, to wystarczy przyjąć <math>k = a t^2 + 2 t</math>, wtedy | Dowód twierdzenia Dirichleta jest bardzo trudny. Natomiast bardzo łatwo można pokazać, że dowolny ciąg arytmetyczny <math>a k + b</math> zawiera nieskończenie wiele liczb złożonych. Istotnie, jeżeli liczby <math>a, b</math> nie są względnie pierwsze, to wszystkie wyrazy ciągu są liczbami złożonymi. Jeżeli <math>a, b</math> są względnie pierwsze i <math>b > 1 ,</math> to wystarczy przyjąć <math>k = b t</math>. Jeżeli są względnie pierwsze i <math>b = 1</math>, to wystarczy przyjąć <math>k = a t^2 + 2 t</math>, wtedy | ||
| Linia 493: | Linia 540: | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C31" style="font-size: 110%; font-weight: bold;">Uwaga C31</span><br/> | ||
Wiemy już, że w przypadku gdy liczby <math>a</math> i <math>b</math> są względnie pierwsze, to w ciągu arytmetycznym <math>a k + b</math> występuje nieskończenie wiele liczb pierwszych. Pojawia się pytanie o to, czy możliwe jest oszacowanie najmniejszej liczby pierwszej <math>p</math> w takim ciągu. Jakkolwiek przypuszczamy, że prawdziwe jest oszacowanie <math>p < a^2</math>, to stan naszej obecnej wiedzy ujmuje twierdzenie Linnika<ref name="Linnik1"/><ref name="Linnik2"/><ref name="Linnik3"/><ref name="Linnik4"/>, które podajemy niżej. Trzeba było ponad pół wieku wysiłku wielu matematyków, aby pokazać, że w twierdzeniu Linnika możemy przyjąć <math>L = 5</math><ref name="Xylouris1"/>. Bombieri, Friedlander i Iwaniec udowodnili<ref name="Bombieri1"/>, że dla prawie wszystkich liczb <math>a</math> prawdziwe jest oszacowanie <math>L \leqslant 2</math>. | Wiemy już, że w przypadku gdy liczby <math>a</math> i <math>b</math> są względnie pierwsze, to w ciągu arytmetycznym <math>a k + b</math> występuje nieskończenie wiele liczb pierwszych. Pojawia się pytanie o to, czy możliwe jest oszacowanie najmniejszej liczby pierwszej <math>p</math> w takim ciągu. Jakkolwiek przypuszczamy, że prawdziwe jest oszacowanie <math>p < a^2</math>, to stan naszej obecnej wiedzy ujmuje twierdzenie Linnika<ref name="Linnik1"/><ref name="Linnik2"/><ref name="Linnik3"/><ref name="Linnik4"/>, które podajemy niżej. Trzeba było ponad pół wieku wysiłku wielu matematyków, aby pokazać, że w twierdzeniu Linnika możemy przyjąć <math>L = 5</math><ref name="Xylouris1"/>. Bombieri, Friedlander i Iwaniec udowodnili<ref name="Bombieri1"/>, że dla prawie wszystkich liczb <math>a</math> prawdziwe jest oszacowanie <math>L \leqslant 2</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C32" style="font-size: 110%; font-weight: bold;">Twierdzenie C32* (Jurij Linnik, 1944)</span><br/> Niech <math>a, b \in \mathbb{Z}_+</math> i <math>p_{\min} (a, b)</math> oznacza najmniejszą liczbę pierwszą w ciągu arytmetycznym <math>a k + b</math>, gdzie <math>k \in \mathbb{Z}_+</math>. Jeżeli <math>\gcd (a, b) = 1</math> i <math>b \in [1, a - 1]</math>, to istnieją takie stałe <math>L > 0</math> i <math>a_0 \geqslant 2</math>, że dla wszystkich <math>a > a_0</math> prawdziwe jest oszacowanie | ||
::<math>p_{\min} (a, b) < a^L</math> | ::<math>p_{\min} (a, b) < a^L</math> | ||
| Linia 504: | Linia 551: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C33" style="font-size: 110%; font-weight: bold;">Zadanie C33</span><br/> | ||
Pokazać, że z twierdzenia Linnika wynika istnienie takich stałych <math>c, L > 0</math>, że dla każdego <math>a \geqslant 2</math> prawdziwe jest oszacowanie | Pokazać, że z twierdzenia Linnika wynika istnienie takich stałych <math>c, L > 0</math>, że dla każdego <math>a \geqslant 2</math> prawdziwe jest oszacowanie | ||
::<math>p(a) < c a^L</math> | ::<math>p(a) < c a^L</math> | ||
| Linia 514: | Linia 561: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
Oszacowanie podane w twierdzeniu Linnika | Oszacowanie podane w twierdzeniu Linnika | ||
::<math>p_{\min} (a, b) < a^L</math> | ::<math>p_{\min} (a, b) < a^L</math> | ||
| Linia 526: | Linia 573: | ||
::<math>p(a) < a^L</math> | ::<math>p(a) < a^L</math> | ||
dla wszystkich <math>a > a_0</math>. Ponieważ dla <math>a \in [2, a_0]</math> funkcja <math>p(a)</math> przyjmuje wartości skończone, a dla <math>a > a_0</math> jest <math>p(a) < a^L</math>, to funkcja <math>{\small\frac{p (a)}{a^L}}</math> jest ograniczona od góry, czyli istnieje taka stała <math>c</math>, że | dla wszystkich <math>a > a_0</math>. Ponieważ dla <math>a \in [2, a_0]</math> funkcja <math>p(a)</math> przyjmuje wartości skończone, a dla <math>a > a_0</math> jest <math>p(a) < a^L</math>, to funkcja <math>{\small\frac{p (a)}{a^L}}</math> jest ograniczona od góry, czyli istnieje taka stała <math>c</math>, że | ||
::<math>{\small\frac{p (a)}{a^L}} < c</math> | ::<math>{\small\frac{p (a)}{a^L}} < c</math> | ||
| Linia 536: | Linia 583: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C34" style="font-size: 110%; font-weight: bold;">Przykład C34</span><br/> | ||
Pokazaliśmy (zobacz | Pokazaliśmy (zobacz [[#C33|C33]]), że istnieją takie stałe <math>c, L > 0</math>, że dla każdego <math>a \geqslant 2</math> prawdziwe jest oszacowanie | ||
::<math>p(a) < c a^L</math> | ::<math>p(a) < c a^L</math> | ||
| Linia 555: | Linia 602: | ||
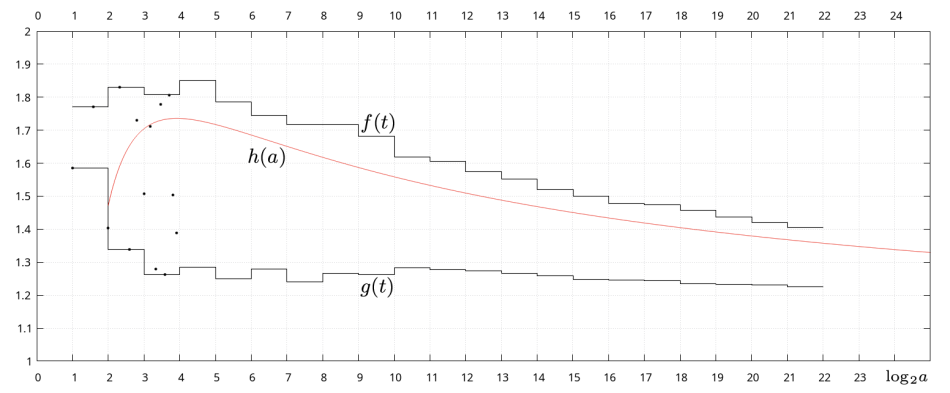
Na zamieszczonym niżej obrazku przedstawiono pierwszych czternaście punktów funkcji <math>{\small\frac{\log p (a)}{\log a}}</math>. Ze względu na skokowy charakter zmian tej funkcji najwygodniej będzie przedstawić jej wykres, pokazując jedynie jej maksymalne i minimalne wartości w wybranych podprzedziałach <math>\mathbb{Z}_+</math>. Mówiąc precyzyjnie, zamieszczone zostały wykresy funkcji | |||
::<math>f(t) = \max_{2^t \leqslant a < 2^{t + 1}} {\small\frac{\log p (a)}{\log a}} \qquad \qquad | ::<math>f(t) = \max_{2^t \leqslant a < 2^{t + 1}} {\small\frac{\log p (a)}{\log a}} \qquad \qquad \qquad \qquad g(t) = \min_{2^t \leqslant a < 2^{t + 1}} {\small\frac{\log p (a)}{\log a}} \qquad \qquad \qquad \qquad h(a) = 1 + {\small\frac{2 \log \log a}{\log a}}</math> | ||
gdzie <math>t \in \mathbb{Z}_+</math>. | gdzie <math>t \in \mathbb{Z}_+</math>. | ||
::[[File: Linnik-22.png|950px|none]] | |||
:: | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż kod i dane do wykresu|Hide=Ukryj kod i dane do wykresu}} | ||
W tabeli przedstawiamy dane, na podstawie których sporządziliśmy zamieszczony wyżej wykres. Mamy kolejno | |||
:* przedział <math>U</math> | |||
:* minimalną wartość <math>{\small\frac{\log p(a)}{\log a}}</math> w przedziale <math>U</math> | |||
:* liczbę <math>a</math>, która odpowiada minimalnej wartości <math>{\small\frac{\log p(a)}{\log a}}</math> | |||
:* wartość <math>p(a) = \underset{\gcd (a, b) = 1}{\max_{1 \leqslant b < a}} p_{\min} (a, b)</math> | |||
:* liczbę <math>b</math> taką, że najmniejsza liczba pierwsza w ciągu <math>a k + b</math> jest równa <math>p ( a )</math> | |||
Następnie podajemy analogiczne wartości dla maksymalnej wartości <math>{\small\frac{\log p(a)}{\log a}}</math> w przedziale <math>U</math>. Pominęliśmy dane dla początkowych przedziałów <math>[2^{n},2^{n + 1})</math>, ponieważ Czytelnik z łatwością policzy je samodzielnie. Prosty kod do obliczeń w PARI/GP zamieściliśmy pod tabelą. | |||
::{| class="wikitable plainlinks" style="font-size: 85%; text-align: right; margin-right: auto;" | |||
::{| class="wikitable plainlinks" style="font-size: | |||
|- | |- | ||
! <math>\boldsymbol{ | ! <math>\boldsymbol{U}</math> || <math>\boldsymbol{\min_{a \in U} {\small\frac{\log p(a)}{\log a}}}</math> || <math>\boldsymbol{a}</math> || <math>\boldsymbol{p(a)}</math> || <math>\boldsymbol{b}</math> || <math>\boldsymbol{\max_{a \in U} {\small\frac{\log p(a)}{\log a}}}</math> || <math>\boldsymbol{a}</math> || <math>\boldsymbol{p(a)}</math> || <math>\boldsymbol{b}</math> | ||
|- | |- | ||
| <math> | | <math>[2^{12},2^{13})</math> || <math>1.273691</math> || <math>6840</math> || <math>76679</math> || <math>1439</math> || <math>1.574826</math> || <math>4177</math> || <math>503771</math> || <math>2531</math> | ||
|- | |- | ||
| <math> | | <math>[2^{13},2^{14})</math> || <math>1.265227</math> || <math>14490</math> || <math>183949</math> || <math>10069</math> || <math>1.551307</math> || <math>8941</math> || <math>1348387</math> || <math>7237</math> | ||
|- | |- | ||
| <math> | | <math>[2^{14},2^{15})</math> || <math>1.257880</math> || <math>20790</math> || <math>269987</math> || <math>20507</math> || <math>1.519764</math> || <math>22133</math> || <math>4012709</math> || <math>6636</math> | ||
|- | |- | ||
| <math>47</math> || <math>5.55</math> || <math>967</math> || <math>1.785437</math> | | <math>[2^{15},2^{16})</math> || <math>1.247285</math> || <math>39270</math> || <math>537157</math> || <math>26647</math> || <math>1.500736</math> || <math>40951</math> || <math>8352037</math> || <math>38984</math> | ||
|- | |||
| <math>[2^{16},2^{17})</math> || <math>1.244884</math> || <math>106260</math> || <math>1808207</math> || <math>1787</math> || <math>1.477806</math> || <math>84229</math> || <math>19005359</math> || <math>53834</math> | |||
|- | |||
| <math>[2^{17},2^{18})</math> || <math>1.243658</math> || <math>150150</math> || <math>2740469</math> || <math>37769</math> || <math>1.474387</math> || <math>132331</math> || <math>35588503</math> || <math>123795</math> | |||
|- | |||
| <math>[2^{18},2^{19})</math> || <math>1.233771</math> || <math>510510</math> || <math>11024723</math> || <math>304013</math> || <math>1.457138</math> || <math>297491</math> || <math>94537921</math> || <math>233274</math> | |||
|- | |||
| <math>[2^{19},2^{20})</math> || <math>1.233150</math> || <math>1021020</math> || <math>25706531</math> || <math>181031</math> || <math>1.437418</math> || <math>596081</math> || <math>200230391</math> || <math>543256</math> | |||
|- | |||
| <math>[2^{20},2^{21})</math> || <math>1.231259</math> || <math>2072070</math> || <math>59859383</math> || <math>1841423</math> || <math>1.419752</math> || <math>1181311</math> || <math>418069567</math> || <math>1066784</math> | |||
|- | |||
| <math>[2^{21},2^{22})</math> || <math>1.224444</math> || <math>3543540</math> || <math>104573173</math> || <math>1810513</math> || <math>1.405843</math> || <math>2753747</math> || <math>1131160207</math> || <math>2123937</math> | |||
|} | |||
<span style="font-size: 90%; color:black;">pmin(a, b) = | |||
\\ zwraca najmniejszą liczbę pierwszą w ciągu a*k + b, gdzie k >= 1 i gcd(a, b) = 1 | |||
{ | |||
'''local'''(k, p); | |||
k = 1; | |||
p = a*k + b; | |||
'''while'''( !'''isprime'''(p), p = a*(k++) + b ); | |||
'''return'''(p); | |||
}</span> | |||
<span style="font-size: 90%; color:black;">PMAX(a) = | |||
\\ zwraca największą ze wszystkich najmniejszych liczb pierwszych | |||
\\ w ciągach a*k + b, gdzie k >= 1, 0 < b < a i gcd(a, b) = 1 | |||
{ | |||
'''local'''(b, p, w); | |||
w = [0, 0]; | |||
b = 0; | |||
'''while'''( b++ < a, | |||
'''if'''( '''gcd'''(a, b) > 1, '''next'''() ); | |||
p = pmin(a, b); | |||
'''if'''( w[1] < p, w = [p, b] ); | |||
); | |||
'''return'''(w); | |||
}</span> | |||
<span style="font-size: 90%; color:black;">Linnik(n) = | |||
\\ n >= 1, sprawdzamy przedział U = [ 2^n , 2^(n + 1) ), czyli 2^n <= a < 2^(n+1) | |||
{ | |||
'''local'''(a, b, p4a, sep, txt, w, y, Ymin, Ymax); | |||
sep = ", "; \\ separator | |||
Ymin = [100, 1, 0, 0]; \\ najmniejsza wartość funkcji log( p(a) ) / log(a) w przedziale U | |||
Ymax = [0, 1, 0, 0]; \\ największa wartość funkcji log( p(a) ) / log(a) w przedziale U | |||
a = 2^n - 1; | |||
'''while'''( a++ < 2^(n+1), | |||
w = PMAX(a); | |||
p4a = w[1]; | |||
b = w[2]; | |||
y = '''log'''(p4a) / '''log'''(a); | |||
if( y < Ymin[1], Ymin = [y, a, p4a, b] ); | |||
if( y > Ymax[1], Ymax = [y, a, p4a, b] ); | |||
); | |||
txt = '''Str'''(n, sep, Ymin[1], sep, Ymin[2], sep, Ymin[3], sep, Ymin[4], sep, Ymax[1], sep, Ymax[2], sep, Ymax[3], sep, Ymax[4]); | |||
'''print'''(txt); | |||
}</span> | |||
{{\Spoiler}} | |||
Przypuszczamy, że prawdziwe jest znacznie silniejsze oszacowanie najmniejszej liczby pierwszej w ciągu arytmetycznym<ref name="Turan1"/><ref name="Wagstaff1"/> | |||
::<math>p(a) \sim a \log^2 \! a</math> | |||
W takim przypadku mielibyśmy | |||
::<math>{\small\frac{\log p (a)}{\log a}} \sim 1 + {\small\frac{2 \log \log a}{\log a}}</math> | |||
Rzeczywiście, porównanie wykresów funkcji <math>f(t)</math> i <math>h(a)</math> wydaje się potwierdzać to przypuszczenie dla <math>a \in [2, 2^{22}]</math>. | |||
W tabeli zestawiliśmy wszystkie wartości funkcji <math>{\small\frac{\log p (a)}{\log a}}</math> większe od <math>1.75</math> dla <math>a \in [2, 2^{22}]</math> | |||
::{| class="wikitable plainlinks" style="font-size: 80%; text-align: center; margin-right: auto;" | |||
|- | |||
! <math>\boldsymbol{a}</math> || <math>\boldsymbol{\log_2 \! a}</math> || <math>\boldsymbol{p(a)}</math> || <math>\boldsymbol{{\small\frac{\log p(a)}{\log a}}}</math> | |||
|- | |||
| <math>31</math> || <math>4.95</math> || <math>577</math> || <math>1.851446</math> | |||
|- | |||
| <math>5</math> || <math>2.32</math> || <math>19</math> || <math>1.829482</math> | |||
|- | |||
| <math>13</math> || <math>3.70</math> || <math>103</math> || <math>1.806947</math> | |||
|- | |||
| <math>47</math> || <math>5.55</math> || <math>967</math> || <math>1.785437</math> | |||
|- | |- | ||
| <math>19</math> || <math>4.24</math> || <math>191</math> || <math>1.783794</math> | | <math>19</math> || <math>4.24</math> || <math>191</math> || <math>1.783794</math> | ||
| Linia 589: | Linia 727: | ||
::{| class="wikitable plainlinks" style="font-size: | Rozważmy zbiór <math>S</math> takich liczb <math>a</math>, że prawdziwe jest oszacowanie <math>p (a) < a \log^2 \! a</math>. Bez trudu możemy podać przykłady takich liczb, ale nie wiemy, czy jest ich nieskończenie wiele. | ||
::{| class="wikitable plainlinks" style="font-size: 80%; text-align: center; margin-right: auto;" | |||
|- | |- | ||
! <math>\boldsymbol{n}</math> || <math>\boldsymbol{a=p_1 \cdot \ldots \cdot p_n}</math> || <math>\boldsymbol{\log_2 \! a}</math> || <math>\boldsymbol{p(a)}</math> || <math>\boldsymbol{{\small\frac{a | ! <math>\boldsymbol{n}</math> || <math>\boldsymbol{a=p_1 \cdot \ldots \cdot p_n}</math> || <math>\boldsymbol{\log_2 \! a}</math> || <math>\boldsymbol{p(a)}</math> || <math>\boldsymbol{{\small\frac{a \log^2 \! a}{p(a)}}}</math> || <math>\boldsymbol{{\small\frac{\log p(a)}{\log a}}}</math> | ||
|- | |- | ||
| <math>2</math> || <math>6</math> || <math>2.584</math> || <math>11</math> || <math>1.751</math> || <math>1.338290</math> | | <math>2</math> || <math>6</math> || <math>2.584</math> || <math>11</math> || <math>1.751</math> || <math>1.338290</math> | ||
| Linia 623: | Linia 762: | ||
::<math>1 < {\small\frac{\log p (a)}{\log a}} < 1 + {\small\frac{2 \log \log a}{\log a}}</math> | ::<math>1 < {\small\frac{\log p (a)}{\log a}} < 1 + {\small\frac{2 \log \log a}{\log a}}</math> | ||
Jeżeli zbiór <math>S</math> jest nieskończony, to z twierdzenia o trzech ciągach otrzymujemy | Jeżeli zbiór <math>S</math> jest nieskończony, to z twierdzenia o trzech ciągach otrzymujemy | ||
::<math>\underset{a \in S}{\lim_{a \rightarrow \infty}} {\small\frac{\log p (a)}{\log a}} = 1</math> | ::<math>\underset{a \in S}{\lim_{a \rightarrow \infty}} {\small\frac{\log p (a)}{\log a}} = 1</math> | ||
| Linia 635: | Linia 774: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C35" style="font-size: 110%; font-weight: bold;">Zadanie C35</span><br/> | ||
Pokazać, że istnieje nieskończenie wiele liczb pierwszych zakończonych cyframi 99, przykładowo 199, 499, 599, 1399, 1499, ... | Pokazać, że istnieje nieskończenie wiele liczb pierwszych zakończonych cyframi 99, przykładowo 199, 499, 599, 1399, 1499, ... | ||
| Linia 645: | Linia 784: | ||
<span style="font-size: 110%; font-weight: bold;">Definicja | <span id="C36" style="font-size: 110%; font-weight: bold;">Definicja C36</span><br/> | ||
Niech <math>a \geqslant 2</math> będzie liczbą całkowitą. Wartość funkcji <math>\pi(n; a, b)</math> jest równa ilości liczb pierwszych nie większych od <math>n</math>, które przy dzieleniu przez <math>a</math> dają resztę <math>b</math>. | Niech <math>a \geqslant 2</math> będzie liczbą całkowitą. Wartość funkcji <math>\pi(n; a, b)</math> jest równa ilości liczb pierwszych nie większych od <math>n</math>, które przy dzieleniu przez <math>a</math> dają resztę <math>b</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C37" style="font-size: 110%; font-weight: bold;">Uwaga C37</span><br/> | ||
Zauważmy, że w twierdzeniu Dirichleta na liczby <math>a</math> oraz <math>b</math> nałożone są minimalne warunki: <math>a \in \mathbb{Z}_+</math> i <math>b \in \mathbb{Z}</math>. Sytuacja w przypadku funkcji <math>\pi (n ; a, b)</math> jest odmienna – tutaj mamy <math>a \geqslant 2</math> oraz <math>0 \leqslant b \leqslant a - 1</math>. Jest tak dlatego, że podział liczb pierwszych, który odzwierciedla funkcja <math>\pi (n ; a, b)</math> jest podziałem pierwotnym, a twierdzenie Dirichleta jest tylko jego uzasadnieniem. Podział | Zauważmy, że w twierdzeniu Dirichleta na liczby <math>a</math> oraz <math>b</math> nałożone są minimalne warunki: <math>a \in \mathbb{Z}_+</math> i <math>b \in \mathbb{Z}</math>. Sytuacja w przypadku funkcji <math>\pi (n ; a, b)</math> jest odmienna – tutaj mamy <math>a \geqslant 2</math> oraz <math>0 \leqslant b \leqslant a - 1</math>. Jest tak dlatego, że podział liczb pierwszych, który odzwierciedla funkcja <math>\pi (n ; a, b)</math>, jest podziałem pierwotnym, a twierdzenie Dirichleta jest tylko jego uzasadnieniem. Podział | ||
liczb pierwszych musi być też precyzyjnie określony, tak aby zachodził naturalny związek | liczb pierwszych musi być też precyzyjnie określony, tak aby zachodził naturalny związek | ||
| Linia 666: | Linia 805: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C38" style="font-size: 110%; font-weight: bold;">Zadanie C38</span><br/> | ||
Pokazać, że dla dowolnej liczby całkowitej <math>m \geqslant 1</math> | Pokazać, że dla dowolnej liczby całkowitej <math>m \geqslant 1</math> | ||
| Linia 674: | Linia 813: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
'''Punkt 1.'''<br/> | '''Punkt 1.'''<br/> | ||
W przypadku liczb naturalnych | W przypadku liczb naturalnych łatwo widzimy, że kolejne liczby | ||
::<math>(m + 1) ! + 2, \quad (m + 1) ! + 3, \quad \ldots, \quad (m + 1) ! + (m + 1)</math> | ::<math>(m + 1) ! + 2, \quad (m + 1) ! + 3, \quad \ldots, \quad (m + 1) ! + (m + 1)</math> | ||
| Linia 703: | Linia 842: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C39" style="font-size: 110%; font-weight: bold;">Przykład C39</span><br/> | ||
Rozważmy ciąg arytmetyczny <math>u_k = 3 k + 2</math> i wskaźnik | Rozważmy ciąg arytmetyczny <math>u_k = 3 k + 2</math> i wskaźnik | ||
| Linia 710: | Linia 849: | ||
Trzynaście wyrazów tego szeregu dla <math>k = k_0 + t</math>, gdzie <math>t = 0, 1, \ldots, 12</math> to oczywiście liczby złożone, ale wyrazy dla <math>k = k_0 - 1</math> i <math>k = k_0 + 13</math> są liczbami pierwszymi. | Trzynaście wyrazów tego szeregu dla <math>k = k_0 + t</math>, gdzie <math>t = 0, 1, \ldots, 12</math> to oczywiście liczby złożone, ale wyrazy dla <math>k = k_0 - 1</math> i <math>k = k_0 + 13</math> są liczbami pierwszymi. | ||
Przeszukując ciąg <math>u_k = 3 k + 2</math> możemy łatwo znaleźć, że pierwsze trzynaście kolejnych wyrazów złożonych pojawia się już dla <math>k = 370, 371, \ldots, 382</math>. | Przeszukując ciąg <math>u_k = 3 k + 2</math>, możemy łatwo znaleźć, że pierwsze trzynaście kolejnych wyrazów złożonych pojawia się już dla <math>k = 370, 371, \ldots, 382</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C40" style="font-size: 110%; font-weight: bold;">Twierdzenie C40</span><br/> | ||
Jeżeli <math>n \geqslant 3</math>, to istnieje <math>n</math> kolejnych liczb naturalnych, wśród których znajduje się dokładnie <math>r \leqslant \pi (n)</math> liczb pierwszych. | Jeżeli <math>n \geqslant 3</math>, to istnieje <math>n</math> kolejnych liczb naturalnych, wśród których znajduje się dokładnie <math>r \leqslant \pi (n)</math> liczb pierwszych. | ||
| Linia 746: | Linia 885: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C41" style="font-size: 110%; font-weight: bold;">Przykład C41</span><br/> | ||
Czytelnik może łatwo sprawdzić, że ciąg <math>( 1308, \ldots, 1407 )</math> stu kolejnych liczb całkowitych zawiera dokładnie <math>8</math> liczb pierwszych. | Czytelnik może łatwo sprawdzić, że ciąg <math>( 1308, \ldots, 1407 )</math> stu kolejnych liczb całkowitych zawiera dokładnie <math>8</math> liczb pierwszych. | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C42" style="font-size: 110%; font-weight: bold;">Zadanie C42</span><br/> | ||
Pokazać, nie korzystając z twierdzenia | Pokazać, nie korzystając z twierdzenia [[#C40|C40]], że istnieje <math>1000</math> kolejnych liczb naturalnych, wśród których jest dokładnie jedna liczba pierwsza. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| Linia 759: | Linia 898: | ||
::<math>1001! + 2, 1001! + 3, \ldots, 1001! + 1001</math> | ::<math>1001! + 2, 1001! + 3, \ldots, 1001! + 1001</math> | ||
nie zawiera żadnej liczby pierwszej. Wielokrotnie zmniejszając wszystkie wypisane wyżej liczby o jeden, aż do chwili, gdy pierwsza z wypisanych liczb będzie liczbą pierwszą uzyskamy <math>1000</math> kolejnych liczb naturalnych, wśród których jest dokładnie jedna liczba pierwsza. | nie zawiera żadnej liczby pierwszej. Wielokrotnie zmniejszając wszystkie wypisane wyżej liczby o jeden, aż do chwili, gdy pierwsza z wypisanych liczb będzie liczbą pierwszą, uzyskamy <math>1000</math> kolejnych liczb naturalnych, wśród których jest dokładnie jedna liczba pierwsza. | ||
Uwaga: dopiero liczba <math>1001! - 1733</math> jest pierwsza.<br/> | Uwaga: dopiero liczba <math>1001! - 1733</math> jest pierwsza.<br/> | ||
| Linia 767: | Linia 906: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C43" style="font-size: 110%; font-weight: bold;">Zadanie C43</span><br/> | ||
Pokazać, że istnieje <math>20</math> kolejnych liczb naturalnych postaci <math>6 k + 1</math>, wśród których jest dokładnie <math>5</math> liczb pierwszych. | Pokazać, że istnieje <math>20</math> kolejnych liczb naturalnych postaci <math>6 k + 1</math>, wśród których jest dokładnie <math>5</math> liczb pierwszych. | ||
| Linia 774: | Linia 913: | ||
:* wśród pierwszych <math>20</math> liczb naturalnych postaci <math>6 k + 1</math> jest <math>13</math> liczb pierwszych | :* wśród pierwszych <math>20</math> liczb naturalnych postaci <math>6 k + 1</math> jest <math>13</math> liczb pierwszych | ||
:* w ciągu <math>6 k + 1</math> istnieją dowolnie długie przedziały pozbawione liczb pierwszych (zobacz zadanie | :* w ciągu <math>6 k + 1</math> istnieją dowolnie długie przedziały pozbawione liczb pierwszych (zobacz zadanie [[#C38|C38]]), zatem istnieje <math>20</math> kolejnych liczb naturalnych postaci <math>6 k + 1</math>, wśród których nie ma ani jednej liczby pierwszej | ||
Pierwsze spostrzeżenie pokazuje, że rozwiązanie problemu jest potencjalnie możliwe. Rozwiązanie mogłoby nie istnieć, gdybyśmy szukali <math>20</math> liczb naturalnych postaci <math>6 k + 1</math> wśród których jest, powiedzmy, <math>15</math> liczb pierwszych. | Pierwsze spostrzeżenie pokazuje, że rozwiązanie problemu jest potencjalnie możliwe. Rozwiązanie mogłoby nie istnieć, gdybyśmy szukali <math>20</math> liczb naturalnych postaci <math>6 k + 1</math>, wśród których jest, powiedzmy, <math>15</math> liczb pierwszych. | ||
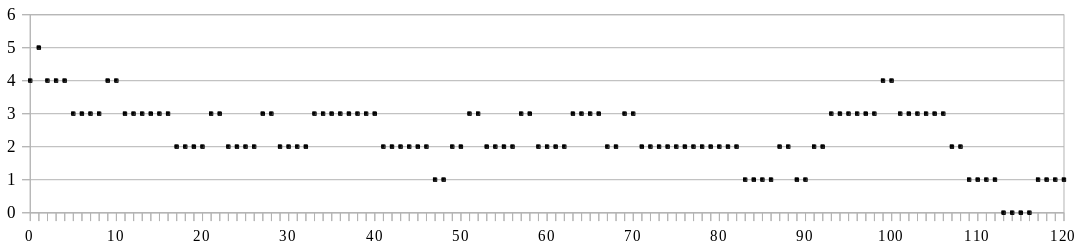
Drugie spostrzeżenie mówi nam, że ilość liczb pierwszych wśród kolejnych <math>20</math> liczb naturalnych postaci <math>6 k + 1</math> zmienia się od <math>13</math> do <math>0</math>. Analiza przebiegu tych zmian jest kluczem do dowodu twierdzenia. | Drugie spostrzeżenie mówi nam, że ilość liczb pierwszych wśród kolejnych <math>20</math> liczb naturalnych postaci <math>6 k + 1</math> zmienia się od <math>13</math> do <math>0</math>. Analiza przebiegu tych zmian jest kluczem do dowodu twierdzenia. | ||
| Linia 809: | Linia 948: | ||
Wynika stąd, że przechodząc od ciągu <math>(B^n)</math> do ciągu <math>(B^{n + 1})</math> ilość liczb pierwszych może się zmienić o <math>- 1</math>, <math>0</math> lub <math>1</math>. Z drugiego ze spostrzeżeń uczynionych na początku dowodu wynika istnienie takiej liczby <math>r</math>, że wśród ciągów | Wynika stąd, że przechodząc od ciągu <math>(B^n)</math> do ciągu <math>(B^{n + 1})</math>, ilość liczb pierwszych może się zmienić o <math>- 1</math>, <math>0</math> lub <math>1</math>. Z drugiego ze spostrzeżeń uczynionych na początku dowodu wynika istnienie takiej liczby <math>r</math>, że wśród ciągów | ||
::<math>(B^1), (B^2), \ldots, (B^r)</math> | ::<math>(B^1), (B^2), \ldots, (B^r)</math> | ||
| Linia 819: | Linia 958: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C44" style="font-size: 110%; font-weight: bold;">Twierdzenie C44</span><br/> | ||
Niech <math>a, b \in \mathbb{Z}</math> oraz <math>a \geqslant 2</math> i <math>0 \leqslant b \leqslant a - 1</math>. Jeżeli liczby <math>a</math> oraz <math>b</math> są względnie pierwsze, to istnieje <math>n</math> kolejnych liczb postaci <math>a k + b</math>, wśród których znajduje się dokładnie <math>r \leqslant \pi (a (n - 1) + b ; a, b)</math> liczb pierwszych. | Niech <math>a, b \in \mathbb{Z}</math> oraz <math>a \geqslant 2</math> i <math>0 \leqslant b \leqslant a - 1</math>. Jeżeli liczby <math>a</math> oraz <math>b</math> są względnie pierwsze, to istnieje <math>n</math> kolejnych liczb postaci <math>a k + b</math>, wśród których znajduje się dokładnie <math>r \leqslant \pi (a (n - 1) + b ; a, b)</math> liczb pierwszych. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Twierdzenie można udowodnić uogólniając dowód twierdzenia | Twierdzenie można udowodnić, uogólniając dowód twierdzenia [[#C40|C40]] lub wykorzystując metodę zastosowaną w rozwiązaniu zadania [[#C43|C43]].<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 829: | Linia 968: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C45" style="font-size: 110%; font-weight: bold;">Zadanie C45</span><br/> | ||
Niech <math>p \geqslant 5</math> będzie liczbą pierwszą. Pokazać, że w ciągu <math>6 k + 1</math> występują kwadraty wszystkich liczb pierwszych <math>p</math>. | Niech <math>p \geqslant 5</math> będzie liczbą pierwszą. Pokazać, że w ciągu <math>6 k + 1</math> występują kwadraty wszystkich liczb pierwszych <math>p</math>. | ||
| Linia 845: | Linia 984: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C46" style="font-size: 110%; font-weight: bold;">Zadanie C46</span><br/> | ||
Dany jest ciąg arytmetyczny <math>a k + b</math>, gdzie liczby <math>a</math> i <math>b</math> są względnie pierwsze. Pokazać, że | Dany jest ciąg arytmetyczny <math>a k + b</math>, gdzie liczby <math>a</math> i <math>b</math> są względnie pierwsze. Pokazać, że | ||
| Linia 869: | Linia 1008: | ||
::<math>p \mid a (j - i)</math> | ::<math>p \mid a (j - i)</math> | ||
Ponieważ <math>p \nmid a</math> to na mocy lematu Euklidesa (twierdzenie | Ponieważ <math>p \nmid a</math> to na mocy lematu Euklidesa (twierdzenie [[#C79|C79]]), mamy | ||
::<math>p \mid (j - i)</math> | ::<math>p \mid (j - i)</math> | ||
| Linia 887: | Linia 1026: | ||
::<math>n p - a k = b</math> | ::<math>n p - a k = b</math> | ||
Zauważmy, że ponieważ <math>p \nmid a</math>, to liczby <math>a</math> i <math>p</math> są względnie pierwsze. Zatem ich największym wspólnym dzielnikiem jest liczba <math>1</math>. Na mocy twierdzenia | Zauważmy, że ponieważ <math>p \nmid a</math>, to liczby <math>a</math> i <math>p</math> są względnie pierwsze. Zatem ich największym wspólnym dzielnikiem jest liczba <math>1</math>. Na mocy twierdzenia [[#C83|C83]] równanie to ma nieskończenie wiele rozwiązań w liczbach całkowitych | ||
::<math>n = n_0 + p t</math> | ::<math>n = n_0 + p t</math> | ||
| Linia 922: | Linia 1061: | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C47" style="font-size: 110%; font-weight: bold;">Uwaga C47</span><br/> | ||
Łatwo możemy napisać w PARI/GP funkcję, która zwraca najmniejszą liczbę naturalną <math>k_0</math>, dla której wyraz ciągu arytmetycznego <math>a k + b</math> jest podzielny przez <math>p</math> (przy założeniu, że liczby <math>a</math> i <math>p</math> są względnie pierwsze). | Łatwo możemy napisać w PARI/GP funkcję, która zwraca najmniejszą liczbę naturalną <math>k_0</math>, dla której wyraz ciągu arytmetycznego <math>a k + b</math> jest podzielny przez <math>p</math> (przy założeniu, że liczby <math>a</math> i <math>p</math> są względnie pierwsze). | ||
| Linia 933: | Linia 1072: | ||
== Ciągi nieskończone i liczby pierwsze == | == Ciągi nieskończone i liczby pierwsze == | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C48" style="font-size: 110%; font-weight: bold;">Uwaga C48</span><br/> | ||
Choć wiele ciągów jest dobrze znanych i równie dobrze zbadanych, to nie wiemy, czy zawierają one nieskończenie wiele liczb pierwszych. Przykładowo | Choć wiele ciągów jest dobrze znanych i równie dobrze zbadanych, to nie wiemy, czy zawierają one nieskończenie wiele liczb pierwszych. Przykładowo | ||
| Linia 979: | Linia 1118: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C49" style="font-size: 110%; font-weight: bold;">Przykład C49</span><br/> | ||
Łatwo sprawdzić, że wartości wielomianu <math>W(n) = n^2 + n + 41</math> są liczbami pierwszymi dla <math>1 \leqslant n \leqslant 39</math>. Oczywiście <math>41 \mid W(41)</math>. | Łatwo sprawdzić, że wartości wielomianu <math>W(n) = n^2 + n + 41</math> są liczbami pierwszymi dla <math>1 \leqslant n \leqslant 39</math>. Oczywiście <math>41 \mid W(41)</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C50" style="font-size: 110%; font-weight: bold;">Twierdzenie C50</span><br/> | ||
Niech <math>a, n</math> | Niech <math>a, n \in \mathbb{Z}_+</math> i <math>a \geqslant 2</math>. Jeżeli liczba <math>a^n + 1</math> jest liczbą pierwszą, to <math>a</math> jest liczbą parzystą i <math>n = 2^m</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Gdyby liczba <math>a</math> była nieparzysta, to <math>a^n + 1 \geqslant 4</math> | Gdyby liczba <math>a</math> była nieparzysta, to liczba <math>a^n + 1 \geqslant 4</math> byłaby parzysta i nie mogłaby być liczbą pierwszą. | ||
Niech | Niech wykładnik <math>n = x y</math> będzie liczbą złożoną, a <math>x</math> będzie liczbą nieparzystą. Wtedy | ||
::<math>a^n + 1 = (a^y)^x + 1</math> | ::<math>a^n + 1 = (a^y)^x + 1</math> | ||
Oznaczając <math>b = a^y</math> oraz <math>x = 2 k + 1</math> | Oznaczając <math>b = a^y</math> oraz <math>x = 2 k + 1</math>, otrzymujemy | ||
::<math>a^n + 1 = (a^y)^x + 1 | ::<math>a^n + 1 = (a^y)^x + 1</math> | ||
::::<math>\: = b^x + 1 | ::::<math>\: = b^x + 1</math> | ||
::::<math>\: = b^{2 k + 1} + 1 | ::::<math>\: = b^{2 k + 1} + 1</math> | ||
::::<math>\: = (b + 1) \cdot (b^{2 k} - b^{2 k - 1} | ::::<math>\: = (b + 1) \cdot (1 - b + b^2 - b^3 + \ldots + b^{2 k - 2} - b^{2 k - 1} + b^{2 k})</math> | ||
Czyli <math>a^n + 1</math> jest liczbą złożoną. Wynika stąd, że wykładnik <math>n</math> nie może zawierać czynników nieparzystych, czyli musi być <math>n = 2^m</math>. Co należało pokazać.<br/> | |||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 1010: | Linia 1149: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C51" style="font-size: 110%; font-weight: bold;">Twierdzenie C51</span><br/> | ||
Dla dowolnej liczby naturalnej <math>n \geqslant 1</math> liczba <math>x - y</math> jest dzielnikiem wyrażenia <math>x^n - y^n</math>. | Dla dowolnej liczby naturalnej <math>n \geqslant 1</math> liczba <math>x - y</math> jest dzielnikiem wyrażenia <math>x^n - y^n</math>. | ||
| Linia 1030: | Linia 1169: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C52" style="font-size: 110%; font-weight: bold;">Twierdzenie C52</span><br/> | ||
Jeżeli <math>n \geqslant 2</math> oraz <math>a^n - 1</math> jest liczbą pierwszą, to <math>a = 2</math> i <math>n</math> jest liczbą pierwszą. | Jeżeli <math>n \geqslant 2</math> oraz <math>a^n - 1</math> jest liczbą pierwszą, to <math>a = 2</math> i <math>n</math> jest liczbą pierwszą. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Z twierdzenia | Z twierdzenia [[#C51|C51]] wiemy, że <math>x - y \mid x^n - y^n</math>. W przypadku gdy <math>a > 2</math> mamy | ||
::<math>a - 1 \mid a^n - 1</math> | ::<math>a - 1 \mid a^n - 1</math> | ||
| Linia 1053: | Linia 1192: | ||
== Ciągi arytmetyczne liczb pierwszych == | == Ciągi arytmetyczne liczb pierwszych == | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C53" style="font-size: 110%; font-weight: bold;">Uwaga C53</span><br/> | ||
Ciągi arytmetyczne liczb pierwszych<ref name="PAPWiki"/><ref name="PAPMathWorld"/> zbudowane z dwóch liczb pierwszych nie są interesujące, bo dowolne dwie liczby tworzą ciąg arytmetyczny. Dlatego będziemy się zajmowali ciągami arytmetycznymi liczb pierwszych o długości <math>n \geqslant 3</math>. | Ciągi arytmetyczne liczb pierwszych<ref name="PAPWiki"/><ref name="PAPMathWorld"/> zbudowane z dwóch liczb pierwszych nie są interesujące, bo dowolne dwie liczby tworzą ciąg arytmetyczny. Dlatego będziemy się zajmowali ciągami arytmetycznymi liczb pierwszych o długości <math>n \geqslant 3</math>. | ||
| Linia 1064: | Linia 1203: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C54" style="font-size: 110%; font-weight: bold;">Twierdzenie C54* (Ben Green i Terence Tao, 2004)</span><br/> | ||
Dla dowolnej liczby naturalnej <math>n \geqslant 2</math> istnieje nieskończenie wiele <math>n</math>-wyrazowych ciągów arytmetycznych liczb pierwszych. | Dla dowolnej liczby naturalnej <math>n \geqslant 2</math> istnieje nieskończenie wiele <math>n</math>-wyrazowych ciągów arytmetycznych liczb pierwszych. | ||
| Linia 1070: | Linia 1209: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C55" style="font-size: 110%; font-weight: bold;">Przykład C55</span><br/> | ||
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 3</math> i <math>n = 4</math>. | Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 3</math> i <math>n = 4</math>. | ||
| Linia 1418: | Linia 1557: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C56" style="font-size: 110%; font-weight: bold;">Przykład C56</span><br/> | ||
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 5</math> i <math>n = 6</math>. | Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 5</math> i <math>n = 6</math>. | ||
| Linia 1710: | Linia 1849: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C57" style="font-size: 110%; font-weight: bold;">Przykład C57</span><br/> | ||
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 7</math> i <math>n = 8</math>. | Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 7</math> i <math>n = 8</math>. | ||
| Linia 1974: | Linia 2113: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C58" style="font-size: 110%; font-weight: bold;">Przykład C58</span><br/> | ||
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 9</math> i <math>n = 10</math>. | Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości <math>n = 9</math> i <math>n = 10</math>. | ||
| Linia 2406: | Linia 2545: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C59" style="font-size: 110%; font-weight: bold;">Twierdzenie C59</span><br/> | ||
Niech <math>n \in \mathbb{Z}_+</math> oraz <math>a, d, k, k_0 \in \mathbb{Z}</math>. Jeżeli liczby <math>d</math> i <math>n</math> są względnie pierwsze, to reszty <math>r_1, r_2, \ldots, r_n</math> z dzielenia <math>n</math> liczb <math>x_k</math> postaci | Niech <math>n \in \mathbb{Z}_+</math> oraz <math>a, d, k, k_0 \in \mathbb{Z}</math>. Jeżeli liczby <math>d</math> i <math>n</math> są względnie pierwsze, to reszty <math>r_1, r_2, \ldots, r_n</math> z dzielenia <math>n</math> liczb <math>x_k</math> postaci | ||
| Linia 2422: | Linia 2561: | ||
::<math>n \mid d (j - i)</math> | ::<math>n \mid d (j - i)</math> | ||
Ponieważ liczby <math>d</math> i <math>n</math> są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie | Ponieważ liczby <math>d</math> i <math>n</math> są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie [[#C79|C79]]), mamy | ||
::<math>n \mid (j - i)</math> | ::<math>n \mid (j - i)</math> | ||
| Linia 2434: | Linia 2573: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C60" style="font-size: 110%; font-weight: bold;">Twierdzenie C60</span><br/> | ||
Niech <math>d \in \mathbb{Z}_+</math> i niech będzie dany ciąg arytmetyczny liczb pierwszych o długości <math>n</math> | Niech <math>d \in \mathbb{Z}_+</math> i niech będzie dany ciąg arytmetyczny liczb pierwszych o długości <math>n</math> | ||
| Linia 2450: | Linia 2589: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
'''Punkt 1.'''<br/> | '''Punkt 1.'''<br/> | ||
Gdyby <math>p_0 \mid d</math>, to dla <math>k \geqslant 1</math> mielibyśmy <math>p_k = p_0 \left( 1 + k \cdot \frac{d}{p_0} \right)</math> i wszystkie te liczby byłyby złożone. | Gdyby <math>p_0 \mid d</math>, to dla <math>k \geqslant 1</math> mielibyśmy <math>p_k = p_0 \left( 1 + k \cdot {\small\frac{d}{p_0}} \right)</math> i wszystkie te liczby byłyby złożone. | ||
'''Punkt 2.'''<br/> | '''Punkt 2.'''<br/> | ||
| Linia 2456: | Linia 2595: | ||
'''Punkt 3.'''<br/> | '''Punkt 3.'''<br/> | ||
Niech <math>q</math> będzie liczbą pierwszą mniejszą od <math>n</math>, a liczby <math>r_k</math> będą resztami uzyskanymi z dzielenia liczb <math>p_k = p_0 + k d</math> przez <math>q</math>, dla <math>k = 0, 1, \ldots, q - 1</math>. Ponieważ z założenia liczby <math>p_0, \ldots, p_{n - 1}</math> są liczbami pierwszymi większymi od <math>q</math> (zauważmy, że <math>p_0 \geqslant n</math>), to żadna z reszt <math>r_k</math> nie może być równa zeru. Czyli mamy <math>q</math> reszt mogących przyjmować jedynie <math>q - 1</math> różnych wartości. Zatem istnieją różne liczby <math>i, j</math>, | Niech <math>q</math> będzie liczbą pierwszą mniejszą od <math>n</math>, a liczby <math>r_k</math> będą resztami uzyskanymi z dzielenia liczb <math>p_k = p_0 + k d</math> przez <math>q</math>, dla <math>k = 0, 1, \ldots, q - 1</math>. Ponieważ z założenia liczby <math>p_0, \ldots, p_{n - 1}</math> są liczbami pierwszymi większymi od <math>q</math> (zauważmy, że <math>p_0 \geqslant n</math>), to żadna z reszt <math>r_k</math> nie może być równa zeru. Czyli mamy <math>q</math> reszt mogących przyjmować jedynie <math>q - 1</math> różnych wartości. Zatem istnieją różne liczby <math>i, j</math> takie, że <math>0 \leqslant i < j \leqslant q - 1</math>, dla których <math>r_i = r_j</math>. Wynika stąd, że różnica liczb | ||
::<math>p_j - p_i = (p_0 + j d) - (p_0 + i d) = d (j - i)</math> | ::<math>p_j - p_i = (p_0 + j d) - (p_0 + i d) = d (j - i)</math> | ||
| Linia 2473: | Linia 2612: | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C61" style="font-size: 110%; font-weight: bold;">Uwaga C61</span><br/> | ||
Czasami, zamiast pisać „ciąg arytmetyczny liczb pierwszych”, będziemy posługiwali się skrótem PAP od angielskiej nazwy „''prime arithmetic progression''”. Konsekwentnie zapis PAP-<math>n</math> będzie oznaczał ciąg arytmetyczny liczb pierwszych o długości <math>n</math>, a zapis PAP<math>(n, d, q)</math> ciąg arytmetyczny liczb pierwszych o długości <math>n</math>, pierwszym wyrazie <math>q</math> i różnicy <math>d</math>. | Czasami, zamiast pisać „ciąg arytmetyczny liczb pierwszych”, będziemy posługiwali się skrótem PAP od angielskiej nazwy „''prime arithmetic progression''”. Konsekwentnie zapis PAP-<math>n</math> będzie oznaczał ciąg arytmetyczny liczb pierwszych o długości <math>n</math>, a zapis PAP<math>(n, d, q)</math> ciąg arytmetyczny liczb pierwszych o długości <math>n</math>, pierwszym wyrazie <math>q</math> i różnicy <math>d</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C62" style="font-size: 110%; font-weight: bold;">Uwaga C62</span><br/> | ||
Jakkolwiek sądzimy, że istnieje nieskończenie wiele ciągów arytmetycznych liczb pierwszych rozpoczynających się od dowolnej liczby pierwszej <math>q</math> i o dowolnej długości <math>3 \leqslant n \leqslant q</math>, to obecnie jest to tylko nieudowodnione przypuszczenie. | Jakkolwiek sądzimy, że istnieje nieskończenie wiele ciągów arytmetycznych liczb pierwszych rozpoczynających się od dowolnej liczby pierwszej <math>q</math> i o dowolnej długości <math>3 \leqslant n \leqslant q</math>, to obecnie jest to tylko nieudowodnione przypuszczenie. | ||
Dlatego '''nawet dla najmniejszej''' liczby pierwszej <math>q</math> takiej, że <math>q \nmid d</math> nierówność <math>n \leqslant q</math>, pokazana w twierdzeniu | Dlatego '''nawet dla najmniejszej''' liczby pierwszej <math>q</math> takiej, że <math>q \nmid d</math> nierówność <math>n \leqslant q</math>, pokazana w twierdzeniu [[#C60|C60]], pozostaje nadal tylko oszacowaniem. W szczególności nie możemy z góry przyjmować, że dla liczby <math>n = q</math> znajdziemy taką liczbę <math>d</math> będącą wielokrotnością liczby <math>P(q - 1)</math> i niepodzielną przez <math>q</math>, że będzie istniał PAP<math>(q, d, q)</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C63" style="font-size: 110%; font-weight: bold;">Przykład C63</span><br/> | ||
Rozważmy dwie różnice <math>d_1 = 6 = 2 \cdot 3</math> oraz <math>d_2 = 42 = 2 \cdot 3 \cdot 7</math>. Zauważmy, że liczba pierwsza <math>5</math> nie dzieli ani <math>d_1</math>, ani <math>d_2</math>. Co więcej, liczba pierwsza <math>5</math> jest '''najmniejszą''' liczbą pierwszą, która nie dzieli rozpatrywanych różnic, zatem nierówność <math>n \leqslant 5</math> zapewnia najmocniejsze oszacowanie długości ciągu <math>n</math>. Łatwo sprawdzamy w zamieszczonych tabelach, że dla <math>d = 6</math> oraz dla <math>d = 42</math> są ciągi o długości <math>3, 4, 5</math>, ale nie ma ciągów o długości <math>6, 7, \ldots</math> | Rozważmy dwie różnice <math>d_1 = 6 = 2 \cdot 3</math> oraz <math>d_2 = 42 = 2 \cdot 3 \cdot 7</math>. Zauważmy, że liczba pierwsza <math>5</math> nie dzieli ani <math>d_1</math>, ani <math>d_2</math>. Co więcej, liczba pierwsza <math>5</math> jest '''najmniejszą''' liczbą pierwszą, która nie dzieli rozpatrywanych różnic, zatem nierówność <math>n \leqslant 5</math> zapewnia najmocniejsze oszacowanie długości ciągu <math>n</math>. Łatwo sprawdzamy w zamieszczonych tabelach, że dla <math>d = 6</math> oraz dla <math>d = 42</math> są ciągi o długości <math>3, 4, 5</math>, ale nie ma ciągów o długości <math>6, 7, \ldots</math> | ||
W szczególności z twierdzenia | W szczególności z twierdzenia [[#C60|C60]] wynika, że szukając ciągów arytmetycznych liczb pierwszych o określonej długości <math>n</math>, należy szukać ich tylko dla różnic <math>d</math> będących wielokrotnością liczby <math>P(n - 1)</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C64" style="font-size: 110%; font-weight: bold;">Zadanie C64</span><br/> | ||
Wiemy, że liczby pierwsze <math>p > 3</math> można przedstawić w jednej z postaci <math>6 k - 1</math> lub <math>6 k + 1</math>. Pokazać, że jeżeli <math>p_0 = 3</math>, to dwa następne wyrazu rosnącego ciągu arytmetycznego liczb pierwszych są różnych postaci. | Wiemy, że liczby pierwsze <math>p > 3</math> można przedstawić w jednej z postaci <math>6 k - 1</math> lub <math>6 k + 1</math>. Pokazać, że jeżeli <math>p_0 = 3</math>, to dwa następne wyrazu rosnącego ciągu arytmetycznego liczb pierwszych są różnych postaci. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
Ponieważ <math>p_0 = 3</math>, a rozpatrywany PAP jest rosnący, to kolejne wyrazy ciągu są większe od liczby <math>3</math> i mogą być przedstawione w jednej z postaci <math>6 k - 1</math> lub <math>6 k + 1</math>. Z twierdzenia | Ponieważ <math>p_0 = 3</math>, a rozpatrywany PAP jest rosnący, to kolejne wyrazy ciągu są większe od liczby <math>3</math> i mogą być przedstawione w jednej z postaci <math>6 k - 1</math> lub <math>6 k + 1</math>. Z twierdzenia [[#C60|C60]] wiemy, że musi być <math>n \leqslant p_0 = 3</math>, czyli długość rozpatrywanego ciągu arytmetycznego liczb pierwszych wynosi dokładnie <math>3</math> i istnieją tylko dwa następne wyrazy. | ||
Rozważmy ciąg arytmetyczny liczb pierwszych składający się z trzech wyrazów <math>p, q, r</math> takich, że <math>p = 3</math>. Mamy | Rozważmy ciąg arytmetyczny liczb pierwszych składający się z trzech wyrazów <math>p, q, r</math> takich, że <math>p = 3</math>. Mamy | ||
| Linia 2512: | Linia 2651: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C65" style="font-size: 110%; font-weight: bold;">Zadanie C65</span><br/> | ||
Wiemy, że liczby pierwsze <math>p > 3</math> można przedstawić w jednej z postaci <math>6 k - 1</math> lub <math>6 k + 1</math>. Pokazać, że wszystkie wyrazy rosnącego ciągu arytmetycznego liczb pierwszych <math>p_0, p_1, \ldots, p_{n - 1}</math>, gdzie <math>p_0 \geqslant 5</math> i <math>n \geqslant 3</math> muszą być jednakowej postaci. | Wiemy, że liczby pierwsze <math>p > 3</math> można przedstawić w jednej z postaci <math>6 k - 1</math> lub <math>6 k + 1</math>. Pokazać, że wszystkie wyrazy rosnącego ciągu arytmetycznego liczb pierwszych <math>p_0, p_1, \ldots, p_{n - 1}</math>, gdzie <math>p_0 \geqslant 5</math> i <math>n \geqslant 3</math> muszą być jednakowej postaci. | ||
| Linia 2534: | Linia 2673: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C66" style="font-size: 110%; font-weight: bold;">Zadanie C66</span><br/> | ||
Niech <math>d > 0</math> będzie różnicą ciągu arytmetycznego liczb pierwszych o długości <math>n</math> | Niech <math>d > 0</math> będzie różnicą ciągu arytmetycznego liczb pierwszych o długości <math>n</math> | ||
::<math>p_k = p_0 + k d \qquad</math> dla <math>\; k = 0, 1, \ldots, n - 1</math> | ::<math>p_k = p_0 + k d \qquad</math> dla <math>\; k = 0, 1, \ldots, n - 1</math> | ||
Pokazać, nie korzystając z twierdzenia | Pokazać, nie korzystając z twierdzenia [[#C60|C60]], że jeżeli liczba pierwsza <math>q</math> nie dzieli <math>d</math>, to <math>n \leqslant q</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| Linia 2546: | Linia 2685: | ||
::<math>q < p_k = p_0 + k d \qquad</math> dla <math>\; k = 0, 1, \ldots, n - 1</math> | ::<math>q < p_k = p_0 + k d \qquad</math> dla <math>\; k = 0, 1, \ldots, n - 1</math> | ||
Ponieważ <math>q \nmid d</math>, to na mocy twierdzenia | Ponieważ <math>q \nmid d</math>, to na mocy twierdzenia [[#C59|C59]] wśród <math>q</math> kolejnych wyrazów <math>p_0, p_1, \ldots, p_{q - 1}</math> (zauważmy, że <math>q - 1 < n - 1</math>) jedna liczba pierwsza <math>p_k</math> musi być podzielna przez <math>q</math>, zatem musi być równa <math>q</math>. Jednak jest to niemożliwe, bo <math>q < p_k</math> dla wszystkich <math>k = 0, 1, \ldots, n - 1</math>. Zatem nie może być <math>n > q</math>.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 2552: | Linia 2691: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C67" style="font-size: 110%; font-weight: bold;">Twierdzenie C67</span><br/> | ||
Niech <math>q</math> będzie liczbą pierwszą, a liczby pierwsze | Niech <math>q</math> będzie liczbą pierwszą, a liczby pierwsze | ||
| Linia 2569: | Linia 2708: | ||
Gdyby <math>q \mid d</math>, to mielibyśmy | Gdyby <math>q \mid d</math>, to mielibyśmy | ||
::<math>p_k = q \left( 1 + k \cdot \frac{d}{q} \right)</math> | ::<math>p_k = q \left( 1 + k \cdot {\small\frac{d}{q}} \right)</math> | ||
i wszystkie liczby <math>p_k</math> dla <math>k \geqslant 1</math> byłyby złożone, wbrew założeniu, że <math>p_k</math> tworzą <math>q</math>-wyrazowy ciąg arytmetyczny liczb pierwszych. | i wszystkie liczby <math>p_k</math> dla <math>k \geqslant 1</math> byłyby złożone, wbrew założeniu, że <math>p_k</math> tworzą <math>q</math>-wyrazowy ciąg arytmetyczny liczb pierwszych. | ||
<math>\Longleftarrow</math><br/> | <math>\Longleftarrow</math><br/> | ||
Ponieważ <math>q</math> jest długością rozpatrywanego ciągu arytmetycznego liczb pierwszych, to z twierdzenia | Ponieważ <math>q</math> jest długością rozpatrywanego ciągu arytmetycznego liczb pierwszych, to z twierdzenia [[#C60|C60]] wynika, że musi być <math>q \leqslant p_0</math>. | ||
Z założenia liczba pierwsza <math>q</math> nie dzieli <math>d</math>, zatem z twierdzenia | Z założenia liczba pierwsza <math>q</math> nie dzieli <math>d</math>, zatem z twierdzenia [[#C59|C59]] wiemy, że <math>q</math> musi dzielić jedną z liczb <math>p_0, p_1, \ldots, p_{q - 1}</math>. | ||
Jeżeli <math>q \mid p_k</math>, to <math>p_k = q</math>. Ponieważ <math>q \leqslant p_0</math>, to możliwe jest jedynie <math>q \mid p_0</math> i musi być <math>p_0 = q</math>.<br/> | Jeżeli <math>q \mid p_k</math>, to <math>p_k = q</math>. Ponieważ <math>q \leqslant p_0</math>, to możliwe jest jedynie <math>q \mid p_0</math> i musi być <math>p_0 = q</math>.<br/> | ||
| Linia 2584: | Linia 2723: | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C68" style="font-size: 110%; font-weight: bold;">Uwaga C68</span><br/> | ||
Niech ciąg arytmetyczny liczb pierwszych o długości <math>n</math> ma postać | Niech ciąg arytmetyczny liczb pierwszych o długości <math>n</math> ma postać | ||
::<math>p_k = p_0 + k d \qquad</math> dla <math>\; k = 0, 1, \ldots, n - 1</math> | ::<math>p_k = p_0 + k d \qquad</math> dla <math>\; k = 0, 1, \ldots, n - 1</math> | ||
Z udowodnionych wyżej twierdzeń | Z udowodnionych wyżej twierdzeń [[#C60|C60]] i [[#C67|C67]] wynika, że ciągi arytmetyczne liczb pierwszych o długości <math>n</math> można podzielić na dwie grupy | ||
:* jeżeli <math>n</math> jest liczbą pierwszą i <math>n \nmid d</math>, to <math>P(n - 1) \mid d</math> oraz <math>p_0 = n</math> (dla ustalonego <math>d</math> może istnieć tylko jeden ciąg) | :* jeżeli <math>n</math> jest liczbą pierwszą i <math>n \nmid d</math>, to <math>P(n - 1) \mid d</math> oraz <math>p_0 = n</math> (dla ustalonego <math>d</math> może istnieć tylko jeden ciąg) | ||
| Linia 2598: | Linia 2737: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C69" style="font-size: 110%; font-weight: bold;">Przykład C69</span><br/> | ||
Niech różnica ciągu arytmetycznego liczb pierwszych wynosi <math>d = 10^t</math>, gdzie <math>t \geqslant 1</math>. Zauważmy, że dla dowolnego <math>t</math> liczba <math>3</math> jest najmniejszą liczbą pierwszą, która nie dzieli <math>d</math>. Z oszacowania <math>n \leqslant 3</math> wynika, że musi być <math>n = 3</math>. | Niech różnica ciągu arytmetycznego liczb pierwszych wynosi <math>d = 10^t</math>, gdzie <math>t \geqslant 1</math>. Zauważmy, że dla dowolnego <math>t</math> liczba <math>3</math> jest najmniejszą liczbą pierwszą, która nie dzieli <math>d</math>. Z oszacowania <math>n \leqslant 3</math> wynika, że musi być <math>n = 3</math>. | ||
| Linia 2605: | Linia 2744: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C70" style="font-size: 110%; font-weight: bold;">Zadanie C70</span><br/> | ||
Znaleźć wszystkie PAP<math>(n, d, p)</math> dla <math>d = 2, 4, 8, 10, 14, 16</math>. | Znaleźć wszystkie PAP<math>(n, d, p)</math> dla <math>d = 2, 4, 8, 10, 14, 16</math>. | ||
| Linia 2621: | Linia 2760: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C71" style="font-size: 110%; font-weight: bold;">Zadanie C71</span><br/> | ||
Znaleźć wszystkie PAP<math>(n, d, p)</math> dla <math>n = 3, 5, 7, 11</math> i <math>d = P (n - 1)</math>. | Znaleźć wszystkie PAP<math>(n, d, p)</math> dla <math>n = 3, 5, 7, 11</math> i <math>d = P (n - 1)</math>. | ||
| Linia 2639: | Linia 2778: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C72" style="font-size: 110%; font-weight: bold;">Przykład C72</span><br/> | ||
Przedstawiamy przykładowe ciągi arytmetyczne liczb pierwszych, | Przedstawiamy przykładowe ciągi arytmetyczne liczb pierwszych takie, że <math>n = p_0</math> dla <math>n = 3, 5, 7, 11, 13</math>. Zauważmy, że wypisane w tabeli wartości <math>d</math> są wielokrotnościami liczby <math>P(n - 1)</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż tabelę|Hide=Ukryj tabelę}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Pokaż tabelę|Hide=Ukryj tabelę}} | ||
| Linia 2667: | Linia 2806: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C73" style="font-size: 110%; font-weight: bold;">Przykład C73</span><br/> | ||
Liczby <math>3, 5, 7</math> są najprostszym przykładem ciągu arytmetycznego '''kolejnych''' liczb pierwszych. Zauważmy, że tylko w przypadku <math>n = 3</math> możliwa jest sytuacja, że <math>n = p_0 = 3</math>. Istotnie, łatwo stwierdzamy, że | Liczby <math>3, 5, 7</math> są najprostszym przykładem ciągu arytmetycznego '''kolejnych''' liczb pierwszych. Zauważmy, że tylko w przypadku <math>n = 3</math> możliwa jest sytuacja, że <math>n = p_0 = 3</math>. Istotnie, łatwo stwierdzamy, że | ||
:* ponieważ <math>p_0</math> i <math>p_1</math> są '''kolejnymi''' liczbami pierwszymi, to <math>p_1 - p_0 < p_0</math> (zobacz zadanie B22) | :* ponieważ <math>p_0</math> i <math>p_1</math> są '''kolejnymi''' liczbami pierwszymi, to <math>p_1 - p_0 < p_0</math> (zobacz zadanie [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B22|B22]]) | ||
:* dla dowolnej liczby pierwszej <math>q \geqslant 5</math> jest <math>q < P (q - 1)</math> (zobacz zadanie B26) | :* dla dowolnej liczby pierwszej <math>q \geqslant 5</math> jest <math>q < P (q - 1)</math> (zobacz zadanie [[Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n#B26|B26]]) | ||
Przypuśćmy teraz, że istnieje ciąg arytmetyczny '''kolejnych''' liczb pierwszych, | Przypuśćmy teraz, że istnieje ciąg arytmetyczny '''kolejnych''' liczb pierwszych taki, że <math>n = p_0 \geqslant 5</math>. Mamy | ||
::<math>d = p_1 - p_0 < p_0 < P (p_0 - 1) = P (n - 1)</math> | ::<math>d = p_1 - p_0 < p_0 < P (p_0 - 1) = P (n - 1)</math> | ||
| Linia 2679: | Linia 2818: | ||
Zatem <math>P(n - 1) \nmid d</math>, co jest niemożliwe. | Zatem <math>P(n - 1) \nmid d</math>, co jest niemożliwe. | ||
Wynika stąd, że poza przypadkiem <math>n = p_0 = 3</math> ciąg arytmetyczny kolejnych liczb pierwszych musi spełniać warunek <math>P(n) | Wynika stąd, że poza przypadkiem <math>n = p_0 = 3</math> ciąg arytmetyczny kolejnych liczb pierwszych musi spełniać warunek <math>P(n) \mid d</math>, czyli <math>P(n) \mid (p_1 - p_0)</math>. | ||
Poniższe tabele przedstawiają przykładowe ciągi arytmetyczne kolejnych liczb pierwszych o długościach <math>n = 3, 4, 5, 6</math> dla rosnących wartości <math>p_0</math>. Nie istnieje ciąg arytmetyczny kolejnych liczb pierwszych o długości <math>n = 7</math> dla <math>p_0 < 10^{13}</math>. Prawdopodobnie CPAP-7 pojawią się dopiero dla <math>p_0 \sim 10^{20}</math>. | Poniższe tabele przedstawiają przykładowe ciągi arytmetyczne kolejnych liczb pierwszych o długościach <math>n = 3, 4, 5, 6</math> dla rosnących wartości <math>p_0</math>. Nie istnieje ciąg arytmetyczny kolejnych liczb pierwszych o długości <math>n = 7</math> dla <math>p_0 < 10^{13}</math>. Prawdopodobnie CPAP-7 pojawią się dopiero dla <math>p_0 \sim 10^{20}</math>. | ||
| Linia 2819: | Linia 2958: | ||
<span style="font-size: 110%; font-weight: bold;">Zadanie | <span id="C74" style="font-size: 110%; font-weight: bold;">Zadanie C74</span><br/> | ||
Uzasadnij przypuszczenie, że ciągów arytmetycznych '''kolejnych''' liczb pierwszych o długości <math>n = 7</math> możemy oczekiwać dopiero dla <math>p_0 \sim 10^{20}</math>. | Uzasadnij przypuszczenie, że ciągów arytmetycznych '''kolejnych''' liczb pierwszych o długości <math>n = 7</math> możemy oczekiwać dopiero dla <math>p_0 \sim 10^{20}</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
Zauważmy, że ilość liczb pierwszych nie większych od <math>x</math> w dobrym przybliżeniu jest określona funkcją <math>\frac{x}{\log x}</math>. Ponieważ funkcja <math>\log x</math> zmienia się bardzo wolno, to odcinki liczb naturalnych o tej samej długości położone w niewielkiej odległości od siebie będą zawierały podobne ilości liczb pierwszych. Przykładowo, dla dużych wartości <math>x</math>, ilość liczb pierwszych w przedziale <math>(x, 2 x)</math> jest tego samego rzędu, co ilość liczb pierwszych w przedziale <math>(1, x)</math><ref name="PrimesInInterval"/>. | Zauważmy, że ilość liczb pierwszych nie większych od <math>x</math> w dobrym przybliżeniu jest określona funkcją <math>{\small\frac{x}{\log x}}</math>. Ponieważ funkcja <math>\log x</math> zmienia się bardzo wolno, to odcinki liczb naturalnych o tej samej długości położone w niewielkiej odległości od siebie będą zawierały podobne ilości liczb pierwszych. Przykładowo, dla dużych wartości <math>x</math>, ilość liczb pierwszych w przedziale <math>(x, 2 x)</math> jest tego samego rzędu, co ilość liczb pierwszych w przedziale <math>(1, x)</math><ref name="PrimesInInterval"/>. | ||
Zatem liczbę <math>\frac{1}{\log x}</math> możemy traktować jako prawdopodobieństwo trafienia na liczbę pierwszą wśród liczb znajdujących się w pobliżu liczby <math>x</math>. Zakładając, że liczby pierwsze są rozłożone przypadkowo, możemy wyliczyć prawdopodobieństwo tego, że <math>n</math> kolejnych liczb pierwszych, położonych w pobliżu liczby <math>x</math>, utworzy ciąg arytmetyczny | Zatem liczbę <math>{\small\frac{1}{\log x}}</math> możemy traktować jako prawdopodobieństwo trafienia na liczbę pierwszą wśród liczb znajdujących się w pobliżu liczby <math>x</math>. Zakładając, że liczby pierwsze są rozłożone przypadkowo, możemy wyliczyć prawdopodobieństwo tego, że <math>n</math> kolejnych liczb pierwszych, położonych w pobliżu liczby <math>x</math>, utworzy ciąg arytmetyczny | ||
::<math>\text{prob}_{\text{cpap}} (n, x) = \left( \frac{1}{\log x} \right)^n \left( 1 - \frac{1}{\log x} \right)^{(n - 1) (d - 1)}</math> | ::<math>\text{prob}_{\text{cpap}} (n, x) = \left( {\small\frac{1}{\log x}} \right)^n \left( 1 - {\small\frac{1}{\log x}} \right)^{(n - 1) (d - 1)}</math> | ||
gdzie <math>d = P (n)</math>. Jest tak, ponieważ w ciągu kolejnych liczb całkowitych musimy trafić na liczbę pierwszą, następnie na <math>d - 1</math> liczb złożonych, taka sytuacja musi się powtórzyć dokładnie <math>n - 1</math> razy, a na koniec znowu musimy trafić na liczbę pierwszą. Czyli potrzebujemy <math>n</math> liczb pierwszych, na które trafiamy z prawdopodobieństwem <math>\frac{1}{\log x}</math> oraz <math>(n - 1) (d - 1)</math> liczb złożonych, na które trafiamy z prawdopodobieństwem <math>1 - \frac{1}{\log x}</math>, a liczby te muszą pojawiać się w ściśle określonej kolejności. | gdzie <math>d = P (n)</math>. Jest tak, ponieważ w ciągu kolejnych liczb całkowitych musimy trafić na liczbę pierwszą, następnie na <math>d - 1</math> liczb złożonych, taka sytuacja musi się powtórzyć dokładnie <math>n - 1</math> razy, a na koniec znowu musimy trafić na liczbę pierwszą. Czyli potrzebujemy <math>n</math> liczb pierwszych, na które trafiamy z prawdopodobieństwem <math>{\small\frac{1}{\log x}}</math> oraz <math>(n - 1) (d - 1)</math> liczb złożonych, na które trafiamy z prawdopodobieństwem <math>1 - {\small\frac{1}{\log x}}</math>, a liczby te muszą pojawiać się w ściśle określonej kolejności. | ||
Ilość ciągów arytmetycznych utworzonych przez <math>n</math> kolejnych liczb pierwszych należących do przedziału <math>(x, 2 x)</math> możemy zatem oszacować na równą około | Ilość ciągów arytmetycznych utworzonych przez <math>n</math> kolejnych liczb pierwszych należących do przedziału <math>(x, 2 x)</math> możemy zatem oszacować na równą około | ||
::<math>Q_{\text{cpap}}(n, x) = x \cdot \left( \frac{1}{\log x} \right)^n \left( 1 - \frac{1}{\log x} \right)^{(n - 1) (d - 1)}</math> | ::<math>Q_{\text{cpap}}(n, x) = x \cdot \left( {\small\frac{1}{\log x}} \right)^n \left( 1 - {\small\frac{1}{\log x}} \right)^{(n - 1) (d - 1)}</math> | ||
| Linia 2886: | Linia 3025: | ||
Możemy ją łatwo wyliczyć w PARI/GP. Oczywiście funkcję <math>f(7, x)</math> zastąpiliśmy jej oszacowaniem <math>C_7 = 2500</math> | Możemy ją łatwo wyliczyć w PARI/GP. Oczywiście funkcję <math>f(7, x)</math> zastąpiliśmy jej oszacowaniem <math>C_7 = 2500</math> | ||
P(n) = prod(k=2, n, if( isprime(k), k, 1 )) | <span style="font-size: 90%; color:black;">P(n) = '''prod'''(k = 2, n, '''if'''( '''isprime'''(k), k, 1 ))</span> | ||
Q(x) = 2500 * x * ( 1/log(x) )^7 * ( 1 - 1/log(x) )^( (7-1)*(P(7)-1) ) | |||
solve(x=10^10, 10^23, Q(x) - 1 ) | <span style="font-size: 90%; color:black;">Q(x) = 2500 * x * ( 1/'''log'''(x) )^7 * ( 1 - 1/'''log'''(x) )^( (7 - 1)*(P(7) - 1) )</span> | ||
<br/> | |||
<span style="font-size: 90%; color:black;">'''solve'''(x = 10^10, 10^23, Q(x) - 1 )</span> | |||
□ | |||
{{\Spoiler}} | |||
== Podciągi nieskończone i ich granice == | |||
<span id="C75" style="font-size: 110%; font-weight: bold;">Definicja C75</span><br/> | |||
Niech <math>(a_k)</math> będzie ciągiem nieskończonym liczb rzeczywistych. Jeżeli <math>k_j</math> jest silnie rosnącym nieskończonym ciągiem liczb naturalnych, to powiemy, że ciąg <math>(a_{k_j})</math> jest podciągiem nieskończonym ciągu <math>(a_k)</math>. | |||
<span id="C76" style="font-size: 110%; font-weight: bold;">Uwaga C76</span><br/> | |||
Podciąg powstaje z ciągu wyjściowego przez '''wybieranie niektórych jego wyrazów''', w tej samej kolejności, ale pomijając dowolnie wiele z nich. Dla przykładu: podciągiem ciągu liczb naturalnych <math>(a_k) = (1, 2, 3, 4, 5, 6, \ldots)</math> jest ciąg liczb parzystych dodatnich <math>(2, 4, 6, 8, 10, \ldots)</math> – zauważmy, że ciąg i podciąg są rozbieżne. Podciągiem ciągu <math>(a_k) = (1, - 1, 1, - 1, 1, - 1, \ldots)</math> jest ciąg <math>(1, 1, 1, 1, \ldots)</math> – zauważmy, że ciąg <math>(a_k)</math> jest rozbieżny, ale podciąg <math>(a_{k_j})</math>, gdzie <math>k_j = 2 j - 1</math> jest zbieżny. | |||
<span id="C77" style="font-size: 110%; font-weight: bold;">Twierdzenie C77</span><br/> | |||
Jeżeli <math>(a_{k_j})</math> jest nieskończonym podciągiem ciągu zbieżnego <math>(a_k)</math>, to podciąg <math>(a_{k_j})</math> też jest zbieżny i <math>\lim_{j \rightarrow \infty} | |||
a_{k_j} = \lim_{k \rightarrow \infty} a_k</math>. | |||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | |||
Niech <math>(a_k)</math> będzie ciągiem zbieżnym do <math>g</math>, czyli <math>\lim_{k \rightarrow \infty} a_k = g</math>. Oznacza to, że prawie wszystkie wyrazy ciągu <math>(a_k)</math> | |||
znajdują się w przedziale <math>(g - \varepsilon, g + \varepsilon)</math>. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od pewnego <math>K_0</math>. | |||
Z założenia <math>(a_{k_j})</math> jest nieskończonym podciągiem ciągu <math>(a_k)</math>, zatem indeksy <math>k_j</math> są silnie rosnącym nieskończonym ciągiem liczb naturalnych i dla pewnego <math>j > J_0</math> musi być <math>k_j > K_0</math>. | |||
Wynika stąd, że prawie wszystkie wyrazy podciągu <math>(a_{k_j})</math> znajdują się w przedziale <math>(g - \varepsilon, g + \varepsilon)</math>. Co oznacza, że liczba <math>g</math> jest granicą podciągu <math>(a_{k_j})</math> i co należało pokazać.<br/> | |||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 2899: | Linia 3069: | ||
== Uzupełnienie == | == Uzupełnienie == | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C78" style="font-size: 110%; font-weight: bold;">Twierdzenie C78 (lemat Bézouta)</span><br/> | ||
Jeżeli liczby całkowite <math>a</math> i <math>b</math> nie są jednocześnie równe zeru, a największy wspólny dzielnik tych liczb jest równy <math>D</math>, to istnieją takie liczby całkowite <math>x, y</math>, że | Jeżeli liczby całkowite <math>a</math> i <math>b</math> nie są jednocześnie równe zeru, a największy wspólny dzielnik tych liczb jest równy <math>D</math>, to istnieją takie liczby całkowite <math>x, y</math>, że | ||
| Linia 2926: | Linia 3096: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C79" style="font-size: 110%; font-weight: bold;">Twierdzenie C79 (lemat Euklidesa)</span><br/> | ||
Niech <math>p</math> będzie liczbą pierwszą oraz <math>a, b, d \in \mathbb{Z}</math>. | Niech <math>p</math> będzie liczbą pierwszą oraz <math>a, b, d \in \mathbb{Z}</math>. | ||
:* jeżeli <math>d \mid a b</math> i liczba <math>d</math> jest względnie pierwsza z <math>a</math>, to <math>d \mid b</math> | :* jeżeli <math>d \mid a b</math> i liczba <math>d</math> jest względnie pierwsza z <math>a</math>, to <math>d \mid b</math> | ||
:* jeżeli <math>p \mid a b</math>, to <math>p \mid a</math> lub <math>p \mid b</math> | :* jeżeli <math>p \mid a b</math>, to <math>p \mid a</math> lub <math>p \mid b</math> | ||
| Linia 2937: | Linia 3107: | ||
'''Punkt 1.''' | '''Punkt 1.''' | ||
Z założenia liczby <math>d</math> i <math>a</math> są względnie pierwsze, zatem na mocy lematu Bézouta (twierdzenie | Z założenia liczby <math>d</math> i <math>a</math> są względnie pierwsze, zatem na mocy lematu Bézouta (twierdzenie [[#C78|C78]]) istnieją takie liczby całkowite <math>x</math> i <math>y</math>, że | ||
::<math>d x + a y = 1</math> | ::<math>d x + a y = 1</math> | ||
| Linia 2945: | Linia 3115: | ||
::<math>d b x + a b y = b</math> | ::<math>d b x + a b y = b</math> | ||
Obydwa wyrazy po | Obydwa wyrazy po lewej stronie są podzielne przez <math>d</math>, bo z założenia <math>d \mid a b</math>. Zatem prawa strona również jest podzielna przez <math>d</math>, czyli <math>d \mid b</math>. Co kończy dowód punktu pierwszego. | ||
'''Punkt 2.''' | '''Punkt 2.''' | ||
Jeżeli <math>p \nmid a</math>, to <math>\gcd (p, a) = 1</math>, zatem z punktu pierwszego wynika, że <math>p \mid b</math>. | Jeżeli <math>p \nmid a</math>, to <math>\gcd (p, a) = 1</math>, zatem z punktu pierwszego wynika, że <math>p \mid b</math>. | ||
Jeżeli <math>p \nmid b</math>, to <math>\gcd (p, b) = 1</math>, zatem z punktu pierwszego wynika, że <math>p \mid a</math>. | Jeżeli <math>p \nmid b</math>, to <math>\gcd (p, b) = 1</math>, zatem z punktu pierwszego wynika, że <math>p \mid a</math>. | ||
Czyli <math>p</math> musi dzielić przynajmniej jedną z liczb <math>a, b</math>. Co należało pokazać.<br/> | Czyli <math>p</math> musi dzielić przynajmniej jedną z liczb <math>a, b</math>. Co należało pokazać.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 2959: | Linia 3129: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C80" style="font-size: 110%; font-weight: bold;">Twierdzenie C80</span><br/> | ||
Niech <math>a, b, m \in \mathbb{Z}</math>. Jeżeli <math>a \mid m</math> i <math>b \mid m</math> oraz <math>\gcd (a, b) = 1</math>, to <math>a b \mid m</math>. | Niech <math>a, b, m \in \mathbb{Z}</math>. Jeżeli <math>a \mid m \;</math> i <math>\; b \mid m</math> oraz <math>\gcd (a, b) = 1</math>, to <math>a b \mid m</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| Linia 2968: | Linia 3138: | ||
::<math>a x + b y = 1</math> | ::<math>a x + b y = 1</math> | ||
(zobacz | (zobacz [[#C78|C78]]). Zatem | ||
::<math>m = m (a x + b y)</math> | ::<math>m = m (a x + b y)</math> | ||
| Linia 2984: | Linia 3154: | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C81" style="font-size: 110%; font-weight: bold;">Twierdzenie C81</span><br/> | ||
Niech <math>a, b, c \in \mathbb{Z}</math>. Równanie <math>a x + b y = c</math> ma rozwiązanie wtedy i tylko wtedy, gdy największy wspólny dzielnik liczb <math>a</math> i <math>b</math> jest dzielnikiem liczby <math>c</math>. | Niech <math>a, b, c \in \mathbb{Z}</math>. Równanie <math>a x + b y = c</math> ma rozwiązanie wtedy i tylko wtedy, gdy największy wspólny dzielnik liczb <math>a</math> i <math>b</math> jest dzielnikiem liczby <math>c</math>. | ||
| Linia 2996: | Linia 3166: | ||
::<math>a x_0 + b y_0 = c</math> | ::<math>a x_0 + b y_0 = c</math> | ||
Ponieważ <math>D</math> dzieli lewą stronę równania, to musi również dzielić prawą, zatem musi być <math>D | Ponieważ <math>D</math> dzieli lewą stronę równania, to musi również dzielić prawą, zatem musi być <math>D \mid c</math>. | ||
<math>\Longleftarrow</math> | <math>\Longleftarrow</math> | ||
Jeżeli <math>D | Jeżeli <math>D \mid c</math>, to możemy napisać <math>c = k D</math> i równanie przyjmuje postać | ||
::<math>a x + b y = k D</math> | ::<math>a x + b y = k D</math> | ||
Lemat Bézouta (twierdzenie | Lemat Bézouta (twierdzenie [[#C78|C78]]) zapewnia istnienie liczb całkowitych <math>x_0</math> i <math>y_0</math> takich, że | ||
::<math>a x_0 + b y_0 = D</math> | ::<math>a x_0 + b y_0 = D</math> | ||
| Linia 3022: | Linia 3192: | ||
<span style="font-size: 110%; font-weight: bold;">Uwaga | <span id="C82" style="font-size: 110%; font-weight: bold;">Uwaga C82</span><br/> | ||
Z twierdzenia | Z twierdzenia [[#C81|C81]] wynika, że szukając rozwiązań równania <math>A x + B y = C</math> w liczbach całkowitych, powinniśmy | ||
:* obliczyć największy wspólny dzielnik <math>D</math> liczb <math>A</math> i <math>B</math> | :* obliczyć największy wspólny dzielnik <math>D</math> liczb <math>A</math> i <math>B</math> | ||
:* jeżeli <math>D > 1</math>, należy sprawdzić, czy <math>D | :* jeżeli <math>D > 1</math>, należy sprawdzić, czy <math>D \mid C</math> | ||
:* jeżeli <math>D \nmid C</math>, to równanie <math>A x + B y = C</math> nie ma rozwiązań w liczbach całkowitych | :* jeżeli <math>D \nmid C</math>, to równanie <math>A x + B y = C</math> nie ma rozwiązań w liczbach całkowitych | ||
:* jeżeli <math>D | :* jeżeli <math>D \mid C</math>, należy podzielić obie strony równania <math>A x + B y = C</math> przez <math>D</math> i przejść do rozwiązywania równania równoważnego <math>a x + b y = c</math>, gdzie <math>a = {\small\frac{A}{D}}</math>, <math>b = {\small\frac{B}{D}}</math>, <math>c = {\small\frac{C}{D}}</math>, zaś największy wspólny dzielnik liczb <math>a</math> i <math>b</math> jest równy <math>1</math>. | ||
<span style="font-size: 110%; font-weight: bold;">Twierdzenie | <span id="C83" style="font-size: 110%; font-weight: bold;">Twierdzenie C83</span><br/> | ||
Niech <math>a, b, c \in \mathbb{Z}</math>. Jeżeli liczby <math>a</math> i <math>b</math> są względnie pierwsze, to równanie | Niech <math>a, b, c \in \mathbb{Z}</math>. Jeżeli liczby <math>a</math> i <math>b</math> są względnie pierwsze, to równanie | ||
| Linia 3047: | Linia 3217: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Z założenia liczby <math>a</math> i <math>b</math> są względnie pierwsze, zatem największy wspólny dzielnik tych liczb jest równy <math>1</math> i dzieli liczbę <math>c</math>. Na mocy twierdzenia | Z założenia liczby <math>a</math> i <math>b</math> są względnie pierwsze, zatem największy wspólny dzielnik tych liczb jest równy <math>1</math> i dzieli liczbę <math>c</math>. Na mocy twierdzenia [[#C81|C81]] równanie | ||
::<math>a x + b y = c</math> | ::<math>a x + b y = c</math> | ||
| Linia 3075: | Linia 3245: | ||
Wynika stąd, że musi być spełniony warunek | Wynika stąd, że musi być spełniony warunek | ||
::<math>a(x - x_0) = b (y_0 - y)</math> | ::<math>a (x - x_0) = b (y_0 - y)</math> | ||
Ponieważ liczby <math>a</math> i <math>b</math> są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie | Ponieważ liczby <math>a \,</math> i <math>\, b</math> są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie [[#C79|C79]]) <math>b \mid (x - x_0)</math>. Skąd mamy | ||
::<math>x - x_0 = b t</math> | ::<math>x - x_0 = b t</math> | ||
| Linia 3091: | Linia 3261: | ||
<span style="font-size: 110%; font-weight: bold;">Przykład | <span id="C84" style="font-size: 110%; font-weight: bold;">Przykład C84</span><br/> | ||
Rozwiązania równania | Rozwiązania równania | ||
::<math>a x + b y = c</math> | ::<math>a x + b y = c</math> | ||
gdzie <math>\gcd (a, b) = 1</math>, które omówiliśmy w poprzednim twierdzeniu, najłatwiej znaleźć korzystając w PARI/GP z funkcji <code>gcdext(a, b)</code>. Funkcja ta zwraca wektor liczb <code>[x<sub>0</sub>, y<sub>0</sub>, d]</code>, gdzie <math>d = \gcd (a, b)</math>, a liczby <math>x_0</math> i <math>y_0</math> są rozwiązaniami równania | gdzie <math>\gcd (a, b) = 1</math>, które omówiliśmy w poprzednim twierdzeniu, najłatwiej znaleźć korzystając w PARI/GP z funkcji <span style="font-size: 90%; color:black;"><code>gcdext(a, b)</code></span>. Funkcja ta zwraca wektor liczb <span style="font-size: 90%; color:black;"><code>[x<sub>0</sub>, y<sub>0</sub>, d]</code></span>, gdzie <math>d = \gcd (a, b)</math>, a liczby <math>x_0</math> i <math>y_0</math> są rozwiązaniami równania | ||
::<math>a x_0 + b y_0 = \gcd (a, b)</math> | ::<math>a x_0 + b y_0 = \gcd (a, b)</math> | ||
| Linia 3104: | Linia 3274: | ||
::<math>a(c x_0) + b (c y_0) = c</math> | ::<math>a(c x_0) + b (c y_0) = c</math> | ||
Zatem para liczb całkowitych <math>(c x_0, c y_0)</math> jest jednym z rozwiązań równania | Zatem para liczb całkowitych <math>(c x_0, c y_0)</math> jest jednym z rozwiązań równania | ||
::<math>a x + b y = c</math> | ::<math>a x + b y = c</math> | ||
| Linia 3114: | Linia 3284: | ||
::<math>y = c y_0 - a t</math> | ::<math>y = c y_0 - a t</math> | ||
Niech <math>a = 7</math> i <math>b = 17</math>. Funkcja <code>gcdext(7,17)</code> zwraca wektor <code>[5, -2, 1]</code>, zatem rozwiązaniami równania <math>7 x + 17 y = 1</math> są liczby | Niech <math>a = 7 \;</math> i <math>\; b = 17</math>. Funkcja <span style="font-size: 90%; color:black;"><code>gcdext(7,17)</code></span> zwraca wektor <span style="font-size: 90%; color:black;"><code>[5, -2, 1]</code></span>, zatem rozwiązaniami równania <math>7 x + 17 y = 1</math> są liczby | ||
::<math>x = 5 + 17 t</math> | ::<math>x = 5 + 17 t</math> | ||
| Linia 3157: | Linia 3327: | ||
<ref name="Bombieri1">Enrico Bombieri, John B. Friedlander and Henryk Iwaniec, ''Primes in Arithmetic Progressions to Large Moduli. III'', Journal of the American Mathematical Society 2 (1989) 215-224</ref> | <ref name="Bombieri1">Enrico Bombieri, John B. Friedlander and Henryk Iwaniec, ''Primes in Arithmetic Progressions to Large Moduli. III'', Journal of the American Mathematical Society 2 (1989) 215-224</ref> | ||
<ref name="Turan1">Paul Turán, ''Über die Primzahlen der arithmetischen Progression'', Acta Sci. Szeged 8 (1937), 226-235</ref> | |||
<ref name="Wagstaff1">Samuel S. Wagstaff, Jr., ''Greatest of the Least Primes in Arithmetic Progressions Having a Given Modulus'', Mathematics of Computation Vol. 33, No. 147 (1979), 1073-1080</ref> | |||
<ref name="PAPWiki">Wikipedia, ''Primes in arithmetic progression'', ([https://en.wikipedia.org/wiki/Primes_in_arithmetic_progression Wiki-en])</ref> | <ref name="PAPWiki">Wikipedia, ''Primes in arithmetic progression'', ([https://en.wikipedia.org/wiki/Primes_in_arithmetic_progression Wiki-en])</ref> | ||
Aktualna wersja na dzień 17:59, 16 gru 2025
Ciągi nieskończone
Definicja C1
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Jeżeli każdej liczbie [math]\displaystyle{ n }[/math] przypiszemy pewną liczbę rzeczywistą [math]\displaystyle{ a_n }[/math], to powiemy, że liczby [math]\displaystyle{ a_1, a_2, \ldots, a_n, \ldots }[/math] tworzą ciąg nieskończony.
Uwaga C2
Ciąg nieskończony [math]\displaystyle{ a_1, a_2, \ldots, a_n, \ldots }[/math] będziemy oznaczać [math]\displaystyle{ (a_n) }[/math]. Często, o ile nie będzie prowadziło to do nieporozumień, ciąg nieskończony będziemy nazywać po prostu ciągiem.
Definicja C3
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Ciąg [math]\displaystyle{ (a_n) }[/math] będziemy nazywali
- ciągiem rosnącym, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} \geqslant a_n }[/math]
- ciągiem malejącym, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} \leqslant a_n }[/math]
Ciągi rosnące dzielimy na
- ciągi silnie rosnące, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} > a_n }[/math]
- ciągi słabo rosnące, jeżeli istnieją takie [math]\displaystyle{ n }[/math], że [math]\displaystyle{ a_{n + 1} = a_n }[/math]
Ciągi malejące dzielimy na
- ciągi silnie malejące, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} < a_n }[/math]
- ciągi słabo malejące, jeżeli istnieją takie [math]\displaystyle{ n }[/math], że [math]\displaystyle{ a_{n + 1} = a_n }[/math]
Zadanie C4
Niech [math]\displaystyle{ a \in \mathbb{R}_+ }[/math], [math]\displaystyle{ \, b \in \mathbb{R} \, }[/math] i [math]\displaystyle{ \, n \in \mathbb{Z}_+ }[/math]. Pokazać, że jeżeli ciąg [math]\displaystyle{ (u_n) }[/math] jest ciągiem silnie rosnącym dla [math]\displaystyle{ n > n_0 }[/math], to ciąg [math]\displaystyle{ v_n = a u_n + b }[/math] też jest ciągiem silnie rosnącym dla [math]\displaystyle{ n > n_0 }[/math]. Pokazać, że analogiczne stwierdzenie jest prawdziwe dla ciągów słabo rosnących, słabo malejących i silnie malejących.
Niech [math]\displaystyle{ n > n_0 }[/math], mamy
- [math]\displaystyle{ v_{n + 1} - v_n = (a u_{n + 1} + b) - (a u_n + b) = a (u_{n + 1} - u_n) > 0 }[/math]
Co należało pokazać.
□
Definicja C5
Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Liczbę [math]\displaystyle{ a }[/math] będziemy nazywali granicą ciągu [math]\displaystyle{ (a_n) }[/math], jeżeli dla dowolnego [math]\displaystyle{ \varepsilon }[/math] w przedziale [math]\displaystyle{ (a - \varepsilon, a + \varepsilon) }[/math] znajdują się prawie wszystkie wyrazy ciągu [math]\displaystyle{ (a_n) }[/math] (to znaczy wszystkie poza co najwyżej skończoną ilością).
Uwaga C6
1) sens definicji jest taki: jeżeli liczba [math]\displaystyle{ a }[/math] jest granicą ciągu [math]\displaystyle{ (a_n) }[/math], to dla dowolnie małego [math]\displaystyle{ \varepsilon > 0 }[/math], poza przedziałem [math]\displaystyle{ (a - \varepsilon, a + \varepsilon) }[/math] może się znaleźć co najwyżej skończona ilość wyrazów ciągu [math]\displaystyle{ (a_n) }[/math]
2) słabsze żądanie, aby w przedziale [math]\displaystyle{ (a - \varepsilon, a + \varepsilon) }[/math] znajdowała się nieskończona ilość wyrazów ciągu, nie prowadzi do poprawnej definicji granicy. Przykładowo, w przedziale [math]\displaystyle{ (1 - \varepsilon, 1 + \varepsilon) }[/math] znajduje się nieskończenie wiele wyrazów ciągu [math]\displaystyle{ a_n = (-1)^n }[/math], ale ani liczba [math]\displaystyle{ 1 }[/math], ani liczba [math]\displaystyle{ - 1 }[/math] nie są granicami tego ciągu. O ciągu [math]\displaystyle{ a_n = (- 1)^n }[/math] mówimy, że nie ma granicy.
3) ze względu na równoważność warunków
- [math]\displaystyle{ \quad a_n \in (a - \varepsilon, a + \varepsilon) }[/math]
- [math]\displaystyle{ \quad a - \varepsilon < a_n < a + \varepsilon }[/math]
- [math]\displaystyle{ \quad - \varepsilon < a_n - a < \varepsilon }[/math]
- [math]\displaystyle{ \quad | a_n - a | < \varepsilon }[/math]
definicja C5 może być wypowiedziana następująco
Definicja C7
Liczbę [math]\displaystyle{ a }[/math] będziemy nazywali granicą ciągu [math]\displaystyle{ (a_n) }[/math], jeżeli dla dowolnego [math]\displaystyle{ \varepsilon > 0 }[/math] prawie wszystkie wyrazy ciągu [math]\displaystyle{ (a_n) }[/math] spełniają warunek [math]\displaystyle{ |a_n - a| < \varepsilon }[/math].
Definicja C8
Ciąg [math]\displaystyle{ (a_n) }[/math] mający granicę (w rozumieniu definicji C5 lub C7) będziemy nazywali ciągiem zbieżnym, a fakt ten zapisujemy symbolicznie następująco
- [math]\displaystyle{ \lim_{n \to \infty} a_n = a }[/math] lub [math]\displaystyle{ a_n \longrightarrow a }[/math]
(od łacińskiego słowa limes oznaczającego granicę).
Zauważmy jeszcze, że wprost z definicji granicy wynika
Twierdzenie C9
- 1. [math]\displaystyle{ \quad \lim_{n \to \infty} a_n = a \qquad \iff \qquad \lim_{n \to \infty} (a_n - a) = 0 \qquad \iff \qquad \lim_{n \to \infty} | a_n - a | = 0 }[/math]
- 2. [math]\displaystyle{ \quad \lim_{n \to \infty} a_n = 0 \qquad \iff \qquad \lim_{n \to \infty} | a_n | = 0 }[/math]
- 3. [math]\displaystyle{ \quad \lim_{n \to \infty} a_n = a \qquad \implies \qquad \lim_{n \to \infty} | a_n | = | a | }[/math]
Punkt 1.
Prawdziwość twierdzenia wynika ze względu na identyczność warunków, które muszą spełniać prawie wszystkie wyrazy ciągu
- [math]\displaystyle{ | a_n - a | < \varepsilon \qquad \iff \qquad | (a_n - a) - 0 | < \varepsilon \qquad \iff \qquad \big|| a_n - a | - 0 \big| < \varepsilon }[/math]
Punkt 2.
Jest to jedynie szczególny przypadek punktu 1. dla [math]\displaystyle{ a = 0 }[/math].
Punkt 3.
Dla dowolnych liczb [math]\displaystyle{ x, y \in \mathbb{R} }[/math] prawdziwa jest nierówność
- [math]\displaystyle{ \big|| x | - | y | \big| \leqslant |x - y| }[/math]
Wynika stąd, że jeżeli dla prawie wszystkich wyrazów ciągu [math]\displaystyle{ (a_n) }[/math] spełniona jest nierówność [math]\displaystyle{ |a_n - a| < \varepsilon }[/math], to tym bardziej prawdą jest, że [math]\displaystyle{ \big|| a_n | - | a |\big| < \varepsilon }[/math]
□
Twierdzenie C10
Jeżeli ciąg [math]\displaystyle{ (a_n) }[/math] jest zbieżny, to jest ograniczony.
Z założenia ciąg [math]\displaystyle{ (a_n) }[/math] jest zbieżny, zatem możemy napisać, że [math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = a }[/math]. Z definicji granicy (zobacz C5, C7) dla dowolnego [math]\displaystyle{ \varepsilon > 0 }[/math] prawie wszystkie wyrazy ciągu [math]\displaystyle{ (a_n) }[/math] spełniają warunek [math]\displaystyle{ | a_n - a | < \varepsilon }[/math]. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od pewnego [math]\displaystyle{ N = N (\varepsilon) }[/math]. Zatem dla [math]\displaystyle{ n > N }[/math] jest
- [math]\displaystyle{ a - \varepsilon < a_n < a + \varepsilon }[/math]
Wynika stąd, że dla każdego [math]\displaystyle{ n \geqslant 1 }[/math] jest
- [math]\displaystyle{ m \leqslant a_n \leqslant M }[/math]
gdzie
- [math]\displaystyle{ M = \max (a_1, \ldots, a_N, a + \varepsilon) }[/math]
- [math]\displaystyle{ m = \min (a_1, \ldots, a_N, a - \varepsilon) }[/math]
Ponieważ [math]\displaystyle{ - | m | \leqslant m \; }[/math] i [math]\displaystyle{ \; M \leqslant | M | }[/math], to
- [math]\displaystyle{ - | m | \leqslant a_n \leqslant | M | }[/math]
Jeżeli oznaczymy [math]\displaystyle{ U = \max (| m |, | M |) }[/math], to możemy napisać
- [math]\displaystyle{ - U \leqslant a_n \leqslant U }[/math]
Czyli dla każdego [math]\displaystyle{ n \geqslant 1 }[/math] jest [math]\displaystyle{ | a_n | \leqslant U }[/math]. Co kończy dowód.
□
Twierdzenie C11 (twierdzenie o trzech ciągach)
Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n > N_0 }[/math] jest spełniony warunek
- [math]\displaystyle{ a_n \leqslant x_n \leqslant b_n }[/math]
oraz
- [math]\displaystyle{ \lim_{n \to \infty} a_n = \lim_{n \to \infty} b_n = g }[/math]
to [math]\displaystyle{ \lim_{n \to \infty} x_n = g }[/math].
Niech [math]\displaystyle{ \varepsilon }[/math] będzie dowolną, ustaloną liczbą większą od [math]\displaystyle{ 0 }[/math]. Z założenia prawie wszystkie wyrazy ciągu [math]\displaystyle{ (a_n) }[/math] spełniają warunek [math]\displaystyle{ |a_n - g| < \varepsilon }[/math]. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od wyrazu [math]\displaystyle{ N_a }[/math]. Podobnie prawie wszystkie wyrazy ciągu [math]\displaystyle{ (b_n) }[/math] spełniają warunek [math]\displaystyle{ |b_n - g| < \varepsilon }[/math] i podobnie możemy przyjąć, że są to wszystkie wyrazy, poczynając od wyrazu [math]\displaystyle{ N_b }[/math]
Nierówność [math]\displaystyle{ a_n \leqslant x_n \leqslant b_n }[/math] jest spełniona dla wszystkich wyrazów, poczynając od [math]\displaystyle{ N_0 }[/math], zatem oznaczając przez [math]\displaystyle{ M }[/math] największą z liczb [math]\displaystyle{ N_a }[/math], [math]\displaystyle{ N_b }[/math], [math]\displaystyle{ N_0 }[/math], możemy napisać, że o ile [math]\displaystyle{ n > M }[/math], to spełnione są jednocześnie nierówności
- [math]\displaystyle{ \quad g - \varepsilon < a_n < g + \varepsilon\ }[/math]
- [math]\displaystyle{ \quad g - \varepsilon < b_n < g + \varepsilon\ }[/math]
- [math]\displaystyle{ \quad a_n \leqslant x_n \leqslant b_n }[/math]
Z powyższych nierówności wynika natychmiast następujący ciąg nierówności
- [math]\displaystyle{ g - \varepsilon < a_n \leqslant x_n \leqslant b_n < g + \varepsilon }[/math]
Co oznacza, że dla [math]\displaystyle{ n > M }[/math] zachodzi
- [math]\displaystyle{ g - \varepsilon < x_n < g + \varepsilon }[/math]
Czyli prawie wszystkie wyrazy ciągu [math]\displaystyle{ (x_n) }[/math] spełniają warunek [math]\displaystyle{ |x_n - g| < \varepsilon }[/math]. Co kończy dowód.
□
Bez dowodu podamy kilka ważnych twierdzeń.
Twierdzenie C12*
Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ n }[/math] i rzeczywista [math]\displaystyle{ M }[/math], że dla każdego [math]\displaystyle{ k > n }[/math] jest
- [math]\displaystyle{ a_{k + 1}\geqslant a_k \qquad }[/math] oraz [math]\displaystyle{ \qquad a_k \leqslant M }[/math]
to ciąg [math]\displaystyle{ (a_k) }[/math] jest zbieżny.
Inaczej mówiąc: ciąg rosnący i ograniczony od góry jest zbieżny.
Twierdzenie C13*
Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ n }[/math] i rzeczywista [math]\displaystyle{ M }[/math], że dla każdego [math]\displaystyle{ k > n }[/math] jest
- [math]\displaystyle{ a_{k + 1} \leqslant a_k \qquad }[/math] oraz [math]\displaystyle{ \qquad a_k \geqslant M }[/math]
to ciąg [math]\displaystyle{ (a_k) }[/math] jest zbieżny.
Inaczej mówiąc: ciąg malejący i ograniczony od dołu jest zbieżny.
Twierdzenie C14*
Jeżeli [math]\displaystyle{ \lim_{n \to \infty} a_n = a }[/math] oraz [math]\displaystyle{ \lim_{n \to \infty} b_n = b }[/math], gdzie [math]\displaystyle{ a, b }[/math] są dowolnymi liczbami rzeczywistymi, to
- [math]\displaystyle{ \quad \lim_{n \to \infty} (a_n \pm b_n) = a \pm b }[/math]
- [math]\displaystyle{ \quad \lim_{n \to \infty} (a_n \cdot b_n) = a \cdot b }[/math]
Jeżeli dodatkowo dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ b_n \neq 0 }[/math] i [math]\displaystyle{ b \neq 0 }[/math], to
- 3. [math]\displaystyle{ \quad \lim_{n \to \infty} {\small\frac{a_n}{b_n}} = {\small\frac{a}{b}} }[/math]
Twierdzenie C15
Jeżeli [math]\displaystyle{ \lim_{n \to \infty} a_n = 0 }[/math], zaś ciąg [math]\displaystyle{ (x_n) }[/math] jest ograniczony, czyli istnieje taka liczba [math]\displaystyle{ M > 0 }[/math], że dla każdej wartości [math]\displaystyle{ n }[/math] prawdziwa jest nierówność [math]\displaystyle{ | x_n | < M }[/math], to
- [math]\displaystyle{ \lim_{n \to \infty} (x_n \cdot a_n) = 0 }[/math]
Wystarczy pokazać, że (zobacz twierdzenie C9 p.2)
- [math]\displaystyle{ \lim_{n \to \infty} |x_n \cdot a_n| = 0 }[/math]
Z założenia prawdziwe jest oszacowanie
- [math]\displaystyle{ 0 \leqslant |x_n \cdot a_n| \leqslant |a_n| \cdot M }[/math]
Zatem z twierdzenia o trzech ciągach otrzymujemy natychmiast, że
- [math]\displaystyle{ \lim_{n \to \infty} |x_n \cdot a_n| = 0 }[/math]
Co kończy dowód.
□
Twierdzenie C16
Dla [math]\displaystyle{ a \geqslant 0 }[/math] i [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwa jest nierówność
- [math]\displaystyle{ (1 + a)^{1 / n} \leqslant 1 + {\small\frac{a}{n}} }[/math]
Wzór jest prawdziwy dla [math]\displaystyle{ a = 0 }[/math]. Zakładając, że [math]\displaystyle{ a > 0 }[/math] i korzystając ze wzoru dwumianowego, mamy dla [math]\displaystyle{ n \geqslant 1 }[/math]
- [math]\displaystyle{ \left( 1 + {\small\frac{a}{n}} \right)^n = \sum_{k=0}^{n} \left [ {\small\binom{n}{k}} \cdot \left ( {\small\frac{a}{n}} \right )^k \right ] \geqslant }[/math]
- [math]\displaystyle{ \;\; \geqslant \sum_{k=0}^{1} \left [ {\small\binom{n}{k}} \cdot \left ( {\small\frac{a}{n}} \right )^k \right ] = }[/math]
- [math]\displaystyle{ \;\; = 1 + n \cdot {\small\frac{a}{n}} = }[/math]
- [math]\displaystyle{ \;\; = 1 + a }[/math]
- [math]\displaystyle{ \left( 1 + {\small\frac{a}{n}} \right)^n = \sum_{k=0}^{n} \left [ {\small\binom{n}{k}} \cdot \left ( {\small\frac{a}{n}} \right )^k \right ] \geqslant }[/math]
Co należało pokazać.
□
Twierdzenie C17
Jeżeli [math]\displaystyle{ A > 0 }[/math], to [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]{A} = 1 }[/math].
Dla [math]\displaystyle{ A > 1 }[/math] możemy napisać [math]\displaystyle{ A = 1 + a }[/math], gdzie [math]\displaystyle{ a > 0 }[/math], wtedy z twierdzenia C16 otrzymujemy
- [math]\displaystyle{ 1 < \sqrt[n]{A} = (1 + a)^{1 / n} \leqslant 1 + {\small\frac{a}{n}} }[/math]
Z twierdzenia o trzech ciągach dostajemy natychmiast (dla [math]\displaystyle{ A > 1 }[/math])
- [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]{A} = 1 }[/math]
W przypadku gdy [math]\displaystyle{ 0 < A < 1 }[/math], możemy napisać [math]\displaystyle{ A = {\small\frac{1}{B}} }[/math], gdzie [math]\displaystyle{ B > 1 }[/math], wtedy ze względu na udowodniony wyżej rezultat [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]{B} = 1 }[/math]
- [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]{A} = \lim_{n \to \infty} {\small\frac{1}{\sqrt[n]{B}}} = \frac{1}{\underset{n \rightarrow \infty}{\lim} \sqrt[n]{B}} = 1 }[/math]
Jeżeli [math]\displaystyle{ A = 1 }[/math], to [math]\displaystyle{ \sqrt[n]{A} = 1 }[/math] dla każdego [math]\displaystyle{ n \geqslant 1 }[/math]. Co kończy dowód.
□
Twierdzenie C18
Jeżeli prawie wszystkie wyrazy ciągu [math]\displaystyle{ (a_n) }[/math] spełniają warunek [math]\displaystyle{ 0 < m < a_n < M }[/math], to [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]{a_n} = 1 }[/math]
Z założenia dla prawie wszystkich wyrazów ciągu [math]\displaystyle{ (a_n) }[/math] jest
- [math]\displaystyle{ 0 < m \leqslant a_n \leqslant M }[/math]
Zatem dla prawie wszystkich wyrazów ciągu [math]\displaystyle{ a_n }[/math] mamy
- [math]\displaystyle{ \sqrt[n]{m} \leqslant \sqrt[n]{a_n} \leqslant \sqrt[n]{M} }[/math]
Z twierdzenia C17 wiemy, że [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]{m} = \lim_{n \to \infty} \sqrt[n]{M} = 1 }[/math], zatem na podstawie twierdzenia o trzech ciągach otrzymujemy natychmiast [math]\displaystyle{ \lim_{n \to \infty} \sqrt[n]{a_n} = 1 }[/math]
□
Twierdzenie C19
Następujące ciągi są silnie rosnące i zbieżne
[math]\displaystyle{ \quad 1. \quad }[/math] [math]\displaystyle{ \lim_{n \to \infty} \left( 1 + {\small\frac{1}{n}} \right)^n = e = 2.718281828 \ldots }[/math] [math]\displaystyle{ \quad 2. \quad }[/math] [math]\displaystyle{ \lim_{n \to \infty} \left( 1 - {\small\frac{1}{n}} \right)^n = {\small\frac{1}{e}} = 0.367879441 \ldots }[/math]
Punkt 1
W twierdzeniu A6 pokazaliśmy, że ciąg
- [math]\displaystyle{ a_n = \left( 1 + {\small\frac{1}{n}} \right)^n }[/math]
jest silnie rosnący i ograniczony od góry. Zatem z twierdzenia C12 wynika, że jest zbieżny. Liczbę będącą granicą tego ciągu oznaczamy literą [math]\displaystyle{ e }[/math], jest ona podstawą logarytmu naturalnego.
Punkt 2
Pokażemy najpierw, że ciąg [math]\displaystyle{ \left( 1 - {\small\frac{1}{n}} \right)^n }[/math] jest silnie rosnący. Musimy pokazać, że prawdziwa jest nierówność
- [math]\displaystyle{ \left( 1 - {\small\frac{1}{n + 1}} \right)^{n + 1} > \left( 1 - {\small\frac{1}{n}} \right)^n }[/math]
Łatwo sprawdzamy prawdziwość nierówności dla [math]\displaystyle{ n = 1 }[/math]. Załóżmy teraz, że [math]\displaystyle{ n \geqslant 2 }[/math]. Przekształcając,
- [math]\displaystyle{ \left( {\small\frac{n}{n + 1}} \right)^{n + 1} > \left( {\small\frac{n - 1}{n}} \right)^n }[/math]
- [math]\displaystyle{ {\small\frac{n}{n + 1}} \cdot \left( {\small\frac{n}{n + 1}} \right)^n \cdot \left( {\small\frac{n}{n - 1}} \right)^n > 1 }[/math]
- [math]\displaystyle{ \left( {\small\frac{n^2}{n^2 - 1}} \right)^n > {\small\frac{n + 1}{n}} }[/math]
otrzymujemy nierówność równoważną,
- [math]\displaystyle{ \left( 1 + {\small\frac{1}{n^2 - 1}} \right)^n > 1 + {\small\frac{1}{n}} }[/math]
którą już łatwo udowodnić, bo
- [math]\displaystyle{ \left( 1 + {\small\frac{1}{n^2 - 1}} \right)^n > \left( 1 + {\small\frac{1}{n^2}} \right)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} \cdot \left( {\small\frac{1}{n^2}} \right)^k > \sum_{k = 0}^{1} {\small\binom{n}{k}} \cdot {\small\frac{1}{n^{2k}}} = 1 + {\small\frac{1}{n}} }[/math]
Ponieważ dla każdego [math]\displaystyle{ n \geqslant 1 }[/math] jest [math]\displaystyle{ \left( 1 - {\small\frac{1}{n}} \right)^n \leqslant 1 }[/math] (bo iloczyn liczb mniejszych od [math]\displaystyle{ 1 }[/math] nie może być liczbą większą do jedności), to z twierdzenia C12 wynika, że ciąg ten jest zbieżny. Zatem możemy napisać
- [math]\displaystyle{ \underset{n \rightarrow \infty}{\lim} \left( 1 - {\small\frac{1}{n}} \right)^n = g }[/math]
Rozważmy teraz iloczyn wypisanych w twierdzeniu ciągów
- [math]\displaystyle{ \left( 1 + {\small\frac{1}{n}} \right)^n \cdot \left( 1 - {\small\frac{1}{n}} \right)^n = \left( 1 - {\small\frac{1}{n^2}} \right)^n = \left[ \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \right]^{1 / n} }[/math]
Łatwo widzimy, że ciąg [math]\displaystyle{ \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} }[/math] jest podciągiem ciągu [math]\displaystyle{ \left( 1 - {\small\frac{1}{n}} \right)^n }[/math], zatem jest ograniczony i dla [math]\displaystyle{ n \geqslant 2 }[/math] spełniony jest układ nierówności
- [math]\displaystyle{ 0 < \left( {\small\frac{3}{4}} \right)^4 \leqslant \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \leqslant 1 }[/math]
Z twierdzenia C18 dostajemy
- [math]\displaystyle{ \lim_{n \to \infty} \left[ \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \right]^{1 / n} = 1 }[/math]
Z twierdzenia C14 p. 2 wynika natychmiast, że
- [math]\displaystyle{ e \cdot g = \lim_{n \to \infty} \left[ \left( 1 + {\small\frac{1}{n}} \right)^n \cdot \left( 1 - {\small\frac{1}{n}} \right)^n \right] = \lim_{n \to \infty} \left[ \left( 1 - {\small\frac{1}{n^2}} \right)^{n^2} \right]^{1 / n} = 1 }[/math]
Zatem [math]\displaystyle{ g = {\small\frac{1}{e}} }[/math].
□
Twierdzenie C20
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe są następujące nierówności
[math]\displaystyle{ \quad 1. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{n + 1}} < \log \left( 1 + {\small\frac{1}{n}} \right) < {\small\frac{1}{n}} }[/math] [math]\displaystyle{ \quad 2. \quad }[/math] [math]\displaystyle{ - {\small\frac{1}{n - 1}} < \log \left( 1 - {\small\frac{1}{n}} \right) < - {\small\frac{1}{n}} }[/math]
Ponieważ ciąg [math]\displaystyle{ \left( 1 + {\small\frac{1}{n}} \right)^n }[/math] jest silnie rosnący, to
- [math]\displaystyle{ \left( 1 + {\small\frac{1}{n}} \right)^n < e }[/math]
Logarytmując powyższą nierówność, mamy
- [math]\displaystyle{ n \cdot \log \left( 1 + {\small\frac{1}{n}} \right) < 1 }[/math]
Stąd wynika natychmiast, że
- [math]\displaystyle{ \log \left( 1 + {\small\frac{1}{n}} \right) < {\small\frac{1}{n}} }[/math]
Ponieważ ciąg [math]\displaystyle{ \left( 1 - {\small\frac{1}{n}} \right)^n }[/math] również jest silnie rosnący, to postępując analogicznie, dostajemy
- [math]\displaystyle{ \left( 1 - {\small\frac{1}{n}} \right)^n < {\small\frac{1}{e}} }[/math]
- [math]\displaystyle{ n \cdot \log \left( 1 - {\small\frac{1}{n}} \right) < - 1 }[/math]
- [math]\displaystyle{ \log \left( 1 - {\small\frac{1}{n}} \right) < - {\small\frac{1}{n}} }[/math]
Przekształcając otrzymane wzory, otrzymujemy
- [math]\displaystyle{ - \log \left( 1 + {\small\frac{1}{n}} \right) = - \log \left( {\small\frac{n + 1}{n}} \right) = \log \left( {\small\frac{n}{n + 1}} \right) = \log \left( 1 - {\small\frac{1}{n + 1}} \right) < - {\small\frac{1}{n + 1}} }[/math]
oraz
- [math]\displaystyle{ - \log \left( 1 - {\small\frac{1}{n}} \right) = - \log \left( {\small\frac{n - 1}{n}} \right) = \log \left( {\small\frac{n}{n - 1}} \right) = \log \left( 1 + {\small\frac{1}{n - 1}} \right) < {\small\frac{1}{n - 1}} }[/math]
- [math]\displaystyle{ - \log \left( 1 - {\small\frac{1}{n}} \right) = - \log \left( {\small\frac{n - 1}{n}} \right) = \log \left( {\small\frac{n}{n - 1}} \right) = \log \left( 1 + {\small\frac{1}{n - 1}} \right) < {\small\frac{1}{n - 1}} }[/math]
□
Liczby pierwsze w ciągach arytmetycznych
Twierdzenie C21
Każda liczba naturalna [math]\displaystyle{ n \geqslant 2 }[/math] jest liczbą pierwszą lub iloczynem liczb pierwszych.
Pierwszy sposób
Przypuśćmy, że istnieją liczby naturalne większe od [math]\displaystyle{ 1 }[/math], które nie są liczbami pierwszymi ani nie są iloczynami liczb pierwszych. Niech [math]\displaystyle{ m }[/math] oznacza najmniejszą[1] z takich liczb. Z założenia [math]\displaystyle{ m }[/math] nie jest liczbą pierwszą, zatem [math]\displaystyle{ m }[/math] może być zapisana w postaci [math]\displaystyle{ m = a \cdot b }[/math], gdzie liczby [math]\displaystyle{ a, b }[/math] są liczbami naturalnymi mniejszymi od [math]\displaystyle{ m }[/math].
Ponieważ [math]\displaystyle{ m }[/math] jest najmniejszą liczbą naturalną, która nie jest liczbą pierwszą ani nie jest iloczynem liczb pierwszych, to liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] muszą być liczbami złożonymi, ale jako mniejsze od [math]\displaystyle{ m }[/math] są one iloczynami liczb pierwszych, zatem i liczba [math]\displaystyle{ m }[/math] musi być iloczynem liczb pierwszych.
Uzyskana sprzeczność dowodzi, że nasze przypuszczenie jest fałszywe.
Drugi sposób
Indukcja matematyczna. Twierdzenie jest oczywiście prawdziwe dla [math]\displaystyle{ n = 2 }[/math].
Zakładając, że twierdzenie jest prawdziwe dla wszystkich liczb naturalnych [math]\displaystyle{ k \in [2, n] }[/math], dla liczby [math]\displaystyle{ n + 1 }[/math] mamy dwie możliwości
- [math]\displaystyle{ n + 1 }[/math] jest liczbą pierwszą (wtedy twierdzenie jest prawdziwe w sposób oczywisty)
- [math]\displaystyle{ n + 1 }[/math] jest liczbą złożoną wtedy, [math]\displaystyle{ n + 1 = a b }[/math], gdzie [math]\displaystyle{ 1 < a, b < n + 1 }[/math]; zatem na podstawie założenia indukcyjnego liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są liczbami pierwszymi lub iloczynami liczb pierwszych, czyli [math]\displaystyle{ n + 1 = a b }[/math] jest iloczynem liczb pierwszych.
Co należało pokazać.
□
Twierdzenie C22 (Euklides, IV w. p.n.e.)
Istnieje nieskończenie wiele liczb pierwszych.
Przypuśćmy, że istnieje jedynie skończona ilość liczb pierwszych [math]\displaystyle{ p_1, p_2, \ldots, p_n }[/math] . Wtedy liczba [math]\displaystyle{ a = p_1 \cdot p_2 \cdot \ldots \cdot p_n + 1 }[/math] jest większa od jedności i z twierdzenia C21 wynika, że posiada dzielnik będący liczbą pierwszą, ale jak łatwo zauważyć żadna z liczb pierwszych [math]\displaystyle{ p_1, p_2, \ldots, p_n }[/math] nie jest dzielnikiem liczby [math]\displaystyle{ a }[/math]. Zatem istnieje liczba pierwsza [math]\displaystyle{ p }[/math] będąca dzielnikiem pierwszym liczby [math]\displaystyle{ a }[/math] i różna od każdej z liczb [math]\displaystyle{ p_1, p_2, \ldots, p_n }[/math]. Co kończy dowód.
□
Twierdzenie C23
Jeżeli liczba naturalna [math]\displaystyle{ n }[/math] jest postaci [math]\displaystyle{ 4 k + 3 }[/math][2], to ma dzielnik postaci [math]\displaystyle{ 4 k + 3 }[/math] będący liczbą pierwszą.
Jeżeli [math]\displaystyle{ n }[/math] jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy zatem sytuację, gdy [math]\displaystyle{ n }[/math] jest liczbą złożoną. Z założenia [math]\displaystyle{ n }[/math] jest liczbą nieparzystą, zatem możliwe są trzy typy iloczynów
- [math]\displaystyle{ (4 a + 1) (4 b + 1) = 16 a b + 4 a + 4 b + 1 = 4 (4 a b + a + b) + 1 }[/math]
- [math]\displaystyle{ (4 a + 1) (4 b + 3) = 16 a b + 12 a + 4 b + 3 = 4 (4 a b + 3 a + b) + 3 }[/math]
- [math]\displaystyle{ (4 a + 3) (4 b + 3) = 16 a b + 12 a + 12 b + 9 = 4 (4 a b + 3 a + 3 b + 2) + 1 }[/math]
Widzimy, że liczba złożona postaci [math]\displaystyle{ 4 k + 3 }[/math] jest iloczynem liczb postaci [math]\displaystyle{ 4 k + 1 }[/math] i [math]\displaystyle{ 4 k + 3 }[/math]. Wynika stąd natychmiast, że liczba złożona postaci [math]\displaystyle{ 4 k + 3 }[/math] posiada dzielnik postaci [math]\displaystyle{ 4 k + 3 }[/math]. Niech [math]\displaystyle{ q }[/math] oznacza najmniejszy dzielnik liczby [math]\displaystyle{ n }[/math] postaci [math]\displaystyle{ 4 k + 3 }[/math]. Pokażemy, że [math]\displaystyle{ q }[/math] jest liczbą pierwszą. Istotnie, gdyby [math]\displaystyle{ q }[/math] była liczbą złożoną, to miałaby dzielnik [math]\displaystyle{ d }[/math] postaci [math]\displaystyle{ 4 k + 3 }[/math] i byłoby [math]\displaystyle{ d < q }[/math], wbrew założeniu, że [math]\displaystyle{ q }[/math] jest najmniejszym dzielnikiem liczby [math]\displaystyle{ n }[/math] postaci [math]\displaystyle{ 4 k + 3 }[/math]. Co kończy dowód.
□
Twierdzenie C24
Istnieje nieskończenie wiele liczb pierwszych postaci [math]\displaystyle{ 4 k + 3 }[/math].
Przypuśćmy, że istnieje tylko skończona ilość liczb pierwszych postaci [math]\displaystyle{ 4 k + 3 }[/math]. Niech będą to liczby [math]\displaystyle{ p_1, \ldots, p_s }[/math]. Liczba
- [math]\displaystyle{ M = 4 p_1 \cdot \ldots \cdot p_s - 1 = 4 (p_1 \cdot \ldots \cdot p_s - 1) + 3 }[/math]
jest postaci [math]\displaystyle{ 4 k + 3 }[/math] i jak wiemy z twierdzenia C23, ma dzielnik pierwszy [math]\displaystyle{ q }[/math] postaci [math]\displaystyle{ 4 k + 3 }[/math]. Ale jak łatwo zauważyć, żadna z liczb [math]\displaystyle{ p_1, \ldots, p_s }[/math] nie dzieli liczby [math]\displaystyle{ M }[/math]. Zatem istnieje liczba pierwsza [math]\displaystyle{ q }[/math] postaci [math]\displaystyle{ 4 k + 3 }[/math] różna od każdej z liczb [math]\displaystyle{ p_1, p_2, \ldots, p_s }[/math]. Otrzymana sprzeczność kończy dowód.
□
Twierdzenie C25
Jeżeli liczba naturalna [math]\displaystyle{ n }[/math] jest postaci [math]\displaystyle{ 6 k + 5 }[/math], to ma dzielnik postaci [math]\displaystyle{ 6 k + 5 }[/math] będący liczbą pierwszą.
Jeżeli [math]\displaystyle{ n }[/math] jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy sytuację, gdy [math]\displaystyle{ n }[/math] jest liczbą złożoną. Z twierdzenia C21 wiemy, że w tym przypadku liczba [math]\displaystyle{ n }[/math] będzie iloczynem liczb pierwszych. Zauważmy, że nieparzyste liczby pierwsze mogą być jedynie postaci [math]\displaystyle{ 6 k + 1 }[/math] lub [math]\displaystyle{ 6 k + 5 }[/math] (liczba [math]\displaystyle{ 6 k + 3 }[/math] jest liczbą złożoną). Ponieważ iloczyn liczb postaci [math]\displaystyle{ 6 k + 1 }[/math]
- [math]\displaystyle{ (6 a + 1) (6 b + 1) = 36 a b + 6 a + 6 b + 1 = 6 (6 a b + a + b) + 1 }[/math]
jest liczbą postaci [math]\displaystyle{ 6 k + 1 }[/math], to w rozkładzie liczby [math]\displaystyle{ n }[/math] na czynniki pierwsze musi pojawić się przynajmniej jeden czynnik postaci [math]\displaystyle{ 6 k + 5 }[/math]. Co kończy dowód.
□
Twierdzenie C26
Istnieje nieskończenie wiele liczb pierwszych postaci [math]\displaystyle{ 6 k + 5 }[/math].
Przypuśćmy, że istnieje tylko skończona ilość liczb pierwszych postaci [math]\displaystyle{ 6 k + 5 }[/math]. Niech będą to liczby [math]\displaystyle{ p_1, \ldots, p_s }[/math]. Liczba
- [math]\displaystyle{ M = 6 p_1 \cdot \ldots \cdot p_s - 1 = 6 (p_1 \cdot \ldots \cdot p_s - 1) + 5 }[/math]
jest postaci [math]\displaystyle{ 6 k + 5 }[/math] i ma dzielnik pierwszy [math]\displaystyle{ q }[/math] postaci [math]\displaystyle{ 6 k + 5 }[/math] (zobacz C25). Ale jak łatwo zauważyć żadna z liczb [math]\displaystyle{ p_1, \ldots, p_s }[/math] nie dzieli liczby [math]\displaystyle{ M }[/math]. Zatem istnieje liczba pierwsza [math]\displaystyle{ q }[/math] postaci [math]\displaystyle{ 6 k + 5 }[/math] różna od każdej z liczb [math]\displaystyle{ p_1, p_2, \ldots, p_s }[/math]. Otrzymana sprzeczność kończy dowód.
□
Twierdzenie C27
Istnieje nieskończenie wiele liczb pierwszych postaci [math]\displaystyle{ 3 k + 2 }[/math].
Jeżeli [math]\displaystyle{ k = 2 j }[/math] jest liczbą parzystą, to otrzymujemy ciąg liczb parzystych
- [math]\displaystyle{ 3 k + 2 = 6 j + 2 }[/math]
w którym jedynie liczba [math]\displaystyle{ 2 }[/math] jest liczbą pierwszą (dla [math]\displaystyle{ j = 0 }[/math]).
Jeżeli [math]\displaystyle{ k = 2 j + 1 }[/math] jest liczbą nieparzystą, to otrzymujemy ciąg liczb nieparzystych
- [math]\displaystyle{ 3 k + 2 = 3 (2 j + 1) + 2 = 6 j + 5 }[/math]
o którym wiemy, że zawiera nieskończenie wiele liczb pierwszych (zobacz twierdzenie C26). Zatem w ciągu arytmetycznym postaci [math]\displaystyle{ 3 k + 2 }[/math] występuje nieskończenie wiele liczb pierwszych.
□
Uwaga C28
Zauważmy, że liczby postaci [math]\displaystyle{ 2 k + 1 }[/math] to wszystkie liczby nieparzyste dodatnie. Ponieważ wszystkie liczby pierwsze (poza liczbą [math]\displaystyle{ 2 }[/math]) są liczbami nieparzystymi, to wśród liczb postaci [math]\displaystyle{ 2 k + 1 }[/math] występuje nieskończenie wiele liczb pierwszych.
Wszystkie omówione wyżej przypadki ciągów arytmetycznych: [math]\displaystyle{ 2 k + 1 }[/math], [math]\displaystyle{ 3 k + 2 }[/math], [math]\displaystyle{ 4 k + 3 }[/math] i [math]\displaystyle{ 6 k + 5 }[/math], w których występuje nieskończona ilość liczb pierwszych są szczególnymi przypadkami udowodnionego w 1837 roku twierdzenia
Twierdzenie C29* (Peter Gustav Lejeune Dirichlet, 1837)
Niech [math]\displaystyle{ a \in \mathbb{Z}_+ }[/math] i [math]\displaystyle{ b \in \mathbb{Z} }[/math]. Jeżeli liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze, to w ciągu arytmetycznym [math]\displaystyle{ a k + b }[/math] występuje nieskończenie wiele liczb pierwszych.
Uwaga C30
Dowód twierdzenia Dirichleta jest bardzo trudny. Natomiast bardzo łatwo można pokazać, że dowolny ciąg arytmetyczny [math]\displaystyle{ a k + b }[/math] zawiera nieskończenie wiele liczb złożonych. Istotnie, jeżeli liczby [math]\displaystyle{ a, b }[/math] nie są względnie pierwsze, to wszystkie wyrazy ciągu są liczbami złożonymi. Jeżeli [math]\displaystyle{ a, b }[/math] są względnie pierwsze i [math]\displaystyle{ b > 1 , }[/math] to wystarczy przyjąć [math]\displaystyle{ k = b t }[/math]. Jeżeli są względnie pierwsze i [math]\displaystyle{ b = 1 }[/math], to wystarczy przyjąć [math]\displaystyle{ k = a t^2 + 2 t }[/math], wtedy
- [math]\displaystyle{ a k + 1 = a^2 t^2 + 2 a t + 1 = (a t + 1)^2 }[/math]
Uwaga C31
Wiemy już, że w przypadku gdy liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze, to w ciągu arytmetycznym [math]\displaystyle{ a k + b }[/math] występuje nieskończenie wiele liczb pierwszych. Pojawia się pytanie o to, czy możliwe jest oszacowanie najmniejszej liczby pierwszej [math]\displaystyle{ p }[/math] w takim ciągu. Jakkolwiek przypuszczamy, że prawdziwe jest oszacowanie [math]\displaystyle{ p < a^2 }[/math], to stan naszej obecnej wiedzy ujmuje twierdzenie Linnika[3][4][5][6], które podajemy niżej. Trzeba było ponad pół wieku wysiłku wielu matematyków, aby pokazać, że w twierdzeniu Linnika możemy przyjąć [math]\displaystyle{ L = 5 }[/math][7]. Bombieri, Friedlander i Iwaniec udowodnili[8], że dla prawie wszystkich liczb [math]\displaystyle{ a }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ L \leqslant 2 }[/math].
Twierdzenie C32* (Jurij Linnik, 1944)
Niech [math]\displaystyle{ a, b \in \mathbb{Z}_+ }[/math] i [math]\displaystyle{ p_{\min} (a, b) }[/math] oznacza najmniejszą liczbę pierwszą w ciągu arytmetycznym [math]\displaystyle{ a k + b }[/math], gdzie [math]\displaystyle{ k \in \mathbb{Z}_+ }[/math]. Jeżeli [math]\displaystyle{ \gcd (a, b) = 1 }[/math] i [math]\displaystyle{ b \in [1, a - 1] }[/math], to istnieją takie stałe [math]\displaystyle{ L > 0 }[/math] i [math]\displaystyle{ a_0 \geqslant 2 }[/math], że dla wszystkich [math]\displaystyle{ a > a_0 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ p_{\min} (a, b) < a^L }[/math]
Zadanie C33
Pokazać, że z twierdzenia Linnika wynika istnienie takich stałych [math]\displaystyle{ c, L > 0 }[/math], że dla każdego [math]\displaystyle{ a \geqslant 2 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ p(a) < c a^L }[/math]
gdzie
- [math]\displaystyle{ p(a) = \underset{\gcd (a, b) = 1}{\max_{1 \leqslant b < a}} p_{\min} (a, b) }[/math]
Oszacowanie podane w twierdzeniu Linnika
- [math]\displaystyle{ p_{\min} (a, b) < a^L }[/math]
jest prawdziwe dla dowolnej liczby [math]\displaystyle{ b \in [1, a - 1] }[/math] względnie pierwszej z [math]\displaystyle{ a }[/math]. Jeżeli zdefiniujemy funkcję
- [math]\displaystyle{ p(a) = \underset{\gcd (a, b) = 1}{\max_{1 \leqslant b < a}} p_{\min} (a, b) }[/math]
to możemy zapisać twierdzenie Linnika tak, aby po lewej stronie nie występowała liczba [math]\displaystyle{ b }[/math], co czyni zapis bardziej przejrzystym. Mamy
- [math]\displaystyle{ p(a) < a^L }[/math]
dla wszystkich [math]\displaystyle{ a > a_0 }[/math]. Ponieważ dla [math]\displaystyle{ a \in [2, a_0] }[/math] funkcja [math]\displaystyle{ p(a) }[/math] przyjmuje wartości skończone, a dla [math]\displaystyle{ a > a_0 }[/math] jest [math]\displaystyle{ p(a) < a^L }[/math], to funkcja [math]\displaystyle{ {\small\frac{p (a)}{a^L}} }[/math] jest ograniczona od góry, czyli istnieje taka stała [math]\displaystyle{ c }[/math], że
- [math]\displaystyle{ {\small\frac{p (a)}{a^L}} < c }[/math]
dla dowolnego [math]\displaystyle{ a \geqslant 2 }[/math]. Co należało pokazać.
□
Przykład C34
Pokazaliśmy (zobacz C33), że istnieją takie stałe [math]\displaystyle{ c, L > 0 }[/math], że dla każdego [math]\displaystyle{ a \geqslant 2 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ p(a) < c a^L }[/math]
gdzie
- [math]\displaystyle{ p(a) = \underset{\gcd (a, b) = 1}{\max_{1 \leqslant b < a}} p_{\min} (a, b) }[/math]
Ponieważ [math]\displaystyle{ p(a) > a }[/math], to prawdziwy jest ciąg nierówności
- [math]\displaystyle{ 1 < {\small\frac{\log p (a)}{\log a}} < {\small\frac{\log c}{\log a}} + L \leqslant \left| {\small\frac{\log c}{\log a}} \right| + L \leqslant {\small\frac{\left| \log c \right|}{\log 2}} + L }[/math]
Wynika stąd, że dla [math]\displaystyle{ a \geqslant 2 }[/math] funkcja [math]\displaystyle{ {\small\frac{\log p (a)}{\log a}} }[/math] jest ograniczona.
Na zamieszczonym niżej obrazku przedstawiono pierwszych czternaście punktów funkcji [math]\displaystyle{ {\small\frac{\log p (a)}{\log a}} }[/math]. Ze względu na skokowy charakter zmian tej funkcji najwygodniej będzie przedstawić jej wykres, pokazując jedynie jej maksymalne i minimalne wartości w wybranych podprzedziałach [math]\displaystyle{ \mathbb{Z}_+ }[/math]. Mówiąc precyzyjnie, zamieszczone zostały wykresy funkcji
- [math]\displaystyle{ f(t) = \max_{2^t \leqslant a < 2^{t + 1}} {\small\frac{\log p (a)}{\log a}} \qquad \qquad \qquad \qquad g(t) = \min_{2^t \leqslant a < 2^{t + 1}} {\small\frac{\log p (a)}{\log a}} \qquad \qquad \qquad \qquad h(a) = 1 + {\small\frac{2 \log \log a}{\log a}} }[/math]
gdzie [math]\displaystyle{ t \in \mathbb{Z}_+ }[/math].
W tabeli przedstawiamy dane, na podstawie których sporządziliśmy zamieszczony wyżej wykres. Mamy kolejno
- przedział [math]\displaystyle{ U }[/math]
- minimalną wartość [math]\displaystyle{ {\small\frac{\log p(a)}{\log a}} }[/math] w przedziale [math]\displaystyle{ U }[/math]
- liczbę [math]\displaystyle{ a }[/math], która odpowiada minimalnej wartości [math]\displaystyle{ {\small\frac{\log p(a)}{\log a}} }[/math]
- wartość [math]\displaystyle{ p(a) = \underset{\gcd (a, b) = 1}{\max_{1 \leqslant b < a}} p_{\min} (a, b) }[/math]
- liczbę [math]\displaystyle{ b }[/math] taką, że najmniejsza liczba pierwsza w ciągu [math]\displaystyle{ a k + b }[/math] jest równa [math]\displaystyle{ p ( a ) }[/math]
Następnie podajemy analogiczne wartości dla maksymalnej wartości [math]\displaystyle{ {\small\frac{\log p(a)}{\log a}} }[/math] w przedziale [math]\displaystyle{ U }[/math]. Pominęliśmy dane dla początkowych przedziałów [math]\displaystyle{ [2^{n},2^{n + 1}) }[/math], ponieważ Czytelnik z łatwością policzy je samodzielnie. Prosty kod do obliczeń w PARI/GP zamieściliśmy pod tabelą.
[math]\displaystyle{ \boldsymbol{U} }[/math] [math]\displaystyle{ \boldsymbol{\min_{a \in U} {\small\frac{\log p(a)}{\log a}}} }[/math] [math]\displaystyle{ \boldsymbol{a} }[/math] [math]\displaystyle{ \boldsymbol{p(a)} }[/math] [math]\displaystyle{ \boldsymbol{b} }[/math] [math]\displaystyle{ \boldsymbol{\max_{a \in U} {\small\frac{\log p(a)}{\log a}}} }[/math] [math]\displaystyle{ \boldsymbol{a} }[/math] [math]\displaystyle{ \boldsymbol{p(a)} }[/math] [math]\displaystyle{ \boldsymbol{b} }[/math] [math]\displaystyle{ [2^{12},2^{13}) }[/math] [math]\displaystyle{ 1.273691 }[/math] [math]\displaystyle{ 6840 }[/math] [math]\displaystyle{ 76679 }[/math] [math]\displaystyle{ 1439 }[/math] [math]\displaystyle{ 1.574826 }[/math] [math]\displaystyle{ 4177 }[/math] [math]\displaystyle{ 503771 }[/math] [math]\displaystyle{ 2531 }[/math] [math]\displaystyle{ [2^{13},2^{14}) }[/math] [math]\displaystyle{ 1.265227 }[/math] [math]\displaystyle{ 14490 }[/math] [math]\displaystyle{ 183949 }[/math] [math]\displaystyle{ 10069 }[/math] [math]\displaystyle{ 1.551307 }[/math] [math]\displaystyle{ 8941 }[/math] [math]\displaystyle{ 1348387 }[/math] [math]\displaystyle{ 7237 }[/math] [math]\displaystyle{ [2^{14},2^{15}) }[/math] [math]\displaystyle{ 1.257880 }[/math] [math]\displaystyle{ 20790 }[/math] [math]\displaystyle{ 269987 }[/math] [math]\displaystyle{ 20507 }[/math] [math]\displaystyle{ 1.519764 }[/math] [math]\displaystyle{ 22133 }[/math] [math]\displaystyle{ 4012709 }[/math] [math]\displaystyle{ 6636 }[/math] [math]\displaystyle{ [2^{15},2^{16}) }[/math] [math]\displaystyle{ 1.247285 }[/math] [math]\displaystyle{ 39270 }[/math] [math]\displaystyle{ 537157 }[/math] [math]\displaystyle{ 26647 }[/math] [math]\displaystyle{ 1.500736 }[/math] [math]\displaystyle{ 40951 }[/math] [math]\displaystyle{ 8352037 }[/math] [math]\displaystyle{ 38984 }[/math] [math]\displaystyle{ [2^{16},2^{17}) }[/math] [math]\displaystyle{ 1.244884 }[/math] [math]\displaystyle{ 106260 }[/math] [math]\displaystyle{ 1808207 }[/math] [math]\displaystyle{ 1787 }[/math] [math]\displaystyle{ 1.477806 }[/math] [math]\displaystyle{ 84229 }[/math] [math]\displaystyle{ 19005359 }[/math] [math]\displaystyle{ 53834 }[/math] [math]\displaystyle{ [2^{17},2^{18}) }[/math] [math]\displaystyle{ 1.243658 }[/math] [math]\displaystyle{ 150150 }[/math] [math]\displaystyle{ 2740469 }[/math] [math]\displaystyle{ 37769 }[/math] [math]\displaystyle{ 1.474387 }[/math] [math]\displaystyle{ 132331 }[/math] [math]\displaystyle{ 35588503 }[/math] [math]\displaystyle{ 123795 }[/math] [math]\displaystyle{ [2^{18},2^{19}) }[/math] [math]\displaystyle{ 1.233771 }[/math] [math]\displaystyle{ 510510 }[/math] [math]\displaystyle{ 11024723 }[/math] [math]\displaystyle{ 304013 }[/math] [math]\displaystyle{ 1.457138 }[/math] [math]\displaystyle{ 297491 }[/math] [math]\displaystyle{ 94537921 }[/math] [math]\displaystyle{ 233274 }[/math] [math]\displaystyle{ [2^{19},2^{20}) }[/math] [math]\displaystyle{ 1.233150 }[/math] [math]\displaystyle{ 1021020 }[/math] [math]\displaystyle{ 25706531 }[/math] [math]\displaystyle{ 181031 }[/math] [math]\displaystyle{ 1.437418 }[/math] [math]\displaystyle{ 596081 }[/math] [math]\displaystyle{ 200230391 }[/math] [math]\displaystyle{ 543256 }[/math] [math]\displaystyle{ [2^{20},2^{21}) }[/math] [math]\displaystyle{ 1.231259 }[/math] [math]\displaystyle{ 2072070 }[/math] [math]\displaystyle{ 59859383 }[/math] [math]\displaystyle{ 1841423 }[/math] [math]\displaystyle{ 1.419752 }[/math] [math]\displaystyle{ 1181311 }[/math] [math]\displaystyle{ 418069567 }[/math] [math]\displaystyle{ 1066784 }[/math] [math]\displaystyle{ [2^{21},2^{22}) }[/math] [math]\displaystyle{ 1.224444 }[/math] [math]\displaystyle{ 3543540 }[/math] [math]\displaystyle{ 104573173 }[/math] [math]\displaystyle{ 1810513 }[/math] [math]\displaystyle{ 1.405843 }[/math] [math]\displaystyle{ 2753747 }[/math] [math]\displaystyle{ 1131160207 }[/math] [math]\displaystyle{ 2123937 }[/math]
pmin(a, b) =
\\ zwraca najmniejszą liczbę pierwszą w ciągu a*k + b, gdzie k >= 1 i gcd(a, b) = 1
{
local(k, p);
k = 1;
p = a*k + b;
while( !isprime(p), p = a*(k++) + b );
return(p);
}
PMAX(a) =
\\ zwraca największą ze wszystkich najmniejszych liczb pierwszych
\\ w ciągach a*k + b, gdzie k >= 1, 0 < b < a i gcd(a, b) = 1
{
local(b, p, w);
w = [0, 0];
b = 0;
while( b++ < a,
if( gcd(a, b) > 1, next() );
p = pmin(a, b);
if( w[1] < p, w = [p, b] );
);
return(w);
}
Linnik(n) =
\\ n >= 1, sprawdzamy przedział U = [ 2^n , 2^(n + 1) ), czyli 2^n <= a < 2^(n+1)
{
local(a, b, p4a, sep, txt, w, y, Ymin, Ymax);
sep = ", "; \\ separator
Ymin = [100, 1, 0, 0]; \\ najmniejsza wartość funkcji log( p(a) ) / log(a) w przedziale U
Ymax = [0, 1, 0, 0]; \\ największa wartość funkcji log( p(a) ) / log(a) w przedziale U
a = 2^n - 1;
while( a++ < 2^(n+1),
w = PMAX(a);
p4a = w[1];
b = w[2];
y = log(p4a) / log(a);
if( y < Ymin[1], Ymin = [y, a, p4a, b] );
if( y > Ymax[1], Ymax = [y, a, p4a, b] );
);
txt = Str(n, sep, Ymin[1], sep, Ymin[2], sep, Ymin[3], sep, Ymin[4], sep, Ymax[1], sep, Ymax[2], sep, Ymax[3], sep, Ymax[4]);
print(txt);
}
Przypuszczamy, że prawdziwe jest znacznie silniejsze oszacowanie najmniejszej liczby pierwszej w ciągu arytmetycznym[9][10]
- [math]\displaystyle{ p(a) \sim a \log^2 \! a }[/math]
W takim przypadku mielibyśmy
- [math]\displaystyle{ {\small\frac{\log p (a)}{\log a}} \sim 1 + {\small\frac{2 \log \log a}{\log a}} }[/math]
Rzeczywiście, porównanie wykresów funkcji [math]\displaystyle{ f(t) }[/math] i [math]\displaystyle{ h(a) }[/math] wydaje się potwierdzać to przypuszczenie dla [math]\displaystyle{ a \in [2, 2^{22}] }[/math].
W tabeli zestawiliśmy wszystkie wartości funkcji [math]\displaystyle{ {\small\frac{\log p (a)}{\log a}} }[/math] większe od [math]\displaystyle{ 1.75 }[/math] dla [math]\displaystyle{ a \in [2, 2^{22}] }[/math]
[math]\displaystyle{ \boldsymbol{a} }[/math] [math]\displaystyle{ \boldsymbol{\log_2 \! a} }[/math] [math]\displaystyle{ \boldsymbol{p(a)} }[/math] [math]\displaystyle{ \boldsymbol{{\small\frac{\log p(a)}{\log a}}} }[/math] [math]\displaystyle{ 31 }[/math] [math]\displaystyle{ 4.95 }[/math] [math]\displaystyle{ 577 }[/math] [math]\displaystyle{ 1.851446 }[/math] [math]\displaystyle{ 5 }[/math] [math]\displaystyle{ 2.32 }[/math] [math]\displaystyle{ 19 }[/math] [math]\displaystyle{ 1.829482 }[/math] [math]\displaystyle{ 13 }[/math] [math]\displaystyle{ 3.70 }[/math] [math]\displaystyle{ 103 }[/math] [math]\displaystyle{ 1.806947 }[/math] [math]\displaystyle{ 47 }[/math] [math]\displaystyle{ 5.55 }[/math] [math]\displaystyle{ 967 }[/math] [math]\displaystyle{ 1.785437 }[/math] [math]\displaystyle{ 19 }[/math] [math]\displaystyle{ 4.24 }[/math] [math]\displaystyle{ 191 }[/math] [math]\displaystyle{ 1.783794 }[/math] [math]\displaystyle{ 61 }[/math] [math]\displaystyle{ 5.93 }[/math] [math]\displaystyle{ 1511 }[/math] [math]\displaystyle{ 1.780771 }[/math] [math]\displaystyle{ 11 }[/math] [math]\displaystyle{ 3.46 }[/math] [math]\displaystyle{ 71 }[/math] [math]\displaystyle{ 1.777675 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 1.58 }[/math] [math]\displaystyle{ 7 }[/math] [math]\displaystyle{ 1.771243 }[/math]
Rozważmy zbiór [math]\displaystyle{ S }[/math] takich liczb [math]\displaystyle{ a }[/math], że prawdziwe jest oszacowanie [math]\displaystyle{ p (a) < a \log^2 \! a }[/math]. Bez trudu możemy podać przykłady takich liczb, ale nie wiemy, czy jest ich nieskończenie wiele.
[math]\displaystyle{ \boldsymbol{n} }[/math] [math]\displaystyle{ \boldsymbol{a=p_1 \cdot \ldots \cdot p_n} }[/math] [math]\displaystyle{ \boldsymbol{\log_2 \! a} }[/math] [math]\displaystyle{ \boldsymbol{p(a)} }[/math] [math]\displaystyle{ \boldsymbol{{\small\frac{a \log^2 \! a}{p(a)}}} }[/math] [math]\displaystyle{ \boldsymbol{{\small\frac{\log p(a)}{\log a}}} }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ 6 }[/math] [math]\displaystyle{ 2.584 }[/math] [math]\displaystyle{ 11 }[/math] [math]\displaystyle{ 1.751 }[/math] [math]\displaystyle{ 1.338290 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 30 }[/math] [math]\displaystyle{ 4.906 }[/math] [math]\displaystyle{ 79 }[/math] [math]\displaystyle{ 4.392 }[/math] [math]\displaystyle{ 1.284679 }[/math] [math]\displaystyle{ 4 }[/math] [math]\displaystyle{ 210 }[/math] [math]\displaystyle{ 7.714 }[/math] [math]\displaystyle{ 761 }[/math] [math]\displaystyle{ 7.889 }[/math] [math]\displaystyle{ 1.240789 }[/math] [math]\displaystyle{ 5 }[/math] [math]\displaystyle{ 2310 }[/math] [math]\displaystyle{ 11.173 }[/math] [math]\displaystyle{ 20477 }[/math] [math]\displaystyle{ 6.766 }[/math] [math]\displaystyle{ 1.281737 }[/math] [math]\displaystyle{ 6 }[/math] [math]\displaystyle{ 30030 }[/math] [math]\displaystyle{ 14.874 }[/math] [math]\displaystyle{ 520547 }[/math] [math]\displaystyle{ 6.132 }[/math] [math]\displaystyle{ 1.276692 }[/math] [math]\displaystyle{ 7 }[/math] [math]\displaystyle{ 510510 }[/math] [math]\displaystyle{ 18.961 }[/math] [math]\displaystyle{ 11024723 }[/math] [math]\displaystyle{ 7.999 }[/math] [math]\displaystyle{ 1.233770 }[/math] [math]\displaystyle{ 8 }[/math] [math]\displaystyle{ 9699690 }[/math] [math]\displaystyle{ 23.209 }[/math] [math]\displaystyle{ 375095881 }[/math] [math]\displaystyle{ 6.692 }[/math] [math]\displaystyle{ 1.227199 }[/math] [math]\displaystyle{ 9 }[/math] [math]\displaystyle{ 223092870 }[/math] [math]\displaystyle{ 27.733 }[/math] [math]\displaystyle{ 11799966613 }[/math] [math]\displaystyle{ 6.986 }[/math] [math]\displaystyle{ 1.206432 }[/math] [math]\displaystyle{ 10 }[/math] [math]\displaystyle{ 6469693230 }[/math] [math]\displaystyle{ 32.591 }[/math] [math]\displaystyle{ 451404994867 }[/math] [math]\displaystyle{ 7.314 }[/math] [math]\displaystyle{ 1.187922 }[/math] [math]\displaystyle{ 11 }[/math] [math]\displaystyle{ 200560490130 }[/math] [math]\displaystyle{ 37.545 }[/math] [math]\displaystyle{ 19822720510961 }[/math] [math]\displaystyle{ 6.852 }[/math] [math]\displaystyle{ 1.176506 }[/math] [math]\displaystyle{ 12 }[/math] [math]\displaystyle{ 7420738134810 }[/math] [math]\displaystyle{ 42.754 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]
Ponieważ [math]\displaystyle{ p(a) > a }[/math], to prawdziwy jest układ nierówności
- [math]\displaystyle{ 1 < {\small\frac{\log p (a)}{\log a}} < 1 + {\small\frac{2 \log \log a}{\log a}} }[/math]
Jeżeli zbiór [math]\displaystyle{ S }[/math] jest nieskończony, to z twierdzenia o trzech ciągach otrzymujemy
- [math]\displaystyle{ \underset{a \in S}{\lim_{a \rightarrow \infty}} {\small\frac{\log p (a)}{\log a}} = 1 }[/math]
W konsekwencji wykres funkcji
- [math]\displaystyle{ g(t) = \underset{2^t \leqslant a < 2^{t + 1}}{\min} {\small\frac{\log p (a)}{\log a}} }[/math]
będzie opadał ku prostej [math]\displaystyle{ y = 1 }[/math].
Zadanie C35
Pokazać, że istnieje nieskończenie wiele liczb pierwszych zakończonych cyframi 99, przykładowo 199, 499, 599, 1399, 1499, ...
Wszystkie liczby naturalne zakończone cyframi [math]\displaystyle{ 99 }[/math] możemy zapisać w postaci [math]\displaystyle{ a_n = 100 k + 99 }[/math], gdzie [math]\displaystyle{ k \in \mathbb{N} }[/math]. Ponieważ ciąg [math]\displaystyle{ (a_n) }[/math] jest ciągiem arytmetycznym, a liczby [math]\displaystyle{ 99 }[/math] i [math]\displaystyle{ 100 }[/math] są względnie pierwsze, to na podstawie twierdzenia Dirichleta stwierdzamy, że istnieje nieskończenie wiele liczb pierwszych zakończonych cyframi [math]\displaystyle{ 99 }[/math].
□
Definicja C36
Niech [math]\displaystyle{ a \geqslant 2 }[/math] będzie liczbą całkowitą. Wartość funkcji [math]\displaystyle{ \pi(n; a, b) }[/math] jest równa ilości liczb pierwszych nie większych od [math]\displaystyle{ n }[/math], które przy dzieleniu przez [math]\displaystyle{ a }[/math] dają resztę [math]\displaystyle{ b }[/math].
Uwaga C37
Zauważmy, że w twierdzeniu Dirichleta na liczby [math]\displaystyle{ a }[/math] oraz [math]\displaystyle{ b }[/math] nałożone są minimalne warunki: [math]\displaystyle{ a \in \mathbb{Z}_+ }[/math] i [math]\displaystyle{ b \in \mathbb{Z} }[/math]. Sytuacja w przypadku funkcji [math]\displaystyle{ \pi (n ; a, b) }[/math] jest odmienna – tutaj mamy [math]\displaystyle{ a \geqslant 2 }[/math] oraz [math]\displaystyle{ 0 \leqslant b \leqslant a - 1 }[/math]. Jest tak dlatego, że podział liczb pierwszych, który odzwierciedla funkcja [math]\displaystyle{ \pi (n ; a, b) }[/math], jest podziałem pierwotnym, a twierdzenie Dirichleta jest tylko jego uzasadnieniem. Podział
liczb pierwszych musi być też precyzyjnie określony, tak aby zachodził naturalny związek
- [math]\displaystyle{ \sum_{b = 0}^{a - 1} \pi (n ; a, b) = \pi (n) }[/math]
Oczywiście nie przeszkadza to w liczeniu liczb pierwszych w dowolnym ciągu arytmetycznym. Niech na przykład
- [math]\displaystyle{ u_k = 7 k + 101 = 7 (k + 14) + 3 \qquad }[/math] gdzie [math]\displaystyle{ k = 0, 1, \ldots }[/math]
Ilość liczb pierwszych w ciagu [math]\displaystyle{ (u_k) }[/math] jest równa
- [math]\displaystyle{ \pi (n ; 7, 3) - \pi (7 \cdot 13 + 3 ; 7, 3) = \pi (n ; 7, 3) - 5 }[/math]
Zadanie C38
Pokazać, że dla dowolnej liczby całkowitej [math]\displaystyle{ m \geqslant 1 }[/math]
- wśród liczb naturalnych zawsze można wskazać [math]\displaystyle{ m }[/math] kolejnych liczb, które są złożone
- w ciągu arytmetycznym [math]\displaystyle{ a k + b }[/math], gdzie liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze, zawsze można wskazać [math]\displaystyle{ m }[/math] kolejnych wyrazów, które są złożone
Punkt 1.
W przypadku liczb naturalnych łatwo widzimy, że kolejne liczby
- [math]\displaystyle{ (m + 1) ! + 2, \quad (m + 1) ! + 3, \quad \ldots, \quad (m + 1) ! + (m + 1) }[/math]
są liczbami złożonymi. Co oznacza, że dla dowolnej liczby naturalnej [math]\displaystyle{ m }[/math] zawsze możemy wskazać taką liczbę [math]\displaystyle{ n }[/math], że [math]\displaystyle{ p_{n + 1} - p_n > m }[/math].
Punkt 2.
W przypadku ciągu arytmetycznego [math]\displaystyle{ u_k = a k + b }[/math] rozważmy kolejne wyrazy ciągu począwszy od wskaźnika
- [math]\displaystyle{ k_0 = \prod^{m - 1}_{j = 0} (a j + b) }[/math]
Łatwo zauważamy, że dla [math]\displaystyle{ k = k_0, k_0 + 1, \ldots, k_0 + (m - 1) }[/math] wyrazy ciągu arytmetycznego [math]\displaystyle{ u_k = a k + b }[/math] są liczbami złożonymi. Istotnie, niech [math]\displaystyle{ t = 0, 1, \ldots, m - 1 }[/math] wtedy
- [math]\displaystyle{ u_k = a k + b = }[/math]
- [math]\displaystyle{ \! = a (k_0 + t) + b = }[/math]
- [math]\displaystyle{ \! = a k_0 + (a t + b) = }[/math]
- [math]\displaystyle{ \! = a \prod^{m - 1}_{j = 0} (a j + b) + (a t + b) }[/math]
i liczba [math]\displaystyle{ a t + b }[/math] dzieli iloczyn [math]\displaystyle{ \prod^{m - 1}_{j = 0} (a j + b) }[/math] dla [math]\displaystyle{ t = 0, \ldots, m - 1 }[/math]. Co należało pokazać.
Wiemy, że jeżeli liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze, to w ciągu [math]\displaystyle{ a k + b }[/math] występuje nieskończenie wiele liczb pierwszych. Niech będą to liczby [math]\displaystyle{ q_1, q_2, \ldots, q_r, \ldots }[/math]. Uzyskany rezultat oznacza, że dla dowolnej liczby naturalnej [math]\displaystyle{ m }[/math] zawsze możemy wskazać taką liczbę [math]\displaystyle{ n }[/math], że [math]\displaystyle{ q_{n + 1} - q_n \geqslant a (m + 1) }[/math]
□
Przykład C39
Rozważmy ciąg arytmetyczny [math]\displaystyle{ u_k = 3 k + 2 }[/math] i wskaźnik
- [math]\displaystyle{ k_0 = \prod^{12}_{j = 0} (3 j + 2) = 3091650738176000 }[/math]
Trzynaście wyrazów tego szeregu dla [math]\displaystyle{ k = k_0 + t }[/math], gdzie [math]\displaystyle{ t = 0, 1, \ldots, 12 }[/math] to oczywiście liczby złożone, ale wyrazy dla [math]\displaystyle{ k = k_0 - 1 }[/math] i [math]\displaystyle{ k = k_0 + 13 }[/math] są liczbami pierwszymi.
Przeszukując ciąg [math]\displaystyle{ u_k = 3 k + 2 }[/math], możemy łatwo znaleźć, że pierwsze trzynaście kolejnych wyrazów złożonych pojawia się już dla [math]\displaystyle{ k = 370, 371, \ldots, 382 }[/math].
Twierdzenie C40
Jeżeli [math]\displaystyle{ n \geqslant 3 }[/math], to istnieje [math]\displaystyle{ n }[/math] kolejnych liczb naturalnych, wśród których znajduje się dokładnie [math]\displaystyle{ r \leqslant \pi (n) }[/math] liczb pierwszych.
Warunek [math]\displaystyle{ n \geqslant 3 }[/math] nie wynika z potrzeb dowodu, a jedynie pomija sytuacje nietypowe, których twierdzenie nie obejmuje. Zawsze istnieje jedna liczba naturalna, która jest liczbą pierwszą i łatwo możemy wskazać dwie kolejne liczby naturalne będące liczbami pierwszymi.
Niech [math]\displaystyle{ k \in \mathbb{N} }[/math]. Wartość funkcji
- [math]\displaystyle{ Q(k, n) = \pi (k + n) - \pi (k) }[/math]
jest równa ilości liczb pierwszych wśród [math]\displaystyle{ n }[/math] kolejnych liczb naturalnych od liczby [math]\displaystyle{ k + 1 }[/math] do liczby [math]\displaystyle{ k + n }[/math].
Uwzględniając, że wypisane niżej wyrażenia w nawiasach kwadratowych mogą przyjmować jedynie dwie wartości [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], dostajemy
- [math]\displaystyle{ \biggl| Q (k + 1, n) - Q (k, n) \biggr| = \biggl| \bigl[\pi (k + n + 1) - \pi (k + n) \bigr] - \bigl[\pi (k + 1) - \pi (k) \bigr] \biggr| \leqslant 1 }[/math]
Ponadto mamy
- [math]\displaystyle{ Q(0, n) = \pi (n) \qquad }[/math] bo [math]\displaystyle{ \pi (0) = 0 }[/math]
- [math]\displaystyle{ Q((n + 1) ! + 1, n) = 0 \qquad }[/math] bo liczby [math]\displaystyle{ (n + 1) ! + 2, \ldots, (n + 1) ! + (n + 1) }[/math] są liczbami złożonymi
Ponieważ wartości funkcji [math]\displaystyle{ Q(k, n) }[/math] mogą zmieniać się tylko o [math]\displaystyle{ - 1 }[/math], [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to [math]\displaystyle{ Q(k, n) }[/math] musi przyjmować wszystkie wartości całkowite od [math]\displaystyle{ 0 }[/math] do [math]\displaystyle{ \pi (n) }[/math]. Wynika stąd, że istnieje taka liczba [math]\displaystyle{ k_r }[/math], że [math]\displaystyle{ Q(k_r, n) = r }[/math], gdzie [math]\displaystyle{ 0 \leqslant r \leqslant \pi (n) }[/math].
Fragment wykresu funkcji [math]\displaystyle{ Q(k, 10) }[/math]. Widzimy, że dla [math]\displaystyle{ k = 113 }[/math] po raz pierwszy mamy [math]\displaystyle{ Q(k, 10) = 0 }[/math], a funkcja [math]\displaystyle{ Q(k, 10) }[/math] przyjmuje wszystkie wartości całkowite od [math]\displaystyle{ 0 }[/math] do [math]\displaystyle{ 5 }[/math].
□
Przykład C41
Czytelnik może łatwo sprawdzić, że ciąg [math]\displaystyle{ ( 1308, \ldots, 1407 ) }[/math] stu kolejnych liczb całkowitych zawiera dokładnie [math]\displaystyle{ 8 }[/math] liczb pierwszych.
Zadanie C42
Pokazać, nie korzystając z twierdzenia C40, że istnieje [math]\displaystyle{ 1000 }[/math] kolejnych liczb naturalnych, wśród których jest dokładnie jedna liczba pierwsza.
Zauważmy, że [math]\displaystyle{ 1000 }[/math] kolejnych liczb naturalnych
- [math]\displaystyle{ 1001! + 2, 1001! + 3, \ldots, 1001! + 1001 }[/math]
nie zawiera żadnej liczby pierwszej. Wielokrotnie zmniejszając wszystkie wypisane wyżej liczby o jeden, aż do chwili, gdy pierwsza z wypisanych liczb będzie liczbą pierwszą, uzyskamy [math]\displaystyle{ 1000 }[/math] kolejnych liczb naturalnych, wśród których jest dokładnie jedna liczba pierwsza.
Uwaga: dopiero liczba [math]\displaystyle{ 1001! - 1733 }[/math] jest pierwsza.
□
Zadanie C43
Pokazać, że istnieje [math]\displaystyle{ 20 }[/math] kolejnych liczb naturalnych postaci [math]\displaystyle{ 6 k + 1 }[/math], wśród których jest dokładnie [math]\displaystyle{ 5 }[/math] liczb pierwszych.
Rozwiązywanie zadania rozpoczniemy od dwóch spostrzeżeń
- wśród pierwszych [math]\displaystyle{ 20 }[/math] liczb naturalnych postaci [math]\displaystyle{ 6 k + 1 }[/math] jest [math]\displaystyle{ 13 }[/math] liczb pierwszych
- w ciągu [math]\displaystyle{ 6 k + 1 }[/math] istnieją dowolnie długie przedziały pozbawione liczb pierwszych (zobacz zadanie C38), zatem istnieje [math]\displaystyle{ 20 }[/math] kolejnych liczb naturalnych postaci [math]\displaystyle{ 6 k + 1 }[/math], wśród których nie ma ani jednej liczby pierwszej
Pierwsze spostrzeżenie pokazuje, że rozwiązanie problemu jest potencjalnie możliwe. Rozwiązanie mogłoby nie istnieć, gdybyśmy szukali [math]\displaystyle{ 20 }[/math] liczb naturalnych postaci [math]\displaystyle{ 6 k + 1 }[/math], wśród których jest, powiedzmy, [math]\displaystyle{ 15 }[/math] liczb pierwszych.
Drugie spostrzeżenie mówi nam, że ilość liczb pierwszych wśród kolejnych [math]\displaystyle{ 20 }[/math] liczb naturalnych postaci [math]\displaystyle{ 6 k + 1 }[/math] zmienia się od [math]\displaystyle{ 13 }[/math] do [math]\displaystyle{ 0 }[/math]. Analiza przebiegu tych zmian jest kluczem do dowodu twierdzenia.
Zbadajmy zatem, jak zmienia się ilość liczb pierwszych wśród kolejnych [math]\displaystyle{ 20 }[/math] liczb naturalnych postaci [math]\displaystyle{ 6 k + 1 }[/math]. Rozważmy ciąg [math]\displaystyle{ a_k = 6 k + 1 }[/math], gdzie [math]\displaystyle{ k = 0, 1, 2, \ldots }[/math]
[math]\displaystyle{ (a_k) = (1, \mathbf{7}, \mathbf{13}, \mathbf{19}, 25, \mathbf{31}, \mathbf{37}, \mathbf{43}, 49, 55, \mathbf{61}, \mathbf{67}, \mathbf{73}, \mathbf{79}, 85, 91, \mathbf{97}, \mathbf{103}, \mathbf{109}, 115, 121, \mathbf{127}, 133, \mathbf{139}, 145, \mathbf{151}, \mathbf{157}, \mathbf{163}, 169, 175, \mathbf{181}, 187, \mathbf{193}, \mathbf{199}, 205, \mathbf{211}, \ldots) }[/math]
Liczby pierwsze zostały pogrubione.
Niech [math]\displaystyle{ (B^n) }[/math] będzie fragmentem ciągu [math]\displaystyle{ (a_k) }[/math] rozpoczynającym się od [math]\displaystyle{ n }[/math]-tego wyrazu ciągu i złożonym z [math]\displaystyle{ 20 }[/math] kolejnych wyrazów ciągu [math]\displaystyle{ (a_k) }[/math]. Przykładowo mamy
[math]\displaystyle{ (B^1) = (1, \mathbf{7}, \mathbf{13}, \mathbf{19}, 25, \mathbf{31}, \mathbf{37}, \mathbf{43}, 49, 55, \mathbf{61}, \mathbf{67}, \mathbf{73}, \mathbf{79}, 85, 91, \mathbf{97}, \mathbf{103}, \mathbf{109}, 115 ) }[/math]
[math]\displaystyle{ (B^2) = ( \mathbf{7}, \mathbf{13}, \mathbf{19}, 25, \mathbf{31}, \mathbf{37}, \mathbf{43}, 49, 55, \mathbf{61}, \mathbf{67}, \mathbf{73}, \mathbf{79}, 85, 91, \mathbf{97}, \mathbf{103}, \mathbf{109}, 115, 121 ) }[/math]
[math]\displaystyle{ (B^3) = ( \mathbf{13}, \mathbf{19}, 25, \mathbf{31}, \mathbf{37}, \mathbf{43}, 49, 55, \mathbf{61}, \mathbf{67}, \mathbf{73}, \mathbf{79}, 85, 91, \mathbf{97}, \mathbf{103}, \mathbf{109}, 115, 121, \mathbf{127} ) }[/math]
Musimy zrozumieć, jak przejście od ciągu [math]\displaystyle{ (B^n) }[/math] do ciągu [math]\displaystyle{ (B^{n + 1}) }[/math]
wpływa na ilość liczb pierwszych w tych ciągach.
- jeżeli najmniejszy wyraz ciągu [math]\displaystyle{ (B^n) }[/math] jest liczbą złożoną, to po przejściu do ciągu [math]\displaystyle{ (B^{n + 1}) }[/math] ilość liczb pierwszych w tym ciągu w stosunku do ilości liczb pierwszych w ciągu [math]\displaystyle{ (B^n) }[/math] może
- pozostać bez zmian (w przypadku, gdy największy wyraz ciągu [math]\displaystyle{ (B^{n + 1}) }[/math] jest liczbą złożoną)
- zwiększyć się o jeden (w przypadku, gdy największy wyraz ciągu [math]\displaystyle{ (B^{n + 1}) }[/math] jest liczbą pierwszą)
- jeżeli najmniejszy wyraz ciągu [math]\displaystyle{ (B^n) }[/math] jest liczbą pierwszą, to po przejściu do ciągu [math]\displaystyle{ (B^{n + 1}) }[/math] ilość liczb pierwszych w tym ciągu w stosunku do ilości liczb pierwszych w ciągu [math]\displaystyle{ (B^n) }[/math] może
- zmniejszyć się o jeden (w przypadku, gdy największy wyraz ciągu [math]\displaystyle{ (B^{n + 1}) }[/math] jest liczbą złożoną)
- pozostać bez zmian (w przypadku, gdy największy wyraz ciągu [math]\displaystyle{ (B^{n + 1}) }[/math] jest liczbą pierwszą)
Wynika stąd, że przechodząc od ciągu [math]\displaystyle{ (B^n) }[/math] do ciągu [math]\displaystyle{ (B^{n + 1}) }[/math], ilość liczb pierwszych może się zmienić o [math]\displaystyle{ - 1 }[/math], [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math]. Z drugiego ze spostrzeżeń uczynionych na początku dowodu wynika istnienie takiej liczby [math]\displaystyle{ r }[/math], że wśród ciągów
- [math]\displaystyle{ (B^1), (B^2), \ldots, (B^r) }[/math]
ilość liczb pierwszych będzie przyjmowała wszystkie możliwe wartości od liczby [math]\displaystyle{ 13 }[/math] do liczby [math]\displaystyle{ 0 }[/math]. Co zapewnia istnienie takich [math]\displaystyle{ 20 }[/math] kolejnych liczb naturalnych postaci [math]\displaystyle{ 6 k + 1 }[/math], że wśród nich jest dokładnie [math]\displaystyle{ 5 }[/math] liczb pierwszych.
□
Twierdzenie C44
Niech [math]\displaystyle{ a, b \in \mathbb{Z} }[/math] oraz [math]\displaystyle{ a \geqslant 2 }[/math] i [math]\displaystyle{ 0 \leqslant b \leqslant a - 1 }[/math]. Jeżeli liczby [math]\displaystyle{ a }[/math] oraz [math]\displaystyle{ b }[/math] są względnie pierwsze, to istnieje [math]\displaystyle{ n }[/math] kolejnych liczb postaci [math]\displaystyle{ a k + b }[/math], wśród których znajduje się dokładnie [math]\displaystyle{ r \leqslant \pi (a (n - 1) + b ; a, b) }[/math] liczb pierwszych.
Twierdzenie można udowodnić, uogólniając dowód twierdzenia C40 lub wykorzystując metodę zastosowaną w rozwiązaniu zadania C43.
□
Zadanie C45
Niech [math]\displaystyle{ p \geqslant 5 }[/math] będzie liczbą pierwszą. Pokazać, że w ciągu [math]\displaystyle{ 6 k + 1 }[/math] występują kwadraty wszystkich liczb pierwszych [math]\displaystyle{ p }[/math].
Wiemy, że liczby pierwsze nieparzyste [math]\displaystyle{ p \geqslant 5 }[/math] mogą być postaci [math]\displaystyle{ 6 k + 1 }[/math] lub [math]\displaystyle{ 6 k + 5 }[/math]. Ponieważ
- [math]\displaystyle{ (6 k + 1)^2 = 6 (6 k^2 + 2 k) + 1 }[/math]
- [math]\displaystyle{ (6 k + 5)^2 = 6 (6 k^2 + 10 k + 4) + 1 }[/math]
zatem kwadraty liczb pierwszych są postaci [math]\displaystyle{ 6 k + 1 }[/math] i nie mogą występować w ciągu postaci [math]\displaystyle{ 6 k + 5 }[/math].
□
Zadanie C46
Dany jest ciąg arytmetyczny [math]\displaystyle{ a k + b }[/math], gdzie liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze. Pokazać, że
- jeżeli liczba pierwsza [math]\displaystyle{ p }[/math] dzieli [math]\displaystyle{ a }[/math], to żaden wyraz ciągu [math]\displaystyle{ a k + b }[/math] nie jest podzielny przez [math]\displaystyle{ p }[/math]
- jeżeli liczba pierwsza [math]\displaystyle{ p }[/math] nie dzieli [math]\displaystyle{ a }[/math], to istnieje nieskończenie wiele wyrazów ciągu [math]\displaystyle{ a k + b }[/math], które są podzielne przez [math]\displaystyle{ p }[/math]
Punkt 1.
Zauważmy, że liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze, zatem liczba pierwsza [math]\displaystyle{ p }[/math] nie może jednocześnie dzielić liczb [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math]. Ponieważ z założenia [math]\displaystyle{ p \mid a }[/math], to wynika stąd, że [math]\displaystyle{ p }[/math] nie dzieli [math]\displaystyle{ b }[/math]. Jeśli tak, to
- [math]\displaystyle{ a k + b = (n p) k + b }[/math]
i [math]\displaystyle{ p }[/math] nie dzieli żadnej liczby postaci [math]\displaystyle{ a k + b }[/math].
Punkt 2.
Pierwszy sposób
Niech [math]\displaystyle{ k_0 \in \mathbb{N} }[/math]. Przypuśćmy, że dla pewnych różnych liczb naturalnych [math]\displaystyle{ i, j }[/math] takich, że [math]\displaystyle{ 1 \leqslant i < j \leqslant p }[/math] liczby [math]\displaystyle{ a(k_0 + i) + b }[/math] oraz [math]\displaystyle{ a(k_0 + j) + b }[/math] dają tę samą resztę przy dzieleniu przez liczbę pierwszą [math]\displaystyle{ p }[/math]. Zatem różnica tych liczb jest podzielna przez [math]\displaystyle{ p }[/math]
- [math]\displaystyle{ p \mid [a (k_0 + j) + b] - [a (k_0 + i) + b] }[/math]
czyli
- [math]\displaystyle{ p \mid a (j - i) }[/math]
Ponieważ [math]\displaystyle{ p \nmid a }[/math] to na mocy lematu Euklidesa (twierdzenie C79), mamy
- [math]\displaystyle{ p \mid (j - i) }[/math]
co jest niemożliwe, bo [math]\displaystyle{ 1 \leqslant j - i \leqslant p - 1 < p }[/math].
Zatem reszty [math]\displaystyle{ r_1, r_2, \ldots, r_p }[/math] są wszystkie różne, a ponieważ jest ich [math]\displaystyle{ p }[/math], czyli tyle ile jest różnych reszt z dzielenia przez liczbę [math]\displaystyle{ p }[/math], to zbiór tych reszt jest identyczny ze zbiorem reszt z dzielenia przez [math]\displaystyle{ p }[/math], czyli ze zbiorem [math]\displaystyle{ S = \{ 0, 1, 2, \ldots, p - 1 \} }[/math]. W szczególności wynika stąd, że wśród [math]\displaystyle{ p }[/math] kolejnych wyrazów ciągu arytmetycznego [math]\displaystyle{ a k + b }[/math] jeden z tych wyrazów jest podzielny przez [math]\displaystyle{ p }[/math]. Zatem istnieje nieskończenie wiele wyrazów ciągu [math]\displaystyle{ a k + b }[/math], które są podzielne przez [math]\displaystyle{ p }[/math].
Drugi sposób
Problem sprowadza się do wykazania istnienia nieskończenie wielu par liczb naturalnych [math]\displaystyle{ (k, n) }[/math], takich że
- [math]\displaystyle{ a k + b = n p }[/math]
Co z kolei sprowadza się do badania rozwiązań całkowitych równania
- [math]\displaystyle{ n p - a k = b }[/math]
Zauważmy, że ponieważ [math]\displaystyle{ p \nmid a }[/math], to liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ p }[/math] są względnie pierwsze. Zatem ich największym wspólnym dzielnikiem jest liczba [math]\displaystyle{ 1 }[/math]. Na mocy twierdzenia C83 równanie to ma nieskończenie wiele rozwiązań w liczbach całkowitych
- [math]\displaystyle{ n = n_0 + p t }[/math]
- [math]\displaystyle{ k = k_0 + a t }[/math]
gdzie [math]\displaystyle{ t }[/math] jest dowolną liczbą całkowitą, a para liczb [math]\displaystyle{ (n_0, k_0) }[/math] jest dowolnym rozwiązaniem tego równania. Widzimy, że dla dostatecznie dużych liczb [math]\displaystyle{ t }[/math] zawsze możemy uzyskać takie [math]\displaystyle{ n }[/math] i [math]\displaystyle{ k }[/math], że [math]\displaystyle{ n, k \in \mathbb{Z}_+ }[/math]. Pokazaliśmy w ten sposób, że w ciągu arytmetycznym [math]\displaystyle{ a k + b }[/math] istnieje nieskończenie wiele wyrazów podzielnych przez liczbę pierwszą [math]\displaystyle{ p }[/math].
Trzeci sposób
Zauważmy, że ponieważ [math]\displaystyle{ p \nmid a }[/math], to liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ p }[/math] są względnie pierwsze. Zatem ich największym wspólnym dzielnikiem jest liczba [math]\displaystyle{ 1 }[/math]. Lemat Bézouta zapewnia istnienie takich liczb całkowitych [math]\displaystyle{ x }[/math] i [math]\displaystyle{ y }[/math], że
- [math]\displaystyle{ a x + p y = 1 }[/math]
Niech [math]\displaystyle{ k_0 = r p - b x }[/math], gdzie [math]\displaystyle{ r }[/math] jest dowolną liczbą całkowitą dodatnią, ale na tyle dużą, aby [math]\displaystyle{ k_0 }[/math] była liczbą dodatnią bez względu na znak iloczynu [math]\displaystyle{ b x }[/math]. Łatwo sprawdzamy, że liczba [math]\displaystyle{ a k_0 + b }[/math] jest podzielna przez [math]\displaystyle{ p }[/math]
- [math]\displaystyle{ a k_0 + b = a (r p - b x) + b = }[/math]
- [math]\displaystyle{ \;\; = a r p - a b x + b = }[/math]
- [math]\displaystyle{ \;\; = a r p + b (1 - a x) = }[/math]
- [math]\displaystyle{ \;\; = a r p + b p y = }[/math]
- [math]\displaystyle{ \;\; = p (a r + b y) }[/math]
Zatem w ciągu [math]\displaystyle{ a k + b }[/math] istnieje przynajmniej jeden wyraz podzielny przez liczbę pierwszą [math]\displaystyle{ p }[/math]. Jeśli tak, to w ciągu arytmetycznym [math]\displaystyle{ a k + b }[/math] istnieje nieskończenie wiele liczb podzielnych przez [math]\displaystyle{ p }[/math], bo dla [math]\displaystyle{ k = k_0 + s p }[/math], gdzie [math]\displaystyle{ s \in \mathbb{N} }[/math], mamy
- [math]\displaystyle{ a k + b = a (k_0 + s p) + b = a s p + (a k_0 + b) }[/math]
Czyli [math]\displaystyle{ p \mid a k + b }[/math].
□
Uwaga C47
Łatwo możemy napisać w PARI/GP funkcję, która zwraca najmniejszą liczbę naturalną [math]\displaystyle{ k_0 }[/math], dla której wyraz ciągu arytmetycznego [math]\displaystyle{ a k + b }[/math] jest podzielny przez [math]\displaystyle{ p }[/math] (przy założeniu, że liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ p }[/math] są względnie pierwsze).
f(a,b,p) = lift( Mod(-b,p)*Mod(a,p)^(-1) )
Ciągi nieskończone i liczby pierwsze
Uwaga C48
Choć wiele ciągów jest dobrze znanych i równie dobrze zbadanych, to nie wiemy, czy zawierają one nieskończenie wiele liczb pierwszych. Przykładowo
[math]\displaystyle{ \quad 1. \quad }[/math] [math]\displaystyle{ a_n = n^2 + 1 }[/math] A002496 [math]\displaystyle{ \quad 2. \quad }[/math] [math]\displaystyle{ b_n = n^2 - n - 1 }[/math] A002327 [math]\displaystyle{ \quad 3. \quad }[/math] [math]\displaystyle{ c_n = n^2 + n + 1 }[/math] A002383 [math]\displaystyle{ \quad 4. \quad }[/math] [math]\displaystyle{ d_n = n^4 + 1 }[/math] A000068 [math]\displaystyle{ \quad 5. \quad }[/math] [math]\displaystyle{ u_n = n! + 1 }[/math] A002981 [math]\displaystyle{ \quad 6. \quad }[/math] [math]\displaystyle{ v_n = n! - 1 }[/math] A002982 [math]\displaystyle{ \quad 7. \quad }[/math] [math]\displaystyle{ M_n = 2^n - 1 }[/math] (liczby Mersenne'a) A000043 [math]\displaystyle{ \quad 8. \quad }[/math] [math]\displaystyle{ F_n = 2^{2^n} + 1 }[/math] (liczby Fermata) A019434 [math]\displaystyle{ \quad 9. \quad }[/math] [math]\displaystyle{ F_n (a) = a^{2^n} + 1 }[/math] (uogólnione liczby Fermata, [math]\displaystyle{ a }[/math] parzyste) MathWorld
Nie wiemy, czy istnieje wielomian całkowity [math]\displaystyle{ W(n) }[/math] stopnia większego niż jeden taki, że [math]\displaystyle{ W(n) }[/math] jest liczbą pierwszą dla nieskończenie wielu liczb [math]\displaystyle{ n }[/math].
Przykład C49
Łatwo sprawdzić, że wartości wielomianu [math]\displaystyle{ W(n) = n^2 + n + 41 }[/math] są liczbami pierwszymi dla [math]\displaystyle{ 1 \leqslant n \leqslant 39 }[/math]. Oczywiście [math]\displaystyle{ 41 \mid W(41) }[/math].
Twierdzenie C50
Niech [math]\displaystyle{ a, n \in \mathbb{Z}_+ }[/math] i [math]\displaystyle{ a \geqslant 2 }[/math]. Jeżeli liczba [math]\displaystyle{ a^n + 1 }[/math] jest liczbą pierwszą, to [math]\displaystyle{ a }[/math] jest liczbą parzystą i [math]\displaystyle{ n = 2^m }[/math].
Gdyby liczba [math]\displaystyle{ a }[/math] była nieparzysta, to liczba [math]\displaystyle{ a^n + 1 \geqslant 4 }[/math] byłaby parzysta i nie mogłaby być liczbą pierwszą.
Niech wykładnik [math]\displaystyle{ n = x y }[/math] będzie liczbą złożoną, a [math]\displaystyle{ x }[/math] będzie liczbą nieparzystą. Wtedy
- [math]\displaystyle{ a^n + 1 = (a^y)^x + 1 }[/math]
Oznaczając [math]\displaystyle{ b = a^y }[/math] oraz [math]\displaystyle{ x = 2 k + 1 }[/math], otrzymujemy
- [math]\displaystyle{ a^n + 1 = (a^y)^x + 1 }[/math]
- [math]\displaystyle{ \: = b^x + 1 }[/math]
- [math]\displaystyle{ \: = b^{2 k + 1} + 1 }[/math]
- [math]\displaystyle{ \: = (b + 1) \cdot (1 - b + b^2 - b^3 + \ldots + b^{2 k - 2} - b^{2 k - 1} + b^{2 k}) }[/math]
Czyli [math]\displaystyle{ a^n + 1 }[/math] jest liczbą złożoną. Wynika stąd, że wykładnik [math]\displaystyle{ n }[/math] nie może zawierać czynników nieparzystych, czyli musi być [math]\displaystyle{ n = 2^m }[/math]. Co należało pokazać.
□
Twierdzenie C51
Dla dowolnej liczby naturalnej [math]\displaystyle{ n \geqslant 1 }[/math] liczba [math]\displaystyle{ x - y }[/math] jest dzielnikiem wyrażenia [math]\displaystyle{ x^n - y^n }[/math].
Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], bo [math]\displaystyle{ x - y }[/math] dzieli [math]\displaystyle{ x^1 - y^1 }[/math]. Załóżmy, że [math]\displaystyle{ x - y }[/math] jest dzielnikiem wyrażenia [math]\displaystyle{ x^n - y^n }[/math], czyli [math]\displaystyle{ x^n - y^n = (x - y) \cdot k }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ x^{n + 1} - y^{n + 1} = x x^n - y x^n + y x^n - y y^n = }[/math]
- [math]\displaystyle{ \quad \, = (x - y) x^n + y (x^n - y^n) = }[/math]
- [math]\displaystyle{ \quad \, = (x - y) x^n + y (x - y) \cdot k = }[/math]
- [math]\displaystyle{ \quad \, = (x - y) (x^n + y \cdot k) }[/math]
Czyli [math]\displaystyle{ x - y }[/math] jest dzielnikiem [math]\displaystyle{ x^{n + 1} - y^{n + 1} }[/math]. Co kończy dowód indukcyjny.
□
Twierdzenie C52
Jeżeli [math]\displaystyle{ n \geqslant 2 }[/math] oraz [math]\displaystyle{ a^n - 1 }[/math] jest liczbą pierwszą, to [math]\displaystyle{ a = 2 }[/math] i [math]\displaystyle{ n }[/math] jest liczbą pierwszą.
Z twierdzenia C51 wiemy, że [math]\displaystyle{ x - y \mid x^n - y^n }[/math]. W przypadku gdy [math]\displaystyle{ a > 2 }[/math] mamy
- [math]\displaystyle{ a - 1 \mid a^n - 1 }[/math]
Czyli musi być [math]\displaystyle{ a = 2 }[/math]. Z tego samego twierdzenia wynika też, że jeżeli [math]\displaystyle{ n }[/math] jest liczbą złożoną [math]\displaystyle{ n = r s }[/math], to
- [math]\displaystyle{ 2^r - 1 \mid 2^{r s} - 1 }[/math]
bo [math]\displaystyle{ a^r - b^r \mid (a^r)^s - (b^r)^s }[/math]. Zatem [math]\displaystyle{ n }[/math] musi być liczbą pierwszą. Co kończy dowód.
□
Ciągi arytmetyczne liczb pierwszych
Uwaga C53
Ciągi arytmetyczne liczb pierwszych[11][12] zbudowane z dwóch liczb pierwszych nie są interesujące, bo dowolne dwie liczby tworzą ciąg arytmetyczny. Dlatego będziemy się zajmowali ciągami arytmetycznymi liczb pierwszych o długości [math]\displaystyle{ n \geqslant 3 }[/math].
Ponieważ nie da się zbudować ciągu arytmetycznego liczb pierwszych o długości [math]\displaystyle{ n \geqslant 3 }[/math], w którym pierwszym wyrazem jest liczba [math]\displaystyle{ p_0 = 2 }[/math], to będą nas interesowały ciągi rozpoczynające się od liczby pierwszej [math]\displaystyle{ p_0 \geqslant 3 }[/math]
Jeżeli do liczby pierwszej nieparzystej dodamy dodatnią liczbę nieparzystą, to otrzymamy liczbę parzystą złożoną, zatem różnica ciągu arytmetycznego [math]\displaystyle{ d }[/math] musi być liczbą parzystą, aby zbudowanie jakiegokolwiek ciągu arytmetycznego liczb pierwszych o długości [math]\displaystyle{ n \geqslant 3 }[/math] było możliwe.
Istnienie nieskończenie wiele ciągów arytmetycznych liczb pierwszych o długości [math]\displaystyle{ n = 3 }[/math] pokazano już wiele lat temu[13]. Temat ciągów arytmetycznych liczb pierwszych zyskał na popularności[14] po udowodnieniu przez Bena Greena i Terence'a Tao twierdzenia o istnieniu dowolnie długich (ale skończonych) ciągów arytmetycznych liczb pierwszych[15].
Twierdzenie C54* (Ben Green i Terence Tao, 2004)
Dla dowolnej liczby naturalnej [math]\displaystyle{ n \geqslant 2 }[/math] istnieje nieskończenie wiele [math]\displaystyle{ n }[/math]-wyrazowych ciągów arytmetycznych liczb pierwszych.
Przykład C55
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości [math]\displaystyle{ n = 3 }[/math] i [math]\displaystyle{ n = 4 }[/math].
W przypadku [math]\displaystyle{ n = 3 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 2 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^8 }[/math].
W przypadku [math]\displaystyle{ n = 4 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 6 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^8 }[/math].
Jeżeli w tabeli jest wypisanych sześć wartości [math]\displaystyle{ p_0 }[/math], to oznacza to, że zostało znalezionych co najmniej sześć wartości [math]\displaystyle{ p_0 }[/math].
| [math]\displaystyle{ \mathbf{n = 3} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 2} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 4} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 6} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 41 }[/math] |
| [math]\displaystyle{ \mathbf{ 8} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 10} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 12} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 47 }[/math] |
| [math]\displaystyle{ \mathbf{ 14} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 18} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 61 }[/math] |
| [math]\displaystyle{ \mathbf{ 20} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 24} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 79 }[/math] |
| [math]\displaystyle{ \mathbf{ 28} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 30} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 37 }[/math] |
| [math]\displaystyle{ \mathbf{ 34} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 36} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 67 }[/math] |
| [math]\displaystyle{ \mathbf{ 38} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 40} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 42} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 67 }[/math] |
| [math]\displaystyle{ \mathbf{ 48} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 53 }[/math] |
| [math]\displaystyle{ \mathbf{ 50} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 54} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 73 }[/math] |
| [math]\displaystyle{ \mathbf{ 60} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 43 }[/math] |
| [math]\displaystyle{ \mathbf{ 64} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 66} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 47 }[/math] |
| [math]\displaystyle{ \mathbf{ 68} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 72} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 107 }[/math] |
| [math]\displaystyle{ \mathbf{ 78} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 113 }[/math] |
| [math]\displaystyle{ \mathbf{ 80} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 84} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 73 }[/math] |
| [math]\displaystyle{ \mathbf{ 90} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 59 }[/math] |
| [math]\displaystyle{ \mathbf{ 94} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 96} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 101 }[/math] |
| [math]\displaystyle{ \mathbf{ 98} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 102} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 89 }[/math] |
| [math]\displaystyle{ \mathbf{ 104} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 108} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 131 }[/math] | [math]\displaystyle{ 163 }[/math] | [math]\displaystyle{ 173 }[/math] | [math]\displaystyle{ 223 }[/math] |
| [math]\displaystyle{ \mathbf{ 110} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 114} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 83 }[/math] |
| [math]\displaystyle{ \mathbf{ 120} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 43 }[/math] |
| [math]\displaystyle{ \mathbf{ 124} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 126} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 101 }[/math] |
| [math]\displaystyle{ \mathbf{ 132} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 67 }[/math] |
| [math]\displaystyle{ \mathbf{ 134} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 138} }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 103 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 173 }[/math] |
| [math]\displaystyle{ \mathbf{ 144} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 113 }[/math] |
| [math]\displaystyle{ \mathbf{ 150} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 73 }[/math] |
| [math]\displaystyle{ \mathbf{ 154} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 156} }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 127 }[/math] |
| [math]\displaystyle{ \mathbf{ 162} }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 109 }[/math] | [math]\displaystyle{ 197 }[/math] | [math]\displaystyle{ 239 }[/math] | [math]\displaystyle{ 269 }[/math] |
| [math]\displaystyle{ \mathbf{ 164} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 168} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 61 }[/math] |
| [math]\displaystyle{ \mathbf{ 174} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 109 }[/math] | [math]\displaystyle{ 139 }[/math] |
| [math]\displaystyle{ \mathbf{ 178} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 180} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 83 }[/math] |
| [math]\displaystyle{ \mathbf{ 186} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 107 }[/math] |
| [math]\displaystyle{ \mathbf{ 188} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 190} }[/math] | [math]\displaystyle{ 3 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 192} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 139 }[/math] |
| [math]\displaystyle{ \mathbf{ 198} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 113 }[/math] |
| [math]\displaystyle{ \mathbf{n = 4} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 6} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 251 }[/math] | [math]\displaystyle{ 601 }[/math] |
| [math]\displaystyle{ \mathbf{ 12} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 227 }[/math] |
| [math]\displaystyle{ \mathbf{ 18} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 313 }[/math] | [math]\displaystyle{ 673 }[/math] |
| [math]\displaystyle{ \mathbf{ 24} }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 349 }[/math] | [math]\displaystyle{ 419 }[/math] | [math]\displaystyle{ 499 }[/math] | [math]\displaystyle{ 569 }[/math] |
| [math]\displaystyle{ \mathbf{ 30} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 41 }[/math] |
| [math]\displaystyle{ \mathbf{ 36} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 241 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 311 }[/math] | [math]\displaystyle{ 751 }[/math] | [math]\displaystyle{ 911 }[/math] |
| [math]\displaystyle{ \mathbf{ 42} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 157 }[/math] |
| [math]\displaystyle{ \mathbf{ 48} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 613 }[/math] | [math]\displaystyle{ 643 }[/math] |
| [math]\displaystyle{ \mathbf{ 54} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 239 }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 719 }[/math] |
| [math]\displaystyle{ \mathbf{ 60} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 71 }[/math] |
| [math]\displaystyle{ \mathbf{ 66} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 241 }[/math] | [math]\displaystyle{ 251 }[/math] | [math]\displaystyle{ 521 }[/math] | [math]\displaystyle{ 541 }[/math] |
| [math]\displaystyle{ \mathbf{ 72} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 167 }[/math] | [math]\displaystyle{ 347 }[/math] | [math]\displaystyle{ 947 }[/math] | [math]\displaystyle{ 1217 }[/math] |
| [math]\displaystyle{ \mathbf{ 78} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 233 }[/math] | [math]\displaystyle{ 353 }[/math] | [math]\displaystyle{ 443 }[/math] |
| [math]\displaystyle{ \mathbf{ 84} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 149 }[/math] | [math]\displaystyle{ 179 }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 439 }[/math] |
| [math]\displaystyle{ \mathbf{ 90} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 89 }[/math] |
| [math]\displaystyle{ \mathbf{ 96} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 631 }[/math] | [math]\displaystyle{ 761 }[/math] | [math]\displaystyle{ 1471 }[/math] |
| [math]\displaystyle{ \mathbf{ 102} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 257 }[/math] | [math]\displaystyle{ 337 }[/math] | [math]\displaystyle{ 557 }[/math] |
| [math]\displaystyle{ \mathbf{ 108} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 163 }[/math] | [math]\displaystyle{ 223 }[/math] | [math]\displaystyle{ 293 }[/math] | [math]\displaystyle{ 353 }[/math] | [math]\displaystyle{ 643 }[/math] |
| [math]\displaystyle{ \mathbf{ 114} }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 349 }[/math] | [math]\displaystyle{ 569 }[/math] | [math]\displaystyle{ 709 }[/math] | [math]\displaystyle{ 1259 }[/math] | [math]\displaystyle{ 2039 }[/math] |
| [math]\displaystyle{ \mathbf{ 120} }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 149 }[/math] |
| [math]\displaystyle{ \mathbf{ 126} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 131 }[/math] |
| [math]\displaystyle{ \mathbf{ 132} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 257 }[/math] | [math]\displaystyle{ 277 }[/math] | [math]\displaystyle{ 487 }[/math] |
| [math]\displaystyle{ \mathbf{ 138} }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 173 }[/math] | [math]\displaystyle{ 383 }[/math] | [math]\displaystyle{ 463 }[/math] | [math]\displaystyle{ 563 }[/math] | [math]\displaystyle{ 773 }[/math] |
| [math]\displaystyle{ \mathbf{ 144} }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 509 }[/math] | [math]\displaystyle{ 599 }[/math] | [math]\displaystyle{ 1019 }[/math] | [math]\displaystyle{ 1579 }[/math] | [math]\displaystyle{ 2609 }[/math] |
| [math]\displaystyle{ \mathbf{ 150} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 163 }[/math] |
| [math]\displaystyle{ \mathbf{ 156} }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 151 }[/math] | [math]\displaystyle{ 191 }[/math] | [math]\displaystyle{ 461 }[/math] | [math]\displaystyle{ 571 }[/math] | [math]\displaystyle{ 641 }[/math] |
| [math]\displaystyle{ \mathbf{ 162} }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 197 }[/math] | [math]\displaystyle{ 337 }[/math] | [math]\displaystyle{ 967 }[/math] | [math]\displaystyle{ 1297 }[/math] | [math]\displaystyle{ 1627 }[/math] |
| [math]\displaystyle{ \mathbf{ 168} }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 103 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 373 }[/math] |
| [math]\displaystyle{ \mathbf{ 174} }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 109 }[/math] | [math]\displaystyle{ 139 }[/math] | [math]\displaystyle{ 509 }[/math] | [math]\displaystyle{ 839 }[/math] | [math]\displaystyle{ 929 }[/math] |
| [math]\displaystyle{ \mathbf{ 180} }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 103 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 283 }[/math] |
| [math]\displaystyle{ \mathbf{ 186} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 151 }[/math] | [math]\displaystyle{ 271 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 491 }[/math] | [math]\displaystyle{ 691 }[/math] |
| [math]\displaystyle{ \mathbf{ 192} }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 307 }[/math] | [math]\displaystyle{ 647 }[/math] | [math]\displaystyle{ 1087 }[/math] | [math]\displaystyle{ 1427 }[/math] |
| [math]\displaystyle{ \mathbf{ 198} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 263 }[/math] | [math]\displaystyle{ 373 }[/math] | [math]\displaystyle{ 853 }[/math] |
| [math]\displaystyle{ \mathbf{ 204} }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 149 }[/math] | [math]\displaystyle{ 449 }[/math] | [math]\displaystyle{ 479 }[/math] | [math]\displaystyle{ 569 }[/math] | [math]\displaystyle{ 919 }[/math] |
| [math]\displaystyle{ \mathbf{ 210} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 103 }[/math] |
| [math]\displaystyle{ \mathbf{ 216} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 181 }[/math] | [math]\displaystyle{ 761 }[/math] | [math]\displaystyle{ 1021 }[/math] | [math]\displaystyle{ 1061 }[/math] | [math]\displaystyle{ 1231 }[/math] |
| [math]\displaystyle{ \mathbf{ 222} }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 197 }[/math] | [math]\displaystyle{ 547 }[/math] | [math]\displaystyle{ 617 }[/math] | [math]\displaystyle{ 787 }[/math] |
| [math]\displaystyle{ \mathbf{ 228} }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 263 }[/math] | [math]\displaystyle{ 313 }[/math] | [math]\displaystyle{ 593 }[/math] | [math]\displaystyle{ 953 }[/math] | [math]\displaystyle{ 1093 }[/math] |
| [math]\displaystyle{ \mathbf{ 234} }[/math] | [math]\displaystyle{ 359 }[/math] | [math]\displaystyle{ 499 }[/math] | [math]\displaystyle{ 619 }[/math] | [math]\displaystyle{ 829 }[/math] | [math]\displaystyle{ 1549 }[/math] | [math]\displaystyle{ 2309 }[/math] |
| [math]\displaystyle{ \mathbf{ 240} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 139 }[/math] | [math]\displaystyle{ 263 }[/math] |
| [math]\displaystyle{ \mathbf{ 246} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 331 }[/math] | [math]\displaystyle{ 541 }[/math] | [math]\displaystyle{ 661 }[/math] |
| [math]\displaystyle{ \mathbf{ 252} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 197 }[/math] | [math]\displaystyle{ 257 }[/math] |
| [math]\displaystyle{ \mathbf{ 258} }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 313 }[/math] | [math]\displaystyle{ 503 }[/math] | [math]\displaystyle{ 1103 }[/math] | [math]\displaystyle{ 1873 }[/math] | [math]\displaystyle{ 3253 }[/math] |
| [math]\displaystyle{ \mathbf{ 264} }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 409 }[/math] |
| [math]\displaystyle{ \mathbf{ 270} }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 229 }[/math] | [math]\displaystyle{ 491 }[/math] | [math]\displaystyle{ 557 }[/math] | [math]\displaystyle{ 613 }[/math] |
| [math]\displaystyle{ \mathbf{ 276} }[/math] | [math]\displaystyle{ 181 }[/math] | [math]\displaystyle{ 191 }[/math] | [math]\displaystyle{ 401 }[/math] | [math]\displaystyle{ 601 }[/math] | [math]\displaystyle{ 661 }[/math] | [math]\displaystyle{ 1171 }[/math] |
| [math]\displaystyle{ \mathbf{ 282} }[/math] | [math]\displaystyle{ 137 }[/math] | [math]\displaystyle{ 317 }[/math] | [math]\displaystyle{ 457 }[/math] | [math]\displaystyle{ 1297 }[/math] | [math]\displaystyle{ 1747 }[/math] | [math]\displaystyle{ 1787 }[/math] |
| [math]\displaystyle{ \mathbf{ 288} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 233 }[/math] | [math]\displaystyle{ 353 }[/math] | [math]\displaystyle{ 463 }[/math] | [math]\displaystyle{ 743 }[/math] |
| [math]\displaystyle{ \mathbf{ 294} }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 139 }[/math] | [math]\displaystyle{ 269 }[/math] | [math]\displaystyle{ 349 }[/math] | [math]\displaystyle{ 719 }[/math] |
| [math]\displaystyle{ \mathbf{ 300} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 109 }[/math] | [math]\displaystyle{ 139 }[/math] |
| [math]\displaystyle{ \mathbf{ 306} }[/math] | [math]\displaystyle{ 491 }[/math] | [math]\displaystyle{ 691 }[/math] | [math]\displaystyle{ 971 }[/math] | [math]\displaystyle{ 1321 }[/math] | [math]\displaystyle{ 1471 }[/math] | [math]\displaystyle{ 2341 }[/math] |
| [math]\displaystyle{ \mathbf{ 312} }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 257 }[/math] | [math]\displaystyle{ 347 }[/math] | [math]\displaystyle{ 547 }[/math] | [math]\displaystyle{ 607 }[/math] | [math]\displaystyle{ 757 }[/math] |
| [math]\displaystyle{ \mathbf{ 318} }[/math] | [math]\displaystyle{ 283 }[/math] | [math]\displaystyle{ 373 }[/math] | [math]\displaystyle{ 653 }[/math] | [math]\displaystyle{ 1063 }[/math] | [math]\displaystyle{ 1493 }[/math] | [math]\displaystyle{ 1823 }[/math] |
| [math]\displaystyle{ \mathbf{ 324} }[/math] | [math]\displaystyle{ 179 }[/math] | [math]\displaystyle{ 349 }[/math] | [math]\displaystyle{ 839 }[/math] | [math]\displaystyle{ 2389 }[/math] | [math]\displaystyle{ 2699 }[/math] | [math]\displaystyle{ 2879 }[/math] |
| [math]\displaystyle{ \mathbf{ 330} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 127 }[/math] |
| [math]\displaystyle{ \mathbf{ 336} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 311 }[/math] | [math]\displaystyle{ 421 }[/math] | [math]\displaystyle{ 491 }[/math] |
| [math]\displaystyle{ \mathbf{ 342} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 137 }[/math] | [math]\displaystyle{ 257 }[/math] | [math]\displaystyle{ 467 }[/math] | [math]\displaystyle{ 887 }[/math] |
| [math]\displaystyle{ \mathbf{ 348} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 563 }[/math] | [math]\displaystyle{ 593 }[/math] | [math]\displaystyle{ 743 }[/math] | [math]\displaystyle{ 1373 }[/math] |
| [math]\displaystyle{ \mathbf{ 354} }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 239 }[/math] | [math]\displaystyle{ 389 }[/math] | [math]\displaystyle{ 509 }[/math] | [math]\displaystyle{ 659 }[/math] | [math]\displaystyle{ 739 }[/math] |
| [math]\displaystyle{ \mathbf{ 360} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 107 }[/math] |
| [math]\displaystyle{ \mathbf{ 366} }[/math] | [math]\displaystyle{ 461 }[/math] | [math]\displaystyle{ 571 }[/math] | [math]\displaystyle{ 1481 }[/math] | [math]\displaystyle{ 1511 }[/math] | [math]\displaystyle{ 1901 }[/math] | [math]\displaystyle{ 2111 }[/math] |
| [math]\displaystyle{ \mathbf{ 372} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 547 }[/math] | [math]\displaystyle{ 857 }[/math] | [math]\displaystyle{ 877 }[/math] | [math]\displaystyle{ 1087 }[/math] | [math]\displaystyle{ 2887 }[/math] |
| [math]\displaystyle{ \mathbf{ 378} }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 163 }[/math] | [math]\displaystyle{ 313 }[/math] | [math]\displaystyle{ 503 }[/math] | [math]\displaystyle{ 563 }[/math] |
| [math]\displaystyle{ \mathbf{ 384} }[/math] | [math]\displaystyle{ 139 }[/math] | [math]\displaystyle{ 229 }[/math] | [math]\displaystyle{ 719 }[/math] | [math]\displaystyle{ 1229 }[/math] | [math]\displaystyle{ 1439 }[/math] | [math]\displaystyle{ 1699 }[/math] |
| [math]\displaystyle{ \mathbf{ 390} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 131 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 197 }[/math] |
| [math]\displaystyle{ \mathbf{ 396} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 431 }[/math] | [math]\displaystyle{ 691 }[/math] | [math]\displaystyle{ 701 }[/math] |
| [math]\displaystyle{ \mathbf{ 402} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 167 }[/math] | [math]\displaystyle{ 727 }[/math] | [math]\displaystyle{ 997 }[/math] | [math]\displaystyle{ 1637 }[/math] |
| [math]\displaystyle{ \mathbf{ 408} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 223 }[/math] | [math]\displaystyle{ 643 }[/math] | [math]\displaystyle{ 683 }[/math] | [math]\displaystyle{ 1063 }[/math] | [math]\displaystyle{ 1213 }[/math] |
| [math]\displaystyle{ \mathbf{ 414} }[/math] | [math]\displaystyle{ 269 }[/math] | [math]\displaystyle{ 359 }[/math] | [math]\displaystyle{ 619 }[/math] | [math]\displaystyle{ 1039 }[/math] | [math]\displaystyle{ 1879 }[/math] | [math]\displaystyle{ 2089 }[/math] |
| [math]\displaystyle{ \mathbf{ 420} }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 47 }[/math] |
| [math]\displaystyle{ \mathbf{ 426} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 131 }[/math] | [math]\displaystyle{ 181 }[/math] | [math]\displaystyle{ 431 }[/math] | [math]\displaystyle{ 761 }[/math] | [math]\displaystyle{ 811 }[/math] |
| [math]\displaystyle{ \mathbf{ 432} }[/math] | [math]\displaystyle{ 227 }[/math] | [math]\displaystyle{ 617 }[/math] | [math]\displaystyle{ 857 }[/math] | [math]\displaystyle{ 997 }[/math] | [math]\displaystyle{ 1657 }[/math] | [math]\displaystyle{ 1667 }[/math] |
| [math]\displaystyle{ \mathbf{ 438} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 383 }[/math] | [math]\displaystyle{ 1163 }[/math] | [math]\displaystyle{ 1303 }[/math] | [math]\displaystyle{ 1873 }[/math] |
| [math]\displaystyle{ \mathbf{ 444} }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 409 }[/math] | [math]\displaystyle{ 1109 }[/math] | [math]\displaystyle{ 1669 }[/math] | [math]\displaystyle{ 1889 }[/math] | [math]\displaystyle{ 2029 }[/math] |
| [math]\displaystyle{ \mathbf{ 450} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 149 }[/math] | [math]\displaystyle{ 193 }[/math] | [math]\displaystyle{ 251 }[/math] | [math]\displaystyle{ 359 }[/math] |
| [math]\displaystyle{ \mathbf{ 456} }[/math] | [math]\displaystyle{ 191 }[/math] | [math]\displaystyle{ 521 }[/math] | [math]\displaystyle{ 631 }[/math] | [math]\displaystyle{ 1171 }[/math] | [math]\displaystyle{ 1291 }[/math] | [math]\displaystyle{ 2341 }[/math] |
| [math]\displaystyle{ \mathbf{ 462} }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 137 }[/math] | [math]\displaystyle{ 277 }[/math] | [math]\displaystyle{ 307 }[/math] | [math]\displaystyle{ 367 }[/math] |
| [math]\displaystyle{ \mathbf{ 468} }[/math] | [math]\displaystyle{ 193 }[/math] | [math]\displaystyle{ 293 }[/math] | [math]\displaystyle{ 503 }[/math] | [math]\displaystyle{ 683 }[/math] | [math]\displaystyle{ 733 }[/math] | [math]\displaystyle{ 1013 }[/math] |
| [math]\displaystyle{ \mathbf{ 474} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 479 }[/math] | [math]\displaystyle{ 719 }[/math] | [math]\displaystyle{ 829 }[/math] |
| [math]\displaystyle{ \mathbf{ 480} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 347 }[/math] | [math]\displaystyle{ 439 }[/math] | [math]\displaystyle{ 449 }[/math] |
| [math]\displaystyle{ \mathbf{ 486} }[/math] | [math]\displaystyle{ 241 }[/math] | [math]\displaystyle{ 811 }[/math] | [math]\displaystyle{ 941 }[/math] | [math]\displaystyle{ 1361 }[/math] | [math]\displaystyle{ 1861 }[/math] | [math]\displaystyle{ 1871 }[/math] |
| [math]\displaystyle{ \mathbf{ 492} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 947 }[/math] | [math]\displaystyle{ 1607 }[/math] | [math]\displaystyle{ 2897 }[/math] | [math]\displaystyle{ 3037 }[/math] |
| [math]\displaystyle{ \mathbf{ 498} }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 883 }[/math] | [math]\displaystyle{ 953 }[/math] | [math]\displaystyle{ 983 }[/math] | [math]\displaystyle{ 1723 }[/math] | [math]\displaystyle{ 1913 }[/math] |
| [math]\displaystyle{ \mathbf{ 504} }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 109 }[/math] | [math]\displaystyle{ 229 }[/math] | [math]\displaystyle{ 359 }[/math] | [math]\displaystyle{ 599 }[/math] | [math]\displaystyle{ 619 }[/math] |
| [math]\displaystyle{ \mathbf{ 510} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 167 }[/math] |
| [math]\displaystyle{ \mathbf{ 516} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 1181 }[/math] | [math]\displaystyle{ 1361 }[/math] | [math]\displaystyle{ 1471 }[/math] |
| [math]\displaystyle{ \mathbf{ 522} }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 487 }[/math] | [math]\displaystyle{ 907 }[/math] | [math]\displaystyle{ 1097 }[/math] | [math]\displaystyle{ 1237 }[/math] | [math]\displaystyle{ 1747 }[/math] |
| [math]\displaystyle{ \mathbf{ 528} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 443 }[/math] | [math]\displaystyle{ 503 }[/math] | [math]\displaystyle{ 653 }[/math] | [math]\displaystyle{ 1213 }[/math] |
| [math]\displaystyle{ \mathbf{ 534} }[/math] | [math]\displaystyle{ 839 }[/math] | [math]\displaystyle{ 919 }[/math] | [math]\displaystyle{ 1019 }[/math] | [math]\displaystyle{ 1399 }[/math] | [math]\displaystyle{ 1579 }[/math] | [math]\displaystyle{ 1619 }[/math] |
| [math]\displaystyle{ \mathbf{ 540} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 113 }[/math] |
| [math]\displaystyle{ \mathbf{ 546} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 401 }[/math] | [math]\displaystyle{ 431 }[/math] | [math]\displaystyle{ 821 }[/math] |
| [math]\displaystyle{ \mathbf{ 552} }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 257 }[/math] | [math]\displaystyle{ 277 }[/math] | [math]\displaystyle{ 727 }[/math] | [math]\displaystyle{ 1427 }[/math] | [math]\displaystyle{ 2267 }[/math] |
| [math]\displaystyle{ \mathbf{ 558} }[/math] | [math]\displaystyle{ 463 }[/math] | [math]\displaystyle{ 593 }[/math] | [math]\displaystyle{ 673 }[/math] | [math]\displaystyle{ 1013 }[/math] | [math]\displaystyle{ 1583 }[/math] | [math]\displaystyle{ 2243 }[/math] |
| [math]\displaystyle{ \mathbf{ 564} }[/math] | [math]\displaystyle{ 109 }[/math] | [math]\displaystyle{ 179 }[/math] | [math]\displaystyle{ 659 }[/math] | [math]\displaystyle{ 719 }[/math] | [math]\displaystyle{ 859 }[/math] | [math]\displaystyle{ 1429 }[/math] |
| [math]\displaystyle{ \mathbf{ 570} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 163 }[/math] | [math]\displaystyle{ 241 }[/math] |
| [math]\displaystyle{ \mathbf{ 576} }[/math] | [math]\displaystyle{ 151 }[/math] | [math]\displaystyle{ 401 }[/math] | [math]\displaystyle{ 541 }[/math] | [math]\displaystyle{ 991 }[/math] | [math]\displaystyle{ 1061 }[/math] | [math]\displaystyle{ 1091 }[/math] |
| [math]\displaystyle{ \mathbf{ 582} }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 457 }[/math] | [math]\displaystyle{ 647 }[/math] | [math]\displaystyle{ 967 }[/math] | [math]\displaystyle{ 1087 }[/math] |
| [math]\displaystyle{ \mathbf{ 588} }[/math] | [math]\displaystyle{ 103 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 223 }[/math] | [math]\displaystyle{ 233 }[/math] | [math]\displaystyle{ 443 }[/math] | [math]\displaystyle{ 613 }[/math] |
| [math]\displaystyle{ \mathbf{ 594} }[/math] | [math]\displaystyle{ 5 }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 439 }[/math] | [math]\displaystyle{ 599 }[/math] | [math]\displaystyle{ 839 }[/math] | [math]\displaystyle{ 1019 }[/math] |
| [math]\displaystyle{ \mathbf{ 600} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 173 }[/math] | [math]\displaystyle{ 227 }[/math] | [math]\displaystyle{ 229 }[/math] | [math]\displaystyle{ 239 }[/math] |
□
Przykład C56
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości [math]\displaystyle{ n = 5 }[/math] i [math]\displaystyle{ n = 6 }[/math].
W przypadku [math]\displaystyle{ n = 5 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 6 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^8 }[/math].
W przypadku [math]\displaystyle{ n = 6 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 30 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^8 }[/math].
Jeżeli w tabeli jest wypisanych sześć wartości [math]\displaystyle{ p_0 }[/math], to oznacza to, że zostało znalezionych co najmniej sześć wartości [math]\displaystyle{ p_0 }[/math].
| [math]\displaystyle{ \mathbf{n = 5} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 6} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 12} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 30} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 137 }[/math] | [math]\displaystyle{ 151 }[/math] |
| [math]\displaystyle{ \mathbf{ 42} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 48} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 60} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 571 }[/math] |
| [math]\displaystyle{ \mathbf{ 90} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 103 }[/math] | [math]\displaystyle{ 503 }[/math] |
| [math]\displaystyle{ \mathbf{ 96} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 120} }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 239 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 359 }[/math] | [math]\displaystyle{ 379 }[/math] |
| [math]\displaystyle{ \mathbf{ 126} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 150} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 223 }[/math] |
| [math]\displaystyle{ \mathbf{ 180} }[/math] | [math]\displaystyle{ 101 }[/math] | [math]\displaystyle{ 103 }[/math] | [math]\displaystyle{ 367 }[/math] | [math]\displaystyle{ 397 }[/math] | [math]\displaystyle{ 577 }[/math] | [math]\displaystyle{ 1013 }[/math] |
| [math]\displaystyle{ \mathbf{ 210} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 157 }[/math] |
| [math]\displaystyle{ \mathbf{ 240} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 263 }[/math] | [math]\displaystyle{ 331 }[/math] | [math]\displaystyle{ 571 }[/math] | [math]\displaystyle{ 823 }[/math] | [math]\displaystyle{ 947 }[/math] |
| [math]\displaystyle{ \mathbf{ 252} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 270} }[/math] | [math]\displaystyle{ 491 }[/math] | [math]\displaystyle{ 557 }[/math] | [math]\displaystyle{ 613 }[/math] | [math]\displaystyle{ 641 }[/math] | [math]\displaystyle{ 743 }[/math] | [math]\displaystyle{ 827 }[/math] |
| [math]\displaystyle{ \mathbf{ 300} }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 223 }[/math] | [math]\displaystyle{ 383 }[/math] | [math]\displaystyle{ 419 }[/math] | [math]\displaystyle{ 509 }[/math] | [math]\displaystyle{ 523 }[/math] |
| [math]\displaystyle{ \mathbf{ 330} }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 317 }[/math] | [math]\displaystyle{ 457 }[/math] | [math]\displaystyle{ 491 }[/math] |
| [math]\displaystyle{ \mathbf{ 360} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 227 }[/math] | [math]\displaystyle{ 293 }[/math] | [math]\displaystyle{ 349 }[/math] | [math]\displaystyle{ 577 }[/math] |
| [math]\displaystyle{ \mathbf{ 390} }[/math] | [math]\displaystyle{ 59 }[/math] | [math]\displaystyle{ 229 }[/math] | [math]\displaystyle{ 311 }[/math] | [math]\displaystyle{ 619 }[/math] | [math]\displaystyle{ 1097 }[/math] | [math]\displaystyle{ 1489 }[/math] |
| [math]\displaystyle{ \mathbf{ 420} }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 67 }[/math] | [math]\displaystyle{ 193 }[/math] | [math]\displaystyle{ 199 }[/math] |
| [math]\displaystyle{ \mathbf{ 426} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 450} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 149 }[/math] | [math]\displaystyle{ 193 }[/math] | [math]\displaystyle{ 599 }[/math] | [math]\displaystyle{ 1033 }[/math] | [math]\displaystyle{ 1117 }[/math] |
| [math]\displaystyle{ \mathbf{ 474} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 480} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 347 }[/math] | [math]\displaystyle{ 491 }[/math] | [math]\displaystyle{ 1019 }[/math] | [math]\displaystyle{ 1103 }[/math] | [math]\displaystyle{ 1723 }[/math] |
| [math]\displaystyle{ \mathbf{ 510} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 89 }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 167 }[/math] | [math]\displaystyle{ 229 }[/math] | [math]\displaystyle{ 419 }[/math] |
| [math]\displaystyle{ \mathbf{ 540} }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 211 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 673 }[/math] | [math]\displaystyle{ 919 }[/math] |
| [math]\displaystyle{ \mathbf{ 570} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 241 }[/math] | [math]\displaystyle{ 269 }[/math] | [math]\displaystyle{ 647 }[/math] | [math]\displaystyle{ 839 }[/math] |
| [math]\displaystyle{ \mathbf{ 594} }[/math] | [math]\displaystyle{ 5 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 600} }[/math] | [math]\displaystyle{ 283 }[/math] | [math]\displaystyle{ 311 }[/math] | [math]\displaystyle{ 353 }[/math] | [math]\displaystyle{ 509 }[/math] | [math]\displaystyle{ 1223 }[/math] | [math]\displaystyle{ 1531 }[/math] |
| [math]\displaystyle{ \mathbf{n = 6} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 30} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 359 }[/math] | [math]\displaystyle{ 541 }[/math] | [math]\displaystyle{ 2221 }[/math] | [math]\displaystyle{ 6673 }[/math] |
| [math]\displaystyle{ \mathbf{ 60} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 641 }[/math] | [math]\displaystyle{ 5443 }[/math] | [math]\displaystyle{ 10091 }[/math] | [math]\displaystyle{ 12457 }[/math] |
| [math]\displaystyle{ \mathbf{ 90} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 503 }[/math] | [math]\displaystyle{ 1973 }[/math] | [math]\displaystyle{ 2351 }[/math] | [math]\displaystyle{ 5081 }[/math] | [math]\displaystyle{ 10709 }[/math] |
| [math]\displaystyle{ \mathbf{ 120} }[/math] | [math]\displaystyle{ 239 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 701 }[/math] | [math]\displaystyle{ 2339 }[/math] | [math]\displaystyle{ 2437 }[/math] | [math]\displaystyle{ 10613 }[/math] |
| [math]\displaystyle{ \mathbf{ 150} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 157 }[/math] | [math]\displaystyle{ 2467 }[/math] | [math]\displaystyle{ 4637 }[/math] | [math]\displaystyle{ 6079 }[/math] |
| [math]\displaystyle{ \mathbf{ 180} }[/math] | [math]\displaystyle{ 397 }[/math] | [math]\displaystyle{ 1013 }[/math] | [math]\displaystyle{ 1307 }[/math] | [math]\displaystyle{ 17029 }[/math] | [math]\displaystyle{ 20963 }[/math] | [math]\displaystyle{ 24337 }[/math] |
| [math]\displaystyle{ \mathbf{ 210} }[/math] | [math]\displaystyle{ 13 }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 179 }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 257 }[/math] | [math]\displaystyle{ 389 }[/math] |
| [math]\displaystyle{ \mathbf{ 240} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 331 }[/math] | [math]\displaystyle{ 2207 }[/math] | [math]\displaystyle{ 3677 }[/math] | [math]\displaystyle{ 5021 }[/math] | [math]\displaystyle{ 6323 }[/math] |
| [math]\displaystyle{ \mathbf{ 270} }[/math] | [math]\displaystyle{ 557 }[/math] | [math]\displaystyle{ 1201 }[/math] | [math]\displaystyle{ 2377 }[/math] | [math]\displaystyle{ 8467 }[/math] | [math]\displaystyle{ 9923 }[/math] | [math]\displaystyle{ 12107 }[/math] |
| [math]\displaystyle{ \mathbf{ 300} }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 223 }[/math] | [math]\displaystyle{ 587 }[/math] | [math]\displaystyle{ 1511 }[/math] | [math]\displaystyle{ 4073 }[/math] | [math]\displaystyle{ 4423 }[/math] |
| [math]\displaystyle{ \mathbf{ 330} }[/math] | [math]\displaystyle{ 127 }[/math] | [math]\displaystyle{ 491 }[/math] | [math]\displaystyle{ 2129 }[/math] | [math]\displaystyle{ 2857 }[/math] | [math]\displaystyle{ 3137 }[/math] | [math]\displaystyle{ 5153 }[/math] |
| [math]\displaystyle{ \mathbf{ 360} }[/math] | [math]\displaystyle{ 227 }[/math] | [math]\displaystyle{ 577 }[/math] | [math]\displaystyle{ 1669 }[/math] | [math]\displaystyle{ 9187 }[/math] | [math]\displaystyle{ 13331 }[/math] | [math]\displaystyle{ 13933 }[/math] |
| [math]\displaystyle{ \mathbf{ 390} }[/math] | [math]\displaystyle{ 229 }[/math] | [math]\displaystyle{ 3701 }[/math] | [math]\displaystyle{ 9007 }[/math] | [math]\displaystyle{ 9833 }[/math] | [math]\displaystyle{ 13291 }[/math] | [math]\displaystyle{ 17911 }[/math] |
| [math]\displaystyle{ \mathbf{ 420} }[/math] | [math]\displaystyle{ 41 }[/math] | [math]\displaystyle{ 43 }[/math] | [math]\displaystyle{ 193 }[/math] | [math]\displaystyle{ 613 }[/math] | [math]\displaystyle{ 743 }[/math] | [math]\displaystyle{ 1289 }[/math] |
| [math]\displaystyle{ \mathbf{ 450} }[/math] | [math]\displaystyle{ 149 }[/math] | [math]\displaystyle{ 1381 }[/math] | [math]\displaystyle{ 1451 }[/math] | [math]\displaystyle{ 3607 }[/math] | [math]\displaystyle{ 5651 }[/math] | [math]\displaystyle{ 8521 }[/math] |
| [math]\displaystyle{ \mathbf{ 480} }[/math] | [math]\displaystyle{ 11 }[/math] | [math]\displaystyle{ 5051 }[/math] | [math]\displaystyle{ 8719 }[/math] | [math]\displaystyle{ 10567 }[/math] | [math]\displaystyle{ 11113 }[/math] | [math]\displaystyle{ 13591 }[/math] |
| [math]\displaystyle{ \mathbf{ 510} }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 419 }[/math] | [math]\displaystyle{ 811 }[/math] | [math]\displaystyle{ 3191 }[/math] | [math]\displaystyle{ 3583 }[/math] | [math]\displaystyle{ 4283 }[/math] |
| [math]\displaystyle{ \mathbf{ 540} }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 673 }[/math] | [math]\displaystyle{ 3851 }[/math] | [math]\displaystyle{ 3907 }[/math] | [math]\displaystyle{ 7043 }[/math] | [math]\displaystyle{ 12377 }[/math] |
| [math]\displaystyle{ \mathbf{ 570} }[/math] | [math]\displaystyle{ 269 }[/math] | [math]\displaystyle{ 1039 }[/math] | [math]\displaystyle{ 2887 }[/math] | [math]\displaystyle{ 3853 }[/math] | [math]\displaystyle{ 10979 }[/math] | [math]\displaystyle{ 11399 }[/math] |
| [math]\displaystyle{ \mathbf{ 600} }[/math] | [math]\displaystyle{ 8839 }[/math] | [math]\displaystyle{ 23371 }[/math] | [math]\displaystyle{ 38183 }[/math] | [math]\displaystyle{ 44189 }[/math] | [math]\displaystyle{ 59743 }[/math] | [math]\displaystyle{ 63467 }[/math] |
| [math]\displaystyle{ \mathbf{ 630} }[/math] | [math]\displaystyle{ 179 }[/math] | [math]\displaystyle{ 193 }[/math] | [math]\displaystyle{ 1637 }[/math] | [math]\displaystyle{ 2267 }[/math] | [math]\displaystyle{ 2897 }[/math] | [math]\displaystyle{ 4813 }[/math] |
| [math]\displaystyle{ \mathbf{ 660} }[/math] | [math]\displaystyle{ 163 }[/math] | [math]\displaystyle{ 317 }[/math] | [math]\displaystyle{ 401 }[/math] | [math]\displaystyle{ 2753 }[/math] | [math]\displaystyle{ 3229 }[/math] | [math]\displaystyle{ 5077 }[/math] |
| [math]\displaystyle{ \mathbf{ 690} }[/math] | [math]\displaystyle{ 277 }[/math] | [math]\displaystyle{ 1523 }[/math] | [math]\displaystyle{ 6101 }[/math] | [math]\displaystyle{ 10427 }[/math] | [math]\displaystyle{ 15971 }[/math] | [math]\displaystyle{ 27059 }[/math] |
| [math]\displaystyle{ \mathbf{ 720} }[/math] | [math]\displaystyle{ 1231 }[/math] | [math]\displaystyle{ 3793 }[/math] | [math]\displaystyle{ 4003 }[/math] | [math]\displaystyle{ 6229 }[/math] | [math]\displaystyle{ 7573 }[/math] | [math]\displaystyle{ 10079 }[/math] |
| [math]\displaystyle{ \mathbf{ 750} }[/math] | [math]\displaystyle{ 1051 }[/math] | [math]\displaystyle{ 1289 }[/math] | [math]\displaystyle{ 1583 }[/math] | [math]\displaystyle{ 2857 }[/math] | [math]\displaystyle{ 12377 }[/math] | [math]\displaystyle{ 18523 }[/math] |
| [math]\displaystyle{ \mathbf{ 780} }[/math] | [math]\displaystyle{ 1151 }[/math] | [math]\displaystyle{ 3517 }[/math] | [math]\displaystyle{ 3923 }[/math] | [math]\displaystyle{ 4637 }[/math] | [math]\displaystyle{ 5309 }[/math] | [math]\displaystyle{ 9929 }[/math] |
| [math]\displaystyle{ \mathbf{ 810} }[/math] | [math]\displaystyle{ 1993 }[/math] | [math]\displaystyle{ 7817 }[/math] | [math]\displaystyle{ 11443 }[/math] | [math]\displaystyle{ 17519 }[/math] | [math]\displaystyle{ 52631 }[/math] | [math]\displaystyle{ 109919 }[/math] |
| [math]\displaystyle{ \mathbf{ 840} }[/math] | [math]\displaystyle{ 97 }[/math] | [math]\displaystyle{ 313 }[/math] | [math]\displaystyle{ 1061 }[/math] | [math]\displaystyle{ 1753 }[/math] | [math]\displaystyle{ 1901 }[/math] | [math]\displaystyle{ 2593 }[/math] |
| [math]\displaystyle{ \mathbf{ 870} }[/math] | [math]\displaystyle{ 2039 }[/math] | [math]\displaystyle{ 2179 }[/math] | [math]\displaystyle{ 5273 }[/math] | [math]\displaystyle{ 5987 }[/math] | [math]\displaystyle{ 9431 }[/math] | [math]\displaystyle{ 10957 }[/math] |
| [math]\displaystyle{ \mathbf{ 900} }[/math] | [math]\displaystyle{ 1747 }[/math] | [math]\displaystyle{ 12541 }[/math] | [math]\displaystyle{ 14767 }[/math] | [math]\displaystyle{ 21193 }[/math] | [math]\displaystyle{ 31511 }[/math] | [math]\displaystyle{ 40289 }[/math] |
| [math]\displaystyle{ \mathbf{ 930} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 293 }[/math] | [math]\displaystyle{ 9043 }[/math] | [math]\displaystyle{ 10247 }[/math] | [math]\displaystyle{ 34327 }[/math] | [math]\displaystyle{ 38891 }[/math] |
| [math]\displaystyle{ \mathbf{ 960} }[/math] | [math]\displaystyle{ 4943 }[/math] | [math]\displaystyle{ 8737 }[/math] | [math]\displaystyle{ 15373 }[/math] | [math]\displaystyle{ 28351 }[/math] | [math]\displaystyle{ 35393 }[/math] | [math]\displaystyle{ 36919 }[/math] |
| [math]\displaystyle{ \mathbf{ 990} }[/math] | [math]\displaystyle{ 1249 }[/math] | [math]\displaystyle{ 1319 }[/math] | [math]\displaystyle{ 2467 }[/math] | [math]\displaystyle{ 2957 }[/math] | [math]\displaystyle{ 4049 }[/math] | [math]\displaystyle{ 8291 }[/math] |
| [math]\displaystyle{ \mathbf{ 1020} }[/math] | [math]\displaystyle{ 887 }[/math] | [math]\displaystyle{ 929 }[/math] | [math]\displaystyle{ 2441 }[/math] | [math]\displaystyle{ 4639 }[/math] | [math]\displaystyle{ 15083 }[/math] | [math]\displaystyle{ 19997 }[/math] |
| [math]\displaystyle{ \mathbf{ 1050} }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 257 }[/math] | [math]\displaystyle{ 443 }[/math] | [math]\displaystyle{ 839 }[/math] | [math]\displaystyle{ 1103 }[/math] | [math]\displaystyle{ 3469 }[/math] |
| [math]\displaystyle{ \mathbf{ 1080} }[/math] | [math]\displaystyle{ 1423 }[/math] | [math]\displaystyle{ 9011 }[/math] | [math]\displaystyle{ 10663 }[/math] | [math]\displaystyle{ 27799 }[/math] | [math]\displaystyle{ 36493 }[/math] | [math]\displaystyle{ 51473 }[/math] |
| [math]\displaystyle{ \mathbf{ 1110} }[/math] | [math]\displaystyle{ 3847 }[/math] | [math]\displaystyle{ 9643 }[/math] | [math]\displaystyle{ 10357 }[/math] | [math]\displaystyle{ 11743 }[/math] | [math]\displaystyle{ 16223 }[/math] | [math]\displaystyle{ 21977 }[/math] |
| [math]\displaystyle{ \mathbf{ 1140} }[/math] | [math]\displaystyle{ 1063 }[/math] | [math]\displaystyle{ 1301 }[/math] | [math]\displaystyle{ 1553 }[/math] | [math]\displaystyle{ 1777 }[/math] | [math]\displaystyle{ 5683 }[/math] | [math]\displaystyle{ 6397 }[/math] |
| [math]\displaystyle{ \mathbf{ 1170} }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 701 }[/math] | [math]\displaystyle{ 911 }[/math] | [math]\displaystyle{ 2143 }[/math] | [math]\displaystyle{ 2297 }[/math] | [math]\displaystyle{ 2857 }[/math] |
| [math]\displaystyle{ \mathbf{ 1200} }[/math] | [math]\displaystyle{ 367 }[/math] | [math]\displaystyle{ 2677 }[/math] | [math]\displaystyle{ 3391 }[/math] | [math]\displaystyle{ 18749 }[/math] | [math]\displaystyle{ 34961 }[/math] | [math]\displaystyle{ 59699 }[/math] |
| [math]\displaystyle{ \mathbf{ 1230} }[/math] | [math]\displaystyle{ 2539 }[/math] | [math]\displaystyle{ 6053 }[/math] | [math]\displaystyle{ 6823 }[/math] | [math]\displaystyle{ 9091 }[/math] | [math]\displaystyle{ 12101 }[/math] | [math]\displaystyle{ 14831 }[/math] |
| [math]\displaystyle{ \mathbf{ 1260} }[/math] | [math]\displaystyle{ 359 }[/math] | [math]\displaystyle{ 617 }[/math] | [math]\displaystyle{ 739 }[/math] | [math]\displaystyle{ 1051 }[/math] | [math]\displaystyle{ 1619 }[/math] | [math]\displaystyle{ 1931 }[/math] |
| [math]\displaystyle{ \mathbf{ 1290} }[/math] | [math]\displaystyle{ 149 }[/math] | [math]\displaystyle{ 17747 }[/math] | [math]\displaystyle{ 20981 }[/math] | [math]\displaystyle{ 24481 }[/math] | [math]\displaystyle{ 46643 }[/math] | [math]\displaystyle{ 47917 }[/math] |
| [math]\displaystyle{ \mathbf{ 1320} }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 977 }[/math] | [math]\displaystyle{ 991 }[/math] | [math]\displaystyle{ 2237 }[/math] | [math]\displaystyle{ 9461 }[/math] | [math]\displaystyle{ 20983 }[/math] |
| [math]\displaystyle{ \mathbf{ 1350} }[/math] | [math]\displaystyle{ 811 }[/math] | [math]\displaystyle{ 937 }[/math] | [math]\displaystyle{ 3877 }[/math] | [math]\displaystyle{ 14923 }[/math] | [math]\displaystyle{ 16001 }[/math] | [math]\displaystyle{ 18493 }[/math] |
| [math]\displaystyle{ \mathbf{ 1380} }[/math] | [math]\displaystyle{ 3613 }[/math] | [math]\displaystyle{ 9227 }[/math] | [math]\displaystyle{ 15541 }[/math] | [math]\displaystyle{ 16927 }[/math] | [math]\displaystyle{ 17417 }[/math] | [math]\displaystyle{ 18089 }[/math] |
| [math]\displaystyle{ \mathbf{ 1410} }[/math] | [math]\displaystyle{ 367 }[/math] | [math]\displaystyle{ 2593 }[/math] | [math]\displaystyle{ 12421 }[/math] | [math]\displaystyle{ 50599 }[/math] | [math]\displaystyle{ 60889 }[/math] | [math]\displaystyle{ 80629 }[/math] |
| [math]\displaystyle{ \mathbf{ 1440} }[/math] | [math]\displaystyle{ 439 }[/math] | [math]\displaystyle{ 6277 }[/math] | [math]\displaystyle{ 20753 }[/math] | [math]\displaystyle{ 21929 }[/math] | [math]\displaystyle{ 39079 }[/math] | [math]\displaystyle{ 57727 }[/math] |
| [math]\displaystyle{ \mathbf{ 1470} }[/math] | [math]\displaystyle{ 1279 }[/math] | [math]\displaystyle{ 1877 }[/math] | [math]\displaystyle{ 2383 }[/math] | [math]\displaystyle{ 2393 }[/math] | [math]\displaystyle{ 2749 }[/math] | [math]\displaystyle{ 2801 }[/math] |
| [math]\displaystyle{ \mathbf{ 1500} }[/math] | [math]\displaystyle{ 7331 }[/math] | [math]\displaystyle{ 8423 }[/math] | [math]\displaystyle{ 15493 }[/math] | [math]\displaystyle{ 28513 }[/math] | [math]\displaystyle{ 31607 }[/math] | [math]\displaystyle{ 38453 }[/math] |
| [math]\displaystyle{ \mathbf{ 1530} }[/math] | [math]\displaystyle{ 2741 }[/math] | [math]\displaystyle{ 3203 }[/math] | [math]\displaystyle{ 8537 }[/math] | [math]\displaystyle{ 14389 }[/math] | [math]\displaystyle{ 20143 }[/math] | [math]\displaystyle{ 21277 }[/math] |
| [math]\displaystyle{ \mathbf{ 1560} }[/math] | [math]\displaystyle{ 419 }[/math] | [math]\displaystyle{ 727 }[/math] | [math]\displaystyle{ 3499 }[/math] | [math]\displaystyle{ 3919 }[/math] | [math]\displaystyle{ 6257 }[/math] | [math]\displaystyle{ 9029 }[/math] |
| [math]\displaystyle{ \mathbf{ 1590} }[/math] | [math]\displaystyle{ 2213 }[/math] | [math]\displaystyle{ 2339 }[/math] | [math]\displaystyle{ 4523 }[/math] | [math]\displaystyle{ 6469 }[/math] | [math]\displaystyle{ 9241 }[/math] | [math]\displaystyle{ 9857 }[/math] |
| [math]\displaystyle{ \mathbf{ 1620} }[/math] | [math]\displaystyle{ 7717 }[/math] | [math]\displaystyle{ 9103 }[/math] | [math]\displaystyle{ 12379 }[/math] | [math]\displaystyle{ 37607 }[/math] | [math]\displaystyle{ 43613 }[/math] | [math]\displaystyle{ 46567 }[/math] |
| [math]\displaystyle{ \mathbf{ 1650} }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 3001 }[/math] | [math]\displaystyle{ 3659 }[/math] | [math]\displaystyle{ 4051 }[/math] | [math]\displaystyle{ 4289 }[/math] | [math]\displaystyle{ 11527 }[/math] |
| [math]\displaystyle{ \mathbf{ 1680} }[/math] | [math]\displaystyle{ 197 }[/math] | [math]\displaystyle{ 997 }[/math] | [math]\displaystyle{ 1289 }[/math] | [math]\displaystyle{ 1319 }[/math] | [math]\displaystyle{ 2309 }[/math] | [math]\displaystyle{ 2683 }[/math] |
| [math]\displaystyle{ \mathbf{ 1710} }[/math] | [math]\displaystyle{ 373 }[/math] | [math]\displaystyle{ 1549 }[/math] | [math]\displaystyle{ 1913 }[/math] | [math]\displaystyle{ 2711 }[/math] | [math]\displaystyle{ 12539 }[/math] | [math]\displaystyle{ 15031 }[/math] |
| [math]\displaystyle{ \mathbf{ 1740} }[/math] | [math]\displaystyle{ 1621 }[/math] | [math]\displaystyle{ 5387 }[/math] | [math]\displaystyle{ 6269 }[/math] | [math]\displaystyle{ 15551 }[/math] | [math]\displaystyle{ 61723 }[/math] | [math]\displaystyle{ 77543 }[/math] |
| [math]\displaystyle{ \mathbf{ 1770} }[/math] | [math]\displaystyle{ 1483 }[/math] | [math]\displaystyle{ 13691 }[/math] | [math]\displaystyle{ 15329 }[/math] | [math]\displaystyle{ 20873 }[/math] | [math]\displaystyle{ 23869 }[/math] | [math]\displaystyle{ 29917 }[/math] |
| [math]\displaystyle{ \mathbf{ 1800} }[/math] | [math]\displaystyle{ 421 }[/math] | [math]\displaystyle{ 967 }[/math] | [math]\displaystyle{ 1499 }[/math] | [math]\displaystyle{ 6217 }[/math] | [math]\displaystyle{ 30983 }[/math] | [math]\displaystyle{ 37171 }[/math] |
| [math]\displaystyle{ \mathbf{ 1830} }[/math] | [math]\displaystyle{ 31 }[/math] | [math]\displaystyle{ 17909 }[/math] | [math]\displaystyle{ 46567 }[/math] | [math]\displaystyle{ 89057 }[/math] | [math]\displaystyle{ 105619 }[/math] | [math]\displaystyle{ 128341 }[/math] |
| [math]\displaystyle{ \mathbf{ 1860} }[/math] | [math]\displaystyle{ 5087 }[/math] | [math]\displaystyle{ 6151 }[/math] | [math]\displaystyle{ 9133 }[/math] | [math]\displaystyle{ 16567 }[/math] | [math]\displaystyle{ 23819 }[/math] | [math]\displaystyle{ 29881 }[/math] |
| [math]\displaystyle{ \mathbf{ 1890} }[/math] | [math]\displaystyle{ 23 }[/math] | [math]\displaystyle{ 727 }[/math] | [math]\displaystyle{ 1109 }[/math] | [math]\displaystyle{ 1279 }[/math] | [math]\displaystyle{ 1409 }[/math] | [math]\displaystyle{ 1543 }[/math] |
| [math]\displaystyle{ \mathbf{ 1920} }[/math] | [math]\displaystyle{ 79 }[/math] | [math]\displaystyle{ 1493 }[/math] | [math]\displaystyle{ 13967 }[/math] | [math]\displaystyle{ 19973 }[/math] | [math]\displaystyle{ 41351 }[/math] | [math]\displaystyle{ 46867 }[/math] |
| [math]\displaystyle{ \mathbf{ 1950} }[/math] | [math]\displaystyle{ 3259 }[/math] | [math]\displaystyle{ 4813 }[/math] | [math]\displaystyle{ 8803 }[/math] | [math]\displaystyle{ 12373 }[/math] | [math]\displaystyle{ 13577 }[/math] | [math]\displaystyle{ 13619 }[/math] |
| [math]\displaystyle{ \mathbf{ 1980} }[/math] | [math]\displaystyle{ 1511 }[/math] | [math]\displaystyle{ 3863 }[/math] | [math]\displaystyle{ 4969 }[/math] | [math]\displaystyle{ 5039 }[/math] | [math]\displaystyle{ 7027 }[/math] | [math]\displaystyle{ 9337 }[/math] |
| [math]\displaystyle{ \mathbf{ 2010} }[/math] | [math]\displaystyle{ 1303 }[/math] | [math]\displaystyle{ 3739 }[/math] | [math]\displaystyle{ 7309 }[/math] | [math]\displaystyle{ 13763 }[/math] | [math]\displaystyle{ 22093 }[/math] | [math]\displaystyle{ 31151 }[/math] |
| [math]\displaystyle{ \mathbf{ 2040} }[/math] | [math]\displaystyle{ 1039 }[/math] | [math]\displaystyle{ 6779 }[/math] | [math]\displaystyle{ 7507 }[/math] | [math]\displaystyle{ 8963 }[/math] | [math]\displaystyle{ 10069 }[/math] | [math]\displaystyle{ 12281 }[/math] |
| [math]\displaystyle{ \mathbf{ 2070} }[/math] | [math]\displaystyle{ 1097 }[/math] | [math]\displaystyle{ 2063 }[/math] | [math]\displaystyle{ 2917 }[/math] | [math]\displaystyle{ 4289 }[/math] | [math]\displaystyle{ 6571 }[/math] | [math]\displaystyle{ 11149 }[/math] |
| [math]\displaystyle{ \mathbf{ 2100} }[/math] | [math]\displaystyle{ 29 }[/math] | [math]\displaystyle{ 281 }[/math] | [math]\displaystyle{ 757 }[/math] | [math]\displaystyle{ 1459 }[/math] | [math]\displaystyle{ 1847 }[/math] | [math]\displaystyle{ 2503 }[/math] |
| [math]\displaystyle{ \mathbf{ 2130} }[/math] | [math]\displaystyle{ 3677 }[/math] | [math]\displaystyle{ 5077 }[/math] | [math]\displaystyle{ 11699 }[/math] | [math]\displaystyle{ 17159 }[/math] | [math]\displaystyle{ 21149 }[/math] | [math]\displaystyle{ 31159 }[/math] |
| [math]\displaystyle{ \mathbf{ 2160} }[/math] | [math]\displaystyle{ 5849 }[/math] | [math]\displaystyle{ 6619 }[/math] | [math]\displaystyle{ 24329 }[/math] | [math]\displaystyle{ 43019 }[/math] | [math]\displaystyle{ 114419 }[/math] | [math]\displaystyle{ 126823 }[/math] |
| [math]\displaystyle{ \mathbf{ 2190} }[/math] | [math]\displaystyle{ 643 }[/math] | [math]\displaystyle{ 4283 }[/math] | [math]\displaystyle{ 4339 }[/math] | [math]\displaystyle{ 23743 }[/math] | [math]\displaystyle{ 24821 }[/math] | [math]\displaystyle{ 30211 }[/math] |
| [math]\displaystyle{ \mathbf{ 2220} }[/math] | [math]\displaystyle{ 4229 }[/math] | [math]\displaystyle{ 11243 }[/math] | [math]\displaystyle{ 11467 }[/math] | [math]\displaystyle{ 12503 }[/math] | [math]\displaystyle{ 13693 }[/math] | [math]\displaystyle{ 26209 }[/math] |
| [math]\displaystyle{ \mathbf{ 2250} }[/math] | [math]\displaystyle{ 4721 }[/math] | [math]\displaystyle{ 6359 }[/math] | [math]\displaystyle{ 17321 }[/math] | [math]\displaystyle{ 19477 }[/math] | [math]\displaystyle{ 21661 }[/math] | [math]\displaystyle{ 23117 }[/math] |
| [math]\displaystyle{ \mathbf{ 2280} }[/math] | [math]\displaystyle{ 719 }[/math] | [math]\displaystyle{ 2399 }[/math] | [math]\displaystyle{ 15797 }[/math] | [math]\displaystyle{ 22391 }[/math] | [math]\displaystyle{ 23189 }[/math] | [math]\displaystyle{ 27809 }[/math] |
| [math]\displaystyle{ \mathbf{ 2310} }[/math] | [math]\displaystyle{ 37 }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 83 }[/math] | [math]\displaystyle{ 547 }[/math] | [math]\displaystyle{ 661 }[/math] | [math]\displaystyle{ 859 }[/math] |
| [math]\displaystyle{ \mathbf{ 2340} }[/math] | [math]\displaystyle{ 107 }[/math] | [math]\displaystyle{ 4363 }[/math] | [math]\displaystyle{ 5483 }[/math] | [math]\displaystyle{ 9613 }[/math] | [math]\displaystyle{ 12413 }[/math] | [math]\displaystyle{ 14737 }[/math] |
| [math]\displaystyle{ \mathbf{ 2370} }[/math] | [math]\displaystyle{ 1187 }[/math] | [math]\displaystyle{ 1831 }[/math] | [math]\displaystyle{ 4211 }[/math] | [math]\displaystyle{ 7963 }[/math] | [math]\displaystyle{ 9419 }[/math] | [math]\displaystyle{ 15607 }[/math] |
| [math]\displaystyle{ \mathbf{ 2400} }[/math] | [math]\displaystyle{ 503 }[/math] | [math]\displaystyle{ 853 }[/math] | [math]\displaystyle{ 4787 }[/math] | [math]\displaystyle{ 15091 }[/math] | [math]\displaystyle{ 20327 }[/math] | [math]\displaystyle{ 23603 }[/math] |
| [math]\displaystyle{ \mathbf{ 2430} }[/math] | [math]\displaystyle{ 13217 }[/math] | [math]\displaystyle{ 31039 }[/math] | [math]\displaystyle{ 38851 }[/math] | [math]\displaystyle{ 43261 }[/math] | [math]\displaystyle{ 46747 }[/math] | [math]\displaystyle{ 67481 }[/math] |
| [math]\displaystyle{ \mathbf{ 2460} }[/math] | [math]\displaystyle{ 227 }[/math] | [math]\displaystyle{ 1459 }[/math] | [math]\displaystyle{ 6779 }[/math] | [math]\displaystyle{ 6863 }[/math] | [math]\displaystyle{ 18553 }[/math] | [math]\displaystyle{ 29207 }[/math] |
| [math]\displaystyle{ \mathbf{ 2490} }[/math] | [math]\displaystyle{ 1237 }[/math] | [math]\displaystyle{ 7621 }[/math] | [math]\displaystyle{ 14411 }[/math] | [math]\displaystyle{ 19801 }[/math] | [math]\displaystyle{ 46457 }[/math] | [math]\displaystyle{ 55921 }[/math] |
| [math]\displaystyle{ \mathbf{ 2520} }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 709 }[/math] | [math]\displaystyle{ 1013 }[/math] | [math]\displaystyle{ 1181 }[/math] | [math]\displaystyle{ 1303 }[/math] | [math]\displaystyle{ 1409 }[/math] |
| [math]\displaystyle{ \mathbf{ 2550} }[/math] | [math]\displaystyle{ 1871 }[/math] | [math]\displaystyle{ 9403 }[/math] | [math]\displaystyle{ 33203 }[/math] | [math]\displaystyle{ 36241 }[/math] | [math]\displaystyle{ 70009 }[/math] | [math]\displaystyle{ 74587 }[/math] |
| [math]\displaystyle{ \mathbf{ 2580} }[/math] | [math]\displaystyle{ 277 }[/math] | [math]\displaystyle{ 6101 }[/math] | [math]\displaystyle{ 29383 }[/math] | [math]\displaystyle{ 35851 }[/math] | [math]\displaystyle{ 55871 }[/math] | [math]\displaystyle{ 61723 }[/math] |
| [math]\displaystyle{ \mathbf{ 2610} }[/math] | [math]\displaystyle{ 5179 }[/math] | [math]\displaystyle{ 8539 }[/math] | [math]\displaystyle{ 8861 }[/math] | [math]\displaystyle{ 10093 }[/math] | [math]\displaystyle{ 15679 }[/math] | [math]\displaystyle{ 17989 }[/math] |
| [math]\displaystyle{ \mathbf{ 2640} }[/math] | [math]\displaystyle{ 9283 }[/math] | [math]\displaystyle{ 10781 }[/math] | [math]\displaystyle{ 12377 }[/math] | [math]\displaystyle{ 12433 }[/math] | [math]\displaystyle{ 13679 }[/math] | [math]\displaystyle{ 22751 }[/math] |
| [math]\displaystyle{ \mathbf{ 2670} }[/math] | [math]\displaystyle{ 1039 }[/math] | [math]\displaystyle{ 4133 }[/math] | [math]\displaystyle{ 12589 }[/math] | [math]\displaystyle{ 14731 }[/math] | [math]\displaystyle{ 16411 }[/math] | [math]\displaystyle{ 23789 }[/math] |
| [math]\displaystyle{ \mathbf{ 2700} }[/math] | [math]\displaystyle{ 8629 }[/math] | [math]\displaystyle{ 10267 }[/math] | [math]\displaystyle{ 16217 }[/math] | [math]\displaystyle{ 17477 }[/math] | [math]\displaystyle{ 18149 }[/math] | [math]\displaystyle{ 19843 }[/math] |
| [math]\displaystyle{ \mathbf{ 2730} }[/math] | [math]\displaystyle{ 19 }[/math] | [math]\displaystyle{ 631 }[/math] | [math]\displaystyle{ 761 }[/math] | [math]\displaystyle{ 811 }[/math] | [math]\displaystyle{ 1091 }[/math] | [math]\displaystyle{ 1423 }[/math] |
| [math]\displaystyle{ \mathbf{ 2760} }[/math] | [math]\displaystyle{ 7 }[/math] | [math]\displaystyle{ 2473 }[/math] | [math]\displaystyle{ 2767 }[/math] | [math]\displaystyle{ 9137 }[/math] | [math]\displaystyle{ 9403 }[/math] | [math]\displaystyle{ 9767 }[/math] |
| [math]\displaystyle{ \mathbf{ 2790} }[/math] | [math]\displaystyle{ 6899 }[/math] | [math]\displaystyle{ 15733 }[/math] | [math]\displaystyle{ 20353 }[/math] | [math]\displaystyle{ 20899 }[/math] | [math]\displaystyle{ 23447 }[/math] | [math]\displaystyle{ 29201 }[/math] |
| [math]\displaystyle{ \mathbf{ 2820} }[/math] | [math]\displaystyle{ 727 }[/math] | [math]\displaystyle{ 1259 }[/math] | [math]\displaystyle{ 3023 }[/math] | [math]\displaystyle{ 7951 }[/math] | [math]\displaystyle{ 17989 }[/math] | [math]\displaystyle{ 20201 }[/math] |
| [math]\displaystyle{ \mathbf{ 2850} }[/math] | [math]\displaystyle{ 379 }[/math] | [math]\displaystyle{ 463 }[/math] | [math]\displaystyle{ 2843 }[/math] | [math]\displaystyle{ 4831 }[/math] | [math]\displaystyle{ 9661 }[/math] | [math]\displaystyle{ 10067 }[/math] |
| [math]\displaystyle{ \mathbf{ 2880} }[/math] | [math]\displaystyle{ 1459 }[/math] | [math]\displaystyle{ 2803 }[/math] | [math]\displaystyle{ 4973 }[/math] | [math]\displaystyle{ 7283 }[/math] | [math]\displaystyle{ 8543 }[/math] | [math]\displaystyle{ 12281 }[/math] |
| [math]\displaystyle{ \mathbf{ 2910} }[/math] | [math]\displaystyle{ 397 }[/math] | [math]\displaystyle{ 12409 }[/math] | [math]\displaystyle{ 19087 }[/math] | [math]\displaystyle{ 25121 }[/math] | [math]\displaystyle{ 37441 }[/math] | [math]\displaystyle{ 41081 }[/math] |
| [math]\displaystyle{ \mathbf{ 2940} }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 383 }[/math] | [math]\displaystyle{ 691 }[/math] | [math]\displaystyle{ 983 }[/math] | [math]\displaystyle{ 2393 }[/math] | [math]\displaystyle{ 2797 }[/math] |
| [math]\displaystyle{ \mathbf{ 2970} }[/math] | [math]\displaystyle{ 1031 }[/math] | [math]\displaystyle{ 2879 }[/math] | [math]\displaystyle{ 3593 }[/math] | [math]\displaystyle{ 5147 }[/math] | [math]\displaystyle{ 6029 }[/math] | [math]\displaystyle{ 6673 }[/math] |
| [math]\displaystyle{ \mathbf{ 3000} }[/math] | [math]\displaystyle{ 907 }[/math] | [math]\displaystyle{ 35543 }[/math] | [math]\displaystyle{ 45413 }[/math] | [math]\displaystyle{ 60337 }[/math] | [math]\displaystyle{ 65713 }[/math] | [math]\displaystyle{ 89009 }[/math] |
□
Przykład C57
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości [math]\displaystyle{ n = 7 }[/math] i [math]\displaystyle{ n = 8 }[/math].
W przypadku [math]\displaystyle{ n = 7 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 30 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^8 }[/math].
W przypadku [math]\displaystyle{ n = 8 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 210 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^8 }[/math].
Jeżeli w tabeli jest wypisanych sześć wartości [math]\displaystyle{ p_0 }[/math], to oznacza to, że zostało znalezionych co najmniej sześć wartości [math]\displaystyle{ p_0 }[/math].
| [math]\displaystyle{ \mathbf{n = 7} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 150} }[/math] | [math]\displaystyle{ 7 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 210} }[/math] | [math]\displaystyle{ 47 }[/math] | [math]\displaystyle{ 179 }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 409 }[/math] | [math]\displaystyle{ 619 }[/math] | [math]\displaystyle{ 829 }[/math] |
| [math]\displaystyle{ \mathbf{ 420} }[/math] | [math]\displaystyle{ 193 }[/math] | [math]\displaystyle{ 1619 }[/math] | [math]\displaystyle{ 2239 }[/math] | [math]\displaystyle{ 2659 }[/math] | [math]\displaystyle{ 4259 }[/math] | [math]\displaystyle{ 5849 }[/math] |
| [math]\displaystyle{ \mathbf{ 630} }[/math] | [math]\displaystyle{ 1637 }[/math] | [math]\displaystyle{ 2267 }[/math] | [math]\displaystyle{ 5569 }[/math] | [math]\displaystyle{ 8369 }[/math] | [math]\displaystyle{ 11003 }[/math] | [math]\displaystyle{ 11633 }[/math] |
| [math]\displaystyle{ \mathbf{ 840} }[/math] | [math]\displaystyle{ 1061 }[/math] | [math]\displaystyle{ 1753 }[/math] | [math]\displaystyle{ 3623 }[/math] | [math]\displaystyle{ 4493 }[/math] | [math]\displaystyle{ 5651 }[/math] | [math]\displaystyle{ 6043 }[/math] |
| [math]\displaystyle{ \mathbf{ 1050} }[/math] | [math]\displaystyle{ 53 }[/math] | [math]\displaystyle{ 3469 }[/math] | [math]\displaystyle{ 6653 }[/math] | [math]\displaystyle{ 8629 }[/math] | [math]\displaystyle{ 8783 }[/math] | [math]\displaystyle{ 8837 }[/math] |
| [math]\displaystyle{ \mathbf{ 1260} }[/math] | [math]\displaystyle{ 359 }[/math] | [math]\displaystyle{ 1931 }[/math] | [math]\displaystyle{ 2063 }[/math] | [math]\displaystyle{ 3323 }[/math] | [math]\displaystyle{ 4583 }[/math] | [math]\displaystyle{ 13933 }[/math] |
| [math]\displaystyle{ \mathbf{ 1470} }[/math] | [math]\displaystyle{ 1279 }[/math] | [math]\displaystyle{ 2393 }[/math] | [math]\displaystyle{ 2801 }[/math] | [math]\displaystyle{ 8117 }[/math] | [math]\displaystyle{ 8191 }[/math] | [math]\displaystyle{ 9661 }[/math] |
| [math]\displaystyle{ \mathbf{ 1680} }[/math] | [math]\displaystyle{ 1289 }[/math] | [math]\displaystyle{ 1319 }[/math] | [math]\displaystyle{ 2683 }[/math] | [math]\displaystyle{ 2969 }[/math] | [math]\displaystyle{ 11261 }[/math] | [math]\displaystyle{ 12941 }[/math] |
| [math]\displaystyle{ \mathbf{ 1890} }[/math] | [math]\displaystyle{ 1279 }[/math] | [math]\displaystyle{ 1723 }[/math] | [math]\displaystyle{ 1811 }[/math] | [math]\displaystyle{ 1879 }[/math] | [math]\displaystyle{ 2693 }[/math] | [math]\displaystyle{ 4583 }[/math] |
| [math]\displaystyle{ \mathbf{ 2100} }[/math] | [math]\displaystyle{ 1847 }[/math] | [math]\displaystyle{ 3947 }[/math] | [math]\displaystyle{ 26497 }[/math] | [math]\displaystyle{ 34913 }[/math] | [math]\displaystyle{ 35771 }[/math] | [math]\displaystyle{ 36187 }[/math] |
| [math]\displaystyle{ \mathbf{ 2310} }[/math] | [math]\displaystyle{ 71 }[/math] | [math]\displaystyle{ 547 }[/math] | [math]\displaystyle{ 1019 }[/math] | [math]\displaystyle{ 1063 }[/math] | [math]\displaystyle{ 1367 }[/math] | [math]\displaystyle{ 1747 }[/math] |
| [math]\displaystyle{ \mathbf{ 2520} }[/math] | [math]\displaystyle{ 113 }[/math] | [math]\displaystyle{ 1181 }[/math] | [math]\displaystyle{ 1409 }[/math] | [math]\displaystyle{ 5413 }[/math] | [math]\displaystyle{ 7109 }[/math] | [math]\displaystyle{ 7933 }[/math] |
| [math]\displaystyle{ \mathbf{ 2730} }[/math] | [math]\displaystyle{ 631 }[/math] | [math]\displaystyle{ 811 }[/math] | [math]\displaystyle{ 1091 }[/math] | [math]\displaystyle{ 2417 }[/math] | [math]\displaystyle{ 3643 }[/math] | [math]\displaystyle{ 3821 }[/math] |
| [math]\displaystyle{ \mathbf{ 2760} }[/math] | [math]\displaystyle{ 7 }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 2940} }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 6317 }[/math] | [math]\displaystyle{ 6911 }[/math] | [math]\displaystyle{ 9433 }[/math] | [math]\displaystyle{ 11927 }[/math] | [math]\displaystyle{ 12373 }[/math] |
| [math]\displaystyle{ \mathbf{n = 8} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 210} }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 409 }[/math] | [math]\displaystyle{ 619 }[/math] | [math]\displaystyle{ 881 }[/math] | [math]\displaystyle{ 3499 }[/math] | [math]\displaystyle{ 3709 }[/math] |
| [math]\displaystyle{ \mathbf{ 420} }[/math] | [math]\displaystyle{ 2239 }[/math] | [math]\displaystyle{ 10243 }[/math] | [math]\displaystyle{ 18493 }[/math] | [math]\displaystyle{ 29297 }[/math] | [math]\displaystyle{ 39199 }[/math] | [math]\displaystyle{ 40343 }[/math] |
| [math]\displaystyle{ \mathbf{ 630} }[/math] | [math]\displaystyle{ 1637 }[/math] | [math]\displaystyle{ 11003 }[/math] | [math]\displaystyle{ 38693 }[/math] | [math]\displaystyle{ 53161 }[/math] | [math]\displaystyle{ 56477 }[/math] | [math]\displaystyle{ 198971 }[/math] |
| [math]\displaystyle{ \mathbf{ 840} }[/math] | [math]\displaystyle{ 6043 }[/math] | [math]\displaystyle{ 6883 }[/math] | [math]\displaystyle{ 10861 }[/math] | [math]\displaystyle{ 11701 }[/math] | [math]\displaystyle{ 84521 }[/math] | [math]\displaystyle{ 103837 }[/math] |
| [math]\displaystyle{ \mathbf{ 1050} }[/math] | [math]\displaystyle{ 8837 }[/math] | [math]\displaystyle{ 41507 }[/math] | [math]\displaystyle{ 246289 }[/math] | [math]\displaystyle{ 302273 }[/math] | [math]\displaystyle{ 382727 }[/math] | [math]\displaystyle{ 499679 }[/math] |
| [math]\displaystyle{ \mathbf{ 1260} }[/math] | [math]\displaystyle{ 2063 }[/math] | [math]\displaystyle{ 3323 }[/math] | [math]\displaystyle{ 87511 }[/math] | [math]\displaystyle{ 145949 }[/math] | [math]\displaystyle{ 208099 }[/math] | [math]\displaystyle{ 213247 }[/math] |
| [math]\displaystyle{ \mathbf{ 1470} }[/math] | [math]\displaystyle{ 8191 }[/math] | [math]\displaystyle{ 15289 }[/math] | [math]\displaystyle{ 101027 }[/math] | [math]\displaystyle{ 102497 }[/math] | [math]\displaystyle{ 187931 }[/math] | [math]\displaystyle{ 227399 }[/math] |
| [math]\displaystyle{ \mathbf{ 1680} }[/math] | [math]\displaystyle{ 1289 }[/math] | [math]\displaystyle{ 11261 }[/math] | [math]\displaystyle{ 31333 }[/math] | [math]\displaystyle{ 33013 }[/math] | [math]\displaystyle{ 133919 }[/math] | [math]\displaystyle{ 193283 }[/math] |
| [math]\displaystyle{ \mathbf{ 1890} }[/math] | [math]\displaystyle{ 2693 }[/math] | [math]\displaystyle{ 15493 }[/math] | [math]\displaystyle{ 15607 }[/math] | [math]\displaystyle{ 17497 }[/math] | [math]\displaystyle{ 45767 }[/math] | [math]\displaystyle{ 47657 }[/math] |
| [math]\displaystyle{ \mathbf{ 2100} }[/math] | [math]\displaystyle{ 1847 }[/math] | [math]\displaystyle{ 34913 }[/math] | [math]\displaystyle{ 37013 }[/math] | [math]\displaystyle{ 39113 }[/math] | [math]\displaystyle{ 83311 }[/math] | [math]\displaystyle{ 102871 }[/math] |
| [math]\displaystyle{ \mathbf{ 2310} }[/math] | [math]\displaystyle{ 1019 }[/math] | [math]\displaystyle{ 3823 }[/math] | [math]\displaystyle{ 5557 }[/math] | [math]\displaystyle{ 6133 }[/math] | [math]\displaystyle{ 7853 }[/math] | [math]\displaystyle{ 9941 }[/math] |
| [math]\displaystyle{ \mathbf{ 2520} }[/math] | [math]\displaystyle{ 5413 }[/math] | [math]\displaystyle{ 7109 }[/math] | [math]\displaystyle{ 19141 }[/math] | [math]\displaystyle{ 21661 }[/math] | [math]\displaystyle{ 23509 }[/math] | [math]\displaystyle{ 24763 }[/math] |
| [math]\displaystyle{ \mathbf{ 2730} }[/math] | [math]\displaystyle{ 1091 }[/math] | [math]\displaystyle{ 4721 }[/math] | [math]\displaystyle{ 7451 }[/math] | [math]\displaystyle{ 22079 }[/math] | [math]\displaystyle{ 49339 }[/math] | [math]\displaystyle{ 53759 }[/math] |
| [math]\displaystyle{ \mathbf{ 2940} }[/math] | [math]\displaystyle{ 9433 }[/math] | [math]\displaystyle{ 11927 }[/math] | [math]\displaystyle{ 14867 }[/math] | [math]\displaystyle{ 50587 }[/math] | [math]\displaystyle{ 80933 }[/math] | [math]\displaystyle{ 127207 }[/math] |
| [math]\displaystyle{ \mathbf{ 3150} }[/math] | [math]\displaystyle{ 433 }[/math] | [math]\displaystyle{ 3583 }[/math] | [math]\displaystyle{ 7877 }[/math] | [math]\displaystyle{ 24677 }[/math] | [math]\displaystyle{ 27827 }[/math] | [math]\displaystyle{ 49031 }[/math] |
| [math]\displaystyle{ \mathbf{ 3360} }[/math] | [math]\displaystyle{ 6571 }[/math] | [math]\displaystyle{ 9041 }[/math] | [math]\displaystyle{ 39791 }[/math] | [math]\displaystyle{ 210391 }[/math] | [math]\displaystyle{ 213751 }[/math] | [math]\displaystyle{ 217111 }[/math] |
| [math]\displaystyle{ \mathbf{ 3570} }[/math] | [math]\displaystyle{ 8971 }[/math] | [math]\displaystyle{ 10429 }[/math] | [math]\displaystyle{ 27737 }[/math] | [math]\displaystyle{ 28387 }[/math] | [math]\displaystyle{ 37313 }[/math] | [math]\displaystyle{ 57047 }[/math] |
| [math]\displaystyle{ \mathbf{ 3780} }[/math] | [math]\displaystyle{ 45767 }[/math] | [math]\displaystyle{ 82037 }[/math] | [math]\displaystyle{ 155569 }[/math] | [math]\displaystyle{ 473513 }[/math] | [math]\displaystyle{ 477293 }[/math] | [math]\displaystyle{ 511873 }[/math] |
| [math]\displaystyle{ \mathbf{ 3990} }[/math] | [math]\displaystyle{ 1699 }[/math] | [math]\displaystyle{ 2909 }[/math] | [math]\displaystyle{ 5689 }[/math] | [math]\displaystyle{ 25033 }[/math] | [math]\displaystyle{ 29873 }[/math] | [math]\displaystyle{ 40559 }[/math] |
| [math]\displaystyle{ \mathbf{ 4200} }[/math] | [math]\displaystyle{ 12547 }[/math] | [math]\displaystyle{ 16747 }[/math] | [math]\displaystyle{ 37013 }[/math] | [math]\displaystyle{ 57139 }[/math] | [math]\displaystyle{ 89899 }[/math] | [math]\displaystyle{ 94099 }[/math] |
| [math]\displaystyle{ \mathbf{ 4410} }[/math] | [math]\displaystyle{ 20809 }[/math] | [math]\displaystyle{ 87623 }[/math] | [math]\displaystyle{ 142271 }[/math] | [math]\displaystyle{ 262733 }[/math] | [math]\displaystyle{ 267143 }[/math] | [math]\displaystyle{ 439009 }[/math] |
| [math]\displaystyle{ \mathbf{ 4620} }[/math] | [math]\displaystyle{ 103 }[/math] | [math]\displaystyle{ 1531 }[/math] | [math]\displaystyle{ 3083 }[/math] | [math]\displaystyle{ 3257 }[/math] | [math]\displaystyle{ 6427 }[/math] | [math]\displaystyle{ 9461 }[/math] |
| [math]\displaystyle{ \mathbf{ 4830} }[/math] | [math]\displaystyle{ 3907 }[/math] | [math]\displaystyle{ 13313 }[/math] | [math]\displaystyle{ 30427 }[/math] | [math]\displaystyle{ 35257 }[/math] | [math]\displaystyle{ 40087 }[/math] | [math]\displaystyle{ 72547 }[/math] |
| [math]\displaystyle{ \mathbf{ 5040} }[/math] | [math]\displaystyle{ 13477 }[/math] | [math]\displaystyle{ 14951 }[/math] | [math]\displaystyle{ 25073 }[/math] | [math]\displaystyle{ 25931 }[/math] | [math]\displaystyle{ 30113 }[/math] | [math]\displaystyle{ 57457 }[/math] |
| [math]\displaystyle{ \mathbf{ 5250} }[/math] | [math]\displaystyle{ 3413 }[/math] | [math]\displaystyle{ 8663 }[/math] | [math]\displaystyle{ 44179 }[/math] | [math]\displaystyle{ 49429 }[/math] | [math]\displaystyle{ 111109 }[/math] | [math]\displaystyle{ 648107 }[/math] |
| [math]\displaystyle{ \mathbf{ 5460} }[/math] | [math]\displaystyle{ 1559 }[/math] | [math]\displaystyle{ 18899 }[/math] | [math]\displaystyle{ 36389 }[/math] | [math]\displaystyle{ 43711 }[/math] | [math]\displaystyle{ 59393 }[/math] | [math]\displaystyle{ 75541 }[/math] |
| [math]\displaystyle{ \mathbf{ 5670} }[/math] | [math]\displaystyle{ 187477 }[/math] | [math]\displaystyle{ 231109 }[/math] | [math]\displaystyle{ 402137 }[/math] | [math]\displaystyle{ 680123 }[/math] | [math]\displaystyle{ 706463 }[/math] | [math]\displaystyle{ 712133 }[/math] |
| [math]\displaystyle{ \mathbf{ 5880} }[/math] | [math]\displaystyle{ 73 }[/math] | [math]\displaystyle{ 29959 }[/math] | [math]\displaystyle{ 152389 }[/math] | [math]\displaystyle{ 158269 }[/math] | [math]\displaystyle{ 317021 }[/math] | [math]\displaystyle{ 2115961 }[/math] |
| [math]\displaystyle{ \mathbf{ 6090} }[/math] | [math]\displaystyle{ 12239 }[/math] | [math]\displaystyle{ 22469 }[/math] | [math]\displaystyle{ 38543 }[/math] | [math]\displaystyle{ 50893 }[/math] | [math]\displaystyle{ 72533 }[/math] | [math]\displaystyle{ 90863 }[/math] |
| [math]\displaystyle{ \mathbf{ 6300} }[/math] | [math]\displaystyle{ 37097 }[/math] | [math]\displaystyle{ 86869 }[/math] | [math]\displaystyle{ 92639 }[/math] | [math]\displaystyle{ 224633 }[/math] | [math]\displaystyle{ 440269 }[/math] | [math]\displaystyle{ 641327 }[/math] |
| [math]\displaystyle{ \mathbf{ 6510} }[/math] | [math]\displaystyle{ 1063 }[/math] | [math]\displaystyle{ 20599 }[/math] | [math]\displaystyle{ 21701 }[/math] | [math]\displaystyle{ 27109 }[/math] | [math]\displaystyle{ 41611 }[/math] | [math]\displaystyle{ 46187 }[/math] |
| [math]\displaystyle{ \mathbf{ 6720} }[/math] | [math]\displaystyle{ 3167 }[/math] | [math]\displaystyle{ 7457 }[/math] | [math]\displaystyle{ 22669 }[/math] | [math]\displaystyle{ 62347 }[/math] | [math]\displaystyle{ 69067 }[/math] | [math]\displaystyle{ 75787 }[/math] |
| [math]\displaystyle{ \mathbf{ 6930} }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 5581 }[/math] | [math]\displaystyle{ 6947 }[/math] | [math]\displaystyle{ 7151 }[/math] | [math]\displaystyle{ 13469 }[/math] | [math]\displaystyle{ 14081 }[/math] |
| [math]\displaystyle{ \mathbf{ 7140} }[/math] | [math]\displaystyle{ 3347 }[/math] | [math]\displaystyle{ 53309 }[/math] | [math]\displaystyle{ 281557 }[/math] | [math]\displaystyle{ 370879 }[/math] | [math]\displaystyle{ 380447 }[/math] | [math]\displaystyle{ 466897 }[/math] |
| [math]\displaystyle{ \mathbf{ 7350} }[/math] | [math]\displaystyle{ 206047 }[/math] | [math]\displaystyle{ 348163 }[/math] | [math]\displaystyle{ 363037 }[/math] | [math]\displaystyle{ 435661 }[/math] | [math]\displaystyle{ 576677 }[/math] | [math]\displaystyle{ 906107 }[/math] |
| [math]\displaystyle{ \mathbf{ 7560} }[/math] | [math]\displaystyle{ 29387 }[/math] | [math]\displaystyle{ 36947 }[/math] | [math]\displaystyle{ 39191 }[/math] | [math]\displaystyle{ 44267 }[/math] | [math]\displaystyle{ 342389 }[/math] | [math]\displaystyle{ 349949 }[/math] |
| [math]\displaystyle{ \mathbf{ 7770} }[/math] | [math]\displaystyle{ 6553 }[/math] | [math]\displaystyle{ 14323 }[/math] | [math]\displaystyle{ 25169 }[/math] | [math]\displaystyle{ 28549 }[/math] | [math]\displaystyle{ 36319 }[/math] | [math]\displaystyle{ 42061 }[/math] |
| [math]\displaystyle{ \mathbf{ 7980} }[/math] | [math]\displaystyle{ 137 }[/math] | [math]\displaystyle{ 4091 }[/math] | [math]\displaystyle{ 7237 }[/math] | [math]\displaystyle{ 8117 }[/math] | [math]\displaystyle{ 12071 }[/math] | [math]\displaystyle{ 24029 }[/math] |
| [math]\displaystyle{ \mathbf{ 8190} }[/math] | [math]\displaystyle{ 3593 }[/math] | [math]\displaystyle{ 21017 }[/math] | [math]\displaystyle{ 35591 }[/math] | [math]\displaystyle{ 43781 }[/math] | [math]\displaystyle{ 49727 }[/math] | [math]\displaystyle{ 59021 }[/math] |
| [math]\displaystyle{ \mathbf{ 8400} }[/math] | [math]\displaystyle{ 86599 }[/math] | [math]\displaystyle{ 173909 }[/math] | [math]\displaystyle{ 788413 }[/math] | [math]\displaystyle{ 1251869 }[/math] | [math]\displaystyle{ 1365019 }[/math] | [math]\displaystyle{ 1392731 }[/math] |
| [math]\displaystyle{ \mathbf{ 8610} }[/math] | [math]\displaystyle{ 541 }[/math] | [math]\displaystyle{ 1867 }[/math] | [math]\displaystyle{ 63703 }[/math] | [math]\displaystyle{ 132283 }[/math] | [math]\displaystyle{ 140893 }[/math] | [math]\displaystyle{ 175837 }[/math] |
| [math]\displaystyle{ \mathbf{ 8820} }[/math] | [math]\displaystyle{ 9403 }[/math] | [math]\displaystyle{ 83563 }[/math] | [math]\displaystyle{ 84421 }[/math] | [math]\displaystyle{ 93241 }[/math] | [math]\displaystyle{ 187823 }[/math] | [math]\displaystyle{ 296983 }[/math] |
| [math]\displaystyle{ \mathbf{ 9030} }[/math] | [math]\displaystyle{ 11087 }[/math] | [math]\displaystyle{ 195203 }[/math] | [math]\displaystyle{ 219799 }[/math] | [math]\displaystyle{ 352813 }[/math] | [math]\displaystyle{ 426973 }[/math] | [math]\displaystyle{ 487651 }[/math] |
| [math]\displaystyle{ \mathbf{ 9240} }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 937 }[/math] | [math]\displaystyle{ 10177 }[/math] | [math]\displaystyle{ 21031 }[/math] | [math]\displaystyle{ 27961 }[/math] | [math]\displaystyle{ 30271 }[/math] |
| [math]\displaystyle{ \mathbf{ 9450} }[/math] | [math]\displaystyle{ 1609 }[/math] | [math]\displaystyle{ 157181 }[/math] | [math]\displaystyle{ 182867 }[/math] | [math]\displaystyle{ 663049 }[/math] | [math]\displaystyle{ 1028479 }[/math] | [math]\displaystyle{ 1037929 }[/math] |
| [math]\displaystyle{ \mathbf{ 9660} }[/math] | [math]\displaystyle{ 521 }[/math] | [math]\displaystyle{ 3449 }[/math] | [math]\displaystyle{ 10181 }[/math] | [math]\displaystyle{ 50417 }[/math] | [math]\displaystyle{ 84229 }[/math] | [math]\displaystyle{ 218363 }[/math] |
| [math]\displaystyle{ \mathbf{ 9870} }[/math] | [math]\displaystyle{ 61 }[/math] | [math]\displaystyle{ 43013 }[/math] | [math]\displaystyle{ 89923 }[/math] | [math]\displaystyle{ 220333 }[/math] | [math]\displaystyle{ 294479 }[/math] | [math]\displaystyle{ 490493 }[/math] |
| [math]\displaystyle{ \mathbf{ 10080} }[/math] | [math]\displaystyle{ 6949 }[/math] | [math]\displaystyle{ 17029 }[/math] | [math]\displaystyle{ 54293 }[/math] | [math]\displaystyle{ 99023 }[/math] | [math]\displaystyle{ 125353 }[/math] | [math]\displaystyle{ 125899 }[/math] |
| [math]\displaystyle{ \mathbf{ 10290} }[/math] | [math]\displaystyle{ 6143 }[/math] | [math]\displaystyle{ 16433 }[/math] | [math]\displaystyle{ 179057 }[/math] | [math]\displaystyle{ 211777 }[/math] | [math]\displaystyle{ 681949 }[/math] | [math]\displaystyle{ 1018357 }[/math] |
| [math]\displaystyle{ \mathbf{ 10500} }[/math] | [math]\displaystyle{ 9109 }[/math] | [math]\displaystyle{ 91153 }[/math] | [math]\displaystyle{ 218527 }[/math] | [math]\displaystyle{ 447817 }[/math] | [math]\displaystyle{ 513167 }[/math] | [math]\displaystyle{ 1113239 }[/math] |
| [math]\displaystyle{ \mathbf{ 10710} }[/math] | [math]\displaystyle{ 9419 }[/math] | [math]\displaystyle{ 28603 }[/math] | [math]\displaystyle{ 28871 }[/math] | [math]\displaystyle{ 37861 }[/math] | [math]\displaystyle{ 43691 }[/math] | [math]\displaystyle{ 75041 }[/math] |
| [math]\displaystyle{ \mathbf{ 10920} }[/math] | [math]\displaystyle{ 14657 }[/math] | [math]\displaystyle{ 21491 }[/math] | [math]\displaystyle{ 52321 }[/math] | [math]\displaystyle{ 63241 }[/math] | [math]\displaystyle{ 79997 }[/math] | [math]\displaystyle{ 80621 }[/math] |
| [math]\displaystyle{ \mathbf{ 11130} }[/math] | [math]\displaystyle{ 49681 }[/math] | [math]\displaystyle{ 70607 }[/math] | [math]\displaystyle{ 187009 }[/math] | [math]\displaystyle{ 198139 }[/math] | [math]\displaystyle{ 209269 }[/math] | [math]\displaystyle{ 219613 }[/math] |
| [math]\displaystyle{ \mathbf{ 11340} }[/math] | [math]\displaystyle{ 24197 }[/math] | [math]\displaystyle{ 57143 }[/math] | [math]\displaystyle{ 68483 }[/math] | [math]\displaystyle{ 158617 }[/math] | [math]\displaystyle{ 212297 }[/math] | [math]\displaystyle{ 237257 }[/math] |
| [math]\displaystyle{ \mathbf{ 11550} }[/math] | [math]\displaystyle{ 4483 }[/math] | [math]\displaystyle{ 4673 }[/math] | [math]\displaystyle{ 9619 }[/math] | [math]\displaystyle{ 16223 }[/math] | [math]\displaystyle{ 21169 }[/math] | [math]\displaystyle{ 66161 }[/math] |
| [math]\displaystyle{ \mathbf{ 11760} }[/math] | [math]\displaystyle{ 3511 }[/math] | [math]\displaystyle{ 241793 }[/math] | [math]\displaystyle{ 469613 }[/math] | [math]\displaystyle{ 517949 }[/math] | [math]\displaystyle{ 548263 }[/math] | [math]\displaystyle{ 643469 }[/math] |
| [math]\displaystyle{ \mathbf{ 11970} }[/math] | [math]\displaystyle{ 6221 }[/math] | [math]\displaystyle{ 10531 }[/math] | [math]\displaystyle{ 22501 }[/math] | [math]\displaystyle{ 40343 }[/math] | [math]\displaystyle{ 216233 }[/math] | [math]\displaystyle{ 280187 }[/math] |
| [math]\displaystyle{ \mathbf{ 12180} }[/math] | [math]\displaystyle{ 18211 }[/math] | [math]\displaystyle{ 65437 }[/math] | [math]\displaystyle{ 126943 }[/math] | [math]\displaystyle{ 137239 }[/math] | [math]\displaystyle{ 149939 }[/math] | [math]\displaystyle{ 361213 }[/math] |
| [math]\displaystyle{ \mathbf{ 12390} }[/math] | [math]\displaystyle{ 7477 }[/math] | [math]\displaystyle{ 24391 }[/math] | [math]\displaystyle{ 41669 }[/math] | [math]\displaystyle{ 76913 }[/math] | [math]\displaystyle{ 95213 }[/math] | [math]\displaystyle{ 181211 }[/math] |
| [math]\displaystyle{ \mathbf{ 12600} }[/math] | [math]\displaystyle{ 26003 }[/math] | [math]\displaystyle{ 435577 }[/math] | [math]\displaystyle{ 448177 }[/math] | [math]\displaystyle{ 558431 }[/math] | [math]\displaystyle{ 571031 }[/math] | [math]\displaystyle{ 583631 }[/math] |
| [math]\displaystyle{ \mathbf{ 12810} }[/math] | [math]\displaystyle{ 19289 }[/math] | [math]\displaystyle{ 35437 }[/math] | [math]\displaystyle{ 40949 }[/math] | [math]\displaystyle{ 53791 }[/math] | [math]\displaystyle{ 59357 }[/math] | [math]\displaystyle{ 94309 }[/math] |
| [math]\displaystyle{ \mathbf{ 13020} }[/math] | [math]\displaystyle{ 15913 }[/math] | [math]\displaystyle{ 55843 }[/math] | [math]\displaystyle{ 77773 }[/math] | [math]\displaystyle{ 179519 }[/math] | [math]\displaystyle{ 418927 }[/math] | [math]\displaystyle{ 670853 }[/math] |
| [math]\displaystyle{ \mathbf{ 13230} }[/math] | [math]\displaystyle{ 5843 }[/math] | [math]\displaystyle{ 7433 }[/math] | [math]\displaystyle{ 9391 }[/math] | [math]\displaystyle{ 31729 }[/math] | [math]\displaystyle{ 40543 }[/math] | [math]\displaystyle{ 53773 }[/math] |
| [math]\displaystyle{ \mathbf{ 13440} }[/math] | [math]\displaystyle{ 2141 }[/math] | [math]\displaystyle{ 15581 }[/math] | [math]\displaystyle{ 270143 }[/math] | [math]\displaystyle{ 335021 }[/math] | [math]\displaystyle{ 405269 }[/math] | [math]\displaystyle{ 448741 }[/math] |
| [math]\displaystyle{ \mathbf{ 13650} }[/math] | [math]\displaystyle{ 3343 }[/math] | [math]\displaystyle{ 12097 }[/math] | [math]\displaystyle{ 16993 }[/math] | [math]\displaystyle{ 19259 }[/math] | [math]\displaystyle{ 63611 }[/math] | [math]\displaystyle{ 81001 }[/math] |
| [math]\displaystyle{ \mathbf{ 13860} }[/math] | [math]\displaystyle{ 6029 }[/math] | [math]\displaystyle{ 6211 }[/math] | [math]\displaystyle{ 26171 }[/math] | [math]\displaystyle{ 27653 }[/math] | [math]\displaystyle{ 32441 }[/math] | [math]\displaystyle{ 51839 }[/math] |
| [math]\displaystyle{ \mathbf{ 14070} }[/math] | [math]\displaystyle{ 40879 }[/math] | [math]\displaystyle{ 87793 }[/math] | [math]\displaystyle{ 87991 }[/math] | [math]\displaystyle{ 159491 }[/math] | [math]\displaystyle{ 285497 }[/math] | [math]\displaystyle{ 485389 }[/math] |
| [math]\displaystyle{ \mathbf{ 14280} }[/math] | [math]\displaystyle{ 6947 }[/math] | [math]\displaystyle{ 15923 }[/math] | [math]\displaystyle{ 27337 }[/math] | [math]\displaystyle{ 79481 }[/math] | [math]\displaystyle{ 111227 }[/math] | [math]\displaystyle{ 364687 }[/math] |
| [math]\displaystyle{ \mathbf{ 14490} }[/math] | [math]\displaystyle{ 41039 }[/math] | [math]\displaystyle{ 48491 }[/math] | [math]\displaystyle{ 142049 }[/math] | [math]\displaystyle{ 144667 }[/math] | [math]\displaystyle{ 159157 }[/math] | [math]\displaystyle{ 161263 }[/math] |
| [math]\displaystyle{ \mathbf{ 14700} }[/math] | [math]\displaystyle{ 12409 }[/math] | [math]\displaystyle{ 36583 }[/math] | [math]\displaystyle{ 51283 }[/math] | [math]\displaystyle{ 161363 }[/math] | [math]\displaystyle{ 218989 }[/math] | [math]\displaystyle{ 578267 }[/math] |
| [math]\displaystyle{ \mathbf{ 14910} }[/math] | [math]\displaystyle{ 23957 }[/math] | [math]\displaystyle{ 74161 }[/math] | [math]\displaystyle{ 79633 }[/math] | [math]\displaystyle{ 89071 }[/math] | [math]\displaystyle{ 109367 }[/math] | [math]\displaystyle{ 120977 }[/math] |
| [math]\displaystyle{ \mathbf{ 15120} }[/math] | [math]\displaystyle{ 33997 }[/math] | [math]\displaystyle{ 121853 }[/math] | [math]\displaystyle{ 136973 }[/math] | [math]\displaystyle{ 203429 }[/math] | [math]\displaystyle{ 330413 }[/math] | [math]\displaystyle{ 379369 }[/math] |
| [math]\displaystyle{ \mathbf{ 15330} }[/math] | [math]\displaystyle{ 12781 }[/math] | [math]\displaystyle{ 64613 }[/math] | [math]\displaystyle{ 505559 }[/math] | [math]\displaystyle{ 588529 }[/math] | [math]\displaystyle{ 614071 }[/math] | [math]\displaystyle{ 873121 }[/math] |
| [math]\displaystyle{ \mathbf{ 15540} }[/math] | [math]\displaystyle{ 15053 }[/math] | [math]\displaystyle{ 33071 }[/math] | [math]\displaystyle{ 41131 }[/math] | [math]\displaystyle{ 160781 }[/math] | [math]\displaystyle{ 176321 }[/math] | [math]\displaystyle{ 209357 }[/math] |
| [math]\displaystyle{ \mathbf{ 15750} }[/math] | [math]\displaystyle{ 7001 }[/math] | [math]\displaystyle{ 10459 }[/math] | [math]\displaystyle{ 64579 }[/math] | [math]\displaystyle{ 80329 }[/math] | [math]\displaystyle{ 103409 }[/math] | [math]\displaystyle{ 119159 }[/math] |
| [math]\displaystyle{ \mathbf{ 15960} }[/math] | [math]\displaystyle{ 1847 }[/math] | [math]\displaystyle{ 6037 }[/math] | [math]\displaystyle{ 17807 }[/math] | [math]\displaystyle{ 21997 }[/math] | [math]\displaystyle{ 33767 }[/math] | [math]\displaystyle{ 71917 }[/math] |
| [math]\displaystyle{ \mathbf{ 16170} }[/math] | [math]\displaystyle{ 32321 }[/math] | [math]\displaystyle{ 66179 }[/math] | [math]\displaystyle{ 82349 }[/math] | [math]\displaystyle{ 99661 }[/math] | [math]\displaystyle{ 130343 }[/math] | [math]\displaystyle{ 219451 }[/math] |
| [math]\displaystyle{ \mathbf{ 16380} }[/math] | [math]\displaystyle{ 22859 }[/math] | [math]\displaystyle{ 28579 }[/math] | [math]\displaystyle{ 43759 }[/math] | [math]\displaystyle{ 43913 }[/math] | [math]\displaystyle{ 60139 }[/math] | [math]\displaystyle{ 95107 }[/math] |
| [math]\displaystyle{ \mathbf{ 16590} }[/math] | [math]\displaystyle{ 6703 }[/math] | [math]\displaystyle{ 23293 }[/math] | [math]\displaystyle{ 29009 }[/math] | [math]\displaystyle{ 45599 }[/math] | [math]\displaystyle{ 51341 }[/math] | [math]\displaystyle{ 57917 }[/math] |
| [math]\displaystyle{ \mathbf{ 16800} }[/math] | [math]\displaystyle{ 91463 }[/math] | [math]\displaystyle{ 276037 }[/math] | [math]\displaystyle{ 524857 }[/math] | [math]\displaystyle{ 874063 }[/math] | [math]\displaystyle{ 940319 }[/math] | [math]\displaystyle{ 957119 }[/math] |
| [math]\displaystyle{ \mathbf{ 17010} }[/math] | [math]\displaystyle{ 6571 }[/math] | [math]\displaystyle{ 70529 }[/math] | [math]\displaystyle{ 117037 }[/math] | [math]\displaystyle{ 227147 }[/math] | [math]\displaystyle{ 797119 }[/math] | [math]\displaystyle{ 814129 }[/math] |
| [math]\displaystyle{ \mathbf{ 17220} }[/math] | [math]\displaystyle{ 120713 }[/math] | [math]\displaystyle{ 225769 }[/math] | [math]\displaystyle{ 242989 }[/math] | [math]\displaystyle{ 343601 }[/math] | [math]\displaystyle{ 819229 }[/math] | [math]\displaystyle{ 965711 }[/math] |
| [math]\displaystyle{ \mathbf{ 17430} }[/math] | [math]\displaystyle{ 4219 }[/math] | [math]\displaystyle{ 6101 }[/math] | [math]\displaystyle{ 15643 }[/math] | [math]\displaystyle{ 25471 }[/math] | [math]\displaystyle{ 33073 }[/math] | [math]\displaystyle{ 42901 }[/math] |
| [math]\displaystyle{ \mathbf{ 17640} }[/math] | [math]\displaystyle{ 12917 }[/math] | [math]\displaystyle{ 34877 }[/math] | [math]\displaystyle{ 59407 }[/math] | [math]\displaystyle{ 62047 }[/math] | [math]\displaystyle{ 85667 }[/math] | [math]\displaystyle{ 193607 }[/math] |
| [math]\displaystyle{ \mathbf{ 17850} }[/math] | [math]\displaystyle{ 9803 }[/math] | [math]\displaystyle{ 129379 }[/math] | [math]\displaystyle{ 147229 }[/math] | [math]\displaystyle{ 238229 }[/math] | [math]\displaystyle{ 270157 }[/math] | [math]\displaystyle{ 289253 }[/math] |
| [math]\displaystyle{ \mathbf{ 18060} }[/math] | [math]\displaystyle{ 87613 }[/math] | [math]\displaystyle{ 90583 }[/math] | [math]\displaystyle{ 117223 }[/math] | [math]\displaystyle{ 512671 }[/math] | [math]\displaystyle{ 574297 }[/math] | [math]\displaystyle{ 623353 }[/math] |
| [math]\displaystyle{ \mathbf{ 18270} }[/math] | [math]\displaystyle{ 29567 }[/math] | [math]\displaystyle{ 47837 }[/math] | [math]\displaystyle{ 86491 }[/math] | [math]\displaystyle{ 268189 }[/math] | [math]\displaystyle{ 424819 }[/math] | [math]\displaystyle{ 511201 }[/math] |
| [math]\displaystyle{ \mathbf{ 18480} }[/math] | [math]\displaystyle{ 1861 }[/math] | [math]\displaystyle{ 2711 }[/math] | [math]\displaystyle{ 8093 }[/math] | [math]\displaystyle{ 10831 }[/math] | [math]\displaystyle{ 11161 }[/math] | [math]\displaystyle{ 11909 }[/math] |
| [math]\displaystyle{ \mathbf{ 18690} }[/math] | [math]\displaystyle{ 881 }[/math] | [math]\displaystyle{ 19571 }[/math] | [math]\displaystyle{ 79531 }[/math] | [math]\displaystyle{ 529829 }[/math] | [math]\displaystyle{ 654767 }[/math] | [math]\displaystyle{ 812353 }[/math] |
| [math]\displaystyle{ \mathbf{ 18900} }[/math] | [math]\displaystyle{ 6899 }[/math] | [math]\displaystyle{ 23201 }[/math] | [math]\displaystyle{ 52267 }[/math] | [math]\displaystyle{ 73823 }[/math] | [math]\displaystyle{ 92723 }[/math] | [math]\displaystyle{ 462079 }[/math] |
| [math]\displaystyle{ \mathbf{ 19110} }[/math] | [math]\displaystyle{ 8941 }[/math] | [math]\displaystyle{ 30091 }[/math] | [math]\displaystyle{ 39367 }[/math] | [math]\displaystyle{ 58603 }[/math] | [math]\displaystyle{ 63737 }[/math] | [math]\displaystyle{ 80611 }[/math] |
| [math]\displaystyle{ \mathbf{ 19320} }[/math] | [math]\displaystyle{ 6857 }[/math] | [math]\displaystyle{ 218761 }[/math] | [math]\displaystyle{ 236699 }[/math] | [math]\displaystyle{ 237733 }[/math] | [math]\displaystyle{ 300319 }[/math] | [math]\displaystyle{ 300499 }[/math] |
| [math]\displaystyle{ \mathbf{ 19530} }[/math] | [math]\displaystyle{ 33829 }[/math] | [math]\displaystyle{ 46183 }[/math] | [math]\displaystyle{ 50929 }[/math] | [math]\displaystyle{ 70459 }[/math] | [math]\displaystyle{ 283859 }[/math] | [math]\displaystyle{ 361651 }[/math] |
| [math]\displaystyle{ \mathbf{ 19740} }[/math] | [math]\displaystyle{ 1117 }[/math] | [math]\displaystyle{ 2729 }[/math] | [math]\displaystyle{ 22469 }[/math] | [math]\displaystyle{ 30757 }[/math] | [math]\displaystyle{ 50497 }[/math] | [math]\displaystyle{ 165391 }[/math] |
| [math]\displaystyle{ \mathbf{ 19950} }[/math] | [math]\displaystyle{ 13339 }[/math] | [math]\displaystyle{ 23767 }[/math] | [math]\displaystyle{ 44549 }[/math] | [math]\displaystyle{ 47791 }[/math] | [math]\displaystyle{ 92399 }[/math] | [math]\displaystyle{ 142699 }[/math] |
| [math]\displaystyle{ \mathbf{ 20160} }[/math] | [math]\displaystyle{ 2857 }[/math] | [math]\displaystyle{ 5821 }[/math] | [math]\displaystyle{ 147089 }[/math] | [math]\displaystyle{ 948263 }[/math] | [math]\displaystyle{ 1044859 }[/math] | [math]\displaystyle{ 1094123 }[/math] |
| [math]\displaystyle{ \mathbf{ 20370} }[/math] | [math]\displaystyle{ 81649 }[/math] | [math]\displaystyle{ 154073 }[/math] | [math]\displaystyle{ 164239 }[/math] | [math]\displaystyle{ 398539 }[/math] | [math]\displaystyle{ 443881 }[/math] | [math]\displaystyle{ 556123 }[/math] |
| [math]\displaystyle{ \mathbf{ 20580} }[/math] | [math]\displaystyle{ 9689 }[/math] | [math]\displaystyle{ 30269 }[/math] | [math]\displaystyle{ 105379 }[/math] | [math]\displaystyle{ 316501 }[/math] | [math]\displaystyle{ 337081 }[/math] | [math]\displaystyle{ 398023 }[/math] |
| [math]\displaystyle{ \mathbf{ 20790} }[/math] | [math]\displaystyle{ 12713 }[/math] | [math]\displaystyle{ 20023 }[/math] | [math]\displaystyle{ 33503 }[/math] | [math]\displaystyle{ 40813 }[/math] | [math]\displaystyle{ 69829 }[/math] | [math]\displaystyle{ 92251 }[/math] |
| [math]\displaystyle{ \mathbf{ 21000} }[/math] | [math]\displaystyle{ 5501 }[/math] | [math]\displaystyle{ 19471 }[/math] | [math]\displaystyle{ 26501 }[/math] | [math]\displaystyle{ 29153 }[/math] | [math]\displaystyle{ 40471 }[/math] | [math]\displaystyle{ 56773 }[/math] |
□
Przykład C58
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości [math]\displaystyle{ n = 9 }[/math] i [math]\displaystyle{ n = 10 }[/math].
W przypadku [math]\displaystyle{ n = 9 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 210 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^9 }[/math].
W przypadku [math]\displaystyle{ n = 10 }[/math] wyszukiwanie ciągów zostało przeprowadzone dla [math]\displaystyle{ d = 210 k }[/math], gdzie [math]\displaystyle{ 1 \leqslant k \leqslant 100 }[/math] i (przy ustalonym [math]\displaystyle{ d }[/math]) dla kolejnych liczb pierwszych [math]\displaystyle{ p_0 \leqslant 10^{10} }[/math].
Jeżeli w tabeli jest wypisanych sześć wartości [math]\displaystyle{ p_0 }[/math], to oznacza to, że zostało znalezionych co najmniej sześć wartości [math]\displaystyle{ p_0 }[/math].
| [math]\displaystyle{ \mathbf{n = 9} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 210} }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 409 }[/math] | [math]\displaystyle{ 3499 }[/math] | [math]\displaystyle{ 10859 }[/math] | [math]\displaystyle{ 564973 }[/math] | [math]\displaystyle{ 1288607 }[/math] |
| [math]\displaystyle{ \mathbf{ 420} }[/math] | [math]\displaystyle{ 52879 }[/math] | [math]\displaystyle{ 53299 }[/math] | [math]\displaystyle{ 56267 }[/math] | [math]\displaystyle{ 61637 }[/math] | [math]\displaystyle{ 3212849 }[/math] | [math]\displaystyle{ 3544939 }[/math] |
| [math]\displaystyle{ \mathbf{ 630} }[/math] | [math]\displaystyle{ 279857 }[/math] | [math]\displaystyle{ 514949 }[/math] | [math]\displaystyle{ 939359 }[/math] | [math]\displaystyle{ 964417 }[/math] | [math]\displaystyle{ 965047 }[/math] | [math]\displaystyle{ 1003819 }[/math] |
| [math]\displaystyle{ \mathbf{ 840} }[/math] | [math]\displaystyle{ 6043 }[/math] | [math]\displaystyle{ 10861 }[/math] | [math]\displaystyle{ 103837 }[/math] | [math]\displaystyle{ 201781 }[/math] | [math]\displaystyle{ 915611 }[/math] | [math]\displaystyle{ 916451 }[/math] |
| [math]\displaystyle{ \mathbf{ 1050} }[/math] | [math]\displaystyle{ 26052251 }[/math] | [math]\displaystyle{ 33267943 }[/math] | [math]\displaystyle{ 54730813 }[/math] | [math]\displaystyle{ 87640921 }[/math] | [math]\displaystyle{ 112704443 }[/math] | [math]\displaystyle{ 115677517 }[/math] |
| [math]\displaystyle{ \mathbf{ 1260} }[/math] | [math]\displaystyle{ 2063 }[/math] | [math]\displaystyle{ 1040089 }[/math] | [math]\displaystyle{ 2166511 }[/math] | [math]\displaystyle{ 2202547 }[/math] | [math]\displaystyle{ 4152847 }[/math] | [math]\displaystyle{ 4400639 }[/math] |
| [math]\displaystyle{ \mathbf{ 1470} }[/math] | [math]\displaystyle{ 101027 }[/math] | [math]\displaystyle{ 363949 }[/math] | [math]\displaystyle{ 1936289 }[/math] | [math]\displaystyle{ 2534561 }[/math] | [math]\displaystyle{ 2536031 }[/math] | [math]\displaystyle{ 3248197 }[/math] |
| [math]\displaystyle{ \mathbf{ 1680} }[/math] | [math]\displaystyle{ 31333 }[/math] | [math]\displaystyle{ 216947 }[/math] | [math]\displaystyle{ 258527 }[/math] | [math]\displaystyle{ 316621 }[/math] | [math]\displaystyle{ 607109 }[/math] | [math]\displaystyle{ 4635361 }[/math] |
| [math]\displaystyle{ \mathbf{ 1890} }[/math] | [math]\displaystyle{ 15607 }[/math] | [math]\displaystyle{ 45767 }[/math] | [math]\displaystyle{ 194113 }[/math] | [math]\displaystyle{ 534211 }[/math] | [math]\displaystyle{ 997201 }[/math] | [math]\displaystyle{ 1442173 }[/math] |
| [math]\displaystyle{ \mathbf{ 2100} }[/math] | [math]\displaystyle{ 34913 }[/math] | [math]\displaystyle{ 37013 }[/math] | [math]\displaystyle{ 102871 }[/math] | [math]\displaystyle{ 176087 }[/math] | [math]\displaystyle{ 581393 }[/math] | [math]\displaystyle{ 583493 }[/math] |
| [math]\displaystyle{ \mathbf{ 2310} }[/math] | [math]\displaystyle{ 3823 }[/math] | [math]\displaystyle{ 60317 }[/math] | [math]\displaystyle{ 80761 }[/math] | [math]\displaystyle{ 563117 }[/math] | [math]\displaystyle{ 574813 }[/math] | [math]\displaystyle{ 1215583 }[/math] |
| [math]\displaystyle{ \mathbf{ 2520} }[/math] | [math]\displaystyle{ 19141 }[/math] | [math]\displaystyle{ 23509 }[/math] | [math]\displaystyle{ 1058597 }[/math] | [math]\displaystyle{ 1061117 }[/math] | [math]\displaystyle{ 1465993 }[/math] | [math]\displaystyle{ 5650097 }[/math] |
| [math]\displaystyle{ \mathbf{ 2730} }[/math] | [math]\displaystyle{ 4721 }[/math] | [math]\displaystyle{ 65881 }[/math] | [math]\displaystyle{ 122069 }[/math] | [math]\displaystyle{ 123059 }[/math] | [math]\displaystyle{ 124799 }[/math] | [math]\displaystyle{ 125789 }[/math] |
| [math]\displaystyle{ \mathbf{ 2940} }[/math] | [math]\displaystyle{ 11927 }[/math] | [math]\displaystyle{ 145723 }[/math] | [math]\displaystyle{ 1222279 }[/math] | [math]\displaystyle{ 12424921 }[/math] | [math]\displaystyle{ 23527081 }[/math] | [math]\displaystyle{ 33820273 }[/math] |
| [math]\displaystyle{ \mathbf{ 3150} }[/math] | [math]\displaystyle{ 433 }[/math] | [math]\displaystyle{ 24677 }[/math] | [math]\displaystyle{ 49031 }[/math] | [math]\displaystyle{ 348763 }[/math] | [math]\displaystyle{ 1243393 }[/math] | [math]\displaystyle{ 1640071 }[/math] |
| [math]\displaystyle{ \mathbf{ 3360} }[/math] | [math]\displaystyle{ 210391 }[/math] | [math]\displaystyle{ 213751 }[/math] | [math]\displaystyle{ 245173 }[/math] | [math]\displaystyle{ 1863509 }[/math] | [math]\displaystyle{ 3831437 }[/math] | [math]\displaystyle{ 6470249 }[/math] |
| [math]\displaystyle{ \mathbf{ 3570} }[/math] | [math]\displaystyle{ 57047 }[/math] | [math]\displaystyle{ 133271 }[/math] | [math]\displaystyle{ 150343 }[/math] | [math]\displaystyle{ 153913 }[/math] | [math]\displaystyle{ 399433 }[/math] | [math]\displaystyle{ 920827 }[/math] |
| [math]\displaystyle{ \mathbf{ 3780} }[/math] | [math]\displaystyle{ 473513 }[/math] | [math]\displaystyle{ 1282607 }[/math] | [math]\displaystyle{ 3536881 }[/math] | [math]\displaystyle{ 4045763 }[/math] | [math]\displaystyle{ 4049543 }[/math] | [math]\displaystyle{ 5655283 }[/math] |
| [math]\displaystyle{ \mathbf{ 3990} }[/math] | [math]\displaystyle{ 1699 }[/math] | [math]\displaystyle{ 99877 }[/math] | [math]\displaystyle{ 103867 }[/math] | [math]\displaystyle{ 649217 }[/math] | [math]\displaystyle{ 1614973 }[/math] | [math]\displaystyle{ 2732441 }[/math] |
| [math]\displaystyle{ \mathbf{ 4200} }[/math] | [math]\displaystyle{ 12547 }[/math] | [math]\displaystyle{ 89899 }[/math] | [math]\displaystyle{ 835721 }[/math] | [math]\displaystyle{ 2544221 }[/math] | [math]\displaystyle{ 5013919 }[/math] | [math]\displaystyle{ 11254637 }[/math] |
| [math]\displaystyle{ \mathbf{ 4410} }[/math] | [math]\displaystyle{ 262733 }[/math] | [math]\displaystyle{ 439009 }[/math] | [math]\displaystyle{ 12940541 }[/math] | [math]\displaystyle{ 15091459 }[/math] | [math]\displaystyle{ 27878321 }[/math] | [math]\displaystyle{ 29196199 }[/math] |
| [math]\displaystyle{ \mathbf{ 4620} }[/math] | [math]\displaystyle{ 55697 }[/math] | [math]\displaystyle{ 64919 }[/math] | [math]\displaystyle{ 85363 }[/math] | [math]\displaystyle{ 89983 }[/math] | [math]\displaystyle{ 217409 }[/math] | [math]\displaystyle{ 372751 }[/math] |
| [math]\displaystyle{ \mathbf{ 4830} }[/math] | [math]\displaystyle{ 30427 }[/math] | [math]\displaystyle{ 35257 }[/math] | [math]\displaystyle{ 72547 }[/math] | [math]\displaystyle{ 351749 }[/math] | [math]\displaystyle{ 2985809 }[/math] | [math]\displaystyle{ 6020477 }[/math] |
| [math]\displaystyle{ \mathbf{ 5040} }[/math] | [math]\displaystyle{ 25073 }[/math] | [math]\displaystyle{ 57457 }[/math] | [math]\displaystyle{ 531359 }[/math] | [math]\displaystyle{ 1245479 }[/math] | [math]\displaystyle{ 2491381 }[/math] | [math]\displaystyle{ 7136659 }[/math] |
| [math]\displaystyle{ \mathbf{ 5250} }[/math] | [math]\displaystyle{ 3413 }[/math] | [math]\displaystyle{ 44179 }[/math] | [math]\displaystyle{ 2117239 }[/math] | [math]\displaystyle{ 2122489 }[/math] | [math]\displaystyle{ 2649067 }[/math] | [math]\displaystyle{ 4895993 }[/math] |
| [math]\displaystyle{ \mathbf{ 5460} }[/math] | [math]\displaystyle{ 144779 }[/math] | [math]\displaystyle{ 913921 }[/math] | [math]\displaystyle{ 1280987 }[/math] | [math]\displaystyle{ 2243491 }[/math] | [math]\displaystyle{ 2283571 }[/math] | [math]\displaystyle{ 2289031 }[/math] |
| [math]\displaystyle{ \mathbf{ 5670} }[/math] | [math]\displaystyle{ 706463 }[/math] | [math]\displaystyle{ 915221 }[/math] | [math]\displaystyle{ 10882211 }[/math] | [math]\displaystyle{ 21206993 }[/math] | [math]\displaystyle{ 21212663 }[/math] | [math]\displaystyle{ 23859467 }[/math] |
| [math]\displaystyle{ \mathbf{ 5880} }[/math] | [math]\displaystyle{ 152389 }[/math] | [math]\displaystyle{ 4896887 }[/math] | [math]\displaystyle{ 6559873 }[/math] | [math]\displaystyle{ 9131321 }[/math] | [math]\displaystyle{ 19210043 }[/math] | [math]\displaystyle{ 24248461 }[/math] |
| [math]\displaystyle{ \mathbf{ 6090} }[/math] | [math]\displaystyle{ 206191 }[/math] | [math]\displaystyle{ 357661 }[/math] | [math]\displaystyle{ 517003 }[/math] | [math]\displaystyle{ 1910927 }[/math] | [math]\displaystyle{ 5835283 }[/math] | [math]\displaystyle{ 10292729 }[/math] |
| [math]\displaystyle{ \mathbf{ 6300} }[/math] | [math]\displaystyle{ 641327 }[/math] | [math]\displaystyle{ 1962449 }[/math] | [math]\displaystyle{ 2797723 }[/math] | [math]\displaystyle{ 3626881 }[/math] | [math]\displaystyle{ 4663249 }[/math] | [math]\displaystyle{ 5601139 }[/math] |
| [math]\displaystyle{ \mathbf{ 6510} }[/math] | [math]\displaystyle{ 20599 }[/math] | [math]\displaystyle{ 155461 }[/math] | [math]\displaystyle{ 161971 }[/math] | [math]\displaystyle{ 573437 }[/math] | [math]\displaystyle{ 4395739 }[/math] | [math]\displaystyle{ 6457669 }[/math] |
| [math]\displaystyle{ \mathbf{ 6720} }[/math] | [math]\displaystyle{ 62347 }[/math] | [math]\displaystyle{ 69067 }[/math] | [math]\displaystyle{ 5072869 }[/math] | [math]\displaystyle{ 9545051 }[/math] | [math]\displaystyle{ 10379081 }[/math] | [math]\displaystyle{ 11184743 }[/math] |
| [math]\displaystyle{ \mathbf{ 6930} }[/math] | [math]\displaystyle{ 17 }[/math] | [math]\displaystyle{ 7151 }[/math] | [math]\displaystyle{ 13469 }[/math] | [math]\displaystyle{ 36469 }[/math] | [math]\displaystyle{ 38261 }[/math] | [math]\displaystyle{ 309167 }[/math] |
| [math]\displaystyle{ \mathbf{ 7140} }[/math] | [math]\displaystyle{ 1241197 }[/math] | [math]\displaystyle{ 1247479 }[/math] | [math]\displaystyle{ 2614559 }[/math] | [math]\displaystyle{ 4496813 }[/math] | [math]\displaystyle{ 4575947 }[/math] | [math]\displaystyle{ 7799837 }[/math] |
| [math]\displaystyle{ \mathbf{ 7350} }[/math] | [math]\displaystyle{ 1445303 }[/math] | [math]\displaystyle{ 8526533 }[/math] | [math]\displaystyle{ 12683299 }[/math] | [math]\displaystyle{ 12690649 }[/math] | [math]\displaystyle{ 21459209 }[/math] | [math]\displaystyle{ 21466559 }[/math] |
| [math]\displaystyle{ \mathbf{ 7560} }[/math] | [math]\displaystyle{ 29387 }[/math] | [math]\displaystyle{ 342389 }[/math] | [math]\displaystyle{ 539839 }[/math] | [math]\displaystyle{ 2141497 }[/math] | [math]\displaystyle{ 7573327 }[/math] | [math]\displaystyle{ 7580887 }[/math] |
| [math]\displaystyle{ \mathbf{ 7770} }[/math] | [math]\displaystyle{ 6553 }[/math] | [math]\displaystyle{ 28549 }[/math] | [math]\displaystyle{ 36319 }[/math] | [math]\displaystyle{ 90373 }[/math] | [math]\displaystyle{ 819317 }[/math] | [math]\displaystyle{ 827087 }[/math] |
| [math]\displaystyle{ \mathbf{ 7980} }[/math] | [math]\displaystyle{ 137 }[/math] | [math]\displaystyle{ 4091 }[/math] | [math]\displaystyle{ 24029 }[/math] | [math]\displaystyle{ 31393 }[/math] | [math]\displaystyle{ 165313 }[/math] | [math]\displaystyle{ 182687 }[/math] |
| [math]\displaystyle{ \mathbf{ 8190} }[/math] | [math]\displaystyle{ 35591 }[/math] | [math]\displaystyle{ 59021 }[/math] | [math]\displaystyle{ 287629 }[/math] | [math]\displaystyle{ 401627 }[/math] | [math]\displaystyle{ 410257 }[/math] | [math]\displaystyle{ 702323 }[/math] |
| [math]\displaystyle{ \mathbf{ 8400} }[/math] | [math]\displaystyle{ 6127909 }[/math] | [math]\displaystyle{ 8133469 }[/math] | [math]\displaystyle{ 8528483 }[/math] | [math]\displaystyle{ 8536883 }[/math] | [math]\displaystyle{ 14448397 }[/math] | [math]\displaystyle{ 19175929 }[/math] |
| [math]\displaystyle{ \mathbf{ 8610} }[/math] | [math]\displaystyle{ 132283 }[/math] | [math]\displaystyle{ 2164387 }[/math] | [math]\displaystyle{ 6903121 }[/math] | [math]\displaystyle{ 10892747 }[/math] | [math]\displaystyle{ 10901357 }[/math] | [math]\displaystyle{ 17489623 }[/math] |
| [math]\displaystyle{ \mathbf{ 8820} }[/math] | [math]\displaystyle{ 84421 }[/math] | [math]\displaystyle{ 466451 }[/math] | [math]\displaystyle{ 3052177 }[/math] | [math]\displaystyle{ 3905777 }[/math] | [math]\displaystyle{ 11397371 }[/math] | [math]\displaystyle{ 53189407 }[/math] |
| [math]\displaystyle{ \mathbf{ 9030} }[/math] | [math]\displaystyle{ 2630153 }[/math] | [math]\displaystyle{ 4927921 }[/math] | [math]\displaystyle{ 5686141 }[/math] | [math]\displaystyle{ 6043399 }[/math] | [math]\displaystyle{ 8411567 }[/math] | [math]\displaystyle{ 8510357 }[/math] |
| [math]\displaystyle{ \mathbf{ 9240} }[/math] | [math]\displaystyle{ 937 }[/math] | [math]\displaystyle{ 21031 }[/math] | [math]\displaystyle{ 53681 }[/math] | [math]\displaystyle{ 62921 }[/math] | [math]\displaystyle{ 95339 }[/math] | [math]\displaystyle{ 495791 }[/math] |
| [math]\displaystyle{ \mathbf{ 9450} }[/math] | [math]\displaystyle{ 1028479 }[/math] | [math]\displaystyle{ 1832711 }[/math] | [math]\displaystyle{ 8104549 }[/math] | [math]\displaystyle{ 15802459 }[/math] | [math]\displaystyle{ 43975031 }[/math] | [math]\displaystyle{ 97126691 }[/math] |
| [math]\displaystyle{ \mathbf{ 9660} }[/math] | [math]\displaystyle{ 521 }[/math] | [math]\displaystyle{ 464413 }[/math] | [math]\displaystyle{ 707071 }[/math] | [math]\displaystyle{ 716731 }[/math] | [math]\displaystyle{ 1197121 }[/math] | [math]\displaystyle{ 1259053 }[/math] |
| [math]\displaystyle{ \mathbf{ 9870} }[/math] | [math]\displaystyle{ 576439 }[/math] | [math]\displaystyle{ 1115923 }[/math] | [math]\displaystyle{ 7516427 }[/math] | [math]\displaystyle{ 9249301 }[/math] | [math]\displaystyle{ 16561691 }[/math] | [math]\displaystyle{ 16571561 }[/math] |
| [math]\displaystyle{ \mathbf{ 10080} }[/math] | [math]\displaystyle{ 6949 }[/math] | [math]\displaystyle{ 125353 }[/math] | [math]\displaystyle{ 156941 }[/math] | [math]\displaystyle{ 949517 }[/math] | [math]\displaystyle{ 3363089 }[/math] | [math]\displaystyle{ 3373169 }[/math] |
| [math]\displaystyle{ \mathbf{ 10290} }[/math] | [math]\displaystyle{ 6143 }[/math] | [math]\displaystyle{ 1535489 }[/math] | [math]\displaystyle{ 2477177 }[/math] | [math]\displaystyle{ 4259887 }[/math] | [math]\displaystyle{ 5294563 }[/math] | [math]\displaystyle{ 10818191 }[/math] |
| [math]\displaystyle{ \mathbf{ 10500} }[/math] | [math]\displaystyle{ 1113239 }[/math] | [math]\displaystyle{ 1841087 }[/math] | [math]\displaystyle{ 7005059 }[/math] | [math]\displaystyle{ 8026327 }[/math] | [math]\displaystyle{ 13707959 }[/math] | [math]\displaystyle{ 22837799 }[/math] |
| [math]\displaystyle{ \mathbf{ 10710} }[/math] | [math]\displaystyle{ 314299 }[/math] | [math]\displaystyle{ 439123 }[/math] | [math]\displaystyle{ 735467 }[/math] | [math]\displaystyle{ 1784911 }[/math] | [math]\displaystyle{ 1923049 }[/math] | [math]\displaystyle{ 2781203 }[/math] |
| [math]\displaystyle{ \mathbf{ 10920} }[/math] | [math]\displaystyle{ 52321 }[/math] | [math]\displaystyle{ 285521 }[/math] | [math]\displaystyle{ 527909 }[/math] | [math]\displaystyle{ 538829 }[/math] | [math]\displaystyle{ 1673941 }[/math] | [math]\displaystyle{ 2214349 }[/math] |
| [math]\displaystyle{ \mathbf{ 11130} }[/math] | [math]\displaystyle{ 187009 }[/math] | [math]\displaystyle{ 198139 }[/math] | [math]\displaystyle{ 255803 }[/math] | [math]\displaystyle{ 547499 }[/math] | [math]\displaystyle{ 2160253 }[/math] | [math]\displaystyle{ 11518723 }[/math] |
| [math]\displaystyle{ \mathbf{ 11340} }[/math] | [math]\displaystyle{ 57143 }[/math] | [math]\displaystyle{ 559051 }[/math] | [math]\displaystyle{ 1091561 }[/math] | [math]\displaystyle{ 10756139 }[/math] | [math]\displaystyle{ 13865323 }[/math] | [math]\displaystyle{ 13876663 }[/math] |
| [math]\displaystyle{ \mathbf{ 11550} }[/math] | [math]\displaystyle{ 4673 }[/math] | [math]\displaystyle{ 9619 }[/math] | [math]\displaystyle{ 89659 }[/math] | [math]\displaystyle{ 112643 }[/math] | [math]\displaystyle{ 155317 }[/math] | [math]\displaystyle{ 166601 }[/math] |
| [math]\displaystyle{ \mathbf{ 11760} }[/math] | [math]\displaystyle{ 3458731 }[/math] | [math]\displaystyle{ 5759843 }[/math] | [math]\displaystyle{ 6305939 }[/math] | [math]\displaystyle{ 6904789 }[/math] | [math]\displaystyle{ 11527693 }[/math] | [math]\displaystyle{ 15296227 }[/math] |
| [math]\displaystyle{ \mathbf{ 11970} }[/math] | [math]\displaystyle{ 10531 }[/math] | [math]\displaystyle{ 1911199 }[/math] | [math]\displaystyle{ 2210573 }[/math] | [math]\displaystyle{ 2298397 }[/math] | [math]\displaystyle{ 15519563 }[/math] | [math]\displaystyle{ 21608347 }[/math] |
| [math]\displaystyle{ \mathbf{ 12180} }[/math] | [math]\displaystyle{ 1067597 }[/math] | [math]\displaystyle{ 1778461 }[/math] | [math]\displaystyle{ 1784599 }[/math] | [math]\displaystyle{ 3551221 }[/math] | [math]\displaystyle{ 7384493 }[/math] | [math]\displaystyle{ 12485003 }[/math] |
| [math]\displaystyle{ \mathbf{ 12390} }[/math] | [math]\displaystyle{ 184291 }[/math] | [math]\displaystyle{ 651017 }[/math] | [math]\displaystyle{ 804493 }[/math] | [math]\displaystyle{ 1536187 }[/math] | [math]\displaystyle{ 4158103 }[/math] | [math]\displaystyle{ 4751293 }[/math] |
| [math]\displaystyle{ \mathbf{ 12600} }[/math] | [math]\displaystyle{ 435577 }[/math] | [math]\displaystyle{ 558431 }[/math] | [math]\displaystyle{ 571031 }[/math] | [math]\displaystyle{ 727369 }[/math] | [math]\displaystyle{ 2890117 }[/math] | [math]\displaystyle{ 3367363 }[/math] |
| [math]\displaystyle{ \mathbf{ 12810} }[/math] | [math]\displaystyle{ 116953 }[/math] | [math]\displaystyle{ 166909 }[/math] | [math]\displaystyle{ 5627029 }[/math] | [math]\displaystyle{ 6623117 }[/math] | [math]\displaystyle{ 10981339 }[/math] | [math]\displaystyle{ 10994149 }[/math] |
| [math]\displaystyle{ \mathbf{ 13020} }[/math] | [math]\displaystyle{ 1691411 }[/math] | [math]\displaystyle{ 3574871 }[/math] | [math]\displaystyle{ 22963981 }[/math] | [math]\displaystyle{ 27098723 }[/math] | [math]\displaystyle{ 29812603 }[/math] | [math]\displaystyle{ 31218403 }[/math] |
| [math]\displaystyle{ \mathbf{ 13230} }[/math] | [math]\displaystyle{ 40543 }[/math] | [math]\displaystyle{ 104651 }[/math] | [math]\displaystyle{ 313219 }[/math] | [math]\displaystyle{ 4705247 }[/math] | [math]\displaystyle{ 4718477 }[/math] | [math]\displaystyle{ 6268289 }[/math] |
| [math]\displaystyle{ \mathbf{ 13440} }[/math] | [math]\displaystyle{ 2141 }[/math] | [math]\displaystyle{ 448741 }[/math] | [math]\displaystyle{ 815261 }[/math] | [math]\displaystyle{ 1560997 }[/math] | [math]\displaystyle{ 1574437 }[/math] | [math]\displaystyle{ 2070517 }[/math] |
| [math]\displaystyle{ \mathbf{ 13650} }[/math] | [math]\displaystyle{ 3343 }[/math] | [math]\displaystyle{ 96997 }[/math] | [math]\displaystyle{ 110647 }[/math] | [math]\displaystyle{ 521047 }[/math] | [math]\displaystyle{ 1590961 }[/math] | [math]\displaystyle{ 2276503 }[/math] |
| [math]\displaystyle{ \mathbf{ 13860} }[/math] | [math]\displaystyle{ 110437 }[/math] | [math]\displaystyle{ 124297 }[/math] | [math]\displaystyle{ 138157 }[/math] | [math]\displaystyle{ 148891 }[/math] | [math]\displaystyle{ 152017 }[/math] | [math]\displaystyle{ 152947 }[/math] |
| [math]\displaystyle{ \mathbf{ 14070} }[/math] | [math]\displaystyle{ 2679239 }[/math] | [math]\displaystyle{ 2886281 }[/math] | [math]\displaystyle{ 3817111 }[/math] | [math]\displaystyle{ 6446353 }[/math] | [math]\displaystyle{ 6460423 }[/math] | [math]\displaystyle{ 6976289 }[/math] |
| [math]\displaystyle{ \mathbf{ 14280} }[/math] | [math]\displaystyle{ 364687 }[/math] | [math]\displaystyle{ 749773 }[/math] | [math]\displaystyle{ 1867573 }[/math] | [math]\displaystyle{ 2146181 }[/math] | [math]\displaystyle{ 2434997 }[/math] | [math]\displaystyle{ 4112627 }[/math] |
| [math]\displaystyle{ \mathbf{ 14490} }[/math] | [math]\displaystyle{ 144667 }[/math] | [math]\displaystyle{ 161263 }[/math] | [math]\displaystyle{ 259603 }[/math] | [math]\displaystyle{ 286333 }[/math] | [math]\displaystyle{ 336251 }[/math] | [math]\displaystyle{ 377809 }[/math] |
| [math]\displaystyle{ \mathbf{ 14700} }[/math] | [math]\displaystyle{ 36583 }[/math] | [math]\displaystyle{ 578267 }[/math] | [math]\displaystyle{ 8529749 }[/math] | [math]\displaystyle{ 14365553 }[/math] | [math]\displaystyle{ 14380253 }[/math] | [math]\displaystyle{ 14830787 }[/math] |
| [math]\displaystyle{ \mathbf{ 14910} }[/math] | [math]\displaystyle{ 74161 }[/math] | [math]\displaystyle{ 109367 }[/math] | [math]\displaystyle{ 120977 }[/math] | [math]\displaystyle{ 1260011 }[/math] | [math]\displaystyle{ 1372211 }[/math] | [math]\displaystyle{ 11898287 }[/math] |
| [math]\displaystyle{ \mathbf{ 15120} }[/math] | [math]\displaystyle{ 121853 }[/math] | [math]\displaystyle{ 689459 }[/math] | [math]\displaystyle{ 822383 }[/math] | [math]\displaystyle{ 11354437 }[/math] | [math]\displaystyle{ 37245407 }[/math] | [math]\displaystyle{ 48384221 }[/math] |
| [math]\displaystyle{ \mathbf{ 15330} }[/math] | [math]\displaystyle{ 7713709 }[/math] | [math]\displaystyle{ 8049187 }[/math] | [math]\displaystyle{ 11583113 }[/math] | [math]\displaystyle{ 12934973 }[/math] | [math]\displaystyle{ 16769749 }[/math] | [math]\displaystyle{ 30793649 }[/math] |
| [math]\displaystyle{ \mathbf{ 15540} }[/math] | [math]\displaystyle{ 160781 }[/math] | [math]\displaystyle{ 580577 }[/math] | [math]\displaystyle{ 4095187 }[/math] | [math]\displaystyle{ 5838409 }[/math] | [math]\displaystyle{ 9523079 }[/math] | [math]\displaystyle{ 10473559 }[/math] |
| [math]\displaystyle{ \mathbf{ 15750} }[/math] | [math]\displaystyle{ 64579 }[/math] | [math]\displaystyle{ 103409 }[/math] | [math]\displaystyle{ 182587 }[/math] | [math]\displaystyle{ 849869 }[/math] | [math]\displaystyle{ 865619 }[/math] | [math]\displaystyle{ 1468729 }[/math] |
| [math]\displaystyle{ \mathbf{ 15960} }[/math] | [math]\displaystyle{ 1847 }[/math] | [math]\displaystyle{ 6037 }[/math] | [math]\displaystyle{ 17807 }[/math] | [math]\displaystyle{ 137147 }[/math] | [math]\displaystyle{ 652969 }[/math] | [math]\displaystyle{ 989977 }[/math] |
| [math]\displaystyle{ \mathbf{ 16170} }[/math] | [math]\displaystyle{ 66179 }[/math] | [math]\displaystyle{ 219451 }[/math] | [math]\displaystyle{ 511843 }[/math] | [math]\displaystyle{ 583421 }[/math] | [math]\displaystyle{ 812431 }[/math] | [math]\displaystyle{ 848567 }[/math] |
| [math]\displaystyle{ \mathbf{ 16380} }[/math] | [math]\displaystyle{ 43759 }[/math] | [math]\displaystyle{ 339263 }[/math] | [math]\displaystyle{ 355643 }[/math] | [math]\displaystyle{ 695047 }[/math] | [math]\displaystyle{ 2011517 }[/math] | [math]\displaystyle{ 2893309 }[/math] |
| [math]\displaystyle{ \mathbf{ 16590} }[/math] | [math]\displaystyle{ 6703 }[/math] | [math]\displaystyle{ 29009 }[/math] | [math]\displaystyle{ 2489183 }[/math] | [math]\displaystyle{ 4028743 }[/math] | [math]\displaystyle{ 9340181 }[/math] | [math]\displaystyle{ 10005263 }[/math] |
| [math]\displaystyle{ \mathbf{ 16800} }[/math] | [math]\displaystyle{ 940319 }[/math] | [math]\displaystyle{ 3772907 }[/math] | [math]\displaystyle{ 3873007 }[/math] | [math]\displaystyle{ 9905921 }[/math] | [math]\displaystyle{ 79622351 }[/math] | [math]\displaystyle{ 95679271 }[/math] |
| [math]\displaystyle{ \mathbf{ 17010} }[/math] | [math]\displaystyle{ 797119 }[/math] | [math]\displaystyle{ 18296627 }[/math] | [math]\displaystyle{ 23152907 }[/math] | [math]\displaystyle{ 38133913 }[/math] | [math]\displaystyle{ 60796007 }[/math] | [math]\displaystyle{ 83709047 }[/math] |
| [math]\displaystyle{ \mathbf{ 17220} }[/math] | [math]\displaystyle{ 225769 }[/math] | [math]\displaystyle{ 1452511 }[/math] | [math]\displaystyle{ 1469731 }[/math] | [math]\displaystyle{ 1606379 }[/math] | [math]\displaystyle{ 2415473 }[/math] | [math]\displaystyle{ 3469069 }[/math] |
| [math]\displaystyle{ \mathbf{ 17430} }[/math] | [math]\displaystyle{ 15643 }[/math] | [math]\displaystyle{ 25471 }[/math] | [math]\displaystyle{ 42901 }[/math] | [math]\displaystyle{ 1170599 }[/math] | [math]\displaystyle{ 3120547 }[/math] | [math]\displaystyle{ 3983249 }[/math] |
| [math]\displaystyle{ \mathbf{ 17640} }[/math] | [math]\displaystyle{ 193607 }[/math] | [math]\displaystyle{ 211247 }[/math] | [math]\displaystyle{ 7624613 }[/math] | [math]\displaystyle{ 10290239 }[/math] | [math]\displaystyle{ 16104047 }[/math] | [math]\displaystyle{ 22618907 }[/math] |
| [math]\displaystyle{ \mathbf{ 17850} }[/math] | [math]\displaystyle{ 129379 }[/math] | [math]\displaystyle{ 289253 }[/math] | [math]\displaystyle{ 1341433 }[/math] | [math]\displaystyle{ 1728911 }[/math] | [math]\displaystyle{ 1746761 }[/math] | [math]\displaystyle{ 2918737 }[/math] |
| [math]\displaystyle{ \mathbf{ 18060} }[/math] | [math]\displaystyle{ 1013921 }[/math] | [math]\displaystyle{ 1038209 }[/math] | [math]\displaystyle{ 2703941 }[/math] | [math]\displaystyle{ 3580333 }[/math] | [math]\displaystyle{ 3914689 }[/math] | [math]\displaystyle{ 11110339 }[/math] |
| [math]\displaystyle{ \mathbf{ 18270} }[/math] | [math]\displaystyle{ 29567 }[/math] | [math]\displaystyle{ 511201 }[/math] | [math]\displaystyle{ 1615723 }[/math] | [math]\displaystyle{ 1890701 }[/math] | [math]\displaystyle{ 1989811 }[/math] | [math]\displaystyle{ 2008081 }[/math] |
| [math]\displaystyle{ \mathbf{ 18480} }[/math] | [math]\displaystyle{ 2711 }[/math] | [math]\displaystyle{ 25643 }[/math] | [math]\displaystyle{ 40853 }[/math] | [math]\displaystyle{ 149143 }[/math] | [math]\displaystyle{ 194839 }[/math] | [math]\displaystyle{ 213319 }[/math] |
| [math]\displaystyle{ \mathbf{ 18690} }[/math] | [math]\displaystyle{ 881 }[/math] | [math]\displaystyle{ 9421469 }[/math] | [math]\displaystyle{ 10687877 }[/math] | [math]\displaystyle{ 11455753 }[/math] | [math]\displaystyle{ 14740463 }[/math] | [math]\displaystyle{ 21499799 }[/math] |
| [math]\displaystyle{ \mathbf{ 18900} }[/math] | [math]\displaystyle{ 73823 }[/math] | [math]\displaystyle{ 462079 }[/math] | [math]\displaystyle{ 804113 }[/math] | [math]\displaystyle{ 823013 }[/math] | [math]\displaystyle{ 1323799 }[/math] | [math]\displaystyle{ 1370987 }[/math] |
| [math]\displaystyle{ \mathbf{ 19110} }[/math] | [math]\displaystyle{ 63737 }[/math] | [math]\displaystyle{ 322171 }[/math] | [math]\displaystyle{ 520193 }[/math] | [math]\displaystyle{ 999763 }[/math] | [math]\displaystyle{ 1023487 }[/math] | [math]\displaystyle{ 1032067 }[/math] |
| [math]\displaystyle{ \mathbf{ 19320} }[/math] | [math]\displaystyle{ 682411 }[/math] | [math]\displaystyle{ 743747 }[/math] | [math]\displaystyle{ 1343669 }[/math] | [math]\displaystyle{ 1373233 }[/math] | [math]\displaystyle{ 1782499 }[/math] | [math]\displaystyle{ 2574437 }[/math] |
| [math]\displaystyle{ \mathbf{ 19530} }[/math] | [math]\displaystyle{ 50929 }[/math] | [math]\displaystyle{ 738919 }[/math] | [math]\displaystyle{ 1773689 }[/math] | [math]\displaystyle{ 1793219 }[/math] | [math]\displaystyle{ 6121807 }[/math] | [math]\displaystyle{ 18867007 }[/math] |
| [math]\displaystyle{ \mathbf{ 19740} }[/math] | [math]\displaystyle{ 2729 }[/math] | [math]\displaystyle{ 30757 }[/math] | [math]\displaystyle{ 360163 }[/math] | [math]\displaystyle{ 1652591 }[/math] | [math]\displaystyle{ 18160973 }[/math] | [math]\displaystyle{ 18862889 }[/math] |
| [math]\displaystyle{ \mathbf{ 19950} }[/math] | [math]\displaystyle{ 142699 }[/math] | [math]\displaystyle{ 162649 }[/math] | [math]\displaystyle{ 239957 }[/math] | [math]\displaystyle{ 302287 }[/math] | [math]\displaystyle{ 322237 }[/math] | [math]\displaystyle{ 661547 }[/math] |
| [math]\displaystyle{ \mathbf{ 20160} }[/math] | [math]\displaystyle{ 3330211 }[/math] | [math]\displaystyle{ 5620609 }[/math] | [math]\displaystyle{ 6413401 }[/math] | [math]\displaystyle{ 15055609 }[/math] | [math]\displaystyle{ 32094917 }[/math] | [math]\displaystyle{ 52863893 }[/math] |
| [math]\displaystyle{ \mathbf{ 20370} }[/math] | [math]\displaystyle{ 1158881 }[/math] | [math]\displaystyle{ 1216213 }[/math] | [math]\displaystyle{ 1236583 }[/math] | [math]\displaystyle{ 3893899 }[/math] | [math]\displaystyle{ 7991839 }[/math] | [math]\displaystyle{ 8012209 }[/math] |
| [math]\displaystyle{ \mathbf{ 20580} }[/math] | [math]\displaystyle{ 9689 }[/math] | [math]\displaystyle{ 316501 }[/math] | [math]\displaystyle{ 398023 }[/math] | [math]\displaystyle{ 2047813 }[/math] | [math]\displaystyle{ 2219557 }[/math] | [math]\displaystyle{ 2240137 }[/math] |
| [math]\displaystyle{ \mathbf{ 20790} }[/math] | [math]\displaystyle{ 12713 }[/math] | [math]\displaystyle{ 20023 }[/math] | [math]\displaystyle{ 141079 }[/math] | [math]\displaystyle{ 159571 }[/math] | [math]\displaystyle{ 296117 }[/math] | [math]\displaystyle{ 914813 }[/math] |
| [math]\displaystyle{ \mathbf{ 21000} }[/math] | [math]\displaystyle{ 5501 }[/math] | [math]\displaystyle{ 19471 }[/math] | [math]\displaystyle{ 65837 }[/math] | [math]\displaystyle{ 688139 }[/math] | [math]\displaystyle{ 3980407 }[/math] | [math]\displaystyle{ 8983031 }[/math] |
| [math]\displaystyle{ \mathbf{n = 10} }[/math] | ||||||
| [math]\displaystyle{ \mathbf{d} }[/math] | [math]\displaystyle{ \mathbf{p_0} }[/math] | |||||
| [math]\displaystyle{ \mathbf{ 210} }[/math] | [math]\displaystyle{ 199 }[/math] | [math]\displaystyle{ 243051733 }[/math] | [math]\displaystyle{ 498161423 }[/math] | [math]\displaystyle{ 2490123989 }[/math] | [math]\displaystyle{ 5417375591 }[/math] | [math]\displaystyle{ 8785408259 }[/math] |
| [math]\displaystyle{ \mathbf{ 420} }[/math] | [math]\displaystyle{ 52879 }[/math] | [math]\displaystyle{ 3544939 }[/math] | [math]\displaystyle{ 725283077 }[/math] | [math]\displaystyle{ 1580792347 }[/math] | [math]\displaystyle{ 1931425157 }[/math] | [math]\displaystyle{ 8392393693 }[/math] |
| [math]\displaystyle{ \mathbf{ 630} }[/math] | [math]\displaystyle{ 964417 }[/math] | [math]\displaystyle{ 1021331 }[/math] | [math]\displaystyle{ 3710699 }[/math] | [math]\displaystyle{ 174610351 }[/math] | [math]\displaystyle{ 396598051 }[/math] | [math]\displaystyle{ 525173641 }[/math] |
| [math]\displaystyle{ \mathbf{ 840} }[/math] | [math]\displaystyle{ 915611 }[/math] | [math]\displaystyle{ 24748189 }[/math] | [math]\displaystyle{ 33791509 }[/math] | [math]\displaystyle{ 314727967 }[/math] | [math]\displaystyle{ 510756371 }[/math] | [math]\displaystyle{ 1079797657 }[/math] |
| [math]\displaystyle{ \mathbf{ 1050} }[/math] | [math]\displaystyle{ 130006783 }[/math] | [math]\displaystyle{ 208734751 }[/math] | [math]\displaystyle{ 400663741 }[/math] | [math]\displaystyle{ 963551671 }[/math] | [math]\displaystyle{ 1219200119 }[/math] | [math]\displaystyle{ 1231110787 }[/math] |
| [math]\displaystyle{ \mathbf{ 1260} }[/math] | [math]\displaystyle{ 6722909 }[/math] | [math]\displaystyle{ 27846803 }[/math] | [math]\displaystyle{ 63289771 }[/math] | [math]\displaystyle{ 1000262819 }[/math] | [math]\displaystyle{ 1476482057 }[/math] | [math]\displaystyle{ 4565705117 }[/math] |
| [math]\displaystyle{ \mathbf{ 1470} }[/math] | [math]\displaystyle{ 2534561 }[/math] | [math]\displaystyle{ 189999707 }[/math] | [math]\displaystyle{ 833570987 }[/math] | [math]\displaystyle{ 1168004581 }[/math] | [math]\displaystyle{ 2010828277 }[/math] | [math]\displaystyle{ 3182258251 }[/math] |
| [math]\displaystyle{ \mathbf{ 1680} }[/math] | [math]\displaystyle{ 1343205113 }[/math] | [math]\displaystyle{ 3033769813 }[/math] | [math]\displaystyle{ 4093882757 }[/math] | [math]\displaystyle{ 4112814241 }[/math] | [math]\displaystyle{ 4348188919 }[/math] | [math]\displaystyle{ 4749575333 }[/math] |
| [math]\displaystyle{ \mathbf{ 1890} }[/math] | [math]\displaystyle{ 41513261 }[/math] | [math]\displaystyle{ 95317913 }[/math] | [math]\displaystyle{ 6232033069 }[/math] | [math]\displaystyle{ 6361761239 }[/math] | [math]\displaystyle{ 6709899029 }[/math] | [math]\displaystyle{ 8521839071 }[/math] |
| [math]\displaystyle{ \mathbf{ 2100} }[/math] | [math]\displaystyle{ 34913 }[/math] | [math]\displaystyle{ 581393 }[/math] | [math]\displaystyle{ 8397091 }[/math] | [math]\displaystyle{ 10200607 }[/math] | [math]\displaystyle{ 31913837 }[/math] | [math]\displaystyle{ 258411317 }[/math] |
| [math]\displaystyle{ \mathbf{ 2310} }[/math] | [math]\displaystyle{ 2564251 }[/math] | [math]\displaystyle{ 7245143 }[/math] | [math]\displaystyle{ 15898823 }[/math] | [math]\displaystyle{ 34834237 }[/math] | [math]\displaystyle{ 51404371 }[/math] | [math]\displaystyle{ 60858179 }[/math] |
| [math]\displaystyle{ \mathbf{ 2520} }[/math] | [math]\displaystyle{ 1058597 }[/math] | [math]\displaystyle{ 8226307 }[/math] | [math]\displaystyle{ 438716653 }[/math] | [math]\displaystyle{ 799422581 }[/math] | [math]\displaystyle{ 975166567 }[/math] | [math]\displaystyle{ 983999677 }[/math] |
| [math]\displaystyle{ \mathbf{ 2730} }[/math] | [math]\displaystyle{ 122069 }[/math] | [math]\displaystyle{ 123059 }[/math] | [math]\displaystyle{ 158633 }[/math] | [math]\displaystyle{ 3319219 }[/math] | [math]\displaystyle{ 3427393 }[/math] | [math]\displaystyle{ 5082629 }[/math] |
| [math]\displaystyle{ \mathbf{ 2940} }[/math] | [math]\displaystyle{ 2546781317 }[/math] | [math]\displaystyle{ 3736609957 }[/math] | [math]\displaystyle{ 4895747497 }[/math] | |||
| [math]\displaystyle{ \mathbf{ 3150} }[/math] | [math]\displaystyle{ 34071019 }[/math] | [math]\displaystyle{ 1174379903 }[/math] | [math]\displaystyle{ 1247572429 }[/math] | [math]\displaystyle{ 1914733781 }[/math] | [math]\displaystyle{ 5502174781 }[/math] | [math]\displaystyle{ 5598860513 }[/math] |
| [math]\displaystyle{ \mathbf{ 3360} }[/math] | [math]\displaystyle{ 210391 }[/math] | [math]\displaystyle{ 762261571 }[/math] | [math]\displaystyle{ 2289797801 }[/math] | [math]\displaystyle{ 5842998881 }[/math] | [math]\displaystyle{ 5973997177 }[/math] | [math]\displaystyle{ 6486241481 }[/math] |
| [math]\displaystyle{ \mathbf{ 3570} }[/math] | [math]\displaystyle{ 150343 }[/math] | [math]\displaystyle{ 920827 }[/math] | [math]\displaystyle{ 47896129 }[/math] | [math]\displaystyle{ 110935963 }[/math] | [math]\displaystyle{ 124813783 }[/math] | [math]\displaystyle{ 253908793 }[/math] |
| [math]\displaystyle{ \mathbf{ 3780} }[/math] | [math]\displaystyle{ 4045763 }[/math] | [math]\displaystyle{ 162045979 }[/math] | [math]\displaystyle{ 3611162221 }[/math] | [math]\displaystyle{ 3953439013 }[/math] | [math]\displaystyle{ 5751477079 }[/math] | [math]\displaystyle{ 6389572141 }[/math] |
| [math]\displaystyle{ \mathbf{ 3990} }[/math] | [math]\displaystyle{ 99877 }[/math] | [math]\displaystyle{ 2732441 }[/math] | [math]\displaystyle{ 145829681 }[/math] | [math]\displaystyle{ 1512868211 }[/math] | [math]\displaystyle{ 1519374557 }[/math] | [math]\displaystyle{ 1905288811 }[/math] |
| [math]\displaystyle{ \mathbf{ 4200} }[/math] | [math]\displaystyle{ 75187297 }[/math] | [math]\displaystyle{ 436800197 }[/math] | [math]\displaystyle{ 825073159 }[/math] | [math]\displaystyle{ 953483507 }[/math] | [math]\displaystyle{ 1237285949 }[/math] | [math]\displaystyle{ 1620977257 }[/math] |
| [math]\displaystyle{ \mathbf{ 4410} }[/math] | [math]\displaystyle{ 343475219 }[/math] | [math]\displaystyle{ 718394137 }[/math] | [math]\displaystyle{ 1714841501 }[/math] | [math]\displaystyle{ 4312513897 }[/math] | [math]\displaystyle{ 4433557501 }[/math] | [math]\displaystyle{ 7302174197 }[/math] |
| [math]\displaystyle{ \mathbf{ 4620} }[/math] | [math]\displaystyle{ 85363 }[/math] | [math]\displaystyle{ 372751 }[/math] | [math]\displaystyle{ 926879 }[/math] | [math]\displaystyle{ 10645541 }[/math] | [math]\displaystyle{ 11022827 }[/math] | [math]\displaystyle{ 11027447 }[/math] |
| [math]\displaystyle{ \mathbf{ 4830} }[/math] | [math]\displaystyle{ 30427 }[/math] | [math]\displaystyle{ 6020477 }[/math] | [math]\displaystyle{ 16424981 }[/math] | [math]\displaystyle{ 151254533 }[/math] | [math]\displaystyle{ 229780123 }[/math] | [math]\displaystyle{ 482610239 }[/math] |
| [math]\displaystyle{ \mathbf{ 5040} }[/math] | [math]\displaystyle{ 145866041 }[/math] | [math]\displaystyle{ 226851517 }[/math] | [math]\displaystyle{ 292104419 }[/math] | [math]\displaystyle{ 517266257 }[/math] | [math]\displaystyle{ 986618569 }[/math] | [math]\displaystyle{ 1785262393 }[/math] |
| [math]\displaystyle{ \mathbf{ 5250} }[/math] | [math]\displaystyle{ 2117239 }[/math] | [math]\displaystyle{ 134051459 }[/math] | [math]\displaystyle{ 444256783 }[/math] | [math]\displaystyle{ 635071121 }[/math] | [math]\displaystyle{ 3239335223 }[/math] | [math]\displaystyle{ 3689988833 }[/math] |
| [math]\displaystyle{ \mathbf{ 5460} }[/math] | [math]\displaystyle{ 2283571 }[/math] | [math]\displaystyle{ 11988607 }[/math] | [math]\displaystyle{ 17327831 }[/math] | [math]\displaystyle{ 18230447 }[/math] | [math]\displaystyle{ 97175423 }[/math] | [math]\displaystyle{ 168445523 }[/math] |
| [math]\displaystyle{ \mathbf{ 5670} }[/math] | [math]\displaystyle{ 21206993 }[/math] | [math]\displaystyle{ 42322087 }[/math] | [math]\displaystyle{ 232282121 }[/math] | [math]\displaystyle{ 530515507 }[/math] | [math]\displaystyle{ 2074726021 }[/math] | [math]\displaystyle{ 2176462667 }[/math] |
| [math]\displaystyle{ \mathbf{ 5880} }[/math] | [math]\displaystyle{ 769792447 }[/math] | [math]\displaystyle{ 1028745119 }[/math] | [math]\displaystyle{ 2716511507 }[/math] | [math]\displaystyle{ 2850255403 }[/math] | [math]\displaystyle{ 4059527753 }[/math] | [math]\displaystyle{ 4338343433 }[/math] |
| [math]\displaystyle{ \mathbf{ 6090} }[/math] | [math]\displaystyle{ 98202331 }[/math] | [math]\displaystyle{ 218657237 }[/math] | [math]\displaystyle{ 508050341 }[/math] | [math]\displaystyle{ 965528153 }[/math] | [math]\displaystyle{ 1963343323 }[/math] | [math]\displaystyle{ 2133623147 }[/math] |
| [math]\displaystyle{ \mathbf{ 6300} }[/math] | [math]\displaystyle{ 46452799 }[/math] | [math]\displaystyle{ 161073877 }[/math] | [math]\displaystyle{ 416581987 }[/math] | [math]\displaystyle{ 444443777 }[/math] | [math]\displaystyle{ 799148171 }[/math] | [math]\displaystyle{ 1536915817 }[/math] |
| [math]\displaystyle{ \mathbf{ 6510} }[/math] | [math]\displaystyle{ 155461 }[/math] | [math]\displaystyle{ 11699279 }[/math] | [math]\displaystyle{ 59259649 }[/math] | [math]\displaystyle{ 82736531 }[/math] | [math]\displaystyle{ 138908647 }[/math] | [math]\displaystyle{ 156852947 }[/math] |
| [math]\displaystyle{ \mathbf{ 6720} }[/math] | [math]\displaystyle{ 62347 }[/math] | [math]\displaystyle{ 18249241 }[/math] | [math]\displaystyle{ 402509117 }[/math] | [math]\displaystyle{ 646946233 }[/math] | [math]\displaystyle{ 694032349 }[/math] | [math]\displaystyle{ 748855249 }[/math] |
| [math]\displaystyle{ \mathbf{ 6930} }[/math] | [math]\displaystyle{ 1664417 }[/math] | [math]\displaystyle{ 3306839 }[/math] | [math]\displaystyle{ 6703841 }[/math] | [math]\displaystyle{ 10343167 }[/math] | [math]\displaystyle{ 16988767 }[/math] | [math]\displaystyle{ 17046329 }[/math] |
| [math]\displaystyle{ \mathbf{ 7140} }[/math] | [math]\displaystyle{ 12331793 }[/math] | [math]\displaystyle{ 21994589 }[/math] | [math]\displaystyle{ 32695477 }[/math] | [math]\displaystyle{ 135554233 }[/math] | [math]\displaystyle{ 355138829 }[/math] | [math]\displaystyle{ 730901161 }[/math] |
| [math]\displaystyle{ \mathbf{ 7350} }[/math] | [math]\displaystyle{ 12683299 }[/math] | [math]\displaystyle{ 21459209 }[/math] | [math]\displaystyle{ 38446267 }[/math] | [math]\displaystyle{ 423264613 }[/math] | [math]\displaystyle{ 3158377081 }[/math] | [math]\displaystyle{ 5208862573 }[/math] |
| [math]\displaystyle{ \mathbf{ 7560} }[/math] | [math]\displaystyle{ 7573327 }[/math] | [math]\displaystyle{ 369901513 }[/math] | [math]\displaystyle{ 2755541693 }[/math] | [math]\displaystyle{ 2774476609 }[/math] | [math]\displaystyle{ 3311703233 }[/math] | [math]\displaystyle{ 5004136327 }[/math] |
| [math]\displaystyle{ \mathbf{ 7770} }[/math] | [math]\displaystyle{ 28549 }[/math] | [math]\displaystyle{ 819317 }[/math] | [math]\displaystyle{ 3721051 }[/math] | [math]\displaystyle{ 11941571 }[/math] | [math]\displaystyle{ 35273473 }[/math] | [math]\displaystyle{ 46949093 }[/math] |
| [math]\displaystyle{ \mathbf{ 7980} }[/math] | [math]\displaystyle{ 1024853 }[/math] | [math]\displaystyle{ 355670309 }[/math] | [math]\displaystyle{ 446786191 }[/math] | [math]\displaystyle{ 547343483 }[/math] | [math]\displaystyle{ 682871447 }[/math] | [math]\displaystyle{ 1772834893 }[/math] |
| [math]\displaystyle{ \mathbf{ 8190} }[/math] | [math]\displaystyle{ 7328437 }[/math] | [math]\displaystyle{ 15275849 }[/math] | [math]\displaystyle{ 17503261 }[/math] | [math]\displaystyle{ 22737017 }[/math] | [math]\displaystyle{ 27294053 }[/math] | [math]\displaystyle{ 45150331 }[/math] |
| [math]\displaystyle{ \mathbf{ 8400} }[/math] | [math]\displaystyle{ 8528483 }[/math] | [math]\displaystyle{ 40313929 }[/math] | [math]\displaystyle{ 243787771 }[/math] | [math]\displaystyle{ 385895737 }[/math] | [math]\displaystyle{ 467671013 }[/math] | [math]\displaystyle{ 797154607 }[/math] |
| [math]\displaystyle{ \mathbf{ 8610} }[/math] | [math]\displaystyle{ 10892747 }[/math] | [math]\displaystyle{ 17489623 }[/math] | [math]\displaystyle{ 28416517 }[/math] | [math]\displaystyle{ 55350017 }[/math] | [math]\displaystyle{ 200631439 }[/math] | [math]\displaystyle{ 449962543 }[/math] |
| [math]\displaystyle{ \mathbf{ 8820} }[/math] | [math]\displaystyle{ 275550449 }[/math] | [math]\displaystyle{ 340210649 }[/math] | [math]\displaystyle{ 375439381 }[/math] | [math]\displaystyle{ 1299902701 }[/math] | [math]\displaystyle{ 7189505563 }[/math] | [math]\displaystyle{ 8000213747 }[/math] |
| [math]\displaystyle{ \mathbf{ 9030} }[/math] | [math]\displaystyle{ 31057003 }[/math] | [math]\displaystyle{ 150282967 }[/math] | [math]\displaystyle{ 634308509 }[/math] | [math]\displaystyle{ 643690123 }[/math] | [math]\displaystyle{ 2295863833 }[/math] | [math]\displaystyle{ 2515095703 }[/math] |
| [math]\displaystyle{ \mathbf{ 9240} }[/math] | [math]\displaystyle{ 53681 }[/math] | [math]\displaystyle{ 14224981 }[/math] | [math]\displaystyle{ 14432399 }[/math] | [math]\displaystyle{ 23559377 }[/math] | [math]\displaystyle{ 28467293 }[/math] | [math]\displaystyle{ 42049001 }[/math] |
| [math]\displaystyle{ \mathbf{ 9450} }[/math] | [math]\displaystyle{ 334554023 }[/math] | [math]\displaystyle{ 488051653 }[/math] | [math]\displaystyle{ 2038389299 }[/math] | [math]\displaystyle{ 2162899399 }[/math] | [math]\displaystyle{ 2445407273 }[/math] | [math]\displaystyle{ 3057392207 }[/math] |
| [math]\displaystyle{ \mathbf{ 9660} }[/math] | [math]\displaystyle{ 707071 }[/math] | [math]\displaystyle{ 125628439 }[/math] | [math]\displaystyle{ 303544463 }[/math] | [math]\displaystyle{ 441911263 }[/math] | [math]\displaystyle{ 449336813 }[/math] | [math]\displaystyle{ 511484261 }[/math] |
| [math]\displaystyle{ \mathbf{ 9870} }[/math] | [math]\displaystyle{ 16561691 }[/math] | [math]\displaystyle{ 26691349 }[/math] | [math]\displaystyle{ 373909451 }[/math] | [math]\displaystyle{ 558247033 }[/math] | [math]\displaystyle{ 626630117 }[/math] | [math]\displaystyle{ 1074793063 }[/math] |
| [math]\displaystyle{ \mathbf{ 10080} }[/math] | [math]\displaystyle{ 3363089 }[/math] | [math]\displaystyle{ 35937059 }[/math] | [math]\displaystyle{ 57814343 }[/math] | [math]\displaystyle{ 83864653 }[/math] | [math]\displaystyle{ 264068017 }[/math] | [math]\displaystyle{ 2293066417 }[/math] |
| [math]\displaystyle{ \mathbf{ 10290} }[/math] | [math]\displaystyle{ 459609859 }[/math] | [math]\displaystyle{ 522069971 }[/math] | [math]\displaystyle{ 535273337 }[/math] | [math]\displaystyle{ 720980111 }[/math] | [math]\displaystyle{ 1617247087 }[/math] | [math]\displaystyle{ 1769323693 }[/math] |
| [math]\displaystyle{ \mathbf{ 10500} }[/math] | [math]\displaystyle{ 38610347 }[/math] | [math]\displaystyle{ 185388121 }[/math] | [math]\displaystyle{ 511207351 }[/math] | [math]\displaystyle{ 512002717 }[/math] | [math]\displaystyle{ 573447551 }[/math] | [math]\displaystyle{ 728734969 }[/math] |
| [math]\displaystyle{ \mathbf{ 10710} }[/math] | [math]\displaystyle{ 2781203 }[/math] | [math]\displaystyle{ 10327159 }[/math] | [math]\displaystyle{ 15741997 }[/math] | [math]\displaystyle{ 161184019 }[/math] | [math]\displaystyle{ 290334601 }[/math] | [math]\displaystyle{ 387848743 }[/math] |
| [math]\displaystyle{ \mathbf{ 10920} }[/math] | [math]\displaystyle{ 527909 }[/math] | [math]\displaystyle{ 8754457 }[/math] | [math]\displaystyle{ 19711711 }[/math] | [math]\displaystyle{ 68442943 }[/math] | [math]\displaystyle{ 70092481 }[/math] | [math]\displaystyle{ 108555763 }[/math] |
| [math]\displaystyle{ \mathbf{ 11130} }[/math] | [math]\displaystyle{ 187009 }[/math] | [math]\displaystyle{ 74743931 }[/math] | [math]\displaystyle{ 1717072597 }[/math] | [math]\displaystyle{ 2241197341 }[/math] | [math]\displaystyle{ 3885152797 }[/math] | [math]\displaystyle{ 5442728839 }[/math] |
| [math]\displaystyle{ \mathbf{ 11340} }[/math] | [math]\displaystyle{ 13865323 }[/math] | [math]\displaystyle{ 151172779 }[/math] | [math]\displaystyle{ 155052347 }[/math] | [math]\displaystyle{ 169766761 }[/math] | [math]\displaystyle{ 417004037 }[/math] | [math]\displaystyle{ 759377761 }[/math] |
| [math]\displaystyle{ \mathbf{ 11550} }[/math] | [math]\displaystyle{ 166601 }[/math] | [math]\displaystyle{ 178151 }[/math] | [math]\displaystyle{ 189701 }[/math] | [math]\displaystyle{ 2902951 }[/math] | [math]\displaystyle{ 2939267 }[/math] | [math]\displaystyle{ 6906061 }[/math] |
| [math]\displaystyle{ \mathbf{ 11760} }[/math] | [math]\displaystyle{ 15296227 }[/math] | [math]\displaystyle{ 115733179 }[/math] | [math]\displaystyle{ 793412467 }[/math] | [math]\displaystyle{ 2045327461 }[/math] | [math]\displaystyle{ 3317282629 }[/math] | [math]\displaystyle{ 3405094727 }[/math] |
| [math]\displaystyle{ \mathbf{ 11970} }[/math] | [math]\displaystyle{ 70627031 }[/math] | [math]\displaystyle{ 81131437 }[/math] | [math]\displaystyle{ 190977547 }[/math] | [math]\displaystyle{ 295424263 }[/math] | [math]\displaystyle{ 435613939 }[/math] | [math]\displaystyle{ 436230467 }[/math] |
| [math]\displaystyle{ \mathbf{ 12180} }[/math] | [math]\displaystyle{ 96579871 }[/math] | [math]\displaystyle{ 196123667 }[/math] | [math]\displaystyle{ 1414855181 }[/math] | [math]\displaystyle{ 1594532899 }[/math] | [math]\displaystyle{ 1852156771 }[/math] | [math]\displaystyle{ 5477685029 }[/math] |
| [math]\displaystyle{ \mathbf{ 12390} }[/math] | [math]\displaystyle{ 355974491 }[/math] | [math]\displaystyle{ 1228212781 }[/math] | [math]\displaystyle{ 1597738157 }[/math] | [math]\displaystyle{ 2356239043 }[/math] | [math]\displaystyle{ 2537515919 }[/math] | [math]\displaystyle{ 2664004501 }[/math] |
| [math]\displaystyle{ \mathbf{ 12600} }[/math] | [math]\displaystyle{ 558431 }[/math] | [math]\displaystyle{ 4885897 }[/math] | [math]\displaystyle{ 62631409 }[/math] | [math]\displaystyle{ 222308641 }[/math] | [math]\displaystyle{ 247236973 }[/math] | [math]\displaystyle{ 597208309 }[/math] |
| [math]\displaystyle{ \mathbf{ 12810} }[/math] | [math]\displaystyle{ 10981339 }[/math] | [math]\displaystyle{ 73391203 }[/math] | [math]\displaystyle{ 614195423 }[/math] | [math]\displaystyle{ 722428933 }[/math] | [math]\displaystyle{ 1804485667 }[/math] | [math]\displaystyle{ 2011342889 }[/math] |
| [math]\displaystyle{ \mathbf{ 13020} }[/math] | [math]\displaystyle{ 37278391 }[/math] | [math]\displaystyle{ 396360829 }[/math] | [math]\displaystyle{ 477013687 }[/math] | [math]\displaystyle{ 1035592279 }[/math] | [math]\displaystyle{ 1668997513 }[/math] | [math]\displaystyle{ 1740405707 }[/math] |
| [math]\displaystyle{ \mathbf{ 13230} }[/math] | [math]\displaystyle{ 4705247 }[/math] | [math]\displaystyle{ 43971617 }[/math] | [math]\displaystyle{ 150462859 }[/math] | [math]\displaystyle{ 3214143193 }[/math] | [math]\displaystyle{ 4385611183 }[/math] | [math]\displaystyle{ 6156888427 }[/math] |
| [math]\displaystyle{ \mathbf{ 13440} }[/math] | [math]\displaystyle{ 1560997 }[/math] | [math]\displaystyle{ 2070517 }[/math] | [math]\displaystyle{ 319796189 }[/math] | [math]\displaystyle{ 397320779 }[/math] | [math]\displaystyle{ 534628103 }[/math] | [math]\displaystyle{ 1466338729 }[/math] |
| [math]\displaystyle{ \mathbf{ 13650} }[/math] | [math]\displaystyle{ 96997 }[/math] | [math]\displaystyle{ 8628157 }[/math] | [math]\displaystyle{ 23309989 }[/math] | [math]\displaystyle{ 84831493 }[/math] | [math]\displaystyle{ 95865989 }[/math] | [math]\displaystyle{ 183786877 }[/math] |
| [math]\displaystyle{ \mathbf{ 13860} }[/math] | [math]\displaystyle{ 110437 }[/math] | [math]\displaystyle{ 124297 }[/math] | [math]\displaystyle{ 138157 }[/math] | [math]\displaystyle{ 152947 }[/math] | [math]\displaystyle{ 166807 }[/math] | [math]\displaystyle{ 180667 }[/math] |
| [math]\displaystyle{ \mathbf{ 14070} }[/math] | [math]\displaystyle{ 6446353 }[/math] | [math]\displaystyle{ 6976289 }[/math] | [math]\displaystyle{ 9167027 }[/math] | [math]\displaystyle{ 315420997 }[/math] | [math]\displaystyle{ 324294169 }[/math] | [math]\displaystyle{ 850130293 }[/math] |
| [math]\displaystyle{ \mathbf{ 14280} }[/math] | [math]\displaystyle{ 8022137 }[/math] | [math]\displaystyle{ 46017523 }[/math] | [math]\displaystyle{ 49573471 }[/math] | [math]\displaystyle{ 84264127 }[/math] | [math]\displaystyle{ 201286747 }[/math] | [math]\displaystyle{ 664107853 }[/math] |
| [math]\displaystyle{ \mathbf{ 14490} }[/math] | [math]\displaystyle{ 4421849 }[/math] | [math]\displaystyle{ 7258067 }[/math] | [math]\displaystyle{ 55181701 }[/math] | [math]\displaystyle{ 266196461 }[/math] | [math]\displaystyle{ 400560449 }[/math] | [math]\displaystyle{ 658093439 }[/math] |
| [math]\displaystyle{ \mathbf{ 14700} }[/math] | [math]\displaystyle{ 14365553 }[/math] | [math]\displaystyle{ 79088123 }[/math] | [math]\displaystyle{ 578429339 }[/math] | [math]\displaystyle{ 1590374273 }[/math] | [math]\displaystyle{ 1620663103 }[/math] | [math]\displaystyle{ 1692678277 }[/math] |
| [math]\displaystyle{ \mathbf{ 14910} }[/math] | [math]\displaystyle{ 1313271217 }[/math] | [math]\displaystyle{ 1398822683 }[/math] | [math]\displaystyle{ 3458123993 }[/math] | [math]\displaystyle{ 5050258823 }[/math] | [math]\displaystyle{ 8564509277 }[/math] | |
| [math]\displaystyle{ \mathbf{ 15120} }[/math] | [math]\displaystyle{ 643929523 }[/math] | [math]\displaystyle{ 1697175937 }[/math] | [math]\displaystyle{ 3456724013 }[/math] | [math]\displaystyle{ 3604668029 }[/math] | [math]\displaystyle{ 5105194837 }[/math] | [math]\displaystyle{ 5972188679 }[/math] |
| [math]\displaystyle{ \mathbf{ 15330} }[/math] | [math]\displaystyle{ 423644591 }[/math] | [math]\displaystyle{ 792183047 }[/math] | [math]\displaystyle{ 1013912467 }[/math] | [math]\displaystyle{ 1239474463 }[/math] | [math]\displaystyle{ 1707297247 }[/math] | [math]\displaystyle{ 1918187839 }[/math] |
| [math]\displaystyle{ \mathbf{ 15540} }[/math] | [math]\displaystyle{ 15113711 }[/math] | [math]\displaystyle{ 49877209 }[/math] | [math]\displaystyle{ 90195289 }[/math] | [math]\displaystyle{ 113317157 }[/math] | [math]\displaystyle{ 542625751 }[/math] | [math]\displaystyle{ 801528769 }[/math] |
| [math]\displaystyle{ \mathbf{ 15750} }[/math] | [math]\displaystyle{ 849869 }[/math] | [math]\displaystyle{ 281904709 }[/math] | [math]\displaystyle{ 741349123 }[/math] | [math]\displaystyle{ 1196157763 }[/math] | [math]\displaystyle{ 1264569469 }[/math] | [math]\displaystyle{ 1628362679 }[/math] |
| [math]\displaystyle{ \mathbf{ 15960} }[/math] | [math]\displaystyle{ 1847 }[/math] | [math]\displaystyle{ 3178141 }[/math] | [math]\displaystyle{ 47378869 }[/math] | [math]\displaystyle{ 105168887 }[/math] | [math]\displaystyle{ 140273363 }[/math] | [math]\displaystyle{ 315104063 }[/math] |
| [math]\displaystyle{ \mathbf{ 16170} }[/math] | [math]\displaystyle{ 3360767 }[/math] | [math]\displaystyle{ 7292851 }[/math] | [math]\displaystyle{ 8511059 }[/math] | [math]\displaystyle{ 10038841 }[/math] | [math]\displaystyle{ 26643899 }[/math] | [math]\displaystyle{ 35098631 }[/math] |
| [math]\displaystyle{ \mathbf{ 16380} }[/math] | [math]\displaystyle{ 339263 }[/math] | [math]\displaystyle{ 2893309 }[/math] | [math]\displaystyle{ 7118387 }[/math] | [math]\displaystyle{ 189387287 }[/math] | [math]\displaystyle{ 209606629 }[/math] | [math]\displaystyle{ 266620267 }[/math] |
| [math]\displaystyle{ \mathbf{ 16590} }[/math] | [math]\displaystyle{ 381816437 }[/math] | [math]\displaystyle{ 695288453 }[/math] | [math]\displaystyle{ 1555003309 }[/math] | [math]\displaystyle{ 2096563163 }[/math] | [math]\displaystyle{ 2844269837 }[/math] | [math]\displaystyle{ 4876784057 }[/math] |
| [math]\displaystyle{ \mathbf{ 16800} }[/math] | [math]\displaystyle{ 143614397 }[/math] | [math]\displaystyle{ 681135667 }[/math] | [math]\displaystyle{ 1337835403 }[/math] | [math]\displaystyle{ 1547432483 }[/math] | [math]\displaystyle{ 1809315247 }[/math] | [math]\displaystyle{ 2850704453 }[/math] |
| [math]\displaystyle{ \mathbf{ 17010} }[/math] | [math]\displaystyle{ 83709047 }[/math] | [math]\displaystyle{ 1041057263 }[/math] | [math]\displaystyle{ 1265416651 }[/math] | [math]\displaystyle{ 1665987569 }[/math] | [math]\displaystyle{ 2529254831 }[/math] | [math]\displaystyle{ 4576482871 }[/math] |
| [math]\displaystyle{ \mathbf{ 17220} }[/math] | [math]\displaystyle{ 1452511 }[/math] | [math]\displaystyle{ 10612519 }[/math] | [math]\displaystyle{ 16814099 }[/math] | [math]\displaystyle{ 216348577 }[/math] | [math]\displaystyle{ 382728461 }[/math] | [math]\displaystyle{ 532388587 }[/math] |
| [math]\displaystyle{ \mathbf{ 17430} }[/math] | [math]\displaystyle{ 25471 }[/math] | [math]\displaystyle{ 137293657 }[/math] | [math]\displaystyle{ 632342783 }[/math] | [math]\displaystyle{ 960368107 }[/math] | [math]\displaystyle{ 5503090291 }[/math] | [math]\displaystyle{ 6704824913 }[/math] |
| [math]\displaystyle{ \mathbf{ 17640} }[/math] | [math]\displaystyle{ 193607 }[/math] | [math]\displaystyle{ 33411011 }[/math] | [math]\displaystyle{ 511632469 }[/math] | [math]\displaystyle{ 819466853 }[/math] | [math]\displaystyle{ 960062011 }[/math] | [math]\displaystyle{ 1178974859 }[/math] |
| [math]\displaystyle{ \mathbf{ 17850} }[/math] | [math]\displaystyle{ 1728911 }[/math] | [math]\displaystyle{ 4584401 }[/math] | [math]\displaystyle{ 7627309 }[/math] | [math]\displaystyle{ 77294621 }[/math] | [math]\displaystyle{ 99462899 }[/math] | [math]\displaystyle{ 170832131 }[/math] |
| [math]\displaystyle{ \mathbf{ 18060} }[/math] | [math]\displaystyle{ 51826531 }[/math] | [math]\displaystyle{ 210101329 }[/math] | [math]\displaystyle{ 235062067 }[/math] | [math]\displaystyle{ 605501191 }[/math] | [math]\displaystyle{ 1083324911 }[/math] | [math]\displaystyle{ 2230437163 }[/math] |
| [math]\displaystyle{ \mathbf{ 18270} }[/math] | [math]\displaystyle{ 1989811 }[/math] | [math]\displaystyle{ 825611753 }[/math] | [math]\displaystyle{ 2281896011 }[/math] | [math]\displaystyle{ 2468212757 }[/math] | [math]\displaystyle{ 2968471043 }[/math] | [math]\displaystyle{ 4958366753 }[/math] |
| [math]\displaystyle{ \mathbf{ 18480} }[/math] | [math]\displaystyle{ 194839 }[/math] | [math]\displaystyle{ 1044739 }[/math] | [math]\displaystyle{ 1075237 }[/math] | [math]\displaystyle{ 2169967 }[/math] | [math]\displaystyle{ 2467369 }[/math] | [math]\displaystyle{ 3135841 }[/math] |
| [math]\displaystyle{ \mathbf{ 18690} }[/math] | [math]\displaystyle{ 90365419 }[/math] | [math]\displaystyle{ 551760331 }[/math] | [math]\displaystyle{ 1165944209 }[/math] | [math]\displaystyle{ 1887703247 }[/math] | [math]\displaystyle{ 1932471091 }[/math] | [math]\displaystyle{ 3396823123 }[/math] |
| [math]\displaystyle{ \mathbf{ 18900} }[/math] | [math]\displaystyle{ 804113 }[/math] | [math]\displaystyle{ 1087721813 }[/math] | [math]\displaystyle{ 2462595313 }[/math] | [math]\displaystyle{ 3420103007 }[/math] | [math]\displaystyle{ 5068097201 }[/math] | [math]\displaystyle{ 5268928117 }[/math] |
| [math]\displaystyle{ \mathbf{ 19110} }[/math] | [math]\displaystyle{ 1023487 }[/math] | [math]\displaystyle{ 6202067 }[/math] | [math]\displaystyle{ 6640901 }[/math] | [math]\displaystyle{ 19304167 }[/math] | [math]\displaystyle{ 78325591 }[/math] | [math]\displaystyle{ 152030453 }[/math] |
| [math]\displaystyle{ \mathbf{ 19320} }[/math] | [math]\displaystyle{ 13154717 }[/math] | [math]\displaystyle{ 123351947 }[/math] | [math]\displaystyle{ 180065461 }[/math] | [math]\displaystyle{ 191400653 }[/math] | [math]\displaystyle{ 307980523 }[/math] | [math]\displaystyle{ 526607503 }[/math] |
| [math]\displaystyle{ \mathbf{ 19530} }[/math] | [math]\displaystyle{ 1773689 }[/math] | [math]\displaystyle{ 128832049 }[/math] | [math]\displaystyle{ 226504217 }[/math] | [math]\displaystyle{ 544697521 }[/math] | [math]\displaystyle{ 880832749 }[/math] | [math]\displaystyle{ 1511819633 }[/math] |
| [math]\displaystyle{ \mathbf{ 19740} }[/math] | [math]\displaystyle{ 216443629 }[/math] | [math]\displaystyle{ 1460073841 }[/math] | [math]\displaystyle{ 2172351869 }[/math] | [math]\displaystyle{ 3696955411 }[/math] | [math]\displaystyle{ 4020404251 }[/math] | [math]\displaystyle{ 4234603313 }[/math] |
| [math]\displaystyle{ \mathbf{ 19950} }[/math] | [math]\displaystyle{ 142699 }[/math] | [math]\displaystyle{ 302287 }[/math] | [math]\displaystyle{ 661547 }[/math] | [math]\displaystyle{ 64740661 }[/math] | [math]\displaystyle{ 176566177 }[/math] | [math]\displaystyle{ 562542581 }[/math] |
| [math]\displaystyle{ \mathbf{ 20160} }[/math] | [math]\displaystyle{ 77727823 }[/math] | [math]\displaystyle{ 585546277 }[/math] | [math]\displaystyle{ 1013154997 }[/math] | [math]\displaystyle{ 1309662637 }[/math] | [math]\displaystyle{ 2007871577 }[/math] | [math]\displaystyle{ 2231189419 }[/math] |
| [math]\displaystyle{ \mathbf{ 20370} }[/math] | [math]\displaystyle{ 1216213 }[/math] | [math]\displaystyle{ 7991839 }[/math] | [math]\displaystyle{ 156234857 }[/math] | [math]\displaystyle{ 1222246309 }[/math] | [math]\displaystyle{ 2382533789 }[/math] | [math]\displaystyle{ 2523592993 }[/math] |
| [math]\displaystyle{ \mathbf{ 20580} }[/math] | [math]\displaystyle{ 2219557 }[/math] | [math]\displaystyle{ 508048529 }[/math] | [math]\displaystyle{ 906000787 }[/math] | [math]\displaystyle{ 1111806827 }[/math] | [math]\displaystyle{ 2134225213 }[/math] | [math]\displaystyle{ 6894499589 }[/math] |
| [math]\displaystyle{ \mathbf{ 20790} }[/math] | [math]\displaystyle{ 2397931 }[/math] | [math]\displaystyle{ 4022297 }[/math] | [math]\displaystyle{ 4043087 }[/math] | [math]\displaystyle{ 15314617 }[/math] | [math]\displaystyle{ 26974879 }[/math] | [math]\displaystyle{ 35575247 }[/math] |
| [math]\displaystyle{ \mathbf{ 21000} }[/math] | [math]\displaystyle{ 49402277 }[/math] | [math]\displaystyle{ 263368843 }[/math] | [math]\displaystyle{ 701455591 }[/math] | [math]\displaystyle{ 2403274567 }[/math] | [math]\displaystyle{ 3097244987 }[/math] | [math]\displaystyle{ 5984865767 }[/math] |
□
Twierdzenie C59
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] oraz [math]\displaystyle{ a, d, k, k_0 \in \mathbb{Z} }[/math]. Jeżeli liczby [math]\displaystyle{ d }[/math] i [math]\displaystyle{ n }[/math] są względnie pierwsze, to reszty [math]\displaystyle{ r_1, r_2, \ldots, r_n }[/math] z dzielenia [math]\displaystyle{ n }[/math] liczb [math]\displaystyle{ x_k }[/math] postaci
- [math]\displaystyle{ x_k = a + k d \qquad }[/math] dla [math]\displaystyle{ \; k = k_0 + 1, \ldots, k_0 + n }[/math]
przez liczbę [math]\displaystyle{ n }[/math] są wszystkie różne i tworzą zbiór [math]\displaystyle{ S = \{ 0, 1, \ldots, n - 1 \} }[/math]. W szczególności wynika stąd, że wśród liczb [math]\displaystyle{ x_k }[/math] jedna jest podzielna przez [math]\displaystyle{ n }[/math].
Przypuśćmy, że dla pewnych różnych liczb naturalnych [math]\displaystyle{ i, j }[/math] takich, że [math]\displaystyle{ 1 \leqslant i < j \leqslant n }[/math] liczby [math]\displaystyle{ a + (k_0 + i) d }[/math] oraz [math]\displaystyle{ a + (k_0 + j) d }[/math] dają tę samą resztę przy dzieleniu przez [math]\displaystyle{ n }[/math]. Zatem różnica tych liczb jest podzielna przez [math]\displaystyle{ n }[/math]
- [math]\displaystyle{ n \mid [a + (k_0 + j) d] - [a + (k_0 + i) d] }[/math]
Czyli
- [math]\displaystyle{ n \mid d (j - i) }[/math]
Ponieważ liczby [math]\displaystyle{ d }[/math] i [math]\displaystyle{ n }[/math] są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie C79), mamy
- [math]\displaystyle{ n \mid (j - i) }[/math]
Co jest niemożliwe, bo [math]\displaystyle{ 1 \leqslant j - i \leqslant n - 1 < n }[/math].
Zatem reszty [math]\displaystyle{ r_1, r_2, \ldots, r_n }[/math] są wszystkie różne, a ponieważ jest ich [math]\displaystyle{ n }[/math], czyli tyle ile jest różnych reszt z dzielenia przez liczbę [math]\displaystyle{ n }[/math], to zbiór tych reszt jest identyczny ze zbiorem reszt z dzielenia przez [math]\displaystyle{ n }[/math], czyli ze zbiorem [math]\displaystyle{ S = \{ 0, 1, 2, \ldots, n - 1 \} }[/math].
□
Twierdzenie C60
Niech [math]\displaystyle{ d \in \mathbb{Z}_+ }[/math] i niech będzie dany ciąg arytmetyczny liczb pierwszych o długości [math]\displaystyle{ n }[/math]
- [math]\displaystyle{ p_k = p_0 + k d \qquad }[/math] dla [math]\displaystyle{ \; k = 0, 1, \ldots, n - 1 }[/math]
Z żądania, aby dany ciąg arytmetyczny był ciągiem arytmetycznym liczb pierwszych, wynika, że muszą być spełnione następujące warunki
- [math]\displaystyle{ p_0 \nmid d }[/math]
- [math]\displaystyle{ n \leqslant p_0 }[/math]
- [math]\displaystyle{ P(n - 1) \mid d }[/math]
- jeżeli liczba pierwsza [math]\displaystyle{ q }[/math] nie dzieli [math]\displaystyle{ d }[/math], to [math]\displaystyle{ n \leqslant q }[/math]
gdzie [math]\displaystyle{ P(t) }[/math] jest iloczynem wszystkich liczb pierwszych nie większych od [math]\displaystyle{ t }[/math].
Punkt 1.
Gdyby [math]\displaystyle{ p_0 \mid d }[/math], to dla [math]\displaystyle{ k \geqslant 1 }[/math] mielibyśmy [math]\displaystyle{ p_k = p_0 \left( 1 + k \cdot {\small\frac{d}{p_0}} \right) }[/math] i wszystkie te liczby byłyby złożone.
Punkt 2.
Ponieważ [math]\displaystyle{ p_0 }[/math] dzieli [math]\displaystyle{ p_0 + p_0 d }[/math], więc musi być [math]\displaystyle{ n - 1 < p_0 }[/math], czyli [math]\displaystyle{ n \leqslant p_0 }[/math].
Punkt 3.
Niech [math]\displaystyle{ q }[/math] będzie liczbą pierwszą mniejszą od [math]\displaystyle{ n }[/math], a liczby [math]\displaystyle{ r_k }[/math] będą resztami uzyskanymi z dzielenia liczb [math]\displaystyle{ p_k = p_0 + k d }[/math] przez [math]\displaystyle{ q }[/math], dla [math]\displaystyle{ k = 0, 1, \ldots, q - 1 }[/math]. Ponieważ z założenia liczby [math]\displaystyle{ p_0, \ldots, p_{n - 1} }[/math] są liczbami pierwszymi większymi od [math]\displaystyle{ q }[/math] (zauważmy, że [math]\displaystyle{ p_0 \geqslant n }[/math]), to żadna z reszt [math]\displaystyle{ r_k }[/math] nie może być równa zeru. Czyli mamy [math]\displaystyle{ q }[/math] reszt mogących przyjmować jedynie [math]\displaystyle{ q - 1 }[/math] różnych wartości. Zatem istnieją różne liczby [math]\displaystyle{ i, j }[/math] takie, że [math]\displaystyle{ 0 \leqslant i < j \leqslant q - 1 }[/math], dla których [math]\displaystyle{ r_i = r_j }[/math]. Wynika stąd, że różnica liczb
- [math]\displaystyle{ p_j - p_i = (p_0 + j d) - (p_0 + i d) = d (j - i) }[/math]
musi być podzielna przez [math]\displaystyle{ q }[/math]. Ponieważ [math]\displaystyle{ q \nmid (j - i) }[/math], bo [math]\displaystyle{ 1 \leqslant j - i \leqslant q - 1 < q }[/math], zatem z lematu Euklidesa [math]\displaystyle{ q \mid d }[/math].
Z uwagi na fakt, że jest tak dla każdej liczby pierwszej [math]\displaystyle{ q < n }[/math], liczba [math]\displaystyle{ d }[/math] musi być podzielna przez
- [math]\displaystyle{ P(n - 1) = \prod_{q < n} q }[/math]
Punkt 4.
Ponieważ [math]\displaystyle{ P(n - 1)|d }[/math], to wszystkie liczby pierwsze mniejsze od [math]\displaystyle{ n }[/math] muszą być dzielnikami [math]\displaystyle{ d }[/math]. Wynika stąd, że jeśli liczba pierwsza [math]\displaystyle{ q }[/math] nie dzieli [math]\displaystyle{ d }[/math], to musi być [math]\displaystyle{ q \geqslant n }[/math]. Co należało pokazać.
□
Uwaga C61
Czasami, zamiast pisać „ciąg arytmetyczny liczb pierwszych”, będziemy posługiwali się skrótem PAP od angielskiej nazwy „prime arithmetic progression”. Konsekwentnie zapis PAP-[math]\displaystyle{ n }[/math] będzie oznaczał ciąg arytmetyczny liczb pierwszych o długości [math]\displaystyle{ n }[/math], a zapis PAP[math]\displaystyle{ (n, d, q) }[/math] ciąg arytmetyczny liczb pierwszych o długości [math]\displaystyle{ n }[/math], pierwszym wyrazie [math]\displaystyle{ q }[/math] i różnicy [math]\displaystyle{ d }[/math].
Uwaga C62
Jakkolwiek sądzimy, że istnieje nieskończenie wiele ciągów arytmetycznych liczb pierwszych rozpoczynających się od dowolnej liczby pierwszej [math]\displaystyle{ q }[/math] i o dowolnej długości [math]\displaystyle{ 3 \leqslant n \leqslant q }[/math], to obecnie jest to tylko nieudowodnione przypuszczenie.
Dlatego nawet dla najmniejszej liczby pierwszej [math]\displaystyle{ q }[/math] takiej, że [math]\displaystyle{ q \nmid d }[/math] nierówność [math]\displaystyle{ n \leqslant q }[/math], pokazana w twierdzeniu C60, pozostaje nadal tylko oszacowaniem. W szczególności nie możemy z góry przyjmować, że dla liczby [math]\displaystyle{ n = q }[/math] znajdziemy taką liczbę [math]\displaystyle{ d }[/math] będącą wielokrotnością liczby [math]\displaystyle{ P(q - 1) }[/math] i niepodzielną przez [math]\displaystyle{ q }[/math], że będzie istniał PAP[math]\displaystyle{ (q, d, q) }[/math].
Przykład C63
Rozważmy dwie różnice [math]\displaystyle{ d_1 = 6 = 2 \cdot 3 }[/math] oraz [math]\displaystyle{ d_2 = 42 = 2 \cdot 3 \cdot 7 }[/math]. Zauważmy, że liczba pierwsza [math]\displaystyle{ 5 }[/math] nie dzieli ani [math]\displaystyle{ d_1 }[/math], ani [math]\displaystyle{ d_2 }[/math]. Co więcej, liczba pierwsza [math]\displaystyle{ 5 }[/math] jest najmniejszą liczbą pierwszą, która nie dzieli rozpatrywanych różnic, zatem nierówność [math]\displaystyle{ n \leqslant 5 }[/math] zapewnia najmocniejsze oszacowanie długości ciągu [math]\displaystyle{ n }[/math]. Łatwo sprawdzamy w zamieszczonych tabelach, że dla [math]\displaystyle{ d = 6 }[/math] oraz dla [math]\displaystyle{ d = 42 }[/math] są ciągi o długości [math]\displaystyle{ 3, 4, 5 }[/math], ale nie ma ciągów o długości [math]\displaystyle{ 6, 7, \ldots }[/math]
W szczególności z twierdzenia C60 wynika, że szukając ciągów arytmetycznych liczb pierwszych o określonej długości [math]\displaystyle{ n }[/math], należy szukać ich tylko dla różnic [math]\displaystyle{ d }[/math] będących wielokrotnością liczby [math]\displaystyle{ P(n - 1) }[/math].
Zadanie C64
Wiemy, że liczby pierwsze [math]\displaystyle{ p > 3 }[/math] można przedstawić w jednej z postaci [math]\displaystyle{ 6 k - 1 }[/math] lub [math]\displaystyle{ 6 k + 1 }[/math]. Pokazać, że jeżeli [math]\displaystyle{ p_0 = 3 }[/math], to dwa następne wyrazu rosnącego ciągu arytmetycznego liczb pierwszych są różnych postaci.
Ponieważ [math]\displaystyle{ p_0 = 3 }[/math], a rozpatrywany PAP jest rosnący, to kolejne wyrazy ciągu są większe od liczby [math]\displaystyle{ 3 }[/math] i mogą być przedstawione w jednej z postaci [math]\displaystyle{ 6 k - 1 }[/math] lub [math]\displaystyle{ 6 k + 1 }[/math]. Z twierdzenia C60 wiemy, że musi być [math]\displaystyle{ n \leqslant p_0 = 3 }[/math], czyli długość rozpatrywanego ciągu arytmetycznego liczb pierwszych wynosi dokładnie [math]\displaystyle{ 3 }[/math] i istnieją tylko dwa następne wyrazy.
Rozważmy ciąg arytmetyczny liczb pierwszych składający się z trzech wyrazów [math]\displaystyle{ p, q, r }[/math] takich, że [math]\displaystyle{ p = 3 }[/math]. Mamy
- [math]\displaystyle{ r = q + d = q + (q - p) = 2 q - p }[/math]
Zatem
- [math]\displaystyle{ r + q = 3 q - 3 }[/math]
Widzimy, że prawa strona powyższej równości jest podzielna przez [math]\displaystyle{ 3 }[/math]. Zatem liczby po lewej stronie wypisanych wyżej równości muszą być różnych postaci, bo tylko w takim przypadku lewa strona równości będzie również podzielna przez [math]\displaystyle{ 3 }[/math].
□
Zadanie C65
Wiemy, że liczby pierwsze [math]\displaystyle{ p > 3 }[/math] można przedstawić w jednej z postaci [math]\displaystyle{ 6 k - 1 }[/math] lub [math]\displaystyle{ 6 k + 1 }[/math]. Pokazać, że wszystkie wyrazy rosnącego ciągu arytmetycznego liczb pierwszych [math]\displaystyle{ p_0, p_1, \ldots, p_{n - 1} }[/math], gdzie [math]\displaystyle{ p_0 \geqslant 5 }[/math] i [math]\displaystyle{ n \geqslant 3 }[/math] muszą być jednakowej postaci.
Niech liczby [math]\displaystyle{ p, q, r }[/math] będą trzema kolejnymi (dowolnie wybranymi) wyrazami rozpatrywanego ciągu. Łatwo zauważmy, że
- [math]\displaystyle{ r = q + d = q + (q - p) = 2 q - p }[/math]
Zatem
- [math]\displaystyle{ p + q = 3 q - r }[/math]
- [math]\displaystyle{ q + r = 3 q - p }[/math]
- [math]\displaystyle{ p + r = 2 q }[/math]
Zauważmy, że prawa strona wypisanych wyżej równości nie jest podzielna przez [math]\displaystyle{ 3 }[/math], bo liczby [math]\displaystyle{ p, q, r }[/math] są liczbami pierwszymi większymi od liczby [math]\displaystyle{ 3 }[/math]. Zatem liczby po lewej stronie wypisanych wyżej równości muszą być tej samej postaci, bo gdyby było inaczej, to lewa strona tych równości byłaby podzielna przez [math]\displaystyle{ 3 }[/math], a prawa nie. Czyli każda para liczb z trójki [math]\displaystyle{ p, q, r }[/math] musi być tej samej postaci i wynika stąd, że wszystkie trzy liczby muszą być tej samej postaci. Ponieważ trzy kolejne wyrazy ciągu [math]\displaystyle{ p_0, p_1, \ldots, p_{n - 1} }[/math] były wybrane dowolnie, to wszystkie wyrazy tego ciągu muszą być tej samej postaci.
□
Zadanie C66
Niech [math]\displaystyle{ d > 0 }[/math] będzie różnicą ciągu arytmetycznego liczb pierwszych o długości [math]\displaystyle{ n }[/math]
- [math]\displaystyle{ p_k = p_0 + k d \qquad }[/math] dla [math]\displaystyle{ \; k = 0, 1, \ldots, n - 1 }[/math]
Pokazać, nie korzystając z twierdzenia C60, że jeżeli liczba pierwsza [math]\displaystyle{ q }[/math] nie dzieli [math]\displaystyle{ d }[/math], to [math]\displaystyle{ n \leqslant q }[/math].
Przypuśćmy, że [math]\displaystyle{ n > q }[/math] tak, że [math]\displaystyle{ q < n \leqslant p_0 }[/math], zatem
- [math]\displaystyle{ q < p_k = p_0 + k d \qquad }[/math] dla [math]\displaystyle{ \; k = 0, 1, \ldots, n - 1 }[/math]
Ponieważ [math]\displaystyle{ q \nmid d }[/math], to na mocy twierdzenia C59 wśród [math]\displaystyle{ q }[/math] kolejnych wyrazów [math]\displaystyle{ p_0, p_1, \ldots, p_{q - 1} }[/math] (zauważmy, że [math]\displaystyle{ q - 1 < n - 1 }[/math]) jedna liczba pierwsza [math]\displaystyle{ p_k }[/math] musi być podzielna przez [math]\displaystyle{ q }[/math], zatem musi być równa [math]\displaystyle{ q }[/math]. Jednak jest to niemożliwe, bo [math]\displaystyle{ q < p_k }[/math] dla wszystkich [math]\displaystyle{ k = 0, 1, \ldots, n - 1 }[/math]. Zatem nie może być [math]\displaystyle{ n > q }[/math].
□
Twierdzenie C67
Niech [math]\displaystyle{ q }[/math] będzie liczbą pierwszą, a liczby pierwsze
- [math]\displaystyle{ p_k = p_0 + k d \qquad }[/math] gdzie [math]\displaystyle{ \; k = 0, 1, \ldots, q - 1 }[/math]
tworzą ciąg arytmetyczny o długości [math]\displaystyle{ q }[/math] i różnicy [math]\displaystyle{ d > 0 }[/math].
Równość [math]\displaystyle{ p_0 = q }[/math] zachodzi wtedy i tylko wtedy, gdy [math]\displaystyle{ q \nmid d }[/math].
[math]\displaystyle{ \Longrightarrow }[/math]
Jeżeli [math]\displaystyle{ p_0 = q }[/math], to [math]\displaystyle{ q }[/math]-wyrazowy ciąg arytmetyczny liczb pierwszych ma postać
- [math]\displaystyle{ p_k = q + k d \qquad }[/math] dla [math]\displaystyle{ \; k = 0, 1, \ldots, q - 1 }[/math]
Gdyby [math]\displaystyle{ q \mid d }[/math], to mielibyśmy
- [math]\displaystyle{ p_k = q \left( 1 + k \cdot {\small\frac{d}{q}} \right) }[/math]
i wszystkie liczby [math]\displaystyle{ p_k }[/math] dla [math]\displaystyle{ k \geqslant 1 }[/math] byłyby złożone, wbrew założeniu, że [math]\displaystyle{ p_k }[/math] tworzą [math]\displaystyle{ q }[/math]-wyrazowy ciąg arytmetyczny liczb pierwszych.
[math]\displaystyle{ \Longleftarrow }[/math]
Ponieważ [math]\displaystyle{ q }[/math] jest długością rozpatrywanego ciągu arytmetycznego liczb pierwszych, to z twierdzenia C60 wynika, że musi być [math]\displaystyle{ q \leqslant p_0 }[/math].
Z założenia liczba pierwsza [math]\displaystyle{ q }[/math] nie dzieli [math]\displaystyle{ d }[/math], zatem z twierdzenia C59 wiemy, że [math]\displaystyle{ q }[/math] musi dzielić jedną z liczb [math]\displaystyle{ p_0, p_1, \ldots, p_{q - 1} }[/math].
Jeżeli [math]\displaystyle{ q \mid p_k }[/math], to [math]\displaystyle{ p_k = q }[/math]. Ponieważ [math]\displaystyle{ q \leqslant p_0 }[/math], to możliwe jest jedynie [math]\displaystyle{ q \mid p_0 }[/math] i musi być [math]\displaystyle{ p_0 = q }[/math].
□
Uwaga C68
Niech ciąg arytmetyczny liczb pierwszych o długości [math]\displaystyle{ n }[/math] ma postać
- [math]\displaystyle{ p_k = p_0 + k d \qquad }[/math] dla [math]\displaystyle{ \; k = 0, 1, \ldots, n - 1 }[/math]
Z udowodnionych wyżej twierdzeń C60 i C67 wynika, że ciągi arytmetyczne liczb pierwszych o długości [math]\displaystyle{ n }[/math] można podzielić na dwie grupy
- jeżeli [math]\displaystyle{ n }[/math] jest liczbą pierwszą i [math]\displaystyle{ n \nmid d }[/math], to [math]\displaystyle{ P(n - 1) \mid d }[/math] oraz [math]\displaystyle{ p_0 = n }[/math] (dla ustalonego [math]\displaystyle{ d }[/math] może istnieć tylko jeden ciąg)
- jeżeli [math]\displaystyle{ n }[/math] jest liczbą złożoną lub [math]\displaystyle{ n \mid d }[/math], to [math]\displaystyle{ P(n) \mid d }[/math] oraz [math]\displaystyle{ p_0 > n }[/math]
Funkcja [math]\displaystyle{ P(t) }[/math] jest iloczynem wszystkich liczb pierwszych nie większych od [math]\displaystyle{ t }[/math].
Przykład C69
Niech różnica ciągu arytmetycznego liczb pierwszych wynosi [math]\displaystyle{ d = 10^t }[/math], gdzie [math]\displaystyle{ t \geqslant 1 }[/math]. Zauważmy, że dla dowolnego [math]\displaystyle{ t }[/math] liczba [math]\displaystyle{ 3 }[/math] jest najmniejszą liczbą pierwszą, która nie dzieli [math]\displaystyle{ d }[/math]. Z oszacowania [math]\displaystyle{ n \leqslant 3 }[/math] wynika, że musi być [math]\displaystyle{ n = 3 }[/math].
Jeżeli długość ciągu [math]\displaystyle{ n = 3 }[/math] i [math]\displaystyle{ n \nmid d }[/math], to musi być [math]\displaystyle{ p_0 = n = 3 }[/math] i może istnieć tylko jeden PAP dla każdego [math]\displaystyle{ d }[/math]. W przypadku [math]\displaystyle{ t \leqslant 10000 }[/math] jedynie dla [math]\displaystyle{ t = 1, 5, 6, 17 }[/math] wszystkie liczby ciągu arytmetycznego [math]\displaystyle{ (3, 3 + 10^t, 3 + 2 \cdot 10^t) }[/math] są pierwsze.
Zadanie C70
Znaleźć wszystkie PAP[math]\displaystyle{ (n, d, p) }[/math] dla [math]\displaystyle{ d = 2, 4, 8, 10, 14, 16 }[/math].
Zauważmy, że dla każdej z podanych różnic [math]\displaystyle{ d }[/math], liczba [math]\displaystyle{ 3 }[/math] jest najmniejszą liczbą pierwszą, która nie dzieli [math]\displaystyle{ d }[/math]. Z oszacowania [math]\displaystyle{ n \leqslant 3 }[/math] wynika, że musi być [math]\displaystyle{ n = 3 }[/math].
Ponieważ [math]\displaystyle{ n = 3 }[/math] jest liczbą pierwszą i dla wypisanych [math]\displaystyle{ d }[/math] liczba [math]\displaystyle{ n \nmid d }[/math], to w każdym przypadku może istnieć tylko jeden ciąg, którego pierwszym wyrazem jest liczba pierwsza [math]\displaystyle{ p_0 = n = 3 }[/math]. Dla [math]\displaystyle{ d = 2, 4, 8, 10, 14 }[/math] łatwo znajdujemy odpowiednie ciągi
- [math]\displaystyle{ (3, 5, 7) }[/math], [math]\displaystyle{ \qquad (3, 7, 11) }[/math], [math]\displaystyle{ \qquad (3, 11, 19) }[/math], [math]\displaystyle{ \qquad (3, 13, 23) }[/math], [math]\displaystyle{ \qquad (3, 17, 31) }[/math]
Dla [math]\displaystyle{ d = 16 }[/math] szukany ciąg nie istnieje, bo [math]\displaystyle{ 35 = 5 \cdot 7 }[/math].
□
Zadanie C71
Znaleźć wszystkie PAP[math]\displaystyle{ (n, d, p) }[/math] dla [math]\displaystyle{ n = 3, 5, 7, 11 }[/math] i [math]\displaystyle{ d = P (n - 1) }[/math].
Z założenia PAP ma długość [math]\displaystyle{ n }[/math], liczba [math]\displaystyle{ n }[/math] jest liczbą pierwszą i [math]\displaystyle{ n \nmid d }[/math]. Zatem może istnieć tylko jeden PAP taki, że [math]\displaystyle{ p_0 = n }[/math]. Dla [math]\displaystyle{ n = 3, 5 }[/math] i odpowiednio [math]\displaystyle{ d = 2, 6 }[/math] otrzymujemy ciągi arytmetyczne liczb pierwszych
- [math]\displaystyle{ (3, 5, 7) }[/math], [math]\displaystyle{ \qquad (5, 11, 17, 23, 29) }[/math]
Ale dla [math]\displaystyle{ n = 7, 11 }[/math] i odpowiednio [math]\displaystyle{ d = 30, 210 }[/math] szukane ciągi nie istnieją, bo
- [math]\displaystyle{ (7, 37, 67, 97, 127, 157, {\color{Red} 187 = 11 \cdot 17}) }[/math]
- [math]\displaystyle{ (11, {\color{Red} 221 = 13 \cdot 17}, 431, 641, {\color{Red} 851 = 23 \cdot 37}, 1061, {\color{Red} 1271 = 31 \cdot 41}, 1481, {\color{Red} 1691 = 19 \cdot 89}, 1901, 2111) }[/math]
- [math]\displaystyle{ (11, {\color{Red} 221 = 13 \cdot 17}, 431, 641, {\color{Red} 851 = 23 \cdot 37}, 1061, {\color{Red} 1271 = 31 \cdot 41}, 1481, {\color{Red} 1691 = 19 \cdot 89}, 1901, 2111) }[/math]
□
Przykład C72
Przedstawiamy przykładowe ciągi arytmetyczne liczb pierwszych takie, że [math]\displaystyle{ n = p_0 }[/math] dla [math]\displaystyle{ n = 3, 5, 7, 11, 13 }[/math]. Zauważmy, że wypisane w tabeli wartości [math]\displaystyle{ d }[/math] są wielokrotnościami liczby [math]\displaystyle{ P(n - 1) }[/math].
| [math]\displaystyle{ \mathbf{n = p_0} }[/math] | [math]\displaystyle{ \mathbf{d} }[/math] | |||||||||
| [math]\displaystyle{ \mathbf{3} }[/math] | [math]\displaystyle{ 2 }[/math] | [math]\displaystyle{ 4 }[/math] | [math]\displaystyle{ 8 }[/math] | [math]\displaystyle{ 10 }[/math] | [math]\displaystyle{ 14 }[/math] | [math]\displaystyle{ 20 }[/math] | [math]\displaystyle{ 28 }[/math] | [math]\displaystyle{ 34 }[/math] | [math]\displaystyle{ 38 }[/math] | [math]\displaystyle{ 40 }[/math] |
| [math]\displaystyle{ \mathbf{5} }[/math] | [math]\displaystyle{ 6 }[/math] | [math]\displaystyle{ 12 }[/math] | [math]\displaystyle{ 42 }[/math] | [math]\displaystyle{ 48 }[/math] | [math]\displaystyle{ 96 }[/math] | [math]\displaystyle{ 126 }[/math] | [math]\displaystyle{ 252 }[/math] | [math]\displaystyle{ 426 }[/math] | [math]\displaystyle{ 474 }[/math] | [math]\displaystyle{ 594 }[/math] |
| [math]\displaystyle{ \mathbf{7} }[/math] | [math]\displaystyle{ 150 }[/math] | [math]\displaystyle{ 2760 }[/math] | [math]\displaystyle{ 3450 }[/math] | [math]\displaystyle{ 9150 }[/math] | [math]\displaystyle{ 14190 }[/math] | [math]\displaystyle{ 20040 }[/math] | [math]\displaystyle{ 21240 }[/math] | [math]\displaystyle{ 63600 }[/math] | [math]\displaystyle{ 76710 }[/math] | [math]\displaystyle{ 117420 }[/math] |
| [math]\displaystyle{ \mathbf{11} }[/math] | [math]\displaystyle{ 1536160080 }[/math] | [math]\displaystyle{ 4911773580 }[/math] | [math]\displaystyle{ 25104552900 }[/math] | [math]\displaystyle{ 77375139660 }[/math] | [math]\displaystyle{ 83516678490 }[/math] | [math]\displaystyle{ 100070721660 }[/math] | [math]\displaystyle{ 150365447400 }[/math] | [math]\displaystyle{ 300035001630 }[/math] | [math]\displaystyle{ 318652145070 }[/math] | [math]\displaystyle{ 369822103350 }[/math] |
| [math]\displaystyle{ \mathbf{13} }[/math] | [math]\displaystyle{ 9918821194590 }[/math] | [math]\displaystyle{ 104340979077720 }[/math] | [math]\displaystyle{ 187635245859600 }[/math] | [math]\displaystyle{ 232320390245790 }[/math] | [math]\displaystyle{ 391467874710990 }[/math] | [math]\displaystyle{ 859201916576850 }[/math] | [math]\displaystyle{ 1024574038282410 }[/math] | [math]\displaystyle{ 1074380369464710 }[/math] | [math]\displaystyle{ 1077624363457950 }[/math] | [math]\displaystyle{ 1185763337651970 }[/math] |
Przykłady takich ciągów dla jeszcze większych liczb pierwszych Czytelnik znajdzie na stronie A088430.
□
Przykład C73
Liczby [math]\displaystyle{ 3, 5, 7 }[/math] są najprostszym przykładem ciągu arytmetycznego kolejnych liczb pierwszych. Zauważmy, że tylko w przypadku [math]\displaystyle{ n = 3 }[/math] możliwa jest sytuacja, że [math]\displaystyle{ n = p_0 = 3 }[/math]. Istotnie, łatwo stwierdzamy, że
- ponieważ [math]\displaystyle{ p_0 }[/math] i [math]\displaystyle{ p_1 }[/math] są kolejnymi liczbami pierwszymi, to [math]\displaystyle{ p_1 - p_0 < p_0 }[/math] (zobacz zadanie B22)
- dla dowolnej liczby pierwszej [math]\displaystyle{ q \geqslant 5 }[/math] jest [math]\displaystyle{ q < P (q - 1) }[/math] (zobacz zadanie B26)
Przypuśćmy teraz, że istnieje ciąg arytmetyczny kolejnych liczb pierwszych taki, że [math]\displaystyle{ n = p_0 \geqslant 5 }[/math]. Mamy
- [math]\displaystyle{ d = p_1 - p_0 < p_0 < P (p_0 - 1) = P (n - 1) }[/math]
Zatem [math]\displaystyle{ P(n - 1) \nmid d }[/math], co jest niemożliwe.
Wynika stąd, że poza przypadkiem [math]\displaystyle{ n = p_0 = 3 }[/math] ciąg arytmetyczny kolejnych liczb pierwszych musi spełniać warunek [math]\displaystyle{ P(n) \mid d }[/math], czyli [math]\displaystyle{ P(n) \mid (p_1 - p_0) }[/math].
Poniższe tabele przedstawiają przykładowe ciągi arytmetyczne kolejnych liczb pierwszych o długościach [math]\displaystyle{ n = 3, 4, 5, 6 }[/math] dla rosnących wartości [math]\displaystyle{ p_0 }[/math]. Nie istnieje ciąg arytmetyczny kolejnych liczb pierwszych o długości [math]\displaystyle{ n = 7 }[/math] dla [math]\displaystyle{ p_0 < 10^{13} }[/math]. Prawdopodobnie CPAP-7 pojawią się dopiero dla [math]\displaystyle{ p_0 \sim 10^{20} }[/math].
Znane są ciągi arytmetyczne kolejnych liczb pierwszych o długościach [math]\displaystyle{ n \leqslant 10 }[/math][16].
| [math]\displaystyle{ \mathbf{n = 3} }[/math] | |
| [math]\displaystyle{ \mathbf{p_0 \leqslant 10^{3}} }[/math] | [math]\displaystyle{ \mathbf{d} }[/math] |
| [math]\displaystyle{ \mathbf{3} }[/math] | [math]\displaystyle{ 2 }[/math] |
| [math]\displaystyle{ \mathbf{47} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{151} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{167} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{199} }[/math] | [math]\displaystyle{ 12 }[/math] |
| [math]\displaystyle{ \mathbf{251} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{257} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{367} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{557} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{587} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{601} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{647} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{727} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{941} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{971} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{n = 4} }[/math] | |
| [math]\displaystyle{ \mathbf{p_0 \leqslant 10^{4}} }[/math] | [math]\displaystyle{ \mathbf{d} }[/math] |
| [math]\displaystyle{ \mathbf{251} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{1741} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{3301} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{5101} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{5381} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{6311} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{6361} }[/math] | [math]\displaystyle{ 6 }[/math] |
| [math]\displaystyle{ \mathbf{n = 5} }[/math] | |
| [math]\displaystyle{ \mathbf{p_0 \leqslant 10^{8}} }[/math] | [math]\displaystyle{ \mathbf{d} }[/math] |
| [math]\displaystyle{ \mathbf{9843019} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{37772429} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{53868649} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{71427757} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{78364549} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{79080577} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{98150021} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{99591433} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{n = 6} }[/math] | |
| [math]\displaystyle{ \mathbf{p_0 \leqslant 10^{10}} }[/math] | [math]\displaystyle{ \mathbf{d} }[/math] |
| [math]\displaystyle{ \mathbf{121174811} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{1128318991} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{2201579179} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{2715239543} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{2840465567} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{3510848161} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{3688067693} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{3893783651} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{5089850089} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{5825680093} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{6649068043} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{6778294049} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{7064865859} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{7912975891} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{8099786711} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{9010802341} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{9327115723} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{9491161423} }[/math] | [math]\displaystyle{ 30 }[/math] |
| [math]\displaystyle{ \mathbf{9544001791} }[/math] | [math]\displaystyle{ 30 }[/math] |
□
Zadanie C74
Uzasadnij przypuszczenie, że ciągów arytmetycznych kolejnych liczb pierwszych o długości [math]\displaystyle{ n = 7 }[/math] możemy oczekiwać dopiero dla [math]\displaystyle{ p_0 \sim 10^{20} }[/math].
Zauważmy, że ilość liczb pierwszych nie większych od [math]\displaystyle{ x }[/math] w dobrym przybliżeniu jest określona funkcją [math]\displaystyle{ {\small\frac{x}{\log x}} }[/math]. Ponieważ funkcja [math]\displaystyle{ \log x }[/math] zmienia się bardzo wolno, to odcinki liczb naturalnych o tej samej długości położone w niewielkiej odległości od siebie będą zawierały podobne ilości liczb pierwszych. Przykładowo, dla dużych wartości [math]\displaystyle{ x }[/math], ilość liczb pierwszych w przedziale [math]\displaystyle{ (x, 2 x) }[/math] jest tego samego rzędu, co ilość liczb pierwszych w przedziale [math]\displaystyle{ (1, x) }[/math][17].
Zatem liczbę [math]\displaystyle{ {\small\frac{1}{\log x}} }[/math] możemy traktować jako prawdopodobieństwo trafienia na liczbę pierwszą wśród liczb znajdujących się w pobliżu liczby [math]\displaystyle{ x }[/math]. Zakładając, że liczby pierwsze są rozłożone przypadkowo, możemy wyliczyć prawdopodobieństwo tego, że [math]\displaystyle{ n }[/math] kolejnych liczb pierwszych, położonych w pobliżu liczby [math]\displaystyle{ x }[/math], utworzy ciąg arytmetyczny
- [math]\displaystyle{ \text{prob}_{\text{cpap}} (n, x) = \left( {\small\frac{1}{\log x}} \right)^n \left( 1 - {\small\frac{1}{\log x}} \right)^{(n - 1) (d - 1)} }[/math]
gdzie [math]\displaystyle{ d = P (n) }[/math]. Jest tak, ponieważ w ciągu kolejnych liczb całkowitych musimy trafić na liczbę pierwszą, następnie na [math]\displaystyle{ d - 1 }[/math] liczb złożonych, taka sytuacja musi się powtórzyć dokładnie [math]\displaystyle{ n - 1 }[/math] razy, a na koniec znowu musimy trafić na liczbę pierwszą. Czyli potrzebujemy [math]\displaystyle{ n }[/math] liczb pierwszych, na które trafiamy z prawdopodobieństwem [math]\displaystyle{ {\small\frac{1}{\log x}} }[/math] oraz [math]\displaystyle{ (n - 1) (d - 1) }[/math] liczb złożonych, na które trafiamy z prawdopodobieństwem [math]\displaystyle{ 1 - {\small\frac{1}{\log x}} }[/math], a liczby te muszą pojawiać się w ściśle określonej kolejności.
Ilość ciągów arytmetycznych utworzonych przez [math]\displaystyle{ n }[/math] kolejnych liczb pierwszych należących do przedziału [math]\displaystyle{ (x, 2 x) }[/math] możemy zatem oszacować na równą około
- [math]\displaystyle{ Q_{\text{cpap}}(n, x) = x \cdot \left( {\small\frac{1}{\log x}} \right)^n \left( 1 - {\small\frac{1}{\log x}} \right)^{(n - 1) (d - 1)} }[/math]
Porównując powyższe oszacowanie z rzeczywistą ilością [math]\displaystyle{ \# \text{CPAP}(n, x) }[/math] ciągów arytmetycznych kolejnych liczb pierwszych w przedziale [math]\displaystyle{ (x, 2x) }[/math] dostajemy
- [math]\displaystyle{ \frac{\# \text{CPAP}(n, x)}{Q_{\text{cpap}} (n, x)} = f (n, x) }[/math]
gdzie w możliwym do zbadania zakresie, czyli dla [math]\displaystyle{ x < 2^{42} \approx 4.4 \cdot 10^{12} }[/math] mamy
- [math]\displaystyle{ f(n, x) \approx a_n \cdot \log x + b_n }[/math]
Stałe [math]\displaystyle{ a_n }[/math] i [math]\displaystyle{ b_n }[/math] wyznaczamy metodą regresji liniowej. Musimy pamiętać, że uzyskanych w ten sposób wyników nie możemy ekstrapolować dla dowolnie dużych [math]\displaystyle{ x }[/math].
W przypadku [math]\displaystyle{ n = 5 }[/math] oraz [math]\displaystyle{ n = 6 }[/math] dysponowaliśmy zbyt małą liczbą danych, aby wyznaczyć stałe [math]\displaystyle{ a_n }[/math] i [math]\displaystyle{ b_n }[/math] z wystarczającą dokładnością. Dlatego w tych przypadkach ograniczyliśmy się do podania oszacowania funkcji [math]\displaystyle{ f(n, x) }[/math].
Uzyskany wyżej rezultaty są istotne, bo z wyliczonych postaci funkcji [math]\displaystyle{ f(n, x) }[/math] wynika, że są to funkcje bardzo wolno zmienne, a ich ekstrapolacja jest w pełni uprawniona.
W zamieszczonej niżej tabeli mamy kolejno
- [math]\displaystyle{ n }[/math], czyli długość CPAP
- wartość iloczynu [math]\displaystyle{ n \cdot P (n) }[/math]
- znalezioną postać funkcji [math]\displaystyle{ f(n, x) }[/math] lub oszacowanie wartości tej funkcji [math]\displaystyle{ C_n }[/math] na podstawie uzyskanych danych; w przypadku [math]\displaystyle{ n = 7 }[/math] jest to oszacowanie wynikające z obserwacji, że wartości funkcji [math]\displaystyle{ f(n, x) }[/math] są rzędu [math]\displaystyle{ n \cdot P (n) }[/math]
- wyliczoną wartość [math]\displaystyle{ \frac{\# \text{CPAP}(n, 2^{40})}{Q_{\text{cpap}}(n, 2^{40})} }[/math], czyli [math]\displaystyle{ f(n, 2^{40}) }[/math]
- wartość funkcji [math]\displaystyle{ f(n, 2^{70}) }[/math] wynikające z ekstrapolacji wzoru [math]\displaystyle{ f(n, x) = a_n \cdot \log x + b_n \qquad }[/math] (dla [math]\displaystyle{ n = 3, 4 }[/math])
- wartość [math]\displaystyle{ x }[/math] wynikającą z rozwiązania równania
- [math]\displaystyle{ \qquad (a_n \cdot \log x + b_n) \cdot Q_{\text{cpap}} (n, x) = 1 \qquad }[/math] (dla [math]\displaystyle{ n = 3, 4 }[/math])
- [math]\displaystyle{ \qquad C_n \cdot Q_{\text{cpap}} (n, x) = 1 \qquad }[/math] (dla [math]\displaystyle{ n = 5, 6, 7 }[/math])
- dla porównania w kolejnych kolumnach zostały podane dwie najmniejsze wartości [math]\displaystyle{ p_0 }[/math] dla CPAP-n
[math]\displaystyle{ n }[/math] [math]\displaystyle{ n \cdot P(n) }[/math] [math]\displaystyle{ f (n, x) \quad \text{lub} \quad C_n }[/math] [math]\displaystyle{ f (n, 2^{40}) }[/math] [math]\displaystyle{ f (n, 2^{70}) }[/math] [math]\displaystyle{ \sim p_0 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ \quad 3 \quad }[/math] [math]\displaystyle{ 18 }[/math] [math]\displaystyle{ 0.52 \cdot \log x + 6.3 }[/math] [math]\displaystyle{ 20.94 }[/math] [math]\displaystyle{ 30 }[/math] [math]\displaystyle{ 130 }[/math] [math]\displaystyle{ 47 }[/math] [math]\displaystyle{ 151 }[/math] [math]\displaystyle{ \quad 4 \quad }[/math] [math]\displaystyle{ 24 }[/math] [math]\displaystyle{ 0.53 \cdot \log x + 11.6 }[/math] [math]\displaystyle{ 26.61 }[/math] [math]\displaystyle{ 36 }[/math] [math]\displaystyle{ 1.5 \cdot 10^3 }[/math] [math]\displaystyle{ 251 }[/math] [math]\displaystyle{ 1741 }[/math] [math]\displaystyle{ \quad 5 \quad }[/math] [math]\displaystyle{ 150 }[/math] [math]\displaystyle{ 120 }[/math] [math]\displaystyle{ 121.45 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ 15 \cdot 10^6 }[/math] [math]\displaystyle{ 9843019 }[/math] [math]\displaystyle{ 37772429 }[/math] [math]\displaystyle{ \quad 6 \quad }[/math] [math]\displaystyle{ 180 }[/math] [math]\displaystyle{ 235 }[/math] [math]\displaystyle{ 228.27 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ 540 \cdot 10^6 }[/math] [math]\displaystyle{ 121174811 }[/math] [math]\displaystyle{ 1128318991 }[/math] [math]\displaystyle{ \quad 7 \quad }[/math] [math]\displaystyle{ 1470 }[/math] [math]\displaystyle{ 2500 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ 2 \cdot 10^{20} }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]
Zauważając, że funkcje [math]\displaystyle{ f(n, x) }[/math] są rzędu [math]\displaystyle{ n \cdot P (n) }[/math] i przyjmując, że podobnie będzie dla [math]\displaystyle{ f(7, x) }[/math], możemy wyliczyć wartość [math]\displaystyle{ x }[/math], dla której może pojawić się pierwszy CPAP-7. Wartość ta jest równa w przybliżeniu [math]\displaystyle{ 2 \cdot 10^{20} }[/math] i wynika z rozwiązania równania
- [math]\displaystyle{ f(7, x) \cdot Q_{\text{cpap}}(7, x) = 1 }[/math]
Możemy ją łatwo wyliczyć w PARI/GP. Oczywiście funkcję [math]\displaystyle{ f(7, x) }[/math] zastąpiliśmy jej oszacowaniem [math]\displaystyle{ C_7 = 2500 }[/math]
P(n) = prod(k = 2, n, if( isprime(k), k, 1 ))
Q(x) = 2500 * x * ( 1/log(x) )^7 * ( 1 - 1/log(x) )^( (7 - 1)*(P(7) - 1) )
solve(x = 10^10, 10^23, Q(x) - 1 )
□
Podciągi nieskończone i ich granice
Definicja C75
Niech [math]\displaystyle{ (a_k) }[/math] będzie ciągiem nieskończonym liczb rzeczywistych. Jeżeli [math]\displaystyle{ k_j }[/math] jest silnie rosnącym nieskończonym ciągiem liczb naturalnych, to powiemy, że ciąg [math]\displaystyle{ (a_{k_j}) }[/math] jest podciągiem nieskończonym ciągu [math]\displaystyle{ (a_k) }[/math].
Uwaga C76
Podciąg powstaje z ciągu wyjściowego przez wybieranie niektórych jego wyrazów, w tej samej kolejności, ale pomijając dowolnie wiele z nich. Dla przykładu: podciągiem ciągu liczb naturalnych [math]\displaystyle{ (a_k) = (1, 2, 3, 4, 5, 6, \ldots) }[/math] jest ciąg liczb parzystych dodatnich [math]\displaystyle{ (2, 4, 6, 8, 10, \ldots) }[/math] – zauważmy, że ciąg i podciąg są rozbieżne. Podciągiem ciągu [math]\displaystyle{ (a_k) = (1, - 1, 1, - 1, 1, - 1, \ldots) }[/math] jest ciąg [math]\displaystyle{ (1, 1, 1, 1, \ldots) }[/math] – zauważmy, że ciąg [math]\displaystyle{ (a_k) }[/math] jest rozbieżny, ale podciąg [math]\displaystyle{ (a_{k_j}) }[/math], gdzie [math]\displaystyle{ k_j = 2 j - 1 }[/math] jest zbieżny.
Twierdzenie C77
Jeżeli [math]\displaystyle{ (a_{k_j}) }[/math] jest nieskończonym podciągiem ciągu zbieżnego [math]\displaystyle{ (a_k) }[/math], to podciąg [math]\displaystyle{ (a_{k_j}) }[/math] też jest zbieżny i [math]\displaystyle{ \lim_{j \rightarrow \infty}
a_{k_j} = \lim_{k \rightarrow \infty} a_k }[/math].
Niech [math]\displaystyle{ (a_k) }[/math] będzie ciągiem zbieżnym do [math]\displaystyle{ g }[/math], czyli [math]\displaystyle{ \lim_{k \rightarrow \infty} a_k = g }[/math]. Oznacza to, że prawie wszystkie wyrazy ciągu [math]\displaystyle{ (a_k) }[/math] znajdują się w przedziale [math]\displaystyle{ (g - \varepsilon, g + \varepsilon) }[/math]. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od pewnego [math]\displaystyle{ K_0 }[/math].
Z założenia [math]\displaystyle{ (a_{k_j}) }[/math] jest nieskończonym podciągiem ciągu [math]\displaystyle{ (a_k) }[/math], zatem indeksy [math]\displaystyle{ k_j }[/math] są silnie rosnącym nieskończonym ciągiem liczb naturalnych i dla pewnego [math]\displaystyle{ j > J_0 }[/math] musi być [math]\displaystyle{ k_j > K_0 }[/math].
Wynika stąd, że prawie wszystkie wyrazy podciągu [math]\displaystyle{ (a_{k_j}) }[/math] znajdują się w przedziale [math]\displaystyle{ (g - \varepsilon, g + \varepsilon) }[/math]. Co oznacza, że liczba [math]\displaystyle{ g }[/math] jest granicą podciągu [math]\displaystyle{ (a_{k_j}) }[/math] i co należało pokazać.
□
Uzupełnienie
Twierdzenie C78 (lemat Bézouta)
Jeżeli liczby całkowite [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] nie są jednocześnie równe zeru, a największy wspólny dzielnik tych liczb jest równy [math]\displaystyle{ D }[/math], to istnieją takie liczby całkowite [math]\displaystyle{ x, y }[/math], że
- [math]\displaystyle{ a x + b y = D }[/math]
Niech [math]\displaystyle{ S }[/math] będzie zbiorem wszystkich liczb całkowitych dodatnich postaci [math]\displaystyle{ a n + b m }[/math], gdzie [math]\displaystyle{ n, m }[/math] są dowolnymi liczbami całkowitymi. Zbiór [math]\displaystyle{ S }[/math] nie jest zbiorem pustym, bo przykładowo liczba [math]\displaystyle{ a^2 + b^2 \in S }[/math]. Z zasady dobrego uporządkowania liczb naturalnych wynika, że zbiór [math]\displaystyle{ S }[/math] ma element najmniejszy, oznaczmy go literą [math]\displaystyle{ d }[/math].
Pokażemy, że [math]\displaystyle{ d \mid a }[/math] i [math]\displaystyle{ d \mid b }[/math]. Z twierdzenia o dzieleniu z resztą możemy napisać [math]\displaystyle{ a = k d + r }[/math], gdzie [math]\displaystyle{ 0 \leqslant r < d }[/math].
Przypuśćmy, że [math]\displaystyle{ d \nmid a }[/math], czyli że [math]\displaystyle{ r > 0 }[/math]. Ponieważ [math]\displaystyle{ d \in S }[/math], to mamy [math]\displaystyle{ d = a u + b v }[/math] dla pewnych liczb całkowitych [math]\displaystyle{ u }[/math] i [math]\displaystyle{ v }[/math]. Zatem
- [math]\displaystyle{ r = a - k d = }[/math]
- [math]\displaystyle{ \;\;\, = a - k (a u + b v) = }[/math]
- [math]\displaystyle{ \;\;\, = a \cdot (1 - k u) + b \cdot (- k v) }[/math]
Wynika stąd, że dodatnia liczba [math]\displaystyle{ r }[/math] należy do zbioru [math]\displaystyle{ S }[/math] oraz [math]\displaystyle{ r < d }[/math], wbrew określeniu liczby [math]\displaystyle{ d }[/math], czyli musi być [math]\displaystyle{ r = 0 }[/math] i [math]\displaystyle{ d \mid a }[/math]. Podobnie pokazujemy, że [math]\displaystyle{ d \mid b }[/math].
Jeżeli [math]\displaystyle{ d' }[/math] jest innym dzielnikiem liczb [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math], to [math]\displaystyle{ d' \mid d }[/math], bo [math]\displaystyle{ d' \mid (a u + b v) }[/math]. Zatem [math]\displaystyle{ d' \leqslant d }[/math], skąd wynika natychmiast, że liczba [math]\displaystyle{ d }[/math] jest największym z dzielników, które jednocześnie dzielą liczby [math]\displaystyle{ a }[/math] oraz [math]\displaystyle{ b }[/math].
Czyli [math]\displaystyle{ d = D }[/math].
□
Twierdzenie C79 (lemat Euklidesa)
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą oraz [math]\displaystyle{ a, b, d \in \mathbb{Z} }[/math].
- jeżeli [math]\displaystyle{ d \mid a b }[/math] i liczba [math]\displaystyle{ d }[/math] jest względnie pierwsza z [math]\displaystyle{ a }[/math], to [math]\displaystyle{ d \mid b }[/math]
- jeżeli [math]\displaystyle{ p \mid a b }[/math], to [math]\displaystyle{ p \mid a }[/math] lub [math]\displaystyle{ p \mid b }[/math]
Punkt 1.
Z założenia liczby [math]\displaystyle{ d }[/math] i [math]\displaystyle{ a }[/math] są względnie pierwsze, zatem na mocy lematu Bézouta (twierdzenie C78) istnieją takie liczby całkowite [math]\displaystyle{ x }[/math] i [math]\displaystyle{ y }[/math], że
- [math]\displaystyle{ d x + a y = 1 }[/math]
Mnożąc obie strony równania przez [math]\displaystyle{ b }[/math], dostajemy
- [math]\displaystyle{ d b x + a b y = b }[/math]
Obydwa wyrazy po lewej stronie są podzielne przez [math]\displaystyle{ d }[/math], bo z założenia [math]\displaystyle{ d \mid a b }[/math]. Zatem prawa strona również jest podzielna przez [math]\displaystyle{ d }[/math], czyli [math]\displaystyle{ d \mid b }[/math]. Co kończy dowód punktu pierwszego.
Punkt 2.
Jeżeli [math]\displaystyle{ p \nmid a }[/math], to [math]\displaystyle{ \gcd (p, a) = 1 }[/math], zatem z punktu pierwszego wynika, że [math]\displaystyle{ p \mid b }[/math].
Jeżeli [math]\displaystyle{ p \nmid b }[/math], to [math]\displaystyle{ \gcd (p, b) = 1 }[/math], zatem z punktu pierwszego wynika, że [math]\displaystyle{ p \mid a }[/math].
Czyli [math]\displaystyle{ p }[/math] musi dzielić przynajmniej jedną z liczb [math]\displaystyle{ a, b }[/math]. Co należało pokazać.
□
Twierdzenie C80
Niech [math]\displaystyle{ a, b, m \in \mathbb{Z} }[/math]. Jeżeli [math]\displaystyle{ a \mid m \; }[/math] i [math]\displaystyle{ \; b \mid m }[/math] oraz [math]\displaystyle{ \gcd (a, b) = 1 }[/math], to [math]\displaystyle{ a b \mid m }[/math].
Z założenia istnieją takie liczby [math]\displaystyle{ r, s, x, y \in \mathbb{Z} }[/math], że [math]\displaystyle{ m = a r }[/math] i [math]\displaystyle{ m = b s }[/math] oraz
- [math]\displaystyle{ a x + b y = 1 }[/math]
(zobacz C78). Zatem
- [math]\displaystyle{ m = m (a x + b y) }[/math]
- [math]\displaystyle{ \quad \, = m a x + m b y }[/math]
- [math]\displaystyle{ \quad \, = b s a x + a r b y }[/math]
- [math]\displaystyle{ \quad \, = a b (s x + r y) }[/math]
Czyli [math]\displaystyle{ a b \mid m }[/math]. Co należało pokazać.
□
Twierdzenie C81
Niech [math]\displaystyle{ a, b, c \in \mathbb{Z} }[/math]. Równanie [math]\displaystyle{ a x + b y = c }[/math] ma rozwiązanie wtedy i tylko wtedy, gdy największy wspólny dzielnik liczb [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] jest dzielnikiem liczby [math]\displaystyle{ c }[/math].
Niech [math]\displaystyle{ D }[/math] oznacza największy wspólny dzielnik liczb [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math].
[math]\displaystyle{ \Longrightarrow }[/math]
Jeżeli liczby całkowite [math]\displaystyle{ x_0 }[/math] i [math]\displaystyle{ y_0 }[/math] są rozwiązaniem rozpatrywanego równania, to
- [math]\displaystyle{ a x_0 + b y_0 = c }[/math]
Ponieważ [math]\displaystyle{ D }[/math] dzieli lewą stronę równania, to musi również dzielić prawą, zatem musi być [math]\displaystyle{ D \mid c }[/math].
[math]\displaystyle{ \Longleftarrow }[/math]
Jeżeli [math]\displaystyle{ D \mid c }[/math], to możemy napisać [math]\displaystyle{ c = k D }[/math] i równanie przyjmuje postać
- [math]\displaystyle{ a x + b y = k D }[/math]
Lemat Bézouta (twierdzenie C78) zapewnia istnienie liczb całkowitych [math]\displaystyle{ x_0 }[/math] i [math]\displaystyle{ y_0 }[/math] takich, że
- [math]\displaystyle{ a x_0 + b y_0 = D }[/math]
Czyli z lematu Bézouta wynika, że równanie [math]\displaystyle{ a x + b y = D }[/math] ma rozwiązanie w liczbach całkowitych. Przekształcając, dostajemy
- [math]\displaystyle{ a(k x_0) + b (k y_0) = k D }[/math]
Zatem liczby [math]\displaystyle{ k x_0 }[/math] i [math]\displaystyle{ k y_0 }[/math] są rozwiązaniem równania
- [math]\displaystyle{ a x + b y = k D }[/math]
Co oznacza, że równianie [math]\displaystyle{ a x + b y = c }[/math] ma rozwiązanie.
□
Uwaga C82
Z twierdzenia C81 wynika, że szukając rozwiązań równania [math]\displaystyle{ A x + B y = C }[/math] w liczbach całkowitych, powinniśmy
- obliczyć największy wspólny dzielnik [math]\displaystyle{ D }[/math] liczb [math]\displaystyle{ A }[/math] i [math]\displaystyle{ B }[/math]
- jeżeli [math]\displaystyle{ D > 1 }[/math], należy sprawdzić, czy [math]\displaystyle{ D \mid C }[/math]
- jeżeli [math]\displaystyle{ D \nmid C }[/math], to równanie [math]\displaystyle{ A x + B y = C }[/math] nie ma rozwiązań w liczbach całkowitych
- jeżeli [math]\displaystyle{ D \mid C }[/math], należy podzielić obie strony równania [math]\displaystyle{ A x + B y = C }[/math] przez [math]\displaystyle{ D }[/math] i przejść do rozwiązywania równania równoważnego [math]\displaystyle{ a x + b y = c }[/math], gdzie [math]\displaystyle{ a = {\small\frac{A}{D}} }[/math], [math]\displaystyle{ b = {\small\frac{B}{D}} }[/math], [math]\displaystyle{ c = {\small\frac{C}{D}} }[/math], zaś największy wspólny dzielnik liczb [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] jest równy [math]\displaystyle{ 1 }[/math].
Twierdzenie C83
Niech [math]\displaystyle{ a, b, c \in \mathbb{Z} }[/math]. Jeżeli liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze, to równanie
- [math]\displaystyle{ a x + b y = c }[/math]
ma nieskończenie wiele rozwiązań w liczbach całkowitych.
Jeżeli para liczb całkowitych [math]\displaystyle{ (x_0, y_0) }[/math] jest jednym z tych rozwiązań, to wszystkie pozostałe rozwiązania całkowite można otrzymać ze wzorów
- [math]\displaystyle{ x = x_0 + b t }[/math]
- [math]\displaystyle{ y = y_0 - a t }[/math]
gdzie [math]\displaystyle{ t }[/math] jest dowolną liczbą całkowitą.
Z założenia liczby [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] są względnie pierwsze, zatem największy wspólny dzielnik tych liczb jest równy [math]\displaystyle{ 1 }[/math] i dzieli liczbę [math]\displaystyle{ c }[/math]. Na mocy twierdzenia C81 równanie
- [math]\displaystyle{ a x + b y = c }[/math]
ma rozwiązanie w liczbach całkowitych.
Zauważmy, że jeżeli para liczb całkowitych [math]\displaystyle{ (x_0, y_0) }[/math] jest rozwiązaniem równania [math]\displaystyle{ a x + b y = c }[/math], to para liczb [math]\displaystyle{ (x_0 + b t, y_0 - a t) }[/math] również jest rozwiązaniem. Istotnie
- [math]\displaystyle{ a(x_0 + b t) + b (y_0 - a t) = a x_0 + a b t + b y_0 - b a t = }[/math]
- [math]\displaystyle{ \, = a x_0 + b y_0 = }[/math]
- [math]\displaystyle{ \, = c }[/math]
Pokażmy teraz, że nie istnieją inne rozwiązania niż określone wzorami
- [math]\displaystyle{ x = x_0 + b t }[/math]
- [math]\displaystyle{ y = y_0 - a t }[/math]
gdzie [math]\displaystyle{ t }[/math] jest dowolną liczbą całkowitą.
Przypuśćmy, że pary liczb całkowitych [math]\displaystyle{ (x, y) }[/math] oraz [math]\displaystyle{ (x_0, y_0) }[/math] są rozwiązaniami rozpatrywanego równania, zatem
- [math]\displaystyle{ a x + b y = c = a x_0 + b y_0 }[/math]
Wynika stąd, że musi być spełniony warunek
- [math]\displaystyle{ a (x - x_0) = b (y_0 - y) }[/math]
Ponieważ liczby [math]\displaystyle{ a \, }[/math] i [math]\displaystyle{ \, b }[/math] są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie C79) [math]\displaystyle{ b \mid (x - x_0) }[/math]. Skąd mamy
- [math]\displaystyle{ x - x_0 = b t }[/math]
gdzie [math]\displaystyle{ t }[/math] jest dowolną liczbą całkowitą. Po podstawieniu dostajemy natychmiast
- [math]\displaystyle{ y - y_0 = - a t }[/math]
Co kończy dowód.
□
Przykład C84
Rozwiązania równania
- [math]\displaystyle{ a x + b y = c }[/math]
gdzie [math]\displaystyle{ \gcd (a, b) = 1 }[/math], które omówiliśmy w poprzednim twierdzeniu, najłatwiej znaleźć korzystając w PARI/GP z funkcji gcdext(a, b). Funkcja ta zwraca wektor liczb [x0, y0, d], gdzie [math]\displaystyle{ d = \gcd (a, b) }[/math], a liczby [math]\displaystyle{ x_0 }[/math] i [math]\displaystyle{ y_0 }[/math] są rozwiązaniami równania
- [math]\displaystyle{ a x_0 + b y_0 = \gcd (a, b) }[/math]
Ponieważ założyliśmy, że [math]\displaystyle{ \gcd (a, b) = 1 }[/math], to łatwo zauważmy, że
- [math]\displaystyle{ a(c x_0) + b (c y_0) = c }[/math]
Zatem para liczb całkowitych [math]\displaystyle{ (c x_0, c y_0) }[/math] jest jednym z rozwiązań równania
- [math]\displaystyle{ a x + b y = c }[/math]
i wszystkie pozostałe rozwiązania uzyskujemy ze wzorów
- [math]\displaystyle{ x = c x_0 + b t }[/math]
- [math]\displaystyle{ y = c y_0 - a t }[/math]
Niech [math]\displaystyle{ a = 7 \; }[/math] i [math]\displaystyle{ \; b = 17 }[/math]. Funkcja gcdext(7,17) zwraca wektor [5, -2, 1], zatem rozwiązaniami równania [math]\displaystyle{ 7 x + 17 y = 1 }[/math] są liczby
- [math]\displaystyle{ x = 5 + 17 t }[/math]
- [math]\displaystyle{ y = - 2 - 7 t }[/math]
A rozwiązaniami równania [math]\displaystyle{ 7 x + 17 y = 10 }[/math] są liczby
- [math]\displaystyle{ x = 50 + 17 t }[/math]
- [math]\displaystyle{ y = - 20 - 7 t }[/math]
Przypisy
- ↑ Korzystamy w tym momencie z zasady dobrego uporządkowania zbioru liczb naturalnych, która stwierdza, że każdy niepusty podzbiór zbioru liczb naturalnych zawiera element najmniejszy. (Wiki-pl), (Wiki-en)
- ↑ Określenie, że „liczba [math]\displaystyle{ n }[/math] jest postaci [math]\displaystyle{ a k + b }[/math]”, jest jedynie bardziej czytelnym (obrazowym) zapisem stwierdzenia, że reszta z dzielenia liczby [math]\displaystyle{ n }[/math] przez [math]\displaystyle{ a }[/math] wynosi [math]\displaystyle{ b }[/math]. Zapis „liczba [math]\displaystyle{ n }[/math] jest postaci [math]\displaystyle{ a k - 1 }[/math]” oznacza, że reszta z dzielenia liczby [math]\displaystyle{ n }[/math] przez [math]\displaystyle{ a }[/math] wynosi [math]\displaystyle{ a - 1 }[/math].
- ↑ Wikipedia, Linnik's theorem, (Wiki-en)
- ↑ MathWorld, Linnik's Theorem. (MathWorld)
- ↑ Yuri Linnik, On the least prime in an arithmetic progression. I. The basic theorem, Mat. Sb. (N.S.) 15 (1944) 139–178.
- ↑ Yuri Linnik, On the least prime in an arithmetic progression. II. The Deuring-Heilbronn phenomenon, Mat. Sb. (N.S.) 15 (1944) 347–368.
- ↑ Triantafyllos Xylouris, Über die Nullstellen der Dirichletschen L-Funktionen und die kleinste Primzahl in einer arithmetischen Progression, Bonner Mathematische Schriften, vol. 404, Univ. Bonn, 2011, Diss.
- ↑ Enrico Bombieri, John B. Friedlander and Henryk Iwaniec, Primes in Arithmetic Progressions to Large Moduli. III, Journal of the American Mathematical Society 2 (1989) 215-224
- ↑ Paul Turán, Über die Primzahlen der arithmetischen Progression, Acta Sci. Szeged 8 (1937), 226-235
- ↑ Samuel S. Wagstaff, Jr., Greatest of the Least Primes in Arithmetic Progressions Having a Given Modulus, Mathematics of Computation Vol. 33, No. 147 (1979), 1073-1080
- ↑ Wikipedia, Primes in arithmetic progression, (Wiki-en)
- ↑ MathWorld, Prime Arithmetic Progression, (LINK)
- ↑ J. G. van der Corput, Über Summen von Primzahlen und Primzahlquadraten, Mathematische Annalen, 116 (1939) 1-50, (LINK)
- ↑ Wikipedia, Largest known primes in AP, (Wiki-en)
- ↑ Ben Green and Terence Tao, The Primes Contain Arbitrarily Long Arithmetic Progressions., Ann. of Math. (2) 167 (2008), 481-547, (LINK1), Preprint. 8 Apr 2004, (LINK2)
- ↑ Wikipedia, Primes in arithmetic progression - Largest known consecutive primes in AP, (Wiki-en)
- ↑ Henryk Dąbrowski, Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n - Uwagi do twierdzenia, (LINK)