Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n: Różnice pomiędzy wersjami
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 9: | Linia 9: | ||
W 1852 roku rosyjski matematyk Czebyszew<ref name="Czebyszew1"/><ref name="Czebyszew2"/> udowodnił, że dla funkcji <math>\pi (n)</math> prawdziwe jest następujące oszacowanie | W 1852 roku rosyjski matematyk Czebyszew<ref name="Czebyszew1"/><ref name="Czebyszew2"/> udowodnił, że dla funkcji <math>\pi (n)</math> prawdziwe jest następujące oszacowanie | ||
| − | ::<math>a \cdot \frac{n}{\log n} \: \underset{n \geqslant 11}{<} \: \pi (n) \: \underset{n \geqslant 96098}{<} \: b \cdot \frac{n}{\log n}</math> | + | ::<math>a \cdot {\small\frac{n}{\log n}} \: \underset{n \geqslant 11}{<} \: \pi (n) \: \underset{n \geqslant 96098}{<} \: b \cdot {\small\frac{n}{\log n}}</math> |
gdzie | gdzie | ||
| Linia 17: | Linia 17: | ||
Dysponując tak dokładnym oszacowaniem funkcji <math>\pi (n)</math>, Czebyszew mógł bez trudu udowodnić następujące twierdzenie<br/> | Dysponując tak dokładnym oszacowaniem funkcji <math>\pi (n)</math>, Czebyszew mógł bez trudu udowodnić następujące twierdzenie<br/> | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B1 (twierdzenie Czebyszewa)</span><br/> | + | <span id="B1" style="font-size: 110%; font-weight: bold;">Twierdzenie B1 (twierdzenie Czebyszewa)</span><br/> |
Dla <math>n \geqslant 2</math> między liczbami naturalnymi <math>n</math> i <math>2 n</math> znajduje się przynajmniej jedna liczba pierwsza. | Dla <math>n \geqslant 2</math> między liczbami naturalnymi <math>n</math> i <math>2 n</math> znajduje się przynajmniej jedna liczba pierwsza. | ||
| Linia 23: | Linia 23: | ||
W rzeczywistości Czebyszew mógł udowodnić znacznie silniejsze twierdzenie<br/> | W rzeczywistości Czebyszew mógł udowodnić znacznie silniejsze twierdzenie<br/> | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B2</span><br/> | + | <span id="B2" style="font-size: 110%; font-weight: bold;">Twierdzenie B2</span><br/> |
| − | Niech <math>n \in \mathbb{N}</math>. Dla <math>n \geqslant 3</math> w każdym z przedziałów <math>(n, 2 | + | Niech <math>n \in \mathbb{N}</math>. Dla <math>n \geqslant 3</math> w każdym z przedziałów <math>(n, 2 |
n)</math>, <math>(2 n, 3 n)</math>, <math>(3 n, 4 n)</math> oraz <math>(4 n, 5 n)</math> znajduje się przynajmniej jedna liczba pierwsza. | n)</math>, <math>(2 n, 3 n)</math>, <math>(3 n, 4 n)</math> oraz <math>(4 n, 5 n)</math> znajduje się przynajmniej jedna liczba pierwsza. | ||
| − | Przeprowadzimy obliczenia dla przedziału <math>(4 n, 5 n)</math>. Czytelnik w identyczny sposób może powtórzyć obliczenia dla pozostałych przypadków. Mamy | + | Przeprowadzimy obliczenia dla przedziału <math>(4 n, 5 n)</math>. Czytelnik w identyczny sposób może powtórzyć obliczenia dla pozostałych przypadków. Mamy |
| − | ::<math>\pi (5 n) - \pi (4 n) > a \cdot \frac{5 n}{\log (5 n)} - b \cdot \frac{4 n}{\log (4 n)} =</math> | + | ::<math>\pi (5 n) - \pi (4 n) > a \cdot {\small\frac{5 n}{\log (5 n)}} - b \cdot {\small\frac{4 n}{\log (4 n)}} =</math> |
| − | ::::::<math>\quad = \frac{5 a n}{\log (5 n)} - \frac{4 b n}{\log (4 n)} =</math> | + | ::::::<math>\quad = {\small\frac{5 a n}{\log (5 n)}} - {\small\frac{4 b n}{\log (4 n)}} =</math> |
| − | ::::::<math>\quad = \frac{5 a n}{\log (5 n)} \left( 1 - \frac{4 b}{5 a} \cdot \frac{\log (5 n)}{\log (4 n)} \right) =</math> | + | ::::::<math>\quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log (5 n)}{\log (4 n)}} \right) =</math> |
| − | ::::::<math>\quad = \frac{5 a n}{\log (5 n)} \left( 1 - \frac{4 b}{5 a} \cdot \frac{\log \left( 4 n \cdot \frac{5}{4} \right)}{\log (4 n)} \right) =</math> | + | ::::::<math>\quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log \left( 4 n \cdot {\small\frac{5}{4}} \right)}{\log (4 n)}} \right) =</math> |
| − | ::::::<math>\quad = \frac{5 a n}{\log (5 n)} \left( 1 - \frac{4 b}{5 a} \cdot \frac{\log (4 n) + \log (5 / 4)}{\log (4 n)} \right) =</math> | + | ::::::<math>\quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log (4 n) + \log (5 / 4)}{\log (4 n)}} \right) =</math> |
| − | ::::::<math>\quad = \frac{5 a n}{\log (5 n)} \left[ 1 - \frac{4 b}{5 a} \cdot \left( 1 + \frac{\log (5 / 4)}{\log (4 n)} \right) \right]</math> | + | ::::::<math>\quad = {\small\frac{5 a n}{\log (5 n)}} \left[ 1 - {\small\frac{4 b}{5 a}} \cdot \left( 1 + {\small\frac{\log (5 / 4)}{\log (4 n)}} \right) \right]</math> |
| − | Dla dużych wartości <math>n</math> wyrażenie w nawiasie zwykłym dąży do <math>1</math>, a wyrażenie w nawiasie kwadratowym do <math>0.03999826 \ldots</math> Można łatwo sprawdzić, że wypisane oszacowanie <math>\pi (5 n) - \pi (4 n)</math> jest większe od <math>1</math> dla <math>n \geqslant 193</math>. Zatem pozostaje sprawdzenie prawdziwości dowodzonego twierdzenia dla <math>4 n < 96098</math>. | + | Dla dużych wartości <math>n</math> wyrażenie w nawiasie zwykłym dąży do <math>1</math>, a wyrażenie w nawiasie kwadratowym do <math>0.03999826 \ldots</math> Można łatwo sprawdzić, że wypisane oszacowanie <math>\pi (5 n) - \pi (4 n)</math> jest większe od <math>1</math> dla <math>n \geqslant 193</math>. Zatem pozostaje sprawdzenie prawdziwości dowodzonego twierdzenia dla <math>4 n < 96098</math>. |
Dysponując odpowiednio dokładnym oszacowaniem typu | Dysponując odpowiednio dokładnym oszacowaniem typu | ||
| − | ::<math>a \cdot \frac{n}{\log n} < \pi (n) < b \cdot \frac{n}{\log n}</math> | + | ::<math>a \cdot {\small\frac{n}{\log n}} < \pi (n) < b \cdot {\small\frac{n}{\log n}}</math> |
możemy dla ustalonej liczby <math>r</math> próbować udowodnić następujące twierdzenie | możemy dla ustalonej liczby <math>r</math> próbować udowodnić następujące twierdzenie | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B3</span><br/> | + | <span id="B3" style="font-size: 110%; font-weight: bold;">Twierdzenie B3</span><br/> |
Niech <math>n, n_0, r \in \mathbb{Z}_+</math>. Istnieje taka liczba <math>n_0</math>, że dla <math>n \geqslant n_0</math> między liczbami <math>r n</math> oraz <math>(r + 1) n</math> znajduje się przynajmniej jedna liczba pierwsza. | Niech <math>n, n_0, r \in \mathbb{Z}_+</math>. Istnieje taka liczba <math>n_0</math>, że dla <math>n \geqslant n_0</math> między liczbami <math>r n</math> oraz <math>(r + 1) n</math> znajduje się przynajmniej jedna liczba pierwsza. | ||
| − | Dowodząc analogicznie, jak to uczyniliśmy wyżej (w przypadku twierdzenia B2), łatwo możemy pokazać, że aby taki dowód był możliwy musi być spełniony warunek | + | Dowodząc analogicznie, jak to uczyniliśmy wyżej (w przypadku twierdzenia [[#B2|B2]]), łatwo możemy pokazać, że aby taki dowód był możliwy musi być spełniony warunek |
| − | ::<math>\frac{b}{a} < \frac{r + 1}{r}</math> | + | ::<math>{\small\frac{b}{a}} < {\small\frac{r + 1}{r}}</math> |
| − | Niestety, elementarny dowód twierdzenia Czebyszewa o funkcji <math>\pi (n)</math> nie dostarczył nam odpowiednio silnego oszacowania, aby dowód twierdzenia Czebyszewa (czyli twierdzenia B3 w przypadku <math>r = 1</math>) był możliwy. Dlatego będziemy musieli to zrobić innym sposobem. Podstawą dowodu będzie dalsze badanie rozwinięcia symbolu Newtona <math>\binom{2 n}{n}</math> na czynniki pierwsze. | + | Niestety, elementarny dowód twierdzenia Czebyszewa o funkcji <math>\pi (n)</math> nie dostarczył nam odpowiednio silnego oszacowania, aby dowód twierdzenia Czebyszewa (czyli twierdzenia [[#B3|B3]] w przypadku <math>r = 1</math>) był możliwy. Dlatego będziemy musieli to zrobić innym sposobem. Podstawą dowodu będzie dalsze badanie rozwinięcia symbolu Newtona <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze. |
| − | Rozpoczniemy od oszacowania funkcji <math>\pi (n)</math>, z którego w przyszłości skorzystamy. | + | Rozpoczniemy od oszacowania funkcji <math>\pi (n)</math>, z którego w przyszłości skorzystamy. |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B4</span><br/> | + | <span id="B4" style="font-size: 110%; font-weight: bold;">Twierdzenie B4</span><br/> |
Dla funkcji <math>\pi (n)</math> prawdziwe są oszacowania: | Dla funkcji <math>\pi (n)</math> prawdziwe są oszacowania: | ||
| − | ::1. <math>\pi (n) \underset{n \geqslant 34}{<} \frac{n}{3}</math><br/> | + | ::1. <math>\pi (n) \underset{n \geqslant 34}{<} {\small\frac{n}{3}}</math><br/> |
| − | ::2. <math>\pi (n) \underset{n \geqslant 15}{<} \frac{n}{2} - 1</math> | + | ::2. <math>\pi (n) \underset{n \geqslant 15}{<} {\small\frac{n}{2}} - 1</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| Linia 77: | Linia 77: | ||
Indukcja matematyczna. Ponieważ wśród kolejnych sześciu liczb naturalnych, co najwyżej dwie mogą być liczbami pierwszymi, zatem <math>\pi (n) \leqslant \pi (n - 6) + 2</math> dla <math>n \geqslant 9 .</math> Musimy sprawdzić prawdziwość twierdzenia dla kolejnych sześciu liczb naturalnych. Istotnie dla <math>n = 34, 35, 36, 37, 38, 39</math> twierdzenie jest prawdziwe. Zakładając prawdziwość twierdzenia dla wszystkich liczb naturalnych należących do przedziału <math>[34, n]</math> otrzymujemy dla <math>n + 1</math> | Indukcja matematyczna. Ponieważ wśród kolejnych sześciu liczb naturalnych, co najwyżej dwie mogą być liczbami pierwszymi, zatem <math>\pi (n) \leqslant \pi (n - 6) + 2</math> dla <math>n \geqslant 9 .</math> Musimy sprawdzić prawdziwość twierdzenia dla kolejnych sześciu liczb naturalnych. Istotnie dla <math>n = 34, 35, 36, 37, 38, 39</math> twierdzenie jest prawdziwe. Zakładając prawdziwość twierdzenia dla wszystkich liczb naturalnych należących do przedziału <math>[34, n]</math> otrzymujemy dla <math>n + 1</math> | ||
| − | ::<math>\pi (n + 1) \leqslant \pi (n - 5) + 2 < \frac{n - 5}{3} + 2 = \frac{n + 1}{3}</math> | + | ::<math>\pi (n + 1) \leqslant \pi (n - 5) + 2 < {\small\frac{n - 5}{3}} + 2 = {\small\frac{n + 1}{3}}</math> |
Co należało pokazać. | Co należało pokazać. | ||
'''Punkt 2.'''<br/> | '''Punkt 2.'''<br/> | ||
| − | Ponieważ dla <math>n \geqslant 34</math> prawdziwa jest nierówność <math>\pi (n) < \frac{n}{3}</math>, a dla <math>n \geqslant 6</math> prawdziwa jest nierówność <math>\frac{n}{3} \leqslant \frac{n}{2} - 1</math>, zatem dla <math>n \geqslant 34</math> prawdziwa jest nierówność <math>\pi (n) < \frac{n}{2} - 1</math>. Wystarczy sprawdzić jej prawdziwość dla <math>15 \leqslant n \leqslant 33</math>.<br/> | + | Ponieważ dla <math>n \geqslant 34</math> prawdziwa jest nierówność <math>\pi (n) < {\small\frac{n}{3}}</math>, a dla <math>n \geqslant 6</math> prawdziwa jest nierówność <math>{\small\frac{n}{3}} \leqslant {\small\frac{n}{2}} - 1</math>, zatem dla <math>n \geqslant 34</math> prawdziwa jest nierówność <math>\pi (n) < {\small\frac{n}{2}} - 1</math>. Wystarczy sprawdzić jej prawdziwość dla <math>15 \leqslant n \leqslant 33</math>.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 88: | Linia 88: | ||
| − | Potrzebne nam też będzie nowe oszacowanie współczynnika dwumianowego <math>\binom{2n}{n}</math> od dołu. | + | Potrzebne nam też będzie nowe oszacowanie współczynnika dwumianowego <math>{\small\binom{2n}{n}}</math> od dołu. |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B5</span><br/> | + | <span id="B5" style="font-size: 110%; font-weight: bold;">Twierdzenie B5</span><br/> |
| − | Dla <math>n \geqslant 2</math> prawdziwa jest nierówność <math>\binom{2n}{n} > \frac{4^n}{2 n}</math> | + | Dla <math>n \geqslant 2</math> prawdziwa jest nierówność <math>{\small\binom{2n}{n}} > {\small\frac{4^n}{2 n}}</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Łatwo zauważamy, że | Łatwo zauważamy, że | ||
| − | ::<math>\binom{2n}{n} = \frac{(2 n) !}{(n!)^2} = \left( \overset{n}{\underset{k = 1}{\prod}} \frac{2 k}{k} \right) \cdot \left( \overset{n - 1}{\underset{k = | + | ::<math>{\small\binom{2n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = \left( \overset{n}{\underset{k = 1}{\prod}} {\small\frac{2 k}{k}} \right) \cdot \left( \overset{n - 1}{\underset{k = |
| − | 1}{\prod}} \frac{2 k + 1}{k} \right) \cdot \frac{1}{n} > \frac{2^{2 n - 1}}{n} = \frac{2^{2 n}}{2 n}</math> | + | 1}{\prod}} {\small\frac{2 k + 1}{k}} \right) \cdot {\small\frac{1}{n}} > {\small\frac{2^{2 n - 1}}{n}} = {\small\frac{2^{2 n}}{2 n}}</math> |
| − | Iloczyn w pierwszym nawiasie uwzględnia wszystkie liczby parzyste licznika od <math>2</math> do <math>2 n</math>, a każdy czynnik tego iloczynu jest równy <math>2</math>. Iloczyn w drugim nawiasie uwzględnia wszystkie liczby nieparzyste licznika od <math>3</math> do <math>2 n - 1</math>. Każdy czynnik tego iloczynu jest większy od <math>2</math>. Wynika stąd natychmiast wypisana nierówność.<br/> | + | Iloczyn w pierwszym nawiasie uwzględnia wszystkie liczby parzyste licznika od <math>2</math> do <math>2 n</math>, a każdy czynnik tego iloczynu jest równy <math>2</math>. Iloczyn w drugim nawiasie uwzględnia wszystkie liczby nieparzyste licznika od <math>3</math> do <math>2 n - 1</math>. Każdy czynnik tego iloczynu jest większy od <math>2</math>. Wynika stąd natychmiast wypisana nierówność.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 105: | Linia 105: | ||
| − | Poniższe twierdzenie zostało już udowodnione (zobacz twierdzenie A25<ref name="p1"/>), ale przedstawimy tutaj inny dowód. | + | Poniższe twierdzenie zostało już udowodnione (zobacz twierdzenie [[Twierdzenie Czebyszewa o funkcji π(n)#A25|A25]]<ref name="p1"/>), ale przedstawimy tutaj inny dowód. |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B6</span><br/> | + | <span id="B6" style="font-size: 110%; font-weight: bold;">Twierdzenie B6</span><br/> |
| − | Liczby pierwsze <math>p > \sqrt{2 n}</math> występują w rozwinięciu współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem <math>u = 0</math> lub <math>u = 1</math>. | + | Liczby pierwsze <math>p > \sqrt{2 n}</math> występują w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze z wykładnikiem <math>u = 0</math> lub <math>u = 1</math>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia A26 wiemy, że jeżeli liczba pierwsza <math>p</math> występuje w rozwinięciu współczynnika dwumianowego <math>\binom{2n}{n}</math> z wykładnikiem <math>u</math>, to <math>p^u \leqslant 2 n</math>. Gdyby liczba pierwsza <math>p > \sqrt{2 n}</math> występowała w rozwinięciu współczynnika dwumianowego <math>\binom{2n}{n}</math> na czynniki pierwsze z wykładnikiem <math>u \geqslant 2</math>, to mielibyśmy <math>p^u \geqslant p^2 > 2 n</math>. Co jest niemożliwe.<br/> | + | Z twierdzenia [[Twierdzenie Czebyszewa o funkcji π(n)#A26|A26]] wiemy, że jeżeli liczba pierwsza <math>p</math> występuje w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2n}{n}}</math> z wykładnikiem <math>u</math>, to <math>p^u \leqslant 2 n</math>. Gdyby liczba pierwsza <math>p > \sqrt{2 n}</math> występowała w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2n}{n}}</math> na czynniki pierwsze z wykładnikiem <math>u \geqslant 2</math>, to mielibyśmy <math>p^u \geqslant p^2 > 2 n</math>. Co jest niemożliwe.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 117: | Linia 117: | ||
| − | Następne twierdzenie jest prostym wnioskiem z twierdzenia A45 (przypadek dla <math>k = 1</math>), ale załączyliśmy dowód dla tego konkretnego przypadku. | + | Następne twierdzenie jest prostym wnioskiem z twierdzenia [[Twierdzenie Czebyszewa o funkcji π(n)#A45|A45]] (przypadek dla <math>k = 1</math>), ale załączyliśmy dowód dla tego konkretnego przypadku. |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B7</span><br/> | + | <span id="B7" style="font-size: 110%; font-weight: bold;">Twierdzenie B7</span><br/> |
| − | Jeżeli <math>n \geqslant 3</math> i liczba pierwsza <math>p \in \left ( \ | + | Jeżeli <math>n \geqslant 3</math> i liczba pierwsza <math>p \in \left ( \tfrac{2}{3} n, n \right ]</math>, to <math>p</math> nie występuje w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2n}{n}}</math> na czynniki pierwsze. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| Linia 126: | Linia 126: | ||
Zauważmy, że liczba pierwsza <math>p = 2</math> nie spełnia warunku <math>p \in \left ( \tfrac{2}{3} n, n \right ]</math> dla <math>n \geqslant 3</math>. | Zauważmy, że liczba pierwsza <math>p = 2</math> nie spełnia warunku <math>p \in \left ( \tfrac{2}{3} n, n \right ]</math> dla <math>n \geqslant 3</math>. | ||
| − | Zapiszmy liczbę <math>\binom{2n}{n}</math> w postaci ułamka: | + | Zapiszmy liczbę <math>{\small\binom{2n}{n}}</math> w postaci ułamka: |
| − | ::<math>\binom{2n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}</math> | + | ::<math>{\small\binom{2n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}}</math> |
| − | Rozważmy dowolną liczbę pierwszą <math>p</math> występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby <math>p</math> spełniała następujące warunki: | + | Rozważmy dowolną liczbę pierwszą <math>p</math> występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby <math>p</math> spełniała następujące warunki: |
| − | :* <math>p \leqslant n</math> — warunek ten zapewnia nam, że liczba <math>p</math> pojawi się co najmniej jeden raz w mianowniku | + | :* <math>p \leqslant n</math> — warunek ten zapewnia nam, że liczba <math>p</math> pojawi się co najmniej jeden raz w mianowniku |
| − | :* <math>2 p > n</math> — warunek ten zapewnia nam, że liczba <math>p</math> pojawi się dokładnie jeden raz w mianowniku | + | :* <math>2 p > n</math> — warunek ten zapewnia nam, że liczba <math>p</math> pojawi się dokładnie jeden raz w mianowniku |
| − | :* <math>2 p \leqslant 2 n</math> — warunek ten (łącznie z warunkiem <math>2 p > n</math>) zapewnia nam, że liczba <math>p</math> pojawi się co najmniej jeden raz w liczniku | + | :* <math>2 p \leqslant 2 n</math> — warunek ten (łącznie z warunkiem <math>2 p > n</math>) zapewnia nam, że liczba <math>p</math> pojawi się co najmniej jeden raz w liczniku |
| − | :* <math>3 p > 2 n</math> — warunek ten (łącznie z warunkiem <math>2 p \leqslant 2 n</math>) zapewnia nam, że liczba <math>p</math> pojawi się dokładnie raz w liczniku (jako <math>2 p</math>) | + | :* <math>3 p > 2 n</math> — warunek ten (łącznie z warunkiem <math>2 p \leqslant 2 n</math>) zapewnia nam, że liczba <math>p</math> pojawi się dokładnie raz w liczniku (jako <math>2 p</math>) |
| − | Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza <math>p \in \left ( \tfrac{2}{3} n, n \right ]</math> pojawia się dokładnie jeden raz w mianowniku i dokładnie jeden raz w liczniku ułamka | + | Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza <math>p \in \left ( \tfrac{2}{3} n, n \right ]</math> pojawia się dokładnie jeden raz w mianowniku i dokładnie jeden raz w liczniku ułamka |
| − | ::<math>\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}</math> | + | ::<math>{\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}}</math> |
| − | Zatem liczba pierwsza <math>p</math> nie występuje w rozwinięciu współczynnika dwumianowego <math>\binom{2n}{n}</math> na czynniki pierwsze. | + | Zatem liczba pierwsza <math>p</math> nie występuje w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2n}{n}}</math> na czynniki pierwsze. |
| − | <span style="border-bottom-style: double;">Dowód na podstawie twierdzenia A24</span><br/><br/> | + | <span style="border-bottom-style: double;">Dowód na podstawie twierdzenia [[Twierdzenie Czebyszewa o funkcji π(n)#A24|A24]]</span><br/><br/> |
Rozważmy najpierw pierwszy składnik sumy | Rozważmy najpierw pierwszy składnik sumy | ||
| − | ::<math>\sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right )</math> | + | ::<math>\sum^{\infty}_{k = 1} \left ( \left \lfloor {\small\frac{2 n}{p^{k}}} \right \rfloor - 2 \left \lfloor {\small\frac{n}{p^{k}}} \right \rfloor \right )</math> |
Ponieważ przypuszczamy, że składnik ten będzie równy <math>0</math>, to będziemy szukali oszacowania od góry. Z założenia mamy | Ponieważ przypuszczamy, że składnik ten będzie równy <math>0</math>, to będziemy szukali oszacowania od góry. Z założenia mamy | ||
| − | :1) <math>p > \frac{2 n}{3} \ | + | :1) <math>p > {\small\frac{2 n}{3}} \qquad \Longrightarrow \qquad {\small\frac{2 n}{p}} < 3 \qquad \Longrightarrow \qquad \left\lfloor {\small\frac{2 n}{p}} \right\rfloor \leqslant 2</math> |
| − | :2) <math>p \leqslant n \ | + | :2) <math>p \leqslant n \qquad \;\:\, \Longrightarrow \qquad {\small\frac{n}{p}} \geqslant 1 \qquad \;\: \Longrightarrow \qquad \left\lfloor {\small\frac{n}{p}} \right\rfloor \geqslant 1</math> |
Zatem | Zatem | ||
| − | ::<math>\left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \leqslant 2 - 2 = 0</math> | + | ::<math>\left\lfloor {\small\frac{2 n}{p}} \right\rfloor - 2 \left\lfloor {\small\frac{n}{p}} \right\rfloor \leqslant 2 - 2 = 0</math> |
Ponieważ każdy ze składników szukanej sumy może być równy tylko <math>0</math> lub <math>1</math>, to otrzymujemy | Ponieważ każdy ze składników szukanej sumy może być równy tylko <math>0</math> lub <math>1</math>, to otrzymujemy | ||
| − | ::<math>\left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 0</math> | + | ::<math>\left\lfloor {\small\frac{2 n}{p}} \right\rfloor - 2 \left\lfloor {\small\frac{n}{p}} \right\rfloor = 0</math> |
| − | Założenie, że <math>n \geqslant 5</math> pozwoli uprościć obliczenia dla drugiego i następnych składników sumy | + | Założenie, że <math>n \geqslant 5</math> pozwoli uprościć obliczenia dla drugiego i następnych składników sumy |
| − | ::<math>p > | + | ::<math>p > {\small\frac{2 n}{3}} \qquad \Longrightarrow \qquad {\small\frac{(2 n)^k}{p^k}} < 3^k</math> |
| − | + | :::::<math> \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} < {\small\frac{9}{2 n}} \cdot \left( {\small\frac{3}{2 n}} \right)^{k - 2}</math> | |
| − | ::<math>\ | + | :::::<math> \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \leqslant {\small\frac{9}{2 n}}</math> |
| − | Dla <math>n = 3</math> i <math>n = 4</math> łatwo sprawdzamy, że liczba <math>3</math> nie dzieli liczb <math>\binom{6}{3} = 20</math> oraz <math>\binom{8}{4} = 70</math>. Zatem dla <math>n \geqslant 3</math> liczba pierwsza <math>p \in \left( \tfrac{2}{3} n, n \right]</math> nie dzieli liczby <math>\binom{2 n}{n}</math>.<br/> | + | :::::<math> \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \leqslant {\small\frac{9}{10}}</math> |
| + | |||
| + | :::::<math> \;\;\;\,\, \Longrightarrow \qquad \left\lfloor {\small\frac{2 n}{p^k}} \right\rfloor = 0</math> | ||
| + | |||
| + | Jeżeli <math>\left\lfloor {\small\frac{2 n}{p^k}} \right\rfloor = 0</math>, to również musi być <math>\left\lfloor {\small\frac{n}{p^k}} \right\rfloor = 0</math>. Pokazaliśmy, że dla <math>n \geqslant 5</math> jest | ||
| + | |||
| + | ::<math>\sum^{\infty}_{k = 1} \left ( \left \lfloor {\small\frac{2 n}{p^{k}}} \right \rfloor - 2 \left \lfloor {\small\frac{n}{p^{k}}} \right \rfloor \right ) = 0</math> | ||
| + | |||
| + | Dla <math>n = 3 \;</math> i <math>\; n = 4</math> łatwo sprawdzamy, że liczba <math>3</math> nie dzieli liczb <math>{\small\binom{6}{3}} = 20</math> oraz <math>{\small\binom{8}{4}} = 70</math>. Zatem dla <math>n \geqslant 3</math> liczba pierwsza <math>p \in \left( \tfrac{2}{3} n, n \right]</math> nie dzieli liczby <math>{\small\binom{2 n}{n}}</math>.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 181: | Linia 189: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B8</span><br/> | + | <span id="B8" style="font-size: 110%; font-weight: bold;">Twierdzenie B8</span><br/> |
| − | Każda liczba pierwsza <math>p \in (n, 2 n]</math> występuje w rozwinięciu współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze z wykładnikiem <math>u = 1</math>. | + | Każda liczba pierwsza <math>p \in (n, 2 n]</math> występuje w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze z wykładnikiem <math>u = 1</math>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Każda liczba pierwsza <math>p \in (n, 2 n]</math> występuje dokładnie jeden raz w liczniku ułamka | + | Każda liczba pierwsza <math>p \in (n, 2 n]</math> występuje dokładnie jeden raz w liczniku ułamka |
| − | ::<math>\binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}</math> | + | ::<math>{\small\binom{2 n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}}</math> |
| − | i nie występuje w mianowniku. Zatem w rozwinięciu współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze wystąpi z wykładnikiem <math>u = 1</math>.<br/> | + | i nie występuje w mianowniku. Zatem w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze wystąpi z wykładnikiem <math>u = 1</math>.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 195: | Linia 203: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Przykład B9</span><br/> | + | <span id="B9" style="font-size: 110%; font-weight: bold;">Przykład B9</span><br/> |
| − | Nawiasami <math>(), [], \{ \}</math> zaznaczyliśmy liczby pierwsze należące odpowiednio do przedziałów <math>\left( \sqrt{2 n}, \tfrac{2}{3} n \right]</math>, <math>\left( \tfrac{2}{3} n, n \right]</math>, <math>(n, 2 n]</math>. Zauważmy, że istnieją liczby pierwsze <math>p \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right]</math>, które nie występują w rozwinięciu współczynnika dwumianowego <math>\binom{2n}{n}</math> na czynniki pierwsze. Zaznaczyliśmy je grubą czcionką. | + | Nawiasami <math>(), [], \{ \}</math> zaznaczyliśmy liczby pierwsze należące odpowiednio do przedziałów <math>\left( \sqrt{2 n}, \tfrac{2}{3} n \right]</math>, <math>\left( \tfrac{2}{3} n, n \right]</math>, <math>(n, 2 n]</math>. Zauważmy, że istnieją liczby pierwsze <math>p \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right]</math>, które nie występują w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2n}{n}}</math> na czynniki pierwsze. Zaznaczyliśmy je grubą czcionką. |
| − | ::<math>\binom{20}{10} = 2^2 \cdot (\mathbf{5^0}) \cdot [7^0] \cdot \{ 11^1 \cdot 13^1 \cdot 17^1 \cdot 19^1 \}</math> | + | ::<math>{\small\binom{20}{10}} = 2^2 \cdot (\mathbf{5^0}) \cdot [7^0] \cdot \{ 11^1 \cdot 13^1 \cdot 17^1 \cdot 19^1 \}</math> |
| − | ::<math>\binom{42}{21} = 2^3 \cdot 3^1 \cdot 5^1 \cdot (\mathbf{7^0} \cdot 11^1 \cdot 13^1) \cdot [17^0 \cdot 19^0] \cdot \{ 23^1 \cdot 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \}</math> | + | ::<math>{\small\binom{42}{21}} = 2^3 \cdot 3^1 \cdot 5^1 \cdot (\mathbf{7^0} \cdot 11^1 \cdot 13^1) \cdot [17^0 \cdot 19^0] \cdot \{ 23^1 \cdot 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \}</math> |
| − | ::<math>\binom{48}{24} = 2^2 \cdot 3^2 \cdot 5^2 \cdot (\mathbf{7^0} \cdot \mathbf{11^0} \cdot 13^1) \cdot [17^0 \cdot 19^0 \cdot 23^0] \cdot \{ 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \}</math> | + | ::<math>{\small\binom{48}{24}} = 2^2 \cdot 3^2 \cdot 5^2 \cdot (\mathbf{7^0} \cdot \mathbf{11^0} \cdot 13^1) \cdot [17^0 \cdot 19^0 \cdot 23^0] \cdot \{ 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \}</math> |
| − | ::<math>\binom{60}{30} = 2^4 \cdot 7^1 \cdot (11^1 \cdot \mathbf{13^0} \cdot 17^1 \cdot 19^1) \cdot [23^0 \cdot 29^0] \cdot \{ 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \cdot 53^1 \cdot 59^1 \}</math> | + | ::<math>{\small\binom{60}{30}} = 2^4 \cdot 7^1 \cdot (11^1 \cdot \mathbf{13^0} \cdot 17^1 \cdot 19^1) \cdot [23^0 \cdot 29^0] \cdot \{ 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \cdot 53^1 \cdot 59^1 \}</math> |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B10</span><br/> | + | <span id="B10" style="font-size: 110%; font-weight: bold;">Twierdzenie B10</span><br/> |
| − | Niech <math>n \geqslant 15</math>. Dla iloczynu liczb pierwszych <math>p_1 \cdot \ldots \cdot p_u</math> występujących w rozwinięciu współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze i spełniających warunek <math>p_i \in (n, 2 n]</math> prawdziwe jest następujące oszacowanie | + | Niech <math>n \geqslant 15</math>. Dla iloczynu liczb pierwszych <math>p_1 \cdot \ldots \cdot p_u</math> występujących w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze i spełniających warunek <math>p_i \in (n, 2 n]</math> prawdziwe jest następujące oszacowanie |
::<math>p_1 \cdot \ldots \cdot p_u > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> | ::<math>p_1 \cdot \ldots \cdot p_u > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Zapiszmy rozwinięcie współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze w postaci: | + | Zapiszmy rozwinięcie współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze w postaci: |
| − | ::<math>\binom{2 n}{n} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u)</math> | + | ::<math>{\small\binom{2 n}{n}} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u)</math> |
| − | gdzie liczby pierwsze <math>r_i</math>, <math>q_i</math>, <math>p_i</math> spełniają warunki: <math>r_i \in \left[ 2, \sqrt{2 n} \right]</math>, <math>q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right]</math> i <math>p_i \in (n, 2 n]</math>. Pominęliśmy liczby pierwsze należące do przedziału <math>\left( \tfrac{2}{3} n, n \right]</math>, bo z twierdzenia B7 wiemy, że nie występują one w rozwinięciu współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze. | + | gdzie liczby pierwsze <math>r_i</math>, <math>q_i</math>, <math>p_i</math> spełniają warunki: <math>r_i \in \left[ 2, \sqrt{2 n} \right]</math>, <math>\; q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right] \;</math> i <math>\; p_i \in (n, 2 n]</math>. Pominęliśmy liczby pierwsze należące do przedziału <math>\left( \tfrac{2}{3} n, n \right]</math>, bo z twierdzenia [[#B7|B7]] wiemy, że nie występują one w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze. |
Zauważmy: | Zauważmy: | ||
| − | 1) z twierdzenia A26 wiemy, że <math>r^{a_i}_i \leqslant 2 n</math>, zatem | + | 1) z twierdzenia [[Twierdzenie Czebyszewa o funkcji π(n)#A26|A26]] wiemy, że <math>r^{a_i}_i \leqslant 2 n</math>, zatem |
::<math>r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s \leqslant (2 n)^s \leqslant (2 n)^{\pi \left( \sqrt{2 n} \right)} < (2 n)^{\sqrt{2 n} / 2 - 1}</math> | ::<math>r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s \leqslant (2 n)^s \leqslant (2 n)^{\pi \left( \sqrt{2 n} \right)} < (2 n)^{\sqrt{2 n} / 2 - 1}</math> | ||
| − | gdzie skorzystaliśmy z oszacowania <math>\pi (n) < \frac{n}{2} - 1</math> prawdziwego dla <math>n \geqslant 15</math> (twierdzenie B4 punkt 2). | + | gdzie skorzystaliśmy z oszacowania <math>\pi (n) < {\small\frac{n}{2}} - 1</math> prawdziwego dla <math>n \geqslant 15</math> (twierdzenie [[#B4|B4]] punkt 2). |
| − | 2) z twierdzenia B6 wiemy, że czynniki <math>q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right]</math> występują z wykładnikiem równym <math>0</math> lub <math>1</math>, zatem: | + | 2) z twierdzenia [[#B6|B6]] wiemy, że czynniki <math>q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right]</math> występują z wykładnikiem równym <math>0</math> lub <math>1</math>, zatem: |
| − | ::<math>q_1 \cdot \ldots \cdot q_t \leqslant \frac{P \left( \frac{2}{3} n \right)}{P \left( \sqrt{2 n} \right)} < P \left( \ | + | ::<math>q_1 \cdot \ldots \cdot q_t \leqslant \frac{P \left( {\small\frac{2}{3}} n \right)}{P \left( \sqrt{2 n} \right)} < P \left( \tfrac{2}{3} n \right) < 4^{2 n / 3}</math> |
| − | gdzie ostatnia nierówność wynika z twierdzenia A9. | + | gdzie ostatnia nierówność wynika z twierdzenia [[Twierdzenie Czebyszewa o funkcji π(n)#A9|A9]]. |
| − | 3) z twierdzenia B5 wiemy, że dla <math>n \geqslant 2</math> prawdziwe jest oszacowanie <math>\binom{2 n}{n} > \frac{4^n}{2 n}</math> | + | 3) z twierdzenia [[#B5|B5]] wiemy, że dla <math>n \geqslant 2</math> prawdziwe jest oszacowanie <math>{\small\binom{2 n}{n}} > {\small\frac{4^n}{2 n}}</math> |
| − | Z punktów 1) - 3) wynika, że dla rozwinięcia współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze prawdziwe jest następujące oszacowanie | + | Z punktów 1) - 3) wynika, że dla rozwinięcia współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze prawdziwe jest następujące oszacowanie |
| − | ::<math>\frac{4^n}{2 n} < \binom{2 n}{n} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u) < (2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u)</math> | + | ::<math>{\small\frac{4^n}{2 n}} < {\small\binom{2 n}{n}} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u) < (2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u)</math> |
Skąd otrzymujemy natychmiast: | Skąd otrzymujemy natychmiast: | ||
| − | ::<math>(2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u) > \frac{4^n}{2 n}</math> | + | ::<math>(2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u) > {\small\frac{4^n}{2 n}}</math> |
| − | ::<math>p_1 \cdot \ldots \cdot p_u > \frac{4^n}{2 n} \cdot (2 n)^{- \sqrt{2 n} / 2 + 1} \cdot 4^{- 2 n / 3} = 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math><br/> | + | ::<math>p_1 \cdot \ldots \cdot p_u > {\small\frac{4^n}{2 n}} \cdot (2 n)^{- \sqrt{2 n} / 2 + 1} \cdot 4^{- 2 n / 3} = 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math><br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 252: | Linia 260: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B11</span><br/> | + | <span id="B11" style="font-size: 110%; font-weight: bold;">Twierdzenie B11</span><br/> |
Dla <math>n \geqslant 15</math> prawdziwe jest następujące oszacowanie | Dla <math>n \geqslant 15</math> prawdziwe jest następujące oszacowanie | ||
| − | ::<math>\frac{P (2 n)}{P (n)} > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> | + | ::<math>{\small\frac{P (2 n)}{P (n)}} > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | W twierdzeniu B10 pokazaliśmy, że dla iloczynu liczb pierwszych <math>p_1 \cdot \ldots \cdot p_u</math> występujących w rozwinięciu współczynnika dwumianowego <math>\binom{2 n}{n}</math> na czynniki pierwsze i spełniających warunek <math>p_i \in (n, 2 n]</math> prawdziwe jest następujące oszacowanie | + | W twierdzeniu [[#B10|B10]] pokazaliśmy, że dla iloczynu liczb pierwszych <math>p_1 \cdot \ldots \cdot p_u</math> występujących w rozwinięciu współczynnika dwumianowego <math>{\small\binom{2 n}{n}}</math> na czynniki pierwsze i spełniających warunek <math>p_i \in (n, 2 n]</math> prawdziwe jest następujące oszacowanie |
::<math>p_1 \cdot \ldots \cdot p_u > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> | ::<math>p_1 \cdot \ldots \cdot p_u > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> | ||
| − | Zauważmy, że liczby pierwsze <math>p_i</math> występują z wykładnikiem równym <math>1</math> (twierdzenie B8) i iloczyn <math>p_1 \cdot \ldots \cdot p_u</math> jest iloczynem '''wszystkich''' liczb <math>p_i \in (n, 2 n]</math>, bo każda liczba pierwsza <math>p_i \in (n, 2 n]</math> występuje w liczniku ułamka | + | Zauważmy, że liczby pierwsze <math>p_i</math> występują z wykładnikiem równym <math>1</math> (twierdzenie [[#B8|B8]]) i iloczyn <math>p_1 \cdot \ldots \cdot p_u</math> jest iloczynem '''wszystkich''' liczb <math>p_i \in (n, 2 n]</math>, bo każda liczba pierwsza <math>p_i \in (n, 2 n]</math> występuje w liczniku ułamka |
| − | ::<math>\binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}</math> | + | ::<math>{\small\binom{2 n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}}</math> |
| − | i nie występuje w mianowniku. Wynika stąd natychmiast, że: | + | i nie występuje w mianowniku. Wynika stąd natychmiast, że: |
| − | ::<math>\frac{P (2 n)}{P (n)} = p_1 \cdot \ldots \cdot p_u > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math><br/> | + | ::<math>{\small\frac{P (2 n)}{P (n)}} = p_1 \cdot \ldots \cdot p_u > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math><br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 274: | Linia 282: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B12</span><br/> | + | <span id="B12" style="font-size: 110%; font-weight: bold;">Twierdzenie B12</span><br/> |
Niech <math>n \in \mathbb{Z}_+</math>. Prawdziwe jest oszacowanie | Niech <math>n \in \mathbb{Z}_+</math>. Prawdziwe jest oszacowanie | ||
| − | ::<math>\frac{P (2 n)}{P (n)} > 2^{n / 2}</math> | + | ::<math>{\small\frac{P (2 n)}{P (n)}} > 2^{n / 2}</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia B11 wiemy, że dla dowolnego <math>n \geqslant 15</math> jest | + | Z twierdzenia [[#B11|B11]] wiemy, że dla dowolnego <math>n \geqslant 15</math> jest |
| − | ::<math>\frac{P (2 n)}{P (n)} > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> | + | ::<math>{\small\frac{P (2 n)}{P (n)}} > 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2}</math> |
| − | + | Chcemy pokazać, że | |
| − | ::<math> | + | ::<math>4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} > 2^{n / 2}</math> |
| − | + | Logarytmując tę nierówność, otrzymujemy | |
| − | ::<math>\frac{ | + | ::<math>{\small\frac{2 n}{3}} \cdot \log 2 - {\small\frac{\sqrt{2 n}}{2}} \cdot \log (2 n) > {\small\frac{n}{2}} \cdot \log 2</math> |
| − | ::<math> | + | ::<math>{\small\frac{\sqrt{2 n}}{2}} \cdot \log (2 n) < {\small\frac{n}{6}} \cdot \log 2</math> |
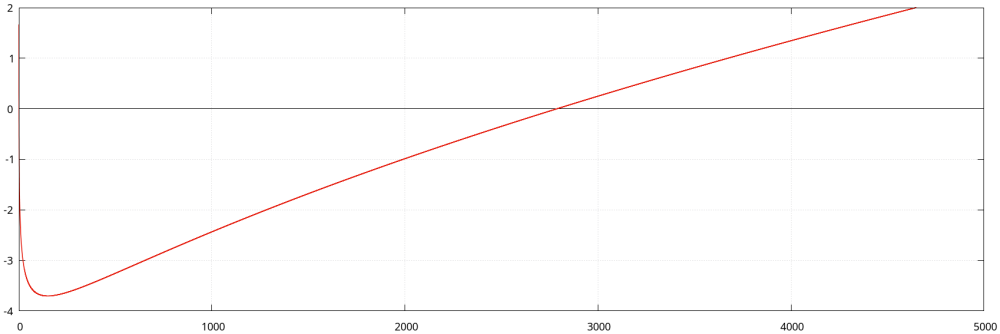
| − | + | ::<math>\log (2 n) < {\small\frac{\log 2}{6}} \cdot \sqrt{2 n}</math> | |
| − | + | Zamieszczony niżej obrazek prezentuje wykres funkcji <math>f(n) = {\small\frac{\log 2}{6}} \cdot \sqrt{2 n} - \log (2 n)</math> | |
| + | ::[[File: B_Czebyszew-wykres-1.png|1000px|none]] | ||
| − | |||
| − | + | Wpisując w PARI/GP polecenie | |
| − | + | <span style="font-size: 90%; color:black;">'''solve'''(n = 2000, 4000, '''log'''(2)/6 * '''sqrt'''(2*n) - '''log'''(2*n))</span> | |
| − | + | znajdujemy, że funkcja <math>f(n)</math> jest większa od zera dla <math>n > 2787.755</math> | |
| − | + | Pozostaje sprawdzić, przez bezpośrednie obliczenie, prawdziwość nierówności | |
| − | + | ::<math>{\small\frac{P (2 n)}{P (n)}} > 2^{n / 2}</math> | |
| − | W programie PARI/GP wystarczy napisać polecenia | + | dla wszystkich <math>n \leqslant 2787</math>. W programie PARI/GP wystarczy napisać polecenia |
<span style="font-size: 90%; color:black;">P(n) = '''prod'''(k = 2, n, '''if'''( '''isprime'''(k), k, 1 )) \\ definicja funkcji P(n)</span> | <span style="font-size: 90%; color:black;">P(n) = '''prod'''(k = 2, n, '''if'''( '''isprime'''(k), k, 1 )) \\ definicja funkcji P(n)</span> | ||
| Linia 321: | Linia 329: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Uwaga B13</span><br/> | + | <span id="B13" style="font-size: 110%; font-weight: bold;">Uwaga B13</span><br/> |
| − | Dowodząc analogicznie jak w twierdzeniu B12, moglibyśmy bez trudu pokazać, że dla <math>n \geqslant 6</math> prawdziwe jest silniejsze oszacowanie <math>\frac{P (2 n)}{P | + | Dowodząc analogicznie jak w twierdzeniu [[#B12|B12]], moglibyśmy bez trudu pokazać, że dla <math>n \geqslant 6</math> prawdziwe jest silniejsze oszacowanie <math>{\small\frac{P (2 n)}{P (n)}} > 2^{3 n / 5}</math>. |
| − | (n)} > 2^{3 n / 5}</math>. | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B14</span><br/> | + | <span id="B14" style="font-size: 110%; font-weight: bold;">Twierdzenie B14</span><br/> |
| − | Dla <math>n \geqslant 1</math> prawdziwe jest oszacowanie <math>\pi (2 n) - \pi (n) > \frac{\log 2}{2} \cdot \frac{n}{\log 2 n}</math> | + | Dla <math>n \geqslant 1</math> prawdziwe jest oszacowanie <math>\pi (2 n) - \pi (n) > {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}}</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Korzystając z twierdzenia B12, możemy napisać | + | Korzystając z twierdzenia [[#B12|B12]], możemy napisać |
| − | ::<math>2^{n / 2} < \frac{P (2 n)}{P (n)} < (2 n)^{\pi (2 n) - \pi (n)}</math> | + | ::<math>2^{n / 2} < {\small\frac{P (2 n)}{P (n)}} < (2 n)^{\pi (2 n) - \pi (n)}</math> |
| − | Oszacowanie z prawej jest oczywiste. Logarytmując obie strony, otrzymujemy | + | Oszacowanie z prawej jest oczywiste. Logarytmując obie strony, otrzymujemy |
| − | ::<math>\frac{n}{2} \cdot \log 2 < [\pi (2 n) - \pi (n)] \cdot \log 2 n</math> | + | ::<math>{\small\frac{n}{2}} \cdot \log 2 < [\pi (2 n) - \pi (n)] \cdot \log 2 n</math> |
a stąd łatwo wyliczamy różnicę <math>\pi (2 n) - \pi (n)</math>.<br/> | a stąd łatwo wyliczamy różnicę <math>\pi (2 n) - \pi (n)</math>.<br/> | ||
| Linia 347: | Linia 354: | ||
Korzystając ze znalezionego oszacowania, udowodnimy | Korzystając ze znalezionego oszacowania, udowodnimy | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B15</span><br/> | + | <span id="B15" style="font-size: 110%; font-weight: bold;">Twierdzenie B15</span><br/> |
Przedział otwarty <math>(n, 2 n)</math> zawiera co najmniej | Przedział otwarty <math>(n, 2 n)</math> zawiera co najmniej | ||
| Linia 363: | Linia 370: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia B14 wiemy, że | + | Z twierdzenia [[#B14|B14]] wiemy, że |
| − | ::<math>\pi (2 n) - \pi (n) > \frac{\log 2}{2} \cdot \frac{n}{\log 2 n}</math> | + | ::<math>\pi (2 n) - \pi (n) > {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}}</math> |
| − | Łatwo sprawdzamy dla jakich wartości <math>n</math> funkcja <math>\frac{\log 2}{2} \cdot \frac{n}{\log 2 n}</math> jest większa od <math>1</math>, <math>2</math>, itd. Wyniki zabraliśmy w tabelce: | + | Łatwo sprawdzamy dla jakich wartości <math>n</math> funkcja <math>{\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}}</math> jest większa od <math>1</math>, <math>2</math>, itd. Wyniki zabraliśmy w tabelce: |
::<math>\begin{array}{|c|c|c|c|c|c|c|} \hline | ::<math>\begin{array}{|c|c|c|c|c|c|c|} \hline | ||
| − | \frac{\log 2}{2} \cdot \frac{n}{\log 2 n} & > 1 & > 2 & > 3 & > 4 & > 5 & > 6\\ \hline | + | {\normalsize\frac{\log 2}{2}} \cdot {\normalsize\frac{n}{\log 2 n}} & > 1 & > 2 & > 3 & > 4 & > 5 & > 6\\ \hline |
\text{dla } n & \geqslant 9 & \geqslant 22 & \geqslant 38 & \geqslant 55 & \geqslant 72 & \geqslant 90\\ \hline | \text{dla } n & \geqslant 9 & \geqslant 22 & \geqslant 38 & \geqslant 55 & \geqslant 72 & \geqslant 90\\ \hline | ||
\end{array}</math> | \end{array}</math> | ||
| Linia 384: | Linia 391: | ||
== Uwagi do twierdzenia == | == Uwagi do twierdzenia == | ||
| − | Już pod koniec XVIII wieku Gauss i Legendre przypuszczali, że <math>\frac{n}{\log n}</math> jest dobrym przybliżeniem wartości funkcji <math>\pi (n)</math>. | + | Już pod koniec XVIII wieku Gauss i Legendre przypuszczali, że <math>{\small\frac{n}{\log n}}</math> jest dobrym przybliżeniem wartości funkcji <math>\pi (n)</math>. |
{| class="wikitable" | {| class="wikitable" | ||
| Linia 391: | Linia 398: | ||
Obecnie wiemy, że dokładnie tak jest<ref name="Dusart06"/> | Obecnie wiemy, że dokładnie tak jest<ref name="Dusart06"/> | ||
| − | ::<math>1 + \frac{1}{\log n} + \frac{1}{\log^2 n} \: \underset{n \geqslant 3527}{<} \: \pi (n) \cdot \frac{\log n}{n} \: \underset{n \geqslant 2}{<} \: 1 + \frac{1}{\log n} + \frac{2.54}{\log^2 n}</math> | + | ::<math>1 + {\small\frac{1}{\log n}} + {\small\frac{1}{\log^2 n}} \: \underset{n \geqslant 3527}{<} \: \pi (n) \cdot {\small\frac{\log n}{n}} \: \underset{n \geqslant 2}{<} \: 1 + {\small\frac{1}{\log n}} + {\small\frac{2.54}{\log^2 n}}</math> |
|} | |} | ||
| − | Jeśli tak, to ilość liczb pierwszych w przedziale <math>(n, 2 n]</math> jest tego samego rzędu, co ilość liczb pierwszych w przedziale <math>(1, n]</math>. Istotnie | + | Jeśli tak, to ilość liczb pierwszych w przedziale <math>(n, 2 n]</math> jest tego samego rzędu, co ilość liczb pierwszych w przedziale <math>(1, n]</math>. Istotnie |
| − | ::<math>\pi (n) \approx \frac{n}{\log n} | + | ::<math>\pi (n) \approx {\small\frac{n}{\log n}}</math> |
| − | :::<math>\;\;\; = \frac{n}{\log n} \cdot \frac{\log n + \log 2}{\log (2 n)} | + | :::<math>\;\;\; = {\small\frac{n}{\log n}} \cdot {\small\frac{\log n + \log 2}{\log (2 n)}}</math> |
| − | :::<math>\;\;\; = \frac{n}{\log (2 n)} \cdot \left( 1 + \frac{\log 2}{\log n} \right)</math> | + | :::<math>\;\;\; = {\small\frac{n}{\log (2 n)}} \cdot \left( 1 + {\small\frac{\log 2}{\log n}} \right)</math> |
| − | ::<math>\pi (2 n) - \pi (n) \approx \frac{2 n}{\log (2 n)} - \frac{n}{\log n} | + | ::<math>\pi (2 n) - \pi (n) \approx {\small\frac{2 n}{\log (2 n)}} - {\small\frac{n}{\log n}}</math> |
| − | ::::::<math>\;\: = \frac{2 n}{\log (2 n)} - \frac{n}{\log (2 n)} \cdot \left( 1 + \frac{\log 2}{\log n} \right) | + | ::::::<math>\;\: = {\small\frac{2 n}{\log (2 n)}} - {\small\frac{n}{\log (2 n)}} \cdot \left( 1 + {\small\frac{\log 2}{\log n}} \right)</math> |
| − | ::::::<math>\;\: = \frac{n}{\log (2 n)} \cdot \left( 1 - \frac{\log 2}{\log n} \right)</math> | + | ::::::<math>\;\: = {\small\frac{n}{\log (2 n)}} \cdot \left( 1 - {\small\frac{\log 2}{\log n}} \right)</math> |
Zatem przypuszczenie, że między liczbami <math>n</math> i <math>2 n</math> znajduje się przynajmniej jedna liczba pierwsza, jest bardzo słabym oczekiwaniem.<br/> | Zatem przypuszczenie, że między liczbami <math>n</math> i <math>2 n</math> znajduje się przynajmniej jedna liczba pierwsza, jest bardzo słabym oczekiwaniem.<br/> | ||
| − | Co więcej, począwszy od pewnego <math>n_0</math> między liczbami <math>n</math> i <math>2 n</math> znajduje przynajmniej jedna liczba będąca kwadratem, sześcianem, czwartą i piątą potęgą liczby naturalnej. Liczby <math>n^2</math>, <math>n^3</math>, <math>n^4</math> czy <math>n^5</math> występują znacznie rzadziej niż liczby pierwsze <math>p_n \approx n \log n</math>.<br/> | + | Co więcej, począwszy od pewnego <math>n_0</math> między liczbami <math>n</math> i <math>2 n</math> znajduje przynajmniej jedna liczba będąca kwadratem, sześcianem, czwartą i piątą potęgą liczby naturalnej. Liczby <math>n^2</math>, <math>n^3</math>, <math>n^4</math> czy <math>n^5</math> występują znacznie rzadziej niż liczby pierwsze <math>p_n \approx n \log n</math>.<br/> |
Pokażemy też, że twierdzenie Czebyszewa wynika ze sformułowanej w 1742 roku hipotezy Goldbacha. Oczywiście ścisły dowód twierdzenia Czebyszewa stał się możliwy dopiero po znalezieniu dokładnego oszacowania funkcji <math>\pi (n)</math>.<br/> | Pokażemy też, że twierdzenie Czebyszewa wynika ze sformułowanej w 1742 roku hipotezy Goldbacha. Oczywiście ścisły dowód twierdzenia Czebyszewa stał się możliwy dopiero po znalezieniu dokładnego oszacowania funkcji <math>\pi (n)</math>.<br/> | ||
| Linia 420: | Linia 427: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B16</span><br/> | + | <span id="B16" style="font-size: 110%; font-weight: bold;">Twierdzenie B16</span><br/> |
| − | Niech <math>n, k, k_0 \in \mathbb{Z}_+</math> i <math>f(k)</math> będzie funkcją rosnącą o wartościach całkowitych dodatnich. Jeżeli spełnione są warunki | + | Niech <math>n, k, k_0 \in \mathbb{Z}_+</math> i <math>f(k)</math> będzie funkcją rosnącą o wartościach całkowitych dodatnich. Jeżeli spełnione są warunki |
::1) <math>\quad f(k + 1) < 2 f (k) \quad</math> dla <math>\quad k \geqslant k_0</math> | ::1) <math>\quad f(k + 1) < 2 f (k) \quad</math> dla <math>\quad k \geqslant k_0</math> | ||
| − | ::2) <math>\quad n \geqslant \left\lfloor \frac{f (k_0)}{2} \right\rfloor + 1</math> | + | ::2) <math>\quad n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1</math> |
to między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba należąca do zbioru wartości funkcji <math>f(k)</math>. | to między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba należąca do zbioru wartości funkcji <math>f(k)</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Niech <math>n \geqslant f (k_0)</math>, a liczba <math>k \geqslant k_0</math> będzie największą liczbą taką, że <math>f(k) \leqslant n</math>. Z określenia liczby <math>k</math> i założenia twierdzenia prawdziwy jest ciąg nierówności | + | Niech <math>n \geqslant f (k_0)</math>, a liczba <math>k \geqslant k_0</math> będzie największą liczbą taką, że <math>f(k) \leqslant n</math>. Z określenia liczby <math>k</math> i założenia twierdzenia prawdziwy jest ciąg nierówności |
::<math>f(k) \leqslant n < f (k + 1) < 2 f (k) \leqslant 2 n</math> | ::<math>f(k) \leqslant n < f (k + 1) < 2 f (k) \leqslant 2 n</math> | ||
| Linia 436: | Linia 443: | ||
Zatem między liczbami <math>n</math> i <math>2 n</math> leży przynajmniej jedna liczba należąca do zbioru wartości funkcji <math>f(k)</math>. | Zatem między liczbami <math>n</math> i <math>2 n</math> leży przynajmniej jedna liczba należąca do zbioru wartości funkcji <math>f(k)</math>. | ||
| − | W szczególności liczba <math>f(k_0)</math> leży między liczbami <math>\; \left\lfloor \frac{f (k_0)}{2} \right\rfloor + j \;</math> oraz <math>\; 2 \left\lfloor \frac{f (k_0)}{2} | + | W szczególności liczba <math>f(k_0)</math> leży między liczbami <math>\; \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + j \;</math> oraz <math>\; 2 \left\lfloor {\small\frac{f (k_0)}{2}} |
| − | \right\rfloor + 2 j \;</math> dla <math>\; j = 1, 2, \ldots, f (k_0) - \left\lfloor \frac{f (k_0)}{2} \right\rfloor - 1</math>. | + | \right\rfloor + 2 j \;</math> dla <math>\; j = 1, 2, \ldots, f (k_0) - \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor - 1</math>. |
| − | Łatwo sprawdzamy, że dla kolejnej liczby <math>j = f (k_0) - \left\lfloor \frac{f (k_0)}{2} \right\rfloor</math> liczba <math>f(k_0)</math> nie leży między liczbami <math>f(k_0)</math> oraz <math>2 f (k_0)</math> — między tymi liczbami leży liczba <math>f(k_0 + 1)</math>. | + | Łatwo sprawdzamy, że dla kolejnej liczby <math>j = f (k_0) - \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor</math> liczba <math>f(k_0)</math> nie leży między liczbami <math>f(k_0)</math> oraz <math>2 f (k_0)</math> — między tymi liczbami leży liczba <math>f(k_0 + 1)</math>. |
| − | Wynika stąd, że twierdzenie jest prawdziwe dla liczb <math>n \geqslant \left\lfloor \frac{f (k_0)}{2} \right\rfloor + 1</math>.<br/> | + | Wynika stąd, że twierdzenie jest prawdziwe dla liczb <math>n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1</math>.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 447: | Linia 454: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Zadanie B17</span><br/> | + | <span id="B17" style="font-size: 110%; font-weight: bold;">Zadanie B17</span><br/> |
| − | Niech <math>x \in \mathbb{R}</math>. Dla <math>n \geqslant 1</math> oraz <math>x > \frac{1}{\sqrt[n]{2} - 1}</math> prawdziwa jest nierówność <math>2 x^n > (x + 1)^n</math>. | + | Niech <math>x \in \mathbb{R}</math>. Dla <math>n \geqslant 1</math> oraz <math>x > {\small\frac{1}{\sqrt[n]{2} - 1}}</math> prawdziwa jest nierówność <math>2 x^n > (x + 1)^n</math>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| Linia 457: | Linia 464: | ||
::<math>x \cdot \sqrt[n]{2} > x + 1</math> | ::<math>x \cdot \sqrt[n]{2} > x + 1</math> | ||
| − | Podnosząc obie strony nierówności do <math>n</math>-tej potęgi | + | Podnosząc obie strony nierówności do <math>n</math>-tej potęgi, otrzymujemy |
::<math>\left( x \cdot \sqrt[n]{2} \right)^n > (x + 1)^n</math> | ::<math>\left( x \cdot \sqrt[n]{2} \right)^n > (x + 1)^n</math> | ||
| Linia 471: | Linia 478: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B18</span><br/> | + | <span id="B18" style="font-size: 110%; font-weight: bold;">Twierdzenie B18</span><br/> |
Niech <math>n \in \mathbb{N}</math>. Jeżeli <math>n \geqslant 5</math>, to między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba będąca kwadratem liczby naturalnej. | Niech <math>n \in \mathbb{N}</math>. Jeżeli <math>n \geqslant 5</math>, to między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba będąca kwadratem liczby naturalnej. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Funkcja <math>f(k) = k^2</math> jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania B17 łatwo stwierdzamy, że warunek z twierdzenia B16 | + | Funkcja <math>f(k) = k^2</math> jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania [[#B17|B17]] łatwo stwierdzamy, że warunek z twierdzenia [[#B16|B16]] |
::<math>(k + 1)^2 < 2 k^2</math> | ::<math>(k + 1)^2 < 2 k^2</math> | ||
| Linia 481: | Linia 488: | ||
jest spełniony dla | jest spełniony dla | ||
| − | ::<math>k_0 = \left\lfloor \frac{1}{\sqrt{2} - 1} \right\rfloor + 1 = 3</math> | + | ::<math>k_0 = \left\lfloor {\small\frac{1}{\sqrt{2} - 1}} \right\rfloor + 1 = 3</math> |
Twierdzenie jest prawdziwe dla liczb | Twierdzenie jest prawdziwe dla liczb | ||
| − | ::<math>n \geqslant \left\lfloor \frac{f (k_0)}{2} \right\rfloor + 1 = \left\lfloor \frac{9}{2} \right\rfloor + 1 = 5</math> | + | ::<math>n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 = \left\lfloor {\small\frac{9}{2}} \right\rfloor + 1 = 5</math> |
Co kończy dowód.<br/> | Co kończy dowód.<br/> | ||
| Linia 493: | Linia 500: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B19</span><br/> | + | <span id="B19" style="font-size: 110%; font-weight: bold;">Twierdzenie B19</span><br/> |
Niech <math>n \in \mathbb{N}</math>. Jeżeli <math>n \geqslant 33</math>, to między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba będąca sześcianem liczby naturalnej. | Niech <math>n \in \mathbb{N}</math>. Jeżeli <math>n \geqslant 33</math>, to między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba będąca sześcianem liczby naturalnej. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Funkcja <math>f(k) = k^3</math> jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania B17 łatwo stwierdzamy, że warunek z twierdzenia B16 | + | Funkcja <math>f(k) = k^3</math> jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania [[#B17|B17]] łatwo stwierdzamy, że warunek z twierdzenia [[#B16|B16]] |
::<math>(k + 1)^3 < 2 k^3</math> | ::<math>(k + 1)^3 < 2 k^3</math> | ||
| Linia 503: | Linia 510: | ||
jest spełniony dla | jest spełniony dla | ||
| − | ::<math>k_0 = \left\lfloor \frac{1}{\sqrt[3]{2} - 1} \right\rfloor + 1 = 4</math> | + | ::<math>k_0 = \left\lfloor {\small\frac{1}{\sqrt[3]{2} - 1}} \right\rfloor + 1 = 4</math> |
Twierdzenie jest prawdziwe dla liczb | Twierdzenie jest prawdziwe dla liczb | ||
| − | ::<math>n \geqslant \left\lfloor \frac{f (k_0)}{2} \right\rfloor + 1 = \left\lfloor \frac{64}{2} \right\rfloor + 1 = 33</math> | + | ::<math>n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 = \left\lfloor {\small\frac{64}{2}} \right\rfloor + 1 = 33</math> |
Co kończy dowód.<br/> | Co kończy dowód.<br/> | ||
| Linia 516: | Linia 523: | ||
Podobnie możemy udowodnić, że dla <math>n \geqslant 649</math> (odpowiednio: <math>n \geqslant 8404</math>) między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba będąca czwartą (odpowiednio: piątą) potęgą liczby naturalnej. Oczywiście analogiczne twierdzenie możemy sformułować dla dowolnej funkcji <math>f(k) = k^u</math>, gdzie <math>u \in \mathbb{Z}_+</math>. | Podobnie możemy udowodnić, że dla <math>n \geqslant 649</math> (odpowiednio: <math>n \geqslant 8404</math>) między liczbami <math>n</math> oraz <math>2 n</math> leży przynajmniej jedna liczba będąca czwartą (odpowiednio: piątą) potęgą liczby naturalnej. Oczywiście analogiczne twierdzenie możemy sformułować dla dowolnej funkcji <math>f(k) = k^u</math>, gdzie <math>u \in \mathbb{Z}_+</math>. | ||
| − | Bez trudu pokażemy też, że twierdzenie Czebyszewa wynika z ponad sto lat od niego starszej hipotezy Goldbacha<ref name="Goldbach1"/>. Hipoteza Goldbacha może być sformułowana w różny sposób, poniżej przedstawimy te formuły i udowodnimy ich równoważność. | + | Bez trudu pokażemy też, że twierdzenie Czebyszewa wynika z ponad sto lat od niego starszej hipotezy Goldbacha<ref name="Goldbach1"/>. Hipoteza Goldbacha może być sformułowana w różny sposób, poniżej przedstawimy te formuły i udowodnimy ich równoważność. |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B20 (hipoteza Goldbacha, 1742)</span><br/> | + | <span id="B20" style="font-size: 110%; font-weight: bold;">Twierdzenie B20 (hipoteza Goldbacha, 1742)</span><br/> |
Następujące warunki są równoważne | Następujące warunki są równoważne | ||
:* <math>( \text{G1} )</math> Każda liczba naturalna parzysta <math>n \geqslant 4</math> jest sumą dwóch liczb pierwszych | :* <math>( \text{G1} )</math> Każda liczba naturalna parzysta <math>n \geqslant 4</math> jest sumą dwóch liczb pierwszych | ||
| Linia 526: | Linia 533: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Pokażemy równoważność warunków <math>( \text{G1} )</math> i <math>( \text{G2} )</math>, a następnie równoważność warunków <math>( \text{G1} )</math> i <math>( \text{G3} )</math> | + | Pokażemy równoważność warunków <math>( \text{G1} )</math> i <math>( \text{G2} )</math>, a następnie równoważność warunków <math>( \text{G1} )</math> i <math>( \text{G3} )</math> |
<math>( \text{G1} ) \quad \implies \quad ( \text{G2} )</math><br/> | <math>( \text{G1} ) \quad \implies \quad ( \text{G2} )</math><br/> | ||
| Linia 538: | Linia 545: | ||
<math>( \text{G3} ) \quad \implies \quad ( \text{G1} )</math><br/> | <math>( \text{G3} ) \quad \implies \quad ( \text{G1} )</math><br/> | ||
| − | Z założenia dla każdego <math>k \geqslant 3</math> jest <math>n = 2 k = p + q + r</math>, gdzie <math>p, q, r</math> są liczbami pierwszymi. Wypisana równość nie jest możliwa w przypadku, gdy wszystkie liczby <math>p, q, r</math> są nieparzyste. Niech <math>r = 2</math> | + | Z założenia dla każdego <math>k \geqslant 3</math> jest <math>n = 2 k = p + q + r</math>, gdzie <math>p, q, r</math> są liczbami pierwszymi. Wypisana równość nie jest możliwa w przypadku, gdy wszystkie liczby <math>p, q, r</math> są nieparzyste. Niech <math>r = 2</math> |
będzie liczbą pierwszą parzystą, wtedy <math>2 k - 2 = p + q</math>.<br/> | będzie liczbą pierwszą parzystą, wtedy <math>2 k - 2 = p + q</math>.<br/> | ||
□ | □ | ||
| Linia 545: | Linia 552: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B21</span><br/> | + | <span id="B21" style="font-size: 110%; font-weight: bold;">Twierdzenie B21</span><br/> |
Niech <math>n \in \mathbb{N}</math> i <math>n \geqslant 2</math>. Jeżeli prawdziwa jest hipoteza Goldbacha, to między <math>n</math> i <math>2 n</math> znajduje się co najmniej jedna liczba pierwsza. | Niech <math>n \in \mathbb{N}</math> i <math>n \geqslant 2</math>. Jeżeli prawdziwa jest hipoteza Goldbacha, to między <math>n</math> i <math>2 n</math> znajduje się co najmniej jedna liczba pierwsza. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Rozważmy liczbę <math>2 n + 2</math> dla <math>n \geqslant 2</math>. Z hipotezy Goldbacha <math>( \text{G2} )</math> wynika, że <math>2 n + 2 = p + q</math> jest sumą dwóch liczb pierwszych nieparzystych. | + | Rozważmy liczbę <math>2 n + 2</math> dla <math>n \geqslant 2</math>. Z hipotezy Goldbacha <math>( \text{G2} )</math> wynika, że <math>2 n + 2 = p + q</math> jest sumą dwóch liczb pierwszych nieparzystych. |
Nie zmniejszając ogólności, możemy założyć, że <math>p \leqslant q</math>, zatem | Nie zmniejszając ogólności, możemy założyć, że <math>p \leqslant q</math>, zatem | ||
| Linia 555: | Linia 562: | ||
::<math>2 n + 2 = p + q \leqslant 2 q</math> | ::<math>2 n + 2 = p + q \leqslant 2 q</math> | ||
| − | Czyli <math>q \geqslant n + 1</math>. Ponieważ <math>p \geqslant 3</math>, to z drugiej strony mamy | + | Czyli <math>q \geqslant n + 1</math>. Ponieważ <math>p \geqslant 3</math>, to z drugiej strony mamy |
::<math>2 n + 2 = p + q \geqslant q + 3</math> | ::<math>2 n + 2 = p + q \geqslant q + 3</math> | ||
| Linia 568: | Linia 575: | ||
== Zastosowania == | == Zastosowania == | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B22</span><br/> | + | <span id="B22" style="font-size: 110%; font-weight: bold;">Twierdzenie B22</span><br/> |
Niech <math>n \in \mathbb{Z}_+</math>. Prawdziwe jest oszacowanie <math>p_{n + 1} < 2 p_n</math>. | Niech <math>n \in \mathbb{Z}_+</math>. Prawdziwe jest oszacowanie <math>p_{n + 1} < 2 p_n</math>. | ||
| Linia 584: | Linia 591: | ||
Prawdziwe jest również twierdzenie odwrotne. | Prawdziwe jest również twierdzenie odwrotne. | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B23</span><br/> | + | <span id="B23" style="font-size: 110%; font-weight: bold;">Twierdzenie B23</span><br/> |
Niech <math>k, n \in \mathbb{Z}_+</math>. Jeżeli dla każdego <math>k</math> prawdziwa jest nierówność <math>p_{k + 1} < 2 p_k</math>, to dla dowolnego <math>n \geqslant 2</math> między liczbami <math>n</math> i <math>2 n</math> znajduje się co najmniej jedna liczba pierwsza. | Niech <math>k, n \in \mathbb{Z}_+</math>. Jeżeli dla każdego <math>k</math> prawdziwa jest nierówność <math>p_{k + 1} < 2 p_k</math>, to dla dowolnego <math>n \geqslant 2</math> między liczbami <math>n</math> i <math>2 n</math> znajduje się co najmniej jedna liczba pierwsza. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Ponieważ <math>n \geqslant 2</math>, to istnieje co najmniej jedna liczba pierwsza <math>q</math> taka, że <math>q \leqslant n</math>. Niech <math>p_k</math> oznacza największą liczbę pierwszą ze zbioru liczb <math>q</math> spełniających warunek <math>q \leqslant n</math>. Z definicji liczby <math>p_k</math> wynika natychmiast, że musi być <math>p_{k + 1} > n</math>. Konsekwentnie otrzymujemy ciąg nierówności | + | Ponieważ <math>n \geqslant 2</math>, to istnieje co najmniej jedna liczba pierwsza <math>q</math> taka, że <math>q \leqslant n</math>. Niech <math>p_k</math> oznacza największą liczbę pierwszą ze zbioru liczb <math>q</math> spełniających warunek <math>q \leqslant n</math>. Z definicji liczby <math>p_k</math> wynika natychmiast, że musi być <math>p_{k + 1} > n</math>. Konsekwentnie otrzymujemy ciąg nierówności |
::<math>p_k \leqslant n < p_{k + 1} < 2 p_k \leqslant 2 n</math> | ::<math>p_k \leqslant n < p_{k + 1} < 2 p_k \leqslant 2 n</math> | ||
| − | gdzie skorzystaliśmy z założonej prawdziwości oszacowania <math>p_{k + 1} < 2 p_k</math>. Zatem między liczbami <math>n</math> i <math>2 n</math> znajduje się liczba pierwsza <math>p_{k + 1}</math>.<br/> | + | gdzie skorzystaliśmy z założonej prawdziwości oszacowania <math>p_{k + 1} < 2 p_k</math>. Zatem między liczbami <math>n</math> i <math>2 n</math> znajduje się liczba pierwsza <math>p_{k + 1}</math>.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 598: | Linia 605: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B24</span><br/> | + | <span id="B24" style="font-size: 110%; font-weight: bold;">Twierdzenie B24</span><br/> |
Niech <math>n \geqslant 3</math>. Prawdziwe jest oszacowanie <math>p_{n + 1} < p_n + p_{n - 1}</math>. | Niech <math>n \geqslant 3</math>. Prawdziwe jest oszacowanie <math>p_{n + 1} < p_n + p_{n - 1}</math>. | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia B15 (punkt 2) wiemy, że dla <math>k \geqslant 6</math> między liczbami <math>k</math> i <math>2 k</math> znajdują się co najmniej dwie liczby pierwsze. Zatem dla <math>n \geqslant 5</math> w przedziale <math>(p_{n - 1}, 2 p_{n - 1})</math> znajduje się co najmniej dwie liczby pierwsze <math>q</math> i <math>r</math>. Nie zmniejszając ogólności, możemy założyć, że <math>q < r</math>. Ponieważ <math>q > p_{n - 1}</math>, to musi być <math>q \geqslant p_n</math>, a ponieważ <math>r > q \geqslant p_n</math>, to musi być <math>r \geqslant p_{n + 1}</math>. Łącząc powyższe spostrzeżenia, otrzymujemy ciąg nierówności | + | Z twierdzenia [[#B15|B15]] (punkt 2) wiemy, że dla <math>k \geqslant 6</math> między liczbami <math>k</math> i <math>2 k</math> znajdują się co najmniej dwie liczby pierwsze. Zatem dla <math>n \geqslant 5</math> w przedziale <math>(p_{n - 1}, 2 p_{n - 1})</math> znajduje się co najmniej dwie liczby pierwsze <math>q</math> i <math>r</math>. Nie zmniejszając ogólności, możemy założyć, że <math>q < r</math>. Ponieważ <math>q > p_{n - 1}</math>, to musi być <math>q \geqslant p_n</math>, a ponieważ <math>r > q \geqslant p_n</math>, to musi być <math>r \geqslant p_{n + 1}</math>. Łącząc powyższe spostrzeżenia, otrzymujemy ciąg nierówności |
::<math>p_{n - 1} < p_n < p_{n + 1} \leqslant r < 2 p_{n - 1} < p_n + p_{n - 1}</math> | ::<math>p_{n - 1} < p_n < p_{n + 1} \leqslant r < 2 p_{n - 1} < p_n + p_{n - 1}</math> | ||
| Linia 612: | Linia 619: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Zadanie B25</span><br/> | + | <span id="B25" style="font-size: 110%; font-weight: bold;">Zadanie B25</span><br/> |
Jeżeli <math>p</math> i <math>q</math> są różnymi liczbami pierwszymi, to <math>p q > p + q</math>. | Jeżeli <math>p</math> i <math>q</math> są różnymi liczbami pierwszymi, to <math>p q > p + q</math>. | ||
| Linia 618: | Linia 625: | ||
Nie zmniejszając ogólności, możemy założyć, że <math>p < q</math>. Zatem <math>p \geqslant 2</math> i <math>q \geqslant 3</math>. Łatwo znajdujemy, że | Nie zmniejszając ogólności, możemy założyć, że <math>p < q</math>. Zatem <math>p \geqslant 2</math> i <math>q \geqslant 3</math>. Łatwo znajdujemy, że | ||
| − | ::<math>\frac{1}{p} + \frac{1}{q} \leqslant \frac{1}{2} + \frac{1}{3} < 1</math> | + | ::<math>{\small\frac{1}{p}} + {\small\frac{1}{q}} \leqslant {\small\frac{1}{2}} + {\small\frac{1}{3}} < 1</math> |
skąd natychmiast otrzymujemy, że <math>p q > p + q</math>.<br/> | skąd natychmiast otrzymujemy, że <math>p q > p + q</math>.<br/> | ||
| Linia 626: | Linia 633: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Zadanie B26</span><br/> | + | <span id="B26" style="font-size: 110%; font-weight: bold;">Zadanie B26</span><br/> |
Niech <math>n \geqslant 2</math>. Pokazać, że prawdziwe jest oszacowanie <math>p_{n + 1} < p_n \cdot p_{n - 1}</math>. | Niech <math>n \geqslant 2</math>. Pokazać, że prawdziwe jest oszacowanie <math>p_{n + 1} < p_n \cdot p_{n - 1}</math>. | ||
| − | <span style="font-size: 110%; font-weight: bold;">Zadanie B27</span><br/> | + | <span id="B27" style="font-size: 110%; font-weight: bold;">Zadanie B27</span><br/> |
Niech <math>n</math> będzie dowolną liczbą naturalną, a <math>p_k</math> oznacza największą liczbę pierwszą mniejszą od <math>n</math>. Pokazać, że tylko dla <math>n = 5</math> spełnione jest równanie | Niech <math>n</math> będzie dowolną liczbą naturalną, a <math>p_k</math> oznacza największą liczbę pierwszą mniejszą od <math>n</math>. Pokazać, że tylko dla <math>n = 5</math> spełnione jest równanie | ||
| Linia 637: | Linia 644: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| − | Równanie nie może być spełnione dla <math>n \leqslant 3</math>, bo nie istnieją dwie różne liczby pierwsze mniejsze od takich liczb <math>n</math>. Sprawdzamy, że równanie nie jest spełnione dla <math>n = 4</math>. Niech <math>n \geqslant 6</math>. Zauważmy, że teraz <math>p_k \geqslant 5</math>, czyli <math>k \geqslant 3</math>. Z określenia liczby <math>p_k</math> i twierdzenia B24 prawdziwy jest ciąg nierówności | + | Równanie nie może być spełnione dla <math>n \leqslant 3</math>, bo nie istnieją dwie różne liczby pierwsze mniejsze od takich liczb <math>n</math>. Sprawdzamy, że równanie nie jest spełnione dla <math>n = 4</math>. Niech <math>n \geqslant 6</math>. Zauważmy, że teraz <math>p_k \geqslant 5</math>, czyli <math>k \geqslant 3</math>. Z określenia liczby <math>p_k</math> i twierdzenia [[#B24|B24]] prawdziwy jest ciąg nierówności |
::<math>p_k < n \leqslant p_{k + 1} < p_k + p_{k - 1}</math> | ::<math>p_k < n \leqslant p_{k + 1} < p_k + p_{k - 1}</math> | ||
| Linia 647: | Linia 654: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B28</span><br/> | + | <span id="B28" style="font-size: 110%; font-weight: bold;">Twierdzenie B28</span><br/> |
| − | Jeżeli <math>n \in \mathbb{Z}</math> i <math>n \geqslant 2</math>, to w przedziale <math>\left( \frac{n}{2}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. | + | Jeżeli <math>n \in \mathbb{Z}</math> i <math>n \geqslant 2</math>, to w przedziale <math>\left( {\small\frac{n}{2}}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia Czebyszewa wiemy, że dla <math>n \geqslant 2</math> w przedziale <math>(n, 2 n)</math> znajduje się przynajmniej jedna liczba pierwsza. Zatem jeżeli <math>n \geqslant 4</math> jest liczbą parzystą, to w przedziale <math>\left( \frac{n}{2}, n \right) \subset \left( \frac{n}{2}, n \right]</math> znajduje się co najmniej jedna liczba pierwsza. Jeżeli <math>n \geqslant 3</math> jest liczbą nieparzystą, to w przedziale <math>\left( \frac{n + 1}{2}, n + 1 \right) = \left( \frac{n + 1}{2}, n \right] \subset \left( \frac{n}{2}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Wynika stąd, że bez względu na parzystość liczby <math>n</math>, dla <math>n \geqslant 3</math> w przedziale <math>\left( \frac{n}{2}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Oczywiście dla <math>n = 2</math> twierdzenie również jest prawdziwe.<br/> | + | Z twierdzenia Czebyszewa wiemy, że dla <math>n \geqslant 2</math> w przedziale <math>(n, 2 n)</math> znajduje się przynajmniej jedna liczba pierwsza. Zatem jeżeli <math>n \geqslant 4</math> jest liczbą parzystą, to w przedziale <math>\left( {\small\frac{n}{2}}, n \right) \subset \left( {\small\frac{n}{2}}, n \right]</math> znajduje się co najmniej jedna liczba pierwsza. Jeżeli <math>n \geqslant 3</math> jest liczbą nieparzystą, to w przedziale <math>\left( {\small\frac{n + 1}{2}}, n + 1 \right) = \left( {\small\frac{n + 1}{2}}, n \right] \subset \left( {\small\frac{n}{2}}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Wynika stąd, że bez względu na parzystość liczby <math>n</math>, dla <math>n \geqslant 3</math> w przedziale <math>\left( {\small\frac{n}{2}}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Oczywiście dla <math>n = 2</math> twierdzenie również jest prawdziwe.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 657: | Linia 664: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B29</span><br/> | + | <span id="B29" style="font-size: 110%; font-weight: bold;">Twierdzenie B29</span><br/> |
| − | Dla <math>n \geqslant 2</math> liczby <math>n!</math> nie można przedstawić w postaci potęgi liczby naturalnej o wykładniku wyższym niż <math>1</math>. | + | Dla <math>n \geqslant 2</math> liczby <math>n!</math> nie można przedstawić w postaci potęgi liczby naturalnej o wykładniku wyższym niż <math>1</math>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia A42 wiemy, że każda liczba pierwsza <math>p</math> taka, że <math>p \in \left( \frac{n}{2}, n \right]</math> występuje w rozkładzie liczby <math>n!</math> na czynniki pierwsze z wykładnikiem <math>1</math>. Z twierdzenia B28 wiemy, że przedziale <math>\left( \frac{n}{2}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Łącząc te fakty, otrzymujemy natychmiast tezę.<br/> | + | Z twierdzenia [[Twierdzenie Czebyszewa o funkcji π(n)#A42|A42]] wiemy, że każda liczba pierwsza <math>p</math> taka, że <math>p \in \left( {\small\frac{n}{2}}, n \right]</math> występuje w rozkładzie liczby <math>n!</math> na czynniki pierwsze z wykładnikiem <math>1</math>. Z twierdzenia [[#B28|B28]] wiemy, że przedziale <math>\left( {\small\frac{n}{2}}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Łącząc te fakty, otrzymujemy natychmiast tezę.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 667: | Linia 674: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B30</span><br/> | + | <span id="B30" style="font-size: 110%; font-weight: bold;">Twierdzenie B30</span><br/> |
Każda liczba naturalna <math>n \geqslant 12</math> jest sumą różnych liczb pierwszych. | Każda liczba naturalna <math>n \geqslant 12</math> jest sumą różnych liczb pierwszych. | ||
| Linia 673: | Linia 680: | ||
Indukcja matematyczna. Twierdzenie jest prawdziwe dla <math>n = 12 = 5 + 7</math>. Zakładając, że twierdzenie jest prawdziwe dla każdej liczby naturalnej należącej do przedziału <math>[12, n]</math>, udowodnimy, że liczba <math>n + 1</math> jest sumą różnych liczb pierwszych. | Indukcja matematyczna. Twierdzenie jest prawdziwe dla <math>n = 12 = 5 + 7</math>. Zakładając, że twierdzenie jest prawdziwe dla każdej liczby naturalnej należącej do przedziału <math>[12, n]</math>, udowodnimy, że liczba <math>n + 1</math> jest sumą różnych liczb pierwszych. | ||
| − | Z twierdzenia B28 wiemy, że dla <math>n \geqslant 2</math> w przedziale <math>\left(\frac{n}{2}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Niech <math>p_k</math> będzie największą liczbą pierwszą w tym przedziale. Z określenia liczby <math>p_k</math> wynika następujący ciąg nierówności | + | Z twierdzenia [[#B28|B28]] wiemy, że dla <math>n \geqslant 2</math> w przedziale <math>\left(\frac{n}{2}, n \right]</math> znajduje się przynajmniej jedna liczba pierwsza. Niech <math>p_k</math> będzie największą liczbą pierwszą w tym przedziale. Z określenia liczby <math>p_k</math> wynika następujący ciąg nierówności |
| − | ::<math>\frac{n}{2} < p_k \leqslant n < n + 1 \leqslant p_{k + 1}</math> | + | ::<math>{\small\frac{n}{2}} < p_k \leqslant n < n + 1 \leqslant p_{k + 1}</math> |
| − | Korzystając z twierdzenia B22 i ostatniej z wypisanych wyżej nierówności, dostajemy | + | Korzystając z twierdzenia [[#B22|B22]] i ostatniej z wypisanych wyżej nierówności, dostajemy |
::<math>n + 1 - p_k \leqslant p_{k + 1} - p_k < p_k \leqslant n</math> | ::<math>n + 1 - p_k \leqslant p_{k + 1} - p_k < p_k \leqslant n</math> | ||
| Linia 699: | Linia 706: | ||
Skąd dostajemy | Skąd dostajemy | ||
| − | ::<math>n \geqslant 11 + p_k > 11 + \frac{n}{2}</math> | + | ::<math>n \geqslant 11 + p_k > 11 + {\small\frac{n}{2}}</math> |
Zatem dopiero dla <math>n > 22</math> warunek <math>n + 1 - p_k \geqslant 12</math> będzie na pewno spełniony. Łatwo sprawdzamy, że dla liczb <math>12, 13, \ldots, 22</math> twierdzenie jest prawdziwe | Zatem dopiero dla <math>n > 22</math> warunek <math>n + 1 - p_k \geqslant 12</math> będzie na pewno spełniony. Łatwo sprawdzamy, że dla liczb <math>12, 13, \ldots, 22</math> twierdzenie jest prawdziwe | ||
| Linia 709: | Linia 716: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B31</span><br/> | + | <span id="B31" style="font-size: 110%; font-weight: bold;">Twierdzenie B31</span><br/> |
Dla <math>n \geqslant 3</math> prawdziwe jest następujące oszacowanie funkcji <math>P(n)</math> od dołu | Dla <math>n \geqslant 3</math> prawdziwe jest następujące oszacowanie funkcji <math>P(n)</math> od dołu | ||
| Linia 717: | Linia 724: | ||
Indukcja matematyczna. Mamy <math>P(3) = 6 > 2^{3 / 2} = 2 \sqrt{2}</math> oraz <math>P(4) = 6 > 2^{4 / 2} = 4</math>, czyli nierówność jest prawdziwa dla <math>n = 3, 4</math>. Zakładając prawdziwość nierówności dla wszystkich liczb naturalnych należących do przedziału <math>\left [ 3, n \right ]</math>, otrzymujemy dla <math>n + 1</math> | Indukcja matematyczna. Mamy <math>P(3) = 6 > 2^{3 / 2} = 2 \sqrt{2}</math> oraz <math>P(4) = 6 > 2^{4 / 2} = 4</math>, czyli nierówność jest prawdziwa dla <math>n = 3, 4</math>. Zakładając prawdziwość nierówności dla wszystkich liczb naturalnych należących do przedziału <math>\left [ 3, n \right ]</math>, otrzymujemy dla <math>n + 1</math> | ||
| − | a) jeżeli <math>n + 1</math> jest liczbą parzystą, to <math>n + 1 = 2 m</math> i wtedy | + | a) jeżeli <math>n + 1</math> jest liczbą parzystą, to <math>n + 1 = 2 m</math> i wtedy |
| − | ::<math>P(n + 1) = P (2 m) = P (m) \cdot \frac{P (2 m)}{P (m)} > 2^{m / 2} \cdot 2^{m / 2} = 2^m = 2^{2 m / 2} = 2^{(n + 1) / 2}</math> | + | ::<math>P(n + 1) = P (2 m) = P (m) \cdot {\small\frac{P (2 m)}{P (m)}} > 2^{m / 2} \cdot 2^{m / 2} = 2^m = 2^{2 m / 2} = 2^{(n + 1) / 2}</math> |
| − | gdzie skorzystaliśmy z założenia indukcyjnego i twierdzenia B12. | + | gdzie skorzystaliśmy z założenia indukcyjnego i twierdzenia [[#B12|B12]]. |
| − | b) jeżeli <math>n + 1</math> jest liczbą nieparzystą, to <math>n + 1 = 2 m + 1</math> i wtedy | + | b) jeżeli <math>n + 1</math> jest liczbą nieparzystą, to <math>n + 1 = 2 m + 1</math> i wtedy |
| − | ::<math>P(n + 1) = P (2 m + 1) = P (2 m + 2) = P (m + 1) \cdot \frac{P (2 m + 2)}{P (m + 1)} > 2^{(m + 1) / 2} \cdot 2^{(m + 1) / 2} = 2^{(2 m + 2) / 2} > 2^{(2 m + 1) / 2} = 2^{(n + 1) / 2}</math> | + | ::<math>P(n + 1) = P (2 m + 1) = P (2 m + 2) = P (m + 1) \cdot {\small\frac{P (2 m + 2)}{P (m + 1)}} > 2^{(m + 1) / 2} \cdot 2^{(m + 1) / 2} = 2^{(2 m + 2) / 2} > 2^{(2 m + 1) / 2} = 2^{(n + 1) / 2}</math> |
Co kończy dowód indukcyjny.<br/> | Co kończy dowód indukcyjny.<br/> | ||
| Linia 733: | Linia 740: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Zadanie B32</span><br/> | + | <span id="B32" style="font-size: 110%; font-weight: bold;">Zadanie B32</span><br/> |
| − | Niech <math>p_n</math> oznaczą <math>n</math>-tą liczbę pierwszą. Korzystając z twierdzenia Czebyszewa pokazać, że dla <math>n \geqslant 1</math> jest <math>p_n \leqslant 2^n</math>. | + | Niech <math>p_n</math> oznaczą <math>n</math>-tą liczbę pierwszą. Korzystając z twierdzenia Czebyszewa pokazać, że dla <math>n \geqslant 1</math> jest <math>p_n \leqslant 2^n</math>. |
| Linia 740: | Linia 747: | ||
| − | == Rozbieżność sumy <math>\textstyle \sum\limits_{p \geqslant 2} \frac{1}{p}</math> == | + | == Rozbieżność sumy <math>\textstyle \sum\limits_{p \geqslant 2} {\small\frac{1}{p}}</math> == |
| − | Rozpoczniemy od prostszego twierdzenia dotyczącego rozbieżności sumy odwrotności wszystkich liczb całkowitych dodatnich. Już sam wzór, w którym pogrupowaliśmy wyrazy tej sumy | + | Rozpoczniemy od prostszego twierdzenia dotyczącego rozbieżności sumy odwrotności wszystkich liczb całkowitych dodatnich. Już sam wzór, w którym pogrupowaliśmy wyrazy tej sumy |
| − | ::<math>S = 1 + \frac{1}{2} + \left( \frac{1}{3} + \frac{1}{4} \right) + \left( \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} \right) + \left( \frac{1}{9} + \frac{1}{10} + \frac{1}{11} + \frac{1}{12} + \frac{1}{13} + \frac{1}{14} + \frac{1}{15} + \frac{1}{16} \right) + \ldots</math> | + | ::<math>S = 1 + {\small\frac{1}{2}} + \left( {\small\frac{1}{3}} + {\small\frac{1}{4}} \right) + \left( {\small\frac{1}{5}} + {\small\frac{1}{6}} + {\small\frac{1}{7}} + {\small\frac{1}{8}} \right) + \left( {\small\frac{1}{9}} + {\small\frac{1}{10}} + {\small\frac{1}{11}} + {\small\frac{1}{12}} + {\small\frac{1}{13}} + {\small\frac{1}{14}} + {\small\frac{1}{15}} + {\small\frac{1}{16}} \right) + \ldots</math> |
| − | mógłby wystarczyć za dowód, bo każda suma w nawiasach jest większa od <math>\frac{1}{2}</math>, ale dowód formalny okaże się pożytecznym ćwiczeniem. | + | mógłby wystarczyć za dowód, bo każda suma w nawiasach jest większa od <math>{\small\frac{1}{2}}</math>, ale dowód formalny okaże się pożytecznym ćwiczeniem. |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B33</span><br/> | + | <span id="B33" style="font-size: 110%; font-weight: bold;">Twierdzenie B33</span><br/> |
Niech <math>S(k)</math> oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od <math>k</math>. Prawdziwa jest nierówność | Niech <math>S(k)</math> oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od <math>k</math>. Prawdziwa jest nierówność | ||
| − | ::<math>S(2^n) > \frac{n + 1}{2}</math>. | + | ::<math>S(2^n) > {\small\frac{n + 1}{2}}</math>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Indukcja matematyczna. Twierdzenie jest prawdziwe dla <math>n = 1</math>, bo | Indukcja matematyczna. Twierdzenie jest prawdziwe dla <math>n = 1</math>, bo | ||
| − | ::<math>S(2^1) = 1 + \frac{1}{2} > 1</math> | + | ::<math>S(2^1) = 1 + {\small\frac{1}{2}} > 1</math> |
Zakładając, że twierdzenie jest prawdziwe dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | Zakładając, że twierdzenie jest prawdziwe dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | ||
| − | ::<math>S(2^{n + 1}) = 1 + \frac{1}{2} + \ldots + \frac{1}{2^n - 1} + \frac{1}{2^n} + \left( \frac{1}{2^n + 1} + \ldots + \frac{1}{2^{n + 1}} \right) =</math> | + | ::<math>S(2^{n + 1}) = 1 + {\small\frac{1}{2}} + \ldots + {\small\frac{1}{2^n - 1}} + {\small\frac{1}{2^n}} + \left( {\small\frac{1}{2^n + 1}} + \ldots + {\small\frac{1}{2^{n + 1}}} \right) =</math> |
| − | ::::<math>\; \; \: = S (2^n) + \left( \frac{1}{2^n + 1} + \ldots + \frac{1}{2^{n + 1}} \right)</math> | + | ::::<math>\; \; \: = S (2^n) + \left( {\small\frac{1}{2^n + 1}} + \ldots + {\small\frac{1}{2^{n + 1}}} \right)</math> |
| − | Ponieważ wyrażenie w nawiasie zawiera <math>2^{n + 1} - 2^n = 2^n</math> wyrazów, z których każdy jest nie mniejszy niż <math>\frac{1}{2^{n + 1}}</math>, to prawdziwe jest oszacowanie | + | Ponieważ wyrażenie w nawiasie zawiera <math>2^{n + 1} - 2^n = 2^n</math> wyrazów, z których każdy jest nie mniejszy niż <math>{\small\frac{1}{2^{n + 1}}}</math>, to prawdziwe jest oszacowanie |
| − | ::<math>S(2^{n + 1}) > \frac{n + 1}{2} + 2^n \cdot \frac{1}{2^{n + 1}} =</math> | + | ::<math>S(2^{n + 1}) > {\small\frac{n + 1}{2}} + 2^n \cdot {\small\frac{1}{2^{n + 1}}} =</math> |
| − | ::::<math>\; \; \: = \frac{n + 2}{2}</math> | + | ::::<math>\; \; \: = {\small\frac{n + 2}{2}}</math> |
| − | Gdzie skorzystaliśmy z założenia indukcyjnego i oszacowaliśmy sumę w nawiasie.<br/> | + | Gdzie skorzystaliśmy z założenia indukcyjnego i oszacowaliśmy sumę w nawiasie.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 778: | Linia 785: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B34</span><br/> | + | <span id="B34" style="font-size: 110%; font-weight: bold;">Twierdzenie B34</span><br/> |
Niech <math>S(k)</math> oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od <math>k</math>. Prawdziwa jest nierówność | Niech <math>S(k)</math> oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od <math>k</math>. Prawdziwa jest nierówność | ||
| Linia 790: | Linia 797: | ||
Zatem | Zatem | ||
| − | ::<math>S(k) \geqslant S (2^n) > \frac{n + 1}{2} = \ | + | ::<math>S(k) \geqslant S (2^n) > {\small\frac{n + 1}{2}} = \tfrac{1}{2} (\lfloor \log_2 \! k \rfloor + 1) > \tfrac{1}{2} \log_2 \! k</math><br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| − | Z twierdzenia B34 wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb całkowitych dodatnich. | + | Z twierdzenia [[#B34|B34]] wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb całkowitych dodatnich. |
{| class="wikitable" | {| class="wikitable" | ||
| Linia 802: | Linia 809: | ||
Dokładniejsze oszacowanie sumy odwrotności liczb całkowitych dodatnich<ref name="harmoniczny1"/> nie większych od <math>k</math> jest dane wzorem | Dokładniejsze oszacowanie sumy odwrotności liczb całkowitych dodatnich<ref name="harmoniczny1"/> nie większych od <math>k</math> jest dane wzorem | ||
| − | ::<math>\sum_{j=1}^{k}\frac{1}{j} = \log k + \gamma + \frac{1}{2 k} - \frac{1}{12 k^2} + \frac{1}{120 k^4} + \ldots</math> | + | ::<math>\sum_{j=1}^{k}\frac{1}{j} = \log k + \gamma + {\small\frac{1}{2 k}} - {\small\frac{1}{12 k^2}} + {\small\frac{1}{120 k^4}} + \ldots</math> |
gdzie <math>\gamma = 0.5772156649 \ldots</math> jest stałą Eulera<ref name="Euler1"/>. | gdzie <math>\gamma = 0.5772156649 \ldots</math> jest stałą Eulera<ref name="Euler1"/>. | ||
| Linia 813: | Linia 820: | ||
Oznaczmy przez <math>Q</math> sumę odwrotności wszystkich liczb pierwszych | Oznaczmy przez <math>Q</math> sumę odwrotności wszystkich liczb pierwszych | ||
| − | ::<math>Q = \frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \frac{1}{13} + \frac{1}{17} + \frac{1}{19} + \frac{1}{23} + \frac{1}{29} + \frac{1}{31} + \frac{1}{37} + \frac{1}{41} + \frac{1}{43} + \frac{1}{47} + \ldots</math> | + | ::<math>Q = {\small\frac{1}{2}} + {\small\frac{1}{3}} + {\small\frac{1}{5}} + {\small\frac{1}{7}} + {\small\frac{1}{11}} + {\small\frac{1}{13}} + {\small\frac{1}{17}} + {\small\frac{1}{19}} + {\small\frac{1}{23}} + {\small\frac{1}{29}} + {\small\frac{1}{31}} + {\small\frac{1}{37}} + {\small\frac{1}{41}} + {\small\frac{1}{43}} + {\small\frac{1}{47}} + \ldots</math> |
a przez <math>Q(k)</math> sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Dla przykładu mamy | a przez <math>Q(k)</math> sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Dla przykładu mamy | ||
| Linia 819: | Linia 826: | ||
::<math>Q(1) = 0</math> | ::<math>Q(1) = 0</math> | ||
| − | ::<math>Q(2) = \frac{1}{2}</math> | + | ::<math>Q(2) = {\small\frac{1}{2}}</math> |
| − | ::<math>Q(3) = \frac{1}{2} + \frac{1}{3}</math> | + | ::<math>Q(3) = {\small\frac{1}{2}} + {\small\frac{1}{3}}</math> |
| − | ::<math>Q(4) = \frac{1}{2} + \frac{1}{3}</math> | + | ::<math>Q(4) = {\small\frac{1}{2}} + {\small\frac{1}{3}}</math> |
| − | Korzystając z twierdzenia B14, udowodnimy | + | Korzystając z twierdzenia [[#B14|B14]], udowodnimy |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B35</span><br/> | + | <span id="B35" style="font-size: 110%; font-weight: bold;">Twierdzenie B35</span><br/> |
Niech <math>Q(k)</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Dla <math>k \geqslant 1</math> prawdziwe jest oszacowanie | Niech <math>Q(k)</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Dla <math>k \geqslant 1</math> prawdziwe jest oszacowanie | ||
| − | ::<math>Q(2 k) - Q (k) > \frac{\log 2}{4} \cdot \frac{1}{\log (2 k)}</math> | + | ::<math>Q(2 k) - Q (k) > {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2 k)}}</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Zauważmy, że | Zauważmy, że | ||
| − | ::<math>Q(2 k) - Q (k) = \sum_{k < p \leqslant 2k} \frac{1}{p} \geqslant</math> | + | ::<math>Q(2 k) - Q (k) = \sum_{k < p \leqslant 2k} {\small\frac{1}{p}} \geqslant</math> |
| − | ::::::<math>\; \: \geqslant \sum_{k < p \leqslant 2k} \frac{1}{2 k} =</math> | + | ::::::<math>\; \: \geqslant \sum_{k < p \leqslant 2k} {\small\frac{1}{2 k}} =</math> |
| − | ::::::<math>\; \: = \frac{1}{2 k} \cdot [\pi (2 k) - \pi (k)] ></math> | + | ::::::<math>\; \: = {\small\frac{1}{2 k}} \cdot [\pi (2 k) - \pi (k)] ></math> |
| − | ::::::<math>\; \: > \frac{1}{2 k} \cdot \frac{\log 2}{2} \cdot \frac{k}{\log (2 k)} =</math> | + | ::::::<math>\; \: > {\small\frac{1}{2 k}} \cdot {\small\frac{\log 2}{2}} \cdot {\small\frac{k}{\log (2 k)}} =</math> |
| − | ::::::<math>\; \: = \frac{\log 2}{4} \cdot \frac{1}{\log (2 k)}</math> | + | ::::::<math>\; \: = {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2 k)}}</math> |
| − | Pierwsza nierówność (nieostra) wynika z faktu, że <math>\frac{1}{p} \geqslant \frac{1}{2 k}</math> dla wszystkich liczb pierwszych <math>p \leqslant 2 k</math>. Kolejna nierówność wynika z twierdzenia B14.<br/> | + | Pierwsza nierówność (nieostra) wynika z faktu, że <math>{\small\frac{1}{p}} \geqslant {\small\frac{1}{2 k}}</math> dla wszystkich liczb pierwszych <math>p \leqslant 2 k</math>. Kolejna nierówność wynika z twierdzenia [[#B14|B14]].<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 852: | Linia 859: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B36</span><br/> | + | <span id="B36" style="font-size: 110%; font-weight: bold;">Twierdzenie B36</span><br/> |
Niech <math>Q(k)</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Prawdziwa jest nierówność | Niech <math>Q(k)</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Prawdziwa jest nierówność | ||
| − | ::<math>Q(2^n) > \frac{1}{4} \cdot \sum_{j = 1}^{n + 1} \frac{1}{j}</math> | + | ::<math>Q(2^n) > {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 1} {\small\frac{1}{j}}</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Indukcja matematyczna. Twierdzenie jest prawdziwe dla <math>n = 1</math>, bo | Indukcja matematyczna. Twierdzenie jest prawdziwe dla <math>n = 1</math>, bo | ||
| − | ::<math>Q(2^1) = \frac{1}{2} > \frac{3}{8}</math> | + | ::<math>Q(2^1) = {\small\frac{1}{2}} > {\small\frac{3}{8}}</math> |
Zakładając, że twierdzenie jest prawdziwe dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | Zakładając, że twierdzenie jest prawdziwe dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | ||
| Linia 866: | Linia 873: | ||
::<math>Q(2^{n + 1}) = Q (2^n) + [Q (2^{n + 1}) - Q (2^n)] ></math> | ::<math>Q(2^{n + 1}) = Q (2^n) + [Q (2^{n + 1}) - Q (2^n)] ></math> | ||
| − | ::::<math>\; \: \: \, > Q (2^n) + \frac{\log 2}{4} \cdot \frac{1}{\log (2^{n + 1})} =</math> | + | ::::<math>\; \: \: \, > Q (2^n) + {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2^{n + 1})}} =</math> |
| − | ::::<math>\; \: \: \, = Q (2^n) + \frac{1}{4} \cdot \frac{1}{n + 1} ></math> | + | ::::<math>\; \: \: \, = Q (2^n) + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 1}} ></math> |
| − | ::::<math>\; \: \: \, > Q (2^n) + \frac{1}{4} \cdot \frac{1}{n + 2} ></math> | + | ::::<math>\; \: \: \, > Q (2^n) + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 2}} ></math> |
| − | ::::<math>\; \: \: \, > \frac{1}{4} \cdot \sum_{j = 1}^{n + 1} \frac{1}{j} + \frac{1}{4} \cdot \frac{1}{n + 2} =</math> | + | ::::<math>\; \: \: \, > {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 1} {\small\frac{1}{j}} + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 2}} =</math> |
| − | ::::<math>\; \: \: \, = \frac{1}{4} \cdot \sum_{j = 1}^{n + 2} \frac{1}{j}</math> | + | ::::<math>\; \: \: \, = {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 2} {\small\frac{1}{j}}</math> |
| − | Pierwsza nierówność wynika z twierdzenia B35, druga z faktu, że <math>\frac{1}{n + 1} > \frac{1}{n + 2}</math>, a trzecia z założenia indukcyjnego.<br/> | + | Pierwsza nierówność wynika z twierdzenia [[#B35|B35]], druga z faktu, że <math>{\small\frac{1}{n + 1}} > {\small\frac{1}{n + 2}}</math>, a trzecia z założenia indukcyjnego.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 882: | Linia 889: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B37</span><br/> | + | <span id="B37" style="font-size: 110%; font-weight: bold;">Twierdzenie B37</span><br/> |
Niech <math>Q(k)</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Prawdziwa jest nierówność | Niech <math>Q(k)</math> oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od <math>k</math>. Prawdziwa jest nierówność | ||
| Linia 896: | Linia 903: | ||
::<math>Q(k) \geqslant Q (2^n) ></math> | ::<math>Q(k) \geqslant Q (2^n) ></math> | ||
| − | :::<math>\quad > \frac{1}{4} \cdot \underset{j = 1}{\overset{n + 1}{\sum}} \frac{1}{j} ></math> | + | :::<math>\quad > {\small\frac{1}{4}} \cdot \underset{j = 1}{\overset{n + 1}{\sum}} {\small\frac{1}{j}} ></math> |
| − | :::<math>\quad > \frac{1}{8} \cdot \log_2 (n + 1) =</math> | + | :::<math>\quad > {\small\frac{1}{8}} \cdot \log_2 (n + 1) =</math> |
| − | :::<math>\quad = \frac{1}{8} \cdot \log_2 (\lfloor \log_2 \! k \rfloor + 1) ></math> | + | :::<math>\quad = {\small\frac{1}{8}} \cdot \log_2 (\lfloor \log_2 \! k \rfloor + 1) ></math> |
| − | :::<math>\quad > \frac{1}{8} \cdot \log_2 (\log_2 \! k)</math> | + | :::<math>\quad > {\small\frac{1}{8}} \cdot \log_2 (\log_2 \! k)</math> |
| − | Pierwsza nierówność (ostra) wynika z twierdzenia B36, kolejna nierówność wynika z twierdzenia B34.<br/> | + | Pierwsza nierówność (ostra) wynika z twierdzenia [[#B36|B36]], kolejna nierówność wynika z twierdzenia [[#B34|B34]].<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| − | Z twierdzenia B37 wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb pierwszych. | + | Z twierdzenia [[#B37|B37]] wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb pierwszych. |
{| class="wikitable" | {| class="wikitable" | ||
| Linia 916: | Linia 923: | ||
Dokładniejsze oszacowanie sumy odwrotności liczb pierwszych nie większych od <math>k</math> jest dane wzorem | Dokładniejsze oszacowanie sumy odwrotności liczb pierwszych nie większych od <math>k</math> jest dane wzorem | ||
| − | ::<math>\sum_{p\leqslant k}\frac{1}{p} = \log \log k + M + \ldots</math> | + | ::<math>\sum_{p\leqslant k} {\small\frac{1}{p}} = \log \log k + M + \ldots</math> |
gdzie <math>M = 0.261497212847 \ldots</math> jest stałą Mertensa<ref name="Mertens1"/>. | gdzie <math>M = 0.261497212847 \ldots</math> jest stałą Mertensa<ref name="Mertens1"/>. | ||
| Linia 923: | Linia 930: | ||
Dla <math>k \geqslant 286</math> prawdziwe jest następujące oszacowanie odchylenia od podanej wyżej wartości<ref name="Rosser1"/> | Dla <math>k \geqslant 286</math> prawdziwe jest następujące oszacowanie odchylenia od podanej wyżej wartości<ref name="Rosser1"/> | ||
| − | <math>\left| \sum_{p\leqslant k}\frac{1}{p} - \log \log k - M \right| < \frac{1}{2 (\log k)^2}</math> | + | <math>\left| \sum_{p\leqslant k} {\small\frac{1}{p}} - \log \log k - M \right| < {\small\frac{1}{2 (\log k)^2}}</math> |
|} | |} | ||
| Linia 931: | Linia 938: | ||
| − | == Zbieżność sumy <math>\textstyle \sum\limits_{p \geqslant 2} \frac{1}{p \log p}</math> == | + | == Zbieżność sumy <math>\textstyle \sum\limits_{p \geqslant 2} {\small\frac{1}{p \log p}}</math> == |
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B38</span><br/> | + | <span id="B38" style="font-size: 110%; font-weight: bold;">Twierdzenie B38</span><br/> |
| − | Niech <math>T = \sum_{p \geqslant 2} \frac{1}{p \log p}</math> będzie sumą odwrotności wszystkich iloczynów <math>p \! \cdot \! \log p</math>, gdzie <math>p</math> oznacza liczbę pierwszą, | + | Niech <math>T = \sum_{p \geqslant 2} {\small\frac{1}{p \log p}}</math> będzie sumą odwrotności wszystkich iloczynów <math>p \! \cdot \! \log p</math>, gdzie <math>p</math> oznacza liczbę pierwszą, a <math>T(k)</math> będzie sumą częściową sumy <math>T</math> |
| − | ::<math>T(k) = \sum_{p \leqslant k} \frac{1}{p \log p}</math> | + | ::<math>T(k) = \sum_{p \leqslant k} {\small\frac{1}{p \log p}}</math> |
Dla <math>k \geqslant 2</math> prawdziwe jest oszacowanie | Dla <math>k \geqslant 2</math> prawdziwe jest oszacowanie | ||
| − | ::<math>T(2 k) - T (k) < \frac{2 \log 2}{\log^2 \! k}</math> | + | ::<math>T(2 k) - T (k) < {\small\frac{2 \log 2}{\log^2 \! k}}</math> |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
Zauważmy, że | Zauważmy, że | ||
| − | ::<math>T(2 k) - T (k) = \sum_{k < p \leqslant 2 k} \frac{1}{p \log p} | + | ::<math>T(2 k) - T (k) = \sum_{k < p \leqslant 2 k} {\small\frac{1}{p \log p}}</math> |
| − | ::::::<math>\; < \sum_{k < p \leqslant 2 k} \frac{1}{k \log k} | + | ::::::<math>\; < \sum_{k < p \leqslant 2 k} {\small\frac{1}{k \log k}}</math> |
| − | ::::::<math>\; = \frac{1}{k \log k} \cdot [\pi (2 k) - \pi (k)] | + | ::::::<math>\; = {\small\frac{1}{k \log k}} \cdot [\pi (2 k) - \pi (k)]</math> |
| − | ::::::<math>\; < \frac{1}{k \log k} \cdot 2 \log 2 \cdot \frac{k}{\log k} | + | ::::::<math>\; < {\small\frac{1}{k \log k}} \cdot 2 \log 2 \cdot {\small\frac{k}{\log k}}</math> |
| − | ::::::<math>\; = \frac{2 \log 2}{(\log k)^2}</math> | + | ::::::<math>\; = {\small\frac{2 \log 2}{(\log k)^2}}</math> |
| − | Pierwsza nierówność wynika z faktu, że <math>\frac{1}{p \log p} < \frac{1}{k \log k}</math> dla wszystkich liczb pierwszych <math>p > k</math>. Kolejna nierówność wynika z twierdzenia A11.<br/> | + | Pierwsza nierówność wynika z faktu, że <math>{\small\frac{1}{p \log p}} < {\small\frac{1}{k \log k}}</math> dla wszystkich liczb pierwszych <math>p > k</math>. Kolejna nierówność wynika z twierdzenia [[Twierdzenie Czebyszewa o funkcji π(n)#A11|A11]].<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 961: | Linia 968: | ||
| − | <span style="font-size: 110%; font-weight: bold;">Twierdzenie B39</span><br/> | + | <span id="B39" style="font-size: 110%; font-weight: bold;">Twierdzenie B39</span><br/> |
| − | Suma <math>\sum_{p \geqslant 2} \frac{1}{p \log p}</math>, gdzie <math>p</math> oznacza liczbę pierwszą, jest skończona<ref name="A137245"/>. | + | Suma <math>\sum_{p \geqslant 2} {\small\frac{1}{p \log p}}</math>, gdzie <math>p</math> oznacza liczbę pierwszą, jest skończona<ref name="A137245"/>. |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Niech <math>p</math> oznacza liczbę pierwszą i niech | + | Niech <math>p</math> oznacza liczbę pierwszą i niech |
| − | ::<math>T(k) = \sum_{p \leqslant k} \frac{1}{p \log p}</math> | + | ::<math>T(k) = \sum_{p \leqslant k} {\small\frac{1}{p \log p}}</math> |
Pokażemy najpierw, że dla <math>n \geqslant 1</math> prawdziwa jest nierówność | Pokażemy najpierw, że dla <math>n \geqslant 1</math> prawdziwa jest nierówność | ||
| − | ::<math>T(2^n) < \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{n} \right)</math> | + | ::<math>T(2^n) < {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} \right)</math> |
'''Indukcja matematyczna'''. Twierdzenie jest prawdziwe dla <math>n = 1</math>, bo | '''Indukcja matematyczna'''. Twierdzenie jest prawdziwe dla <math>n = 1</math>, bo | ||
| Linia 979: | Linia 986: | ||
Zakładając, że twierdzenie jest prawdziwe dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | Zakładając, że twierdzenie jest prawdziwe dla <math>n</math>, otrzymujemy dla <math>n + 1</math> | ||
| − | ::<math>T(2^{n + 1}) = T (2^n) + [T (2^{n + 1}) - T (2^n)] | + | ::<math>T(2^{n + 1}) = T (2^n) + [T (2^{n + 1}) - T (2^n)]</math> |
| − | ::::<math>\;\;\: < T (2^n) + 2 \log 2 \cdot \frac{1}{[\log (2^n)]^2} | + | ::::<math>\;\;\: < T (2^n) + 2 \log 2 \cdot {\small\frac{1}{[\log (2^n)]^2}}</math> |
| − | ::::<math>\;\;\: < \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{n} \right) + 2 \log 2 \cdot \frac{1}{n^2 (\log 2)^2} | + | ::::<math>\;\;\: < {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} \right) + 2 \log 2 \cdot {\small\frac{1}{n^2 (\log 2)^2}}</math> |
| − | ::::<math>\;\;\: = \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{n} + \frac{1}{n^2} \right) | + | ::::<math>\;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} + {\small\frac{1}{n^2}} \right)</math> |
| − | ::::<math>\;\;\: = \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{n + 1} + \left( \frac{2}{n + 1} - \frac{2}{n} + \frac{1}{n^2} \right) \right) | + | ::::<math>\;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} + \left( {\small\frac{2}{n + 1}} - {\small\frac{2}{n}} + {\small\frac{1}{n^2}} \right) \right)</math> |
| − | ::::<math>\;\;\: = \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{n + 1} - \frac{n - 1}{n^2 (n + 1)} \right) | + | ::::<math>\;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} - {\small\frac{n - 1}{n^2 (n + 1)}} \right)</math> |
| − | ::::<math>\;\;\: < \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{n + 1} \right)</math> | + | ::::<math>\;\;\: < {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} \right)</math> |
| − | Pierwsza nierówność wynika z twierdzenia B38, a druga z założenia indukcyjnego. Co kończy dowód indukcyjny. | + | Pierwsza nierówność wynika z twierdzenia [[#B38|B38]], a druga z założenia indukcyjnego. Co kończy dowód indukcyjny. |
| Linia 1006: | Linia 1013: | ||
to łatwo otrzymujemy | to łatwo otrzymujemy | ||
| − | ::<math>T(k) \leqslant T (2^{n + 1}) < \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{n + 1} \right) \leqslant \frac{2}{\log 2} \cdot \left( 3 - \frac{2}{\log_2 \! k + 1} \right) < \frac{6}{\log 2}</math> | + | ::<math>T(k) \leqslant T (2^{n + 1}) < {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} \right) \leqslant {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{\log_2 \! k + 1}} \right) < {\small\frac{6}{\log 2}}</math> |
| − | Ponieważ ciąg sum częściowych <math>T(k)</math> jest rosnący i ograniczony<ref name="Wiki1"/><ref name="Wiki2"/>, to suma odwrotności wszystkich iloczynów <math>p \! \cdot \! \log p</math> jest skończona.<br/> | + | Ponieważ ciąg sum częściowych <math>T(k)</math> jest rosnący i ograniczony<ref name="Wiki1"/><ref name="Wiki2"/>, to suma odwrotności wszystkich iloczynów <math>p \! \cdot \! \log p</math> jest skończona.<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 1033: | Linia 1040: | ||
<ref name="Czebyszew2">P. L. Chebyshev, ''Mémoire sur les nombres premiers'', J. de Math. Pures Appl. (1) 17 (1852), 366-390, ([http://sites.mathdoc.fr/JMPA/PDF/JMPA_1852_1_17_A19_0.pdf LINK])</ref> | <ref name="Czebyszew2">P. L. Chebyshev, ''Mémoire sur les nombres premiers'', J. de Math. Pures Appl. (1) 17 (1852), 366-390, ([http://sites.mathdoc.fr/JMPA/PDF/JMPA_1852_1_17_A19_0.pdf LINK])</ref> | ||
| − | <ref name="p1">Literą "A" poprzedzamy numery twierdzeń, które zostały sformułowane i udowodnione w artykule ''Twierdzenie Czebyszewa o funkcji <math>\pi (n)</math>'', ([https://henryk-dabrowski.pl/index.php?title=Twierdzenie_Czebyszewa_o_funkcji_%CF%80(n) LINK])</ref> | + | <ref name="p1">Literą "A" poprzedzamy numery twierdzeń, które zostały sformułowane i udowodnione w artykule ''Twierdzenie Czebyszewa o funkcji <math>\pi (n)</math>'', ([https://henryk-dabrowski.pl/index.php?title=Twierdzenie_Czebyszewa_o_funkcji_%CF%80(n) LINK])</ref> |
<ref name="Dusart06">P. Dusart, ''Sharper bounds for <math>\psi</math>, <math>\theta</math>, <math>\pi</math>, <math>p_k</math>'', Rapport de recherche no. 1998-06, Université de Limoges</ref> | <ref name="Dusart06">P. Dusart, ''Sharper bounds for <math>\psi</math>, <math>\theta</math>, <math>\pi</math>, <math>p_k</math>'', Rapport de recherche no. 1998-06, Université de Limoges</ref> | ||
| Linia 1049: | Linia 1056: | ||
<ref name="A137245">The On-Line Encyclopedia of Integer Sequences, ''A137245 - Decimal expansion of Sum_{p prime} 1/(p * log p)'', ([https://oeis.org/A137245 LINK])</ref> | <ref name="A137245">The On-Line Encyclopedia of Integer Sequences, ''A137245 - Decimal expansion of Sum_{p prime} 1/(p * log p)'', ([https://oeis.org/A137245 LINK])</ref> | ||
| − | <ref name="Wiki1">Wikipedia, ''Twierdzenie o zbieżności ciągu monotonicznego'', ([https://pl.wikipedia.org/wiki/Twierdzenie_o_zbie%C5%BCno%C5%9Bci_ci%C4%85gu_monotonicznego Wiki-pl])</ref> | + | <ref name="Wiki1">Wikipedia, ''Twierdzenie o zbieżności ciągu monotonicznego'', ([https://pl.wikipedia.org/wiki/Twierdzenie_o_zbie%C5%BCno%C5%9Bci_ci%C4%85gu_monotonicznego Wiki-pl])</ref> |
<ref name="Wiki2">Wikipedia, ''Aksjomat ciągłości'', ([https://pl.wikipedia.org/wiki/Aksjomat_ci%C4%85g%C5%82o%C5%9Bci Wiki-pl])</ref> | <ref name="Wiki2">Wikipedia, ''Aksjomat ciągłości'', ([https://pl.wikipedia.org/wiki/Aksjomat_ci%C4%85g%C5%82o%C5%9Bci Wiki-pl])</ref> | ||
Aktualna wersja na dzień 12:59, 6 cze 2024
Twierdzenie Czebyszewa
W 1852 roku rosyjski matematyk Czebyszew[1][2] udowodnił, że dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ a \cdot {\small\frac{n}{\log n}} \: \underset{n \geqslant 11}{\lt } \: \pi (n) \: \underset{n \geqslant 96098}{\lt } \: b \cdot {\small\frac{n}{\log n}} }[/math]
gdzie
- [math]\displaystyle{ a = \log (2^{1 / 2} \cdot 3^{1 / 3} \cdot 5^{1 / 5} \cdot 30^{- 1 / 30}) = 0.921292022 \qquad \quad b = \tfrac{6}{5} a = 1.105550428 }[/math]
Dysponując tak dokładnym oszacowaniem funkcji [math]\displaystyle{ \pi (n) }[/math], Czebyszew mógł bez trudu udowodnić następujące twierdzenie
Twierdzenie B1 (twierdzenie Czebyszewa)
Dla [math]\displaystyle{ n \geqslant 2 }[/math] między liczbami naturalnymi [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się przynajmniej jedna liczba pierwsza.
W rzeczywistości Czebyszew mógł udowodnić znacznie silniejsze twierdzenie
Twierdzenie B2
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math]. Dla [math]\displaystyle{ n \geqslant 3 }[/math] w każdym z przedziałów [math]\displaystyle{ (n, 2
n) }[/math], [math]\displaystyle{ (2 n, 3 n) }[/math], [math]\displaystyle{ (3 n, 4 n) }[/math] oraz [math]\displaystyle{ (4 n, 5 n) }[/math] znajduje się przynajmniej jedna liczba pierwsza.
Przeprowadzimy obliczenia dla przedziału [math]\displaystyle{ (4 n, 5 n) }[/math]. Czytelnik w identyczny sposób może powtórzyć obliczenia dla pozostałych przypadków. Mamy
- [math]\displaystyle{ \pi (5 n) - \pi (4 n) \gt a \cdot {\small\frac{5 n}{\log (5 n)}} - b \cdot {\small\frac{4 n}{\log (4 n)}} = }[/math]
- [math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} - {\small\frac{4 b n}{\log (4 n)}} = }[/math]
- [math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log (5 n)}{\log (4 n)}} \right) = }[/math]
- [math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log \left( 4 n \cdot {\small\frac{5}{4}} \right)}{\log (4 n)}} \right) = }[/math]
- [math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log (4 n) + \log (5 / 4)}{\log (4 n)}} \right) = }[/math]
- [math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left[ 1 - {\small\frac{4 b}{5 a}} \cdot \left( 1 + {\small\frac{\log (5 / 4)}{\log (4 n)}} \right) \right] }[/math]
Dla dużych wartości [math]\displaystyle{ n }[/math] wyrażenie w nawiasie zwykłym dąży do [math]\displaystyle{ 1 }[/math], a wyrażenie w nawiasie kwadratowym do [math]\displaystyle{ 0.03999826 \ldots }[/math] Można łatwo sprawdzić, że wypisane oszacowanie [math]\displaystyle{ \pi (5 n) - \pi (4 n) }[/math] jest większe od [math]\displaystyle{ 1 }[/math] dla [math]\displaystyle{ n \geqslant 193 }[/math]. Zatem pozostaje sprawdzenie prawdziwości dowodzonego twierdzenia dla [math]\displaystyle{ 4 n \lt 96098 }[/math].
Dysponując odpowiednio dokładnym oszacowaniem typu
- [math]\displaystyle{ a \cdot {\small\frac{n}{\log n}} \lt \pi (n) \lt b \cdot {\small\frac{n}{\log n}} }[/math]
możemy dla ustalonej liczby [math]\displaystyle{ r }[/math] próbować udowodnić następujące twierdzenie
Twierdzenie B3
Niech [math]\displaystyle{ n, n_0, r \in \mathbb{Z}_+ }[/math]. Istnieje taka liczba [math]\displaystyle{ n_0 }[/math], że dla [math]\displaystyle{ n \geqslant n_0 }[/math] między liczbami [math]\displaystyle{ r n }[/math] oraz [math]\displaystyle{ (r + 1) n }[/math] znajduje się przynajmniej jedna liczba pierwsza.
Dowodząc analogicznie, jak to uczyniliśmy wyżej (w przypadku twierdzenia B2), łatwo możemy pokazać, że aby taki dowód był możliwy musi być spełniony warunek
- [math]\displaystyle{ {\small\frac{b}{a}} \lt {\small\frac{r + 1}{r}} }[/math]
Niestety, elementarny dowód twierdzenia Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math] nie dostarczył nam odpowiednio silnego oszacowania, aby dowód twierdzenia Czebyszewa (czyli twierdzenia B3 w przypadku [math]\displaystyle{ r = 1 }[/math]) był możliwy. Dlatego będziemy musieli to zrobić innym sposobem. Podstawą dowodu będzie dalsze badanie rozwinięcia symbolu Newtona [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze.
Rozpoczniemy od oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math], z którego w przyszłości skorzystamy.
Twierdzenie B4
Dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe są oszacowania:
- 1. [math]\displaystyle{ \pi (n) \underset{n \geqslant 34}{\lt } {\small\frac{n}{3}} }[/math]
- 1. [math]\displaystyle{ \pi (n) \underset{n \geqslant 34}{\lt } {\small\frac{n}{3}} }[/math]
- 2. [math]\displaystyle{ \pi (n) \underset{n \geqslant 15}{\lt } {\small\frac{n}{2}} - 1 }[/math]
Punkt 1.
Indukcja matematyczna. Ponieważ wśród kolejnych sześciu liczb naturalnych, co najwyżej dwie mogą być liczbami pierwszymi, zatem [math]\displaystyle{ \pi (n) \leqslant \pi (n - 6) + 2 }[/math] dla [math]\displaystyle{ n \geqslant 9 . }[/math] Musimy sprawdzić prawdziwość twierdzenia dla kolejnych sześciu liczb naturalnych. Istotnie dla [math]\displaystyle{ n = 34, 35, 36, 37, 38, 39 }[/math] twierdzenie jest prawdziwe. Zakładając prawdziwość twierdzenia dla wszystkich liczb naturalnych należących do przedziału [math]\displaystyle{ [34, n] }[/math] otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ \pi (n + 1) \leqslant \pi (n - 5) + 2 \lt {\small\frac{n - 5}{3}} + 2 = {\small\frac{n + 1}{3}} }[/math]
Co należało pokazać.
Punkt 2.
Ponieważ dla [math]\displaystyle{ n \geqslant 34 }[/math] prawdziwa jest nierówność [math]\displaystyle{ \pi (n) \lt {\small\frac{n}{3}} }[/math], a dla [math]\displaystyle{ n \geqslant 6 }[/math] prawdziwa jest nierówność [math]\displaystyle{ {\small\frac{n}{3}} \leqslant {\small\frac{n}{2}} - 1 }[/math], zatem dla [math]\displaystyle{ n \geqslant 34 }[/math] prawdziwa jest nierówność [math]\displaystyle{ \pi (n) \lt {\small\frac{n}{2}} - 1 }[/math]. Wystarczy sprawdzić jej prawdziwość dla [math]\displaystyle{ 15 \leqslant n \leqslant 33 }[/math].
□
Potrzebne nam też będzie nowe oszacowanie współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] od dołu.
Twierdzenie B5
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwa jest nierówność [math]\displaystyle{ {\small\binom{2n}{n}} \gt {\small\frac{4^n}{2 n}} }[/math]
Łatwo zauważamy, że
- [math]\displaystyle{ {\small\binom{2n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = \left( \overset{n}{\underset{k = 1}{\prod}} {\small\frac{2 k}{k}} \right) \cdot \left( \overset{n - 1}{\underset{k = 1}{\prod}} {\small\frac{2 k + 1}{k}} \right) \cdot {\small\frac{1}{n}} \gt {\small\frac{2^{2 n - 1}}{n}} = {\small\frac{2^{2 n}}{2 n}} }[/math]
Iloczyn w pierwszym nawiasie uwzględnia wszystkie liczby parzyste licznika od [math]\displaystyle{ 2 }[/math] do [math]\displaystyle{ 2 n }[/math], a każdy czynnik tego iloczynu jest równy [math]\displaystyle{ 2 }[/math]. Iloczyn w drugim nawiasie uwzględnia wszystkie liczby nieparzyste licznika od [math]\displaystyle{ 3 }[/math] do [math]\displaystyle{ 2 n - 1 }[/math]. Każdy czynnik tego iloczynu jest większy od [math]\displaystyle{ 2 }[/math]. Wynika stąd natychmiast wypisana nierówność.
□
Poniższe twierdzenie zostało już udowodnione (zobacz twierdzenie A25[3]), ale przedstawimy tutaj inny dowód.
Twierdzenie B6
Liczby pierwsze [math]\displaystyle{ p \gt \sqrt{2 n} }[/math] występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u = 0 }[/math] lub [math]\displaystyle{ u = 1 }[/math].
Z twierdzenia A26 wiemy, że jeżeli liczba pierwsza [math]\displaystyle{ p }[/math] występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] z wykładnikiem [math]\displaystyle{ u }[/math], to [math]\displaystyle{ p^u \leqslant 2 n }[/math]. Gdyby liczba pierwsza [math]\displaystyle{ p \gt \sqrt{2 n} }[/math] występowała w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u \geqslant 2 }[/math], to mielibyśmy [math]\displaystyle{ p^u \geqslant p^2 \gt 2 n }[/math]. Co jest niemożliwe.
□
Następne twierdzenie jest prostym wnioskiem z twierdzenia A45 (przypadek dla [math]\displaystyle{ k = 1 }[/math]), ale załączyliśmy dowód dla tego konkretnego przypadku.
Twierdzenie B7
Jeżeli [math]\displaystyle{ n \geqslant 3 }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left ( \tfrac{2}{3} n, n \right ] }[/math], to [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze.
Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]
Zauważmy, że liczba pierwsza [math]\displaystyle{ p = 2 }[/math] nie spełnia warunku [math]\displaystyle{ p \in \left ( \tfrac{2}{3} n, n \right ] }[/math] dla [math]\displaystyle{ n \geqslant 3 }[/math].
Zapiszmy liczbę [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] w postaci ułamka:
- [math]\displaystyle{ {\small\binom{2n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]
Rozważmy dowolną liczbę pierwszą [math]\displaystyle{ p }[/math] występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:
- [math]\displaystyle{ p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej jeden raz w mianowniku
- [math]\displaystyle{ 2 p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie jeden raz w mianowniku
- [math]\displaystyle{ 2 p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej jeden raz w liczniku
- [math]\displaystyle{ 3 p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie raz w liczniku (jako [math]\displaystyle{ 2 p }[/math])
Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left ( \tfrac{2}{3} n, n \right ] }[/math] pojawia się dokładnie jeden raz w mianowniku i dokładnie jeden raz w liczniku ułamka
- [math]\displaystyle{ {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]
Zatem liczba pierwsza [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze.
Dowód na podstawie twierdzenia A24
Rozważmy najpierw pierwszy składnik sumy
- [math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor {\small\frac{2 n}{p^{k}}} \right \rfloor - 2 \left \lfloor {\small\frac{n}{p^{k}}} \right \rfloor \right ) }[/math]
Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 0 }[/math], to będziemy szukali oszacowania od góry. Z założenia mamy
- 1) [math]\displaystyle{ p \gt {\small\frac{2 n}{3}} \qquad \Longrightarrow \qquad {\small\frac{2 n}{p}} \lt 3 \qquad \Longrightarrow \qquad \left\lfloor {\small\frac{2 n}{p}} \right\rfloor \leqslant 2 }[/math]
- 2) [math]\displaystyle{ p \leqslant n \qquad \;\:\, \Longrightarrow \qquad {\small\frac{n}{p}} \geqslant 1 \qquad \;\: \Longrightarrow \qquad \left\lfloor {\small\frac{n}{p}} \right\rfloor \geqslant 1 }[/math]
Zatem
- [math]\displaystyle{ \left\lfloor {\small\frac{2 n}{p}} \right\rfloor - 2 \left\lfloor {\small\frac{n}{p}} \right\rfloor \leqslant 2 - 2 = 0 }[/math]
Ponieważ każdy ze składników szukanej sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy
- [math]\displaystyle{ \left\lfloor {\small\frac{2 n}{p}} \right\rfloor - 2 \left\lfloor {\small\frac{n}{p}} \right\rfloor = 0 }[/math]
Założenie, że [math]\displaystyle{ n \geqslant 5 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy
- [math]\displaystyle{ p \gt {\small\frac{2 n}{3}} \qquad \Longrightarrow \qquad {\small\frac{(2 n)^k}{p^k}} \lt 3^k }[/math]
- [math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \lt {\small\frac{9}{2 n}} \cdot \left( {\small\frac{3}{2 n}} \right)^{k - 2} }[/math]
- [math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \leqslant {\small\frac{9}{2 n}} }[/math]
- [math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \leqslant {\small\frac{9}{10}} }[/math]
- [math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad \left\lfloor {\small\frac{2 n}{p^k}} \right\rfloor = 0 }[/math]
Jeżeli [math]\displaystyle{ \left\lfloor {\small\frac{2 n}{p^k}} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor {\small\frac{n}{p^k}} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 5 }[/math] jest
- [math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor {\small\frac{2 n}{p^{k}}} \right \rfloor - 2 \left \lfloor {\small\frac{n}{p^{k}}} \right \rfloor \right ) = 0 }[/math]
Dla [math]\displaystyle{ n = 3 \; }[/math] i [math]\displaystyle{ \; n = 4 }[/math] łatwo sprawdzamy, że liczba [math]\displaystyle{ 3 }[/math] nie dzieli liczb [math]\displaystyle{ {\small\binom{6}{3}} = 20 }[/math] oraz [math]\displaystyle{ {\small\binom{8}{4}} = 70 }[/math]. Zatem dla [math]\displaystyle{ n \geqslant 3 }[/math] liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{2}{3} n, n \right] }[/math] nie dzieli liczby [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math].
□
Twierdzenie B8
Każda liczba pierwsza [math]\displaystyle{ p \in (n, 2 n] }[/math] występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u = 1 }[/math].
Każda liczba pierwsza [math]\displaystyle{ p \in (n, 2 n] }[/math] występuje dokładnie jeden raz w liczniku ułamka
- [math]\displaystyle{ {\small\binom{2 n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]
i nie występuje w mianowniku. Zatem w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze wystąpi z wykładnikiem [math]\displaystyle{ u = 1 }[/math].
□
Przykład B9
Nawiasami [math]\displaystyle{ (), [], \{ \} }[/math] zaznaczyliśmy liczby pierwsze należące odpowiednio do przedziałów [math]\displaystyle{ \left( \sqrt{2 n}, \tfrac{2}{3} n \right] }[/math], [math]\displaystyle{ \left( \tfrac{2}{3} n, n \right] }[/math], [math]\displaystyle{ (n, 2 n] }[/math]. Zauważmy, że istnieją liczby pierwsze [math]\displaystyle{ p \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right] }[/math], które nie występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze. Zaznaczyliśmy je grubą czcionką.
- [math]\displaystyle{ {\small\binom{20}{10}} = 2^2 \cdot (\mathbf{5^0}) \cdot [7^0] \cdot \{ 11^1 \cdot 13^1 \cdot 17^1 \cdot 19^1 \} }[/math]
- [math]\displaystyle{ {\small\binom{42}{21}} = 2^3 \cdot 3^1 \cdot 5^1 \cdot (\mathbf{7^0} \cdot 11^1 \cdot 13^1) \cdot [17^0 \cdot 19^0] \cdot \{ 23^1 \cdot 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \} }[/math]
- [math]\displaystyle{ {\small\binom{48}{24}} = 2^2 \cdot 3^2 \cdot 5^2 \cdot (\mathbf{7^0} \cdot \mathbf{11^0} \cdot 13^1) \cdot [17^0 \cdot 19^0 \cdot 23^0] \cdot \{ 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \} }[/math]
- [math]\displaystyle{ {\small\binom{60}{30}} = 2^4 \cdot 7^1 \cdot (11^1 \cdot \mathbf{13^0} \cdot 17^1 \cdot 19^1) \cdot [23^0 \cdot 29^0] \cdot \{ 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \cdot 53^1 \cdot 59^1 \} }[/math]
Twierdzenie B10
Niech [math]\displaystyle{ n \geqslant 15 }[/math]. Dla iloczynu liczb pierwszych [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u }[/math] występujących w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze i spełniających warunek [math]\displaystyle{ p_i \in (n, 2 n] }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
Zapiszmy rozwinięcie współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze w postaci:
- [math]\displaystyle{ {\small\binom{2 n}{n}} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u) }[/math]
gdzie liczby pierwsze [math]\displaystyle{ r_i }[/math], [math]\displaystyle{ q_i }[/math], [math]\displaystyle{ p_i }[/math] spełniają warunki: [math]\displaystyle{ r_i \in \left[ 2, \sqrt{2 n} \right] }[/math], [math]\displaystyle{ \; q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right] \; }[/math] i [math]\displaystyle{ \; p_i \in (n, 2 n] }[/math]. Pominęliśmy liczby pierwsze należące do przedziału [math]\displaystyle{ \left( \tfrac{2}{3} n, n \right] }[/math], bo z twierdzenia B7 wiemy, że nie występują one w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze.
Zauważmy:
1) z twierdzenia A26 wiemy, że [math]\displaystyle{ r^{a_i}_i \leqslant 2 n }[/math], zatem
- [math]\displaystyle{ r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s \leqslant (2 n)^s \leqslant (2 n)^{\pi \left( \sqrt{2 n} \right)} \lt (2 n)^{\sqrt{2 n} / 2 - 1} }[/math]
gdzie skorzystaliśmy z oszacowania [math]\displaystyle{ \pi (n) \lt {\small\frac{n}{2}} - 1 }[/math] prawdziwego dla [math]\displaystyle{ n \geqslant 15 }[/math] (twierdzenie B4 punkt 2).
2) z twierdzenia B6 wiemy, że czynniki [math]\displaystyle{ q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right] }[/math] występują z wykładnikiem równym [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], zatem:
- [math]\displaystyle{ q_1 \cdot \ldots \cdot q_t \leqslant \frac{P \left( {\small\frac{2}{3}} n \right)}{P \left( \sqrt{2 n} \right)} \lt P \left( \tfrac{2}{3} n \right) \lt 4^{2 n / 3} }[/math]
gdzie ostatnia nierówność wynika z twierdzenia A9.
3) z twierdzenia B5 wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ {\small\binom{2 n}{n}} \gt {\small\frac{4^n}{2 n}} }[/math]
Z punktów 1) - 3) wynika, że dla rozwinięcia współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ {\small\frac{4^n}{2 n}} \lt {\small\binom{2 n}{n}} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u) \lt (2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u) }[/math]
Skąd otrzymujemy natychmiast:
- [math]\displaystyle{ (2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u) \gt {\small\frac{4^n}{2 n}} }[/math]
- [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u \gt {\small\frac{4^n}{2 n}} \cdot (2 n)^{- \sqrt{2 n} / 2 + 1} \cdot 4^{- 2 n / 3} = 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
- [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u \gt {\small\frac{4^n}{2 n}} \cdot (2 n)^{- \sqrt{2 n} / 2 + 1} \cdot 4^{- 2 n / 3} = 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
□
Twierdzenie B11
Dla [math]\displaystyle{ n \geqslant 15 }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
W twierdzeniu B10 pokazaliśmy, że dla iloczynu liczb pierwszych [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u }[/math] występujących w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze i spełniających warunek [math]\displaystyle{ p_i \in (n, 2 n] }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
Zauważmy, że liczby pierwsze [math]\displaystyle{ p_i }[/math] występują z wykładnikiem równym [math]\displaystyle{ 1 }[/math] (twierdzenie B8) i iloczyn [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u }[/math] jest iloczynem wszystkich liczb [math]\displaystyle{ p_i \in (n, 2 n] }[/math], bo każda liczba pierwsza [math]\displaystyle{ p_i \in (n, 2 n] }[/math] występuje w liczniku ułamka
- [math]\displaystyle{ {\small\binom{2 n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]
i nie występuje w mianowniku. Wynika stąd natychmiast, że:
- [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} = p_1 \cdot \ldots \cdot p_u \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
- [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} = p_1 \cdot \ldots \cdot p_u \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
□
Twierdzenie B12
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Prawdziwe jest oszacowanie
- [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 2^{n / 2} }[/math]
Z twierdzenia B11 wiemy, że dla dowolnego [math]\displaystyle{ n \geqslant 15 }[/math] jest
- [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]
Chcemy pokazać, że
- [math]\displaystyle{ 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} \gt 2^{n / 2} }[/math]
Logarytmując tę nierówność, otrzymujemy
- [math]\displaystyle{ {\small\frac{2 n}{3}} \cdot \log 2 - {\small\frac{\sqrt{2 n}}{2}} \cdot \log (2 n) \gt {\small\frac{n}{2}} \cdot \log 2 }[/math]
- [math]\displaystyle{ {\small\frac{\sqrt{2 n}}{2}} \cdot \log (2 n) \lt {\small\frac{n}{6}} \cdot \log 2 }[/math]
- [math]\displaystyle{ \log (2 n) \lt {\small\frac{\log 2}{6}} \cdot \sqrt{2 n} }[/math]
Zamieszczony niżej obrazek prezentuje wykres funkcji [math]\displaystyle{ f(n) = {\small\frac{\log 2}{6}} \cdot \sqrt{2 n} - \log (2 n) }[/math]
Wpisując w PARI/GP polecenie
solve(n = 2000, 4000, log(2)/6 * sqrt(2*n) - log(2*n))
znajdujemy, że funkcja [math]\displaystyle{ f(n) }[/math] jest większa od zera dla [math]\displaystyle{ n \gt 2787.755 }[/math]
Pozostaje sprawdzić, przez bezpośrednie obliczenie, prawdziwość nierówności
- [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 2^{n / 2} }[/math]
dla wszystkich [math]\displaystyle{ n \leqslant 2787 }[/math]. W programie PARI/GP wystarczy napisać polecenia
P(n) = prod(k = 2, n, if( isprime(k), k, 1 )) \\ definicja funkcji P(n)
for(n = 1, 2788, if( P(2*n)/P(n) <= 2^(n/2), print(n) ))
□
Uwaga B13
Dowodząc analogicznie jak w twierdzeniu B12, moglibyśmy bez trudu pokazać, że dla [math]\displaystyle{ n \geqslant 6 }[/math] prawdziwe jest silniejsze oszacowanie [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 2^{3 n / 5} }[/math].
Twierdzenie B14
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (2 n) - \pi (n) \gt {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}} }[/math]
Korzystając z twierdzenia B12, możemy napisać
- [math]\displaystyle{ 2^{n / 2} \lt {\small\frac{P (2 n)}{P (n)}} \lt (2 n)^{\pi (2 n) - \pi (n)} }[/math]
Oszacowanie z prawej jest oczywiste. Logarytmując obie strony, otrzymujemy
- [math]\displaystyle{ {\small\frac{n}{2}} \cdot \log 2 \lt [\pi (2 n) - \pi (n)] \cdot \log 2 n }[/math]
a stąd łatwo wyliczamy różnicę [math]\displaystyle{ \pi (2 n) - \pi (n) }[/math].
□
Korzystając ze znalezionego oszacowania, udowodnimy
Twierdzenie B15
Przedział otwarty [math]\displaystyle{ (n, 2 n) }[/math] zawiera co najmniej
- jedną liczbę pierwszą, o ile [math]\displaystyle{ n \geqslant 2 }[/math]
- dwie liczby pierwsze, o ile [math]\displaystyle{ n \geqslant 6 }[/math]
- trzy liczby pierwsze, o ile [math]\displaystyle{ n \geqslant 9 }[/math]
- cztery liczby pierwsze, o ile [math]\displaystyle{ n \geqslant 15 }[/math]
- pięć liczb pierwszych, o ile [math]\displaystyle{ n \geqslant 21 }[/math]
- sześć liczb pierwszych, o ile [math]\displaystyle{ n \geqslant 24 }[/math]
Z twierdzenia B14 wiemy, że
- [math]\displaystyle{ \pi (2 n) - \pi (n) \gt {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}} }[/math]
Łatwo sprawdzamy dla jakich wartości [math]\displaystyle{ n }[/math] funkcja [math]\displaystyle{ {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}} }[/math] jest większa od [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], itd. Wyniki zabraliśmy w tabelce:
- [math]\displaystyle{ \begin{array}{|c|c|c|c|c|c|c|} \hline {\normalsize\frac{\log 2}{2}} \cdot {\normalsize\frac{n}{\log 2 n}} & \gt 1 & \gt 2 & \gt 3 & \gt 4 & \gt 5 & \gt 6\\ \hline \text{dla } n & \geqslant 9 & \geqslant 22 & \geqslant 38 & \geqslant 55 & \geqslant 72 & \geqslant 90\\ \hline \end{array} }[/math]
Bezpośrednie sprawdzenie dla [math]\displaystyle{ 2 \leqslant n \leqslant 8 }[/math] kończy dowód twierdzenia Czebyszewa. Analogicznie kończymy dowody pozostałych pozycji.
□
Uwagi do twierdzenia
Już pod koniec XVIII wieku Gauss i Legendre przypuszczali, że [math]\displaystyle{ {\small\frac{n}{\log n}} }[/math] jest dobrym przybliżeniem wartości funkcji [math]\displaystyle{ \pi (n) }[/math].
|
Obecnie wiemy, że dokładnie tak jest[4]
|
Jeśli tak, to ilość liczb pierwszych w przedziale [math]\displaystyle{ (n, 2 n] }[/math] jest tego samego rzędu, co ilość liczb pierwszych w przedziale [math]\displaystyle{ (1, n] }[/math]. Istotnie
- [math]\displaystyle{ \pi (n) \approx {\small\frac{n}{\log n}} }[/math]
- [math]\displaystyle{ \;\;\; = {\small\frac{n}{\log n}} \cdot {\small\frac{\log n + \log 2}{\log (2 n)}} }[/math]
- [math]\displaystyle{ \;\;\; = {\small\frac{n}{\log (2 n)}} \cdot \left( 1 + {\small\frac{\log 2}{\log n}} \right) }[/math]
- [math]\displaystyle{ \pi (2 n) - \pi (n) \approx {\small\frac{2 n}{\log (2 n)}} - {\small\frac{n}{\log n}} }[/math]
- [math]\displaystyle{ \;\: = {\small\frac{2 n}{\log (2 n)}} - {\small\frac{n}{\log (2 n)}} \cdot \left( 1 + {\small\frac{\log 2}{\log n}} \right) }[/math]
- [math]\displaystyle{ \;\: = {\small\frac{n}{\log (2 n)}} \cdot \left( 1 - {\small\frac{\log 2}{\log n}} \right) }[/math]
Zatem przypuszczenie, że między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się przynajmniej jedna liczba pierwsza, jest bardzo słabym oczekiwaniem.
Co więcej, począwszy od pewnego [math]\displaystyle{ n_0 }[/math] między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje przynajmniej jedna liczba będąca kwadratem, sześcianem, czwartą i piątą potęgą liczby naturalnej. Liczby [math]\displaystyle{ n^2 }[/math], [math]\displaystyle{ n^3 }[/math], [math]\displaystyle{ n^4 }[/math] czy [math]\displaystyle{ n^5 }[/math] występują znacznie rzadziej niż liczby pierwsze [math]\displaystyle{ p_n \approx n \log n }[/math].
Pokażemy też, że twierdzenie Czebyszewa wynika ze sformułowanej w 1742 roku hipotezy Goldbacha. Oczywiście ścisły dowód twierdzenia Czebyszewa stał się możliwy dopiero po znalezieniu dokładnego oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math].
Twierdzenie B16
Niech [math]\displaystyle{ n, k, k_0 \in \mathbb{Z}_+ }[/math] i [math]\displaystyle{ f(k) }[/math] będzie funkcją rosnącą o wartościach całkowitych dodatnich. Jeżeli spełnione są warunki
- 1) [math]\displaystyle{ \quad f(k + 1) \lt 2 f (k) \quad }[/math] dla [math]\displaystyle{ \quad k \geqslant k_0 }[/math]
- 2) [math]\displaystyle{ \quad n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 }[/math]
to między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba należąca do zbioru wartości funkcji [math]\displaystyle{ f(k) }[/math].
Niech [math]\displaystyle{ n \geqslant f (k_0) }[/math], a liczba [math]\displaystyle{ k \geqslant k_0 }[/math] będzie największą liczbą taką, że [math]\displaystyle{ f(k) \leqslant n }[/math]. Z określenia liczby [math]\displaystyle{ k }[/math] i założenia twierdzenia prawdziwy jest ciąg nierówności
- [math]\displaystyle{ f(k) \leqslant n \lt f (k + 1) \lt 2 f (k) \leqslant 2 n }[/math]
Zatem między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba należąca do zbioru wartości funkcji [math]\displaystyle{ f(k) }[/math].
W szczególności liczba [math]\displaystyle{ f(k_0) }[/math] leży między liczbami [math]\displaystyle{ \; \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + j \; }[/math] oraz [math]\displaystyle{ \; 2 \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 2 j \; }[/math] dla [math]\displaystyle{ \; j = 1, 2, \ldots, f (k_0) - \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor - 1 }[/math].
Łatwo sprawdzamy, że dla kolejnej liczby [math]\displaystyle{ j = f (k_0) - \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor }[/math] liczba [math]\displaystyle{ f(k_0) }[/math] nie leży między liczbami [math]\displaystyle{ f(k_0) }[/math] oraz [math]\displaystyle{ 2 f (k_0) }[/math] — między tymi liczbami leży liczba [math]\displaystyle{ f(k_0 + 1) }[/math].
Wynika stąd, że twierdzenie jest prawdziwe dla liczb [math]\displaystyle{ n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 }[/math].
□
Zadanie B17
Niech [math]\displaystyle{ x \in \mathbb{R} }[/math]. Dla [math]\displaystyle{ n \geqslant 1 }[/math] oraz [math]\displaystyle{ x \gt {\small\frac{1}{\sqrt[n]{2} - 1}} }[/math] prawdziwa jest nierówność [math]\displaystyle{ 2 x^n \gt (x + 1)^n }[/math].
Z założenia
- [math]\displaystyle{ \left( \sqrt[n]{2} - 1 \right) x \gt 1 }[/math]
- [math]\displaystyle{ x \cdot \sqrt[n]{2} \gt x + 1 }[/math]
Podnosząc obie strony nierówności do [math]\displaystyle{ n }[/math]-tej potęgi, otrzymujemy
- [math]\displaystyle{ \left( x \cdot \sqrt[n]{2} \right)^n \gt (x + 1)^n }[/math]
Czyli
- [math]\displaystyle{ 2 x^n \gt (x + 1)^n }[/math]
Co należało pokazać.
□
Twierdzenie B18
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math]. Jeżeli [math]\displaystyle{ n \geqslant 5 }[/math], to między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba będąca kwadratem liczby naturalnej.
Funkcja [math]\displaystyle{ f(k) = k^2 }[/math] jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania B17 łatwo stwierdzamy, że warunek z twierdzenia B16
- [math]\displaystyle{ (k + 1)^2 \lt 2 k^2 }[/math]
jest spełniony dla
- [math]\displaystyle{ k_0 = \left\lfloor {\small\frac{1}{\sqrt{2} - 1}} \right\rfloor + 1 = 3 }[/math]
Twierdzenie jest prawdziwe dla liczb
- [math]\displaystyle{ n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 = \left\lfloor {\small\frac{9}{2}} \right\rfloor + 1 = 5 }[/math]
Co kończy dowód.
□
Twierdzenie B19
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math]. Jeżeli [math]\displaystyle{ n \geqslant 33 }[/math], to między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba będąca sześcianem liczby naturalnej.
Funkcja [math]\displaystyle{ f(k) = k^3 }[/math] jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania B17 łatwo stwierdzamy, że warunek z twierdzenia B16
- [math]\displaystyle{ (k + 1)^3 \lt 2 k^3 }[/math]
jest spełniony dla
- [math]\displaystyle{ k_0 = \left\lfloor {\small\frac{1}{\sqrt[3]{2} - 1}} \right\rfloor + 1 = 4 }[/math]
Twierdzenie jest prawdziwe dla liczb
- [math]\displaystyle{ n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 = \left\lfloor {\small\frac{64}{2}} \right\rfloor + 1 = 33 }[/math]
Co kończy dowód.
□
Podobnie możemy udowodnić, że dla [math]\displaystyle{ n \geqslant 649 }[/math] (odpowiednio: [math]\displaystyle{ n \geqslant 8404 }[/math]) między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba będąca czwartą (odpowiednio: piątą) potęgą liczby naturalnej. Oczywiście analogiczne twierdzenie możemy sformułować dla dowolnej funkcji [math]\displaystyle{ f(k) = k^u }[/math], gdzie [math]\displaystyle{ u \in \mathbb{Z}_+ }[/math].
Bez trudu pokażemy też, że twierdzenie Czebyszewa wynika z ponad sto lat od niego starszej hipotezy Goldbacha[5]. Hipoteza Goldbacha może być sformułowana w różny sposób, poniżej przedstawimy te formuły i udowodnimy ich równoważność.
Twierdzenie B20 (hipoteza Goldbacha, 1742)
Następujące warunki są równoważne
- [math]\displaystyle{ ( \text{G1} ) }[/math] Każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 4 }[/math] jest sumą dwóch liczb pierwszych
- [math]\displaystyle{ ( \text{G2} ) }[/math] Każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 6 }[/math] jest sumą dwóch liczb pierwszych nieparzystych
- [math]\displaystyle{ ( \text{G3} ) }[/math] Każda liczba naturalna [math]\displaystyle{ n \geqslant 6 }[/math] jest sumą trzech liczb pierwszych
Pokażemy równoważność warunków [math]\displaystyle{ ( \text{G1} ) }[/math] i [math]\displaystyle{ ( \text{G2} ) }[/math], a następnie równoważność warunków [math]\displaystyle{ ( \text{G1} ) }[/math] i [math]\displaystyle{ ( \text{G3} ) }[/math]
[math]\displaystyle{ ( \text{G1} ) \quad \implies \quad ( \text{G2} ) }[/math]
Z założenia każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 4 }[/math] jest sumą dwóch liczb pierwszych, czyli [math]\displaystyle{ n = 2 k = p + q }[/math], gdzie [math]\displaystyle{ p, q }[/math] są liczbami pierwszymi. Zauważmy, że liczby [math]\displaystyle{ p, q }[/math] muszą mieć taką samą parzystość. Ponieważ istnieje tylko jedna liczba pierwsza parzysta, to istnieje tylko jedna liczba naturalna, która jest sumą dwóch liczb pierwszych parzystych. Oczywiście jest to liczba [math]\displaystyle{ 4 = 2 + 2 }[/math]. Wszystkie liczby naturalne parzyste większe od [math]\displaystyle{ 4 }[/math] muszą być sumą dwóch liczb pierwszych nieparzystych.
[math]\displaystyle{ ( \text{G2} ) \quad \implies \quad ( \text{G1} ) }[/math]
Z założenia każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 6 }[/math] jest sumą dwóch liczb pierwszych. Ponieważ [math]\displaystyle{ 4 = 2 + 2 }[/math] jest sumą dwóch liczb pierwszych, to każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 4 }[/math] jest sumą dwóch liczb pierwszych.
[math]\displaystyle{ ( \text{G1} ) \quad \implies \quad ( \text{G3} ) }[/math]
Z założenia dla każdego [math]\displaystyle{ k \geqslant 3 }[/math] jest [math]\displaystyle{ n = 2 k - 2 = p + q }[/math], gdzie [math]\displaystyle{ p, q }[/math] są liczbami pierwszymi. Zatem [math]\displaystyle{ 2 k = p + q + 2 }[/math] oraz [math]\displaystyle{ 2 k + 1 = p + q + 3 }[/math].
[math]\displaystyle{ ( \text{G3} ) \quad \implies \quad ( \text{G1} ) }[/math]
Z założenia dla każdego [math]\displaystyle{ k \geqslant 3 }[/math] jest [math]\displaystyle{ n = 2 k = p + q + r }[/math], gdzie [math]\displaystyle{ p, q, r }[/math] są liczbami pierwszymi. Wypisana równość nie jest możliwa w przypadku, gdy wszystkie liczby [math]\displaystyle{ p, q, r }[/math] są nieparzyste. Niech [math]\displaystyle{ r = 2 }[/math]
będzie liczbą pierwszą parzystą, wtedy [math]\displaystyle{ 2 k - 2 = p + q }[/math].
□
Twierdzenie B21
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math] i [math]\displaystyle{ n \geqslant 2 }[/math]. Jeżeli prawdziwa jest hipoteza Goldbacha, to między [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się co najmniej jedna liczba pierwsza.
Rozważmy liczbę [math]\displaystyle{ 2 n + 2 }[/math] dla [math]\displaystyle{ n \geqslant 2 }[/math]. Z hipotezy Goldbacha [math]\displaystyle{ ( \text{G2} ) }[/math] wynika, że [math]\displaystyle{ 2 n + 2 = p + q }[/math] jest sumą dwóch liczb pierwszych nieparzystych.
Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ p \leqslant q }[/math], zatem
- [math]\displaystyle{ 2 n + 2 = p + q \leqslant 2 q }[/math]
Czyli [math]\displaystyle{ q \geqslant n + 1 }[/math]. Ponieważ [math]\displaystyle{ p \geqslant 3 }[/math], to z drugiej strony mamy
- [math]\displaystyle{ 2 n + 2 = p + q \geqslant q + 3 }[/math]
Czyli [math]\displaystyle{ q \leqslant 2 n - 1 }[/math]. Zatem [math]\displaystyle{ n + 1 \leqslant q \leqslant 2 n - 1 }[/math], co oznacza, że [math]\displaystyle{ n \lt q \lt 2 n }[/math].
□
Zastosowania
Twierdzenie B22
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Prawdziwe jest oszacowanie [math]\displaystyle{ p_{n + 1} \lt 2 p_n }[/math].
Z twierdzenia Czebyszewa wiemy, że między liczbami [math]\displaystyle{ p_n }[/math] i [math]\displaystyle{ 2 p_n }[/math] znajduje się przynajmniej jedna liczba pierwsza [math]\displaystyle{ q }[/math]. Ponieważ [math]\displaystyle{ q \gt p_n }[/math], to musi być [math]\displaystyle{ q \geqslant p_{n + 1} }[/math]. Otrzymujemy ciąg nierówności
- [math]\displaystyle{ p_n \lt p_{n + 1} \leqslant q \lt 2 p_n }[/math]
Skąd wynika natychmiast, że [math]\displaystyle{ p_{n + 1} \lt 2 p_n }[/math].
□
Prawdziwe jest również twierdzenie odwrotne.
Twierdzenie B23
Niech [math]\displaystyle{ k, n \in \mathbb{Z}_+ }[/math]. Jeżeli dla każdego [math]\displaystyle{ k }[/math] prawdziwa jest nierówność [math]\displaystyle{ p_{k + 1} \lt 2 p_k }[/math], to dla dowolnego [math]\displaystyle{ n \geqslant 2 }[/math] między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się co najmniej jedna liczba pierwsza.
Ponieważ [math]\displaystyle{ n \geqslant 2 }[/math], to istnieje co najmniej jedna liczba pierwsza [math]\displaystyle{ q }[/math] taka, że [math]\displaystyle{ q \leqslant n }[/math]. Niech [math]\displaystyle{ p_k }[/math] oznacza największą liczbę pierwszą ze zbioru liczb [math]\displaystyle{ q }[/math] spełniających warunek [math]\displaystyle{ q \leqslant n }[/math]. Z definicji liczby [math]\displaystyle{ p_k }[/math] wynika natychmiast, że musi być [math]\displaystyle{ p_{k + 1} \gt n }[/math]. Konsekwentnie otrzymujemy ciąg nierówności
- [math]\displaystyle{ p_k \leqslant n \lt p_{k + 1} \lt 2 p_k \leqslant 2 n }[/math]
gdzie skorzystaliśmy z założonej prawdziwości oszacowania [math]\displaystyle{ p_{k + 1} \lt 2 p_k }[/math]. Zatem między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się liczba pierwsza [math]\displaystyle{ p_{k + 1} }[/math].
□
Twierdzenie B24
Niech [math]\displaystyle{ n \geqslant 3 }[/math]. Prawdziwe jest oszacowanie [math]\displaystyle{ p_{n + 1} \lt p_n + p_{n - 1} }[/math].
Z twierdzenia B15 (punkt 2) wiemy, że dla [math]\displaystyle{ k \geqslant 6 }[/math] między liczbami [math]\displaystyle{ k }[/math] i [math]\displaystyle{ 2 k }[/math] znajdują się co najmniej dwie liczby pierwsze. Zatem dla [math]\displaystyle{ n \geqslant 5 }[/math] w przedziale [math]\displaystyle{ (p_{n - 1}, 2 p_{n - 1}) }[/math] znajduje się co najmniej dwie liczby pierwsze [math]\displaystyle{ q }[/math] i [math]\displaystyle{ r }[/math]. Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ q \lt r }[/math]. Ponieważ [math]\displaystyle{ q \gt p_{n - 1} }[/math], to musi być [math]\displaystyle{ q \geqslant p_n }[/math], a ponieważ [math]\displaystyle{ r \gt q \geqslant p_n }[/math], to musi być [math]\displaystyle{ r \geqslant p_{n + 1} }[/math]. Łącząc powyższe spostrzeżenia, otrzymujemy ciąg nierówności
- [math]\displaystyle{ p_{n - 1} \lt p_n \lt p_{n + 1} \leqslant r \lt 2 p_{n - 1} \lt p_n + p_{n - 1} }[/math]
Zatem [math]\displaystyle{ p_{n + 1} \lt p_n + p_{n - 1} }[/math]. Dla [math]\displaystyle{ n \lt 5 }[/math] nierówność sprawdzamy bezpośrednio.
□
Zadanie B25
Jeżeli [math]\displaystyle{ p }[/math] i [math]\displaystyle{ q }[/math] są różnymi liczbami pierwszymi, to [math]\displaystyle{ p q \gt p + q }[/math].
Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ p \lt q }[/math]. Zatem [math]\displaystyle{ p \geqslant 2 }[/math] i [math]\displaystyle{ q \geqslant 3 }[/math]. Łatwo znajdujemy, że
- [math]\displaystyle{ {\small\frac{1}{p}} + {\small\frac{1}{q}} \leqslant {\small\frac{1}{2}} + {\small\frac{1}{3}} \lt 1 }[/math]
skąd natychmiast otrzymujemy, że [math]\displaystyle{ p q \gt p + q }[/math].
□
Zadanie B26
Niech [math]\displaystyle{ n \geqslant 2 }[/math]. Pokazać, że prawdziwe jest oszacowanie [math]\displaystyle{ p_{n + 1} \lt p_n \cdot p_{n - 1} }[/math].
Zadanie B27
Niech [math]\displaystyle{ n }[/math] będzie dowolną liczbą naturalną, a [math]\displaystyle{ p_k }[/math] oznacza największą liczbę pierwszą mniejszą od [math]\displaystyle{ n }[/math]. Pokazać, że tylko dla [math]\displaystyle{ n = 5 }[/math] spełnione jest równanie
- [math]\displaystyle{ n = p_k + p_{k - 1} }[/math]
Równanie nie może być spełnione dla [math]\displaystyle{ n \leqslant 3 }[/math], bo nie istnieją dwie różne liczby pierwsze mniejsze od takich liczb [math]\displaystyle{ n }[/math]. Sprawdzamy, że równanie nie jest spełnione dla [math]\displaystyle{ n = 4 }[/math]. Niech [math]\displaystyle{ n \geqslant 6 }[/math]. Zauważmy, że teraz [math]\displaystyle{ p_k \geqslant 5 }[/math], czyli [math]\displaystyle{ k \geqslant 3 }[/math]. Z określenia liczby [math]\displaystyle{ p_k }[/math] i twierdzenia B24 prawdziwy jest ciąg nierówności
- [math]\displaystyle{ p_k \lt n \leqslant p_{k + 1} \lt p_k + p_{k - 1} }[/math]
Zatem liczba [math]\displaystyle{ n \geqslant 6 }[/math] nie może być sumą dwóch największych liczb pierwszych od niej mniejszych [math]\displaystyle{ p_k }[/math] i [math]\displaystyle{ p_{k - 1} }[/math], gdzie [math]\displaystyle{ p_k \lt n \leqslant p_{k + 1} }[/math].
□
Twierdzenie B28
Jeżeli [math]\displaystyle{ n \in \mathbb{Z} }[/math] i [math]\displaystyle{ n \geqslant 2 }[/math], to w przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza.
Z twierdzenia Czebyszewa wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] w przedziale [math]\displaystyle{ (n, 2 n) }[/math] znajduje się przynajmniej jedna liczba pierwsza. Zatem jeżeli [math]\displaystyle{ n \geqslant 4 }[/math] jest liczbą parzystą, to w przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right) \subset \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się co najmniej jedna liczba pierwsza. Jeżeli [math]\displaystyle{ n \geqslant 3 }[/math] jest liczbą nieparzystą, to w przedziale [math]\displaystyle{ \left( {\small\frac{n + 1}{2}}, n + 1 \right) = \left( {\small\frac{n + 1}{2}}, n \right] \subset \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Wynika stąd, że bez względu na parzystość liczby [math]\displaystyle{ n }[/math], dla [math]\displaystyle{ n \geqslant 3 }[/math] w przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Oczywiście dla [math]\displaystyle{ n = 2 }[/math] twierdzenie również jest prawdziwe.
□
Twierdzenie B29
Dla [math]\displaystyle{ n \geqslant 2 }[/math] liczby [math]\displaystyle{ n! }[/math] nie można przedstawić w postaci potęgi liczby naturalnej o wykładniku wyższym niż [math]\displaystyle{ 1 }[/math].
Z twierdzenia A42 wiemy, że każda liczba pierwsza [math]\displaystyle{ p }[/math] taka, że [math]\displaystyle{ p \in \left( {\small\frac{n}{2}}, n \right] }[/math] występuje w rozkładzie liczby [math]\displaystyle{ n! }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ 1 }[/math]. Z twierdzenia B28 wiemy, że przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Łącząc te fakty, otrzymujemy natychmiast tezę.
□
Twierdzenie B30
Każda liczba naturalna [math]\displaystyle{ n \geqslant 12 }[/math] jest sumą różnych liczb pierwszych.
Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 12 = 5 + 7 }[/math]. Zakładając, że twierdzenie jest prawdziwe dla każdej liczby naturalnej należącej do przedziału [math]\displaystyle{ [12, n] }[/math], udowodnimy, że liczba [math]\displaystyle{ n + 1 }[/math] jest sumą różnych liczb pierwszych.
Z twierdzenia B28 wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] w przedziale [math]\displaystyle{ \left(\frac{n}{2}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Niech [math]\displaystyle{ p_k }[/math] będzie największą liczbą pierwszą w tym przedziale. Z określenia liczby [math]\displaystyle{ p_k }[/math] wynika następujący ciąg nierówności
- [math]\displaystyle{ {\small\frac{n}{2}} \lt p_k \leqslant n \lt n + 1 \leqslant p_{k + 1} }[/math]
Korzystając z twierdzenia B22 i ostatniej z wypisanych wyżej nierówności, dostajemy
- [math]\displaystyle{ n + 1 - p_k \leqslant p_{k + 1} - p_k \lt p_k \leqslant n }[/math]
Widzimy, że liczba [math]\displaystyle{ n + 1 - p_k }[/math] jest mniejsza od liczb [math]\displaystyle{ p_k }[/math] oraz [math]\displaystyle{ n }[/math]. Zatem na mocy założenia indukcyjnego jest sumą różnych liczb pierwszych mniejszych od [math]\displaystyle{ p_k }[/math]. Wynika stąd, że liczba
- [math]\displaystyle{ n + 1 = p_k + (n + 1 - p_k) }[/math]
jest sumą różnych liczb pierwszych.
Gdybyśmy na tym zakończyli dowód, to równie dobrze moglibyśmy uznać, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n \geqslant 5 = 2 + 3 }[/math]. Wtedy łatwo zauważymy, że liczba pierwsza [math]\displaystyle{ 11 }[/math] nie jest sumą różnych liczb pierwszych. Ratując sytuację, moglibyśmy przyjąć, że [math]\displaystyle{ 11 }[/math] jest sumą tylko jednej liczby pierwszej, czyli samej siebie. Jednak liczba [math]\displaystyle{ 6 }[/math] też nie jest sumą różnych liczb pierwszych i nie ma sposobu obejścia tego problemu.
Błąd polega na tym, że musimy sprawdzić, czy liczba [math]\displaystyle{ n + 1 - p_k }[/math] spełnia założenia twierdzenia, czyli czy jest
- [math]\displaystyle{ n + 1 - p_k \in [12, n] }[/math]
Na razie pokazaliśmy tylko, że liczba ta jest mniejsza od [math]\displaystyle{ n }[/math]. Musimy jeszcze pokazać, że
- [math]\displaystyle{ n + 1 - p_k \geqslant 12 }[/math]
Skąd dostajemy
- [math]\displaystyle{ n \geqslant 11 + p_k \gt 11 + {\small\frac{n}{2}} }[/math]
Zatem dopiero dla [math]\displaystyle{ n \gt 22 }[/math] warunek [math]\displaystyle{ n + 1 - p_k \geqslant 12 }[/math] będzie na pewno spełniony. Łatwo sprawdzamy, że dla liczb [math]\displaystyle{ 12, 13, \ldots, 22 }[/math] twierdzenie jest prawdziwe
[math]\displaystyle{ \mathbf{12} = 5 + 7 }[/math], [math]\displaystyle{ \mathbf{13} = 2 + 11 }[/math], [math]\displaystyle{ \mathbf{14} = 3 + 11 }[/math], [math]\displaystyle{ \mathbf{15} = 2 + 13 }[/math], [math]\displaystyle{ \mathbf{16} = 3 + 13 }[/math], [math]\displaystyle{ \mathbf{17} = 2 + 3 + 5 + 7 }[/math], [math]\displaystyle{ \mathbf{18} = 5 + 13 }[/math], [math]\displaystyle{ \mathbf{19} = 2 + 17 }[/math], [math]\displaystyle{ \mathbf{20} = 3 + 17 }[/math], [math]\displaystyle{ \mathbf{21} = 2 + 19 }[/math], [math]\displaystyle{ \mathbf{22} = 3 + 19 }[/math], [math]\displaystyle{ \mathbf{23} = 3 + 7 + 13 }[/math]
□
Twierdzenie B31
Dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest następujące oszacowanie funkcji [math]\displaystyle{ P(n) }[/math] od dołu
- [math]\displaystyle{ P (n) \gt 2^{n / 2} }[/math]
Indukcja matematyczna. Mamy [math]\displaystyle{ P(3) = 6 \gt 2^{3 / 2} = 2 \sqrt{2} }[/math] oraz [math]\displaystyle{ P(4) = 6 \gt 2^{4 / 2} = 4 }[/math], czyli nierówność jest prawdziwa dla [math]\displaystyle{ n = 3, 4 }[/math]. Zakładając prawdziwość nierówności dla wszystkich liczb naturalnych należących do przedziału [math]\displaystyle{ \left [ 3, n \right ] }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
a) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą parzystą, to [math]\displaystyle{ n + 1 = 2 m }[/math] i wtedy
- [math]\displaystyle{ P(n + 1) = P (2 m) = P (m) \cdot {\small\frac{P (2 m)}{P (m)}} \gt 2^{m / 2} \cdot 2^{m / 2} = 2^m = 2^{2 m / 2} = 2^{(n + 1) / 2} }[/math]
gdzie skorzystaliśmy z założenia indukcyjnego i twierdzenia B12.
b) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą nieparzystą, to [math]\displaystyle{ n + 1 = 2 m + 1 }[/math] i wtedy
- [math]\displaystyle{ P(n + 1) = P (2 m + 1) = P (2 m + 2) = P (m + 1) \cdot {\small\frac{P (2 m + 2)}{P (m + 1)}} \gt 2^{(m + 1) / 2} \cdot 2^{(m + 1) / 2} = 2^{(2 m + 2) / 2} \gt 2^{(2 m + 1) / 2} = 2^{(n + 1) / 2} }[/math]
Co kończy dowód indukcyjny.
□
Zadanie B32
Niech [math]\displaystyle{ p_n }[/math] oznaczą [math]\displaystyle{ n }[/math]-tą liczbę pierwszą. Korzystając z twierdzenia Czebyszewa pokazać, że dla [math]\displaystyle{ n \geqslant 1 }[/math] jest [math]\displaystyle{ p_n \leqslant 2^n }[/math].
Rozbieżność sumy [math]\displaystyle{ \textstyle \sum\limits_{p \geqslant 2} {\small\frac{1}{p}} }[/math]
Rozpoczniemy od prostszego twierdzenia dotyczącego rozbieżności sumy odwrotności wszystkich liczb całkowitych dodatnich. Już sam wzór, w którym pogrupowaliśmy wyrazy tej sumy
- [math]\displaystyle{ S = 1 + {\small\frac{1}{2}} + \left( {\small\frac{1}{3}} + {\small\frac{1}{4}} \right) + \left( {\small\frac{1}{5}} + {\small\frac{1}{6}} + {\small\frac{1}{7}} + {\small\frac{1}{8}} \right) + \left( {\small\frac{1}{9}} + {\small\frac{1}{10}} + {\small\frac{1}{11}} + {\small\frac{1}{12}} + {\small\frac{1}{13}} + {\small\frac{1}{14}} + {\small\frac{1}{15}} + {\small\frac{1}{16}} \right) + \ldots }[/math]
mógłby wystarczyć za dowód, bo każda suma w nawiasach jest większa od [math]\displaystyle{ {\small\frac{1}{2}} }[/math], ale dowód formalny okaże się pożytecznym ćwiczeniem.
Twierdzenie B33
Niech [math]\displaystyle{ S(k) }[/math] oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność
- [math]\displaystyle{ S(2^n) \gt {\small\frac{n + 1}{2}} }[/math].
Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], bo
- [math]\displaystyle{ S(2^1) = 1 + {\small\frac{1}{2}} \gt 1 }[/math]
Zakładając, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ S(2^{n + 1}) = 1 + {\small\frac{1}{2}} + \ldots + {\small\frac{1}{2^n - 1}} + {\small\frac{1}{2^n}} + \left( {\small\frac{1}{2^n + 1}} + \ldots + {\small\frac{1}{2^{n + 1}}} \right) = }[/math]
- [math]\displaystyle{ \; \; \: = S (2^n) + \left( {\small\frac{1}{2^n + 1}} + \ldots + {\small\frac{1}{2^{n + 1}}} \right) }[/math]
Ponieważ wyrażenie w nawiasie zawiera [math]\displaystyle{ 2^{n + 1} - 2^n = 2^n }[/math] wyrazów, z których każdy jest nie mniejszy niż [math]\displaystyle{ {\small\frac{1}{2^{n + 1}}} }[/math], to prawdziwe jest oszacowanie
- [math]\displaystyle{ S(2^{n + 1}) \gt {\small\frac{n + 1}{2}} + 2^n \cdot {\small\frac{1}{2^{n + 1}}} = }[/math]
- [math]\displaystyle{ \; \; \: = {\small\frac{n + 2}{2}} }[/math]
Gdzie skorzystaliśmy z założenia indukcyjnego i oszacowaliśmy sumę w nawiasie.
□
Twierdzenie B34
Niech [math]\displaystyle{ S(k) }[/math] oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność
- [math]\displaystyle{ S(k) \gt \tfrac{1}{2} \, \log_2 \! k }[/math]
Niech [math]\displaystyle{ n = \lfloor \log_2 \! k \rfloor }[/math] dla dowolnego [math]\displaystyle{ k \geqslant 1 }[/math]. Mamy
- [math]\displaystyle{ k = 2^{\log_2 \! k} \geqslant 2^{\lfloor \log_2 \! k \rfloor} = 2^n }[/math]
Zatem
- [math]\displaystyle{ S(k) \geqslant S (2^n) \gt {\small\frac{n + 1}{2}} = \tfrac{1}{2} (\lfloor \log_2 \! k \rfloor + 1) \gt \tfrac{1}{2} \log_2 \! k }[/math]
- [math]\displaystyle{ S(k) \geqslant S (2^n) \gt {\small\frac{n + 1}{2}} = \tfrac{1}{2} (\lfloor \log_2 \! k \rfloor + 1) \gt \tfrac{1}{2} \log_2 \! k }[/math]
□
Z twierdzenia B34 wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb całkowitych dodatnich.
|
Dokładniejsze oszacowanie sumy odwrotności liczb całkowitych dodatnich[6] nie większych od [math]\displaystyle{ k }[/math] jest dane wzorem
gdzie [math]\displaystyle{ \gamma = 0.5772156649 \ldots }[/math] jest stałą Eulera[7]. |
Oznaczmy przez [math]\displaystyle{ Q }[/math] sumę odwrotności wszystkich liczb pierwszych
- [math]\displaystyle{ Q = {\small\frac{1}{2}} + {\small\frac{1}{3}} + {\small\frac{1}{5}} + {\small\frac{1}{7}} + {\small\frac{1}{11}} + {\small\frac{1}{13}} + {\small\frac{1}{17}} + {\small\frac{1}{19}} + {\small\frac{1}{23}} + {\small\frac{1}{29}} + {\small\frac{1}{31}} + {\small\frac{1}{37}} + {\small\frac{1}{41}} + {\small\frac{1}{43}} + {\small\frac{1}{47}} + \ldots }[/math]
a przez [math]\displaystyle{ Q(k) }[/math] sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Dla przykładu mamy
- [math]\displaystyle{ Q(1) = 0 }[/math]
- [math]\displaystyle{ Q(2) = {\small\frac{1}{2}} }[/math]
- [math]\displaystyle{ Q(3) = {\small\frac{1}{2}} + {\small\frac{1}{3}} }[/math]
- [math]\displaystyle{ Q(4) = {\small\frac{1}{2}} + {\small\frac{1}{3}} }[/math]
Korzystając z twierdzenia B14, udowodnimy
Twierdzenie B35
Niech [math]\displaystyle{ Q(k) }[/math] oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Dla [math]\displaystyle{ k \geqslant 1 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ Q(2 k) - Q (k) \gt {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2 k)}} }[/math]
Zauważmy, że
- [math]\displaystyle{ Q(2 k) - Q (k) = \sum_{k \lt p \leqslant 2k} {\small\frac{1}{p}} \geqslant }[/math]
- [math]\displaystyle{ \; \: \geqslant \sum_{k \lt p \leqslant 2k} {\small\frac{1}{2 k}} = }[/math]
- [math]\displaystyle{ \; \: = {\small\frac{1}{2 k}} \cdot [\pi (2 k) - \pi (k)] \gt }[/math]
- [math]\displaystyle{ \; \: \gt {\small\frac{1}{2 k}} \cdot {\small\frac{\log 2}{2}} \cdot {\small\frac{k}{\log (2 k)}} = }[/math]
- [math]\displaystyle{ \; \: = {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2 k)}} }[/math]
Pierwsza nierówność (nieostra) wynika z faktu, że [math]\displaystyle{ {\small\frac{1}{p}} \geqslant {\small\frac{1}{2 k}} }[/math] dla wszystkich liczb pierwszych [math]\displaystyle{ p \leqslant 2 k }[/math]. Kolejna nierówność wynika z twierdzenia B14.
□
Twierdzenie B36
Niech [math]\displaystyle{ Q(k) }[/math] oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność
- [math]\displaystyle{ Q(2^n) \gt {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 1} {\small\frac{1}{j}} }[/math]
Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], bo
- [math]\displaystyle{ Q(2^1) = {\small\frac{1}{2}} \gt {\small\frac{3}{8}} }[/math]
Zakładając, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ Q(2^{n + 1}) = Q (2^n) + [Q (2^{n + 1}) - Q (2^n)] \gt }[/math]
- [math]\displaystyle{ \; \: \: \, \gt Q (2^n) + {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2^{n + 1})}} = }[/math]
- [math]\displaystyle{ \; \: \: \, = Q (2^n) + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 1}} \gt }[/math]
- [math]\displaystyle{ \; \: \: \, \gt Q (2^n) + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 2}} \gt }[/math]
- [math]\displaystyle{ \; \: \: \, \gt {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 1} {\small\frac{1}{j}} + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 2}} = }[/math]
- [math]\displaystyle{ \; \: \: \, = {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 2} {\small\frac{1}{j}} }[/math]
Pierwsza nierówność wynika z twierdzenia B35, druga z faktu, że [math]\displaystyle{ {\small\frac{1}{n + 1}} \gt {\small\frac{1}{n + 2}} }[/math], a trzecia z założenia indukcyjnego.
□
Twierdzenie B37
Niech [math]\displaystyle{ Q(k) }[/math] oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność
- [math]\displaystyle{ Q(k) \gt \tfrac{1}{8} \, \log_2 \! \log_2 \! k }[/math]
Niech [math]\displaystyle{ n = \lfloor \log_2 \! k \rfloor }[/math] dla dowolnego [math]\displaystyle{ k \geqslant 1 }[/math]. Mamy
- [math]\displaystyle{ k = 2^{\log_2 \! k} \geqslant 2^{\lfloor \log_2 \! k \rfloor} = 2^n }[/math]
Ponieważ
- [math]\displaystyle{ Q(k) \geqslant Q (2^n) \gt }[/math]
- [math]\displaystyle{ \quad \gt {\small\frac{1}{4}} \cdot \underset{j = 1}{\overset{n + 1}{\sum}} {\small\frac{1}{j}} \gt }[/math]
- [math]\displaystyle{ \quad \gt {\small\frac{1}{8}} \cdot \log_2 (n + 1) = }[/math]
- [math]\displaystyle{ \quad = {\small\frac{1}{8}} \cdot \log_2 (\lfloor \log_2 \! k \rfloor + 1) \gt }[/math]
- [math]\displaystyle{ \quad \gt {\small\frac{1}{8}} \cdot \log_2 (\log_2 \! k) }[/math]
Pierwsza nierówność (ostra) wynika z twierdzenia B36, kolejna nierówność wynika z twierdzenia B34.
□
Z twierdzenia B37 wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb pierwszych.
|
Dokładniejsze oszacowanie sumy odwrotności liczb pierwszych nie większych od [math]\displaystyle{ k }[/math] jest dane wzorem
gdzie [math]\displaystyle{ M = 0.261497212847 \ldots }[/math] jest stałą Mertensa[8].
[math]\displaystyle{ \left| \sum_{p\leqslant k} {\small\frac{1}{p}} - \log \log k - M \right| \lt {\small\frac{1}{2 (\log k)^2}} }[/math] |
Zbieżność sumy [math]\displaystyle{ \textstyle \sum\limits_{p \geqslant 2} {\small\frac{1}{p \log p}} }[/math]
Twierdzenie B38
Niech [math]\displaystyle{ T = \sum_{p \geqslant 2} {\small\frac{1}{p \log p}} }[/math] będzie sumą odwrotności wszystkich iloczynów [math]\displaystyle{ p \! \cdot \! \log p }[/math], gdzie [math]\displaystyle{ p }[/math] oznacza liczbę pierwszą, a [math]\displaystyle{ T(k) }[/math] będzie sumą częściową sumy [math]\displaystyle{ T }[/math]
- [math]\displaystyle{ T(k) = \sum_{p \leqslant k} {\small\frac{1}{p \log p}} }[/math]
Dla [math]\displaystyle{ k \geqslant 2 }[/math] prawdziwe jest oszacowanie
- [math]\displaystyle{ T(2 k) - T (k) \lt {\small\frac{2 \log 2}{\log^2 \! k}} }[/math]
Zauważmy, że
- [math]\displaystyle{ T(2 k) - T (k) = \sum_{k \lt p \leqslant 2 k} {\small\frac{1}{p \log p}} }[/math]
- [math]\displaystyle{ \; \lt \sum_{k \lt p \leqslant 2 k} {\small\frac{1}{k \log k}} }[/math]
- [math]\displaystyle{ \; = {\small\frac{1}{k \log k}} \cdot [\pi (2 k) - \pi (k)] }[/math]
- [math]\displaystyle{ \; \lt {\small\frac{1}{k \log k}} \cdot 2 \log 2 \cdot {\small\frac{k}{\log k}} }[/math]
- [math]\displaystyle{ \; = {\small\frac{2 \log 2}{(\log k)^2}} }[/math]
Pierwsza nierówność wynika z faktu, że [math]\displaystyle{ {\small\frac{1}{p \log p}} \lt {\small\frac{1}{k \log k}} }[/math] dla wszystkich liczb pierwszych [math]\displaystyle{ p \gt k }[/math]. Kolejna nierówność wynika z twierdzenia A11.
□
Twierdzenie B39
Suma [math]\displaystyle{ \sum_{p \geqslant 2} {\small\frac{1}{p \log p}} }[/math], gdzie [math]\displaystyle{ p }[/math] oznacza liczbę pierwszą, jest skończona[10].
Niech [math]\displaystyle{ p }[/math] oznacza liczbę pierwszą i niech
- [math]\displaystyle{ T(k) = \sum_{p \leqslant k} {\small\frac{1}{p \log p}} }[/math]
Pokażemy najpierw, że dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwa jest nierówność
- [math]\displaystyle{ T(2^n) \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} \right) }[/math]
Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], bo
- [math]\displaystyle{ T(2^1) \approx 0.721 \lt 2.885 }[/math]
Zakładając, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ T(2^{n + 1}) = T (2^n) + [T (2^{n + 1}) - T (2^n)] }[/math]
- [math]\displaystyle{ \;\;\: \lt T (2^n) + 2 \log 2 \cdot {\small\frac{1}{[\log (2^n)]^2}} }[/math]
- [math]\displaystyle{ \;\;\: \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} \right) + 2 \log 2 \cdot {\small\frac{1}{n^2 (\log 2)^2}} }[/math]
- [math]\displaystyle{ \;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} + {\small\frac{1}{n^2}} \right) }[/math]
- [math]\displaystyle{ \;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} + \left( {\small\frac{2}{n + 1}} - {\small\frac{2}{n}} + {\small\frac{1}{n^2}} \right) \right) }[/math]
- [math]\displaystyle{ \;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} - {\small\frac{n - 1}{n^2 (n + 1)}} \right) }[/math]
- [math]\displaystyle{ \;\;\: \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} \right) }[/math]
Pierwsza nierówność wynika z twierdzenia B38, a druga z założenia indukcyjnego. Co kończy dowód indukcyjny.
Niech [math]\displaystyle{ n = \lfloor \log_2 \! k \rfloor }[/math] dla dowolnego [math]\displaystyle{ k \geqslant 1 }[/math]. Ponieważ
- [math]\displaystyle{ k = 2^{\log_2 \! k} \lt 2^{\lfloor \log_2 \! k \rfloor + 1} = 2^{n + 1} }[/math]
oraz
- [math]\displaystyle{ n + 1 = \lfloor \log_2 \! k \rfloor + 1 \leqslant \log_2 \! k + 1 }[/math]
to łatwo otrzymujemy
- [math]\displaystyle{ T(k) \leqslant T (2^{n + 1}) \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} \right) \leqslant {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{\log_2 \! k + 1}} \right) \lt {\small\frac{6}{\log 2}} }[/math]
Ponieważ ciąg sum częściowych [math]\displaystyle{ T(k) }[/math] jest rosnący i ograniczony[11][12], to suma odwrotności wszystkich iloczynów [math]\displaystyle{ p \! \cdot \! \log p }[/math] jest skończona.
□
Przypisy
- ↑ Wikipedia, Pafnuty Czebyszew (1821 - 1893), (Wiki-pl), (Wiki-ru)
- ↑ P. L. Chebyshev, Mémoire sur les nombres premiers, J. de Math. Pures Appl. (1) 17 (1852), 366-390, (LINK)
- ↑ Literą "A" poprzedzamy numery twierdzeń, które zostały sformułowane i udowodnione w artykule Twierdzenie Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math], (LINK)
- ↑ P. Dusart, Sharper bounds for [math]\displaystyle{ \psi }[/math], [math]\displaystyle{ \theta }[/math], [math]\displaystyle{ \pi }[/math], [math]\displaystyle{ p_k }[/math], Rapport de recherche no. 1998-06, Université de Limoges
- ↑ Wikipedia, Hipoteza Goldbacha, (Wiki-pl)
- ↑ Wikipedia, Szereg harmoniczny, (Wiki-pl)
- ↑ Wikipedia, Stała Eulera, (Wiki-pl)
- ↑ Wikipedia, Stała Meissela-Mertensa, (Wiki-pl)
- ↑ J. B. Rosser and L. Schoenfeld, Approximate formulas for some functions of prime numbers, Illinois J. Math. 6 (1962), 64-94, (LINK)
- ↑ The On-Line Encyclopedia of Integer Sequences, A137245 - Decimal expansion of Sum_{p prime} 1/(p * log p), (LINK)
- ↑ Wikipedia, Twierdzenie o zbieżności ciągu monotonicznego, (Wiki-pl)
- ↑ Wikipedia, Aksjomat ciągłości, (Wiki-pl)