Szeregi liczbowe: Różnice pomiędzy wersjami
| (Nie pokazano 14 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 3043: | Linia 3043: | ||
'''Punkt 4.''' | '''Punkt 4.''' | ||
| − | Dowód tego punktu został umieszczony w Uzupełnieniu (zobacz [[# | + | Dowód tego punktu został umieszczony w Uzupełnieniu (zobacz [[#D109|D109]]).<br/> |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 3050: | Linia 3050: | ||
<span id="D85" style="font-size: 110%; font-weight: bold;">Zadanie D85</span><br/> | <span id="D85" style="font-size: 110%; font-weight: bold;">Zadanie D85</span><br/> | ||
| − | Niech <math>C_n</math> oznacza <math>n</math>-tą liczbę Catalana i niech <math>\sum_{n = 0}^{\infty} x_n</math> oznacza szereg, który otrzymujemy, mnożąc szereg <math>\sum_{ | + | Niech <math>C_n</math> oznacza <math>n</math>-tą liczbę Catalana i niech <math>\sum_{n = 0}^{\infty} x_n</math> oznacza szereg, który otrzymujemy, mnożąc szereg <math>\sum_{n = 0}^{\infty} a_n</math> przez siebie według reguły Cauchy'ego. Pokazać, że |
:* jeżeli <math>a_n = C_n</math>, to <math>x_n = C_{n + 1}</math> | :* jeżeli <math>a_n = C_n</math>, to <math>x_n = C_{n + 1}</math> | ||
| Linia 3093: | Linia 3093: | ||
= {\small\frac{2 (2 n - 1)}{n + 1}}</math> | = {\small\frac{2 (2 n - 1)}{n + 1}}</math> | ||
| − | Z kryterium d'Alemberta dla szeregu <math>\sum_{ | + | Z kryterium d'Alemberta dla szeregu <math>\sum_{n = 0}^{\infty} a_n</math> i szeregu <math>\sum_{n = 0}^{\infty} x_n</math> otrzymujemy |
| − | ::<math>\left| {\small\frac{a_{ | + | ::<math>\left| {\small\frac{a_{n + 1}}{a_n}} \right| = \left| {\small\frac{r^n C_n}{r^{n - 1} C_{n - 1}}} \right| = | r | \cdot {\small\frac{C_n}{C_{n - 1}}} = | r | \cdot {\small\frac{2 (2 n - 1)}{n + 1}} \xrightarrow{\; n \rightarrow \infty \;} 4 | r |</math> |
| − | ::<math>\left| {\small\frac{x_{ | + | ::<math>\left| {\small\frac{x_{n + 1}}{x_n}} \right| = \left| {\small\frac{r^{n - 1} C_n (1 + 2 \alpha r)}{r^{n - 2} C_{n - 1} (1 + 2 \alpha r)}} \right| = | r | \cdot {\small\frac{C_n}{C_{n - 1}}} \xrightarrow{\; n \rightarrow \infty \;} 4 | r |</math> |
Zatem szeregi te są bezwzględnie zbieżne w przypadku, gdy <math>| r | < {\small\frac{1}{4}}</math>. W szczególności dla <math>\alpha = - {\small\frac{1}{2 r}}</math> szereg <math>\sum_{n = 0}^{\infty} x_n</math> zawsze będzie zbieżny, bo od trzeciego wyrazu będzie się składał z samych zer. Wiemy, że w przypadku, gdy <math>r = {\small\frac{1}{4}}</math> szereg <math>\sum_{n = 0}^{\infty} {\small\frac{C_n}{4^n}} = 2</math> jest zbieżny.<br/> | Zatem szeregi te są bezwzględnie zbieżne w przypadku, gdy <math>| r | < {\small\frac{1}{4}}</math>. W szczególności dla <math>\alpha = - {\small\frac{1}{2 r}}</math> szereg <math>\sum_{n = 0}^{\infty} x_n</math> zawsze będzie zbieżny, bo od trzeciego wyrazu będzie się składał z samych zer. Wiemy, że w przypadku, gdy <math>r = {\small\frac{1}{4}}</math> szereg <math>\sum_{n = 0}^{\infty} {\small\frac{C_n}{4^n}} = 2</math> jest zbieżny.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Sumy współczynników dwumianowych == | ||
| + | |||
| + | <span id="D86" style="font-size: 110%; font-weight: bold;">Twierdzenie D86</span><br/> | ||
| + | Dla <math>n \geqslant 0 \;</math> i <math>\; r \in \mathbb{R}</math> prawdziwe są wzory | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} r^k {\small\binom{n}{k}} = (r + 1)^n</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\frac{r^{k + 1}}{k + 1}} {\small\binom{n}{k}} = {\small\frac{(r + 1)^{n + 1} - 1}{n + 1}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k {\small\binom{n}{k}} = n 2^{n - 1}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} = n (n + 1) 2^{n - 2}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | |||
| + | '''Punkt 1.''' | ||
| + | |||
| + | Ze wzoru dwumianowego natychmiast otrzymujemy | ||
| + | |||
| + | ::<math>(1 + r)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} r^k</math> | ||
| + | |||
| + | '''Punkt 2.''' | ||
| + | |||
| + | Całkując obie strony wzoru dwumianowego | ||
| + | |||
| + | ::<math>(1 + x)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} x^k</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>\int^r_0 (1 + x)^n d x = \sum_{k = 0}^{n} {\small\binom{n}{k}} \int^r_0 x^k d x</math> | ||
| + | |||
| + | ::<math>{\small\frac{(r + 1)^{n + 1} - 1}{n + 1}} = \sum_{k = 0}^{n} {\small\frac{r^{k + 1}}{k + 1}} {\small\binom{n}{k}}</math> | ||
| + | |||
| + | '''Punkt 3.''' | ||
| + | |||
| + | Obliczając pochodną każdej ze stron wzoru dwumianowego | ||
| + | |||
| + | ::<math>(1 + x)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} x^k</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>n (1 + x)^{n - 1} = \sum_{k = 0}^{n} {\small\binom{n}{k}} k x^{k - 1}</math> | ||
| + | |||
| + | Kładąc <math>x = 1</math>, dostajemy dowodzony wzór. | ||
| + | |||
| + | '''Punkt 4.''' | ||
| + | |||
| + | Obliczając drugą pochodną każdej ze stron wzoru dwumianowego | ||
| + | |||
| + | ::<math>(1 + x)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} x^k</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>n(n - 1) (1 + x)^{n - 2} = \sum_{k = 0}^{n} {\small\binom{n}{k}} k (k - 1) x^{k - 1}</math> | ||
| + | |||
| + | Kładąc <math>x = 1</math>, dostajemy | ||
| + | |||
| + | ::<math>n(n - 1) 2^{n - 2} = \sum_{k = 0}^{n} {\small\binom{n}{k}} k (k - 1) = \sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} - \sum_{k = 0}^{n} k {\small\binom{n}{k}} = \sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} - n 2^{n - 1}</math> | ||
| + | |||
| + | Skąd natychmiast wynika dowodzony wzór.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D87" style="font-size: 110%; font-weight: bold;">Twierdzenie D87</span><br/> | ||
| + | Dla <math>n, m \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{m} {\small\binom{n + k}{n}} = {\small\binom{n + m + 1}{n}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Ze wzoru Pascala | ||
| + | |||
| + | ::<math>{\small\binom{a}{k}} = {\small\binom{a - 1}{k}} + {\small\binom{a - 1}{k - 1}}</math> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>{\small\binom{a - 1}{k}} = {\small\binom{a}{k}} - {\small\binom{a - 1}{k - 1}}</math> | ||
| + | |||
| + | Kładąc <math>a = n + k + 1</math>, mamy | ||
| + | |||
| + | ::<math>{\small\binom{n + k}{k}} = {\small\binom{n + k + 1}{k}} - {\small\binom{n + k}{k - 1}}</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>{\small\binom{n + k}{n}} = {\small\binom{n + k + 1}{n + 1}} - {\small\binom{n + k}{n + 1}}</math> | ||
| + | |||
| + | Wykorzystując powyższy wzór, łatwo pokazujemy, że (zobacz [[#D12|D12]]) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{m} {\small\binom{n + k}{n}} = 1 + \sum_{k = 1}^{m} {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = 1 + \sum_{k = 1}^{m} \left[ {\small\binom{n + k + 1}{n + 1}} - {\small\binom{n + k}{n + 1}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = 1 - \sum_{k = 1}^{m} \left[ {\small\binom{n + k}{n + 1}} - {\small\binom{n + k + 1}{n + 1}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = 1 - \left[ 1 - {\small\binom{n + m + 1}{n + 1}} \right]</math> | ||
| + | |||
| + | :::::<math>\;\;\,\, = {\small\binom{n + m + 1}{n}}</math> | ||
| + | |||
| + | Co kończy dowód.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | === <span style="border-bottom:2px solid #000;">Suma nieoznaczona</span> === | ||
| + | |||
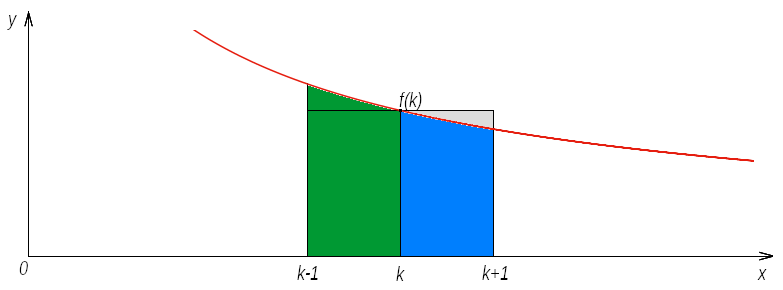
| + | <span id="D88" style="font-size: 110%; font-weight: bold;">Uwaga D88</span><br/> | ||
| + | Sumą nieoznaczoną<ref name="IndefiniteSum1"/> (lub antyróżnicą) funkcji <math>f(k)</math>, będziemy nazywali dowolną funkcję <math>F(k)</math> taką, że | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>F(k + 1) - F (k) = f (k)</math> | ||
| + | </div> | ||
| + | |||
| + | Łatwo zauważamy, że istnieje cała rodzina funkcji <math>F(k)</math>, bo jeżeli <math>F (k)</math> jest sumą nieoznaczoną, to <math>F (k) + C</math>, gdzie <math>C</math> jest stałą, również jest sumą nieoznaczoną. W szczególności | ||
| + | |||
| + | ::<math>\sum_{k = a}^{b} f (k) = \sum_{k = a}^{b} (F (k + 1) - F (k))</math> | ||
| + | |||
| + | ::::<math>\;\;\;\: = - \sum_{k = a}^{b} (F (k) - F (k + 1))</math> | ||
| + | |||
| + | <div style="margin-top: 1.1em; margin-bottom: 1em;"> | ||
| + | ::::<math>\;\;\;\: = - ( F (a) - F (b + 1) )</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 1.5em; margin-bottom: 1em;"> | ||
| + | ::::<math>\;\;\;\: = F (b + 1) - F (a)</math> | ||
| + | </div> | ||
| + | |||
| + | Co przez analogię do całki nieoznaczonej możemy zapisać jako | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | ::<math>\sum_{k = a}^{b} f (k) = F (k) \biggr\rvert_{a}^{b + 1} \qquad \qquad \qquad ( 1 )</math> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | Należy podkreślić różnicę między sumą oznaczoną <math>S(n)</math> a sumą nieoznaczoną <math>F(k)</math>. Niech <math>f(k) = k^2</math>. Oczywiście | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} k^2 = {\small\frac{1}{6}} n (n + 1) (2 n + 1)</math> | ||
| + | |||
| + | ::<math>F(k) = {\small\frac{1}{6}} (k - 1) k (2 k - 1)</math> | ||
| + | |||
| + | Ponieważ dla sumy <math>S(n)</math> prawdziwy jest związek <math>S(n + 1) - S (n) = f (n + 1)</math>, to otrzymujemy <math>F(k) = S (k - 1)</math>. Weźmy kolejny przykład, niech <math>f(k) = r^k</math>, gdzie <math>r</math> jest stałą. Mamy | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} r^k = {\small\frac{r^{n + 1} - 1}{r - 1}}</math> | ||
| + | |||
| + | ale | ||
| + | |||
| + | ::<math>F(k) = {\small\frac{r^k}{r - 1}}</math> | ||
| + | |||
| + | i nie jest prawdą, że <math>F(k) = S (k - 1)</math>, bo pominięty został wyraz <math>{\small\frac{- 1}{r - 1}}</math>, który jest stałą, ale jest to zrozumiałe. | ||
| + | |||
| + | Niech teraz <math>f(n, k) = {\small\binom{n + k}{n}}</math>. Wiemy, że (zobacz [[#D87|D87]]) | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | ::<math>F(n, k) = {\small\frac{k}{n + 1}} {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | Tym razem otrzymujemy zupełnie inne wyniki: suma <math>S(n)</math> nie zależy od dwóch zmiennych, bo jest to niemożliwe, a suma nieoznaczona nadal zależy od <math>k</math>, bo dla <math>F(n, k)</math> musi być prawdziwy wzór <math>(1)</math>. Łatwo widzimy, że | ||
| + | |||
| + | ::<math>S (n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1}</math> | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D89" style="font-size: 110%; font-weight: bold;">Uwaga D89</span><br/> | ||
| + | Powiedzmy, że dysponujemy wzorem <math>S(b) = \sum_{k = a}^{b} f (k)</math> i chcemy udowodnić jego poprawność. W prostych przypadkach możemy wykorzystać indukcję matematyczną: wystarczy pokazać, że | ||
| + | |||
| + | ::<math>S(k + 1) = S (k) + f (k + 1)</math> | ||
| + | |||
| + | Jeżeli już udało nam się pokazać związek <math>f(k) = S (k) - S (k - 1)</math>, to równie dobrze możemy zamienić sumę na sumę teleskopową (zobacz [[#D12|D12]]), aby otrzymać, że | ||
| + | |||
| + | ::<math>\sum_{k = a + 1}^{b} f (k) = \sum_{k = a + 1}^{b} ( S (k) - S (k - 1) )</math> | ||
| + | |||
| + | :::::<math>\;\, = - \sum_{k = a + 1}^{b} ( S (k - 1) - S (k) )</math> | ||
| + | |||
| + | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| + | :::::<math>\;\, = - ( S (a) - S (b) )</math> | ||
| + | </div> | ||
| + | |||
| + | <div style="margin-top: 2em; margin-bottom: 1em;"> | ||
| + | :::::<math>\;\, = S (b) - S (a)</math> | ||
| + | </div> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>S(b) = \sum_{k = a + 1}^{b} f (k) + S (a) = \sum_{k = a}^{b} f (k)</math> | ||
| + | |||
| + | bo <math>S(a) = f (a)</math>. | ||
| + | |||
| + | |||
| + | W przypadkach bardziej skomplikowanych nie możemy tak postąpić. W poprzedniej uwadze rozważaliśmy sumę | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | ale | ||
| + | |||
| + | ::<math>S(n) - S (n - 1) = {\small\frac{3 n + 1}{2 (n + 1)}} {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | I nie da się pokazać związku <math>S(k) - S (k - 1) = f (n, k)</math>, bo różnica <math>S(k) - S (k - 1)</math> nie zależy od <math>n</math>. | ||
| + | |||
| + | Tutaj z pomocą przychodzi nam suma nieoznaczona. W programie Maxima możemy ją policzyć, wpisując polecenia | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">'''load''' ("zeilberger"); | ||
| + | '''AntiDifference'''('''binomial'''(n+k, n), k);</span> | ||
| + | |||
| + | Otrzymujemy | ||
| + | |||
| + | ::<math>F(n, k) = {\small\frac{k}{n + 1}} {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | Oczywiście | ||
| + | |||
| + | ::<math>F(n, k + 1) - F (n, k) = {\small\binom{n + k}{n}}</math> | ||
| + | |||
| + | i | ||
| + | |||
| + | ::<math>S(n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | Podsumujmy. Jakkolwiek znalezienie ogólnego wzoru na sumę <math>S (n) = \sum_{k = 0}^{n} f (k)</math> może być bardzo trudne, to udowodnienie poprawności tego wzoru może być znacznie łatwiejsze (metodą indukcji matematycznej lub obliczając sumę teleskopową). Podobnie jest w bardziej skomplikowanym przypadku, gdy szukamy ogólnego wzoru na sumę <math>S(n) = \sum_{k = 0}^{n} f (n, k)</math>. Tutaj wymienionych przed chwilą metod zastosować nie można, a znalezienie wzoru na sumę nieoznaczoną <math>F(n, k)</math> może być jeszcze trudniejsze, ale gdy już taki wzór mamy, to sprawdzenie jego poprawności, czyli związku <math>F(n, k + 1) - F (n, k) = f (n, k)</math>, może być bardzo łatwe, a wtedy otrzymujemy natychmiast | ||
| + | |||
| + | ::<math>S(n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1}</math> | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D90" style="font-size: 110%; font-weight: bold;">Zadanie D90</span><br/> | ||
| + | Korzystając z programu Maxima znaleźć sumę nieoznaczoną <math>F(n, k)</math> dla funkcji | ||
| + | |||
| + | ::<math>f(n, k) = {\small\frac{1}{(k + 1) (n - k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | i pokazać, że prawdziwy jest wzór <math>C_{n + 1} = \sum_{k = 0}^{n} C_k C_{n - k}</math>, gdzie <math>C_n</math> są liczbami Catalana. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Wpisując w programie Maxima polecenia | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">'''load''' ("zeilberger"); | ||
| + | '''AntiDifference'''( 1/(k+1) * 1/(n-k+1) * '''binomial'''(2*k, k) * '''binomial'''(2*n-2*k, n-k), k);</span> | ||
| + | |||
| + | otrzymujemy | ||
| + | |||
| + | ::<math>F(n, k) = - {\small\frac{(n - 2 k + 1) (2 n - 2 k + 1)}{(n + 1) (n + 2) (n - k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 (n - k)}{n - k}}</math> | ||
| + | |||
| + | Czytelnik bez trudu pokaże, że | ||
| + | |||
| + | ::<math>F(n, k + 1) = - {\small\frac{(2 k + 1) (n - 2 k - 1)}{(n + 1) (n + 2) (k + 1)}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}}</math> | ||
| + | |||
| + | oraz łatwo sprawdzi związek <math>F(n, k + 1) - F (n, k) = f (n, k)</math> i wyliczy sumę oznaczoną. | ||
| + | |||
| + | Chcemy zwrócić uwagę na występującą tutaj trudność. Oczywiście | ||
| + | |||
| + | ::<math>S (n) = F (n, k) \biggr\rvert_{k = 0}^{k = n + 1}</math> | ||
| + | |||
| + | ale funkcja <math>F(n, k)</math> nie jest określona dla <math>k = n + 1</math>. Żeby ominąć ten problem, możemy przekształcić funkcję <math>F(n, k)</math> tak, aby możliwe było obliczenie jej wartości dla <math>k = n + 1</math> | ||
| + | |||
| + | ::<math>F(n, k) = - {\small\frac{n - 2 k + 1}{2 (n + 1) (n + 2)}} {\small\binom{2 k}{k}} {\small\binom{2 (n - k + 1)}{n - k + 1}}</math> | ||
| + | |||
| + | lub zapisać sumę w postaci | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n, k) = \sum_{k = 0}^{n - 1} f (n, k) + f (n, n) = F (n, k) \biggr\rvert_{k = 0}^{k = n} + f (n, n)</math><br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | === <span style="border-bottom:2px solid #000;">Znajdowanie równania rekurencyjnego dla sumy <math>\boldsymbol{S(n)}</math></span> === | ||
| + | |||
| + | <span id="D91" style="font-size: 110%; font-weight: bold;">Uwaga D91</span><br/> | ||
| + | Rozważmy sumę | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} f (n, k)</math> | ||
| + | |||
| + | W twierdzeniach [[#D107|D107]] i [[#D108|D108]] wyliczyliśmy <math>S(n)</math>, znajdując najpierw równanie rekurencyjne dla sumy. Możemy przypuszczać, że równanie rekurencyjne dla sumy <math>S(n)</math> wynika z istnienia odpowiedniego równania rekurencyjnego dla składników sumy <math>f(n, k)</math>. Zagadnieniem tym zajmowała się siostra Mary Celine Fasenmyer, która podała algorytm postępowania<ref name="Fasenmyer1"/><ref name="Fasenmyer2"/>. Prace Zeilbergera oraz Wilfa i Zeilbergera uogólniły ten algorytm<ref name="Zeilberger1"/><ref name="WilfZeilberger1"/>. My przedstawimy jedynie kilka prostych przypadków, które zilustrujemy przykładami. Szersze omówienie tematu Czytelnik znajdzie w książce Petkovšeka, Wilfa i Zeilbergera<ref name="PetkovsekWilfZeilberger1"/>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D92" style="font-size: 110%; font-weight: bold;">Twierdzenie D92</span><br/> | ||
| + | Niech <math>S(n) = \sum_{k = 0}^{n} f (n, k)</math>. Jeżeli składniki sumy <math>f(n, k)</math> spełniają równanie rekurencyjne | ||
| + | |||
| + | ::<math>a \cdot f (n + 1, k + 1) + b \cdot f (n + 1, k) + c \cdot f (n, k + 1) + d \cdot f (n, k) = 0</math> | ||
| + | |||
| + | gdzie współczynniki <math>a, b, c, d</math> są funkcjami tylko <math>n</math>, to suma <math>S (n)</math> spełnia równanie rekurencyjne | ||
| + | |||
| + | ::<math>(a + b) S (n + 1) + (c + d) S (n) - a \cdot f (n + 1, 0) - b \cdot f (n + 1, n + 1) - c [f (n, 0) - f (n, n + 1)] = 0</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Łatwo zauważamy, że | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n + 1, k + 1) = \sum_{j = 1}^{n + 1} f (n + 1, j)</math> | ||
| + | |||
| + | :::::::<math>\;\;\;\,\, = - f (n + 1, 0) + \sum^{n + 1}_{j = 0} f (n + 1, j)</math> | ||
| + | |||
| + | :::::::<math>\;\;\;\,\, = - f (n + 1, 0) + S (n + 1)</math> | ||
| + | |||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n + 1, k) = - f (n + 1, n + 1) + \sum_{k = 0}^{n + 1} f (n + 1, k) =</math> | ||
| + | |||
| + | ::::::<math>\;\;\; = - f (n + 1, n + 1) + S (n + 1)</math> | ||
| + | |||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} f (n, k + 1) = \sum_{j = 1}^{n + 1} f (n, j)</math> | ||
| + | |||
| + | ::::::<math>\;\;\; = - f (n, 0) + f (n, n + 1) + \sum_{j = 0}^{n} f (n, j)</math> | ||
| + | |||
| + | ::::::<math>\;\;\; = - f (n, 0) + f (n, n + 1) + S (n)</math> | ||
| + | |||
| + | |||
| + | Zatem sumując założone równanie rekurencyjne | ||
| + | |||
| + | ::<math>a \cdot f (n + 1, k + 1) + b \cdot f (n + 1, k) + c \cdot f (n, k + 1) + d \cdot f (n, k) = 0</math> | ||
| + | |||
| + | po <math>k</math> od <math>k = 0</math> do <math>k = n</math>, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot [- f (n + 1, 0) + S (n + 1)] + b \cdot [- f (n + 1, n + 1) + S (n + 1)] + c \cdot [- f (n, 0) + f (n, n + 1) + S (n)] + d \cdot S (n) = 0</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>(a + b) S (n + 1) + (c + d) S (n) - a \cdot f (n + 1, 0) - b \cdot f (n + 1, n + 1) - c [f (n, 0) - f (n, n + 1)] = 0</math> | ||
| + | |||
| + | Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D93" style="font-size: 110%; font-weight: bold;">Uwaga D93</span><br/> | ||
| + | Nie ma sensu stosowanie opisanej powyżej metody do prostych sum postaci <math>\sum_{k = 0}^{n} f (k)</math>, bo równanie rekurencyjne otrzymujemy w takim przypadku natychmiast: <math>S(n + 1) - S (n) = f (n + 1)</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D94" style="font-size: 110%; font-weight: bold;">Zadanie D94</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D87|D87]]) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\binom{n + k}{n}} = {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | W tym przypadku nie otrzymamy równania rekurencyjnego, ale od razu wzór ogólny na sumę <math>S(n)</math>. | ||
| + | |||
| + | Oczywiście <math>f(n, k) = {\small\binom{n + k}{n}}</math>. Po podstawieniu do równania (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{f (n + 1, k + 1)}{f (n, k)}} + b \cdot {\small\frac{f (n + 1, k)}{f (n, k)}} + c \cdot {\small\frac{f (n, k + 1)}{f (n, k)}} + d = 0</math> | ||
| + | |||
| + | i zredukowaniu silni, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{(n + k + 1) (n + k + 2)}{(k + 1) (n + 1)}} + b \cdot {\small\frac{n + k + 1}{n + 1}} + c \cdot {\small\frac{n + k + 1}{k + 1}} + d = 0</math> | ||
| + | |||
| + | Sprowadzając do wspólnego mianownika, mamy | ||
| + | |||
| + | ::<math>(a + b) k^2 + ((2 a + b + c + d) n + 3 a + 2 b + c + d) k + (a + c) n^2 + (3 a + b + 2 c + d) n + 2 a + b + c + d = 0</math> | ||
| + | |||
| + | Ponieważ powyższe równanie musi być prawdziwe dla każdego <math>k</math>, to współczynniki przy potęgach <math>k</math> muszą być równe zero. Zatem dostajemy układ równań | ||
| + | |||
| + | ::<math> | ||
| + | \begin{cases} | ||
| + | a + b = 0 \ | ||
| + | (2 a + b + c + d) n + 3 a + 2 b + c + d = 0 \ | ||
| + | (a + c) n^2 + (3 a + b + 2 c + d) n + 2 a + b + c + d = 0 \ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Łatwo znajdujemy rozwiązania: <math>b = - a</math>, <math>c = - a</math>, <math>d = 0</math>. Skąd wynika związek dla <math>S(n)</math> (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>- a S (n) = a - a {\small\binom{2 n + 2}{n + 1}} - a \left( 1 - {\small\binom{2 n + 1}{n}} \right)</math> | ||
| + | |||
| + | ::::<math>\;\;\: = - a \left[ {\small\binom{2 n + 2}{n + 1}} - {\small\binom{2 n + 1}{n}} \right]</math> | ||
| + | |||
| + | ::::<math>\;\;\: = - a {\small\binom{2 n + 1}{n}}</math> | ||
| + | |||
| + | I otrzymaliśmy dowodzony wzór. | ||
| + | |||
| + | |||
| + | Do obliczeń wykorzystaliśmy oprogramowanie Maxima. Poniżej podajemy kod procedury.<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum1() := | ||
| + | ( | ||
| + | f(n, k):= '''binomial'''(n+k, n), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n,k) ), | ||
| + | F1: a * f(n+1,k+1)/f(n,k) + b * f(n+1,k)/f(n,k) + c * f(n,k+1)/f(n,k) + d, /* równanie rekurencyjne dla składników sumy f(n, k) */<!--\--> | ||
| + | S1: (a+b) * S[n+1] + (c+d) * S[n] - a * f(n+1, 0) - b * f(n+1, n+1) - c * ( f(n, 0) - f(n, n+1) ), /* równanie rekurencyjne dla sumy S(n) */<!--\--> | ||
| + | /* przekształcamy F1, S1 */<!--\--> | ||
| + | F2: '''minfactorial'''( '''makefact'''(F1) ), /* zamień na silnie i uprość silnie */<!--\--> | ||
| + | '''print'''("równanie: ", F2),<!--\--> | ||
| + | F3: '''num'''( '''factor'''(F2) ), /* faktoryzuj i weź licznik */<!--\--> | ||
| + | '''print'''("licznik = ", '''rat'''(F3, k)),<!--\--> | ||
| + | deg: '''hipow'''(F3, k),<!--\--> | ||
| + | '''print'''("stopień = ", deg), | ||
| + | /* stopień wielomianu F3 jest równy deg i mamy deg+1 równań */<!--\--> | ||
| + | LE: ['''subst'''(0, k, F3) = 0],<!--\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F3, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\--> | ||
| + | '''print'''("lista równań: ", LE), | ||
| + | sol: '''solve'''( LE, [a, b, c, d] ), /* lista rozwiązań */ | ||
| + | '''print'''("rozwiązanie: ", sol), | ||
| + | S2: '''minfactorial'''( '''makefact'''(S1) ), /* zamień na silnie i uprość silnie */<!--\--> | ||
| + | S3: '''subst'''( sol[1], S2 ), /* pierwszy element listy sol */<!--\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\--> | ||
| + | '''solve'''( S4 = 0, S[n] )<!--\--> | ||
| + | /* S[n] = (2*n+1)! / (n! * (n+1)!) */ | ||
| + | )$</span> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D95" style="font-size: 110%; font-weight: bold;">Zadanie D95</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D86|D86]] p.1) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} r^k {\small\binom{n}{k}} = (r + 1)^n</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Oczywiście <math>f(n, k) = r^k {\small\binom{n}{k}}</math>. Po podstawieniu do równania (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{f (n + 1, k + 1)}{f (n, k)}} + b \cdot {\small\frac{f (n + 1, k)}{f (n, k)}} + c \cdot {\small\frac{f (n, k + 1)}{f (n, k)}} + d = 0</math> | ||
| + | |||
| + | i zredukowaniu silni, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{(n + 1) r}{k + 1}} + b \cdot {\small\frac{n + 1}{n - k + 1}} + c \cdot {\small\frac{(n - k) r}{k + 1}} + d = 0</math> | ||
| + | |||
| + | Sprowadzając do wspólnego mianownika, mamy | ||
| + | |||
| + | ::<math>(c r - d) k^2 + (- ((a + 2 c) n + a + c) r + (b + d) n + b) k + ((a + c) n^2 + (2 a + c) n + a) r + (b + d) n + b + d = 0</math> | ||
| + | |||
| + | Ponieważ powyższe równanie musi być prawdziwe dla każdego <math>k</math>, to współczynniki przy potęgach <math>k</math> muszą być równe zero. Zatem dostajemy układ równań | ||
| + | |||
| + | ::<math> | ||
| + | \begin{cases} | ||
| + | c r - d = 0 \ | ||
| + | - ((a + 2 c) n + a + c) r + (b + d) n + b = 0 \ | ||
| + | ((a + c) n^2 + (2 a + c) n + a) r + (b + d) n + b + d = 0 \ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Łatwo znajdujemy rozwiązania: <math>b = 0</math>, <math>c = - a</math>, <math>d = - a \cdot r</math>. Skąd wynika związek dla <math>S(n)</math> (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>S(n + 1) = (r + 1) S (n)</math> | ||
| + | |||
| + | Metodą indukcji matematycznej dowodzimy, że <math>S(n) = (r + 1)^n</math>. | ||
| + | |||
| + | |||
| + | Do obliczeń wykorzystaliśmy oprogramowanie Maxima. Poniżej podajemy kod procedury.<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum2() := | ||
| + | ( | ||
| + | f(n, k):= r^k * '''binomial'''(n, k), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n,k) ), | ||
| + | F1: a * f(n+1,k+1)/f(n,k) + b * f(n+1,k)/f(n,k) + c * f(n,k+1)/f(n,k) + d, /* równanie rekurencyjne dla składników sumy f(n, k) */<!--\--> | ||
| + | S1: (a+b) * S[n+1] + (c+d) * S[n] - a * f(n+1, 0) - b * f(n+1, n+1) - c * ( f(n, 0) - f(n, n+1) ), /* równanie rekurencyjne dla sumy S(n) */<!--\--> | ||
| + | /* przekształcamy F1, S1 */<!--\--> | ||
| + | F2: '''minfactorial'''( '''makefact'''(F1) ), /* zamień na silnie i uprość silnie */<!--\--> | ||
| + | '''print'''("równanie: ", F2),<!--\--> | ||
| + | F3: '''num'''( '''factor'''(F2) ), /* faktoryzuj i weź licznik */<!--\--> | ||
| + | '''print'''("licznik = ", '''rat'''(F3, k)),<!--\--> | ||
| + | deg: '''hipow'''(F3, k),<!--\--> | ||
| + | '''print'''("stopień = ", deg), | ||
| + | /* stopień wielomianu F3 jest równy deg i mamy deg+1 równań */<!--\--> | ||
| + | LE: ['''subst'''(0, k, F3) = 0],<!--\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F3, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\--> | ||
| + | '''print'''("lista równań: ", LE), | ||
| + | sol: '''solve'''( LE, [a, b, c, d] ), /* lista rozwiązań */ | ||
| + | '''print'''("rozwiązanie: ", sol), | ||
| + | S2: '''minfactorial'''( '''makefact'''(S1) ), /* zamień na silnie i uprość silnie */<!--\--> | ||
| + | S3: '''subst'''( sol[1], S2), /* pierwszy element listy sol */<!--\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\--> | ||
| + | /* S[n+1] = (r+1)*S[n] */ | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S4 = 0, S[n] ) /* S[n] = C*(r+1)^n */<!--\--> | ||
| + | )$</span> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D96" style="font-size: 110%; font-weight: bold;">Zadanie D96</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D86|D86]] p.2) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{n}{k}} = {\small\frac{2^{n + 1} - 1}{n + 1}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Oczywiście <math>f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math>. Po podstawieniu do równania (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{f (n + 1, k + 1)}{f (n, k)}} + b \cdot {\small\frac{f (n + 1, k)}{f (n, k)}} + c \cdot {\small\frac{f (n, k + 1)}{f (n, k)}} + d = 0</math> | ||
| + | |||
| + | i zredukowaniu silni, otrzymujemy | ||
| + | |||
| + | ::<math>a \cdot {\small\frac{n + 1}{k + 2}} + b \cdot {\small\frac{n + 1}{n - k + 1}} + c \cdot {\small\frac{n - k}{k + 2}} + d = 0</math> | ||
| + | |||
| + | Sprowadzając do wspólnego mianownika, mamy | ||
| + | |||
| + | ::<math>(c - d) k^2 + ((- a + b - 2 c + d) n - a + b - c - d) k + (a + c) n^2 + (2 a + 2 b + c + 2 d) n + a + 2 b + 2 d = 0</math> | ||
| + | |||
| + | Ponieważ powyższe równanie musi być prawdziwe dla każdego <math>k</math>, to współczynniki przy potęgach <math>k</math> muszą być równe zero. Zatem dostajemy układ równań | ||
| + | |||
| + | ::<math> | ||
| + | \begin{cases} | ||
| + | c - d = 0 \ | ||
| + | (- a + b - 2 c + d) n - a + b - c - d = 0 \ | ||
| + | (a + c) n^2 + (2 a + 2 b + c + 2 d) n + a + 2 b + 2 d = 0 \ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Łatwo znajdujemy rozwiązania: <math>b = 0</math>, <math>c = - a \cdot {\small\frac{n + 1}{n + 2}}</math>, <math>d = - a \cdot {\small\frac{n + 1}{n + 2}}</math>. Skąd wynika związek dla <math>S(n)</math> (zobacz [[#D92|D92]]) | ||
| + | |||
| + | ::<math>(n + 2) S (n + 1) = 2 (n + 1) S (n) + 1</math> | ||
| + | |||
| + | Metodą indukcji matematycznej łatwo dowodzimy, że <math>S(n) = {\small\frac{2^{n + 1} - 1}{n + 1}}</math>. | ||
| + | |||
| + | |||
| + | Do obliczeń wykorzystaliśmy oprogramowanie Maxima. Poniżej podajemy kod procedury.<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum3() := | ||
| + | ( | ||
| + | f(n, k):= 1/(k+1) * '''binomial'''(n, k), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n,k) ), | ||
| + | F1: a * f(n+1,k+1)/f(n,k) + b * f(n+1,k)/f(n,k) + c * f(n,k+1)/f(n,k) + d, /* równanie rekurencyjne dla składników sumy f(n, k) */<!--\--> | ||
| + | S1: (a+b) * S[n+1] + (c+d) * S[n] - a * f(n+1, 0) - b * f(n+1, n+1) - c * ( f(n, 0) - f(n, n+1) ), /* równanie rekurencyjne dla sumy S(n) */<!--\--> | ||
| + | /* przekształcamy F1, S1 */<!--\--> | ||
| + | F2: '''minfactorial'''( '''makefact'''(F1) ), /* zamień na silnie i uprość silnie */<!--\--> | ||
| + | '''print'''("równanie: ", F2),<!--\--> | ||
| + | F3: '''num'''( '''factor'''(F2) ), /* faktoryzuj i weź licznik */<!--\--> | ||
| + | '''print'''("licznik = ", '''rat'''(F3, k)),<!--\--> | ||
| + | deg: '''hipow'''(F3, k),<!--\--> | ||
| + | '''print'''("stopień = ", deg), | ||
| + | /* stopień wielomianu F3 jest równy deg i mamy deg+1 równań */<!--\--> | ||
| + | LE: ['''subst'''(0, k, F3) = 0],<!--\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F3, k^i)=0, LE), /* kolejne równania wpisujemy do listy LE */<!--\--> | ||
| + | '''print'''("lista równań: ", LE), | ||
| + | sol: '''solve'''( LE, [a, b, c, d] ), /* lista rozwiązań */ | ||
| + | '''print'''("rozwiązanie: ", sol), | ||
| + | S2: '''minfactorial'''( '''makefact'''(S1) ), /* zamień na silnie i uprość silnie */<!--\--> | ||
| + | S3: '''subst'''( sol[1], S2), /* pierwszy element listy sol */<!--\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\--> | ||
| + | /* (n+2)*S[n+1] = 2*(n+1)*S[n] + 1 */ | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S4 = 0, S[n] ) /* S[n] = ( (C+1) * 2^n - 1 )/(n + 1) */<!--\--> | ||
| + | )$</span> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D97" style="font-size: 110%; font-weight: bold;">Zadanie D97</span><br/> | ||
| + | Niech <math>n \in \mathbb{N}_0 \;</math> i <math>\; k \in \mathbb{Z}</math>. Uzasadnić, dlaczego przyjmujemy, że <math>{\small\binom{n}{k}} = 0</math>, gdy <math>k < 0 \;</math> lub <math>\; k > n</math>. | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Jeżeli zapiszmy <math>{\small\binom{n}{k}}</math> w postaci | ||
| + | |||
| + | ::<math>{\small\binom{n}{k}} = {\small\frac{n!}{k! (n - k) !}} = {\small\frac{n \cdot (n - 1) \cdot \ldots \cdot (n - k + 1)}{k!}}</math> | ||
| + | |||
| + | to natychmiast widzimy, że prawa strona musi być równa zero dla <math>k > n</math>. | ||
| + | |||
| + | Jeżeli we wzorze Pascala | ||
| + | |||
| + | ::<math>{\small\binom{n}{k}} = {\small\binom{n - 1}{k}} + {\small\binom{n - 1}{k - 1}}</math> | ||
| + | |||
| + | położymy <math>n = m + 1 \;</math> i <math>\; k = 0</math>, to otrzymamy | ||
| + | |||
| + | ::<math>1 = 1 + {\small\binom{m}{- 1}}</math> | ||
| + | |||
| + | czyli <math>{\small\binom{m}{- 1}} = 0</math> | ||
| + | |||
| + | I tak samo dla wszystkich <math>k < 0</math>. | ||
| + | |||
| + | |||
| + | Znacznie mocniejszego uzasadnienia dostarczy nam funkcja gamma (zobacz [[#D110|D110]]), która jest uogólnieniem silni na liczby rzeczywiste. Rozważmy funkcję | ||
| + | |||
| + | ::<math>g(n, x) = {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1) \Gamma (n - x + 1)}}</math> | ||
| + | |||
| + | Jeżeli <math>k \in \mathbb{Z} \;</math> i <math>\; 0 \leqslant k \leqslant n</math>, to funkcja <math>g(n, k)</math> jest równa współczynnikowi dwumianowemu <math>{\small\binom{n}{k}}</math>. | ||
| + | |||
| + | ::<math>g(n, k) = {\small\frac{\Gamma (n + 1)}{\Gamma (k + 1) \Gamma (n - k + 1)}} = {\small\frac{n!}{k! (n - k) !}} = {\small\binom{n}{k}}</math> | ||
| + | |||
| + | |||
| + | W przypadku, gdy <math>k < 0</math>, mamy | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow k} g (n, x) = \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1) \Gamma (n - x + 1)}} = \lim_{x \rightarrow k} {\small\frac{1}{\Gamma (x + 1)}} \cdot \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (n - x + 1)}} = 0 \cdot {\small\frac{\Gamma (n + 1)}{\Gamma (n - k + 1)}} = 0</math> | ||
| + | |||
| + | |||
| + | W przypadku, gdy <math>k > n</math>, dostajemy | ||
| + | |||
| + | ::<math>\lim_{x \rightarrow k} g (n, x) = \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1) \Gamma (n - x + 1)}} = \lim_{x \rightarrow k} {\small\frac{\Gamma (n + 1)}{\Gamma (x + 1)}} \cdot \lim_{x \rightarrow k} {\small\frac{1}{\Gamma (n - x + 1)}} = {\small\frac{\Gamma (n + 1)}{\Gamma (k + 1)}} \cdot 0 = 0</math> | ||
| + | |||
| + | |||
| + | Co najlepiej wyjaśnia, dlaczego przyjmujemy, że <math>{\small\binom{n}{k}} = 0</math>, gdy <math>k < 0 \;</math> lub <math>\; k > n</math>.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D98" style="font-size: 110%; font-weight: bold;">Twierdzenie D98</span><br/> | ||
| + | Niech <math>n, I, J \in \mathbb{N}_0 \;</math> i <math>\; k \in \mathbb{Z}</math>. Jeżeli <math>f(n, k) = 0</math> | ||
| + | dla <math>k \notin [0, n] \,</math> i składniki sumy <math>f(n, k)</math> spełniają równanie rekurencyjne | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = 0</math> | ||
| + | |||
| + | gdzie współczynniki <math>a_{i j}</math> są funkcjami tylko <math>n</math>, to suma | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} f (n, k)</math> | ||
| + | |||
| + | spełnia następujące równanie rekurencyjne | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} S (n + i) \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| + | Z założenia <math>f(n, k) = 0</math> dla <math>k \notin [0, n]</math>, zatem sumę <math>S(n)</math> możemy zapisać w postaci | ||
| + | |||
| + | ::<math>S(n) = \sum_{k = 0}^{n} f (n, k) = \sum_{k = - \infty}^{+ \infty} f (n, k)</math> | ||
| + | |||
| + | Niech <math>0 \leqslant i \leqslant I</math> oraz <math>0 \leqslant j \leqslant J</math>. Rozważmy sumę | ||
| + | |||
| + | ::<math>\sum_{k = - J}^{n + I} f (n + i, k + j)</math> | ||
| + | |||
| + | Zauważmy, że <math>f(n + i, k + j) = 0</math> dla <math>k \notin [- J, n + I]</math>, bo | ||
| + | |||
| + | :* dla <math>k < - J</math> mamy <math>k + j < - J + j \leqslant 0</math> | ||
| + | :* dla <math>k > n + I</math> mamy <math>k + j > n + I + j \geqslant n + I \geqslant n + i</math> | ||
| + | |||
| + | Wynika stąd, że rozszerzając rozpatrywaną sumę na cały zbiór liczb całkowitych, nie zmienimy wartości sumy. Czyli, że | ||
| + | |||
| + | ::<math>\sum_{k = - J}^{n + I} f (n + i, k + j) = \sum_{k = - \infty}^{+ \infty} f (n + i, k + j)</math> | ||
| + | |||
| + | |||
| + | Teraz już łatwo otrzymujemy równanie rekurencyjne dla sumy <math>S(n)</math> | ||
| + | |||
| + | ::<math>0 = \sum_{k = - J}^{n + I} \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{k = - J}^{n + I} f (n + i, k + j) \,</math><span style="color: Green"><sup>[a]</sup></span> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{k = - \infty}^{+ \infty} f (n + i, k + j)</math> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum^{+ \infty}_{l = - \infty} f (n + i, l)</math> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot S (n + i)</math> | ||
| + | |||
| + | ::::::::::::<math>\;\;\;\:\, = \sum_{i = 0}^{I} S (n + i) \left[ \sum_{j = 0}^{J} a_{i j} \right]</math> | ||
| + | |||
| + | Co należało pokazać. | ||
| + | |||
| + | |||
| + | <hr style="width: 25%; height: 2px; " /> | ||
| + | <span style="color: Green">[a]</span> W przypadku wielokrotnych sum skończonych możemy dowolnie zmieniać ich kolejność ze względu na łączność dodawania.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D99" style="font-size: 110%; font-weight: bold;">Uwaga D99</span><br/> | ||
| + | Z zadania [[#D97|D97]] wynika, że jeżeli funkcja <math>f(n, k)</math> zawiera czynnik <math>{\small\binom{n}{k}}</math>, to może spełniać warunek <math>f(n, k) = 0</math> dla <math>k \notin [0, n]</math>. Oczywiście nie jest to warunek wystarczający, bo funkcja <math>f (n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math> jest różna od zera dla <math>k = - 1</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D100" style="font-size: 110%; font-weight: bold;">Zadanie D100</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór (zobacz [[#D86|D86]] p.3) | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k {\small\binom{n}{k}} = n 2^{n - 1}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Oczywiście <math>f(n, k) = k {\small\binom{n}{k}}</math>. Do rozwiązania problemu wykorzystamy oprogramowanie Maxima i procedurę<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum5(I, J) := | ||
| + | ( | ||
| + | '''read'''("podaj definicję f(n, k)"), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n, k) ), | ||
| + | F1: '''sum'''( '''sum'''( a[i,j] * f(n+i, k+j), i, 0, I), j, 0, J) / f(n, k),<!--\--> | ||
| + | F2: '''num'''( '''factor'''( '''minfactorial'''( '''makefact'''( '''expand'''( F1 ) ) ) ) ),<!--\--> | ||
| + | deg: '''hipow'''(F2, k),<!--\--> | ||
| + | LE: ['''subst'''(0, k, F2) = 0],<!--\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F2, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\--> | ||
| + | LV: '''create_list'''(a[i, j], i, 0, I , j, 0, J), /* lista zmiennych */ | ||
| + | sol: '''solve'''( LE, LV ), /* lista rozwiązań */ | ||
| + | S1: '''sum'''( S[n+i] * '''sum'''(a[i,j], j, 0, J), i, 0, I),<!--\--> | ||
| + | S2: '''subst'''( sol[1], S1 ), /* pierwszy element listy sol */<!--\--> | ||
| + | S3: '''num'''( '''factor'''( '''expand'''( S2 ) ) ),<!--\--> | ||
| + | '''print'''("rekurencja: ", S3 = 0),<!--\--> | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S3 = 0, S[n] )<!--\--> | ||
| + | )$</span> | ||
| + | |||
| + | |||
| + | Wywołujemy procedurę <span style="font-size: 90%; color:black;"><code>sum5(1, 2)</code></span> i wpisujemy funkcję | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">f(n, k):= k * '''binomial'''(n, k)</span> | ||
| + | |||
| + | W wyniku otrzymujemy równanie rekurencyjne | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">n * S[n+1] = 2 * (n+1) * S[n]</span> | ||
| + | |||
| + | którego rozwiązanie jest postaci | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">S[n] = C * n * 2^(n-1)</span> | ||
| + | |||
| + | Łatwo sprawdzamy, że <span style="font-size: 90%; color:black;"><code>C = 1</code></span>. Co należało pokazać.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D101" style="font-size: 110%; font-weight: bold;">Zadanie D101</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwe są wzory | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^2 {\small\binom{n}{k}} = n (n + 1) 2^{n - 2}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^3 {\small\binom{n}{k}} = n^2 (n + 3) 2^{n - 3}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\binom{n}{k}}^2 = {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k {\small\binom{n}{k}}^2 = {\small\frac{1}{2}} n {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^2 {\small\binom{n}{k}}^2 = n^2 {\small\binom{2 n - 2}{n - 1}}</math> | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} k^3 {\small\binom{n}{k}}^2 = {\small\frac{1}{2}} n^2 (n + 1) {\small\binom{2 n - 2}{n - 1}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Wskazówki: | ||
| + | |||
| + | Korzystamy z procedury <span style="font-size: 90%; color:black;"><code>sum5()</code></span>, której kod został podany w zadaniu [[#D100|D100]]. | ||
| + | |||
| + | Zawsze próbujemy znaleźć rozwiązanie dla najmniejszych wartości parametrów <span style="font-size: 90%; color:black;"><code>I, J</code></span>. | ||
| + | |||
| + | ::<math>\Gamma \left( n + {\small\frac{1}{2}} \right) = 2^{- 2 n} \sqrt{\pi} \cdot {\small\frac{(2 n) !}{n!}} = 2^{- 2 n} \sqrt{\pi} \cdot n! \cdot {\small\binom{2 n}{n}}</math> | ||
| + | |||
| + | '''Punkt 1.''' <span style="font-size: 90%; color:black;"><code>sum5(1, 2)</code></span>, zobacz też <span style="font-size: 90%; color:black;"><code>sum5(2, 1)</code></span> | ||
| + | |||
| + | '''Punkt 2.''' <span style="font-size: 90%; color:black;"><code>sum5(1, 3)</code></span>, zobacz też <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 3.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 4.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 5.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 2)</code></span> | ||
| + | |||
| + | '''Punkt 6.''' <span style="font-size: 90%; color:black;"><code>sum5(2, 3)</code></span>, zobacz też <span style="font-size: 90%; color:black;"><code>sum5(3, 2)</code></span><br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D102" style="font-size: 110%; font-weight: bold;">Uwaga D102</span><br/> | ||
| + | Niech <math>S(n) = \sum_{k = 0}^{n} f (n, k)</math>. Wiemy (zobacz [[#D98|D98]]), że jeżeli dla dowolnego <math>n</math> wartość funkcji <math>f(n, k)</math> jest określona dla wszystkich <math>k \in \mathbb{Z} \;</math> i <math>\; f(n, k) = 0</math> dla <math>k \notin [0, n]</math>, to sumę <math>S(n)</math> możemy zapisać w równoważnej postaci | ||
| + | <math>S(n) = \sum_{k = 0}^{n} f (n, k) = \sum_{k \in \mathbb{Z}} f (n, k)</math> | ||
| + | |||
| + | |||
| + | Rozważmy teraz funkcję <math>f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math>, która powyższego warunku nie spełnia, bo jest różna od zera dla <math>k = - 1</math>. Jeżeli zapiszemy <math>f(n, k)</math> w postaci | ||
| + | |||
| + | ::<math>f(n, k) = {\small\frac{1}{k + 1}} {\small\binom{n}{k}} = {\small\frac{1}{k + 1}} \cdot {\small\frac{n!}{k! (n - k) !}} = {\small\frac{n!}{(k + 1) ! (n - k) !}}</math> | ||
| + | |||
| + | to natychmiast widzimy, że | ||
| + | |||
| + | ::<math>f(n, - 1) = {\small\frac{n!}{0! (n + 1) !}} = {\small\frac{1}{n + 1}}</math> | ||
| + | |||
| + | Zatem w przypadku tej funkcji mamy | ||
| + | |||
| + | ::<math>\sum_{k \in \mathbb{Z}} f (n, k) = \sum_{k = 0}^{n} f (n, k) + f (n, - 1) = S (n) + {\small\frac{1}{n + 1}}</math> | ||
| + | |||
| + | |||
| + | '''Zakładając''', że spełnione jest równanie | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = 0</math> | ||
| + | |||
| + | otrzymujemy następujące równanie rekurencyjne dla sumy <math>S(n) = \sum_{k \in \mathbb{Z}} f (n, k)</math> | ||
| + | |||
| + | ::<math>\sum_{k \in \mathbb{Z}} \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot f (n + i, k + j) = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{k \in \mathbb{Z}} f (n + i, k + j)</math> | ||
| + | |||
| + | :::::::::::<math>\;\;\;\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \sum_{l \in \mathbb{Z}} f (n + i, l)</math> | ||
| + | |||
| + | :::::::::::<math>\;\;\;\, = \sum_{i = 0}^{I} \sum_{j = 0}^{J} a_{i j} \cdot \left[ S (n + i) + {\small\frac{1}{n + i + 1}} \right]</math> | ||
| + | |||
| + | :::::::::::<math>\;\;\;\, = \sum_{i = 0}^{I} \left[ S (n + i) + {\small\frac{1}{n + i + 1}} \right] \cdot \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0</math> | ||
| + | |||
| + | |||
| + | Jeżeli mamy skończoną liczbę punktów <math>k_r \notin [0, n]</math>, w których funkcja <math>f(n, k)</math> jest określona i różna od zera, to możemy zdefiniować funkcję | ||
| + | |||
| + | ::<math>T(n) = f (n, k_1) + f (n, k_2) + f (n, k_3) + \ldots = \sum_r f (n, k_r)</math> | ||
| + | |||
| + | W takim przypadku otrzymamy następujące równanie rekurencyjne dla sumy <math>S (n) = \sum_{k = 0}^{n} f (n, k)</math> | ||
| + | |||
| + | ::<math>\sum_{i = 0}^{I} [S (n + i) + T (n + i)] \cdot \left[ \sum_{j = 0}^{J} a_{i j} \right] = 0</math> | ||
| + | |||
| + | |||
| + | Wystarczy drobna modyfikacja procedury <span style="font-size: 90%; color:black;"><code>sum5()</code></span>, aby obejmowała ona również takie przypadki<!-- aby uniknąć formatowania zmiennych F1, S1 wstawiamy znaki \ --> | ||
| + | |||
| + | <span style="font-size: 90%; color:black;">sum6(I, J):= | ||
| + | ( | ||
| + | '''read'''("podaj definicję f(n, k)"), /* składnik sumy */ | ||
| + | '''print'''("f(n, k) = ", f(n, k) ), | ||
| + | '''read'''("podaj definicję T(n)"), /* suma skończonych wartości funkcji f(n, k), gdzie k<0 lub k>n */ | ||
| + | '''print'''("T(n) = ", T(n) ), | ||
| + | F1: '''sum'''( '''sum'''( a[i,j] * f(n+i, k+j), i, 0, I), j, 0, J) / f(n, k),<!--\--> | ||
| + | F2: '''num'''( '''factor'''( '''minfactorial'''( '''makefact'''( '''expand'''( F1 ) ) ) ) ),<!--\--> | ||
| + | deg: '''hipow'''(F2, k),<!--\--> | ||
| + | LE: ['''subst'''(0, k, F2) = 0],<!--\--> | ||
| + | '''for''' i: 1 '''thru''' deg '''do''' '''push'''('''coeff'''(F2, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */<!--\--> | ||
| + | LV: '''create_list'''(a[i, j], i, 0, I , j, 0, J), /* lista zmiennych */ | ||
| + | sol: '''solve'''( LE, LV ), /* lista rozwiązań */ | ||
| + | S1: '''sum'''( ( S[n+i] + T(n+i) ) * '''sum'''( a[i,j], j, 0, J ), i, 0, I ),<!--\--> | ||
| + | S2: '''num'''( '''factor'''( '''minfactorial'''( '''makefact'''( '''expand'''( S1 ) ) ) ) ),<!--\--> | ||
| + | S3: '''subst'''( sol[1], S2 ), /* pierwszy element listy sol */<!--\--> | ||
| + | S4: '''num'''( '''factor'''( '''expand'''( S3 ) ) ),<!--\--> | ||
| + | '''print'''("rekurencja: ", S4 = 0),<!--\--> | ||
| + | '''load'''("solve_rec"), | ||
| + | '''solve_rec'''( S4 = 0, S[n] )<!--\--> | ||
| + | )$</span> | ||
| + | |||
| + | |||
| + | Korzystając z powyższej procedury, Czytelnik może łatwo policzyć wypisane poniżej sumy. | ||
| + | |||
| + | ::{| class="wikitable plainlinks" style="font-size: 90%; text-align: center; margin-right: auto;" | ||
| + | |- | ||
| + | ! <math>\boldsymbol{f(n,k)}</math> || <math>\boldsymbol{f(n,-1)}</math> || <math>\boldsymbol{f(n,-2)}</math> || <math>\boldsymbol{\sum_{k = 0}^n f(n,k)}</math> || WolframAlpha | ||
| + | |- | ||
| + | | <math>{\small\frac{1}{k + 1}} {\small\binom{n}{k}}</math> || <math>{\small\frac{1}{n + 1}}</math> || <math>0</math> || <math>{\small\frac{2^{n + 1} - 1}{n + 1}}</math> || [https://www.wolframalpha.com/input?i=Sum%5B1%2F%28k%2B1%29+*+binomial%28n%2Ck%29%2C+%7Bk%2C+0%2C+n%7D%5D LINK1] | ||
| + | |- | ||
| + | | <math>{\small\frac{1}{k + 2}} {\small\binom{n}{k}}</math> || <math>0</math> || <math>- {\small\frac{1}{(n + 1) (n + 2)}}</math> || <math>{\small\frac{n 2^{n + 1} + 1}{(n + 1) (n + 2)}}</math> || [https://www.wolframalpha.com/input?i=Sum%5B1%2F%28k%2B2%29+*+binomial%28n%2C+k%29%2C+%7Bk%2C+0%2C+n%7D%5D LINK2] | ||
| + | |- | ||
| + | | <math>{\small\frac{1}{(k + 1) (k + 2)}} {\small\binom{n}{k}}</math> || <math>{\small\frac{1}{n + 1}}</math> || <math>{\small\frac{1}{(n + 1) (n + 2)}}</math> || <math>{\small\frac{2^{n + 2} - n - 3}{(n + 1) (n + 2)}}</math> || [https://www.wolframalpha.com/input?i=Sum%5B1%2F%28k%2B1%29+*+1%2F%28k%2B2%29+*+binomial%28n%2C+k%29%2C+%7Bk%2C+0%2C+n%7D%5D LINK3] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D103" style="font-size: 110%; font-weight: bold;">Zadanie D103</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = 4^n</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Zauważmy, że składniki sumy są równe zero dla <math>k \notin [0, n]</math> (zobacz zadanie [[#D115|D115]]). Zatem korzystając z procedury <span style="font-size: 90%; color:black;"><code>sum6(2, 1)</code></span>, otrzymujemy równanie rekurencyjne | ||
| + | |||
| + | ::<math>(n + 2) S (n + 2) - 4 (2 n + 3) S (n + 1) + 16 (n + 1) S (n) = 0</math> | ||
| + | |||
| + | i rozwiązanie | ||
| + | |||
| + | ::<math>S(n) = C \cdot 4^n</math> | ||
| + | |||
| + | Łatwo sprawdzamy, że <math>C = 1</math>.<br/> | ||
| + | □ | ||
| + | {{\Spoiler}} | ||
| + | |||
| + | |||
| + | |||
| + | <span id="D104" style="font-size: 110%; font-weight: bold;">Zadanie D104</span><br/> | ||
| + | Pokazać, że dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| + | |||
| + | ::<math>\sum_{k = 0}^{n} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Rozwiązanie|Hide=Ukryj rozwiązanie}} | ||
| + | Zauważmy, że składniki sumy są równe zero dla <math>k \notin [0, n]</math> (zobacz [[#D115|D115]]) poza punktem <math>k = - 1</math>. Wiemy, że (zobacz [[#D116|D116]]) | ||
| + | |||
| + | ::<math>\lim_{k \rightarrow - 1} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} = - {\small\frac{1}{2}}</math> | ||
| + | |||
| + | Zatem | ||
| + | |||
| + | ::<math>\lim_{k \rightarrow - 1} {\small\frac{1}{k + 1}} {\small\binom{2 k}{k}} {\small\binom{2 n - 2 k}{n - k}} = - {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | Czyli | ||
| + | |||
| + | ::<math>f(n, - 1) = - {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> | ||
| + | |||
| + | |||
| + | Korzystając z procedury <span style="font-size: 90%; color:black;"><code>sum6(2, 1)</code></span>, otrzymujemy równanie rekurencyjne | ||
| + | |||
| + | ::<math>(n^2 + 5 n + 6) S (n + 2) - 8 (n^2 + 4 n + 4) S (n + 1) + 16 (n^2 + 3 n + 2) S (n) + 2 \cdot {\small\frac{(2 n + 2) !}{[(n + 1) !]^2}} = 0</math> | ||
| + | |||
| + | ::<math>(n + 2) (n + 3) S (n + 2) - 8 (n + 2)^2 S (n + 1) + 16 (n + 1) (n + 2) S (n) + 2 \cdot {\small\frac{(2 n + 2) !}{[(n + 1) !]^2}} = 0</math> | ||
| + | |||
| + | ::<math>(n + 3) S (n + 2) - 8 (n + 2) S (n + 1) + 16 (n + 1) S (n) + 2 \cdot {\small\frac{(2 n + 2) !}{(n + 1) ! (n + 2) !}} = 0</math> | ||
| + | |||
| + | Maxima nie potrafi rozwiązać tego równania rekurencyjnego, ale można sprawdzić, że <math>S(n) = {\small\frac{1}{2}} {\small\binom{2 n + 2}{n + 1}}</math> jest jego rozwiązaniem.<br/> | ||
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 3112: | Linia 3984: | ||
| | ||
| − | === <span style=" | + | === <span style="border-bottom:2px solid #000; padding-bottom: 0.2em">Dowód własności liczb Catalana <math>{\small C_{n + 1} = \textstyle\sum_{k = 0}^{n} C_k C_{n - k}}</math></span> === |
| − | <span id=" | + | <span id="D105" style="font-size: 110%; font-weight: bold;">Uwaga D105</span><br/> |
Przedstawiony poniżej dowód czwartego punktu twierdzenia [[#D84|D84]] został oparty na pracy Jovana Mikicia<ref name="JovanMikic1"/>. | Przedstawiony poniżej dowód czwartego punktu twierdzenia [[#D84|D84]] został oparty na pracy Jovana Mikicia<ref name="JovanMikic1"/>. | ||
| − | <span id=" | + | <span id="D106" style="font-size: 110%; font-weight: bold;">Twierdzenie D106</span><br/> |
Jeżeli funkcja <math>f(k)</math> nie zależy od <math>n</math> i dane są sumy | Jeżeli funkcja <math>f(k)</math> nie zależy od <math>n</math> i dane są sumy | ||
| Linia 3151: | Linia 4023: | ||
| − | <span id=" | + | <span id="D107" style="font-size: 110%; font-weight: bold;">Twierdzenie D107</span><br/> |
Dla <math>n \geqslant 0</math> prawdziwy jest wzór | Dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| Linia 3179: | Linia 4051: | ||
:::<math>\;\;\:\, = {\small\frac{n S (n)}{2}}</math> | :::<math>\;\;\:\, = {\small\frac{n S (n)}{2}}</math> | ||
| − | Ponieważ <math>T(n) = {\small\frac{n S (n)}{2}} \;</math> i <math>\; T(n) = 4 T (n - 1) + 2 S (n - 1)</math> (zobacz [[# | + | Ponieważ <math>T(n) = {\small\frac{n S (n)}{2}} \;</math> i <math>\; T(n) = 4 T (n - 1) + 2 S (n - 1)</math> (zobacz [[#D106|D106]]), to otrzymujemy |
::<math>{\small\frac{n S (n)}{2}} = 4 \cdot {\small\frac{(n - 1) S (n - 1)}{2}} + 2 S (n - 1)</math> | ::<math>{\small\frac{n S (n)}{2}} = 4 \cdot {\small\frac{(n - 1) S (n - 1)}{2}} + 2 S (n - 1)</math> | ||
| Linia 3195: | Linia 4067: | ||
| − | <span id=" | + | <span id="D108" style="font-size: 110%; font-weight: bold;">Twierdzenie D108</span><br/> |
Dla <math>n \geqslant 0</math> prawdziwy jest wzór | Dla <math>n \geqslant 0</math> prawdziwy jest wzór | ||
| Linia 3219: | Linia 4091: | ||
</div> | </div> | ||
| − | Ponieważ <math>T(n) = (n + 1) S (n) - 4^n \;</math> i <math>\; T(n) = 4 T (n - 1) + 2 S (n - 1)</math> (zobacz [[# | + | Ponieważ <math>T(n) = (n + 1) S (n) - 4^n \;</math> i <math>\; T(n) = 4 T (n - 1) + 2 S (n - 1)</math> (zobacz [[#D106|D106]]), to otrzymujemy |
<div style="margin-top: 1em; margin-bottom: 1em;"> | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| Linia 3249: | Linia 4121: | ||
| − | <span id=" | + | <span id="D109" style="font-size: 110%; font-weight: bold;">Twierdzenie D109</span><br/> |
Jeżeli <math>C_n</math> są liczbami Catalana, to | Jeżeli <math>C_n</math> są liczbami Catalana, to | ||
| Linia 3286: | Linia 4158: | ||
| | ||
| − | <span id=" | + | <span id="D110" style="font-size: 110%; font-weight: bold;">Definicja D110</span><br/> |
Funkcja <math>\Gamma (z)</math><ref name="gamma1"/> jest zdefiniowana równoważnymi wzorami | Funkcja <math>\Gamma (z)</math><ref name="gamma1"/> jest zdefiniowana równoważnymi wzorami | ||
| Linia 3404: | Linia 4276: | ||
| − | <span id=" | + | <span id="D111" style="font-size: 110%; font-weight: bold;">Twierdzenie D111</span><br/> |
Dla funkcji <math>\Gamma (z)</math> prawdziwe są następujące wzory | Dla funkcji <math>\Gamma (z)</math> prawdziwe są następujące wzory | ||
| Linia 3419: | Linia 4291: | ||
</div> | </div> | ||
| − | :* <math>\Gamma (z) | + | :* <math>\Gamma (2 z) = {\small\frac{2^{2 z - 1}}{\sqrt{\pi}}} \cdot \Gamma (z) \Gamma \left( z + {\small\frac{1}{2}} \right) \qquad 2 z \notin \mathbb{Z}_- \cup \{ 0 \} \qquad \qquad </math> (wzór Legendre'a o podwajaniu) |
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| Linia 3429: | Linia 4301: | ||
'''Punkt 2.''' | '''Punkt 2.''' | ||
| − | Z definicji Gaussa otrzymujemy | + | Z definicji Gaussa funkcji <math>\Gamma (z)</math> otrzymujemy |
::<math>\Gamma (z) = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ::<math>\Gamma (z) = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | ||
| Linia 3437: | Linia 4309: | ||
Zatem | Zatem | ||
| − | ::<math> | + | ::<math>z \Gamma (z) = z \cdot \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> |
| − | + | :::<math>\;\;\;\;\, = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{(z + 1) \cdot \ldots \cdot (z + n)}} \cdot {\small\frac{n}{z + n + 1}} \cdot {\small\frac{z + n + 1}{n}}</math> | |
| − | + | :::<math>\;\;\;\;\, = \lim_{n \rightarrow \infty} {\small\frac{n^{z + 1} n!}{(z + 1) \cdot \ldots \cdot (z + n) (z + n + 1)}} \cdot \left( 1 + {\small\frac{z + 1}{n}} \right)</math> | |
| − | ::::<math>\;\;\ | + | :::<math>\;\;\;\;\, = \lim_{n \rightarrow \infty} {\small\frac{n^{z + 1} n!}{(z + 1) \cdot \ldots \cdot (z + n) (z + n + 1)}} \cdot \lim_{n \rightarrow \infty} \left( 1 + {\small\frac{z + 1}{n}} \right)</math> |
| + | |||
| + | :::<math>\;\;\;\;\, = \Gamma (z + 1)</math> | ||
'''Punkt 3.''' | '''Punkt 3.''' | ||
| Linia 3470: | Linia 4344: | ||
'''Punkt 4.''' | '''Punkt 4.''' | ||
| − | Z definicji Gaussa funkcji gamma | + | Z definicji Gaussa funkcji gamma mamy |
| − | ::<math>\Gamma (z) = \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}}</math> | + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{n^{2 z} n!}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + n)}}</math> |
| + | |||
| + | Jeżeli w powyższym równaniu położymy <math>2 n</math> zamiast <math>n</math>, to dostaniemy | ||
| + | |||
| + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n)}}</math> | ||
| + | |||
| + | |||
| + | Zauważmy teraz, że | ||
| + | |||
| + | ::<math>2^{2 n + 2} [z (z + 1) \cdot \ldots \cdot (z + n)] \cdot \left[ \left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right) \right] = [2 z (2 z + 2) \cdot \ldots \cdot (2 z + 2 n)] \cdot [(2 z + 1) (2 z + 3) \cdot \ldots \cdot (2 z + 2 n + 1)]</math> | ||
| − | + | ::::::::::::::::::::::<math>\;\;\;\,\, = 2 z (2 z + 1) (2 z + 2) (2 z + 3) \cdot \ldots \cdot (2 z + 2 n) (2 z + 2 n + 1)</math> | |
| − | + | Czyli | |
| − | + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n)}}</math> | |
| − | <div style="margin-top: | + | <div style="margin-top: 1em; margin-bottom: 1em;"> |
| − | ::<math>\ | + | :::<math>\;\;\;\:\, = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n) (2 z + 2 n + 1)}} \cdot (2 z + 2 n + 1)</math> |
</div> | </div> | ||
| − | + | <div style="margin-top: 1em; margin-bottom: 1em;"> | |
| + | :::<math>\;\;\;\:\, = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2^{2 n + 2} [z (z + 1) \cdot \ldots \cdot (z + n)] \cdot \left[ \left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right) \right]}} \cdot 2 n \left( 1 + {\small\frac{2 z + 1}{2 n}} \right)</math> | ||
| + | </div> | ||
<div style="margin-top: 1em; margin-bottom: 1em;"> | <div style="margin-top: 1em; margin-bottom: 1em;"> | ||
| − | ::<math>\ | + | :::<math>\;\;\;\:\, = 2^{2 z} \cdot \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \cdot {\small\frac{n^{z + (1 / 2)} n!}{\left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right)}} \cdot {\small\frac{(2 n) !}{(n!)^2}} \cdot {\small\frac{\sqrt{n}}{2^{2 n + 1}}} \cdot \left( 1 + {\small\frac{2 z + 1}{2 n}} \right)</math> |
</div> | </div> | ||
| − | + | <div style="margin-top: 1em; margin-bottom: 1em;"> | |
| + | :::<math>\;\;\;\:\, = 2^{2 z} \cdot \lim_{n \rightarrow \infty} {\small\frac{n^z n!}{z (z + 1) \cdot \ldots \cdot (z + n)}} \cdot \lim_{n \rightarrow \infty}{\small\frac{n^{z + (1 / 2)} n!}{\left( z + {\small\frac{1}{2}} \right) \left( z + {\small\frac{3}{2}} \right) \cdot \ldots \cdot \left( z + n + {\small\frac{1}{2}} \right)}} \cdot \lim_{n \rightarrow \infty} {\small\frac{(2 n) !}{(n!)^2}} \cdot {\small\frac{\sqrt{n}}{2^{2 n + 1}}} \cdot \lim_{n \rightarrow \infty} \left( 1 + {\small\frac{2 z + 1}{2 n}} \right)</math> | ||
| + | </div> | ||
| − | ::<math> | + | :::<math>\;\;\;\:\, = 2^{2 z} \cdot \Gamma (z) \cdot \Gamma \left( z + {\small\frac{1}{2}} \right) \cdot C \cdot 1</math> |
| − | |||
| − | + | Ponieważ wyrażenie | |
| − | ::<math>\ | + | ::<math>\lim_{n \rightarrow \infty} {\small\frac{(2 n) !}{(n!)^2}} \cdot {\small\frac{\sqrt{n}}{2^{2 n + 1}}}</math> |
| − | + | nie zależy od <math>z</math>, a wartości funkcji <math>\Gamma (2 z)</math>, <math>\Gamma (z)</math> i <math>\Gamma \left( z + {\small\frac{1}{2}} \right)</math> są określone dla <math>2 z \notin \mathbb{Z}_- \cup \{ 0 \}</math>, to powyższa granica musi być pewną stałą. Jeżeli po lewej stronie położymy <math>z = {\small\frac{1}{2}}</math>, to otrzymamy | |
| − | ::<math> | + | ::<math>\Gamma (1) = 2 \cdot \Gamma \left( {\small\frac{1}{2}} \right) \Gamma (1) \cdot C</math> |
| − | + | Czyli | |
| − | + | ::<math>C = {\small\frac{1}{2 \sqrt{\pi}}}</math> | |
| − | + | I ostatecznie dostajemy | |
| + | ::<math>\Gamma (2 z) = {\small\frac{2^{2 z - 1}}{\sqrt{\pi}}} \cdot \Gamma (z) \Gamma \left( z + {\small\frac{1}{2}} \right)</math> | ||
| − | |||
| − | + | Przy okazji pokazaliśmy asymptotykę: <math>{\small\binom{2 n}{n}} \sim {\small\frac{2^{2 n}}{\sqrt{\pi \, n}}}</math> | |
| − | |||
| − | + | Zauważmy jeszcze, że gdy położymy <math>2 n + 1</math> zamiast <math>n</math>, to otrzymamy taki sam rezultat, bo | |
| − | + | ::<math>\Gamma (2 z) = \lim_{n \rightarrow \infty} {\small\frac{(2 n + 1)^{2 z} (2 n + 1) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n + 1)}} = \lim_{n \rightarrow \infty} {\small\frac{(2 n)^{2 z} (2 n) !}{2 z (2 z + 1) \cdot \ldots \cdot (2 z + 2 n)}} \cdot \left( 1 + {\small\frac{1}{2 n}} \right)^{\! 2 z} \cdot \left( {\small\frac{1}{1 + {\normalsize\frac{2 z}{2 n + 1}}}} \right)</math><br/> | |
□ | □ | ||
{{\Spoiler}} | {{\Spoiler}} | ||
| Linia 3525: | Linia 4410: | ||
| − | Ze wzorów podanych w twierdzeniu [[# | + | Ze wzorów podanych w twierdzeniu [[#D111|D111]] otrzymujemy<br/> |
| − | <span id=" | + | <span id="D112" style="font-size: 110%; font-weight: bold;">Twierdzenie D112</span><br/> |
Niech <math>k \in \mathbb{Z} \;</math> i <math>\; n \in \mathbb{N}_0</math> | Niech <math>k \in \mathbb{Z} \;</math> i <math>\; n \in \mathbb{N}_0</math> | ||
| Linia 3561: | Linia 4446: | ||
'''Punkt 1.''' | '''Punkt 1.''' | ||
| − | Wystarczy położyć <math>z = {\small\frac{1}{2}}</math> we wzorze 3. twierdzenia [[# | + | Wystarczy położyć <math>z = {\small\frac{1}{2}}</math> we wzorze 3. twierdzenia [[#D111|D111]] |
'''Punkt 2.''' | '''Punkt 2.''' | ||
| Linia 3573: | Linia 4458: | ||
'''Punkt 3.''' | '''Punkt 3.''' | ||
| − | Wystarczy położyć <math>z = z' + {\small\frac{1}{2}}</math> we wzorze 3. twierdzenia [[# | + | Wystarczy położyć <math>z = z' + {\small\frac{1}{2}}</math> we wzorze 3. twierdzenia [[#D111|D111]] |
'''Punkt 4.''' | '''Punkt 4.''' | ||
| Linia 3625: | Linia 4510: | ||
| − | <span id=" | + | <span id="D113" style="font-size: 110%; font-weight: bold;">Twierdzenie D113</span><br/> |
Jeżeli <math>n \in \mathbb{N}_0 \,</math> i <math>\; a \in \mathbb{Z}_+</math>, to | Jeżeli <math>n \in \mathbb{N}_0 \,</math> i <math>\; a \in \mathbb{Z}_+</math>, to | ||
| Linia 3631: | Linia 4516: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Wiemy, że jeżeli <math>z</math> nie jest liczbą całkowitą, to prawdziwy jest wzór (zobacz [[# | + | Wiemy, że jeżeli <math>z</math> nie jest liczbą całkowitą, to prawdziwy jest wzór (zobacz [[#D111|D111]] p.3) |
::<math>\Gamma (z) \Gamma (- z + 1) = {\small\frac{\pi}{\sin (\pi z)}}</math> | ::<math>\Gamma (z) \Gamma (- z + 1) = {\small\frac{\pi}{\sin (\pi z)}}</math> | ||
| Linia 3661: | Linia 4546: | ||
| − | <span id=" | + | <span id="D114" style="font-size: 110%; font-weight: bold;">Twierdzenie D114</span><br/> |
Jeżeli <math>n \in \mathbb{N}_0 \,</math> i <math>\; a \in \mathbb{Z}_+</math>, to | Jeżeli <math>n \in \mathbb{N}_0 \,</math> i <math>\; a \in \mathbb{Z}_+</math>, to | ||
| Linia 3667: | Linia 4552: | ||
{{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | {{Spoiler|Style = font-style: italic; font-weight: bold; color: olive; text-decoration: underline;|Show=Dowód|Hide=Ukryj dowód}} | ||
| − | Z twierdzenia [[# | + | Z twierdzenia [[#D111|D111]] p.2 wynika, że |
::<math>\Gamma (a z + a n + 1) = \Gamma (a z + 1) \cdot \prod^{a n}_{j = 1} (a z + j)</math> | ::<math>\Gamma (a z + a n + 1) = \Gamma (a z + 1) \cdot \prod^{a n}_{j = 1} (a z + j)</math> | ||
| Linia 3679: | Linia 4564: | ||
Zatem | Zatem | ||
| − | ::<math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (a z + 1)}{\Gamma (b z + 1)}} = {\small\frac{b}{a}} \cdot \frac{\displaystyle\prod^{b n - 1}_{j = 1} (- b n + j)}{\displaystyle\prod^{a n - 1}_{j = 1} (- a n + j)} \cdot {\small\frac{\Gamma (1)}{\Gamma (1)}} = {\small\frac{b}{a}} \cdot \frac{(- 1)^{b n - 1} \cdot \displaystyle\prod^{b n - 1}_{j = 1} ( | + | ::<math>\lim_{z \rightarrow - n} {\small\frac{\Gamma (a z + 1)}{\Gamma (b z + 1)}} = |
| + | {\small\frac{b}{a}} \cdot \frac{\displaystyle\prod^{b n - 1}_{j = 1} (- b n + j)}{\displaystyle\prod^{a n - 1}_{j = 1} (- a n + j)} \cdot {\small\frac{\Gamma (1)}{\Gamma (1)}} = | ||
| + | {\small\frac{b}{a}} \cdot \frac{(- 1)^{b n - 1} \cdot \displaystyle\prod^{b n - 1}_{j = 1} (b n - j)}{(- 1)^{a n - 1} \cdot \displaystyle\prod^{a n - 1}_{j = 1} (a n - j)} = | ||
| + | {\small\frac{b}{a}} \cdot (- 1)^{(a - b) n} \cdot {\small\frac{(b n - 1) !}{(a n - 1) !}} = | ||
| + | (- 1)^{(a - b) n} \cdot {\small\frac{(b n) !}{(a n) !}}</math> | ||
Co należało pokazać.<br/> | Co należało pokazać.<br/> | ||
| Linia 3687: | Linia 4576: | ||
| − | <span id=" | + | <span id="D115" style="font-size: 110%; font-weight: bold;">Zadanie D115</span><br/> |
| − | Niech <math>n \in \mathbb{ | + | Niech <math>n \in \mathbb{Z}_+ \,</math> i <math>\; g(n) = {\small\binom{2 n}{n}}</math>. Pokazać, że |
:* rozszerzając funkcję <math>g(n)</math> na zbiór liczb rzeczywistych, otrzymujemy <math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)^2}}</math> | :* rozszerzając funkcję <math>g(n)</math> na zbiór liczb rzeczywistych, otrzymujemy <math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)^2}}</math> | ||
| Linia 3705: | Linia 4594: | ||
bo funkcja <math>\Gamma (x)</math> jest rozszerzeniem pojęcia silni na zbiór liczb rzeczywistych. | bo funkcja <math>\Gamma (x)</math> jest rozszerzeniem pojęcia silni na zbiór liczb rzeczywistych. | ||
| − | Korzystając z twierdzenia [[# | + | Korzystając z twierdzenia [[#D114|D114]], otrzymujemy |
::<math>\lim_{x \rightarrow - n} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)}} = (- 1)^n \cdot {\small\frac{n!}{(2 n) !}}</math> | ::<math>\lim_{x \rightarrow - n} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)}} = (- 1)^n \cdot {\small\frac{n!}{(2 n) !}}</math> | ||
| − | Ale wiemy, że (zobacz [[# | + | Ale wiemy, że (zobacz [[#D110|D110]]) |
::<math>\lim_{x \rightarrow - n} {\small\frac{1}{\Gamma (x + 1)}} = 0</math> | ::<math>\lim_{x \rightarrow - n} {\small\frac{1}{\Gamma (x + 1)}} = 0</math> | ||
| Linia 3725: | Linia 4614: | ||
| − | <span id=" | + | <span id="D116" style="font-size: 110%; font-weight: bold;">Zadanie D116</span><br/> |
| − | Niech <math>n \in \mathbb{N}_0</math> i <math>g(n) = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}}</math>. Pokazać, że | + | Niech <math>n \in \mathbb{N}_0 \,</math> i <math>\; g(n) = {\small\frac{1}{n + 1}} {\small\binom{2 n}{n}}</math>. Pokazać, że |
:* rozszerzając funkcję <math>g(n)</math> na zbiór liczb rzeczywistych, otrzymujemy <math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 2) \Gamma (x + 1)}}</math> | :* rozszerzając funkcję <math>g(n)</math> na zbiór liczb rzeczywistych, otrzymujemy <math>g(x) = {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 2) \Gamma (x + 1)}}</math> | ||
| Linia 3743: | Linia 4632: | ||
to łatwo pokażemy, że granica funkcji <math>g(x)</math> w punkcje <math>x = - 1</math> istnieje i jest równa <math>- {\small\frac{1}{2}}</math>. | to łatwo pokażemy, że granica funkcji <math>g(x)</math> w punkcje <math>x = - 1</math> istnieje i jest równa <math>- {\small\frac{1}{2}}</math>. | ||
| − | Z twierdzenia [[# | + | Z twierdzenia [[#D114|D114]] dostajemy |
::<math>\lim_{x \rightarrow - 1} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)}} = (- 1) \cdot {\small\frac{1}{2}} = - {\small\frac{1}{2}}</math> | ::<math>\lim_{x \rightarrow - 1} {\small\frac{\Gamma (2 x + 1)}{\Gamma (x + 1)}} = (- 1) \cdot {\small\frac{1}{2}} = - {\small\frac{1}{2}}</math> | ||
| Linia 3813: | Linia 4702: | ||
<ref name="CesaroSum1">Wikipedia, ''Sumowalność metodą Cesàro'', ([https://pl.wikipedia.org/wiki/Sumowalno%C5%9B%C4%87_metod%C4%85_Ces%C3%A0ro Wiki-pl]), ([https://en.wikipedia.org/wiki/Ces%C3%A0ro_summation Wiki-en])</ref> | <ref name="CesaroSum1">Wikipedia, ''Sumowalność metodą Cesàro'', ([https://pl.wikipedia.org/wiki/Sumowalno%C5%9B%C4%87_metod%C4%85_Ces%C3%A0ro Wiki-pl]), ([https://en.wikipedia.org/wiki/Ces%C3%A0ro_summation Wiki-en])</ref> | ||
| + | |||
| + | <ref name="IndefiniteSum1">Wikipedia, ''Indefinite sum'', ([https://en.wikipedia.org/wiki/Indefinite_sum Wiki-en])</ref> | ||
| + | |||
| + | <ref name="Fasenmyer1">Sister Mary Celine Fasenmyer, ''Some Generalized Hypergeometric Polynomials'', Bull. Amer. Math. Soc. 53 (1947), 806-812</ref> | ||
| + | |||
| + | <ref name="Fasenmyer2">Sister Mary Celine Fasenmyer, ''A Note on Pure Recurrence Relations'', Amer. Math. Monthly 56 (1949), 14-17</ref> | ||
| + | |||
| + | <ref name="Zeilberger1">Doron Zeilberger, ''Sister Celine's technique and its generalizations'', Journal of Mathematical Analysis and Applications, 85 (1982), 114-145</ref> | ||
| + | |||
| + | <ref name="WilfZeilberger1">Herbert Wilf and Doron Zeilberger, ''Rational Functions Certify Combinatorial Identities'', J. Amer. Math. Soc. 3 (1990), 147-158</ref> | ||
| + | |||
| + | <ref name="PetkovsekWilfZeilberger1">Marko Petkovšek, Herbert Wilf and Doron Zeilberger, ''A = B'', AK Peters, Ltd., 1996</ref> | ||
<ref name="JovanMikic1">Jovan Mikić, ''A Proof of a Famous Identity Concerning the Convolution of the Central Binomial Coefficients'', Journal of Integer Sequences, Vol. 19, No. 6 (2016), pp. 1 - 10, ([https://cs.uwaterloo.ca/journals/JIS/VOL19/Mikic2/mikic15.html LINK])</ref> | <ref name="JovanMikic1">Jovan Mikić, ''A Proof of a Famous Identity Concerning the Convolution of the Central Binomial Coefficients'', Journal of Integer Sequences, Vol. 19, No. 6 (2016), pp. 1 - 10, ([https://cs.uwaterloo.ca/journals/JIS/VOL19/Mikic2/mikic15.html LINK])</ref> | ||
Aktualna wersja na dzień 11:37, 28 sty 2025
Szeregi nieskończone
Definicja D1
Sumę wszystkich wyrazów ciągu nieskończonego
nazywamy szeregiem nieskończonym o wyrazach
Definicja D2
Ciąg
Definicja D3
Szereg
Twierdzenie D4 (warunek konieczny zbieżności szeregu)
Jeżeli szereg
Okazuje się, że bardzo łatwo podać przykład szeregów, dla których warunek
Twierdzenie D5 (kryterium Leibniza)
Niech ciąg
to szereg
Twierdzenie D6
Dla
Przykład D7
Szeregi niekończone często definiują ważne funkcje. Dobrym przykładem może być funkcja eta Dirichleta[1], którą definiuje szereg naprzemienny
lub funkcja dzeta Riemanna[2], którą definiuje inny szereg
Na podstawie twierdzenia D6 funkcje te są związane wzorem
Dla
Twierdzenie D8
Niech
Twierdzenie D9 (kryterium porównawcze)
Jeżeli istnieje taka liczba całkowita
to
- zbieżność szeregu
- rozbieżność szeregu
Twierdzenie D10
Jeżeli szereg
Definicja D11
Powiemy, że szereg
Powiemy, że szereg
Twierdzenie D12
Niech
to odpowiadający temu ciągowi szereg nazywamy szeregiem teleskopowym. Suma częściowa szeregu teleskopowego jest odpowiednio równa
Twierdzenie D13
Następujące szeregi są zbieżne
1. 2. 3. 4. A013661, WolframAlpha
Twierdzenie D14
Następujące szeregi są zbieżne
Przykład D15
Na przykładzie szeregu
Ponieważ nie jesteśmy w stanie zsumować nieskończenie wielu wyrazów, zatem najlepiej będzie podzielić szereg na dwie części
Wartość pierwszej części możemy policzyć bezpośrednio, a dla drugiej części powinniśmy znaleźć jak najlepsze oszacowanie.
Dowodząc twierdzenie D14, w punkcie 4. pokazaliśmy, że prawdziwy jest ciąg nierówności
Wykorzystamy powyższy wzór do znalezienia potrzebnego nam oszacowania. Sumując strony nierówności, dostajemy
Ponieważ szeregi po lewej i po prawej stronie są szeregami teleskopowymi, to łatwo znajdujemy, że
Przechodząc z
Teraz pozostaje dodać sumę wyrazów szeregu od
Poniżej przedstawiamy wartości oszacowania sumy szeregu znalezione przy pomocy programu PARI/GP dla kolejnych wartości
for(n = 1, 8, s = sum( k = 3, 10^n, 1/k/(log(k))^2 ); print( "n= ", n, " a= ", s + 1/log(10^n+1), " b= ", s + 1/log(10^n) ))
Dysponując oszacowaniem reszty szeregu, znaleźliśmy wartość sumy szeregu z dokładnością 10 miejsc po przecinku.
Natomiast samo zsumowanie
Zatem mimo zsumowania stu milionów(!) wyrazów szeregu otrzymaliśmy rezultat z dokładnością jednego(!) miejsca po przecinku. Co więcej, nie wiemy, jaka jest dokładność uzyskanego rezultatu. Znając oszacowanie od dołu i od góry, dokładność jednego miejsca po przecinku uzyskaliśmy po zsumowaniu dziesięciu(!) wyrazów szeregu.
Rozpatrywana wyżej sytuacja pokazuje, że w przypadku znajdowania przybliżonej wartości sumy szeregu ważniejsze od sumowania ogromnej ilości wyrazów jest posiadanie oszacowania nieskończonej reszty szeregu. Ponieważ wyznaczenie tego oszacowania na ogół nie jest proste, pokażemy jak ten problem rozwiązać przy pomocy całki oznaczonej.
Szeregi nieskończone i całka oznaczona
Twierdzenie D16
Jeżeli funkcja
Przykład D17
Rozważmy szereg
Funkcja
Przy obliczaniu całek oznaczonych Czytelnik może skorzystać ze strony WolframAlpha.
Ponieważ
to dostajemy
Zauważmy: nie tylko wiemy, że szereg
Twierdzenie D18 (kryterium całkowe zbieżności szeregów)
Załóżmy, że funkcja
Przykład D19
Przykłady zebraliśmy w tabeli. Przy obliczaniu całek nieoznaczonych Czytelnik może skorzystać ze strony WolframAlpha.
szereg funkcja całka granica wynik 1. szereg rozbieżny 2. szereg rozbieżny 3. szereg zbieżny 4. szereg rozbieżny 5. szereg zbieżny
Stosując kryterium całkowe, można łatwo pokazać, że szeregi
są zbieżne dla
Twierdzenie D20
Jeżeli funkcja
gdzie
Przykład D21
Twierdzenie D20 umożliwia określenie, z jaką dokładnością została wyznaczona suma szeregu. Wyznaczmy sumę szeregu
Zatem
Dla kolejnych wartości
W programie PARI/GP wystarczy napisać:
f(k) = 1.0 / (k+1) / sqrt(k) S(m) = sum( k = 1, m, f(k) ) R(m) = Pi - 2*atan( sqrt(m) ) for(j = 1, 9, m = 10^j; suma = S(m); reszta = R(m); print( "j= ", j, " a= ", suma + reszta - f(m), " b= ", suma + reszta ))
Prostym wnioskiem z twierdzenia D16 jest następujące
Twierdzenie D22
Niech
Twierdzenie D23
Niech
gdzie
Uwaga D24
Niech
- korzystając z całkowego kryterium zbieżności, możemy łatwo zbadać, czy szereg
- jeżeli szereg jest zbieżny, to ponownie wykorzystując całki (twierdzenie D23), możemy znaleźć oszacowanie sumy częściowej szeregu
Jednak dysponując już oszacowaniem sumy częściowej szeregu
Czasami potrzebujemy takiego uproszczenia problemu, aby udowodnić zbieżność szeregów bez odwoływania się do całek. Zauważmy, że Czytelnik nawet nie musi znać całek – wystarczy, że policzy je przy pomocy programów, które potrafią to robić (np. WolframAlpha). Kiedy już znajdziemy oszacowanie sumy częściowej szeregu, nie musimy wyjaśniać, w jaki sposób je znaleźliśmy – wystarczy udowodnić, że jest ono poprawne, a do tego wystarczy indukcja matematyczna.
Zamieszczonej niżej zadania pokazują, jak wykorzystać w tym celu twierdzenie D23.
Zadanie D25
Korzystając z twierdzenia D23, znaleźć oszacowania sumy częściowej szeregów
Zadanie D26
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania
Zadanie D27
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania
Szeregi nieskończone i liczby pierwsze
Twierdzenie D28
Następujące szeregi są zbieżne
Twierdzenie D29
Następujące szeregi są zbieżne
Twierdzenie D30
Szereg
Uwaga D31
Moglibyśmy oszacować rozbieżność szeregu
Twierdzenie D32
Niech
Twierdzenie D33
Niech
Twierdzenie D34
Dla dowolnego
Twierdzenie D35 (pierwsze twierdzenie Mertensa[5][6], 1874)
Dla dowolnego
Twierdzenie D36 (pierwsze twierdzenie Mertensa[5][6], 1874)
Dla dowolnego
Twierdzenie D37
Dla dowolnego
Uwaga D38
|
Dokładniejsze oszacowanie sumy gdzie Dla |
Uwaga D39
|
Dokładniejsze oszacowanie sumy gdzie Dla |
Uwaga D40
Dla
są liczbami dodatnimi.
Twierdzenie D41
Prawdziwy jest następujący związek
gdzie
Twierdzenie D42
Dla
Zadanie D43
Niech
wynika twierdzenie Czebyszewa.
Definicja D44
Powiemy, że liczby pierwsze
Twierdzenie D45* (Viggo Brun, 1919)
Suma odwrotności par liczb pierwszych
gdzie
Zadanie D46
Pokazać, że istnieje nieskończenie wiele liczb pierwszych nietworzących par liczb bliźniaczych.
Dowód z Księgi. Rozbieżność sumy
Twierdzenie D47
Suma odwrotności liczb pierwszych jest rozbieżna.
Sumowanie przez części
Uwaga D48
Omawianie metody sumowania przez części[16] rozpoczniemy od udowodnienia prostego twierdzenia, które dobrze ilustruje tę metodę i ułatwi zrozumienie uogólnienia. Potrzebna nam będzie następująca funkcja
Łatwo znajdujemy związek funkcji
Twierdzenie D49
Niech
Zadanie D50
Pokazać, że dla
Zadanie D51
Pokazać, że oszacowanie
Twierdzenie D52 (sumowanie przez części)
Niech
gdzie
Zadanie D53
Niech
Twierdzenie D54 (kryterium Dirichleta)
Niech
- ciąg
- ciąg
- istnieje taka stała
- istnieje taka stała
to szereg
Zadanie D55
Udowodnić następujące wzory
Zadanie D56
Pokazać, że szereg
Zadanie D57
Pokazać, że szereg
Zadanie D58
Niech
Twierdzenie D59
Niech
Uwaga D60
Funkcja
Z twierdzenia D59 wynika, że jeżeli istnieje granica
Wiemy, że dla funkcji
Zadanie D61
Niech
Iloczyn Cauchy'ego szeregów
Twierdzenie D62 (kryterium d'Alemberta)
Niech
Jeżeli
-
-
-
-
Uwaga C62
W przypadku, gdy
Przykład D64
Niech
Ponieważ
to z kryterium d'Alemberta wynika, że szereg jest bezwzględnie zbieżny.
Zadanie D65
Pokazać, że szereg
Uwaga D66
W twierdzeniu A37, korzystając z następującej definicji funkcji
pominęliśmy dowód własności
Oznaczmy
Zastępując sumowanie po kolejnych liniach poziomych sumowaniem po kolejnych przekątnych, otrzymamy taki rysunek
Co odpowiada sumie
Ponieważ
to otrzymujemy
Pokazaliśmy tym samym, że z definicji
wynika podstawowa własność funkcji wykładniczej
Mamy świadomość, że dokonana przez nas zmiana sposobu sumowania była nieformalna i w związku z tym nie wiemy, czy była poprawna. Zatem musimy precyzyjnie zdefiniować takie sumowanie i zbadać, kiedy jest dopuszczalne. Dopiero wtedy będziemy mogli być pewni, że policzony rezultat jest poprawny.
Definicja D67
Iloczynem Cauchy'ego szeregów
W przypadku szeregów, których wyrazy są numerowane od liczby
Zadanie D68
Niech
- jeżeli
- jeżeli
- jeżeli
- jeżeli
- jeżeli
- jeżeli
- jeżeli
- jeżeli
- jeżeli
- jeżeli
Przykład D69
Ostatni punkt zadania D68 pozwala stworzyć wiele przykładowych szeregów i ich iloczynów Cauchy'ego. Przypomnijmy, że
Przykłady zebraliśmy w tabeli.
zbieżny zbieżny zbieżny rozbieżny rozbieżny zbieżny zbieżny / rozbieżny zbieżny / rozbieżny zbieżny / rozbieżny zbieżny zbieżny zbieżny rozbieżny zbieżny zbieżny rozbieżny rozbieżny rozbieżny rozbieżny rozbieżny zbieżny rozbieżny rozbieżny zbieżny rozbieżny rozbieżny rozbieżny rozbieżny zbieżny zbieżny rozbieżny zbieżny rozbieżny rozbieżny zbieżny / rozbieżny zbieżny / rozbieżny rozbieżny rozbieżny rozbieżny rozbieżny zbieżny zbieżny
Przykład D70
Podamy przykład szeregów zbieżnych, których iloczyn Cauchy'ego jest rozbieżny. Rozważmy zbieżny szereg (zobacz D5)
Mnożąc powyższy szereg przez siebie według reguły Cauchy'ego, otrzymujemy
Ale
Czyli
Ponieważ
Zadanie D71
Pokazać, że jeżeli
Uwaga D72
Przykłady D69 i D70 pokazują, że w ogólności nie jest prawdziwy wzór
Skoro iloczyn sum szeregów nie zawsze jest równy sumie iloczynu Cauchy'ego tych szeregów, to musimy ustalić, jakie warunki muszą być spełnione, aby tak było.
Uwaga D73
Nim przejdziemy do dowodu twierdzenia Mertensa, zauważmy, że od sumowania po
możemy łatwo przejść do sumowania po liniach poziomych lub po liniach pionowych. Rysunek przedstawia sytuację, gdy
Przejście do sumowania po liniach poziomych
Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach poziomych, a druga po kolejnych elementach w
Przejście do sumowania po liniach pionowych
Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach pionowych, a druga po kolejnych elementach w
Twierdzenie D74 (Franciszek Mertens)
Jeżeli szereg
Zadanie D75
Pokazać, że iloczyn Cauchy'ego dwóch szeregów bezwzględnie zbieżnych jest bezwzględnie zbieżny.
Zadanie D76
Podać przykład szeregów zbieżnych, z których tylko jeden jest bezwzględnie zbieżny i których iloczyn Cauchy'ego jest warunkowo zbieżny.
Zadanie D77
Podać przykład szeregów warunkowo zbieżnych, których iloczyn Cauchy'ego jest warunkowo zbieżny.
Uwaga D78
Nim przejdziemy do dowodu twierdzenia Abela, musimy udowodnić trzy twierdzenia dotyczące pewnych granic. Warto zauważyć, że twierdzenie D80 pozwala przypisać wartość sumy do szeregów, których suma w zwykłym sensie nie istnieje. Uogólnienie to nazywamy sumowalnością w sensie Cesàro[20]. Nie będziemy zajmowali się tym tematem, ale podamy ciekawy przykład.
Rozważmy szereg
Zatem szereg
Twierdzenie D79
Jeżeli
Twierdzenie D80
Jeżeli ciąg
Twierdzenie D81
Niech
Twierdzenie D82 (Niels Henrik Abel)
Jeżeli szeregi
Liczby Catalana
Definicja D83
Liczby Catalana
gdzie
Twierdzenie D84
Liczby Catalana
-
-
Zadanie D85
Niech
- jeżeli
- jeżeli
- jeżeli
- jeżeli
Dla jakich wartości
Sumy współczynników dwumianowych
Twierdzenie D86
Dla
Twierdzenie D87
Dla
Suma nieoznaczona
Uwaga D88
Sumą nieoznaczoną[21] (lub antyróżnicą) funkcji
Łatwo zauważamy, że istnieje cała rodzina funkcji
Co przez analogię do całki nieoznaczonej możemy zapisać jako
Należy podkreślić różnicę między sumą oznaczoną
Ponieważ dla sumy
ale
i nie jest prawdą, że
Niech teraz
Tym razem otrzymujemy zupełnie inne wyniki: suma
Uwaga D89
Powiedzmy, że dysponujemy wzorem
Jeżeli już udało nam się pokazać związek
Czyli
bo
W przypadkach bardziej skomplikowanych nie możemy tak postąpić. W poprzedniej uwadze rozważaliśmy sumę
ale
I nie da się pokazać związku
Tutaj z pomocą przychodzi nam suma nieoznaczona. W programie Maxima możemy ją policzyć, wpisując polecenia
load ("zeilberger");
AntiDifference(binomial(n+k, n), k);
Otrzymujemy
Oczywiście
i
Podsumujmy. Jakkolwiek znalezienie ogólnego wzoru na sumę
Zadanie D90
Korzystając z programu Maxima znaleźć sumę nieoznaczoną
i pokazać, że prawdziwy jest wzór
Znajdowanie równania rekurencyjnego dla sumy
Uwaga D91
Rozważmy sumę
W twierdzeniach D107 i D108 wyliczyliśmy
Twierdzenie D92
Niech
gdzie współczynniki
Uwaga D93
Nie ma sensu stosowanie opisanej powyżej metody do prostych sum postaci
Zadanie D94
Pokazać, że dla
Zadanie D95
Pokazać, że dla
Zadanie D96
Pokazać, że dla
Zadanie D97
Niech
Twierdzenie D98
Niech
gdzie współczynniki
spełnia następujące równanie rekurencyjne
Uwaga D99
Z zadania D97 wynika, że jeżeli funkcja
Zadanie D100
Pokazać, że dla
Zadanie D101
Pokazać, że dla
Uwaga D102
Niech
Rozważmy teraz funkcję
to natychmiast widzimy, że
Zatem w przypadku tej funkcji mamy
Zakładając, że spełnione jest równanie
otrzymujemy następujące równanie rekurencyjne dla sumy
Jeżeli mamy skończoną liczbę punktów
W takim przypadku otrzymamy następujące równanie rekurencyjne dla sumy
Wystarczy drobna modyfikacja procedury sum5(), aby obejmowała ona również takie przypadki
sum6(I, J):=
(
read("podaj definicję f(n, k)"), /* składnik sumy */
print("f(n, k) = ", f(n, k) ),
read("podaj definicję T(n)"), /* suma skończonych wartości funkcji f(n, k), gdzie k<0 lub k>n */
print("T(n) = ", T(n) ),
F1: sum( sum( a[i,j] * f(n+i, k+j), i, 0, I), j, 0, J) / f(n, k),
F2: num( factor( minfactorial( makefact( expand( F1 ) ) ) ) ),
deg: hipow(F2, k),
LE: [subst(0, k, F2) = 0],
for i: 1 thru deg do push(coeff(F2, k^i) = 0, LE), /* kolejne równania wpisujemy do listy LE */
LV: create_list(a[i, j], i, 0, I , j, 0, J), /* lista zmiennych */
sol: solve( LE, LV ), /* lista rozwiązań */
S1: sum( ( S[n+i] + T(n+i) ) * sum( a[i,j], j, 0, J ), i, 0, I ),
S2: num( factor( minfactorial( makefact( expand( S1 ) ) ) ) ),
S3: subst( sol[1], S2 ), /* pierwszy element listy sol */
S4: num( factor( expand( S3 ) ) ),
print("rekurencja: ", S4 = 0),
load("solve_rec"),
solve_rec( S4 = 0, S[n] )
)$
Korzystając z powyższej procedury, Czytelnik może łatwo policzyć wypisane poniżej sumy.
Zadanie D103
Pokazać, że dla
Zadanie D104
Pokazać, że dla
Uzupełnienie
Dowód własności liczb Catalana
Uwaga D105
Przedstawiony poniżej dowód czwartego punktu twierdzenia D84 został oparty na pracy Jovana Mikicia[27].
Twierdzenie D106
Jeżeli funkcja
to
Twierdzenie D107
Dla
Twierdzenie D108
Dla
Twierdzenie D109
Jeżeli
Funkcja gamma
Definicja D110
Funkcja
Trzy ostatnie wzory możemy wykorzystać do zdefiniowania funkcji
Twierdzenie D111
Dla funkcji
-
-
Ze wzorów podanych w twierdzeniu D111 otrzymujemy
Twierdzenie D112
Niech
Twierdzenie D113
Jeżeli
Twierdzenie D114
Jeżeli
Zadanie D115
Niech
- rozszerzając funkcję
- rozszerzając funkcję
Zadanie D116
Niech
- rozszerzając funkcję
- rozszerzając funkcję
Przypisy
- ↑ Wikipedia, Funkcja η, (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Funkcja dzeta Riemanna, (Wiki-pl), (Wiki-en)
- ↑ Twierdzenie: funkcja ciągła w przedziale domkniętym jest całkowalna w tym przedziale.
- ↑ W szczególności: funkcja ograniczona i mająca skończoną liczbę punktów nieciągłości w przedziale domkniętym jest w tym przedziale całkowalna.
- ↑ Skocz do: 5,0 5,1 Wikipedia, Twierdzenia Mertensa, (Wiki-pl), (Wiki-en)
- ↑ Skocz do: 6,0 6,1 Wikipedia, Franciszek Mertens, (Wiki-pl)
- ↑ J. B. Rosser and L. Schoenfeld, Approximate formulas for some functions of prime numbers, Illinois J. Math. 6 (1962), 64-94, (LINK)
- ↑ Zobacz twierdzenie D42.
- ↑ The On-Line Encyclopedia of Integer Sequences, A001620 - Decimal expansion of Euler's constant, (A001620)
- ↑ The On-Line Encyclopedia of Integer Sequences, A083343 - Decimal expansion of constant B3 (or B_3) related to the Mertens constant, (A083343)
- ↑ The On-Line Encyclopedia of Integer Sequences, A138312 - Decimal expansion of Mertens's constant minus Euler's constant, (A138312)
- ↑ Pierre Dusart, Estimates of Some Functions Over Primes without R.H., 2010, (LINK)
- ↑ Wikipedia, Stałe Bruna, (Wiki-pl), (Wiki-en)
- ↑ The On-Line Encyclopedia of Integer Sequences, A065421 - Decimal expansion of Viggo Brun's constant B, (A065421)
- ↑ Paul Erdős, Über die Reihe
- ↑ sumowanie przez części (ang. summation by parts)
- ↑ ciąg wypukły (ang. convex sequence)
- ↑ Pierre Dusart, Explicit estimates of some functions over primes, The Ramanujan Journal, vol. 45(1), 2018, 227-251.
- ↑ Skocz do: 19,0 19,1 Wikipedia, Szereg geometryczny, (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Sumowalność metodą Cesàro, (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Indefinite sum, (Wiki-en)
- ↑ Sister Mary Celine Fasenmyer, Some Generalized Hypergeometric Polynomials, Bull. Amer. Math. Soc. 53 (1947), 806-812
- ↑ Sister Mary Celine Fasenmyer, A Note on Pure Recurrence Relations, Amer. Math. Monthly 56 (1949), 14-17
- ↑ Doron Zeilberger, Sister Celine's technique and its generalizations, Journal of Mathematical Analysis and Applications, 85 (1982), 114-145
- ↑ Herbert Wilf and Doron Zeilberger, Rational Functions Certify Combinatorial Identities, J. Amer. Math. Soc. 3 (1990), 147-158
- ↑ Marko Petkovšek, Herbert Wilf and Doron Zeilberger, A = B, AK Peters, Ltd., 1996
- ↑ Jovan Mikić, A Proof of a Famous Identity Concerning the Convolution of the Central Binomial Coefficients, Journal of Integer Sequences, Vol. 19, No. 6 (2016), pp. 1 - 10, (LINK)
- ↑ Wikipedia, Funkcja Γ, (Wiki-pl), (Wiki-en)