Szeregi liczbowe

07.04.2022

Szeregi nieskończone

Definicja D1
Sumę wszystkich wyrazów ciągu nieskończonego [math]\displaystyle{ (a_n) }[/math]

[math]\displaystyle{ a_1 + a_2 + a_3 + \ldots + a_n + \ldots = \sum_{k = 1}^{\infty} a_k }[/math]

nazywamy szeregiem nieskończonym o wyrazach [math]\displaystyle{ a_n }[/math].

Definicja D2
Ciąg [math]\displaystyle{ S_n = \sum_{k = 1}^{n} a_k }[/math] nazywamy ciągiem sum częściowych szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math].

Definicja D3
Szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] będziemy nazywali zbieżnym, jeżeli ciąg sum częściowych [math]\displaystyle{ \left ( S_n \right ) }[/math] jest zbieżny.

Twierdzenie D4 (warunek konieczny zbieżności szeregu)
Jeżeli szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] jest zbieżny, to [math]\displaystyle{ \lim_{n \to \infty} a_n = 0 }[/math].

Dowód

Niech [math]\displaystyle{ S_n = \sum_{k = 1}^{n} a_k }[/math] będzie ciągiem sum częściowych, wtedy [math]\displaystyle{ a_{n + 1} = S_{n + 1} - S_n }[/math]. Z założenia ciąg [math]\displaystyle{ (S_n) }[/math] jest zbieżny, zatem

[math]\displaystyle{ \lim_{n \to \infty} a_{n + 1} = \lim_{n \to \infty} \left ( S_{n+1} - S_{n} \right ) = \lim_{n \to \infty} S_{n + 1} - \lim_{n \to \infty} S_n = 0 }[/math]

□

Okazuje się, że bardzo łatwo podać przykład szeregów, dla których warunek [math]\displaystyle{ \lim_{n \to \infty} a_n = 0 }[/math] jest warunkiem wystarczającym. Opisany w poniższym twierdzeniu rodzaj szeregów nazywamy szeregami naprzemiennymi.
Twierdzenie D5 (kryterium Leibniza)
Niech ciąg [math]\displaystyle{ (a_n) }[/math] będzie ciągiem malejącym o wyrazach nieujemnych. Jeżeli

[math]\displaystyle{ \underset{n \rightarrow \infty}{\lim} a_n = 0 }[/math]

to szereg [math]\displaystyle{ \underset{k = 1}{\overset{\infty}{\sum}} (- 1)^{k + 1} \cdot a_k }[/math] jest zbieżny.

Dowód

Grupując wyrazy szeregu po dwa, otrzymujemy sumę częściową postaci

[math]\displaystyle{ S_{2 m} = (a_1 - a_2) + (a_3 - a_4) + \ldots + (a_{2 m - 1} - a_{2 m}) }[/math]

Ponieważ ciąg [math]\displaystyle{ (a_n) }[/math] jest ciągiem malejącym, to każde wyrażenie w nawiasie jest liczbą nieujemną. Z drugiej strony

[math]\displaystyle{ S_{2 m} = a_1 - (a_2 - a_3) - (a_4 - a_5) - \ldots - (a_{2 m - 2} - a_{2 m - 1}) {- a_{2 m}} \lt a_1 }[/math]

Zatem dla każdego [math]\displaystyle{ m }[/math] ciąg sum częściowych [math]\displaystyle{ S_{2 m} }[/math] jest rosnący i ograniczony od góry, skąd na mocy twierdzenia C10 jest zbieżny, czyli

[math]\displaystyle{ \lim_{m \to \infty} S_{2 m} = g }[/math]

Pozostaje zbadać sumy częściowe [math]\displaystyle{ S_{2 m + 1} }[/math]. Rezultat jest natychmiastowy

[math]\displaystyle{ \lim_{m \to \infty} S_{2 m + 1} = \lim_{m \to \infty} (S_{2 m} + a_{2 m + 1}) = \lim_{m \to \infty} S_{2 m} + \lim_{m \to \infty} a_{2 m + 1} = g + 0 = g }[/math]

Co kończy dowód.
□

Twierdzenie D6
Dla [math]\displaystyle{ s \gt 1 }[/math] prawdziwy jest następujący związek

[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{k^s} = (1 - 2^{1 - s}) \sum_{k = 1}^{\infty} \frac{1}{k^s} }[/math]

Dowód

Zauważmy, że założenie [math]\displaystyle{ s \gt 1 }[/math] zapewnia zbieżność szeregu po prawej stronie. Zapiszmy szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^s} }[/math] w postaci sumy dla [math]\displaystyle{ k }[/math] parzystych i nieparzystych

[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^s} = 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \frac{1}{5^s} + \ldots = }[/math]

[math]\displaystyle{ \:\, = \sum_{k = 1}^{\infty} \frac{1}{(2 k - 1)^s} + \sum_{k = 1}^{\infty} \frac{1}{(2 k)^s} = }[/math]

[math]\displaystyle{ \:\, = \sum_{k = 1}^{\infty} \frac{1}{(2 k - 1)^s} + \frac{1}{2^s} \sum_{k = 1}^{\infty} \frac{1}{k^s} }[/math]

Otrzymujemy wzór

[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{(2 k - 1)^s} = (1 - 2^{- s}) \sum_{k = 1}^{\infty} \frac{1}{k^s} }[/math]

Podobnie rozpiszmy szereg naprzemienny

[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{k^s} = 1 - \frac{1}{2^s} + \frac{1}{3^s} - \frac{1}{4^s} + \frac{1}{5^s} - \ldots = }[/math]

[math]\displaystyle{ = \sum_{k = 1}^{\infty} \frac{1}{(2 k - 1)^s} - \sum_{k = 1}^{\infty} \frac{1}{(2 k)^s} = }[/math]

[math]\displaystyle{ = (1 - 2^{- s}) \sum_{k = 1}^{\infty} \frac{1}{k^s} - \frac{1}{2^s} \sum_{k = 1}^{\infty} \frac{1}{k^s} = }[/math]

[math]\displaystyle{ = (1 - 2^{1 - s}) \sum_{k = 1}^{\infty} \frac{1}{k^s} }[/math]

gdzie skorzystaliśmy ze znalezionego wyżej wzoru dla sumy szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{(2 k - 1)^s} }[/math]
□

Przykład D7
Szeregi niekończone często definiują ważne funkcje. Dobrym przykładem może być funkcja eta Dirichleta, którą definiuje szereg naprzemienny

[math]\displaystyle{ \eta (s) = \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{k^s} }[/math]

lub funkcja dzeta Riemanna, którą definiuje inny szereg

[math]\displaystyle{ \zeta (s) = \sum_{k = 1}^{\infty} \frac{1}{k^s} }[/math]

Na podstawie twierdzenia D6 funkcje te są związane wzorem

[math]\displaystyle{ \eta (s) = (1 - 2^{1 - s}) \zeta (s) }[/math]

Dla [math]\displaystyle{ s \in \mathbb{R}_+ }[/math] funkcja eta Dirichleta jest zbieżna. Możemy ją wykorzystać do znajdowania sumy szeregu naprzemiennego [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{k^s} }[/math].

[math]\displaystyle{ s = \frac{1}{2} }[/math]	[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{\sqrt{k}} = 0.604898643421 \ldots }[/math]	WolframAlpha
[math]\displaystyle{ s = 1 }[/math]	[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{k} = \log 2 = 0.693147180559 \ldots }[/math]	WolframAlpha
[math]\displaystyle{ s = 2 }[/math]	[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{k^2} = \frac{\pi^2}{12} = 0.822467033424 \ldots }[/math]	WolframAlpha

Twierdzenie D8
Niech [math]\displaystyle{ N \in \mathbb{Z}_+ }[/math]. Szeregi [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] oraz [math]\displaystyle{ \sum_{k = N}^{\infty} a_k }[/math] są jednocześnie zbieżne lub jednocześnie rozbieżne. W przypadku zbieżności zachodzi związek

[math]\displaystyle{ \sum_{k = 1}^{\infty} a_k = \left ( a_1 + a_2 + \ldots + a_{N - 1} \right ) + \sum_{k = N}^{\infty} a_k }[/math]

Dowód

Niech [math]\displaystyle{ S(n) =\sum_{k = 1}^{n} a_k }[/math] (gdzie [math]\displaystyle{ n \geqslant 1 }[/math]) oznacza sumę częściową pierwszego szeregu, a [math]\displaystyle{ T(n) = \sum_{k = N}^{\infty} a_k }[/math] (gdzie [math]\displaystyle{ n \geqslant N }[/math]) oznacza sumę częściową drugiego szeregu. Dla [math]\displaystyle{ n \geqslant N }[/math] mamy

[math]\displaystyle{ S(n) = (a_1 + a_2 + \ldots + a_{N - 1}) + T (n) }[/math]

Widzimy, że dla [math]\displaystyle{ n }[/math] dążącego do nieskończoności zbieżność (rozbieżność) jednego ciągu implikuje zbieżność (rozbieżność) drugiego.
□

Twierdzenie D9 (kryterium porównawcze)
Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ k \gt N_0 }[/math] jest spełniony warunek

[math]\displaystyle{ 0 \leqslant a_k \leqslant b_k }[/math]

to

1.    zbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} b_k }[/math] pociąga za sobą zbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math]
2.    rozbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] pociąga za sobą rozbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} b_k }[/math]

Dowód

Dowód przeprowadzimy dla szeregów [math]\displaystyle{ \sum_{k = N_0}^{\infty} a_k }[/math] oraz [math]\displaystyle{ \sum_{k = N_0}^{\infty} b_k }[/math], które są (odpowiednio) jednocześnie zbieżne lub jednocześnie rozbieżne z szeregami [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] oraz [math]\displaystyle{ \sum_{k = 1}^{\infty} b_k }[/math].

Punkt 1.
Z założenia szereg [math]\displaystyle{ \sum_{k = N_0}^{\infty} b_k }[/math] jest zbieżny. Niech [math]\displaystyle{ \sum_{k = N_0}^{\infty} b_k = b }[/math], zatem z założonych w twierdzeniu nierówności dostajemy

[math]\displaystyle{ 0 \leqslant \sum_{k = N_0}^{n} a_k \leqslant \sum_{k = N_0}^{n} b_k \leqslant b }[/math]

Zauważmy, że ciąg sum częściowych [math]\displaystyle{ A_n = \sum_{k = N_0}^{n} a_k }[/math] jest ciągiem rosnącym (bo [math]\displaystyle{ a_k \geqslant 0 }[/math]) i ograniczonym od góry. Wynika stąd, że ciąg [math]\displaystyle{ \left ( A_n \right ) }[/math] jest zbieżny, zatem szereg [math]\displaystyle{ \sum_{k = N_0}^{\infty} a_k }[/math] jest zbieżny.

Punkt 2.
Z założenia szereg [math]\displaystyle{ \sum_{k = N_0}^{\infty} a_k }[/math] jest rozbieżny, a z założonych w twierdzeniu nierówności dostajemy

[math]\displaystyle{ 0 \leqslant \sum_{k = N_0}^{n} a_k \leqslant \sum_{k = N_0}^{n} b_k }[/math]

Rosnący ciąg sum częściowych [math]\displaystyle{ A_n = \sum_{k = N_0}^{n} a_k }[/math] nie może być ograniczony od góry, bo przeczyłoby to założeniu, że szereg [math]\displaystyle{ \sum_{k = N_0}^{\infty} a_k }[/math] jest rozbieżny. Wynika stąd i z wypisanych wyżej nierówności, że również ciąg sum częściowych [math]\displaystyle{ B_n = \sum_{k = N_0}^{n} b_k }[/math] nie może być ograniczony od góry, zatem szereg [math]\displaystyle{ \sum_{k = N_0}^{\infty} b_k }[/math] jest rozbieżny.
□

Twierdzenie D10
Jeżeli szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \left | a_k \right | }[/math] jest zbieżny, to szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math] jest również zbieżny.

Dowód

Niech [math]\displaystyle{ b_k = a_k + | a_k | }[/math]. Z definicji prawdziwe jest następujące kryterium porównawcze

[math]\displaystyle{ 0 \leqslant b_k \leqslant 2 | a_k | }[/math]

Zatem z punktu 1. twierdzenia D9 wynika, że szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} b_k }[/math] jest zbieżny. Z definicji wyrazów ciągu [math]\displaystyle{ \left ( b_k \right ) }[/math] mamy [math]\displaystyle{ a_k = b_k - | a_k | }[/math] i możemy napisać

[math]\displaystyle{ \sum_{k = 1}^{\infty} a_k = \sum_{k = 1}^{\infty} b_k - \sum_{k = 1}^{\infty} | a_k | }[/math]

Ponieważ szeregi po prawej stronie są zbieżne, to zbieżny jest też szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math]. Zauważmy, że jedynie w przypadku, gdyby obydwa szeregi po prawej stronie były rozbieżne, nie moglibyśmy wnioskować o zbieżności / rozbieżności szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} a_k }[/math], bo suma szeregów rozbieżnych może być zbieżna.
□

Twierdzenie D11
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Jeżeli wyrazy ciągu [math]\displaystyle{ (a_n) }[/math] można zapisać w jednej z postaci

1. [math]\displaystyle{ \quad a_k = f_k - f_{k + 1} }[/math]
2. [math]\displaystyle{ \quad a_k = f_{k - 1} - f_k }[/math]

to odpowiadający temu ciągowi szereg nazywamy szeregiem teleskopowym. Suma częściowa szeregu teleskopowego jest odpowiednio równa

1. [math]\displaystyle{ \quad \sum_{k = m}^{n} a_k = f_m - f_{n + 1} }[/math]
2. [math]\displaystyle{ \quad \sum_{k = m}^{n} a_k = f_{m - 1} - f_n }[/math]

Dowód

[math]\displaystyle{ \sum_{k = m}^{n} a_k = \sum_{k = m}^{n} (f_k - f_{k + 1}) = }[/math]

[math]\displaystyle{ = (f_m - f_{m + 1}) + (f_{m + 1} - f_{m + 2}) + (f_{m + 2} - f_{m + 3}) + \ldots + (f_{n - 1} - f_n) + (f_n - f_{n + 1}) = }[/math]

[math]\displaystyle{ = f_m - f_{m + 1} + f_{m + 1} - f_{m + 2} + f_{m + 2} - f_{m + 3} + \ldots + f_{n - 1} - f_n + f_n - f_{n + 1} = }[/math]

[math]\displaystyle{ = f_m + (- f_{m + 1} + f_{m + 1}) + (- f_{m + 2} + f_{m + 2}) + (- f_{m + 3} + \ldots + f_{n - 1}) + (- f_n + f_n) - f_{n + 1} = }[/math]

[math]\displaystyle{ = f_m - f_{n + 1} }[/math]

[math]\displaystyle{ \sum_{k = m}^{n} a_k = \sum_{k = m}^{n} (f_{k - 1} - f_k) = }[/math]

[math]\displaystyle{ = (f_{m - 1} - f_m) + (f_m - f_{m + 1}) + (f_{m + 1} - f_{m + 2}) + \ldots + (f_{n - 2} - f_{n - 1}) + (f_{n - 1} - f_n) = }[/math]

[math]\displaystyle{ = f_{m - 1} - f_m + f_m - f_{m + 1} + f_{m + 1} - f_{m + 2} + \ldots + f_{n - 2} - f_{n - 1} + f_{n - 1} - f_n = }[/math]

[math]\displaystyle{ = f_{m - 1} + (- f_m + f_m) + (- f_{m + 1} + f_{m + 1}) + (- f_{m + 2} + \ldots + f_{n - 2}) + (- f_{n - 1} + f_{n - 1}) - f_n = }[/math]

[math]\displaystyle{ = f_{m - 1} - f_n }[/math]

□

Twierdzenie D12
Następujące szeregi są zbieżne

1. [math]\displaystyle{ \quad \sum^{\infty}_{k = 1} \frac{1}{k (k + 1)} = 1 }[/math]
2. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} \frac{1}{k (k - 1)} = 1 }[/math]
3. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} \frac{1}{k^2 - 1} = \frac{3}{4} }[/math]
4. [math]\displaystyle{ \quad \sum^{\infty}_{k = 1} \frac{1}{k^2} = \frac{\pi^2}{6} = 1.644934066848 \ldots }[/math]	A013661, WolframAlpha

Dowód

Punkt 1.
Dla dowodu wykorzystamy fakt, że rozpatrywany szereg jest szeregiem teleskopowym

[math]\displaystyle{ \frac{1}{k (k + 1)} = \frac{1}{k} - \frac{1}{k + 1} }[/math]

Zatem

[math]\displaystyle{ \sum^n_{k = 1} \frac{1}{k (k + 1)} = \sum^n_{k = 1} \left( \frac{1}{k} - \frac{1}{k + 1} \right) = 1 - \frac{1}{n + 1} }[/math]

Przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, dostajemy

[math]\displaystyle{ \sum^{\infty}_{k = 1} \frac{1}{k (k + 1)} = 1 }[/math]

Punkt 2.
Szereg jest identyczny z szeregiem z punktu 1., co łatwo zauważyć zmieniając zmienną sumowania [math]\displaystyle{ k = s + 1 }[/math] i odpowiednio granice sumowania.

Punkt 3.
Należy skorzystać z tożsamości

[math]\displaystyle{ \frac{1}{k^2 - 1} = \frac{1}{2} \left[ \left( \frac{1}{k} - \frac{1}{k + 1} \right) + \left( \frac{1}{k - 1} - \frac{1}{k} \right) \right] }[/math]

Punkt 4.
Ponieważ dla [math]\displaystyle{ k \geqslant 2 }[/math] prawdziwa jest nierówność

[math]\displaystyle{ 0 \lt \frac{1}{k^2} \lt \frac{1}{k^2 - 1} }[/math]

to na mocy kryterium porównawczego (twierdzenie D9) ze zbieżności szeregu [math]\displaystyle{ \sum^{\infty}_{k = 2} \frac{1}{k^2 - 1} }[/math] wynika zbieżność szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^2} }[/math]
□

Twierdzenie D13
Następujące szeregi są zbieżne

1. [math]\displaystyle{ \quad \sum_{k = 1}^{\infty} \frac{1}{(k + 1) \sqrt{k}} = 1.860025079221 \ldots }[/math]
2. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} \frac{\log k}{k (k + 1)} = 0.788530565911 \ldots }[/math]	A085361
3. [math]\displaystyle{ \quad \sum^{\infty}_{k = 2} \frac{\log k}{k (k - 1)} = 1.257746886944 \ldots }[/math]	A131688
4. [math]\displaystyle{ \quad \sum^{\infty}_{k = 3} \frac{1}{k \cdot \log^2 \! k} = 1.069058310734 \ldots }[/math]	A115563

Dowód

Punkt 1.

Wystarczy zauważyć, że

[math]\displaystyle{ \frac{1}{\sqrt{k}} - \frac{1}{\sqrt{k + 1}} = \frac{\sqrt{k + 1} - \sqrt{k}}{\sqrt{k} \cdot \sqrt{k + 1}} = }[/math]

[math]\displaystyle{ \quad\: = \frac{1}{\sqrt{k} \cdot \sqrt{k + 1} \cdot \left( \sqrt{k + 1} + \sqrt{k} \right)} \gt }[/math]

[math]\displaystyle{ \quad\: \gt \frac{1}{\sqrt{k} \cdot \sqrt{k + 1} \cdot 2 \sqrt{k + 1}} }[/math]

[math]\displaystyle{ \quad\: = \frac{1}{2 (k + 1) \sqrt{k}} }[/math]

Zatem

[math]\displaystyle{ \sum_{k = 1}^n \frac{1}{(k + 1) \sqrt{k}} = 2 \sum_{k = 1}^n \frac{1}{2 (k + 1) \sqrt{k}} \lt }[/math]

[math]\displaystyle{ \;\;\;\: \lt 2 \sum_{k = 1}^n \left( \frac{1}{\sqrt{k}} - \frac{1}{\sqrt{k + 1}} \right) = }[/math]

[math]\displaystyle{ \;\;\;\: = 2 \left( 1 - \frac{1}{\sqrt{n + 1}} \right) \lt }[/math]

[math]\displaystyle{ \;\;\;\: \lt 2 }[/math]

Ponieważ ciąg sum częściowych szeregu jest rosnący i ograniczony, to szereg jest zbieżny.

Punkt 2.
Korzystając z twierdzenia A37, możemy napisać oszacowanie

[math]\displaystyle{ 0 \lt \frac{\log k}{k (k + 1)} \lt \frac{2 \sqrt{k}}{k (k + 1)} \lt \frac{2}{(k + 1) \sqrt{k}} }[/math]

Zatem na mocy kryterium porównawczego ze zbieżności szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{(k + 1) \sqrt{k}} }[/math] wynika zbieżność szeregu [math]\displaystyle{ \sum^{\infty}_{k = 2} \frac{\log k}{k (k + 1)} }[/math]

Punkt 3.
Zauważmy, że

[math]\displaystyle{ \frac{\log (k - 1)}{k - 1} - \frac{\log (k)}{k} = \frac{k \log (k - 1) - (k - 1) \log (k)}{k (k - 1)} = }[/math]

[math]\displaystyle{ \;\;\, = \frac{k \log \left( k \left( 1 - \frac{1}{k} \right) \right) - (k - 1) \log (k)}{k (k - 1)} = }[/math]

[math]\displaystyle{ \;\;\, = \frac{k \log (k) + k \log \left( 1 - \frac{1}{k} \right) - k \log (k) + \log (k)}{k (k - 1)} \gt }[/math]

[math]\displaystyle{ \;\;\, \gt \frac{\log (k) - k \cdot \frac{1}{k - 1}}{k (k - 1)} = }[/math]

[math]\displaystyle{ \;\;\, = \frac{\log (k)}{k (k - 1)} - \frac{1}{(k - 1)^2} }[/math]

Czyli prawdziwe jest oszacowanie

[math]\displaystyle{ \frac{\log (k)}{k (k - 1)} \lt \left[ \frac{\log (k - 1)}{k - 1} - \frac{\log (k)}{k} \right] + \frac{1}{(k - 1)^2} }[/math]

Zatem możemy napisać

[math]\displaystyle{ \sum_{k = 2}^{n} \frac{\log (k)}{k (k - 1)} \lt \sum_{k = 2}^{n} \left[ \frac{\log (k - 1)}{k - 1} - \frac{\log (k)}{k} \right] + \sum_{k = 2}^{n} \frac{1}{(k - 1)^2} }[/math]

[math]\displaystyle{ \: \lt - \frac{\log (n)}{n} + \sum_{j = 1}^{n - 1} \frac{1}{j^2} }[/math]

[math]\displaystyle{ \: \lt \sum_{j = 1}^{\infty} \frac{1}{j^2} = }[/math]

[math]\displaystyle{ \: = \frac{\pi^2}{6} }[/math]

Ponieważ ciąg sum częściowych szeregu jest rosnący i ograniczony, to szereg jest zbieżny.

Punkt 4.
Zauważmy, że

[math]\displaystyle{ \frac{1}{\log (k)} - \frac{1}{\log (k + 1)} = \frac{\log (k + 1) - \log (k)}{\log (k) \log (k + 1)} = }[/math]

[math]\displaystyle{ \;\;\, = \frac{\log \left( 1 + \frac{1}{k} \right)}{\log (k) \log (k + 1)} \lt }[/math]

[math]\displaystyle{ \;\;\, \lt \frac{1}{k \cdot \log (k) \log (k + 1)} \lt }[/math]

[math]\displaystyle{ \;\;\, \lt \frac{1}{k \cdot \log^2 \! k} }[/math]

Z drugiej strony mamy

[math]\displaystyle{ \frac{1}{\log (k - 1)} - \frac{1}{\log (k)} = \frac{\log (k) - \log (k - 1)}{\log (k - 1) \log (k)} = }[/math]

[math]\displaystyle{ \;\;\, = \frac{\log \left( 1 + \frac{1}{k - 1} \right)}{\log (k - 1) \log (k)} \gt }[/math]

[math]\displaystyle{ \;\;\, \gt \frac{1}{k \cdot \log (k - 1) \log (k)} \gt }[/math]

[math]\displaystyle{ \;\;\, \gt \frac{1}{k \cdot \log^2 \! k} }[/math]

Wynika stąd następujący ciąg nierówności

[math]\displaystyle{ \frac{1}{\log (k)} - \frac{1}{\log (k + 1)} \lt \frac{1}{k \cdot \log^2 \! k} \lt \frac{1}{\log (k - 1)} - \frac{1}{\log (k)} }[/math]

Rezultat ten wykorzystamy w pełni w przykładzie D14, a do pokazania zbieżności szeregu wystarczy nam prawa nierówność. Mamy

[math]\displaystyle{ \sum_{k = 3}^{n} \frac{1}{k \cdot \log^2 \! k} \lt \sum_{k = 3}^{n} \left[ \frac{1}{\log (k - 1)} - \frac{1}{\log (k)} \right] = }[/math]

[math]\displaystyle{ \; = \frac{1}{\log 2} - \frac{1}{\log (n)} \lt }[/math]

[math]\displaystyle{ \; \lt \frac{1}{\log 2} }[/math]

Ponieważ ciąg sum częściowych szeregu jest rosnący i ograniczony, to szereg jest zbieżny.
□

Przykład D14
Na przykładzie szeregu [math]\displaystyle{ \sum_{k = 3}^{\infty} \frac{1}{k \cdot \log^2 k} }[/math] pokażemy, jak należy obliczać przybliżoną wartość sumy szeregu.

Ponieważ nie jesteśmy w stanie zsumować nieskończenie wielu wyrazów, zatem najlepiej będzie podzielić szereg na dwie części

[math]\displaystyle{ \sum_{k = 3}^{\infty} \frac{1}{k \cdot \log^2 k} = \sum_{k = 3}^{m} \frac{1}{k \cdot \log^2 k} + \sum_{k = m + 1}^{\infty} \frac{1}{k \cdot \log^2 k} }[/math]

Wartość pierwszej części możemy policzyć bezpośrednio, a dla drugiej części powinniśmy znaleźć jak najlepsze oszacowanie.

Dowodząc twierdzenie D13, w punkcie 4. pokazaliśmy, że prawdziwy jest ciąg nierówności

[math]\displaystyle{ \frac{1}{\log (k)} - \frac{1}{\log (k + 1)} \lt \frac{1}{k \cdot \log^2 k} \lt \frac{1}{\log (k - 1)} - \frac{1}{\log (k)} }[/math]

Wykorzystamy powyższy wzór do znalezienia potrzebnego nam oszacowania. Sumując strony nierówności, dostajemy

[math]\displaystyle{ \sum_{k = m + 1}^{n} \left( \frac{1}{\log (k)} - \frac{1}{\log (k + 1)} \right) \lt \sum_{k = m + 1}^{n} \frac{1}{k \cdot \log^2 k} \lt \sum_{k = m + 1}^{n} \left( \frac{1}{\log (k - 1)} - \frac{1}{\log (k)} \right) }[/math]

Ponieważ szeregi po lewej i po prawej stronie są szeregami teleskopowymi, to łatwo znajdujemy, że

[math]\displaystyle{ \frac{1}{\log (m + 1)} - \frac{1}{\log (n + 1)} \lt \sum_{k = m + 1}^{n} \frac{1}{k \cdot \log^2 k} \lt \frac{1}{\log m} - \frac{1}{\log n} }[/math]

Przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, otrzymujemy oszacowanie

[math]\displaystyle{ \frac{1}{\log (m + 1)} \lt \sum_{k = m + 1}^{\infty} \frac{1}{k \cdot \log^2 k} \lt \frac{1}{\log m} }[/math]

Teraz pozostaje dodać sumę wyrazów szeregu od [math]\displaystyle{ k = 3 }[/math] do [math]\displaystyle{ k = m }[/math]

[math]\displaystyle{ \frac{1}{\log (m + 1)} + \sum_{k = 3}^{m} \frac{1}{k \cdot \log^2 k} \lt \sum_{k = 3}^{\infty} \frac{1}{k \cdot \log^2 k} \lt \frac{1}{\log m} + \sum_{k = 3}^{m} \frac{1}{k \cdot \log^2 k} }[/math]

Poniżej przedstawiamy wartości oszacowania sumy szeregu znalezione przy pomocy programu PARI/GP dla kolejnych wartości [math]\displaystyle{ m }[/math]. Wystarczy proste polecenie

for(n=1, 8, s = sum( k = 3, 10^n, 1/k/(log(k))^2 ); print("n= ", n, "   a= ", s+1/log(10^n+1), "   b= ", s+1/log(10^n) ))

[math]\displaystyle{ m = 10^1 }[/math]	[math]\displaystyle{ 1.06 }[/math]	[math]\displaystyle{ 1.07 }[/math]
[math]\displaystyle{ m = 10^2 }[/math]	[math]\displaystyle{ 1.068 }[/math]	[math]\displaystyle{ 1.069 }[/math]
[math]\displaystyle{ m = 10^3 }[/math]	[math]\displaystyle{ 1.06904 }[/math]	[math]\displaystyle{ 1.06906 }[/math]
[math]\displaystyle{ m = 10^4 }[/math]	[math]\displaystyle{ 1.069057 }[/math]	[math]\displaystyle{ 1.069058 }[/math]
[math]\displaystyle{ m = 10^5 }[/math]	[math]\displaystyle{ 1.0690582 }[/math]	[math]\displaystyle{ 1.0690583 }[/math]
[math]\displaystyle{ m = 10^6 }[/math]	[math]\displaystyle{ 1.06905830 }[/math]	[math]\displaystyle{ 1.06905831 }[/math]
[math]\displaystyle{ m = 10^7 }[/math]	[math]\displaystyle{ 1.0690583105 }[/math]	[math]\displaystyle{ 1.0690583109 }[/math]
[math]\displaystyle{ m = 10^8 }[/math]	[math]\displaystyle{ 1.06905831071 }[/math]	[math]\displaystyle{ 1.06905831074 }[/math]

Dysponując oszacowaniem reszty szeregu, znaleźliśmy wartość sumy szeregu z dokładnością 10 miejsc po przecinku.

Natomiast samo zsumowanie [math]\displaystyle{ 10^8 }[/math] wyrazów szeregu daje wynik

[math]\displaystyle{ \sum_{k = 3}^{10^8} \frac{1}{k \cdot \log^2 k} = 1.014 771 500 510 916 \ldots }[/math]

Zatem mimo zsumowania stu milionów(!) wyrazów szeregu otrzymaliśmy rezultat z dokładnością jednego(!) miejsca po przecinku. Co więcej, nie wiemy, jaka jest dokładność uzyskanego rezultatu. Znając oszacowanie od dołu i od góry, dokładność jednego miejsca po przecinku uzyskaliśmy po zsumowaniu dziesięciu(!) wyrazów szeregu.

Rozpatrywana wyżej sytuacja pokazuje, że w przypadku znajdowania przybliżonej wartości sumy szeregu ważniejsze od sumowania ogromnej ilości wyrazów jest posiadanie oszacowania nieskończonej reszty szeregu. Ponieważ wyznaczenie tego oszacowania na ogół nie jest proste, pokażemy jak ten problem rozwiązać przy pomocy całki oznaczonej.

Szeregi nieskończone i całka oznaczona

Twierdzenie D15
Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] jest ciągła, dodatnia i malejąca w przedziale [math]\displaystyle{ [m, n + 1] }[/math], to prawdziwy jest następujący ciąg nierówności

[math]\displaystyle{ 0 \leqslant \int_{m}^{n + 1} f(x) d x \leqslant \sum_{k = m}^{n} f(k) \leqslant f (m) + \int_{m}^{n} f(x) d x }[/math]

Dowód

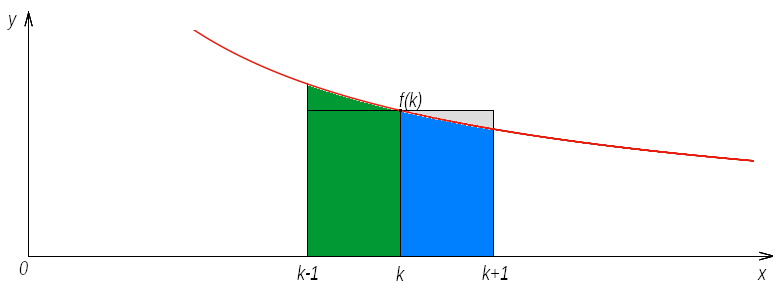
Ponieważ funkcja [math]\displaystyle{ f(x) }[/math] jest z założenia ciągła, dodatnia i malejąca, to zamieszczony niżej rysunek dobrze prezentuje problem.

Przedstawiona na rysunku krzywa odpowiada funkcji [math]\displaystyle{ f(x) }[/math]. Dla współrzędnej [math]\displaystyle{ x = k }[/math] zaznaczyliśmy wartość funkcji [math]\displaystyle{ f(k) }[/math], a po lewej i prawej stronie tych punktów zaznaczyliśmy pasy o jednostkowej szerokości. Łatwo zauważamy, że

• po lewej stronie pole pod krzywą (zaznaczone kolorem zielonym) jest większe od pola prostokąta o wysokości [math]\displaystyle{ f(k) }[/math] i jednostkowej szerokości
• po prawej stronie pole pod krzywą (zaznaczone kolorem niebieskim) jest mniejsze od pola prostokąta o wysokości [math]\displaystyle{ f(k) }[/math] i jednostkowej szerokości

Korzystając z własności całki oznaczonej, otrzymujemy ciąg nierówności

[math]\displaystyle{ \int_{k}^{k + 1} f(x) d x \leqslant f(k) \leqslant \int_{k - 1}^{k} f(x) d x }[/math]

W powyższym wzorze występują nierówności nieostre, bo rysunek przedstawia funkcję silnie malejącą, ale zgodnie z uczynionym założeniem funkcja [math]\displaystyle{ f(x) }[/math] może być funkcją słabo malejącą.

Sumując lewą nierówność od [math]\displaystyle{ k = m }[/math] do [math]\displaystyle{ k = n }[/math], a prawą od [math]\displaystyle{ k = m + 1 }[/math] do [math]\displaystyle{ k = n }[/math], dostajemy

[math]\displaystyle{ \int_{m}^{n + 1} f (x) d x \leqslant \sum_{k = m}^{n} f (k) }[/math]

[math]\displaystyle{ \sum_{k = m + 1}^{n} f (k) \leqslant \int_{m}^{n} f (x) d x }[/math]

Dodając [math]\displaystyle{ f(m) }[/math] do obydwu stron drugiej z powyższych nierówności i łącząc je ze sobą, otrzymujemy kolejny i docelowy ciąg nierówności

[math]\displaystyle{ 0 \leqslant \int_{m}^{n + 1} f (x) d x \leqslant \sum_{k = m}^{n} f (k) \leqslant f (m) + \int_{m}^{n} f (x) d x }[/math]

□

Przykład D16
Rozważmy szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k} }[/math].

Funkcja [math]\displaystyle{ f(x) = \frac{1}{x} }[/math] jest ciągła, dodatnia i silnie malejąca w przedziale [math]\displaystyle{ (0, + \infty) }[/math], zatem dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ \int_{1}^{n + 1} \frac{d x}{x} \lt \sum_{k = 1}^{n} \frac{1}{k} \lt 1 + \int_{1}^{n} \frac{d x}{x} }[/math]

Przy obliczaniu całek oznaczonych Czytelnik może skorzystać ze strony WolframAlpha.

[math]\displaystyle{ \log (n + 1) \lt \sum_{k = 1}^{n} \frac{1}{k} \lt 1 + \log n }[/math]

Ponieważ

[math]\displaystyle{ \log (n + 1) = \log \left( n \left( 1 + \frac{1}{n} \right) \right) = \log n + \log \left( 1 + \frac{1}{n} \right) \gt \log n + \frac{1}{n + 1} }[/math]

to dostajemy

[math]\displaystyle{ \frac{1}{n + 1} \lt \sum_{k = 1}^{n} \frac{1}{k} - \log n \lt 1 }[/math]

Zauważmy: nie tylko wiemy, że szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k} }[/math] jest rozbieżny, ale jeszcze potrafimy określić, jaka funkcja tę rozbieżność opisuje! Mamy zatem podstawy, by przypuszczać, że całki umożliwią opracowanie metody, która pozwoli rozstrzygać o zbieżności szeregów.

Twierdzenie D17 (kryterium całkowe zbieżności szeregów)
Załóżmy, że funkcja [math]\displaystyle{ f(x) }[/math] jest ciągła, dodatnia i malejąca w przedziale [math]\displaystyle{ [m, + \infty) }[/math]. Szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f(k) }[/math] jest zbieżny lub rozbieżny w zależności od tego, czy funkcja pierwotna [math]\displaystyle{ F(x) = \int f (x) d x }[/math] ma dla [math]\displaystyle{ x \rightarrow \infty }[/math] granicę skończoną, czy nie.

Dowód

Nim przejdziemy do dowodu, wyjaśnimy uczynione założenia. Założenie, że funkcja [math]\displaystyle{ f(x) }[/math] jest malejąca, będzie wykorzystane w czasie dowodu twierdzenia, ale rozważanie przypadku, gdy [math]\displaystyle{ f(x) }[/math] jest rosnąca, nie ma sensu, bo wtedy nie mógłby być spełniony warunek konieczny zbieżności szeregu [math]\displaystyle{ \sum_{k = m}^{\infty} f(k) }[/math] (zobacz twierdzenie D4).

Moglibyśmy założyć bardziej ogólnie, że funkcja jest nieujemna, ale wtedy twierdzenie obejmowałoby przypadki funkcji takich, że dla pewnego [math]\displaystyle{ x_0 }[/math] byłoby [math]\displaystyle{ f(x_0) = 0 }[/math]. Ponieważ z założenia funkcja [math]\displaystyle{ f(x) }[/math] jest malejąca, zatem mielibyśmy [math]\displaystyle{ f(x) = 0 }[/math] dla [math]\displaystyle{ x \geqslant x_0 }[/math]. Odpowiadający tej funkcji szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math] miałby dla [math]\displaystyle{ k \geqslant x_0 }[/math] tylko wyrazy zerowe i byłby w sposób oczywisty zbieżny.

Założenie ciągłości funkcji [math]\displaystyle{ f(x) }[/math] ma zapewnić całkowalność funkcji [math]\displaystyle{ f(x) }[/math]. Założenie to można osłabić, ale nie będziemy zajmowali się tym problemem – ograniczymy się do podania przykładów. Niech [math]\displaystyle{ a, b \in \mathbb{R} }[/math], mamy

[math]\displaystyle{ \int_a^b \text{sgn}(x) d x = | b | - | a | }[/math] [math]\displaystyle{ \qquad \qquad \int_0^a \lfloor x \rfloor d x = \frac{1}{2} \lfloor a \rfloor (2 a - \lfloor a \rfloor - 1) }[/math] [math]\displaystyle{ \qquad \qquad \int_{-a}^a \lfloor x \rfloor d x = - a }[/math]

Po tych uwagach dotyczących założeń możemy przejść do właściwego dowodu. Korzystając ze wzoru udowodnionego w twierdzeniu D15 i przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, dostajemy

[math]\displaystyle{ 0 \leqslant \int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f (m) + \int_{m}^{\infty} f(x) d x }[/math]

Z drugiej nierówności wynika, że jeżeli całka [math]\displaystyle{ \int_{m}^{\infty} f(x) d x }[/math] jest rozbieżna, to rosnący ciąg kolejnych całek oznaczonych [math]\displaystyle{ C_j = \int_{m}^{j} f (x) d x }[/math] nie może być ograniczony od góry (w przeciwnym wypadku całka [math]\displaystyle{ \int_{m}^{\infty} f (x) d x }[/math] byłby zbieżna), zatem również rosnący ciąg sum częściowych [math]\displaystyle{ F_j = \sum_{k = m}^{j} f(k) }[/math] nie może być ograniczony od góry, co oznacza, że szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f(k) }[/math] jest rozbieżny.

Z trzeciej nierówności wynika, że jeżeli całka [math]\displaystyle{ \int_{m}^{\infty} f(x) d x }[/math] jest zbieżna, to ciąg sum częściowych [math]\displaystyle{ F_j = \sum_{k = m}^{j} f (k) }[/math] jest ciągiem rosnącym i ograniczonym od góry. Wynika stąd, że ciąg [math]\displaystyle{ F_j }[/math] jest zbieżny, zatem szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f(k) }[/math] jest zbieżny.

Ponieważ zbieżność (rozbieżność) całki [math]\displaystyle{ \int_{m}^{\infty} f(x) d x }[/math] nie zależy od wyboru dolnej granicy całkowania, to wystarczy badać granicę [math]\displaystyle{ \lim_{x \to \infty} F (x) }[/math], gdzie [math]\displaystyle{ F(x) = \int f (x) d x }[/math] jest dowolną funkcją pierwotną.
□

Przykład D18
Przykłady zebraliśmy w tabeli. Przy obliczaniu całek nieoznaczonych Czytelnik może skorzystać ze strony WolframAlpha.

	szereg [math]\displaystyle{ \sum_{k = m}^{\infty} a_k }[/math]	funkcja [math]\displaystyle{ f(x) }[/math]	całka [math]\displaystyle{ F(x) = \int f(x) d x }[/math]	granica [math]\displaystyle{ \lim_{x \to \infty} F(x) }[/math]	wynik
1.	[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k} }[/math]	[math]\displaystyle{ \frac{1}{x} }[/math]	[math]\displaystyle{ \log x }[/math]	[math]\displaystyle{ \infty }[/math]	szereg rozbieżny
2.	[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{\sqrt{k}} }[/math]	[math]\displaystyle{ \frac{1}{\sqrt{x}} }[/math]	[math]\displaystyle{ 2 \sqrt{x} }[/math]	[math]\displaystyle{ \infty }[/math]	szereg rozbieżny
3.	[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^2} }[/math]	[math]\displaystyle{ \frac{1}{x^2} }[/math]	[math]\displaystyle{ - \frac{1}{x} }[/math]	[math]\displaystyle{ 0 }[/math]	szereg zbieżny
4.	[math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{k \log k} }[/math]	[math]\displaystyle{ \frac{1}{x \log x} }[/math]	[math]\displaystyle{ \log \log x }[/math]	[math]\displaystyle{ \infty }[/math]	szereg rozbieżny
5.	[math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{k \log^2 \! k} }[/math]	[math]\displaystyle{ \frac{1}{x \log^2 \! x} }[/math]	[math]\displaystyle{ - \frac{1}{\log x} }[/math]	[math]\displaystyle{ 0 }[/math]	szereg zbieżny

Stosując kryterium całkowe można łatwo pokazać, że szeregi

[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^s} }[/math]

[math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{k \log^s \! k} }[/math]

są zbieżne dla [math]\displaystyle{ s \gt 1 }[/math] i rozbieżne dla [math]\displaystyle{ s \leqslant 1 }[/math].

Twierdzenie D19
Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] jest ciągła, dodatnia i malejąca w przedziale [math]\displaystyle{ [m, \infty) }[/math] oraz

[math]\displaystyle{ R(m) = \int_{m}^{\infty} f(x) d x }[/math]

[math]\displaystyle{ S(m) = \sum_{k = a}^{m} f(k) }[/math]

gdzie [math]\displaystyle{ a \lt m }[/math], to prawdziwe jest następujące oszacowanie sumy szeregu nieskończonego [math]\displaystyle{ \sum_{k = a}^{\infty} f (k) }[/math]

[math]\displaystyle{ S(m) + R(m) - f(m) \leqslant \sum_{k = a}^{\infty} f(k) \leqslant S(m) + R(m) }[/math]

Dowód

Korzystając ze wzoru udowodnionego w twierdzeniu D15 i przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, dostajemy

[math]\displaystyle{ \int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f(m) + \int_{m}^{\infty} f(x) d x }[/math]

Czyli

[math]\displaystyle{ R(m) \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f(m) + R (m) }[/math]

Odejmując od każdej ze stron nierówności liczbę [math]\displaystyle{ f(m) }[/math] i dodając do każdej ze stron nierówności sumę skończoną [math]\displaystyle{ S(m) = \sum_{k = a}^{m} f(k) }[/math], otrzymujemy

[math]\displaystyle{ S(m) + R (m) - f(m) \leqslant \sum_{k = a}^{\infty} f(k) \leqslant S(m) + R (m) }[/math]

Co należało pokazać.
□

Przykład D20
Twierdzenie D19 umożliwia określenie, z jaką dokładnością została wyznaczona suma szeregu. Wyznaczmy sumę szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{(k + 1) \sqrt{k}} }[/math]. Mamy

[math]\displaystyle{ S(m) = \sum_{k = 1}^{m} \frac{1}{(k + 1) \sqrt{k}} }[/math]

[math]\displaystyle{ \int \frac{d x}{(x + 1) \sqrt{x}} = 2 \text{arctg} \left( \sqrt{x} \right) }[/math]

[math]\displaystyle{ R(m) = \int_{m}^{\infty} \frac{d x}{(x + 1) \sqrt{x}} = \pi - 2 \text{arctg} \left( \sqrt{m} \right) }[/math]

Zatem

[math]\displaystyle{ S(m) + R (m) - f (m) \leqslant \sum_{k = 1}^{\infty} \frac{1}{(k + 1) \sqrt{k}} \leqslant S (m) + R (m) }[/math]

Dla kolejnych wartości [math]\displaystyle{ m }[/math] otrzymujemy

[math]\displaystyle{ m }[/math]	[math]\displaystyle{ S(m) + R(m) - f(m) }[/math]	[math]\displaystyle{ S(m) + R(m) }[/math]
[math]\displaystyle{ 10^1 }[/math]	[math]\displaystyle{ 1.84 }[/math]	[math]\displaystyle{ 1.87 }[/math]
[math]\displaystyle{ 10^2 }[/math]	[math]\displaystyle{ 1.85 }[/math]	[math]\displaystyle{ 1.86 }[/math]
[math]\displaystyle{ 10^3 }[/math]	[math]\displaystyle{ 1.86000 }[/math]	[math]\displaystyle{ 1.86004 }[/math]
[math]\displaystyle{ 10^4 }[/math]	[math]\displaystyle{ 1.860024 }[/math]	[math]\displaystyle{ 1.860025 }[/math]
[math]\displaystyle{ 10^5 }[/math]	[math]\displaystyle{ 1.86002506 }[/math]	[math]\displaystyle{ 1.86002509 }[/math]
[math]\displaystyle{ 10^6 }[/math]	[math]\displaystyle{ 1.860025078 }[/math]	[math]\displaystyle{ 1.860025079 }[/math]
[math]\displaystyle{ 10^7 }[/math]	[math]\displaystyle{ 1.86002507920 }[/math]	[math]\displaystyle{ 1.86002507923 }[/math]
[math]\displaystyle{ 10^8 }[/math]	[math]\displaystyle{ 1.860025079220 }[/math]	[math]\displaystyle{ 1.860025079221 }[/math]
[math]\displaystyle{ 10^9 }[/math]	[math]\displaystyle{ 1.8600250792211 }[/math]	[math]\displaystyle{ 1.8600250792212 }[/math]

W programie PARI/GP wystarczy napisać:

f(k) = 1.0/(k+1)/sqrt(k)
S(m) = sum( k = 1, m, f(k) )
R(m) = Pi - 2*atan( sqrt(m) )
for(j=1, 9, m=10^j; suma=S(m); reszta=R(m); print( "j= ", j, "   a= ", suma + reszta - f(m), "   b= ", suma + reszta ))

Prostym wnioskiem z twierdzenia D15 jest następujące
Twierdzenie D21
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ [m, + \infty) }[/math]. Jeżeli przy wyliczaniu sumy szeregu nieskończonego [math]\displaystyle{ \sum_{k = a}^{\infty} f (k) }[/math] (gdzie [math]\displaystyle{ a \lt m }[/math]) zastąpimy sumę [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math] całką [math]\displaystyle{ \int_{m}^{\infty} f (x) d x }[/math], to błąd wyznaczenia sumy szeregu nie przekroczy [math]\displaystyle{ f(m) }[/math].

Dowód

Korzystając ze wzoru z twierdzenia D15 i przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, otrzymujemy

[math]\displaystyle{ \int_{m}^{\infty} f(x) d x \leqslant \sum_{k = m}^{\infty} f(k) \leqslant f(m) + \int_{m}^{\infty} f(x) d x }[/math]

Dodając do każdej ze stron nierówności wyrażenie [math]\displaystyle{ - f(m) + \sum_{k = a}^{m} f(k) }[/math], dostajemy

[math]\displaystyle{ - f(m) + \sum_{k = a}^{m} f(k) + \int_{m}^{\infty} f(x) d x \leqslant \sum_{k = a}^{\infty} f(k) \leqslant \sum_{k = a}^{m} f(k) + \int_{m}^{\infty} f(x) d x }[/math]

Skąd wynika natychmiast

[math]\displaystyle{ - f(m) \leqslant \sum_{k = a}^{\infty} f(k) - \left( \sum_{k = a}^{m} f(k) + \int_{m}^{\infty} f(x) d x \right) \leqslant 0 \lt f(m) }[/math]

Czyli

[math]\displaystyle{ \left| \sum_{k = a}^{\infty} f(k) - \left( \sum_{k = a}^{m} f(k) + \int_{m}^{\infty} f(x) d x \right) \right| \leqslant f(m) }[/math]

Co kończy dowód.
□

Twierdzenie D22
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ [m, + \infty) }[/math]. Jeżeli szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math] jest zbieżny, to dla każdego [math]\displaystyle{ n \geqslant m }[/math] prawdziwe jest następujące oszacowanie sumy częściowej szeregu [math]\displaystyle{ S(n) }[/math]

[math]\displaystyle{ S(n) = \sum_{k = m}^{n} f (k) \leqslant C - B \int_{n}^{\infty} f (x) d x }[/math]

gdzie [math]\displaystyle{ B }[/math] oraz [math]\displaystyle{ C }[/math] są dowolnymi stałymi spełniającymi nierówności

[math]\displaystyle{ B \geqslant 1 }[/math]

[math]\displaystyle{ C \geqslant f (m) + B \int_{m}^{\infty} f (x) d x }[/math]

Dowód

Z twierdzenia D15 mamy

[math]\displaystyle{ S(n) = \sum_{k = m}^{n} f (k) \leqslant f (m) + \int_{m}^{n} f (x) d x \leqslant }[/math]

[math]\displaystyle{ \;\! \leqslant f (m) + B \int_{m}^{n} f (x) d x = }[/math]

[math]\displaystyle{ \;\! = f (m) + B \int_{m}^{n} f (x) d x - B \int_{m}^{\infty} f (x) d x + B \int_{m}^{\infty} f (x) d x = }[/math]

[math]\displaystyle{ \;\! = f (m) + B \int_{m}^{n} f (x) d x - B \int^n_m f (x) d x - B \int_{n}^{\infty} f (x) d x + B \int_{m}^{\infty} f (x) d x = }[/math]

[math]\displaystyle{ \;\! = f (m) - B \int_{n}^{\infty} f (x) d x + B \int_{m}^{\infty} f (x) d x = }[/math]

[math]\displaystyle{ \;\! = \left[ f (m) + B \int_{m}^{\infty} f (x) d x \right] - B \int_{n}^{\infty} f (x) d x \leqslant }[/math]

[math]\displaystyle{ \;\! \leqslant C - B \int_{n}^{\infty} f (x) d x }[/math]

□

Uwaga D23
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ [m, \infty) }[/math]. Rozważmy szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math]. Zauważmy, że:

• korzystając z całkowego kryterium zbieżności, możemy łatwo zbadać, czy szereg [math]\displaystyle{ \sum_{k = m}^{\infty} f (k) }[/math] jest zbieżny
• jeżeli szereg jest zbieżny, to ponownie wykorzystując całki (twierdzenie D22), możemy znaleźć oszacowanie sumy częściowej szeregu [math]\displaystyle{ S(n) = \sum_{k = m}^{n} f(k) }[/math]

Jednak dysponując już oszacowaniem sumy częściowej szeregu [math]\displaystyle{ S(n) = \sum_{k = m}^{n} f(k) }[/math], możemy udowodnić jego poprawność przy pomocy indukcji matematycznej, a stąd łatwo pokazać zbieżność szeregu [math]\displaystyle{ \sum_{k = m}^{\infty} f(k) }[/math]. Zauważmy, że wybór większego [math]\displaystyle{ B }[/math] ułatwia dowód indukcyjny. Stałą [math]\displaystyle{ C }[/math] najlepiej zaokrąglić w górę do wygodnej dla nas wartości.

Czasami potrzebujemy takiego uproszczenia problemu, aby udowodnić zbieżność szeregów bez odwoływania się do całek. Zauważmy, że Czytelnik nawet nie musi znać całek – wystarczy, że policzy je przy pomocy programów, które potrafią to robić (np. WolframAlpha). Kiedy już znajdziemy oszacowanie sumy częściowej szeregu, nie musimy wyjaśniać, w jaki sposób je znaleźliśmy – wystarczy udowodnić, że jest ono poprawne, a do tego wystarczy indukcja matematyczna.

Zamieszczonej niżej zadania pokazują, jak wykorzystać w tym celu twierdzenie D22.

Zadanie D24
Korzystając z twierdzenia D22, znaleźć oszacowania sumy częściowej szeregów

[math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^2} \qquad }[/math] oraz [math]\displaystyle{ \qquad \sum_{k = 2}^{\infty} \frac{1}{k (\log k)^2} }[/math]

Rozwiązanie

Rozważmy szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^2} }[/math]. Funkcja [math]\displaystyle{ f(x) = \frac{1}{x^2} }[/math] jest funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ (0, + \infty) }[/math]. Dla [math]\displaystyle{ n \gt 0 }[/math] jest

[math]\displaystyle{ \int_{n}^{\infty} \frac{1}{x^2} d x = \frac{1}{n} \qquad }[/math] (zobacz: WolframAlpha)

[math]\displaystyle{ C \geqslant 1 + \int_{1}^{\infty} \frac{1}{x^2} d x = 2 }[/math]

Zatem

[math]\displaystyle{ \sum_{k = 1}^{n} \frac{1}{k^2} \leqslant 2 - \frac{1}{n} }[/math]

Rozważmy szereg [math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{k (\log k)^2} }[/math]. Funkcja [math]\displaystyle{ f(x) = \frac{1}{x (\log x)^2} }[/math] jest funkcją ciągłą, dodatnią i malejącą w przedziale [math]\displaystyle{ (1, + \infty) }[/math]. Dla [math]\displaystyle{ n \gt 1 }[/math] jest

[math]\displaystyle{ \int_{n}^{\infty} \frac{1}{x (\log x)^2} d x = \frac{1}{\log n} \qquad }[/math] (zobacz: WolframAlpha)

[math]\displaystyle{ C \geqslant \frac{1}{2 \cdot (\log 2)^2} + \int_{2}^{\infty} \frac{1}{x (\log x)^2} d x = \frac{1}{2 \cdot (\log 2)^2} + \frac{1}{\log 2} = 2.483379 \ldots }[/math]

Przyjmijmy [math]\displaystyle{ C = 2.5 }[/math], zatem

[math]\displaystyle{ \sum_{k = 2}^{n} \frac{1}{k (\log k)^2} \lt 2.5 - \frac{1}{\log n} }[/math]

□

Zadanie D25
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania [math]\displaystyle{ \sum_{k = 1}^{n} \frac{1}{k^2} \leqslant 2 - \frac{1}{n} }[/math] i udowodnić, że szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^2} }[/math] jest zbieżny.

Rozwiązanie

Indukcja matematyczna. Łatwo zauważamy, że oszacowanie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math]. Zakładając, że oszacowanie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ \sum_{k = 1}^{n + 1} \frac{1}{k^2} = \sum_{k = 1}^{n} \frac{1}{k^2} + \frac{1}{(n + 1)^2} \leqslant }[/math]

[math]\displaystyle{ \;\: \leqslant 2 - \frac{1}{n} + \frac{1}{(n + 1)^2} \leqslant }[/math]

[math]\displaystyle{ \;\: \leqslant 2 - \frac{1}{n + 1} + \left( \frac{1}{n + 1} - \frac{1}{n} + \frac{1}{(n + 1)^2} \right) = }[/math]

[math]\displaystyle{ \;\: = 2 - \frac{1}{n + 1} - \frac{1}{n (n + 1)^2} \lt }[/math]

[math]\displaystyle{ \;\: \lt 2 - \frac{1}{n + 1} }[/math]

Co kończy dowód indukcyjny. Zatem dla [math]\displaystyle{ n \geqslant 1 }[/math] mamy

[math]\displaystyle{ S(n) = \sum_{k = 1}^{n} \frac{1}{k^2} \leqslant 2 - \frac{1}{n} \lt 2 }[/math]

Czyli ciąg sum częściowych [math]\displaystyle{ S(n) = \sum_{k = 1}^{n} \frac{1}{k^2} }[/math] szeregu [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{k^2} }[/math] jest rosnący i ograniczony od góry, a zatem zbieżny. Co oznacza, że szereg jest zbieżny.
□

Zadanie D26
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania [math]\displaystyle{ \sum_{k = 2}^{n} \frac{1}{k (\log k)^2} \lt 2.5 - \frac{1}{\log n} }[/math] i udowodnić, że szereg [math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{k (\log k)^2} }[/math] jest zbieżny.

Rozwiązanie

Indukcja matematyczna. Łatwo sprawdzamy, że oszacowanie jest prawdziwe dla [math]\displaystyle{ n = 2 }[/math]

[math]\displaystyle{ \sum_{k = 2}^{2} \frac{1}{k (\log k)^2} \approx 1.040684 \lt 2.5 - \frac{1}{\log 2} \approx 1.05730 }[/math]

Zakładając, że oszacowanie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ \sum_{k = m}^{n + 1} \frac{1}{k (\log k)^2} = \sum_{k = m}^{n} \frac{1}{k (\log k)^2} + \frac{1}{(n + 1) \cdot (\log (n + 1))^2} \lt }[/math]

[math]\displaystyle{ \;\: \lt 2.5 - \frac{1}{\log n} + \frac{1}{(n + 1) \cdot (\log (n + 1))^2} = }[/math]

[math]\displaystyle{ \;\: = 2.5 - \frac{1}{\log (n + 1)} + \left( \frac{1}{\log (n + 1)} - \frac{1}{\log n} + \frac{1}{(n + 1) \cdot (\log (n + 1))^2} \right) = }[/math]

[math]\displaystyle{ \;\: = 2.5 - \frac{1}{\log (n + 1)} + \frac{1}{\log (n + 1)} \left( 1 - \frac{\log (n + 1)}{\log n} + \frac{1}{(n + 1) \cdot \log (n + 1)} \right) = }[/math]

[math]\displaystyle{ \;\: = 2.5 - \frac{1}{\log (n + 1)} + \frac{1}{\log (n + 1)} \left( 1 - \frac{\log \left( n \left( 1 + \frac{1}{n} \right) \right)}{\log n} + \frac{1}{(n + 1) \cdot \log (n + 1)} \right) = }[/math]

[math]\displaystyle{ \;\: = 2.5 - \frac{1}{\log (n + 1)} + \frac{1}{\log (n + 1)} \left( 1 - 1 - \frac{\log \left( 1 + \frac{1}{n} \right)}{\log n} + \frac{1}{(n + 1) \cdot \log (n + 1)} \right) \lt }[/math]

[math]\displaystyle{ \;\: \lt 2.5 - \frac{1}{\log (n + 1)} + \frac{1}{\log (n + 1)} \left( - \frac{1}{(n + 1) \log n} + \frac{1}{(n + 1) \cdot \log (n + 1)} \right) \lt }[/math]

[math]\displaystyle{ \;\: \lt 2.5 - \frac{1}{\log (n + 1)} }[/math]

Co kończy dowód indukcyjny. Zatem dla [math]\displaystyle{ n \geqslant 2 }[/math] mamy

[math]\displaystyle{ S(n) = \sum_{k = 2}^{n} \frac{1}{k (\log k)^2} \lt 2.5 - \frac{1}{\log n} \lt 2.5 }[/math]

Czyli ciąg sum częściowych [math]\displaystyle{ S(n) }[/math] szeregu [math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{k (\log k)^2} }[/math] jest rosnący i ograniczony od góry, a zatem zbieżny. Co oznacza, że szereg jest zbieżny.
□

Szeregi nieskończone i liczby pierwsze

Twierdzenie D27
Następujące szeregi są zbieżne

1. [math]\displaystyle{ \quad \sum_{k = 1}^{\infty} \frac{(- 1)^{k + 1}}{p_k} = 0.269605966 \ldots }[/math]
2. [math]\displaystyle{ \quad \sum_{p \geqslant 2} \frac{1}{p^2} = 0.452247420041 \ldots }[/math]	A085548
3. [math]\displaystyle{ \quad \sum_{p \geqslant 2} \frac{1}{(p - 1)^2} = 1.375064994748 \ldots }[/math]	A086242
4. [math]\displaystyle{ \quad \sum_{p \geqslant 2} \frac{1}{p (p - 1)} = 0.773156669049 \ldots }[/math]	A136141

Dowód

Punkt 1.
Szereg jest szeregiem naprzemiennym i jego zbieżność wynika z twierdzenia D5.

Punkt 2.
Szereg jest zbieżny, bo sumy częściowe tego szeregu tworzą ciąg rosnący i ograniczony

[math]\displaystyle{ \sum_{p \leqslant n} \frac{1}{p^2} \lt \sum_{k = 2}^{\infty} \frac{1}{k^2} \lt \frac{\pi^2}{6} }[/math]

Punkt 3.
Szereg jest zbieżny, bo sumy częściowe tego szeregu tworzą ciąg rosnący i ograniczony

[math]\displaystyle{ \sum_{p \leqslant n} \frac{1}{(p - 1)^2} \lt \sum_{j = 2}^{\infty} \frac{1}{(j - 1)^2} = \sum_{k = 1}^{\infty} \frac{1}{k^2} = \frac{\pi^2}{6} }[/math]

Punkt 4.
Zbieżność wzoru wynika z kryterium porównawczego, bo dla każdego [math]\displaystyle{ p \geqslant 2 }[/math] jest

[math]\displaystyle{ 0 \lt \frac{1}{p (p - 1)} \lt \frac{1}{(p - 1)^2} }[/math]

□

Twierdzenie D28
Następujące szeregi są zbieżne

1. [math]\displaystyle{ \quad \sum_{p \geqslant 2} \frac{1}{p \log p} = 1.636616323351 \ldots }[/math]	A137245
2. [math]\displaystyle{ \quad \sum_{p \geqslant 2} \frac{1}{p^2 \log p} = 0.507782187859 \ldots }[/math]	A221711
3. [math]\displaystyle{ \quad \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} = 0.755366610831 \ldots }[/math]	A138312
4. [math]\displaystyle{ \quad \sum_{p \geqslant 2} \frac{\log p}{p^2} = 0.493091109368 \ldots }[/math]	A136271

Dowód

Punkt 1.
Zbieżność tego szeregu udowodniliśmy w twierdzeniu B39, ale obecnie potrafimy uzyskać rezultat znacznie łatwiej. Zauważmy, że rozpatrywaną sumę możemy zapisać w postaci

[math]\displaystyle{ \sum_{p \geqslant 2} \frac{1}{p \log p} = \sum_{k = 1}^{\infty} \frac{1}{p_k \log p_k} = \frac{1}{2 \log 2} + \sum_{k = 2}^{\infty} \frac{1}{p_k \log p_k} }[/math]

Wyrażenie w mianowniku ułamka możemy łatwo oszacować. Z twierdzenia A1 mamy ([math]\displaystyle{ a = 0.72 }[/math])

[math]\displaystyle{ p_k \log p_k \gt a \cdot k \log k \cdot \log (a \cdot k \log k) = }[/math]

[math]\displaystyle{ \;\;\:\, = a \cdot k \log k \cdot (\log a + \log k + \log \log k) = }[/math]

[math]\displaystyle{ \;\;\:\, = a \cdot k \cdot (\log k)^2 \cdot \left( 1 + \frac{\log a + \log \log k}{\log k} \right) }[/math]

Ponieważ dla [math]\displaystyle{ k \gt \exp \left( \tfrac{1}{a} \right) = 4.01039 \ldots }[/math] jest

[math]\displaystyle{ \log a + \log \log k \gt 0 }[/math]

to dla [math]\displaystyle{ k \geqslant 5 }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ p_k \log p_k \gt a \cdot k \cdot (\log k)^2 }[/math]

Wynika stąd, że dla [math]\displaystyle{ k \geqslant 5 }[/math] prawdziwy jest ciąg nierówności

[math]\displaystyle{ 0 \lt \frac{1}{p_k \log p_k} \lt \frac{1}{a \cdot k \cdot (\log k)^2} }[/math]

Zatem na mocy kryterium porównawczego ze zbieżności szeregu [math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{k \cdot (\log k)^2} }[/math] (zobacz twierdzenie D13 p. 4 lub przykład D18 p. 5) wynika zbieżność szeregu [math]\displaystyle{ \sum_{k = 2}^{\infty} \frac{1}{p_k \log p_k} }[/math]

Punkt 2.
Zbieżność szeregu wynika z kryterium porównawczego (twierdzenie D9), bo

[math]\displaystyle{ 0 \lt \frac{1}{p^2 \log p} \lt \frac{1}{p \log p} }[/math]

Punkt 3.
Szereg jest zbieżny, bo sumy częściowe tego szeregu tworzą ciąg rosnący i ograniczony

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} \lt \sum_{k = 2}^{\infty} \frac{\log k}{k (k - 1)} = 1.2577 \ldots }[/math]

Punkt 4.
Zbieżność szeregu wynika z kryterium porównawczego, bo dla każdego [math]\displaystyle{ p \geqslant 2 }[/math] jest

[math]\displaystyle{ 0 \lt \frac{\log p}{p^2} \lt \frac{\log p}{p (p - 1)} }[/math]

□

Twierdzenie D29
Szereg [math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p} }[/math] jest rozbieżny.

Dowód

Dla potrzeb dowodu zapiszmy szereg w innej postaci

[math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p} = \sum_{k = 1}^{\infty} \frac{\log p_k}{p_k} }[/math]

Zauważmy, że dla [math]\displaystyle{ k \geqslant 3 }[/math] wyrazy szeregów [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{p_k} }[/math] oraz [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{\log p_k}{p_k} }[/math] spełniają nierówności

[math]\displaystyle{ 0 \leqslant \frac{1}{p_k} \leqslant \frac{\log p_k}{p_k} }[/math]

Ponieważ szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{1}{p_k} }[/math] jest rozbieżny, to na mocy kryterium porównawczego (twierdzenie D9) rozbieżny jest również szereg [math]\displaystyle{ \sum_{k = 1}^{\infty} \frac{\log p_k}{p_k} }[/math]
□

Uwaga D30
Moglibyśmy oszacować rozbieżność szeregu [math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p} }[/math] podobnie, jak to uczyniliśmy w przypadku twierdzenia B37, ale tym razem zastosujemy inną metodę, która pozwoli nam uzyskać bardziej precyzyjny rezultat.

Twierdzenie D31
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Prawdziwe są następujące nierówności

[math]\displaystyle{ \quad 1. \quad }[/math]	[math]\displaystyle{ n! \gt n^n e^{- n} }[/math]	[math]\displaystyle{ \text{dla} \;\; n \geqslant 1 }[/math]
[math]\displaystyle{ \quad 2. \quad }[/math]	[math]\displaystyle{ n! \lt n^{n + 1} e^{- n} }[/math]	[math]\displaystyle{ \text{dla} \;\; n \geqslant 7 }[/math]

Dowód

Punkt 1. (indukcja matematyczna)
Łatwo sprawdzić prawdziwość nierówności dla [math]\displaystyle{ n = 1 }[/math]. Zakładając prawdziwość dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ (n + 1) ! = n! \cdot (n + 1) \gt }[/math]

[math]\displaystyle{ \;\;\; \gt n^n \cdot e^{- n} \cdot (n + 1) = }[/math]

[math]\displaystyle{ \;\;\; = (n + 1)^{n + 1} \cdot \frac{n^n}{(n + 1)^n} \cdot e^{- n} = }[/math]

[math]\displaystyle{ \;\;\; = (n + 1)^{n + 1} \cdot \frac{1}{\left( 1 + \frac{1}{n} \right)^n} \cdot e^{- n} \gt }[/math]

[math]\displaystyle{ \;\;\; \gt (n + 1)^{n + 1} \cdot \frac{1}{e} \cdot e^{- n} = }[/math]

[math]\displaystyle{ \;\;\; = (n + 1)^{n + 1} e^{- (n + 1)} }[/math]

Ponieważ [math]\displaystyle{ \left( 1 + \frac{1}{n} \right)^n \lt e }[/math], zatem [math]\displaystyle{ \frac{1}{\left( 1 + \frac{1}{n} \right)^n} \gt \frac{1}{e} }[/math]. Co kończy dowód punktu 1.

Punkt 2. (indukcja matematyczna)
Łatwo sprawdzić prawdziwość nierówności dla [math]\displaystyle{ n = 7 }[/math]. Zakładając prawdziwość dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ (n + 1) ! = n! \cdot (n + 1) \lt }[/math]

[math]\displaystyle{ \;\;\; \lt n^{n + 1} \cdot e^{- n} \cdot (n + 1) = }[/math]

[math]\displaystyle{ \;\;\; = (n + 1)^{n + 2} \cdot \frac{n^{n + 1}}{(n + 1)^{n + 1}} \cdot e^{- n} = }[/math]

[math]\displaystyle{ \;\;\; = (n + 1)^{n + 2} \cdot \left( \frac{n}{n + 1} \right)^{n + 1} \cdot e^{- n} = }[/math]

[math]\displaystyle{ \;\;\; = (n + 1)^{n + 2} \cdot \left( 1 - \frac{1}{n + 1} \right)^{n + 1} \cdot e^{- n} \lt }[/math]

[math]\displaystyle{ \;\;\; \lt (n + 1)^{n + 2} \cdot \frac{1}{e} \cdot e^{- n} = }[/math]

[math]\displaystyle{ \;\;\; = (n + 1)^{n + 2} \cdot e^{- (n + 1)} }[/math]

Ostatnia nierówność wynika z faktu, że [math]\displaystyle{ \left( 1 - \frac{1}{n + 1} \right)^{n + 1} \lt \frac{1}{e} }[/math]. Co kończy dowód punktu 2.
□

Twierdzenie D32
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Dla wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ n! }[/math] na czynniki pierwsze, prawdziwe są oszacowania

[math]\displaystyle{ \quad 1. \quad }[/math]	[math]\displaystyle{ \frac{n}{p} - 1 \lt W_p (n!) \lt \frac{n}{p - 1} }[/math]
[math]\displaystyle{ \quad 2. \quad }[/math]	[math]\displaystyle{ \frac{n + 1}{p} - 1 \leqslant W_p (n!) \leqslant \frac{n - 1}{p - 1} }[/math]

Dowód

Punkt 1. (prawa nierówność)

Zauważmy, że

[math]\displaystyle{ W_p (n!) = \left\lfloor \frac{n}{p} \right\rfloor + \left\lfloor \frac{n}{p^2} \right\rfloor + \left\lfloor \frac{n}{p^3} \right\rfloor + \ldots \lt }[/math]

[math]\displaystyle{ \;\, \lt \frac{n}{p} + \frac{n}{p^2} + \frac{n}{p^3} + \ldots + \frac{n}{p^k} + \ldots = }[/math]

[math]\displaystyle{ \;\, = \frac{n}{p} \cdot \frac{1}{1 - \frac{1}{p}} = }[/math]

[math]\displaystyle{ \;\, = \frac{n}{p - 1} }[/math]

Punkt 1. (lewa nierówność)

Łatwo znajdujemy, że

[math]\displaystyle{ W_p (n!) = \sum_{k = 1}^{\infty} \left\lfloor \frac{n}{p^k} \right\rfloor \geqslant \left\lfloor \frac{n}{p} \right\rfloor \gt \frac{n}{p} - 1 }[/math]

Punkt 2. (prawa nierówność)

Z uzyskanego w punkcie 1. oszacowania wynika, że [math]\displaystyle{ (p - 1) W_p (n!) \lt n }[/math]. Ponieważ nierówność ta dotyczy liczb całkowitych, to możemy napisać

[math]\displaystyle{ (p - 1) W_p (n!) \leqslant n - 1 }[/math]

Skąd otrzymujemy natychmiast nierówność nieostrą [math]\displaystyle{ W_p (n!) \leqslant \frac{n - 1}{p - 1} }[/math].

Punkt 2. (lewa nierówność)

Z uzyskanego w punkcie 1. oszacowania wynika, że [math]\displaystyle{ n - p \lt p \cdot W_p (n!) }[/math]. Ponieważ nierówność ta dotyczy liczb całkowitych, to możemy napisać

[math]\displaystyle{ n - p \leqslant p \cdot W_p (n!) - 1 }[/math]

Skąd otrzymujemy natychmiast nierówność nieostrą [math]\displaystyle{ W_p (n!) \geqslant \frac{n + 1}{p} - 1 }[/math].
□

Twierdzenie D33
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \gt - 1 }[/math]

Dowód

Z oszacowania wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ n! }[/math] na czynniki pierwsze, wynika natychmiast, że dla [math]\displaystyle{ n \geqslant 2 }[/math] mamy

[math]\displaystyle{ n! \lt \prod_{p \leqslant n} p^{n / (p - 1)} }[/math]

Ponieważ dla [math]\displaystyle{ n \geqslant 1 }[/math] jest [math]\displaystyle{ n! \gt n^n e^{- n} }[/math] (zobacz punkt 1. twierdzenia D31), to

[math]\displaystyle{ n^n e^{- n} \lt \prod_{p \leqslant n} p^{n / (p - 1)} }[/math]

Logarytmując, otrzymujemy

[math]\displaystyle{ n \log n - n \lt \sum_{p \leqslant n} \frac{n \log p}{p - 1} = n \sum_{p \leqslant n} \frac{\log p}{p - 1} }[/math]

Dzieląc strony przez [math]\displaystyle{ n }[/math], dostajemy szukaną nierówność.
□

Twierdzenie D34 (pierwsze twierdzenie Mertensa, 1874)
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} - \log n \gt - 1.755367 }[/math]

Dowód

Ponieważ

[math]\displaystyle{ \frac{1}{p - 1} = \frac{1}{p} + \frac{1}{p (p - 1)} }[/math]

to z twierdzenia D33 dostajemy

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} + \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} - \log n \gt - 1 }[/math]

Czyli

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} - \log n \gt - 1 - \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} }[/math]

[math]\displaystyle{ \;\, \gt - 1 - \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} }[/math]

[math]\displaystyle{ \;\, = - 1 - 0.755366610831 \ldots }[/math]

[math]\displaystyle{ \;\, \gt - 1.755367 }[/math]

Gdzie wykorzystaliśmy zbieżność szeregu [math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} }[/math] (twierdzenie D28 p. 3).
□

Twierdzenie D35 (pierwsze twierdzenie Mertensa, 1874)
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} - \log n \lt 0.386295 }[/math]

Dowód

Z oszacowania wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ n! }[/math] na czynniki pierwsze, wynika natychmiast, że dla [math]\displaystyle{ n \geqslant 1 }[/math] mamy

[math]\displaystyle{ n! \geqslant \prod_{p \leqslant n} p^{(n + 1) / p \: - \: 1} }[/math]

Ponieważ dla [math]\displaystyle{ n \geqslant 7 }[/math] jest [math]\displaystyle{ n! \lt n^{n + 1} e^{- n} }[/math], to

[math]\displaystyle{ \prod_{p \leqslant n} p^{(n + 1) / p \: - \: 1} \lt n^{n + 1} e^{- n} }[/math]

Logarytmując, otrzymujemy

[math]\displaystyle{ \sum_{p \leqslant n} \left( \frac{n + 1}{p} - 1 \right) \cdot \log p \lt (n + 1) \cdot \log n - n }[/math]

[math]\displaystyle{ (n + 1) \sum_{p \leqslant n} \frac{\log p}{p} - \sum_{p \leqslant n} \log p \lt (n + 1) \cdot \log n - n }[/math]

Skąd natychmiast wynika, że

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} - \log n \lt - \frac{n}{n + 1} + \frac{1}{n + 1} \cdot \log \left( \prod_{p \leqslant n} p \right) }[/math]

[math]\displaystyle{ \;\: = - 1 + \frac{1}{n + 1} + \frac{1}{n + 1} \cdot \log (P (n)) }[/math]

[math]\displaystyle{ \;\: \lt - 1 + \frac{1}{n + 1} + \frac{n \cdot \log 4}{n + 1} }[/math]

[math]\displaystyle{ \;\: = - 1 + \frac{1}{n + 1} + \log 4 - \frac{\log 4}{n + 1} }[/math]

[math]\displaystyle{ \;\: = \log 4 - 1 + \frac{1 - \log 4}{n + 1} }[/math]

[math]\displaystyle{ \;\: = \log 4 - 1 - \frac{0.386294 \ldots}{n + 1} }[/math]

[math]\displaystyle{ \;\: \lt \log 4 - 1 }[/math]

[math]\displaystyle{ \;\: = 0.386294361 \ldots }[/math]

Druga nierówność wynika z twierdzenia A9. Bezpośrednio sprawdzamy, że powyższa nierówność jest prawdziwa dla [math]\displaystyle{ n \lt 7 }[/math].
□

Twierdzenie D36
Dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \lt 1.141661 }[/math]

Dowód

Ponieważ

[math]\displaystyle{ \frac{1}{p} = \frac{1}{p - 1} - \frac{1}{p (p - 1)} }[/math]

to z twierdzenia D35 dostajemy

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} - \log n \lt \log 4 - 1 }[/math]

Czyli

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \lt \log 4 - 1 + \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} }[/math]

[math]\displaystyle{ \;\;\: \lt \log 4 - 1 + \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} }[/math]

[math]\displaystyle{ \;\;\: = \log 4 - 1 + 0.755366610831 \ldots }[/math]

[math]\displaystyle{ \;\;\: \lt 1.141661 }[/math]

□

Uwaga D37

Dokładniejsze oszacowanie sumy [math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} }[/math] jest dane wzorem [math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} = \log n - E + \ldots }[/math] gdzie [math]\displaystyle{ E = 1.332582275733 \ldots }[/math] Dla [math]\displaystyle{ n \geqslant 319 }[/math] mamy też [math]\displaystyle{ \left| \sum_{p \leqslant n} \frac{\log p}{p} - \log n + E \right| \lt \frac{1}{2 \log n} }[/math]

Uwaga D38

Dokładniejsze oszacowanie sumy [math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} }[/math] jest dane wzorem [math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} = \log n - \gamma + \ldots }[/math] gdzie [math]\displaystyle{ \gamma = 0.5772156649 \ldots }[/math] jest stałą Eulera. Dla [math]\displaystyle{ n \geqslant 318 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \left| \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n + \gamma \right| \lt \frac{1}{2 \log n} }[/math]

Uwaga D39
Dla [math]\displaystyle{ n \leqslant 10^{10} }[/math] wartości wyrażeń

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p} - \log n + E }[/math]

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n + \gamma }[/math]

są liczbami dodatnimi.

Twierdzenie D40
Prawdziwy jest następujący związek

[math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} = \sum_{n = 2}^{\infty} \left( \sum_{p \geqslant 2} \frac{\log p}{p^n} \right) = E - \gamma }[/math]

gdzie

• [math]\displaystyle{ \quad \gamma = 0.577215664901532 \ldots }[/math] jest stałą Eulera
• [math]\displaystyle{ \quad E = 1.332582275733220 \ldots }[/math]
• [math]\displaystyle{ \quad E - \gamma = 0.755366610831688 \ldots }[/math]

Dowód

Ponieważ

[math]\displaystyle{ \frac{1}{p (p - 1)} = \frac{1}{p - 1} - \frac{1}{p} }[/math]

zatem

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} = \sum_{p \leqslant n} \frac{\log p}{p - 1} - \sum_{p \leqslant n} \frac{\log p}{p} = (\log n - \gamma + \ldots) - (\log n - E + \ldots) }[/math]

Przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, otrzymujemy

[math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} = E - \gamma }[/math]

Zauważmy teraz, że

[math]\displaystyle{ \frac{1}{p - 1} = \frac{1}{p} \cdot \frac{1}{1 - \frac{1}{p}} = }[/math]

[math]\displaystyle{ \;\! = \frac{1}{p} \cdot \left( 1 + \frac{1}{p} + \frac{1}{p^2} + \frac{1}{p^3} + \ldots + \frac{1}{p^k} + \ldots \right) = }[/math]

[math]\displaystyle{ \;\! = \frac{1}{p} + \frac{1}{p^2} + \frac{1}{p^3} + \ldots + \frac{1}{p^k} + \ldots }[/math]

Zatem

[math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} = \sum_{p \geqslant 2} \frac{\log p}{p} \cdot \left( \frac{1}{p} + \frac{1}{p^2} + \frac{1}{p^3} + \ldots + \frac{1}{p^k} + \ldots \right) = \sum_{n = 2}^{\infty} \left( \sum_{p \geqslant 2} \frac{\log p}{p^n} \right) }[/math]

□

Twierdzenie D41
Dla [math]\displaystyle{ n \geqslant 318 }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ \left| \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n + \gamma \right| \lt \frac{1}{2 \log n} }[/math]

Dowód

Należy zauważyć, że tak dokładnego oszacowania nie można udowodnić metodami elementarnymi, dlatego punktem wyjścia jest oszacowanie podane w pracy Pierre'a Dusarta

[math]\displaystyle{ - \left( \frac{0.2}{\log n} + \frac{0.2}{\log^2 n} \right) \; \underset{n \geqslant 2}{\lt } \; \sum_{p \leqslant n} \frac{\log p}{p} - \log n + E \; \underset{n \geqslant 2974}{\lt } \; \frac{0.2}{\log n} + \frac{0.2}{\log^2 n} }[/math]

Ponieważ dla [math]\displaystyle{ x \gt e^2 \approx 7.389 }[/math] jest [math]\displaystyle{ 1 + \frac{1}{\log x} \lt 1.5 }[/math], to dla [math]\displaystyle{ n \geqslant 8 }[/math] mamy

[math]\displaystyle{ \frac{0.2}{\log n} + \frac{0.2}{\log^2 n} = \frac{0.2}{\log n} \left( 1 + \frac{1}{\log n} \right) \lt \frac{0.3}{\log n} }[/math]

Zatem wyjściowy układ nierówności możemy zapisać w postaci

[math]\displaystyle{ - \frac{0.3}{\log n} \; \underset{n \geqslant 8}{\lt } \; \sum_{p \leqslant n} \frac{\log p}{p} - \log n + E \; \underset{n \geqslant 2974}{\lt } \; \frac{0.3}{\log n} }[/math]

Z tożsamości

[math]\displaystyle{ \frac{1}{p} = \frac{1}{p - 1} - \frac{1}{p (p - 1)} }[/math]

wynika natychmiast, że

[math]\displaystyle{ - \frac{0.3}{\log n} \; \underset{n \geqslant 8}{\lt } \; \sum_{p \leqslant n} \frac{\log p}{p - 1} - \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} - \log n + E \; \underset{n \geqslant 2974}{\lt } \; \frac{0.3}{\log n} }[/math]

Prawa nierówność

Rozważmy prawą nierówność prawdziwą dla [math]\displaystyle{ n \geqslant 2974 }[/math]

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} - \log n + E \lt \frac{0.3}{\log n} }[/math]

Z twierdzenia D40 wiemy, że

[math]\displaystyle{ \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} - E = - \gamma }[/math]

Zatem

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \lt \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} - E + \frac{0.3}{\log n} }[/math]

[math]\displaystyle{ \;\;\: \lt \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} - E + \frac{0.3}{\log n} }[/math]

[math]\displaystyle{ \;\;\: = - \gamma + \frac{0.3}{\log n} }[/math]

[math]\displaystyle{ \;\;\: \lt - \gamma + \frac{0.5}{\log n} }[/math]

Bezpośrednio obliczając, sprawdzamy, że nierówność

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \lt - \gamma + \frac{0.5}{\log n} }[/math]

jest prawdziwa dla wszystkich liczb [math]\displaystyle{ 318 \leqslant n \leqslant 3000 }[/math]

Lewa nierówność

Rozważmy teraz lewą nierówność prawdziwą dla [math]\displaystyle{ n \geqslant 8 }[/math]

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} - \log n + E \gt - \frac{0.3}{\log n} }[/math]

Mamy

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \gt \sum_{p \leqslant n} \frac{\log p}{p (p - 1)} - E - \frac{0.3}{\log n} }[/math]

[math]\displaystyle{ \;\;\, = \sum_{p \geqslant 2} \frac{\log p}{p (p - 1)} - \sum_{p \gt n} \frac{\log p}{p (p - 1)} - E - \frac{0.3}{\log n} }[/math]

[math]\displaystyle{ \;\;\, = - \gamma - \frac{0.3}{\log n} - \sum_{p \gt n} \frac{\log p}{p (p - 1)} }[/math]

[math]\displaystyle{ \;\;\, \gt - \gamma - \frac{0.3}{\log n} - \sum_{k = n + 1}^{\infty} \frac{\log k}{k (k - 1)} }[/math]

[math]\displaystyle{ \;\;\, \gt - \gamma - \frac{0.3}{\log n} - \sum_{k = n + 1}^{\infty} \frac{\log k}{(k - 1)^2} }[/math]

Korzystając kolejno z twierdzeń D15 i C18, dostajemy

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \gt - \gamma - \frac{0.3}{\log n} - \int_{n}^{\infty} \frac{\log x}{(x - 1)^2} d x }[/math]

[math]\displaystyle{ \;\;\, = - \gamma - \frac{0.3}{\log n} - \frac{\log n}{n - 1} + \log \left( 1 - \frac{1}{n} \right) }[/math]

[math]\displaystyle{ \;\;\, \gt - \gamma - \frac{0.3}{\log n} - \frac{\log n}{n - 1} - \frac{1}{n - 1} }[/math]

[math]\displaystyle{ \;\;\, = - \gamma - \frac{0.5}{\log n} + \left( \frac{0.2}{\log n} - \frac{\log n + 1}{n - 1} \right) }[/math]

[math]\displaystyle{ \;\;\, \gt - \gamma - \frac{0.5}{\log n} }[/math]

Do znalezienia całki oznaczonej Czytelnik może wykorzystać stronę WolframAlpha. Ostatnia nierówność jest prawdziwa dla [math]\displaystyle{ n \geqslant 153 }[/math]. Bezpośrednio obliczając, sprawdzamy, że nierówność

[math]\displaystyle{ \sum_{p \leqslant n} \frac{\log p}{p - 1} - \log n \gt - \gamma - \frac{0.5}{\log n} }[/math]

jest prawdziwa dla wszystkich [math]\displaystyle{ 2 \leqslant n \leqslant 200 }[/math].
□

Zadanie D42
Niech [math]\displaystyle{ r = 1 - \log (2) \approx 0.30685281944 }[/math]. Pokazać, że z nierówności prawdziwej dla [math]\displaystyle{ x \geqslant 32 }[/math]

[math]\displaystyle{ \sum_{p \leqslant x} \frac{\log p}{p - 1} \lt \log x - r }[/math]

wynika twierdzenie Czebyszewa.

Rozwiązanie

Z twierdzenia D41 wiemy, że dla [math]\displaystyle{ x \geqslant 318 }[/math] jest

[math]\displaystyle{ \sum_{p \leqslant x} \frac{\log p}{p - 1} - \log x \lt - \gamma + \frac{1}{2\log x} \leqslant - \gamma + \frac{1}{2 \log (318)} = - 0.490441 \ldots \lt - 0.306852 \ldots = - r }[/math]

Zatem postulowane oszacowanie jest prawdziwe dla [math]\displaystyle{ n \geqslant 318 }[/math]. Sprawdzając bezpośrednio dla [math]\displaystyle{ 2 \leqslant x \leqslant 317 }[/math], łatwo potwierdzamy prawdziwość nierówności

[math]\displaystyle{ \sum_{p \leqslant x} \frac{\log p}{p - 1} \lt \log x - r }[/math]

dla [math]\displaystyle{ x \geqslant 32 }[/math].

Niech [math]\displaystyle{ a \in \mathbb{Z} }[/math] i [math]\displaystyle{ a \geqslant 32 }[/math]. Korzystając z twierdzenia D32, łatwo znajdujemy oszacowanie

[math]\displaystyle{ a! = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_n}_n }[/math]

[math]\displaystyle{ \quad \leqslant p^{(a - 1) / (p_1 - 1)}_1 \cdot \ldots \cdot p^{(a - 1) / (p_n - 1)}_n }[/math]

[math]\displaystyle{ \quad = (p^{1 / (p_1 - 1)}_1 \cdot \ldots \cdot p^{1 / (p_n - 1)}_n)^{a - 1} }[/math]

gdzie [math]\displaystyle{ p_n \leqslant a \lt p_{n + 1} }[/math]. Oznaczając wyrażenie w nawiasie przez [math]\displaystyle{ U }[/math], mamy

[math]\displaystyle{ \log U = \frac{\log p_1}{p_1 - 1} + \ldots + \frac{\log p_n}{p_n - 1} = \sum_{p \leqslant a} \frac{\log p}{p - 1} \lt \log a - r }[/math]

gdzie skorzystaliśmy z oszacowania wskazanego w treści zadania. Zatem [math]\displaystyle{ U \lt a \cdot e^{- r} }[/math].

Przypuśćmy, że mnożymy liczbę [math]\displaystyle{ a! }[/math] przez kolejne liczby naturalne [math]\displaystyle{ a + 1, a + 2, \ldots, b - 1, b }[/math]. Możemy postawić pytanie: kiedy w rozkładzie na czynniki pierwsze liczby [math]\displaystyle{ b! }[/math] musi pojawić się nowy czynnik pierwszy? Jeżeli takiego nowego czynnika pierwszego nie ma, to

[math]\displaystyle{ a! \cdot (a + 1) \cdot \ldots \cdot b = b! }[/math]

[math]\displaystyle{ \;\;\; = p^{\beta_1}_1 \cdot \ldots \cdot p^{\beta_n}_n }[/math]

[math]\displaystyle{ \;\;\; \leqslant p^{(b - 1) / (p_1 - 1)}_1 \cdot \ldots \cdot p^{(b - 1) / (p_n - 1)}_n }[/math]

[math]\displaystyle{ \;\;\; = (p^{1 / (p_1 - 1)}_1 \cdot \ldots \cdot p^{1 / (p_n - 1)}_n)^{b - 1} }[/math]

[math]\displaystyle{ \;\;\; = U^{b - 1} }[/math]

[math]\displaystyle{ \;\;\; \lt (a \cdot e^{- r})^{b - 1} }[/math]

Jednocześnie z twierdzenia D31 wiemy, że prawdziwa jest nierówność [math]\displaystyle{ b! \gt b^b e^{- b} }[/math], zatem

[math]\displaystyle{ b^b e^{- b} \lt b! \lt \frac{(a \cdot e^{- r})^b}{a \cdot e^{-r}} }[/math]

[math]\displaystyle{ b e^{- 1} \lt \frac{a \cdot e^{- r}}{(a \cdot e^{- r})^{1 / b}} }[/math]

[math]\displaystyle{ b \lt \frac{a \cdot e^{1 - r}}{(a \cdot e^{- r})^{1 / b}} }[/math]

Ponieważ [math]\displaystyle{ e^{1 - r} = e^{\log (2)} = 2 }[/math], to

[math]\displaystyle{ b \lt \frac{2 a}{(a \cdot e^{- r})^{1 / b}} \lt 2 a }[/math]

Z oszacowania [math]\displaystyle{ b \lt 2 a }[/math] wynika, że [math]\displaystyle{ (a \cdot e^{- r})^{1 / b} \gt (a \cdot e^{-r})^{1 / 2 a} }[/math]. Możemy teraz zapisać uzyskane wyżej oszacowanie w postaci, w której prawa strona nierówności nie zależy od [math]\displaystyle{ b }[/math]

[math]\displaystyle{ b \lt \frac{2 a}{(a \cdot e^{- r})^{1 / b}} \lt \frac{2 a}{(a \cdot e^{- r})^{1 / 2 a}} }[/math]

Ponieważ [math]\displaystyle{ e^{- r} = 0.735758 \ldots }[/math], to [math]\displaystyle{ (a \cdot e^{- r})^{1 / 2 a} \gt (a / 2)^{1 / 2 a} }[/math], co pozwala uprościć uzyskane oszacowanie

[math]\displaystyle{ b \lt \frac{2 a}{(a \cdot e^{- r})^{1 / 2 a}} \lt \frac{2 a}{(a / 2)^{1 / 2 a}} }[/math]

Pokażemy, że dla [math]\displaystyle{ a \gt 303.05 }[/math]

[math]\displaystyle{ \frac{2 a}{(a / 2)^{1 / 2 a}} \lt 2 a - 5 }[/math]

Istotnie

[math]\displaystyle{ \frac{1}{(a / 2)^{1 / 2 a}} \lt 1 - \frac{5}{2 a} }[/math]

[math]\displaystyle{ \frac{a}{2} \cdot \left( 1 - \frac{5}{2 a} \right)^{2 a} \gt 1 }[/math]

[math]\displaystyle{ \frac{a}{2} \cdot \left[ \left( 1 - \frac{5}{2 a} \right)^{\tfrac{2 a}{5}} \right]^5 \gt 1 }[/math]

Wyrażenie w nawiasie kwadratowym jest funkcją rosnącą i ograniczoną (zobacz twierdzenie C17) i dla [math]\displaystyle{ a \geqslant 32 }[/math] przyjmuje wartości z przedziału [math]\displaystyle{ [0.353 \ldots, e^{- 1}) }[/math]. Zatem dla odpowiednio dużego [math]\displaystyle{ a }[/math] powyższa nierówność z pewnością jest prawdziwa. Łatwo sprawdzamy, że dla [math]\displaystyle{ a = 304 }[/math] jest

[math]\displaystyle{ \frac{a}{2} \cdot \left( 1 - \frac{5}{2 a} \right)^{2 a} = 1.003213 \ldots }[/math]

Wynika stąd, że wszystkie kolejne liczby naturalne [math]\displaystyle{ a + 1, a + 2, \ldots, b - 1, b }[/math] mogą być liczbami złożonymi co najwyżej do chwili, gdy [math]\displaystyle{ b \lt 2 a - 5 }[/math], czyli [math]\displaystyle{ b \leqslant 2 a - 6 }[/math]. Zatem w przedziale [math]\displaystyle{ (a, 2 a) }[/math] musi znajdować się przynajmniej jedna liczba pierwsza. Dla [math]\displaystyle{ a \leqslant 303 }[/math] prawdziwość twierdzenia sprawdzamy bezpośrednio.
□

Definicja D43
Powiemy, że liczby pierwsze [math]\displaystyle{ p, q }[/math] są liczbami bliźniaczymi (tworzą parę liczb bliźniaczych), jeżeli [math]\displaystyle{ \left | p - q \right | = 2 }[/math]

Twierdzenie D44* (Viggo Brun, 1919)
Suma odwrotności par liczb pierwszych [math]\displaystyle{ p }[/math] i [math]\displaystyle{ p + 2 }[/math], takich że liczba [math]\displaystyle{ p + 2 }[/math] jest również pierwsza, jest skończona

[math]\displaystyle{ \underset{p + 2 \in \mathbb{P}}{\sum_{p \geqslant 2}} \left( \frac{1}{p} + \frac{1}{p + 2} \right) = \left( \frac{1}{3} + \frac{1}{5} \right) + \left( \frac{1}{5} + \frac{1}{7} \right) + \left( \frac{1}{11} + \frac{1}{13} \right) + \left( \frac{1}{17} + \frac{1}{19} \right) + \ldots = B_2 }[/math]

gdzie [math]\displaystyle{ B_2 = 1.90216058 \ldots }[/math] jest stałą Bruna.

Zadanie D45
Pokazać, że istnieje nieskończenie wiele liczb pierwszych nie tworzących par liczb bliźniaczych.

Rozwiązanie

Niech [math]\displaystyle{ p }[/math] i [math]\displaystyle{ q = p + 4 }[/math] będą liczbami pierwszymi i [math]\displaystyle{ n \geqslant 1 }[/math]. Ponieważ liczby [math]\displaystyle{ p q }[/math] i [math]\displaystyle{ p + 2 }[/math] są względnie pierwsze, to z twierdzenia Dirichleta wiemy, że wśród liczb [math]\displaystyle{ a_n = p q n + (p + 2) }[/math] jest nieskończenie wiele liczb pierwszych, a jednocześnie żadna z liczb [math]\displaystyle{ a_n }[/math] nie tworzy pary liczb bliźniaczych, bo

[math]\displaystyle{ a_n - 2 = p q n + p = p (q n + 1) }[/math]

[math]\displaystyle{ a_n + 2 = p q n + (p + 4) = q (p n + 1) }[/math]

są liczbami złożonymi. Najprostsze przykłady to [math]\displaystyle{ a_n = 21 n + 5 }[/math] i [math]\displaystyle{ b_n = 77 n + 9 }[/math]

Najłatwiej wszystkie przypadki takich ciągów wyszukać w programie PARI/GP. Polecenie

for(a=1,50, for(b=3,floor(a/2), g=gcd(a,b); g1=gcd(a,b-2); g2=gcd(a,b+2); if( g==1 && g1>1 && g2>1, print("a= ", a, "   b= ",b) )))

wyszukuje wszystkie liczby dodatnie [math]\displaystyle{ a, b }[/math], gdzie [math]\displaystyle{ b \leqslant \left\lfloor \frac{a}{2} \right\rfloor }[/math], które tworzą ciągi [math]\displaystyle{ a k + b }[/math] o poszukiwanych właściwościach. Oczywiście ciągi [math]\displaystyle{ a k + (a - b) }[/math] również są odpowiednie. Przykładowo dla [math]\displaystyle{ a \leqslant 50 }[/math] mamy

[math]\displaystyle{ 15 k + 7, \quad 21 k + 5, \quad 30 k + 7, \quad 33 k + 13, \quad 35 k + 12, \quad 39 k + 11, \quad 42 k + 5, \quad 45 k + 7, \quad 45 k + 8, \quad 45 k + 22 }[/math]

□