Ciągi liczbowe: Różnice pomiędzy wersjami

Wersja z 19:13, 20 lut 2024

12.03.2022

Ciągi nieskończone

Definicja C1
Niech $n \in Z_{+}$ . Jeżeli każdej liczbie $n$ przypiszemy pewną liczbę rzeczywistą $a_{n}$ , to powiemy, że liczby $a_{1}, a_{2}, \dots, a_{n}, \dots$ tworzą ciąg nieskończony.

Uwaga C2
Ciąg nieskończony $a_{1}, a_{2}, \dots, a_{n}, \dots$ będziemy oznaczać $(a_{n})$ . Często, o ile nie będzie prowadziło to do nieporozumień, ciąg nieskończony będziemy nazywać po prostu ciągiem.

Definicja C3
Niech $n \in Z_{+}$ . Ciąg $(a_{n})$ będziemy nazywali

ciągiem rosnącym, jeżeli dla każdego $n$ jest $a_{n + 1} ⩾ a_{n}$
ciągiem malejącym, jeżeli dla każdego $n$ jest $a_{n + 1} ⩽ a_{n}$

Ciągi rosnące dzielimy na

ciągi silnie rosnące, jeżeli dla każdego $n$ jest $a_{n + 1} > a_{n}$
ciągi słabo rosnące, jeżeli istnieją takie $n$ , że $a_{n + 1} = a_{n}$

Ciągi malejące dzielimy na

ciągi silnie malejące, jeżeli dla każdego $n$ jest $a_{n + 1} < a_{n}$
ciągi słabo malejące, jeżeli istnieją takie $n$ , że $a_{n + 1} = a_{n}$

Definicja C4
Niech $ε \in R_{+}$ . Liczbę $a$ będziemy nazywali granicą ciągu $(a_{n})$ , jeżeli dla dowolnego $ε$ w przedziale $(a - ε, a + ε)$ znajdują się prawie wszystkie wyrazy ciągu $(a_{n})$ (to znaczy wszystkie poza co najwyżej skończoną ilością).

Uwaga C5
1) sens definicji jest taki: jeżeli liczba $a$ jest granicą ciągu $(a_{n})$ , to dla dowolnie małego $ε > 0$ , poza przedziałem $(a - ε, a + ε)$ może się znaleźć co najwyżej skończona ilość wyrazów ciągu $(a_{n})$

2) słabsze żądanie, aby w przedziale $(a - ε, a + ε)$ znajdowała się nieskończona ilość wyrazów ciągu nie prowadzi do poprawnej definicji granicy. Przykładowo, w przedziale $(1 - ε, 1 + ε)$ znajduje się nieskończenie wiele wyrazów ciągu $a_{n} = (- 1)^{n}$ , ale ani liczba $1$ , ani liczba $- 1$ nie są granicami tego ciągu. O ciągu $a_{n} = (- 1)^{n}$ mówimy, że nie ma granicy.

3) ze względu na równoważność warunków

$a_{n} \in (a - ε, a + ε)$
$a - ε < a_{n} < a + ε$
$- ε < a_{n} - a < ε$
$| a_{n} - a | < ε$

definicja C4 może być wypowiedziana następująco

Definicja C6
Liczbę $a$ będziemy nazywali granicą ciągu $(a_{n})$ , jeżeli dla dowolnego $ε > 0$ prawie wszystkie wyrazy ciągu $(a_{n})$ spełniają warunek $| a_{n} - a | < ε$ .

Definicja C7
Ciąg $(a_{n})$ mający granicę (w rozumieniu definicji C4 lub C6) będziemy nazywali ciągiem zbieżnym, a fakt ten zapisujemy symbolicznie następująco

lim_{n \to \infty} a_{n} = a

lub

a_{n} ⟶ a

(od łacińskiego słowa limes oznaczającego granicę).

Zauważmy jeszcze, że wprost z definicji granicy wynika
Twierdzenie C8

1.

lim_{n \to \infty} a_{n} = a ⟺ lim_{n \to \infty} (a_{n} - a) = 0 ⟺ lim_{n \to \infty} | a_{n} - a | = 0

2.

lim_{n \to \infty} a_{n} = 0 ⟺ lim_{n \to \infty} | a_{n} | = 0

3.

lim_{n \to \infty} a_{n} = a ⟹ lim_{n \to \infty} | a_{n} | = | a |

Dowód

Punkt 1.
Prawdziwość twierdzenia wynika ze względu na identyczność warunków, które muszą spełniać prawie wszystkie wyrazy ciągu

| a_{n} - a | < ε ⟺ | (a_{n} - a) - 0 | < ε ⟺ | | a_{n} - a | - 0 | < ε

Punkt 2.
Jest to jedynie szczególny przypadek punktu 1. dla $a = 0$ .

Punkt 3.
Dla dowolnych liczb $x, y \in R$ prawdziwa jest nierówność

| | x | - | y | | ⩽ | x - y |

Wynika stąd, że jeżeli dla prawie wszystkich wyrazów ciągu $(a_{n})$ spełniona jest nierówność $| a_{n} - a | < ε$ , to tym bardziej prawdą jest, że $| | a_{n} | - | a | | < ε$
□

Twierdzenie C9 (twierdzenie o trzech ciągach)
Jeżeli istnieje taka liczba całkowita $N_{0}$ , że dla każdego $n > N_{0}$ jest spełniony warunek

a_{n} ⩽ x_{n} ⩽ b_{n}

oraz

lim_{n \to \infty} a_{n} = lim_{n \to \infty} b_{n} = g

to $lim_{n \to \infty} x_{n} = g$ .

Dowód

Niech $ε$ będzie dowolną, ustaloną liczbą większą od $0$ . Z założenia prawie wszystkie wyrazy ciągu $(a_{n})$ spełniają warunek $| a_{n} - g | < ε$ . Możemy założyć, że są to wszystkie wyrazy, poczynając od wyrazu $N_{a}$ . Podobnie prawie wszystkie wyrazy ciągu $(b_{n})$ spełniają warunek $| b_{n} - g | < ε$ i podobnie możemy założyć, że są to wszystkie wyrazy, poczynając od wyrazu $N_{b}$

Nierówność $a_{n} ⩽ x_{n} ⩽ b_{n}$ jest spełniona dla wszystkich wyrazów, poczynając od $N_{0}$ , zatem oznaczając przez $M$ największą z liczb $N_{a}$ , $N_{b}$ , $N_{0}$ , możemy napisać, że o ile $n > M$ , to spełnione są jednocześnie nierówności

$g - ε < a_{n} < g + ε$
$g - ε < b_{n} < g + ε$
$a_{n} ⩽ x_{n} ⩽ b_{n}$

Z powyższych nierówności wynika natychmiast następujący ciąg nierówności

g - ε < a_{n} ⩽ x_{n} ⩽ b_{n} < g + ε

Co oznacza, że dla $n > M$ zachodzi

g - ε < x_{n} < g + ε

Czyli prawie wszystkie wyrazy ciągu $(x_{n})$ spełniają warunek $| x_{n} - g | < ε$ . Co kończy dowód.
□

Bez dowodu podamy kilka ważnych twierdzeń.
Twierdzenie C10*
Jeżeli istnieje taka liczba całkowita $n$ i rzeczywista $M$ , że dla każdego $k > n$ jest

a_{k + 1} ⩾ a_{k}

oraz

a_{k} ⩽ M

to ciąg $(a_{k})$ jest zbieżny.
Inaczej mówiąc: ciąg rosnący i ograniczony od góry jest zbieżny.

Twierdzenie C11*
Jeżeli istnieje taka liczba całkowita $n$ i rzeczywista $M$ , że dla każdego $k > n$ jest

a_{k + 1} ⩽ a_{k}

oraz

a_{k} ⩾ M

to ciąg $(a_{k})$ jest zbieżny.
Inaczej mówiąc: ciąg malejący i ograniczony od dołu jest zbieżny.

Twierdzenie C12*
Jeżeli $lim_{n \to \infty} a_{n} = a$ oraz $lim_{n \to \infty} b_{n} = b$ , gdzie $a, b$ są dowolnymi liczbami rzeczywistymi, to

$lim_{n \to \infty} (a_{n} \pm b_{n}) = a \pm b$
$lim_{n \to \infty} (a_{n} \cdot b_{n}) = a \cdot b$

Jeżeli dodatkowo dla każdego $n$ jest $b_{n} \neq 0$ i $b \neq 0$ , to

3.

lim_{n \to \infty} \frac{a_{n}}{b_{n}} = \frac{a}{b}

Twierdzenie C13
Jeżeli $lim_{n \to \infty} a_{n} = 0$ , zaś ciąg $(x_{n})$ jest ograniczony, czyli istnieje taka liczba $M > 0$ , że dla każdej wartości $n$ prawdziwa jest nierówność $| x_{n} | < M$ , to

lim_{n \to \infty} (x_{n} \cdot a_{n}) = 0

Dowód

Wystarczy pokazać, że (zobacz twierdzenie C8 p.2)

lim_{n \to \infty} | x_{n} \cdot a_{n} | = 0

Z założenia prawdziwe jest oszacowanie

0 ⩽ | x_{n} \cdot a_{n} | ⩽ | a_{n} | \cdot M

Zatem z twierdzenia o trzech ciągach otrzymujemy natychmiast, że

lim_{n \to \infty} | x_{n} \cdot a_{n} | = 0

Co kończy dowód.
□

Twierdzenie C14
Dla $a ⩾ 0$ i $n ⩾ 1$ prawdziwa jest nierówność

(1 + a)^{1 / n} ⩽ 1 + \frac{a}{n}

Dowód

Wzór jest prawdziwy dla $a = 0$ . Zakładając, że $a > 0$ i korzystając ze wzoru dwumianowego, mamy dla $n ⩾ 1$

{(1 + \frac{a}{n})}^{n} = \sum_{k = 0}^{n} [(\binom{n}{k}) \cdot {(\frac{a}{n})}^{k}] ⩾

⩾ \sum_{k = 0}^{1} [(\binom{n}{k}) \cdot {(\frac{a}{n})}^{k}] =

= 1 + n \cdot \frac{a}{n} =

= 1 + a

Co należało pokazać.
□

Twierdzenie C15
Jeżeli $A > 0$ , to $lim_{n \to \infty} \sqrt[n]{A} = 1$ .

Dowód

Dla $A > 1$ możemy napisać $A = 1 + a$ , gdzie $a > 0$ , wtedy z twierdzenia C14 otrzymujemy

1 < \sqrt[n]{A} = (1 + a)^{1 / n} ⩽ 1 + \frac{a}{n}

Z twierdzenia o trzech ciągach dostajemy natychmiast (dla $A > 1$ )

lim_{n \to \infty} \sqrt[n]{A} = 1

W przypadku gdy $0 < A < 1$ , możemy napisać $A = \frac{1}{B}$ , gdzie $B > 1$ , wtedy ze względu na udowodniony wyżej rezultat $lim_{n \to \infty} \sqrt[n]{B} = 1$

lim_{n \to \infty} \sqrt[n]{A} = lim_{n \to \infty} \frac{1}{\sqrt[n]{B}} = \frac{1}{lim_{n \to \infty} \sqrt[n]{B}} = 1

Jeżeli $A = 1$ , to $\sqrt[n]{A} = 1$ dla każdego $n ⩾ 1$ . Co kończy dowód.
□

Twierdzenie C16
Jeżeli prawie wszystkie wyrazy ciągu ciągu $(a_{n})$ spełniają warunek $0 < m < a_{n} < M$ , to $lim_{n \to \infty} \sqrt[n]{a_{n}} = 1$

Dowód

Z założenia dla prawie wszystkich wyrazów ciągu $(a_{n})$ jest

0 < m ⩽ a_{n} ⩽ M

Zatem dla prawie wszystkich wyrazów ciągu $a_{n}$ mamy

\sqrt[n]{m} ⩽ \sqrt[n]{a_{n}} ⩽ \sqrt[n]{M}

Z twierdzenia C15 wiemy, że $lim_{n \to \infty} \sqrt[n]{m} = lim_{n \to \infty} \sqrt[n]{M} = 1$ , zatem na podstawie twierdzenia o trzech ciągach otrzymujemy natychmiast $lim_{n \to \infty} \sqrt[n]{a_{n}} = 1$
□

Twierdzenie C17
Następujące ciągi są silnie rosnące i zbieżne

$1.$	$lim_{n \to \infty} {(1 + \frac{1}{n})}^{n} = e = 2.718281828 \dots$
$2.$	$lim_{n \to \infty} {(1 - \frac{1}{n})}^{n} = \frac{1}{e} = 0.367879441 \dots$

Dowód

Punkt 1
W twierdzeniu A6 pokazaliśmy, że ciąg

a_{n} = {(1 + \frac{1}{n})}^{n}

jest silnie rosnący i ograniczony od góry. Zatem z twierdzenia C10 wynika, że jest zbieżny. Liczbę będącą granicą tego ciągu oznaczamy literą $e$ , jest ona podstawą logarytmu naturalnego.

Punkt 2
Pokażemy najpierw, że ciąg ${(1 - \frac{1}{n})}^{n}$ jest silnie rosnący. Musimy pokazać, że prawdziwa jest nierówność

{(1 - \frac{1}{n + 1})}^{n + 1} > {(1 - \frac{1}{n})}^{n}

Łatwo sprawdzamy prawdziwość nierówności dla $n = 1$ . Załóżmy teraz, że $n ⩾ 2$ . Przekształcając,

{(\frac{n}{n + 1})}^{n + 1} > {(\frac{n - 1}{n})}^{n}

\frac{n}{n + 1} \cdot {(\frac{n}{n + 1})}^{n} \cdot {(\frac{n}{n - 1})}^{n} > 1

{(\frac{n^{2}}{n^{2} - 1})}^{n} > \frac{n + 1}{n}

otrzymujemy nierówność równoważną,

{(1 + \frac{1}{n^{2} - 1})}^{n} > 1 + \frac{1}{n}

którą już łatwo udowodnić, bo

{(1 + \frac{1}{n^{2} - 1})}^{n} > {(1 + \frac{1}{n^{2}})}^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) \cdot {(\frac{1}{n^{2}})}^{k} > \sum_{k = 0}^{1} (\binom{n}{k}) \cdot \frac{1}{n^{2 k}} = 1 + \frac{1}{n}

Ponieważ dla każdego $n ⩾ 1$ jest ${(1 - \frac{1}{n})}^{n} ⩽ 1$ (bo iloczyn liczb mniejszych od $1$ nie może być liczbą większą do jedności), to z twierdzenia C10 wynika, że ciąg ten jest zbieżny. Zatem możemy napisać

lim_{n \to \infty} {(1 - \frac{1}{n})}^{n} = g

Rozważmy teraz iloczyn wypisanych w twierdzeniu ciągów

{(1 + \frac{1}{n})}^{n} \cdot {(1 - \frac{1}{n})}^{n} = {(1 - \frac{1}{n^{2}})}^{n} = {[{(1 - \frac{1}{n^{2}})}^{n^{2}}]}^{1 / n}

Łatwo widzimy, że ciąg ${(1 - \frac{1}{n^{2}})}^{n^{2}}$ jest podciągiem ciągu ${(1 - \frac{1}{n})}^{n}$ , zatem jest ograniczony i dla $n ⩾ 2$ spełniony jest układ nierówności

0 < {(\frac{3}{4})}^{4} ⩽ {(1 - \frac{1}{n^{2}})}^{n^{2}} ⩽ 1

Z twierdzenia C16 dostajemy

lim_{n \to \infty} {[{(1 - \frac{1}{n^{2}})}^{n^{2}}]}^{1 / n} = 1

Z twierdzenia C12 p. 2 wynika natychmiast, że

e \cdot g = lim_{n \to \infty} [{(1 + \frac{1}{n})}^{n} \cdot {(1 - \frac{1}{n})}^{n}] = lim_{n \to \infty} {[{(1 - \frac{1}{n^{2}})}^{n^{2}}]}^{1 / n} = 1

Zatem $g = \frac{1}{e}$ .
□

Twierdzenie C18
Dla $n ⩾ 2$ prawdziwe są następujące nierówności

$1.$	$\frac{1}{n + 1} < \log (1 + \frac{1}{n}) < \frac{1}{n}$
$2.$	$- \frac{1}{n - 1} < \log (1 - \frac{1}{n}) < - \frac{1}{n}$

Dowód

Ponieważ ciąg ${(1 + \frac{1}{n})}^{n}$ jest silnie rosnący, to

{(1 + \frac{1}{n})}^{n} < e

Logarytmując powyższą nierówność, mamy

n \cdot \log (1 + \frac{1}{n}) < 1

Stąd wynika natychmiast, że

\log (1 + \frac{1}{n}) < \frac{1}{n}

Ponieważ ciąg ${(1 - \frac{1}{n})}^{n}$ również jest silnie rosnący, to postępując analogicznie, dostajemy

{(1 - \frac{1}{n})}^{n} < \frac{1}{e}

n \cdot \log (1 - \frac{1}{n}) < - 1

\log (1 - \frac{1}{n}) < - \frac{1}{n}

Przekształcając otrzymane wzory, otrzymujemy

- \log (1 + \frac{1}{n}) = - \log (\frac{n + 1}{n}) = \log (\frac{n}{n + 1}) = \log (1 - \frac{1}{n + 1}) < - \frac{1}{n + 1}

oraz

- \log (1 - \frac{1}{n}) = - \log (\frac{n - 1}{n}) = \log (\frac{n}{n - 1}) = \log (1 + \frac{1}{n - 1}) < \frac{1}{n - 1}

□

Liczby pierwsze w ciągach arytmetycznych

Twierdzenie C19
Każda liczba naturalna $n ⩾ 2$ jest liczbą pierwszą lub iloczynem liczb pierwszych.

Dowód

Pierwszy sposób

Przypuśćmy, że istnieją liczby naturalne większe od $1$ , które nie są liczbami pierwszymi ani nie są iloczynami liczb pierwszych. Niech $m$ oznacza najmniejszą^[1] z takich liczb. Z założenia $m$ nie jest liczbą pierwszą, zatem $m$ może być zapisana w postaci $m = a \cdot b$ , gdzie liczby $a, b$ są liczbami naturalnymi mniejszymi od $m$ .

Ponieważ $m$ jest najmniejszą liczbą naturalną, która nie jest liczbą pierwszą ani nie jest iloczynem liczb pierwszych, to liczby $a$ i $b$ muszą być liczbami złożonymi, ale jako mniejsze od $m$ są one iloczynami liczb pierwszych, zatem i liczba $m$ musi być iloczynem liczb pierwszych.

Uzyskana sprzeczność dowodzi, że nasze przypuszczenie jest fałszywe.

Drugi sposób

Indukcja matematyczna. Twierdzenie jest oczywiście prawdziwe dla $n = 2$ . Zakładając, że twierdzenie jest prawdziwe dla wszystkich liczb naturalnych $k \in [2, n]$ , dla liczby $n + 1$ mamy dwie możliwości

$n + 1$ jest liczbą pierwszą (wtedy twierdzenie jest prawdziwe w sposób oczywisty)
$n + 1$ jest liczbą złożoną wtedy, $n + 1 = a b$ , gdzie $1 < a, b < n + 1$ ; zatem na podstawie założenia indukcyjnego liczby $a$ i $b$ są liczbami pierwszymi lub iloczynami liczb pierwszych, czyli $n + 1 = a b$ jest iloczynem liczb pierwszych.

Co należało pokazać.
□

Twierdzenie C20 (Euklides, IV w. p.n.e.)
Istnieje nieskończenie wiele liczb pierwszych.

Dowód

Przypuśćmy, że istnieje jedynie skończona ilość liczb pierwszych $p_{1}, p_{2}, \dots, p_{n}$ . Wtedy liczba $a = p_{1} \cdot p_{2} \cdot \dots \cdot p_{n} + 1$ jest większa od jedności i z twierdzenia C19 wynika, że posiada dzielnik będący liczbą pierwszą, ale jak łatwo zauważyć żadna z liczb pierwszych $p_{1}, p_{2}, \dots, p_{n}$ nie jest dzielnikiem liczby $a$ . Zatem istnieje liczba pierwsza $p$ będąca dzielnikiem pierwszym liczby $a$ i różna od każdej z liczb $p_{1}, p_{2}, \dots, p_{n}$ . Co kończy dowód.
□

Twierdzenie C21
Jeżeli liczba naturalna $n$ jest postaci $4 k + 3$ ^[2], to ma dzielnik postaci $4 k + 3$ będący liczbą pierwszą.

Dowód

Jeżeli $n$ jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy zatem sytuację gdy $n$ jest liczbą złożoną. Z założenia $n$ jest liczbą nieparzystą, zatem możliwe są trzy typy iloczynów

(4 a + 1) (4 b + 1) = 16 a b + 4 a + 4 b + 1 = 4 (4 a b + a + b) + 1

(4 a + 1) (4 b + 3) = 16 a b + 12 a + 4 b + 3 = 4 (4 a b + 3 a + b) + 3

(4 a + 3) (4 b + 3) = 16 a b + 12 a + 12 b + 9 = 4 (4 a b + 3 a + 3 b + 2) + 1

Widzimy, że liczba złożona postaci $4 k + 3$ jest iloczynem liczb postaci $4 k + 1$ i $4 k + 3$ . Wynika stąd natychmiast, że liczba złożona postaci $4 k + 3$ posiada dzielnik postaci $4 k + 3$ . Niech $q$ oznacza najmniejszy dzielnik liczby $n$ postaci $4 k + 3$ . Pokażemy, że $q$ jest liczbą pierwszą. Istotnie, gdyby $q$ była liczbą złożoną, to miałaby dzielnik $d$ postaci $4 k + 3$ i byłoby $d < q$ , wbrew założeniu, że $q$ jest najmniejszym dzielnikiem liczby $n$ postaci $4 k + 3$ . Co kończy dowód.
□

Twierdzenie C22
Istnieje nieskończenie wiele liczb pierwszych postaci $4 k + 3$ .

Dowód

Przypuśćmy, że istnieje tylko skończona ilość liczb pierwszych postaci $4 k + 3$ . Niech będą to liczby $p_{1}, \dots, p_{s}$ . Liczba

M = 4 p_{1} \cdot \dots \cdot p_{s} - 1 = 4 (p_{1} \cdot \dots \cdot p_{s} - 1) + 3

jest postaci $4 k + 3$ i jak wiemy z twierdzenia C21, ma dzielnik pierwszy $q$ postaci $4 k + 3$ . Ale jak łatwo zauważyć, żadna z liczb $p_{1}, \dots, p_{s}$ nie dzieli liczby $M$ . Zatem istnieje liczba pierwsza $q$ postaci $4 k + 3$ różna od każdej z liczb $p_{1}, p_{2}, \dots, p_{s}$ . Otrzymana sprzeczność kończy dowód.
□

Twierdzenie C23
Jeżeli liczba naturalna $n$ jest postaci $6 k + 5$ , to ma dzielnik postaci $6 k + 5$ będący liczbą pierwszą.

Dowód

Jeżeli $n$ jest liczbą pierwszą, to twierdzenie jest dowiedzione. Zbadajmy sytuację gdy $n$ jest liczbą złożoną. Z twierdzenia C19 wiemy, że w tym przypadku liczba $n$ będzie iloczynem liczb pierwszych. Zauważmy, że nieparzyste liczby pierwsze mogą być jedynie postaci $6 k + 1$ lub $6 k + 5$ (liczba $6 k + 3$ jest liczbą złożoną). Ponieważ iloczyn liczb postaci $6 k + 1$

(6 a + 1) (6 b + 1) = 36 a b + 6 a + 6 b + 1 = 6 (6 a b + a + b) + 1

jest liczbą postaci $6 k + 1$ , to w rozkładzie liczby $n$ na czynniki pierwsze musi pojawić się przynajmniej jeden czynnik postaci $6 k + 5$ . Co kończy dowód.
□

Twierdzenie C24
Istnieje nieskończenie wiele liczb pierwszych postaci $6 k + 5$ .

Dowód

Przypuśćmy, że istnieje tylko skończona ilość liczb pierwszych postaci $6 k + 5$ . Niech będą to liczby $p_{1}, \dots, p_{s}$ . Liczba

M = 6 p_{1} \cdot \dots \cdot p_{s} - 1 = 6 (p_{1} \cdot \dots \cdot p_{s} - 1) + 5

jest postaci $6 k + 5$ i jak wiemy z twierdzenia C23 ma dzielnik pierwszy $q$ postaci $6 k + 5$ . Ale jak łatwo zauważyć żadna z liczb $p_{1}, \dots, p_{s}$ nie dzieli liczby $M$ . Zatem istnieje liczba pierwsza $q$ postaci $6 k + 5$ różna od każdej z liczb $p_{1}, p_{2}, \dots, p_{s}$ . Otrzymana sprzeczność kończy dowód.
□

Twierdzenie C25
Istnieje nieskończenie wiele liczb pierwszych postaci $3 k + 2$ .

Dowód

Jeżeli $k = 2 j$ jest liczbą parzystą, to otrzymujemy ciąg liczb parzystych

3 k + 2 = 6 j + 2

w którym jedynie liczba $2$ jest liczbą pierwszą (dla $j = 0$ ).

Jeżeli $k = 2 j + 1$ jest liczbą nieparzystą, to otrzymujemy ciąg liczb nieparzystych

3 k + 2 = 3 (2 j + 1) + 2 = 6 j + 5

o którym wiemy, że zawiera nieskończenie wiele liczb pierwszych (zobacz twierdzenie C24). Zatem w ciągu arytmetycznym postaci $3 k + 2$ występuje nieskończenie wiele liczb pierwszych.
□

Uwaga C26
Zauważmy, że liczby postaci $2 k + 1$ to wszystkie liczby nieparzyste dodatnie. Ponieważ wszystkie liczby pierwsze (poza liczbą $2$ ) są liczbami nieparzystymi, to wśród liczb postaci $2 k + 1$ występuje nieskończenie wiele liczb pierwszych.

Wszystkie omówione wyżej przypadki ciągów arytmetycznych: $2 k + 1$ , $3 k + 2$ , $4 k + 3$ i $6 k + 5$ , w których występuje nieskończona ilość liczb pierwszych są szczególnymi przypadkami udowodnionego w 1837 roku twierdzenia

Twierdzenie C27* (Peter Gustav Lejeune Dirichlet, 1837)
Niech $a \in Z_{+}$ i $b \in Z$ . Jeżeli liczby $a$ i $b$ są względnie pierwsze, to w ciągu arytmetycznym $a k + b$ występuje nieskończenie wiele liczb pierwszych.

Uwaga C28
Dowód twierdzenia Dirichleta jest bardzo trudny. Natomiast bardzo łatwo można pokazać, że dowolny ciąg arytmetyczny $a k + b$ zawiera nieskończenie wiele liczb złożonych. Istotnie, jeżeli liczby $a, b$ nie są względnie pierwsze, to wszystkie wyrazy ciągu są liczbami złożonymi. Jeżeli $a, b$ są względnie pierwsze i $b > 1,$ to wystarczy przyjąć $k = b t$ . Jeżeli są względnie pierwsze i $b = 1$ , to wystarczy przyjąć $k = a t^{2} + 2 t$ , wtedy

a k + 1 = a^{2} t^{2} + 2 a t + 1 = (a t + 1)^{2}

Uwaga C29
Wiemy już, że w przypadku gdy liczby $a$ i $b$ są względnie pierwsze, to w ciągu arytmetycznym $a k + b$ występuje nieskończenie wiele liczb pierwszych. Pojawia się pytanie o to, czy możliwe jest oszacowanie najmniejszej liczby pierwszej $p$ w takim ciągu. Jakkolwiek przypuszczamy, że prawdziwe jest oszacowanie $p < a^{2}$ , to stan naszej obecnej wiedzy ujmuje twierdzenie Linnika^[3]^[4]^[5]^[6], które podajemy niżej. Trzeba było ponad pół wieku wysiłku wielu matematyków, aby pokazać, że w twierdzeniu Linnika możemy przyjąć $L = 5$ ^[7]. Bombieri, Friedlander i Iwaniec udowodnili^[8], że dla prawie wszystkich liczb $a$ prawdziwe jest oszacowanie $L ⩽ 2$ .

Twierdzenie C30* (Jurij Linnik, 1944)
Niech $a, b \in Z_{+}$ i $p_{min} (a, b)$ oznacza najmniejszą liczbę pierwszą w ciągu arytmetycznym $a k + b$ , gdzie $k \in Z_{+}$ . Jeżeli $gcd (a, b) = 1$ i $b \in [1, a - 1]$ , to istnieją takie stałe $L > 0$ i $a_{0} ⩾ 2$ , że dla wszystkich $a > a_{0}$ prawdziwe jest oszacowanie

p_{min} (a, b) < a^{L}

Zadanie C31
Pokazać, że z twierdzenia Linnika wynika istnienie takich stałych $c, L > 0$ , że dla każdego $a ⩾ 2$ prawdziwe jest oszacowanie

p (a) < c a^{L}

gdzie

p (a) = \underset{gcd (a, b) = 1}{max_{1 ⩽ b < a}} p_{min} (a, b)

Rozwiązanie

Oszacowanie podane w twierdzeniu Linnika

p_{min} (a, b) < a^{L}

jest prawdziwe dla dowolnej liczby $b \in [1, a - 1]$ względnie pierwszej z $a$ . Jeżeli zdefiniujemy funkcję

p (a) = \underset{gcd (a, b) = 1}{max_{1 ⩽ b < a}} p_{min} (a, b)

to możemy zapisać twierdzenie Linnika tak, aby po lewej stronie nie występowała liczba $b$ , co czyni zapis bardziej przejrzystym. Mamy

p (a) < a^{L}

dla wszystkich $a > a_{0}$ . Ponieważ dla $a \in [2, a_{0}]$ funkcja $p (a)$ przyjmuje wartości skończone, a dla $a > a_{0}$ jest $p (a) < a^{L}$ , to funkcja $\frac{p (a)}{a^{L}}$ jest ograniczona od góry, czyli istnieje taka stała $c$ , że

\frac{p (a)}{a^{L}} < c

dla dowolnego $a ⩾ 2$ . Co należało pokazać.
□

Przykład C32
Pokazaliśmy (zobacz C31), że istnieją takie stałe $c, L > 0$ , że dla każdego $a ⩾ 2$ prawdziwe jest oszacowanie

p (a) < c a^{L}

gdzie

p (a) = \underset{gcd (a, b) = 1}{max_{1 ⩽ b < a}} p_{min} (a, b)

Ponieważ $p (a) > a$ , to prawdziwy jest ciąg nierówności

1 < \frac{\log p (a)}{\log a} < \frac{\log c}{\log a} + L ⩽ | \frac{\log c}{\log a} | + L ⩽ \frac{| \log c |}{\log 2} + L

Wynika stąd, że dla $a ⩾ 2$ funkcja $\frac{\log p (a)}{\log a}$ jest ograniczona.

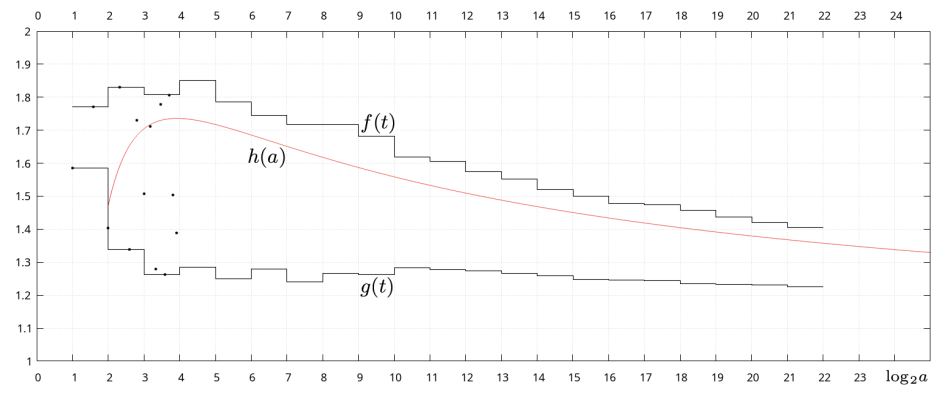
Na zamieszczonym niżej obrazku przedstawiono pierwszych czternaście punktów funkcji $\frac{\log p (a)}{\log a}$ . Ze względu na skokowy charakter zmian tej funkcji najwygodniej będzie przedstawić jej wykres, pokazując jedynie jej maksymalne i minimalne wartości w wybranych podprzedziałach $Z_{+}$ . Mówiąc precyzyjnie, zamieszczone zostały wykresy funkcji

f (t) = max_{2^{t} ⩽ a < 2^{t + 1}} \frac{\log p (a)}{\log a} g (t) = min_{2^{t} ⩽ a < 2^{t + 1}} \frac{\log p (a)}{\log a} h (a) = 1 + \frac{2 \log \log a}{\log a}

gdzie $t \in Z_{+}$ .

Pokaż kod i dane do wykresu

W tabeli przedstawiamy dane, na podstawie których sporządziliśmy zamieszczony wyżej wykres. Mamy kolejno

przedział $U$
minimalną wartość $\frac{\log p (a)}{\log a}$ w przedziale $U$
liczbę $a$ , która odpowiada minimalnej wartości $\frac{\log p (a)}{\log a}$
wartość $p (a) = \underset{gcd (a, b) = 1}{max_{1 ⩽ b < a}} p_{min} (a, b)$
liczbę $b$ taką, że najmniejsza liczba pierwsza w ciągu $a k + b$ jest równa $p (a)$

Następnie podajemy analogiczne wartości dla maksymalnej wartości $\frac{\log p (a)}{\log a}$ w przedziale $U$ . Pominęliśmy dane dla początkowych przedziałów $[2^{n}, 2^{n + 1})$ , ponieważ Czytelnik z łatwością policzy je samodzielnie. Prosty kod do obliczeń w PARI/GP zamieściliśmy pod tabelą.

$U$	$min_{a \in U} \frac{\log p (a)}{\log a}$	$a$	$p (a)$	$b$	$max_{a \in U} \frac{\log p (a)}{\log a}$	$a$	$p (a)$	$b$
$[2^{12}, 2^{13})$	$1.273691$	$6840$	$76679$	$1439$	$1.574826$	$4177$	$503771$	$2531$
$[2^{13}, 2^{14})$	$1.265227$	$14490$	$183949$	$10069$	$1.551307$	$8941$	$1348387$	$7237$
$[2^{14}, 2^{15})$	$1.257880$	$20790$	$269987$	$20507$	$1.519764$	$22133$	$4012709$	$6636$
$[2^{15}, 2^{16})$	$1.247285$	$39270$	$537157$	$26647$	$1.500736$	$40951$	$8352037$	$38984$
$[2^{16}, 2^{17})$	$1.244884$	$106260$	$1808207$	$1787$	$1.477806$	$84229$	$19005359$	$53834$
$[2^{17}, 2^{18})$	$1.243658$	$150150$	$2740469$	$37769$	$1.474387$	$132331$	$35588503$	$123795$
$[2^{18}, 2^{19})$	$1.233771$	$510510$	$11024723$	$304013$	$1.457138$	$297491$	$94537921$	$233274$
$[2^{19}, 2^{20})$	$1.233150$	$1021020$	$25706531$	$181031$	$1.437418$	$596081$	$200230391$	$543256$
$[2^{20}, 2^{21})$	$1.231259$	$2072070$	$59859383$	$1841423$	$1.419752$	$1181311$	$418069567$	$1066784$
$[2^{21}, 2^{22})$	$1.224444$	$3543540$	$104573173$	$1810513$	$1.405843$	$2753747$	$1131160207$	$2123937$

pmin(a, b) = 
\\ zwraca najmniejszą liczbę pierwszą w ciągu a*k + b, gdzie k >= 1 i gcd(a, b) = 1
{
local(k, p);
k = 1;
p = a*k + b;
while( !isprime(p), p = a*(k++) + b );
return(p);
}

PMAX(a) = 
\\ zwraca największą ze wszystkich najmniejszych liczb pierwszych
\\ w ciągach a*k + b, gdzie k >= 1, 0 < b < a i gcd(a, b) = 1
{
local(b, p, w);
w = [0, 0];
b = 0;
while( b++ < a,
       if( gcd(a, b) > 1, next() );
       p = pmin(a, b);
       if( w[1] < p, w = [p, b] );
     );
return(w);
}

Linnik(n) = 
\\ n >= 1, sprawdzamy przedział U = [ 2^n , 2^(n + 1) ), czyli  2^n <= a < 2^(n+1)
{
local(a, b, p4a, sep, txt, w, y, Ymin, Ymax);
sep = ", "; \\ separator
Ymin = [100, 1, 0, 0]; \\ najmniejsza wartość funkcji log( p(a) ) / log(a) w przedziale U
Ymax = [0, 1, 0, 0]; \\ największa wartość funkcji log( p(a) ) / log(a) w przedziale U
a = 2^n - 1;
while( a++ < 2^(n+1),
       w = PMAX(a);
       p4a = w[1];
       b = w[2];
       y = log(p4a) / log(a);
       if( y < Ymin[1], Ymin = [y, a, p4a, b] );
       if( y > Ymax[1], Ymax = [y, a, p4a, b] );
     );
txt = Str(n, sep, Ymin[1], sep, Ymin[2], sep, Ymin[3], sep, Ymin[4], sep, Ymax[1], sep, Ymax[2], sep, Ymax[3], sep, Ymax[4]);
print(txt);
}

Przypuszczamy, że prawdziwe jest znacznie silniejsze oszacowanie najmniejszej liczby pierwszej w ciągu arytmetycznym^[9]^[10]

p (a) \sim a \log^{2} a

W takim przypadku mielibyśmy

\frac{\log p (a)}{\log a} \sim 1 + \frac{2 \log \log a}{\log a}

Rzeczywiście, porównanie wykresów funkcji $f (t)$ i $h (a)$ wydaje się potwierdzać to przypuszczenie dla $a \in [2, 2^{22}]$ .

W tabeli zestawiliśmy wszystkie wartości funkcji $\frac{\log p (a)}{\log a}$ większe od $1.75$ dla $a \in [2, 2^{22}]$

$a$	$\log_{2} a$	$p (a)$	$\frac{\log p (a)}{\log a}$
$31$	$4.95$	$577$	$1.851446$
$5$	$2.32$	$19$	$1.829482$
$13$	$3.70$	$103$	$1.806947$
$47$	$5.55$	$967$	$1.785437$
$19$	$4.24$	$191$	$1.783794$
$61$	$5.93$	$1511$	$1.780771$
$11$	$3.46$	$71$	$1.777675$
$3$	$1.58$	$7$	$1.771243$

Rozważmy zbiór $S$ takich liczb $a$ , że prawdziwe jest oszacowanie $p (a) < a \log^{2} a$ . Bez trudu możemy podać przykłady takich liczb, ale nie wiemy, czy jest ich nieskończenie wiele.

$n$	$a = p_{1} \cdot \dots \cdot p_{n}$	$\log_{2} a$	$p (a)$	$\frac{a \log^{2} a}{p (a)}$	$\frac{\log p (a)}{\log a}$
$2$	$6$	$2.584$	$11$	$1.751$	$1.338290$
$3$	$30$	$4.906$	$79$	$4.392$	$1.284679$
$4$	$210$	$7.714$	$761$	$7.889$	$1.240789$
$5$	$2310$	$11.173$	$20477$	$6.766$	$1.281737$
$6$	$30030$	$14.874$	$520547$	$6.132$	$1.276692$
$7$	$510510$	$18.961$	$11024723$	$7.999$	$1.233770$
$8$	$9699690$	$23.209$	$375095881$	$6.692$	$1.227199$
$9$	$223092870$	$27.733$	$11799966613$	$6.986$	$1.206432$
$10$	$6469693230$	$32.591$	$451404994867$	$7.314$	$1.187922$
$11$	$200560490130$	$37.545$	$19822720510961$	$6.852$	$1.176506$
$12$	$7420738134810$	$42.754$

Ponieważ $p (a) > a$ , to prawdziwy jest układ nierówności

1 < \frac{\log p (a)}{\log a} < 1 + \frac{2 \log \log a}{\log a}

Jeżeli zbiór $S$ jest nieskończony, to z twierdzenia o trzech ciągach otrzymujemy

\underset{a \in S}{lim_{a \to \infty}} \frac{\log p (a)}{\log a} = 1

W konsekwencji wykres funkcji

g (t) = min_{2^{t} ⩽ a < 2^{t + 1}} \frac{\log p (a)}{\log a}

będzie opadał ku prostej $y = 1$ .

Zadanie C33
Pokazać, że istnieje nieskończenie wiele liczb pierwszych zakończonych cyframi 99, przykładowo 199, 499, 599, 1399, 1499, ...

Rozwiązanie

Wszystkie liczby naturalne zakończone cyframi $99$ możemy zapisać w postaci $a_{n} = 100 k + 99$ , gdzie $k \in N$ . Ponieważ ciąg $(a_{n})$ jest ciągiem arytmetycznym, a liczby $99$ i $100$ są względnie pierwsze, to na podstawie twierdzenia Dirichleta stwierdzamy, że istnieje nieskończenie wiele liczb pierwszych zakończonych cyframi $99$ .
□

Definicja C34
Niech $a ⩾ 2$ będzie liczbą całkowitą. Wartość funkcji $π (n; a, b)$ jest równa ilości liczb pierwszych nie większych od $n$ , które przy dzieleniu przez $a$ dają resztę $b$ .

Uwaga C35
Zauważmy, że w twierdzeniu Dirichleta na liczby $a$ oraz $b$ nałożone są minimalne warunki: $a \in Z_{+}$ i $b \in Z$ . Sytuacja w przypadku funkcji $π (n; a, b)$ jest odmienna – tutaj mamy $a ⩾ 2$ oraz $0 ⩽ b ⩽ a - 1$ . Jest tak dlatego, że podział liczb pierwszych, który odzwierciedla funkcja $π (n; a, b)$ jest podziałem pierwotnym, a twierdzenie Dirichleta jest tylko jego uzasadnieniem. Podział liczb pierwszych musi być też precyzyjnie określony, tak aby zachodził naturalny związek

\sum_{b = 0}^{a - 1} π (n; a, b) = π (n)

Oczywiście nie przeszkadza to w liczeniu liczb pierwszych w dowolnym ciągu arytmetycznym. Niech na przykład

u_{k} = 7 k + 101 = 7 (k + 14) + 3

gdzie

k = 0, 1, \dots

Ilość liczb pierwszych w ciagu $(u_{k})$ jest równa

π (n; 7, 3) - π (7 \cdot 13 + 3; 7, 3) = π (n; 7, 3) - 5

Zadanie C36
Pokazać, że dla dowolnej liczby całkowitej $m ⩾ 1$

wśród liczb naturalnych zawsze można wskazać $m$ kolejnych liczb, które są złożone
w ciągu arytmetycznym $a k + b$ , gdzie liczby $a$ i $b$ są względnie pierwsze, zawsze można wskazać $m$ kolejnych wyrazów, które są złożone

Rozwiązanie

Punkt 1.
W przypadku liczb naturalnych, łatwo widzimy, że kolejne liczby

(m + 1)! + 2, (m + 1)! + 3, \dots, (m + 1)! + (m + 1)

są liczbami złożonymi. Co oznacza, że dla dowolnej liczby naturalnej $m$ zawsze możemy wskazać taką liczbę $n$ , że $p_{n + 1} - p_{n} > m$ .

Punkt 2.
W przypadku ciągu arytmetycznego $u_{k} = a k + b$ rozważmy kolejne wyrazy ciągu począwszy od wskaźnika

k_{0} = \prod_{j = 0}^{m - 1} (a j + b)

Łatwo zauważamy, że dla $k = k_{0}, k_{0} + 1, \dots, k_{0} + (m - 1)$ wyrazy ciągu arytmetycznego $u_{k} = a k + b$ są liczbami złożonymi. Istotnie, niech $t = 0, 1, \dots, m - 1$ wtedy

u_{k} = a k + b =

= a (k_{0} + t) + b =

= a k_{0} + (a t + b) =

= a \prod_{j = 0}^{m - 1} (a j + b) + (a t + b)

i liczba $a t + b$ dzieli iloczyn $\prod_{j = 0}^{m - 1} (a j + b)$ dla $t = 0, \dots, m - 1$ . Co należało pokazać.

Wiemy, że jeżeli liczby $a$ i $b$ są względnie pierwsze, to w ciągu $a k + b$ występuje nieskończenie wiele liczb pierwszych. Niech będą to liczby $q_{1}, q_{2}, \dots, q_{r}, \dots$ . Uzyskany rezultat oznacza, że dla dowolnej liczby naturalnej $m$ zawsze możemy wskazać taką liczbę $n$ , że $q_{n + 1} - q_{n} ⩾ a (m + 1)$
□

Przykład C37
Rozważmy ciąg arytmetyczny $u_{k} = 3 k + 2$ i wskaźnik

k_{0} = \prod_{j = 0}^{12} (3 j + 2) = 3091650738176000

Trzynaście wyrazów tego szeregu dla $k = k_{0} + t$ , gdzie $t = 0, 1, \dots, 12$ to oczywiście liczby złożone, ale wyrazy dla $k = k_{0} - 1$ i $k = k_{0} + 13$ są liczbami pierwszymi.

Przeszukując ciąg $u_{k} = 3 k + 2$ możemy łatwo znaleźć, że pierwsze trzynaście kolejnych wyrazów złożonych pojawia się już dla $k = 370, 371, \dots, 382$ .

Twierdzenie C38
Jeżeli $n ⩾ 3$ , to istnieje $n$ kolejnych liczb naturalnych, wśród których znajduje się dokładnie $r ⩽ π (n)$ liczb pierwszych.

Dowód

Warunek $n ⩾ 3$ nie wynika z potrzeb dowodu, a jedynie pomija sytuacje nietypowe, których twierdzenie nie obejmuje. Zawsze istnieje jedna liczba naturalna, która jest liczbą pierwszą i łatwo możemy wskazać dwie kolejne liczby naturalne będące liczbami pierwszymi.

Niech $k \in N$ . Wartość funkcji

Q (k, n) = π (k + n) - π (k)

jest równa ilości liczb pierwszych wśród $n$ kolejnych liczb naturalnych od liczby $k + 1$ do liczby $k + n$ .

Uwzględniając, że wypisane niżej wyrażenia w nawiasach kwadratowych mogą przyjmować jedynie dwie wartości $0$ lub $1$ , dostajemy

$| Q (k + 1, n) - Q (k, n) | = | [π (k + n + 1) - π (k + n)] - [π (k + 1) - π (k)] | ⩽ 1$

Ponadto mamy

$Q (0, n) = π (n)$ bo $π (0) = 0$
$Q ((n + 1)! + 1, n) = 0$ bo liczby $(n + 1)! + 2, \dots, (n + 1)! + (n + 1)$ są liczbami złożonymi

Ponieważ wartości funkcji $Q (k, n)$ mogą zmieniać się tylko o $- 1$ , $0$ lub $1$ , to $Q (k, n)$ musi przyjmować wszystkie wartości całkowite od $0$ do $π (n)$ . Wynika stąd, że istnieje taka liczba $k_{r}$ , że $Q (k_{r}, n) = r$ , gdzie $0 ⩽ r ⩽ π (n)$ .

Fragment wykresu funkcji $Q (k, 10)$ . Widzimy, że dla $k = 113$ po raz pierwszy mamy $Q (k, 10) = 0$ , a funkcja $Q (k, 10)$ przyjmuje wszystkie wartości całkowite od $0$ do $5$ .
□

Przykład C39
Czytelnik może łatwo sprawdzić, że ciąg $(1308, \dots, 1407)$ stu kolejnych liczb całkowitych zawiera dokładnie $8$ liczb pierwszych.

Zadanie C40
Pokazać, nie korzystając z twierdzenia C38, że istnieje $1000$ kolejnych liczb naturalnych, wśród których jest dokładnie jedna liczba pierwsza.

Rozwiązanie

Zauważmy, że $1000$ kolejnych liczb naturalnych

1001! + 2, 1001! + 3, \dots, 1001! + 1001

nie zawiera żadnej liczby pierwszej. Wielokrotnie zmniejszając wszystkie wypisane wyżej liczby o jeden, aż do chwili, gdy pierwsza z wypisanych liczb będzie liczbą pierwszą uzyskamy $1000$ kolejnych liczb naturalnych, wśród których jest dokładnie jedna liczba pierwsza.

Uwaga: dopiero liczba $1001! - 1733$ jest pierwsza.
□

Zadanie C41
Pokazać, że istnieje $20$ kolejnych liczb naturalnych postaci $6 k + 1$ , wśród których jest dokładnie $5$ liczb pierwszych.

Rozwiązanie

Rozwiązywanie zadania rozpoczniemy od dwóch spostrzeżeń

wśród pierwszych $20$ liczb naturalnych postaci $6 k + 1$ jest $13$ liczb pierwszych
w ciągu $6 k + 1$ istnieją dowolnie długie przedziały pozbawione liczb pierwszych (zobacz zadanie C36), zatem istnieje $20$ kolejnych liczb naturalnych postaci $6 k + 1$ , wśród których nie ma ani jednej liczby pierwszej

Pierwsze spostrzeżenie pokazuje, że rozwiązanie problemu jest potencjalnie możliwe. Rozwiązanie mogłoby nie istnieć, gdybyśmy szukali $20$ liczb naturalnych postaci $6 k + 1$ wśród których jest, powiedzmy, $15$ liczb pierwszych.

Drugie spostrzeżenie mówi nam, że ilość liczb pierwszych wśród kolejnych $20$ liczb naturalnych postaci $6 k + 1$ zmienia się od $13$ do $0$ . Analiza przebiegu tych zmian jest kluczem do dowodu twierdzenia.

Zbadajmy zatem, jak zmienia się ilość liczb pierwszych wśród kolejnych $20$ liczb naturalnych postaci $6 k + 1$ . Rozważmy ciąg $a_{k} = 6 k + 1$ , gdzie $k = 0, 1, 2, \dots$

$(a_{k}) = (1, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115, 121, 127, 133, 139, 145, 151, 157, 163, 169, 175, 181, 187, 193, 199, 205, 211, \dots)$

Liczby pierwsze zostały pogrubione.

Niech $(B^{n})$ będzie fragmentem ciągu $(a_{k})$ rozpoczynającym się od $n$ -tego wyrazu ciągu i złożonym z $20$ kolejnych wyrazów ciągu $(a_{k})$ . Przykładowo mamy

$(B^{1}) = (1, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115)$

$(B^{2}) = (7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115, 121)$

$(B^{3}) = (13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115, 121, 127)$

Musimy zrozumieć, jak przejście od ciągu $(B^{n})$ do ciągu $(B^{n + 1})$ wpływa na ilość liczb pierwszych w tych ciągach.

jeżeli najmniejszy wyraz ciągu $(B^{n})$ jest liczbą złożoną, to po przejściu do ciągu $(B^{n + 1})$ ilość liczb pierwszych w tym ciągu w stosunku do ilości liczb pierwszych w ciągu $(B^{n})$ może
- pozostać bez zmian (w przypadku, gdy największy wyraz ciągu $(B^{n + 1})$ jest liczbą złożoną)
- zwiększyć się o jeden (w przypadku, gdy największy wyraz ciągu $(B^{n + 1})$ jest liczbą pierwszą)

jeżeli najmniejszy wyraz ciągu $(B^{n})$ jest liczbą pierwszą, to po przejściu do ciągu $(B^{n + 1})$ ilość liczb pierwszych w tym ciągu w stosunku do ilości liczb pierwszych w ciągu $(B^{n})$ może
- zmniejszyć się o jeden (w przypadku, gdy największy wyraz ciągu $(B^{n + 1})$ jest liczbą złożoną)
- pozostać bez zmian (w przypadku, gdy największy wyraz ciągu $(B^{n + 1})$ jest liczbą pierwszą)

Wynika stąd, że przechodząc od ciągu $(B^{n})$ do ciągu $(B^{n + 1})$ ilość liczb pierwszych może się zmienić o $- 1$ , $0$ lub $1$ . Z drugiego ze spostrzeżeń uczynionych na początku dowodu wynika istnienie takiej liczby $r$ , że wśród ciągów

(B^{1}), (B^{2}), \dots, (B^{r})

ilość liczb pierwszych będzie przyjmowała wszystkie możliwe wartości od liczby $13$ do liczby $0$ . Co zapewnia istnienie takich $20$ kolejnych liczb naturalnych postaci $6 k + 1$ , że wśród nich jest dokładnie $5$ liczb pierwszych.
□

Twierdzenie C42
Niech $a, b \in Z$ oraz $a ⩾ 2$ i $0 ⩽ b ⩽ a - 1$ . Jeżeli liczby $a$ oraz $b$ są względnie pierwsze, to istnieje $n$ kolejnych liczb postaci $a k + b$ , wśród których znajduje się dokładnie $r ⩽ π (a (n - 1) + b; a, b)$ liczb pierwszych.

Dowód

Zadanie C43
Niech $p ⩾ 5$ będzie liczbą pierwszą. Pokazać, że w ciągu $6 k + 1$ występują kwadraty wszystkich liczb pierwszych $p$ .

Rozwiązanie

Wiemy, że liczby pierwsze nieparzyste $p ⩾ 5$ mogą być postaci $6 k + 1$ lub $6 k + 5$ . Ponieważ

(6 k + 1)^{2} = 6 (6 k^{2} + 2 k) + 1

(6 k + 5)^{2} = 6 (6 k^{2} + 10 k + 4) + 1

zatem kwadraty liczb pierwszych są postaci $6 k + 1$ i nie mogą występować w ciągu postaci $6 k + 5$ .
□

Zadanie C44
Dany jest ciąg arytmetyczny $a k + b$ , gdzie liczby $a$ i $b$ są względnie pierwsze. Pokazać, że

jeżeli liczba pierwsza $p$ dzieli $a$ , to żaden wyraz ciągu $a k + b$ nie jest podzielny przez $p$
jeżeli liczba pierwsza $p$ nie dzieli $a$ , to istnieje nieskończenie wiele wyrazów ciągu $a k + b$ , które są podzielne przez $p$

Rozwiązanie

Punkt 1.
Zauważmy, że liczby $a$ i $b$ są względnie pierwsze, zatem liczba pierwsza $p$ nie może jednocześnie dzielić liczb $a$ i $b$ . Ponieważ z założenia $p ∣ a$ , to wynika stąd, że $p$ nie dzieli $b$ . Jeśli tak, to

a k + b = (n p) k + b

i $p$ nie dzieli żadnej liczby postaci $a k + b$ .

Punkt 2.
Pierwszy sposób

Niech $k_{0} \in N$ . Przypuśćmy, że dla pewnych różnych liczb naturalnych $i, j$ takich, że $1 ⩽ i < j ⩽ p$ liczby $a (k_{0} + i) + b$ oraz $a (k_{0} + j) + b$ dają tę samą resztę przy dzieleniu przez liczbę pierwszą $p$ . Zatem różnica tych liczb jest podzielna przez $p$

p ∣ [a (k_{0} + j) + b] - [a (k_{0} + i) + b]

czyli

p ∣ a (j - i)

Ponieważ $p ∤ a$ to na mocy lematu Euklidesa (twierdzenie C74), mamy

p ∣ (j - i)

co jest niemożliwe, bo $1 ⩽ j - i ⩽ p - 1 < p$ .

Zatem reszty $r_{1}, r_{2}, \dots, r_{p}$ są wszystkie różne, a ponieważ jest ich $p$ , czyli tyle ile jest różnych reszt z dzielenia przez liczbę $p$ , to zbiór tych reszt jest identyczny ze zbiorem reszt z dzielenia przez $p$ , czyli ze zbiorem $S = {0, 1, 2, \dots, p - 1}$ . W szczególności wynika stąd, że wśród $p$ kolejnych wyrazów ciągu arytmetycznego $a k + b$ jeden z tych wyrazów jest podzielny przez $p$ . Zatem istnieje nieskończenie wiele wyrazów ciągu $a k + b$ , które są podzielne przez $p$ .

Drugi sposób

Problem sprowadza się do wykazania istnienia nieskończenie wielu par liczb naturalnych $(k, n)$ , takich że

a k + b = n p

Co z kolei sprowadza się do badania rozwiązań całkowitych równania

n p - a k = b

Zauważmy, że ponieważ $p ∤ a$ , to liczby $a$ i $p$ są względnie pierwsze. Zatem ich największym wspólnym dzielnikiem jest liczba $1$ . Na mocy twierdzenia C78 równanie to ma nieskończenie wiele rozwiązań w liczbach całkowitych

n = n_{0} + p t

k = k_{0} + a t

gdzie $t$ jest dowolną liczbą całkowitą, a para liczb $(n_{0}, k_{0})$ jest dowolnym rozwiązaniem tego równania. Widzimy, że dla dostatecznie dużych liczb $t$ zawsze możemy uzyskać takie $n$ i $k$ , że $n, k \in Z_{+}$ . Pokazaliśmy w ten sposób, że w ciągu arytmetycznym $a k + b$ istnieje nieskończenie wiele wyrazów podzielnych przez liczbę pierwszą $p$ .

Trzeci sposób

Zauważmy, że ponieważ $p ∤ a$ , to liczby $a$ i $p$ są względnie pierwsze. Zatem ich największym wspólnym dzielnikiem jest liczba $1$ . Lemat Bézouta zapewnia istnienie takich liczb całkowitych $x$ i $y$ , że

a x + p y = 1

Niech $k_{0} = r p - b x$ , gdzie $r$ jest dowolną liczbą całkowitą dodatnią, ale na tyle dużą, aby $k_{0}$ była liczbą dodatnią bez względu na znak iloczynu $b x$ . Łatwo sprawdzamy, że liczba $a k_{0} + b$ jest podzielna przez $p$

a k_{0} + b = a (r p - b x) + b =

= a r p - a b x + b =

= a r p + b (1 - a x) =

= a r p + b p y =

= p (a r + b y)

Zatem w ciągu $a k + b$ istnieje przynajmniej jeden wyraz podzielny przez liczbę pierwszą $p$ . Jeśli tak, to w ciągu arytmetycznym $a k + b$ istnieje nieskończenie wiele liczb podzielnych przez $p$ , bo dla $k = k_{0} + s p$ , gdzie $s \in N$ , mamy

a k + b = a (k_{0} + s p) + b = a s p + (a k_{0} + b)

Czyli $p ∣ a k + b$ .
□

Uwaga C45
Łatwo możemy napisać w PARI/GP funkcję, która zwraca najmniejszą liczbę naturalną $k_{0}$ , dla której wyraz ciągu arytmetycznego $a k + b$ jest podzielny przez $p$ (przy założeniu, że liczby $a$ i $p$ są względnie pierwsze).

f(a,b,p) = lift( Mod(-b,p)*Mod(a,p)^(-1) )

Ciągi nieskończone i liczby pierwsze

Uwaga C46
Choć wiele ciągów jest dobrze znanych i równie dobrze zbadanych, to nie wiemy, czy zawierają one nieskończenie wiele liczb pierwszych. Przykładowo

$1.$	$a_{n} = n^{2} + 1$	A002496
$2.$	$b_{n} = n^{2} - n - 1$	A002327
$3.$	$c_{n} = n^{2} + n + 1$	A002383
$4.$	$d_{n} = n^{4} + 1$	A000068
$5.$	$u_{n} = n! + 1$	A002981
$6.$	$v_{n} = n! - 1$	A002982
$7.$	$M_{n} = 2^{n} - 1$ (liczby Mersenne'a)	A000043
$8.$	$F_{n} = 2^{2^{n}} + 1$ (liczby Fermata)	A019434
$9.$	$F_{n} (a) = a^{2^{n}} + 1$ (uogólnione liczby Fermata, $a$ parzyste)	MathWorld

Nie wiemy, czy istnieje wielomian całkowity $W (n)$ stopnia większego niż jeden taki, że $W (n)$ jest liczbą pierwszą dla nieskończenie wielu liczb $n$ .

Przykład C47
Łatwo sprawdzić, że wartości wielomianu $W (n) = n^{2} + n + 41$ są liczbami pierwszymi dla $1 ⩽ n ⩽ 39$ . Oczywiście $41 ∣ W (41)$ .

Twierdzenie C48
Niech $a, n \in Z_{+}$ i $a ⩾ 2$ . Jeżeli liczba $a^{n} + 1$ jest liczbą pierwszą, to $a$ jest liczbą parzystą i $n = 2^{m}$ .

Dowód

Gdyby liczba $a$ była nieparzysta, to liczba $a^{n} + 1 ⩾ 4$ byłaby parzysta i nie mogłaby być liczbą pierwszą.

Niech wykładnik $n = x y$ będzie liczbą złożoną, a $x$ będzie liczbą nieparzystą. Wtedy

a^{n} + 1 = (a^{y})^{x} + 1

Oznaczając $b = a^{y}$ oraz $x = 2 k + 1$ , otrzymujemy

a^{n} + 1 = (a^{y})^{x} + 1

= b^{x} + 1

= b^{2 k + 1} + 1

= (b + 1) \cdot (1 - b + b^{2} - b^{3} + \dots + b^{2 k - 2} - b^{2 k - 1} + b^{2 k})

Czyli $a^{n} + 1$ jest liczbą złożoną. Wynika stąd, że wykładnik $n$ nie może zawierać czynników nieparzystych, czyli musi być $n = 2^{m}$ . Co należało pokazać.
□

Twierdzenie C49
Dla dowolnej liczby naturalnej $n ⩾ 1$ liczba $x - y$ jest dzielnikiem wyrażenia $x^{n} - y^{n}$ .

Dowód

Indukcja matematyczna. Twierdzenie jest prawdziwe dla $n = 1$ , bo $x - y$ dzieli $x^{1} - y^{1}$ . Załóżmy, że $x - y$ jest dzielnikiem wyrażenia $x^{n} - y^{n}$ , czyli $x^{n} - y^{n} = (x - y) \cdot k$ , otrzymujemy dla $n + 1$

x^{n + 1} - y^{n + 1} = x x^{n} - y x^{n} + y x^{n} - y y^{n} =

= (x - y) x^{n} + y (x^{n} - y^{n}) =

= (x - y) x^{n} + y (x - y) \cdot k =

= (x - y) (x^{n} + y \cdot k)

Czyli $x - y$ jest dzielnikiem $x^{n + 1} - y^{n + 1}$ . Co kończy dowód indukcyjny.
□

Twierdzenie C50
Jeżeli $n ⩾ 2$ oraz $a^{n} - 1$ jest liczbą pierwszą, to $a = 2$ i $n$ jest liczbą pierwszą.

Dowód

Z twierdzenia C49 wiemy, że $x - y ∣ x^{n} - y^{n}$ . W przypadku gdy $a > 2$ mamy

a - 1 ∣ a^{n} - 1

Czyli musi być $a = 2$ . Z tego samego twierdzenia wynika też, że jeżeli $n$ jest liczbą złożoną $n = r s$ , to

2^{r} - 1 ∣ 2^{r s} - 1

bo $a^{r} - b^{r} ∣ (a^{r})^{s} - (b^{r})^{s}$ . Zatem $n$ musi być liczbą pierwszą. Co kończy dowód.
□

Ciągi arytmetyczne liczb pierwszych

Uwaga C51
Ciągi arytmetyczne liczb pierwszych^[11]^[12] zbudowane z dwóch liczb pierwszych nie są interesujące, bo dowolne dwie liczby tworzą ciąg arytmetyczny. Dlatego będziemy się zajmowali ciągami arytmetycznymi liczb pierwszych o długości $n ⩾ 3$ .

Ponieważ nie da się zbudować ciągu arytmetycznego liczb pierwszych o długości $n ⩾ 3$ , w którym pierwszym wyrazem jest liczba $p_{0} = 2$ , to będą nas interesowały ciągi rozpoczynające się od liczby pierwszej $p_{0} ⩾ 3$

Jeżeli do liczby pierwszej nieparzystej dodamy dodatnią liczbę nieparzystą, to otrzymamy liczbę parzystą złożoną, zatem różnica ciągu arytmetycznego $d$ musi być liczbą parzystą, aby zbudowanie jakiegokolwiek ciągu arytmetycznego liczb pierwszych o długości $n ⩾ 3$ było możliwe.

Istnienie nieskończenie wiele ciągów arytmetycznych liczb pierwszych o długości $n = 3$ pokazano już wiele lat temu^[13]. Temat ciągów arytmetycznych liczb pierwszych zyskał na popularności^[14] po udowodnieniu przez Bena Greena i Terence'a Tao twierdzenia o istnieniu dowolnie długich (ale skończonych) ciągów arytmetycznych liczb pierwszych^[15].

Twierdzenie C52* (Ben Green i Terence Tao, 2004)
Dla dowolnej liczby naturalnej $n ⩾ 2$ istnieje nieskończenie wiele $n$ -wyrazowych ciągów arytmetycznych liczb pierwszych.

Przykład C53
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości $n = 3$ i $n = 4$ .

Pokaż tabele

W przypadku $n = 3$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 2 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{8}$ .

W przypadku $n = 4$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 6 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{8}$ .

Jeżeli w tabeli jest wypisanych sześć wartości $p_{0}$ , to oznacza to, że zostało znalezionych co najmniej sześć wartości $p_{0}$ .

$n = 3$
$d$	$p_{0}$
$2$	$3$
$4$	$3$
$6$	$5$	$7$	$11$	$17$	$31$	$41$
$8$	$3$
$10$	$3$
$12$	$5$	$7$	$17$	$19$	$29$	$47$
$14$	$3$
$18$	$5$	$11$	$23$	$43$	$53$	$61$
$20$	$3$
$24$	$5$	$13$	$19$	$23$	$59$	$79$
$28$	$3$
$30$	$7$	$11$	$13$	$23$	$29$	$37$
$34$	$3$
$36$	$7$	$11$	$17$	$31$	$37$	$67$
$38$	$3$
$40$	$3$
$42$	$5$	$17$	$19$	$29$	$47$	$67$
$48$	$5$	$11$	$13$	$31$	$41$	$53$
$50$	$3$
$54$	$5$	$19$	$29$	$43$	$59$	$73$
$60$	$7$	$11$	$19$	$29$	$37$	$43$
$64$	$3$
$66$	$5$	$7$	$17$	$31$	$41$	$47$
$68$	$3$
$72$	$7$	$29$	$37$	$67$	$79$	$107$
$78$	$11$	$23$	$71$	$73$	$101$	$113$
$80$	$3$
$84$	$5$	$13$	$23$	$29$	$43$	$73$
$90$	$11$	$13$	$17$	$19$	$47$	$59$
$94$	$3$
$96$	$5$	$7$	$31$	$41$	$71$	$101$
$98$	$3$
$102$	$7$	$29$	$37$	$47$	$79$	$89$
$104$	$3$
$108$	$23$	$41$	$131$	$163$	$173$	$223$
$110$	$3$
$114$	$13$	$23$	$43$	$53$	$79$	$83$
$120$	$11$	$17$	$29$	$31$	$37$	$43$
$124$	$3$
$126$	$5$	$11$	$31$	$41$	$97$	$101$
$132$	$5$	$7$	$17$	$19$	$47$	$67$
$134$	$3$
$138$	$41$	$61$	$73$	$103$	$113$	$173$
$144$	$5$	$19$	$23$	$29$	$79$	$113$
$150$	$7$	$13$	$17$	$31$	$47$	$73$
$154$	$3$
$156$	$37$	$41$	$67$	$71$	$107$	$127$
$162$	$29$	$107$	$109$	$197$	$239$	$269$
$164$	$3$
$168$	$11$	$13$	$23$	$31$	$43$	$61$
$174$	$5$	$19$	$53$	$83$	$109$	$139$
$178$	$3$
$180$	$13$	$19$	$59$	$61$	$71$	$83$
$186$	$7$	$11$	$37$	$47$	$71$	$107$
$188$	$3$
$190$	$3$
$192$	$5$	$37$	$47$	$59$	$79$	$139$
$198$	$13$	$43$	$53$	$71$	$83$	$113$

$n = 4$
$d$	$p_{0}$
$6$	$5$	$11$	$41$	$61$	$251$	$601$
$12$	$5$	$7$	$17$	$47$	$127$	$227$
$18$	$5$	$43$	$53$	$113$	$313$	$673$
$24$	$59$	$79$	$349$	$419$	$499$	$569$
$30$	$7$	$11$	$13$	$23$	$37$	$41$
$36$	$31$	$241$	$281$	$311$	$751$	$911$
$42$	$5$	$47$	$67$	$97$	$107$	$157$
$48$	$5$	$13$	$53$	$83$	$613$	$643$
$54$	$5$	$19$	$29$	$239$	$379$	$719$
$60$	$11$	$19$	$43$	$47$	$53$	$71$
$66$	$31$	$41$	$241$	$251$	$521$	$541$
$72$	$7$	$67$	$167$	$347$	$947$	$1217$
$78$	$23$	$73$	$113$	$233$	$353$	$443$
$84$	$5$	$29$	$149$	$179$	$379$	$439$
$90$	$11$	$13$	$47$	$61$	$83$	$89$
$96$	$5$	$71$	$101$	$631$	$761$	$1471$
$102$	$7$	$47$	$127$	$257$	$337$	$557$
$108$	$23$	$163$	$223$	$293$	$353$	$643$
$114$	$79$	$349$	$569$	$709$	$1259$	$2039$
$120$	$29$	$37$	$71$	$73$	$107$	$149$
$126$	$5$	$11$	$31$	$41$	$101$	$131$
$132$	$5$	$47$	$67$	$257$	$277$	$487$
$138$	$73$	$173$	$383$	$463$	$563$	$773$
$144$	$29$	$509$	$599$	$1019$	$1579$	$2609$
$150$	$7$	$13$	$17$	$73$	$157$	$163$
$156$	$41$	$151$	$191$	$461$	$571$	$641$
$162$	$107$	$197$	$337$	$967$	$1297$	$1627$
$168$	$43$	$73$	$83$	$103$	$113$	$373$
$174$	$19$	$109$	$139$	$509$	$839$	$929$
$180$	$59$	$61$	$101$	$103$	$281$	$283$
$186$	$11$	$151$	$271$	$281$	$491$	$691$
$192$	$37$	$157$	$307$	$647$	$1087$	$1427$
$198$	$13$	$53$	$83$	$263$	$373$	$853$
$204$	$79$	$149$	$449$	$479$	$569$	$919$
$210$	$13$	$23$	$29$	$47$	$71$	$103$
$216$	$11$	$181$	$761$	$1021$	$1061$	$1231$
$222$	$17$	$157$	$197$	$547$	$617$	$787$
$228$	$43$	$263$	$313$	$593$	$953$	$1093$
$234$	$359$	$499$	$619$	$829$	$1549$	$2309$
$240$	$23$	$41$	$67$	$107$	$139$	$263$
$246$	$31$	$71$	$101$	$331$	$541$	$661$
$252$	$5$	$17$	$97$	$127$	$197$	$257$
$258$	$53$	$313$	$503$	$1103$	$1873$	$3253$
$264$	$19$	$29$	$89$	$199$	$379$	$409$
$270$	$47$	$67$	$229$	$491$	$557$	$613$
$276$	$181$	$191$	$401$	$601$	$661$	$1171$
$282$	$137$	$317$	$457$	$1297$	$1747$	$1787$
$288$	$23$	$43$	$233$	$353$	$463$	$743$
$294$	$59$	$89$	$139$	$269$	$349$	$719$
$300$	$7$	$47$	$53$	$83$	$109$	$139$
$306$	$491$	$691$	$971$	$1321$	$1471$	$2341$
$312$	$127$	$257$	$347$	$547$	$607$	$757$
$318$	$283$	$373$	$653$	$1063$	$1493$	$1823$
$324$	$179$	$349$	$839$	$2389$	$2699$	$2879$
$330$	$23$	$59$	$79$	$101$	$113$	$127$
$336$	$11$	$61$	$281$	$311$	$421$	$491$
$342$	$7$	$67$	$137$	$257$	$467$	$887$
$348$	$5$	$73$	$563$	$593$	$743$	$1373$
$354$	$89$	$239$	$389$	$509$	$659$	$739$
$360$	$7$	$13$	$23$	$37$	$101$	$107$
$366$	$461$	$571$	$1481$	$1511$	$1901$	$2111$
$372$	$7$	$547$	$857$	$877$	$1087$	$2887$
$378$	$53$	$83$	$163$	$313$	$503$	$563$
$384$	$139$	$229$	$719$	$1229$	$1439$	$1699$
$390$	$31$	$43$	$59$	$131$	$157$	$197$
$396$	$5$	$61$	$71$	$431$	$691$	$701$
$402$	$7$	$17$	$167$	$727$	$997$	$1637$
$408$	$13$	$223$	$643$	$683$	$1063$	$1213$
$414$	$269$	$359$	$619$	$1039$	$1879$	$2089$
$420$	$19$	$23$	$37$	$41$	$43$	$47$
$426$	$5$	$131$	$181$	$431$	$761$	$811$
$432$	$227$	$617$	$857$	$997$	$1657$	$1667$
$438$	$5$	$53$	$383$	$1163$	$1303$	$1873$
$444$	$199$	$409$	$1109$	$1669$	$1889$	$2029$
$450$	$11$	$97$	$149$	$193$	$251$	$359$
$456$	$191$	$521$	$631$	$1171$	$1291$	$2341$
$462$	$47$	$107$	$137$	$277$	$307$	$367$
$468$	$193$	$293$	$503$	$683$	$733$	$1013$
$474$	$5$	$29$	$379$	$479$	$719$	$829$
$480$	$7$	$11$	$127$	$347$	$439$	$449$
$486$	$241$	$811$	$941$	$1361$	$1861$	$1871$
$492$	$7$	$107$	$947$	$1607$	$2897$	$3037$
$498$	$73$	$883$	$953$	$983$	$1723$	$1913$
$504$	$89$	$109$	$229$	$359$	$599$	$619$
$510$	$13$	$67$	$83$	$89$	$97$	$167$
$516$	$31$	$61$	$71$	$1181$	$1361$	$1471$
$522$	$47$	$487$	$907$	$1097$	$1237$	$1747$
$528$	$13$	$73$	$443$	$503$	$653$	$1213$
$534$	$839$	$919$	$1019$	$1399$	$1579$	$1619$
$540$	$7$	$17$	$37$	$73$	$101$	$113$
$546$	$31$	$61$	$71$	$401$	$431$	$821$
$552$	$67$	$257$	$277$	$727$	$1427$	$2267$
$558$	$463$	$593$	$673$	$1013$	$1583$	$2243$
$564$	$109$	$179$	$659$	$719$	$859$	$1429$
$570$	$23$	$31$	$73$	$157$	$163$	$241$
$576$	$151$	$401$	$541$	$991$	$1061$	$1091$
$582$	$37$	$127$	$457$	$647$	$967$	$1087$
$588$	$103$	$113$	$223$	$233$	$443$	$613$
$594$	$5$	$89$	$439$	$599$	$839$	$1019$
$600$	$31$	$101$	$173$	$227$	$229$	$239$

□

Przykład C54
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości $n = 5$ i $n = 6$ .

Pokaż tabele

W przypadku $n = 5$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 6 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{8}$ .

W przypadku $n = 6$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 30 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{8}$ .

Jeżeli w tabeli jest wypisanych sześć wartości $p_{0}$ , to oznacza to, że zostało znalezionych co najmniej sześć wartości $p_{0}$ .

$n = 5$
$d$	$p_{0}$
$6$	$5$
$12$	$5$
$30$	$7$	$11$	$37$	$107$	$137$	$151$
$42$	$5$
$48$	$5$
$60$	$11$	$43$	$53$	$71$	$113$	$571$
$90$	$13$	$61$	$83$	$89$	$103$	$503$
$96$	$5$
$120$	$29$	$107$	$239$	$281$	$359$	$379$
$126$	$5$
$150$	$7$	$13$	$17$	$73$	$157$	$223$
$180$	$101$	$103$	$367$	$397$	$577$	$1013$
$210$	$13$	$23$	$47$	$71$	$127$	$157$
$240$	$23$	$263$	$331$	$571$	$823$	$947$
$252$	$5$
$270$	$491$	$557$	$613$	$641$	$743$	$827$
$300$	$83$	$223$	$383$	$419$	$509$	$523$
$330$	$79$	$113$	$127$	$317$	$457$	$491$
$360$	$7$	$13$	$227$	$293$	$349$	$577$
$390$	$59$	$229$	$311$	$619$	$1097$	$1489$
$420$	$19$	$41$	$43$	$67$	$193$	$199$
$426$	$5$
$450$	$11$	$149$	$193$	$599$	$1033$	$1117$
$474$	$5$
$480$	$11$	$347$	$491$	$1019$	$1103$	$1723$
$510$	$13$	$89$	$97$	$167$	$229$	$419$
$540$	$113$	$211$	$281$	$379$	$673$	$919$
$570$	$31$	$157$	$241$	$269$	$647$	$839$
$594$	$5$
$600$	$283$	$311$	$353$	$509$	$1223$	$1531$

$n = 6$
$d$	$p_{0}$
$30$	$7$	$107$	$359$	$541$	$2221$	$6673$
$60$	$11$	$53$	$641$	$5443$	$10091$	$12457$
$90$	$13$	$503$	$1973$	$2351$	$5081$	$10709$
$120$	$239$	$281$	$701$	$2339$	$2437$	$10613$
$150$	$7$	$73$	$157$	$2467$	$4637$	$6079$
$180$	$397$	$1013$	$1307$	$17029$	$20963$	$24337$
$210$	$13$	$47$	$179$	$199$	$257$	$389$
$240$	$23$	$331$	$2207$	$3677$	$5021$	$6323$
$270$	$557$	$1201$	$2377$	$8467$	$9923$	$12107$
$300$	$83$	$223$	$587$	$1511$	$4073$	$4423$
$330$	$127$	$491$	$2129$	$2857$	$3137$	$5153$
$360$	$227$	$577$	$1669$	$9187$	$13331$	$13933$
$390$	$229$	$3701$	$9007$	$9833$	$13291$	$17911$
$420$	$41$	$43$	$193$	$613$	$743$	$1289$
$450$	$149$	$1381$	$1451$	$3607$	$5651$	$8521$
$480$	$11$	$5051$	$8719$	$10567$	$11113$	$13591$
$510$	$97$	$419$	$811$	$3191$	$3583$	$4283$
$540$	$379$	$673$	$3851$	$3907$	$7043$	$12377$
$570$	$269$	$1039$	$2887$	$3853$	$10979$	$11399$
$600$	$8839$	$23371$	$38183$	$44189$	$59743$	$63467$
$630$	$179$	$193$	$1637$	$2267$	$2897$	$4813$
$660$	$163$	$317$	$401$	$2753$	$3229$	$5077$
$690$	$277$	$1523$	$6101$	$10427$	$15971$	$27059$
$720$	$1231$	$3793$	$4003$	$6229$	$7573$	$10079$
$750$	$1051$	$1289$	$1583$	$2857$	$12377$	$18523$
$780$	$1151$	$3517$	$3923$	$4637$	$5309$	$9929$
$810$	$1993$	$7817$	$11443$	$17519$	$52631$	$109919$
$840$	$97$	$313$	$1061$	$1753$	$1901$	$2593$
$870$	$2039$	$2179$	$5273$	$5987$	$9431$	$10957$
$900$	$1747$	$12541$	$14767$	$21193$	$31511$	$40289$
$930$	$7$	$293$	$9043$	$10247$	$34327$	$38891$
$960$	$4943$	$8737$	$15373$	$28351$	$35393$	$36919$
$990$	$1249$	$1319$	$2467$	$2957$	$4049$	$8291$
$1020$	$887$	$929$	$2441$	$4639$	$15083$	$19997$
$1050$	$53$	$257$	$443$	$839$	$1103$	$3469$
$1080$	$1423$	$9011$	$10663$	$27799$	$36493$	$51473$
$1110$	$3847$	$9643$	$10357$	$11743$	$16223$	$21977$
$1140$	$1063$	$1301$	$1553$	$1777$	$5683$	$6397$
$1170$	$379$	$701$	$911$	$2143$	$2297$	$2857$
$1200$	$367$	$2677$	$3391$	$18749$	$34961$	$59699$
$1230$	$2539$	$6053$	$6823$	$9091$	$12101$	$14831$
$1260$	$359$	$617$	$739$	$1051$	$1619$	$1931$
$1290$	$149$	$17747$	$20981$	$24481$	$46643$	$47917$
$1320$	$53$	$977$	$991$	$2237$	$9461$	$20983$
$1350$	$811$	$937$	$3877$	$14923$	$16001$	$18493$
$1380$	$3613$	$9227$	$15541$	$16927$	$17417$	$18089$
$1410$	$367$	$2593$	$12421$	$50599$	$60889$	$80629$
$1440$	$439$	$6277$	$20753$	$21929$	$39079$	$57727$
$1470$	$1279$	$1877$	$2383$	$2393$	$2749$	$2801$
$1500$	$7331$	$8423$	$15493$	$28513$	$31607$	$38453$
$1530$	$2741$	$3203$	$8537$	$14389$	$20143$	$21277$
$1560$	$419$	$727$	$3499$	$3919$	$6257$	$9029$
$1590$	$2213$	$2339$	$4523$	$6469$	$9241$	$9857$
$1620$	$7717$	$9103$	$12379$	$37607$	$43613$	$46567$
$1650$	$19$	$3001$	$3659$	$4051$	$4289$	$11527$
$1680$	$197$	$997$	$1289$	$1319$	$2309$	$2683$
$1710$	$373$	$1549$	$1913$	$2711$	$12539$	$15031$
$1740$	$1621$	$5387$	$6269$	$15551$	$61723$	$77543$
$1770$	$1483$	$13691$	$15329$	$20873$	$23869$	$29917$
$1800$	$421$	$967$	$1499$	$6217$	$30983$	$37171$
$1830$	$31$	$17909$	$46567$	$89057$	$105619$	$128341$
$1860$	$5087$	$6151$	$9133$	$16567$	$23819$	$29881$
$1890$	$23$	$727$	$1109$	$1279$	$1409$	$1543$
$1920$	$79$	$1493$	$13967$	$19973$	$41351$	$46867$
$1950$	$3259$	$4813$	$8803$	$12373$	$13577$	$13619$
$1980$	$1511$	$3863$	$4969$	$5039$	$7027$	$9337$
$2010$	$1303$	$3739$	$7309$	$13763$	$22093$	$31151$
$2040$	$1039$	$6779$	$7507$	$8963$	$10069$	$12281$
$2070$	$1097$	$2063$	$2917$	$4289$	$6571$	$11149$
$2100$	$29$	$281$	$757$	$1459$	$1847$	$2503$
$2130$	$3677$	$5077$	$11699$	$17159$	$21149$	$31159$
$2160$	$5849$	$6619$	$24329$	$43019$	$114419$	$126823$
$2190$	$643$	$4283$	$4339$	$23743$	$24821$	$30211$
$2220$	$4229$	$11243$	$11467$	$12503$	$13693$	$26209$
$2250$	$4721$	$6359$	$17321$	$19477$	$21661$	$23117$
$2280$	$719$	$2399$	$15797$	$22391$	$23189$	$27809$
$2310$	$37$	$71$	$83$	$547$	$661$	$859$
$2340$	$107$	$4363$	$5483$	$9613$	$12413$	$14737$
$2370$	$1187$	$1831$	$4211$	$7963$	$9419$	$15607$
$2400$	$503$	$853$	$4787$	$15091$	$20327$	$23603$
$2430$	$13217$	$31039$	$38851$	$43261$	$46747$	$67481$
$2460$	$227$	$1459$	$6779$	$6863$	$18553$	$29207$
$2490$	$1237$	$7621$	$14411$	$19801$	$46457$	$55921$
$2520$	$113$	$709$	$1013$	$1181$	$1303$	$1409$
$2550$	$1871$	$9403$	$33203$	$36241$	$70009$	$74587$
$2580$	$277$	$6101$	$29383$	$35851$	$55871$	$61723$
$2610$	$5179$	$8539$	$8861$	$10093$	$15679$	$17989$
$2640$	$9283$	$10781$	$12377$	$12433$	$13679$	$22751$
$2670$	$1039$	$4133$	$12589$	$14731$	$16411$	$23789$
$2700$	$8629$	$10267$	$16217$	$17477$	$18149$	$19843$
$2730$	$19$	$631$	$761$	$811$	$1091$	$1423$
$2760$	$7$	$2473$	$2767$	$9137$	$9403$	$9767$
$2790$	$6899$	$15733$	$20353$	$20899$	$23447$	$29201$
$2820$	$727$	$1259$	$3023$	$7951$	$17989$	$20201$
$2850$	$379$	$463$	$2843$	$4831$	$9661$	$10067$
$2880$	$1459$	$2803$	$4973$	$7283$	$8543$	$12281$
$2910$	$397$	$12409$	$19087$	$25121$	$37441$	$41081$
$2940$	$17$	$383$	$691$	$983$	$2393$	$2797$
$2970$	$1031$	$2879$	$3593$	$5147$	$6029$	$6673$
$3000$	$907$	$35543$	$45413$	$60337$	$65713$	$89009$

□

Przykład C55
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości $n = 7$ i $n = 8$ .

Pokaż tabele

W przypadku $n = 7$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 30 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{8}$ .

W przypadku $n = 8$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 210 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{8}$ .

Jeżeli w tabeli jest wypisanych sześć wartości $p_{0}$ , to oznacza to, że zostało znalezionych co najmniej sześć wartości $p_{0}$ .

$n = 7$
$d$	$p_{0}$
$150$	$7$
$210$	$47$	$179$	$199$	$409$	$619$	$829$
$420$	$193$	$1619$	$2239$	$2659$	$4259$	$5849$
$630$	$1637$	$2267$	$5569$	$8369$	$11003$	$11633$
$840$	$1061$	$1753$	$3623$	$4493$	$5651$	$6043$
$1050$	$53$	$3469$	$6653$	$8629$	$8783$	$8837$
$1260$	$359$	$1931$	$2063$	$3323$	$4583$	$13933$
$1470$	$1279$	$2393$	$2801$	$8117$	$8191$	$9661$
$1680$	$1289$	$1319$	$2683$	$2969$	$11261$	$12941$
$1890$	$1279$	$1723$	$1811$	$1879$	$2693$	$4583$
$2100$	$1847$	$3947$	$26497$	$34913$	$35771$	$36187$
$2310$	$71$	$547$	$1019$	$1063$	$1367$	$1747$
$2520$	$113$	$1181$	$1409$	$5413$	$7109$	$7933$
$2730$	$631$	$811$	$1091$	$2417$	$3643$	$3821$
$2760$	$7$
$2940$	$17$	$6317$	$6911$	$9433$	$11927$	$12373$

$n = 8$
$d$	$p_{0}$
$210$	$199$	$409$	$619$	$881$	$3499$	$3709$
$420$	$2239$	$10243$	$18493$	$29297$	$39199$	$40343$
$630$	$1637$	$11003$	$38693$	$53161$	$56477$	$198971$
$840$	$6043$	$6883$	$10861$	$11701$	$84521$	$103837$
$1050$	$8837$	$41507$	$246289$	$302273$	$382727$	$499679$
$1260$	$2063$	$3323$	$87511$	$145949$	$208099$	$213247$
$1470$	$8191$	$15289$	$101027$	$102497$	$187931$	$227399$
$1680$	$1289$	$11261$	$31333$	$33013$	$133919$	$193283$
$1890$	$2693$	$15493$	$15607$	$17497$	$45767$	$47657$
$2100$	$1847$	$34913$	$37013$	$39113$	$83311$	$102871$
$2310$	$1019$	$3823$	$5557$	$6133$	$7853$	$9941$
$2520$	$5413$	$7109$	$19141$	$21661$	$23509$	$24763$
$2730$	$1091$	$4721$	$7451$	$22079$	$49339$	$53759$
$2940$	$9433$	$11927$	$14867$	$50587$	$80933$	$127207$
$3150$	$433$	$3583$	$7877$	$24677$	$27827$	$49031$
$3360$	$6571$	$9041$	$39791$	$210391$	$213751$	$217111$
$3570$	$8971$	$10429$	$27737$	$28387$	$37313$	$57047$
$3780$	$45767$	$82037$	$155569$	$473513$	$477293$	$511873$
$3990$	$1699$	$2909$	$5689$	$25033$	$29873$	$40559$
$4200$	$12547$	$16747$	$37013$	$57139$	$89899$	$94099$
$4410$	$20809$	$87623$	$142271$	$262733$	$267143$	$439009$
$4620$	$103$	$1531$	$3083$	$3257$	$6427$	$9461$
$4830$	$3907$	$13313$	$30427$	$35257$	$40087$	$72547$
$5040$	$13477$	$14951$	$25073$	$25931$	$30113$	$57457$
$5250$	$3413$	$8663$	$44179$	$49429$	$111109$	$648107$
$5460$	$1559$	$18899$	$36389$	$43711$	$59393$	$75541$
$5670$	$187477$	$231109$	$402137$	$680123$	$706463$	$712133$
$5880$	$73$	$29959$	$152389$	$158269$	$317021$	$2115961$
$6090$	$12239$	$22469$	$38543$	$50893$	$72533$	$90863$
$6300$	$37097$	$86869$	$92639$	$224633$	$440269$	$641327$
$6510$	$1063$	$20599$	$21701$	$27109$	$41611$	$46187$
$6720$	$3167$	$7457$	$22669$	$62347$	$69067$	$75787$
$6930$	$17$	$5581$	$6947$	$7151$	$13469$	$14081$
$7140$	$3347$	$53309$	$281557$	$370879$	$380447$	$466897$
$7350$	$206047$	$348163$	$363037$	$435661$	$576677$	$906107$
$7560$	$29387$	$36947$	$39191$	$44267$	$342389$	$349949$
$7770$	$6553$	$14323$	$25169$	$28549$	$36319$	$42061$
$7980$	$137$	$4091$	$7237$	$8117$	$12071$	$24029$
$8190$	$3593$	$21017$	$35591$	$43781$	$49727$	$59021$
$8400$	$86599$	$173909$	$788413$	$1251869$	$1365019$	$1392731$
$8610$	$541$	$1867$	$63703$	$132283$	$140893$	$175837$
$8820$	$9403$	$83563$	$84421$	$93241$	$187823$	$296983$
$9030$	$11087$	$195203$	$219799$	$352813$	$426973$	$487651$
$9240$	$199$	$937$	$10177$	$21031$	$27961$	$30271$
$9450$	$1609$	$157181$	$182867$	$663049$	$1028479$	$1037929$
$9660$	$521$	$3449$	$10181$	$50417$	$84229$	$218363$
$9870$	$61$	$43013$	$89923$	$220333$	$294479$	$490493$
$10080$	$6949$	$17029$	$54293$	$99023$	$125353$	$125899$
$10290$	$6143$	$16433$	$179057$	$211777$	$681949$	$1018357$
$10500$	$9109$	$91153$	$218527$	$447817$	$513167$	$1113239$
$10710$	$9419$	$28603$	$28871$	$37861$	$43691$	$75041$
$10920$	$14657$	$21491$	$52321$	$63241$	$79997$	$80621$
$11130$	$49681$	$70607$	$187009$	$198139$	$209269$	$219613$
$11340$	$24197$	$57143$	$68483$	$158617$	$212297$	$237257$
$11550$	$4483$	$4673$	$9619$	$16223$	$21169$	$66161$
$11760$	$3511$	$241793$	$469613$	$517949$	$548263$	$643469$
$11970$	$6221$	$10531$	$22501$	$40343$	$216233$	$280187$
$12180$	$18211$	$65437$	$126943$	$137239$	$149939$	$361213$
$12390$	$7477$	$24391$	$41669$	$76913$	$95213$	$181211$
$12600$	$26003$	$435577$	$448177$	$558431$	$571031$	$583631$
$12810$	$19289$	$35437$	$40949$	$53791$	$59357$	$94309$
$13020$	$15913$	$55843$	$77773$	$179519$	$418927$	$670853$
$13230$	$5843$	$7433$	$9391$	$31729$	$40543$	$53773$
$13440$	$2141$	$15581$	$270143$	$335021$	$405269$	$448741$
$13650$	$3343$	$12097$	$16993$	$19259$	$63611$	$81001$
$13860$	$6029$	$6211$	$26171$	$27653$	$32441$	$51839$
$14070$	$40879$	$87793$	$87991$	$159491$	$285497$	$485389$
$14280$	$6947$	$15923$	$27337$	$79481$	$111227$	$364687$
$14490$	$41039$	$48491$	$142049$	$144667$	$159157$	$161263$
$14700$	$12409$	$36583$	$51283$	$161363$	$218989$	$578267$
$14910$	$23957$	$74161$	$79633$	$89071$	$109367$	$120977$
$15120$	$33997$	$121853$	$136973$	$203429$	$330413$	$379369$
$15330$	$12781$	$64613$	$505559$	$588529$	$614071$	$873121$
$15540$	$15053$	$33071$	$41131$	$160781$	$176321$	$209357$
$15750$	$7001$	$10459$	$64579$	$80329$	$103409$	$119159$
$15960$	$1847$	$6037$	$17807$	$21997$	$33767$	$71917$
$16170$	$32321$	$66179$	$82349$	$99661$	$130343$	$219451$
$16380$	$22859$	$28579$	$43759$	$43913$	$60139$	$95107$
$16590$	$6703$	$23293$	$29009$	$45599$	$51341$	$57917$
$16800$	$91463$	$276037$	$524857$	$874063$	$940319$	$957119$
$17010$	$6571$	$70529$	$117037$	$227147$	$797119$	$814129$
$17220$	$120713$	$225769$	$242989$	$343601$	$819229$	$965711$
$17430$	$4219$	$6101$	$15643$	$25471$	$33073$	$42901$
$17640$	$12917$	$34877$	$59407$	$62047$	$85667$	$193607$
$17850$	$9803$	$129379$	$147229$	$238229$	$270157$	$289253$
$18060$	$87613$	$90583$	$117223$	$512671$	$574297$	$623353$
$18270$	$29567$	$47837$	$86491$	$268189$	$424819$	$511201$
$18480$	$1861$	$2711$	$8093$	$10831$	$11161$	$11909$
$18690$	$881$	$19571$	$79531$	$529829$	$654767$	$812353$
$18900$	$6899$	$23201$	$52267$	$73823$	$92723$	$462079$
$19110$	$8941$	$30091$	$39367$	$58603$	$63737$	$80611$
$19320$	$6857$	$218761$	$236699$	$237733$	$300319$	$300499$
$19530$	$33829$	$46183$	$50929$	$70459$	$283859$	$361651$
$19740$	$1117$	$2729$	$22469$	$30757$	$50497$	$165391$
$19950$	$13339$	$23767$	$44549$	$47791$	$92399$	$142699$
$20160$	$2857$	$5821$	$147089$	$948263$	$1044859$	$1094123$
$20370$	$81649$	$154073$	$164239$	$398539$	$443881$	$556123$
$20580$	$9689$	$30269$	$105379$	$316501$	$337081$	$398023$
$20790$	$12713$	$20023$	$33503$	$40813$	$69829$	$92251$
$21000$	$5501$	$19471$	$26501$	$29153$	$40471$	$56773$

□

Przykład C56
Tabela zawiera przykładowe ciągi arytmetyczne liczb pierwszych o długości $n = 9$ i $n = 10$ .

Pokaż tabele

W przypadku $n = 9$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 210 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{9}$ .

W przypadku $n = 10$ wyszukiwanie ciągów zostało przeprowadzone dla $d = 210 k$ , gdzie $1 ⩽ k ⩽ 100$ i (przy ustalonym $d$ ) dla kolejnych liczb pierwszych $p_{0} ⩽ 10^{10}$ .

Jeżeli w tabeli jest wypisanych sześć wartości $p_{0}$ , to oznacza to, że zostało znalezionych co najmniej sześć wartości $p_{0}$ .

$n = 9$
$d$	$p_{0}$
$210$	$199$	$409$	$3499$	$10859$	$564973$	$1288607$
$420$	$52879$	$53299$	$56267$	$61637$	$3212849$	$3544939$
$630$	$279857$	$514949$	$939359$	$964417$	$965047$	$1003819$
$840$	$6043$	$10861$	$103837$	$201781$	$915611$	$916451$
$1050$	$26052251$	$33267943$	$54730813$	$87640921$	$112704443$	$115677517$
$1260$	$2063$	$1040089$	$2166511$	$2202547$	$4152847$	$4400639$
$1470$	$101027$	$363949$	$1936289$	$2534561$	$2536031$	$3248197$
$1680$	$31333$	$216947$	$258527$	$316621$	$607109$	$4635361$
$1890$	$15607$	$45767$	$194113$	$534211$	$997201$	$1442173$
$2100$	$34913$	$37013$	$102871$	$176087$	$581393$	$583493$
$2310$	$3823$	$60317$	$80761$	$563117$	$574813$	$1215583$
$2520$	$19141$	$23509$	$1058597$	$1061117$	$1465993$	$5650097$
$2730$	$4721$	$65881$	$122069$	$123059$	$124799$	$125789$
$2940$	$11927$	$145723$	$1222279$	$12424921$	$23527081$	$33820273$
$3150$	$433$	$24677$	$49031$	$348763$	$1243393$	$1640071$
$3360$	$210391$	$213751$	$245173$	$1863509$	$3831437$	$6470249$
$3570$	$57047$	$133271$	$150343$	$153913$	$399433$	$920827$
$3780$	$473513$	$1282607$	$3536881$	$4045763$	$4049543$	$5655283$
$3990$	$1699$	$99877$	$103867$	$649217$	$1614973$	$2732441$
$4200$	$12547$	$89899$	$835721$	$2544221$	$5013919$	$11254637$
$4410$	$262733$	$439009$	$12940541$	$15091459$	$27878321$	$29196199$
$4620$	$55697$	$64919$	$85363$	$89983$	$217409$	$372751$
$4830$	$30427$	$35257$	$72547$	$351749$	$2985809$	$6020477$
$5040$	$25073$	$57457$	$531359$	$1245479$	$2491381$	$7136659$
$5250$	$3413$	$44179$	$2117239$	$2122489$	$2649067$	$4895993$
$5460$	$144779$	$913921$	$1280987$	$2243491$	$2283571$	$2289031$
$5670$	$706463$	$915221$	$10882211$	$21206993$	$21212663$	$23859467$
$5880$	$152389$	$4896887$	$6559873$	$9131321$	$19210043$	$24248461$
$6090$	$206191$	$357661$	$517003$	$1910927$	$5835283$	$10292729$
$6300$	$641327$	$1962449$	$2797723$	$3626881$	$4663249$	$5601139$
$6510$	$20599$	$155461$	$161971$	$573437$	$4395739$	$6457669$
$6720$	$62347$	$69067$	$5072869$	$9545051$	$10379081$	$11184743$
$6930$	$17$	$7151$	$13469$	$36469$	$38261$	$309167$
$7140$	$1241197$	$1247479$	$2614559$	$4496813$	$4575947$	$7799837$
$7350$	$1445303$	$8526533$	$12683299$	$12690649$	$21459209$	$21466559$
$7560$	$29387$	$342389$	$539839$	$2141497$	$7573327$	$7580887$
$7770$	$6553$	$28549$	$36319$	$90373$	$819317$	$827087$
$7980$	$137$	$4091$	$24029$	$31393$	$165313$	$182687$
$8190$	$35591$	$59021$	$287629$	$401627$	$410257$	$702323$
$8400$	$6127909$	$8133469$	$8528483$	$8536883$	$14448397$	$19175929$
$8610$	$132283$	$2164387$	$6903121$	$10892747$	$10901357$	$17489623$
$8820$	$84421$	$466451$	$3052177$	$3905777$	$11397371$	$53189407$
$9030$	$2630153$	$4927921$	$5686141$	$6043399$	$8411567$	$8510357$
$9240$	$937$	$21031$	$53681$	$62921$	$95339$	$495791$
$9450$	$1028479$	$1832711$	$8104549$	$15802459$	$43975031$	$97126691$
$9660$	$521$	$464413$	$707071$	$716731$	$1197121$	$1259053$
$9870$	$576439$	$1115923$	$7516427$	$9249301$	$16561691$	$16571561$
$10080$	$6949$	$125353$	$156941$	$949517$	$3363089$	$3373169$
$10290$	$6143$	$1535489$	$2477177$	$4259887$	$5294563$	$10818191$
$10500$	$1113239$	$1841087$	$7005059$	$8026327$	$13707959$	$22837799$
$10710$	$314299$	$439123$	$735467$	$1784911$	$1923049$	$2781203$
$10920$	$52321$	$285521$	$527909$	$538829$	$1673941$	$2214349$
$11130$	$187009$	$198139$	$255803$	$547499$	$2160253$	$11518723$
$11340$	$57143$	$559051$	$1091561$	$10756139$	$13865323$	$13876663$
$11550$	$4673$	$9619$	$89659$	$112643$	$155317$	$166601$
$11760$	$3458731$	$5759843$	$6305939$	$6904789$	$11527693$	$15296227$
$11970$	$10531$	$1911199$	$2210573$	$2298397$	$15519563$	$21608347$
$12180$	$1067597$	$1778461$	$1784599$	$3551221$	$7384493$	$12485003$
$12390$	$184291$	$651017$	$804493$	$1536187$	$4158103$	$4751293$
$12600$	$435577$	$558431$	$571031$	$727369$	$2890117$	$3367363$
$12810$	$116953$	$166909$	$5627029$	$6623117$	$10981339$	$10994149$
$13020$	$1691411$	$3574871$	$22963981$	$27098723$	$29812603$	$31218403$
$13230$	$40543$	$104651$	$313219$	$4705247$	$4718477$	$6268289$
$13440$	$2141$	$448741$	$815261$	$1560997$	$1574437$	$2070517$
$13650$	$3343$	$96997$	$110647$	$521047$	$1590961$	$2276503$
$13860$	$110437$	$124297$	$138157$	$148891$	$152017$	$152947$
$14070$	$2679239$	$2886281$	$3817111$	$6446353$	$6460423$	$6976289$
$14280$	$364687$	$749773$	$1867573$	$2146181$	$2434997$	$4112627$
$14490$	$144667$	$161263$	$259603$	$286333$	$336251$	$377809$
$14700$	$36583$	$578267$	$8529749$	$14365553$	$14380253$	$14830787$
$14910$	$74161$	$109367$	$120977$	$1260011$	$1372211$	$11898287$
$15120$	$121853$	$689459$	$822383$	$11354437$	$37245407$	$48384221$
$15330$	$7713709$	$8049187$	$11583113$	$12934973$	$16769749$	$30793649$
$15540$	$160781$	$580577$	$4095187$	$5838409$	$9523079$	$10473559$
$15750$	$64579$	$103409$	$182587$	$849869$	$865619$	$1468729$
$15960$	$1847$	$6037$	$17807$	$137147$	$652969$	$989977$
$16170$	$66179$	$219451$	$511843$	$583421$	$812431$	$848567$
$16380$	$43759$	$339263$	$355643$	$695047$	$2011517$	$2893309$
$16590$	$6703$	$29009$	$2489183$	$4028743$	$9340181$	$10005263$
$16800$	$940319$	$3772907$	$3873007$	$9905921$	$79622351$	$95679271$
$17010$	$797119$	$18296627$	$23152907$	$38133913$	$60796007$	$83709047$
$17220$	$225769$	$1452511$	$1469731$	$1606379$	$2415473$	$3469069$
$17430$	$15643$	$25471$	$42901$	$1170599$	$3120547$	$3983249$
$17640$	$193607$	$211247$	$7624613$	$10290239$	$16104047$	$22618907$
$17850$	$129379$	$289253$	$1341433$	$1728911$	$1746761$	$2918737$
$18060$	$1013921$	$1038209$	$2703941$	$3580333$	$3914689$	$11110339$
$18270$	$29567$	$511201$	$1615723$	$1890701$	$1989811$	$2008081$
$18480$	$2711$	$25643$	$40853$	$149143$	$194839$	$213319$
$18690$	$881$	$9421469$	$10687877$	$11455753$	$14740463$	$21499799$
$18900$	$73823$	$462079$	$804113$	$823013$	$1323799$	$1370987$
$19110$	$63737$	$322171$	$520193$	$999763$	$1023487$	$1032067$
$19320$	$682411$	$743747$	$1343669$	$1373233$	$1782499$	$2574437$
$19530$	$50929$	$738919$	$1773689$	$1793219$	$6121807$	$18867007$
$19740$	$2729$	$30757$	$360163$	$1652591$	$18160973$	$18862889$
$19950$	$142699$	$162649$	$239957$	$302287$	$322237$	$661547$
$20160$	$3330211$	$5620609$	$6413401$	$15055609$	$32094917$	$52863893$
$20370$	$1158881$	$1216213$	$1236583$	$3893899$	$7991839$	$8012209$
$20580$	$9689$	$316501$	$398023$	$2047813$	$2219557$	$2240137$
$20790$	$12713$	$20023$	$141079$	$159571$	$296117$	$914813$
$21000$	$5501$	$19471$	$65837$	$688139$	$3980407$	$8983031$

$n = 10$
$d$	$p_{0}$
$210$	$199$	$243051733$	$498161423$	$2490123989$	$5417375591$	$8785408259$
$420$	$52879$	$3544939$	$725283077$	$1580792347$	$1931425157$	$8392393693$
$630$	$964417$	$1021331$	$3710699$	$174610351$	$396598051$	$525173641$
$840$	$915611$	$24748189$	$33791509$	$314727967$	$510756371$	$1079797657$
$1050$	$130006783$	$208734751$	$400663741$	$963551671$	$1219200119$	$1231110787$
$1260$	$6722909$	$27846803$	$63289771$	$1000262819$	$1476482057$	$4565705117$
$1470$	$2534561$	$189999707$	$833570987$	$1168004581$	$2010828277$	$3182258251$
$1680$	$1343205113$	$3033769813$	$4093882757$	$4112814241$	$4348188919$	$4749575333$
$1890$	$41513261$	$95317913$	$6232033069$	$6361761239$	$6709899029$	$8521839071$
$2100$	$34913$	$581393$	$8397091$	$10200607$	$31913837$	$258411317$
$2310$	$2564251$	$7245143$	$15898823$	$34834237$	$51404371$	$60858179$
$2520$	$1058597$	$8226307$	$438716653$	$799422581$	$975166567$	$983999677$
$2730$	$122069$	$123059$	$158633$	$3319219$	$3427393$	$5082629$
$2940$	$2546781317$	$3736609957$	$4895747497$
$3150$	$34071019$	$1174379903$	$1247572429$	$1914733781$	$5502174781$	$5598860513$
$3360$	$210391$	$762261571$	$2289797801$	$5842998881$	$5973997177$	$6486241481$
$3570$	$150343$	$920827$	$47896129$	$110935963$	$124813783$	$253908793$
$3780$	$4045763$	$162045979$	$3611162221$	$3953439013$	$5751477079$	$6389572141$
$3990$	$99877$	$2732441$	$145829681$	$1512868211$	$1519374557$	$1905288811$
$4200$	$75187297$	$436800197$	$825073159$	$953483507$	$1237285949$	$1620977257$
$4410$	$343475219$	$718394137$	$1714841501$	$4312513897$	$4433557501$	$7302174197$
$4620$	$85363$	$372751$	$926879$	$10645541$	$11022827$	$11027447$
$4830$	$30427$	$6020477$	$16424981$	$151254533$	$229780123$	$482610239$
$5040$	$145866041$	$226851517$	$292104419$	$517266257$	$986618569$	$1785262393$
$5250$	$2117239$	$134051459$	$444256783$	$635071121$	$3239335223$	$3689988833$
$5460$	$2283571$	$11988607$	$17327831$	$18230447$	$97175423$	$168445523$
$5670$	$21206993$	$42322087$	$232282121$	$530515507$	$2074726021$	$2176462667$
$5880$	$769792447$	$1028745119$	$2716511507$	$2850255403$	$4059527753$	$4338343433$
$6090$	$98202331$	$218657237$	$508050341$	$965528153$	$1963343323$	$2133623147$
$6300$	$46452799$	$161073877$	$416581987$	$444443777$	$799148171$	$1536915817$
$6510$	$155461$	$11699279$	$59259649$	$82736531$	$138908647$	$156852947$
$6720$	$62347$	$18249241$	$402509117$	$646946233$	$694032349$	$748855249$
$6930$	$1664417$	$3306839$	$6703841$	$10343167$	$16988767$	$17046329$
$7140$	$12331793$	$21994589$	$32695477$	$135554233$	$355138829$	$730901161$
$7350$	$12683299$	$21459209$	$38446267$	$423264613$	$3158377081$	$5208862573$
$7560$	$7573327$	$369901513$	$2755541693$	$2774476609$	$3311703233$	$5004136327$
$7770$	$28549$	$819317$	$3721051$	$11941571$	$35273473$	$46949093$
$7980$	$1024853$	$355670309$	$446786191$	$547343483$	$682871447$	$1772834893$
$8190$	$7328437$	$15275849$	$17503261$	$22737017$	$27294053$	$45150331$
$8400$	$8528483$	$40313929$	$243787771$	$385895737$	$467671013$	$797154607$
$8610$	$10892747$	$17489623$	$28416517$	$55350017$	$200631439$	$449962543$
$8820$	$275550449$	$340210649$	$375439381$	$1299902701$	$7189505563$	$8000213747$
$9030$	$31057003$	$150282967$	$634308509$	$643690123$	$2295863833$	$2515095703$
$9240$	$53681$	$14224981$	$14432399$	$23559377$	$28467293$	$42049001$
$9450$	$334554023$	$488051653$	$2038389299$	$2162899399$	$2445407273$	$3057392207$
$9660$	$707071$	$125628439$	$303544463$	$441911263$	$449336813$	$511484261$
$9870$	$16561691$	$26691349$	$373909451$	$558247033$	$626630117$	$1074793063$
$10080$	$3363089$	$35937059$	$57814343$	$83864653$	$264068017$	$2293066417$
$10290$	$459609859$	$522069971$	$535273337$	$720980111$	$1617247087$	$1769323693$
$10500$	$38610347$	$185388121$	$511207351$	$512002717$	$573447551$	$728734969$
$10710$	$2781203$	$10327159$	$15741997$	$161184019$	$290334601$	$387848743$
$10920$	$527909$	$8754457$	$19711711$	$68442943$	$70092481$	$108555763$
$11130$	$187009$	$74743931$	$1717072597$	$2241197341$	$3885152797$	$5442728839$
$11340$	$13865323$	$151172779$	$155052347$	$169766761$	$417004037$	$759377761$
$11550$	$166601$	$178151$	$189701$	$2902951$	$2939267$	$6906061$
$11760$	$15296227$	$115733179$	$793412467$	$2045327461$	$3317282629$	$3405094727$
$11970$	$70627031$	$81131437$	$190977547$	$295424263$	$435613939$	$436230467$
$12180$	$96579871$	$196123667$	$1414855181$	$1594532899$	$1852156771$	$5477685029$
$12390$	$355974491$	$1228212781$	$1597738157$	$2356239043$	$2537515919$	$2664004501$
$12600$	$558431$	$4885897$	$62631409$	$222308641$	$247236973$	$597208309$
$12810$	$10981339$	$73391203$	$614195423$	$722428933$	$1804485667$	$2011342889$
$13020$	$37278391$	$396360829$	$477013687$	$1035592279$	$1668997513$	$1740405707$
$13230$	$4705247$	$43971617$	$150462859$	$3214143193$	$4385611183$	$6156888427$
$13440$	$1560997$	$2070517$	$319796189$	$397320779$	$534628103$	$1466338729$
$13650$	$96997$	$8628157$	$23309989$	$84831493$	$95865989$	$183786877$
$13860$	$110437$	$124297$	$138157$	$152947$	$166807$	$180667$
$14070$	$6446353$	$6976289$	$9167027$	$315420997$	$324294169$	$850130293$
$14280$	$8022137$	$46017523$	$49573471$	$84264127$	$201286747$	$664107853$
$14490$	$4421849$	$7258067$	$55181701$	$266196461$	$400560449$	$658093439$
$14700$	$14365553$	$79088123$	$578429339$	$1590374273$	$1620663103$	$1692678277$
$14910$	$1313271217$	$1398822683$	$3458123993$	$5050258823$	$8564509277$
$15120$	$643929523$	$1697175937$	$3456724013$	$3604668029$	$5105194837$	$5972188679$
$15330$	$423644591$	$792183047$	$1013912467$	$1239474463$	$1707297247$	$1918187839$
$15540$	$15113711$	$49877209$	$90195289$	$113317157$	$542625751$	$801528769$
$15750$	$849869$	$281904709$	$741349123$	$1196157763$	$1264569469$	$1628362679$
$15960$	$1847$	$3178141$	$47378869$	$105168887$	$140273363$	$315104063$
$16170$	$3360767$	$7292851$	$8511059$	$10038841$	$26643899$	$35098631$
$16380$	$339263$	$2893309$	$7118387$	$189387287$	$209606629$	$266620267$
$16590$	$381816437$	$695288453$	$1555003309$	$2096563163$	$2844269837$	$4876784057$
$16800$	$143614397$	$681135667$	$1337835403$	$1547432483$	$1809315247$	$2850704453$
$17010$	$83709047$	$1041057263$	$1265416651$	$1665987569$	$2529254831$	$4576482871$
$17220$	$1452511$	$10612519$	$16814099$	$216348577$	$382728461$	$532388587$
$17430$	$25471$	$137293657$	$632342783$	$960368107$	$5503090291$	$6704824913$
$17640$	$193607$	$33411011$	$511632469$	$819466853$	$960062011$	$1178974859$
$17850$	$1728911$	$4584401$	$7627309$	$77294621$	$99462899$	$170832131$
$18060$	$51826531$	$210101329$	$235062067$	$605501191$	$1083324911$	$2230437163$
$18270$	$1989811$	$825611753$	$2281896011$	$2468212757$	$2968471043$	$4958366753$
$18480$	$194839$	$1044739$	$1075237$	$2169967$	$2467369$	$3135841$
$18690$	$90365419$	$551760331$	$1165944209$	$1887703247$	$1932471091$	$3396823123$
$18900$	$804113$	$1087721813$	$2462595313$	$3420103007$	$5068097201$	$5268928117$
$19110$	$1023487$	$6202067$	$6640901$	$19304167$	$78325591$	$152030453$
$19320$	$13154717$	$123351947$	$180065461$	$191400653$	$307980523$	$526607503$
$19530$	$1773689$	$128832049$	$226504217$	$544697521$	$880832749$	$1511819633$
$19740$	$216443629$	$1460073841$	$2172351869$	$3696955411$	$4020404251$	$4234603313$
$19950$	$142699$	$302287$	$661547$	$64740661$	$176566177$	$562542581$
$20160$	$77727823$	$585546277$	$1013154997$	$1309662637$	$2007871577$	$2231189419$
$20370$	$1216213$	$7991839$	$156234857$	$1222246309$	$2382533789$	$2523592993$
$20580$	$2219557$	$508048529$	$906000787$	$1111806827$	$2134225213$	$6894499589$
$20790$	$2397931$	$4022297$	$4043087$	$15314617$	$26974879$	$35575247$
$21000$	$49402277$	$263368843$	$701455591$	$2403274567$	$3097244987$	$5984865767$

□

Twierdzenie C57
Niech $n \in Z_{+}$ oraz $a, d, k, k_{0} \in Z$ . Jeżeli liczby $d$ i $n$ są względnie pierwsze, to reszty $r_{1}, r_{2}, \dots, r_{n}$ z dzielenia $n$ liczb $x_{k}$ postaci

x_{k} = a + k d

dla

k = k_{0} + 1, \dots, k_{0} + n

przez liczbę $n$ są wszystkie różne i tworzą zbiór $S = {0, 1, \dots, n - 1}$ . W szczególności wynika stąd, że wśród liczb $x_{k}$ jedna jest podzielna przez $n$ .

Dowód

Przypuśćmy, że dla pewnych różnych liczb naturalnych $i, j$ takich, że $1 ⩽ i < j ⩽ n$ liczby $a + (k_{0} + i) d$ oraz $a + (k_{0} + j) d$ dają tę samą resztę przy dzieleniu przez $n$ . Zatem różnica tych liczb jest podzielna przez $n$

n ∣ [a + (k_{0} + j) d] - [a + (k_{0} + i) d]

Czyli

n ∣ d (j - i)

Ponieważ liczby $d$ i $n$ są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie C74), mamy

n ∣ (j - i)

Co jest niemożliwe, bo $1 ⩽ j - i ⩽ n - 1 < n$ .

Zatem reszty $r_{1}, r_{2}, \dots, r_{n}$ są wszystkie różne, a ponieważ jest ich $n$ , czyli tyle ile jest różnych reszt z dzielenia przez liczbę $n$ , to zbiór tych reszt jest identyczny ze zbiorem reszt z dzielenia przez $n$ , czyli ze zbiorem $S = {0, 1, 2, \dots, n - 1}$ .
□

Twierdzenie C58
Niech $d \in Z_{+}$ i niech będzie dany ciąg arytmetyczny liczb pierwszych o długości $n$

p_{k} = p_{0} + k d

dla

k = 0, 1, \dots, n - 1

Z żądania, aby dany ciąg arytmetyczny był ciągiem arytmetycznym liczb pierwszych, wynika, że muszą być spełnione następujące warunki

$p_{0} ∤ d$
$n ⩽ p_{0}$
$P (n - 1) ∣ d$
jeżeli liczba pierwsza $q$ nie dzieli $d$ , to $n ⩽ q$

gdzie $P (t)$ jest iloczynem wszystkich liczb pierwszych nie większych od $t$ .

Dowód

Punkt 1.
Gdyby $p_{0} ∣ d$ , to dla $k ⩾ 1$ mielibyśmy $p_{k} = p_{0} (1 + k \cdot \frac{d}{p_{0}})$ i wszystkie te liczby byłyby złożone.

Punkt 2.
Ponieważ $p_{0}$ dzieli $p_{0} + p_{0} d$ , więc musi być $n - 1 < p_{0}$ , czyli $n ⩽ p_{0}$ .

Punkt 3.
Niech $q$ będzie liczbą pierwszą mniejszą od $n$ , a liczby $r_{k}$ będą resztami uzyskanymi z dzielenia liczb $p_{k} = p_{0} + k d$ przez $q$ , dla $k = 0, 1, \dots, q - 1$ . Ponieważ z założenia liczby $p_{0}, \dots, p_{n - 1}$ są liczbami pierwszymi większymi od $q$ (zauważmy, że $p_{0} ⩾ n$ ), to żadna z reszt $r_{k}$ nie może być równa zeru. Czyli mamy $q$ reszt mogących przyjmować jedynie $q - 1$ różnych wartości. Zatem istnieją różne liczby $i, j$ , takie że $0 ⩽ i < j ⩽ q - 1$ , dla których $r_{i} = r_{j}$ . Wynika stąd, że różnica liczb

p_{j} - p_{i} = (p_{0} + j d) - (p_{0} + i d) = d (j - i)

musi być podzielna przez $q$ . Ponieważ $q ∤ (j - i)$ , bo $1 ⩽ j - i ⩽ q - 1 < q$ , zatem z lematu Euklidesa $q ∣ d$ .

Z uwagi na fakt, że jest tak dla każdej liczby pierwszej $q < n$ , liczba $d$ musi być podzielna przez

P (n - 1) = \prod_{q < n} q

Punkt 4.
Ponieważ $P (n - 1) | d$ , to wszystkie liczby pierwsze mniejsze od $n$ muszą być dzielnikami $d$ . Wynika stąd, że jeśli liczba pierwsza $q$ nie dzieli $d$ , to musi być $q ⩾ n$ . Co należało pokazać.
□

Uwaga C59
Czasami, zamiast pisać „ciąg arytmetyczny liczb pierwszych”, będziemy posługiwali się skrótem PAP od angielskiej nazwy „prime arithmetic progression”. Konsekwentnie zapis PAP- $n$ będzie oznaczał ciąg arytmetyczny liczb pierwszych o długości $n$ , a zapis PAP $(n, d, q)$ ciąg arytmetyczny liczb pierwszych o długości $n$ , pierwszym wyrazie $q$ i różnicy $d$ .

Uwaga C60
Jakkolwiek sądzimy, że istnieje nieskończenie wiele ciągów arytmetycznych liczb pierwszych rozpoczynających się od dowolnej liczby pierwszej $q$ i o dowolnej długości $3 ⩽ n ⩽ q$ , to obecnie jest to tylko nieudowodnione przypuszczenie.

Dlatego nawet dla najmniejszej liczby pierwszej $q$ takiej, że $q ∤ d$ nierówność $n ⩽ q$ , pokazana w twierdzeniu C58, pozostaje nadal tylko oszacowaniem. W szczególności nie możemy z góry przyjmować, że dla liczby $n = q$ znajdziemy taką liczbę $d$ będącą wielokrotnością liczby $P (q - 1)$ i niepodzielną przez $q$ , że będzie istniał PAP $(q, d, q)$ .

Przykład C61
Rozważmy dwie różnice $d_{1} = 6 = 2 \cdot 3$ oraz $d_{2} = 42 = 2 \cdot 3 \cdot 7$ . Zauważmy, że liczba pierwsza $5$ nie dzieli ani $d_{1}$ , ani $d_{2}$ . Co więcej, liczba pierwsza $5$ jest najmniejszą liczbą pierwszą, która nie dzieli rozpatrywanych różnic, zatem nierówność $n ⩽ 5$ zapewnia najmocniejsze oszacowanie długości ciągu $n$ . Łatwo sprawdzamy w zamieszczonych tabelach, że dla $d = 6$ oraz dla $d = 42$ są ciągi o długości $3, 4, 5$ , ale nie ma ciągów o długości $6, 7, \dots$

W szczególności z twierdzenia C58 wynika, że szukając ciągów arytmetycznych liczb pierwszych o określonej długości $n$ , należy szukać ich tylko dla różnic $d$ będących wielokrotnością liczby $P (n - 1)$ .

Zadanie C62
Wiemy, że liczby pierwsze $p > 3$ można przedstawić w jednej z postaci $6 k - 1$ lub $6 k + 1$ . Pokazać, że jeżeli $p_{0} = 3$ , to dwa następne wyrazu rosnącego ciągu arytmetycznego liczb pierwszych są różnych postaci.

Rozwiązanie

Ponieważ $p_{0} = 3$ , a rozpatrywany PAP jest rosnący, to kolejne wyrazy ciągu są większe od liczby $3$ i mogą być przedstawione w jednej z postaci $6 k - 1$ lub $6 k + 1$ . Z twierdzenia C58 wiemy, że musi być $n ⩽ p_{0} = 3$ , czyli długość rozpatrywanego ciągu arytmetycznego liczb pierwszych wynosi dokładnie $3$ i istnieją tylko dwa następne wyrazy.

Rozważmy ciąg arytmetyczny liczb pierwszych składający się z trzech wyrazów $p, q, r$ takich, że $p = 3$ . Mamy

r = q + d = q + (q - p) = 2 q - p

Zatem

r + q = 3 q - 3

Widzimy, że prawa strona powyższej równości jest podzielna przez $3$ . Zatem liczby po lewej stronie wypisanych wyżej równości muszą być różnych postaci, bo tylko w takim przypadku lewa strona równości będzie również podzielna przez $3$ .
□

Zadanie C63
Wiemy, że liczby pierwsze $p > 3$ można przedstawić w jednej z postaci $6 k - 1$ lub $6 k + 1$ . Pokazać, że wszystkie wyrazy rosnącego ciągu arytmetycznego liczb pierwszych $p_{0}, p_{1}, \dots, p_{n - 1}$ , gdzie $p_{0} ⩾ 5$ i $n ⩾ 3$ muszą być jednakowej postaci.

Rozwiązanie

Niech liczby $p, q, r$ będą trzema kolejnymi (dowolnie wybranymi) wyrazami rozpatrywanego ciągu. Łatwo zauważmy, że

r = q + d = q + (q - p) = 2 q - p

Zatem

p + q = 3 q - r

q + r = 3 q - p

p + r = 2 q

Zauważmy, że prawa strona wypisanych wyżej równości nie jest podzielna przez $3$ , bo liczby $p, q, r$ są liczbami pierwszymi większymi od liczby $3$ . Zatem liczby po lewej stronie wypisanych wyżej równości muszą być tej samej postaci, bo gdyby było inaczej, to lewa strona tych równości byłaby podzielna przez $3$ , a prawa nie. Czyli każda para liczb z trójki $p, q, r$ musi być tej samej postaci i wynika stąd, że wszystkie trzy liczby muszą być tej samej postaci. Ponieważ trzy kolejne wyrazy ciągu $p_{0}, p_{1}, \dots, p_{n - 1}$ były wybrane dowolnie, to wszystkie wyrazy tego ciągu muszą być tej samej postaci.
□

Zadanie C64
Niech $d > 0$ będzie różnicą ciągu arytmetycznego liczb pierwszych o długości $n$

p_{k} = p_{0} + k d

dla

k = 0, 1, \dots, n - 1

Pokazać, nie korzystając z twierdzenia C58, że jeżeli liczba pierwsza $q$ nie dzieli $d$ , to $n ⩽ q$ .

Rozwiązanie

Przypuśćmy, że $n > q$ tak, że $q < n ⩽ p_{0}$ , zatem

q < p_{k} = p_{0} + k d

dla

k = 0, 1, \dots, n - 1

Ponieważ $q ∤ d$ , to na mocy twierdzenia C57 wśród $q$ kolejnych wyrazów $p_{0}, p_{1}, \dots, p_{q - 1}$ (zauważmy, że $q - 1 < n - 1$ ) jedna liczba pierwsza $p_{k}$ musi być podzielna przez $q$ , zatem musi być równa $q$ . Jednak jest to niemożliwe, bo $q < p_{k}$ dla wszystkich $k = 0, 1, \dots, n - 1$ . Zatem nie może być $n > q$ .
□

Twierdzenie C65
Niech $q$ będzie liczbą pierwszą, a liczby pierwsze

p_{k} = p_{0} + k d

gdzie

k = 0, 1, \dots, q - 1

tworzą ciąg arytmetyczny o długości $q$ i różnicy $d > 0$ .

Równość $p_{0} = q$ zachodzi wtedy i tylko wtedy, gdy $q ∤ d$ .

Dowód

$⟹$
Jeżeli $p_{0} = q$ , to $q$ -wyrazowy ciąg arytmetyczny liczb pierwszych ma postać

p_{k} = q + k d

dla

k = 0, 1, \dots, q - 1

Gdyby $q ∣ d$ , to mielibyśmy

p_{k} = q (1 + k \cdot \frac{d}{q})

i wszystkie liczby $p_{k}$ dla $k ⩾ 1$ byłyby złożone, wbrew założeniu, że $p_{k}$ tworzą $q$ -wyrazowy ciąg arytmetyczny liczb pierwszych.

$⟸$
Ponieważ $q$ jest długością rozpatrywanego ciągu arytmetycznego liczb pierwszych, to z twierdzenia C58 wynika, że musi być $q ⩽ p_{0}$ .

Z założenia liczba pierwsza $q$ nie dzieli $d$ , zatem z twierdzenia C57 wiemy, że $q$ musi dzielić jedną z liczb $p_{0}, p_{1}, \dots, p_{q - 1}$ .

Jeżeli $q ∣ p_{k}$ , to $p_{k} = q$ . Ponieważ $q ⩽ p_{0}$ , to możliwe jest jedynie $q ∣ p_{0}$ i musi być $p_{0} = q$ .
□

Uwaga C66
Niech ciąg arytmetyczny liczb pierwszych o długości $n$ ma postać

p_{k} = p_{0} + k d

dla

k = 0, 1, \dots, n - 1

Z udowodnionych wyżej twierdzeń C58 i C65 wynika, że ciągi arytmetyczne liczb pierwszych o długości $n$ można podzielić na dwie grupy

jeżeli $n$ jest liczbą pierwszą i $n ∤ d$ , to $P (n - 1) ∣ d$ oraz $p_{0} = n$ (dla ustalonego $d$ może istnieć tylko jeden ciąg)
jeżeli $n$ jest liczbą złożoną lub $n ∣ d$ , to $P (n) ∣ d$ oraz $p_{0} > n$

Funkcja $P (t)$ jest iloczynem wszystkich liczb pierwszych nie większych od $t$ .

Przykład C67
Niech różnica ciągu arytmetycznego liczb pierwszych wynosi $d = 10^{t}$ , gdzie $t ⩾ 1$ . Zauważmy, że dla dowolnego $t$ liczba $3$ jest najmniejszą liczbą pierwszą, która nie dzieli $d$ . Z oszacowania $n ⩽ 3$ wynika, że musi być $n = 3$ .

Jeżeli długość ciągu $n = 3$ i $n ∤ d$ , to musi być $p_{0} = n = 3$ i może istnieć tylko jeden PAP dla każdego $d$ . W przypadku $t ⩽ 10000$ jedynie dla $t = 1, 5, 6, 17$ wszystkie liczby ciągu arytmetycznego $(3, 3 + 10^{t}, 3 + 2 \cdot 10^{t})$ są pierwsze.

Zadanie C68
Znaleźć wszystkie PAP $(n, d, p)$ dla $d = 2, 4, 8, 10, 14, 16$ .

Rozwiązanie

Zauważmy, że dla każdej z podanych różnic $d$ , liczba $3$ jest najmniejszą liczbą pierwszą, która nie dzieli $d$ . Z oszacowania $n ⩽ 3$ wynika, że musi być $n = 3$ .

Ponieważ $n = 3$ jest liczbą pierwszą i dla wypisanych $d$ liczba $n ∤ d$ , to w każdym przypadku może istnieć tylko jeden ciąg, którego pierwszym wyrazem jest liczba pierwsza $p_{0} = n = 3$ . Dla $d = 2, 4, 8, 10, 14$ łatwo znajdujemy odpowiednie ciągi

(3, 5, 7)

,

(3, 7, 11)

,

(3, 11, 19)

,

(3, 13, 23)

,

(3, 17, 31)

Dla $d = 16$ szukany ciąg nie istnieje, bo $35 = 5 \cdot 7$ .
□

Zadanie C69
Znaleźć wszystkie PAP $(n, d, p)$ dla $n = 3, 5, 7, 11$ i $d = P (n - 1)$ .

Rozwiązanie

Z założenia PAP ma długość $n$ , liczba $n$ jest liczbą pierwszą i $n ∤ d$ . Zatem może istnieć tylko jeden PAP taki, że $p_{0} = n$ . Dla $n = 3, 5$ i odpowiednio $d = 2, 6$ otrzymujemy ciągi arytmetyczne liczb pierwszych

(3, 5, 7)

,

(5, 11, 17, 23, 29)

Ale dla $n = 7, 11$ i odpowiednio $d = 30, 210$ szukane ciągi nie istnieją, bo

(7, 37, 67, 97, 127, 157, 187 = 11 \cdot 17)

(11, 221 = 13 \cdot 17, 431, 641, 851 = 23 \cdot 37, 1061, 1271 = 31 \cdot 41, 1481, 1691 = 19 \cdot 89, 1901, 2111)

□

Przykład C70
Przedstawiamy przykładowe ciągi arytmetyczne liczb pierwszych, takie że $n = p_{0}$ dla $n = 3, 5, 7, 11, 13$ . Zauważmy, że wypisane w tabeli wartości $d$ są wielokrotnościami liczby $P (n - 1)$ .

Pokaż tabelę

$n = p_{0}$	$d$
$3$	$2$	$4$	$8$	$10$	$14$	$20$	$28$	$34$	$38$	$40$
$5$	$6$	$12$	$42$	$48$	$96$	$126$	$252$	$426$	$474$	$594$
$7$	$150$	$2760$	$3450$	$9150$	$14190$	$20040$	$21240$	$63600$	$76710$	$117420$
$11$	$1536160080$	$4911773580$	$25104552900$	$77375139660$	$83516678490$	$100070721660$	$150365447400$	$300035001630$	$318652145070$	$369822103350$
$13$	$9918821194590$	$104340979077720$	$187635245859600$	$232320390245790$	$391467874710990$	$859201916576850$	$1024574038282410$	$1074380369464710$	$1077624363457950$	$1185763337651970$

Przykłady takich ciągów dla jeszcze większych liczb pierwszych Czytelnik znajdzie na stronie A088430.
□

Przykład C71
Liczby $3, 5, 7$ są najprostszym przykładem ciągu arytmetycznego kolejnych liczb pierwszych. Zauważmy, że tylko w przypadku $n = 3$ możliwa jest sytuacja, że $n = p_{0} = 3$ . Istotnie, łatwo stwierdzamy, że

ponieważ $p_{0}$ i $p_{1}$ są kolejnymi liczbami pierwszymi, to $p_{1} - p_{0} < p_{0}$ (zobacz zadanie B22)
dla dowolnej liczby pierwszej $q ⩾ 5$ jest $q < P (q - 1)$ (zobacz zadanie B26)

Przypuśćmy teraz, że istnieje ciąg arytmetyczny kolejnych liczb pierwszych, taki że $n = p_{0} ⩾ 5$ . Mamy

d = p_{1} - p_{0} < p_{0} < P (p_{0} - 1) = P (n - 1)

Zatem $P (n - 1) ∤ d$ , co jest niemożliwe.

Wynika stąd, że poza przypadkiem $n = p_{0} = 3$ ciąg arytmetyczny kolejnych liczb pierwszych musi spełniać warunek $P (n) | d$ , czyli $P (n) | (p_{1} - p_{0})$ .

Poniższe tabele przedstawiają przykładowe ciągi arytmetyczne kolejnych liczb pierwszych o długościach $n = 3, 4, 5, 6$ dla rosnących wartości $p_{0}$ . Nie istnieje ciąg arytmetyczny kolejnych liczb pierwszych o długości $n = 7$ dla $p_{0} < 10^{13}$ . Prawdopodobnie CPAP-7 pojawią się dopiero dla $p_{0} \sim 10^{20}$ .

Znane są ciągi arytmetyczne kolejnych liczb pierwszych o długościach $n ⩽ 10$ ^[16].

Pokaż tabele

$n = 3$
$p_{0} ⩽ 10^{3}$	$d$
$3$	$2$
$47$	$6$
$151$	$6$
$167$	$6$
$199$	$12$
$251$	$6$
$257$	$6$
$367$	$6$
$557$	$6$
$587$	$6$
$601$	$6$
$647$	$6$
$727$	$6$
$941$	$6$
$971$	$6$

$n = 4$
$p_{0} ⩽ 10^{4}$	$d$
$251$	$6$
$1741$	$6$
$3301$	$6$
$5101$	$6$
$5381$	$6$
$6311$	$6$
$6361$	$6$

$n = 5$
$p_{0} ⩽ 10^{8}$	$d$
$9843019$	$30$
$37772429$	$30$
$53868649$	$30$
$71427757$	$30$
$78364549$	$30$
$79080577$	$30$
$98150021$	$30$
$99591433$	$30$

$n = 6$
$p_{0} ⩽ 10^{10}$	$d$
$121174811$	$30$
$1128318991$	$30$
$2201579179$	$30$
$2715239543$	$30$
$2840465567$	$30$
$3510848161$	$30$
$3688067693$	$30$
$3893783651$	$30$
$5089850089$	$30$
$5825680093$	$30$
$6649068043$	$30$
$6778294049$	$30$
$7064865859$	$30$
$7912975891$	$30$
$8099786711$	$30$
$9010802341$	$30$
$9327115723$	$30$
$9491161423$	$30$
$9544001791$	$30$

□

Zadanie C72
Uzasadnij przypuszczenie, że ciągów arytmetycznych kolejnych liczb pierwszych o długości $n = 7$ możemy oczekiwać dopiero dla $p_{0} \sim 10^{20}$ .

Rozwiązanie

Zauważmy, że ilość liczb pierwszych nie większych od $x$ w dobrym przybliżeniu jest określona funkcją $\frac{x}{\log x}$ . Ponieważ funkcja $\log x$ zmienia się bardzo wolno, to odcinki liczb naturalnych o tej samej długości położone w niewielkiej odległości od siebie będą zawierały podobne ilości liczb pierwszych. Przykładowo, dla dużych wartości $x$ , ilość liczb pierwszych w przedziale $(x, 2 x)$ jest tego samego rzędu, co ilość liczb pierwszych w przedziale $(1, x)$ ^[17].

Zatem liczbę $\frac{1}{\log x}$ możemy traktować jako prawdopodobieństwo trafienia na liczbę pierwszą wśród liczb znajdujących się w pobliżu liczby $x$ . Zakładając, że liczby pierwsze są rozłożone przypadkowo, możemy wyliczyć prawdopodobieństwo tego, że $n$ kolejnych liczb pierwszych, położonych w pobliżu liczby $x$ , utworzy ciąg arytmetyczny

{prob}_{cpap} (n, x) = {(\frac{1}{\log x})}^{n} {(1 - \frac{1}{\log x})}^{(n - 1) (d - 1)}

gdzie $d = P (n)$ . Jest tak, ponieważ w ciągu kolejnych liczb całkowitych musimy trafić na liczbę pierwszą, następnie na $d - 1$ liczb złożonych, taka sytuacja musi się powtórzyć dokładnie $n - 1$ razy, a na koniec znowu musimy trafić na liczbę pierwszą. Czyli potrzebujemy $n$ liczb pierwszych, na które trafiamy z prawdopodobieństwem $\frac{1}{\log x}$ oraz $(n - 1) (d - 1)$ liczb złożonych, na które trafiamy z prawdopodobieństwem $1 - \frac{1}{\log x}$ , a liczby te muszą pojawiać się w ściśle określonej kolejności.

Ilość ciągów arytmetycznych utworzonych przez $n$ kolejnych liczb pierwszych należących do przedziału $(x, 2 x)$ możemy zatem oszacować na równą około

Q_{cpap} (n, x) = x \cdot {(\frac{1}{\log x})}^{n} {(1 - \frac{1}{\log x})}^{(n - 1) (d - 1)}

Porównując powyższe oszacowanie z rzeczywistą ilością $# CPAP (n, x)$ ciągów arytmetycznych kolejnych liczb pierwszych w przedziale $(x, 2 x)$ dostajemy

\frac{# CPAP (n, x)}{Q_{cpap} (n, x)} = f (n, x)

gdzie w możliwym do zbadania zakresie, czyli dla $x < 2^{42} \approx 4.4 \cdot 10^{12}$ mamy

f (n, x) \approx a_{n} \cdot \log x + b_{n}

Stałe $a_{n}$ i $b_{n}$ wyznaczamy metodą regresji liniowej. Musimy pamiętać, że uzyskanych w ten sposób wyników nie możemy ekstrapolować dla dowolnie dużych $x$ .

W przypadku $n = 5$ oraz $n = 6$ dysponowaliśmy zbyt małą liczbą danych, aby wyznaczyć stałe $a_{n}$ i $b_{n}$ z wystarczającą dokładnością. Dlatego w tych przypadkach ograniczyliśmy się do podania oszacowania funkcji $f (n, x)$ .

Uzyskany wyżej rezultaty są istotne, bo z wyliczonych postaci funkcji $f (n, x)$ wynika, że są to funkcje bardzo wolno zmienne, a ich ekstrapolacja jest w pełni uprawniona.

W zamieszczonej niżej tabeli mamy kolejno

$n$ , czyli długość CPAP
wartość iloczynu $n \cdot P (n)$
znalezioną postać funkcji $f (n, x)$ lub oszacowanie wartości tej funkcji $C_{n}$ na podstawie uzyskanych danych; w przypadku $n = 7$ jest to oszacowanie wynikające z obserwacji, że wartości funkcji $f (n, x)$ są rzędu $n \cdot P (n)$
wyliczoną wartość $\frac{# CPAP (n, 2^{40})}{Q_{cpap} (n, 2^{40})}$ , czyli $f (n, 2^{40})$
wartość funkcji $f (n, 2^{70})$ wynikające z ekstrapolacji wzoru $f (n, x) = a_{n} \cdot \log x + b_{n}$ (dla $n = 3, 4$ )
wartość $x$ wynikającą z rozwiązania równania

(a_{n} \cdot \log x + b_{n}) \cdot Q_{cpap} (n, x) = 1

(dla

n = 3, 4

)

C_{n} \cdot Q_{cpap} (n, x) = 1

(dla

n = 5, 6, 7

)

dla porównania w kolejnych kolumnach zostały podane dwie najmniejsze wartości $p_{0}$ dla CPAP-n

$n$	$n \cdot P (n)$	$f (n, x) lub C_{n}$	$f (n, 2^{40})$	$f (n, 2^{70})$	$\sim p_{0}$
$3$	$18$	$0.52 \cdot \log x + 6.3$	$20.94$	$30$	$130$	$47$	$151$
$4$	$24$	$0.53 \cdot \log x + 11.6$	$26.61$	$36$	$1.5 \cdot 10^{3}$	$251$	$1741$
$5$	$150$	$120$	$121.45$		$15 \cdot 10^{6}$	$9843019$	$37772429$
$6$	$180$	$235$	$228.27$		$540 \cdot 10^{6}$	$121174811$	$1128318991$
$7$	$1470$	$2500$	$0$		$2 \cdot 10^{20}$

Zauważając, że funkcje $f (n, x)$ są rzędu $n \cdot P (n)$ i przyjmując, że podobnie będzie dla $f (7, x)$ , możemy wyliczyć wartość $x$ , dla której może pojawić się pierwszy CPAP-7. Wartość ta jest równa w przybliżeniu $2 \cdot 10^{20}$ i wynika z rozwiązania równania

f (7, x) \cdot Q_{cpap} (7, x) = 1

Możemy ją łatwo wyliczyć w PARI/GP. Oczywiście funkcję $f (7, x)$ zastąpiliśmy jej oszacowaniem $C_{7} = 2500$

P(n) = prod(k=2, n, if( isprime(k), k, 1 ))
Q(x) = 2500 * x * ( 1/log(x) )^7 * ( 1 - 1/log(x) )^( (7-1)*(P(7)-1) )
solve(x=10^10, 10^23, Q(x) - 1 )

□

Uzupełnienie

Twierdzenie C73 (lemat Bézouta)
Jeżeli liczby całkowite $a$ i $b$ nie są jednocześnie równe zeru, a największy wspólny dzielnik tych liczb jest równy $D$ , to istnieją takie liczby całkowite $x, y$ , że

a x + b y = D

Dowód

Niech $S$ będzie zbiorem wszystkich liczb całkowitych dodatnich postaci $a n + b m$ , gdzie $n, m$ są dowolnymi liczbami całkowitymi. Zbiór $S$ nie jest zbiorem pustym, bo przykładowo liczba $a^{2} + b^{2} \in S$ . Z zasady dobrego uporządkowania liczb naturalnych wynika, że zbiór $S$ ma element najmniejszy, oznaczmy go literą $d$ .

Pokażemy, że $d ∣ a$ i $d ∣ b$ . Z twierdzenia o dzieleniu z resztą możemy napisać $a = k d + r$ , gdzie $0 ⩽ r < d$ .

Przypuśćmy, że $d ∤ a$ , czyli że $r > 0$ . Ponieważ $d \in S$ , to mamy $d = a u + b v$ dla pewnych liczb całkowitych $u$ i $v$ . Zatem

r = a - k d =

= a - k (a u + b v) =

= a \cdot (1 - k u) + b \cdot (- k v)

Wynika stąd, że dodatnia liczba $r$ należy do zbioru $S$ oraz $r < d$ , wbrew określeniu liczby $d$ , czyli musi być $r = 0$ i $d ∣ a$ . Podobnie pokazujemy, że $d ∣ b$ .

Jeżeli $d^{'}$ jest innym dzielnikiem liczb $a$ i $b$ , to $d^{'} ∣ d$ , bo $d^{'} ∣ (a u + b v)$ . Zatem $d^{'} ⩽ d$ , skąd wynika natychmiast, że liczba $d$ jest największym z dzielników, które jednocześnie dzielą liczby $a$ oraz $b$ . Czyli $d = D$ .
□

Twierdzenie C74 (lemat Euklidesa)
Niech $p$ będzie liczbą pierwszą oraz $a, b, d \in Z$ .

jeżeli $d ∣ a b$ i liczba $d$ jest względnie pierwsza z $a$ , to $d ∣ b$

jeżeli $p ∣ a b$ , to $p ∣ a$ lub $p ∣ b$

Dowód

Punkt 1.

Z założenia liczby $d$ i $a$ są względnie pierwsze, zatem na mocy lematu Bézouta (twierdzenie C73) istnieją takie liczby całkowite $x$ i $y$ , że

d x + a y = 1

Mnożąc obie strony równania przez $b$ , dostajemy

d b x + a b y = b

Obydwa wyrazy po prawej stronie są podzielne przez $d$ , bo z założenia $d ∣ a b$ . Zatem prawa strona również jest podzielna przez $d$ , czyli $d ∣ b$ . Co kończy dowód punktu pierwszego.

Punkt 2.

Jeżeli $p ∤ a$ , to $gcd (p, a) = 1$ , zatem z punktu pierwszego wynika, że $p ∣ b$ .

Jeżeli $p ∤ b$ , to $gcd (p, b) = 1$ , zatem z punktu pierwszego wynika, że $p ∣ a$ .

Czyli $p$ musi dzielić przynajmniej jedną z liczb $a, b$ . Co należało pokazać.
□

Twierdzenie C75
Niech $a, b, m \in Z$ . Jeżeli $a ∣ m$ i $b ∣ m$ oraz $gcd (a, b) = 1$ , to $a b ∣ m$ .

Dowód

Z założenia istnieją takie liczby $r, s, x, y \in Z$ , że $m = a r$ i $m = b s$ oraz

a x + b y = 1

(zobacz C73). Zatem

m = m (a x + b y)

= m a x + m b y

= b s a x + a r b y

= a b (s x + r y)

Czyli $a b ∣ m$ . Co należało pokazać.
□

Twierdzenie C76
Niech $a, b, c \in Z$ . Równanie $a x + b y = c$ ma rozwiązanie wtedy i tylko wtedy, gdy największy wspólny dzielnik liczb $a$ i $b$ jest dzielnikiem liczby $c$ .

Dowód

Niech $D$ oznacza największy wspólny dzielnik liczb $a$ i $b$ .

$⟹$

Jeżeli liczby całkowite $x_{0}$ i $y_{0}$ są rozwiązaniem rozpatrywanego równania, to

a x_{0} + b y_{0} = c

Ponieważ $D$ dzieli lewą stronę równania, to musi również dzielić prawą, zatem musi być $D | c$ .

$⟸$

Jeżeli $D | c$ , to możemy napisać $c = k D$ i równanie przyjmuje postać

a x + b y = k D

Lemat Bézouta (twierdzenie C73) zapewnia istnienie liczb całkowitych $x_{0}$ i $y_{0}$ takich, że

a x_{0} + b y_{0} = D

Czyli z lematu Bézouta wynika, że równanie $a x + b y = D$ ma rozwiązanie w liczbach całkowitych. Przekształcając, dostajemy

a (k x_{0}) + b (k y_{0}) = k D

Zatem liczby $k x_{0}$ i $k y_{0}$ są rozwiązaniem równania

a x + b y = k D

Co oznacza, że równianie $a x + b y = c$ ma rozwiązanie.
□

Uwaga C77
Z twierdzenia C76 wynika, że szukając rozwiązań równania $A x + B y = C$ w liczbach całkowitych, powinniśmy

obliczyć największy wspólny dzielnik $D$ liczb $A$ i $B$
jeżeli $D > 1$ , należy sprawdzić, czy $D | C$
jeżeli $D ∤ C$ , to równanie $A x + B y = C$ nie ma rozwiązań w liczbach całkowitych
jeżeli $D | C$ , należy podzielić obie strony równania $A x + B y = C$ przez $D$ i przejść do rozwiązywania równania równoważnego $a x + b y = c$ , gdzie $a = \frac{A}{D}$ , $b = \frac{B}{D}$ , $c = \frac{C}{D}$ , zaś największy wspólny dzielnik liczb $a$ i $b$ jest równy $1$ .

Twierdzenie C78
Niech $a, b, c \in Z$ . Jeżeli liczby $a$ i $b$ są względnie pierwsze, to równanie

a x + b y = c

ma nieskończenie wiele rozwiązań w liczbach całkowitych.

Jeżeli para liczb całkowitych $(x_{0}, y_{0})$ jest jednym z tych rozwiązań, to wszystkie pozostałe rozwiązania całkowite można otrzymać ze wzorów

x = x_{0} + b t

y = y_{0} - a t

gdzie $t$ jest dowolną liczbą całkowitą.

Dowód

Z założenia liczby $a$ i $b$ są względnie pierwsze, zatem największy wspólny dzielnik tych liczb jest równy $1$ i dzieli liczbę $c$ . Na mocy twierdzenia C76 równanie

a x + b y = c

ma rozwiązanie w liczbach całkowitych.

Zauważmy, że jeżeli para liczb całkowitych $(x_{0}, y_{0})$ jest rozwiązaniem równania $a x + b y = c$ , to para liczb $(x_{0} + b t, y_{0} - a t)$ również jest rozwiązaniem. Istotnie

a (x_{0} + b t) + b (y_{0} - a t) = a x_{0} + a b t + b y_{0} - b a t =

= a x_{0} + b y_{0} =

= c

Pokażmy teraz, że nie istnieją inne rozwiązania niż określone wzorami

x = x_{0} + b t

y = y_{0} - a t

gdzie $t$ jest dowolną liczbą całkowitą.

Przypuśćmy, że pary liczb całkowitych $(x, y)$ oraz $(x_{0}, y_{0})$ są rozwiązaniami rozpatrywanego równania, zatem

a x + b y = c = a x_{0} + b y_{0}

Wynika stąd, że musi być spełniony warunek

a (x - x_{0}) = b (y_{0} - y)

Ponieważ liczby $a$ i $b$ są względnie pierwsze, to na mocy lematu Euklidesa (twierdzenie C74) $b | (x - x_{0})$ . Skąd mamy

x - x_{0} = b t

gdzie $t$ jest dowolną liczbą całkowitą. Po podstawieniu dostajemy natychmiast

y - y_{0} = - a t

Co kończy dowód.
□

Przykład C79
Rozwiązania równania

a x + b y = c

gdzie $gcd (a, b) = 1$ , które omówiliśmy w poprzednim twierdzeniu, najłatwiej znaleźć korzystając w PARI/GP z funkcji gcdext(a, b). Funkcja ta zwraca wektor liczb [x₀, y₀, d], gdzie $d = gcd (a, b)$ , a liczby $x_{0}$ i $y_{0}$ są rozwiązaniami równania

a x_{0} + b y_{0} = gcd (a, b)

Ponieważ założyliśmy, że $gcd (a, b) = 1$ , to łatwo zauważmy, że

a (c x_{0}) + b (c y_{0}) = c

Zatem para liczb całkowitych $(c x_{0}, c y_{0})$ jest jednym z rozwiązań równania

a x + b y = c

i wszystkie pozostałe rozwiązania uzyskujemy ze wzorów

x = c x_{0} + b t

y = c y_{0} - a t

Niech $a = 7$ i $b = 17$ . Funkcja gcdext(7,17) zwraca wektor [5, -2, 1], zatem rozwiązaniami równania $7 x + 17 y = 1$ są liczby

x = 5 + 17 t

y = - 2 - 7 t

A rozwiązaniami równania $7 x + 17 y = 10$ są liczby

x = 50 + 17 t

y = - 20 - 7 t

Przypisy

↑ Korzystamy w tym momencie z zasady dobrego uporządkowania zbioru liczb naturalnych, która stwierdza, że każdy niepusty podzbiór zbioru liczb naturalnych zawiera element najmniejszy. (Wiki-pl), (Wiki-en)
↑ Określenie, że „liczba $n$ jest postaci $a k + b$ ”, jest jedynie bardziej czytelnym (obrazowym) zapisem stwierdzenia, że reszta z dzielenia liczby $n$ przez $a$ wynosi $b$ . Zapis „liczba $n$ jest postaci $a k - 1$ ” oznacza, że reszta z dzielenia liczby $n$ przez $a$ wynosi $a - 1$ .
↑ Wikipedia, Linnik's theorem, (Wiki-en)
↑ MathWorld, Linnik's Theorem. (MathWorld)
↑ Yuri Linnik, On the least prime in an arithmetic progression. I. The basic theorem, Mat. Sb. (N.S.) 15 (1944) 139–178.
↑ Yuri Linnik, On the least prime in an arithmetic progression. II. The Deuring-Heilbronn phenomenon, Mat. Sb. (N.S.) 15 (1944) 347–368.
↑ Triantafyllos Xylouris, Über die Nullstellen der Dirichletschen L-Funktionen und die kleinste Primzahl in einer arithmetischen Progression, Bonner Mathematische Schriften, vol. 404, Univ. Bonn, 2011, Diss.
↑ Enrico Bombieri, John B. Friedlander and Henryk Iwaniec, Primes in Arithmetic Progressions to Large Moduli. III, Journal of the American Mathematical Society 2 (1989) 215-224
↑ Paul Turán, Über die Primzahlen der arithmetischen Progression, Acta Sci. Szeged 8 (1937), 226-235
↑ Samuel S. Wagstaff, Jr., Greatest of the Least Primes in Arithmetic Progressions Having a Given Modulus, Mathematics of Computation Vol. 33, No. 147 (1979), 1073-1080
↑ Wikipedia, Primes in arithmetic progression, (Wiki-en)
↑ MathWorld, Prime Arithmetic Progression, (LINK)
↑ J. G. van der Corput, Über Summen von Primzahlen und Primzahlquadraten, Mathematische Annalen, 116 (1939) 1-50, (LINK)
↑ Wikipedia, Largest known primes in AP, (Wiki-en)
↑ Ben Green and Terence Tao, The Primes Contain Arbitrarily Long Arithmetic Progressions., Ann. of Math. (2) 167 (2008), 481-547, (LINK1), Preprint. 8 Apr 2004, (LINK2)
↑ Wikipedia, Primes in arithmetic progression - Largest known consecutive primes in AP, (Wiki-en)
↑ Henryk Dąbrowski, Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n - Uwagi do twierdzenia, (LINK)

[WellOrdering-1] Korzystamy w tym momencie z zasady dobrego uporządkowania zbioru liczb naturalnych, która stwierdza, że każdy niepusty podzbiór zbioru liczb naturalnych zawiera element najmniejszy. (Wiki-pl), (Wiki-en)

[LiczbaJestPostaci-2] Określenie, że „liczba $n$ jest postaci $a k + b$ ”, jest jedynie bardziej czytelnym (obrazowym) zapisem stwierdzenia, że reszta z dzielenia liczby $n$ przez $a$ wynosi $b$ . Zapis „liczba $n$ jest postaci $a k - 1$ ” oznacza, że reszta z dzielenia liczby $n$ przez $a$ wynosi $a - 1$ .

[Linnik1-3] Wikipedia, Linnik's theorem, (Wiki-en)

[Linnik2-4] MathWorld, Linnik's Theorem. (MathWorld)

[Linnik3-5] Yuri Linnik, On the least prime in an arithmetic progression. I. The basic theorem, Mat. Sb. (N.S.) 15 (1944) 139–178.

[Linnik4-6] Yuri Linnik, On the least prime in an arithmetic progression. II. The Deuring-Heilbronn phenomenon, Mat. Sb. (N.S.) 15 (1944) 347–368.

[Xylouris1-7] Triantafyllos Xylouris, Über die Nullstellen der Dirichletschen L-Funktionen und die kleinste Primzahl in einer arithmetischen Progression, Bonner Mathematische Schriften, vol. 404, Univ. Bonn, 2011, Diss.

[Bombieri1-8] Enrico Bombieri, John B. Friedlander and Henryk Iwaniec, Primes in Arithmetic Progressions to Large Moduli. III, Journal of the American Mathematical Society 2 (1989) 215-224

[Turan1-9] Paul Turán, Über die Primzahlen der arithmetischen Progression, Acta Sci. Szeged 8 (1937), 226-235

[Wagstaff1-10] Samuel S. Wagstaff, Jr., Greatest of the Least Primes in Arithmetic Progressions Having a Given Modulus, Mathematics of Computation Vol. 33, No. 147 (1979), 1073-1080

[PAPWiki-11] Wikipedia, Primes in arithmetic progression, (Wiki-en)

[PAPMathWorld-12] MathWorld, Prime Arithmetic Progression, (LINK)

[Corput-13] J. G. van der Corput, Über Summen von Primzahlen und Primzahlquadraten, Mathematische Annalen, 116 (1939) 1-50, (LINK)

[largestPAP-14] Wikipedia, Largest known primes in AP, (Wiki-en)

[GeenTao-15] Ben Green and Terence Tao, The Primes Contain Arbitrarily Long Arithmetic Progressions., Ann. of Math. (2) 167 (2008), 481-547, (LINK1), Preprint. 8 Apr 2004, (LINK2)

[CPAP1-16] Wikipedia, Primes in arithmetic progression - Largest known consecutive primes in AP, (Wiki-en)

[PrimesInInterval-17] Henryk Dąbrowski, Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n - Uwagi do twierdzenia, (LINK)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

@@ Linia 1089: / Linia 1089: @@
 Oznaczając <math>b = a^y</math> oraz <math>x = 2 k + 1</math>, otrzymujemy
-::<math>a^n + 1 = (a^y)^x + 1 =</math>
+::<math>a^n + 1 = (a^y)^x + 1</math>
-::::<math>\: = b^x + 1 =</math>
+::::<math>\: = b^x + 1</math>
-::::<math>\: = b^{2 k + 1} + 1 =</math>
+::::<math>\: = b^{2 k + 1} + 1</math>
 ::::<math>\: = (b + 1) \cdot (1 - b + b^2 - b^3 + \ldots + b^{2 k - 2} - b^{2 k - 1} + b^{2 k})</math>

Ciągi liczbowe: Różnice pomiędzy wersjami

Wersja z 19:13, 20 lut 2024

Spis treści

Ciągi nieskończone

Liczby pierwsze w ciągach arytmetycznych

Ciągi nieskończone i liczby pierwsze

Ciągi arytmetyczne liczb pierwszych

Uzupełnienie

Przypisy

Menu nawigacyjne

Szukaj