Twierdzenie Czebyszewa o funkcji π(n)

07.11.2021

Oznaczenia

Będziemy stosowali następujące oznaczenia:

[math]\displaystyle{ \mathbb{Z} }[/math] — zbiór liczb całkowitych

[math]\displaystyle{ \mathbb{Z}_+ }[/math] — zbiór liczb całkowitych dodatnich

[math]\displaystyle{ \mathbb{N} }[/math] — zbiór liczb naturalnych [math]\displaystyle{ \mathbb{N} = \mathbb{Z}_{+} }[/math]

[math]\displaystyle{ \mathbb{N}_0 }[/math] — zbiór liczb całkowitych nieujemnych [math]\displaystyle{ \mathbb{N}_0 = \mathbb{Z}_{+} \cup \left \{ 0 \right \} }[/math]

[math]\displaystyle{ \mathbb{R} }[/math] — zbiór liczb rzeczywistych

[math]\displaystyle{ d \mid n }[/math] — czytaj: d dzieli n ([math]\displaystyle{ d }[/math] jest dzielnikiem liczby [math]\displaystyle{ n }[/math])

[math]\displaystyle{ d \nmid n }[/math] — czytaj: d nie dzieli n ([math]\displaystyle{ d }[/math] nie jest dzielnikiem liczby [math]\displaystyle{ n }[/math])

[math]\displaystyle{ p_n }[/math] — [math]\displaystyle{ n }[/math]-ta liczba pierwsza

[math]\displaystyle{ \pi (n) }[/math] — ilość liczb pierwszych nie większych od [math]\displaystyle{ n }[/math]

[math]\displaystyle{ P(n) }[/math] — iloczyn liczb pierwszych nie większych od [math]\displaystyle{ n }[/math]

[math]\displaystyle{ \lfloor x \rfloor }[/math] — największa liczba całkowita nie większa od [math]\displaystyle{ x }[/math]

[math]\displaystyle{ \binom{n}{m} }[/math] — współczynnik dwumianowy (symbol Newtona), [math]\displaystyle{ \binom{n}{m} = \frac{n!}{m! \cdot (n - m) !} }[/math]

[math]\displaystyle{ \log (x) }[/math] — logarytm naturalny liczby [math]\displaystyle{ x \gt 0 }[/math]

[math]\displaystyle{ W_p (n) }[/math] — wykładnik z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze liczby [math]\displaystyle{ n }[/math]

[math]\displaystyle{ n }[/math] — oznacza zawsze liczbę naturalną

[math]\displaystyle{ p }[/math] — oznacza zawsze liczbę pierwszą

Przykładowe wartości niektórych wypisanych wyżej funkcji:

[math]\displaystyle{ p_2 = 3 }[/math],   [math]\displaystyle{ p_{10} = 29 }[/math],   [math]\displaystyle{ p_{100} = 541 }[/math]

[math]\displaystyle{ \pi (10) = 4 }[/math],   [math]\displaystyle{ \pi (100) = 25 }[/math],   [math]\displaystyle{ \pi (541) = 100 }[/math]

[math]\displaystyle{ P(5) = 30 }[/math],   [math]\displaystyle{ P(10) = 210 }[/math],   [math]\displaystyle{ P(50) = 614889782588491410 }[/math]

[math]\displaystyle{ \lfloor 1.2 \rfloor = 1 }[/math],   [math]\displaystyle{ \lfloor 2.8 \rfloor = 2 }[/math],   [math]\displaystyle{ \lfloor - 1.5 \rfloor = - 2 }[/math]

[math]\displaystyle{ \binom{5}{2} = 10 }[/math],   [math]\displaystyle{ \binom{10}{5} = 252 }[/math],   [math]\displaystyle{ \binom{9}{3} = 84 }[/math]

[math]\displaystyle{ W_2 (8) = 3 }[/math],   [math]\displaystyle{ W_3 (18) = 2 }[/math],   [math]\displaystyle{ W_7 (28) = 1 }[/math]

Funkcje te są zaimplementowane w PARI/GP

[math]\displaystyle{ p_n }[/math] = prime(n)

[math]\displaystyle{ \pi (n) }[/math] = primepi(n)

[math]\displaystyle{ P(n) }[/math] = prodeuler(p=2, n, p)

[math]\displaystyle{ \lfloor x \rfloor }[/math] = floor(x)

[math]\displaystyle{ \binom{n}{m} }[/math] = binomial(n, m)

[math]\displaystyle{ W_p (n) }[/math] = valuation(n, p)

Twierdzenie Czebyszewa

W 1852 roku rosyjski matematyk Czebyszew udowodnił, że dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ a \cdot \frac{n}{\log n} \: \underset{n \geqslant 11}{\lt } \: \pi (n) \: \underset{n \geqslant 96098}{\lt } \: b \cdot \frac{n}{\log n} }[/math]

gdzie

[math]\displaystyle{ a = \log (2^{1 / 2} \cdot 3^{1 / 3} \cdot 5^{1 / 5} \cdot 30^{- 1 / 30}) = 0.921292022 \qquad \quad b = \tfrac{6}{5} a = 1.105550428 }[/math]

Dziwnym zrządzeniem losu rezultat ten określany jest jako nierówności Czebyszewa (których nie należy mylić z nierównościami udowodnionymi przez Czebyszewa w teorii prawdopodobieństwa), a twierdzeniem Czebyszewa nazywany jest łatwy wniosek z tych nierówności. Stąd tytuł tego artykułu: „Twierdzenie Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math]”

Twierdzenie Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math] nabrało nowego życia, gdy w 1936 Erdos zelementaryzował jego dowód. Elementarny dowód daje mniej dokładne oszacowania, ale pozwala zapoznać się z tym pięknym twierdzeniem nawet uczniom szkoły podstawowej.

Czytelnik powinien mieć świadomość, że rezultat ten ma już jedynie znaczenie historyczne – dzisiaj dysponujemy znacznie lepszymi oszacowaniami funkcji [math]\displaystyle{ \pi (n) }[/math] oraz [math]\displaystyle{ p_n }[/math]

[math]\displaystyle{ \frac{n}{\log n} \left( 1 + \frac{1}{\log n} \right) \underset{n \geqslant 599}{\lt } \pi (n) \underset{n \geqslant 2}{\lt } \frac{n}{\log n} \left( 1 + \frac{1.28}{\log n} \right) }[/math]

[math]\displaystyle{ n (\log n + \log \log n - 1) \underset{n \geqslant 2}{\lt } p_n \underset{n \geqslant 6}{\lt } n (\log n + \log \log n) }[/math]

Przedstawimy tutaj elementarny dowód twierdzenia Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math] oraz analogiczne oszacowanie dla funkcji [math]\displaystyle{ p_n }[/math].

Twierdzenie A1
Prawdziwe są następujące oszacowania:

[math]\displaystyle{ 0.72 \cdot n \log n \underset{n \geqslant 1}{\lt } p_n \underset{n \geqslant 3}{\lt } 2n \log n }[/math]

[math]\displaystyle{ \frac{2}{3} \cdot \frac{n}{\log n} \underset{n \geqslant 3}{\lt } \pi (n) \underset{n \geqslant 2}{\lt } \frac{2 n}{\log n} }[/math]

Dowód powyższego twierdzenia jest łatwy, ale wymaga udowodnienia kolejno wielu, przeważnie bardzo prostych, twierdzeń pomocniczych.

Oszacowanie [math]\displaystyle{ p_n }[/math] od dołu i [math]\displaystyle{ \pi (n) }[/math] od góry

Rozpoczniemy od oszacowania liczby [math]\displaystyle{ \binom{2n}{n} }[/math]. Badanie właściwości tego współczynnika dwumianowego jest kluczowe dla naszego dowodu.

Twierdzenie A2
Niech [math]\displaystyle{ n, k \in \mathbb{N} }[/math]. Współczynnik dwumianowy [math]\displaystyle{ \binom{n}{k} }[/math] jest zawsze liczbą całkowitą dodatnią.

Dowód

Indukcja matematyczna. Ponieważ

[math]\displaystyle{ \binom{0}{0} = \binom{1}{0} = \binom{1}{1} = 1 }[/math]

to twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math]. Zakładając prawdziwość twierdzenia dla wszystkich liczb całkowitych należących do przedziału [math]\displaystyle{ [1, n] }[/math] mamy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ \binom{n + 1}{0} = \binom{n + 1}{n + 1} = 1 }[/math]

Dla [math]\displaystyle{ k }[/math] spełniającego warunek [math]\displaystyle{ 1 \leqslant k \leqslant n }[/math], jest

[math]\displaystyle{ \binom{n + 1}{k} = \binom{n}{k} + \binom{n}{k - 1} }[/math]

Na podstawie założenia indukcyjnego liczby po prawej stronie są liczbami całkowitymi dodatnimi, zatem [math]\displaystyle{ \binom{n + 1}{k} }[/math] dla wszystkich wartości [math]\displaystyle{ k }[/math] jest liczbą całkowitą dodatnią. Co należało pokazać.
□

Twierdzenie A3
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] jest liczbą parzystą.

Dowód

Łatwo zauważamy, że

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{n! \cdot n!} = \frac{2 n \cdot (2 n - 1)!}{n \cdot (n - 1) ! \cdot n!} = 2 \cdot \binom{2 n - 1}{n - 1} }[/math]

□

Twierdzenie A4
Prawdziwe są następujące oszacowania współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math]

[math]\displaystyle{ 3.8^{n + 1} \underset{n \geqslant 80}{\lt } \binom{2 n}{n} \underset{n \geqslant 5}{\lt } 4^{n - 1} }[/math]

Dowód

Indukcja matematyczna. W przypadku lewej nierówności łatwo sprawdzamy, że [math]\displaystyle{ 3.8^{81} \lt \binom{160}{80} }[/math]. Zakładając prawdziwość nierówności dla [math]\displaystyle{ n \geqslant 80 }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ \binom{2 (n + 1)}{n + 1} = \binom{2 n}{n} \cdot \frac{(2 n + 2) (2 n + 1)}{(n + 1) (n + 1)} \gt 3.8^{n + 1} \cdot 2 \cdot \left( 2 - \frac{1}{n + 1} \right) \geqslant 3.8^{n + 1} \cdot 2 \cdot \left( 2 - \frac{1}{80 + 1} \right) \gt 3.8^{n + 1} \cdot 3.9753 \gt 3.8^{n + 2} }[/math]

Prawa nierówność jest prawdziwa dla [math]\displaystyle{ n = 5 }[/math]. Zakładając prawdziwość nierówności dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]:

[math]\displaystyle{ \binom{2 (n + 1)}{n + 1} = \binom{2 n}{n} \cdot \frac{(2 n + 2) (2 n + 1)}{(n + 1) (n + 1)} \lt 4^{n -1} \cdot 2 \cdot \left( 2 - \frac{1}{n + 1} \right) \lt 4^n }[/math]

□

Twierdzenie A5
Dla [math]\displaystyle{ n \geqslant 12 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \gt 3 n }[/math].

Dowód

Indukcja matematyczna. Dowód oprzemy na spostrzeżeniu, że wśród kolejnych sześciu liczb naturalnych [math]\displaystyle{ 6 k, 6 k + 1, 6 k + 2, 6 k + 3, 6 k + 4, 6 k + 5 }[/math] jedynie dwie: [math]\displaystyle{ 6 k + 1 }[/math] i [math]\displaystyle{ 6 k + 5 }[/math] mogą być pierwsze. Wynika stąd, że [math]\displaystyle{ p_{n + 2} \geqslant p_n + 6 }[/math] dla [math]\displaystyle{ n \geqslant 4 }[/math]. Dowód indukcyjny przeprowadzimy, stosując krok równy [math]\displaystyle{ 2 }[/math]. Twierdzenie jest oczywiście prawdziwe dla [math]\displaystyle{ n = 12 }[/math], bowiem [math]\displaystyle{ p_{12} = 37 \gt 3 \cdot 12 = 36 }[/math], podobnie [math]\displaystyle{ p_{13} = 41 \gt 3 \cdot 13 = 39 }[/math]. Zakładając prawdziwość twierdzenia dla wszystkich liczb naturalnych [math]\displaystyle{ k \in [12, n] }[/math], otrzymujemy dla [math]\displaystyle{ n + 2 }[/math]:

[math]\displaystyle{ p_{n + 2} \geqslant p_n + 6 \gt 3 n + 6 = 3 \cdot (n + 2) }[/math]

Uwaga: inaczej mówiąc, dowodzimy twierdzenie osobno dla [math]\displaystyle{ n }[/math] parzystych [math]\displaystyle{ (n \geqslant 12) }[/math] i osobno dla [math]\displaystyle{ n }[/math] nieparzystych [math]\displaystyle{ (n \geqslant 13) }[/math].
□

Twierdzenie A6
Ciąg [math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n }[/math] jest rosnący i ograniczony. Dla wyrazów ciągu [math]\displaystyle{ (a_n) }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ 2 \leqslant a_n \lt 3 }[/math].

Dowód

W artykule, w którym pojęcie współczynnika dwumianowego odgrywa główną rolę, nie mogło zabraknąć dowodu odwołującego się do wzoru dwumianowego

[math]\displaystyle{ \left ( x + y \right )^{n} = \sum_{k=0}^{n} \binom{n}{k} x^{n-k}y^{k} = \binom{n}{0} x^{n} + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^{2} + \ldots + \binom{n}{n}y^{n} }[/math]

gdzie [math]\displaystyle{ \binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} }[/math].

Dowód opiera się na spostrzeżeniu, że [math]\displaystyle{ e = \sum_{k=0}^{\infty} \frac{1}{k!} = 2.718281828 \ldots }[/math], a wykorzystanie wzoru dwumianowego pozwala przekształcić wyrażenie [math]\displaystyle{ \left( 1 + \frac{1}{n} \right)^n }[/math] do postaci sumy z wyraźnie wydzielonym czynnikiem [math]\displaystyle{ \frac{1}{k!} }[/math]. Stosując wzór dwumianowy, możemy zapisać [math]\displaystyle{ n }[/math]-ty wyraz ciągu [math]\displaystyle{ (a_n) }[/math] w postaci

[math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n = }[/math]

[math]\displaystyle{ \quad \; = \sum_{k=0}^{n} \binom{n}{k} \frac{1}{n^k} = }[/math]

[math]\displaystyle{ \quad \; = 2 + \sum_{k=2}^{n} \frac{n!}{k! \cdot (n - k)!} \cdot \frac{1}{n^k} = }[/math]

[math]\displaystyle{ \quad \; = 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \frac{n \cdot (n - 1) \cdot \ldots \cdot (n - (k - 1))}{n^k} = }[/math]

[math]\displaystyle{ \quad \; = 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n} \right) }[/math]

Odpowiednio dla wyrazu [math]\displaystyle{ a_{n + 1} }[/math] mamy

[math]\displaystyle{ a_{n + 1} = \left( 1 + \frac{1}{n + 1} \right)^{n + 1} = }[/math]

[math]\displaystyle{ \qquad \: = 2 + \sum_{k=2}^{n + 1} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n + 1} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n + 1} \right) \gt }[/math]

[math]\displaystyle{ \qquad \: \gt 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n + 1} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n + 1} \right) \gt }[/math]

[math]\displaystyle{ \qquad \: \gt 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n} \right) = }[/math]

[math]\displaystyle{ \qquad \: = a_n }[/math]

Ostatnia nierówność jest prawdziwa, bo dla dowolnej liczby [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] jest [math]\displaystyle{ 1 - \frac{x}{n + 1} \gt 1 - \frac{x}{n} }[/math]

Zatem ciąg [math]\displaystyle{ (a_n) }[/math] jest rosnący. Musimy jeszcze wykazać, że jest ograniczony od góry. Pokazaliśmy wyżej, że wyraz [math]\displaystyle{ a_n }[/math] może być zapisany w postaci

[math]\displaystyle{ a_n = 2 + \sum_{k=2}^{n} \frac{1}{k!} \cdot \left( 1 - \frac{1}{n} \right) \cdot \ldots \cdot \left( 1 - \frac{k - 1}{n} \right) }[/math]

Ponieważ czynniki w nawiasach są dodatnie i mniejsze od jedności, to

[math]\displaystyle{ a_n \leqslant 2 + \sum_{k=2}^{n} \frac{1}{k!} = }[/math]

[math]\displaystyle{ \quad \; \leqslant 1 + 1 + \sum_{k=2}^{n} \frac{1}{2^{k-1}} = }[/math]

[math]\displaystyle{ \quad \; = 1 + \left ( 1 + \frac{1}{2} + \frac{1}{2^2} + \ldots + \frac{1}{2^{n-1}}\right ) = }[/math]

[math]\displaystyle{ \quad \; = 1 + \frac{1 - \left ( \frac{1}{2} \right )^{n}}{1 - \frac{1}{2}} = }[/math]

[math]\displaystyle{ \quad \; = 1 + 2 - \frac{1}{2^{n-1}} \lt }[/math]

[math]\displaystyle{ \quad \; \lt 3 }[/math]

Druga nierówność (nieostra) jest prawdziwa, bo dla [math]\displaystyle{ k \geqslant 2 }[/math] zachodzi oczywista nierówność [math]\displaystyle{ k! \geqslant 2^{k - 1} }[/math]. Do sumy ujętej w nawiasy zastosowaliśmy wzór na sumę częściową szeregu geometrycznego.

Ponieważ [math]\displaystyle{ a_1 = 2 }[/math], to prawdziwe jest oszacowanie [math]\displaystyle{ 2 \leqslant a_n \lt 3 }[/math]. Zauważmy jeszcze (już bez dowodu), że ciąg [math]\displaystyle{ (a_n) }[/math], jako rosnący i ograniczony od góry, jest zbieżny. Granicą ciągu [math]\displaystyle{ (a_n) }[/math] jest liczba niewymierna [math]\displaystyle{ e = 2.718281828 \ldots }[/math], która jest podstawą logarytmu naturalnego.
□

Twierdzenie A7
Prawdziwe są następujące oszacowania:

[math]\displaystyle{ n^n \underset{n \geqslant 13}{\lt } p_1 p_2 \cdot \ldots \cdot p_n \underset{n \geqslant 3}{\lt } (n \log n)^n }[/math]

Dowód

Indukcja matematyczna. Udowodnimy tylko oszacowanie od dołu. Dowód oszacowania od góry przedstawimy po zakończeniu dowodu twierdzenia A1. Łatwo sprawdzamy, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 13 }[/math]. Zakładając prawdziwość twierdzenia dla liczb naturalnych [math]\displaystyle{ k \in [13, n] }[/math] mamy dla [math]\displaystyle{ n + 1 }[/math]:

[math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n p_{n + 1} \gt n^n \cdot p_{n + 1} \gt n^n \cdot 3 (n + 1) \gt n^n \cdot \left( 1 + \frac{1}{n} \right)^n \cdot (n + 1) = (n + 1)^{n + 1} }[/math]

Gdzie skorzystaliśmy z faktu, że [math]\displaystyle{ p_n \gt 3 n }[/math] dla [math]\displaystyle{ n \geqslant 12 }[/math] oraz z właściwości rosnącego ciągu [math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n \lt e = 2.718281828 \ldots \lt 3 }[/math] (zobacz twierdzenie A6).
□

Twierdzenie A8
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \frac{P (2 n)}{P (n)} \lt 4^{n - 1} }[/math], gdzie [math]\displaystyle{ P (n) }[/math] oznacza iloczyn wszystkich liczb pierwszych nie większych od [math]\displaystyle{ n }[/math].

Dowód

Rozważmy współczynnik dwumianowy

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{n! \cdot n!} = \frac{2 n \cdot (2 n - 1) \cdot \ldots \cdot (n + 1)}{n!} }[/math]

Każda liczba pierwsza należąca do przedziału [math]\displaystyle{ [n + 1, 2 n] }[/math] występuje w liczniku wypisanego wyżej ułamka i nie występuje w mianowniku. Wynika stąd oszacowanie

[math]\displaystyle{ \binom{2 n}{n} = C \cdot \underset{n + 1 \leqslant p_k \leqslant 2 n}{\prod p_k} \gt \underset{n + 1 \leqslant p_k \leqslant 2 n}{\prod p_k} = \frac{P (2 n)}{P (n)} }[/math]

Zauważmy, że wypisany w powyższej nierówności iloczyn liczb pierwszych jest liczbą nieparzystą. Ponieważ współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] jest dodatnią liczbą całkowitą parzystą, zatem również czynnik [math]\displaystyle{ C \geqslant 2 }[/math] musi być dodatnią liczbą całkowitą parzystą. Łącząc uzyskaną nierówność z oszacowaniem z twierdzenia A4, otrzymujemy natychmiast:

[math]\displaystyle{ \frac{P (2 n)}{P (n)} \lt \binom{2 n}{n} \lt 4^{n - 1} }[/math]

Dla [math]\displaystyle{ n = 2, 3, 4 }[/math] sprawdzamy uzyskany rezultat bezpośrednio.
□

Twierdzenie A9
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ P(n) \lt 4^n }[/math]

Dowód

Indukcja matematyczna. Oszacowanie [math]\displaystyle{ P(n) \lt 4^n }[/math] jest prawdziwe dla [math]\displaystyle{ n = 1, 2 }[/math]. Zakładając prawdziwość oszacowania dla wszystkich liczb całkowitych nie większych od [math]\displaystyle{ n }[/math], dla [math]\displaystyle{ n + 1 }[/math] rozpatrzymy dwa przypadki. Jeżeli [math]\displaystyle{ n + 1 = 2 k + 1 }[/math] jest liczbą nieparzystą większą lub równą [math]\displaystyle{ 3 }[/math], to mamy

[math]\displaystyle{ P(n + 1) = P (2 k + 1) = P (2 k + 2) = P (k + 1) \cdot \frac{P (2 k + 2)}{P (k + 1)} \lt 4^{k + 1} \cdot 4^k = 4^{2 k + 1} = 4^{n + 1} }[/math]

gdzie skorzystaliśmy z założenia indukcyjnego i oszacowania z twierdzenia A8.

Jeżeli [math]\displaystyle{ n + 1 = 2 k }[/math] jest liczbą parzystą większą lub równą [math]\displaystyle{ 4 }[/math], to mamy

[math]\displaystyle{ P(n + 1) = P (2 k) = P (k) \cdot \frac{P (2 k)}{P (k)} \lt 4^k \cdot 4^{k - 1} = 4^{2 k - 1} \lt 4^{2 k} = 4^{n + 1} }[/math]

gdzie ponownie skorzystaliśmy z założenia indukcyjnego i oszacowania z twierdzenia A8.
□

Twierdzenie A10
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \gt \frac{1}{2 \log 2} \cdot n \log n }[/math].

Dowód

Ponieważ z definicji [math]\displaystyle{ P(p_n) = p_1 p_2 \cdot \ldots \cdot p_n }[/math], to korzystając z oszacowań uzyskanych w twierdzeniach A7 i A9 dostajemy dla [math]\displaystyle{ n \geqslant 13 }[/math]

[math]\displaystyle{ n^n \lt p_1 p_2 \cdot \ldots \cdot p_n = P (p_n) \lt 4^{p_n} }[/math]

Logarytmując obie strony nierówności, mamy

[math]\displaystyle{ n \log n \lt p_n \cdot \log 4 }[/math]

Skąd natychmiast wynika dowodzone oszacowanie

[math]\displaystyle{ p_n \gt \frac{1}{2 \log 2} \cdot n \log n \gt 0.72 \cdot n \log n }[/math]

Prawdziwość powyższej nierówności dla [math]\displaystyle{ n \leqslant 12 }[/math] sprawdzamy bezpośrednio.
□

Twierdzenie A11
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (2 n) - \pi (n) \lt 2 \log 2 \cdot \frac{n}{\log n} }[/math].

Dowód

Każda liczba pierwsza należąca do przedziału [math]\displaystyle{ [n + 1, 2 n] }[/math] jest dzielnikiem współczynnika dwumianowego

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{n! \cdot n!} = \frac{2 n \cdot (2 n - 1) \cdot \ldots \cdot (n + 1)}{n!} }[/math]

bowiem dzieli licznik i nie dzieli mianownika. Ponieważ dla każdej z tych liczb jest [math]\displaystyle{ p \gt n }[/math], to

[math]\displaystyle{ n^{\pi (2 n) - \pi (n)} \lt \prod_{n \lt p_i \leqslant 2 n} p_i \lt \binom{2 n}{n} \lt 4^n }[/math]

Ostatnia nierówność wynika z twierdzenia A4. Logarytmując, dostajemy

[math]\displaystyle{ [\pi (2 n) - \pi (n)] \cdot \log n \lt 2 n \cdot \log 2 }[/math]

Czyli

[math]\displaystyle{ \pi (2 n) - \pi (n) \lt 2 \log 2 \cdot \frac{n}{\log n} }[/math]

□

Twierdzenie A12
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (n) \lt 2 \cdot \frac{n}{\log n} }[/math].

Dowód

Indukcja matematyczna. Oszacowanie [math]\displaystyle{ \pi (n) \lt 2 \cdot \frac{n}{\log n} }[/math] jest prawdziwe dla [math]\displaystyle{ 2 \leqslant n \leqslant 62 }[/math], co łatwo sprawdzamy przez bezpośrednie wyliczenie. W programie GP/PARI wystarczy wpisać polecenie:

for(n = 2, 62, if( primepi(n) >= 2 * n/log(n), print(n) ))

Zakładając prawdziwość wzoru dla wszystkich liczb naturalnych należących do przedziału [math]\displaystyle{ [2, n] }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

a) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą parzystą, to:

[math]\displaystyle{ \pi (n + 1) = \pi (n) = 2 \cdot \frac{n}{\log n} \lt 2 \cdot \frac{n + 1}{\log (n + 1)} }[/math]

Ostatnia nierówność wynika ze spostrzeżenia, że funkcja [math]\displaystyle{ \frac{x}{\log x} }[/math] jest funkcją rosnącą dla [math]\displaystyle{ x \gt e \approx 2.71828 }[/math]. Można też wykorzystać oszacowanie [math]\displaystyle{ \log(1 + x) \lt x }[/math] prawdziwe dla [math]\displaystyle{ x \gt 0 }[/math].

b) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą nieparzystą, to możemy położyć [math]\displaystyle{ n + 1 = 2 k + 1 }[/math] i otrzymujemy:

[math]\displaystyle{ \pi (n + 1) = \pi (2 k + 1) }[/math]

[math]\displaystyle{ \quad = \pi (2 k + 2) }[/math]

[math]\displaystyle{ \quad = \pi (k + 1) + [\pi (2 k + 2) - \pi (k + 1)] }[/math]

[math]\displaystyle{ \quad \lt 2 \cdot \frac{k + 1}{\log (k + 1)} + 2 \log 2 \cdot \frac{k + 1}{\log (k + 1)} }[/math]

[math]\displaystyle{ \quad = (1 + \log 2) \cdot \frac{2 k + 2}{\log (k + 1)} }[/math]

[math]\displaystyle{ \quad \lt \left[ 1.7 \cdot \frac{2 k + 2}{\log (k + 1)} \cdot \frac{\log (2 k + 1)}{2 k + 1} \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]

[math]\displaystyle{ \quad = \left[ 1.7 \cdot \frac{2 k + 2}{2 k + 1} \cdot \frac{\log (2 k + 2)}{\log (k + 1)} \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]

[math]\displaystyle{ \quad = \left[ 1.7 \cdot \left( 1 + \frac{1}{2 k + 1} \right) \cdot \frac{\log (k + 1) + \log 2}{\log (k + 1)} \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]

[math]\displaystyle{ \quad = \left[ 1.7 \cdot \left( 1 + \frac{1}{2 k + 1} \right) \cdot \left( 1 + \frac{\log 2}{\log (k + 1)} \right) \right] \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]

[math]\displaystyle{ \quad \lt 2 \cdot \frac{2 k + 1}{\log (2 k + 1)} }[/math]

[math]\displaystyle{ \quad = 2 \cdot \frac{n + 1}{\log (n + 1)} }[/math]

Ostatnia nierówność wynika z faktu, że czynnik w nawiasie kwadratowym maleje wraz ze wzrostem [math]\displaystyle{ k }[/math] i dla [math]\displaystyle{ k = 63 }[/math] osiąga wartość [math]\displaystyle{ 1.9989 \ldots }[/math]
□

Wykładnik z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w [math]\displaystyle{ n! }[/math]

Uzyskanie kolejnych oszacowań wymaga znalezienia wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} }[/math].

Definicja A13
Funkcję [math]\displaystyle{ \lfloor x \rfloor }[/math] (czytaj: całość z [math]\displaystyle{ x }[/math]) definiujemy jako największą liczbę całkowitą nie większą od [math]\displaystyle{ x }[/math]. Operacyjnie możemy ją zdefiniować następująco: niech liczby [math]\displaystyle{ x, \varepsilon \in \mathbb{R} }[/math], liczba [math]\displaystyle{ k \in \mathbb{Z} }[/math] oraz [math]\displaystyle{ 0 \leqslant \varepsilon \lt 1 }[/math], jeżeli [math]\displaystyle{ x = k + \varepsilon }[/math], to [math]\displaystyle{ \lfloor x \rfloor = \lfloor k + \varepsilon \rfloor = k }[/math].

Twierdzenie A14
Dla [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math], [math]\displaystyle{ x \in \mathbb{R} }[/math] jest [math]\displaystyle{ \left \lfloor \frac{x}{n} \right\rfloor = \left \lfloor \frac{\left \lfloor x \right \rfloor}{n} \right \rfloor }[/math].

Dowód

Korzystając z definicji A13, przedstawmy liczbę w postaci [math]\displaystyle{ x = k + \varepsilon }[/math], gdzie [math]\displaystyle{ 0 \leqslant \varepsilon \lt 1 }[/math].

Z twierdzenia o dzieleniu z resztą liczbę [math]\displaystyle{ k }[/math] możemy zapisać w postaci [math]\displaystyle{ k = q n + r }[/math], gdzie [math]\displaystyle{ 0 \leqslant r \leqslant n - 1 }[/math], mamy zatem [math]\displaystyle{ x = q n + r + \varepsilon }[/math]. Ponieważ [math]\displaystyle{ 0 \leqslant r + \varepsilon \lt n }[/math], to po podzieleniu przez [math]\displaystyle{ n }[/math] dostajemy

[math]\displaystyle{ 0 \leqslant \frac{r + \varepsilon}{n} \lt 1 }[/math]

czyli

[math]\displaystyle{ \left \lfloor \frac{x}{n} \right \rfloor = \left \lfloor \frac{qn + r + \varepsilon }{n} \right \rfloor = \left \lfloor q + \frac{r + \varepsilon }{n} \right \rfloor = q }[/math]

Podobnie, ponieważ [math]\displaystyle{ 0 \leqslant r \lt n }[/math], to [math]\displaystyle{ 0 \leqslant \frac{r}{n} \lt 1 }[/math] i otrzymujemy

[math]\displaystyle{ \left\lfloor \frac{\left \lfloor x \right\rfloor}{n} \right\rfloor = \left \lfloor \frac{\left \lfloor qn + r + \varepsilon \right \rfloor}{n} \right \rfloor = \left \lfloor \frac{qn + r}{n} \right \rfloor = \left \lfloor q + \frac{r}{n} \right \rfloor = q }[/math]

□

Twierdzenie A15
Niech [math]\displaystyle{ x \in \mathbb{R} }[/math]. Liczba [math]\displaystyle{ \lfloor 2 x \rfloor - 2 \lfloor x \rfloor }[/math] przyjmuje wartości [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math].

Dowód

Niech [math]\displaystyle{ x = k + \varepsilon }[/math], gdzie [math]\displaystyle{ 0 \leqslant \varepsilon \lt 1 }[/math]. Mamy

[math]\displaystyle{ \lfloor 2 x \rfloor - 2 \lfloor x \rfloor = \lfloor 2 k + 2 \varepsilon \rfloor - 2 \lfloor k + \varepsilon \rfloor = 2 k + \lfloor 2 \varepsilon \rfloor - 2 k -2 \lfloor \varepsilon \rfloor = \lfloor 2 \varepsilon \rfloor }[/math]

Ponieważ [math]\displaystyle{ 0 \leqslant 2 \varepsilon \lt 2 }[/math], zatem [math]\displaystyle{ \lfloor 2 \varepsilon \rfloor = 0 }[/math] lub [math]\displaystyle{ \lfloor 2 \varepsilon \rfloor = 1 }[/math].
□

Bardzo istotnym rezultatem (z punktu widzenia przyszłych obliczeń) będzie znalezienie wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w iloczynie [math]\displaystyle{ 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n = n! }[/math]

Definicja A16
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą, zaś [math]\displaystyle{ a }[/math] dowolną liczbą naturalną. Jeżeli liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia liczby naturalnej [math]\displaystyle{ n \geqslant 2 }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ a }[/math], to powiemy, że funkcja [math]\displaystyle{ W_p (n) }[/math] przyjmuje wartość [math]\displaystyle{ a }[/math]. Fakt ten możemy zapisać następująco

[math]\displaystyle{ W_p (n) = a \qquad\qquad \iff \qquad\qquad p^{a} \mid n \qquad \text{i} \qquad p^{a + 1} \nmid n }[/math]

Przykład A17
[math]\displaystyle{ W_5 (100) = 2 }[/math],   [math]\displaystyle{ W_7 (42) = 1 }[/math],   ponieważ [math]\displaystyle{ 11! = 2^8 \cdot 3^4 \cdot 5^2 \cdot 7 \cdot 11 }[/math], to [math]\displaystyle{ W_3 (11!) = 4 }[/math]

Wprost z definicji funkcji [math]\displaystyle{ W_p (n) }[/math] wynikają następujące właściwości:

Twierdzenie A18

Podstawowe własności funkcji [math]\displaystyle{ W_p (n) }[/math]

1. [math]\displaystyle{ \;\; W_p (n \cdot m) = W_p (n) + W_p (m) }[/math]
2. [math]\displaystyle{ \;\; W_p (n \cdot p^a) = a + W_p (n) }[/math]
3. [math]\displaystyle{ \;\; W_{p}\left ( \frac{n}{m} \right ) = W_{p}\left ( n \right ) - W_{p}\left ( m \right ) \quad \text{o ile} \quad \frac{n}{m}\in \mathbb{Z}_{+} }[/math]
4. [math]\displaystyle{ \;\; p \nmid n \quad\quad \iff \quad\quad W_p (n) = 0 }[/math]

Twierdzenie A19
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą. Ilość liczb podzielnych przez [math]\displaystyle{ p }[/math] i występujących w ciągu [math]\displaystyle{ 1, 2, 3, \ldots, n }[/math] wynosi [math]\displaystyle{ r = \left\lfloor \frac{n}{p} \right\rfloor }[/math].

Dowód

Wśród liczb naturalnych [math]\displaystyle{ 1, 2, 3, \ldots, n }[/math] istnieje pewna ilość liczb podzielnych przez [math]\displaystyle{ p }[/math]. Liczby te możemy z łatwością wypisać, będą nimi

[math]\displaystyle{ 1 \cdot p, 2 \cdot p, 3 \cdot p, \ldots, r \cdot p }[/math]

Gdzie [math]\displaystyle{ r }[/math] jest największą liczbą całkowitą nie większą niż [math]\displaystyle{ \frac{n}{p} }[/math], czyli [math]\displaystyle{ r = \left\lfloor \frac{n}{p} \right\rfloor }[/math].
□

Przykład A20
Ilość liczb całkowitych dodatnich podzielnych przez [math]\displaystyle{ 5 }[/math] i nie większych od [math]\displaystyle{ 63 }[/math] wynosi [math]\displaystyle{ \left\lfloor \frac{63}{5} \right\rfloor = 12 }[/math]. Liczby te to [math]\displaystyle{ 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 }[/math].

Twierdzenie A19 umożliwi nam określenie wykładnika, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] występuje w [math]\displaystyle{ n! }[/math]

Twierdzenie A21
Liczba pierwsza [math]\displaystyle{ p }[/math] występuje w iloczynie [math]\displaystyle{ n! }[/math] z wykładnikiem [math]\displaystyle{ W_p (n!) = \sum_{k = 1}^{\infty} \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]

Dowód

Dowód sprowadza się do znalezienia wartości funkcji [math]\displaystyle{ W_p (n!) }[/math].

[math]\displaystyle{ W_p (n!) = W_p (1 \cdot 2 \cdot 3 \cdot \ldots \cdot n) = W_p \left( p \cdot 2 p \cdot 3 p \cdot \ldots \cdot \left\lfloor \frac{n}{p} \right\rfloor \cdot p \right) }[/math]

Pozostawiliśmy jedynie czynniki podzielne przez [math]\displaystyle{ p }[/math] (czynniki niepodzielne przez [math]\displaystyle{ p }[/math] nie dają wkładu do wykładnika, z jakim [math]\displaystyle{ p }[/math] występuje w [math]\displaystyle{ n! }[/math]), wyłączając czynnik [math]\displaystyle{ p }[/math] z każdej z liczb [math]\displaystyle{ p, 2 p, 3 p, \ldots, \left\lfloor \frac{n}{p} \right\rfloor \cdot p }[/math] mamy

[math]\displaystyle{ W_p (n!) = W_p \left( p^{\lfloor n / p \rfloor} \cdot 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p} \right\rfloor \right) = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p} \right\rfloor \right) }[/math]

Otrzymane wyrażenie przekształcamy analogicznie jak wyżej

[math]\displaystyle{ W_p (n!) = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( p \cdot 2 p \cdot 3 p \cdot \ldots \cdot \left\lfloor \frac{\lfloor n / p \rfloor}{p} \right\rfloor \cdot p \right) }[/math]

Z twierdzenia A14 wiemy, że dla [math]\displaystyle{ x \in \mathbb{R} }[/math] i [math]\displaystyle{ n \in \mathbb{Z}_{+} }[/math] jest:

[math]\displaystyle{ \left\lfloor \frac{\lfloor x \rfloor}{n} \right\rfloor = \left \lfloor \frac{x}{n} \right \rfloor }[/math]

zatem

[math]\displaystyle{ W_p (n!) = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( p \cdot 2 p \cdot 3 p \cdot \ldots \cdot \left\lfloor \frac{n}{p^2} \right\rfloor \cdot p \right) = }[/math]

[math]\displaystyle{ \;\, = \left\lfloor \frac{n}{p} \right\rfloor + W_p \left( p^{\lfloor n / p^2 \rfloor} \cdot 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p^2} \right\rfloor \right) = }[/math]

[math]\displaystyle{ \;\, = \left\lfloor \frac{n}{p} \right\rfloor + \left\lfloor \frac{n}{p^2} \right\rfloor + W_p \left( 1 \cdot 2 \cdot 3 \cdot \ldots \cdot \left\lfloor \frac{n}{p^2} \right\rfloor \right) }[/math]

Oczywiście opisaną wyżej procedurę możemy powtarzać wielokrotnie. Zakończenie następuje wtedy, gdy wykładnik liczby pierwszej [math]\displaystyle{ p }[/math] osiągnie wartość tak dużą, że [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math]. Ponieważ nie wiemy, jaka to wartość (choć możemy ją oszacować), to stosujemy zapis

[math]\displaystyle{ W_p (n!) = \sum_{k = 1}^{\infty} \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]

zdając sobie sprawę z tego, że w rzeczywistości sumowanie obejmuje jedynie skończoną liczbę składników.
□

Uwaga A22
Należy zauważyć, że liczba sumowań jest skończona, bowiem bardziej precyzyjnie możemy powyższy wzór zapisać w postaci

[math]\displaystyle{ W_p (n!) = \sum_{k = 1}^B \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]

gdzie [math]\displaystyle{ B = \lfloor \log_2 (n) \rfloor }[/math]. Jest tak dlatego, że jeżeli [math]\displaystyle{ k }[/math] przekroczy [math]\displaystyle{ \lfloor \log_2 (n) \rfloor }[/math], to dla liczby pierwszej [math]\displaystyle{ p = 2 }[/math], jak również dla wszystkich innych liczb pierwszych mamy

[math]\displaystyle{ \frac{n}{p^k} \lt 1 }[/math]

czyli dla [math]\displaystyle{ k \gt B }[/math] sumujemy same zera.

Przykład A23
Niech [math]\displaystyle{ n = 30 }[/math], [math]\displaystyle{ p = 3 }[/math]

[math]\displaystyle{ W_3 (30!) = W_3 (1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 30) = }[/math]

[math]\displaystyle{ \quad = W_3 (3\cdot 6 \cdot 9 \cdot 12 \cdot 15 \cdot 18 \cdot 21 \cdot 24 \cdot 27 \cdot 30) = }[/math]

[math]\displaystyle{ \quad = W_3 (3^{10} \cdot 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10) = }[/math]

[math]\displaystyle{ \quad = 10 + W_3 (1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10) = }[/math]

[math]\displaystyle{ \quad = 10 + W_3 (3 \cdot 6 \cdot 9) = }[/math]

[math]\displaystyle{ \quad = 10 + W_3 (3^3 \cdot 1 \cdot 2 \cdot 3) = }[/math]

[math]\displaystyle{ \quad = 10 + 3 + W_3 (1 \cdot 2 \cdot 3) = }[/math]

[math]\displaystyle{ \quad = 10 + 3 + W_3 (3) = }[/math]

[math]\displaystyle{ \quad = 10 + 3 + 1 = }[/math]

[math]\displaystyle{ \quad = 14 }[/math]

Co jest zgodne ze wzorem:

[math]\displaystyle{ W_3 (30!) = \left\lfloor \frac{30}{3} \right\rfloor + \left\lfloor \frac{30}{3^2} \right\rfloor + \left\lfloor \frac{30}{3^3} \right\rfloor = 10 + 3 + 1 = 14 }[/math]

Podobnie jak w poprzednim podrozdziale będziemy badali współczynnik dwumianowy postaci [math]\displaystyle{ \binom{2 n}{n} }[/math]. Teraz już łatwo możemy policzyć wykładnik, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze tego współczynnika dwumianowego.

Twierdzenie A24
Liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] z wykładnikiem

[math]\displaystyle{ u = \sum^{\infty}_{k = 1} \left( \left \lfloor \frac{2n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right) }[/math]

Dowód

Ponieważ [math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} }[/math], to liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia na czynniki pierwsze liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] z wykładnikiem:

[math]\displaystyle{ W_p \left( \binom{2 n}{n} \right) = W_p ((2 n) !) - 2 W_p (n!) = \sum^{\infty}_{k = 1} \left \lfloor \frac{2n}{p^{k}} \right \rfloor - 2 \sum^{\infty}_{k = 1} \left \lfloor \frac{n}{p^{k}} \right \rfloor = \sum^{\infty}_{k = 1} \left( \left \lfloor \frac{2n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right) }[/math]

□

Twierdzenie A25
Liczby pierwsze spełniające warunek [math]\displaystyle{ p \gt \sqrt{2 n} }[/math] występują w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u = 1 }[/math] lub [math]\displaystyle{ u = 0 }[/math].

Dowód

Jeżeli [math]\displaystyle{ p \gt \sqrt{2 n} }[/math], to dla [math]\displaystyle{ k \geqslant 2 }[/math] mamy [math]\displaystyle{ p^k \geqslant p^2 \gt 2 n \gt n }[/math]. Zatem dla [math]\displaystyle{ k \geqslant 2 }[/math] jest [math]\displaystyle{ \left\lfloor \frac{2 n}{p^k} \right\rfloor = \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math] i otrzymujemy

[math]\displaystyle{ u = \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) = \left \lfloor \frac{2 n}{p} \right \rfloor - 2 \left \lfloor \frac{n}{p} \right \rfloor }[/math]

Na mocy twierdzenia A15 (dla [math]\displaystyle{ x = \tfrac{n}{p} }[/math]), dostajemy natychmiast, że [math]\displaystyle{ u = 1 }[/math] lub [math]\displaystyle{ u = 0 }[/math].
□

Twierdzenie A26
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą. Jeżeli [math]\displaystyle{ p^a \biggr\rvert \binom{2 n}{n} }[/math], to [math]\displaystyle{ p^a \leqslant 2 n }[/math].

Dowód

Niech [math]\displaystyle{ u }[/math] oznacza wykładnik, z jakim liczba pierwsza [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze. Mamy

[math]\displaystyle{ u = \sum_{k = 1}^{\infty} \left( \left\lfloor \frac{2 n}{p^k} \right\rfloor - 2 \left\lfloor \frac{n}{p^k} \right\rfloor \right) }[/math]

gdzie sumowanie przebiega w rzeczywistości od [math]\displaystyle{ k = 1 }[/math] do [math]\displaystyle{ k = s }[/math], a wartość liczby [math]\displaystyle{ s }[/math] wynika z warunku [math]\displaystyle{ p^s \leqslant 2 n \lt p^{s + 1} }[/math]. Ponieważ sumowane wyrazy są równe [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy natychmiast oszacowanie [math]\displaystyle{ u \leqslant s }[/math], skąd wynika następujący ciąg nierówności

[math]\displaystyle{ p^a \leqslant p^u \leqslant p^s \leqslant 2 n }[/math]

□

Oszacowanie [math]\displaystyle{ p_n }[/math] od góry i [math]\displaystyle{ \pi (n) }[/math] od dołu

Z twierdzenia A26 wynika natychmiast

Twierdzenie A27
Niech [math]\displaystyle{ \binom{2 n}{n} = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s }[/math] będzie rozkładem współczynnika dwumianowego na czynniki pierwsze. Dla każdej liczby pierwszej [math]\displaystyle{ q_i }[/math], [math]\displaystyle{ i = 1, \ldots, s }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ q^{\alpha_i}_i \leqslant 2 n }[/math].

Uwaga: w powyższym twierdzeniu [math]\displaystyle{ q_i }[/math] nie oznacza [math]\displaystyle{ i }[/math]-tej liczby pierwszej, a pewną liczbą pierwszą o indeksie [math]\displaystyle{ i }[/math] ze zboru liczb pierwszych [math]\displaystyle{ q_1, \ldots q_s }[/math], które wchodzą do rozkładu współczynnika dwumianowego na czynniki pierwsze z wykładnikiem większym od zera.

Twierdzenie A28
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest następujące oszacowanie współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math]

[math]\displaystyle{ \binom{2 n}{n} \leqslant (2 n)^{\pi (2 n)} \lt (2 n + 1)^{\pi (2 n + 1)} }[/math]

Dowód

Dowód wynika natychmiast z twierdzenia A27, bowiem

[math]\displaystyle{ \binom{2 n}{n} = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s \leqslant (2 n)^s \leqslant (2 n)^{\pi (2 n)} \lt (2 n + 1)^{\pi (2 n + 1)} }[/math]

□

Twierdzenie A29
Dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]

Dowód

W twierdzeniu A4 oszacowaliśmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math]. Przepiszemy, to twierdzenie w postaci bardziej czytelnej dla potrzeb tego dowodu

[math]\displaystyle{ \left( \sqrt{3.8} \right)^{2 n} \lt \left( \sqrt{3.8} \right)^{2 n + 1} \lt \left( \sqrt{3.8} \right)^{2 n + 2} = 3.8^{n + 1} \lt \binom{2 n}{n} }[/math]

Nierówności te są prawdziwe dla [math]\displaystyle{ n \geqslant 80 }[/math]. Z twierdzenia A28 mamy

[math]\displaystyle{ \left( \sqrt{3.8} \right)^{2 n} \lt \left( \sqrt{3.8} \right)^{2 n + 1} \lt \binom{2 n}{n} \leqslant (2 n)^{\pi (2 n)} \lt (2 n + 1)^{\pi (2 n + 1)} }[/math]

Łącząc odpowiednie oszacowania współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] od góry z odpowiednimi oszacowaniami od dołu, dostajemy

[math]\displaystyle{ (2 n + 1)^{\pi (2 n + 1)} \gt \left( \sqrt{3.8} \right)^{2 n + 1} }[/math]

[math]\displaystyle{ (2 n)^{\pi (2 n)} \gt \left( \sqrt{3.8} \right)^{2 n} }[/math]

Zatem zarówno dla parzystych, jak i nieparzystych liczb [math]\displaystyle{ m \geqslant 160 }[/math] jest

[math]\displaystyle{ m^{\pi (m)} \gt \left( \sqrt{3.8} \right)^m }[/math]

[math]\displaystyle{ \pi (m) \cdot \log m \gt m \cdot \log \left( \sqrt{3.8} \right) }[/math]

Czyli

[math]\displaystyle{ \pi (m) \gt \frac{1}{2} \cdot \log \left ( 3.8 \right ) \cdot \frac{m}{\log m} \gt 0.6675 \cdot \frac{m}{\log m} \gt \frac{2}{3} \cdot \frac{m}{\log m} }[/math]

Dla [math]\displaystyle{ m = 3, 4, \ldots, 159 }[/math] prawdziwość nierówności sprawdzamy przez bezpośrednie wyliczenie. W programie GP/PARI wystarczy wykonać polecenie

for(n = 2, 200, if( primepi(n) <= 2/3 * n/log(n), print(n) ))

□

Twierdzenie A30
Niech [math]\displaystyle{ n \geqslant 3 }[/math]. Dla [math]\displaystyle{ n }[/math]-tej liczby pierwszej [math]\displaystyle{ p_n }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \lt 2 n \log n }[/math]

Dowód

Rozpoczniemy od pokazania, że dla [math]\displaystyle{ x \gt 83499.14 }[/math] prawdziwe jest następujące oszacowanie funkcji [math]\displaystyle{ \log x }[/math] od góry

[math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 4} }[/math]

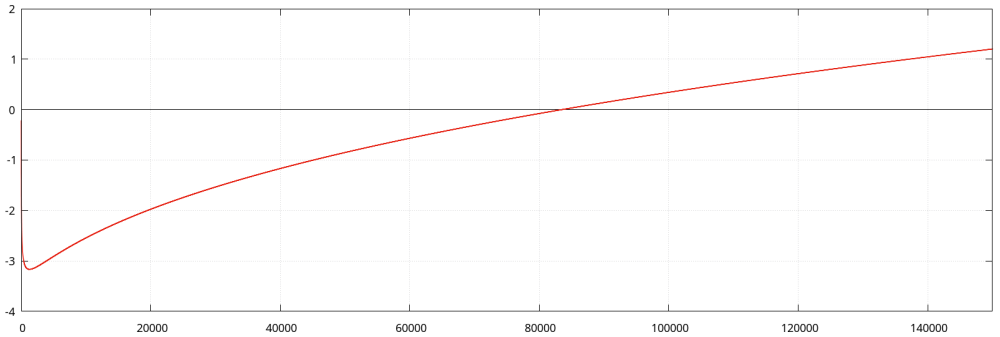
Wiemy, że dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] istnieje takie [math]\displaystyle{ x_0 }[/math], że dla [math]\displaystyle{ x \gt x_0 }[/math] jest [math]\displaystyle{ \log x \lt x^{1 / n} }[/math]. Zatem dla odpowiednio dużych [math]\displaystyle{ x }[/math] z pewnością będzie [math]\displaystyle{ \tfrac{2}{3} \cdot x^{1 / 4} \gt \log x \, }[/math]^[a]. Zamieszczony niżej obrazek przedstawia wykres funkcji [math]\displaystyle{ f( x ) = \tfrac{2}{3} \cdot x^{1 / 4} - \log x }[/math].

Wpisując w PARI/GP polecenie

solve(x = 80000, 10^5, 2/3 * x^(1/4) - log(x))

wyliczamy, że funkcja [math]\displaystyle{ f( x ) }[/math] przecina oś [math]\displaystyle{ O X }[/math] w punkcie [math]\displaystyle{ x = 83499.136 \ldots }[/math] Wynika stąd, że dla [math]\displaystyle{ x \gt 83499.14 }[/math] prawdziwa jest nierówność

[math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 4} }[/math]

Z twierdzenia A29 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]. Kładąc [math]\displaystyle{ n = p_k }[/math], otrzymujemy dla [math]\displaystyle{ k \geqslant 2 }[/math]

[math]\displaystyle{ k = \pi (p_k) \gt \frac{2}{3} \cdot \frac{p_k}{\log p_k} }[/math]

Zatem

[math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \log p_k \qquad \qquad (1) }[/math]

Korzystając z wcześniej pokazanego oszacowania, otrzymujemy nierówność prawdziwą dla [math]\displaystyle{ p_k \gt 83499 }[/math]

[math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{2}{3} \cdot (p_k)^{1 / 4} }[/math]

czyli

[math]\displaystyle{ (p_k)^{3 / 4} \lt k }[/math]

[math]\displaystyle{ p_k \lt k^{4 / 3} }[/math]

Wstawiając to oszacowanie ponownie do [math]\displaystyle{ (1) }[/math], dostajemy

[math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{4}{3} \cdot \log k = 2 k \log k }[/math]

Wpisując w PARI/GP polecenie

for(k = 1, 10^5, p = prime(k); if( p > 83499, print("end"); break() ); if( p >= 2 * k * log(k), print(k) ))

łatwo sprawdzamy, że oszacowanie [math]\displaystyle{ p_k \lt 2 k \log k }[/math] jest prawdziwe dla [math]\displaystyle{ k \geqslant 3 }[/math].

---

[a] Bardziej precyzyjnie: pochodna funkcji [math]\displaystyle{ f(x) = \tfrac{2}{3} \cdot x^{1 / 4} - \log x }[/math] jest równa [math]\displaystyle{ \frac{1}{6 x^{3 / 4}} - \frac{1}{x} }[/math] (zobacz WolframAlpha). Łatwo sprawdzamy, że pochodna jest ujemna w przedziale [math]\displaystyle{ (0, 1296) }[/math] i dodatnia w przedziale [math]\displaystyle{ (1296, \infty) }[/math]. Wynika stąd, że funkcja [math]\displaystyle{ f( x ) }[/math] jest funkcją malejącą dla [math]\displaystyle{ x \lt 1296 }[/math] i rosnącą dla [math]\displaystyle{ x \gt 1296 }[/math].
□

Dowód twierdzenia A30 kończy dowód całego twierdzenia A1. Możemy teraz dokończyć dowód twierdzenia A7 i pokazać, że dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest oszacowanie:

[math]\displaystyle{ p_1 \cdot \ldots \cdot p_n \lt (n \log n)^n }[/math]

Dowód

Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 3 }[/math]. Zakładając prawdziwość twierdzenia dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]:

[math]\displaystyle{ p_1 \cdot \ldots \cdot p_n p_{n + 1} \lt (n \log n)^n \cdot p_{n + 1} \lt }[/math]

[math]\displaystyle{ \quad \lt n^n \cdot (\log n)^n \cdot 2 (n + 1) \log (n + 1) \leqslant }[/math]

[math]\displaystyle{ \quad \leqslant n^n \cdot \left( 1 + \frac{1}{n} \right)^n \cdot (n + 1) \cdot (\log n)^n \cdot \log (n + 1) \lt }[/math]

[math]\displaystyle{ \quad \lt (n + 1)^{n + 1} \cdot [\log (n + 1)]^n \cdot \log (n + 1) = }[/math]

[math]\displaystyle{ \quad = [(n + 1) \cdot \log (n + 1)]^{n + 1} }[/math]

Gdzie skorzystaliśmy z twierdzenia A30 oraz z faktu, że ciąg [math]\displaystyle{ a_n = \left( 1 + \frac{1}{n} \right)^n }[/math] jest ciągiem ograniczonym [math]\displaystyle{ 2 \leqslant a_n \lt 3 }[/math] (zobacz twierdzenie A6).
□

Uwagi do dowodu

Wydłużając znacząco czas obliczeń, moglibyśmy nieco poprawić uzyskane wyżej oszacowanie i udowodnić

Twierdzenie A31
Niech [math]\displaystyle{ n \geqslant 3 }[/math]. Dla [math]\displaystyle{ n }[/math]-tej liczby pierwszej [math]\displaystyle{ p_n }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ p_n \lt 1.875 \cdot n \log n }[/math]

Dowód

Rozpoczniemy od pokazania, że dla [math]\displaystyle{ x \gt 7572437.23 }[/math] prawdziwe jest następujące oszacowanie funkcji [math]\displaystyle{ \log x }[/math] od góry

[math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 5} }[/math]

Wiemy, że dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] istnieje takie [math]\displaystyle{ x_0 }[/math], że dla [math]\displaystyle{ x \gt x_0 }[/math] jest [math]\displaystyle{ \log x \lt x^{1 / n} }[/math]. Zatem dla odpowiednio dużych [math]\displaystyle{ x }[/math] z pewnością będzie [math]\displaystyle{ \tfrac{2}{3} \cdot x^{1 / 5} \gt \log x \, }[/math]^[a]. Wpisując w PARI/GP polecenie

solve(x = 10^6, 10^7, 2/3 * x^(1/5) - log(x))

wyliczamy, że funkcja [math]\displaystyle{ f(x) = \tfrac{2}{3} \cdot x^{1 / 5} - \log x }[/math] przecina oś [math]\displaystyle{ O X }[/math] w punkcie [math]\displaystyle{ x = 7572437.223 \ldots }[/math] Wynika stąd, że dla [math]\displaystyle{ x \gt 7572437.23 }[/math] prawdziwa jest nierówność

[math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 5} }[/math]

Z twierdzenia A29 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]. Kładąc [math]\displaystyle{ n = p_k }[/math], otrzymujemy dla [math]\displaystyle{ k \geqslant 2 }[/math]

[math]\displaystyle{ k = \pi (p_k) \gt \frac{2}{3} \cdot \frac{p_k}{\log p_k} }[/math]

Zatem

[math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \log p_k \qquad \qquad (1) }[/math]

Korzystając z wcześniej pokazanego oszacowania, otrzymujemy nierówność prawdziwą dla [math]\displaystyle{ p_k \gt 7572437 }[/math]

[math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{2}{3} \cdot (p_k)^{1 / 5} }[/math]

czyli

[math]\displaystyle{ (p_k)^{4 / 5} \lt k }[/math]

[math]\displaystyle{ p_k \lt k^{5 / 4} }[/math]

Wstawiając to oszacowanie ponownie do [math]\displaystyle{ (1) }[/math], dostajemy

[math]\displaystyle{ p_k \lt \frac{3}{2} \cdot k \cdot \frac{5}{4} \cdot \log k = 1.875 \cdot k \log k }[/math]

Wpisując w PARI/GP polecenie

for(k = 1, 10^7, p = prime(k); if( p > 7572437, print("end"); break() ); if( p >= 2 * k * log(k), print(k) ))

łatwo sprawdzamy, że oszacowanie [math]\displaystyle{ p_k \lt 1.875 \cdot k \log k }[/math] jest prawdziwe dla [math]\displaystyle{ k \geqslant 3 }[/math].

---

[a] Bardziej precyzyjnie: pochodna funkcji [math]\displaystyle{ f(x) = \tfrac{2}{3} \cdot x^{1 / 5} - \log x }[/math] jest równa [math]\displaystyle{ \frac{2}{15 x^{4 / 5}} - \frac{1}{x} }[/math] (zobacz WolframAlpha). Łatwo sprawdzamy, że pochodna jest ujemna w przedziale [math]\displaystyle{ (0, 23730.46875) }[/math] i dodatnia w przedziale [math]\displaystyle{ (23730.46875, \infty) }[/math]. Wynika stąd, że funkcja [math]\displaystyle{ f( x ) }[/math] jest funkcją malejącą dla [math]\displaystyle{ x \lt 23730.46875 }[/math] i rosnącą dla [math]\displaystyle{ x \gt 23730.46875 }[/math].
□

Twierdzenie A32
Niech [math]\displaystyle{ n \geqslant 2 }[/math]. Dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ \pi (n) \lt 1.733 \cdot \frac{n}{\log n} }[/math]

Dowód

Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] jest

[math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} \gt n^{4 / 5} }[/math]

Ostatnia nierówność wynika z faktu, że dla [math]\displaystyle{ x \gt 7572437.223 \ldots }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ \frac{2}{3} \cdot \frac{x}{\log x} \gt x^{4 / 5} }[/math]

Korzystając z twierdzenia A9 możemy napisać ciąg nierówności

[math]\displaystyle{ 4^n \gt P (n) = p_1 p_2 \cdot \ldots \cdot p_{\pi (n)} \gt \pi (n)^{\pi (n)} \gt (n^{4 / 5})^{\pi (n)} = n^{4 \pi (n) / 5} }[/math]

skąd otrzymujemy, że dla [math]\displaystyle{ n \geqslant 7572438 }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ \pi (n) \lt 1.733 \cdot \frac{n}{\log n} }[/math]

W GP/PARI sprawdzamy, że otrzymana nierówność jest prawdziwa dla [math]\displaystyle{ n \geqslant 2 }[/math]

for(n = 2, 8*10^6, if( primepi(n) >= 1.733 * n/log(n), print(n) ))

□

Uwaga A33
Dowód twierdzenia A31 wymagał wykorzystania polecenia PARI/GP, w którym wielokrotnie była wywoływana funkcja prime(n). Analogiczna sytuacja miała miejsce w przypadku twierdzenia A32 – tam musieliśmy wielokrotnie wywoływać funkcję primepi(n). Znacznie lepiej w takim przypadku jest napisać krótki program, który zamiast wielokrotnie wywoływać te funkcje, będzie je obliczał w sposób ciągły w całym testowanym przedziale wartości. Taka zmiana znacząco skraca czas obliczeń. Podane niżej programy Test1(n) i Test2(n) wywołane z parametrami n = 520000 i odpowiednio n = 8*10^6 odpowiadają poleceniom

for(s = 1, 520000, if( prime(s) >= s^(5/4), print(s) ))

for(n = 2, 8 * 10^6, if( primepi(n) >= 1.733 * n / log(n), print(n) ))

ale wykonywane są znacznie szybciej.

Test1(n) = 
\\ test oszacowania: prime(k) >= k^(5/4) dla 1 <= k <= n
\\ bez bezpośredniego odwoływania się do funkcji prime(k)
{
local(p, k);
k = 1;
p = 2;
while( k <= n,
       if( p >= k^(5/4), print(k) );
       k = k + 1;
       p = nextprime(p + 1);  \\ liczba p ma wartość prime(k)
     );
}

Test2(n) = 
\\ test oszacowania: primepi(k) < 1.733*k/log(k) dla 2 <= k <= n 
\\ bez bezpośredniego odwoływania się do funkcji primepi(k)
{
local(s, k);
s = 1;
k = 2;
while( k <= n,
       if( s >= 1.733 * k / log(k), print(k) );
       k = k + 1;
       s = s + isprime(k);  \\ dla kolejnych k liczba s ma wartość primepi(k)
     );
}

Uwaga A34
Czytelnik nie powinien mieć złudzeń, że postępując podobnie, uzyskamy istotne polepszenie oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math] lub [math]\displaystyle{ p_n }[/math]. Już osiągnięcie tą drogą oszacowania [math]\displaystyle{ p_n \lt 1.6 \cdot n \log n }[/math] przekracza możliwości obliczeniowe współczesnych komputerów. Wystarczy zauważyć, że nierówność

[math]\displaystyle{ \log x \lt \frac{2}{3} \cdot x^{1 / 16} }[/math]

jest prawdziwa dla [math]\displaystyle{ x \gt 7.671 \cdot 10^{32} }[/math].

Zastosowania

Ciekawy rezultat wynika z twierdzenia A7, ale wcześniej musimy udowodnić twierdzenie o średniej arytmetycznej i geometrycznej.

Twierdzenie A35
Dla dowolnych liczb dodatnich [math]\displaystyle{ a_1, a_2, \ldots, a_n }[/math] średnia arytmetyczna jest nie mniejsza od średniej geometrycznej

[math]\displaystyle{ \frac{a_1 + a_2 + \ldots + a_n}{n} \geqslant \sqrt[n]{a_1 a_2 \cdot \ldots \cdot a_n} }[/math]

Dowód

Twierdzenie jest w sposób oczywisty prawdziwe dla [math]\displaystyle{ n = 1 }[/math]. Równie łatwo stwierdzamy prawdziwość nierówności dla [math]\displaystyle{ n = 2 }[/math]

[math]\displaystyle{ (a_1 - a_2)^2 \geqslant 0 }[/math]

[math]\displaystyle{ a^2_1 - 2 a_1 a_2 + a^2_2 \geqslant 0 }[/math]

[math]\displaystyle{ a^2_1 + 2 a_1 a_2 + a^2_2 \geqslant 4 a_1 a_2 }[/math]

[math]\displaystyle{ (a_1 + a_2)^2 \geqslant 4 a_1 a_2 }[/math]

[math]\displaystyle{ \frac{a_1 + a_2}{2} \geqslant \sqrt{a_1 a_2} }[/math]

Dla potrzeb dowodu zapiszemy dowodzoną nierówność w postaci

[math]\displaystyle{ \left( \frac{a_1 + a_2 + \ldots + a_n}{n} \right)^n \geqslant a_1 a_2 \cdot \ldots \cdot a_n }[/math]

Zakładając, że twierdzenie jest prawdziwe dla wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ n }[/math] dla [math]\displaystyle{ n + 1 }[/math] mamy

a) w przypadku gdy [math]\displaystyle{ n + 1 = 2 k }[/math] jest liczbą parzystą

[math]\displaystyle{ \left( \frac{a_1 + a_2 + \ldots + a_{n + 1}}{n + 1} \right)^{n + 1} = \left( \frac{a_1 + a_2 + \ldots + a_{2 k}}{2 k} \right)^{2 k} = }[/math]

[math]\displaystyle{ \quad = \left[ \left( \frac{\frac{a_1 + a_2}{2} + \frac{a_3 + a_4}{2} + \ldots + \frac{a_{2 k - 1} + a_{2 k}}{2}}{k} \right)^k \right]^2 \geqslant }[/math]

[math]\displaystyle{ \quad \geqslant \left( \frac{a_1 + a_2}{2} \cdot \frac{a_3 + a_4}{2} \cdot \ldots \cdot \frac{a_{2 k - 1} + a_{2 k}}{2} \right)^2 \geqslant }[/math]

[math]\displaystyle{ \quad \geqslant \left( \sqrt{a_1 a_2} \cdot \sqrt{a_3 a_4} \cdot \ldots \cdot \sqrt{a_{2 k - 1} a_{2 k}} \right)^2 = }[/math]

[math]\displaystyle{ \quad = a_1 a_2 \cdot \ldots \cdot a_{2 k} = }[/math]

[math]\displaystyle{ \quad = a_1 a_2 \cdot \ldots \cdot a_{n + 1} }[/math]

Gdzie skorzystaliśmy z założenia indukcyjnego i prawdziwości dowodzonego twierdzenia dla [math]\displaystyle{ n = 2 }[/math].

b) w przypadku gdy [math]\displaystyle{ n + 1 = 2 k - 1 }[/math] jest liczbą nieparzystą, możemy skorzystać z udowodnionego wyżej punktu a) dla parzystej ilości liczb

[math]\displaystyle{ a_1, a_2, \ldots, a_{2 k - 1}, S }[/math]

gdzie przez [math]\displaystyle{ S }[/math] oznaczyliśmy średnią arytmetyczną liczb [math]\displaystyle{ a_1, a_2, \ldots, a_{2 k - 1} }[/math]

[math]\displaystyle{ S = \frac{a_1 + a_2 + \ldots + a_{2 k - 1}}{2 k - 1} }[/math]

Na mocy punktu a) prawdziwa jest nierówność

[math]\displaystyle{ \left( \frac{a_1 + a_2 + \ldots + a_{2 k - 1} + S}{2 k} \right)^{2 k} = \left( \frac{(2 k - 1) S + S}{2 k} \right)^{2 k} \geqslant a_1 a_2 \cdot \ldots \cdot a_{2 k - 1} \cdot S }[/math]

Skąd otrzymujemy

[math]\displaystyle{ S^{2 k} \geqslant a_1 a_2 \cdot \ldots \cdot a_{2 k - 1} \cdot S }[/math]

[math]\displaystyle{ S^{2 k - 1} \geqslant a_1 a_2 \cdot \ldots \cdot a_{2 k - 1} }[/math]

Co należało pokazać.
□

Twierdzenie A36
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwa jest nierówność [math]\displaystyle{ p_1 + p_2 + \ldots + p_n \gt n^2 }[/math].

Dowód

Korzystając z twierdzeń A7 i A35 możemy napisać następujący ciąg nierówności dla [math]\displaystyle{ n }[/math] kolejnych liczb pierwszych

[math]\displaystyle{ \frac{p_1 + p_2 + \ldots + p_n}{n} \geqslant \sqrt[n]{p_1 \cdot p_2 \cdot \ldots \cdot p_n} \gt \sqrt[n]{n^n} = n }[/math]

Stąd otrzymujemy natychmiast tezę twierdzenia, którą sprawdzamy dla [math]\displaystyle{ n \lt 13 }[/math]. Do sprawdzenia można wykorzystać proste polecenie w PARI/GP

for(n = 1, 20, s = 0; for(k = 1, n, s = s + prime(k)); if( s <= n^2, print(n) ))

□

Twierdzenie A1 pozwala nam udowodnić różne oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math] i [math]\displaystyle{ p_n }[/math], które byłyby trudne do uzyskania inną drogą. Wykorzystujemy do tego znany fakt, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ n_0 }[/math], że dla każdego [math]\displaystyle{ n \gt n_0 }[/math] prawdziwa jest nierówność [math]\displaystyle{ \log x \lt x^{\varepsilon} }[/math]. Inaczej mówiąc, funkcja [math]\displaystyle{ \log x }[/math] rośnie wolniej niż najwolniej rosnąca funkcja potęgowa. Nim przejdziemy do dowodu takich przykładowych oszacowań, udowodnimy pomocnicze twierdzenie, które wykorzystamy przy szacowaniu.

Twierdzenie A37
Prawdziwe są następujące nierówności:

1.    [math]\displaystyle{ e^x \gt x \qquad \qquad \qquad \quad \:\, }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R} }[/math]

2.    [math]\displaystyle{ e^x \gt 2 x \qquad \qquad \qquad \;\;\,\, }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R} }[/math]

3.    [math]\displaystyle{ \log x \lt n \cdot x^{1 / n} \qquad \quad \;\;\: }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] i dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]

4.    [math]\displaystyle{ \log x \leqslant n (x^{1 / n} - 1) \qquad }[/math] dla każdego [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] i dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]

Dowód

Punkt 1. i punkt 2.

Ponieważ funkcję [math]\displaystyle{ \exp (x) }[/math] możemy zdefiniować w sposób równoważny wzorem

[math]\displaystyle{ e^x = \sum_{k = 0}^{\infty} \frac{x^k}{k!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} + \ldots }[/math]

to funkcja [math]\displaystyle{ e^x }[/math] jest funkcją dodatnią, bo dla [math]\displaystyle{ x \gt 0 }[/math] sumujemy tylko wyrazy dodatnie, dla [math]\displaystyle{ x = 0 }[/math] mamy [math]\displaystyle{ e^0 = 1 }[/math], a dla [math]\displaystyle{ x \lt 0 }[/math] możemy napisać [math]\displaystyle{ e^x = \frac{1}{e^{| x |}} \gt 0 }[/math].

Ponieważ funkcje [math]\displaystyle{ x \, }[/math] i [math]\displaystyle{ \, 2 x }[/math] są ujemne lub równe zero dla [math]\displaystyle{ x \leqslant 0 }[/math], to pozostaje rozważyć jedynie przypadek, gdy [math]\displaystyle{ x \gt 0 }[/math]. Łatwo zauważmy, że

[math]\displaystyle{ e^x - x = \sum_{k = 0}^{\infty} \frac{x^k}{k!} - x = 1 + \sum^{\infty}_{k = 2} \frac{x^k}{k!} \gt 0 }[/math]

[math]\displaystyle{ e^x - 2 x = \sum_{k = 0}^{\infty} \frac{x^k}{k!} - 2 x = 1 - x + \frac{x^2}{2} + \sum_{k = 3}^{\infty} \frac{x^k}{k!} = \frac{1}{2} + \frac{(x - 1)^2}{2} + \sum_{k = 3}^{\infty} \frac{x^k}{k!} \gt 0 }[/math]

Punkt 3.

W rozpatrywanej nierówności połóżmy zmienną pomocniczą [math]\displaystyle{ x = e^y }[/math], gdzie [math]\displaystyle{ y \in \mathbb{R} }[/math]. Otrzymujemy

[math]\displaystyle{ y \lt n \cdot (e^y)^{1 / n} }[/math]

Czyli

[math]\displaystyle{ \frac{y}{n} \lt e^{y / n} }[/math]

Otrzymana nierówność jest prawdziwa dla dowolnego [math]\displaystyle{ \frac{y}{n} \in \mathbb{R} }[/math] na mocy punktu 1. tego twierdzenia.

Punkt 4.

Rozważmy funkcję

[math]\displaystyle{ f(x) = n \cdot x^{1 / n} - \log x }[/math]

Pochodna tej funkcji jest równa

[math]\displaystyle{ f' (x) = \frac{x^{1 / n} - 1}{x} }[/math]

Pochodna jest równa zero dla [math]\displaystyle{ x = 1 }[/math]. Dla [math]\displaystyle{ 0 \lt x \lt 1 }[/math] pochodna jest ujemna, a dla [math]\displaystyle{ x \gt 1 }[/math] jest dodatnia, zatem w punkcie [math]\displaystyle{ x = 1 }[/math] funkcja [math]\displaystyle{ f(x) }[/math] ma minimum i [math]\displaystyle{ f(1) = n }[/math]. Wynika stąd oszacowanie

[math]\displaystyle{ f(x) = n \cdot x^{1 / n} - \log x \geqslant n }[/math]

Skąd otrzymujemy

[math]\displaystyle{ \log x \leqslant n (x^{1 / n} - 1) }[/math]

□

Zadanie A38
Niech [math]\displaystyle{ x \in \mathbb{R}_+ }[/math]. Pokazać, że dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] istnieje takie [math]\displaystyle{ x_0 }[/math], że dla każdego [math]\displaystyle{ x \gt x_0 }[/math] jest [math]\displaystyle{ \log x \lt x^{1 / n} }[/math].

Rozwiązanie

Pierwszy sposób
Rozważmy ciąg nierówności

[math]\displaystyle{ \log x \lt 2 n \cdot x^{1 / 2 n} \lt x^{1 / n} }[/math]

Z twierdzenia A37 wiemy, że pierwsza nierówność jest prawdziwa dla dowolnych [math]\displaystyle{ x \in \mathbb{R}_+ }[/math] i [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Podnosząc strony drugiej nierówności do potęgi [math]\displaystyle{ 2 n }[/math] otrzymujemy [math]\displaystyle{ (2 n)^{2 n} \cdot x \lt x^2 }[/math], czyli nierówność ta jest prawdziwa dla [math]\displaystyle{ x \gt (2 n)^{2 n} }[/math]. Wynika stąd, że wystarczy przyjąć [math]\displaystyle{ x_0 = (2 n)^{2 n} }[/math].

Drugi sposób
Nierówność [math]\displaystyle{ \log x \lt x^{1 / n} }[/math] możemy równoważnie zapisać w postaci [math]\displaystyle{ x \lt \exp (x^{1 / n}) }[/math]. Jeżeli położymy [math]\displaystyle{ x = t^n }[/math], to otrzymamy nierówność [math]\displaystyle{ t^n {\lt e^t} }[/math]. Ponieważ

[math]\displaystyle{ e^t = \sum_{k = 0}^{\infty} \frac{t^k}{k!} = 1 + t + \frac{t^2}{2} + \frac{t^3}{6} + \frac{t^4}{24} + \frac{t^5}{120} + \ldots }[/math]

to

[math]\displaystyle{ e^t \gt \frac{t^{n + 1}}{(n + 1) !} \gt t^n }[/math]

Pierwsza nierówność jest prawdziwa dla [math]\displaystyle{ t \gt 0 }[/math], bo pomijamy wyrazy dodatnie, a druga dla [math]\displaystyle{ t \gt (n + 1) ! }[/math] Wystarczy zatem przyjąć [math]\displaystyle{ x_0 = [(n + 1) !]^n }[/math]. Ponieważ [math]\displaystyle{ [(n + 1) !]^n \gt (2 n)^{2 n} }[/math] dla [math]\displaystyle{ n \geqslant 4 }[/math], to jest to gorsze oszacowanie wartości [math]\displaystyle{ x_0 }[/math].
□

Twierdzenie A39
Dla funkcji [math]\displaystyle{ p_n }[/math] i [math]\displaystyle{ \pi (n) }[/math] prawdziwe są następujące oszacowania:

[math]\displaystyle{ 10 n \underset{n \geqslant 6473}{\lt } p_n \underset{n \geqslant 2}{\lt } n^2 }[/math]

[math]\displaystyle{ \sqrt{n} \underset{n \geqslant 5}{\lt } \pi (n) \underset{n \geqslant 64721}{\lt } \frac{n}{10} }[/math]

Dowód

Lewa górna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 1 }[/math] jest [math]\displaystyle{ p_n \gt 0.72 \cdot n \log n }[/math]. Wystarczy rozwiązać nierówność:

[math]\displaystyle{ 0.72 \cdot \log n \gt 10 }[/math]

czyli [math]\displaystyle{ n \gt \exp \left( \frac{10}{0.72} \right) = 1076137.5 }[/math]

W PARI/GP wpisujemy polecenie:

for(n=1, 11*10^5, if( prime(n) <= 10*n, print(n) ))

Prawa górna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] jest [math]\displaystyle{ p_n \lt 2 n \log n }[/math]. Zatem wystarczy pokazać, że [math]\displaystyle{ 2 n \log n \lt n^2 }[/math]. Korzystając z twierdzenia A37, łatwo zauważmy, że dla [math]\displaystyle{ n \gt 16 }[/math] jest:

[math]\displaystyle{ n - 2 \log n \gt n - 2 \cdot 2 \cdot n^{1 / 2} = \sqrt{n} \left( \sqrt{n} - 4 \right) \gt 0 }[/math]

Przypadki [math]\displaystyle{ n \leqslant 16 }[/math] sprawdzamy bezpośrednio.

Lewa dolna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 3 }[/math] jest [math]\displaystyle{ \pi (n) \gt \frac{2}{3} \cdot \frac{n}{\log n} }[/math]. Zatem wystarczy pokazać, że [math]\displaystyle{ \frac{2}{3} \cdot \frac{n}{\log n} \gt \sqrt{n} }[/math]. Korzystając z twierdzenia A37, łatwo zauważmy, że dla [math]\displaystyle{ n \gt 6^4 = 1296 }[/math] jest:

[math]\displaystyle{ \frac{2}{3} \cdot \frac{n}{\log n} - \sqrt{n} \gt \frac{2}{3} \cdot \frac{n}{4 \cdot n^{1 / 4}} - \sqrt{n} = \frac{1}{6} \cdot n^{3 / 4} - \sqrt{n} = \frac{1}{6} \sqrt{n} (n^{1 / 4} - 6) \gt 0 }[/math]

Sprawdzenie przypadków [math]\displaystyle{ n \leqslant 1296 }[/math] sprowadza się do wpisania w PARI/GP polecenia:

for(n=1, 2000, if( primepi(n) <= sqrt(n), print(n) ))

Prawa dolna nierówność. Z twierdzenia A1 wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] jest [math]\displaystyle{ \pi (n) \lt \frac{2 n}{\log n} }[/math]. Zatem wystarczy pokazać, że [math]\displaystyle{ \frac{2 n}{\log n} \lt \frac{n}{10} }[/math]. Nierówność ta jest prawdziwa dla [math]\displaystyle{ \log n \gt 20 }[/math], czyli dla

[math]\displaystyle{ n \gt e^{20} \gt 485165195.4 }[/math]

Sprawdzenie przypadków dla [math]\displaystyle{ n \leqslant 490 \cdot 10^6 }[/math] będzie wymagało napisania w PARI/GP krótkiego programu i wywołania go z parametrem n = 490*10^6

Test3(n) =
\\ test oszacowania: primepi(k) < k/10 dla 2 <= k <= n 
\\ bez bezpośredniego odwoływania się do funkcji primepi(k)
{
local(s, k);
s = 1;
k = 2;
while( k <= n,
       if( s >= k/10, print(k) );
       k = k + 1;
       s = s + isprime(k);  \\ dla kolejnych k liczba s ma wartość primepi(k)
     );
}

□

Twierdzenie A40
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n^2})^{n / 3} }[/math]

Dowód

Korzystając kolejno z twierdzeń A30, A37 i A7, łatwo otrzymujemy

[math]\displaystyle{ (p_{n^2})^{n / 3} \lt (2 \cdot n^2 \cdot \log n^2)^{n / 3} }[/math]

[math]\displaystyle{ \;\; = (4 \cdot n^2 \cdot \log n)^{n / 3} }[/math]

[math]\displaystyle{ \;\; \lt (8 \cdot n^{5 / 2})^{n / 3} }[/math]

[math]\displaystyle{ \;\; = (2 \cdot n^{5 / 6})^n }[/math]

[math]\displaystyle{ \;\; \lt n^n }[/math]

[math]\displaystyle{ \;\; \lt p_1 p_2 \cdot \ldots \cdot p_n }[/math]

Zauważmy, że nierówność [math]\displaystyle{ 2 \cdot n^{5 / 6} \lt n }[/math] jest prawdziwa dla [math]\displaystyle{ n \gt 2^6 }[/math]. Sprawdzając bezpośrednio dla [math]\displaystyle{ n \leqslant 64 }[/math] stwierdzamy, że dowodzona nierówność jest prawdziwa dla [math]\displaystyle{ n \geqslant 1 }[/math].
□

Zadanie A41
Korzystając z twierdzenia A40 pokazać, że

•    [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n + 1})^2 \qquad \qquad \text{dla } \; n \geqslant 4 }[/math]
•    [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{2 n})^3 \qquad \qquad \;\; \text{dla } \; n \geqslant 7 }[/math]

Rozwiązanie

Punkt 1.

Ponieważ [math]\displaystyle{ n^2 \gt n + 1 }[/math] dla [math]\displaystyle{ n \geqslant 2 }[/math] oraz [math]\displaystyle{ {\small\frac{n}{3}} \gt 2 }[/math] dla [math]\displaystyle{ n \gt 6 }[/math], to dla [math]\displaystyle{ n \gt 6 }[/math] jest

[math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n^2})^{n / 3} \gt (p_{n + 1})^2 }[/math]

Sprawdzając bezpośrednio dla [math]\displaystyle{ n \leqslant 6 }[/math], łatwo stwierdzamy prawdziwość oszacowania dla [math]\displaystyle{ n \geqslant 4 }[/math].

Punkt 2.

Ponieważ [math]\displaystyle{ n^2 \gt 2 n }[/math] dla [math]\displaystyle{ n \gt 2 }[/math] oraz [math]\displaystyle{ {\small\frac{n}{3}} \gt 3 }[/math] dla [math]\displaystyle{ n \gt 9 }[/math], to dla [math]\displaystyle{ n \gt 9 }[/math] jest

[math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_n \gt (p_{n^2})^{n / 3} \gt (p_{2 n})^3 }[/math]

Sprawdzając bezpośrednio dla [math]\displaystyle{ n \leqslant 9 }[/math], łatwo stwierdzamy prawdziwość oszacowania dla [math]\displaystyle{ n \geqslant 7 }[/math].
□

Twierdzenie A42
Każda liczba pierwsza [math]\displaystyle{ p }[/math], taka że [math]\displaystyle{ p \in \left( \frac{n}{2}, n \right] }[/math] występuje w rozwinięciu [math]\displaystyle{ n! }[/math] na czynniki pierwsze z wykładnikiem równym jeden.

Dowód

Z twierdzenia A21 wiemy, że każda liczba pierwsza [math]\displaystyle{ p }[/math] występuje w iloczynie [math]\displaystyle{ n! }[/math] z wykładnikiem [math]\displaystyle{ W_p (n!) = \sum_{k = 1}^{\infty} \left\lfloor \frac{n}{p^k} \right\rfloor }[/math]

Z założenia [math]\displaystyle{ p \leqslant n }[/math] i [math]\displaystyle{ 2 p \gt n }[/math], zatem:

1.    [math]\displaystyle{ \frac{n}{p} \geqslant 1 }[/math]   oraz   [math]\displaystyle{ \frac{n}{p} \lt 2 }[/math],   czyli   [math]\displaystyle{ \left\lfloor \frac{n}{p} \right\rfloor = 1 }[/math]

2.    [math]\displaystyle{ \frac{n}{p^2} \lt \frac{2}{p} \leqslant 1 }[/math],   czyli   [math]\displaystyle{ \left\lfloor \frac{n}{p^2} \right\rfloor = 0 }[/math]   i tym bardziej   [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math]   dla   [math]\displaystyle{ k \geqslant 3 }[/math]

□

Rezultat uzyskany w twierdzeniu A25 zainspirował nas do postawienia pytania: jakie warunki musi spełniać liczba pierwsza [math]\displaystyle{ p }[/math], aby występowała w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden lub równym zero? Twierdzenia A43 i A45 udzielają na to pytanie precyzyjnej odpowiedzi. Przykłady A44 i A46 to tylko twierdzenia A43 i A45 dla wybranych wartości liczby [math]\displaystyle{ k }[/math]. Jeśli Czytelnik nie miał problemów ze zrozumieniem dowodów twierdzeń A43 i A45, to może je pominąć.

Twierdzenie A43
Niech [math]\displaystyle{ k }[/math] będzie dowolną ustaloną liczbą naturalną. Jeżeli [math]\displaystyle{ n \geqslant 2 (k + 1) \left( k + \tfrac{1}{2} \right) }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left( {\small\frac{n}{k + 1}}, {\small\frac{n}{k + \tfrac{1}{2}}} \right] }[/math], to [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden.

Dowód

Najpierw udowodnimy przypadek [math]\displaystyle{ k = 0 }[/math].

Zauważmy, że każda liczba pierwsza [math]\displaystyle{ p \in (n, 2 n] }[/math] występuje dokładnie jeden raz w liczniku ułamka

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

i nie występuje w mianowniku. Zatem w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze wystąpi z wykładnikiem równym [math]\displaystyle{ 1 }[/math].

Co kończy dowód twierdzenia w przypadku, gdy [math]\displaystyle{ k = 0 }[/math].

Możemy teraz przejść do dowodu dla wszystkich [math]\displaystyle{ k \geqslant 1 }[/math].

Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]

Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Rozważmy dowolną liczbę pierwszą występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:

• [math]\displaystyle{ k p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k }[/math] razy w mianowniku
• [math]\displaystyle{ (k + 1) p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku (jako [math]\displaystyle{ p, 2 p, \ldots, k p }[/math])
• [math]\displaystyle{ (2 k + 1) p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ (k + 1) p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k + 1 }[/math] razy w liczniku
• [math]\displaystyle{ (2 k + 2) p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ (2 k + 1) p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k + 1 }[/math] razy w liczniku (jako [math]\displaystyle{ (k + 1) p, (k + 2) p, \ldots, (2 k + 1) p }[/math])

Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left(\frac{n}{k + 1}, \frac{n}{k + \frac{1}{2}} \right] }[/math] pojawia się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku i dokładnie [math]\displaystyle{ k + 1 }[/math] razy w liczniku ułamka

[math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Zatem występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem jeden.

Niech [math]\displaystyle{ q }[/math] będzie największą liczbą pierwszą nie większą od ustalonej liczby [math]\displaystyle{ 2 k + 1 }[/math]. Rozpatrywane przez nas wielokrotności liczby zwiększają wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ r_i \in \{ 2, 3, \ldots, q \} }[/math]. Dlatego twierdzenie nie może dotyczyć tych liczb i musimy nałożyć warunek

[math]\displaystyle{ r_i \notin \left( \frac{n}{k + 1}, \frac{n}{k + \frac{1}{2}} \right] }[/math]

Warunek ten będzie z pewnością spełniony, gdy

[math]\displaystyle{ q \leqslant 2 k + 1 \leqslant \frac{n}{k + 1} }[/math]

czyli dla [math]\displaystyle{ n }[/math] spełniających nierówność [math]\displaystyle{ n \geqslant (k + 1) (2 k + 1) }[/math].

Oczywiście nie wyklucza to możliwości, że istnieją liczby [math]\displaystyle{ n \lt 2 (k + 1) (k + \tfrac{1}{2}) }[/math], dla których twierdzenie jest prawdziwe. Pozostaje (przy ustalonej wartości liczby [math]\displaystyle{ k }[/math]) bezpośrednio sprawdzić prawdziwość twierdzenia dla [math]\displaystyle{ n \lt 2 (k + 1) (k + \tfrac{1}{2}) }[/math].

Dowód na podstawie twierdzenia A24

Rozważmy najpierw pierwszy składnik sumy

[math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) }[/math]

Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 1 }[/math], to będziemy szukali oszacowania od dołu. Z założenia mamy

1)    [math]\displaystyle{ p \gt \frac{n}{k + 1} \quad\ \implies \quad \frac{n}{p} \lt k + 1 \quad\ \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \leqslant k }[/math]

2)    [math]\displaystyle{ p \leqslant \frac{n}{k + \tfrac{1}{2}} \quad\ \implies \quad \frac{2 n}{p} \geqslant 2 k + 1 \quad\ \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \geqslant 2 k + 1 }[/math]

Zatem

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \geqslant 2 k + 1 - 2 k = 1 }[/math]

Ponieważ każdy ze składników sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 1 }[/math]

Założenie, że [math]\displaystyle{ n \geqslant 2 (k + 1)^2 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy

[math]\displaystyle{ p \gt \frac{n}{k + 1} \quad \implies \quad \frac{2 n}{p} \lt 2 k + 2 \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{(2 n)^s}{p^s} \lt (2 k + 2)^s \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 2)^2}{2 n} \cdot \left( \frac{2 k + 2}{2 n} \right)^{s - 2} \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 2)^2}{2 n} \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \frac{2 n}{p^s} \lt 1 \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \! \! \implies \quad \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math]

Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^s} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 2 (k + 1)^2 }[/math] jest

[math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) = 1 }[/math]

Pozostaje bezpośrednio sprawdzić, dla jakich wartości [math]\displaystyle{ n \lt 2 (k + 1)^2 }[/math] twierdzenie pozostaje prawdziwe.

Ponieważ analiza krotności pojawiania się liczby pierwszej [math]\displaystyle{ p }[/math] jest bardziej precyzyjna, to podajemy, że twierdzenie jest z pewnością prawdziwe dla [math]\displaystyle{ n \geqslant 2 (k + 1) (k + \tfrac{1}{2}) }[/math]
□

Przykład A44
Jeżeli [math]\displaystyle{ n \geqslant 6 }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left( \frac{n}{2}, \frac{2 n}{3} \right] }[/math], to [math]\displaystyle{ p }[/math] występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden.

Dowód

Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]

Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Rozważmy dowolną liczbę pierwszą występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:

• [math]\displaystyle{ p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej jeden raz w mianowniku
• [math]\displaystyle{ 2 p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie jeden raz w mianowniku (jako [math]\displaystyle{ p }[/math])
• [math]\displaystyle{ 3 p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej dwa razy w liczniku
• [math]\displaystyle{ 4 p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 3 p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie dwa razy w liczniku (jako [math]\displaystyle{ 2 p }[/math] i [math]\displaystyle{ 3 p }[/math])

Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math] pojawia się dokładnie jeden raz w mianowniku i dokładnie dwa razy w liczniku ułamka

[math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Zatem występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem jeden.

Wielokrotności liczby [math]\displaystyle{ p }[/math] podnoszą wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ p = 2, 3 }[/math]. Dlatego zakładamy, że [math]\displaystyle{ n \geqslant 6 }[/math], bo dla [math]\displaystyle{ n \geqslant 6 }[/math] liczby pierwsze [math]\displaystyle{ p = 2, 3 }[/math] nie spełniają warunku [math]\displaystyle{ p \in \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math].

Bezpośrednio sprawdzamy, że twierdzenie nie jest prawdziwe dla [math]\displaystyle{ n = 5 }[/math] i liczba [math]\displaystyle{ 3^2 }[/math] dzieli liczbę [math]\displaystyle{ \binom{10}{5} = 252 = 9 \cdot 28 }[/math]

Dowód na podstawie twierdzenia A24

Rozważmy najpierw pierwszy składnik sumy

[math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) }[/math]

Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 1 }[/math], to będziemy szukali oszacowania od dołu. Z założenia mamy

1)    [math]\displaystyle{ p \gt \frac{n}{2} \quad \implies \quad \frac{n}{p} \lt 2 \quad \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \leqslant 1 }[/math]

2)    [math]\displaystyle{ p \leqslant \frac{2 n}{3} \quad \implies \quad \frac{2 n}{p} \geqslant 3 \quad \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \geqslant 3 }[/math]

Zatem

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \geqslant 3 - 2 = 1 }[/math]

Ponieważ każdy ze składników sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 1 }[/math]

Założenie, że [math]\displaystyle{ n \geqslant 9 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy

[math]\displaystyle{ p \gt \frac{n}{2} \quad \implies \quad \frac{(2 n)^k}{p^k} \lt 4^k \quad \implies \quad \frac{2 n}{p^k} \lt \frac{16}{2 n} \cdot \left( \frac{4}{2 n} \right)^{k - 2} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{16}{2 n} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{16}{18} \quad \implies \quad \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math]

Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 9 }[/math] jest

[math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) = 1 }[/math]

Dla [math]\displaystyle{ n = 6, 7 }[/math] żadna liczba pierwsza nie należy do [math]\displaystyle{ \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math]. Dla [math]\displaystyle{ n = 8 }[/math] łatwo sprawdzamy, że liczba [math]\displaystyle{ 5 }[/math] wchodzi do rozkładu liczby [math]\displaystyle{ \binom{16}{8} = 12870 }[/math] na czynniki pierwsze z wykładnikiem równym jeden.

Zatem dla [math]\displaystyle{ n \geqslant 6 }[/math] liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{n}{2}, \tfrac{2 n}{3} \right] }[/math] wchodzi do rozkładu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze z wykładnikiem równym jeden.
□

Twierdzenie A45
Niech [math]\displaystyle{ k }[/math] będzie dowolną ustaloną liczbą całkowitą dodatnią. Jeżeli liczba pierwsza [math]\displaystyle{ p \in \left( \frac{n}{k + \tfrac{1}{2}}, \frac{n}{k} \right] }[/math], to dla [math]\displaystyle{ n \geqslant 2 k (k + \tfrac{1}{2}) }[/math] liczba [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.

Dowód

Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]

Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Rozważmy dowolną liczbę pierwszą [math]\displaystyle{ p }[/math] występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:

• [math]\displaystyle{ k p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k }[/math] razy w mianowniku
• [math]\displaystyle{ (k + 1) p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku (jako [math]\displaystyle{ p, 2 p, \ldots, k p }[/math])
• [math]\displaystyle{ 2 k p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ (k + 1) p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej [math]\displaystyle{ k }[/math] razy w liczniku
• [math]\displaystyle{ (2 k + 1) p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 k p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie [math]\displaystyle{ k }[/math] razy w liczniku (jako [math]\displaystyle{ (k + 1) p, (k + 2) p, \ldots, 2 k p }[/math])

Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left( \frac{n}{k + \frac{1}{2}}, \frac{n}{k} \right] }[/math] pojawia się dokładnie [math]\displaystyle{ k }[/math] razy w mianowniku i dokładnie [math]\displaystyle{ k }[/math] razy w liczniku ułamka

[math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Co oznacza, że [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.

Niech [math]\displaystyle{ q }[/math] będzie największą liczbą pierwszą nie większą od ustalonej liczby [math]\displaystyle{ 2 k }[/math]. Rozpatrywane przez nas wielokrotności liczby [math]\displaystyle{ p }[/math] zwiększają wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ r_i \in \{ 2, 3, \ldots, q \} }[/math]. Dlatego twierdzenie nie może dotyczyć tych liczb i musimy nałożyć warunek

[math]\displaystyle{ r_i \notin \left( \frac{n}{k + \frac{1}{2}}, \frac{n}{k} \right] }[/math]

Warunek ten będzie z pewnością spełniony, gdy

[math]\displaystyle{ q \leqslant 2 k \leqslant \frac{n}{k + \frac{1}{2}} }[/math]

czyli dla [math]\displaystyle{ n }[/math] spełniających nierówność [math]\displaystyle{ n \geqslant 2 k (k + \tfrac{1}{2}) }[/math]. Oczywiście nie wyklucza to możliwości, że istnieją liczby [math]\displaystyle{ n \lt 2 k (k + \tfrac{1}{2}) }[/math], dla których twierdzenie jest prawdziwe. Pozostaje (przy ustalonej wartości liczby [math]\displaystyle{ k }[/math]) bezpośrednio sprawdzić prawdziwość twierdzenia dla [math]\displaystyle{ n \lt 2 k (k + \tfrac{1}{2}) }[/math].

Dowód na podstawie twierdzenia A24

Rozważmy najpierw pierwszy składnik sumy

[math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) }[/math]

Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 0 }[/math], to będziemy szukali oszacowania od góry. Z założenia mamy

1)    [math]\displaystyle{ p \gt \frac{n}{k + \frac{1}{2}} \quad\ \implies \quad \frac{2 n}{p} \lt 2 k + 1 \quad\ \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \leqslant 2 k }[/math]

2)    [math]\displaystyle{ p \leqslant \frac{n}{k} \quad\ \implies \quad \frac{n}{p} \geqslant k \quad\ \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \geqslant k }[/math]

Zatem

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \leqslant 2 k - 2 k = 0 }[/math]

Ponieważ każdy ze składników sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 0 }[/math]

Założenie, że [math]\displaystyle{ 2 n \geqslant (2 k + 1)^2 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy

[math]\displaystyle{ p \gt \frac{2 n}{2 k + 1} \quad \implies \quad \frac{(2 n)^s}{p^s} \lt (2 k + 1)^s \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 1)^2}{2 n} \cdot \left( \frac{2 k + 1}{2 n} \right)^{s - 2} \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \frac{2 n}{p^s} \lt \frac{(2 k + 1)^2}{2 n} \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \frac{2 n}{p^s} \lt 1 \quad \implies }[/math]

[math]\displaystyle{ \qquad \qquad \qquad \; \implies \quad \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math]

Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^s} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^s} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ 2 n \geqslant (2 k + 1)^2 }[/math] jest

[math]\displaystyle{ \sum^{\infty}_{s = 1} \left ( \left \lfloor \frac{2 n}{p^{s}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{s}} \right \rfloor \right ) = 0 }[/math]

Pozostaje bezpośrednio sprawdzić, dla jakich wartości [math]\displaystyle{ n \lt \frac{1}{2} (2 k + 1)^2 }[/math] twierdzenie pozostaje prawdziwe.

Ponieważ analiza krotności pojawiania się liczby pierwszej [math]\displaystyle{ p }[/math] jest bardziej precyzyjna, to podajemy, że twierdzenie jest z pewnością prawdziwe dla [math]\displaystyle{ n \geqslant 2 k (k + \tfrac{1}{2}) }[/math].
□

Przykład A46
Jeżeli [math]\displaystyle{ n \geqslant 8 }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left( \frac{2 n}{5}, \frac{n}{2} \right] }[/math], to [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu liczby [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.

Dowód

Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]

Zapiszmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 n}{n} }[/math] w postaci ułamka

[math]\displaystyle{ \binom{2 n}{n} = \frac{(2 n) !}{(n!)^2} = \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Rozważmy dowolną liczbę pierwszą [math]\displaystyle{ p }[/math] występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:

• [math]\displaystyle{ 2 p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej dwa razy w mianowniku
• [math]\displaystyle{ 3 p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie dwa razy w mianowniku (jako [math]\displaystyle{ p }[/math] i [math]\displaystyle{ 2 p }[/math])
• [math]\displaystyle{ 4 p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 3 p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej dwa razy w liczniku
• [math]\displaystyle{ 5 p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 4 p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie dwa razy w liczniku (jako [math]\displaystyle{ 3 p }[/math] i [math]\displaystyle{ 4 p }[/math])

Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math] pojawia się dokładnie dwa razy w mianowniku i dokładnie dwa razy w liczniku ułamka

[math]\displaystyle{ \frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n} }[/math]

Zatem nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 n}{n} }[/math] na czynniki pierwsze.

Wielokrotności liczby [math]\displaystyle{ p }[/math] podnoszą wykładniki, z jakimi występują liczby pierwsze [math]\displaystyle{ 2 }[/math] i [math]\displaystyle{ 3 }[/math]. Dlatego zakładamy, że [math]\displaystyle{ n \geqslant 8 }[/math], bo dla [math]\displaystyle{ n \geqslant 8 }[/math] liczby pierwsze [math]\displaystyle{ 2, 3 }[/math] nie spełniają warunku [math]\displaystyle{ p \in \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math].

Bezpośrednio sprawdzamy, że twierdzenie nie jest prawdziwe dla [math]\displaystyle{ n = 7 }[/math] i liczba [math]\displaystyle{ 3 }[/math] dzieli liczbę [math]\displaystyle{ \binom{14}{7} = 3432 }[/math]

Dowód na podstawie twierdzenia A24

Rozważmy najpierw pierwszy składnik sumy

[math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) }[/math]

Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 0 }[/math], to będziemy szukali oszacowania od góry. Z założenia mamy

1)    [math]\displaystyle{ p \gt \frac{2 n}{5} \quad \implies \quad \frac{2 n}{p} \lt 5 \quad \implies \quad \left\lfloor \frac{2 n}{p} \right\rfloor \leqslant 4 }[/math]

2)    [math]\displaystyle{ p \leqslant \frac{n}{2} \quad \implies \quad \frac{n}{p} \geqslant 2 \quad \implies \quad \left\lfloor \frac{n}{p} \right\rfloor \geqslant 2 }[/math]

Zatem

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor \leqslant 4 - 4 = 0 }[/math]

Ponieważ każdy ze składników szukanej sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy

[math]\displaystyle{ \left\lfloor \frac{2 n}{p} \right\rfloor - 2 \left\lfloor \frac{n}{p} \right\rfloor = 0 }[/math]

Założenie, że [math]\displaystyle{ n \geqslant 13 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy

[math]\displaystyle{ p \gt \frac{2 n}{5} \quad \implies \quad \frac{(2 n)^k}{p^k} \lt 5^k \quad \implies \quad \frac{2 n}{p^k} \lt \frac{25}{2 n} \cdot \left( \frac{5}{2 n} \right)^{k - 2} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{25}{2 n} \quad \implies \quad \frac{2 n}{p^k} \leqslant \frac{25}{26} \quad \implies \quad \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math]

Jeżeli [math]\displaystyle{ \left\lfloor \frac{2 n}{p^k} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor \frac{n}{p^k} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 13 }[/math] jest

[math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor \frac{2 n}{p^{k}} \right \rfloor - 2 \left \lfloor \frac{n}{p^{k}} \right \rfloor \right ) = 0 }[/math]

Dla [math]\displaystyle{ n = 8, 9 }[/math] żadna liczba pierwsza nie należy do [math]\displaystyle{ \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math].

Dla [math]\displaystyle{ n = 10, 11, 12 }[/math] łatwo sprawdzamy, że liczba [math]\displaystyle{ 5 }[/math] nie dzieli liczb [math]\displaystyle{ \binom{20}{10} = 184756 }[/math], [math]\displaystyle{ \binom{22}{11} = 705432 }[/math] oraz [math]\displaystyle{ \binom{24}{12} = 2704156 }[/math].

Zatem dla [math]\displaystyle{ n \geqslant 8 }[/math] liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{2 n}{5}, \tfrac{n}{2} \right] }[/math] nie dzieli liczby [math]\displaystyle{ \binom{2 n}{n} }[/math].
□

Uwaga A47
Z przykładu A44 nie wynika, że w przedziale [math]\displaystyle{ \left( \frac{n}{2}, \frac{2 n}{3} \right] }[/math] znajduje się choćby jedna liczba pierwsza [math]\displaystyle{ p }[/math]. Analogiczna uwaga jest prawdziwa w przypadku przykładu A46 oraz twierdzeń A43 i A45. Istnienie liczby pierwszej w określonym przedziale będzie tematem kolejnego artykułu.

Przykład A48
Pokazujemy i omawiamy wynik zastosowania twierdzeń A43 i A45 do współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math]. Można udowodnić, że granicę stosowalności obu twierdzeń bardzo dokładnie opisuje warunek [math]\displaystyle{ p \gt \sqrt{2 n} }[/math], co w naszym przypadku daje [math]\displaystyle{ p \gt \sqrt{2 \cdot 3284} \approx 81.04 }[/math].

Pokaż przykład

Wybraliśmy współczynnik dwumianowy [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] dlatego, że w rozkładzie tego współczynnika na czynniki pierwsze występują wszystkie liczby pierwsze [math]\displaystyle{ p \leqslant 107 }[/math], co ułatwia analizowanie występowania liczb pierwszych. Tylko sześć liczb pierwszych: 2, 3, 59, 61, 73, 79 występuje z wykładnikiem większym niż jeden. Ponieważ [math]\displaystyle{ \sqrt{2 \cdot 3284} \approx 81.043 }[/math], zatem liczba 79 jest ostatnią liczbą pierwszą, która mogłaby wystąpić z wykładnikiem większym niż jeden i tak właśnie jest.

Poniżej wypisaliśmy wszystkie liczby pierwsze [math]\displaystyle{ p \leqslant 3284 }[/math], które występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] na czynniki pierwsze. Pogrubienie oznacza, że dana liczba rozpoczyna nowy wiersz w tabeli. Ostatnią pogrubioną i dodatkowo podkreśloną liczbą jest liczba 107, bo wszystkie liczby pierwsze mniejsze od 107 powinny pojawić się w tabeli – oczywiście tak się nie stanie, bo twierdzeń A43 i A45 nie można stosować bez ograniczeń dla coraz większych liczb [math]\displaystyle{ k }[/math].

2⁶, 3⁸, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59², 61², 67, 71, 73², 79², 83, 89, 97, 101, 103, 107, 127, 137, 139, 151, 157, 167, 173, 197, 199, 211, 223, 239, 241, 257, 277, 281, 283, 307, 311, 331, 337, 367, 373, 379, 383, 419, 421, 431, 433, 479, 487, 491, 499, 503, 557, 563, 569, 571, 577, 587, 593, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179

Liczba 821 została pogrubiona (w tabeli), bo jest liczbą pierwszą i wyznacza początek przedziału otwartego, konsekwentnie liczba 821 nie występuje w rozkładzie współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] na czynniki pierwsze.

Czytelnik łatwo sprawdzi, że największą wartością liczby [math]\displaystyle{ k }[/math], dla jakiej można jeszcze stosować twierdzenie A43, jest [math]\displaystyle{ k = 39 }[/math]. Podobnie największą wartością liczby [math]\displaystyle{ k }[/math], dla jakiej można jeszcze stosować twierdzenie A45, jest [math]\displaystyle{ k = 40 }[/math]. Wartości te i odpowiadające im przedziały zostały pogrubione, aby uwidocznić granicę stosowania tych twierdzeń. Łatwo odczytujemy, że twierdzenia A43 i A45 można stosować dla liczb pierwszych [math]\displaystyle{ p }[/math] spełniających warunek [math]\displaystyle{ p \gt 81.09 }[/math]. Co bardzo dokładnie pokrywa się z warunkiem [math]\displaystyle{ p \gt \sqrt{2 \cdot 3284} \approx 81.04 }[/math]

Liczba 73 jest ostatnią poprawnie pokazaną liczbą pierwszą. Po niej nie pojawiają się liczby pierwsze 71 i 67, które występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ \binom{2 \cdot 3284}{3284} }[/math] na czynniki pierwsze.

[math]\displaystyle{ k }[/math]	[math]\displaystyle{ \frac{3284}{k+1} }[/math]	[math]\displaystyle{ p \in \left ( \frac{3284}{k + 1}, \frac{3284}{k + \tfrac{1}{2}} \right ] }[/math]	[math]\displaystyle{ \frac{3284}{k+\tfrac{1}{2}} }[/math]	[math]\displaystyle{ \frac{3284}{k} }[/math]
0	3284	{3299, 3301, ..., 6553, 6563}	6568
1	1642	{1657, 1663, ..., 2161, 2179}	2189,33	3284
2	1094,67	{1097, 1103, ..., 1303, 1307}	1313,60	1642
3	821	{823, 827, ..., 929, 937}	938,29	1094,67
4	656,80	{659, 661, 673, 677, 683, 691, 701, 709, 719, 727}	729,78	821
5	547,33	{557, 563, 569, 571, 577, 587, 593}	597,09	656,80
6	469,14	{479, 487, 491, 499, 503}	505,23	547,33
7	410,50	{419, 421, 431, 433}	437,87	469,14
8	364,89	{367, 373, 379, 383}	386,35	410,50
9	328,40	{331, 337}	345,68	364,89
10	298,55	{307, 311}	312,76	328,40
11	273,67	{277, 281, 283}	285,57	298,55
12	252,62	{257}	262,72	273,67
13	234,57	{239, 241}	243,26	252,62
14	218,93	{223}	226,48	234,57
15	205,25	{211}	211,87	218,93
16	193,18	{197, 199}	199,03	205,25
17	182,44	{}	187,66	193,18
18	172,84	{173}	177,51	182,44
19	164,20	{167}	168,41	172,84
20	156,38	{157}	160,20	164,20
21	149,27	{151}	152,74	156,38
22	142,78	{}	145,96	149,27
23	136,83	{137, 139}	139,74	142,78
24	131,36	{}	134,04	136,83
25	126,31	{127}	128,78	131,36
26	121,63	{}	123,92	126,31
27	117,29	{}	119,42	121,63
28	113,24	{}	115,23	117,29
29	109,47	{}	111,32	113,24
30	105,94	{107}	107,67	109,47
31	102,63	{103}	104,25	105,94
32	99,52	{101}	101,05	102,63
33	96,59	{97}	98,03	99,52
34	93,83	{}	95,19	96,59
35	91,22	{}	92,51	93,83
36	88,76	{89}	89,97	91,22
37	86,42	{}	87,57	88,76
38	84,21	{}	85,30	86,42
39	82,10	{83}	83,14	84,21
40	80,10	{}	81,09	82,10
41	78,19	{79}	79,13	80,10
42	76,37	{}	77,27	78,19
43	74,64	{}	75,49	76,37
44	72,98	{73}	73,80	74,64
45	71,39	{}	72,18	72,98
46	69,87	{}	70,62	71,39
47	68,42	{}	69,14	69,87
48	67,02	{}	67,71	68,42
49	65,68	{}	66,34	67,02
50	64,39	{}	65,03	65,68
51	63,15	{}	63,77	64,39
52	61,96	{}	62,55	63,15
53	60,81	{61}	61,38	61,96
54	59,71	{}	60,26	60,81
55	58,64	{59}	59,17	59,71
56	57,61	{}	58,12	58,64
57	56,62	{}	57,11	57,61
58	55,66	{}	56,14	56,62
59	54,73	{}	55,19	55,66
60	53,84	{}	54,28	54,73
61	52,97	{53}	53,40	53,84
62	52,13	{}	52,54	52,97
63	51,31	{}	51,72	52,13
64	50,52	{}	50,91	51,31
65	49,76	{}	50,14	50,52
66	49,01	{}	49,38	49,76
67	48,29	{}	48,65	49,01
68	47,59	{}	47,94	48,29
69	46,91	{47}	47,25	47,59
70	46,25	{}	46,58	46,91

□