Szeregi liczbowe

07.04.2022

Szeregi nieskończone

Definicja D1
Sumę wszystkich wyrazów ciągu nieskończonego $(a_n)$

$a_1+a_2+a_3+\dots +a_n+\dots =\sum _{k=1}^{\mathrm{\infty }}{a}_k$

nazywamy szeregiem nieskończonym o wyrazach $a_n$.

Definicja D2
Ciąg $S_n=\sum _{k=1}^n{a}_k$ nazywamy ciągiem sum częściowych szeregu $\sum _{k=1}^{\mathrm{\infty }}{a}_k$.

Definicja D3
Szereg $\sum _{k=1}^{\mathrm{\infty }}{a}_k$ będziemy nazywali zbieżnym, jeżeli ciąg sum częściowych $\left(S_n\right)$ jest zbieżny.

Twierdzenie D4 (warunek konieczny zbieżności szeregu)
Jeżeli szereg $\sum _{k=1}^{\mathrm{\infty }}{a}_k$ jest zbieżny, to $\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$.

Dowód

Niech $S_n=\sum _{k=1}^n{a}_k$ będzie ciągiem sum częściowych, wtedy $a_{n+1}=S_{n+1}-S_n$. Z założenia ciąg $(S_n)$ jest zbieżny, zatem

$\underset{n\to \mathrm{\infty }}{lim}{a}_{n+1}=\underset{n\to \mathrm{\infty }}{lim}(S_{n+1}-S_n)=\underset{n\to \mathrm{\infty }}{lim}{S}_{n+1}-\underset{n\to \mathrm{\infty }}{lim}{S}_n=0$

□

Okazuje się, że bardzo łatwo podać przykład szeregów, dla których warunek $\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$ jest warunkiem wystarczającym. Opisany w poniższym twierdzeniu rodzaj szeregów nazywamy szeregami naprzemiennymi.
Twierdzenie D5 (kryterium Leibniza)
Niech ciąg $(a_n)$ będzie ciągiem malejącym o wyrazach nieujemnych. Jeżeli

$\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$

to szereg $\underset{k=1}{\sum ^{\mathrm{\infty }}}(-1{)}^{k+1}\cdot a_k$ jest zbieżny.

Dowód

Grupując wyrazy szeregu po dwa, otrzymujemy sumę częściową postaci

$S_{2m}=(a_1-a_2)+(a_3-a_4)+\dots +(a_{2m-1}-a_{2m})$

Ponieważ ciąg $(a_n)$ jest ciągiem malejącym, to każde wyrażenie w nawiasie jest liczbą nieujemną. Z drugiej strony

$S_{2m}=a_1-(a_2-a_3)-(a_4-a_5)-\dots -(a_{2m-2}-a_{2m-1})-a_{2m}<a_1$

Zatem dla każdego $m$ ciąg sum częściowych $S_{2m}$ jest rosnący i ograniczony od góry, skąd na mocy twierdzenia C11 jest zbieżny, czyli

$\underset{m\to \mathrm{\infty }}{lim}{S}_{2m}=g$

Pozostaje zbadać sumy częściowe $S_{2m+1}$. Rezultat jest natychmiastowy

$\underset{m\to \mathrm{\infty }}{lim}{S}_{2m+1}=\underset{m\to \mathrm{\infty }}{lim}(S_{2m}+a_{2m+1})=\underset{m\to \mathrm{\infty }}{lim}{S}_{2m}+\underset{m\to \mathrm{\infty }}{lim}{a}_{2m+1}=g+0=g$

Co kończy dowód.
□

Twierdzenie D6
Dla $s>1$ prawdziwy jest następujący związek

$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{k^s}=(1-2^{1-s})\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$

Dowód

Zauważmy, że założenie $s>1$ zapewnia zbieżność szeregu po prawej stronie. Zapiszmy szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$ w postaci sumy dla $k$ parzystych i nieparzystych

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\dots$

$=\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(2k-1{)}^s}+\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(2k{)}^s}$

$=\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(2k-1{)}^s}+\frac{1}{2^s}\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$

Otrzymujemy wzór

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(2k-1{)}^s}=(1-2^{-s})\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$

Podobnie rozpiszmy szereg naprzemienny

$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{k^s}=1-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+\frac{1}{5^s}-\dots$

$=\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(2k-1{)}^s}-\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(2k{)}^s}$

$=(1-2^{-s})\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}-\frac{1}{2^s}\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$

$=(1-2^{1-s})\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$

gdzie skorzystaliśmy ze znalezionego wyżej wzoru dla sumy szeregu $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(2k-1{)}^s}$
□

Przykład D7
Szeregi niekończone często definiują ważne funkcje. Dobrym przykładem może być funkcja eta Dirichleta, którą definiuje szereg naprzemienny

$\eta (s)=\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{k^s}$

lub funkcja dzeta Riemanna, którą definiuje inny szereg

$\zeta (s)=\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$

Na podstawie twierdzenia D6 funkcje te są związane wzorem

$\eta (s)=(1-2^{1-s})\zeta (s)$

Dla $s\in {\mathbb{R}}_{+}$ funkcja eta Dirichleta jest zbieżna. Możemy ją wykorzystać do znajdowania sumy szeregu naprzemiennego $\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{k^s}$.

$s=\frac{1}{2}$	$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{\sqrt{k}}=0.604898643421\dots$	WolframAlpha
$s=1$	$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{k}=\log 2=0.693147180559\dots$	WolframAlpha
$s=2$	$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{k^2}=\frac{{\pi }^2}{12}=0.822467033424\dots$	WolframAlpha

Twierdzenie D8
Niech $N\in {\mathbb{Z}}_{+}$. Szeregi $\sum _{k=1}^{\mathrm{\infty }}{a}_k$ oraz $\sum _{k=N}^{\mathrm{\infty }}{a}_k$ są jednocześnie zbieżne lub jednocześnie rozbieżne. W przypadku zbieżności zachodzi związek

$\sum _{k=1}^{\mathrm{\infty }}{a}_k=(a_1+a_2+\dots +a_{N-1})+\sum _{k=N}^{\mathrm{\infty }}{a}_k$

Dowód

Niech $S(n)=\sum _{k=1}^n{a}_k$ (gdzie $n⩾1$) oznacza sumę częściową pierwszego szeregu, a $T(n)=\sum _{k=N}^{\mathrm{\infty }}{a}_k$ (gdzie $n⩾N$) oznacza sumę częściową drugiego szeregu. Dla $n⩾N$ mamy

$S(n)=(a_1+a_2+\dots +a_{N-1})+T(n)$

Widzimy, że dla $n$ dążącego do nieskończoności zbieżność (rozbieżność) jednego ciągu implikuje zbieżność (rozbieżność) drugiego.
□

Twierdzenie D9 (kryterium porównawcze)
Jeżeli istnieje taka liczba całkowita $N_0$, że dla każdego $k>N_0$ jest spełniony warunek

$0⩽a_k⩽b_k$

to

1.    zbieżność szeregu $\sum _{k=1}^{\mathrm{\infty }}{b}_k$ pociąga za sobą zbieżność szeregu $\sum _{k=1}^{\mathrm{\infty }}{a}_k$
2.    rozbieżność szeregu $\sum _{k=1}^{\mathrm{\infty }}{a}_k$ pociąga za sobą rozbieżność szeregu $\sum _{k=1}^{\mathrm{\infty }}{b}_k$

Dowód

Dowód przeprowadzimy dla szeregów $\sum _{k=N_0}^{\mathrm{\infty }}{a}_k$ oraz $\sum _{k=N_0}^{\mathrm{\infty }}{b}_k$, które są (odpowiednio) jednocześnie zbieżne lub jednocześnie rozbieżne z szeregami $\sum _{k=1}^{\mathrm{\infty }}{a}_k$ oraz $\sum _{k=1}^{\mathrm{\infty }}{b}_k$.

Punkt 1.
Z założenia szereg $\sum _{k=N_0}^{\mathrm{\infty }}{b}_k$ jest zbieżny. Niech $\sum _{k=N_0}^{\mathrm{\infty }}{b}_k=b$, zatem z założonych w twierdzeniu nierówności dostajemy

$0⩽\sum _{k=N_0}^n{a}_k⩽\sum _{k=N_0}^n{b}_k⩽b$

Zauważmy, że ciąg sum częściowych $A_n=\sum _{k=N_0}^n{a}_k$ jest ciągiem rosnącym (bo $a_k⩾0$) i ograniczonym od góry. Wynika stąd, że ciąg $\left(A_n\right)$ jest zbieżny, zatem szereg $\sum _{k=N_0}^{\mathrm{\infty }}{a}_k$ jest zbieżny.

Punkt 2.
Z założenia szereg $\sum _{k=N_0}^{\mathrm{\infty }}{a}_k$ jest rozbieżny, a z założonych w twierdzeniu nierówności dostajemy

$0⩽\sum _{k=N_0}^n{a}_k⩽\sum _{k=N_0}^n{b}_k$

Rosnący ciąg sum częściowych $A_n=\sum _{k=N_0}^n{a}_k$ nie może być ograniczony od góry, bo przeczyłoby to założeniu, że szereg $\sum _{k=N_0}^{\mathrm{\infty }}{a}_k$ jest rozbieżny. Wynika stąd i z wypisanych wyżej nierówności, że również ciąg sum częściowych $B_n=\sum _{k=N_0}^n{b}_k$ nie może być ograniczony od góry, zatem szereg $\sum _{k=N_0}^{\mathrm{\infty }}{b}_k$ jest rozbieżny.
□

Twierdzenie D10
Jeżeli szereg $\sum _{k=1}^{\mathrm{\infty }}\left|a_k\right|$ jest zbieżny, to szereg $\sum _{k=1}^{\mathrm{\infty }}{a}_k$ jest również zbieżny.

Dowód

Niech $b_k=a_k+|a_k|$. Z definicji prawdziwe jest następujące kryterium porównawcze

$0⩽b_k⩽2|a_k|$

Zatem z punktu 1. twierdzenia D9 wynika, że szereg $\sum _{k=1}^{\mathrm{\infty }}{b}_k$ jest zbieżny. Z definicji wyrazów ciągu $\left(b_k\right)$ mamy $a_k=b_k-|a_k|$ i możemy napisać

$\sum _{k=1}^{\mathrm{\infty }}{a}_k=\sum _{k=1}^{\mathrm{\infty }}{b}_k-\sum _{k=1}^{\mathrm{\infty }}|a_k|$

Ponieważ szeregi po prawej stronie są zbieżne, to zbieżny jest też szereg $\sum _{k=1}^{\mathrm{\infty }}{a}_k$. Zauważmy, że jedynie w przypadku, gdyby obydwa szeregi po prawej stronie były rozbieżne, nie moglibyśmy wnioskować o zbieżności / rozbieżności szeregu $\sum _{k=1}^{\mathrm{\infty }}{a}_k$, bo suma szeregów rozbieżnych może być zbieżna.
□

Definicja D11
Powiemy, że szereg $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ jest bezwzględnie zbieżny, jeżeli szereg $\sum _{n=0}^{\mathrm{\infty }}|a_n|$ jest zbieżny.

Powiemy, że szereg $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ jest warunkowo zbieżny, jeżeli szereg $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ jest zbieżny, ale szereg $\sum _{n=0}^{\mathrm{\infty }}|a_n|$ jest rozbieżny.

Twierdzenie D12
Niech $n\in {\mathbb{Z}}_{+}$. Jeżeli wyrazy ciągu $(a_n)$ można zapisać w jednej z postaci

1. $a_k=f_k-f_{k+1}$
2. $a_k=f_{k-1}-f_k$

to odpowiadający temu ciągowi szereg nazywamy szeregiem teleskopowym. Suma częściowa szeregu teleskopowego jest odpowiednio równa

1. $\sum _{k=m}^n{a}_k=f_m-f_{n+1}$
2. $\sum _{k=m}^n{a}_k=f_{m-1}-f_n$

Dowód

$\sum _{k=m}^n{a}_k=\sum _{k=m}^n(f_k-f_{k+1})=$

$=(f_m-f_{m+1})+(f_{m+1}-f_{m+2})+(f_{m+2}-f_{m+3})+\dots +(f_{n-1}-f_n)+(f_n-f_{n+1})$

$=f_m-f_{m+1}+f_{m+1}-f_{m+2}+f_{m+2}-f_{m+3}+\dots +f_{n-1}-f_n+f_n-f_{n+1}$

$=f_m+(-f_{m+1}+f_{m+1})+(-f_{m+2}+f_{m+2})+(-f_{m+3}+\dots +f_{n-1})+(-f_n+f_n)-f_{n+1}$

$=f_m-f_{n+1}$

$\sum _{k=m}^n{a}_k=\sum _{k=m}^n(f_{k-1}-f_k)=$

$=(f_{m-1}-f_m)+(f_m-f_{m+1})+(f_{m+1}-f_{m+2})+\dots +(f_{n-2}-f_{n-1})+(f_{n-1}-f_n)$

$=f_{m-1}-f_m+f_m-f_{m+1}+f_{m+1}-f_{m+2}+\dots +f_{n-2}-f_{n-1}+f_{n-1}-f_n$

$=f_{m-1}+(-f_m+f_m)+(-f_{m+1}+f_{m+1})+(-f_{m+2}+\dots +f_{n-2})+(-f_{n-1}+f_{n-1})-f_n$

$=f_{m-1}-f_n$

□

Twierdzenie D13
Następujące szeregi są zbieżne

1. $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k(k+1)}=1$
2. $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k(k-1)}=1$
3. $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k^2-1}=\frac{3}{4}$
4. $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}=\frac{{\pi }^2}{6}=1.644934066848\dots$	A013661, WolframAlpha

Dowód

Punkt 1.
Dla dowodu wykorzystamy fakt, że rozpatrywany szereg jest szeregiem teleskopowym

$\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}$

Zatem

$\sum _{k=1}^n\frac{1}{k(k+1)}=\sum _{k=1}^n(\frac{1}{k}-\frac{1}{k+1})=1-\frac{1}{n+1}$

Przechodząc z $n$ do nieskończoności, dostajemy

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k(k+1)}=1$

Punkt 2.
Szereg jest identyczny z szeregiem z punktu 1., co łatwo zauważyć zmieniając zmienną sumowania $k=s+1$ i odpowiednio granice sumowania.

Punkt 3.
Należy skorzystać z tożsamości

$\frac{1}{k^2-1}=\frac{1}{2}[(\frac{1}{k}-\frac{1}{k+1})+(\frac{1}{k-1}-\frac{1}{k})]$

Punkt 4.
Ponieważ dla $k⩾2$ prawdziwa jest nierówność

$0<\frac{1}{k^2}<\frac{1}{k^2-1}$

to na mocy kryterium porównawczego (twierdzenie D9) ze zbieżności szeregu $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k^2-1}$ wynika zbieżność szeregu $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}$
□

Twierdzenie D14
Następujące szeregi są zbieżne

1. $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(k+1)\sqrt{k}}=1.860025079221\dots$
2. $\sum _{k=2}^{\mathrm{\infty }}\frac{\log k}{k(k+1)}=0.788530565911\dots$	A085361
3. $\sum _{k=2}^{\mathrm{\infty }}\frac{\log k}{k(k-1)}=1.257746886944\dots$	A131688
4. $\sum _{k=3}^{\mathrm{\infty }}\frac{1}{k\cdot {\log }^{2}k}=1.069058310734\dots$	A115563

Dowód

Punkt 1.

Wystarczy zauważyć, że

$\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}=\frac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k}\cdot \sqrt{k+1}}$

$=\frac{1}{\sqrt{k}\cdot \sqrt{k+1}\cdot (\sqrt{k+1}+\sqrt{k})}$

$>\frac{1}{\sqrt{k}\cdot \sqrt{k+1}\cdot 2\sqrt{k+1}}$

$=\frac{1}{2(k+1)\sqrt{k}}$

Zatem

$\sum _{k=1}^n\frac{1}{(k+1)\sqrt{k}}=2\sum _{k=1}^n\frac{1}{2(k+1)\sqrt{k}}$

$<2\sum _{k=1}^n(\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}})$

$=2(1-\frac{1}{\sqrt{n+1}})$

$<2$

Ponieważ ciąg sum częściowych szeregu jest rosnący i ograniczony, to szereg jest zbieżny.

Punkt 2.
Korzystając z twierdzenia A37 p.4, możemy napisać oszacowanie

$0<\frac{\log k}{k(k+1)}<\frac{\sqrt{k}}{k(k+1)}=\frac{1}{(k+1)\sqrt{k}}$

Zatem na mocy kryterium porównawczego ze zbieżności szeregu $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(k+1)\sqrt{k}}$ wynika zbieżność szeregu $\sum _{k=2}^{\mathrm{\infty }}\frac{\log k}{k(k+1)}$

Punkt 3.
Zauważmy, że

$\frac{\log (k-1)}{k-1}-\frac{\log (k)}{k}=\frac{k\log (k-1)-(k-1)\log (k)}{k(k-1)}$

$=\frac{k\log \left(k(1-\frac{1}{k})\right)-(k-1)\log (k)}{k(k-1)}$

$=\frac{k\log (k)+k\log (1-\frac{1}{k})-k\log (k)+\log (k)}{k(k-1)}$

$>\frac{\log (k)-k\cdot \frac{1}{k-1}}{k(k-1)}$

$=\frac{\log (k)}{k(k-1)}-\frac{1}{(k-1{)}^2}$

Czyli prawdziwe jest oszacowanie

$\frac{\log (k)}{k(k-1)}<[\frac{\log (k-1)}{k-1}-\frac{\log (k)}{k}]+\frac{1}{(k-1{)}^2}$

Zatem możemy napisać

$\sum _{k=2}^n\frac{\log (k)}{k(k-1)}<\sum _{k=2}^n[\frac{\log (k-1)}{k-1}-\frac{\log (k)}{k}]+\sum _{k=2}^n\frac{1}{(k-1{)}^2}$

$<-\frac{\log (n)}{n}+\sum _{j=1}^{n-1}\frac{1}{j^2}$

$<\sum _{j=1}^{\mathrm{\infty }}\frac{1}{j^2}$

$=\frac{{\pi }^2}{6}$

Ponieważ ciąg sum częściowych szeregu jest rosnący i ograniczony, to szereg jest zbieżny.

Punkt 4.
Zauważmy, że

$\frac{1}{\log (k)}-\frac{1}{\log (k+1)}=\frac{\log (k+1)-\log (k)}{\log (k)\log (k+1)}$

$=\frac{\log (1+\frac{1}{k})}{\log (k)\log (k+1)}$

$<\frac{1}{k\cdot \log (k)\log (k+1)}$

$<\frac{1}{k\cdot {\log }^{2}k}$

Z drugiej strony mamy

$\frac{1}{\log (k-1)}-\frac{1}{\log (k)}=\frac{\log (k)-\log (k-1)}{\log (k-1)\log (k)}$

$=\frac{\log (1+\frac{1}{k-1})}{\log (k-1)\log (k)}$

$>\frac{1}{k\cdot \log (k-1)\log (k)}$

$>\frac{1}{k\cdot {\log }^{2}k}$

Wynika stąd następujący ciąg nierówności

$\frac{1}{\log (k)}-\frac{1}{\log (k+1)}<\frac{1}{k\cdot {\log }^{2}k}<\frac{1}{\log (k-1)}-\frac{1}{\log (k)}$

Rezultat ten wykorzystamy w pełni w przykładzie D15, a do pokazania zbieżności szeregu wystarczy nam prawa nierówność. Mamy

$\sum _{k=3}^n\frac{1}{k\cdot {\log }^{2}k}<\sum _{k=3}^n[\frac{1}{\log (k-1)}-\frac{1}{\log (k)}]$

$=\frac{1}{\log 2}-\frac{1}{\log (n)}$

$<\frac{1}{\log 2}$

Ponieważ ciąg sum częściowych szeregu jest rosnący i ograniczony, to szereg jest zbieżny.
□

Przykład D15
Na przykładzie szeregu $\sum _{k=3}^{\mathrm{\infty }}\frac{1}{k\cdot {\log }^{2}k}$ pokażemy, jak należy obliczać przybliżoną wartość sumy szeregu.

Ponieważ nie jesteśmy w stanie zsumować nieskończenie wielu wyrazów, zatem najlepiej będzie podzielić szereg na dwie części

$\sum _{k=3}^{\mathrm{\infty }}\frac{1}{k\cdot {\log }^{2}k}=\sum _{k=3}^m\frac{1}{k\cdot {\log }^{2}k}+\sum _{k=m+1}^{\mathrm{\infty }}\frac{1}{k\cdot {\log }^{2}k}$

Wartość pierwszej części możemy policzyć bezpośrednio, a dla drugiej części powinniśmy znaleźć jak najlepsze oszacowanie.

Dowodząc twierdzenie D14, w punkcie 4. pokazaliśmy, że prawdziwy jest ciąg nierówności

$\frac{1}{\log (k)}-\frac{1}{\log (k+1)}<\frac{1}{k\cdot {\log }^{2}k}<\frac{1}{\log (k-1)}-\frac{1}{\log (k)}$

Wykorzystamy powyższy wzór do znalezienia potrzebnego nam oszacowania. Sumując strony nierówności, dostajemy

$\sum _{k=m+1}^n(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})<\sum _{k=m+1}^n\frac{1}{k\cdot {\log }^{2}k}<\sum _{k=m+1}^n(\frac{1}{\log (k-1)}-\frac{1}{\log (k)})$

Ponieważ szeregi po lewej i po prawej stronie są szeregami teleskopowymi, to łatwo znajdujemy, że

$\frac{1}{\log (m+1)}-\frac{1}{\log (n+1)}<\sum _{k=m+1}^n\frac{1}{k\cdot {\log }^{2}k}<\frac{1}{\log m}-\frac{1}{\log n}$

Przechodząc z $n$ do nieskończoności, otrzymujemy oszacowanie

$\frac{1}{\log (m+1)}<\sum _{k=m+1}^{\mathrm{\infty }}\frac{1}{k\cdot {\log }^{2}k}<\frac{1}{\log m}$

Teraz pozostaje dodać sumę wyrazów szeregu od $k=3$ do $k=m$

$\frac{1}{\log (m+1)}+\sum _{k=3}^m\frac{1}{k\cdot {\log }^{2}k}<\sum _{k=3}^{\mathrm{\infty }}\frac{1}{k\cdot {\log }^{2}k}<\frac{1}{\log m}+\sum _{k=3}^m\frac{1}{k\cdot {\log }^{2}k}$

Poniżej przedstawiamy wartości oszacowania sumy szeregu znalezione przy pomocy programu PARI/GP dla kolejnych wartości $m$. Wystarczy proste polecenie

for(n = 1, 8, s = sum( k = 3, 10^n, 1/k/(log(k))^2 ); print( "n= ", n, "   a= ", s + 1/log(10^n+1), "   b= ", s + 1/log(10^n) ))

$m={10}^1$	$1.06$	$1.07$
$m={10}^2$	$1.068$	$1.069$
$m={10}^3$	$1.06904$	$1.06906$
$m={10}^4$	$1.069057$	$1.069058$
$m={10}^5$	$1.0690582$	$1.0690583$
$m={10}^6$	$1.06905830$	$1.06905831$
$m={10}^7$	$1.0690583105$	$1.0690583109$
$m={10}^8$	$1.06905831071$	$1.06905831074$

Dysponując oszacowaniem reszty szeregu, znaleźliśmy wartość sumy szeregu z dokładnością 10 miejsc po przecinku.

Natomiast samo zsumowanie ${10}^8$ wyrazów szeregu daje wynik

$\sum _{k=3}^{{10}^8}\frac{1}{k\cdot {\log }^{2}k}=1.014771500510916\dots$

Zatem mimo zsumowania stu milionów(!) wyrazów szeregu otrzymaliśmy rezultat z dokładnością jednego(!) miejsca po przecinku. Co więcej, nie wiemy, jaka jest dokładność uzyskanego rezultatu. Znając oszacowanie od dołu i od góry, dokładność jednego miejsca po przecinku uzyskaliśmy po zsumowaniu dziesięciu(!) wyrazów szeregu.

Rozpatrywana wyżej sytuacja pokazuje, że w przypadku znajdowania przybliżonej wartości sumy szeregu ważniejsze od sumowania ogromnej ilości wyrazów jest posiadanie oszacowania nieskończonej reszty szeregu. Ponieważ wyznaczenie tego oszacowania na ogół nie jest proste, pokażemy jak ten problem rozwiązać przy pomocy całki oznaczonej.

Szeregi nieskończone i całka oznaczona

Twierdzenie D16
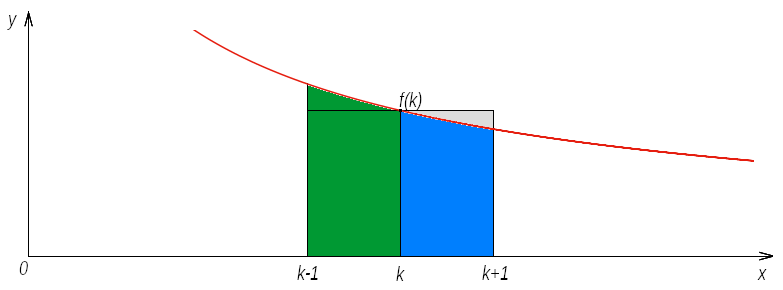
Jeżeli funkcja $f(x)$ jest ciągła, dodatnia i malejąca w przedziale $[m,n+1]$, to prawdziwy jest następujący ciąg nierówności

$0⩽{\int }_m^{n+1}f(x)dx⩽\sum _{k=m}^{n}f(k)⩽f(m)+{\int }_m^{n}f(x)dx$

Dowód

Ponieważ funkcja $f(x)$ jest z założenia ciągła, dodatnia i malejąca, to zamieszczony niżej rysunek dobrze prezentuje problem.

Przedstawiona na rysunku krzywa odpowiada funkcji $f(x)$. Dla współrzędnej $x=k$ zaznaczyliśmy wartość funkcji $f(k)$, a po lewej i prawej stronie tych punktów zaznaczyliśmy pasy o jednostkowej szerokości. Łatwo zauważamy, że

• po lewej stronie pole pod krzywą (zaznaczone kolorem zielonym) jest większe od pola prostokąta o wysokości $f(k)$ i jednostkowej szerokości
• po prawej stronie pole pod krzywą (zaznaczone kolorem niebieskim) jest mniejsze od pola prostokąta o wysokości $f(k)$ i jednostkowej szerokości

Korzystając z własności całki oznaczonej, otrzymujemy ciąg nierówności

${\int }_k^{k+1}f(x)dx⩽f(k)⩽{\int }_{k-1}^{k}f(x)dx$

W powyższym wzorze występują nierówności nieostre, bo rysunek przedstawia funkcję silnie malejącą, ale zgodnie z uczynionym założeniem funkcja $f(x)$ może być funkcją słabo malejącą.

Sumując lewą nierówność od $k=m$ do $k=n$, a prawą od $k=m+1$ do $k=n$, dostajemy

${\int }_m^{n+1}f(x)dx⩽\sum _{k=m}^{n}f(k)$

$\sum _{k=m+1}^{n}f(k)⩽{\int }_m^{n}f(x)dx$

Dodając $f(m)$ do obydwu stron drugiej z powyższych nierówności i łącząc je ze sobą, otrzymujemy kolejny i docelowy ciąg nierówności

$0⩽{\int }_m^{n+1}f(x)dx⩽\sum _{k=m}^{n}f(k)⩽f(m)+{\int }_m^{n}f(x)dx$

□

Przykład D17
Rozważmy szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}$.

Funkcja $f(x)=\frac{1}{x}$ jest ciągła, dodatnia i silnie malejąca w przedziale $(0,+\mathrm{\infty })$, zatem dla dowolnego $n\in {\mathbb{Z}}_{+}$ prawdziwe jest oszacowanie

${\int }_1^{n+1}\frac{dx}{x}<\sum _{k=1}^n\frac{1}{k}<1+{\int }_1^n\frac{dx}{x}$

Przy obliczaniu całek oznaczonych Czytelnik może skorzystać ze strony WolframAlpha.

$\log (n+1)<\sum _{k=1}^n\frac{1}{k}<1+\log n$

Ponieważ

$\log (n+1)=\log \left(n(1+\frac{1}{n})\right)=\log n+\log (1+\frac{1}{n})>\log n+\frac{1}{n+1}$

to dostajemy

$\frac{1}{n+1}<\sum _{k=1}^n\frac{1}{k}-\log n<1$

Zauważmy: nie tylko wiemy, że szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}$ jest rozbieżny, ale jeszcze potrafimy określić, jaka funkcja tę rozbieżność opisuje! Mamy zatem podstawy, by przypuszczać, że całki umożliwią opracowanie metody, która pozwoli rozstrzygać o zbieżności szeregów.

Twierdzenie D18 (kryterium całkowe zbieżności szeregów)
Załóżmy, że funkcja $f(x)$ jest ciągła, dodatnia i malejąca w przedziale $[m,+\mathrm{\infty })$. Szereg $\sum _{k=m}^{\mathrm{\infty }}f(k)$ jest zbieżny lub rozbieżny w zależności od tego, czy funkcja pierwotna $F(x)=\int f(x)dx$ ma dla $x\to \mathrm{\infty }$ granicę skończoną, czy nie.

Dowód

Nim przejdziemy do dowodu, wyjaśnimy uczynione założenia. Założenie, że funkcja $f(x)$ jest malejąca, będzie wykorzystane w czasie dowodu twierdzenia, ale rozważanie przypadku, gdy $f(x)$ jest rosnąca, nie ma sensu, bo wtedy nie mógłby być spełniony warunek konieczny zbieżności szeregu $\sum _{k=m}^{\mathrm{\infty }}f(k)$ (zobacz twierdzenie D4).

Moglibyśmy założyć bardziej ogólnie, że funkcja jest nieujemna, ale wtedy twierdzenie obejmowałoby przypadki funkcji takich, że dla pewnego $x_0$ byłoby $f(x_0)=0$. Ponieważ z założenia funkcja $f(x)$ jest malejąca, zatem mielibyśmy $f(x)=0$ dla $x⩾x_0$. Odpowiadający tej funkcji szereg $\sum _{k=m}^{\mathrm{\infty }}f(k)$ miałby dla $k⩾x_0$ tylko wyrazy zerowe i byłby w sposób oczywisty zbieżny.

Założenie ciągłości funkcji $f(x)$ ma zapewnić całkowalność funkcji $f(x)$. Założenie to można osłabić, tutaj ograniczymy się tylko do podania przykładów. Niech $a,b\in \mathbb{R}$, mamy

${\int }_a^b\text{sgn}(x)dx=|b|-|a|$ ${\int }_0^a\lfloor x\rfloor dx=\frac{1}{2}\lfloor a\rfloor (2a-\lfloor a\rfloor -1)$ ${\int }_{-a}^a\lfloor x\rfloor dx=-a$

Po tych uwagach dotyczących założeń możemy przejść do właściwego dowodu. Korzystając ze wzoru udowodnionego w twierdzeniu D16 i przechodząc z $n$ do nieskończoności, dostajemy

$0⩽{\int }_m^{\mathrm{\infty }}f(x)dx⩽\sum _{k=m}^{\mathrm{\infty }}f(k)⩽f(m)+{\int }_m^{\mathrm{\infty }}f(x)dx$

Z drugiej nierówności wynika, że jeżeli całka ${\int }_m^{\mathrm{\infty }}f(x)dx$ jest rozbieżna, to rosnący ciąg kolejnych całek oznaczonych $C_j={\int }_m^{j}f(x)dx$ nie może być ograniczony od góry (w przeciwnym wypadku całka ${\int }_m^{\mathrm{\infty }}f(x)dx$ byłby zbieżna), zatem również rosnący ciąg sum częściowych $F_j=\sum _{k=m}^{j}f(k)$ nie może być ograniczony od góry, co oznacza, że szereg $\sum _{k=m}^{\mathrm{\infty }}f(k)$ jest rozbieżny.

Z trzeciej nierówności wynika, że jeżeli całka ${\int }_m^{\mathrm{\infty }}f(x)dx$ jest zbieżna, to ciąg sum częściowych $F_j=\sum _{k=m}^{j}f(k)$ jest ciągiem rosnącym i ograniczonym od góry. Wynika stąd, że ciąg $F_j$ jest zbieżny, zatem szereg $\sum _{k=m}^{\mathrm{\infty }}f(k)$ jest zbieżny.

Ponieważ zbieżność (rozbieżność) całki ${\int }_m^{\mathrm{\infty }}f(x)dx$ nie zależy od wyboru dolnej granicy całkowania, to wystarczy badać granicę $\underset{x\to \mathrm{\infty }}{lim}F(x)$, gdzie $F(x)=\int f(x)dx$ jest dowolną funkcją pierwotną.
□

Przykład D19
Przykłady zebraliśmy w tabeli. Przy obliczaniu całek nieoznaczonych Czytelnik może skorzystać ze strony WolframAlpha.

	szereg $\sum _{k=m}^{\mathrm{\infty }}{a}_k$	funkcja $f(x)$	całka $F(x)=\int f(x)dx$	granica $\underset{x\to \mathrm{\infty }}{lim}F(x)$	wynik
1.	$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}$	$\frac{1}{x}$	$\log x$	$\mathrm{\infty }$	szereg rozbieżny
2.	$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{\sqrt{k}}$	$\frac{1}{\sqrt{x}}$	$2\sqrt{x}$	$\mathrm{\infty }$	szereg rozbieżny
3.	$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}$	$\frac{1}{x^2}$	$-\frac{1}{x}$	$0$	szereg zbieżny
4.	$\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k\log k}$	$\frac{1}{x\log x}$	$\log \log x$	$\mathrm{\infty }$	szereg rozbieżny
5.	$\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k{\log }^{2}k}$	$\frac{1}{x{\log }^{2}x}$	$-\frac{1}{\log x}$	$0$	szereg zbieżny

Stosując kryterium całkowe, można łatwo pokazać, że szeregi

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^s}$

$\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k{\log }^{s}k}$

są zbieżne dla $s>1$ i rozbieżne dla $s⩽1$.

Twierdzenie D20
Jeżeli funkcja $f(x)$ jest ciągła, dodatnia i malejąca w przedziale $[m,\mathrm{\infty })$ oraz

$R(m)={\int }_m^{\mathrm{\infty }}f(x)dx$

$S(m)=\sum _{k=a}^{m}f(k)$

gdzie $a<m$, to prawdziwe jest następujące oszacowanie sumy szeregu nieskończonego $\sum _{k=a}^{\mathrm{\infty }}f(k)$

$S(m)+R(m)-f(m)⩽\sum _{k=a}^{\mathrm{\infty }}f(k)⩽S(m)+R(m)$

Dowód

Korzystając ze wzoru udowodnionego w twierdzeniu D16 i przechodząc z $n$ do nieskończoności, dostajemy

${\int }_m^{\mathrm{\infty }}f(x)dx⩽\sum _{k=m}^{\mathrm{\infty }}f(k)⩽f(m)+{\int }_m^{\mathrm{\infty }}f(x)dx$

Czyli

$R(m)⩽\sum _{k=m}^{\mathrm{\infty }}f(k)⩽f(m)+R(m)$

Odejmując od każdej ze stron nierówności liczbę $f(m)$ i dodając do każdej ze stron nierówności sumę skończoną $S(m)=\sum _{k=a}^{m}f(k)$, otrzymujemy

$S(m)+R(m)-f(m)⩽\sum _{k=a}^{\mathrm{\infty }}f(k)⩽S(m)+R(m)$

Co należało pokazać.
□

Przykład D21
Twierdzenie D20 umożliwia określenie, z jaką dokładnością została wyznaczona suma szeregu. Wyznaczmy sumę szeregu $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(k+1)\sqrt{k}}$. Mamy

$S(m)=\sum _{k=1}^m\frac{1}{(k+1)\sqrt{k}}$

$\int \frac{dx}{(x+1)\sqrt{x}}=2\text{arctg}\left(\sqrt{x}\right)$

$R(m)={\int }_m^{\mathrm{\infty }}\frac{dx}{(x+1)\sqrt{x}}=\pi -2\text{arctg}\left(\sqrt{m}\right)$

Zatem

$S(m)+R(m)-f(m)⩽\sum _{k=1}^{\mathrm{\infty }}\frac{1}{(k+1)\sqrt{k}}⩽S(m)+R(m)$

Dla kolejnych wartości $m$ otrzymujemy

$m$	$S(m)+R(m)-f(m)$	$S(m)+R(m)$
${10}^1$	$1.84$	$1.87$
${10}^2$	$1.85$	$1.86$
${10}^3$	$1.86000$	$1.86004$
${10}^4$	$1.860024$	$1.860025$
${10}^5$	$1.86002506$	$1.86002509$
${10}^6$	$1.860025078$	$1.860025079$
${10}^7$	$1.86002507920$	$1.86002507923$
${10}^8$	$1.860025079220$	$1.860025079221$
${10}^9$	$1.8600250792211$	$1.8600250792212$

W programie PARI/GP wystarczy napisać:

f(k) = 1.0 / (k+1) / sqrt(k)
S(m) = sum( k = 1, m, f(k) )
R(m) = Pi - 2*atan( sqrt(m) )
for(j = 1, 9, m = 10^j; suma = S(m); reszta = R(m); print( "j= ", j, "   a= ", suma + reszta - f(m), "   b= ", suma + reszta ))

Prostym wnioskiem z twierdzenia D16 jest następujące
Twierdzenie D22
Niech $f(x)$ będzie funkcją ciągłą, dodatnią i malejącą w przedziale $[m,+\mathrm{\infty })$. Jeżeli przy wyliczaniu sumy szeregu nieskończonego $\sum _{k=a}^{\mathrm{\infty }}f(k)$ (gdzie $a<m$) zastąpimy sumę $\sum _{k=m}^{\mathrm{\infty }}f(k)$ całką ${\int }_m^{\mathrm{\infty }}f(x)dx$, to błąd wyznaczenia sumy szeregu nie przekroczy $f(m)$.

Dowód

Korzystając ze wzoru z twierdzenia D16 i przechodząc z $n$ do nieskończoności, otrzymujemy

${\int }_m^{\mathrm{\infty }}f(x)dx⩽\sum _{k=m}^{\mathrm{\infty }}f(k)⩽f(m)+{\int }_m^{\mathrm{\infty }}f(x)dx$

Dodając do każdej ze stron nierówności wyrażenie $-f(m)+\sum _{k=a}^{m}f(k)$, dostajemy

$-f(m)+\sum _{k=a}^{m}f(k)+{\int }_m^{\mathrm{\infty }}f(x)dx⩽\sum _{k=a}^{\mathrm{\infty }}f(k)⩽\sum _{k=a}^{m}f(k)+{\int }_m^{\mathrm{\infty }}f(x)dx$

Skąd wynika natychmiast

$-f(m)⩽\sum _{k=a}^{\mathrm{\infty }}f(k)-(\sum _{k=a}^{m}f(k)+{\int }_m^{\mathrm{\infty }}f(x)dx)⩽0<f(m)$

Czyli

$|\sum _{k=a}^{\mathrm{\infty }}f(k)-(\sum _{k=a}^{m}f(k)+{\int }_m^{\mathrm{\infty }}f(x)dx)|⩽f(m)$

Co kończy dowód.
□

Twierdzenie D23
Niech $f(x)$ będzie funkcją ciągłą, dodatnią i malejącą w przedziale $[m,+\mathrm{\infty })$. Jeżeli szereg $\sum _{k=m}^{\mathrm{\infty }}f(k)$ jest zbieżny, to dla każdego $n⩾m$ prawdziwe jest następujące oszacowanie sumy częściowej szeregu $S(n)$

$S(n)=\sum _{k=m}^{n}f(k)⩽C-B{\int }_n^{\mathrm{\infty }}f(x)dx$

gdzie $B$ oraz $C$ są dowolnymi stałymi spełniającymi nierówności

$B⩾1$

$C⩾f(m)+B{\int }_m^{\mathrm{\infty }}f(x)dx$

Dowód

Z twierdzenia D16 mamy

$S(n)=\sum _{k=m}^{n}f(k)⩽f(m)+{\int }_m^{n}f(x)dx$

$⩽f(m)+B{\int }_m^{n}f(x)dx$

$=f(m)+B{\int }_m^{n}f(x)dx-B{\int }_m^{\mathrm{\infty }}f(x)dx+B{\int }_m^{\mathrm{\infty }}f(x)dx$

$=f(m)+B{\int }_m^{n}f(x)dx-B{\int }_m^{n}f(x)dx-B{\int }_n^{\mathrm{\infty }}f(x)dx+B{\int }_m^{\mathrm{\infty }}f(x)dx$

$=f(m)-B{\int }_n^{\mathrm{\infty }}f(x)dx+B{\int }_m^{\mathrm{\infty }}f(x)dx$

$=[f(m)+B{\int }_m^{\mathrm{\infty }}f(x)dx]-B{\int }_n^{\mathrm{\infty }}f(x)dx$

$⩽C-B{\int }_n^{\mathrm{\infty }}f(x)dx$

□

Uwaga D24
Niech $f(x)$ będzie funkcją ciągłą, dodatnią i malejącą w przedziale $[m,\mathrm{\infty })$. Rozważmy szereg $\sum _{k=m}^{\mathrm{\infty }}f(k)$. Zauważmy, że:

• korzystając z całkowego kryterium zbieżności, możemy łatwo zbadać, czy szereg $\sum _{k=m}^{\mathrm{\infty }}f(k)$ jest zbieżny
• jeżeli szereg jest zbieżny, to ponownie wykorzystując całki (twierdzenie D23), możemy znaleźć oszacowanie sumy częściowej szeregu $S(n)=\sum _{k=m}^{n}f(k)$

Jednak dysponując już oszacowaniem sumy częściowej szeregu $S(n)=\sum _{k=m}^{n}f(k)$, możemy udowodnić jego poprawność przy pomocy indukcji matematycznej, a stąd łatwo pokazać zbieżność szeregu $\sum _{k=m}^{\mathrm{\infty }}f(k)$. Zauważmy, że wybór większego $B$ ułatwia dowód indukcyjny. Stałą $C$ najlepiej zaokrąglić w górę do wygodnej dla nas wartości.

Czasami potrzebujemy takiego uproszczenia problemu, aby udowodnić zbieżność szeregów bez odwoływania się do całek. Zauważmy, że Czytelnik nawet nie musi znać całek – wystarczy, że policzy je przy pomocy programów, które potrafią to robić (np. WolframAlpha). Kiedy już znajdziemy oszacowanie sumy częściowej szeregu, nie musimy wyjaśniać, w jaki sposób je znaleźliśmy – wystarczy udowodnić, że jest ono poprawne, a do tego wystarczy indukcja matematyczna.

Zamieszczonej niżej zadania pokazują, jak wykorzystać w tym celu twierdzenie D23.

Zadanie D25
Korzystając z twierdzenia D23, znaleźć oszacowania sumy częściowej szeregów

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}$ oraz $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k(\log k{)}^2}$

Rozwiązanie

Rozważmy szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}$. Funkcja $f(x)=\frac{1}{x^2}$ jest funkcją ciągłą, dodatnią i malejącą w przedziale $(0,+\mathrm{\infty })$. Dla $n>0$ jest

${\int }_n^{\mathrm{\infty }}\frac{dx}{x^2}=\frac{1}{n}$ (zobacz: WolframAlpha)

$C⩾1+{\int }_1^{\mathrm{\infty }}\frac{dx}{x^2}=2$

Zatem

$\sum _{k=1}^n\frac{1}{k^2}⩽2-\frac{1}{n}$

Rozważmy szereg $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k(\log k{)}^2}$. Funkcja $f(x)=\frac{1}{x(\log x{)}^2}$ jest funkcją ciągłą, dodatnią i malejącą w przedziale $(1,+\mathrm{\infty })$. Dla $n>1$ jest

${\int }_n^{\mathrm{\infty }}\frac{dx}{x(\log x{)}^2}=\frac{1}{\log n}$ (zobacz: WolframAlpha)

$C⩾\frac{1}{2\cdot (\log 2{)}^2}+{\int }_2^{\mathrm{\infty }}\frac{dx}{x(\log x{)}^2}=\frac{1}{2\cdot (\log 2{)}^2}+\frac{1}{\log 2}=2.483379\dots$

Przyjmijmy $C=2.5$, zatem

$\sum _{k=2}^n\frac{1}{k(\log k{)}^2}<2.5-\frac{1}{\log n}$

□

Zadanie D26
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania $\sum _{k=1}^n\frac{1}{k^2}⩽2-\frac{1}{n}$ i udowodnić, że szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}$ jest zbieżny.

Rozwiązanie

Indukcja matematyczna. Łatwo zauważamy, że oszacowanie jest prawdziwe dla $n=1$. Zakładając, że oszacowanie jest prawdziwe dla $n$, otrzymujemy dla $n+1$

$\sum _{k=1}^{n+1}\frac{1}{k^2}=\sum _{k=1}^n\frac{1}{k^2}+\frac{1}{(n+1{)}^2}$

$⩽2-\frac{1}{n}+\frac{1}{(n+1{)}^2}$

$⩽2-\frac{1}{n+1}+(\frac{1}{n+1}-\frac{1}{n}+\frac{1}{(n+1{)}^2})$

$=2-\frac{1}{n+1}-\frac{1}{n(n+1{)}^2}$

$<2-\frac{1}{n+1}$

Co kończy dowód indukcyjny. Zatem dla $n⩾1$ mamy

$S(n)=\sum _{k=1}^n\frac{1}{k^2}⩽2-\frac{1}{n}<2$

Czyli ciąg sum częściowych $S(n)=\sum _{k=1}^n\frac{1}{k^2}$ szeregu $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}$ jest rosnący i ograniczony od góry, a zatem zbieżny. Co oznacza, że szereg jest zbieżny.
□

Zadanie D27
Stosując indukcję matematyczną, udowodnić prawdziwość oszacowania $\sum _{k=2}^n\frac{1}{k(\log k{)}^2}<2.5-\frac{1}{\log n}$ i udowodnić, że szereg $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k(\log k{)}^2}$ jest zbieżny.

Rozwiązanie

Indukcja matematyczna. Łatwo sprawdzamy, że oszacowanie jest prawdziwe dla $n=2$

$\sum _{k=2}^2\frac{1}{k(\log k{)}^2}\approx 1.040684<2.5-\frac{1}{\log 2}\approx 1.05730$

Zakładając, że oszacowanie jest prawdziwe dla $n$, otrzymujemy dla $n+1$

$\sum _{k=m}^{n+1}\frac{1}{k(\log k{)}^2}=\sum _{k=m}^n\frac{1}{k(\log k{)}^2}+\frac{1}{(n+1)\cdot (\log (n+1){)}^2}$

$<2.5-\frac{1}{\log n}+\frac{1}{(n+1)\cdot (\log (n+1){)}^2}$

$=2.5-\frac{1}{\log (n+1)}+(\frac{1}{\log (n+1)}-\frac{1}{\log n}+\frac{1}{(n+1)\cdot (\log (n+1){)}^2})$

$=2.5-\frac{1}{\log (n+1)}+\frac{1}{\log (n+1)}(1-\frac{\log (n+1)}{\log n}+\frac{1}{(n+1)\cdot \log (n+1)})$

$=2.5-\frac{1}{\log (n+1)}+\frac{1}{\log (n+1)}(1-\frac{\log \left(n(1+\frac{1}{n})\right)}{\log n}+\frac{1}{(n+1)\cdot \log (n+1)})$

$=2.5-\frac{1}{\log (n+1)}+\frac{1}{\log (n+1)}(1-1-\frac{\log (1+\frac{1}{n})}{\log n}+\frac{1}{(n+1)\cdot \log (n+1)})$

$<2.5-\frac{1}{\log (n+1)}+\frac{1}{\log (n+1)}(-\frac{1}{(n+1)\log n}+\frac{1}{(n+1)\cdot \log (n+1)})$

$<2.5-\frac{1}{\log (n+1)}$

Co kończy dowód indukcyjny. Zatem dla $n⩾2$ mamy

$S(n)=\sum _{k=2}^n\frac{1}{k(\log k{)}^2}<2.5-\frac{1}{\log n}<2.5$

Czyli ciąg sum częściowych $S(n)$ szeregu $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k(\log k{)}^2}$ jest rosnący i ograniczony od góry, a zatem zbieżny. Co oznacza, że szereg jest zbieżny.
□

Szeregi nieskończone i liczby pierwsze

Twierdzenie D28
Następujące szeregi są zbieżne

1. $\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{p_k}=0.269605966\dots$
2. $\sum _{p⩾2}\frac{1}{p^2}=0.452247420041\dots$	A085548
3. $\sum _{p⩾2}\frac{1}{(p-1{)}^2}=1.375064994748\dots$	A086242
4. $\sum _{p⩾2}\frac{1}{p(p-1)}=0.773156669049\dots$	A136141

Dowód

Punkt 1.
Szereg jest szeregiem naprzemiennym i jego zbieżność wynika z twierdzenia D5.

Punkt 2.
Szereg jest zbieżny, bo sumy częściowe tego szeregu tworzą ciąg rosnący i ograniczony

$\sum _{p⩽n}\frac{1}{p^2}<\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k^2}<\frac{{\pi }^2}{6}$

Punkt 3.
Szereg jest zbieżny, bo sumy częściowe tego szeregu tworzą ciąg rosnący i ograniczony

$\sum _{p⩽n}\frac{1}{(p-1{)}^2}<\sum _{j=2}^{\mathrm{\infty }}\frac{1}{(j-1{)}^2}=\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}=\frac{{\pi }^2}{6}$

Punkt 4.
Zbieżność wzoru wynika z kryterium porównawczego, bo dla każdego $p⩾2$ jest

$0<\frac{1}{p(p-1)}<\frac{1}{(p-1{)}^2}$

□

Twierdzenie D29
Następujące szeregi są zbieżne

1. $\sum _{p⩾2}\frac{1}{p\log p}=1.636616323351\dots$	A137245
2. $\sum _{p⩾2}\frac{1}{p^2\log p}=0.507782187859\dots$	A221711
3. $\sum _{p⩾2}\frac{\log p}{p(p-1)}=0.755366610831\dots$	A138312
4. $\sum _{p⩾2}\frac{\log p}{p^2}=0.493091109368\dots$	A136271

Dowód

Punkt 1.
Zbieżność tego szeregu udowodniliśmy w twierdzeniu B39, ale obecnie potrafimy uzyskać rezultat znacznie łatwiej. Zauważmy, że rozpatrywaną sumę możemy zapisać w postaci

$\sum _{p⩾2}\frac{1}{p\log p}=\sum _{k=1}^{\mathrm{\infty }}\frac{1}{p_k\log p_k}=\frac{1}{2\log 2}+\sum _{k=2}^{\mathrm{\infty }}\frac{1}{p_k\log p_k}$

Wyrażenie w mianowniku ułamka możemy łatwo oszacować. Z twierdzenia A1 mamy ($a=0.72$)

$p_k\log p_k>a\cdot k\log k\cdot \log (a\cdot k\log k)=$

$=a\cdot k\log k\cdot (\log a+\log k+\log \log k)=$

$=a\cdot k\cdot (\log k{)}^2\cdot (1+\frac{\log a+\log \log k}{\log k})$

Ponieważ dla $k>\exp \left(\frac{1}{a}\right)=4.01039\dots$ jest

$\log a+\log \log k>0$

to dla $k⩾5$ prawdziwe jest oszacowanie

$p_k\log p_k>a\cdot k\cdot (\log k{)}^2$

Wynika stąd, że dla $k⩾5$ prawdziwy jest ciąg nierówności

$0<\frac{1}{p_k\log p_k}<\frac{1}{a\cdot k\cdot (\log k{)}^2}$

Zatem na mocy kryterium porównawczego ze zbieżności szeregu $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{k\cdot (\log k{)}^2}$ (zobacz twierdzenie D14 p. 4 lub przykład D19 p. 5) wynika zbieżność szeregu $\sum _{k=2}^{\mathrm{\infty }}\frac{1}{p_k\log p_k}$

Punkt 2.
Zbieżność szeregu wynika z kryterium porównawczego (twierdzenie D9), bo

$0<\frac{1}{p^2\log p}<\frac{1}{p\log p}$

Punkt 3.
Szereg jest zbieżny, bo sumy częściowe tego szeregu tworzą ciąg rosnący i ograniczony

$\sum _{p⩽n}\frac{\log p}{p(p-1)}<\sum _{k=2}^{\mathrm{\infty }}\frac{\log k}{k(k-1)}=1.2577\dots$

Punkt 4.
Zbieżność szeregu wynika z kryterium porównawczego, bo dla każdego $p⩾2$ jest

$0<\frac{\log p}{p^2}<\frac{\log p}{p(p-1)}$

□

Twierdzenie D30
Szereg $\sum _{p⩾2}\frac{\log p}{p}$ jest rozbieżny.

Dowód

Dla potrzeb dowodu zapiszmy szereg w innej postaci

$\sum _{p⩾2}\frac{\log p}{p}=\sum _{k=1}^{\mathrm{\infty }}\frac{\log p_k}{p_k}$

Zauważmy, że dla $k⩾3$ wyrazy szeregów $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{p_k}$ oraz $\sum _{k=1}^{\mathrm{\infty }}\frac{\log p_k}{p_k}$ spełniają nierówności

$0⩽\frac{1}{p_k}⩽\frac{\log p_k}{p_k}$

Ponieważ szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{p_k}$ jest rozbieżny (zobacz B37), to na mocy kryterium porównawczego rozbieżny jest również szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{\log p_k}{p_k}$
□

Uwaga D31
Moglibyśmy oszacować rozbieżność szeregu $\sum _{p⩾2}\frac{\log p}{p}$ podobnie, jak to uczyniliśmy w przypadku twierdzenia B37, ale tym razem zastosujemy inną metodę, która pozwoli nam uzyskać bardziej precyzyjny rezultat.

Twierdzenie D32
Niech $n\in {\mathbb{Z}}_{+}$. Prawdziwe są następujące nierówności

$1.$	$n!>n^n{e}^{-n}$	$\text{dla}n⩾1$
$2.$	$n!<n^{n+1}{e}^{-n}$	$\text{dla}n⩾7$

Dowód

Punkt 1. (indukcja matematyczna)
Łatwo sprawdzić prawdziwość nierówności dla $n=1$. Zakładając prawdziwość dla $n$, otrzymujemy dla $n+1$

$(n+1)!=n!\cdot (n+1)>$

$>n^n\cdot e^{-n}\cdot (n+1)=$

$=(n+1{)}^{n+1}\cdot \frac{n^n}{(n+1{)}^n}\cdot e^{-n}=$

$=(n+1{)}^{n+1}\cdot \frac{1}{{(1+\frac{1}{n})}^n}\cdot e^{-n}>$

$>(n+1{)}^{n+1}\cdot \frac{1}{e}\cdot e^{-n}=$

$=(n+1{)}^{n+1}{e}^{-(n+1)}$

Ponieważ ${(1+\frac{1}{n})}^n<e$, zatem $\frac{1}{{(1+\frac{1}{n})}^n}>\frac{1}{e}$. Co kończy dowód punktu 1.

Punkt 2. (indukcja matematyczna)
Łatwo sprawdzić prawdziwość nierówności dla $n=7$. Zakładając prawdziwość dla $n$, otrzymujemy dla $n+1$

$(n+1)!=n!\cdot (n+1)<$

$<n^{n+1}\cdot e^{-n}\cdot (n+1)=$

$=(n+1{)}^{n+2}\cdot \frac{n^{n+1}}{(n+1{)}^{n+1}}\cdot e^{-n}=$

$=(n+1{)}^{n+2}\cdot {\left(\frac{n}{n+1}\right)}^{n+1}\cdot e^{-n}=$

$=(n+1{)}^{n+2}\cdot {(1-\frac{1}{n+1})}^{n+1}\cdot e^{-n}<$

$<(n+1{)}^{n+2}\cdot \frac{1}{e}\cdot e^{-n}=$

$=(n+1{)}^{n+2}\cdot e^{-(n+1)}$

Ostatnia nierówność wynika z faktu, że ${(1-\frac{1}{n+1})}^{n+1}<\frac{1}{e}$. Co kończy dowód punktu 2.
□

Twierdzenie D33
Niech $n\in {\mathbb{Z}}_{+}$. Dla wykładnika, z jakim liczba pierwsza $p$ występuje w rozwinięciu liczby $n!$ na czynniki pierwsze, prawdziwe są oszacowania

$1.$	$\frac{n}{p}-1<W_p(n!)<\frac{n}{p-1}$
$2.$	$\frac{n+1}{p}-1⩽W_p(n!)⩽\frac{n-1}{p-1}$

Dowód

Punkt 1. (prawa nierówność)

Zauważmy, że

$W_p(n!)=\lfloor \frac{n}{p}\rfloor +\lfloor \frac{n}{p^2}\rfloor +\lfloor \frac{n}{p^3}\rfloor +\dots$

$<\frac{n}{p}+\frac{n}{p^2}+\frac{n}{p^3}+\dots +\frac{n}{p^k}+\dots$

$=\frac{n}{p}\cdot \frac{1}{1-\frac{1}{p}}$

$=\frac{n}{p-1}$

Punkt 1. (lewa nierówność)

Łatwo znajdujemy, że

$W_p(n!)=\sum _{k=1}^{\mathrm{\infty }}\lfloor \frac{n}{p^k}\rfloor ⩾\lfloor \frac{n}{p}\rfloor >\frac{n}{p}-1$

Punkt 2. (prawa nierówność)

Z uzyskanego w punkcie 1. oszacowania wynika, że $(p-1)W_p(n!)<n$. Ponieważ nierówność ta dotyczy liczb całkowitych, to możemy napisać

$(p-1)W_p(n!)⩽n-1$

Skąd otrzymujemy natychmiast nierówność nieostrą $W_p(n!)⩽\frac{n-1}{p-1}$.

Punkt 2. (lewa nierówność)

Z uzyskanego w punkcie 1. oszacowania wynika, że $n-p<p\cdot W_p(n!)$. Ponieważ nierówność ta dotyczy liczb całkowitych, to możemy napisać

$n-p⩽p\cdot W_p(n!)-1$

Skąd otrzymujemy natychmiast nierówność nieostrą $W_p(n!)⩾\frac{n+1}{p}-1$.
□

Twierdzenie D34
Dla dowolnego $n\in {\mathbb{Z}}_{+}$ prawdziwe jest następujące oszacowanie

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n>-1$

Dowód

Z oszacowania wykładnika, z jakim liczba pierwsza $p$ występuje w rozwinięciu liczby $n!$ na czynniki pierwsze, wynika natychmiast, że dla $n⩾2$ mamy

$n!<\prod _{p⩽n}{p}^{n/(p-1)}$

Ponieważ dla $n⩾1$ jest $n!>n^n{e}^{-n}$ (zobacz punkt 1. twierdzenia D32), to

$n^n{e}^{-n}<\prod _{p⩽n}{p}^{n/(p-1)}$

Logarytmując, otrzymujemy

$n\log n-n<\sum _{p⩽n}\frac{n\log p}{p-1}=n\sum _{p⩽n}\frac{\log p}{p-1}$

Dzieląc strony przez $n$, dostajemy szukaną nierówność.
□

Twierdzenie D35 (pierwsze twierdzenie Mertensa, 1874)
Dla dowolnego $n\in {\mathbb{Z}}_{+}$ prawdziwe jest następujące oszacowanie

$\sum _{p⩽n}\frac{\log p}{p}-\log n>-1.755367$

Dowód

Ponieważ

$\frac{1}{p-1}=\frac{1}{p}+\frac{1}{p(p-1)}$

to z twierdzenia D34 dostajemy

$\sum _{p⩽n}\frac{\log p}{p}+\sum _{p⩽n}\frac{\log p}{p(p-1)}-\log n>-1$

Czyli

$\sum _{p⩽n}\frac{\log p}{p}-\log n>-1-\sum _{p⩽n}\frac{\log p}{p(p-1)}$

$>-1-\sum _{p⩾2}\frac{\log p}{p(p-1)}$

$=-1-0.755366610831\dots$

$>-1.755367$

Gdzie wykorzystaliśmy zbieżność szeregu $\sum _{p⩾2}\frac{\log p}{p(p-1)}$ (twierdzenie D29 p. 3).
□

Twierdzenie D36 (pierwsze twierdzenie Mertensa, 1874)
Dla dowolnego $n\in {\mathbb{Z}}_{+}$ prawdziwe jest następujące oszacowanie

$\sum _{p⩽n}\frac{\log p}{p}-\log n<0.386295$

Dowód

Z oszacowania wykładnika, z jakim liczba pierwsza $p$ występuje w rozwinięciu liczby $n!$ na czynniki pierwsze, wynika natychmiast, że dla $n⩾1$ mamy

$n!⩾\prod _{p⩽n}{p}^{(n+1)/p-1}$

Ponieważ dla $n⩾7$ jest $n!<n^{n+1}{e}^{-n}$, to

$\prod _{p⩽n}{p}^{(n+1)/p-1}<n^{n+1}{e}^{-n}$

Logarytmując, otrzymujemy

$\sum _{p⩽n}(\frac{n+1}{p}-1)\cdot \log p<(n+1)\cdot \log n-n$

$(n+1)\sum _{p⩽n}\frac{\log p}{p}-\sum _{p⩽n}\log p<(n+1)\cdot \log n-n$

Skąd natychmiast wynika, że

$\sum _{p⩽n}\frac{\log p}{p}-\log n<-\frac{n}{n+1}+\frac{1}{n+1}\cdot \log \left(\prod _{p⩽n}p\right)$

$=-1+\frac{1}{n+1}+\frac{1}{n+1}\cdot \log (P(n))$

$<-1+\frac{1}{n+1}+\frac{n\cdot \log 4}{n+1}$

$=-1+\frac{1}{n+1}+\log 4-\frac{\log 4}{n+1}$

$=\log 4-1+\frac{1-\log 4}{n+1}$

$=\log 4-1-\frac{0.386294\dots }{n+1}$

$<\log 4-1$

$=0.386294361\dots$

Druga nierówność wynika z twierdzenia A9. Bezpośrednio sprawdzamy, że powyższa nierówność jest prawdziwa dla $n<7$.
□

Twierdzenie D37
Dla dowolnego $n\in {\mathbb{Z}}_{+}$ prawdziwe jest następujące oszacowanie

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n<1.141661$

Dowód

Ponieważ

$\frac{1}{p}=\frac{1}{p-1}-\frac{1}{p(p-1)}$

to z twierdzenia D36 dostajemy

$\sum _{p⩽n}\frac{\log p}{p-1}-\sum _{p⩽n}\frac{\log p}{p(p-1)}-\log n<\log 4-1$

Czyli

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n<\log 4-1+\sum _{p⩽n}\frac{\log p}{p(p-1)}$

$<\log 4-1+\sum _{p⩾2}\frac{\log p}{p(p-1)}$

$=\log 4-1+0.755366610831\dots$

$<1.141661$

□

Uwaga D38

Dokładniejsze oszacowanie sumy $\sum _{p⩽n}\frac{\log p}{p}$ jest dane wzorem $\sum _{p⩽n}\frac{\log p}{p}=\log n-E+\dots$ gdzie $E=1.332582275733\dots$ Dla $n⩾319$ mamy też $|\sum _{p⩽n}\frac{\log p}{p}-\log n+E|<\frac{1}{2\log n}$

Uwaga D39

Dokładniejsze oszacowanie sumy $\sum _{p⩽n}\frac{\log p}{p-1}$ jest dane wzorem $\sum _{p⩽n}\frac{\log p}{p-1}=\log n-\gamma +\dots$ gdzie $\gamma =0.5772156649\dots$ jest stałą Eulera. Dla $n⩾318$ prawdziwe jest oszacowanie $|\sum _{p⩽n}\frac{\log p}{p-1}-\log n+\gamma |<\frac{1}{2\log n}$

Uwaga D40
Dla $n⩽{10}^{10}$ wartości wyrażeń

$\sum _{p⩽n}\frac{\log p}{p}-\log n+E$

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n+\gamma$

są liczbami dodatnimi.

Twierdzenie D41
Prawdziwy jest następujący związek

$\sum _{p⩾2}\frac{\log p}{p(p-1)}=\sum _{n=2}^{\mathrm{\infty }}\left(\sum _{p⩾2}\frac{\log p}{p^n}\right)=E-\gamma$

gdzie

• $\gamma =0.577215664901532\dots$ jest stałą Eulera
• $E=1.332582275733220\dots$
• $E-\gamma =0.755366610831688\dots$

Dowód

Ponieważ

$\frac{1}{p(p-1)}=\frac{1}{p-1}-\frac{1}{p}$

zatem

$\sum _{p⩽n}\frac{\log p}{p(p-1)}=\sum _{p⩽n}\frac{\log p}{p-1}-\sum _{p⩽n}\frac{\log p}{p}=(\log n-\gamma +\dots )-(\log n-E+\dots )$

Przechodząc z $n$ do nieskończoności, otrzymujemy

$\sum _{p⩾2}\frac{\log p}{p(p-1)}=E-\gamma$

Zauważmy teraz, że

$\frac{1}{p-1}=\frac{1}{p}\cdot \frac{1}{1-\frac{1}{p}}$

$=\frac{1}{p}\cdot (1+\frac{1}{p}+\frac{1}{p^2}+\frac{1}{p^3}+\dots +\frac{1}{p^k}+\dots )$

$=\frac{1}{p}+\frac{1}{p^2}+\frac{1}{p^3}+\dots +\frac{1}{p^k}+\dots$

Zatem

$\sum _{p⩾2}\frac{\log p}{p(p-1)}=\sum _{p⩾2}\frac{\log p}{p}\cdot (\frac{1}{p}+\frac{1}{p^2}+\frac{1}{p^3}+\dots +\frac{1}{p^k}+\dots )=\sum _{n=2}^{\mathrm{\infty }}\left(\sum _{p⩾2}\frac{\log p}{p^n}\right)$

□

Twierdzenie D42
Dla $n⩾318$ prawdziwe jest oszacowanie

$|\sum _{p⩽n}\frac{\log p}{p-1}-\log n+\gamma |<\frac{1}{2\log n}$

Dowód

Należy zauważyć, że tak dokładnego oszacowania nie można udowodnić metodami elementarnymi, dlatego punktem wyjścia jest oszacowanie podane w pracy Pierre'a Dusarta

$-(\frac{0.2}{\log n}+\frac{0.2}{{\log }^{2}n})\underset{n⩾2}{<}\sum _{p⩽n}\frac{\log p}{p}-\log n+E\underset{n⩾2974}{<}\frac{0.2}{\log n}+\frac{0.2}{{\log }^{2}n}$

Ponieważ dla $x>e^2\approx 7.389$ jest $1+\frac{1}{\log x}<1.5$, to dla $n⩾8$ mamy

$\frac{0.2}{\log n}+\frac{0.2}{{\log }^{2}n}=\frac{0.2}{\log n}(1+\frac{1}{\log n})<\frac{0.3}{\log n}$

Zatem wyjściowy układ nierówności możemy zapisać w postaci

$-\frac{0.3}{\log n}\underset{n⩾8}{<}\sum _{p⩽n}\frac{\log p}{p}-\log n+E\underset{n⩾2974}{<}\frac{0.3}{\log n}$

Z tożsamości

$\frac{1}{p}=\frac{1}{p-1}-\frac{1}{p(p-1)}$

wynika natychmiast, że

$-\frac{0.3}{\log n}\underset{n⩾8}{<}\sum _{p⩽n}\frac{\log p}{p-1}-\sum _{p⩽n}\frac{\log p}{p(p-1)}-\log n+E\underset{n⩾2974}{<}\frac{0.3}{\log n}$

Prawa nierówność

Rozważmy prawą nierówność prawdziwą dla $n⩾2974$

$\sum _{p⩽n}\frac{\log p}{p-1}-\sum _{p⩽n}\frac{\log p}{p(p-1)}-\log n+E<\frac{0.3}{\log n}$

Z twierdzenia D41 wiemy, że

$\sum _{p⩾2}\frac{\log p}{p(p-1)}-E=-\gamma$

Zatem

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n<\sum _{p⩽n}\frac{\log p}{p(p-1)}-E+\frac{0.3}{\log n}$

$<\sum _{p⩾2}\frac{\log p}{p(p-1)}-E+\frac{0.3}{\log n}$

$=-\gamma +\frac{0.3}{\log n}$

$<-\gamma +\frac{0.5}{\log n}$

Bezpośrednio obliczając, sprawdzamy, że nierówność

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n<-\gamma +\frac{0.5}{\log n}$

jest prawdziwa dla wszystkich liczb $318⩽n⩽3000$

Lewa nierówność

Rozważmy teraz lewą nierówność prawdziwą dla $n⩾8$

$\sum _{p⩽n}\frac{\log p}{p-1}-\sum _{p⩽n}\frac{\log p}{p(p-1)}-\log n+E>-\frac{0.3}{\log n}$

Mamy

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n>\sum _{p⩽n}\frac{\log p}{p(p-1)}-E-\frac{0.3}{\log n}$

$=\sum _{p⩾2}\frac{\log p}{p(p-1)}-\sum _{p>n}\frac{\log p}{p(p-1)}-E-\frac{0.3}{\log n}$

$=-\gamma -\frac{0.3}{\log n}-\sum _{p>n}\frac{\log p}{p(p-1)}$

$>-\gamma -\frac{0.3}{\log n}-\sum _{k=n+1}^{\mathrm{\infty }}\frac{\log k}{k(k-1)}$

$>-\gamma -\frac{0.3}{\log n}-\sum _{k=n+1}^{\mathrm{\infty }}\frac{\log k}{(k-1{)}^2}$

Korzystając kolejno z twierdzeń D16 i C18, dostajemy

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n>-\gamma -\frac{0.3}{\log n}-{\int }_n^{\mathrm{\infty }}\frac{\log x}{(x-1{)}^2}dx$

$=-\gamma -\frac{0.3}{\log n}-\frac{\log n}{n-1}+\log (1-\frac{1}{n})$

$>-\gamma -\frac{0.3}{\log n}-\frac{\log n}{n-1}-\frac{1}{n-1}$

$=-\gamma -\frac{0.5}{\log n}+(\frac{0.2}{\log n}-\frac{\log n+1}{n-1})$

$>-\gamma -\frac{0.5}{\log n}$

Do znalezienia całki oznaczonej Czytelnik może wykorzystać stronę WolframAlpha. Ostatnia nierówność jest prawdziwa dla $n⩾153$. Bezpośrednio obliczając, sprawdzamy, że nierówność

$\sum _{p⩽n}\frac{\log p}{p-1}-\log n>-\gamma -\frac{0.5}{\log n}$

jest prawdziwa dla wszystkich $2⩽n⩽200$.
□

Zadanie D43
Niech $r=1-\log (2)\approx 0.30685281944$. Pokazać, że z nierówności prawdziwej dla $x⩾32$

$\sum _{p⩽x}\frac{\log p}{p-1}<\log x-r$

wynika twierdzenie Czebyszewa.

Rozwiązanie

Z twierdzenia D42 wiemy, że dla $x⩾318$ jest

$\sum _{p⩽x}\frac{\log p}{p-1}-\log x<-\gamma +\frac{1}{2\log x}⩽-\gamma +\frac{1}{2\log (318)}=-0.490441\dots <-0.306852\dots =-r$

Zatem postulowane oszacowanie jest prawdziwe dla $n⩾318$. Sprawdzając bezpośrednio dla $2⩽x⩽317$, łatwo potwierdzamy prawdziwość nierówności

$\sum _{p⩽x}\frac{\log p}{p-1}<\log x-r$

dla $x⩾32$.

Niech $a\in \mathbb{Z}$ i $a⩾32$. Korzystając z twierdzenia D33, łatwo znajdujemy oszacowanie

$a!=p_1^{{\alpha }_1}\cdot \dots \cdot p_n^{{\alpha }_n}$

$⩽p_1^{(a-1)/(p_1-1)}\cdot \dots \cdot p_n^{(a-1)/(p_n-1)}$

$=(p_1^{1/(p_1-1)}\cdot \dots \cdot p_n^{1/(p_n-1)}{)}^{a-1}$

gdzie $p_n⩽a<p_{n+1}$. Oznaczając wyrażenie w nawiasie przez $U$, mamy

$\log U=\frac{\log p_1}{p_1-1}+\dots +\frac{\log p_n}{p_n-1}=\sum _{p⩽a}\frac{\log p}{p-1}<\log a-r$

gdzie skorzystaliśmy z oszacowania wskazanego w treści zadania. Zatem $U<a\cdot e^{-r}$.

Przypuśćmy, że mnożymy liczbę $a!$ przez kolejne liczby naturalne $a+1,a+2,\dots ,b-1,b$. Możemy postawić pytanie: kiedy w rozkładzie na czynniki pierwsze liczby $b!$ musi pojawić się nowy czynnik pierwszy? Jeżeli takiego nowego czynnika pierwszego nie ma, to

$a!\cdot (a+1)\cdot \dots \cdot b=b!$

$=p_1^{{\beta }_1}\cdot \dots \cdot p_n^{{\beta }_n}$

$⩽p_1^{(b-1)/(p_1-1)}\cdot \dots \cdot p_n^{(b-1)/(p_n-1)}$

$=(p_1^{1/(p_1-1)}\cdot \dots \cdot p_n^{1/(p_n-1)}{)}^{b-1}$

$=U^{b-1}$

$<(a\cdot e^{-r}{)}^{b-1}$

Jednocześnie z twierdzenia D32 wiemy, że prawdziwa jest nierówność $b!>b^b{e}^{-b}$, zatem

$b^b{e}^{-b}<b!<\frac{(a\cdot e^{-r}{)}^b}{a\cdot e^{-r}}$

$b{e}^{-1}<\frac{a\cdot e^{-r}}{(a\cdot e^{-r}{)}^{1/b}}$

$b<\frac{a\cdot e^{1-r}}{(a\cdot e^{-r}{)}^{1/b}}$

Ponieważ $e^{1-r}=e^{\log (2)}=2$, to

$b<\frac{2a}{(a\cdot e^{-r}{)}^{1/b}}<2a$

Z oszacowania $b<2a$ wynika, że $(a\cdot e^{-r}{)}^{1/b}>(a\cdot e^{-r}{)}^{1/2a}$. Możemy teraz zapisać uzyskane wyżej oszacowanie w postaci, w której prawa strona nierówności nie zależy od $b$

$b<\frac{2a}{(a\cdot e^{-r}{)}^{1/b}}<\frac{2a}{(a\cdot e^{-r}{)}^{1/2a}}$

Ponieważ $e^{-r}=0.735758\dots$, to $(a\cdot e^{-r}{)}^{1/2a}>(a/2{)}^{1/2a}$, co pozwala uprościć uzyskane oszacowanie

$b<\frac{2a}{(a\cdot e^{-r}{)}^{1/2a}}<\frac{2a}{(a/2{)}^{1/2a}}$

Pokażemy, że dla $a>303.05$

$\frac{2a}{(a/2{)}^{1/2a}}<2a-5$

Istotnie

$\frac{1}{(a/2{)}^{1/2a}}<1-\frac{5}{2a}$

$\frac{a}{2}\cdot {(1-\frac{5}{2a})}^{2a}>1$

$\frac{a}{2}\cdot {\left[{(1-\frac{5}{2a})}^{\frac{2a}{5}}\right]}^5>1$

Wyrażenie w nawiasie kwadratowym jest funkcją rosnącą i ograniczoną (zobacz twierdzenie C17) i dla $a⩾32$ przyjmuje wartości z przedziału $[0.353\dots ,e^{-1})$. Zatem dla odpowiednio dużego $a$ powyższa nierówność z pewnością jest prawdziwa. Łatwo sprawdzamy, że dla $a=304$ jest

$\frac{a}{2}\cdot {(1-\frac{5}{2a})}^{2a}=1.003213\dots$

Wynika stąd, że wszystkie kolejne liczby naturalne $a+1,a+2,\dots ,b-1,b$ mogą być liczbami złożonymi co najwyżej do chwili, gdy $b<2a-5$, czyli $b⩽2a-6$. Zatem w przedziale $(a,2a)$ musi znajdować się przynajmniej jedna liczba pierwsza. Dla $a⩽303$ prawdziwość twierdzenia sprawdzamy bezpośrednio.
□

Definicja D44
Powiemy, że liczby pierwsze $p,q$ są liczbami bliźniaczymi (tworzą parę liczb bliźniaczych), jeżeli $|p-q|=2$

Twierdzenie D45* (Viggo Brun, 1919)
Suma odwrotności par liczb pierwszych $p$ i $p+2$, takich że liczba $p+2$ jest również pierwsza, jest skończona

$\underset{p+2\in \mathbb{P}}{\sum _{p⩾2}}(\frac{1}{p}+\frac{1}{p+2})=(\frac{1}{3}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{7})+(\frac{1}{11}+\frac{1}{13})+(\frac{1}{17}+\frac{1}{19})+\dots =B_2$

gdzie $B_2=1.90216058\dots$ jest stałą Bruna.

Zadanie D46
Pokazać, że istnieje nieskończenie wiele liczb pierwszych nietworzących par liczb bliźniaczych.

Rozwiązanie

Niech $p$ i $q=p+4$ będą liczbami pierwszymi i $n⩾1$. Ponieważ liczby $pq$ i $p+2$ są względnie pierwsze, to z twierdzenia Dirichleta wiemy, że wśród liczb $a_n=pqn+(p+2)$ jest nieskończenie wiele liczb pierwszych, a jednocześnie żadna z liczb $a_n$ nie tworzy pary liczb bliźniaczych, bo

$a_n-2=pqn+p=p(qn+1)$

$a_n+2=pqn+(p+4)=q(pn+1)$

są liczbami złożonymi. Najprostsze przykłady to $a_n=21n+5$ i $b_n=77n+9$

Najłatwiej wszystkie przypadki takich ciągów wyszukać w programie PARI/GP. Polecenie

for(a=1,50, for(b=3,floor(a/2), g=gcd(a,b); g1=gcd(a,b-2); g2=gcd(a,b+2); if( g==1 && g1>1 && g2>1, print("a= ", a, "   b= ",b) )))

wyszukuje wszystkie liczby dodatnie $a,b$, gdzie $b⩽\lfloor \frac{a}{2}\rfloor$, które tworzą ciągi $ak+b$ o poszukiwanych właściwościach. Oczywiście ciągi $ak+(a-b)$ również są odpowiednie. Przykładowo dla $a⩽50$ mamy

$15k+7,21k+5,30k+7,33k+13,35k+12,39k+11,42k+5,45k+7,45k+8,45k+22$

□

Dowód z Księgi. Rozbieżność sumy $\sum _{p⩾2}\frac{1}{p}$

Twierdzenie D47
Suma odwrotności liczb pierwszych jest rozbieżna.

Dowód

Poniższy dowód został przedstawiony przez Erdősa w pracy z 1938 roku. Jest to bardzo elegancki i chyba najprostszy dowód tego twierdzenia.

Załóżmy, dla otrzymania sprzeczności, że rozważana suma jest zbieżna, czyli $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{p_k}=C$, gdzie $C$ jest pewną stałą. Zbieżność szeregu o wyrazach dodatnich oznacza, że różnica między sumą tego szeregu i sumami częściowymi, które uwzględniają coraz więcej wyrazów ciągu, musi być coraz mniejsza. Wynika stąd istnienie najmniejszej liczby $r$ takiej, że $\sum _{k=r+1}^{\mathrm{\infty }}\frac{1}{p_k}<\frac{1}{2}$.

Oznacza to, że zbiór liczb pierwszych rozpada się na dwa rozłączne podzbiory $P=\{p_1,p_2,\dots ,p_r\}$ i $Q=\{p_{r+1},p_{r+2,}\dots \}$.

Konsekwentnie zbiór liczb całkowitych dodatnich możemy podzielić na dwa rozłączne podzbiory: zbiór ${\mathbb{Z}}_Q$ liczb podzielnych przez dowolną liczbę pierwszą ze zbioru $Q$ i zbiór ${\mathbb{Z}}_P$ liczb, które nie są podzielne przez żadną liczbę pierwszą ze zbioru $Q$. Czyli liczby ze zbioru ${\mathbb{Z}}_P$ muszą być iloczynami potęg liczb pierwszych ze zbioru $P$.

Niech $M$ będzie dostatecznie dużą liczbą całkowitą.

Oszacowanie od góry ilości liczb $k\in {\mathbb{Z}}_Q$ takich, że $k⩽M$

Zauważmy, że liczb nie większych od $M$ i podzielnych przez liczbę pierwszą $p$ jest dokładnie $\lfloor \frac{M}{p}\rfloor$ (zobacz A19). Łatwo otrzymujemy oszacowanie^[a]

$\sum _{p\in Q}\lfloor \frac{M}{p}\rfloor <M\cdot \sum _{p\in Q}\frac{1}{p}<\frac{1}{2}M$

bo z założenia $\sum _{p\in Q}\frac{1}{p}<\frac{1}{2}$. Zatem liczb takich, że $k\in {\mathbb{Z}}_Q$ i $k⩽M$ jest mniej niż $\frac{M}{2}$.

Oszacowanie od góry ilości liczb $k\in {\mathbb{Z}}_P$ takich, że $k⩽M$

Każdą liczbę ze zbioru ${\mathbb{Z}}_P$ możemy zapisać w postaci $k=p_1^{{\alpha }_1}\cdot \dots \cdot p_r^{{\alpha }_r}$. Niech ${\alpha }_i=2{\beta }_i+{\delta }_i$, gdzie ${\delta }_i$ jest resztą z dzielenia liczby ${\alpha }_i$ przez $2$. Zatem

$k=p_1^{{\alpha }_1}\cdot \dots \cdot p_r^{{\alpha }_r}=(p_1^{{\beta }_1}\cdot \dots \cdot p_r^{{\beta }_r}{)}^2\cdot (p_1^{{\delta }_1}\cdot \dots \cdot p_r^{{\delta }_r})$

Ponieważ ${\delta }_i$ może przybierać tylko dwie wartości: zero lub jeden, to liczb postaci $p_1^{{\delta }_1}\cdot \dots \cdot p_r^{{\delta }_r}$ jest dokładnie $2^r$, a kwadratów liczb całkowitych nie większych od $M$ jest dokładnie $\lfloor \sqrt{M}\rfloor ⩽\sqrt{M}$. Zatem liczb $k\in {\mathbb{Z}}_P$ takich, że $k⩽M$ jest nie więcej niż $2^r\sqrt{M}$^[b].

Ponieważ ${\mathbb{Z}}_P\cup {\mathbb{Z}}_Q={\mathbb{Z}}_{+}$ i liczb $k\in {\mathbb{Z}}_{+}$ takich, że $k⩽M$ jest po prostu $M$, to musi być prawdziwe oszacowanie

$M<2^r\sqrt{M}+\frac{M}{2}$

Czyli

$2^{r+1}>\sqrt{M}$

Co jest niemożliwe, bo $r$ jest ustalone, a $M$ może być dowolnie duże. Wystarczy przyjąć $M⩾2^{2r+2}$.

---

[a] Zauważmy, że suma po lewej stronie może być większa od rzeczywistej ilości liczb $k$. Dla przykładu: gdy $M>p_{r+1}{p}_{r+2}$, to liczba $p_{r+1}{p}_{r+2}$ zostanie policzona dwukrotnie: raz jako podzielna przez $p_{r+1}$ i drugi raz jako podzielna przez $p_{r+2}$. Co oczywiście nie wpływa na poprawność przedstawionego oszacowania.

[b] Zauważmy, że dla $M>8$ liczba $a^2$ taka, że $a^2⩽M<(a+1{)}^2$ wystąpi dokładnie jeden raz (jako $a^2\cdot 1$), ale my oszacujemy, że pojawiła się $2^r$ razy. Można pokazać, że dla dowolnych $r⩾1$ i $M⩾1$, liczb $k\in {\mathbb{Z}}_P$ takich, że $k⩽M$, jest mniej niż $2^r\sqrt{M}$. Jest ich nawet mniej niż $2^r\lfloor \sqrt{M}\rfloor$, poza przypadkami $r=1$ i $M=2,3,8$, kiedy to ilość takich liczb jest równa $2^r\lfloor \sqrt{M}\rfloor <2^r\sqrt{M}$.
□

Sumowanie przez części

Uwaga D48
Omawianie metody sumowania przez części rozpoczniemy od udowodnienia prostego twierdzenia, które dobrze ilustruje tę metodę i ułatwi zrozumienie uogólnienia. Potrzebna nam będzie następująca funkcja

$D(k)=\{\begin{array}{ll}1& \text{gdy }k\text{ jest liczbą pierwszą}\\ 0& \text{gdy }k\text{ nie jest liczbą pierwszą}\end{array}$

Łatwo znajdujemy związek funkcji $D(k)$ z funkcją $\pi (k)$

$\pi (k)-\pi (k-1)=\sum _{p⩽k}1-\sum _{p⩽k-1}1$

$=\sum _{i=1}^{k}D(i)-\sum _{i=1}^{k-1}D(i)$

$=D(k)+\sum _{i=1}^{k-1}D(i)-\sum _{i=1}^{k-1}D(i)$

$=D(k)$

Twierdzenie D49
Niech $n\in {\mathbb{Z}}_{+}$ i niech $\sum _{p⩽n}\frac{1}{p}$ oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od $n$. Prawdziwy jest następujący związek

$\sum _{p⩽n}\frac{1}{p}=\frac{\pi (n)}{n}+\sum _{k=2}^{n-1}\frac{\pi (k)}{k(k+1)}$

Dowód

Rozpatrywaną sumę możemy zapisać w postaci

$\sum _{p⩽n}\frac{1}{p}=\sum _{k=2}^n\frac{D(k)}{k}$

$=\sum _{k=2}^n\frac{\pi (k)-\pi (k-1)}{k}$

$=\sum _{k=2}^n\frac{\pi (k)}{k}-\sum _{k=2}^n\frac{\pi (k-1)}{k}$

W drugiej sumie zmieniamy zmienną sumowania. Niech $j=k-1$. Sumowanie po $k$ przebiegało od $2$ do $n$, zatem sumowanie po $j$ będzie przebiegało od $1$ do $n-1$. Otrzymujemy

$\sum _{p⩽n}\frac{1}{p}=\sum _{k=2}^n\frac{\pi (k)}{k}-\sum _{j=1}^{n-1}\frac{\pi (j)}{j+1}$

$=\frac{\pi (n)}{n}+\sum _{k=2}^{n-1}\frac{\pi (k)}{k}-\sum _{j=2}^{n-1}\frac{\pi (j)}{j+1}$

Ponieważ $\pi (1)=0$. Zmieniając jedynie oznaczenie zmiennej sumowania, mamy

$\sum _{p⩽n}\frac{1}{p}=\frac{\pi (n)}{n}+\sum _{k=2}^{n-1}\frac{\pi (k)}{k}-\sum _{k=2}^{n-1}\frac{\pi (k)}{k+1}$

$=\frac{\pi (n)}{n}+\sum _{k=2}^n\pi (k)(\frac{1}{k}-\frac{1}{k+1})$

$=\frac{\pi (n)}{n}+\sum _{k=2}^{n-1}\frac{\pi (k)}{k(k+1)}$

Co należało pokazać.
□

Zadanie D50
Pokazać, że dla $n⩾1$ prawdziwe jest oszacowanie $\sum _{p⩽n}\frac{1}{p}>\frac{2}{3}\cdot \log \log (n+1)$.

Rozwiązanie

Z twierdzenia D49 wiemy, że dla $n⩾1$ prawdziwy jest wzór

$\sum _{p⩽n}\frac{1}{p}=\frac{\pi (n)}{n}+\sum _{k=2}^{n-1}\frac{\pi (k)}{k(k+1)}$

Z twierdzenia A1 wiemy, że dla $n⩾3$ prawdziwe jest oszacowanie $\pi (n)>\frac{2}{3}\cdot \frac{n}{\log n}$. Zatem dla $n⩾4$ jest

$\sum _{p⩽n}\frac{1}{p}=\frac{\pi (n)}{n}+\sum _{k=2}^{n-1}\frac{\pi (k)}{k(k+1)}$

$=\frac{\pi (n)}{n}+\frac{1}{3}+\sum _{k=4}^{n-1}\frac{\pi (k)}{k(k+1)}$

$>\frac{2}{3}\cdot \frac{1}{\log n}+\frac{1}{3}+\frac{2}{3}\cdot \sum _{k=4}^{n-1}\frac{k}{\log k\cdot k(k+1)}$

$>\frac{1}{3}+\frac{2}{3}\cdot \sum _{k=4}^{n-1}\frac{1}{(k+1)\log k}$

$>\frac{1}{3}+\frac{2}{3}\cdot \sum _{k=4}^{n-1}\frac{1}{(k+1)\log (k+1)}$

$=\frac{1}{3}+\frac{2}{3}\cdot \sum _{j=5}^n\frac{1}{j\log j}$

Korzystając z twierdzenia D16, otrzymujemy

$\sum _{p⩽n}\frac{1}{p}⩾\frac{1}{3}+\frac{2}{3}\cdot {\int }_5^{n+1}\frac{dx}{x\log x}$

$=\frac{2}{3}\cdot \log \log x{|}_5^{n+1}+\frac{1}{3}$

$=\frac{2}{3}\cdot \log \log (n+1)-\frac{2}{3}\cdot \log \log 5+\frac{1}{3}$

$>\frac{2}{3}\cdot \log \log (n+1)$

Zauważmy, że znacznie mniejszym nakładem pracy otrzymaliśmy lepsze oszacowanie sumy $\sum _{p⩽n}\frac{1}{p}$ (porównaj B37).
□

Zadanie D51
Pokazać, że oszacowanie $\pi (n)<n^{1-\epsilon }$, gdzie $\epsilon \in (0,1)$, nie może być prawdziwe dla prawie wszystkich liczb naturalnych.

Rozwiązanie

Przypuśćmy, że dla prawie wszystkich liczb naturalnych jest $\pi (n)<n^{1-\epsilon }$. Zatem istnieje taka liczba $n_0$, że dla wszystkich $n⩾n_0$ jest $\pi (n)<n^{1-\epsilon }$. Korzystając ze wzoru (zobacz D49)

$\sum _{p⩽n}\frac{1}{p}=\frac{\pi (n)}{n}+\sum _{k=2}^{n-1}\frac{\pi (k)}{k(k+1)}$

dla liczby $n>n_0$ otrzymujemy oszacowanie

$\sum _{p⩽n}\frac{1}{p}<\frac{n^{1-\epsilon }}{n}+\sum _{k=2}^{n_0-1}\frac{\pi (k)}{k(k+1)}+\sum _{k=n_0}^{n-1}\frac{k^{1-\epsilon }}{k(k+1)}$

$=\frac{1}{n^{\epsilon }}+C_1+\sum _{k=n_0}^{n-1}\frac{1}{k^{\epsilon }(k+1)}$

$<\frac{1}{(n_0{)}^{\epsilon }}+C_1+\sum _{k=n_0}^n\frac{1}{k^{1+\epsilon }}$

$⩽\frac{1}{(n_0{)}^{\epsilon }}+C_1+\frac{1}{(n_0{)}^{1+\epsilon }}+{\int }_{n_0}^n\frac{dx}{x^{1+\epsilon }}$

$=C_2+[-\frac{1}{\epsilon \cdot x^{\epsilon }}{|}_{n_0}^n]$

$=C_2-\frac{1}{\epsilon n^{\epsilon }}+\frac{1}{\epsilon (n_0{)}^{\epsilon }}$

$<C_2+\frac{1}{\epsilon (n_0{)}^{\epsilon }}$

$=C_3$

Co jest niemożliwe, bo lewa strona rośnie nieograniczenie wraz ze wzrostem $n$ (zobacz B37, D47, D50).
□

Twierdzenie D52 (sumowanie przez części)
Niech $a_j$, $b_j$ będą ciągami określonymi przynajmniej dla $s⩽j⩽n$. Prawdziwy jest następujący wzór

$\sum _{k=s}^n{a}_k{b}_k=a_n\cdot B(n)-\sum _{k=s}^{n-1}(a_{k+1}-a_k)B(k)$

gdzie $B(k)=\sum _{j=s}^k{b}_j$. Wzór ten nazywamy wzorem na sumowanie przez części.

Dowód

Jeżeli potrafimy wyliczyć lub oszacować sumę liczoną dla jednego z czynników (powiedzmy, że dla $b_j$), to do wyliczenia lub oszacowania sumy $\sum _{j=s}^n{a}_j{b}_j$ może być pomocny dowodzony wzór

$\sum _{k=s}^n{a}_k{b}_k=a_n\cdot B(n)-\sum _{k=s}^{n-1}(a_{k+1}-a_k)B(k)$

gdzie $B(k)=\sum _{j=s}^k{b}_j$. Nim przejdziemy do dowodu, zauważmy, że wprost z definicji funkcji $B(k)$ otrzymujemy

$B(s)=\sum _{j=s}^s{b}_j=b_s$

oraz

$B(k)-B(k-1)=\sum _{j=s}^k{b}_j-\sum _{j=s}^{k-1}{b}_j=b_k+\sum _{j=s}^{k-1}{b}_j-\sum _{j=s}^{k-1}{b}_j=b_k$

Przekształcając prawą stronę dowodzonego wzoru, pokażemy, że obie strony są równe.

$\sum _{k=s}^n{a}_k{b}_k=a_n\cdot B(n)-\sum _{k=s}^{n-1}(a_{k+1}-a_k)B(k)$

$=a_{n}B(n)-\sum _{k=s}^{n-1}{a}_{k+1}B(k)+\sum _{k=s}^{n-1}{a}_{k}B(k)$

W pierwszej sumie po prawej stronie zmieniamy wskaźnik sumowania na $j=k+1$, a w drugiej sumie zmieniamy tylko nazwę wskaźnika

$\sum _{k=s}^n{a}_k{b}_k=a_{n}B(n)-\sum _{j=s+1}^n{a}_{j}B(j-1)+\sum _{j=s}^{n-1}{a}_{j}B(j)$

$=-\sum _{j=s+1}^n{a}_{j}B(j-1)+\sum _{j=s}^n{a}_{j}B(j)$

$=-\sum _{j=s+1}^n{a}_{j}B(j-1)+\sum _{j=s+1}^n{a}_{j}B(j)+a_{s}B(s)$

$=\sum _{j=s+1}^n{a}_j[B(j)-B(j-1)]+a_s{b}_s$

$=\sum _{j=s+1}^n{a}_j{b}_j+a_s{b}_s$

$=\sum _{j=s}^n{a}_j{b}_j$

Co należało pokazać.
□

Zadanie D53
Niech $r\ne 1$. Pokazać, że $\sum _{k=1}^{n}k{r}^k=\frac{n{r}^{n+2}-(n+1)r^{n+1}+r}{(r-1{)}^2}$.

Rozwiązanie

Korzystając ze wzoru na sumowanie przez części, połóżmy $s=0$, $a_k=k$ i $b_k=r^k$. Zauważmy, że sumowanie od $k=0$ nic nie zmienia, a nieco upraszcza przekształcenia, bo możemy korzystać wprost ze wzoru na sumę częściową szeregu geometrycznego. Otrzymujemy

$\sum _{k=0}^{n}k{r}^k=n\cdot B(n)-\sum _{k=0}^{n-1}(k+1-k)B(k)$

gdzie

$B(k)=\sum _{j=0}^k{r}^j=\frac{r^{k+1}-1}{r-1}$

Zatem

$\sum _{k=0}^{n}k{r}^k=n\cdot \frac{r^{n+1}-1}{r-1}-\sum _{k=0}^{n-1}\frac{r^{k+1}-1}{r-1}$

$=\frac{1}{r-1}(n{r}^{n+1}-n-\sum _{k=0}^{n-1}{r}^{k+1}+\sum _{k=0}^{n-1}1)$

$=\frac{1}{r-1}(n{r}^{n+1}-n-r\sum _{k=0}^{n-1}{r}^k+n)$

$=\frac{1}{r-1}(n{r}^{n+1}-r\cdot \frac{r^n-1}{r-1})$

$=\frac{1}{(r-1{)}^2}(n{r}^{n+2}-n{r}^{n+1}-r^{n+1}+r)$

$=\frac{n{r}^{n+2}-(n+1)r^{n+1}+r}{(r-1{)}^2}$

Co należało pokazać.
□

Twierdzenie D54 (kryterium Dirichleta)
Niech $(a_k)$ i $(b_k)$ będą ciągami liczb rzeczywistych. Jeżeli

•    ciąg $(a_k)$ jest monotoniczny
  
  

•    $\underset{k\to \mathrm{\infty }}{lim}{a}_k=0$

•    istnieje taka stała $M$, że $\left|\sum _{j=1}^k{b}_j\right|⩽M$ dla dowolnej liczby $k$

to szereg $\sum _{k=1}^{\mathrm{\infty }}{a}_k{b}_k$ jest zbieżny.

Dowód

Korzystając ze wzoru na sumowanie przez części, możemy napisać

$\sum _{k=1}^n{a}_k{b}_k=a_n\cdot B(n)-\sum _{k=1}^{n-1}(a_{k+1}-a_k)B(k)$

$=a_n\cdot B(n)+\sum _{k=1}^{n-1}(a_k-a_{k+1})B(k)$

gdzie $B(k)=\sum _{j=1}^k{b}_j$. Z założenia ciąg $B(n)$ jest ograniczony i $\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$, zatem (zobacz C13)

$\underset{n\to \mathrm{\infty }}{lim}{a}_n\cdot B(n)=0$

Z założenia ciąg $(a_k)$ jest monotoniczny. Jeżeli jest malejący, to

$\sum _{k=1}^{n-1}|(a_k-a_{k+1})B(k)|⩽\sum _{k=1}^{n-1}M(a_k-a_{k+1})$

$=M\sum _{k=1}^{n-1}(a_k-a_{k+1})$

$=M(a_1-a_n)$

(zobacz D12). Jeżeli ciąg $(a_k)$ jest rosnący, to

$\sum _{k=1}^{n-1}|(a_k-a_{k+1})B(k)|⩽\sum _{k=1}^{n-1}M(a_{k+1}-a_k)$

$=-M\sum _{k=1}^{n-1}(a_k-a_{k+1})$

$=-M(a_1-a_n)$

Łącząc uzyskane rezultaty oraz uwzględniając fakt, że ciąg $(a_n)$ jest ograniczony, bo jest zbieżny (zobacz C9), możemy napisać

$\sum _{k=1}^{n-1}|(a_k-a_{k+1})B(k)|⩽M|a_1-a_n|⩽M(|a_1|+|a_n|)⩽2MU$

Ponieważ sumy częściowe szeregu $\sum _{k=1}^{\mathrm{\infty }}|(a_k-a_{k+1})B(k)|$ tworzą ciąg rosnący i ograniczony od góry, to szereg ten jest zbieżny (zobacz C10). Wynika stąd zbieżność szeregu $\sum _{k=1}^{\mathrm{\infty }}(a_k-a_{k+1})B(k)$ (zobacz D10). Zatem szereg $\sum _{k=1}^{\mathrm{\infty }}{a}_k{b}_k$ musi być zbieżny. Co należało pokazać.
□

Zadanie D55
Udowodnić następujące wzory

$\sum _{j=1}^k\sin j=\frac{\cos \left(\frac{1}{2}\right)-\cos (k+\frac{1}{2})}{2\sin \left(\frac{1}{2}\right)}=\frac{\sin \left(\frac{k}{2}\right)\cdot \sin \left(\frac{k+1}{2}\right)}{\sin \left(\frac{1}{2}\right)}$

$\sum _{j=1}^k\cos (j+\frac{1}{2})=\frac{\sin (k+1)-\sin (1)}{2\sin \left(\frac{1}{2}\right)}=\frac{\sin \left(\frac{k}{2}\right)\cos (\frac{k}{2}+1)}{\sin \left(\frac{1}{2}\right)}$

Rozwiązanie

Punkt 1.

Stosując metodę indukcji matematycznej, udowodnimy, że prawdziwy jest wzór

$2\sin \left(\frac{1}{2}\right)\cdot \sum _{j=1}^k\sin j=\cos \left(\frac{1}{2}\right)-\cos (k+\frac{1}{2})$

Ponieważ

$2\sin x\cdot \sin y=\cos (x-y)-\cos (x+y)$

to wzór jest prawdziwy dla $k=1$. Zakładając, że wzór jest prawdziwy dla $k$, otrzymujemy dla $k+1$

$2\sin \left(\frac{1}{2}\right)\cdot \sum _{j=1}^{k+1}\sin j=2\sin \left(\frac{1}{2}\right)\cdot \sum _{j=1}^k\sin j+2\sin \left(\frac{1}{2}\right)\sin (k+1)$

$=\cos \left(\frac{1}{2}\right)-\cos (k+\frac{1}{2})+\cos (k+\frac{1}{2})-\cos (k+1+\frac{1}{2})$

$=\cos \left(\frac{1}{2}\right)-\cos (k+1+\frac{1}{2})$

Na mocy zasady indukcji matematycznej wzór jest prawdziwy dla dowolnej liczby naturalnej.

Punkt 2.

Stosując metodę indukcji matematycznej, udowodnimy, że prawdziwy jest wzór

$2\sin \left(\frac{1}{2}\right)\cdot \sum _{j=1}^k\cos (j+\frac{1}{2})=\sin (k+1)-\sin (1)$

Ponieważ

$2\sin x\cos y=\sin (x-y)+\sin (x+y)$

to wzór jest prawdziwy dla $k=1$. Zakładając, że wzór jest prawdziwy dla $k$, otrzymujemy dla $k+1$

$2\sin \left(\frac{1}{2}\right)\cdot \sum _{j=1}^{k+1}\cos (j+\frac{1}{2})=2\sin \left(\frac{1}{2}\right)\cdot \sum _{j=1}^k\cos (j+\frac{1}{2})+2\sin \left(\frac{1}{2}\right)\cdot \cos (k+1+\frac{1}{2})$

$=\sin (k+1)-\sin (1)-\sin (k+1)+\sin (k+2)$

$=\sin (k+2)-\sin (1)$

Na mocy zasady indukcji matematycznej wzór jest prawdziwy dla dowolnej liczby naturalnej.
□

Zadanie D56
Pokazać, że szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{\sin k}{k}$ jest zbieżny.

Rozwiązanie

W zadaniu D55 p.1 pokazaliśmy, że prawdziwy jest wzór

$\sum _{j=1}^k\sin j=\frac{\cos \left(\frac{1}{2}\right)-\cos (k+\frac{1}{2})}{2\sin \left(\frac{1}{2}\right)}=\frac{\sin \left(\frac{k}{2}\right)\cdot \sin \left(\frac{k+1}{2}\right)}{\sin \left(\frac{1}{2}\right)}$

Skąd natychmiast otrzymujemy oszacowanie^[a]

$|\sum _{j=1}^k\sin j|=\left|\frac{\sin \left(\frac{k}{2}\right)\cdot \sin \left(\frac{k+1}{2}\right)}{\sin \left(\frac{1}{2}\right)}\right|⩽\frac{1}{\sin \left(\frac{1}{2}\right)}$

Ponieważ spełnione są założenia kryterium Dirichleta, to szereg $\sum _{k=1}^{\mathrm{\infty }}\frac{\sin k}{k}$ jest zbieżny. Wiemy, że $\sum _{k=1}^{\mathrm{\infty }}\frac{\sin k}{k}=\frac{1}{2}(\pi -1)=1.070796\dots$ (WolframAlpha).

---

[a] Zauważmy, że bez trudu możemy otrzymać dokładniejsze oszacowanie

$-0.127671<\frac{\cos \left(\frac{1}{2}\right)-1}{2\sin \left(\frac{1}{2}\right)}⩽\sum _{j=1}^k\sin j⩽\frac{\cos \left(\frac{1}{2}\right)+1}{2\sin \left(\frac{1}{2}\right)}<1.958159$

□

Zadanie D57
Pokazać, że szereg $\sum _{k=2}^{\mathrm{\infty }}\frac{\sin k}{\log k}$ jest zbieżny, a suma tego szeregu jest w przybliżeniu równa $0.6839137864\dots$

Rozwiązanie

Zbieżność szeregu wynika z kryterium Dirichleta, co pokazujemy tak samo jak w zadaniu poprzednim. Oszacowanie sumy szeregu jest znacznie trudniejsze, bo ciąg sum częściowych $S_n=\sum _{k=2}^n\frac{\sin k}{\log k}$ silnie oscyluje i dopiero dla bardzo dużych $n$ wynik sumowania mógłby być znaczący. Przykładowo:

$S_{{10}^6}=0.609189S_{{10}^7}=0.748477S_{{10}^8}=0.727256S_{{10}^9}=0.660078$

Okazuje się, że tutaj też będzie pomocne sumowanie przez części. We wzorze na sumowanie przez części połóżmy $s=2$, $a_k=\frac{1}{\log k}$ i $b_k=\sin k$. Korzystając ze wzoru pokazanego w zadaniu D55 p.1, otrzymujemy

$B(k)=\sum _{j=2}^k\sin j=\frac{\cos \left(\frac{1}{2}\right)-\cos (k+\frac{1}{2})}{2\sin \left(\frac{1}{2}\right)}-\sin (1)=C_1+C_2\cos (k+\frac{1}{2})$

gdzie

$C_1=\frac{1}{2}\mathrm{ctg}\left(\frac{1}{2}\right)-\sin (1)C_2=-\frac{1}{2\sin \left(\frac{1}{2}\right)}$

Sumując przez części, dostajemy

$\sum _{k=2}^n\frac{\sin k}{\log k}=\frac{1}{\log n}\cdot B(n)-\sum _{k=2}^{n-1}(\frac{1}{\log (k+1)}-\frac{1}{\log (k)})B(k)$

$=\frac{1}{\log n}\cdot B(n)+\sum _{k=2}^{n-1}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})(C_1+C_2\cos (k+\frac{1}{2}))$

$=\frac{1}{\log n}\cdot B(n)+C_1\sum _{k=2}^{n-1}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})+C_2\sum _{k=2}^{n-1}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})\cos (k+\frac{1}{2})$

$=\frac{1}{\log n}\cdot B(n)+C_1(\frac{1}{\log (2)}-\frac{1}{\log (n)})+C_2\sum _{k=2}^{n-1}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})\cos (k+\frac{1}{2})$

Przechodząc z $n$ do nieskończoności, mamy

$\sum _{k=2}^{\mathrm{\infty }}\frac{\sin k}{\log k}=\frac{C_1}{\log 2}+C_2\sum _{k=2}^{\mathrm{\infty }}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})\cos (k+\frac{1}{2})$

Zauważmy, że szereg po prawej stronie jest zbieżny nawet bez uzbieżniającego czynnika $\cos (k+\frac{1}{2})$, bo bez tego czynnika mielibyśmy szereg teleskopowy (zobacz D12). Pozwala to oczekiwać, że sumy częściowe szeregu po prawej stronie będą znacznie szybciej zbiegały do sumy szeregu. Rzeczywiście, tym razem dla sum

$S_n=\frac{C_1}{\log 2}+C_2\sum _{k=2}^n(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})\cos (k+\frac{1}{2})$

otrzymujemy

$S_{{10}^6}=0.683913783004S_{{10}^7}=0.683913786642S_{{10}^8}=0.683913786411S_{{10}^9}=0.683913786415$

Jest to przybliżona wartość sumy szeregu $\sum _{k=2}^{\mathrm{\infty }}\frac{\sin k}{\log k}$.

Oszacowanie błędu z jakim wyznaczona została wartość sumy

Kolejne sumowanie przez części pozwoli określić błąd z jakim wyznaczona została wartość sumy $\sum _{k=2}^{\mathrm{\infty }}\frac{\sin k}{\log k}$. Rozważmy sumę

$\sum _{k=2}^{\mathrm{\infty }}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})\cos (k+\frac{1}{2})$

We wzorze na sumowanie przez części połóżmy $s=2$, $a_k=\frac{1}{\log (k)}-\frac{1}{\log (k+1)}$ i $b_k=\cos (k+\frac{1}{2})$. Korzystając ze wzoru pokazanego w zadaniu D55 p.2, otrzymujemy

$B(k)=\sum _{j=2}^k{b}_j=\sum _{j=2}^k\cos (j+\frac{1}{2})=\frac{\sin (k+1)-\sin (1)}{2\sin \left(\frac{1}{2}\right)}-\cos \left(\frac{3}{2}\right)=C_3+C_4\cdot \sin (k+1)$

gdzie

$C_3=-\cos \left(\frac{3}{2}\right)-\frac{\sin (1)}{2\sin \left(\frac{1}{2}\right)}{C}_4=\frac{1}{2\sin \left(\frac{1}{2}\right)}$

Wzór na sumowanie przez części ma teraz postać

$\sum _{k=2}^n(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})\cos (k+\frac{1}{2})=(\frac{1}{\log (n)}-\frac{1}{\log (n+1)})B(n)-\sum _{k=2}^{n-1}(\frac{1}{\log (k+1)}-\frac{1}{\log (k+2)}-\frac{1}{\log (k)}+\frac{1}{\log (k+1)})B(k)$

$=(\frac{1}{\log (n)}-\frac{1}{\log (n+1)})B(n)+\sum _{k=2}^{n-1}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)})(C_3+C_4\cdot \sin (k+1))$

Zauważmy, że

$C_3\sum _{k=2}^{n-1}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)})=C_3\sum _{k=2}^{n-1}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})-C_3\sum _{k=2}^{n-1}(\frac{1}{\log (k+1)}-\frac{1}{\log (k+2)})$

$=C_3(\frac{1}{\log (2)}-\frac{1}{\log (n)})-C_3(\frac{1}{\log (3)}-\frac{1}{\log (n+1)})$

bo szeregi po prawej stronie są szeregami teleskopowymi.

Przechodząc z $n$ do nieskończoności, otrzymujemy

$\sum _{k=2}^{\mathrm{\infty }}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})\cos (k+\frac{1}{2})=\frac{C_3}{\log (2)}-\frac{C_3}{\log (3)}+C_4\sum _{k=2}^{\mathrm{\infty }}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)})\sin (k+1)$

Zbierając, otrzymaliśmy wzór

$\sum _{k=2}^{\mathrm{\infty }}\frac{\sin k}{\log k}=\frac{C_1}{\log (2)}+C_2{C}_3(\frac{1}{\log (2)}-\frac{1}{\log (3)})+C_2{C}_4\sum _{k=2}^{\mathrm{\infty }}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)})\sin (k+1)$

gdzie

$C_1=\frac{1}{2}\mathrm{ctg}\left(\frac{1}{2}\right)-\sin (1)C_2=-\frac{1}{2\sin \left(\frac{1}{2}\right)}$

$C_3=-\cos \left(\frac{3}{2}\right)-\frac{\sin (1)}{2\sin \left(\frac{1}{2}\right)}{C}_4=\frac{1}{2\sin \left(\frac{1}{2}\right)}$

Dla sum

$S_n=\frac{C_1}{\log (2)}+C_2{C}_3(\frac{1}{\log (2)}-\frac{1}{\log (3)})+C_2{C}_4\sum _{k=2}^n(\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)})\sin (k+1)$

dostajemy

$S_{{10}^7}=0.68391378641827479894S_{{10}^8}=0.68391378641827482233S_{{10}^9}=0.68391378641827482268$

Łatwo oszacujemy błąd z jakim wyliczyliśmy wartość sumy szeregu $S$

$|S-S_n|=|C_2{C}_4\sum _{k=n+1}^{\mathrm{\infty }}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)})\sin (k+1)|$

$=|C_2{C}_4|\cdot |\sum _{k=n+1}^{\mathrm{\infty }}(\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)})\sin (k+1)|$

$⩽|C_2{C}_4|\cdot \sum _{k=n+1}^{\mathrm{\infty }}|\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)}||\sin (k+1)|$

$⩽|C_2{C}_4|\cdot \sum _{k=n+1}^{\mathrm{\infty }}|\frac{1}{\log (k)}-\frac{1}{\log (k+1)}-\frac{1}{\log (k+1)}+\frac{1}{\log (k+2)}|$                (zobacz przypis [a])

$=|C_2{C}_4|\cdot \sum _{k=n+1}^{\mathrm{\infty }}[(\frac{1}{\log (k)}-\frac{1}{\log (k+1)})-(\frac{1}{\log (k+1)}-\frac{1}{\log (k+2)})]$

$=|C_2{C}_4|\cdot (\frac{1}{\log (n+1)}-\frac{1}{\log (n+2)})$

Dla $n={10}^9$ otrzymujemy

$|S-S_n|<2.533\cdot {10}^{-12}$

Zatem $S=0.6839137864\dots$, gdzie wszystkie wypisane cyfry są prawidłowe.

---

[a] Z łatwego do sprawdzenia wzoru

$\frac{1}{\log (k)}-\frac{1}{\log (k+1)}=\frac{\log (1+\frac{1}{k})}{\log (k)\log (k+1)}$

wynika, że wyrażenie $\frac{1}{\log (k)}-\frac{1}{\log (k+1)}$ maleje ze wzrostem $k$, czyli ciąg $a_k=\frac{1}{\log (k)}-\frac{1}{\log (k+1)}$ jest ciągiem malejącym, zatem

$\frac{1}{\log (k)}-\frac{1}{\log (k+1)}>\frac{1}{\log (k+1)}-\frac{1}{\log (k+2)}$

Ciągi $(a_k{)}_{k=1}^n$ liczb rzeczywistych takie, że $2a_k⩽a_{k-1}+a_{k+1}$ dla $k=2,\dots ,n-1$ nazywamy ciągami wypukłymi. Wprost z definicji funkcji wypukłej wynika, że jeżeli $f(x)$ jest funkcją wypukłą i $a_k=f(k)$, to ciąg $(a_k)$ jest ciągiem wypukłym.
□

Zadanie D58
Niech $\theta (n)=\sum _{p⩽n}\log p$. Pokazać, że

$\theta (n)=\log n\cdot \pi (n)-\sum _{k=2}^{n-1}\log (1+\frac{1}{k})\pi (k)$

Rozwiązanie

Korzystając ze wzoru na sumowanie przez części, połóżmy $s=2$, $a_k=\log k$ i $b_k=D(k)$. Otrzymujemy

$\sum _{k=2}^n\log k\cdot D(k)=\log n\cdot B(n)-\sum _{k=2}^{n-1}(\log (k+1)-\log k)B(k)$

gdzie

$B(k)=\sum _{j=2}^{k}D(k)=\pi (k)$

$\sum _{k=2}^n\log k\cdot D(k)=\sum _{p⩽n}\log p=\theta (n)$

Zatem

$\theta (n)=\log n\cdot \pi (n)-\sum _{k=2}^{n-1}\log (1+\frac{1}{k})\pi (k)$

Co należało pokazać.
□

Twierdzenie D59
Niech $\theta (n)=\sum _{p⩽n}\log p$. Jeżeli prawdziwe jest oszacowanie $\frac{A\cdot n}{\log n}<\pi (n)<\frac{B\cdot n}{\log n}$, gdzie $A,B\in {\mathbb{R}}_{+}$, to istnieje granica

$\underset{n\to \mathrm{\infty }}{lim}\frac{\theta (n)}{\pi (n)\cdot \log n}=1$

Dowód

Z definicji funkcji $\theta (n)$ łatwo otrzymujemy

$\theta (n)=\sum _{p⩽n}\log p<\sum _{p⩽n}\log n=\log n\cdot \pi (n)$

Skąd wynika, że

$\frac{\theta (n)}{\log n\cdot \pi (n)}<1$

Oszacowanie wyrażenia $\frac{\theta (n)}{\log n\cdot \pi (n)}$ od dołu będzie wymagało więcej pracy. Ze wzoru

$\theta (n)=\log n\cdot \pi (n)-\sum _{k=2}^{n-1}\log (1+\frac{1}{k})\pi (k)$

(zobacz D58) otrzymujemy

$\frac{\theta (n)}{\log n\cdot \pi (n)}=1-\frac{1}{\log n\cdot \pi (n)}\cdot \sum _{k=2}^{n-1}\log (1+\frac{1}{k})\pi (k)$

Z twierdzenia C18 i założonego oszacowania funkcji $\pi (n)$

$\frac{A\cdot n}{\log n}<\pi (n)<\frac{B\cdot n}{\log n}$

dostajemy

$\frac{1}{\log n\cdot \pi (n)}\cdot \sum _{k=2}^{n-1}\log (1+\frac{1}{k})\pi (k)<\frac{\log n}{\log n\cdot A\cdot n}\cdot \sum _{k=2}^{n-1}\frac{1}{k}\cdot \frac{B\cdot k}{\log k}$

$<\frac{B}{A\cdot n}\cdot \sum _{k=2}^{n-1}\frac{1}{\log k}$

Nie możemy oszacować sumy całką, bo całka $\int \frac{dx}{\log x}$ jest funkcją nieelementarną. Nie możemy też pozwolić sobie na zbyt niedokładne oszacowanie sumy i nie możemy napisać

$\sum _{k=2}^{n-1}\frac{1}{\log k}<\frac{n-2}{\log 2}<\frac{n}{\log 2}$

Wyjściem z tej sytuacji jest odpowiedni podział przedziału sumowania i szacowanie w każdym przedziale osobno. Niech punkt podziału $M$ spełnia warunek $\sqrt{n}⩽M<\sqrt{n}+1$. Mamy

$\sum _{k=2}^{n-1}\frac{1}{\log k}=\sum _{k=2}^{M-1}\frac{1}{\log k}+\sum _{k=M}^{n-1}\frac{1}{\log k}$

$<\frac{M-2}{\log 2}+\frac{n-M}{\log M}$

$<\frac{M}{\log 2}+\frac{n}{\log M}$

$<\frac{\sqrt{n}}{\log 2}+\frac{n}{\log \sqrt{n}}$

$<\frac{\sqrt{n}}{\log 2}+\frac{2n}{\log n}$

Zatem

$\frac{1}{\log n\cdot \pi (n)}\cdot \sum _{k=2}^{n-1}\log (1+\frac{1}{k})\pi (k)<\frac{B}{A\cdot n}\cdot (\frac{\sqrt{n}}{\log 2}+\frac{2n}{\log n})$

$<\frac{B}{A}\cdot (\frac{1}{\sqrt{n}\cdot \log 2}+\frac{2}{\log n})$

Łącząc otrzymane rezultaty, otrzymujemy

$1-\frac{B}{A}\cdot (\frac{1}{\sqrt{n}\cdot \log 2}+\frac{2}{\log n})<\frac{\theta (n)}{\log n\cdot \pi (n)}<1$

Na mocy twierdzenia o trzech ciągach (zobacz C9) mamy

$\underset{n\to \mathrm{\infty }}{lim}\frac{\theta (n)}{\pi (n)\cdot \log n}=1$

Co należało pokazać.
□

Uwaga D60
Funkcja $\theta (n)$ jest ściśle związana z dobrze nam znaną funkcją $P(n)$. Ponieważ $P(n)=\prod _{p⩽n}p$, to

$\log P(n)=\log \left(\prod _{p⩽n}p\right)=\sum _{p⩽n}\log p=\theta (n)$.

Z twierdzenia D59 wynika, że jeżeli istnieje granica $\frac{\theta (n)}{n}$, to będzie istniała granica dla $\frac{\pi (n)\cdot \log n}{n}$. Jeżeli istnieje granica $\frac{\pi (n)\cdot \log n}{n}$, to będzie istniała granica dla $\frac{\theta (n)}{n}$ (zobacz C12 p.3).

Wiemy, że dla funkcji $\theta (n)$, gdzie $n⩾2$, prawdziwe jest oszacowanie

$|\frac{\theta (n)}{n}-1|⩽\frac{151.3}{{\log }^{4}n}$

Zadanie D61
Niech $\theta (n)=\sum _{p⩽n}\log p$. Pokazać, że

$\pi (n)=\frac{\theta (n)}{\log n}+\sum _{k=2}^{n-1}\frac{\log (1+\frac{1}{k})}{\log k\cdot \log (k+1)}\cdot \theta (k)$

Rozwiązanie

Kładąc we wzorze na sumowanie przez części (zobacz D52) $s=2$, $a_k=\frac{1}{\log k}$ i $b_k=D(k)\cdot \log k$. Otrzymujemy

$\sum _{k=2}^{n}D(k)=\frac{1}{\log n}\cdot B(n)-\sum _{k=2}^{n-1}(\frac{1}{\log (k+1)}-\frac{1}{\log k})B(k)$

gdzie

$B(k)=\sum _{j=2}^{k}D(k)\cdot \log k=\sum _{p⩽k}\log p=\theta (k)$

$\sum _{k=2}^{n}D(k)=\sum _{p⩽n}1=\pi (n)$

Zatem

$\pi (n)=\frac{\theta (n)}{\log n}-\sum _{k=2}^{n-1}(\frac{1}{\log (k+1)}-\frac{1}{\log k})\theta (k)$

$=\frac{\theta (n)}{\log n}-\sum _{k=2}^{n-1}\frac{\log k-\log (k+1)}{\log k\cdot \log (k+1)}\cdot \theta (k)$

$=\frac{\theta (n)}{\log n}+\sum _{k=2}^{n-1}\frac{\log (1+\frac{1}{k})}{\log k\cdot \log (k+1)}\cdot \theta (k)$

Co należało pokazać.
□

Iloczyn Cauchy'ego szeregów

Twierdzenie D62 (kryterium d'Alemberta)
Niech $(a_n)$ będzie ciągiem liczb rzeczywistych i istnieje granica

$g=\underset{n\to \mathrm{\infty }}{lim}\left|\frac{a_{n+1}}{a_n}\right|$

Jeżeli

•    $g<1$, to szereg $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ jest bezwzględnie zbieżny

•    $g>1$, to szereg $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ jest rozbieżny

Dowód

Rozważmy najpierw przypadek, gdy $g=\underset{n\to \mathrm{\infty }}{lim}\left|\frac{a_{n+1}}{a_n}\right|<1$. Niech $r$ będzie dowolną liczbą rzeczywistą taką, że $g<r<1$ i przyjmijmy $\epsilon =r-g$. Z definicji granicy ciągu wiemy, że prawie wszystkie wyrazy ciągu $\left(\left|\frac{a_{n+1}}{a_n}\right|\right)$ spełniają warunek

$-\epsilon <\left|\frac{a_{n+1}}{a_n}\right|-g<\epsilon$

Możemy przyjąć, że są to wszystkie wyrazy, poczynając od $N$. Z prawej nierówności otrzymujemy, że dla $n⩾N$ jest

$\left|\frac{a_{n+1}}{a_n}\right|<r$

$|a_{n+1}|<r|a_n|$

$|a_{n+k}|<r^k|a_n|$

Ostatnią nierówność można łatwo udowodnić metodą indukcji matematycznej względem $k$. Korzystając ze wzoru na sumę szeregu geometrycznego, otrzymujemy

$\sum _{k=N+1}^{\mathrm{\infty }}|a_k|=\sum _{k=1}^{\mathrm{\infty }}|a_{N+k}|<\sum _{k=1}^{\mathrm{\infty }}{r}^k|a_n|=r|a_n|\sum _{k=1}^{\mathrm{\infty }}{r}^{k-1}=|a_n|\cdot \frac{r}{1-r}$

Zatem szereg $\sum _{i=0}^{\mathrm{\infty }}{a}_i$ jest bezwzględnie zbieżny.

W przypadku, gdy $g=\underset{n\to \mathrm{\infty }}{lim}\left|\frac{a_{n+1}}{a_n}\right|>1$ wybieramy liczbę $r$ tak, aby spełniała warunek $1<r<g$ i przyjmujemy $\epsilon =g-r$. Z definicji granicy ciągu wiemy, że prawie wszystkie wyrazy ciągu $\left(\left|\frac{a_{n+1}}{a_n}\right|\right)$ spełniają warunek

$-\epsilon <\left|\frac{a_{n+1}}{a_n}\right|-g<\epsilon$

Przyjmując, że są to wszystkie wyrazy, poczynając od $N$, z lewej nierówności otrzymujemy dla $n⩾N$

$\left|\frac{a_{n+1}}{a_n}\right|>r>1$

Czyli $|a_{n+1}|>|a_n|$, zatem dla wszystkich $k>N$ jest $|a_k|>|a_N|>0$ i nie może być spełniony podstawowy warunek zbieżności szeregu (zobacz D4). Zatem szereg jest rozbieżny. Co kończy dowód.
□

Uwaga C62
W przypadku, gdy $\underset{n\to \mathrm{\infty }}{lim}\left|\frac{a_{n+1}}{a_n}\right|=1$ kryterium d'Alemberta nie rozstrzyga o zbieżności lub rozbieżności szeregu $\sum _{n=0}^{\mathrm{\infty }}{a}_n$. Czytelnikowi zostawiamy zastosowanie tego kryterium do szeregów

$\sum _{n=1}^{\mathrm{\infty }}1\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}$

Przykład D64
Niech $x\in \mathbb{R}$. Zbadamy zbieżność szeregu

$e^x=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}+\dots$

Ponieważ

$\underset{n\to \mathrm{\infty }}{lim}|\frac{x^{n+1}}{(n+1)!}\cdot \frac{n!}{x^n}|=\underset{n\to \mathrm{\infty }}{lim}\frac{|x|}{n+1}=0$

to z kryterium d'Alemberta wynika, że szereg jest bezwzględnie zbieżny.

Zadanie D65
Pokazać, że szereg $\sum _{n=0}^{\mathrm{\infty }}\frac{n^n}{n!}$ jest rozbieżny.

Rozwiązanie

Łatwo znajdujemy, że

$\left|\frac{a_{n+1}}{a_n}\right|=\frac{(n+1{)}^{n+1}}{(n+1)!}\cdot \frac{n!}{n^n}=\frac{(n+1)(n+1{)}^n}{(n+1)n!}\cdot \frac{n!}{n^n}={(1+\frac{1}{n})}^n\stackrel{n\to \mathrm{\infty }}{\to }e>1$

Z kryterium d'Alemberta wynika, że szereg jest rozbieżny.
□

Uwaga D66
W twierdzeniu A37, korzystając z następującej definicji funkcji $e^x$

$e^x=\sum _{k=0}^{\mathrm{\infty }}\frac{x^k}{k!}=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}+\dots$

pominęliśmy dowód własności $e^x{e}^{-x}=1$. Spróbujemy teraz pokazać, że $e^x{e}^y=e^{x+y}$.

$e^x{e}^y=\left(\sum _{i=0}^{\mathrm{\infty }}\frac{x^i}{i!}\right)\left(\sum _{j=0}^{\mathrm{\infty }}\frac{y^j}{j!}\right)=\sum _{i=0}^{\mathrm{\infty }}\sum _{j=0}^{\mathrm{\infty }}\frac{x^i{y}^j}{i!\cdot j!}$

Oznaczmy $a_i=\frac{x^i}{i!}$ oraz $b_j=\frac{y^j}{j!}$ i przyjrzyjmy się sumowaniu po $i,j$. W podwójnej sumie po prawej stronie $\sum _{i=0}^{\mathrm{\infty }}\sum _{j=0}^{\mathrm{\infty }}{a}_i{b}_j$ sumujemy po kolejnych liniach poziomych tak, jak to zostało pokazane na rysunku

$a_6{b}_0$	$$	$$	$$	$$	$$	$\cdots$
$a_5{b}_0$	$a_5{b}_1$	$a_5{b}_2$	$a_5{b}_3$	$a_5{b}_4$	$a_5{b}_5$	$\cdots$
$a_4{b}_0$	$a_4{b}_1$	$a_4{b}_2$	$a_4{b}_3$	$a_4{b}_4$	$a_4{b}_5$	$\cdots$
$a_3{b}_0$	$a_3{b}_1$	$a_3{b}_2$	$a_3{b}_3$	$a_3{b}_4$	$a_3{b}_5$	$\cdots$
$a_2{b}_0$	$a_2{b}_1$	$a_2{b}_2$	$a_2{b}_3$	$a_2{b}_4$	$a_2{b}_5$	$\cdots$
$a_1{b}_0$	$a_1{b}_1$	$a_1{b}_2$	$a_1{b}_3$	$a_1{b}_4$	$a_1{b}_5$	$\cdots$
$a_0{b}_0$	$a_0{b}_1$	$a_0{b}_2$	$a_0{b}_3$	$a_0{b}_4$	$a_0{b}_5$	$\cdots$

Zastępując sumowanie po kolejnych liniach poziomych sumowaniem po kolejnych przekątnych, otrzymamy taki rysunek

$a_6{b}_0$	$$
$a_5{b}_0$	$$
$a_4{b}_0$	$a_4{b}_1$	$$
$a_3{b}_0$	$a_3{b}_1$	$a_3{b}_2$	$$
$a_2{b}_0$	$a_2{b}_1$	$a_2{b}_2$	$a_2{b}_3$	$$
$a_1{b}_0$	$a_1{b}_1$	$a_1{b}_2$	$a_1{b}_3$	$a_1{b}_4$	$$
$a_0{b}_0$	$a_0{b}_1$	$a_0{b}_2$	$a_0{b}_3$	$a_0{b}_4$	$a_0{b}_5$	$a_0{b}_6$

Co odpowiada sumie $\sum _{n=0}^{\mathrm{\infty }}\sum _{k=0}^n{a}_k{b}_{n-k}$, gdzie $n$ numeruje kolejne przekątne. Taka zmiana sposobu sumowania powoduje następujące przekształcenie wzoru

$e^x{e}^y=\sum _{i=0}^{\mathrm{\infty }}\sum _{j=0}^{\mathrm{\infty }}\frac{x^i{y}^j}{i!\cdot j!}=\sum _{n=0}^{\mathrm{\infty }}\sum _{k=0}^n\frac{x^k{y}^{n-k}}{k!\cdot (n-k)!}$

Ponieważ

$\frac{1}{k!\cdot (n-k)!}=\frac{1}{n!}\cdot \frac{n!}{k!\cdot (n-k)!}=\frac{1}{n!}\cdot (\genfrac{}{}{0ex}{}{n}{k})$

to otrzymujemy

$e^x{e}^y=\sum _{i=0}^{\mathrm{\infty }}\sum _{j=0}^{\mathrm{\infty }}\frac{x^i{y}^j}{i!\cdot j!}=\sum _{n=0}^{\mathrm{\infty }}\sum _{k=0}^n\frac{x^k{y}^{n-k}}{k!\cdot (n-k)!}=\sum _{n=0}^{\mathrm{\infty }}\sum _{k=0}^n\frac{1}{n!}\cdot (\genfrac{}{}{0ex}{}{n}{k})\cdot x^k{y}^{n-k}=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})\cdot x^k{y}^{n-k}=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}(x+y{)}^n=e^{x+y}$

Pokazaliśmy tym samym, że z definicji

$e^x=\sum _{k=0}^{\mathrm{\infty }}\frac{x^k}{k!}=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}+\dots$

wynika podstawowa własność funkcji wykładniczej $e^x{e}^y=e^{x+y}$.

Mamy świadomość, że dokonana przez nas zmiana sposobu sumowania była nieformalna i w związku z tym nie wiemy, czy była poprawna. Zatem musimy precyzyjnie zdefiniować takie sumowanie i zbadać, kiedy jest dopuszczalne. Dopiero wtedy będziemy mogli być pewni, że policzony rezultat jest poprawny.

Definicja D67
Iloczynem Cauchy'ego szeregów $\sum _{i=0}^{\mathrm{\infty }}{a}_i$ oraz $\sum _{j=0}^{\mathrm{\infty }}{b}_j$ nazywamy szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n$, gdzie

$c_n=\sum _{k=0}^n{a}_k{b}_{n-k}=a_0{b}_n+a_1{b}_{n-1}+\dots +a_{n-1}{b}_1+a_n{b}_0$

W przypadku szeregów, których wyrazy są numerowane od liczby $1$, iloczynem Cauchy'ego szeregów $\sum _{i=1}^{\mathrm{\infty }}{a}_i$ oraz $\sum _{j=1}^{\mathrm{\infty }}{b}_j$ nazywamy szereg $\sum _{n=1}^{\mathrm{\infty }}{c}_n$, gdzie

$c_n=\sum _{k=1}^n{a}_k{b}_{n-k+1}=a_1{b}_n+a_2{b}_{n-1}+\dots +a_{n-1}{b}_2+a_n{b}_1$

Zadanie D68
Niech $c_n=\sum _{k=0}^n{a}_k{b}_{n-k}$. Pokazać, że

•    jeżeli $(a_n)=(1,0,0,0,0,\dots )$, $(b_n)$ jest dowolnym ciągiem, to $c_n=b_n$

•    jeżeli $(a_n)=(1,1,1,1,1,\dots )$, $(b_n)$ jest dowolnym ciągiem, to $c_n=\sum _{k=0}^n{b}_k=B_n$

•    jeżeli $a_n=b_n=\frac{r^n}{n!}$, to $c_n=\frac{(2r{)}^n}{n!}$

•    jeżeli $(a_n)=(a,r,r^2,r^3,\dots )$, $(b_n)=(b,r,r^2,r^3,\dots )$, to $c_n=\{\begin{array}{ll}ab& \text{gdy }n=0\\ (a+b+n-1)r^n& \text{gdy }n⩾1\end{array}$

•    jeżeli $(a_n)=(a,q,q^2,q^3,\dots )$, $(b_n)=(b,r,r^2,r^3,\dots )$, gdzie $q\ne r$, to $c_n=\{\begin{array}{ll}ab& \text{gdy }n=0\\ q^n(b+\frac{r}{q-r})+r^n(a-\frac{q}{q-r})& \text{gdy }n⩾1\end{array}$

Rozwiązanie

Punkt 1.

$c_n=\sum _{k=0}^n{a}_k{b}_{n-k}=a_0{b}_n=b_n$

Punkt 2.

$c_n=\sum _{k=0}^n{a}_k{b}_{n-k}=\sum _{k=0}^n{b}_{n-k}=\sum _{j=0}^n{b}_j=B_n$

Punkt 3.

$c_n=\sum _{k=0}^n{a}_k{b}_{n-k}=\sum _{k=0}^n\frac{r^k{r}^{n-k}}{k!(n-k)!}=\frac{r^n}{n!}\sum _{k=0}^n\frac{n!}{k!(n-k)!}=\frac{r^n}{n!}\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})=\frac{(2r{)}^n}{n!}$

Punkt 4.

Dla $n=0$ mamy $c_0=a_0{b}_0=ab$

Dla $n=1$ mamy $c_1=a_0{b}_1+a_1{b}_0=a\cdot r+r\cdot b=(a+b)r$

Dla $n⩾2$ jest

$c_n=\sum _{k=0}^n{a}_k{b}_{n-k}$

$=a_0{b}_n+a_n{b}_0+\sum _{k=1}^{n-1}{a}_k{b}_{n-k}$

$=a\cdot r^n+r^n\cdot b+\sum _{k=1}^{n-1}{r}^k{r}^{n-k}$

$=(a+b)r^n+\sum _{k=1}^{n-1}{r}^n$

$=(a+b+n-1)r^n$

Zbierając, otrzymujemy

$c_n=\{\begin{array}{ll}ab& \text{gdy }n=0\\ (a+b+n-1)r^n& \text{gdy }n⩾1\end{array}$

Punkt 5.

Dla $n=0$ mamy $c_0=a_0{b}_0=ab$

Dla $n=1$ mamy $c_1=a_0{b}_1+a_1{b}_0=ar+bq$

Dla $n⩾2$ jest

$c_n=\sum _{k=0}^n{a}_k{b}_{n-k}$

$=a_0{b}_n+a_n{b}_0+\sum _{k=1}^{n-1}{a}_k{b}_{n-k}$

$=a{r}^n+b{q}^n+\sum _{k=1}^{n-1}{q}^k{r}^{n-k}$

Jeżeli $r=0$, to $\sum _{k=1}^{n-1}{q}^k{r}^{n-k}=0$. Jeżeli $r\ne 0$, to

$\sum _{k=1}^{n-1}{q}^k{r}^{n-k}=r^n\sum _{k=1}^{n-1}{\left(\frac{q}{r}\right)}^k=r^n\cdot \frac{{\left(\frac{q}{r}\right)}^n-\frac{q}{r}}{\frac{q}{r}-1}=\frac{r{q}^n-q{r}^n}{q-r}$

Zauważmy, że znaleziony wzór obejmuje również przypadek $r=0$. Zatem

$c_n=a{r}^n+b{q}^n+\frac{r{q}^n-q{r}^n}{q-r}$

$=q^n(b+\frac{r}{q-r})+r^n(a-\frac{q}{q-r})$

Zbierając, otrzymujemy

$c_n=\{\begin{array}{ll}ab& \text{gdy }n=0\\ q^n(b+\frac{r}{q-r})+r^n(a-\frac{q}{q-r})& \text{gdy }n⩾1\end{array}$

□

Przykład D69
Ostatni punkt zadania D68 pozwala stworzyć wiele przykładowych szeregów i ich iloczynów Cauchy'ego. Przypomnijmy, że

$(a_n)=(a,q,q^2,q^3,\dots )$, $(b_n)=(b,r,r^2,r^3,\dots )$,  gdzie $q\ne r$

$c_n=\{\begin{array}{ll}ab& \text{gdy }n=0\\ q^n(b+\frac{r}{q-r})+r^n(a-\frac{q}{q-r})& \text{gdy }n⩾1\end{array}$

Przykłady zebraliśmy w tabeli.

$\mathit{a}$	$\mathit{q}$	$\mathit{b}$	$\mathit{r}$	$\mathbf{(}{\mathit{c}}_{\mathit{n}}\mathbf{)}$	$\mathbf{\sum }_{\mathit{n}\mathbf{=}\mathbf{0}}^{\mathbf{\infty }}{\mathit{a}}_{\mathit{n}}$	$\mathbf{\sum }_{\mathit{n}\mathbf{=}\mathbf{0}}^{\mathbf{\infty }}{\mathit{b}}_{\mathit{n}}$	$\mathbf{\sum }_{\mathit{n}\mathbf{=}\mathbf{0}}^{\mathbf{\infty }}{\mathit{c}}_{\mathit{n}}$
$3$	$\frac{1}{2}$	$-2$	$\frac{1}{3}$	$(-6,0,0,0,0,0,\dots )$	zbieżny	zbieżny	zbieżny
$-2$	$2$	$3$	$3$	$(-6,0,0,0,0,0,\dots )$	rozbieżny	rozbieżny	zbieżny
$\frac{r-2q}{r-q}$	$q$	$\frac{r}{r-q}$	$r$	$(\frac{r(r-2q)}{(r-q{)}^2},r,r^2,r^3,r^4,r^5,\dots )$	zbieżny / rozbieżny	zbieżny / rozbieżny	zbieżny / rozbieżny
$4$	$\frac{1}{2}$	$-2$	$\frac{1}{3}$	$(-8,\frac{1}{3},\frac{1}{3^2},\frac{1}{3^3},\frac{1}{3^4},\frac{1}{3^5},\dots )$	zbieżny	zbieżny	zbieżny
$\frac{7}{3}$	$2$	$-\frac{1}{3}$	$\frac{1}{2}$	$(-\frac{7}{9},\frac{1}{2},\frac{1}{2^2},\frac{1}{2^3},\frac{1}{2^4},\frac{1}{2^5},\dots )$	rozbieżny	zbieżny	zbieżny
$-1$	$2$	$3$	$3$	$(-3,3,3^2,3^3,3^4,3^5,\dots )$	rozbieżny	rozbieżny	rozbieżny
$\frac{1}{2}$	$1$	$\frac{1}{2}$	$-1$	$(\frac{1}{4},0,0,0,0,0,\dots )$	rozbieżny	rozbieżny	zbieżny
$-1$	$1$	$2$	$2$	$(-2,0,0,0,0,0,\dots )$	rozbieżny	rozbieżny	zbieżny
$-1$	$1$	$3$	$2$	$(-3,1,1,1,1,1,\dots )$	rozbieżny	rozbieżny	rozbieżny
$2$	$1$	$-1$	$\frac{1}{2}$	$(-2,0,0,0,0,0,\dots )$	rozbieżny	zbieżny	zbieżny
$2$	$1$	$0$	$\frac{1}{2}$	$(0,1,1,1,1,1,\dots )$	rozbieżny	zbieżny	rozbieżny
$\frac{r-2}{r-1}$	$1$	$\frac{r}{r-1}$	$r$	$(\frac{r(r-2)}{(r-1{)}^2},r,r^2,r^3,r^4,r^5,\dots )$	rozbieżny	zbieżny / rozbieżny	zbieżny / rozbieżny
$0$	$1$	$2$	$2$	$(0,2,2^2,2^3,2^4,2^5,\dots )$	rozbieżny	rozbieżny	rozbieżny
$3$	$1$	$-1$	$\frac{1}{2}$	$(-3,\frac{1}{2},\frac{1}{2^2},\frac{1}{2^3},\frac{1}{2^4},\frac{1}{2^5},\dots )$	rozbieżny	zbieżny	zbieżny

Przykład D70
Podamy przykład szeregów zbieżnych, których iloczyn Cauchy'ego jest rozbieżny. Rozważmy zbieżny szereg (zobacz D5)

$\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{\sqrt{k+1}}=0.604898643\dots$ (WolframAlpha)

Mnożąc powyższy szereg przez siebie według reguły Cauchy'ego, otrzymujemy

$c_n=\sum _{k=0}^n\frac{(-1{)}^k}{\sqrt{k+1}}\cdot \frac{(-1{)}^{n-k}}{\sqrt{n-k+1}}=(-1{)}^n\cdot \sum _{k=0}^n\frac{1}{\sqrt{(k+1)(n-k+1)}}$

Ale $k⩽n$ i $n-k⩽n$, zatem

$\frac{1}{\sqrt{(k+1)(n-k+1)}}⩾\frac{1}{\sqrt{(n+1)(n+1)}}=\frac{1}{n+1}$

Czyli

$|c_n|⩾\sum _{k=0}^n\frac{1}{n+1}=1$

Ponieważ $\underset{n\to \mathrm{\infty }}{lim}{c}_n\ne 0$, to iloczyn Cauchy'ego jest rozbieżny (zobacz D4).

Zadanie D71
Pokazać, że jeżeli $a_n=b_n=r^n$ i $c_n=(n+1)r^n$ (zobacz D68 p.3), to szeregi $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ oraz $\sum _{n=0}^{\mathrm{\infty }}{c}_n$ są jednocześnie zbieżne lub jednocześnie rozbieżne. Sprawdzić, że w przypadku, gdy szeregi te są zbieżne, prawdziwy jest wzór

$\left(\sum _{i=0}^{\mathrm{\infty }}{a}_i\right)\cdot \left(\sum _{j=0}^{\mathrm{\infty }}{b}_j\right)=\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{k=0}^n{a}_k{b}_{n-k}\right)$

Rozwiązanie

Zbieżność szeregu $\sum _{n=0}^{\mathrm{\infty }}(n+1)r^n$ łatwo zbadamy, stosując kryterium d'Alemberta.

$\left|\frac{c_{n+1}}{c_n}\right|=\left|\frac{(n+2)r^{n+1}}{(n+1)r^n}\right|=\frac{n+2}{n+1}\cdot |r|\stackrel{n\to \mathrm{\infty }}{\to }|r|$

Zatem szereg $\sum _{n=0}^{\mathrm{\infty }}(n+1)r^n$ jest zbieżny, gdy $|r|<1$ i rozbieżny, gdy $|r|>1$, tak samo, jak szereg $\sum _{n=0}^{\mathrm{\infty }}{r}^n$. W przypadku, gdy $r=\pm 1$ szereg $\sum _{n=0}^{\mathrm{\infty }}{r}^n$ jest rozbieżny, a odpowiednie sumy częściowe szeregu $\sum _{n=0}^{\mathrm{\infty }}(n+1)r^n$ są równe

•     gdy $r=1$, $c_n=n+1$, $C_L=\sum _{n=0}^L(n+1)=\frac{(L+1)(L+2)}{2}\stackrel{L\to \mathrm{\infty }}{\to }\mathrm{\infty }$ (zobacz [a], WolframAlpha)

•     gdy $r=-1$, $c_n=(n+1)(-1{)}^n$, $C_L=\sum _{n=0}^L(n+1)(-1{)}^n=(-1{)}^L\cdot \frac{2L+3}{4}+\frac{1}{4}\stackrel{L\to \mathrm{\infty }}{\to }\pm \mathrm{\infty }$ (zobacz D53, WolframAlpha)

W przypadku, gdy $|r|<1$ wiemy, że $\sum _{n=0}^{\mathrm{\infty }}{r}^n=\frac{1}{1-r}$. Korzystając z zadania D53, otrzymujemy

$\sum _{n=0}^L(n+1)r^n=\sum _{n=0}^{L}n{r}^n+\sum _{n=0}^L{r}^n=\frac{L{r}^{L+2}-(L+1)r^{L+1}+r}{(r-1{)}^2}+\frac{r^{L+1}-1}{r-1}=\frac{(L+1)r^{L+2}-(L+2)r^{L+1}+1}{(r-1{)}^2}\stackrel{L\to \mathrm{\infty }}{\to }\frac{1}{(r-1{)}^2}$

Ponieważ szereg $\sum _{n=0}^{\mathrm{\infty }}(n+1)r^n$ jest zbieżny, gdy $|r|<1$, to musi być $\underset{n\to \mathrm{\infty }}{lim}(n+1)r^n=0$ (zobacz D4). Pokazaliśmy, że w rozważanym przypadku iloczyn sum szeregów jest równy sumie iloczynu Cauchy'ego tych szeregów.

---

[a] Zauważmy, że

$\sum _{k=0}^{n}k=\frac{1}{2}(\sum _{k=0}^{n}k+\sum _{k=0}^{n}k)=\frac{1}{2}[\sum _{k=0}^{n}k+\sum _{j=0}^n(n-j)]=\frac{1}{2}[\sum _{k=0}^{n}k+\sum _{k=0}^n(n-k)]=\frac{1}{2}\sum _{k=0}^n(k+n-k)=\frac{n}{2}\sum _{k=0}^{n}1=\frac{n(n+1)}{2}$

□

Uwaga D72
Przykłady D69 i D70 pokazują, że w ogólności nie jest prawdziwy wzór

$\left(\sum _{i=0}^{\mathrm{\infty }}{a}_i\right)\cdot \left(\sum _{j=0}^{\mathrm{\infty }}{b}_j\right)=\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{k=0}^n{a}_k{b}_{n-k}\right)$

Skoro iloczyn sum szeregów nie zawsze jest równy sumie iloczynu Cauchy'ego tych szeregów, to musimy ustalić, jakie warunki muszą być spełnione, aby tak było.

Uwaga D73
Nim przejdziemy do dowodu twierdzenia Mertensa, zauważmy, że od sumowania po $m+1$ kolejnych przekątnych

$\sum _{n=0}^m\sum _{k=0}^n{a}_k{b}_{n-k}$

możemy łatwo przejść do sumowania po liniach poziomych lub po liniach pionowych. Rysunek przedstawia sytuację, gdy $m=5$.

$a_6{b}_0$	$$
$a_5{b}_0$	$$
$a_4{b}_0$	$a_4{b}_1$	$$
$a_3{b}_0$	$a_3{b}_1$	$a_3{b}_2$	$$
$a_2{b}_0$	$a_2{b}_1$	$a_2{b}_2$	$a_2{b}_3$	$$
$a_1{b}_0$	$a_1{b}_1$	$a_1{b}_2$	$a_1{b}_3$	$a_1{b}_4$	$$
$a_0{b}_0$	$a_0{b}_1$	$a_0{b}_2$	$a_0{b}_3$	$a_0{b}_4$	$a_0{b}_5$	$a_0{b}_6$

Przejście do sumowania po liniach poziomych

$\sum _{n=0}^m\sum _{k=0}^n{a}_k{b}_{n-k}=\sum _{i=0}^m\sum _{j=0}^{m-i}{a}_i{b}_j$

Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach poziomych, a druga po kolejnych elementach w $i$-tej linii poziomej.

Przejście do sumowania po liniach pionowych

$\sum _{n=0}^m\sum _{k=0}^n{a}_k{b}_{n-k}=\sum _{i=0}^m\sum _{j=0}^{m-i}{a}_j{b}_i$

Pierwsza suma (po prawej stronie) przebiega po kolejnych liniach pionowych, a druga po kolejnych elementach w $i$-tej linii pionowej.

Twierdzenie D74 (Franciszek Mertens)
Jeżeli szereg $\sum _{i=0}^{\mathrm{\infty }}{a}_i=A$ jest zbieżny bezwzględnie, szereg $\sum _{j=0}^{\mathrm{\infty }}{b}_j=B$ jest zbieżny, to ich iloczyn Cauchy'ego $\sum _{n=0}^{\mathrm{\infty }}{c}_n$, gdzie $c_n=\sum _{k=0}^n{a}_k{b}_{n-k}$, jest zbieżny i $\sum _{n=0}^{\mathrm{\infty }}{c}_n=AB$.

Dowód

Z założenia szereg $\sum _{i=0}^{\mathrm{\infty }}{a}_i$ jest zbieżny bezwzględnie, oznaczmy $\sum _{i=0}^{\mathrm{\infty }}|a_i|=A^{\prime }$. Niech

$A_n=\sum _{i=0}^n{a}_i{B}_n=\sum _{j=0}^n{b}_j{C}_n=\sum _{k=0}^n{c}_k{\beta }_n=B_n-B$

Przekształcając sumę $C_m$, otrzymujemy

$C_m=\sum _{n=0}^m{c}_n$

$=\sum _{n=0}^m\sum _{k=0}^n{a}_k{b}_{n-k}$

Przechodzimy od sumowania po $m+1$ kolejnych przekątnych do sumowania po $m+1$ kolejnych liniach poziomych (zobacz D73).

$C_m=\sum _{i=0}^m\sum _{j=0}^{m-i}{a}_i{b}_j$

$=\sum _{i=0}^m{a}_i\sum _{j=0}^{m-i}{b}_j$

$=\sum _{i=0}^m{a}_i{B}_{m-i}$

$=\sum _{i=0}^m{a}_i\left(B+{\beta }_{m-i}\right)$

$=\sum _{i=0}^m{a}_{i}B+\sum _{i=0}^m{a}_i{\beta }_{m-i}$

$=B\sum _{i=0}^m{a}_i+\sum _{i=0}^m{a}_i{\beta }_{m-i}$

$=A_{m}B+\sum _{k=0}^m{\beta }_k{a}_{m-k}$

Zatem

$C_m-A_{m}B=\sum _{k=0}^m{\beta }_k{a}_{m-k}$

Niech

${\delta }_m=\sum _{k=0}^m{\beta }_k{a}_{m-k}$

Oczywiście chcemy pokazać, że $C_m⟶AB$. Ponieważ $A_{m}B⟶AB$, to wystarczy pokazać, że ${\delta }_m⟶0$.

Z założenia $B_m⟶B$, zatem ${\beta }_m⟶0$. Ze zbieżności ciągu $({\beta }_k)$ wynika, że

•    ciąg $({\beta }_k)$ jest ograniczony, czyli istnieje taka liczba $U>0$, że dla każdego $k⩾0$ jest $|{\beta }_k|⩽U$ (zobacz C9)

•    dla dowolnego ${\epsilon }_1>0$ prawie wszystkie wyrazy ciągu $({\beta }_k)$ spełniają warunek $|{\beta }_k|<{\epsilon }_1$ (zobacz C4, C6)

Możemy przyjąć, że warunek $|{\beta }_k|<{\epsilon }_1$ spełniają wszystkie wyrazy, poczynając od $M=M({\epsilon }_1)$. Zatem dla $m>M$ dostajemy

$|{\delta }_m|⩽\sum _{k=0}^M|{\beta }_k||a_{m-k}|+\sum _{k=M+1}^m|{\beta }_k||a_{m-k}|$

$<U(|a_m|+\dots +|a_{m-M}|)+{\epsilon }_1\sum _{k=M+1}^m|a_{m-k}|$

$<U(|a_{m-M}|+\dots +|a_m|)+{\epsilon }_1{A}^{\prime }$

Z założenia szereg $\sum _{i=0}^{\mathrm{\infty }}{a}_i$ jest zbieżny, zatem musi być $\underset{m\to \mathrm{\infty }}{lim}{a}_m=0$ (zobacz D4). Czyli dla dowolnego ${\epsilon }_2>0$ prawie wszystkie wyrazy ciągu $(a_k)$ spełniają warunek $|a_k|<{\epsilon }_2$. Możemy przyjąć, że są to wszystkie wyrazy, poczynając od $N=N({\epsilon }_2)$. Zatem dla $m>M+N$ otrzymujemy

$|{\delta }_m|<U(|a_{m-M}|+\dots +|a_m|)+{\epsilon }_1{A}^{\prime }$

$<{\epsilon }_2(M+1)U+{\epsilon }_1{A}^{\prime }$

Prawa strona nierówności jest dowolnie mała. Przykładowo dla dowolnego $\epsilon >0$ wystarczy wybrać ${\epsilon }_1=\frac{\epsilon /2}{A^{\prime }}$ i ${\epsilon }_2=\frac{\epsilon /2}{(M+1)U}$, aby otrzymać $|{\delta }_m|<\epsilon$ dla wszystkich $m>M+N$. Ponieważ prawie wszystkie wyrazy ciągu ${\delta }_m$ spełniają warunek $|{\delta }_m|<\epsilon$, to $\underset{m\to \mathrm{\infty }}{lim}{\delta }_m=0$. Co należało pokazać.
□

Zadanie D75
Pokazać, że iloczyn Cauchy'ego dwóch szeregów bezwzględnie zbieżnych jest bezwzględnie zbieżny.

Rozwiązanie

Z założenia szeregi $\sum _{i=0}^{\mathrm{\infty }}{a}_i$ oraz $\sum _{j=0}^{\mathrm{\infty }}{b}_j$ są bezwzględnie zbieżne, zatem możemy napisać

$\sum _{i=0}^{\mathrm{\infty }}|a_i|=A^{\prime }\sum _{j=0}^{\mathrm{\infty }}|b_j|=B^{\prime }$

Zauważmy, że suma $\sum _{n=0}^m\sum _{k=0}^n|a_k||b_{n-k}|$ obejmuje $m+1$ przekątnych. Łatwo możemy przejść od sumowania po kolejnych przekątnych do sumowana po $m+1$ kolejnych liniach poziomych (zobacz D73).

$C_m^{\prime }=\sum _{n=0}^m|c_n|$

$=\sum _{n=0}^m\left|\sum _{k=0}^n{a}_k{b}_{n-k}\right|$

$⩽\sum _{n=0}^m\sum _{k=0}^n|a_k{b}_{n-k}|$

$=\sum _{n=0}^m\sum _{k=0}^n|a_k||b_{n-k}|$

$=\sum _{i=0}^m\sum _{j=0}^{m-i}|a_i||b_j|$ (zmieniliśmy sposób sumowania)

$=\sum _{i=0}^m|a_i|\sum _{j=0}^{m-i}|b_j|$

$⩽A^{\prime }{B}^{\prime }$

Ponieważ ciąg sum częściowych $C_m^{\prime }$ jest rosnący (bo sumujemy wartości nieujemne) i ograniczony od góry, to jest zbieżny.
□

Zadanie D76
Podać przykład szeregów zbieżnych, z których tylko jeden jest bezwzględnie zbieżny i których iloczyn Cauchy'ego jest warunkowo zbieżny.

Rozwiązanie

Zauważmy, że szereg $\sum _{i=0}^{\mathrm{\infty }}\frac{(-1{)}^i}{2^i}=\frac{2}{3}$ jest bezwzględnie zbieżny, bo $\sum _{i=0}^{\mathrm{\infty }}\frac{1}{2^i}=2$ jest zbieżny. Szereg $\sum _{j=0}^{\mathrm{\infty }}\frac{(-1{)}^j}{j+1}=\log 2$ jest zbieżny na mocy kryterium Leibniza (zobacz D5), ale nie jest bezwzględnie zbieżny (zobacz D17, D19 p.1, B34).

Zatem na podstawie twierdzenia Mertensa iloczyn Cauchy'ego tych szeregów $\sum _{n=0}^{\mathrm{\infty }}{c}_n$, gdzie

$c_n=\sum _{k=0}^n\frac{(-1{)}^k}{2^k}\cdot \frac{(-1{)}^{n-k}}{n-k+1}$

$=(-1{)}^n\sum _{k=0}^n\frac{1}{2^k(n-k+1)}$

jest zbieżny. Łatwo widzimy, że

$|c_n|=\sum _{k=0}^n\frac{1}{2^k(n-k+1)}$

$=\frac{1}{n+1}+\sum _{k=1}^n\frac{1}{2^k(n-k+1)}$

$⩾\frac{1}{n+1}$

Ponieważ szereg $\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n+1}$ jest rozbieżny i

$0⩽\frac{1}{n+1}⩽|c_n|$

to na mocy kryterium porównawczego (zobacz D9) szereg $\sum _{n=0}^{\mathrm{\infty }}|c_n|$ jest rozbieżny. Co należało pokazać.
□

Zadanie D77
Podać przykład szeregów warunkowo zbieżnych, których iloczyn Cauchy'ego jest warunkowo zbieżny.

Rozwiązanie

Szereg $\sum _{j=0}^{\mathrm{\infty }}\frac{(-1{)}^j}{j+1}=\log 2$ jest warunkowo zbieżny (zobacz D5, D17, D19 p.1, B34). Iloczyn Cauchy'ego dwóch takich szeregów jest równy $\sum _{n=0}^{\mathrm{\infty }}{c}_n$, gdzie

$c_n=\sum _{k=0}^n\frac{(-1{)}^k}{k+1}\cdot \frac{(-1{)}^{n-k}}{n-k+1}$

$=(-1{)}^n\sum _{k=0}^n\frac{1}{(k+1)(n-k+1)}$

$=\frac{(-1{)}^n}{n+2}\sum _{k=0}^n\frac{(n-k+1)+(k+1)}{(k+1)(n-k+1)}$

$=\frac{(-1{)}^n}{n+2}\sum _{k=0}^n(\frac{1}{k+1}+\frac{1}{n-k+1})$

$=\frac{(-1{)}^n}{n+2}(\sum _{k=0}^n\frac{1}{k+1}+\sum _{j=0}^n\frac{1}{j+1})$

$=\frac{2(-1{)}^n}{n+2}\sum _{k=0}^n\frac{1}{k+1}$

Ponieważ (zobacz D17)

$\log (n+1)<\sum _{k=1}^n\frac{1}{k}<1+\log n$

to

$\frac{2}{n+2}\cdot \log (n+2)<|c_n|<\frac{2}{n+2}\cdot (1+\log (n+1))$

Z twierdzenia o trzech ciągach wynika natychmiast, że $\underset{n\to \mathrm{\infty }}{lim}|c_n|=0$. Pokażemy teraz, że ciąg $(|c_n|)$ jest ciągiem malejącym.

$|c_n|-|c_{n-1}|=\frac{2}{n+2}\sum _{k=0}^n\frac{1}{k+1}-\frac{2}{n+1}\sum _{k=0}^{n-1}\frac{1}{k+1}$

$=\frac{2}{n+2}\cdot \frac{1}{n+1}+\frac{2}{n+2}\sum _{k=0}^{n-1}\frac{1}{k+1}-\frac{2}{n+1}\sum _{k=0}^{n-1}\frac{1}{k+1}$

$=\frac{2}{(n+2)(n+1)}+(\frac{2}{n+2}-\frac{2}{n+1})\sum _{k=0}^{n-1}\frac{1}{k+1}$

$=\frac{2}{(n+2)(n+1)}-\frac{2}{(n+2)(n+1)}\sum _{k=0}^{n-1}\frac{1}{k+1}$

$⩽0$

Bo $\sum _{k=0}^{n-1}\frac{1}{k+1}⩾1$. Ponieważ ciąg $(|c_n|)$ jest malejący i zbieżny do zera, to z kryterium Leibniza (zobacz D5) szereg $\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n|c_n|$ jest zbieżny. Zauważmy jeszcze, że dla $n⩾1$ mamy

$0⩽\frac{1}{n+1}⩽\frac{2\log (n+2)}{n+2}<|c_n|$

Zatem na podstawie kryterium porównawczego (zobacz D9) szereg $\sum _{n=0}^{\mathrm{\infty }}|c_n|$ jest rozbieżny.
□

Uwaga D78
Nim przejdziemy do dowodu twierdzenia Abela, musimy udowodnić trzy twierdzenia dotyczące pewnych granic. Warto zauważyć, że twierdzenie D80 pozwala przypisać wartość sumy do szeregów, których suma w zwykłym sensie nie istnieje. Uogólnienie to nazywamy sumowalnością w sensie Cesàro. Nie będziemy zajmowali się tym tematem, ale podamy ciekawy przykład.

Rozważmy szereg $\sum _{i=0}^{\mathrm{\infty }}(-1{)}^i$. Sumy częściowe tego szeregu wynoszą $S_k=\frac{1+(-1{)}^k}{2}$ i tworzą ciąg rozbieżny, ale ciąg kolejnych średnich arytmetycznych dla ciągu $(S_k)$ jest równy

$x_n=\frac{S_0+\dots +S_n}{n+1}=\frac{1}{n+1}\cdot \sum _{k=0}^n\frac{1+(-1{)}^k}{2}=\frac{1}{2}+\frac{1+(-1{)}^n}{4(n+1)}\stackrel{n\to \mathrm{\infty }}{\to }\frac{1}{2}$ (WolframAlfa)

Zatem szereg $\sum _{i=0}^{\mathrm{\infty }}(-1{)}^i$ jest sumowalny w sensie Cesàro i jego suma jest równa $\frac{1}{2}$.

Twierdzenie D79
Jeżeli $\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$, to $\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n+1}\sum _{k=0}^n|a_k|=0$.

Dowód

Z założenia $\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$. Ze zbieżności ciągu $(a_k)$ wynika, że

•    ciąg $(a_k)$ jest ograniczony, czyli istnieje taka liczba $U>0$, że dla każdego $k⩾0$ jest $|a_k|⩽U$ (zobacz C9)

•    dla dowolnego $\epsilon >0$ prawie wszystkie wyrazy ciągu $(a_k)$ spełniają warunek $|a_k|<\epsilon$ (zobacz C4, C6)

Możemy przyjąć, że warunek $|a_k|<\epsilon$ spełniają wszystkie wyrazy, poczynając od $N=N(\epsilon )$. Zatem dla $n>N$ możemy napisać

$\frac{1}{n+1}\sum _{k=0}^n|a_k|=\frac{|a_0|+\dots +|a_N|+|a_{N+1}|+\dots +|a_n|}{n+1}$

$<\frac{U(N+1)}{n+1}+\frac{\epsilon (n-N)}{n+1}$

$<\frac{U(N+1)}{n+1}+\epsilon$

Ponieważ liczba $n$ może być dowolnie duża, to wyrażenie $\frac{U(N+1)}{n+1}$ może być dowolnie małe. W szczególności warunek

$\frac{U(N+1)}{n+1}<\epsilon$

jest spełniony dla $n>\frac{U(N+1)}{\epsilon }-1$ i otrzymujemy, że

$\frac{1}{n+1}\sum _{k=0}^n|a_k|<2\epsilon$

dla wszystkich $n>max(N,\frac{U(N+1)}{\epsilon }-1)$. Zatem $\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n+1}\sum _{k=0}^n|a_k|=0$. Co należało pokazać.
□

Twierdzenie D80
Jeżeli ciąg $(a_k)$ jest zbieżny, to ciąg kolejnych średnich arytmetycznych $x_n=\frac{a_0+\dots +a_n}{n+1}$ jest zbieżny do tej samej granicy.

Dowód

Z założenia ciąg $(a_k)$ jest zbieżny, zatem możemy napisać

$\underset{k\to \mathrm{\infty }}{lim}{a}_k=g$

Z definicji ciągu $(x_n)$ dostajemy

$x_n-g=\frac{a_0+\dots +a_n}{n+1}-g=\frac{a_0+\dots +a_n-(n+1)g}{n+1}=\frac{(a_0-g)+\dots +(a_n-g)}{n+1}=\frac{a_0-g}{n+1}+\dots +\frac{a_n-g}{n+1}$

Wynika stąd, że

$0⩽|x_n-g|⩽\frac{|a_0-g|}{n+1}+\dots +\frac{|a_n-g|}{n+1}=\frac{1}{n+1}\sum _{k=0}^n|a_k-g|$

W granicy, gdy $n\to \mathrm{\infty }$, z twierdzenia D79 i twierdzenia o trzech ciągach (zobacz C10) otrzymujemy

$\underset{n\to \mathrm{\infty }}{lim}|x_n-g|=0$

Czyli $\underset{n\to \mathrm{\infty }}{lim}{x}_n=g$ (zobacz C8 p.2). Co należało pokazać.
□

Twierdzenie D81
Niech $(a_n)$ i $(b_n)$ będą zbieżnymi ciągami liczb rzeczywistych. Jeżeli $\underset{n\to \mathrm{\infty }}{lim}{a}_n=a$ i $\underset{n\to \mathrm{\infty }}{lim}{b}_n=b$, to $\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n+1}\sum _{k=0}^n{a}_k{b}_{n-k}=ab$.

Dowód

1. Przypadek, gdy $\underset{\mathit{n}\mathbf{\to }\mathbf{\infty }}{\mathbf{lim}}{\mathit{a}}_{\mathit{n}}\mathbf{=}\mathbf{0}$

Ponieważ ciąg $(b_n)$ jest zbieżny, to jest ograniczony (zobacz C9), czyli istnieje taka liczba $U>0$, że dla każdego $k⩾0$ jest $|b_k|⩽U$. Zatem

$0⩽\left|\frac{1}{n+1}\sum _{k=0}^n{a}_k{b}_{n-k}\right|⩽\frac{1}{n+1}\sum _{k=0}^n|a_k||b_{n-k}|⩽\frac{U}{n+1}\sum _{k=0}^n|a_k|$

W granicy, gdy $n\to \mathrm{\infty }$, z twierdzenia D79 i twierdzenia o trzech ciągach (zobacz C10) otrzymujemy

$\underset{n\to \mathrm{\infty }}{lim}\left|\frac{1}{n+1}\sum _{k=0}^n{a}_k{b}_{n-k}\right|=0$

Czyli $\underset{n\to \mathrm{\infty }}{lim}\left(\frac{1}{n+1}\sum _{k=0}^n{a}_k{b}_{n-k}\right)=0$ (zobacz C8 p.2).

2. Przypadek, gdy $\underset{\mathit{n}\mathbf{\to }\mathbf{\infty }}{\mathbf{lim}}{\mathit{a}}_{\mathit{n}}\mathbf{\ne }\mathbf{0}$

Niech $x_n=a_n-a$. Oczywiście $\underset{n\to \mathrm{\infty }}{lim}{x}_n=0$. Podstawiając, otrzymujemy

$\frac{1}{n+1}\sum _{k=0}^n{a}_k{b}_{n-k}=\frac{1}{n+1}\sum _{k=0}^n(a+x_k)b_{n-k}$

$=\frac{1}{n+1}\sum _{k=0}^{n}a{b}_{n-k}+\frac{1}{n+1}\sum _{k=0}^n{x}_k{b}_{n-k}$

$=a\cdot \frac{1}{n+1}\sum _{j=0}^n{b}_j+\frac{1}{n+1}\sum _{k=0}^n{x}_k{b}_{n-k}$

W granicy, gdy $n⟶\mathrm{\infty }$, z twierdzenia D80 i udowodnionego wyżej przypadku, gdy $\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$, dostajemy

$\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n+1}\sum _{k=0}^n{a}_k{b}_{n-k}=ab$

Co kończy dowód.
□

Twierdzenie D82 (Niels Henrik Abel)
Jeżeli szeregi $\sum _{i=0}^{\mathrm{\infty }}{a}_i=A$ oraz $\sum _{j=0}^{\mathrm{\infty }}{b}_j=B$ są zbieżne i ich iloczyn Cauchy'ego $\sum _{n=0}^{\mathrm{\infty }}{c}_n$, gdzie $c_n=\sum _{k=0}^n{a}_k{b}_{n-k}$, jest zbieżny, to $\sum _{n=0}^{\mathrm{\infty }}{c}_n=AB$.

Dowód

Będziemy stosowali następujące oznaczenia

$A_n=\sum _{i=0}^n{a}_i{B}_n=\sum _{i=0}^n{b}_i{C}_n=\sum _{i=0}^n{c}_i$

Z założenia szeregi są zbieżne, zatem możemy napisać

$\underset{n\to \mathrm{\infty }}{lim}{A}_n=A\underset{n\to \mathrm{\infty }}{lim}{B}_n=B\underset{n\to \mathrm{\infty }}{lim}{C}_n=C$

Rozważmy sumę

$\sum _{m=0}^L{C}_m=\sum _{m=0}^L\sum _{n=0}^m{c}_n$

$=\sum _{m=0}^L\sum _{n=0}^m\sum _{k=0}^n{a}_k{b}_{n-k}$

Od sumowania wyrazów $a_k{b}_{n-k}$ po $m+1$ kolejnych przekątnych przechodzimy do sumowania po $m+1$ kolejnych liniach poziomych (zobacz D73).

$\sum _{m=0}^L{C}_m=\sum _{m=0}^L\sum _{i=0}^m\sum _{j=0}^{m-i}{a}_i{b}_j$

$=\sum _{m=0}^L\sum _{i=0}^m{a}_i\sum _{j=0}^{m-i}{b}_j$

$=\sum _{m=0}^L\sum _{i=0}^m{a}_i{B}_{m-i}$

$=\sum _{m=0}^L\sum _{k=0}^m{a}_k{B}_{m-k}$

Od sumowania wyrazów $a_k{B}_{m-k}$ po $L+1$ kolejnych przekątnych przechodzimy do sumowania po $L+1$ kolejnych liniach pionowych (zobacz D73).

$\sum _{m=0}^L{C}_m=\sum _{i=0}^L\sum _{j=0}^{L-i}{a}_j{B}_i$

$=\sum _{i=0}^L{B}_i\sum _{j=0}^{L-i}{a}_j$

$=\sum _{i=0}^L{B}_i{A}_{L-i}$

Zatem

$\frac{1}{L+1}\sum _{m=0}^L{C}_m=\frac{1}{L+1}\sum _{i=0}^L{B}_i{A}_{L-i}$

W granicy, gdy $L⟶\mathrm{\infty }$, z twierdzeń D80 i D81 otrzymujemy $C=AB$. Co należało pokazać.
□

Liczby Catalana

Definicja D83
Liczby Catalana $C_n$ definiujemy wzorem

$C_n=\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})$

gdzie $n⩾0$.

Twierdzenie D84
Liczby Catalana $C_n$ mają następujące własności

•    $C_n$ są liczbami całkowitymi dodatnimi

•    $C_n=\frac{1}{2n+1}(\genfrac{}{}{0ex}{}{2n+1}{n})=\frac{1}{n}(\genfrac{}{}{0ex}{}{2n}{n-1})$

•    $C_{n+1}=\frac{2(2n+1)}{n+2}{C}_n$

•    $C_{n+1}=\sum _{k=0}^n{C}_k{C}_{n-k}$

Dowód

Punkt 1.

Twierdzenie jest prawdziwe dla początkowych wartości $n⩾0$, bo $(C_n)=(1,1,2,5,14,42,132,429,1430,4862,16796,\dots )$. W ogólności wystarczy zauważyć, że dla $n⩾0$ mamy

$(\genfrac{}{}{0ex}{}{2n}{n+1})=\frac{(2n)!}{(n+1)!(n-1)!}=\frac{n}{n+1}\cdot \frac{(2n)!}{n!n!}=\frac{n}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})<(\genfrac{}{}{0ex}{}{2n}{n})$

$(\genfrac{}{}{0ex}{}{2n}{n})-(\genfrac{}{}{0ex}{}{2n}{n+1})=(\genfrac{}{}{0ex}{}{2n}{n})-\frac{n}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})=\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})=C_n$

Zatem $C_n$ jest liczbą całkowitą większą od zera.

Punkt 2.

$\frac{1}{2n+1}(\genfrac{}{}{0ex}{}{2n+1}{n})=\frac{1}{2n+1}\cdot \frac{(2n+1)!}{n!(n+1)!}=\frac{1}{2n+1}\cdot \frac{2n+1}{n+1}\cdot \frac{(2n)!}{n!n!}=\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})=C_n$

$\frac{1}{n}(\genfrac{}{}{0ex}{}{2n}{n-1})=\frac{1}{n}\cdot \frac{(2n)!}{(n-1)!(n+1)!}=\frac{1}{n+1}\cdot \frac{(2n)!}{n!n!}=\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})=C_n$

Punkt 3.

$\frac{C_{n+1}}{C_n}=\frac{1}{n+2}\cdot \frac{(2n+2)!}{(n+1)!(n+1)!}\cdot (n+1)\cdot \frac{n!n!}{(2n)!}$

$=\frac{1}{n+2}\cdot \frac{(2n+2)(2n+1)}{(n+1{)}^2}\cdot \frac{(2n)!}{n!n!}\cdot (n+1)\cdot \frac{n!n!}{(2n)!}=$

$=\frac{2(2n+1)}{n+2}$

Punkt 4.

Dowód tego punktu został umieszczony w Uzupełnieniu (zobacz D90).
□

Zadanie D85
Niech $C_n$ oznacza $n$-tą liczbę Catalana i niech $\sum _{n=0}^{\mathrm{\infty }}{x}_n$ oznacza szereg, który otrzymujemy, mnożąc szereg $\sum _{k=0}^{\mathrm{\infty }}{a}_k$ przez siebie według reguły Cauchy'ego. Pokazać, że

•    jeżeli $a_n=C_n$,  to  $x_n=C_{n+1}$

•    jeżeli $a_0=\alpha$ i $a_n=r^{n-1}{C}_{n-1}$ dla $n⩾1$,  to  $x_0={\alpha }^2$, $x_1=2\alpha C_0$ i $x_n=(1+2\alpha r)r^{n-2}{C}_{n-1}$ dla $n⩾2$

Dla jakich wartości $\alpha ,r$ szereg $\sum _{n=0}^{\mathrm{\infty }}{x}_n$ jest zbieżny?

Rozwiązanie

Punkt 2.

Dla $n=0$ mamy $x_0=a_0{a}_0={\alpha }^2$

Dla $n=1$ mamy $x_1=a_0{a}_1+a_1{a}_0=2a_0{a}_1=2\alpha C_0$

Dla $n⩾2$ jest

$x_n=\sum _{k=0}^n{a}_k{a}_{n-k}$

$=a_0{a}_n+a_n{a}_0+\sum _{k=1}^{n-1}{a}_k{a}_{n-k}$

$=2a_0{a}_n+\sum _{k=1}^{n-1}{r}^{k-1}{C}_{k-1}\cdot r^{n-k-1}{C}_{n-k-1}$

$=2\alpha r^{n-1}{C}_{n-1}+r^{n-2}\sum _{k=1}^{n-1}{C}_{k-1}{C}_{n-k-1}$

$=2\alpha r^{n-1}{C}_{n-1}+r^{n-2}\sum _{j=0}^{n-2}{C}_j{C}_{n-2-j}$

$=2\alpha r^{n-1}{C}_{n-1}+r^{n-2}{C}_{n-1}$

$=r^{n-2}{C}_{n-1}(1+2\alpha r)$

Zauważmy, że

$\frac{C_n}{C_{n-1}}=\frac{\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})}{\frac{1}{n}(\genfrac{}{}{0ex}{}{2n-2}{n-1})}=\frac{n}{n+1}\cdot \frac{2n(2n-1)(2n-2)!}{n^2[(n-1)!{]}^2}\cdot \frac{[(n-1)!{]}^2}{(2n-2)!}=\frac{n}{n+1}\cdot \frac{2n(2n-1)}{n^2}=\frac{2(2n-1)}{n+1}$

Z kryterium d'Alemberta dla szeregu $\sum _{k=0}^{\mathrm{\infty }}{a}_k$ i szeregu $\sum _{k=0}^{\mathrm{\infty }}{x}_k$ otrzymujemy

$\left|\frac{a_{k+1}}{a_k}\right|=\left|\frac{r^n{C}_n}{r^{n-1}{C}_{n-1}}\right|=|r|\cdot \frac{C_n}{C_{n-1}}=|r|\cdot \frac{2(2n-1)}{n+1}\stackrel{n\to \mathrm{\infty }}{\to }4|r|$

$\left|\frac{x_{k+1}}{x_k}\right|=\left|\frac{r^{n-1}{C}_n(1+2\alpha r)}{r^{n-2}{C}_{n-1}(1+2\alpha r)}\right|=|r|\cdot \frac{C_n}{C_{n-1}}\stackrel{n\to \mathrm{\infty }}{\to }4|r|$

Zatem szeregi te są bezwzględnie zbieżne w przypadku, gdy $|r|<\frac{1}{4}$. W szczególności dla $\alpha =-\frac{1}{2r}$ szereg $\sum _{n=0}^{\mathrm{\infty }}{x}_n$ zawsze będzie zbieżny, bo od trzeciego wyrazu będzie się składał z samych zer. Wiemy, że w przypadku, gdy $r=\frac{1}{4}$ szereg $\sum _{n=0}^{\mathrm{\infty }}\frac{C_n}{4^n}=2$ jest zbieżny.
□

Uzupełnienie

Uwaga D86
Przedstawiony poniżej dowód czwartego punktu twierdzenia D84 został oparty na pracy Jovana Mikicia.

Twierdzenie D87
Jeżeli funkcja $f(k)$ nie zależy od $n$ i dane są sumy

$S(n)=\sum _{k=0}^{n}f(k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$T(n)=\sum _{k=0}^n(n-k)f(k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

to

$T(n)=4T(n-1)+2S(n-1)$

Dowód

Z definicji sumy $T(n)$ ostatni wyraz tej sumy jest równy zero, zatem dla $n⩾1$ mamy

$T(n)=\sum _{k=0}^{n-1}(n-k)f(k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\sum _{k=0}^{n-1}(n-k)f(k)\cdot \frac{(2n-2k)(2n-2k-1)}{(n-k{)}^2}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k-2}{n-k-1})$

$=\sum _{k=0}^{n-1}2(2n-2k-1)f(k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k-2}{n-k-1})$

$=\sum _{k=0}^{n-1}[4(n-1-k)+2]f(k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k-2}{n-k-1})$

Czyli

$T(n)=4T(n-1)+2S(n-1)$

Co kończy dowód.
□

Twierdzenie D88
Dla $n⩾0$ prawdziwy jest wzór

$\sum _{k=0}^n(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})=4^n$

Dowód

Niech

$S(n)=\sum _{k=0}^n(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$T(n)=\sum _{k=0}^n(n-k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

Zauważmy, że

$T(n)=\sum _{k=0}^n(n-k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\frac{1}{2}[\sum _{k=0}^n(n-k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})+\sum _{k=0}^n(n-k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})]$

$=\frac{1}{2}[\sum _{k=0}^n(n-k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})+\sum _{j=0}^{n}j(\genfrac{}{}{0ex}{}{2n-2j}{n-j})(\genfrac{}{}{0ex}{}{2j}{j})]$

$=\frac{1}{2}[\sum _{k=0}^n(n-k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})+\sum _{k=0}^{n}k(\genfrac{}{}{0ex}{}{2n-2k}{n-k})(\genfrac{}{}{0ex}{}{2k}{k})]$

$=\frac{1}{2}\sum _{k=0}^n(n-k+k)(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\frac{n}{2}\sum _{k=0}^n(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\frac{nS(n)}{2}$

Ponieważ $T(n)=\frac{nS(n)}{2}$ i $T(n)=4T(n-1)+2S(n-1)$ (zobacz D87), to otrzymujemy

$\frac{nS(n)}{2}=4\cdot \frac{(n-1)S(n-1)}{2}+2S(n-1)$

Czyli

$nS(n)=4nS(n-1)-4S(n-1)+4S(n-1)$

$S(n)=4S(n-1)$

Metodą indukcji matematycznej łatwo dowodzimy, że $S(n)=4^n$. Co należało pokazać.
□

Twierdzenie D89
Dla $n⩾0$ prawdziwy jest wzór

$\sum _{k=0}^n\frac{1}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})=\frac{1}{2}(\genfrac{}{}{0ex}{}{2n+2}{n+1})$

Dowód

Oznaczmy

$S(n)=\sum _{k=0}^n\frac{1}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$T(n)=\sum _{k=0}^n\frac{n-k}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

Zauważmy, że

$T(n)=\sum _{k=0}^n\frac{n-k}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\sum _{k=0}^n\frac{n+1-(k+1)}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=(n+1)\sum _{k=0}^n\frac{1}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})-\sum _{k=0}^n(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=(n+1)S(n)-4^n$

Ponieważ $T(n)=(n+1)S(n)-4^n$ i $T(n)=4T(n-1)+2S(n-1)$ (zobacz D87), to otrzymujemy

$(n+1)S(n)-4^n=4\cdot (nS(n-1)-4^{n-1})+2S(n-1)$

$(n+1)S(n)-4^n=4nS(n-1)-4^n+2S(n-1)$

$S(n)=\frac{2(2n+1)}{n+1}S(n-1)$

Metodą indukcji matematycznej dowodzimy, że $S(n)=\frac{1}{2}(\genfrac{}{}{0ex}{}{2n+2}{n+1})$. Dla $n=0$ mamy $S(0)=1$ i $\frac{1}{2}(\genfrac{}{}{0ex}{}{2}{1})=1$. Zatem wzór jest prawdziwy dla $n=0$. Zakładając, że wzór jest prawdziwy dla $n-1$, otrzymujemy dla $n$

$\frac{2(2n+1)}{n+1}S(n-1)=\frac{2n+1}{n+1}\cdot (\genfrac{}{}{0ex}{}{2n}{n})$

$=\frac{2n+1}{n+1}\cdot \frac{(n+1{)}^2}{(2n+1)(2n+2)}\cdot \frac{(2n+1)(2n+2)}{(n+1{)}^2}\cdot (\genfrac{}{}{0ex}{}{2n}{n})$

$=\frac{1}{2}(\genfrac{}{}{0ex}{}{2n+2}{n+1})$

$=S(n)$

Co kończy dowód.
□

Twierdzenie D90
Jeżeli $C_n$ są liczbami Catalana, to

$C_{n+1}=\sum _{k=0}^n{C}_k{C}_{n-k}$

Dowód

Zauważmy, że

$\sum _{k=0}^n{C}_k{C}_{n-k}=\sum _{k=0}^n\frac{1}{(k+1)(n-k+1)}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\frac{1}{n+2}\sum _{k=0}^n(\frac{1}{k+1}+\frac{1}{n-k+1})(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\frac{1}{n+2}[\sum _{k=0}^n\frac{1}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})+\sum _{k=0}^n\frac{1}{n-k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})]$

$=\frac{1}{n+2}[\sum _{k=0}^n\frac{1}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})+\sum _{j=0}^n\frac{1}{j+1}(\genfrac{}{}{0ex}{}{2n-2j}{n-j})(\genfrac{}{}{0ex}{}{2j}{j})]$

$=\frac{2}{n+2}\sum _{k=0}^n\frac{1}{k+1}(\genfrac{}{}{0ex}{}{2k}{k})(\genfrac{}{}{0ex}{}{2n-2k}{n-k})$

$=\frac{2}{n+2}\cdot \frac{1}{2}(\genfrac{}{}{0ex}{}{2n+2}{n+1})$

$=\frac{1}{n+2}(\genfrac{}{}{0ex}{}{2n+2}{n+1})$

$=C_{n+1}$

Co należało pokazać.
□