Twierdzenie Czebyszewa o liczbie pierwszej między n i 2n

22.12.2021

Twierdzenie Czebyszewa

W 1852 roku rosyjski matematyk Czebyszew udowodnił, że dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ a \cdot {\small\frac{n}{\log n}} \: \underset{n \geqslant 11}{\lt } \: \pi (n) \: \underset{n \geqslant 96098}{\lt } \: b \cdot {\small\frac{n}{\log n}} }[/math]

gdzie

[math]\displaystyle{ a = \log (2^{1 / 2} \cdot 3^{1 / 3} \cdot 5^{1 / 5} \cdot 30^{- 1 / 30}) = 0.921292022 \qquad \quad b = \tfrac{6}{5} a = 1.105550428 }[/math]

Dysponując tak dokładnym oszacowaniem funkcji [math]\displaystyle{ \pi (n) }[/math], Czebyszew mógł bez trudu udowodnić następujące twierdzenie
Twierdzenie B1 (twierdzenie Czebyszewa)
Dla [math]\displaystyle{ n \geqslant 2 }[/math] między liczbami naturalnymi [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się przynajmniej jedna liczba pierwsza.

W rzeczywistości Czebyszew mógł udowodnić znacznie silniejsze twierdzenie
Twierdzenie B2
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math]. Dla [math]\displaystyle{ n \geqslant 3 }[/math] w każdym z przedziałów [math]\displaystyle{ (n, 2 n) }[/math], [math]\displaystyle{ (2 n, 3 n) }[/math], [math]\displaystyle{ (3 n, 4 n) }[/math] oraz [math]\displaystyle{ (4 n, 5 n) }[/math] znajduje się przynajmniej jedna liczba pierwsza.

Przeprowadzimy obliczenia dla przedziału [math]\displaystyle{ (4 n, 5 n) }[/math]. Czytelnik w identyczny sposób może powtórzyć obliczenia dla pozostałych przypadków. Mamy

[math]\displaystyle{ \pi (5 n) - \pi (4 n) \gt a \cdot {\small\frac{5 n}{\log (5 n)}} - b \cdot {\small\frac{4 n}{\log (4 n)}} = }[/math]

[math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} - {\small\frac{4 b n}{\log (4 n)}} = }[/math]

[math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log (5 n)}{\log (4 n)}} \right) = }[/math]

[math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log \left( 4 n \cdot {\small\frac{5}{4}} \right)}{\log (4 n)}} \right) = }[/math]

[math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left( 1 - {\small\frac{4 b}{5 a}} \cdot {\small\frac{\log (4 n) + \log (5 / 4)}{\log (4 n)}} \right) = }[/math]

[math]\displaystyle{ \quad = {\small\frac{5 a n}{\log (5 n)}} \left[ 1 - {\small\frac{4 b}{5 a}} \cdot \left( 1 + {\small\frac{\log (5 / 4)}{\log (4 n)}} \right) \right] }[/math]

Dla dużych wartości [math]\displaystyle{ n }[/math] wyrażenie w nawiasie zwykłym dąży do [math]\displaystyle{ 1 }[/math], a wyrażenie w nawiasie kwadratowym do [math]\displaystyle{ 0.03999826 \ldots }[/math] Można łatwo sprawdzić, że wypisane oszacowanie [math]\displaystyle{ \pi (5 n) - \pi (4 n) }[/math] jest większe od [math]\displaystyle{ 1 }[/math] dla [math]\displaystyle{ n \geqslant 193 }[/math]. Zatem pozostaje sprawdzenie prawdziwości dowodzonego twierdzenia dla [math]\displaystyle{ 4 n \lt 96098 }[/math].

Dysponując odpowiednio dokładnym oszacowaniem typu

[math]\displaystyle{ a \cdot {\small\frac{n}{\log n}} \lt \pi (n) \lt b \cdot {\small\frac{n}{\log n}} }[/math]

możemy dla ustalonej liczby [math]\displaystyle{ r }[/math] próbować udowodnić następujące twierdzenie

Twierdzenie B3
Niech [math]\displaystyle{ n, n_0, r \in \mathbb{Z}_+ }[/math]. Istnieje taka liczba [math]\displaystyle{ n_0 }[/math], że dla [math]\displaystyle{ n \geqslant n_0 }[/math] między liczbami  [math]\displaystyle{ r n }[/math]  oraz  [math]\displaystyle{ (r + 1) n }[/math]  znajduje się przynajmniej jedna liczba pierwsza.

Dowodząc analogicznie, jak to uczyniliśmy wyżej (w przypadku twierdzenia B2), łatwo możemy pokazać, że aby taki dowód był możliwy musi być spełniony warunek

[math]\displaystyle{ {\small\frac{b}{a}} \lt {\small\frac{r + 1}{r}} }[/math]

Niestety, elementarny dowód twierdzenia Czebyszewa o funkcji [math]\displaystyle{ \pi (n) }[/math] nie dostarczył nam odpowiednio silnego oszacowania, aby dowód twierdzenia Czebyszewa (czyli twierdzenia B3 w przypadku [math]\displaystyle{ r = 1 }[/math]) był możliwy. Dlatego będziemy musieli to zrobić innym sposobem. Podstawą dowodu będzie dalsze badanie rozwinięcia symbolu Newtona [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze.

Rozpoczniemy od oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math], z którego w przyszłości skorzystamy.

Twierdzenie B4
Dla funkcji [math]\displaystyle{ \pi (n) }[/math] prawdziwe są oszacowania:

1. [math]\displaystyle{ \pi (n) \underset{n \geqslant 34}{\lt } {\small\frac{n}{3}} }[/math]

2. [math]\displaystyle{ \pi (n) \underset{n \geqslant 15}{\lt } {\small\frac{n}{2}} - 1 }[/math]

Dowód

Punkt 1.
Indukcja matematyczna. Ponieważ wśród kolejnych sześciu liczb naturalnych, co najwyżej dwie mogą być liczbami pierwszymi, zatem [math]\displaystyle{ \pi (n) \leqslant \pi (n - 6) + 2 }[/math] dla [math]\displaystyle{ n \geqslant 9 . }[/math] Musimy sprawdzić prawdziwość twierdzenia dla kolejnych sześciu liczb naturalnych. Istotnie dla [math]\displaystyle{ n = 34, 35, 36, 37, 38, 39 }[/math] twierdzenie jest prawdziwe. Zakładając prawdziwość twierdzenia dla wszystkich liczb naturalnych należących do przedziału [math]\displaystyle{ [34, n] }[/math] otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ \pi (n + 1) \leqslant \pi (n - 5) + 2 \lt {\small\frac{n - 5}{3}} + 2 = {\small\frac{n + 1}{3}} }[/math]

Co należało pokazać.

Punkt 2.
Ponieważ dla [math]\displaystyle{ n \geqslant 34 }[/math] prawdziwa jest nierówność [math]\displaystyle{ \pi (n) \lt {\small\frac{n}{3}} }[/math], a dla [math]\displaystyle{ n \geqslant 6 }[/math] prawdziwa jest nierówność [math]\displaystyle{ {\small\frac{n}{3}} \leqslant {\small\frac{n}{2}} - 1 }[/math], zatem dla [math]\displaystyle{ n \geqslant 34 }[/math] prawdziwa jest nierówność [math]\displaystyle{ \pi (n) \lt {\small\frac{n}{2}} - 1 }[/math]. Wystarczy sprawdzić jej prawdziwość dla [math]\displaystyle{ 15 \leqslant n \leqslant 33 }[/math].
□

Potrzebne nam też będzie nowe oszacowanie współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] od dołu.

Twierdzenie B5
Dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwa jest nierówność [math]\displaystyle{ {\small\binom{2n}{n}} \gt {\small\frac{4^n}{2 n}} }[/math]

Dowód

Łatwo zauważamy, że

[math]\displaystyle{ {\small\binom{2n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = \left( \overset{n}{\underset{k = 1}{\prod}} {\small\frac{2 k}{k}} \right) \cdot \left( \overset{n - 1}{\underset{k = 1}{\prod}} {\small\frac{2 k + 1}{k}} \right) \cdot {\small\frac{1}{n}} \gt {\small\frac{2^{2 n - 1}}{n}} = {\small\frac{2^{2 n}}{2 n}} }[/math]

Iloczyn w pierwszym nawiasie uwzględnia wszystkie liczby parzyste licznika od [math]\displaystyle{ 2 }[/math] do [math]\displaystyle{ 2 n }[/math], a każdy czynnik tego iloczynu jest równy [math]\displaystyle{ 2 }[/math]. Iloczyn w drugim nawiasie uwzględnia wszystkie liczby nieparzyste licznika od [math]\displaystyle{ 3 }[/math] do [math]\displaystyle{ 2 n - 1 }[/math]. Każdy czynnik tego iloczynu jest większy od [math]\displaystyle{ 2 }[/math]. Wynika stąd natychmiast wypisana nierówność.
□

Poniższe twierdzenie zostało już udowodnione (zobacz twierdzenie A25), ale przedstawimy tutaj inny dowód.

Twierdzenie B6
Liczby pierwsze [math]\displaystyle{ p \gt \sqrt{2 n} }[/math] występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u = 0 }[/math] lub [math]\displaystyle{ u = 1 }[/math].

Dowód

Z twierdzenia A26 wiemy, że jeżeli liczba pierwsza [math]\displaystyle{ p }[/math] występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] z wykładnikiem [math]\displaystyle{ u }[/math], to [math]\displaystyle{ p^u \leqslant 2 n }[/math]. Gdyby liczba pierwsza [math]\displaystyle{ p \gt \sqrt{2 n} }[/math] występowała w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u \geqslant 2 }[/math], to mielibyśmy [math]\displaystyle{ p^u \geqslant p^2 \gt 2 n }[/math]. Co jest niemożliwe.
□

Następne twierdzenie jest prostym wnioskiem z twierdzenia A45 (przypadek dla [math]\displaystyle{ k = 1 }[/math]), ale załączyliśmy dowód dla tego konkretnego przypadku.

Twierdzenie B7
Jeżeli [math]\displaystyle{ n \geqslant 3 }[/math] i liczba pierwsza [math]\displaystyle{ p \in \left ( \tfrac{2}{3} n, n \right ] }[/math], to [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze.

Dowód

Dowód na podstawie analizy krotności pojawiania się liczby [math]\displaystyle{ p }[/math]

Zauważmy, że liczba pierwsza [math]\displaystyle{ p = 2 }[/math] nie spełnia warunku [math]\displaystyle{ p \in \left ( \tfrac{2}{3} n, n \right ] }[/math] dla [math]\displaystyle{ n \geqslant 3 }[/math].

Zapiszmy liczbę [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] w postaci ułamka:

[math]\displaystyle{ {\small\binom{2n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]

Rozważmy dowolną liczbę pierwszą [math]\displaystyle{ p }[/math] występującą w mianowniku wypisanego wyżej ułamka. Potrzebujemy, aby [math]\displaystyle{ p }[/math] spełniała następujące warunki:

•    [math]\displaystyle{ p \leqslant n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej jeden raz w mianowniku
•    [math]\displaystyle{ 2 p \gt n }[/math] — warunek ten zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie jeden raz w mianowniku
•    [math]\displaystyle{ 2 p \leqslant 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 p \gt n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się co najmniej jeden raz w liczniku
•    [math]\displaystyle{ 3 p \gt 2 n }[/math] — warunek ten (łącznie z warunkiem [math]\displaystyle{ 2 p \leqslant 2 n }[/math]) zapewnia nam, że liczba [math]\displaystyle{ p }[/math] pojawi się dokładnie raz w liczniku (jako [math]\displaystyle{ 2 p }[/math])

Łącząc otrzymane warunki, otrzymujemy, że liczba pierwsza [math]\displaystyle{ p \in \left ( \tfrac{2}{3} n, n \right ] }[/math] pojawia się dokładnie jeden raz w mianowniku i dokładnie jeden raz w liczniku ułamka

[math]\displaystyle{ {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]

Zatem liczba pierwsza [math]\displaystyle{ p }[/math] nie występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze.

Dowód na podstawie twierdzenia A24

Rozważmy najpierw pierwszy składnik sumy

[math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor {\small\frac{2 n}{p^{k}}} \right \rfloor - 2 \left \lfloor {\small\frac{n}{p^{k}}} \right \rfloor \right ) }[/math]

Ponieważ przypuszczamy, że składnik ten będzie równy [math]\displaystyle{ 0 }[/math], to będziemy szukali oszacowania od góry. Z założenia mamy

1)    [math]\displaystyle{ p \gt {\small\frac{2 n}{3}} \qquad \Longrightarrow \qquad {\small\frac{2 n}{p}} \lt 3 \qquad \Longrightarrow \qquad \left\lfloor {\small\frac{2 n}{p}} \right\rfloor \leqslant 2 }[/math]

2)    [math]\displaystyle{ p \leqslant n \qquad \;\:\, \Longrightarrow \qquad {\small\frac{n}{p}} \geqslant 1 \qquad \;\: \Longrightarrow \qquad \left\lfloor {\small\frac{n}{p}} \right\rfloor \geqslant 1 }[/math]

Zatem

[math]\displaystyle{ \left\lfloor {\small\frac{2 n}{p}} \right\rfloor - 2 \left\lfloor {\small\frac{n}{p}} \right\rfloor \leqslant 2 - 2 = 0 }[/math]

Ponieważ każdy ze składników szukanej sumy może być równy tylko [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], to otrzymujemy

[math]\displaystyle{ \left\lfloor {\small\frac{2 n}{p}} \right\rfloor - 2 \left\lfloor {\small\frac{n}{p}} \right\rfloor = 0 }[/math]

Założenie, że [math]\displaystyle{ n \geqslant 5 }[/math] pozwoli uprościć obliczenia dla drugiego i następnych składników sumy

[math]\displaystyle{ p \gt {\small\frac{2 n}{3}} \qquad \Longrightarrow \qquad {\small\frac{(2 n)^k}{p^k}} \lt 3^k }[/math]

[math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \lt {\small\frac{9}{2 n}} \cdot \left( {\small\frac{3}{2 n}} \right)^{k - 2} }[/math]

[math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \leqslant {\small\frac{9}{2 n}} }[/math]

[math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad {\small\frac{2 n}{p^k}} \leqslant {\small\frac{9}{10}} }[/math]

[math]\displaystyle{ \;\;\;\,\, \Longrightarrow \qquad \left\lfloor {\small\frac{2 n}{p^k}} \right\rfloor = 0 }[/math]

Jeżeli [math]\displaystyle{ \left\lfloor {\small\frac{2 n}{p^k}} \right\rfloor = 0 }[/math], to również musi być [math]\displaystyle{ \left\lfloor {\small\frac{n}{p^k}} \right\rfloor = 0 }[/math]. Pokazaliśmy, że dla [math]\displaystyle{ n \geqslant 5 }[/math] jest

[math]\displaystyle{ \sum^{\infty}_{k = 1} \left ( \left \lfloor {\small\frac{2 n}{p^{k}}} \right \rfloor - 2 \left \lfloor {\small\frac{n}{p^{k}}} \right \rfloor \right ) = 0 }[/math]

Dla [math]\displaystyle{ n = 3 \; }[/math] i [math]\displaystyle{ \; n = 4 }[/math] łatwo sprawdzamy, że liczba [math]\displaystyle{ 3 }[/math] nie dzieli liczb [math]\displaystyle{ {\small\binom{6}{3}} = 20 }[/math] oraz [math]\displaystyle{ {\small\binom{8}{4}} = 70 }[/math]. Zatem dla [math]\displaystyle{ n \geqslant 3 }[/math] liczba pierwsza [math]\displaystyle{ p \in \left( \tfrac{2}{3} n, n \right] }[/math] nie dzieli liczby [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math].
□

Twierdzenie B8
Każda liczba pierwsza [math]\displaystyle{ p \in (n, 2 n] }[/math] występuje w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ u = 1 }[/math].

Dowód

Każda liczba pierwsza [math]\displaystyle{ p \in (n, 2 n] }[/math] występuje dokładnie jeden raz w liczniku ułamka

[math]\displaystyle{ {\small\binom{2 n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]

i nie występuje w mianowniku. Zatem w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze wystąpi z wykładnikiem [math]\displaystyle{ u = 1 }[/math].
□

Przykład B9
Nawiasami [math]\displaystyle{ (), [], \{ \} }[/math] zaznaczyliśmy liczby pierwsze należące odpowiednio do przedziałów [math]\displaystyle{ \left( \sqrt{2 n}, \tfrac{2}{3} n \right] }[/math], [math]\displaystyle{ \left( \tfrac{2}{3} n, n \right] }[/math], [math]\displaystyle{ (n, 2 n] }[/math]. Zauważmy, że istnieją liczby pierwsze [math]\displaystyle{ p \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right] }[/math], które nie występują w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2n}{n}} }[/math] na czynniki pierwsze. Zaznaczyliśmy je grubą czcionką.

[math]\displaystyle{ {\small\binom{20}{10}} = 2^2 \cdot (\mathbf{5^0}) \cdot [7^0] \cdot \{ 11^1 \cdot 13^1 \cdot 17^1 \cdot 19^1 \} }[/math]

[math]\displaystyle{ {\small\binom{42}{21}} = 2^3 \cdot 3^1 \cdot 5^1 \cdot (\mathbf{7^0} \cdot 11^1 \cdot 13^1) \cdot [17^0 \cdot 19^0] \cdot \{ 23^1 \cdot 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \} }[/math]

[math]\displaystyle{ {\small\binom{48}{24}} = 2^2 \cdot 3^2 \cdot 5^2 \cdot (\mathbf{7^0} \cdot \mathbf{11^0} \cdot 13^1) \cdot [17^0 \cdot 19^0 \cdot 23^0] \cdot \{ 29^1 \cdot 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \} }[/math]

[math]\displaystyle{ {\small\binom{60}{30}} = 2^4 \cdot 7^1 \cdot (11^1 \cdot \mathbf{13^0} \cdot 17^1 \cdot 19^1) \cdot [23^0 \cdot 29^0] \cdot \{ 31^1 \cdot 37^1 \cdot 41^1 \cdot 43^1 \cdot 47^1 \cdot 53^1 \cdot 59^1 \} }[/math]

Twierdzenie B10
Niech [math]\displaystyle{ n \geqslant 15 }[/math]. Dla iloczynu liczb pierwszych [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u }[/math] występujących w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze i spełniających warunek [math]\displaystyle{ p_i \in (n, 2 n] }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ p_1 \cdot \ldots \cdot p_u \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]

Dowód

Zapiszmy rozwinięcie współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze w postaci:

[math]\displaystyle{ {\small\binom{2 n}{n}} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u) }[/math]

gdzie liczby pierwsze [math]\displaystyle{ r_i }[/math], [math]\displaystyle{ q_i }[/math], [math]\displaystyle{ p_i }[/math] spełniają warunki: [math]\displaystyle{ r_i \in \left[ 2, \sqrt{2 n} \right] }[/math], [math]\displaystyle{ \; q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right] \; }[/math] i [math]\displaystyle{ \; p_i \in (n, 2 n] }[/math]. Pominęliśmy liczby pierwsze należące do przedziału [math]\displaystyle{ \left( \tfrac{2}{3} n, n \right] }[/math], bo z twierdzenia B7 wiemy, że nie występują one w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze.

Zauważmy:

1) z twierdzenia A26 wiemy, że [math]\displaystyle{ r^{a_i}_i \leqslant 2 n }[/math], zatem

[math]\displaystyle{ r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s \leqslant (2 n)^s \leqslant (2 n)^{\pi \left( \sqrt{2 n} \right)} \lt (2 n)^{\sqrt{2 n} / 2 - 1} }[/math]

gdzie skorzystaliśmy z oszacowania [math]\displaystyle{ \pi (n) \lt {\small\frac{n}{2}} - 1 }[/math] prawdziwego dla [math]\displaystyle{ n \geqslant 15 }[/math] (twierdzenie B4 punkt 2).

2) z twierdzenia B6 wiemy, że czynniki [math]\displaystyle{ q_i \in \left( \sqrt{2 n}, \tfrac{2}{3} n \right] }[/math] występują z wykładnikiem równym [math]\displaystyle{ 0 }[/math] lub [math]\displaystyle{ 1 }[/math], zatem:

[math]\displaystyle{ q_1 \cdot \ldots \cdot q_t \leqslant \frac{P \left( {\small\frac{2}{3}} n \right)}{P \left( \sqrt{2 n} \right)} \lt P \left( \tfrac{2}{3} n \right) \lt 4^{2 n / 3} }[/math]

gdzie ostatnia nierówność wynika z twierdzenia A9.

3) z twierdzenia B5 wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ {\small\binom{2 n}{n}} \gt {\small\frac{4^n}{2 n}} }[/math]

Z punktów 1) - 3) wynika, że dla rozwinięcia współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze prawdziwe jest następujące oszacowanie

[math]\displaystyle{ {\small\frac{4^n}{2 n}} \lt {\small\binom{2 n}{n}} = (r^{a_1}_1 \cdot \ldots \cdot r^{a_s}_s) (q_1 \cdot \ldots \cdot q_t) (p_1 \cdot \ldots \cdot p_u) \lt (2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u) }[/math]

Skąd otrzymujemy natychmiast:

[math]\displaystyle{ (2 n)^{\sqrt{2 n} / 2 - 1} \cdot 4^{2 n / 3} \cdot (p_1 \cdot \ldots \cdot p_u) \gt {\small\frac{4^n}{2 n}} }[/math]

[math]\displaystyle{ p_1 \cdot \ldots \cdot p_u \gt {\small\frac{4^n}{2 n}} \cdot (2 n)^{- \sqrt{2 n} / 2 + 1} \cdot 4^{- 2 n / 3} = 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]

□

Twierdzenie B11
Dla [math]\displaystyle{ n \geqslant 15 }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]

Dowód

W twierdzeniu B10 pokazaliśmy, że dla iloczynu liczb pierwszych [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u }[/math] występujących w rozwinięciu współczynnika dwumianowego [math]\displaystyle{ {\small\binom{2 n}{n}} }[/math] na czynniki pierwsze i spełniających warunek [math]\displaystyle{ p_i \in (n, 2 n] }[/math] prawdziwe jest następujące oszacowanie

[math]\displaystyle{ p_1 \cdot \ldots \cdot p_u \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]

Zauważmy, że liczby pierwsze [math]\displaystyle{ p_i }[/math] występują z wykładnikiem równym [math]\displaystyle{ 1 }[/math] (twierdzenie B8) i iloczyn [math]\displaystyle{ p_1 \cdot \ldots \cdot p_u }[/math] jest iloczynem wszystkich liczb [math]\displaystyle{ p_i \in (n, 2 n] }[/math], bo każda liczba pierwsza [math]\displaystyle{ p_i \in (n, 2 n] }[/math] występuje w liczniku ułamka

[math]\displaystyle{ {\small\binom{2 n}{n}} = {\small\frac{(2 n) !}{(n!)^2}} = {\small\frac{(n + 1) \cdot (n + 2) \cdot \ldots \cdot (2 n - 1) \cdot 2 n}{1 \cdot 2 \cdot \ldots \cdot (n - 1) \cdot n}} }[/math]

i nie występuje w mianowniku. Wynika stąd natychmiast, że:

[math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} = p_1 \cdot \ldots \cdot p_u \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]

□

Twierdzenie B12
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Prawdziwe jest oszacowanie

[math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 2^{n / 2} }[/math]

Dowód

Z twierdzenia B11 wiemy, że dla dowolnego [math]\displaystyle{ n \geqslant 15 }[/math] jest

[math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} }[/math]

Chcemy pokazać, że

[math]\displaystyle{ 4^{n / 3} \cdot (2 n)^{- \sqrt{2 n} / 2} \gt 2^{n / 2} }[/math]

Logarytmując tę nierówność, otrzymujemy

[math]\displaystyle{ {\small\frac{2 n}{3}} \cdot \log 2 - {\small\frac{\sqrt{2 n}}{2}} \cdot \log (2 n) \gt {\small\frac{n}{2}} \cdot \log 2 }[/math]

[math]\displaystyle{ {\small\frac{\sqrt{2 n}}{2}} \cdot \log (2 n) \lt {\small\frac{n}{6}} \cdot \log 2 }[/math]

[math]\displaystyle{ \log (2 n) \lt {\small\frac{\log 2}{6}} \cdot \sqrt{2 n} }[/math]

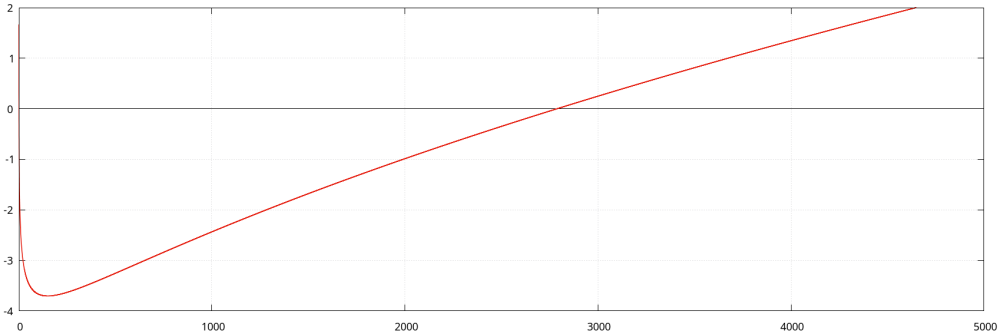
Zamieszczony niżej obrazek prezentuje wykres funkcji [math]\displaystyle{ f(n) = {\small\frac{\log 2}{6}} \cdot \sqrt{2 n} - \log (2 n) }[/math]

Wpisując w PARI/GP polecenie

solve(n = 2000, 4000, log(2)/6 * sqrt(2*n) - log(2*n))

znajdujemy, że funkcja [math]\displaystyle{ f(n) }[/math] jest większa od zera dla [math]\displaystyle{ n \gt 2787.755 }[/math]

Pozostaje sprawdzić, przez bezpośrednie obliczenie, prawdziwość nierówności

[math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 2^{n / 2} }[/math]

dla wszystkich [math]\displaystyle{ n \leqslant 2787 }[/math]. W programie PARI/GP wystarczy napisać polecenia

P(n) = prod(k = 2, n, if( isprime(k), k, 1 ))  \\ definicja funkcji P(n)

for(n = 1, 2788, if( P(2*n)/P(n) <= 2^(n/2), print(n) ))

□

Uwaga B13
Dowodząc analogicznie jak w twierdzeniu B12, moglibyśmy bez trudu pokazać, że dla [math]\displaystyle{ n \geqslant 6 }[/math] prawdziwe jest silniejsze oszacowanie [math]\displaystyle{ {\small\frac{P (2 n)}{P (n)}} \gt 2^{3 n / 5} }[/math].

Twierdzenie B14
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \pi (2 n) - \pi (n) \gt {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}} }[/math]

Dowód

Korzystając z twierdzenia B12, możemy napisać

[math]\displaystyle{ 2^{n / 2} \lt {\small\frac{P (2 n)}{P (n)}} \lt (2 n)^{\pi (2 n) - \pi (n)} }[/math]

Oszacowanie z prawej jest oczywiste. Logarytmując obie strony, otrzymujemy

[math]\displaystyle{ {\small\frac{n}{2}} \cdot \log 2 \lt [\pi (2 n) - \pi (n)] \cdot \log 2 n }[/math]

a stąd łatwo wyliczamy różnicę [math]\displaystyle{ \pi (2 n) - \pi (n) }[/math].
□

Korzystając ze znalezionego oszacowania, udowodnimy

Twierdzenie B15
Przedział otwarty [math]\displaystyle{ (n, 2 n) }[/math] zawiera co najmniej

•    jedną liczbę pierwszą, o ile [math]\displaystyle{ n \geqslant 2 }[/math]

•    dwie liczby pierwsze, o ile [math]\displaystyle{ n \geqslant 6 }[/math]

•    trzy liczby pierwsze, o ile [math]\displaystyle{ n \geqslant 9 }[/math]

•    cztery liczby pierwsze, o ile [math]\displaystyle{ n \geqslant 15 }[/math]

•    pięć liczb pierwszych, o ile [math]\displaystyle{ n \geqslant 21 }[/math]

•    sześć liczb pierwszych, o ile [math]\displaystyle{ n \geqslant 24 }[/math]

Dowód

Z twierdzenia B14 wiemy, że

[math]\displaystyle{ \pi (2 n) - \pi (n) \gt {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}} }[/math]

Łatwo sprawdzamy dla jakich wartości [math]\displaystyle{ n }[/math] funkcja [math]\displaystyle{ {\small\frac{\log 2}{2}} \cdot {\small\frac{n}{\log 2 n}} }[/math] jest większa od [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ 2 }[/math], itd. Wyniki zabraliśmy w tabelce:

[math]\displaystyle{ \begin{array}{|c|c|c|c|c|c|c|} \hline {\normalsize\frac{\log 2}{2}} \cdot {\normalsize\frac{n}{\log 2 n}} & \gt 1 & \gt 2 & \gt 3 & \gt 4 & \gt 5 & \gt 6\\ \hline \text{dla } n & \geqslant 9 & \geqslant 22 & \geqslant 38 & \geqslant 55 & \geqslant 72 & \geqslant 90\\ \hline \end{array} }[/math]

Bezpośrednie sprawdzenie dla [math]\displaystyle{ 2 \leqslant n \leqslant 8 }[/math] kończy dowód twierdzenia Czebyszewa. Analogicznie kończymy dowody pozostałych pozycji.
□

Uwagi do twierdzenia

Już pod koniec XVIII wieku Gauss i Legendre przypuszczali, że [math]\displaystyle{ {\small\frac{n}{\log n}} }[/math] jest dobrym przybliżeniem wartości funkcji [math]\displaystyle{ \pi (n) }[/math].

Obecnie wiemy, że dokładnie tak jest [math]\displaystyle{ 1 + {\small\frac{1}{\log n}} + {\small\frac{1}{\log^2 n}} \: \underset{n \geqslant 3527}{\lt } \: \pi (n) \cdot {\small\frac{\log n}{n}} \: \underset{n \geqslant 2}{\lt } \: 1 + {\small\frac{1}{\log n}} + {\small\frac{2.54}{\log^2 n}} }[/math]

Jeśli tak, to ilość liczb pierwszych w przedziale [math]\displaystyle{ (n, 2 n] }[/math] jest tego samego rzędu, co ilość liczb pierwszych w przedziale [math]\displaystyle{ (1, n] }[/math]. Istotnie

[math]\displaystyle{ \pi (n) \approx {\small\frac{n}{\log n}} = }[/math]

[math]\displaystyle{ \;\;\; = {\small\frac{n}{\log n}} \cdot {\small\frac{\log n + \log 2}{\log (2 n)}} = }[/math]

[math]\displaystyle{ \;\;\; = {\small\frac{n}{\log (2 n)}} \cdot \left( 1 + {\small\frac{\log 2}{\log n}} \right) }[/math]

[math]\displaystyle{ \pi (2 n) - \pi (n) \approx {\small\frac{2 n}{\log (2 n)}} - {\small\frac{n}{\log n}} = }[/math]

[math]\displaystyle{ \;\: = {\small\frac{2 n}{\log (2 n)}} - {\small\frac{n}{\log (2 n)}} \cdot \left( 1 + {\small\frac{\log 2}{\log n}} \right) = }[/math]

[math]\displaystyle{ \;\: = {\small\frac{n}{\log (2 n)}} \cdot \left( 1 - {\small\frac{\log 2}{\log n}} \right) }[/math]

Zatem przypuszczenie, że między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się przynajmniej jedna liczba pierwsza, jest bardzo słabym oczekiwaniem.

Co więcej, począwszy od pewnego [math]\displaystyle{ n_0 }[/math] między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje przynajmniej jedna liczba będąca kwadratem, sześcianem, czwartą i piątą potęgą liczby naturalnej. Liczby [math]\displaystyle{ n^2 }[/math], [math]\displaystyle{ n^3 }[/math], [math]\displaystyle{ n^4 }[/math] czy [math]\displaystyle{ n^5 }[/math] występują znacznie rzadziej niż liczby pierwsze [math]\displaystyle{ p_n \approx n \log n }[/math].

Pokażemy też, że twierdzenie Czebyszewa wynika ze sformułowanej w 1742 roku hipotezy Goldbacha. Oczywiście ścisły dowód twierdzenia Czebyszewa stał się możliwy dopiero po znalezieniu dokładnego oszacowania funkcji [math]\displaystyle{ \pi (n) }[/math].

Twierdzenie B16
Niech [math]\displaystyle{ n, k, k_0 \in \mathbb{Z}_+ }[/math] i [math]\displaystyle{ f(k) }[/math] będzie funkcją rosnącą o wartościach całkowitych dodatnich. Jeżeli spełnione są warunki

1) [math]\displaystyle{ \quad f(k + 1) \lt 2 f (k) \quad }[/math] dla [math]\displaystyle{ \quad k \geqslant k_0 }[/math]

2) [math]\displaystyle{ \quad n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 }[/math]

to między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba należąca do zbioru wartości funkcji [math]\displaystyle{ f(k) }[/math].

Dowód

Niech [math]\displaystyle{ n \geqslant f (k_0) }[/math], a liczba [math]\displaystyle{ k \geqslant k_0 }[/math] będzie największą liczbą taką, że [math]\displaystyle{ f(k) \leqslant n }[/math]. Z określenia liczby [math]\displaystyle{ k }[/math] i założenia twierdzenia prawdziwy jest ciąg nierówności

[math]\displaystyle{ f(k) \leqslant n \lt f (k + 1) \lt 2 f (k) \leqslant 2 n }[/math]

Zatem między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba należąca do zbioru wartości funkcji [math]\displaystyle{ f(k) }[/math].

W szczególności liczba [math]\displaystyle{ f(k_0) }[/math] leży między liczbami [math]\displaystyle{ \; \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + j \; }[/math] oraz [math]\displaystyle{ \; 2 \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 2 j \; }[/math] dla [math]\displaystyle{ \; j = 1, 2, \ldots, f (k_0) - \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor - 1 }[/math].

Łatwo sprawdzamy, że dla kolejnej liczby [math]\displaystyle{ j = f (k_0) - \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor }[/math] liczba [math]\displaystyle{ f(k_0) }[/math] nie leży między liczbami [math]\displaystyle{ f(k_0) }[/math] oraz [math]\displaystyle{ 2 f (k_0) }[/math] — między tymi liczbami leży liczba [math]\displaystyle{ f(k_0 + 1) }[/math].

Wynika stąd, że twierdzenie jest prawdziwe dla liczb [math]\displaystyle{ n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 }[/math].
□

Zadanie B17
Niech [math]\displaystyle{ x \in \mathbb{R} }[/math]. Dla [math]\displaystyle{ n \geqslant 1 }[/math] oraz [math]\displaystyle{ x \gt {\small\frac{1}{\sqrt[n]{2} - 1}} }[/math] prawdziwa jest nierówność [math]\displaystyle{ 2 x^n \gt (x + 1)^n }[/math].

Rozwiązanie

Z założenia

[math]\displaystyle{ \left( \sqrt[n]{2} - 1 \right) x \gt 1 }[/math]

[math]\displaystyle{ x \cdot \sqrt[n]{2} \gt x + 1 }[/math]

Podnosząc obie strony nierówności do [math]\displaystyle{ n }[/math]-tej potęgi, otrzymujemy

[math]\displaystyle{ \left( x \cdot \sqrt[n]{2} \right)^n \gt (x + 1)^n }[/math]

Czyli

[math]\displaystyle{ 2 x^n \gt (x + 1)^n }[/math]

Co należało pokazać.
□

Twierdzenie B18
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math]. Jeżeli [math]\displaystyle{ n \geqslant 5 }[/math], to między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba będąca kwadratem liczby naturalnej.

Dowód

Funkcja [math]\displaystyle{ f(k) = k^2 }[/math] jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania B17 łatwo stwierdzamy, że warunek z twierdzenia B16

[math]\displaystyle{ (k + 1)^2 \lt 2 k^2 }[/math]

jest spełniony dla

[math]\displaystyle{ k_0 = \left\lfloor {\small\frac{1}{\sqrt{2} - 1}} \right\rfloor + 1 = 3 }[/math]

Twierdzenie jest prawdziwe dla liczb

[math]\displaystyle{ n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 = \left\lfloor {\small\frac{9}{2}} \right\rfloor + 1 = 5 }[/math]

Co kończy dowód.
□

Twierdzenie B19
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math]. Jeżeli [math]\displaystyle{ n \geqslant 33 }[/math], to między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba będąca sześcianem liczby naturalnej.

Dowód

Funkcja [math]\displaystyle{ f(k) = k^3 }[/math] jest funkcją rosnącą o wartościach całkowitych dodatnich. Na podstawie zadania B17 łatwo stwierdzamy, że warunek z twierdzenia B16

[math]\displaystyle{ (k + 1)^3 \lt 2 k^3 }[/math]

jest spełniony dla

[math]\displaystyle{ k_0 = \left\lfloor {\small\frac{1}{\sqrt[3]{2} - 1}} \right\rfloor + 1 = 4 }[/math]

Twierdzenie jest prawdziwe dla liczb

[math]\displaystyle{ n \geqslant \left\lfloor {\small\frac{f (k_0)}{2}} \right\rfloor + 1 = \left\lfloor {\small\frac{64}{2}} \right\rfloor + 1 = 33 }[/math]

Co kończy dowód.
□

Podobnie możemy udowodnić, że dla [math]\displaystyle{ n \geqslant 649 }[/math] (odpowiednio: [math]\displaystyle{ n \geqslant 8404 }[/math]) między liczbami [math]\displaystyle{ n }[/math] oraz [math]\displaystyle{ 2 n }[/math] leży przynajmniej jedna liczba będąca czwartą (odpowiednio: piątą) potęgą liczby naturalnej. Oczywiście analogiczne twierdzenie możemy sformułować dla dowolnej funkcji [math]\displaystyle{ f(k) = k^u }[/math], gdzie [math]\displaystyle{ u \in \mathbb{Z}_+ }[/math].

Bez trudu pokażemy też, że twierdzenie Czebyszewa wynika z ponad sto lat od niego starszej hipotezy Goldbacha. Hipoteza Goldbacha może być sformułowana w różny sposób, poniżej przedstawimy te formuły i udowodnimy ich równoważność.

Twierdzenie B20 (hipoteza Goldbacha, 1742)
Następujące warunki są równoważne

•    [math]\displaystyle{ ( \text{G1} ) }[/math]   Każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 4 }[/math] jest sumą dwóch liczb pierwszych
•    [math]\displaystyle{ ( \text{G2} ) }[/math]   Każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 6 }[/math] jest sumą dwóch liczb pierwszych nieparzystych
•    [math]\displaystyle{ ( \text{G3} ) }[/math]   Każda liczba naturalna [math]\displaystyle{ n \geqslant 6 }[/math] jest sumą trzech liczb pierwszych

Dowód

Pokażemy równoważność warunków [math]\displaystyle{ ( \text{G1} ) }[/math] i [math]\displaystyle{ ( \text{G2} ) }[/math], a następnie równoważność warunków [math]\displaystyle{ ( \text{G1} ) }[/math] i [math]\displaystyle{ ( \text{G3} ) }[/math]

[math]\displaystyle{ ( \text{G1} ) \quad \implies \quad ( \text{G2} ) }[/math]
Z założenia każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 4 }[/math] jest sumą dwóch liczb pierwszych, czyli [math]\displaystyle{ n = 2 k = p + q }[/math], gdzie [math]\displaystyle{ p, q }[/math] są liczbami pierwszymi. Zauważmy, że liczby [math]\displaystyle{ p, q }[/math] muszą mieć taką samą parzystość. Ponieważ istnieje tylko jedna liczba pierwsza parzysta, to istnieje tylko jedna liczba naturalna, która jest sumą dwóch liczb pierwszych parzystych. Oczywiście jest to liczba [math]\displaystyle{ 4 = 2 + 2 }[/math]. Wszystkie liczby naturalne parzyste większe od [math]\displaystyle{ 4 }[/math] muszą być sumą dwóch liczb pierwszych nieparzystych.

[math]\displaystyle{ ( \text{G2} ) \quad \implies \quad ( \text{G1} ) }[/math]
Z założenia każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 6 }[/math] jest sumą dwóch liczb pierwszych. Ponieważ [math]\displaystyle{ 4 = 2 + 2 }[/math] jest sumą dwóch liczb pierwszych, to każda liczba naturalna parzysta [math]\displaystyle{ n \geqslant 4 }[/math] jest sumą dwóch liczb pierwszych.

[math]\displaystyle{ ( \text{G1} ) \quad \implies \quad ( \text{G3} ) }[/math]
Z założenia dla każdego [math]\displaystyle{ k \geqslant 3 }[/math] jest [math]\displaystyle{ n = 2 k - 2 = p + q }[/math], gdzie [math]\displaystyle{ p, q }[/math] są liczbami pierwszymi. Zatem  [math]\displaystyle{ 2 k = p + q + 2 }[/math]  oraz  [math]\displaystyle{ 2 k + 1 = p + q + 3 }[/math].

[math]\displaystyle{ ( \text{G3} ) \quad \implies \quad ( \text{G1} ) }[/math]
Z założenia dla każdego [math]\displaystyle{ k \geqslant 3 }[/math] jest [math]\displaystyle{ n = 2 k = p + q + r }[/math], gdzie [math]\displaystyle{ p, q, r }[/math] są liczbami pierwszymi. Wypisana równość nie jest możliwa w przypadku, gdy wszystkie liczby [math]\displaystyle{ p, q, r }[/math] są nieparzyste. Niech [math]\displaystyle{ r = 2 }[/math] będzie liczbą pierwszą parzystą, wtedy [math]\displaystyle{ 2 k - 2 = p + q }[/math].
□

Twierdzenie B21
Niech [math]\displaystyle{ n \in \mathbb{N} }[/math] i [math]\displaystyle{ n \geqslant 2 }[/math]. Jeżeli prawdziwa jest hipoteza Goldbacha, to między [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się co najmniej jedna liczba pierwsza.

Dowód

Rozważmy liczbę [math]\displaystyle{ 2 n + 2 }[/math] dla [math]\displaystyle{ n \geqslant 2 }[/math]. Z hipotezy Goldbacha [math]\displaystyle{ ( \text{G2} ) }[/math] wynika, że [math]\displaystyle{ 2 n + 2 = p + q }[/math] jest sumą dwóch liczb pierwszych nieparzystych.

Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ p \leqslant q }[/math], zatem

[math]\displaystyle{ 2 n + 2 = p + q \leqslant 2 q }[/math]

Czyli [math]\displaystyle{ q \geqslant n + 1 }[/math]. Ponieważ [math]\displaystyle{ p \geqslant 3 }[/math], to z drugiej strony mamy

[math]\displaystyle{ 2 n + 2 = p + q \geqslant q + 3 }[/math]

Czyli [math]\displaystyle{ q \leqslant 2 n - 1 }[/math]. Zatem [math]\displaystyle{ n + 1 \leqslant q \leqslant 2 n - 1 }[/math], co oznacza, że [math]\displaystyle{ n \lt q \lt 2 n }[/math].
□

Zastosowania

Twierdzenie B22
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Prawdziwe jest oszacowanie [math]\displaystyle{ p_{n + 1} \lt 2 p_n }[/math].

Dowód

Z twierdzenia Czebyszewa wiemy, że między liczbami [math]\displaystyle{ p_n }[/math] i [math]\displaystyle{ 2 p_n }[/math] znajduje się przynajmniej jedna liczba pierwsza [math]\displaystyle{ q }[/math]. Ponieważ [math]\displaystyle{ q \gt p_n }[/math], to musi być [math]\displaystyle{ q \geqslant p_{n + 1} }[/math]. Otrzymujemy ciąg nierówności

[math]\displaystyle{ p_n \lt p_{n + 1} \leqslant q \lt 2 p_n }[/math]

Skąd wynika natychmiast, że [math]\displaystyle{ p_{n + 1} \lt 2 p_n }[/math].
□

Prawdziwe jest również twierdzenie odwrotne.

Twierdzenie B23
Niech [math]\displaystyle{ k, n \in \mathbb{Z}_+ }[/math]. Jeżeli dla każdego [math]\displaystyle{ k }[/math] prawdziwa jest nierówność [math]\displaystyle{ p_{k + 1} \lt 2 p_k }[/math], to dla dowolnego [math]\displaystyle{ n \geqslant 2 }[/math] między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się co najmniej jedna liczba pierwsza.

Dowód

Ponieważ [math]\displaystyle{ n \geqslant 2 }[/math], to istnieje co najmniej jedna liczba pierwsza [math]\displaystyle{ q }[/math] taka, że [math]\displaystyle{ q \leqslant n }[/math]. Niech [math]\displaystyle{ p_k }[/math] oznacza największą liczbę pierwszą ze zbioru liczb [math]\displaystyle{ q }[/math] spełniających warunek [math]\displaystyle{ q \leqslant n }[/math]. Z definicji liczby [math]\displaystyle{ p_k }[/math] wynika natychmiast, że musi być [math]\displaystyle{ p_{k + 1} \gt n }[/math]. Konsekwentnie otrzymujemy ciąg nierówności

[math]\displaystyle{ p_k \leqslant n \lt p_{k + 1} \lt 2 p_k \leqslant 2 n }[/math]

gdzie skorzystaliśmy z założonej prawdziwości oszacowania [math]\displaystyle{ p_{k + 1} \lt 2 p_k }[/math]. Zatem między liczbami [math]\displaystyle{ n }[/math] i [math]\displaystyle{ 2 n }[/math] znajduje się liczba pierwsza [math]\displaystyle{ p_{k + 1} }[/math].
□

Twierdzenie B24
Niech [math]\displaystyle{ n \geqslant 3 }[/math]. Prawdziwe jest oszacowanie [math]\displaystyle{ p_{n + 1} \lt p_n + p_{n - 1} }[/math].

Dowód

Z twierdzenia B15 (punkt 2) wiemy, że dla [math]\displaystyle{ k \geqslant 6 }[/math] między liczbami [math]\displaystyle{ k }[/math] i [math]\displaystyle{ 2 k }[/math] znajdują się co najmniej dwie liczby pierwsze. Zatem dla [math]\displaystyle{ n \geqslant 5 }[/math] w przedziale [math]\displaystyle{ (p_{n - 1}, 2 p_{n - 1}) }[/math] znajduje się co najmniej dwie liczby pierwsze [math]\displaystyle{ q }[/math] i [math]\displaystyle{ r }[/math]. Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ q \lt r }[/math]. Ponieważ [math]\displaystyle{ q \gt p_{n - 1} }[/math], to musi być [math]\displaystyle{ q \geqslant p_n }[/math], a ponieważ [math]\displaystyle{ r \gt q \geqslant p_n }[/math], to musi być [math]\displaystyle{ r \geqslant p_{n + 1} }[/math]. Łącząc powyższe spostrzeżenia, otrzymujemy ciąg nierówności

[math]\displaystyle{ p_{n - 1} \lt p_n \lt p_{n + 1} \leqslant r \lt 2 p_{n - 1} \lt p_n + p_{n - 1} }[/math]

Zatem [math]\displaystyle{ p_{n + 1} \lt p_n + p_{n - 1} }[/math]. Dla [math]\displaystyle{ n \lt 5 }[/math] nierówność sprawdzamy bezpośrednio.
□

Zadanie B25
Jeżeli [math]\displaystyle{ p }[/math] i [math]\displaystyle{ q }[/math] są różnymi liczbami pierwszymi, to [math]\displaystyle{ p q \gt p + q }[/math].

Rozwiązanie

Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ p \lt q }[/math]. Zatem [math]\displaystyle{ p \geqslant 2 }[/math] i [math]\displaystyle{ q \geqslant 3 }[/math]. Łatwo znajdujemy, że

[math]\displaystyle{ {\small\frac{1}{p}} + {\small\frac{1}{q}} \leqslant {\small\frac{1}{2}} + {\small\frac{1}{3}} \lt 1 }[/math]

skąd natychmiast otrzymujemy, że [math]\displaystyle{ p q \gt p + q }[/math].
□

Zadanie B26
Niech [math]\displaystyle{ n \geqslant 2 }[/math]. Pokazać, że prawdziwe jest oszacowanie [math]\displaystyle{ p_{n + 1} \lt p_n \cdot p_{n - 1} }[/math].

Zadanie B27
Niech [math]\displaystyle{ n }[/math] będzie dowolną liczbą naturalną, a [math]\displaystyle{ p_k }[/math] oznacza największą liczbę pierwszą mniejszą od [math]\displaystyle{ n }[/math]. Pokazać, że tylko dla [math]\displaystyle{ n = 5 }[/math] spełnione jest równanie

[math]\displaystyle{ n = p_k + p_{k - 1} }[/math]

Rozwiązanie

Równanie nie może być spełnione dla [math]\displaystyle{ n \leqslant 3 }[/math], bo nie istnieją dwie różne liczby pierwsze mniejsze od takich liczb [math]\displaystyle{ n }[/math]. Sprawdzamy, że równanie nie jest spełnione dla [math]\displaystyle{ n = 4 }[/math]. Niech [math]\displaystyle{ n \geqslant 6 }[/math]. Zauważmy, że teraz [math]\displaystyle{ p_k \geqslant 5 }[/math], czyli [math]\displaystyle{ k \geqslant 3 }[/math]. Z określenia liczby [math]\displaystyle{ p_k }[/math] i twierdzenia B24 prawdziwy jest ciąg nierówności

[math]\displaystyle{ p_k \lt n \leqslant p_{k + 1} \lt p_k + p_{k - 1} }[/math]

Zatem liczba [math]\displaystyle{ n \geqslant 6 }[/math] nie może być sumą dwóch największych liczb pierwszych od niej mniejszych [math]\displaystyle{ p_k }[/math] i [math]\displaystyle{ p_{k - 1} }[/math], gdzie [math]\displaystyle{ p_k \lt n \leqslant p_{k + 1} }[/math].
□

Twierdzenie B28
Jeżeli [math]\displaystyle{ n \in \mathbb{Z} }[/math] i [math]\displaystyle{ n \geqslant 2 }[/math], to w przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza.

Dowód

Z twierdzenia Czebyszewa wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] w przedziale [math]\displaystyle{ (n, 2 n) }[/math] znajduje się przynajmniej jedna liczba pierwsza. Zatem jeżeli [math]\displaystyle{ n \geqslant 4 }[/math] jest liczbą parzystą, to w przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right) \subset \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się co najmniej jedna liczba pierwsza. Jeżeli [math]\displaystyle{ n \geqslant 3 }[/math] jest liczbą nieparzystą, to w przedziale [math]\displaystyle{ \left( {\small\frac{n + 1}{2}}, n + 1 \right) = \left( {\small\frac{n + 1}{2}}, n \right] \subset \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Wynika stąd, że bez względu na parzystość liczby [math]\displaystyle{ n }[/math], dla [math]\displaystyle{ n \geqslant 3 }[/math] w przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Oczywiście dla [math]\displaystyle{ n = 2 }[/math] twierdzenie również jest prawdziwe.
□

Twierdzenie B29
Dla [math]\displaystyle{ n \geqslant 2 }[/math] liczby [math]\displaystyle{ n! }[/math] nie można przedstawić w postaci potęgi liczby naturalnej o wykładniku wyższym niż [math]\displaystyle{ 1 }[/math].

Dowód

Z twierdzenia A42 wiemy, że każda liczba pierwsza [math]\displaystyle{ p }[/math] taka, że [math]\displaystyle{ p \in \left( {\small\frac{n}{2}}, n \right] }[/math] występuje w rozkładzie liczby [math]\displaystyle{ n! }[/math] na czynniki pierwsze z wykładnikiem [math]\displaystyle{ 1 }[/math]. Z twierdzenia B28 wiemy, że przedziale [math]\displaystyle{ \left( {\small\frac{n}{2}}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Łącząc te fakty, otrzymujemy natychmiast tezę.
□

Twierdzenie B30
Każda liczba naturalna [math]\displaystyle{ n \geqslant 12 }[/math] jest sumą różnych liczb pierwszych.

Dowód

Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 12 = 5 + 7 }[/math]. Zakładając, że twierdzenie jest prawdziwe dla każdej liczby naturalnej należącej do przedziału [math]\displaystyle{ [12, n] }[/math], udowodnimy, że liczba [math]\displaystyle{ n + 1 }[/math] jest sumą różnych liczb pierwszych.

Z twierdzenia B28 wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] w przedziale [math]\displaystyle{ \left(\frac{n}{2}, n \right] }[/math] znajduje się przynajmniej jedna liczba pierwsza. Niech [math]\displaystyle{ p_k }[/math] będzie największą liczbą pierwszą w tym przedziale. Z określenia liczby [math]\displaystyle{ p_k }[/math] wynika następujący ciąg nierówności

[math]\displaystyle{ {\small\frac{n}{2}} \lt p_k \leqslant n \lt n + 1 \leqslant p_{k + 1} }[/math]

Korzystając z twierdzenia B22 i ostatniej z wypisanych wyżej nierówności, dostajemy

[math]\displaystyle{ n + 1 - p_k \leqslant p_{k + 1} - p_k \lt p_k \leqslant n }[/math]

Widzimy, że liczba [math]\displaystyle{ n + 1 - p_k }[/math] jest mniejsza od liczb [math]\displaystyle{ p_k }[/math] oraz [math]\displaystyle{ n }[/math]. Zatem na mocy założenia indukcyjnego jest sumą różnych liczb pierwszych mniejszych od [math]\displaystyle{ p_k }[/math]. Wynika stąd, że liczba

[math]\displaystyle{ n + 1 = p_k + (n + 1 - p_k) }[/math]

jest sumą różnych liczb pierwszych.

Gdybyśmy na tym zakończyli dowód, to równie dobrze moglibyśmy uznać, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n \geqslant 5 = 2 + 3 }[/math]. Wtedy łatwo zauważymy, że liczba pierwsza [math]\displaystyle{ 11 }[/math] nie jest sumą różnych liczb pierwszych. Ratując sytuację, moglibyśmy przyjąć, że [math]\displaystyle{ 11 }[/math] jest sumą tylko jednej liczby pierwszej, czyli samej siebie. Jednak liczba [math]\displaystyle{ 6 }[/math] też nie jest sumą różnych liczb pierwszych i nie ma sposobu obejścia tego problemu.

Błąd polega na tym, że musimy sprawdzić, czy liczba [math]\displaystyle{ n + 1 - p_k }[/math] spełnia założenia twierdzenia, czyli czy jest

[math]\displaystyle{ n + 1 - p_k \in [12, n] }[/math]

Na razie pokazaliśmy tylko, że liczba ta jest mniejsza od [math]\displaystyle{ n }[/math]. Musimy jeszcze pokazać, że

[math]\displaystyle{ n + 1 - p_k \geqslant 12 }[/math]

Skąd dostajemy

[math]\displaystyle{ n \geqslant 11 + p_k \gt 11 + {\small\frac{n}{2}} }[/math]

Zatem dopiero dla [math]\displaystyle{ n \gt 22 }[/math] warunek [math]\displaystyle{ n + 1 - p_k \geqslant 12 }[/math] będzie na pewno spełniony. Łatwo sprawdzamy, że dla liczb [math]\displaystyle{ 12, 13, \ldots, 22 }[/math] twierdzenie jest prawdziwe

[math]\displaystyle{ \mathbf{12} = 5 + 7 }[/math], [math]\displaystyle{ \mathbf{13} = 2 + 11 }[/math], [math]\displaystyle{ \mathbf{14} = 3 + 11 }[/math], [math]\displaystyle{ \mathbf{15} = 2 + 13 }[/math], [math]\displaystyle{ \mathbf{16} = 3 + 13 }[/math], [math]\displaystyle{ \mathbf{17} = 2 + 3 + 5 + 7 }[/math], [math]\displaystyle{ \mathbf{18} = 5 + 13 }[/math], [math]\displaystyle{ \mathbf{19} = 2 + 17 }[/math], [math]\displaystyle{ \mathbf{20} = 3 + 17 }[/math], [math]\displaystyle{ \mathbf{21} = 2 + 19 }[/math], [math]\displaystyle{ \mathbf{22} = 3 + 19 }[/math], [math]\displaystyle{ \mathbf{23} = 3 + 7 + 13 }[/math]
□

Twierdzenie B31
Dla [math]\displaystyle{ n \geqslant 3 }[/math] prawdziwe jest następujące oszacowanie funkcji [math]\displaystyle{ P(n) }[/math] od dołu

[math]\displaystyle{ P (n) \gt 2^{n / 2} }[/math]

Dowód

Indukcja matematyczna. Mamy [math]\displaystyle{ P(3) = 6 \gt 2^{3 / 2} = 2 \sqrt{2} }[/math] oraz [math]\displaystyle{ P(4) = 6 \gt 2^{4 / 2} = 4 }[/math], czyli nierówność jest prawdziwa dla [math]\displaystyle{ n = 3, 4 }[/math]. Zakładając prawdziwość nierówności dla wszystkich liczb naturalnych należących do przedziału [math]\displaystyle{ \left [ 3, n \right ] }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

a) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą parzystą, to [math]\displaystyle{ n + 1 = 2 m }[/math] i wtedy

[math]\displaystyle{ P(n + 1) = P (2 m) = P (m) \cdot {\small\frac{P (2 m)}{P (m)}} \gt 2^{m / 2} \cdot 2^{m / 2} = 2^m = 2^{2 m / 2} = 2^{(n + 1) / 2} }[/math]

gdzie skorzystaliśmy z założenia indukcyjnego i twierdzenia B12.

b) jeżeli [math]\displaystyle{ n + 1 }[/math] jest liczbą nieparzystą, to [math]\displaystyle{ n + 1 = 2 m + 1 }[/math] i wtedy

[math]\displaystyle{ P(n + 1) = P (2 m + 1) = P (2 m + 2) = P (m + 1) \cdot {\small\frac{P (2 m + 2)}{P (m + 1)}} \gt 2^{(m + 1) / 2} \cdot 2^{(m + 1) / 2} = 2^{(2 m + 2) / 2} \gt 2^{(2 m + 1) / 2} = 2^{(n + 1) / 2} }[/math]

Co kończy dowód indukcyjny.
□

Zadanie B32
Niech [math]\displaystyle{ p_n }[/math] oznaczą [math]\displaystyle{ n }[/math]-tą liczbę pierwszą. Korzystając z twierdzenia Czebyszewa pokazać, że dla [math]\displaystyle{ n \geqslant 1 }[/math] jest [math]\displaystyle{ p_n \leqslant 2^n }[/math].

Rozbieżność sumy [math]\displaystyle{ \textstyle \sum\limits_{p \geqslant 2} {\small\frac{1}{p}} }[/math]

Rozpoczniemy od prostszego twierdzenia dotyczącego rozbieżności sumy odwrotności wszystkich liczb całkowitych dodatnich. Już sam wzór, w którym pogrupowaliśmy wyrazy tej sumy

[math]\displaystyle{ S = 1 + {\small\frac{1}{2}} + \left( {\small\frac{1}{3}} + {\small\frac{1}{4}} \right) + \left( {\small\frac{1}{5}} + {\small\frac{1}{6}} + {\small\frac{1}{7}} + {\small\frac{1}{8}} \right) + \left( {\small\frac{1}{9}} + {\small\frac{1}{10}} + {\small\frac{1}{11}} + {\small\frac{1}{12}} + {\small\frac{1}{13}} + {\small\frac{1}{14}} + {\small\frac{1}{15}} + {\small\frac{1}{16}} \right) + \ldots }[/math]

mógłby wystarczyć za dowód, bo każda suma w nawiasach jest większa od [math]\displaystyle{ {\small\frac{1}{2}} }[/math], ale dowód formalny okaże się pożytecznym ćwiczeniem.

Twierdzenie B33
Niech [math]\displaystyle{ S(k) }[/math] oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność

[math]\displaystyle{ S(2^n) \gt {\small\frac{n + 1}{2}} }[/math].

Dowód

Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], bo

[math]\displaystyle{ S(2^1) = 1 + {\small\frac{1}{2}} \gt 1 }[/math]

Zakładając, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ S(2^{n + 1}) = 1 + {\small\frac{1}{2}} + \ldots + {\small\frac{1}{2^n - 1}} + {\small\frac{1}{2^n}} + \left( {\small\frac{1}{2^n + 1}} + \ldots + {\small\frac{1}{2^{n + 1}}} \right) = }[/math]

[math]\displaystyle{ \; \; \: = S (2^n) + \left( {\small\frac{1}{2^n + 1}} + \ldots + {\small\frac{1}{2^{n + 1}}} \right) }[/math]

Ponieważ wyrażenie w nawiasie zawiera [math]\displaystyle{ 2^{n + 1} - 2^n = 2^n }[/math] wyrazów, z których każdy jest nie mniejszy niż [math]\displaystyle{ {\small\frac{1}{2^{n + 1}}} }[/math], to prawdziwe jest oszacowanie

[math]\displaystyle{ S(2^{n + 1}) \gt {\small\frac{n + 1}{2}} + 2^n \cdot {\small\frac{1}{2^{n + 1}}} = }[/math]

[math]\displaystyle{ \; \; \: = {\small\frac{n + 2}{2}} }[/math]

Gdzie skorzystaliśmy z założenia indukcyjnego i oszacowaliśmy sumę w nawiasie.
□

Twierdzenie B34
Niech [math]\displaystyle{ S(k) }[/math] oznacza sumę odwrotności wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność

[math]\displaystyle{ S(k) \gt \tfrac{1}{2} \, \log_2 \! k }[/math]

Dowód

Niech [math]\displaystyle{ n = \lfloor \log_2 \! k \rfloor }[/math] dla dowolnego [math]\displaystyle{ k \geqslant 1 }[/math]. Mamy

[math]\displaystyle{ k = 2^{\log_2 \! k} \geqslant 2^{\lfloor \log_2 \! k \rfloor} = 2^n }[/math]

Zatem

[math]\displaystyle{ S(k) \geqslant S (2^n) \gt {\small\frac{n + 1}{2}} = \tfrac{1}{2} (\lfloor \log_2 \! k \rfloor + 1) \gt \tfrac{1}{2} \log_2 \! k }[/math]

□

Z twierdzenia B34 wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb całkowitych dodatnich.

Dokładniejsze oszacowanie sumy odwrotności liczb całkowitych dodatnich nie większych od [math]\displaystyle{ k }[/math] jest dane wzorem [math]\displaystyle{ \sum_{j=1}^{k}\frac{1}{j} = \log k + \gamma + {\small\frac{1}{2 k}} - {\small\frac{1}{12 k^2}} + {\small\frac{1}{120 k^4}} + \ldots }[/math] gdzie [math]\displaystyle{ \gamma = 0.5772156649 \ldots }[/math] jest stałą Eulera.

Oznaczmy przez [math]\displaystyle{ Q }[/math] sumę odwrotności wszystkich liczb pierwszych

[math]\displaystyle{ Q = {\small\frac{1}{2}} + {\small\frac{1}{3}} + {\small\frac{1}{5}} + {\small\frac{1}{7}} + {\small\frac{1}{11}} + {\small\frac{1}{13}} + {\small\frac{1}{17}} + {\small\frac{1}{19}} + {\small\frac{1}{23}} + {\small\frac{1}{29}} + {\small\frac{1}{31}} + {\small\frac{1}{37}} + {\small\frac{1}{41}} + {\small\frac{1}{43}} + {\small\frac{1}{47}} + \ldots }[/math]

a przez [math]\displaystyle{ Q(k) }[/math] sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Dla przykładu mamy

[math]\displaystyle{ Q(1) = 0 }[/math]

[math]\displaystyle{ Q(2) = {\small\frac{1}{2}} }[/math]

[math]\displaystyle{ Q(3) = {\small\frac{1}{2}} + {\small\frac{1}{3}} }[/math]

[math]\displaystyle{ Q(4) = {\small\frac{1}{2}} + {\small\frac{1}{3}} }[/math]

Korzystając z twierdzenia B14, udowodnimy

Twierdzenie B35
Niech [math]\displaystyle{ Q(k) }[/math] oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Dla [math]\displaystyle{ k \geqslant 1 }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ Q(2 k) - Q (k) \gt {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2 k)}} }[/math]

Dowód

Zauważmy, że

[math]\displaystyle{ Q(2 k) - Q (k) = \sum_{k \lt p \leqslant 2k} {\small\frac{1}{p}} \geqslant }[/math]

[math]\displaystyle{ \; \: \geqslant \sum_{k \lt p \leqslant 2k} {\small\frac{1}{2 k}} = }[/math]

[math]\displaystyle{ \; \: = {\small\frac{1}{2 k}} \cdot [\pi (2 k) - \pi (k)] \gt }[/math]

[math]\displaystyle{ \; \: \gt {\small\frac{1}{2 k}} \cdot {\small\frac{\log 2}{2}} \cdot {\small\frac{k}{\log (2 k)}} = }[/math]

[math]\displaystyle{ \; \: = {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2 k)}} }[/math]

Pierwsza nierówność (nieostra) wynika z faktu, że [math]\displaystyle{ {\small\frac{1}{p}} \geqslant {\small\frac{1}{2 k}} }[/math] dla wszystkich liczb pierwszych [math]\displaystyle{ p \leqslant 2 k }[/math]. Kolejna nierówność wynika z twierdzenia B14.
□

Twierdzenie B36
Niech [math]\displaystyle{ Q(k) }[/math] oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność

[math]\displaystyle{ Q(2^n) \gt {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 1} {\small\frac{1}{j}} }[/math]

Dowód

Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], bo

[math]\displaystyle{ Q(2^1) = {\small\frac{1}{2}} \gt {\small\frac{3}{8}} }[/math]

Zakładając, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ Q(2^{n + 1}) = Q (2^n) + [Q (2^{n + 1}) - Q (2^n)] \gt }[/math]

[math]\displaystyle{ \; \: \: \, \gt Q (2^n) + {\small\frac{\log 2}{4}} \cdot {\small\frac{1}{\log (2^{n + 1})}} = }[/math]

[math]\displaystyle{ \; \: \: \, = Q (2^n) + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 1}} \gt }[/math]

[math]\displaystyle{ \; \: \: \, \gt Q (2^n) + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 2}} \gt }[/math]

[math]\displaystyle{ \; \: \: \, \gt {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 1} {\small\frac{1}{j}} + {\small\frac{1}{4}} \cdot {\small\frac{1}{n + 2}} = }[/math]

[math]\displaystyle{ \; \: \: \, = {\small\frac{1}{4}} \cdot \sum_{j = 1}^{n + 2} {\small\frac{1}{j}} }[/math]

Pierwsza nierówność wynika z twierdzenia B35, druga z faktu, że [math]\displaystyle{ {\small\frac{1}{n + 1}} \gt {\small\frac{1}{n + 2}} }[/math], a trzecia z założenia indukcyjnego.
□

Twierdzenie B37
Niech [math]\displaystyle{ Q(k) }[/math] oznacza sumę odwrotności wszystkich liczb pierwszych nie większych od [math]\displaystyle{ k }[/math]. Prawdziwa jest nierówność

[math]\displaystyle{ Q(k) \gt \tfrac{1}{8} \, \log_2 \! \log_2 \! k }[/math]

Dowód

Niech [math]\displaystyle{ n = \lfloor \log_2 \! k \rfloor }[/math] dla dowolnego [math]\displaystyle{ k \geqslant 1 }[/math]. Mamy

[math]\displaystyle{ k = 2^{\log_2 \! k} \geqslant 2^{\lfloor \log_2 \! k \rfloor} = 2^n }[/math]

Ponieważ

[math]\displaystyle{ Q(k) \geqslant Q (2^n) \gt }[/math]

[math]\displaystyle{ \quad \gt {\small\frac{1}{4}} \cdot \underset{j = 1}{\overset{n + 1}{\sum}} {\small\frac{1}{j}} \gt }[/math]

[math]\displaystyle{ \quad \gt {\small\frac{1}{8}} \cdot \log_2 (n + 1) = }[/math]

[math]\displaystyle{ \quad = {\small\frac{1}{8}} \cdot \log_2 (\lfloor \log_2 \! k \rfloor + 1) \gt }[/math]

[math]\displaystyle{ \quad \gt {\small\frac{1}{8}} \cdot \log_2 (\log_2 \! k) }[/math]

Pierwsza nierówność (ostra) wynika z twierdzenia B36, kolejna nierówność wynika z twierdzenia B34.
□

Z twierdzenia B37 wynika natychmiast rozbieżność sumy odwrotności wszystkich liczb pierwszych.

Dokładniejsze oszacowanie sumy odwrotności liczb pierwszych nie większych od [math]\displaystyle{ k }[/math] jest dane wzorem [math]\displaystyle{ \sum_{p\leqslant k} {\small\frac{1}{p}} = \log \log k + M + \ldots }[/math] gdzie [math]\displaystyle{ M = 0.261497212847 \ldots }[/math] jest stałą Mertensa. Dla [math]\displaystyle{ k \geqslant 286 }[/math] prawdziwe jest następujące oszacowanie odchylenia od podanej wyżej wartości [math]\displaystyle{ \left| \sum_{p\leqslant k} {\small\frac{1}{p}} - \log \log k - M \right| \lt {\small\frac{1}{2 (\log k)^2}} }[/math]

Zbieżność sumy [math]\displaystyle{ \textstyle \sum\limits_{p \geqslant 2} {\small\frac{1}{p \log p}} }[/math]

Twierdzenie B38
Niech [math]\displaystyle{ T = \sum_{p \geqslant 2} {\small\frac{1}{p \log p}} }[/math] będzie sumą odwrotności wszystkich iloczynów [math]\displaystyle{ p \! \cdot \! \log p }[/math], gdzie [math]\displaystyle{ p }[/math] oznacza liczbę pierwszą, a [math]\displaystyle{ T(k) }[/math] będzie sumą częściową sumy [math]\displaystyle{ T }[/math]

[math]\displaystyle{ T(k) = \sum_{p \leqslant k} {\small\frac{1}{p \log p}} }[/math]

Dla [math]\displaystyle{ k \geqslant 2 }[/math] prawdziwe jest oszacowanie

[math]\displaystyle{ T(2 k) - T (k) \lt {\small\frac{2 \log 2}{\log^2 \! k}} }[/math]

Dowód

Zauważmy, że

[math]\displaystyle{ T(2 k) - T (k) = \sum_{k \lt p \leqslant 2 k} {\small\frac{1}{p \log p}} }[/math]

[math]\displaystyle{ \; \lt \sum_{k \lt p \leqslant 2 k} {\small\frac{1}{k \log k}} }[/math]

[math]\displaystyle{ \; = {\small\frac{1}{k \log k}} \cdot [\pi (2 k) - \pi (k)] }[/math]

[math]\displaystyle{ \; \lt {\small\frac{1}{k \log k}} \cdot 2 \log 2 \cdot {\small\frac{k}{\log k}} }[/math]

[math]\displaystyle{ \; = {\small\frac{2 \log 2}{(\log k)^2}} }[/math]

Pierwsza nierówność wynika z faktu, że [math]\displaystyle{ {\small\frac{1}{p \log p}} \lt {\small\frac{1}{k \log k}} }[/math] dla wszystkich liczb pierwszych [math]\displaystyle{ p \gt k }[/math]. Kolejna nierówność wynika z twierdzenia A11.
□

Twierdzenie B39
Suma [math]\displaystyle{ \sum_{p \geqslant 2} {\small\frac{1}{p \log p}} }[/math], gdzie [math]\displaystyle{ p }[/math] oznacza liczbę pierwszą, jest skończona.

Dowód

Niech [math]\displaystyle{ p }[/math] oznacza liczbę pierwszą i niech

[math]\displaystyle{ T(k) = \sum_{p \leqslant k} {\small\frac{1}{p \log p}} }[/math]

Pokażemy najpierw, że dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwa jest nierówność

[math]\displaystyle{ T(2^n) \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} \right) }[/math]

Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], bo

[math]\displaystyle{ T(2^1) \approx 0.721 \lt 2.885 }[/math]

Zakładając, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ T(2^{n + 1}) = T (2^n) + [T (2^{n + 1}) - T (2^n)] }[/math]

[math]\displaystyle{ \;\;\: \lt T (2^n) + 2 \log 2 \cdot {\small\frac{1}{[\log (2^n)]^2}} }[/math]

[math]\displaystyle{ \;\;\: \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} \right) + 2 \log 2 \cdot {\small\frac{1}{n^2 (\log 2)^2}} }[/math]

[math]\displaystyle{ \;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n}} + {\small\frac{1}{n^2}} \right) }[/math]

[math]\displaystyle{ \;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} + \left( {\small\frac{2}{n + 1}} - {\small\frac{2}{n}} + {\small\frac{1}{n^2}} \right) \right) }[/math]

[math]\displaystyle{ \;\;\: = {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} - {\small\frac{n - 1}{n^2 (n + 1)}} \right) }[/math]

[math]\displaystyle{ \;\;\: \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} \right) }[/math]

Pierwsza nierówność wynika z twierdzenia B38, a druga z założenia indukcyjnego. Co kończy dowód indukcyjny.

Niech [math]\displaystyle{ n = \lfloor \log_2 \! k \rfloor }[/math] dla dowolnego [math]\displaystyle{ k \geqslant 1 }[/math]. Ponieważ

[math]\displaystyle{ k = 2^{\log_2 \! k} \lt 2^{\lfloor \log_2 \! k \rfloor + 1} = 2^{n + 1} }[/math]

oraz

[math]\displaystyle{ n + 1 = \lfloor \log_2 \! k \rfloor + 1 \leqslant \log_2 \! k + 1 }[/math]

to łatwo otrzymujemy

[math]\displaystyle{ T(k) \leqslant T (2^{n + 1}) \lt {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{n + 1}} \right) \leqslant {\small\frac{2}{\log 2}} \cdot \left( 3 - {\small\frac{2}{\log_2 \! k + 1}} \right) \lt {\small\frac{6}{\log 2}} }[/math]

Ponieważ ciąg sum częściowych [math]\displaystyle{ T(k) }[/math] jest rosnący i ograniczony, to suma odwrotności wszystkich iloczynów [math]\displaystyle{ p \! \cdot \! \log p }[/math] jest skończona.
□