Największy wspólny dzielnik, element odwrotny modulo, funkcja Eulera
Największy wspólny dzielnik
Definicja H1
Niech będą dane dwie liczby całkowite [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] niebędące jednocześnie zerami. Największym wspólnym dzielnikiem[1] liczb [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math] będziemy nazywali liczbę całkowitą [math]\displaystyle{ D }[/math] taką, że
- [math]\displaystyle{ D \mid a \quad \text{i} \quad D \mid b }[/math]
- [math]\displaystyle{ \,\, d \mid a \quad \text{i} \quad \; d \mid b \qquad \Longrightarrow \qquad d \leqslant D }[/math]
gdzie [math]\displaystyle{ d }[/math] jest dowolną liczbą całkowitą.
Uwaga H2
Tak zdefiniowaną liczbę [math]\displaystyle{ D }[/math] będziemy oznaczali przez [math]\displaystyle{ \gcd (a, b) }[/math]. Ponieważ [math]\displaystyle{ 1 \mid a \; }[/math] i [math]\displaystyle{ \; 1 \mid b }[/math], to z definicji wynika natychmiast, że [math]\displaystyle{ \gcd (a, b) \geqslant 1 }[/math].
Zadanie H3
Pokazać, że
- [math]\displaystyle{ d \mid \gcd (a, b) \qquad \Longleftrightarrow \qquad d \mid a \quad \text{i} \quad d \mid b }[/math]
[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Z założenia [math]\displaystyle{ d \mid \gcd (a, b) }[/math]. Z definicji największego wspólnego dzielnika [math]\displaystyle{ \gcd (a, b) \mid a }[/math], zatem [math]\displaystyle{ d \mid a }[/math]. Analogicznie pokazujemy, że [math]\displaystyle{ d \mid b }[/math].
[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Z założenia [math]\displaystyle{ a = r d }[/math], [math]\displaystyle{ b = s d }[/math]. Z lematu Bézouta (zobacz C74) istnieją takie liczby całkowite [math]\displaystyle{ x, y }[/math], że
- [math]\displaystyle{ \gcd (a, b) = a x + b y = r d x + s d y = d (r x + s y) }[/math]
Zatem [math]\displaystyle{ d \mid \gcd (a, b) }[/math].
□
Twierdzenie H4
Jeżeli liczby całkowite [math]\displaystyle{ a, b }[/math] nie są jednocześnie równe zero i [math]\displaystyle{ \gcd (a, b) = a x + b y }[/math], to [math]\displaystyle{ \gcd (x, y) = 1 }[/math].
Z lematu Bézouta (zobacz C74) wiemy, że liczby całkowite [math]\displaystyle{ x, y }[/math] zawsze istnieją. Niech [math]\displaystyle{ \gcd (a, b) = d > 0 }[/math], zatem [math]\displaystyle{ a = d k }[/math] i [math]\displaystyle{ b = d m }[/math], czyli
- [math]\displaystyle{ (d k) x + (d m) y = d }[/math]
Co oznacza, że [math]\displaystyle{ k x + m y = 1 }[/math], ale [math]\displaystyle{ \gcd (x, y) }[/math] jest dzielnikiem [math]\displaystyle{ k x + m y }[/math] (bo jest dzielnikiem [math]\displaystyle{ x }[/math] i [math]\displaystyle{ y }[/math]), zatem [math]\displaystyle{ \gcd (x, y) \mid 1 }[/math], czyli [math]\displaystyle{ \gcd (x, y) = 1 }[/math]. Co należało pokazać.
□
Twierdzenie H5
Niech [math]\displaystyle{ a, b, k \in \mathbb{Z} }[/math]. Prawdziwy jest wzór
- [math]\displaystyle{ \gcd (a + k b, b) = \gcd (a, b) }[/math]
Niech [math]\displaystyle{ d_1 = \gcd (a + k b, b) \; }[/math] i [math]\displaystyle{ \; d_2 = \gcd (a, b) }[/math].
Z definicji [math]\displaystyle{ d_1 \mid (a + k b) \; }[/math] i [math]\displaystyle{ \; d_1 \mid b }[/math], zatem [math]\displaystyle{ a + k b = x d_1 \; }[/math] i [math]\displaystyle{ \; b = y d_1 }[/math], czyli [math]\displaystyle{ a + k x d_1 = x d_1 }[/math], skąd natychmiast wynika, że [math]\displaystyle{ d_1 \mid a }[/math]. Ponieważ [math]\displaystyle{ d_1 \mid b }[/math], to [math]\displaystyle{ d_1 \mid d_2 }[/math] (zobacz H3).
Z definicji [math]\displaystyle{ d_2 \mid a \; }[/math] i [math]\displaystyle{ \; d_2 \mid b }[/math], zatem [math]\displaystyle{ d_2 \mid (a + k b) \; }[/math] i [math]\displaystyle{ \; d_2 \mid b }[/math], czyli [math]\displaystyle{ d_2 \mid d_1 }[/math].
Ponieważ [math]\displaystyle{ d_1 \mid d_2 \; }[/math] i [math]\displaystyle{ \; d_2 \mid d_1 }[/math], to [math]\displaystyle{ | d_1 | = | d_2 | }[/math]. Co kończy dowód.
□
Twierdzenie H6
Niech [math]\displaystyle{ a, b, m \in \mathbb{Z} }[/math]. Prawdziwa jest następująca równoważność
- [math]\displaystyle{ \gcd (a, m) = 1 \quad \text{i} \quad \gcd (b, m) = 1 \quad \qquad \Longleftrightarrow \quad \qquad \gcd (a b, m) = 1 }[/math]
[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Niech [math]\displaystyle{ \gcd (a b, m) = d }[/math]. Z definicji [math]\displaystyle{ d \mid a b }[/math] i [math]\displaystyle{ d \mid m }[/math]. Gdyby było [math]\displaystyle{ d > 1 }[/math], to istniałaby liczba pierwsza [math]\displaystyle{ p }[/math] taka, że [math]\displaystyle{ p \mid d }[/math] i mielibyśmy [math]\displaystyle{ p \mid a b }[/math] i [math]\displaystyle{ p \mid m }[/math]. Jeżeli [math]\displaystyle{ p \mid a b }[/math], to [math]\displaystyle{ p \mid a }[/math] lub [math]\displaystyle{ p \mid b }[/math] (zobacz C75). W przypadku, gdy [math]\displaystyle{ p \mid a }[/math] dostajemy [math]\displaystyle{ \gcd (a, m) \geqslant p > 1 }[/math], wbrew założeniu, że [math]\displaystyle{ \gcd (a, m) = 1 }[/math]. Analogicznie pokazujemy sprzeczność, gdy [math]\displaystyle{ p \mid b }[/math].
[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Niech [math]\displaystyle{ \gcd (a, m) = d }[/math]. Z definicji [math]\displaystyle{ d \mid a }[/math] i [math]\displaystyle{ d \mid m }[/math], zatem również [math]\displaystyle{ d \mid a b }[/math] i [math]\displaystyle{ d \mid m }[/math]. Mamy stąd
- [math]\displaystyle{ 1 = \gcd (a b, m) \geqslant d \geqslant 1 }[/math]
Czyli musi być [math]\displaystyle{ d = 1 }[/math]. Analogicznie pokazujemy, że [math]\displaystyle{ \gcd (b, m) = 1 }[/math].
□
Twierdzenie H7
Dla [math]\displaystyle{ a, b, m \in \mathbb{Z} }[/math] jest
- [math]\displaystyle{ \gcd (a b, m) \mid \gcd (a, m) \cdot \gcd (b, m) }[/math]
Wprowadźmy oznaczenia
- [math]\displaystyle{ r = \gcd (a b, m) }[/math]
- [math]\displaystyle{ s = \gcd (a, m) }[/math]
- [math]\displaystyle{ t = \gcd (b, m) }[/math]
Z lematu Bézouta (zobacz C74) istnieją takie liczby [math]\displaystyle{ x, y, X, Y }[/math], że
- [math]\displaystyle{ s = a x + m y }[/math]
- [math]\displaystyle{ t = b X + m Y }[/math]
Zatem
- [math]\displaystyle{ s t = (a x + m y) (b X + m Y) = a b x X + a m x Y + m b y X + m^2 y Y }[/math]
ale [math]\displaystyle{ r \mid a b }[/math] i [math]\displaystyle{ r \mid m }[/math], skąd otrzymujemy, że [math]\displaystyle{ r \mid s t }[/math]. Co należało pokazać.
□
Twierdzenie H8
Jeżeli liczby [math]\displaystyle{ a, b }[/math] są względnie pierwsze, to
- [math]\displaystyle{ \gcd (a b, m) = \gcd (a, m) \cdot \gcd (b, m) }[/math]
Wprowadźmy oznaczenia
- [math]\displaystyle{ r = \gcd (a b, m) }[/math]
- [math]\displaystyle{ s = \gcd (a, m) }[/math]
- [math]\displaystyle{ t = \gcd (b, m) }[/math]
Z założenia [math]\displaystyle{ \gcd (a, b) = 1 }[/math]. Ponieważ [math]\displaystyle{ s \mid a }[/math] oraz [math]\displaystyle{ t \mid b }[/math], to [math]\displaystyle{ \gcd (s, t) = 1 }[/math], zatem (zobacz C76)
- [math]\displaystyle{ s \mid a \qquad \,\, \text{i} \qquad t \mid b \qquad \qquad \;\, \Longrightarrow \qquad \qquad s t \mid a b }[/math]
- [math]\displaystyle{ s \mid m \qquad \text{i} \qquad t \mid m \qquad \qquad \Longrightarrow \qquad \qquad s t \mid m }[/math]
Wynika stąd, że [math]\displaystyle{ s t \mid \gcd (a b, m) }[/math], czyli [math]\displaystyle{ s t \mid r }[/math]. Z poprzedniego twierdzenia wiemy, że [math]\displaystyle{ r \mid s t }[/math], zatem [math]\displaystyle{ |r| = |s t| }[/math]. Co kończy dowód.
□
Twierdzenie H9
Jeżeli liczby [math]\displaystyle{ b, m }[/math] są względnie pierwsze, to
- [math]\displaystyle{ \gcd (a b, m) = \gcd (a, m) }[/math]
Wprowadźmy oznaczenia
- [math]\displaystyle{ r = \gcd (a b, m) }[/math]
- [math]\displaystyle{ s = \gcd (a, m) }[/math]
Z lematu Bézouta istnieją takie liczby [math]\displaystyle{ x, y }[/math], że
- [math]\displaystyle{ r = a b x + m y }[/math]
Ale [math]\displaystyle{ s \mid a \; }[/math] i [math]\displaystyle{ \; s \mid m }[/math], zatem [math]\displaystyle{ s \mid r }[/math].
Z założenia [math]\displaystyle{ \gcd (b, m) = 1 }[/math], zatem z twierdzenia H7 wynika natychmiast, że [math]\displaystyle{ r \mid s }[/math]. Ponieważ [math]\displaystyle{ s \mid r \; }[/math] i [math]\displaystyle{ \; r \mid s }[/math], to [math]\displaystyle{ | r | = | s | }[/math]. Co należało pokazać.
□
Twierdzenie H10
Jeżeli liczby [math]\displaystyle{ a, b }[/math] nie są jednocześnie równe zero i [math]\displaystyle{ m \neq 0 }[/math], to
- [math]\displaystyle{ \gcd (a m, b m) = | m | \cdot \gcd (a, b) }[/math]
Oznaczmy [math]\displaystyle{ d = \gcd (a, b) \; }[/math] i [math]\displaystyle{ \; D = \gcd (a m, b m) }[/math]. Pokażemy, że [math]\displaystyle{ d m \mid D }[/math].
- [math]\displaystyle{ \begin{array}{llll} d = \gcd (a, b) & \qquad \Longrightarrow \qquad & d \mid a \quad \text{i} \quad d \mid b & \text{(zobacz H3)} \\ & & & \\ & \qquad \Longrightarrow \qquad & d m \mid a m \quad \text{i} \quad d m \mid b m & \\ & & & \\ & \qquad \Longrightarrow \qquad & d m \mid \gcd (a m, b m) & \text{(zobacz H3)} \\ & & & \\ & \qquad \Longrightarrow \qquad & d m \mid D & \\ \end{array} }[/math]
Pokażemy, że [math]\displaystyle{ D \mid d m }[/math].
- [math]\displaystyle{ \begin{array}{llll} d = \gcd (a, b) & \qquad \Longrightarrow \qquad & d = a x + b y & \text{(lemat Bézouta C74)} \\ & & & \\ & \qquad \Longrightarrow \qquad & d m = a m x + b m y & \\ & & & \\ & \qquad \Longrightarrow \qquad & D \mid d m & \\ \end{array} }[/math]
Ostatnia implikacja korzysta z tego, że [math]\displaystyle{ D \mid a m \; }[/math] i [math]\displaystyle{ \; D \mid b m }[/math] (zobacz H3). Ponieważ [math]\displaystyle{ d m \mid D \; }[/math] i [math]\displaystyle{ \; D \mid d m }[/math], to [math]\displaystyle{ | D | = | d m | }[/math]. Co należało pokazać.
□
Zadanie H11
Pokazać, że jeżeli liczby [math]\displaystyle{ a, b }[/math] nie są jednocześnie równe zero, to
- [math]\displaystyle{ \gcd \left( {\small\frac{a}{\gcd (a, b)}}, {\small\frac{b}{\gcd (a, b)}} \right) = 1 }[/math]
Z twierdzenia H10 otrzymujemy
- [math]\displaystyle{ \gcd (a, b) = \gcd \left( \gcd (a, b) \cdot {\small\frac{a}{\gcd (a, b)}}, \gcd (a, b) \cdot {\small\frac{b}{\gcd (a, b)}} \right) }[/math]
- [math]\displaystyle{ \;\;\;\; = \gcd (a, b) \cdot \gcd \left( {\small\frac{a}{\gcd (a, b)}}, {\small\frac{b}{\gcd (a, b)}} \right) }[/math]
Zatem
- [math]\displaystyle{ \gcd \left( {\small\frac{a}{\gcd (a, b)}}, {\small\frac{b}{\gcd (a, b)}} \right) = 1 }[/math]
Co należało pokazać.
□
Zadanie H12
Pokazać, że [math]\displaystyle{ a \mid b }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ a \mid \gcd (a, b) }[/math].
[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Zakładając, że [math]\displaystyle{ a \mid b }[/math], dostajemy
- [math]\displaystyle{ \begin{array}{llll} a \mid b & \qquad \Longrightarrow \qquad & b = k a & \\ & & & \\ & \qquad \Longrightarrow \qquad & \gcd (a, b) = \gcd (a, k a) = | a | \cdot \gcd (1, k) = | a | & \qquad \text{(zobacz H10)} \\ & & & \\ & \qquad \Longrightarrow \qquad & a \mid \gcd (a, b) & \\ \end{array} }[/math]
[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Jeżeli [math]\displaystyle{ a \mid \gcd (a, b) }[/math], to [math]\displaystyle{ a \mid b }[/math] (zobacz H3). Co należało pokazać.
□
Zadanie H13
Niech [math]\displaystyle{ \gcd (a, d) = 1 }[/math]. Pokazać, że [math]\displaystyle{ d \nmid a b }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ d \nmid b }[/math].
Korzystając z rezultatu pokazanego w zadaniu H12, dostajemy
- [math]\displaystyle{ \begin{array}{llll} d \nmid a b & \qquad \Longleftrightarrow \qquad & d \nmid \gcd (d, a b) & \\ & & & \\ & \qquad \Longleftrightarrow \qquad & d \nmid \gcd (d, b) & \text{(zobacz H9)} \\ & & & \\ & \qquad \Longleftrightarrow \qquad & d \nmid b & \\ \end{array} }[/math]
Co należało pokazać.
□
Twierdzenie H14
Jeżeli dodatnie liczby [math]\displaystyle{ a, b }[/math] są względnie pierwsze, to każdy dzielnik [math]\displaystyle{ d }[/math] iloczynu [math]\displaystyle{ a b }[/math] można przedstawić jednoznacznie w postaci [math]\displaystyle{ d = d_1 d_2 }[/math], gdzie [math]\displaystyle{ d_1 \mid a , }[/math] [math]\displaystyle{ \; d_2 \mid b \; }[/math] [math]\displaystyle{ \text{i} \; \gcd (d_1, d_2) = 1 }[/math].
Niech [math]\displaystyle{ d_1 = \gcd (d, a) \; }[/math] i [math]\displaystyle{ \; d_2 = \gcd (d, b) }[/math]. Z twierdzenia H8 mamy
- [math]\displaystyle{ d_1 d_2 = \gcd (d, a) \cdot \gcd (d, b) = \gcd (d, a b) = d }[/math]
Bo z założenia [math]\displaystyle{ d \mid a b }[/math]. Z definicji największego wspólnego dzielnika i zadania H3 dostajemy
- [math]\displaystyle{ \gcd (d_1, d_2) = e \qquad \Longrightarrow \qquad e \mid d_1 \quad \text{i} \quad e \mid d_2 }[/math]
- [math]\displaystyle{ \, \Longrightarrow \qquad e \mid \gcd (d, a) \quad \text{i} \quad e \mid \gcd (d, b) }[/math]
- [math]\displaystyle{ \, \Longrightarrow \qquad e \mid a \quad \text{i} \quad e \mid b }[/math]
- [math]\displaystyle{ \, \Longrightarrow \qquad e \mid \gcd (a, b) }[/math]
- [math]\displaystyle{ \, \Longrightarrow \qquad \gcd (a, b) \geqslant e }[/math]
Gdyby było [math]\displaystyle{ \gcd (d_1, d_2) = e > 1 }[/math], to mielibyśmy [math]\displaystyle{ \gcd (a, b) \geqslant e > 1 }[/math]. Wbrew założeniu, że [math]\displaystyle{ \gcd (a, b) = 1 }[/math]. Co kończy dowód.
□
Twierdzenie H15
Jeżeli [math]\displaystyle{ a, m, n \in \mathbb{Z}_+ }[/math], to
- [math]\displaystyle{ \gcd (a^m - 1, a^n - 1) = a^{\gcd (m, n)} - 1 }[/math]
Pokażemy najpierw, że jeżeli [math]\displaystyle{ d }[/math] jest dzielnikiem lewej strony dowodzonej równości, to jest również dzielnikiem prawej strony i odwrotnie.
[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Z założenia [math]\displaystyle{ d }[/math] jest dzielnikiem [math]\displaystyle{ \gcd (a^m - 1, a^n - 1) }[/math], czyli [math]\displaystyle{ d \mid (a^m - 1) \; }[/math] i [math]\displaystyle{ \; d \mid (a^n - 1) }[/math], co możemy zapisać w postaci
- [math]\displaystyle{ a^m \equiv 1 \!\! \pmod{d} \quad \qquad \text{oraz} \quad \qquad a^n \equiv 1 \!\! \pmod{d} }[/math]
Z lematu Bézouta (zobacz C74) wiemy, że istnieją takie liczby [math]\displaystyle{ x, y }[/math], że [math]\displaystyle{ \gcd (m, n) = m x + n y }[/math]. Łatwo znajdujemy, że
- [math]\displaystyle{ a^{\gcd (m, n)} \equiv a^{m x + n y} \equiv (a^m)^x \cdot (a^n)^y \equiv 1^x \cdot 1^y \equiv 1 \!\! \pmod{d} }[/math]
Czyli [math]\displaystyle{ d \, \biggr\rvert \left( a^{\gcd (m, n)} - 1 \right) }[/math].
[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Z założenia [math]\displaystyle{ d \, \biggr\rvert \left( a^{\gcd (m, n)} - 1 \right) }[/math], czyli
- [math]\displaystyle{ a^{\gcd (m, n)} \equiv 1 \!\! \pmod{d} }[/math]
Zatem
- [math]\displaystyle{ a^m \equiv \left[ a^{\gcd (m, n)} \right]^{\tfrac{m}{\gcd (m, n)}} \equiv 1 \!\! \pmod{d} }[/math]
Podobnie otrzymujemy
- [math]\displaystyle{ a^n \equiv 1 \!\! \pmod{d} }[/math]
Zatem [math]\displaystyle{ d }[/math] dzieli [math]\displaystyle{ a^m - 1 \; }[/math] i [math]\displaystyle{ \; a^n - 1 }[/math], czyli
- [math]\displaystyle{ d \mid \gcd (a^m - 1, a^n - 1) }[/math]
W szczególności wynika stąd, że
- [math]\displaystyle{ \gcd (a^m - 1, a^n - 1) \, \biggr\rvert \left( a^{\gcd (m, n)} - 1 \right) }[/math]
- [math]\displaystyle{ \left( a^{\gcd (m, n)} - 1 \right) \, \biggr\rvert \, \gcd (a^m - 1, a^n - 1) }[/math]
Czyli [math]\displaystyle{ \left| \gcd (a^m - 1, a^n - 1) \right| = \left| a^{\gcd (m, n)} - 1 \right| }[/math]. Co kończy dowód.
□
Uwaga H16
W dowodzie twierdzenia H15 pominęliśmy milczeniem fakt, że jedna z liczb [math]\displaystyle{ x, y }[/math] może być (i często jest) ujemna. Choć rezultat jest prawidłowy, to nie wiemy, co oznacza zapis
- [math]\displaystyle{ a^{- 1000} \equiv 1^{- 10} \equiv 1 \!\! \pmod{d} }[/math]
Omówimy ten problem w następnej sekcji. Zauważmy, wyprzedzając materiał, że z kongruencji
- [math]\displaystyle{ a^m \equiv 1 \!\! \pmod{d} \quad \qquad \text{oraz} \quad \qquad a^n \equiv 1 \!\! \pmod{d} }[/math]
wynika, że [math]\displaystyle{ \gcd (a, d) = 1 }[/math] i liczba [math]\displaystyle{ a }[/math] ma element odwrotny modulo [math]\displaystyle{ d }[/math].
Element odwrotny modulo [math]\displaystyle{ m }[/math]
Twierdzenie H17
Niech [math]\displaystyle{ m \in \mathbb{Z}_+ }[/math]. Dla liczby [math]\displaystyle{ a \in \mathbb{Z} }[/math] istnieje taka liczba [math]\displaystyle{ x }[/math], że
- [math]\displaystyle{ a x \equiv 1 \!\! \pmod{m} }[/math]
wtedy i tylko wtedy, gdy [math]\displaystyle{ \gcd (a, m) = 1 }[/math].
[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Z założenia istnieje taka liczba [math]\displaystyle{ x }[/math], że
- [math]\displaystyle{ a x \equiv 1 \!\! \pmod{m} }[/math]
Zatem dla pewnego [math]\displaystyle{ k \in \mathbb{Z} }[/math] jest
- [math]\displaystyle{ a x = 1 + k m }[/math]
Czyli [math]\displaystyle{ a x - k m = 1 }[/math]. Wynika stąd, że [math]\displaystyle{ \gcd (a, m) }[/math] dzieli [math]\displaystyle{ 1 }[/math], co oznacza, że [math]\displaystyle{ \gcd (a, m) = 1 }[/math].
[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Z założenia [math]\displaystyle{ \gcd (a, m) = 1 }[/math]. Z lematu Bézouta (zobacz C74) wynika, że istnieją takie liczby całkowite [math]\displaystyle{ x, y }[/math], że
- [math]\displaystyle{ a x + m y = 1 }[/math]
Zatem modulo [math]\displaystyle{ m }[/math] dostajemy
- [math]\displaystyle{ a x \equiv 1 \!\! \pmod{m} }[/math]
Co kończy dowód.
□
Definicja H18
Niech [math]\displaystyle{ m \in \mathbb{Z}_+ }[/math]. Liczbę [math]\displaystyle{ x }[/math] taką, że
- [math]\displaystyle{ a \cdot x \equiv 1 \!\! \pmod{m} }[/math]
będziemy nazywali elementem odwrotnym liczby [math]\displaystyle{ a }[/math] modulo [math]\displaystyle{ m }[/math] i oznaczali jako [math]\displaystyle{ a^{- 1} }[/math].
Uwaga H19
Oznaczenie elementu odwrotnego ma naturalne uzasadnienie. Zauważmy, że jeżeli [math]\displaystyle{ b \mid a }[/math] oraz [math]\displaystyle{ b }[/math] ma element odwrotny modulo [math]\displaystyle{ m }[/math], to prawdziwa jest kongruencja
- [math]\displaystyle{ {\small\frac{a}{b}} \equiv a b^{- 1} \!\! \pmod{m} }[/math]
Istotnie
- [math]\displaystyle{ {\small\frac{a}{b}} = {\small\frac{a}{b}} \cdot 1 \equiv {\small\frac{a}{b}} \cdot b b^{- 1} \equiv a b^{- 1} \!\! \pmod{m} }[/math]
W PARI/GP odwrotność liczby [math]\displaystyle{ a }[/math] modulo [math]\displaystyle{ m }[/math] znajdujemy, wpisując Mod(a, m)^(-1).
Twierdzenie H20
Niech [math]\displaystyle{ a, k \in \mathbb{Z} }[/math], [math]\displaystyle{ m \in \mathbb{Z}_+ }[/math]. Poniższa tabelka przedstawia elementy odwrotne do elementu [math]\displaystyle{ a }[/math] w przypadku niektórych modułów [math]\displaystyle{ m }[/math]. W szczególności, jeżeli moduł [math]\displaystyle{ m }[/math] jest liczbą nieparzystą, to [math]\displaystyle{ 2^{- 1} \equiv {\small\frac{m + 1}{2}} \!\! \pmod{m} }[/math].
postać
modułu [math]\displaystyle{ \boldsymbol{m} }[/math]odwrotność
elementu [math]\displaystyle{ \boldsymbol{a} }[/math]uwagi [math]\displaystyle{ 1. }[/math] [math]\displaystyle{ m = 2 }[/math] [math]\displaystyle{ 1 }[/math] liczba [math]\displaystyle{ a }[/math]
jest liczbą
nieparzystą[math]\displaystyle{ 2. }[/math] [math]\displaystyle{ m = 4 }[/math] [math]\displaystyle{ R_4(a) }[/math] [math]\displaystyle{ 3. }[/math] [math]\displaystyle{ m = 8 }[/math] [math]\displaystyle{ R_8(a) }[/math] [math]\displaystyle{ 4. }[/math] [math]\displaystyle{ m = a k - 1 }[/math] [math]\displaystyle{ {\small\frac{m + 1}{a}} }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ 5. }[/math] [math]\displaystyle{ m = a k + 1 }[/math] [math]\displaystyle{ - {\small\frac{m - 1}{a}} }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ 6. }[/math] [math]\displaystyle{ m = a k - 2 }[/math] [math]\displaystyle{ {\small\frac{m + 1}{2}} \cdot {\small\frac{m + 2}{a}} }[/math] liczby [math]\displaystyle{ a , m }[/math]
są liczbami
nieparzystymi[math]\displaystyle{ 7. }[/math] [math]\displaystyle{ m = a k + 2 }[/math] [math]\displaystyle{ {\small\frac{m - 1}{2}} \cdot {\small\frac{m - 2}{2}} }[/math]
Punkty 1. - 3.
Ponieważ dla liczb nieparzystych jest
- [math]\displaystyle{ a^2 \equiv 1 \!\! \pmod{2} }[/math]
- [math]\displaystyle{ a^2 \equiv 1 \!\! \pmod{4} }[/math]
- [math]\displaystyle{ a^2 \equiv 1 \!\! \pmod{8} }[/math]
to liczba nieparzysta [math]\displaystyle{ a }[/math] jest swoją odwrotnością modulo [math]\displaystyle{ 2 }[/math], [math]\displaystyle{ 4 }[/math] i [math]\displaystyle{ 8 }[/math]. Ponieważ element odwrotny jest definiowany modulo, zatem możemy napisać
- [math]\displaystyle{ a^{- 1} \equiv R_2 (a) \!\! \pmod{2} }[/math]
- [math]\displaystyle{ a^{- 1} \equiv R_4 (a) \!\! \pmod{4} }[/math]
- [math]\displaystyle{ a^{- 1} \equiv R_8 (a) \!\! \pmod{8} }[/math]
W pierwszym przypadku wynik jest oczywisty, bo [math]\displaystyle{ R_2 (a) = 1 }[/math].
Punkt 4.
Zauważmy, że
- [math]\displaystyle{ \gcd (a, m) = \gcd (a, a k - 1) = \gcd (a, - 1) = 1 }[/math]
oraz [math]\displaystyle{ a \mid (m + 1) }[/math]. Zatem
- [math]\displaystyle{ a \cdot a^{- 1} = a \cdot {\small\frac{m + 1}{a}} = m + 1 \equiv 1 \!\! \pmod{m} }[/math]
Punkt 5.
Zauważmy, że
- [math]\displaystyle{ \gcd (a, m) = \gcd (a, a k + 1) = \gcd (a, 1) = 1 }[/math]
oraz [math]\displaystyle{ a \mid (m - 1) }[/math]. Zatem
- [math]\displaystyle{ a \cdot a^{- 1} = a \cdot \left[ - \left( {\small\frac{m - 1}{a}} \right) \right] = - m + 1 \equiv 1 \!\! \pmod{m} }[/math]
Punkt 6.
Ponieważ zakładamy, że [math]\displaystyle{ 2 \mid (m + 1) }[/math], to [math]\displaystyle{ m }[/math] musi być liczbą nieparzystą, czyli [math]\displaystyle{ a }[/math] też musi być liczbą nieparzystą. Zauważmy, że
- [math]\displaystyle{ \gcd (a, m) = \gcd (a, a k - 2) = \gcd (a, - 2) = 1 }[/math]
oraz [math]\displaystyle{ a \mid (m + 2) }[/math]. Zatem
- [math]\displaystyle{ a \cdot a^{- 1} = a \cdot \left( {\small\frac{m + 1}{2}} \cdot {\small\frac{m + 2}{a}} \right) = {\small\frac{m + 1}{2}} \cdot (m + 2) \equiv {\small\frac{m + 1}{2}} \cdot 2 \equiv m + 1 \equiv 1 \!\! \pmod{m} }[/math]
Podobnie pokazujemy punkt 7. Co kończy dowód.
□
Twierdzenie H21
Niech [math]\displaystyle{ a, b \in \mathbb{Z} }[/math], [math]\displaystyle{ m \in \mathbb{Z}_+ }[/math] i liczba [math]\displaystyle{ a }[/math] ma element odwrotny modulo [math]\displaystyle{ m }[/math]. Jeżeli liczby [math]\displaystyle{ u_1, u_2, \ldots, u_r }[/math] są liczbami różnymi modulo [math]\displaystyle{ m }[/math], to liczby
- 1. [math]\displaystyle{ a u_1, a u_2, \ldots, a u_r }[/math]
- 2. [math]\displaystyle{ a u_1 + b, a u_2 + b, \ldots, a u_r + b }[/math]
są liczbami różnymi modulo [math]\displaystyle{ m }[/math]. Jeżeli ponadto liczby [math]\displaystyle{ u_1, u_2, \ldots, u_r }[/math] są względnie pierwsze z [math]\displaystyle{ m }[/math], to również liczby
- 3. [math]\displaystyle{ u^{- 1}_1, u^{- 1}_2, \ldots, u^{- 1}_r }[/math]
są liczbami różnymi modulo [math]\displaystyle{ m }[/math].
Punkt 1.
Przypuśćmy dla uzyskania sprzeczności, że istnieją takie różne wskaźniki [math]\displaystyle{ i, j }[/math], że
- [math]\displaystyle{ a u_i \equiv a u_j \!\! \pmod{m} }[/math]
Z założenia liczba [math]\displaystyle{ a }[/math] ma element odwrotny modulo [math]\displaystyle{ m }[/math], zatem mnożąc obie strony kongruencji przez [math]\displaystyle{ a^{- 1} }[/math], otrzymujemy
- [math]\displaystyle{ u_i \equiv u_j \!\! \pmod{m} }[/math]
dla [math]\displaystyle{ i \neq j }[/math], wbrew założeniu, że liczby [math]\displaystyle{ u_1, u_2, \ldots, u_r }[/math] są różne modulo [math]\displaystyle{ m }[/math]. Dowód punktu 2. jest analogiczny.
Punkt 3.
Przypuśćmy dla uzyskania sprzeczności, że istnieją takie różne wskaźniki [math]\displaystyle{ i, j }[/math], że
- [math]\displaystyle{ u^{- 1}_i \equiv u^{- 1}_j \!\! \pmod{m} }[/math]
- [math]\displaystyle{ u_j u^{- 1}_i \equiv 1 \!\! \pmod{m} }[/math]
- [math]\displaystyle{ u_j u^{- 1}_i u_i \equiv u_i \!\! \pmod{m} }[/math]
- [math]\displaystyle{ u_j \equiv u_i \!\! \pmod{m} }[/math]
Ponownie otrzymujemy [math]\displaystyle{ u_i \equiv u_j \!\! \pmod{m} }[/math] dla [math]\displaystyle{ i \neq j }[/math], wbrew założeniu, że liczby [math]\displaystyle{ u_1, u_2, \ldots, u_r }[/math] są różne modulo [math]\displaystyle{ m }[/math]. Co należało pokazać.
□
Zadanie H22
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą. Pokazać, że dla [math]\displaystyle{ k \in [0, p - 1] }[/math] prawdziwa jest kongruencja
- [math]\displaystyle{ {\small\binom{p - 1}{k}} \equiv (- 1)^k \pmod{p} }[/math]
Zauważmy, że modulo [math]\displaystyle{ p }[/math] mamy
- [math]\displaystyle{ {\small\binom{p - 1}{k}} = {\small\frac{(p - 1) !}{k! \cdot (p - 1 - k) !}} }[/math]
- [math]\displaystyle{ \;\; = {\small\frac{(p - 1) (p - 2) \cdot \ldots \cdot (p - k)}{k!}} }[/math]
- [math]\displaystyle{ \;\; \equiv (p - 1) (p - 2) \cdot \ldots \cdot (p - k) \cdot (k!)^{- 1} }[/math]
- [math]\displaystyle{ \;\; \equiv (- 1)^k \cdot k! \cdot (k!)^{- 1} }[/math]
- [math]\displaystyle{ \;\; \equiv (- 1)^k \pmod{p} }[/math]
Co należało pokazać.
□
Zadanie H23
Niech [math]\displaystyle{ A }[/math] i [math]\displaystyle{ B }[/math] będą zbiorami skończonymi. Pokazać, że jeżeli [math]\displaystyle{ A \subseteq B \;\; \text{i} \;\; | A | = | B | }[/math], to [math]\displaystyle{ \; A = B }[/math].
Pierwszy sposób
Z definicji zbiory [math]\displaystyle{ A }[/math] i [math]\displaystyle{ B }[/math] są równe wtedy i tylko wtedy, gdy jednocześnie spełnione są warunki
- [math]\displaystyle{ x \in A \qquad \Longrightarrow \qquad x \in B }[/math]
- [math]\displaystyle{ x \in B \qquad \Longrightarrow \qquad x \in A }[/math]
Z założenia [math]\displaystyle{ A \subseteq B }[/math], zatem warunek 1. jest spełniony. Przypuśćmy, że istnieje taki element [math]\displaystyle{ x }[/math], że [math]\displaystyle{ x \in B }[/math], ale [math]\displaystyle{ x \notin A }[/math]. Jeśli tak, to
- [math]\displaystyle{ | B | = | A | + 1 }[/math]
Co jest sprzeczne z założeniem, że [math]\displaystyle{ | A | = | B | }[/math].
Uwaga
Łatwo zauważyć, że wybierając z trzech warunków [math]\displaystyle{ A \subseteq B }[/math], [math]\displaystyle{ B \subseteq A }[/math] i [math]\displaystyle{ | A | = | B | }[/math] dowolne dwa, zawsze otrzymamy z nich trzeci. Oczywiście nie dotyczy to zbiorów nieskończonych. Przykładowo liczby parzyste stanowią podzbiór liczb całkowitych, liczb parzystych jest tyle samo, co liczb całkowitych[2], ale zbiór liczb całkowitych nie jest podzbiorem zbioru liczb parzystych.
Drugi sposób
Ponieważ zbiór [math]\displaystyle{ A }[/math] jest z założenia podzbiorem zbioru [math]\displaystyle{ B }[/math], to zbiór [math]\displaystyle{ B }[/math] można przedstawić w postaci sumy zbioru [math]\displaystyle{ A }[/math] i pewnego zbioru [math]\displaystyle{ C }[/math] takiego, że żaden element zbioru [math]\displaystyle{ C }[/math] nie jest elementem zbioru [math]\displaystyle{ A }[/math]. Zatem
- [math]\displaystyle{ B = A \cup C \qquad \text{i} \qquad A \cap C = \varnothing }[/math]
Ponieważ zbiory [math]\displaystyle{ A }[/math] i [math]\displaystyle{ C }[/math] są rozłączne, to wiemy, że
- [math]\displaystyle{ | A \cup C | = | A | + | C | }[/math]
Czyli
- [math]\displaystyle{ | B | = | A \cup C | = | A | + | C | }[/math]
Skąd wynika, że [math]\displaystyle{ | C | = 0 }[/math], zatem zbiór [math]\displaystyle{ C }[/math] jest zbiorem pustym i otrzymujemy natychmiast [math]\displaystyle{ B = A }[/math]. Co należało pokazać.
Uwaga (przypadek zbiorów skończonych)
Najczęściej prawdziwe jest jedynie oszacowanie [math]\displaystyle{ | A \cup C | \leqslant | A | + | C | }[/math], bo niektóre elementy mogą zostać policzone dwa razy. Elementy liczone dwukrotnie to te, które należą do iloczynu zbiorów [math]\displaystyle{ | A | }[/math] i [math]\displaystyle{ | C | }[/math], zatem od sumy [math]\displaystyle{ | A | + | C | }[/math] musimy odjąć liczbę elementów iloczynu zbiorów [math]\displaystyle{ | A | }[/math] i [math]\displaystyle{ | C | }[/math]. Co daje ogólny wzór[3]
- [math]\displaystyle{ | A \cup C | = | A | + | C | - | A \cap C | }[/math]
- [math]\displaystyle{ | A \cup C | = | A | + | C | - | A \cap C | }[/math]
□
Definicja H24
Niech elementy każdego ze zbiorów [math]\displaystyle{ A = \{ a_1, a_2, \ldots, a_r \} }[/math] oraz [math]\displaystyle{ B = \{ b_1, b_2, \ldots, b_r \} }[/math] będą różne modulo [math]\displaystyle{ m }[/math]. Powiemy, że zbiory [math]\displaystyle{ A, B }[/math] są równe modulo [math]\displaystyle{ m }[/math], jeżeli dla każdego [math]\displaystyle{ k = 1, \ldots, r }[/math] istnieje takie [math]\displaystyle{ j = 1, \ldots, r }[/math], że prawdziwa jest kongruencja [math]\displaystyle{ a_k \equiv b_j \!\! \pmod{m} }[/math].
Twierdzenie H25
Niech elementy każdego ze zbiorów [math]\displaystyle{ A = \{ a_1, a_2, \ldots, a_r \} }[/math] oraz [math]\displaystyle{ B = \{ b_1, b_2, \ldots, b_r \} }[/math] będą różne modulo [math]\displaystyle{ m }[/math]. Zbiory [math]\displaystyle{ A, B }[/math] są równe modulo [math]\displaystyle{ m }[/math] wtedy i tylko wtedy, gdy zbiory [math]\displaystyle{ A' = \{ R_m (a_1), R_m (a_2), \ldots, R_m (a_r) \} }[/math] i [math]\displaystyle{ B' = \{ R_m (b_1), R_m (b_2), \ldots, R_m (b_r) \} }[/math] są równe.
[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Ponieważ elementy każdego ze zbiorów [math]\displaystyle{ A, B }[/math] są różne modulo [math]\displaystyle{ m }[/math], to elementy zbiorów [math]\displaystyle{ A' }[/math] i [math]\displaystyle{ B' }[/math] są wszystkie różne. Czyli [math]\displaystyle{ | A' | = | B' | = r }[/math]. Ponieważ warunek
- [math]\displaystyle{ a_k \equiv b_j \!\! \pmod{m} }[/math]
oznacza, że reszty z dzielenia liczb [math]\displaystyle{ a_k }[/math] i [math]\displaystyle{ b_j }[/math] przez [math]\displaystyle{ m }[/math] są równe, to z założenia dla każdego [math]\displaystyle{ k = 1, \ldots, r }[/math] istnieje takie [math]\displaystyle{ j = 1, \ldots, r }[/math], że
- [math]\displaystyle{ R_m (a_k) = R_m (b_j) }[/math]
A to oznacza, że każdy element zbioru [math]\displaystyle{ A' }[/math] należy do zbioru [math]\displaystyle{ B' }[/math], czyli [math]\displaystyle{ A' \subseteq B' }[/math]. Wynika stąd, że [math]\displaystyle{ A' = B' }[/math] (zobacz H23). Co należało pokazać.
[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Ponieważ zbiory [math]\displaystyle{ A', B' }[/math] są równe, to zbiór [math]\displaystyle{ A' }[/math] jest podzbiorem zbioru [math]\displaystyle{ B' }[/math], czyli dla każdego elementu [math]\displaystyle{ R_m (a_k) \in A' }[/math] istnieje taki element [math]\displaystyle{ R_m (b_j) \in B' }[/math], że
- [math]\displaystyle{ R_m (a_k) = R_m (b_j) }[/math]
Ponieważ równość reszt oznacza równość modulo, zatem
- [math]\displaystyle{ a_k \equiv b_j \!\! \pmod{m} }[/math]
Wynika stąd, że dla każdego [math]\displaystyle{ k = 1, \ldots, r }[/math] istnieje takie [math]\displaystyle{ j = 1, \ldots, r }[/math], że prawdziwa jest kongruencja
- [math]\displaystyle{ a_k \equiv b_j \!\! \pmod{m} }[/math]
czyli zbiory [math]\displaystyle{ A, B }[/math] są równe modulo [math]\displaystyle{ m }[/math]. Co kończy dowód.
□
Twierdzenie H26
Niech będą dane zbiory [math]\displaystyle{ A = \{ 1, 2, \ldots, p - 1 \} }[/math], [math]\displaystyle{ B = \{ b_1, b_2, \ldots, b_{p - 1} \} }[/math], gdzie [math]\displaystyle{ p }[/math] jest liczbą pierwszą. Jeżeli wszystkie elementy zbioru [math]\displaystyle{ B }[/math] są różne modulo [math]\displaystyle{ p }[/math] i żadna z liczb [math]\displaystyle{ b_k \in B }[/math] nie jest podzielna przez [math]\displaystyle{ p }[/math], to zbiory [math]\displaystyle{ A, B, C = \{ b^{- 1}_1, b^{- 1}_2, \ldots, b^{- 1}_{p - 1} \} }[/math] są równe modulo [math]\displaystyle{ p }[/math].
Z definicji zbioru [math]\displaystyle{ A }[/math] wszystkie elementy tego zbioru są różne modulo [math]\displaystyle{ p }[/math]. Łatwo zauważamy, że
- [math]\displaystyle{ A = \{ 1, 2, \ldots, p - 1 \} = \{ R_p (1), R_p (2), \ldots, R_p (p - 1) \} = A' }[/math]
Ponieważ wszystkie liczby [math]\displaystyle{ b_k \in B }[/math], gdzie [math]\displaystyle{ k = 1, \ldots, p - 1 }[/math] są różne modulo [math]\displaystyle{ p }[/math] i nie są podzielne przez [math]\displaystyle{ p }[/math], to reszty [math]\displaystyle{ R_p (b_1), R_p (b_2), \ldots, R_p (b_{p - 1}) }[/math] są wszystkie dodatnie i różne, a ponieważ jest ich [math]\displaystyle{ p - 1 }[/math], czyli dokładnie tyle, ile jest różnych i dodatnich reszt z dzielenia przez liczbę [math]\displaystyle{ p }[/math], to zbiór tych reszt jest identyczny ze zbiorem dodatnich reszt z dzielenia przez [math]\displaystyle{ p }[/math], czyli ze zbiorem [math]\displaystyle{ A }[/math]. Zatem mamy
- [math]\displaystyle{ A = A' = \{ R_p (b_1), R_p (b_2), \ldots, R_p (b_{p - 1}) \} = B' }[/math]
Na mocy twierdzenia H25 zbiory [math]\displaystyle{ A }[/math] i [math]\displaystyle{ B }[/math] są równe modulo [math]\displaystyle{ p }[/math].
Z twierdzenia H21 wiemy, że wszystkie liczby [math]\displaystyle{ b^{- 1}_k \in C }[/math] są różne modulo [math]\displaystyle{ p }[/math]. Zauważmy, że każda z tych liczb jest względnie pierwsza z [math]\displaystyle{ p }[/math], zatem nie może być podzielna przez [math]\displaystyle{ p }[/math]. Wynika stąd, że reszty [math]\displaystyle{ R_p (b^{- 1}_1), R_p (b^{- 1}_2), \ldots, R_p (b^{- 1}_{p - 1}) }[/math] są wszystkie dodatnie i różne, a ponieważ jest ich [math]\displaystyle{ p - 1 }[/math], czyli dokładnie tyle, ile jest różnych i dodatnich reszt z dzielenia przez liczbę [math]\displaystyle{ p }[/math], to zbiór tych reszt jest identyczny ze zbiorem dodatnich reszt z dzielenia przez [math]\displaystyle{ p }[/math], czyli ze zbiorem [math]\displaystyle{ A }[/math]. Zatem mamy
- [math]\displaystyle{ A = A' = \{ R_p (b^{- 1}_1), R_p (b^{- 1}_2), \ldots, R_p (b^{- 1}_{p - 1}) \} = C' }[/math]
Na mocy twierdzenia H25 zbiory [math]\displaystyle{ A }[/math] i [math]\displaystyle{ C }[/math] są równe modulo [math]\displaystyle{ p }[/math]. Ponieważ [math]\displaystyle{ A' = B' }[/math] i [math]\displaystyle{ A' = C' }[/math], to [math]\displaystyle{ B' = C' }[/math] i ponownie na mocy twierdzenia H25 zbiory [math]\displaystyle{ B }[/math] i [math]\displaystyle{ C }[/math] są równe modulo [math]\displaystyle{ p }[/math]. Co należało pokazać.
□
Zadanie H27
Niech [math]\displaystyle{ p }[/math] będzie liczbą pierwszą nieparzystą. Pokazać, że suma [math]\displaystyle{ \sum_{k = 1}^{p - 1} {\small\frac{(p - 1) !}{k}} }[/math] jest podzielna przez [math]\displaystyle{ p }[/math].
Zauważmy najpierw, że modulo [math]\displaystyle{ p }[/math] następujące sumy są równe
- [math]\displaystyle{ \sum_{k = 1}^{p - 1} k \equiv \sum_{k = 1}^{p - 1} k^{- 1} \!\! \pmod{p} }[/math]
Istotnie, jeśli przyjmiemy w twierdzeniu H26, że zbiór [math]\displaystyle{ B = \{ 1, 2, \ldots, p - 1 \} }[/math], to zbiór [math]\displaystyle{ C }[/math] będzie zbiorem liczb, które są odwrotnościami liczb [math]\displaystyle{ 1, 2, \ldots, p - 1 }[/math] modulo [math]\displaystyle{ p }[/math] i możemy napisać
- [math]\displaystyle{ \sum_{x \in B} x \equiv \sum_{y \in C} y \!\! \pmod{p} }[/math]
bo
- gdy [math]\displaystyle{ x }[/math] przebiega kolejne wartości [math]\displaystyle{ b_k }[/math], to [math]\displaystyle{ x }[/math] przyjmuje kolejno wartości [math]\displaystyle{ 1, 2, \ldots, p - 1 }[/math]
- gdy [math]\displaystyle{ y }[/math] przebiega kolejne wartości [math]\displaystyle{ b_k^{- 1} }[/math], to [math]\displaystyle{ y }[/math] (modulo [math]\displaystyle{ p }[/math]) przyjmuje wszystkie wartości ze zbioru [math]\displaystyle{ A = \{ 1, 2, \ldots, p - 1 \} }[/math], czyli liczba [math]\displaystyle{ y }[/math] (modulo [math]\displaystyle{ p }[/math]) przyjmuje wszystkie wartości [math]\displaystyle{ 1, 2, \ldots, p - 1 }[/math], ale w innej kolejności
Ponieważ kolejność sumowania tych samych składników nie wpływa na wartość sumy, to prawdziwa jest wyżej wypisana równość sum modulo [math]\displaystyle{ p }[/math].
Zatem modulo [math]\displaystyle{ p }[/math] otrzymujemy
- [math]\displaystyle{ \sum_{k = 1}^{p - 1} {\small\frac{(p - 1) !}{k}} \equiv \sum_{k = 1}^{p - 1} (p - 1)! \cdot k^{- 1} }[/math]
- [math]\displaystyle{ \;\;\: \equiv (p - 1) ! \cdot \sum_{k = 1}^{p - 1} k^{- 1} }[/math]
- [math]\displaystyle{ \;\;\: \equiv (p - 1) ! \cdot \sum_{k = 1}^{p - 1} k }[/math]
- [math]\displaystyle{ \;\;\: \equiv (p - 1) ! \cdot {\small\frac{(p - 1) p}{2}} }[/math]
- [math]\displaystyle{ \;\;\: \equiv (p - 1) ! \cdot {\small\frac{p - 1}{2}} \cdot p }[/math]
- [math]\displaystyle{ \;\;\: \equiv 0 \!\! \pmod{p} }[/math]
Należy zauważyć, że dla liczby pierwszej nieparzystej [math]\displaystyle{ p }[/math] liczba [math]\displaystyle{ {\small\frac{p - 1}{2}} }[/math] jest liczbą całkowitą.
□
Funkcje multiplikatywne
Definicja H28
Powiemy, że funkcja [math]\displaystyle{ f(n) }[/math] określona w zbiorze liczb całkowitych dodatnich jest funkcją multiplikatywną, jeżeli [math]\displaystyle{ f(1) = 1 }[/math] i dla względnie pierwszych liczb [math]\displaystyle{ a, b }[/math] spełniony jest warunek [math]\displaystyle{ f(a b) = f (a) f (b) }[/math].
Uwaga H29
Założenie [math]\displaystyle{ f(1) = 1 }[/math] możemy równoważnie zastąpić założeniem, że funkcja [math]\displaystyle{ f(n) }[/math] nie jest tożsamościowo równa zero.
Gdyby [math]\displaystyle{ f(n) }[/math] spełniała jedynie warunek [math]\displaystyle{ f(a b) = f (a) f (b) }[/math] dla względnie pierwszych liczb [math]\displaystyle{ a, b }[/math], to mielibyśmy
- a) [math]\displaystyle{ f(n) }[/math] jest tożsamościowo równa zeru wtedy i tylko wtedy, gdy [math]\displaystyle{ f(1) = 0 }[/math]
- b) [math]\displaystyle{ f(n) }[/math] nie jest tożsamościowo równa zeru wtedy i tylko wtedy, gdy [math]\displaystyle{ f(1) = 1 }[/math]
Ponieważ [math]\displaystyle{ f(1) = f (1 \cdot 1) = f (1) f (1) }[/math], zatem [math]\displaystyle{ f(1) = 0 }[/math] lub [math]\displaystyle{ f (1) = 1 }[/math].
Jeżeli [math]\displaystyle{ f(1) = 0 }[/math], to dla dowolnego [math]\displaystyle{ n }[/math] mamy
- [math]\displaystyle{ f(n) = f (n \cdot 1) = f (n) f (1) = 0 }[/math]
Czyli [math]\displaystyle{ f(n) }[/math] jest funkcją tożsamościowo równą zero.
Jeżeli [math]\displaystyle{ f(n) }[/math] nie jest funkcją tożsamościowo równą zero, to istnieje taka liczba [math]\displaystyle{ a \in \mathbb{Z}_+ }[/math], że [math]\displaystyle{ f(a) \neq 0 }[/math]. Zatem
- [math]\displaystyle{ f(a) = f (a \cdot 1) = f (a) f (1) }[/math]
I dzieląc obie strony przez [math]\displaystyle{ f(a) \neq 0 }[/math], dostajemy [math]\displaystyle{ f(1) = 1 }[/math].
Przykład H30
Ponieważ [math]\displaystyle{ \gcd (1, c) = 1 }[/math], to [math]\displaystyle{ \gcd (n, c) }[/math] rozpatrywana jako funkcja [math]\displaystyle{ n }[/math], gdzie [math]\displaystyle{ c }[/math] jest ustaloną liczbą całkowitą, jest funkcją multiplikatywną (zobacz H8).
Twierdzenie H31
Jeżeli funkcja [math]\displaystyle{ f(n) }[/math] jest funkcją multiplikatywną, to funkcja
- [math]\displaystyle{ F(n) = \sum_{d \mid n} f (d) }[/math]
gdzie sumowanie przebiega po wszystkich dzielnikach dodatnich liczby [math]\displaystyle{ n }[/math], jest również funkcją multiplikatywną.
Ponieważ
- [math]\displaystyle{ F(1) = \sum_{d \mid 1} f (d) = f (1) = 1 }[/math]
to funkcja [math]\displaystyle{ F(n) }[/math] spełnia pierwszy warunek definicji H28.
Niech [math]\displaystyle{ a, b }[/math] będą względnie pierwszymi liczbami dodatnimi. Każdy dzielnik dodatni iloczynu [math]\displaystyle{ a b }[/math] można zapisać w postaci [math]\displaystyle{ d = d_1 d_2 }[/math], gdzie [math]\displaystyle{ d_1 \mid a }[/math], [math]\displaystyle{ \; d_2 \mid b \, }[/math] oraz [math]\displaystyle{ \, \gcd (d_1, d_2) = 1 }[/math] (zobacz H14). Niech zbiory
- [math]\displaystyle{ S_a = \{ d \in \mathbb{Z}_+ : d \mid a \} }[/math]
- [math]\displaystyle{ S_b = \{ d \in \mathbb{Z}_+ : d \mid b \} }[/math]
- [math]\displaystyle{ S_{a b} = \{ d \in \mathbb{Z}_+ : d \mid a b \} }[/math]
będą zbiorami dzielników dodatnich liczb [math]\displaystyle{ a, b }[/math] i [math]\displaystyle{ a b }[/math]. Dla przykładu
- [math]\displaystyle{ S_5 = \{ 1, 5 \} }[/math]
- [math]\displaystyle{ S_7 = \{ 1, 7 \} }[/math]
- [math]\displaystyle{ S_{35} = \{ 1, 5, 7, 35 \} }[/math]
Dla dowolnego [math]\displaystyle{ d_1 \in S_a \, }[/math] i [math]\displaystyle{ \, d_2 \in S_b }[/math] musi być [math]\displaystyle{ \gcd (d_1, d_2) = 1 }[/math], bo gdyby było [math]\displaystyle{ \gcd (d_1, d_2) = g > 1 }[/math], to
- [math]\displaystyle{ g \mid d_1 \quad \; \text{i} \quad \; d_1 \mid a \qquad \quad \Longrightarrow \qquad \quad g \mid a }[/math]
- [math]\displaystyle{ g \mid d_2 \quad \; \text{i} \quad \; d_2 \mid b \qquad \quad \Longrightarrow \qquad \quad g \mid b }[/math]
Zatem [math]\displaystyle{ g \mid \gcd (a, b) }[/math] i mielibyśmy [math]\displaystyle{ \gcd (a, b) \geqslant g > 1 }[/math], wbrew założeniu.
Przekształcając, otrzymujemy
- [math]\displaystyle{ F(a b) = \sum_{d \mid a b} f (d) }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \sum_{d \in S_{a b}} f (d) }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \underset{d_2 \in S_{b}}{\sum_{d_1 \in S_{a}}} f (d_1 d_2) }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \underset{d_2 \in S_{b}}{\sum_{d_1 \in S_{a}}} f (d_1) f (d_2) }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \sum_{d_1 \in S_{a}} f (d_1) \sum_{d_2 \in S_{b}} f (d_2) }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \sum_{d_1 \mid a} f (d_1) \sum_{d_2 \mid b} f (d_2) }[/math]
- [math]\displaystyle{ \;\;\;\;\: = F (a) F (b) }[/math]
Co należało pokazać.
□
Funkcja Eulera [math]\displaystyle{ \varphi (n) }[/math]
Definicja H32
Funkcja Eulera [math]\displaystyle{ \varphi (n) }[/math][4] jest równa ilości liczb całkowitych dodatnich nie większych od [math]\displaystyle{ n }[/math] i względnie pierwszych z [math]\displaystyle{ n }[/math].
Twierdzenie H33
Funkcja Eulera [math]\displaystyle{ \varphi (n) }[/math] jest multiplikatywna, czyli dla względnie pierwszych liczb [math]\displaystyle{ m, n }[/math] jest [math]\displaystyle{ \varphi (m n) = \varphi (m) \varphi (n) }[/math].
Niech [math]\displaystyle{ m, n }[/math] będą dodatnimi liczbami całkowitymi takimi, że [math]\displaystyle{ \gcd (m, n) = 1 }[/math]. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math], zatem nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ n > 1 }[/math]. Wypiszmy w tabeli wszystkie liczby od [math]\displaystyle{ 1 }[/math] do [math]\displaystyle{ m n }[/math].
[math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ k }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ m }[/math] [math]\displaystyle{ m + 1 }[/math] [math]\displaystyle{ m + 2 }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ m + k }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ 2 m }[/math] [math]\displaystyle{ 2 m + 1 }[/math] [math]\displaystyle{ 2 m + 2 }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ 2 m + k }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ 3 m }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ (n - 1) m + 1 }[/math] [math]\displaystyle{ (n - 1) m + 2 }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ (n - 1) m + k }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ n m }[/math]
1. Natychmiast widzimy, że w pierwszym wierszu mamy [math]\displaystyle{ \varphi (m) }[/math] liczb względnie pierwszych z [math]\displaystyle{ m }[/math]. Tak samo jest w każdym kolejnym wierszu, bo (zobacz H5)
- [math]\displaystyle{ \gcd (r m + k, m) = \gcd (k, m) }[/math]
Zatem mamy dokładnie [math]\displaystyle{ \varphi (m) }[/math] kolumn liczb względnie pierwszych z [math]\displaystyle{ m }[/math].
2. Załóżmy, że liczba [math]\displaystyle{ k }[/math] jest jedną z liczb względnie pierwszych z [math]\displaystyle{ m }[/math], czyli [math]\displaystyle{ \gcd (k, m) = 1 }[/math]. Przy tym założeniu [math]\displaystyle{ k }[/math]-ta kolumna (pokazana w tabeli) jest kolumną liczb względnie pierwszych z [math]\displaystyle{ m }[/math].
3. Zauważmy, że reszty z dzielenia liczb wypisanych w [math]\displaystyle{ k }[/math]-tej kolumnie przez [math]\displaystyle{ n }[/math] są wszystkie różne. Gdyby tak nie było, to dla pewnych [math]\displaystyle{ i, j }[/math], gdzie [math]\displaystyle{ 0 \leqslant i, j \leqslant n - 1 }[/math], różnica liczb [math]\displaystyle{ i m + k }[/math] oraz [math]\displaystyle{ j m + k }[/math] byłaby podzielna przez [math]\displaystyle{ n }[/math]. Mielibyśmy
- [math]\displaystyle{ n \mid ((i m + k) - (j m + k)) }[/math]
Skąd wynika natychmiast
- [math]\displaystyle{ n \mid (i - j) m }[/math]
Ponieważ założyliśmy, że [math]\displaystyle{ \gcd (n, m) = 1 }[/math], to musi być [math]\displaystyle{ n \mid (i - j) }[/math] (zobacz C75), ale
- [math]\displaystyle{ 0 \leqslant | i - j | \leqslant n - 1 }[/math]
Czyli [math]\displaystyle{ n }[/math] może dzielić [math]\displaystyle{ i - j }[/math] tylko w przypadku, gdy [math]\displaystyle{ i = j }[/math]. Wbrew naszemu przypuszczeniu, że istnieją różne liczby dające takie same reszty przy dzieleniu przez [math]\displaystyle{ n }[/math].
4. Ponieważ w [math]\displaystyle{ k }[/math]-tej kolumnie znajduje się dokładnie [math]\displaystyle{ n }[/math] liczb i reszty z dzielenia tych liczb przez [math]\displaystyle{ n }[/math] są wszystkie różne, to reszty te tworzą zbiór [math]\displaystyle{ S = \{ 0, 1, \ldots, n - 1 \} }[/math]. Wynika stąd, że liczby wypisane w [math]\displaystyle{ k }[/math]-tej kolumnie mogą być zapisane w postaci
- [math]\displaystyle{ a_r = b_r \cdot n + r }[/math]
gdzie [math]\displaystyle{ r = 0, 1, \ldots, n - 1 }[/math] i [math]\displaystyle{ b_r \in \mathbb{Z} }[/math].
Zauważmy, że następujące ilości liczb są sobie równe
- ilość liczb w [math]\displaystyle{ k }[/math]-tej kolumnie względnie pierwszych z [math]\displaystyle{ n }[/math]
- ilość liczb [math]\displaystyle{ r }[/math] względnie pierwszych z [math]\displaystyle{ n }[/math], gdzie [math]\displaystyle{ r = 0, \ldots, n - 1 }[/math], bo [math]\displaystyle{ \gcd (b_r \cdot n + r, n) = \gcd (r, n) }[/math]
- ilość liczb [math]\displaystyle{ r }[/math] względnie pierwszych z [math]\displaystyle{ n }[/math], gdzie [math]\displaystyle{ r = 1, \ldots, n }[/math], bo [math]\displaystyle{ \gcd (n, n) = \gcd (0, n) = | n | > 1 }[/math]
Ostatnia ilość liczb jest równa [math]\displaystyle{ \varphi (n) }[/math], co wynika wprost z definicji funkcji [math]\displaystyle{ \varphi (n) }[/math].
5. Zbierając: mamy w wypisanej tabeli dokładnie [math]\displaystyle{ \varphi (m) \varphi (n) }[/math] liczb [math]\displaystyle{ u \in [1, m n] }[/math], dla których jednocześnie jest
- [math]\displaystyle{ \gcd (u, m) = 1 \quad \text{i} \quad \gcd (u, n) = 1 }[/math]
Z twierdzenia H6 wynika, że w tabeli jest dokładnie [math]\displaystyle{ \varphi (m) \varphi (n) }[/math] liczb [math]\displaystyle{ u \in [1, m n] }[/math], dla których jest
- [math]\displaystyle{ \gcd (u, m n) = 1 }[/math]
Zatem [math]\displaystyle{ \varphi (m n) = \varphi (m) \varphi (n) }[/math]. Co należało pokazać.
□
Twierdzenie H34
Dla dowolnej liczby całkowitej dodatniej [math]\displaystyle{ n }[/math] jest
- [math]\displaystyle{ \varphi (n) = n \cdot \prod_{p|n} \left( 1 - {\small\frac{1}{p}} \right) }[/math]
gdzie iloczyn obliczamy po wszystkich liczbach pierwszych [math]\displaystyle{ p }[/math], będących dzielnikami liczby [math]\displaystyle{ n }[/math].
Ponieważ wszystkie liczby naturalne mniejsze od liczby pierwszej [math]\displaystyle{ p }[/math] są jednocześnie pierwsze względem [math]\displaystyle{ p }[/math], to [math]\displaystyle{ \varphi (p) = p - 1 }[/math].
Równie łatwo znajdujemy wartość funkcji [math]\displaystyle{ \varphi (n) }[/math] w przypadku gdy [math]\displaystyle{ n }[/math] jest potęgą liczby pierwszej [math]\displaystyle{ n = p^k }[/math]. Wystarczy zauważyć, że w ciągu kolejnych liczb
- [math]\displaystyle{ 1, 2, 3, 4, \ldots, p^k - 1, p^k }[/math]
jedynymi liczbami, które nie są pierwsze względem [math]\displaystyle{ p^k }[/math], są te, które dzielą się przez [math]\displaystyle{ p }[/math] i jest ich [math]\displaystyle{ p^{k - 1} }[/math], co widać natychmiast po ich bezpośrednim wypisaniu
- [math]\displaystyle{ 1 \cdot p, 2 \cdot p, 3 \cdot p, \ldots, (p^{k - 1} - 1) \cdot p, p^{k - 1} \cdot p }[/math]
Zatem
- [math]\displaystyle{ \varphi (p^k) = p^k - p^{k - 1} = p^k \left( 1 - {\small\frac{1}{p}} \right) }[/math]
Ponieważ [math]\displaystyle{ \varphi (n) }[/math] jest funkcją multiplikatywną, to dla [math]\displaystyle{ n = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s }[/math] otrzymujemy
- [math]\displaystyle{ \varphi (n) = \prod^s_{k = 1} \varphi (p^{\alpha_k}_k) }[/math]
- [math]\displaystyle{ \;\;\,\, = \prod^s_{k = 1} p^{\alpha_k}_k \left( 1 - {\small\frac{1}{p_k}} \right) }[/math]
- [math]\displaystyle{ \;\;\,\, = \left[ \prod^s_{k = 1} p^{\alpha_k}_k \right] \cdot \left[ \prod^s_{k = 1} \left( 1 - {\small\frac{1}{p_k}} \right) \right] }[/math]
- [math]\displaystyle{ \;\;\,\, = n \cdot \prod^s_{k = 1} \left( 1 - {\small\frac{1}{p_k}} \right) }[/math]
- [math]\displaystyle{ \;\;\,\, = n \cdot \prod_{p|n} \left( 1 - {\small\frac{1}{p}} \right) }[/math]
Co należało pokazać.
□
Twierdzenie H35
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Jeżeli [math]\displaystyle{ q }[/math] jest liczbą pierwszą, to
- [math]\displaystyle{ \varphi (q n) = \left\{ \begin{array}{rl} (q - 1) \varphi (n) & \quad \text{gdy} \quad q \nmid n \\ q \varphi (n) & \quad \text{gdy} \quad q \mid n \\ \end{array} \right. }[/math]
Jeżeli [math]\displaystyle{ q \nmid m }[/math], to [math]\displaystyle{ \gcd (q, m) = 1 }[/math], zatem [math]\displaystyle{ \varphi (q m) = \varphi (q) \varphi (m) = (q - 1) \varphi (m) }[/math]. Jeżeli [math]\displaystyle{ q \mid m }[/math], to liczby [math]\displaystyle{ m }[/math] oraz [math]\displaystyle{ q m }[/math] mają taki sam zbiór dzielników pierwszych, zatem
- [math]\displaystyle{ \varphi (q m) = q m \prod_{p \mid q m} \left( 1 - {\small\frac{1}{p}} \right) = q \cdot \left[ m \prod_{p \mid m} \left( 1 - {\small\frac{1}{p}} \right) \right] = q \varphi (m) }[/math]
Co należało pokazać.
□
Zadanie H36
Niech [math]\displaystyle{ q \in \mathbb{P} }[/math] i [math]\displaystyle{ a, b, m, n \in \mathbb{Z}_+ }[/math]. Pokazać, że
- [math]\displaystyle{ \varphi (q^{a + b}) = q^a \varphi (q^b) }[/math]
- [math]\displaystyle{ \varphi (n^m) = n^{m - 1} \varphi (n) }[/math]
Punkt 1.
- [math]\displaystyle{ \varphi (q^{a + b}) = (q - 1) q^{a + b - 1} = q^a \cdot (q - 1) q^{b - 1} = q^a \varphi (q^b) }[/math]
Punkt 2.
Niech [math]\displaystyle{ n = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s }[/math]
- [math]\displaystyle{ \varphi (n^m) = \varphi (p^{m \alpha_1}_1 \cdot \ldots \cdot p^{m \alpha_s}_s) }[/math]
- [math]\displaystyle{ \, = \varphi (p^{m \alpha_1}_1) \cdot \ldots \cdot \varphi (p^{m \alpha_s}_s) }[/math]
- [math]\displaystyle{ \, = \varphi (p^{(m - 1) \alpha_1 + \alpha_1}_1) \cdot \ldots \cdot \varphi (p^{(m - 1) \alpha_s + \alpha_s}_s) }[/math]
- [math]\displaystyle{ \, = p^{(m - 1) \alpha_1}_1 \varphi (p^{\alpha_1}_1) \cdot \ldots \cdot p^{(m - 1) \alpha_s}_s \varphi (p^{\alpha_s}_s) }[/math]
- [math]\displaystyle{ \, = p^{(m - 1) \alpha_1}_1 \cdot \ldots \cdot p^{(m - 1) \alpha_s}_s \cdot \varphi (p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s) }[/math]
- [math]\displaystyle{ \, = n^{m - 1} \varphi (n) }[/math]
Co należało pokazać.
□
Twierdzenie H37
Niech [math]\displaystyle{ m, n \in \mathbb{Z}_+ }[/math]. Jeżeli [math]\displaystyle{ m \mid n }[/math], to [math]\displaystyle{ \varphi (m) \mid \varphi (n) }[/math].
Niech [math]\displaystyle{ n = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s }[/math]. Ponieważ założyliśmy, że [math]\displaystyle{ m \mid n }[/math], to [math]\displaystyle{ m }[/math] musi być postaci [math]\displaystyle{ m = p^{\beta_1}_1 \cdot \ldots \cdot p^{\beta_s}_s }[/math], gdzie [math]\displaystyle{ 0 \leqslant \beta_i \leqslant \alpha_i }[/math], dla [math]\displaystyle{ i = 1, \ldots, s }[/math]. Łatwo zauważamy, że
- jeżeli [math]\displaystyle{ \beta_i = 0 }[/math], to [math]\displaystyle{ \varphi (p^{\beta_i}_i) = 1 }[/math] i dzieli [math]\displaystyle{ \varphi (p^{\alpha_i}_i) }[/math]
- jeżeli [math]\displaystyle{ 1 \leqslant \beta_i \leqslant \alpha_i }[/math], to [math]\displaystyle{ (p_i - 1) p_i^{\beta_i - 1} \mid (p_i - 1) p_i^{\alpha_i - 1} }[/math], zatem [math]\displaystyle{ \varphi (p^{\beta_i}_i) \mid \varphi (p^{\alpha_i}_i) }[/math]
Skąd natychmiast wynika, że [math]\displaystyle{ \varphi (p^{\beta_1}_1) \cdot \ldots \cdot \varphi (p^{\beta_s}_s) }[/math] dzieli [math]\displaystyle{ \varphi (p^{\alpha_1}_1) \cdot \ldots \cdot \varphi (p^{\alpha_s}_s) }[/math], czyli [math]\displaystyle{ \varphi (m) \mid \varphi (n) }[/math].
Zauważmy, że twierdzenie odwrotne nie jest prawdziwe, bo [math]\displaystyle{ \varphi (7) \mid \varphi (19) }[/math], ale [math]\displaystyle{ 7 \nmid 19 }[/math].
□
Zadanie H38
Dla [math]\displaystyle{ n \geqslant 3 }[/math] wartości [math]\displaystyle{ \varphi (n) }[/math] są liczbami parzystymi.
Jeżeli liczba [math]\displaystyle{ n \geqslant 3 }[/math] jest podzielna przez liczbę pierwszą nieparzystą [math]\displaystyle{ p }[/math], zaś [math]\displaystyle{ k }[/math] jest wykładnikiem, z jakim [math]\displaystyle{ p }[/math] wchodzi do rozwinięcia [math]\displaystyle{ n }[/math] na czynniki pierwsze, to
- [math]\displaystyle{ \varphi (n) = \varphi \left( p^k \cdot {\small\frac{n}{p^k}} \right) = (p - 1) p^{k - 1} \cdot \varphi \left( {\small\frac{n}{p^k}} \right) }[/math]
zatem [math]\displaystyle{ \varphi (n) }[/math] jest liczbą parzystą, ponieważ [math]\displaystyle{ p - 1 }[/math] jest liczbą parzystą.
Jeżeli żadna liczba nieparzysta nie dzieli [math]\displaystyle{ n }[/math], to liczba [math]\displaystyle{ n }[/math] jest postaci [math]\displaystyle{ n = 2^a }[/math] i [math]\displaystyle{ \varphi (n) = 2^{a - 1} }[/math], ale z założenia [math]\displaystyle{ n \geqslant 3 }[/math], zatem [math]\displaystyle{ a \geqslant 2 }[/math] i [math]\displaystyle{ \varphi (n) }[/math] jest liczbą parzystą.
□
Twierdzenie H39
Jeżeli [math]\displaystyle{ n }[/math] jest liczbą złożoną, to [math]\displaystyle{ \varphi (n) \leqslant n - \sqrt{n} }[/math].
Pierwszy sposób
Niech [math]\displaystyle{ n = a b }[/math], gdzie [math]\displaystyle{ 1 < a \leqslant b < n }[/math]. Liczby [math]\displaystyle{ 1 \cdot a, 2 \cdot a, 3 \cdot a, \ldots, b \cdot a }[/math] są nie większe od [math]\displaystyle{ n }[/math] i nie są względnie pierwsze z [math]\displaystyle{ n }[/math], zatem
- [math]\displaystyle{ \varphi (n) \leqslant n - b }[/math]
Ponieważ [math]\displaystyle{ b \geqslant a }[/math], to [math]\displaystyle{ b^2 \geqslant a b = n }[/math] i [math]\displaystyle{ b \geqslant \sqrt{n} }[/math]. Wynika stąd, że
- [math]\displaystyle{ \varphi (n) \leqslant n - b \leqslant n - \sqrt{n} }[/math]
Drugi sposób
Niech [math]\displaystyle{ q }[/math] oznacza najmniejszy dzielnik pierwszy liczby złożonej [math]\displaystyle{ n }[/math], zatem [math]\displaystyle{ q^2 \leqslant n }[/math], czyli [math]\displaystyle{ q \leqslant \sqrt{n} }[/math], a stąd [math]\displaystyle{ {\small\frac{n}{q}} \geqslant \sqrt{n} }[/math] i
- [math]\displaystyle{ \varphi (n) = n \cdot \prod_{p|n} \left( 1 - {\small\frac{1}{p}} \right) \leqslant n \left( 1 - {\small\frac{1}{q}} \right) = n - {\small\frac{n}{q}} \leqslant n - \sqrt{n} }[/math]
Co należało pokazać.
□
Twierdzenie H40
Dla [math]\displaystyle{ n \geqslant 1 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \varphi (n) > {\small\frac{\sqrt{n}}{2}} }[/math].
Dla [math]\displaystyle{ k \geqslant 3 }[/math] jest
- [math]\displaystyle{ \left( 1 - {\small\frac{1}{k}} \right)^2 > {\small\frac{1}{k}} }[/math]
Wynika stąd, że jeżeli [math]\displaystyle{ m \geqslant 3 }[/math] jest liczbą nieparzystą, to
- [math]\displaystyle{ \varphi (m)^2 = m^2 \prod_{p|m} \left( 1 - {\small\frac{1}{p}} \right)^2 > m^2 \prod_{p|m} {\small\frac{1}{p}} \geqslant m }[/math]
bo
- [math]\displaystyle{ \prod_{p|m} p \leqslant m }[/math]
Czyli dla nieparzystych liczb [math]\displaystyle{ m \geqslant 3 }[/math] mamy
- [math]\displaystyle{ \varphi (m) > \sqrt{m} > {\small\frac{\sqrt{m}}{2}} }[/math]
Jeżeli [math]\displaystyle{ d = 2^a }[/math], gdzie [math]\displaystyle{ a \geqslant 1 }[/math], to
- [math]\displaystyle{ \varphi (d) = \varphi (2^a) = 2^{a - 1} > {\small\frac{\sqrt{2^a}}{2}} = {\small\frac{\sqrt{d}}{2}} }[/math]
W przypadku ogólnym, gdy [math]\displaystyle{ n }[/math] jest iloczynem liczby nieparzystej [math]\displaystyle{ m \geqslant 3 }[/math] i potęgi liczby [math]\displaystyle{ 2 }[/math], dostajemy
- [math]\displaystyle{ \varphi (n) = \varphi (2^a m) = \varphi (2^a) \varphi (m) > {\small\frac{\sqrt{2^a}}{2}} \cdot \sqrt{m} = {\small\frac{\sqrt{2^a m}}{2}} = {\small\frac{\sqrt{n}}{2}} }[/math]
Oczywiście nierówność [math]\displaystyle{ \varphi (n) > {\small\frac{\sqrt{n}}{2}} }[/math] jest również prawdziwa dla [math]\displaystyle{ n = 1 }[/math]. Co należało pokazać.
□
Zadanie H41
Pokazać, że dla [math]\displaystyle{ n \geqslant 7 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \varphi (n) > \sqrt{n} }[/math].
Zauważmy, że
- [math]\displaystyle{ n - 1 > \sqrt{n} \qquad \qquad \;\, \text{dla} \; n \geqslant 3 }[/math]
- [math]\displaystyle{ n - 1 > \sqrt{2 n} \qquad \qquad \text{dla} \; n \geqslant 4 }[/math]
Zatem dla liczby pierwszej [math]\displaystyle{ p }[/math] i [math]\displaystyle{ k \geqslant 1 }[/math] jest
- [math]\displaystyle{ \varphi (p^k) = (p - 1) p^{k - 1} > \sqrt{p} \cdot p^{k - 1} = p^{k - \tfrac{1}{2}} \geqslant p^{\tfrac{k}{2}} = \sqrt{p^k} \qquad \qquad \qquad \qquad \quad \; \text{dla} \;\: p \geqslant 3 }[/math]
- [math]\displaystyle{ \varphi (p^k) = (p - 1) p^{k - 1} > \sqrt{2 p} \cdot p^{k - 1} = \sqrt{2} \cdot p^{k - \tfrac{1}{2}} \geqslant \sqrt{2} \cdot p^{\tfrac{k}{2}} = \sqrt{2 p^k} \qquad \qquad \text{dla} \;\, p \geqslant 5 }[/math]
1. Przypadek, gdy [math]\displaystyle{ \boldsymbol{n \geqslant 3} }[/math] jest liczbą nieparzystą
Liczba [math]\displaystyle{ n }[/math] jest iloczynem czynników pierwszych nieparzystych, zatem
- [math]\displaystyle{ \varphi (n) = \varphi (p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s) = \varphi (p^{\alpha_1}_1) \cdot \ldots \cdot \varphi (p^{\alpha_s}_s) > \sqrt{p^{\alpha_1}_1} \cdot \ldots \cdot \sqrt{p^{\alpha_s}_s} = \sqrt{n} }[/math]
2. Przypadek, gdy [math]\displaystyle{ \boldsymbol{n = 2^a m} \; }[/math] i [math]\displaystyle{ \; \boldsymbol{q \mid m ,} \; }[/math] gdzie [math]\displaystyle{ \; \boldsymbol{q \geqslant 5} }[/math]
Z założenia [math]\displaystyle{ n = 2^a m = 2^a q^b r }[/math], gdzie [math]\displaystyle{ r \geqslant 1 }[/math] jest liczbą nieparzystą. Zauważmy, że [math]\displaystyle{ \varphi (r) \geqslant \sqrt{r} }[/math], bo może być [math]\displaystyle{ r = 1 }[/math].
- [math]\displaystyle{ \varphi (n) = \varphi (2^a q^b r) }[/math]
- [math]\displaystyle{ \;\;\,\, = \varphi (2^a) \varphi (q^b) \varphi (r) }[/math]
- [math]\displaystyle{ \;\;\,\, > 2^{a - 1} \sqrt{2 q^b} \sqrt{r} }[/math]
- [math]\displaystyle{ \;\;\,\, = 2^{a - \tfrac{1}{2}} \sqrt{q^b} \sqrt{r} }[/math]
- [math]\displaystyle{ \;\;\,\, \geqslant 2^{\tfrac{a}{2}} \sqrt{q^b r} }[/math]
- [math]\displaystyle{ \;\;\,\, = \sqrt{2^a q^b r} }[/math]
- [math]\displaystyle{ \;\;\,\, = \sqrt{n} }[/math]
3. Przypadek, gdy [math]\displaystyle{ \boldsymbol{n = 2^a m} \; }[/math] i [math]\displaystyle{ \; \boldsymbol{q \nmid m ,} \; }[/math] gdzie [math]\displaystyle{ \; \boldsymbol{q \geqslant 5} }[/math]
Jeżeli żadna liczba pierwsza [math]\displaystyle{ q \geqslant 5 }[/math] nie dzieli [math]\displaystyle{ m }[/math], to możliwe są tylko dwie sytuacje: [math]\displaystyle{ n = 2^a \, }[/math] i [math]\displaystyle{ \, n = 2^a 3^b }[/math].
3a. Przypadek, gdy [math]\displaystyle{ \boldsymbol{n = 2^a} }[/math]
- [math]\displaystyle{ \varphi (n) = \varphi (2^a) = 2^{a - 1} > \sqrt{2^a} = \sqrt{n} \qquad \qquad \;\, \text{dla} \; a \geqslant 3 }[/math]
Twierdzenie nie jest prawdziwe dla [math]\displaystyle{ n = 2 \, }[/math] i [math]\displaystyle{ \, n = 4 \,\, }[/math] (gdy [math]\displaystyle{ a = 1 \, }[/math] lub [math]\displaystyle{ \, a = 2 }[/math]).
3b. Przypadek, gdy [math]\displaystyle{ \boldsymbol{n = 2^a 3^b} }[/math]
- [math]\displaystyle{ \varphi (n) = \varphi (2^a 3^b) = \varphi (2^a) \varphi (3^b) = 2^{a - 1} \cdot 2 \cdot 3^{b - 1} = 2^a 3^{b - 1} = \sqrt{2^a 3^b} \cdot {\small\frac{\sqrt{2^a 3^b}}{3}} > \sqrt{2^a 3^b} }[/math]
Ostatnia nierówność jest prawdziwa, o ile [math]\displaystyle{ \sqrt{2^a 3^b} > 3 }[/math], czyli gdy [math]\displaystyle{ 2^a 3^b > 9 }[/math], co ma miejsce, gdy [math]\displaystyle{ a \geqslant 2 }[/math] lub [math]\displaystyle{ b \geqslant 2 }[/math].
Twierdzenie nie jest prawdziwe dla [math]\displaystyle{ n = 6 \; }[/math] (gdy [math]\displaystyle{ a = 1 \, }[/math] i [math]\displaystyle{ \, b = 1 }[/math]).
Zbierając uzyskane wyniki, otrzymujemy: oszacowanie [math]\displaystyle{ \varphi (n) > \sqrt{n} }[/math] nie jest prawdziwe dla [math]\displaystyle{ n = 1, 2, 4, 6 }[/math]. Co należało pokazać.
□
Zadanie H42
Pokazać, że dla [math]\displaystyle{ n \geqslant 2 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \varphi (n) > {\small\frac{n}{3 \log n}} }[/math]. Korzystając z tego wyniku, pokazać, że [math]\displaystyle{ \varphi (n) > n^{2 / 3} }[/math] dla [math]\displaystyle{ n \geqslant 43 }[/math] oraz że [math]\displaystyle{ \varphi (n) > n^{3 / 4} }[/math] dla [math]\displaystyle{ n \geqslant 211 }[/math].
Niech [math]\displaystyle{ n = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s }[/math], a [math]\displaystyle{ n' = q_1 \cdot \ldots \cdot q_s }[/math] oznacza liczbę, będącą iloczynem dokładnie tych samych czynników pierwszych, jakie występują w liczbie [math]\displaystyle{ n }[/math], natomiast [math]\displaystyle{ n^{\!\ast} = p_1 \cdot \ldots \cdot p_s }[/math] oznacza liczbę, będącą iloczynem dokładnie tej samej ilości czynników pierwszych, przy czym [math]\displaystyle{ p_i }[/math] oznacza teraz [math]\displaystyle{ i }[/math]-tą liczbę pierwszą.
Ponieważ
- [math]\displaystyle{ {\small\frac{\varphi (n)}{n}} = \prod_{p \mid n} \left( 1 - {\small\frac{1}{p}} \right) }[/math]
to
- [math]\displaystyle{ {\small\frac{\varphi (n)}{n}} = {\small\frac{\varphi (n')}{n'}} \geqslant {\small\frac{\varphi (n^{\!\ast})}{n^{\!\ast}}} = \prod^s_{i = 1} \left( 1 - {\small\frac{1}{p_i}} \right) \geqslant \prod^{p_s}_{k = 2} \left( 1 - {\small\frac{1}{k}} \right) = {\small\frac{1}{p_s}} }[/math]
Ostatnia równość wynika z prostego wzoru
- [math]\displaystyle{ \prod^m_{k = 2} \left( 1 - {\small\frac{1}{k}} \right) = {\small\frac{1}{2}} \cdot {\small\frac{2}{3}} \cdot {\small\frac{3}{4}} \cdot \ldots \cdot {\small\frac{m - 2}{m - 1}} \cdot {\small\frac{m - 1}{m}} = {\small\frac{1}{m}} }[/math]
Musimy oszacować wartość liczby [math]\displaystyle{ p_s }[/math]. Z twierdzenia B31 wynika, że dla [math]\displaystyle{ m \geqslant 2 }[/math] jest [math]\displaystyle{ P(m) \geqslant 2^{m / 2} }[/math], gdzie funkcja [math]\displaystyle{ P(m) }[/math] jest równa iloczynowi wszystkich liczb pierwszych nie większych od [math]\displaystyle{ m }[/math]. Zatem dla [math]\displaystyle{ p_s \geqslant 2 }[/math] jest
- [math]\displaystyle{ n^{\!\ast} = p_1 \cdot \ldots \cdot p_s = P (p_s) \geqslant 2^{p_s / 2} }[/math]
Logarytmując, otrzymujemy
- [math]\displaystyle{ p_s \leqslant {\small\frac{2 \log n^{\!\ast}}{\log 2}} }[/math]
Ponieważ [math]\displaystyle{ n \geqslant n' \geqslant n^{\!\ast} }[/math], to
- [math]\displaystyle{ {\small\frac{\varphi (n)}{n}} \geqslant {\small\frac{1}{p_s}} \geqslant {\small\frac{\log 2}{2 \log n^{\!\ast}}} \geqslant {\small\frac{\log 2}{2 \log n}} > {\small\frac{1}{3 \log n}} }[/math]
Ostatecznie otrzymujemy
- [math]\displaystyle{ \varphi (n) > {\small\frac{n}{3 \log n}} }[/math]
Co należało pokazać.
Rozwiązując drugą część zadania, wystarczy znaleźć, dla jakich [math]\displaystyle{ n }[/math] prawdziwa jest nierówność
- [math]\displaystyle{ {\small\frac{n}{3 \log n}} > n^{2 / 3} }[/math]
Czyli
- [math]\displaystyle{ \log n < {\small\frac{1}{3}} n^{1 / 3} }[/math]
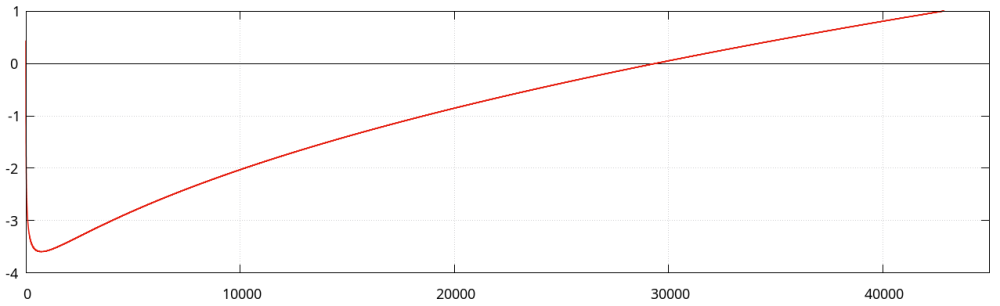
Wiemy (zobacz A38), że dla dowolnego [math]\displaystyle{ a \in \mathbb{Z}_+ }[/math] istnieje takie [math]\displaystyle{ n_0 }[/math], że dla każdego [math]\displaystyle{ n > n_0 }[/math] jest [math]\displaystyle{ \log n < n^{1 / a} }[/math]. Zatem dla odpowiednio dużych [math]\displaystyle{ n }[/math] z pewnością będzie [math]\displaystyle{ \log n < {\small\frac{1}{3}} n^{1 / 3} }[/math]. Zamieszczony niżej obrazek przedstawia wykres funkcji [math]\displaystyle{ f(n) = {\small\frac{1}{3}} n^{1 / 3} - \log n }[/math]
Widoczne na wykresie miejsce zerowe funkcji [math]\displaystyle{ f(n) }[/math] znajdujemy, wpisując w PARI/GP polecenie
solve(n = 20000, 40000, 1/3 * n^(1/3) - log(n))
Otrzymujemy
- [math]\displaystyle{ n = 29409.96 \ldots }[/math]
Zatem [math]\displaystyle{ {\small\frac{n}{3 \log n}} > n^{2 / 3} \; }[/math] dla [math]\displaystyle{ \; n > 29500 }[/math]
Poleceniem
for(n = 1, 29500, if( eulerphi(n) <= n^(2/3), print(n) ))
sprawdzamy, że oszacowanie [math]\displaystyle{ \varphi (n) > n^{2 / 3} }[/math] jest prawdziwe dla [math]\displaystyle{ n \geqslant 43 }[/math].
Postępując analogicznie jak wyżej, znajdujemy, dla jakich [math]\displaystyle{ n }[/math] prawdziwa jest nierówność
- [math]\displaystyle{ {\small\frac{n}{3 \log n}} > n^{3 / 4} }[/math]
Czyli
- [math]\displaystyle{ \log n < {\small\frac{1}{3}} n^{1 / 4} }[/math]
Wpisując w PARI/GP polecenie
solve(n = 10^3, 10^7, 1/3 * n^(1/4) - log(n))
otrzymujemy
- [math]\displaystyle{ n = 4447862.68 \ldots }[/math]
Zatem [math]\displaystyle{ {\small\frac{n}{3 \log n}} > n^{3 / 4} \; }[/math] dla [math]\displaystyle{ \; n > 4.45 \cdot 10^6 }[/math]
Poleceniem
for(n = 1, 5 * 10^6, if( eulerphi(n) <= n^(3/4), print(n) ))
sprawdzamy, że oszacowanie [math]\displaystyle{ \varphi (n) > n^{3 / 4} }[/math] jest prawdziwe dla [math]\displaystyle{ n \geqslant 211 }[/math]. Co należało pokazać.
□
Twierdzenie H43
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Liczba [math]\displaystyle{ n }[/math] jest liczbą pierwszą wtedy i tylko wtedy, gdy [math]\displaystyle{ \varphi (n) = n - 1 }[/math].
Dla liczb złożonych [math]\displaystyle{ n \geqslant 4 }[/math] nigdy nie będzie [math]\displaystyle{ \varphi (n) = n - 1 }[/math], bo
- [math]\displaystyle{ \varphi (n) \leqslant n - \sqrt{n} \leqslant n - 2 }[/math]
Dla [math]\displaystyle{ n = 1, 2, 3 }[/math] sprawdzamy bezpośrednio: [math]\displaystyle{ \varphi (1) = 1 \neq 1 - 1 }[/math], [math]\displaystyle{ \varphi (2) = 1 = 2 - 1 }[/math], [math]\displaystyle{ \varphi (3) = 2 = 3 - 1 }[/math]. Co kończy dowód.
□
Twierdzenie H44
Dla dowolnej liczby całkowitej dodatniej [math]\displaystyle{ n }[/math] jest
- [math]\displaystyle{ n = \sum_{d \mid n} \varphi (d) = \sum_{d \mid n} \varphi \left( {\small\frac{n}{d}} \right) }[/math]
gdzie sumowanie przebiega po wszystkich dzielnikach dodatnich liczby [math]\displaystyle{ n }[/math].
Ponieważ [math]\displaystyle{ \varphi (n) }[/math] jest funkcją multiplikatywną, to funkcja
- [math]\displaystyle{ F(n) = \sum_{d \mid n} \varphi (d) }[/math]
też jest funkcją multiplikatywną (zobacz H31). Łatwo sprawdzamy, że twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math]. Niech [math]\displaystyle{ n > 1 }[/math]. Jeżeli [math]\displaystyle{ n = p^{\alpha} }[/math] jest potęgą liczby pierwszej, to otrzymujemy
- [math]\displaystyle{ F (p^{\alpha}) = \sum_{d \mid p^{\alpha}} \varphi (d) }[/math]
- [math]\displaystyle{ = \varphi (1) + \varphi (p) + \varphi (p^2) + \ldots + \varphi (p^{\alpha}) = }[/math]
- [math]\displaystyle{ = 1 + (p - 1) + p (p - 1) + \ldots + p^{\alpha - 1} (p - 1) = }[/math]
- [math]\displaystyle{ = 1 + (p - 1) + (p^2 - p) + \ldots + (p^{\alpha} - p^{\alpha - 1}) }[/math]
- [math]\displaystyle{ = p^{\alpha} }[/math]
Jeżeli [math]\displaystyle{ n }[/math] jest postaci [math]\displaystyle{ n = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s }[/math], to
- [math]\displaystyle{ F(n) = F (p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s) = }[/math]
- [math]\displaystyle{ \;\;\;\, = F (p^{\alpha_1}_1) \cdot \ldots \cdot F (p^{\alpha_s}_s) = }[/math]
- [math]\displaystyle{ \;\;\;\, = p^{\alpha_1}_1 \cdot \ldots \cdot p^{\alpha_s}_s }[/math]
- [math]\displaystyle{ \;\;\;\, = n }[/math]
Niech [math]\displaystyle{ 1 < d_1 < d_2 < \ldots < n }[/math] będą dzielnikami liczby [math]\displaystyle{ n }[/math]. Zauważmy, że kiedy [math]\displaystyle{ d }[/math] przebiega zbiór dzielników [math]\displaystyle{ \{ 1, d_1, d_2, \ldots, n \} }[/math], to [math]\displaystyle{ e = {\small\frac{n}{d}} }[/math] przebiega wszystkie te liczby tylko w odwrotnej kolejności. Zatem
- [math]\displaystyle{ \sum_{d \mid n} \varphi (d) = \sum_{d \mid n} \varphi \left( {\small\frac{n}{d}} \right) }[/math]
Co należało pokazać.
□
Zadanie H45
Niech [math]\displaystyle{ n \geqslant 2 }[/math]. Pokazać, że suma liczb całkowitych dodatnich nie większych od [math]\displaystyle{ n }[/math] i względnie pierwszych z [math]\displaystyle{ n }[/math] jest równa [math]\displaystyle{ {\small\frac{1}{2}} n \varphi (n) }[/math].
Łatwo sprawdzamy, że wzór jest prawdziwy dla [math]\displaystyle{ n = 2 }[/math] i odtąd będziemy przyjmowali, że [math]\displaystyle{ n \geqslant 3 }[/math]. Zatem wartości [math]\displaystyle{ \varphi (n) }[/math] są liczbami parzystymi i niech [math]\displaystyle{ c = {\small\frac{1}{2}} \varphi (n) }[/math]. Zauważmy, że jeżeli liczba [math]\displaystyle{ a }[/math] jest względnie pierwsza z [math]\displaystyle{ n }[/math], to liczba [math]\displaystyle{ n - a }[/math] jest również względnie pierwsza z [math]\displaystyle{ n }[/math], bo [math]\displaystyle{ \gcd (a, n) = \gcd (n - a, n) }[/math]. Wypiszmy wszystkie liczby całkowite dodatnie nie większe od [math]\displaystyle{ n }[/math] i względnie pierwsze z [math]\displaystyle{ n }[/math] w kolejności rosnącej, a pod spodem w kolejności malejącej
[math]\displaystyle{ 1 }[/math] [math]\displaystyle{ a_2 }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ a_c }[/math] [math]\displaystyle{ n - a_c }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ n - a_2 }[/math] [math]\displaystyle{ n - 1 }[/math] [math]\displaystyle{ n - 1 }[/math] [math]\displaystyle{ n - a_2 }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ n - a_c }[/math] [math]\displaystyle{ a_c }[/math] [math]\displaystyle{ … }[/math] [math]\displaystyle{ a_2 }[/math] [math]\displaystyle{ 1 }[/math]
Suma liczb w każdej kolumnie jest równa [math]\displaystyle{ n }[/math]. Ponieważ ilość liczb względnie pierwszych z [math]\displaystyle{ n }[/math] jest równa [math]\displaystyle{ \varphi (n) }[/math], to podwojona suma liczb całkowitych nie większych od [math]\displaystyle{ n }[/math] i pierwszych względem [math]\displaystyle{ n }[/math] wynosi [math]\displaystyle{ n \varphi (n) }[/math]. Co należało pokazać.
□
Zadanie H46
Pokazać, że dla liczb naturalnych nieparzystych [math]\displaystyle{ n \geqslant 5 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \varphi (n) > \pi (n) }[/math].
1. Jeżeli [math]\displaystyle{ n \geqslant 5 }[/math] jest liczbą pierwszą, to liczbami pierwszymi względem [math]\displaystyle{ n }[/math] są wszystkie liczby pierwsze mniejsze od [math]\displaystyle{ n }[/math] oraz liczby [math]\displaystyle{ 1, 4 }[/math]. Zatem
- [math]\displaystyle{ \varphi (n) \geqslant \pi (n) - 1 + 2 > \pi (n) }[/math].
2. Jeżeli [math]\displaystyle{ n = p^a }[/math], gdzie [math]\displaystyle{ a \geqslant 2 }[/math], jest potęgą liczby pierwszej nieparzystej, to [math]\displaystyle{ n \geqslant 9 }[/math] i liczbami pierwszymi względem [math]\displaystyle{ n }[/math] są wszystkie liczby pierwsze nie większe od [math]\displaystyle{ n }[/math] (oprócz liczby [math]\displaystyle{ p }[/math]) oraz liczby [math]\displaystyle{ 1, 4, 8 }[/math]. Zatem
- [math]\displaystyle{ \varphi (n) \geqslant \pi (n) - 1 + 3 > \pi (n) }[/math].
3. Jeżeli [math]\displaystyle{ n }[/math] ma więcej niż jeden dzielnik pierwszy nieparzysty, to [math]\displaystyle{ n = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s }[/math], gdzie [math]\displaystyle{ s \geqslant 2 }[/math]. Zauważmy, że
- [math]\displaystyle{ n = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s \geqslant q_1 \cdot \ldots \cdot q_s \geqslant 3 \cdot 5^{s - 1} > 2^{2 s - 1} }[/math]
Liczbami pierwszymi względem [math]\displaystyle{ n }[/math] są wszystkie liczby pierwsze nie większe od [math]\displaystyle{ n }[/math] (oprócz liczb [math]\displaystyle{ q_1, \ldots, q_s }[/math]) oraz liczby [math]\displaystyle{ 1, 2^2, 2^3, \ldots, 2^{2 s - 1} }[/math]. Zatem
- [math]\displaystyle{ \varphi (n) \geqslant \pi (n) - s + 2 s - 1 = \pi (n) + s - 1 > \pi (n) }[/math]
Co należało pokazać.
□
Zadanie H47
Pokazać, że dla liczb naturalnych [math]\displaystyle{ n \geqslant 91 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ \varphi (n) > \pi (n) }[/math].
Ponieważ [math]\displaystyle{ p_{2 s} > 1 }[/math] i [math]\displaystyle{ p_{2 s} \geqslant p_{s + 1} }[/math], to z zadania A41 natychmiast wynika nierówność
- [math]\displaystyle{ p_1 p_2 \cdot \ldots \cdot p_s > p_{s + 1} p_{2 s} }[/math]
która jest prawdziwa dla [math]\displaystyle{ n \geqslant 4 }[/math].
Pokażemy najpierw, że dla każdej liczby naturalnej mającej nie mniej niż cztery dzielniki pierwsze nierówność [math]\displaystyle{ \varphi (n) > \pi (n) }[/math] jest zawsze prawdziwa.
Przez [math]\displaystyle{ p_1, p_2, \ldots, p_k, \ldots }[/math] oznaczymy kolejne liczby pierwsze. Niech [math]\displaystyle{ n \geqslant 2 }[/math] będzie liczbą naturalną i [math]\displaystyle{ n = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s }[/math], gdzie [math]\displaystyle{ q_i }[/math] oznaczają dowolne (nie muszą być kolejne) liczby pierwsze.
Wśród kolejnych [math]\displaystyle{ 2 s }[/math] liczb pierwszych znajduje się przynajmniej [math]\displaystyle{ s }[/math] liczb pierwszych różnych od każdej z liczb [math]\displaystyle{ q_1, \ldots, q_s }[/math]. Jeśli oznaczymy te liczby (w rosnącej kolejności) przez [math]\displaystyle{ r_1, \ldots, r_s }[/math], to łatwo zauważymy, że prawdziwe są dla nich następujące oszacowania
- dla najmniejszej liczby [math]\displaystyle{ r_1 \leqslant p_{s + 1} }[/math]
- dla wszystkich liczb [math]\displaystyle{ r_j \leqslant p_{2 s} }[/math] dla [math]\displaystyle{ j = 1, \ldots, s }[/math].
Korzystając z wypisanej na początku dowodu nierówności, dla [math]\displaystyle{ s \geqslant 4 }[/math] mamy
- [math]\displaystyle{ n = q^{\alpha_1}_1 \cdot \ldots \cdot q^{\alpha_s}_s \geqslant q_1 \cdot \ldots \cdot q_s \geqslant p_1 \cdot \ldots \cdot p_s > p_{s + 1} p_{2 s} \geqslant r_1 \cdot r_j }[/math]
gdzie [math]\displaystyle{ j = 1, \ldots, s }[/math].
Wynika stąd, że jeśli [math]\displaystyle{ s \geqslant 4 }[/math], to liczbami pierwszymi względem [math]\displaystyle{ n }[/math] są wszystkie liczby pierwsze nie większe od [math]\displaystyle{ n }[/math] (oprócz liczb pierwszych [math]\displaystyle{ q_1, \ldots, q_s }[/math]) oraz liczby [math]\displaystyle{ 1 }[/math] i [math]\displaystyle{ r_1 r_j }[/math], gdzie [math]\displaystyle{ j = 1, \ldots, s }[/math]. Zatem
- [math]\displaystyle{ \varphi (n) \geqslant \pi (n) - s + s + 1> \pi (n) }[/math]
Co mieliśmy pokazać.
Uwzględniając rezultat pokazany w zadaniu H46, pozostaje sprawdzić przypadki gdy [math]\displaystyle{ n = 2^a }[/math], [math]\displaystyle{ n = 2^a p^b }[/math], [math]\displaystyle{ n = 2^a p^b q^c }[/math], gdzie [math]\displaystyle{ a, b, c \in \mathbb{Z}_+ }[/math].
1. Niech [math]\displaystyle{ n = 2^a }[/math]. Jeśli [math]\displaystyle{ n \geqslant 16 }[/math], to liczbami pierwszymi względem [math]\displaystyle{ n }[/math] są wszystkie liczby pierwsze nie większe od [math]\displaystyle{ n }[/math] (oprócz liczby [math]\displaystyle{ 2 }[/math]) oraz liczby [math]\displaystyle{ 1, 9, 15 }[/math]. Zatem
- [math]\displaystyle{ \varphi (n) \geqslant \pi (n) - 1 + 3 > \pi (n) }[/math]
2. Niech [math]\displaystyle{ n = 2^a p^b }[/math], zaś [math]\displaystyle{ r }[/math] będzie najmniejszą liczbą pierwszą nieparzystą różną od [math]\displaystyle{ p }[/math]. Oczywiście [math]\displaystyle{ r \in \{ 3, 5 \} }[/math] i jeśli tylko [math]\displaystyle{ n > 5^3 = 125 }[/math], to liczbami pierwszymi względem [math]\displaystyle{ n }[/math] są wszystkie liczby pierwsze nie większe od [math]\displaystyle{ n }[/math] (oprócz liczb pierwszych [math]\displaystyle{ 2 }[/math] i [math]\displaystyle{ p }[/math]) oraz liczby [math]\displaystyle{ 1, r^2, r^3 }[/math]. Zatem
- [math]\displaystyle{ \varphi (n) \geqslant \pi (n) - 2 + 3 > \pi (n) }[/math]
3. Niech [math]\displaystyle{ n = 2^a p^b q^c }[/math], zaś [math]\displaystyle{ r }[/math] będzie najmniejszą liczbą pierwszą nieparzystą różną od [math]\displaystyle{ p }[/math] oraz różną od [math]\displaystyle{ q }[/math]. Oczywiście [math]\displaystyle{ r \in \{ 3, 5, 7 \} }[/math] i jeśli [math]\displaystyle{ n > 7^4 = 2401 }[/math], to liczbami pierwszymi względem [math]\displaystyle{ n }[/math] są wszystkie liczby pierwsze nie większe od [math]\displaystyle{ n }[/math] (oprócz liczb pierwszych [math]\displaystyle{ 2 }[/math], [math]\displaystyle{ p }[/math] i [math]\displaystyle{ q }[/math]) oraz liczby [math]\displaystyle{ 1, r^2, r^3, r^4 }[/math]. Zatem
- [math]\displaystyle{ \varphi (n) \geqslant \pi (n) - 3 + 4 > \pi (n) }[/math]
Zbierając: pozostaje sprawdzić bezpośrednio przypadki, gdy [math]\displaystyle{ n }[/math] jest liczbą parzystą i [math]\displaystyle{ n \leqslant 2401 }[/math]. W GP/PARI wystarczy napisać polecenie
for(n = 1, 2500, if( eulerphi(n) <= primepi(n), print(n) ))
Nierówność [math]\displaystyle{ \varphi (n) > \pi (n) }[/math] nie jest prawdziwa dla [math]\displaystyle{ n \in \{ 2, 3, 4, 6, 8, 10, 12, 14, 18, 20, 24, 30, 42, 60, 90 \} }[/math]. Co kończy dowód.
□
Zadanie H48
Pokazać, że [math]\displaystyle{ \varphi (n) = 2^a }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ n = 2^b q_1 \cdot \ldots \cdot q_s }[/math], gdzie [math]\displaystyle{ q_1, \ldots, q_s }[/math] są liczbami pierwszymi Fermata: [math]\displaystyle{ 3, 5, 17, 257, 65537 }[/math].
W przypadku, gdy [math]\displaystyle{ 2 \mid n }[/math], łatwo zauważamy, że liczba [math]\displaystyle{ 2 }[/math] może występować w dowolnej potędze, bo [math]\displaystyle{ \varphi (2^b) = 2^{b - 1} }[/math].
W przypadku, gdy [math]\displaystyle{ p \mid n }[/math], gdzie [math]\displaystyle{ p }[/math] jest liczbą pierwszą nieparzystą, mamy [math]\displaystyle{ \varphi (p^k) = (p - 1) p^{k - 1} }[/math] i równie łatwo zauważmy, że musi być [math]\displaystyle{ k = 1 }[/math], a liczba [math]\displaystyle{ p - 1 }[/math] musi być potęgą liczby [math]\displaystyle{ 2 }[/math]. Zatem liczba pierwsza [math]\displaystyle{ p }[/math] musi być postaci [math]\displaystyle{ p = 2^t + 1 }[/math], co jest możliwe tylko wtedy, gdy [math]\displaystyle{ t }[/math] jest potęgą liczby [math]\displaystyle{ 2 }[/math] (zobacz C49), czyli [math]\displaystyle{ p }[/math] musi być liczbą pierwszą Fermata. Co należało pokazać.
□
Zadanie H49
Pokazać, że funkcja Eulera spełnia warunek [math]\displaystyle{ \varphi (n) = {\small\frac{n}{2}} }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ n = 2^k }[/math].
Zauważmy, że [math]\displaystyle{ n }[/math] musi być liczbą parzystą, zatem [math]\displaystyle{ n = 2^k m }[/math], gdzie [math]\displaystyle{ m }[/math] jest liczbą nieparzystą. Otrzymujemy
- [math]\displaystyle{ \varphi (n) = \varphi (2^k m) = \varphi (2^k) \varphi (m) = 2^{k - 1} \varphi (m) = {\small\frac{2^k m}{2}} \cdot {\small\frac{\varphi (m)}{m}} = {\small\frac{n}{2}} \cdot {\small\frac{\varphi (m)}{m}} }[/math]
ale [math]\displaystyle{ {\small\frac{\varphi (m)}{m}} = 1 }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ m = 1 }[/math]. Co należało pokazać.
□
Zadanie H50
Pokazać, że funkcja Eulera spełnia warunek [math]\displaystyle{ \varphi (n) = {\small\frac{n}{2}} - 1 }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ n = 2 q }[/math], gdzie [math]\displaystyle{ q \geqslant 3 }[/math] jest liczbą pierwszą.
Oczywiście [math]\displaystyle{ n }[/math] musi być liczbą parzystą, zatem [math]\displaystyle{ n = 2^k m }[/math], gdzie [math]\displaystyle{ m }[/math] jest liczbą nieparzystą. Możemy teraz zapisać warunek [math]\displaystyle{ \varphi (n) = {\small\frac{n}{2}} - 1 }[/math] w postaci
- [math]\displaystyle{ \varphi (n) = \varphi (2^k m) = \varphi (2^k) \varphi (m) = 2^{k - 1} \varphi (m) = 2^{k - 1} m - 1 }[/math]
Ponieważ [math]\displaystyle{ \varphi (n) }[/math] dla [math]\displaystyle{ n \geqslant 3 }[/math] jest liczbą parzystą (zobacz H38), to nie może być [math]\displaystyle{ k \geqslant 2 }[/math], bo strony równania miałyby różną parzystość. Zatem musi być [math]\displaystyle{ n = 2 m }[/math], gdzie [math]\displaystyle{ m }[/math] jest liczbą nieparzystą
- [math]\displaystyle{ \varphi (n) = \varphi (2 m) = \varphi (2) \varphi (m) = \varphi (m) = m - 1 }[/math]
Z twierdzenia H43 wynika natychmiast, że [math]\displaystyle{ m }[/math] musi być liczbą pierwszą. Ponieważ najmniejszymi liczbami, dla których warunek [math]\displaystyle{ \varphi (n) = {\small\frac{n}{2}} - 1 }[/math] jest spełniony, są [math]\displaystyle{ n = 6, 10, 14, \ldots }[/math], to musi być [math]\displaystyle{ m \geqslant 3 }[/math]. Co należało pokazać.
□
Przypisy