Liczby losowe – metoda odwracania dystrybuanty
Gęstość prawdopodobieństwa i dystrybuanta
Rozważmy funkcję [math]\displaystyle{ f(x) }[/math] określoną na [math]\displaystyle{ \mathbb{R} }[/math], nieujemną i całkowalną. Powiemy, że [math]\displaystyle{ f(x) }[/math] jest gęstością rozkładu prawdopodobieństwa [math]\displaystyle{ P }[/math], jeżeli dla dowolnego zbioru [math]\displaystyle{ A \subset \mathbb{R} }[/math] jest
- [math]\displaystyle{ P(A)=\int\limits_A f(x)dx }[/math]
gdzie [math]\displaystyle{ P(A) }[/math] jest prawdopodobieństwem przypisanym zbiorowi [math]\displaystyle{ A }[/math].
Z powyższej definicji wynika natychmiast, że funkcja [math]\displaystyle{ f(x) }[/math] musi być unormowana:
- [math]\displaystyle{ \int^{+ \infty}_{- \infty} f(x)dx = 1 }[/math]
Dystrybuantą gęstości prawdopodobieństwa [math]\displaystyle{ f(x) }[/math] nazywamy funkcję:
- [math]\displaystyle{ F(x) = \int^x_{- \infty} f(t)dt }[/math]
Prawdopodobieństwo, że zmienna losowa przyjmie wartość należącą do przedziału [math]\displaystyle{ [a, b] }[/math] wynosi:
- [math]\displaystyle{ P(a \leqslant x \leqslant b) = \int^b_a f(t)dt = F (b) - F (a) }[/math]
Rozkład równomierny [math]\displaystyle{ U(a, b) }[/math]
Rozkładem równomiernym (prostokątnym) nazywamy rozkład prawdopodobieństwa, dla którego gęstość prawdopodobieństwa [math]\displaystyle{ f(x) }[/math] jest równa:
- [math]\displaystyle{ f(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt a\\ \frac{1}{b - a} & \text{dla} & x \in [a, b]\\ 0 & \text{dla} & x \gt b \end{array} \right. }[/math]
Tak zdefiniowany rozkład równomierny będziemy oznaczali [math]\displaystyle{ U(a, b) }[/math]. Dystrybuanta tego rozkładu jest określona wzorem:
- [math]\displaystyle{ F(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt a\\ \frac{x - a}{b - a} & \text{dla} & x \in [a, b]\\ 1 & \text{dla} & x \gt b \end{array} \right. }[/math]
Zbiór liczb należących do rozkładu równomiernego [math]\displaystyle{ U(0, 1) }[/math] możemy łatwo uzyskać. Przykładowo w arkuszu kalkulacyjnym LibreOffice dostępna jest funkcja [math]\displaystyle{ \text{LOS}() }[/math], która zwraca przypadkową liczbę z przedziału [math]\displaystyle{ [0, 1) }[/math]. Pisząc makro mamy dostępną analogiczną funkcję [math]\displaystyle{ \text{Rnd}() }[/math]. Liczby losowe generowane przez programy komputerowe nazywamy liczbami pseudolosowymi.
Dysponując liczbami losowymi [math]\displaystyle{ u_i }[/math] należącymi do rozkładu równomiernego [math]\displaystyle{ U(0, 1) }[/math] możemy łatwo uzyskać liczby losowe [math]\displaystyle{ x_i }[/math] należące do rozkładu równomiernego [math]\displaystyle{ U(a, b) }[/math]. Wystarczy skorzystać ze wzoru:
- [math]\displaystyle{ x_i = a + (b - a) u_i }[/math]
Przykład histogramu rozkładu równomiernego [math]\displaystyle{ U (0, 1) }[/math] Czytelnik znajdzie w arkuszu kalkulacyjnym: Równomierny
Dystrybuanta odwrotna
Dystrybuanta odwrotna [math]\displaystyle{ F^{- 1} (u) }[/math] przekształca zmienną losową [math]\displaystyle{ U(0,1) }[/math] o rozkładzie równomiernym w zmienną losową [math]\displaystyle{ X }[/math] o rozkładzie [math]\displaystyle{ f(x) }[/math], któremu odpowiada dystrybuanta [math]\displaystyle{ F(x) }[/math]:
- [math]\displaystyle{ X = F^{- 1} (U) }[/math]
Punktowi [math]\displaystyle{ u \in [0, 1] }[/math] zostaje przypisany punkt [math]\displaystyle{ x = F^{- 1} (u) \in [a, b] }[/math]. Granice przedziału [math]\displaystyle{ [a, b] }[/math] mogą być w ogólności niewłaściwe.
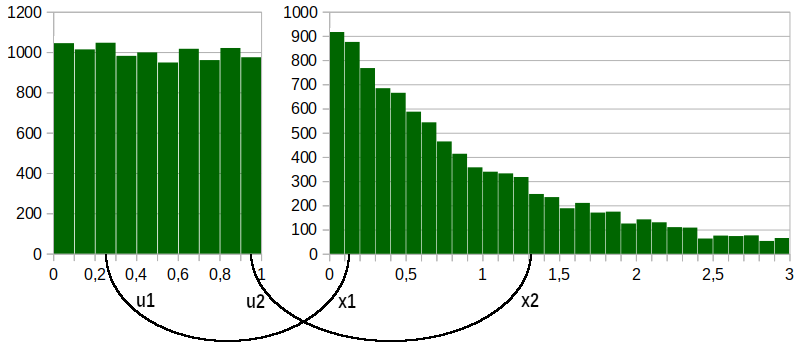
Przykładowo dystrybuanta odwrotna zmiennej losowej o rozkładzie [math]\displaystyle{ f(x) = e^{- x} }[/math], gdzie [math]\displaystyle{ x \in [0, + \infty) }[/math] jest równa [math]\displaystyle{ F^{- 1} (x) = - \log (1 - x) }[/math]. Zatem wylosowana liczba [math]\displaystyle{ u_1 = 0.25 \in [0.2, 0.3) }[/math] z rozkładu [math]\displaystyle{ U[0, 1] }[/math] przejdzie w punkt
- [math]\displaystyle{ x_1 = - \log (1 - u_1) = 0.125 \in [0.1, 0.2) }[/math]
z rozkładu wykładniczego [math]\displaystyle{ f(x) = e^{- x} }[/math]. Podobnie liczba [math]\displaystyle{ u_2 = 0.95 \in [0.9, 0.1) }[/math] przejdzie w punkt
- [math]\displaystyle{ x_2 = - \log (1 - u_2) = 1.301 \in [1.3, 1.4) }[/math]
Czyli liczby te trafią do innych podprzedziałów, będą zliczane w innych miejscach i utworzą inny histogram. Tak jak to pokazano na rysunku:
Przykłady histogramów rozkładu równomiernego [math]\displaystyle{ U (0, 1) }[/math] i wykładniczego [math]\displaystyle{ f(x) = e^{-x} }[/math] (wygenerowanego z rozkładu równomiernego) Czytelnik znajdzie w arkuszach kalkulacyjnych:
Przedstawimy teraz kilka przykładów zastosowania tego faktu.
Rozkład jednomianowy [math]\displaystyle{ f(x) = (n + 1)x^n }[/math]
Rozważmy funkcję gęstości prawdopodobieństwa postaci:
- [math]\displaystyle{ f(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt 0\\ (n + 1) x^n & \text{dla} & x \in [0, 1]\\ 0 & \text{dla} & x \gt 1 \end{array} \right. }[/math]
Łatwo sprawdzamy, że
- [math]\displaystyle{ \int^{+ \infty}_{- \infty} f(t)dt = \int^1_0 f (t) dt = (n + 1) \int^1_0 t^n dt = t^{n + 1} \biggr|^1_0 = 1 }[/math]
Dystrybuanta
- [math]\displaystyle{ F(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt 0\\ x^{n + 1} & \text{dla} & x \in [0, 1]\\ 1 & \text{dla} & x \gt 1 \end{array} \right. }[/math]
Dystrybuanta odwrotna
- [math]\displaystyle{ F^{- 1} (x) = \sqrt[n + 1]{x} }[/math]
Jeżeli [math]\displaystyle{ u_i \in U (0, 1) }[/math], to liczby [math]\displaystyle{ x_i = \sqrt[n + 1]{u_i} \in [0, 1] }[/math] będą należały do rozkładu [math]\displaystyle{ f(x) = (n + 1) x^n }[/math] określonego na odcinku [math]\displaystyle{ [0, 1] }[/math].
Krzywa opisująca histogram
Załóżmy, że:
- wygenerowaliśmy [math]\displaystyle{ N }[/math] liczb losowych [math]\displaystyle{ u_i \in U (0, 1) }[/math]
- obliczyliśmy wartości [math]\displaystyle{ x_i = \sqrt[n + 1]{u_i} }[/math]
- podzieliliśmy przedział zmienności liczb [math]\displaystyle{ x_i }[/math] (w naszym przypadku [math]\displaystyle{ [0, 1] }[/math]) na podprzedziały każdy o ustalonej szerokości [math]\displaystyle{ \Delta }[/math]
- pogrupowaliśmy [math]\displaystyle{ x_i }[/math] w poszczególnych podprzedziałach i wyznaczyliśmy ilość [math]\displaystyle{ g(k) }[/math] liczb [math]\displaystyle{ x_i }[/math] w [math]\displaystyle{ k }[/math]-tym podprzedziale
Jakiej zależności [math]\displaystyle{ g(k) }[/math] należy się spodziewać? Prawdopodobieństwo tego, że zmienna losowa przyjmie wartość z [math]\displaystyle{ k }[/math]-tego przedziału o szerokości [math]\displaystyle{ \Delta }[/math] wyraża się wzorem:
- [math]\displaystyle{ P((k - 1) \Delta \leqslant x_i \leqslant k \Delta) = \int^{k \Delta}_{(k - 1) \Delta} f(t)dt \approx f (k \Delta) \cdot \Delta }[/math]
Przybliżenie jest tym lepsze, im mniejsza jest szerokość przedziałów [math]\displaystyle{ \Delta }[/math]. Należy zatem oczekiwać zależności:
- [math]\displaystyle{ g(k) = N \cdot f (k \Delta) \cdot \Delta = N \Delta \cdot f (k \Delta) }[/math]
Dla rozkładu jednomianowego na odcinku [math]\displaystyle{ [0, 1] }[/math] otrzymamy:
- [math]\displaystyle{ g(k) = N \cdot f (k \Delta) \cdot \Delta = N \cdot (n + 1) \cdot (k \Delta)^n \cdot \Delta = (n + 1) N \cdot \Delta^{n + 1} \cdot k^n }[/math]
Przykład dla [math]\displaystyle{ n = 1 }[/math] i [math]\displaystyle{ n = 2 }[/math]
Niech [math]\displaystyle{ N = 10^5 }[/math], [math]\displaystyle{ \Delta = 0.01 }[/math]
dla [math]\displaystyle{ n = 1 }[/math]: [math]\displaystyle{ g(k) = 20 k }[/math]
dla [math]\displaystyle{ n = 2 }[/math]: [math]\displaystyle{ g(k) = 0.3 k^2 }[/math]
Przykłady histogramów rozkładu jednomianowego [math]\displaystyle{ f(x) = (n + 1)x^n }[/math], dla [math]\displaystyle{ n = 1, 2 }[/math] Czytelnik znajdzie w arkuszach kalkulacyjnych:
Jednomianowy (n = 1)
Jednomianowy (n = 2)
Rozkład postaci [math]\displaystyle{ f(x) = \tfrac{3}{2} \sqrt{x} }[/math]
Rozważmy następującą funkcję gęstości prawdopodobieństwa:
- [math]\displaystyle{ f(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt 0\\ \frac{3}{2} \sqrt{x} & \text{dla} & x \in [0, 1]\\ 0 & \text{dla} & x \gt 1 \end{array} \right. }[/math]
Czytelnik łatwo sprawdzi, że:
- [math]\displaystyle{ \int^{+ \infty}_{- \infty} f(t)dt = 1 }[/math]
Dystrybuanta
- [math]\displaystyle{ F(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt 0\\ x^{3 / 2} & \text{dla} & x \in [0, 1]\\ 1 & \text{dla} & x \gt 1 \end{array} \right. }[/math]
Dystrybuanta odwrotna
- [math]\displaystyle{ F^{- 1} (x) = x^{2 / 3} }[/math]
Jeżeli [math]\displaystyle{ u_i \in U (0, 1) }[/math], to liczby [math]\displaystyle{ x_i = (u_i)^{2 / 3} }[/math] będą należały do rozkładu [math]\displaystyle{ f(x) = \tfrac{3}{2} \sqrt{x} }[/math] określonego na odcinku [math]\displaystyle{ [0, 1] }[/math].
Krzywa opisująca histogram
- [math]\displaystyle{ g(k) = N \cdot f (k \Delta) \cdot \Delta = N \cdot \frac{3}{2} \cdot \sqrt{k \Delta} \cdot \Delta = \frac{3}{2} \cdot N \Delta^{3 / 2} \cdot \sqrt{k} }[/math]
Dla [math]\displaystyle{ N = 10^5 }[/math], [math]\displaystyle{ \Delta = 0.01 }[/math] otrzymujemy: [math]\displaystyle{ g(k) = 150 \sqrt{k} }[/math]
Przykład histogramu rozkładu postaci [math]\displaystyle{ f (x) = \tfrac{3}{2} \sqrt{x} }[/math] Czytelnik znajdzie w arkuszu kalkulacyjnym: Pierwiastek
Rozkład postaci [math]\displaystyle{ f(x) = \tfrac{1}{2 \sqrt{ax}} }[/math]
Dla [math]\displaystyle{ a \gt 0 }[/math] określamy następującą funkcję gęstości prawdopodobieństwa:
- [math]\displaystyle{ f(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \leqslant 0\\ \frac{1}{2 \sqrt{ax}} & \text{dla} & x \in (0, a]\\ 0 & \text{dla} & x \gt a \end{array} \right. }[/math]
Czytelnik łatwo sprawdzi, że:
- [math]\displaystyle{ \int^{+ \infty}_{- \infty} f(t)dt = 1 }[/math]
Dystrybuanta
- [math]\displaystyle{ F(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt 0\\ \sqrt{\frac{x}{a}} & \text{dla} & x \in [0, a]\\ 1 & \text{dla} & x \gt a \end{array} \right. }[/math]
Dystrybuanta odwrotna
- [math]\displaystyle{ F^{- 1} (x) = ax^2 }[/math]
Jeżeli [math]\displaystyle{ u_i \in U (0, 1) }[/math], to liczby [math]\displaystyle{ x_i = au^2_i \in [0, a] }[/math] będą należały do rozkładu [math]\displaystyle{ f(x) = \tfrac{1}{2 \sqrt{ax}} }[/math] określonego na odcinku [math]\displaystyle{ (0, a] }[/math].
Krzywa opisująca histogram
- [math]\displaystyle{ g(k) = N \cdot f (k \Delta) \cdot \Delta = N \cdot \frac{1}{2\sqrt{ak \Delta}} \cdot \Delta = \frac{N \sqrt{\Delta}}{2 \sqrt{a}} \cdot \frac{1}{\sqrt{k}} }[/math]
Dla [math]\displaystyle{ a = 25 }[/math], [math]\displaystyle{ N = 10^5 }[/math], [math]\displaystyle{ \Delta = 0.25 }[/math] otrzymujemy: [math]\displaystyle{ g(k) = \tfrac{5000}{\sqrt{k}} }[/math]
Przykład histogramu rozkładu postaci [math]\displaystyle{ f (x) = \tfrac{1}{10 \sqrt{x}} }[/math] określonego na odcinku [math]\displaystyle{ (0, 25] }[/math] Czytelnik znajdzie w arkuszu kalkulacyjnym: Odwrotność pierwiastka
Rozkład wykładniczy [math]\displaystyle{ f(x) = \lambda e^{- \lambda x} }[/math]
Dla rozkładu wykładniczego funkcja gęstości prawdopodobieństwa jest określona następująco:
- [math]\displaystyle{ f(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt 0\\ \lambda e^{- \lambda x} & \text{dla} & x \geqslant 0 \end{array} \right. }[/math]
gdzie [math]\displaystyle{ \lambda \gt 0 }[/math].
Dystrybuanta
- [math]\displaystyle{ F(x) = \left\{ \begin{array}{lll} 0 & \text{dla} & x \lt 0\\ 1 - e^{- \lambda x} & \text{dla} & x \geqslant 0 \end{array} \right. }[/math]
Dystrybuanta odwrotna
- [math]\displaystyle{ F^{- 1} (x) = - \frac{1}{\lambda} \cdot \log (1 - x) }[/math]
Jeżeli [math]\displaystyle{ u_i \in U (0, 1) }[/math], to liczby [math]\displaystyle{ x_i = - \frac{1}{\lambda} \cdot \log (1 - u_i) }[/math] będą należały do rozkładu wykładniczego [math]\displaystyle{ f(x) = \lambda e^{- \lambda x} }[/math] określonego na półprostej [math]\displaystyle{ [0, +\infty) }[/math].
Krzywa opisująca histogram
- [math]\displaystyle{ g(k) = N \cdot \lambda e^{- \lambda \cdot k \Delta} \cdot \Delta = N \Delta \cdot \exp (- (\lambda \Delta) \cdot k) }[/math]
Dla [math]\displaystyle{ \lambda = 1 }[/math] oraz [math]\displaystyle{ N = 10^5 }[/math], [math]\displaystyle{ \Delta = 0.1 }[/math] otrzymujemy: [math]\displaystyle{ g(k) = 10000 \cdot e^{- 0.1 \cdot k} }[/math]
Przykład histogramu rozkładu wykładniczego [math]\displaystyle{ f(x) = e^{- x} }[/math] Czytelnik znajdzie w arkuszu kalkulacyjnym: Wykładniczy
Rozkład normalny [math]\displaystyle{ N (\mu, \sigma^2) }[/math]
Rozkładem normalnym nazywamy rozkład, dla którego funkcja gęstości prawdopodobieństwa ma postać:
- [math]\displaystyle{ f(x) = \frac{1}{\sigma \sqrt{2 \pi}} \cdot \exp \left( - \frac{(x - \mu)^2}{2 \sigma^2} \right) }[/math]
gdzie [math]\displaystyle{ \mu \in \mathbb{R} }[/math] i [math]\displaystyle{ \sigma \gt 0 }[/math].
Dystrybuanta
- [math]\displaystyle{ F(x) = \int^x_{- \infty} f (t) dt = \frac{1}{\sqrt{\pi}} \int^{\frac{x - \mu}{\sigma \sqrt{2}}}_{- \infty} e^{-u^2} du = \frac{1}{\sqrt{\pi}} \int^0_{- \infty} e^{- u^2} du + \frac{1}{\sqrt{\pi}} \int^{\frac{x - \mu}{\sigma \sqrt{2}}}_0 e^{- u^2} du }[/math]
Ponieważ
- [math]\displaystyle{ \frac{1}{\sqrt{\pi}} \int^0_{- \infty} e^{- u^2} du = \frac{1}{2} }[/math]
to
- [math]\displaystyle{ F(x) = \frac{1}{2} \left( 1 + \text{erf}\left( \frac{x - \mu}{\sigma \sqrt{2}} \right) \right) }[/math]
Funkcję [math]\displaystyle{ \text{erf}(x) }[/math] nazywamy funkcją błędu Gaussa i jest to funkcja nieelementarna:
- [math]\displaystyle{ \text{erf}(x) = \frac{2}{\sqrt{\pi}} \int^x_0 e^{- t^2} dt }[/math]
Łatwo można pokazać, że [math]\displaystyle{ \text{erf}(x) }[/math] jest funkcją nieparzystą:
- [math]\displaystyle{ \text{erf}(-x) = - \text{erf}(x) }[/math]
W arkuszu LibreOffice [math]\displaystyle{ \text{erf}(x) }[/math] jest dostępna pod nazwą FUNKCJA.BŁ.DOKŁ(). Dostępna jest też komplementarna funkcja błędu [math]\displaystyle{ \text{erfc}(x) = 1 - \text{erf}(x) }[/math] pod nazwą KOMP.FUNKCJA.BŁ.DOKŁ(). Funkcja odwrotna funkcji [math]\displaystyle{ \text{erf}(x) }[/math] również nie jest elementarna. Dlatego uzyskanie liczb [math]\displaystyle{ x_i \in N (\mu, \sigma^2) }[/math] na bazie liczb [math]\displaystyle{ u_i \in U (0, 1) }[/math] wymaga nieco innego podejścia.
Metoda Boxa - Mullera
Zamiast jednej zmiennej losowej o standardowym rozkładzie normalnym [math]\displaystyle{ N(0, 1) }[/math], rozważmy dwie niezależne zmienne losowe o takim rozkładzie. Funkcja gęstości prawdopodobieństwa dla takiej pary niezależnych zmiennych losowych będzie iloczynem gęstości prawdopodobieństwa tych funkcji:
- [math]\displaystyle{ f(x, y) = f (x) f (y) = \frac{1}{\sqrt{2 \pi}} e^{- x^2 / 2} \cdot \frac{1}{\sqrt{2 \pi}} e^{- x^2 / 2} = \frac{1}{2 \pi} e^{- (x^2 + y^2) / 2} }[/math]
Przechodząc do współrzędnych biegunowych
- [math]\displaystyle{ \left\{ \begin{array}{l} x = r \cdot \cos (\varphi)\\ y = r \cdot \sin (\varphi) \end{array} \right. }[/math]
gdzie [math]\displaystyle{ r \geqslant 0 }[/math] i [math]\displaystyle{ \varphi \in \left [ 0, 2\pi \right ) }[/math], otrzymujemy:
- [math]\displaystyle{ f (r, \varphi) = \frac{1}{2 \pi} e^{- r^2 / 2} }[/math]
Funkcję gęstości prawdopodobieństwa [math]\displaystyle{ f (r, \varphi) }[/math] możemy zapisać w postaci iloczynu:
- [math]\displaystyle{ f (r, \varphi) = g (r) h (\varphi) }[/math]
Widzimy, że [math]\displaystyle{ h (\varphi) = \frac{1}{2 \pi} = \text{const} }[/math] jest unormowaną funkcją gęstości prawdopodobieństwa zmiennej [math]\displaystyle{ \varphi }[/math]. Oznacza to, że rozkład [math]\displaystyle{ \varphi }[/math] jest rozkładem równomiernym [math]\displaystyle{ U (0, 2 \pi) }[/math], a liczba [math]\displaystyle{ \varphi }[/math] może być zapisana w postaci [math]\displaystyle{ \varphi = 2 \pi \cdot u }[/math], gdzie [math]\displaystyle{ u }[/math] jest liczbą z równomiernego rozkładu [math]\displaystyle{ U(0, 1) }[/math].
Iloczyn dystrybuant [math]\displaystyle{ G(r) H (\varphi) }[/math] jest określony całką we współrzędnych biegunowych:
- [math]\displaystyle{ G (\hat{r}) H (\hat{\varphi}) = \int^{\hat{r}}_0 \int^{\hat{\varphi}}_0 g(r) h (\varphi) rdrd \varphi = \int^{\hat{r}}_0 g(r)rdr \int^{\hat{\varphi}}_0 h (\varphi) d \varphi }[/math]
Zatem dystrybuanta [math]\displaystyle{ G (\hat{r}) }[/math] jest równa:
- [math]\displaystyle{ G (\hat{r}) = \int^{\hat{r}}_0 g(r)rdr = \int^{\hat{r}}_0 e^{- r^2 / 2} rdr = - e^{- r^2 / 2} \biggr|^{\hat{r}}_0 = 1 - e^{- \hat{r}^2 / 2} }[/math]
Całkę nieoznaczoną [math]\displaystyle{ \int e^{- r^2 / 2} rdr = -e^{- r^2 / 2} }[/math] wyliczamy dokonując podstawienia [math]\displaystyle{ t = -r^2/2 }[/math].
Wracając do zmiennej [math]\displaystyle{ r }[/math], mamy:
- [math]\displaystyle{ G(r) = 1 - e^{- r^2 / 2} }[/math]
Łatwo znajdujemy dystrybuantę odwrotną:
- [math]\displaystyle{ G^{- 1} (r) = \sqrt{- 2 \log (1 - r)} }[/math]
Jeżeli [math]\displaystyle{ v_i \in U (0, 1) }[/math], to liczby [math]\displaystyle{ \sqrt{- 2 \log (1 - v_i)} }[/math] będą należały do rozkładu prawdopodobieństwa odpowiadającego funkcji [math]\displaystyle{ g(r) }[/math].
Zatem parze liczb [math]\displaystyle{ u, v \in U (0, 1) }[/math] odpowiadają liczby [math]\displaystyle{ \varphi, r }[/math]
- [math]\displaystyle{ \left\{ \begin{array}{l} \varphi = 2 \pi \cdot u\\ r = \sqrt{- 2 \log (1 - v)} \end{array} \right. }[/math]
z rozkładów opisywanych funkcjami gęstości [math]\displaystyle{ h (\varphi) }[/math] i [math]\displaystyle{ g(r) }[/math], a tym liczbom odpowiada para liczb [math]\displaystyle{ x, y }[/math]
- [math]\displaystyle{ \left\{ \begin{array}{l} x = \sqrt{- 2 \log (1 - v)} \cdot \cos (2 \pi \cdot u)\\ y = \sqrt{- 2 \log (1 - v)} \cdot \sin (2 \pi \cdot u) \end{array} \right. }[/math]
które należą do standardowych rozkładów normalnych [math]\displaystyle{ N(0, 1) }[/math].
Wnioski
Jeżeli [math]\displaystyle{ u, v \in U (0, 1) }[/math], to liczby
- [math]\displaystyle{ \left\{ \begin{array}{l} x = \sqrt{- 2 \log (1 - u)} \cdot \cos (2 \pi \cdot v)\\ y = \sqrt{- 2 \log (1 - u)} \cdot \sin (2 \pi \cdot v) \end{array} \right. }[/math]
będą należały do standardowego rozkładu normalnego [math]\displaystyle{ N(0, 1) }[/math].
Uogólniając postępowanie z poprzedniego punktu, można łatwo pokazać, że jeżeli [math]\displaystyle{ u, v \in U (0, 1) }[/math], to liczby
- [math]\displaystyle{ \left\{ \begin{array}{l} x = \mu + \sigma \sqrt{- 2 \log (1 - u)} \cdot \cos (2 \pi \cdot v)\\ y = \mu + \sigma \sqrt{- 2 \log (1 - u)} \cdot \sin (2 \pi \cdot v) \end{array} \right. }[/math]
będą należały do rozkładu normalnego [math]\displaystyle{ N (\mu, \sigma^2) }[/math].
Przykład histogramu rozkładu normalnego [math]\displaystyle{ f (x) = \frac{1}{\sqrt{2 \pi}} e^{- x^2} }[/math] Czytelnik znajdzie w arkuszu kalkulacyjnym: Normalny