Morderstwa, egzekucje, odstraszanie - amerykański eksperyment

16.10.2015

Wiemy, że przez wiele lat siły Postępu kwestionowały istnienie odstraszającego efektu kary śmierci. Media oraz "autorytety" propagowały oficjalne stanowisko ONZ, a na stronie Amnesty International nadal możemy przeczytać

Wyniki badań relacji między stosowaniem kary śmierci a współczynnikiem zabójstw przeprowadzone dla Organizacji Narodów Zjednoczonych w 1988 roku i uzupełnione w 1996 oraz 2002 roku stwierdzają, że: „...badania nie dostarczyły naukowego dowodu na to, że kara śmierci ma większy efekt odstraszający niż kara dożywotniego więzienia. Jest mało prawdopodobne by udało się uzyskać taki dowód w przyszłości. Hipoteza o odstraszającym działaniu kary śmierci wciąż nie znajduje potwierdzenia”

Godność ofiar nie ma dla ONZ najmniejszego znaczenia. Fakt, że decyzje podjęte na podstawie nieudowodnionego domniemania (o jednakowym odstraszaniu kary śmierci i kary dożywotniego więzienia) mogą skutkować śmiercią wielu niewinnych osób, nie działa na ONZ odstraszająco. Postęp ma swoją cenę, życie ofiar znaczy zbyt mało, a liczy się godność i życie morderców.

Na nieszczęście dla przedstawicieli Postępu, najnowsze, niezależne i nie przeprowadzane dla ONZ badania potwierdzają tezę, że kara śmierci ma duży efekt odstraszający. Jak do tego doszło? Decydujące znaczenie miały następujące wydarzenia w Stanach Zjednoczonych

02.06.1967	Ostatnia egzekucja przed formalnym zawieszeniem kary śmierci. Rozpoczyna się nieformalne moratorium na wykonywanie wyroków śmierci.
02.07.1972	Sąd Najwyższy uznaje, że większość stanowych ustaw dotyczących kary śmierci jest niezgodna z konstytucją (sprawa Furman v. Georgia). Powoduje to faktyczne i formalne zawieszenie wykonywania kary śmierci w USA
02.07.1976	Sąd Najwyższy uznaje karę śmierci za zgodną z konstytucją Stanów Zjednoczonych (sprawa Gregg v. Georgia). Wyrok oznacza, że stany, które dostosowały swoje prawodawstwo mogą wykonywać wyroki śmierci.
17.01.1977	Pierwsza egzekucja po decyzji Sądu Najwyższego w sprawie Gregg v. Georgia. Koniec moratorium na wykonywanie kary śmierci w USA.

Widzimy, że w Stanach Zjednoczonych w okresie od 03.06.1967 do 16.01.1977 nie został wykonany ani jeden wyrok śmierci, zaś okres względnej bierności wymiaru sprawiedliwości trwał jeszcze dłużej. Tabela przedstawia ilość wykonanych wyroków śmierci w poszczególnych latach

Rok	1965	1966	1967	...	1977	1978	1979	1980	1981	1982	1983
Egzekucje	7	1	2	–	1	–	2	–	1	2	5

Fakt ten jest obecnie wykorzystywany do badań statystycznych, których celem jest oszacowanie efektu odstraszającego. Z matematyczną precyzją potwierdzono jego istnienie i pokazano, że każda egzekucja pozwala uniknąć nawet do osiemnastu morderstw. Czytelnik powinien zdawać sobie sprawę, że to właśnie „amerykański eksperyment” umożliwił te badania, które nie byłby możliwe w przypadku stabilnej sytuacji. Przy właściwie dobranym stopniu represji systemu karnego, mielibyśmy niewielkie wahania ilości zabójstw i niewielkie wahania ilości egzekucji, a wielkości te oscylowałyby wokół linii prostej poziomej (zobacz zamieszczone niżej wykresy, lata 1936 – 1956). Żadne badanie statystyczne nie byłoby w stanie wykryć zależności między ilością egzekucji, a ilością zabójstw, bowiem mierzone efekty byłyby zbyt małe i zostałyby przykryte przez wpływ innych czynników.

Dalszy ciąg artykułu odbiega od standardowych tekstów i może być trudny dla części Czytelników. Chciałbym w nim przybliżyć metody stosowane przez badaczy, które pozwalają jawnie uchwycić zależność między ilością wykonywanych egzekucji, a ilością zabójstw. Konieczne będzie wprowadzenie prostych oznaczeń. Niech z_t oznacza ilość zabójstw, zaś w_t ilość egzekucji. W obydwu przypadkach indeks t oznacza rok, do którego odnoszą się te liczby. Poniżej przedstawiamy ilość zabójstw z_t i ilość egzekucji w_t dla lat t = 1936, 1937,..., 2013.

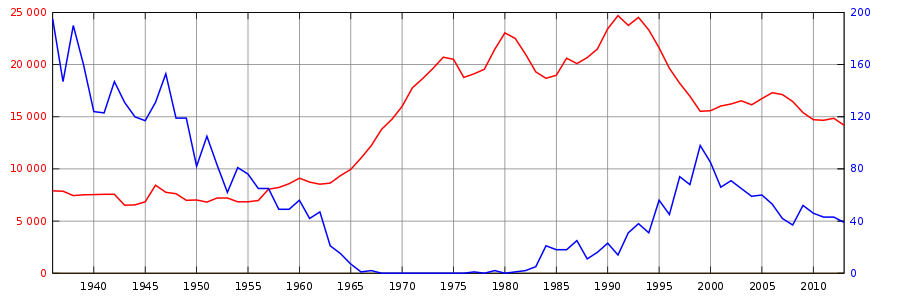
Krzywa o kolorze czerwonym przedstawia ilość zabójstw dokonanych w danym roku. Odpowiednie wartości dla tej krzywej należy odczytywać na skali po lewej stronie. Krzywa niebieska oznacza ilość egzekucji, wartości dla tej krzywej odczytujemy na skali po prawej stronie.

Patrząc na zamieszczony wyżej obrazek dość łatwo można dostrzec jak wraz ze spadkiem ilości egzekucji rośnie ilość zabójstw. Jednak interpretacja jest utrudniona przez znaczne zmiany ilości egzekucji w poszczególnych latach (duże wahania na wykresie). Aby uczynić obraz bardziej czytelnym, będziemy posługiwali się średnią kroczącą. Zamiast ilości zabójstw z_t i ilości egzekucji w_t będziemy używali wielkości z̄_t i w̄_t, które zdefiniujemy jako wartości średnie ilości zabójstw i egzekucji obliczone dla ostatnich pięciu lat

z̄_t = ⅕·(z_t + z_t-1 + z_t-2 + z_t-3 + z_t-4)

w̄_t = ⅕·(w_t + w_t-1 + w_t-2 + w_t-3 + w_t-4)

Posługiwanie się średnią z ostatnich pięciu lat powoduje, że zanikają duże wahania, bardziej widoczne są tendencje, a wykres staje się bardziej czytelny. Poniżej przedstawiamy średnią kroczącą ilość zabójstw z̄_t i średnią kroczącą ilość egzekucji w̄_t dla lat t = 1940, 1941,..., 2013

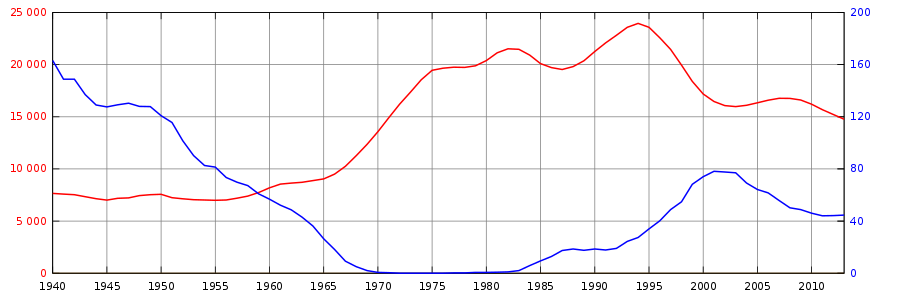
Czytelnik powinien dobrze zrozumieć powody, dla których posługujemy się średnią kroczącą. Nie można uciec od problemu właściwego przedstawienia danych na wykresie. Zastosowanie średniej kroczącej wydaje się najlepszym podejściem, bowiem mimo modyfikacji zostaje zachowane odniesienie do ilości popełnianych zabójstw lub wykonywanych egzekucji w ciągu jednego roku. Natomiast wątpliwości wynikają głównie z naszego przyzwyczajenia do posługiwania się okresem jednego roku w zestawieniach statystycznych. Gdyby Czytelnik otrzymał dane o zabójstwach i egzekucjach z podziałem na poszczególne miesiące (lub kwartały) dla lat 1936 - 2013, to nie miałby najmniejszych wątpliwości, że należy dobrać właściwą metodę dla czytelnego zaprezentowania danych.

Będziemy chcieli wykazać, że widoczny na obydwu rysunkach odstraszający efekt egzekucji nie jest jedynie złudzeniem. Postąpimy analogicznie jak autorzy wielu prac, którzy wykazali związek między ilością zabójstw i ilością egzekucji oraz otrzymali oszacowanie, że każda egzekucja oznacza ochronę życia wielu niewinnych osób.

Myślę, że przynajmniej część Czytelników spotkała się z pojęciami regresji liniowej i metody najmniejszych kwadratów. W przypadku zwykłej regresji liniowej zakładamy, że badane zjawisko jest opisywane linią prostą, a naszym celem jest wyznaczenie takich wartości stałych a i b, aby prosta

y = a·x + b

była jak najlepiej dopasowana do pewnego zbioru punktów (x_k , y_k) na płaszczyźnie. Punkty te wynikają z pomiarów wielkości zależnej y jako funkcji wielkości niezależnej x. Przykładem może być pomiar długości d (zmienna zależna) sprężyny w funkcji siły F (zmienna niezależna) użytej do jej rozciągnięcia. Odpowiednie wzory wynikają z zastosowania metody najmniejszych kwadratów i są dobrze znane.

Metodę tę możemy z powodzeniem przenieść do badania wpływu ilości egzekucji na ilość zabójstw. Tym razem nie będziemy szukali najlepiej dopasowanej prostej, ale będziemy badali pewien model zależności między ilością zabójstw z_t i ilością wykonanych egzekucji w roku poprzednim w_t-1. Nasz prosty model opisuje równanie

z_t = a·w_t-1 + b

Zauważmy też, że jeżeli badamy stosunkowo długi okres czasu, to możemy oczekiwać, że średnia ilość zabójstw będzie wzrastała wraz z upływem czasu z powodu wzrostu liczby ludności w badanym kraju lub jako uboczny skutek systematycznego zmniejszania represyjności systemu karnego. Możemy zatem oczekiwać, że nieco zmodyfikowany model postaci

z_t = a·w_t-1 + b·(t - 1936) + c

będzie lepiej opisywał badany związek między ilością egzekucji, a ilością zabójstw w długim okresie czasu.

Z matematycznego punktu widzenia pierwszy model odpowiada zwykłej regresji liniowej, którą omówiliśmy krótko nieco wcześniej, zaś drugi model opisuje dwukrotna regresja liniowa, mamy bowiem jedną wielkość zależną z_t i dwie wielkości niezależne w_t-1 oraz t. Obliczenia w przypadku podwójnej regresji liniowej nie są skomplikowane, ale w internecie brakuje przejrzystych opisów. Omawiane obliczenia można najłatwiej wykonać w Excelu lub arkuszu kalkulacyjnym pakietu LibreOffice. Obliczenia przeprowadzimy zarówno dla danych wieloletnich (z_t , w_t-1) oraz dla tych samych danych zapisanych w postaci średnich kroczących (z̄_t , w̄_t-1).

Korzystając z dostępnych danych wieloletnich dla lat t = 1936, 1937,..., 2013, otrzymujemy dla przyjętych modeli

zt = -78(±18)·wt-1 + 18700(±1400)				korelacja = 0,707
zt = -48(±18)·wt-1 + 128(±42)·(t - 1936) + 12100(±2500)				korelacja = 0,818

W przypadku analogicznej analizy wykonanej dla średnich kroczących i lat t = 1940, 1941,..., 2013, dostajemy

z̄t = -88(±20)·w̄t-1 + 19200(±1400)				korelacja = 0,728
z̄t = -54(±18)·w̄t-1 + 142(±40)·(t - 1940) + 12200(±2300)				korelacja = 0,854

Liczba w nawiasie umieszczona za współczynnikiem jest błędem z jakim ten współczynnik został wyznaczony. Przyjąłem, że wartość błędu jest równa podwojonej wartości wyliczonego odchylenia standardowego dla odpowiedniego współczynnika, co w przypadku znacznej ilości pomiarów gwarantuje w praktyce, że wartość tego współczynnika mieści się w podanym przedziale z poziomem ufności równym 95%.

Poza wskaźnikiem korelacji, którego wartość jest wysoka, istotnym elementem są wielkości błędów z jakimi zostały wyznaczone współczynniki, bowiem wskazują na stopień dopasowania modelu. W szczególności błąd współczynnika przy zmiennej w_t-1 nigdy nie przekracza 38% wartości tego współczynnika, co jest dobrym rezultatem. Zauważmy, że niemożliwe byłoby uzyskanie tak małych błędów, gdyby egzekucje były wykonywane w sposób losowy. Mniejsze błędy w przypadku średnich kroczących nie powinny dziwić. Już samo użycie średnich kroczących powoduje zmniejszenie rozrzutu danych, co skutkuje zmniejszeniem wyliczonego błędu. Warto też zauważyć, że zmiana psychiki potencjalnych zabójców wymaga czasu, co wyraźnie widzimy na pierwszym wykresie, gdy w latach 1936 - 1956 ilość egzekucji spadała, a ilość zabójstw pozostawała praktycznie niezmienna. Używanie średnich kroczących pozwala częściowo uwzględnić to opóźnienie czasowe i dlatego opis jest bliższy rzeczywistości.

Z przeprowadzonej analizy statystycznej wynika, że każda egzekucja ratuje życie około kilkudziesięciu osób. Decyduje o tym ujemny znak współczynnika przy zmiennej w_t-1. Zauważmy w jak prosty sposób uzyskaliśmy ten rezultat. Wynik ten jest bardzo ważny, bowiem o ile przeciwnicy kary śmierci mogą się z nami spierać, czy na danym wykresie ilość zabójstw rośnie (maleje) przy zmniejszaniu (zwiększaniu) ilości egzekucji (a tutaj dopuszczalne jest każde kłamstwo i każda manipulacja), to wynik matematycznych obliczeń nie podlega dyskusji.

Na zakończenie artykułu chciałbym zwrócić uwagę Czytelnika na okres, kiedy wymiar sprawiedliwości w Stanach Zjednoczonych był najsilniej zdestabilizowany, czyli na lata 1955 – 2001. Patrząc na wykres średnich kroczących łatwo zauważamy, że to w roku 1955 zaczyna docierać do przestępców przekonanie, że są praktycznie bezkarni, bowiem kara śmierci wykonywana jest rzadko (ilość egzekucji spada poniżej osiemdziesięciu rocznie), więzienia zaczynają przypominać hotele, a ilość przestępstw zaczyna zdecydowanie rosnąć. Natomiast w roku 2001 średnia krocząca ilość egzekucji zbliża się do osiemdziesięciu rocznie, zaś w latach 1995 – 2001 widoczny jest zdecydowany spadek ilości zabójstw. Już na początku artykułu pisaliśmy, że okres destabilizacji jest kluczowy dla badań efektu odstraszającego, bowiem efekty gwałtownego zmniejszenia represyjności systemu karnego, następnie zniesienia kary śmierci i w końcu jej przywrócenia są na tyle duże, że wpływy innych czynników na liczbę popełnianych zabójstw nie są w stanie zakryć odstraszającego efektu kary śmierci. Korzystając z dostępnych danych otrzymujemy odpowiednio dla liczby zabójstw z_t i średniej kroczącej liczby zabójstw z̄_t następujące wyniki

zt = -102(±22)·wt-1 + 316(±46)·(t - 1955) + 12200(±1400)				korelacja = 0,927
z̄t = -88(±20)·w̄t-1 + 316(±39)·(t - 1955) + 11500(±1300)				korelacja = 0,953

Uzyskane rezultaty zaskakują bardzo wysokim wskaźnikiem korelacji, bardzo dobrym dopasowaniem i małymi błędami wyznaczonych współczynników regresji, a tym samym potwierdzają, że każda egzekucja oznacza ochronę życia kilkudziesięciu osób.

Należy podkreślić, że autorzy prac naukowych mają dostęp do znacznie większej liczby danych (fachowo nazywanych danymi panelowymi) oraz stosują znacznie bardziej rozbudowane analizy, w których uwzględniają wiele czynników: ilość wykonywanych egzekucji, ilość więźniów w celi śmierci, wskaźnik bezrobocia, procent Murzynów w danej populacji, odsetek ludzi młodych (w wieku 20-35 lat), liczbę więźniów, ilość policjantów, stopień urbanizacji, itd., itp.

Wszystkie te badania niezmiennie prowadzą do wniosku, że każda egzekucja zapobiega znacznej ilości morderstw, a kara śmierci ma silne działanie odstraszające.

PS.
Obawiam się, że część Czytelników może odnieść wrażenie, że przedstawione wyżej wyniki zostały wyczarowane niczym królik ze statystycznego kapelusza. Chciałbym, aby tak nie było i dlatego przygotowałem pewien przykład. Rozważmy funkcje f(t) i g(t) zdefiniowane w przedziale [4, 40] następująco

Przedział	[4, 8)	[8, 12)	[12, 16)	[16, 20)	[20, 24)	[24, 28)	[28, 32)	[32, 36)	[36, 40]
f(t)	2t	t + 8	t/2 + 14	t/4 + 18	23	-t/4 + 29	-t/2 + 36	-t + 52	-2t + 88
g(t)	-t + 12	-t/2 + 8	-t/4 + 5	-t/8 + 3	1/2	t/8 - 2.5	t/4 - 6	t/2 - 14	t - 32

Zauważmy, że w tabeli nie znajdziemy dwóch identycznych funkcji. Co więcej, wykresy funkcji f(t) (oznaczona kolorem czerwonym) i funkcji g(t) (oznaczona kolorem niebieskim) nie wskazują wprost na istnienie zależności między tymi funkcjami

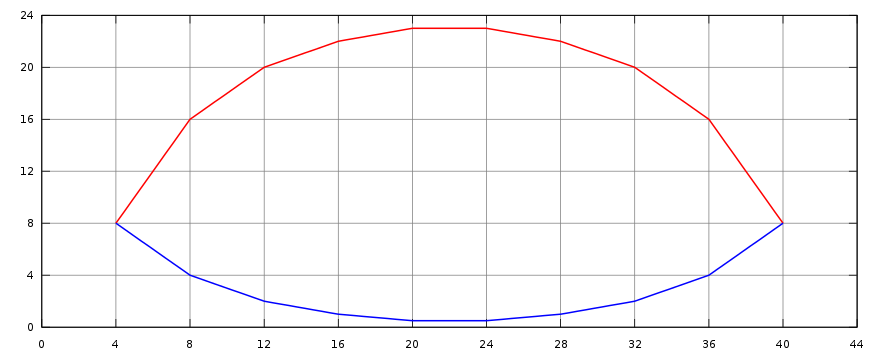
Jednak Czytelnik może łatwo sprawdzić, że dla każdej wartości t należącej do przedziału [4, 40] prawdziwy jest następujący związek między tymi funkcjami: f(t) = -2·g(t) + 24. Czy Czytelnik dostrzega podobieństwo między zamieszczonym wyżej wykresem, a fragmentem wykresu średnich kroczących dla lat 1959 - 2001? Właśnie ze względu na to podobieństwo otrzymaliśmy tak dobrze dopasowane wyniki. Z konieczności związek między funkcjami z_t i w_t-1 znajdujemy statystycznie, czyli najpierw zakładamy postać związku, a współczynniki wyliczamy tak, aby uzyskać najlepsze dopasowanie.