Wzór Eulera-Maclaurina
Wielomiany, liczby i funkcje okresowe Bernoulliego
Definicja E1
Wielomiany [math]\displaystyle{ B_n(x) }[/math] spełniające warunki
● [math]\displaystyle{ B_0(x) = 1 }[/math] ● [math]\displaystyle{ {\small\frac{d}{d x}}B_n(x) = n B_{n - 1}(x) }[/math] ● [math]\displaystyle{ \int_0^1 B_n(t) d t = 0 \qquad \text{dla} \;\; n \geqslant 1 }[/math]
będziemy nazywali wielomianami Bernoulliego[1][2][3][4].
Zadanie E2
Korzystając z definicji E1 znaleźć jawną postać wielomianów [math]\displaystyle{ B_1 (x) }[/math], [math]\displaystyle{ B_2 (x) }[/math] i [math]\displaystyle{ B_3 (x) }[/math].
Z punktu 2. definicji E1 mamy
- [math]\displaystyle{ B'_1 (x) = 1 \cdot B_0 (x) = 1 }[/math]
Zatem
- [math]\displaystyle{ B_1 (x) = \int dx = x + C }[/math]
Stałą [math]\displaystyle{ C }[/math] wyznaczamy z punktu 3. definicji E1
- [math]\displaystyle{ 0 = \int^1_0 B_1 (x) dx = \int^1_0 (x + C) dx = \left( {\small\frac{x^2}{2}} + C x \right) \Biggr\rvert_{0}^{1} = {\small\frac{1}{2}} + C }[/math]
Otrzymujemy, że [math]\displaystyle{ C = - {\small\frac{1}{2}} }[/math], czyli [math]\displaystyle{ \boxed{ B_1 (x) = x - {\small\frac{1}{2}} } }[/math]
Postępując analogicznie dla [math]\displaystyle{ n = 2 }[/math], dostajemy
- [math]\displaystyle{ B'_2 (x) = 2 \cdot B_1 (x) = 2 x - 1 }[/math]
- [math]\displaystyle{ B_2 (x) = \int (2 x - 1) dx = x^2 - x + C }[/math]
- [math]\displaystyle{ 0 = \int^1_0 B_2 (x) dx = \int^1_0 (x^2 - x + C) dx = \left( {\small\frac{x^3}{3}} - {\small\frac{x^2}{2}} + C x \right) \Biggr\rvert_{0}^{1} = {\small\frac{1}{3}} - {\small\frac{1}{2}} + C }[/math]
Otrzymujemy, że [math]\displaystyle{ C = {\small\frac{1}{6}} }[/math], czyli [math]\displaystyle{ \boxed{ B_2 (x) = x^2 - x + {\small\frac{1}{6}} } }[/math]
Powtarzając dla [math]\displaystyle{ n = 3 }[/math], mamy
- [math]\displaystyle{ B'_3 (x) = 3 \cdot B_2 (x) = 3 x^2 - 3 x + {\small\frac{1}{2}} }[/math]
- [math]\displaystyle{ B_3 (x) = \int \left( 3 x^2 - 3 x + {\small\frac{1}{2}} \right) dx = x^3 - {\small\frac{3 x^2}{2}} + {\small\frac{x}{2}} + C }[/math]
- [math]\displaystyle{ 0 = \int^1_0 B_3 (x) dx = \int^1_0 \left( x^3 - {\small\frac{3 x^2}{2}} + {\small\frac{x}{2}} + C \right) dx = \left( {\small\frac{x^4}{4}} - {\small\frac{x^3}{2}} + {\small\frac{x^2}{4}} + C x \right) \Biggr\rvert_{0}^{1} = {\small\frac{1}{4}} - {\small\frac{1}{2}} + {\small\frac{1}{4}} + C }[/math]
Otrzymujemy, że [math]\displaystyle{ C = 0 }[/math], czyli [math]\displaystyle{ \boxed{ B_3 (x) = x^3 - {\small\frac{3 x^2}{2}} + {\small\frac{x}{2}} } }[/math]
□
Twierdzenie E3*
Wielomiany Bernoulliego [math]\displaystyle{ B_n(x) }[/math] określone są następującym wzorem ogólnym
- [math]\displaystyle{ B_n(x) = \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} \sum_{j = 0}^{k} (- 1)^j {\small\binom{k}{j}} (x + j)^n }[/math]
Przykład E4
W tabeli wypisaliśmy początkowe wielomiany Bernoulliego.
[math]\displaystyle{ \quad \;\: n \quad }[/math] [math]\displaystyle{ B_n(x) }[/math] [math]\displaystyle{ \quad \;\: 0 \quad }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ \quad \;\: 1 \quad }[/math] [math]\displaystyle{ x - {\small\frac{1}{2}} }[/math] [math]\displaystyle{ \quad \;\: 2 \quad }[/math] [math]\displaystyle{ x^2 - x + {\small\frac{1}{6}} }[/math] [math]\displaystyle{ \quad \;\: 3 \quad }[/math] [math]\displaystyle{ x^3 - {\small\frac{3}{2}} x^2 + {\small\frac{1}{2}} x }[/math] [math]\displaystyle{ \quad \;\: 4 \quad }[/math] [math]\displaystyle{ x^4 - 2 x^3 + x^2 - \small\frac{1}{30} }[/math] [math]\displaystyle{ \quad \;\: 5 \quad }[/math] [math]\displaystyle{ x^5 - {\small\frac{5}{2}} x^4 + \small\frac{5}{3} x^3 - \small\frac{1}{6} x }[/math] [math]\displaystyle{ \quad \;\: 6 \quad }[/math] [math]\displaystyle{ x^6 - 3 x^5 + \small\frac{5}{2} x^4 - \small\frac{1}{2} x^2 + \small\frac{1}{42} }[/math] [math]\displaystyle{ \quad \;\: 7 \quad }[/math] [math]\displaystyle{ x^7 - {\small\frac{7}{2}} x^6 + {\small\frac{7}{2}} x^5 - {\small\frac{7}{6}} x^3 + {\small\frac{1}{6}} x }[/math] [math]\displaystyle{ \quad \;\: 8 \quad }[/math] [math]\displaystyle{ x^8 - 4 x^7 + \small\frac{14}{3} x^6 - \small\frac{7}{3} x^4 + \small\frac{2}{3} x^2 - \small\frac{1}{30} }[/math] [math]\displaystyle{ \quad \;\: 9 \quad }[/math] [math]\displaystyle{ x^9 - \small\frac{9}{2} x^8 + 6 x^7 - \small\frac{21}{5} x^5 + 2 x^3 - \small\frac{3}{10} x }[/math] [math]\displaystyle{ \quad 10 \quad }[/math] [math]\displaystyle{ x^{10} - 5 x^9 + \small\frac{15}{2} x^8 - 7 x^6 + 5 x^4 - \small\frac{3}{2} x^2 + \small\frac{5}{66} }[/math] [math]\displaystyle{ \quad 11 \quad }[/math] [math]\displaystyle{ x^{11} - \small\frac{11}{2} x^{10} + \small\frac{55}{6} x^9 - 11 x^7 + 11 x^5 - \small\frac{11}{2} x^3 + \small\frac{5}{6} x }[/math] [math]\displaystyle{ \quad 12 \quad }[/math] [math]\displaystyle{ x^{12} - 6 x^{11} + 11 x^{10} - {\small\frac{33}{2}} x^8 + 22 x^6 - {\small\frac{33}{2}} x^4 + 5 x^2 - {\small\frac{691}{2730}} }[/math]
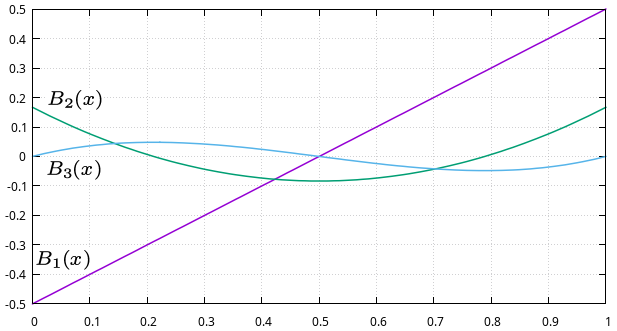
Przykład E5
Przedstawiamy wykresy wielomianów Bernoulliego [math]\displaystyle{ B_n(x) }[/math] dla [math]\displaystyle{ x \in [0, 1] }[/math]
Definicja E6
Liczbami Bernoulliego [math]\displaystyle{ B_n }[/math] będziemy nazywali wartości wielomianów Bernoulliego [math]\displaystyle{ B_n(x) }[/math] dla [math]\displaystyle{ x = 0 }[/math], czyli [math]\displaystyle{ B_n = B_n (0) }[/math].
Uwaga E7
Ze wzoru podanego w twierdzeniu E3 wynika natychmiast wzór ogólny dla liczb Bernoulliego.
- [math]\displaystyle{ B_n = B_n (0) = \sum_{k = 0}^{n} {\small\frac{1}{k + 1}} \sum_{j = 0}^{k} (- 1)^j {\small\binom{k}{j}} j^n }[/math]
Twierdzenie E8
Niech [math]\displaystyle{ B_n (x) }[/math] i [math]\displaystyle{ B_n }[/math] oznaczają odpowiednio wielomiany i liczby Bernoulliego. Prawdziwe są następujące wzory
[math]\displaystyle{ \quad 1. \quad }[/math] [math]\displaystyle{ B_n (1) = B_n (0) }[/math] [math]\displaystyle{ n \geqslant 2 }[/math] [math]\displaystyle{ \quad 2. \quad }[/math] [math]\displaystyle{ B_n (1 - x) = (- 1)^n B_n (x) }[/math] [math]\displaystyle{ n \geqslant 0 }[/math] [math]\displaystyle{ \quad 3. \quad }[/math] [math]\displaystyle{ B_{2 k + 1} (1) = B_{2 k + 1} (0) = B_{2 k + 1} \left( \tfrac{1}{2} \right) = 0 }[/math] [math]\displaystyle{ k \geqslant 1 }[/math] [math]\displaystyle{ \quad 4. \quad }[/math] [math]\displaystyle{ B_n \left( a x \right) = a^{n - 1} \sum_{k = 0}^{a - 1} B_n \left( x + \small\frac{k}{a} \right) }[/math] [math]\displaystyle{ n \geqslant 0 \quad \text{i} \quad a \in \mathbb{Z}_+ }[/math] [math]\displaystyle{ \quad 5. \quad }[/math] [math]\displaystyle{ \sum_{k = 1}^{a - 1} B_n \left( \small\frac{k}{a} \right) = (a^{1 - n} - 1) B_n }[/math] [math]\displaystyle{ n \geqslant 0 \quad \text{i} \quad a \in \mathbb{Z}_+ }[/math] [math]\displaystyle{ \quad 6. \quad }[/math] [math]\displaystyle{ B_n \left( \tfrac{1}{2} \right) = (2^{1 - n} - 1) B_n }[/math] [math]\displaystyle{ n \geqslant 0 }[/math] [math]\displaystyle{ \quad 7. \quad }[/math] [math]\displaystyle{ B_{2 k} \left( \tfrac{1}{3} \right) = \tfrac{1}{2} (3^{1 - 2 k} - 1) B_{2 k} }[/math] [math]\displaystyle{ k \geqslant 0 }[/math] [math]\displaystyle{ \quad 8. \quad }[/math] [math]\displaystyle{ B_{2 k} \left( \tfrac{1}{4} \right) = 2^{- 2 k} (2^{1 - 2 k} - 1) B_{2 k} }[/math] [math]\displaystyle{ k \geqslant 0 }[/math] [math]\displaystyle{ \quad 9. \quad }[/math] [math]\displaystyle{ B_{2 k} \left( \tfrac{1}{6} \right) = \tfrac{1}{2} (2^{1 - 2 k} - 1) (3^{1 - 2 k} - 1) B_{2 k} }[/math] [math]\displaystyle{ k \geqslant 0 }[/math] [math]\displaystyle{ \quad 10. \quad }[/math] [math]\displaystyle{ B_n (x + 1) - B_n (x) = n x^{n - 1} }[/math] [math]\displaystyle{ n \geqslant 0 }[/math]
Punkt 1.
Dla [math]\displaystyle{ n \geqslant 2 }[/math] mamy
- [math]\displaystyle{ B_n (1) - B_n (0) = \int_0^1 B'_n (t) d t = n \int_0^1 B_{n - 1} (t) d t = 0 }[/math]
Punkt 2.
Indukcja matematyczna. Wzór jest prawdziwy dla [math]\displaystyle{ n = 1 }[/math]. Załóżmy, że jest prawdziwy dla wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ n }[/math]. Z założenia mamy
- [math]\displaystyle{ B_n (1 - x) = (- 1)^n B_n (x) }[/math]
- [math]\displaystyle{ - {\small\frac{d}{d x}} B_{n + 1} (1 - x) = (- 1)^n {\small\frac{d}{d x}} B_{n + 1} (x) }[/math]
Całkując, otrzymujemy
- [math]\displaystyle{ B_{n + 1} (1 - x) = (- 1)^{n + 1} B_{n + 1} (x) + C }[/math]
Wystarczy pokazać, że stała [math]\displaystyle{ C }[/math] jest równa zero, istotnie
- [math]\displaystyle{ \int_0^1 B_{n + 1} (1 - t) d t = (- 1)^{n + 1} \int_0^1 B_{n + 1} (t) d t + C \int_0^1 d t }[/math]
- [math]\displaystyle{ - \int_1^0 B_{n + 1}(u) d u = C }[/math]
Punkt 3.
Kładąc we wzorze 2. [math]\displaystyle{ x = 0 }[/math] oraz [math]\displaystyle{ n = 2 k + 1 }[/math], gdzie [math]\displaystyle{ k \geqslant 1 }[/math], otrzymujemy
- [math]\displaystyle{ B_{2 k + 1} (1) = - B_{2 k + 1} (0) }[/math]
ale ze wzoru 1. mamy [math]\displaystyle{ B_{2 k + 1} (1) = B_{2 k + 1} (0) }[/math], dodając równania stronami, dostajemy [math]\displaystyle{ B_{2 k + 1} (1) = 0 }[/math].
Kładąc we wzorze 2. [math]\displaystyle{ x = {\small\frac{1}{2}} }[/math] oraz [math]\displaystyle{ n = 2 k + 1 }[/math], gdzie [math]\displaystyle{ k \geqslant 1 }[/math], mamy
- [math]\displaystyle{ B_{2 k + 1} \left( {\small\frac{1}{2}} \right) = - B_{2 k + 1} \left( {\small\frac{1}{2}} \right) }[/math]
czyli [math]\displaystyle{ B_{2 k + 1} \left( {\small\frac{1}{2}} \right) = 0 }[/math].
Punkt 4.
Indukcja matematyczna. Dla ułatwienia rachunków połóżmy [math]\displaystyle{ x = {\small\frac{y}{a}} }[/math], zatem będziemy dowodzili, że
- [math]\displaystyle{ B_n (y) = a^{n - 1} \sum_{k = 0}^{a - 1} B_n \left( {\small\frac{y + k}{a}} \right) }[/math]
Bez trudu możemy sprawdzić prawdziwość wzoru dla [math]\displaystyle{ n = 1 }[/math].
- [math]\displaystyle{ \sum_{k = 0}^{a - 1} B_1 \left( {\small\frac{y + k}{a}} \right) = \sum_{k = 0}^{a - 1} \left( {\small\frac{y + k}{a}} - {\small\frac{1}{2}} \right) }[/math]
- [math]\displaystyle{ \;\;\;\: = {\small\frac{y}{a}} \cdot a - {\small\frac{1}{2}} \cdot a + \sum_{k = 0}^{a - 1} {\small\frac{k}{a}} }[/math]
- [math]\displaystyle{ \;\;\;\: = y - {\small\frac{a}{2}} + {\small\frac{1}{a}} \cdot {\small\frac{a (a - 1)}{2}} }[/math]
- [math]\displaystyle{ \;\;\;\: = y - {\small\frac{1}{2}} }[/math]
- [math]\displaystyle{ \;\;\;\: = B_1 (y) }[/math]
Załóżmy, że dowodzony wzór jest prawdziwy dla wszystkich liczb naturalnych nie większych od [math]\displaystyle{ n }[/math]. Korzystając z definicji wielomianów Bernoulliego, możemy napisać
- [math]\displaystyle{ {\small\frac{1}{n + 1}} {\small\frac{d}{d y}} B_{n + 1} (y) = a^{n - 1} \sum_{k = 0}^{a - 1} {\small\frac{a}{n + 1}} {\small\frac{d}{d y}} B_{n + 1} \left( {\small\frac{y + k}{a}} \right) }[/math]
Całkując, otrzymujemy
- [math]\displaystyle{ B_{n + 1} (y) = a^n \sum_{k = 0}^{a - 1} B_{n + 1} \left( {\small\frac{y + k}{a}} \right) + C }[/math]
Wystarczy pokazać, że stała [math]\displaystyle{ C }[/math] jest równa zero. Mamy
- [math]\displaystyle{ \int_0^1 \sum_{k = 0}^{a - 1} B_{n + 1} \left( {\small\frac{y + k}{a}} \right) d y = \sum_{k = 0}^{a - 1} \int_0^1 \left[ {\small\frac{a}{n + 2}} {\small\frac{d}{d y}} B_{n + 2} \left( {\small\frac{y + k}{a}} \right) \right] d y }[/math]
- [math]\displaystyle{ \:\, = {\small\frac{a}{n + 2}} \sum_{k = 0}^{a - 1} \biggl[ B_{n + 2} \left( {\small\frac{y + k}{a}} \right) \biggr\rvert_{0}^{1} \biggr] }[/math]
- [math]\displaystyle{ \:\, = {\small\frac{a}{n + 2}} \sum_{k = 0}^{a - 1} \left[ B_{n + 2} \left( {\small\frac{k + 1}{a}} \right) - B_{n + 2} \left( {\small\frac{k}{a}} \right) \right] }[/math]
- [math]\displaystyle{ \:\, = {\small\frac{a}{n + 2}} [B_{n + 2} (1) - B_{n + 2} (0)] }[/math]
- [math]\displaystyle{ \:\, = 0 }[/math]
dla [math]\displaystyle{ n \geqslant 0 }[/math]. Przekształcając, skorzystaliśmy z faktu, że suma jest teleskopowa (zobacz D12). Ponieważ [math]\displaystyle{ \int^1_0 B_{n + 1} (y) d y = 0 }[/math], to [math]\displaystyle{ \int_0^1 C d t = C = 0 }[/math].
Punkt 5.
Połóżmy [math]\displaystyle{ x = 0 }[/math] we wzorze udowodnionym w punkcie 4. Mamy
- [math]\displaystyle{ B_n (0) = a^{n - 1} \sum_{k = 0}^{a - 1} B_n \left( {\small\frac{k}{a}} \right) = a^{n - 1} \sum_{k = 1}^{a - 1} B_n \left( {\small\frac{k}{a}} \right) + a^{n - 1} B_n (0) }[/math]
Skąd natychmiast otrzymujemy
- [math]\displaystyle{ \sum_{k = 1}^{a - 1} B_n \left( {\small\frac{k}{a}} \right) = \left( {\small\frac{1}{a^{n - 1}}} - 1 \right) B_n }[/math]
Punkt 6.
Kładąc [math]\displaystyle{ a = 2 }[/math] we wzorze 5, otrzymujemy
- [math]\displaystyle{ B_n \left( {\small\frac{1}{2}} \right) = \left( {\small\frac{1}{2^{n - 1}}} - 1 \right) B_n }[/math]
Co należało udowodnić.
Punkt 7.
Wzór podany w punkcie 5. dla [math]\displaystyle{ n = 2 m }[/math] i [math]\displaystyle{ a = 3 }[/math] przyjmuje postać
- [math]\displaystyle{ \sum_{k = 1}^2 B_{2 m} \left( {\small\frac{k}{3}} \right) = (3^{1 - 2 m} - 1) B_{2 m} }[/math]
Czyli
- [math]\displaystyle{ B_{2 m} \left( {\small\frac{1}{3}} \right) + B_{2 m} \left( {\small\frac{2}{3}} \right) = (3^{1 - 2 m} - 1) B_{2 m} }[/math]
Korzystając z punktu 2, dostajemy
- [math]\displaystyle{ 2 B_{2 m} \left( {\small\frac{1}{3}} \right) = (3^{1 - 2 m} - 1) B_{2 m} }[/math]
Punkt 8.
Wzór podany w punkcie 5. dla [math]\displaystyle{ n = 2 m }[/math] i [math]\displaystyle{ a = 4 }[/math] przyjmuje postać
- [math]\displaystyle{ \sum_{k = 1}^3 B_{2 m} \left( {\small\frac{k}{4}} \right) = (4^{1 - 2 m} - 1) B_{2 m} }[/math]
Czyli
- [math]\displaystyle{ B_{2 m} \left( {\small\frac{1}{4}} \right) + B_{2 m} \left( {\small\frac{1}{2}} \right) + B_{2 m} \left( {\small\frac{3}{4}} \right) = (2^{2 - 4 m} - 1) B_{2 m} }[/math]
Korzystając z punktów 6. i 2., dostajemy
- [math]\displaystyle{ B_{2 m} \left( {\small\frac{1}{4}} \right) + (2^{1 - 2 m} - 1) B_{2 m} + (- 1)^{2 m} B_{2 m} \left( {\small\frac{1}{4}} \right) = (2^{2 - 4 m} - 1) B_{2 m} }[/math]
- [math]\displaystyle{ 2 B_{2 m} \left( {\small\frac{1}{4}} \right) = B_{2 m} (2^{2 - 4 m} - 2^{1 - 2 m}) }[/math]
Zatem
- [math]\displaystyle{ B_{2 m} \left( {\small\frac{1}{4}} \right) = 2^{- 2 m} (2^{1 - 2 m} - 1) B_{2 m} }[/math]
Punkt 9.
Wzór podany w punkcie 5. dla [math]\displaystyle{ n = 2 m }[/math] i [math]\displaystyle{ a = 6 }[/math] przyjmuje postać
- [math]\displaystyle{ \sum_{k = 1}^5 B_{2 m} \left( {\small\frac{k}{6}} \right) = (6^{1 - 2 m} - 1) B_{2 m} }[/math]
Czyli
- [math]\displaystyle{ B_{2 m} \left( {\small\frac{1}{6}} \right) + B_{2 m} \left( {\small\frac{1}{3}} \right) + B_{2 m} \left( {\small\frac{1}{2}} \right) + B_{2 m} \left( {\small\frac{2}{3}} \right) + B_{2 m} \left( {\small\frac{5}{6}} \right) = (6^{1 - 2 m} - 1) B_{2 m} }[/math]
Korzystając z udowodnionych wyżej wzorów, dostajemy
- [math]\displaystyle{ 2 B_{2 m} \left( {\small\frac{1}{6}} \right) + 2 B_{2 m} \left( {\small\frac{1}{3}} \right) = (6^{1 - 2 m} - 1) B_{2 m} - (2^{1 - 2 m} - 1) B_{2 m} = 6^{1 - 2 m} B_{2 m} - 2^{1 - 2 m} B_{2 m} = 2^{1 - 2 m} (3^{1 - 2 m} - 1) B_{2 m} }[/math]
- [math]\displaystyle{ 2 B_{2 m} \left( {\small\frac{1}{6}} \right) = 2^{1 - 2 m} (3^{1 - 2 m} - 1) B_{2 m} - (3^{1 - 2 m} - 1) B_{2 m} = (2^{1 - 2 m} - 1) (3^{1 - 2 m} - 1) B_{2 m} }[/math]
Zatem
- [math]\displaystyle{ B_{2 m} \left( {\small\frac{1}{6}} \right) = \tfrac{1}{2} (2^{1 - 2 m} - 1) (3^{1 - 2 m} - 1) B_{2 m} }[/math]
Punkt 10.
Indukcja matematyczna. Łatwo sprawdzamy, że wzór jest prawdziwy dla [math]\displaystyle{ n = 0, 1, 2 }[/math]. Zakładając, że wzór jest prawdziwy dla wszystkich liczb całkowitych dodatnich nie większych od [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ x^n = \int^x_0 n t^{n - 1} d t }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \int^x_0 (B_n (t + 1) - B_n (t) ) d t }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \int^x_0 B_n (t + 1) d t - \int^x_0 B_n (t) d t \qquad \qquad \qquad u = t + 1 }[/math]
- [math]\displaystyle{ \;\;\;\;\: = \int_{1}^{x + 1} B_n (u) d u - \int^x_0 B_n (t) d t }[/math]
- [math]\displaystyle{ \;\;\;\;\: = {\small\frac{1}{n + 1}} \int_{1}^{x + 1} B'_{n + 1} (u) d u - {\small\frac{1}{n + 1}} \int^x_0 B'_{n + 1} (t) d t }[/math]
- [math]\displaystyle{ \;\;\;\;\: = {\small\frac{1}{n + 1}} (B_{n + 1} (x + 1) - B_{n + 1} (1) - B_{n + 1} (x) + B_{n + 1} (0)) }[/math]
- [math]\displaystyle{ \;\;\;\;\: = {\small\frac{1}{n + 1}} (B_{n + 1} (x + 1) - B_{n + 1} (x)) }[/math]
Bo [math]\displaystyle{ B_n (1) = B_n (0) }[/math] dla [math]\displaystyle{ n \geqslant 2 }[/math]. Co należało pokazać.
□
Zadanie E9
Niech [math]\displaystyle{ k \in \mathbb{N}_0 }[/math]. Pokazać, że wykres funkcji [math]\displaystyle{ B_{2 k} (x) }[/math] jest symetryczny, a funkcji [math]\displaystyle{ B_{2 k + 1} (x) }[/math] jest antysymetryczny względem prostej [math]\displaystyle{ x = {\small\frac{1}{2}} }[/math].
Jeżeli we wzorze (zobacz E8 p.2)
- [math]\displaystyle{ B_n (1 - x) = (- 1)^n B_n (x) }[/math]
położymy [math]\displaystyle{ x = {\small\frac{1}{2}} + t }[/math], to otrzymamy
- [math]\displaystyle{ B_n \left( {\small\frac{1}{2}} - t \right) = (- 1)^n B_n \left( {\small\frac{1}{2}} + t \right) }[/math]
Zatem
- [math]\displaystyle{ B_{2 k} \left( {\small\frac{1}{2}} - t \right) = B_{2 k} \left( {\small\frac{1}{2}} + t \right) }[/math]
oraz
- [math]\displaystyle{ B_{2 k + 1} \left( {\small\frac{1}{2}} - t \right) = - B_{2 k + 1} \left( {\small\frac{1}{2}} + t \right) }[/math]
Co oznacza, że wykres funkcji [math]\displaystyle{ B_{2 k} (x) }[/math] jest symetryczny, a funkcji [math]\displaystyle{ B_{2 k + 1} (x) }[/math] jest antysymetryczny względem prostej [math]\displaystyle{ x = {\small\frac{1}{2}} }[/math].
□
Zadanie E10
Niech [math]\displaystyle{ k \in \mathbb{N}_0 }[/math]. Pokazać, że
- [math]\displaystyle{ \int_{0}^{1 / 2} B_{2 k + 1} (x) d x = - \int^1_{1 / 2} B_{2 k + 1} (t) d t }[/math]
- [math]\displaystyle{ \int_{0}^{1 / 2} B_{2 k + 2} (x) d x = 0 }[/math]
Ze wzoru E8 p.2 mamy
- [math]\displaystyle{ \int_{0}^{1 / 2} B_n (x) d x = (- 1)^n \int_{0}^{1 / 2} B_n (1 - x) d x }[/math]
Podstawiając [math]\displaystyle{ 1 - x = t }[/math] w całce po prawej stronie, otrzymujemy
- [math]\displaystyle{ \int_{0}^{1 / 2} B_n (x) d x = (- 1)^n \int^1_{1 / 2} B_n (t) d t }[/math]
Dla [math]\displaystyle{ n = 2 k + 1 }[/math] dostajemy natychmiast pierwszy wzór. Dla [math]\displaystyle{ n = 2 k }[/math] mamy
- [math]\displaystyle{ \int_{0}^{1 / 2} B_{2 k} (x) d x = \int^1_{1 / 2} B_{2 k} (t) d t }[/math]
Ponieważ dla [math]\displaystyle{ k \geqslant 1 }[/math] jest
- [math]\displaystyle{ 0 = \int^1_0 B_{2 k} (x) d x = \int_{0}^{1 / 2} B_{2 k} (x) d x + \int^1_{1 / 2} B_{2 k} (x) d x = 2 \int_{0}^{1 / 2} B_{2 k} (x) d x }[/math]
to otrzymujemy
- [math]\displaystyle{ \int_{0}^{1 / 2} B_{2 k} (x) d x = 0 }[/math]
Co należało pokazać.
□
Zadanie E11
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Pokazać, że [math]\displaystyle{ B_n = - {\small\frac{n}{2 (1 - 2^{- n})}} \int_{0}^{1 / 2} B_{n - 1} (t) d t }[/math]
Z definicji E1 p.2 mamy
- [math]\displaystyle{ B \left( {\small\frac{1}{2}} \right) - B (0) = n \int_{0}^{1 / 2} B_{n - 1} (t) d t }[/math]
Z twierdzenia E8 p.6 dostajemy
- [math]\displaystyle{ B \left( {\small\frac{1}{2}} \right) = (2^{1 - n} - 1) B_n (0) }[/math]
Z powyższych wzorów łatwo otrzymujemy, że
- [math]\displaystyle{ B_n = B_n (0) = - {\small\frac{n}{2 (1 - 2^{- n})}} \int_{0}^{1 / 2} B_{n - 1} (t) d t }[/math]
- [math]\displaystyle{ B_n = B_n (0) = - {\small\frac{n}{2 (1 - 2^{- n})}} \int_{0}^{1 / 2} B_{n - 1} (t) d t }[/math]
□
Twierdzenie E12
Niech [math]\displaystyle{ f(x) }[/math] i [math]\displaystyle{ f' (x) }[/math] będą ciągłymi funkcjami rzeczywistymi określonymi w przedziale [math]\displaystyle{ [a, b] }[/math] i różniczkowalnymi w [math]\displaystyle{ (a, b) }[/math]. Jeżeli dla pewnego punktu [math]\displaystyle{ r \in (a, b) }[/math] spełnione są warunki [math]\displaystyle{ f(a) = f (b) = f (r) = 0 }[/math], to istnieje taki punkt [math]\displaystyle{ t \in (a, b) }[/math], że [math]\displaystyle{ f'' (t) = 0 }[/math].
Łatwo zauważamy, że dla funkcji [math]\displaystyle{ f(x) }[/math] i dla każdego z przedziałów [math]\displaystyle{ [a, r] }[/math] oraz [math]\displaystyle{ [r, b] }[/math] spełnione są założenia twierdzenia Rolle'a[5]. Zatem istnieją takie punkty [math]\displaystyle{ s_1 \in (a, r) \, }[/math] i [math]\displaystyle{ \, s_2 \in (r, b) }[/math], że
- [math]\displaystyle{ f' (s_1) = f' (s_2) = 0 }[/math]
Teraz widzimy, że dla funkcji [math]\displaystyle{ f' (x) }[/math] i przedziału [math]\displaystyle{ [s_1, s_2] }[/math] również spełnione są założenia twierdzenia Rolle'a. Zatem istnieje taki punkt [math]\displaystyle{ t \in (s_1, s_2) \subset (a, b) }[/math], że
- [math]\displaystyle{ f'' (t) = 0 }[/math]
Co należało pokazać.
□
Twierdzenie E13
Niech [math]\displaystyle{ k \in \mathbb{Z}_+ }[/math]. Wielomian [math]\displaystyle{ B_{2 k + 1} (x) }[/math] ma dokładnie trzy pierwiastki w przedziale [math]\displaystyle{ [0, 1] }[/math]. Są to liczby [math]\displaystyle{ x = 0 }[/math], [math]\displaystyle{ x = {\small\frac{1}{2}} \, }[/math] i [math]\displaystyle{ \, x = 1 }[/math].
Z twierdzenia E8 p.3 wiemy, że dla [math]\displaystyle{ k \geqslant 1 }[/math] jest
- [math]\displaystyle{ B_{2 k + 1} (0) = B_{2 k + 1} \left( {\small\frac{1}{2}} \right) = B_{2 k + 1} (1) = 0 }[/math]
Zatem dla [math]\displaystyle{ k \geqslant 1 }[/math] każdy wielomian Bernoulliego [math]\displaystyle{ B_{2 k + 1} (x) }[/math] ma trzy pierwiastki: [math]\displaystyle{ x = 0 }[/math], [math]\displaystyle{ x = {\small\frac{1}{2}} }[/math] i [math]\displaystyle{ x = 1 }[/math].
Pozostaje udowodnić, że wielomiany te nie mają innych pierwiastków w przedziale [math]\displaystyle{ [0, 1] }[/math]. Bez trudu możemy sprawdzić, że twierdzenie jest prawdziwe dla początkowych liczb całkowitych dodatnich, np. dla [math]\displaystyle{ k = 1, 2, 3, 4 }[/math] (zobacz WolframAlphaB3, WolframAlphaB5, WolframAlphaB7, WolframAlphaB9).
Przypuśćmy, dla uzyskania sprzeczności, że [math]\displaystyle{ B_{2 k + 1} (x) }[/math] jest wielomianem Bernoulliego o najmniejszym stopniu nieparzystym [math]\displaystyle{ 2 k + 1 }[/math] mającym pierwiastek [math]\displaystyle{ r \in [0, 1] }[/math] różny od [math]\displaystyle{ 0, {\small\frac{1}{2}}, 1 }[/math].
Z twierdzenia E8 p.2 wiemy, że dla [math]\displaystyle{ n \geqslant 0 }[/math] jest
- [math]\displaystyle{ B_n (1 - x) = (- 1)^n B_n (x) }[/math]
Łatwo widzimy, że jeżeli [math]\displaystyle{ r \in [0, 1] }[/math] jest pierwiastkiem [math]\displaystyle{ B_{2 k + 1} (x) }[/math], to [math]\displaystyle{ 1 - r \in [0, 1] }[/math] również jest pierwiastkiem [math]\displaystyle{ B_{2 k + 1} (x) }[/math]. Zatem nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ r \in \left( 0, {\small\frac{1}{2}} \right) }[/math].
Ponieważ wielomiany Bernoulliego są funkcjami różniczkowalnymi i [math]\displaystyle{ B_{2 k + 1} (0) = B_{2 k + 1} (r) = B_{2 k + 1} \left( {\small\frac{1}{2}} \right) = 0 }[/math], to spełnione są założenia twierdzenia E12. Zatem istnieje taka liczba [math]\displaystyle{ t \in \left( 0, {\small\frac{1}{2}} \right) }[/math], że [math]\displaystyle{ B''_{2 k + 1} (t) = 0 }[/math]. Ale
- [math]\displaystyle{ B''_{2 k + 1} (x) = (2 k + 1) B'_{2 k} (x) = 2 k (2 k + 1) B_{2 k - 1} (x) }[/math]
Skąd wynika, że [math]\displaystyle{ B_{2 k - 1} (t) = 0 }[/math], wbrew założeniu, że [math]\displaystyle{ B_{2 k + 1} (x) }[/math] jest wielomianem Bernoulliego o najmniejszym stopniu nieparzystym [math]\displaystyle{ 2 k + 1 }[/math] mającym pierwiastek [math]\displaystyle{ r \in [0, 1] }[/math] różny od [math]\displaystyle{ 0, {\small\frac{1}{2}}, 1 }[/math]. Otrzymana sprzeczność kończy dowód.
□
Twierdzenie E14
Niech [math]\displaystyle{ k \in \mathbb{N}_0 }[/math]. Liczby Bernoulliego [math]\displaystyle{ B_{2 k} }[/math] są różne od zera.
Łatwo sprawdzamy, że [math]\displaystyle{ B_0 = 1 }[/math], [math]\displaystyle{ B_2 = {\small\frac{1}{6}} }[/math], [math]\displaystyle{ B_4 = - {\small\frac{1}{30}} }[/math], [math]\displaystyle{ B_6 = {\small\frac{1}{42}} }[/math]. Przypuśćmy, dla uzyskania sprzeczności, że dla pewnego [math]\displaystyle{ k \gt 3 }[/math] jest [math]\displaystyle{ B_{2 k} = B_{2 k} (0) = 0 }[/math]. Zatem z twierdzenia E8 p.6 mamy
- [math]\displaystyle{ B_{2 k} \left( {\small\frac{1}{2}} \right) = (2^{1 - 2 k} - 1) B_{2 k} = 0 }[/math]
Ponieważ [math]\displaystyle{ B_{2 k} (0) = B_{2 k} \left( {\small\frac{1}{2}} \right) = 0 }[/math], to z twierdzenia Rolle'a[5] wynika, że istnieje taka liczba [math]\displaystyle{ r \in \left( 0, {\small\frac{1}{2}} \right) }[/math], że [math]\displaystyle{ B'_{2 k} (r) = 0 }[/math], czyli [math]\displaystyle{ 2 k B_{2 k - 1} (r) = 0 }[/math]. Wbrew temu, że wielomiany Bernoulliego o indeksie nieparzystym mają dokładnie trzy pierwiastki w przedziale [math]\displaystyle{ [0, 1] }[/math] i są to liczby [math]\displaystyle{ x = 0 }[/math], [math]\displaystyle{ x = {\small\frac{1}{2}} }[/math], [math]\displaystyle{ x = 1 }[/math] (zobacz E13). Otrzymana sprzeczność kończy dowód.
□
Twierdzenie E15
Niech [math]\displaystyle{ k \in \mathbb{N}_0 }[/math]. Dla wielomianów Bernoulliego [math]\displaystyle{ B_{2 k} (x) \, }[/math] i [math]\displaystyle{ \, x \in [0, 1] }[/math] prawdziwe jest następujące oszacowanie
- [math]\displaystyle{ | B_{2 k} (x) | \leqslant | B_{2 k} | }[/math]
Zauważmy, że dla [math]\displaystyle{ k \geqslant 2 }[/math]
- [math]\displaystyle{ B'_{2 k} (x) = 2 k B_{2 k - 1} (x) }[/math]
- wielomian [math]\displaystyle{ B_{2 k - 1} (x) }[/math] ma dokładnie trzy pierwiastki w przedziale [math]\displaystyle{ [0, 1] }[/math]: [math]\displaystyle{ x = 0 }[/math], [math]\displaystyle{ x = {\small\frac{1}{2}} \, }[/math] oraz [math]\displaystyle{ \, x = 1 }[/math] (zobacz E13)
- [math]\displaystyle{ B''_{2 k} (x) = 2 k (2 k - 1) B_{2 k - 2} (x) }[/math]
Zatem wielomian [math]\displaystyle{ B_{2 k} (x) }[/math] ma ekstrema w punktach [math]\displaystyle{ x = 0, {\small\frac{1}{2}}, 1 }[/math]. Łatwo widzimy, że [math]\displaystyle{ B_{2 k} (0) = B_{2 k} (1) = B_{2 k} \, }[/math] i [math]\displaystyle{ \, B_{2 k} \left( {\small\frac{1}{2}} \right) = (2^{1 - 2 k} - 1) B_{2 k} }[/math]. Wynika stąd, że wartości funkcji [math]\displaystyle{ | B_{2 k} (x) | }[/math] nie przekraczają liczby [math]\displaystyle{ | B_{2 k} | }[/math]. Prawdziwość twierdzenia dla wielomianu [math]\displaystyle{ B_0 (x) = 1 }[/math] jest oczywista, a dla wielomianu [math]\displaystyle{ B_2 (x) = x^2 - x + {\small\frac{1}{6}} }[/math] łatwo sprawdzamy ją bezpośrednio, znajdując minimum funkcji [math]\displaystyle{ B_2 (x) }[/math] i wartości [math]\displaystyle{ B_2 (x) }[/math] w punktach [math]\displaystyle{ x = 0 \, }[/math] i [math]\displaystyle{ \, x = 1 }[/math] (zobacz WolframAlphaB2). Co kończy dowód.
□
Przykład E16
W tabeli przedstawiamy liczby Bernoulliego [math]\displaystyle{ B_n }[/math] oraz minimalne [math]\displaystyle{ m_n }[/math] i maksymalne [math]\displaystyle{ M_n }[/math] wartości wielomianów [math]\displaystyle{ B_n(x) }[/math] dla [math]\displaystyle{ x \in [0, 1] }[/math]
[math]\displaystyle{ \quad n \quad }[/math] [math]\displaystyle{ B_n(x) }[/math] [math]\displaystyle{ B_n }[/math] [math]\displaystyle{ m_n }[/math] [math]\displaystyle{ M_n }[/math] [math]\displaystyle{ \quad 0 \quad }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ \quad 1 \quad }[/math] [math]\displaystyle{ x - {\small\frac{1}{2}} }[/math] [math]\displaystyle{ - {\small\frac{1}{2}} }[/math] [math]\displaystyle{ - {\small\frac{1}{2}} }[/math] [math]\displaystyle{ {\small\frac{1}{2}} }[/math] [math]\displaystyle{ \quad 2 \quad }[/math] [math]\displaystyle{ x^2 - x + {\small\frac{1}{6}} }[/math] [math]\displaystyle{ {\small\frac{1}{6}} }[/math] [math]\displaystyle{ - {\small\frac{1}{12}} }[/math] [math]\displaystyle{ {\small\frac{1}{6}} }[/math] [math]\displaystyle{ \quad 3 \quad }[/math] [math]\displaystyle{ x^3 - {\small\frac{3}{2}} x^2 + {\small\frac{1}{2}} x }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - {\small\frac{\sqrt{3}}{36}} }[/math] [math]\displaystyle{ {\small\frac{\sqrt{3}}{36}} }[/math] [math]\displaystyle{ \quad 4 \quad }[/math] [math]\displaystyle{ x^4 - 2 x^3 + x^2 - {\small\frac{1}{30}} }[/math] [math]\displaystyle{ - {\small\frac{1}{30}} }[/math] [math]\displaystyle{ - {\small\frac{1}{30}} }[/math] [math]\displaystyle{ {\small\frac{7}{240}} }[/math] [math]\displaystyle{ \quad 5 \quad }[/math] [math]\displaystyle{ x^5 - {\small\frac{5}{2}} x^4 + {\small\frac{5}{3}} x^3 - {\small\frac{1}{6}} x }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - {\small\frac{1}{6}} \sqrt{{\small\frac{1}{60}} + {\small\frac{\sqrt{30}}{1125}}} }[/math] [math]\displaystyle{ {\small\frac{1}{6}} \sqrt{{\small\frac{1}{60}} + {\small\frac{\sqrt{30}}{1125}}} }[/math] [math]\displaystyle{ \quad 6 \quad }[/math] [math]\displaystyle{ x^6 - 3 x^5 + {\small\frac{5}{2}} x^4 - {\small\frac{1}{2}} x^2 + {\small\frac{1}{42}} }[/math] [math]\displaystyle{ {\small\frac{1}{42}} }[/math] [math]\displaystyle{ - {\small\frac{31}{1344}} }[/math] [math]\displaystyle{ {\small\frac{1}{42}} }[/math]
Zauważmy, że [math]\displaystyle{ M_3 = {\small\frac{\sqrt{3}}{36}} \lt {\small\frac{3}{62}} }[/math], [math]\displaystyle{ \quad M_5 \lt {\small\frac{1}{40}} }[/math], [math]\displaystyle{ \quad M_7 \lt {\small\frac{1}{38}} \quad }[/math] oraz [math]\displaystyle{ \quad M_9 \lt {\small\frac{1}{21}} }[/math]
Przykład E17
Minima [math]\displaystyle{ m_n }[/math] i maksima [math]\displaystyle{ M_n }[/math] wielomianów Bernoulliego [math]\displaystyle{ B_n(x) }[/math] dla [math]\displaystyle{ x \in [0, 1] }[/math] są równe[6]
[math]\displaystyle{ n }[/math] [math]\displaystyle{ m_n }[/math] [math]\displaystyle{ M_n }[/math] [math]\displaystyle{ \text{uwagi} }[/math] [math]\displaystyle{ 2 k + 1 }[/math] [math]\displaystyle{ - \bigl| B_{2 k + 1} (x_{2 k}) \bigr| }[/math] [math]\displaystyle{ \bigl| B_{2 k + 1} (x_{2 k}) \bigr| }[/math] [math]\displaystyle{ B_{2 k} (x_{2 k}) = 0 \;\;\; \text{dla} \;\; x \in \left( 0, \tfrac{1}{2} \right) }[/math] [math]\displaystyle{ 4 k }[/math] [math]\displaystyle{ B_{4 k} (0) }[/math] [math]\displaystyle{ B_{4 k} \left( \tfrac{1}{2} \right) }[/math] [math]\displaystyle{ \text{dla} \;\; k \geqslant 1 }[/math] [math]\displaystyle{ 4 k + 2 }[/math] [math]\displaystyle{ B_{4 k + 2} \left( \tfrac{1}{2} \right) }[/math] [math]\displaystyle{ B_{4 k + 2} (0) }[/math] [math]\displaystyle{ }[/math]
W zamieszczonej niżej tabeli przedstawiamy liczby Bernoulliego [math]\displaystyle{ B_n }[/math] oraz minimalne i maksymalne wartości wielomianów [math]\displaystyle{ B_n(x) }[/math] dla [math]\displaystyle{ x \in [0, 1] }[/math] w zapisie dziesiętnym.
Pogrubiliśmy czcionkę w rzędzie, w którym wartości bezwzględne liczb [math]\displaystyle{ B_n, m_n, M_n }[/math] przyjmują najmniejszą wartość.
[math]\displaystyle{ n }[/math] [math]\displaystyle{ B_n }[/math] [math]\displaystyle{ m_n }[/math] [math]\displaystyle{ M_n }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ - \tfrac{1}{2} }[/math] [math]\displaystyle{ - 0.5 }[/math] [math]\displaystyle{ 0.5 }[/math] [math]\displaystyle{ 2 }[/math] [math]\displaystyle{ \tfrac{1}{6} }[/math] [math]\displaystyle{ - 0.083333333333 }[/math] [math]\displaystyle{ 0.166666666666 }[/math] [math]\displaystyle{ 3 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 0.048112522432 }[/math] [math]\displaystyle{ 0.048112522432 }[/math] [math]\displaystyle{ 4 }[/math] [math]\displaystyle{ - \tfrac{1}{30} }[/math] [math]\displaystyle{ - 0.033333333333 }[/math] [math]\displaystyle{ 0.029166666666 }[/math] [math]\displaystyle{ 5 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 0.024458190869 }[/math] [math]\displaystyle{ 0.024458190869 }[/math] [math]\displaystyle{ \mathbf{6} }[/math] [math]\displaystyle{ \mathbf{\tfrac{1}{42}} }[/math] [math]\displaystyle{ \mathbf{- 0.023065476190} }[/math] [math]\displaystyle{ \mathbf{0.023809523809} }[/math] [math]\displaystyle{ 7 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 0.026065114257 }[/math] [math]\displaystyle{ 0.026065114257 }[/math] [math]\displaystyle{ 8 }[/math] [math]\displaystyle{ - \tfrac{1}{30} }[/math] [math]\displaystyle{ - 0.033333333333 }[/math] [math]\displaystyle{ 0.033072916666 }[/math] [math]\displaystyle{ 9 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 0.047550561639 }[/math] [math]\displaystyle{ 0.047550561639 }[/math] [math]\displaystyle{ 10 }[/math] [math]\displaystyle{ \tfrac{5}{66} }[/math] [math]\displaystyle{ - 0.075609611742 }[/math] [math]\displaystyle{ 0.075757575757 }[/math] [math]\displaystyle{ 11 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 0.132496658444 }[/math] [math]\displaystyle{ 0.132496658444 }[/math] [math]\displaystyle{ 12 }[/math] [math]\displaystyle{ - \tfrac{691}{2730} }[/math] [math]\displaystyle{ - 0.253113553113 }[/math] [math]\displaystyle{ 0.252989962511 }[/math] [math]\displaystyle{ 13 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 0.523566395739 }[/math] [math]\displaystyle{ 0.523566395739 }[/math] [math]\displaystyle{ 14 }[/math] [math]\displaystyle{ \tfrac{7}{6} }[/math] [math]\displaystyle{ - 1.166524251302 }[/math] [math]\displaystyle{ 1.166666666666 }[/math] [math]\displaystyle{ 15 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 2.785040736728 }[/math] [math]\displaystyle{ 2.785040736728 }[/math] [math]\displaystyle{ 16 }[/math] [math]\displaystyle{ - \tfrac{3617}{510} }[/math] [math]\displaystyle{ - 7.092156862745 }[/math] [math]\displaystyle{ 7.091940427293 }[/math] [math]\displaystyle{ 17 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 19.18848758233 }[/math] [math]\displaystyle{ 19.18848758233 }[/math] [math]\displaystyle{ 18 }[/math] [math]\displaystyle{ \tfrac{43867}{798} }[/math] [math]\displaystyle{ - 54.97075854805 }[/math] [math]\displaystyle{ 54.97117794486 }[/math] [math]\displaystyle{ 19 }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ - 166.2291245655 }[/math] [math]\displaystyle{ 166.2291245655 }[/math] [math]\displaystyle{ 20 }[/math] [math]\displaystyle{ - \tfrac{174611}{330} }[/math] [math]\displaystyle{ - 529.1242424242 }[/math] [math]\displaystyle{ 529.1232331998 }[/math]
□
Definicja E18
Funkcje okresowe Bernoulliego [math]\displaystyle{ P_n(x) }[/math] definiujemy następująco
- [math]\displaystyle{ P_n(x) = B_n(x - \lfloor x \rfloor) }[/math]
Uwaga E19
Inaczej mówiąc funkcja okresowa Bernoulliego [math]\displaystyle{ P_n(x) }[/math] na odcinku [math]\displaystyle{ [0, 1] }[/math], przyjmuje te same wartości, co wielomian Bernoulliego [math]\displaystyle{ B_n(x) }[/math]. Wartości te powtarzają się dla kolejnych odcinków [math]\displaystyle{ [k, k + 1] }[/math], gdzie [math]\displaystyle{ k \in \mathbb{Z} }[/math].
Uwaga E20
Wprost z definicji funkcji okresowych Bernoulliego wynika, że dla [math]\displaystyle{ k \in \mathbb{Z} }[/math] jest
- [math]\displaystyle{ P_n (k) = B_n (k - \lfloor k \rfloor) = B_n (0) = B_n }[/math]
Twierdzenie E21
Własności funkcji okresowych Bernoulliego
● funkcja [math]\displaystyle{ P_0 (x) }[/math] jest ciągła i różniczkowalna ● funkcja [math]\displaystyle{ P_1 (x) }[/math] nie jest ciągła w punktach [math]\displaystyle{ x \in \mathbb{Z} }[/math] ● funkcja [math]\displaystyle{ P_2 (x) }[/math] jest ciągła, ale nie jest różniczkowalna w punktach [math]\displaystyle{ x \in \mathbb{Z} }[/math] ● dla [math]\displaystyle{ n \geqslant 3 }[/math] funkcje [math]\displaystyle{ P_n (x) }[/math] są ciągłe i różniczkowalne ● [math]\displaystyle{ {\small\frac{d}{d x}} P_n (x) = n P_{n - 1} (x) \qquad }[/math] o ile [math]\displaystyle{ n \neq 1, 2 }[/math] lub [math]\displaystyle{ n = 1, 2 }[/math] oraz [math]\displaystyle{ x \notin \mathbb{Z} }[/math] ● [math]\displaystyle{ \int^x_0 P_n (t) d t = {\small\frac{P_{n + 1} (x)}{n + 1}} - {\small\frac{B_{n + 1}}{n + 1}} }[/math]
Ciągłość funkcji okresowych Bernoulliego
Policzymy granice prawostronne i granice lewostronne funkcji okresowych Bernoulliego [math]\displaystyle{ P_n (x) }[/math] w punktach [math]\displaystyle{ x = k }[/math], gdzie [math]\displaystyle{ k \in \mathbb{Z} }[/math]. Mamy
- [math]\displaystyle{ \lim_{x \to k^+} P_n (x) = \lim_{\varepsilon \to 0} P_n (k + \varepsilon) }[/math]
- [math]\displaystyle{ \;\,\, = \lim_{\varepsilon \to 0} B_n (k + \varepsilon - \lfloor k + \varepsilon \rfloor) }[/math]
- [math]\displaystyle{ \;\,\, = \lim_{\varepsilon \to 0} B_n (k + \varepsilon - k) }[/math]
- [math]\displaystyle{ \;\,\, = \lim_{\varepsilon \to 0} B_n (\varepsilon) }[/math]
- [math]\displaystyle{ \;\,\, = B_n (0) }[/math]
- [math]\displaystyle{ \lim_{x \to k^-} P_n (x) = \lim_{\varepsilon \to 0} P_n (k - \varepsilon) }[/math]
- [math]\displaystyle{ \;\,\, = \lim_{\varepsilon \to 0} B_n (k - \varepsilon - \lfloor k - \varepsilon \rfloor) }[/math]
- [math]\displaystyle{ \;\,\, = \lim_{\varepsilon \to 0} B_n (k - \varepsilon - (k - 1)) }[/math]
- [math]\displaystyle{ \;\,\, = \lim_{\varepsilon \to 0} B_n (k - \varepsilon - k + 1) }[/math]
- [math]\displaystyle{ \;\,\, = \lim_{\varepsilon \to 0} B_n (1 - \varepsilon) }[/math]
- [math]\displaystyle{ \;\,\, = B_n (1) }[/math]
Z punktu 1. twierdzenia E8 wiemy, że dla [math]\displaystyle{ n \geqslant 2 }[/math] jest [math]\displaystyle{ B_n (0) = B_n (1) }[/math]. Oprócz tego dla [math]\displaystyle{ n = 0 }[/math] i [math]\displaystyle{ n = 1 }[/math] mamy
- [math]\displaystyle{ B_0 (0) = B_0 (1) = 1 }[/math]
oraz
- [math]\displaystyle{ B_1 (0) = - {\small\frac{1}{2}} \neq {\small\frac{1}{2}} = B_1 (1) }[/math]
Wynika stąd, że wszystkie funkcje okresowe Bernoulliego [math]\displaystyle{ P_n (x) }[/math] są ciągłe poza funkcją [math]\displaystyle{ P_1 (x) }[/math].
Różniczkowalność funkcji okresowych Bernoulliego
Pochodne funkcji okresowych Bernoulliego [math]\displaystyle{ P_n (x) }[/math] są równe
- [math]\displaystyle{ {\small\frac{d}{d x}} P_n (x) = {\small\frac{d}{d x}} B_n (x - \lfloor x \rfloor) }[/math]
- [math]\displaystyle{ \;\;\;\;\, = n B_{n - 1} (x - \lfloor x \rfloor) \cdot \left( 1 - {\small\frac{d}{d x}} \lfloor x \rfloor \right) }[/math]
- [math]\displaystyle{ \;\;\;\;\, = n P_{n - 1} (x) \cdot \left( 1 - {\small\frac{d}{d x}} \lfloor x \rfloor \right) }[/math]
Zauważmy, że pochodna [math]\displaystyle{ {\small\frac{d}{d x}} \lfloor x \rfloor = 0 }[/math] dla [math]\displaystyle{ x \notin \mathbb{Z} }[/math], ale funkcja [math]\displaystyle{ \lfloor x \rfloor }[/math] nie jest różniczkowalna w punktach [math]\displaystyle{ x \in \mathbb{Z} }[/math]. Wiemy, że pochodna funkcji w punkcie istnieje wtedy i tylko wtedy, gdy obie pochodne jednostronne w tym punkcie istnieją i są równe. Zatem musimy zbadać, czy pochodne prawostronne i lewostronne funkcji okresowych Bernoulliego [math]\displaystyle{ P_n (x) }[/math] są równe w punktach [math]\displaystyle{ x = k }[/math]. Ponieważ dla [math]\displaystyle{ x \notin \mathbb{Z} }[/math] mamy
- [math]\displaystyle{ {\small\frac{d}{d x}} P_n (x) = n P_{n - 1} (x) }[/math]
a jednocześnie dla [math]\displaystyle{ n \geqslant 3 }[/math] funkcje [math]\displaystyle{ P_{n - 1} (x) }[/math] są ciągłe, to
- [math]\displaystyle{ \lim_{x \to k^+} n P_{n - 1} (x) = \lim_{x \to k^-} n P_{n - 1} (x) }[/math]
Czyli
- [math]\displaystyle{ \lim_{x \to k^+} {\small\frac{d}{d x}} P_n (x) = \lim_{x \to k^-} {\small\frac{d}{d x}} P_n (x) }[/math]
Wynika stąd, że dla [math]\displaystyle{ n \geqslant 3 }[/math] pochodne prawostronne i lewostronne funkcji [math]\displaystyle{ P_n (x) }[/math] są równe w punktach [math]\displaystyle{ x = k }[/math]. Zatem funkcje [math]\displaystyle{ P_n (x) }[/math] są różniczkowalne w tych punktach.
Dla [math]\displaystyle{ n = 0 }[/math] jest [math]\displaystyle{ P_0 (x) = B_0 (x - \lfloor x \rfloor) = 1 }[/math], zatem [math]\displaystyle{ P_0 (x) }[/math] jest ciągła i różniczkowalna.
Dla [math]\displaystyle{ n = 1 }[/math] wiemy już, że funkcja [math]\displaystyle{ P_1 (x) }[/math] nie jest ciągła w punktach [math]\displaystyle{ x \in \mathbb{Z} }[/math], zatem nie jest w nich różniczkowalna.
Dla [math]\displaystyle{ n = 2 }[/math] mamy
- [math]\displaystyle{ \lim_{x \to k^+} 2 P_1 (x) = 2 B_1 (0) = - 1 \neq 1 = 2 B_1 (1) = \lim_{x \to k^-} 2 P_1 (x) }[/math]
Skąd wynika natychmiast, że
- [math]\displaystyle{ \lim_{x \to k^+} {\small\frac{d}{d x}} P_2 (x) \neq \lim_{x \to k^-} {\small\frac{d}{d x}} P_2 (x) }[/math]
Zatem funkcja [math]\displaystyle{ P_2 (x) }[/math] nie jest różniczkowalna w punktach [math]\displaystyle{ x \in \mathbb{Z} }[/math].
Przeprowadzane wyżej rozważania dotyczące ciągłości i różniczkowalności funkcji okresowych Bernoulliego [math]\displaystyle{ P_n (x) }[/math] stanowią dowody pierwszych pięciu punktów twierdzenia.
Punkt 6.
Ponieważ funkcja [math]\displaystyle{ P_n (t) }[/math] jest funkcją okresową o okresie równym [math]\displaystyle{ 1 }[/math], to całka oznaczona będzie równa sumie wielokrotności całek na odcinku [math]\displaystyle{ [0, 1] }[/math] i całce na odcinku [math]\displaystyle{ [0, x - \lfloor x \rfloor] }[/math].
- [math]\displaystyle{ \int^x_0 P_n (t) d t = \int_{0}^{\lfloor x \rfloor} P_n (t) d t + \int^x_{\lfloor x \rfloor} P_n (t) d t }[/math]
- [math]\displaystyle{ \;\;\; = \lfloor x \rfloor \int^1_0 P_n (t) d t + \int_{0}^{x - \lfloor x \rfloor} P_n (t) d t }[/math]
- [math]\displaystyle{ \;\;\; = \int_{0}^{x - \lfloor x \rfloor} B_n (t - \lfloor t \rfloor) d t }[/math]
- [math]\displaystyle{ \;\;\; = \int_{0}^{x - \lfloor x \rfloor} B_n (t) d t }[/math]
- [math]\displaystyle{ \;\;\; = {\small\frac{1}{n + 1}} \int_{0}^{x - \lfloor x \rfloor} \left [ {\small\frac{d}{d t}} B_{n + 1} (t) \right ] d t }[/math]
- [math]\displaystyle{ \;\;\; = {\small\frac{1}{n + 1}} \cdot B_{n + 1} (t) \biggr\rvert_{0}^{x - \lfloor x \rfloor} }[/math]
- [math]\displaystyle{ \;\;\; = {\small\frac{1}{n + 1}} [B_{n + 1} (x - \lfloor x \rfloor) - B_{n + 1} (0)] }[/math]
- [math]\displaystyle{ \;\;\; = {\small\frac{P_{n + 1} (x)}{n + 1}} - {\small\frac{B_{n + 1}}{n + 1}} }[/math]
□
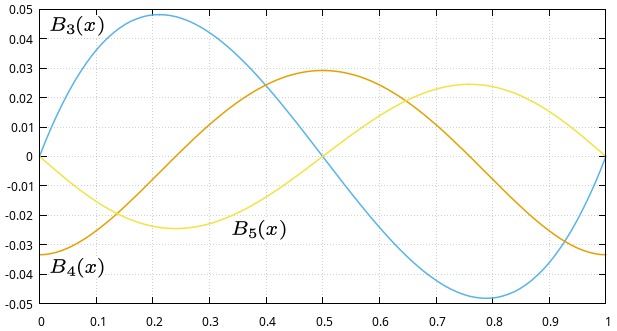
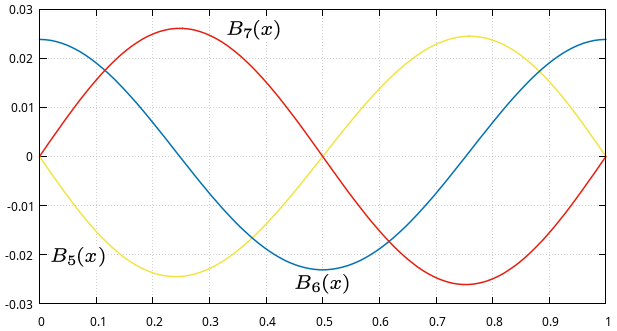
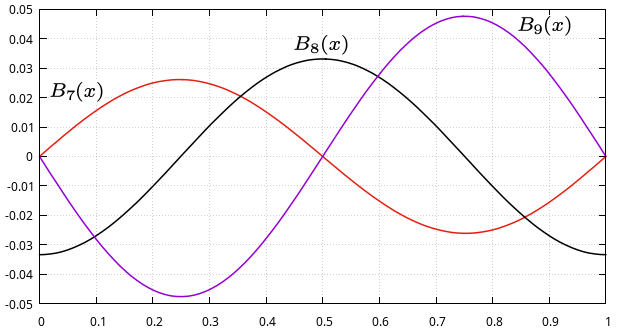
Przykład E22
Przedstawiamy przykładowe wykresy funkcji okresowych Bernoulliego [math]\displaystyle{ P_n (x) }[/math]. Stanowią one bardzo dobrą ilustrację do twierdzenia E21.
Twierdzenie E23*
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Dla liczb Bernoulliego [math]\displaystyle{ B_{2 n} = (- 1)^{n + 1} | B_{2 n} | }[/math] prawdziwe są następujące oszacowania [7][8][9]
- [math]\displaystyle{ {\small\frac{2 (2 n) !}{(2 \pi)^{2 n}}} \cdot {\small\frac{1}{1 - 2^{- 2 n}}} \lt | B_{2 n} | \lt {\small\frac{2 (2 n) !}{(2 \pi)^{2 n}}} \cdot {\small\frac{1}{1 - 2^{1 - 2 n}}} }[/math]
i asymptotyki
- [math]\displaystyle{ B_{2 n} \sim (- 1)^{n + 1} \cdot {\small\frac{2 (2 n) !}{(2 \pi)^{2 n}}} }[/math]
- [math]\displaystyle{ B_{2 n} \sim (- 1)^{n + 1} \cdot 4 \sqrt{\pi n} \cdot \left( {\small\frac{n}{\pi e}} \right)^{2 n} }[/math]
Twierdzenie E24*
Niech [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math]. Dla ilorazu kolejnych liczb Bernoulliego [math]\displaystyle{ B_{2 n} }[/math] prawdziwe są następujące oszacowania[10]
- [math]\displaystyle{ {\small\frac{2^{2 n - 1} - 1}{2^{2 n + 1} - 1}} \cdot {\small\frac{(2 n + 1) (2 n + 2)}{\pi^2}} \lt \left| {\small\frac{B_{2 n + 2}}{B_{2 n}}} \right| \lt {\small\frac{2^{2 n} - 1}{2^{2 n + 2} - 1}} \cdot {\small\frac{(2 n + 1) (2 n + 2)}{\pi^2}} }[/math]
i asymptotyka
- [math]\displaystyle{ {\small\frac{B_{2 n + 2}}{B_{2 n}}} \sim - {\small\frac{n^2}{\pi^2}} }[/math]
Wzór sumacyjny Eulera-Maclaurina
Uwaga E25
Często w twierdzeniu musimy założyć, że rozważana funkcja [math]\displaystyle{ f(x) }[/math] jest określona w pewnym zbiorze liczb rzeczywistych i jest funkcją ciągłą oraz wszystkie jej pochodne od [math]\displaystyle{ f' (x) }[/math] do [math]\displaystyle{ f^{(n)} (x) }[/math] istnieją i są ciągłe w tym zbiorze. Przekazanie tego prostego założenia wymaga użycia wielu słów, a samo twierdzenie staje się mało czytelne. Ze względów czysto praktycznych wprowadzamy pojęcie klasy funkcji.
Definicja E26
Funkcję [math]\displaystyle{ f(x) }[/math] określoną i ciągłą w zbiorze [math]\displaystyle{ A \subset \mathbb{R} }[/math] i mającą kolejno [math]\displaystyle{ n }[/math] ciągłych pochodnych w tym zbiorze będziemy nazywali funkcją klasy [math]\displaystyle{ C^n }[/math]. Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] jest ciągła w [math]\displaystyle{ A }[/math], to powiemy, że jest klasy [math]\displaystyle{ C^0 }[/math]. Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] jest klasy [math]\displaystyle{ C^n }[/math] dla dowolnego [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math], to powiemy, że funkcja [math]\displaystyle{ f(x) }[/math] jest klasy [math]\displaystyle{ C^{\infty} }[/math]. W
przypadku, gdy chcemy jednocześnie zaznaczyć dziedzinę funkcji, to stosujemy zapis [math]\displaystyle{ C^0 (A) }[/math], [math]\displaystyle{ C^n (A) }[/math] i [math]\displaystyle{ C^{\infty} (A) }[/math].
Przykład E27
Tylko dla potrzeb tego przykładu funkcję [math]\displaystyle{ f(x) }[/math] określoną następująco
- [math]\displaystyle{ f(x) = \left\{ \begin{array}{lll} g (x) & & x \lt 0\\ h (x) & & x \geqslant 0 \end{array} \right. }[/math]
będziemy zapisywali jako [math]\displaystyle{ f(x) = \left \{ g (x) \big\rvert h (x) \right \} }[/math].
Przykłady funkcji klasy [math]\displaystyle{ C^0 (\mathbb{R}) }[/math]
- [math]\displaystyle{ \left \{ - x \big\rvert x \right \} \;\; \text{czyli} \;\; | x | , \quad \left \{ 0 \big\rvert x \right \} , \quad \left \{ 1 \big\rvert e^x \right \} , \quad \left \{ 1 + x \big\rvert \cos (x) \right \} }[/math]
Przykłady funkcji klasy [math]\displaystyle{ C^1 (\mathbb{R}) }[/math]
- [math]\displaystyle{ \left \{ 0 \big\rvert x^2 \right \} , \quad \left \{ 1 + x \big\rvert e^x \right \} , \quad \left \{ 1 \big\rvert \cos (x) \right \} }[/math]
Przykłady funkcji klasy [math]\displaystyle{ C^2 (\mathbb{R}) }[/math]
- [math]\displaystyle{ x^2 \sqrt{x^2} , \quad \left \{ 0 \big\rvert x^3 \right \} , \quad \left \{ 1 + x + \tfrac{1}{2} x^2 \big\rvert e^x \right \} , \quad \left \{ x \big\rvert \sin (x) \right \} }[/math]
Przykłady funkcji klasy [math]\displaystyle{ C^3 (\mathbb{R}) }[/math]
- [math]\displaystyle{ \left \{ 0 \big\rvert x^4 \right \} , \quad \left \{ 1 + x + \tfrac{1}{2} x^2 + \tfrac{1}{6} x^3 \big\rvert e^x \right \} , \quad \left \{ 1 - \tfrac{1}{2} x^2 \big\rvert \cos (x) \right \} }[/math]
Przykłady funkcji klasy [math]\displaystyle{ C^n (\mathbb{R}) }[/math]
- [math]\displaystyle{ P_{n + 2} (x) , \quad x^n \sqrt{x^2} , \quad \left \{ 0 \big\rvert x^{n + 1} \right \} , \quad \left\{ \sum_{k = 0}^{n} {\small\frac{x^k}{k!}} \biggr\rvert e^x \right\} }[/math]
Przykłady funkcji klasy [math]\displaystyle{ C^{\infty} (\mathbb{R}) }[/math]
- [math]\displaystyle{ x^k \;\; \text{dla} \;\; k \in \mathbb{N}_0 , \quad e^x , \quad \sin (x) , \quad \cos (x) }[/math]
Przykłady funkcji klasy [math]\displaystyle{ C^{\infty} (\mathbb{R}_+) }[/math]
- [math]\displaystyle{ {\small\frac{1}{x}} }[/math], [math]\displaystyle{ \sqrt{x} }[/math], [math]\displaystyle{ \log x }[/math]
Twierdzenie E28
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją rzeczywistą klasy [math]\displaystyle{ C^1 ( [k, k + 1] ) }[/math], gdzie [math]\displaystyle{ k \in \mathbb{Z} }[/math]. Jeżeli zastąpimy na jednostkowym odcinku pole prostokąta całką, to błąd, jaki popełnimy, jest równy
- [math]\displaystyle{ f(k) - \int_{k}^{k + 1} f(t) d t = \int_k^{k + 1} (t - \lfloor t \rfloor - 1) f'(t) d t }[/math]
Całkując przez części, dostajemy
- [math]\displaystyle{ \int_k^{k + 1} f(t) d t = f(t) \cdot t \biggr\rvert_{k}^{k+1} - \int_k^{k + 1} f'(t) \cdot t d t }[/math]
- [math]\displaystyle{ \quad \, = (k + 1) \cdot f(k + 1) - k \cdot f(k) - \int_k^{k + 1} t \cdot f'(t) d t }[/math]
- [math]\displaystyle{ \quad \, = k \cdot f(k + 1) + f(k + 1) - k \cdot f(k) - \int_k^{k + 1} t \cdot f'(t) d t }[/math]
- [math]\displaystyle{ \quad \, = f(k + 1) + \int_k^{k + 1} k \cdot f'(t) d t - \int_k^{k + 1} t \cdot f'(t) d t }[/math]
Zatem poszukiwaną różnicę możemy zapisać w postaci
- [math]\displaystyle{ f(k) - \int_{k}^{k + 1} f(t) d t = f(k) - f(k + 1) - \int_k^{k + 1} k \cdot f'(t) d t + \int_k^{k + 1} t \cdot f'(t) d t }[/math]
- [math]\displaystyle{ = - \int_k^{k + 1} f'(t) d t - \int_k^{k + 1} k \cdot f'(t) d t + \int_k^{k + 1} t \cdot f'(t) d t }[/math]
- [math]\displaystyle{ = \int_k^{k + 1} (t - k - 1) f'(t) d t }[/math]
- [math]\displaystyle{ = \int_k^{k + 1} (t - \lfloor t \rfloor - 1) f'(t) d t }[/math]
Co należało pokazać.
□
Zadanie E29
Pokazać, że dla [math]\displaystyle{ x \gt 0 }[/math] całka [math]\displaystyle{ \int^x_0 (t - \lfloor t \rfloor)^n d t }[/math] jest równa
- [math]\displaystyle{ \int^x_0 (t - \lfloor t \rfloor)^n d t = {\small\frac{\lfloor x \rfloor + (x - \lfloor x \rfloor)^{n + 1}}{n + 1}} }[/math]
Ponieważ funkcja [math]\displaystyle{ (x - \lfloor x \rfloor)^n }[/math] jest funkcją okresową o okresie równym [math]\displaystyle{ 1 }[/math], to całka oznaczona będzie równa sumie wielokrotności całek na odcinku [math]\displaystyle{ [0, 1] }[/math] i całce na odcinku [math]\displaystyle{ [0, x - \lfloor x \rfloor] }[/math].
- [math]\displaystyle{ \int^x_0 (t - \lfloor t \rfloor)^n d t = \int_{0}^{\lfloor x \rfloor} (t - \lfloor t \rfloor)^n d t + \int^x_{\lfloor x \rfloor} (t - \lfloor t \rfloor)^n d t }[/math]
- [math]\displaystyle{ \;\;\;\; = \lfloor x \rfloor \cdot \int^1_0 (t - \lfloor t \rfloor)^n d t + \int^{x - \lfloor x \rfloor}_0 (t - \lfloor t \rfloor)^n d t }[/math]
- [math]\displaystyle{ \;\;\;\; = \lfloor x \rfloor \cdot \int^1_0 t^n d t + \int_{0}^{x - \lfloor x \rfloor} t^n d t }[/math]
- [math]\displaystyle{ \;\;\;\; = \lfloor x \rfloor \cdot {\normalsize\frac{t^{n + 1}}{n + 1}} \biggr\rvert_{0}^{1} + {\normalsize\frac{t^{n + 1}}{n + 1}} \biggr\rvert_{0}^{x - \lfloor x \rfloor} }[/math]
- [math]\displaystyle{ \;\;\;\; = \lfloor x \rfloor \cdot {\normalsize\frac{1}{n + 1}} + {\normalsize\frac{(x - \lfloor x \rfloor)^{n + 1}}{n + 1}} }[/math]
- [math]\displaystyle{ \;\;\;\; = {\normalsize\frac{\lfloor x \rfloor + (x - \lfloor x \rfloor)^{n + 1}}{n + 1}} }[/math]
Co należało pokazać.
□
Twierdzenie E30
Niech [math]\displaystyle{ f(x) }[/math] będzie funkcją rzeczywistą klasy [math]\displaystyle{ C^1 ( [a, b] ) }[/math], gdzie [math]\displaystyle{ a, b \in \mathbb{Z} }[/math]. Możemy zastąpić sumowanie całkowaniem, stosując wzór
- [math]\displaystyle{ \sum_{k = a}^{b} f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \int_a^b \left( t - \lfloor t \rfloor - {\small\frac{1}{2}} \right) f'(t) d t }[/math]
Powyższy wzór można zapisać w postaci
[math]\displaystyle{ \sum_{k = a}^{b} f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \int_a^b P_1(t) f'(t) d t }[/math]
gdzie [math]\displaystyle{ P_1(t) }[/math] jest funkcją okresową Bernoulliego.
Sumując uzyskany w twierdzeniu E28 związek od [math]\displaystyle{ k = a }[/math] do [math]\displaystyle{ k = b - 1 }[/math], dostajemy
- [math]\displaystyle{ \sum_{k = a}^{b - 1} f(k) - \int^b_a f(t) d t = \int_a^b (t - \lfloor t \rfloor - 1) f'(t) d t }[/math]
Dodając do obydwu stron [math]\displaystyle{ f(b) }[/math] i przekształcając prawą stronę, mamy
- [math]\displaystyle{ \sum_{k = a}^{b} f(k) = f(b) + \int^b_a f(t) d t + \int_a^b \left( t - \lfloor t \rfloor - {\small\frac{1}{2}} \right) f'(t) d t - {\small\frac{1}{2}} f(b) + {\small\frac{1}{2}} f(a) }[/math]
- [math]\displaystyle{ \;\;\:\, = \int^b_a f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \int_a^b \left( t - \lfloor t \rfloor - {\small\frac{1}{2}} \right) f'(t) d t }[/math]
- [math]\displaystyle{ \;\;\:\, = \int^b_a f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \int_a^b \left( t - \lfloor t \rfloor - {\small\frac{1}{2}} \right) f'(t) d t }[/math]
□
Uwaga E31
Czytelnik zapewne już domyśla się, w jakim kierunku zmierzamy. Całkując przez części i korzystając z własności funkcji okresowych Bernoulliego, przekształcimy całkę [math]\displaystyle{ \int_a^b P_1 (t) f' (t) d t }[/math] do postaci [math]\displaystyle{ \int_a^b P_2 (t) f'' (t) d t }[/math], a następnie do postaci [math]\displaystyle{ \int_a^b P_3 (t) f^{(3)} (t) d t }[/math] itd.
Twierdzenie E32
Niech [math]\displaystyle{ a, b \in \mathbb{Z} }[/math], a funkcje [math]\displaystyle{ P_n(t) }[/math], gdzie [math]\displaystyle{ n \geqslant 1 }[/math], będą funkcjami okresowymi Bernoulliego. Jeżeli funkcja rzeczywista [math]\displaystyle{ g(t) }[/math] jest klasy [math]\displaystyle{ C^1 ( [a, b] ) }[/math], to
- [math]\displaystyle{ \int_a^b P_n(t) g(t) d t = {\small\frac{B_{n + 1}}{n + 1}} [g(b) - g(a)] - {\small\frac{1}{n + 1}} \int_a^b P_{n + 1}(t) g'(t) d t }[/math]
Niech [math]\displaystyle{ k \in \mathbb{Z} }[/math]. Rozważmy całkę [math]\displaystyle{ \int_a^b P_n(t) g(t) d t }[/math] na odcinku [math]\displaystyle{ [k, k + 1] \subset [a, b] }[/math]. Całkując przez części, dostajemy
- [math]\displaystyle{ \int_k^{k + 1} P_n(t) g(t) d t = {\small\frac{1}{n + 1}} P_{n + 1}(t) g(t) \biggr\rvert_{k}^{k + 1} - {\small\frac{1}{n + 1}} \int_k^{k + 1} P_{n + 1}(t) g'(t) d t }[/math]
- [math]\displaystyle{ \;\: = {\small\frac{1}{n + 1}} P_{n + 1}(k + 1) g(k + 1) - {\small\frac{1}{n + 1}} P_{n + 1}(k) g(k) - {\small\frac{1}{n + 1}} \int_k^{k + 1} P_{n + 1}(t) g'(t) d t }[/math]
- [math]\displaystyle{ \;\: = {\small\frac{1}{n + 1}} B_{n + 1} \cdot g (k + 1) - {\small\frac{1}{n + 1}} B_{n + 1} \cdot g (k) - {\small\frac{1}{n + 1}} \int_k^{k + 1} P_{n + 1}(t) g'(t) d t }[/math]
- [math]\displaystyle{ \;\: = {\small\frac{B_{n + 1}}{n + 1}} \cdot [g (k + 1) - g (k)] - {\small\frac{1}{n + 1}} \int_k^{k + 1} P_{n + 1}(t) g'(t) d t }[/math]
Przekształcając, skorzystaliśmy z faktu, że dla [math]\displaystyle{ n \geqslant 1 }[/math] jest
- [math]\displaystyle{ P_{n + 1} (k + 1) = P_{n + 1} (k) = B_{n + 1} }[/math]
Sumując po [math]\displaystyle{ k }[/math] od [math]\displaystyle{ k = a }[/math] do [math]\displaystyle{ k = b - 1 }[/math], natychmiast otrzymujemy
- [math]\displaystyle{ \int_a^b P_n(t) g(t) d t = {\small\frac{B_{n + 1}}{n + 1}} [g(b) - g(a)] - {\small\frac{1}{n + 1}} \int_a^b P_{n + 1}(t) g'(t) d t }[/math]
Co należało udowodnić.
□
Twierdzenie E33
Niech [math]\displaystyle{ a, b \in \mathbb{Z} }[/math], a funkcje [math]\displaystyle{ P_n (t) }[/math], gdzie [math]\displaystyle{ n \geqslant 1 }[/math], będą funkcjami okresowymi Bernoulliego. Jeżeli funkcja rzeczywista [math]\displaystyle{ g(t) }[/math] jest klasy [math]\displaystyle{ C^k ( [a, b] ) }[/math], to
- [math]\displaystyle{ \int_a^b P_n (t) g (t) d t = \sum_{j = 1}^k \frac{(- 1)^{j + 1} n! \cdot B_{n + j}}{(n + j) !} [g^{(j - 1)} (b) - g^{(j - 1)} (a)] + {\normalsize\frac{(- 1)^k n!}{(n + k) !}} \int_a^b P_{n + k} (t) g^{(k)} (t) d t }[/math]
Indukcja matematyczna. Dla [math]\displaystyle{ k = 1 }[/math] dostajemy
- [math]\displaystyle{ \int_a^b P_n (t) g (t) d t = {\normalsize\frac{B_{n + 1}}{n + 1}} [g (b) - g (a)] - {\normalsize\frac{1}{n + 1}} \int_a^b P_{n + 1} (t) g^{(1)} (t) d t }[/math]
Czyli wzór udowodniony w twierdzeniu E32. Zatem twierdzenie jest prawdziwe dla [math]\displaystyle{ k = 1 }[/math]. Zauważmy, że z tego samego twierdzenia natychmiast wynika, że
- [math]\displaystyle{ \int_a^b P_{n + k} (t) g^{(k)} (t) d t = {\normalsize\frac{B_{n + k + 1}}{n + k + 1}} [g^{(k)} (b) - g^{(k)} (a)] - {\normalsize\frac{1}{n + k + 1}} \int_a^b P_{n + k + 1} (t) g^{(k + 1)} (t) d t }[/math]
Korzystając z powyższego wyniku, przy założeniu, że dowodzony wzór jest prawdziwy dla [math]\displaystyle{ k \in \mathbb{Z}_+ }[/math], otrzymujemy
- [math]\displaystyle{ \int_a^b P_n (t) g (t) d t = \sum_{j = 1}^k \frac{(- 1)^{j + 1} n! \cdot B_{n + j}}{(n + j) !} [g^{(j - 1)} (b) - g^{(j - 1)} (a)] + {\normalsize\frac{(- 1)^k n!}{(n + k) !}} \int_a^b P_{n + k} (t) g^{(k)} (t) d t }[/math]
- [math]\displaystyle{ \;\;\;\, = \sum_{j = 1}^k \frac{(- 1)^{j + 1} n! \cdot B_{n + j}}{(n + j) !} [g^{(j - 1)} (b) - g^{(j - 1)} (a)] + {\normalsize\frac{(- 1)^k n!}{(n + k) !}} \left[ {\normalsize\frac{B_{n + k + 1}}{n + k + 1}} [g^{(k)} (b) - g^{(k)} (a)] - {\normalsize\frac{1}{n + k + 1}} \int_a^b P_{n + k + 1} (t) g^{(k + 1)} (t) d t \right] }[/math]
- [math]\displaystyle{ \;\;\;\, = \sum_{j = 1}^k \frac{(- 1)^{j + 1} n! \cdot B_{n + j}}{(n + j) !} [g^{(j - 1)} (b) - g^{(j - 1)} (a)] + \frac{(- 1)^{k + 2} n! \cdot B_{n + k + 1}}{(n + k + 1) !} [g^{(k)} (b) - g^{(k)} (a)] + {\normalsize\frac{(- 1)^{k + 1} n!}{(n + k + 1) !}} \int_a^b P_{n + k + 1} (t) g^{(k + 1)} (t) d t }[/math]
- [math]\displaystyle{ \;\;\;\, = \sum_{j = 1}^{k + 1} \frac{(- 1)^{j + 1} n! \cdot B_{n + j}}{(n + j) !} [g^{(j - 1)} (b) - g^{(j - 1)} (a)] + {\normalsize\frac{(- 1)^{k + 1} n!}{(n + k + 1) !}} \int_a^b P_{n + k + 1} (t) g^{(k + 1)} (t) d t }[/math]
Tym samym pokazaliśmy prawdziwość dowodzonego wzoru dla [math]\displaystyle{ k + 1 }[/math]. Na mocy zasady indukcji matematycznej dowodzony wzór jest prawdziwy dla wszystkich [math]\displaystyle{ k \in \mathbb{Z}_+ }[/math].
□
Twierdzenie E34 (wzór sumacyjny Eulera-Maclaurina, [math]\displaystyle{ \sim }[/math]1735)
Niech [math]\displaystyle{ a, b \in \mathbb{Z} }[/math], a funkcje [math]\displaystyle{ P_r (t) }[/math], gdzie [math]\displaystyle{ r \geqslant 1 }[/math], będą funkcjami okresowymi Bernoulliego. Jeżeli funkcja rzeczywista [math]\displaystyle{ f(t) }[/math] jest klasy [math]\displaystyle{ C^r ( [a, b] ) }[/math], to
[math]\displaystyle{ \sum_{k = a}^b f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \sum_{k = 2}^r {\small\frac{B_k}{k!}} [f^{(k - 1)}(b) - f^{(k - 1)}(a)] - {\small\frac{(- 1)^r}{r!}} \int_a^b P_r(t) f^{(r)}(t) d t }[/math]
Lewą stronę wzoru udowodnionego w twierdzeniu E33
- [math]\displaystyle{ \int_a^b P_n (t) g (t) d t = \sum_{j = 1}^k \frac{(- 1)^{j + 1} n! \cdot B_{n + j}}{(n + j) !} [g^{(j - 1)} (b) - g^{(j - 1)} (a)] + {\normalsize\frac{(- 1)^k n!}{(n + k) !}} \int_a^b P_{n + k} (t) g^{(k)} (t) d t }[/math]
chcemy przekształcić do postaci, która występuje po prawej stronie wzoru z twierdzenia E30. Jeżeli położymy [math]\displaystyle{ n = 1 }[/math] oraz [math]\displaystyle{ g(t) = f' (t) = f^{(1)} (t) }[/math], to dostaniemy
- [math]\displaystyle{ \int_a^b P_1 (t) f' (t) d t = \sum_{j = 1}^k \frac{(- 1)^{j + 1} \cdot B_{j + 1}}{(j + 1) !} [f^{(j)} (b) - f^{(j)} (a)] + {\normalsize\frac{(- 1)^k}{(k + 1) !}} \int_a^b P_{k + 1} (t) f^{(k + 1)} (t) d t }[/math]
Niech [math]\displaystyle{ k = r - 1 }[/math]
- [math]\displaystyle{ \int_a^b P_1 (t) f' (t) d t = \sum_{j = 1}^{r - 1} \frac{(- 1)^{j + 1} \cdot B_{j + 1}}{(j + 1) !} [f^{(j)} (b) - f^{(j)} (a)] + {\normalsize\frac{(- 1)^{r - 1}}{r!}} \int_a^b P_r (t) f^{(r)} (t) d t }[/math]
Ponieważ litera [math]\displaystyle{ k }[/math] już nie występuje we wzorze, to wykorzystamy ją jako nowy wskaźnik sumowania. Od sumowania po [math]\displaystyle{ j }[/math] przejdźmy do sumowania po [math]\displaystyle{ k = j + 1 }[/math], czyli [math]\displaystyle{ k }[/math] zmienia się teraz od [math]\displaystyle{ 2 }[/math] do [math]\displaystyle{ r }[/math]
- [math]\displaystyle{ \int_a^b P_1 (t) f' (t) d t = \sum_{k = 2}^r {\normalsize\frac{(- 1)^k \cdot B_k}{k!}} [f^{(k - 1)} (b) - f^{(k - 1)} (a)] - {\normalsize\frac{(- 1)^r}{r!}} \int_a^b P_r (t) f^{(r)} (t) d t }[/math]
Podstawiając powyższy wzór do twierdzenia E30, otrzymujemy, że jeżeli funkcja [math]\displaystyle{ f(t) }[/math] jest klasy [math]\displaystyle{ C^r ( [a, b] ) }[/math], gdzie [math]\displaystyle{ r \geqslant 1 }[/math], to
- [math]\displaystyle{ \sum_{k = a}^{b} f (k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \sum_{k = 2}^r {\small\frac{(- 1)^k B_k}{k!}} [f^{(k - 1)}(b) - f^{(k - 1)}(a)] - {\small\frac{(- 1)^r}{r!}} \int_a^b P_r(t) f^{(r)}(t) d t }[/math]
Zauważmy, że [math]\displaystyle{ (- 1)^k B_k = B_k }[/math], bo dla nieparzystych liczb [math]\displaystyle{ k \geqslant 2 }[/math] mamy [math]\displaystyle{ (- 1)^k B_k = 0 = B_k }[/math], a dla parzystych liczb [math]\displaystyle{ k \geqslant 2 }[/math] jest [math]\displaystyle{ (- 1)^k B_k = B_k }[/math]. Czynnik [math]\displaystyle{ (- 1)^k }[/math] został dodany tylko dla potrzeb dowodu indukcyjnego twierdzenia E33. Zatem otrzymujemy
- [math]\displaystyle{ \sum_{k = a}^b f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \sum_{k = 2}^r {\small\frac{B_k}{k!}} [f^{(k - 1)}(b) - f^{(k - 1)}(a)] - {\small\frac{(- 1)^r}{r!}} \int_a^b P_r(t) f^{(r)}(t) d t }[/math]
Co należało pokazać.
□
Uwaga E35
Uwzględniając, że dla nieparzystych liczb [math]\displaystyle{ k \geqslant 2 }[/math] jest [math]\displaystyle{ B_k = 0 }[/math], możemy dla parzystego [math]\displaystyle{ r = 2 s }[/math] napisać
[math]\displaystyle{ \sum_{k = a}^b f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \sum_{k = 1}^s {\small\frac{B_{2 k}}{(2 k) !}} [f^{(2 k - 1)}(b) - f^{(2 k - 1)}(a)] - {\small\frac{1}{(2 s) !}} \int_a^b P_{2 s}(t) f^{(2 s)}(t) d t }[/math]
W przypadku, gdy [math]\displaystyle{ r = 2 s + 1 }[/math] mamy [math]\displaystyle{ B_{2 s + 1} = 0 }[/math], zatem nie pojawi się nowy składnik sumy, ale ostatni wyraz ulegnie zmianie
[math]\displaystyle{ \sum_{k = a}^b f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \sum_{k = 1}^s {\small\frac{B_{2 k}}{(2 k) !}} [f^{(2 k - 1)}(b) - f^{(2 k - 1)}(a)] + {\small\frac{1}{(2 s + 1) !}} \int_a^b P_{2 s + 1}(t) f^{(2 s + 1)}(t) d t }[/math]
Oczywiście
- [math]\displaystyle{ - {\small\frac{1}{(2 s) !}} \int_a^b P_{2 s} (t) f^{(2 s)} (t) d t = {\small\frac{1}{(2 s + 1) !}} \int_a^b P_{2 s + 1} (t) f^{(2 s + 1)} (t) d t }[/math]
(zobacz twierdzenie E32).
Uwaga E36
Poniżej wypisaliśmy gotowe wzory Eulera-Maclaurina dla [math]\displaystyle{ r = 1, \ldots, 9 }[/math]
- [math]\displaystyle{ \sum_{k = a}^b f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + Q_r }[/math]
gdzie
[math]\displaystyle{ \quad \;\: r \quad }[/math] [math]\displaystyle{ Q_r }[/math] [math]\displaystyle{ \quad \;\: 1. \quad }[/math] [math]\displaystyle{ \int_a^b P_1(t) f'(t) d t }[/math] [math]\displaystyle{ \quad \;\: 2. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] - {\small\frac{1}{2}} \int_a^b P_2(t) f''(t) d t }[/math] [math]\displaystyle{ \quad \;\: 3. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] + {\small\frac{1}{6}} \int_a^b P_3(t) f^{(3)}(t) d t }[/math] [math]\displaystyle{ \quad \;\: 4. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] - {\small\frac{1}{720}} [f^{(3)}(b) - f^{(3)}(a)] - {\small\frac{1}{24}} \int_a^b P_4(t) f^{(4)}(t) d t }[/math] [math]\displaystyle{ \quad \;\: 5. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] - {\small\frac{1}{720}} [f^{(3)}(b) - f^{(3)}(a)] + {\small\frac{1}{120}} \int_a^b P_5(t) f^{(5)}(t) d t }[/math] [math]\displaystyle{ \quad \;\: 6. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] - {\small\frac{1}{720}} [f^{(3)}(b) - f^{(3)}(a)] + {\small\frac{1}{30240}} [f^{(5)}(b) - f^{(5)}(a)] - {\small\frac{1}{720}} \int_a^b P_6(t) f^{(6)}(t) d t }[/math] [math]\displaystyle{ \quad \;\: 7. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] - {\small\frac{1}{720}} [f^{(3)}(b) - f^{(3)}(a)] + {\small\frac{1}{30240}} [f^{(5)}(b) - f^{(5)}(a)] + {\small\frac{1}{5040}} \int_a^b P_7(t) f^{(7)}(t) d t }[/math] [math]\displaystyle{ \quad \;\: 8. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] - {\small\frac{1}{720}} [f^{(3)}(b) - f^{(3)}(a)] + {\small\frac{1}{30240}} [f^{(5)}(b) - f^{(5)}(a)] - {\small\frac{1}{1209600}} [f^{(7)}(b) - f^{(7)}(a)] - {\small\frac{1}{40320}} \int_a^b P_8(t) f^{(8)}(t) d t }[/math] [math]\displaystyle{ \quad \;\: 9. \quad }[/math] [math]\displaystyle{ {\small\frac{1}{12}} [f'(b) - f'(a)] - {\small\frac{1}{720}} [f^{(3)}(b) - f^{(3)}(a)] + {\small\frac{1}{30240}} [f^{(5)}(b) - f^{(5)}(a)] - {\small\frac{1}{1209600}} [f^{(7)}(b) - f^{(7)}(a)] + {\small\frac{1}{362880}} \int_a^b P_9(t) f^{(9)}(t) d t }[/math]
Nim przejdziemy do przykładów, przypomnimy kilka podstawowych definicji i twierdzeń dotyczących całek niewłaściwych.
Całki niewłaściwe – zbieżność i kryteria zbieżności
Definicja E37
Niech funkcja [math]\displaystyle{ f(x) }[/math] będzie określona w przedziale [math]\displaystyle{ [a, + \infty) }[/math] i całkowalna w każdym podprzedziale [math]\displaystyle{ [a, b] }[/math] tego przedziału. Granicę
- [math]\displaystyle{ \lim_{b \to + \infty} \int^b_a f(x) d x }[/math]
będziemy nazywali całką niewłaściwą funkcji [math]\displaystyle{ f(x) }[/math] w granicach od [math]\displaystyle{ a }[/math] do [math]\displaystyle{ + \infty }[/math] i zapisywali symbolicznie jako
- [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math]
Jeżeli powyższa granica jest skończona, to powiemy, że całka [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math] jest zbieżna. Jeżeli granica jest nieskończona lub nie istnieje, to powiemy, że całka jest rozbieżna.
Twierdzenie E38 (kryterium porównawcze)
Jeżeli dla [math]\displaystyle{ x \geqslant a }[/math] funkcje [math]\displaystyle{ f(x) }[/math] i [math]\displaystyle{ g(x) }[/math] spełniają nierówności
- [math]\displaystyle{ 0 \leqslant f(x) \leqslant g(x) }[/math]
to
● ze zbieżności całki [math]\displaystyle{ \int_{a}^{\infty} g(x) d x }[/math] wynika zbieżność całki [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math] ● z rozbieżności całki [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math] wynika rozbieżność całki [math]\displaystyle{ \int_{a}^{\infty} g(x) d x }[/math]
Punkt 1.
Niech [math]\displaystyle{ m \in \mathbb{Z}_+ }[/math] będzie wybrane dowolnie, ale tak, aby [math]\displaystyle{ m \gt a }[/math]. Ponieważ z założenia funkcje [math]\displaystyle{ f(x) }[/math] i [math]\displaystyle{ g(x) }[/math] są całkowalne w dowolnym podprzedziale [math]\displaystyle{ [a, b] }[/math] przedziału [math]\displaystyle{ [a, \infty) }[/math], to całki
- [math]\displaystyle{ \int^m_a f(x) d x \qquad }[/math] oraz [math]\displaystyle{ \qquad \int^m_a g(x) d x }[/math]
istnieją, a ich wartość nie wpływa na zbieżność / rozbieżność odpowiednich całek niewłaściwych. Zatem możemy ograniczyć się do badania zbieżności całek
- [math]\displaystyle{ \int_{m}^{\infty} f(x) d x \qquad }[/math] oraz [math]\displaystyle{ \qquad \int_{m}^{\infty} g(x) d x }[/math]
Niech dla [math]\displaystyle{ k \geqslant m }[/math] ciąg [math]\displaystyle{ (U_k) }[/math] będzie rosnącym ciągiem kolejnych całek oznaczonych
- [math]\displaystyle{ U_k = \int_m^k f(x) d x }[/math]
Ponieważ z założenia dla [math]\displaystyle{ x \geqslant m \gt a }[/math] funkcje [math]\displaystyle{ f(x) }[/math] i [math]\displaystyle{ g(x) }[/math] spełniają nierówności
- [math]\displaystyle{ 0 \leqslant f(x) \leqslant g(x) }[/math]
to ciąg [math]\displaystyle{ (U_k) }[/math] jest ograniczony od góry
- [math]\displaystyle{ U_k = \int^k_m f(x) d x \leqslant \int^k_m g(x) d x \leqslant \int_{m}^{\infty} g(x) d x }[/math]
bo założyliśmy, że całka [math]\displaystyle{ \int_{m}^{\infty} g(x) d x }[/math] jest zbieżna. Ponieważ ciąg [math]\displaystyle{ (U_k) }[/math] jest rosnący i ograniczony od góry, to jest zbieżny. Wynika stąd istnienie granic
- 1. [math]\displaystyle{ \qquad \lim_{k \to \infty} U_k = g }[/math]
- 2. [math]\displaystyle{ \qquad \lim_{k \to \infty} \int_{k}^{k + 1} f(x) d x = \lim_{k \to \infty} U_{k + 1} - \lim_{k \to \infty} U_k = g - g = 0 }[/math]
- 3. [math]\displaystyle{ \qquad \lim_{b \to \infty} \left( \int^b_m f(x) d x - U_{\lfloor b \rfloor} \right) = 0 }[/math]
- 4. [math]\displaystyle{ \qquad \lim_{b \to \infty} \int^b_m f(x) d x = \lim_{b \to \infty} \left[ \left( \int^b_m f(x) d x - U_{\lfloor b \rfloor} \right) + U_{\lfloor b \rfloor} \right] = \lim_{b \to \infty} \left( \int^b_m f(x) d x - U_{\lfloor b \rfloor} \right) + \lim_{b \to \infty} U_{\lfloor b \rfloor} = 0 + g = g }[/math]
Trzecia granica wymaga krótkiego omówienia. Prawdziwy jest następujący ciąg nierówności
- [math]\displaystyle{ 0 \leqslant \int^b_m f(x) d x - U_{\lfloor b \rfloor} = \int^b_m f(x) d x - \int_{m}^{\lfloor b \rfloor} f(x) d x = \int^b_{\lfloor b \rfloor} f(x) d x \leqslant \int^{\lfloor b \rfloor + 1}_{\lfloor b \rfloor} f(x) d x }[/math]
Wystarczy zauważyć, że w granicy dla [math]\displaystyle{ b \rightarrow \infty }[/math] ostatni wyraz po prawej stronie dąży do zera (granica nr 2).
Zatem całka [math]\displaystyle{ \int_{m}^{\infty} f(x) d x }[/math] jest zbieżna. Co kończy dowód punktu 1.
Punkt 2.
Z założenia całka [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math] jest rozbieżna. Przypuśćmy, że całka [math]\displaystyle{ \int_{a}^{\infty} g(x) d x }[/math] jest zbieżna. Jeśli tak, to na podstawie udowodnionego już punktu 1. całka [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math] musiałaby być zbieżna, wbrew założeniu, że jest rozbieżna. Otrzymana sprzeczność dowodzi, że nasze przypuszczenie o zbieżności całki [math]\displaystyle{ \int_{a}^{\infty} g(x) d x }[/math] jest fałszywe. Co kończy dowód punktu 2.
□
Twierdzenie E39
Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] jest całkowalna w każdym podprzedziale [math]\displaystyle{ [a, b] }[/math] przedziału [math]\displaystyle{ [a, + \infty) }[/math] i całka [math]\displaystyle{ \int_{a}^{\infty} | f(x) | d x }[/math] jest zbieżna, to zbieżna jest też całka [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math]. O całce [math]\displaystyle{ \int_{a}^{\infty} f (x) d x }[/math] powiemy wtedy, że jest bezwzględnie zbieżna.
Ponieważ
- [math]\displaystyle{ 0 \leqslant f(x) + | f(x) | \leqslant 2 | f(x) | }[/math]
to z kryterium porównawczego wynika, że całka
- [math]\displaystyle{ \int_{a}^{\infty} (f(x) + | f(x) |) d x }[/math]
jest zbieżna. Zatem całka
- [math]\displaystyle{ \int_{a}^{\infty} f(x) d x = \int_{a}^{\infty} (f(x) + | f(x) |) d x - \int_{a}^{\infty} | f(x) | d x }[/math]
jest różnicą całek zbieżnych i również musi być zbieżna.
□
Twierdzenie E40
Jeżeli całka [math]\displaystyle{ \int_{a}^{\infty} | f(x) | d x }[/math] jest zbieżna, a funkcja [math]\displaystyle{ g(x) }[/math] jest ograniczona, to zbieżna jest też całka [math]\displaystyle{ \int_{a}^{\infty} | f(x) g(x) | d x }[/math].
Z założenia funkcja [math]\displaystyle{ g(x) }[/math] jest ograniczona, zatem istnieje taka liczba [math]\displaystyle{ M \gt 0 }[/math], że dla każdego [math]\displaystyle{ x \geqslant a }[/math] jest [math]\displaystyle{ | g(x) | \leqslant M }[/math]. Zauważmy, że dla [math]\displaystyle{ x \geqslant a }[/math] prawdziwy jest układ nierówności
- [math]\displaystyle{ 0 \leqslant {\small\frac{1}{M}} | f(x) g(x) | \leqslant | f(x) | }[/math]
Zatem na podstawie kryterium porównawczego ze zbieżności całki [math]\displaystyle{ \int_{a}^{\infty} | f(x) | d x }[/math] wynika zbieżność całki [math]\displaystyle{ \int_{a}^{\infty} | f(x) g(x) | d x }[/math].
□
Twierdzenie E41
Niech [math]\displaystyle{ F(x) }[/math] oznacza funkcję pierwotną funkcji [math]\displaystyle{ f(x) }[/math]. Całka [math]\displaystyle{ \int_{a}^{\infty} f(x) d x }[/math] jest zbieżna wtedy i tylko wtedy, gdy granica [math]\displaystyle{ \lim_{x \to \infty} F(x) }[/math] jest skończona.
Z definicji całki niewłaściwej mamy
- [math]\displaystyle{ \int_{a}^{\infty} f(t) d t = \lim_{b \to \infty} \int^b_a f(t) d t }[/math]
- [math]\displaystyle{ \;\; = \lim_{b \to \infty} \biggl[ F(t) \biggr\rvert_{a}^{b} \biggr] }[/math]
- [math]\displaystyle{ \;\; = \lim_{b \to \infty} [F (b) - F (a)] }[/math]
- [math]\displaystyle{ \;\; = - F (a) + \lim_{b \to \infty} F (b) }[/math]
Zauważmy, że aby możliwe było rozważanie, czy całka [math]\displaystyle{ \int_{a}^{\infty} f (x) d x }[/math] jest zbieżna, muszą być spełnione warunki dodatkowe, których już jawnie nie wypisaliśmy
● funkcja [math]\displaystyle{ f(x) }[/math] musi być określona w przedziale [math]\displaystyle{ [a, \infty) }[/math] ● funkcja [math]\displaystyle{ f(x) }[/math] musi być całkowalna w każdym podprzedziale [math]\displaystyle{ [a, b] }[/math] przedziału [math]\displaystyle{ [a, \infty) }[/math]
Ponieważ [math]\displaystyle{ \int^b_a f(t) d t = F(b) - F(a) }[/math], to wartość [math]\displaystyle{ F(a) }[/math] musi być skończona. Zatem granica [math]\displaystyle{ \lim_{x \to \infty} F(x) }[/math] jest skończona wtedy i tylko wtedy, gdy granica [math]\displaystyle{ \lim_{b \to \infty} \int^b_a f (t) d t }[/math] jest skończona. Co należało pokazać.
□
Twierdzenie E42
Jeżeli
● funkcja [math]\displaystyle{ f(x) }[/math] jest funkcją ciągłą i ma stały znak w przedziale [math]\displaystyle{ [a, + \infty) }[/math] ● całka [math]\displaystyle{ \int_{a}^{\infty} f (x) d x }[/math] jest zbieżna ● funkcja [math]\displaystyle{ g(x) }[/math] jest ograniczona w przedziale [math]\displaystyle{ [a, + \infty) }[/math], czyli dla [math]\displaystyle{ x \geqslant a }[/math] jest
- 1. [math]\displaystyle{ \qquad m \leqslant g (x) \leqslant M }[/math]
- 1. [math]\displaystyle{ \qquad m \leqslant g (x) \leqslant M }[/math]
lub
- 2. [math]\displaystyle{ \qquad | g (x) | \leqslant L }[/math]
● całka [math]\displaystyle{ \int^b_a g (x) d x }[/math] istnieje dla każdego [math]\displaystyle{ b \gt a }[/math]
to całki [math]\displaystyle{ \int_{a}^{\infty} | f (x) g (x) | d x }[/math] oraz [math]\displaystyle{ \int_{a}^{\infty} f (x) g (x) d x }[/math] są zbieżne i prawdziwe są następujące oszacowania
- 1. [math]\displaystyle{ \qquad s \:\! m \int_{a}^{\infty} f (x) d x \leqslant s \int_{a}^{\infty} f (x) g (x) d x \leqslant s M \int_{a}^{\infty} f (x) d x }[/math]
lub
- 2. [math]\displaystyle{ \qquad \int_{a}^{\infty} | f (x) g (x) | d x \leqslant L \left| \int_{a}^{\infty} f (x) d x \right| }[/math]
gdzie [math]\displaystyle{ s }[/math] jest znakiem funkcji [math]\displaystyle{ f(x) }[/math] w przedziale [math]\displaystyle{ [a, + \infty) }[/math].
Z założenia funkcja [math]\displaystyle{ f (t) }[/math] ma stały znak w przedziale [math]\displaystyle{ [a, + \infty) }[/math], zatem mamy
- [math]\displaystyle{ \int_{a}^{\infty} f (t) d t = s \int_{a}^{\infty} [s \cdot f (t)] d t = s \int_{a}^{\infty} | f (t) | d t }[/math]
gdzie [math]\displaystyle{ s }[/math] jest znakiem funkcji [math]\displaystyle{ f(x) }[/math] w przedziale [math]\displaystyle{ [a, + \infty) }[/math]. Czyli całka [math]\displaystyle{ \int_{a}^{\infty} f (t) d t }[/math] jest bezwzględnie zbieżna. Ponieważ z założenia funkcja [math]\displaystyle{ g(x) }[/math] jest ograniczona, to z twierdzenia E40 wynika, że całka [math]\displaystyle{ \int_{a}^{\infty} | f (t) g (t) | d t }[/math] jest zbieżna, zatem jest też zbieżna całka [math]\displaystyle{ \int_{a}^{\infty} f (t) g (t) d t }[/math] (twierdzenie E39).
Przypadek 1.
Funkcja [math]\displaystyle{ s \cdot f (t) }[/math] jest dodatnia, gdzie [math]\displaystyle{ s }[/math] jest znakiem funkcji [math]\displaystyle{ f(x) }[/math] w przedziale [math]\displaystyle{ [a, + \infty) }[/math]. Stąd i z założonej postaci ograniczenia funkcji [math]\displaystyle{ g (t) }[/math] wynika, że prawdziwy jest następujący układ nierówności
- [math]\displaystyle{ s \:\! m f (x) \leqslant s f (x) g (x) \leqslant s M f (x) }[/math]
Wynika stąd odpowiedni układ nierówności dla całek oznaczonych właściwych
- [math]\displaystyle{ s \:\! m \int^b_a f (x) d x \leqslant s \int^b_a f (x) g (x) d x \leqslant s M \int^b_a f (x) d x }[/math]
gdzie [math]\displaystyle{ b \gt a }[/math]. Ponieważ całki [math]\displaystyle{ \int_{a}^{\infty} f (x) d x }[/math] oraz [math]\displaystyle{ \int_{a}^{\infty} f (x) g (x) d x }[/math] są zbieżne, to uprawnione jest przejście do granicy i w granicy, gdy [math]\displaystyle{ b }[/math] dąży do nieskończoności, otrzymujemy
- [math]\displaystyle{ s \:\! m \int_{a}^{\infty} f (x) d x \leqslant s \int_{a}^{\infty} f (x) g (x) d x \leqslant s M \int_{a}^{\infty} f (x) d x }[/math]
Przypadek 2.
Ponieważ funkcja [math]\displaystyle{ | f (t) | }[/math] jest dodatnia, to prawdziwe jest oszacowanie
- [math]\displaystyle{ | g (x) | \cdot | f (x) | \leqslant L | f (x) | }[/math]
Wynika stąd oszacowanie dla całek oznaczonych właściwych
- [math]\displaystyle{ \int^b_a | f (x) g (x) | d x \leqslant L \int^b_a | f (x) | d x }[/math]
- [math]\displaystyle{ \, = s L \int^b_a f (x) d x }[/math]
- [math]\displaystyle{ \, = L \left| \int^b_a f (x) d x \right| }[/math]
gdzie [math]\displaystyle{ b \gt a }[/math]. Ponieważ całki [math]\displaystyle{ \int_{a}^{\infty} f (x) d x }[/math] i [math]\displaystyle{ \int_{a}^{\infty} | f (x) g (x) | d x }[/math] są zbieżne, to możemy przejść do granicy i w granicy, gdy [math]\displaystyle{ b }[/math] dąży do nieskończoności, otrzymujemy
- [math]\displaystyle{ \int_{a}^{\infty} | f (x) g (x) | d x \leqslant L \left| \int_{a}^{\infty} f (x) d x \right| }[/math]
Co należało pokazać.
□
Twierdzenie E43
Niech [math]\displaystyle{ P_n(t) }[/math], gdzie [math]\displaystyle{ n \geqslant 1 }[/math], będzie funkcją okresową Bernoulliego. Całka
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_n(t)}{t^{\alpha}}} d t }[/math]
gdzie [math]\displaystyle{ \alpha \gt 1 }[/math], jest zbieżna.
Funkcja [math]\displaystyle{ {\small\frac{1}{t^{\alpha}}} }[/math] spełnia warunki
● jest ciągła i nie zmienia znaku w przedziale [math]\displaystyle{ (0, + \infty) }[/math] ● całka [math]\displaystyle{ \int_1^{\infty} {\small\frac{d t}{t^{\alpha}}} = {\small\frac{1}{\alpha - 1}} }[/math] jest zbieżna
Funkcje okresowe Bernoulliego [math]\displaystyle{ P_r (t) }[/math] są zdefiniowane wzorem
- [math]\displaystyle{ P_r(t) = B_r(t - \lfloor t \rfloor) }[/math]
a wielomiany Bernoulliego [math]\displaystyle{ B_r(t) }[/math] są ograniczone w przedziale [math]\displaystyle{ [0, 1] }[/math][11] (zobacz przykład E17), wynika stąd, że [math]\displaystyle{ P_r(t) }[/math] są funkcjami ograniczonymi. Zatem z twierdzenia E42 otrzymujemy natychmiast, że całka [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_r(t)}{t^{\alpha}}} d t }[/math] jest zbieżna.
□
Twierdzenie E44
Niech [math]\displaystyle{ P_n (t) }[/math], gdzie [math]\displaystyle{ n \geqslant 1 }[/math], będzie funkcją okresową Bernoulliego. Całka
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_n(t)}{t^{\varepsilon}}} d t }[/math]
gdzie [math]\displaystyle{ \varepsilon \gt 0 }[/math], jest zbieżna.
W przypadku funkcji [math]\displaystyle{ g(t) = {\small\frac{1}{t^{\varepsilon}}} }[/math] z twierdzenia E32 otrzymujemy
- [math]\displaystyle{ \int_1^b {\small\frac{P_n(t)}{t^{\varepsilon}}} d t = {\small\frac{B_{n + 1}}{n + 1}} \left[ {\small\frac{1}{b^{\varepsilon}}} - 1 \right] + {\small\frac{\varepsilon}{n + 1}} \int_1^b {\small\frac{P_{n + 1}(t)}{t^{1 + \varepsilon}}} d t }[/math]
W granicy, gdy [math]\displaystyle{ b }[/math] dąży do nieskończoności, mamy
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_n(t)}{t^{\varepsilon}}} d t = - {\small\frac{B_{n + 1}}{n + 1}} + {\small\frac{\varepsilon}{n + 1}} \int_1^{\infty} {\small\frac{P_{n + 1}(t)}{t^{1 + \varepsilon}}} d t }[/math]
Ponieważ na mocy twierdzenia E43 całka po prawej stronie jest zbieżna, to jest też zbieżna całka [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_n (t)}{t^{\varepsilon}}} d t }[/math]. Co należało pokazać.
□
Zadanie E45
Niech [math]\displaystyle{ P_n (t) }[/math], gdzie [math]\displaystyle{ n \geqslant 1 }[/math], będzie funkcją okresową Bernoulliego. Pokazać, że całka
- [math]\displaystyle{ \int_1^{\infty} P_n (t) t^{\varepsilon} d t }[/math]
gdzie [math]\displaystyle{ 0 \lt \varepsilon \lt 1 }[/math], jest rozbieżna.
W przypadku funkcji [math]\displaystyle{ g(t) = t^{\varepsilon} }[/math] z twierdzenia E32 otrzymujemy
- [math]\displaystyle{ \int_1^b P_n(t) t^{\varepsilon} d t = {\small\frac{B_{n + 1}}{n + 1}} [b^{\varepsilon} - 1] - {\small\frac{\varepsilon}{n + 1}} \int_1^b {\small\frac{P_{n + 1}(t)}{t^{1 - \varepsilon}}} d t }[/math]
Dla [math]\displaystyle{ 0 \lt \varepsilon \lt 1 }[/math] całka [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_{n + 1}(t)}{t^{1 - \varepsilon}}} d t }[/math] jest zbieżna, ale pierwszy wyraz po prawej stronie jest rozbieżny, gdy [math]\displaystyle{ b }[/math] dąży do nieskończoności, zatem cała prawa strona jest rozbieżna.
□
Zadanie E46
Niech [math]\displaystyle{ P_n (t) }[/math], gdzie [math]\displaystyle{ n \geqslant 1 }[/math], będzie funkcją okresową Bernoulliego. Pokazać, że całka
- [math]\displaystyle{ \int_2^{\infty} {\small\frac{P_n (t)}{\log t}} d t }[/math]
jest zbieżna.
W przypadku funkcji [math]\displaystyle{ g(t) = {\small\frac{1}{\log t}} }[/math] z twierdzenia E32 otrzymujemy
- [math]\displaystyle{ \int_2^b {\small\frac{P_n(t)}{\log t}} d t = {\small\frac{B_{n + 1}}{n + 1}} \left[ {\small\frac{1}{\log b}} - {\small\frac{1}{\log 2}} \right] + {\small\frac{1}{n + 1}} \int_2^b {\small\frac{P_{n + 1}(t)}{t \cdot \log^2 t}} d t }[/math]
W granicy, gdy [math]\displaystyle{ b }[/math] dąży do nieskończoności, mamy
- [math]\displaystyle{ \int_2^{\infty} {\small\frac{P_n (t)}{\log t}} d t = - {\small\frac{B_{n + 1}}{(n + 1) \log 2}} + {\small\frac{1}{n + 1}} \int_2^{\infty} {\small\frac{P_{n + 1} (t)}{t \cdot \log^2 t}} d t }[/math]
Ponieważ na mocy twierdzenia E44 całka po prawej stronie jest zbieżna, to jest też zbieżna całka [math]\displaystyle{ \int_2^{\infty} {\small\frac{P_n (t)}{\log t}} d t }[/math].
□
Zadanie E47
Niech [math]\displaystyle{ P_r (t) }[/math], gdzie [math]\displaystyle{ r \geqslant 1 }[/math], będzie funkcją okresową Bernoulliego oraz prawdziwe będzie następujące oszacowanie funkcji [math]\displaystyle{ P_r (t) }[/math]
- [math]\displaystyle{ m_r \leqslant P_r (t) \leqslant M_r }[/math]
Pokazać, że dla [math]\displaystyle{ \alpha \gt 1 }[/math] i [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] jest
- [math]\displaystyle{ {\small\frac{m_r}{\alpha - 1}} \cdot {\small\frac{1}{n^{\alpha - 1}}} \leqslant \int_n^{\infty} {\small\frac{P_r(t)}{t^{\alpha}}} d t \leqslant {\small\frac{M_r}{\alpha - 1}} \cdot {\small\frac{1}{n^{\alpha - 1}}} }[/math]
Zauważmy, że
- funkcja [math]\displaystyle{ {\small\frac{1}{t^{\alpha}}} }[/math] jest funkcją ciągłą i zachowuje stały (dodatni) znak w przedziale [math]\displaystyle{ (0, + \infty) }[/math]
- całka [math]\displaystyle{ \int_{n}^{\infty} {\small\frac{d t}{t^{\alpha}}} = {\small\frac{1}{\alpha - 1}} \cdot {\small\frac{1}{n^{\alpha - 1}}} }[/math] jest zbieżna
- funkcja [math]\displaystyle{ P_r (t) }[/math] jest ograniczona i z założenia prawdziwy jest układ nierówności [math]\displaystyle{ m_r \leqslant P_r (t) \leqslant M_r }[/math]
- całka [math]\displaystyle{ \int^b_n P_r (t) d t }[/math] istnieje dla każdego [math]\displaystyle{ b \gt n }[/math]
Zatem spełnione są założenia twierdzenia E42 i natychmiast otrzymujemy, że całka [math]\displaystyle{ \int_{n}^{\infty} {\small\frac{P_r (t)}{t^{\alpha}}} d t }[/math] jest zbieżna i prawdziwe jest oszacowanie
- [math]\displaystyle{ {\small\frac{m_r}{\alpha - 1}} \cdot {\small\frac{1}{n^{\alpha - 1}}} \leqslant \int_n^{\infty} {\small\frac{P_r (t)}{t^{\alpha}}} d t \leqslant {\small\frac{M_r}{\alpha - 1}} \cdot {\small\frac{1}{n^{\alpha - 1}}} }[/math]
Co należało pokazać.
□
Podamy teraz kryterium Dirichleta, dzięki któremu moglibyśmy natychmiast uzyskać dowody twierdzeń E43 i E44 oraz rozwiązanie zadania E46. Celowo nie stosowaliśmy tego kryterium, aby Czytelnik mógł zapoznać się z ciekawym zastosowaniem twierdzenia E32.
Twierdzenie E48* (kryterium Dirichleta)
Jeżeli funkcje [math]\displaystyle{ f(x) }[/math] i [math]\displaystyle{ g(x) }[/math] są całkowalne w każdym podprzedziale [math]\displaystyle{ [a, b] }[/math] przedziału [math]\displaystyle{ [a, + \infty) }[/math] oraz spełniają warunki
● całka z funkcji [math]\displaystyle{ f(x) }[/math] jest ograniczona, czyli istnieje taka stała [math]\displaystyle{ M \gt 0 }[/math], że dla każdego [math]\displaystyle{ b \gt a }[/math] jest [math]\displaystyle{ \left| \int^b_a f(x) d x \right| \leqslant M }[/math] ● funkcja [math]\displaystyle{ g(x) }[/math] jest funkcją monotoniczną (czyli malejącą lub rosnącą) ● [math]\displaystyle{ \lim_{x \to \infty} g (x) = 0 }[/math]
to całka [math]\displaystyle{ \int_{a}^{\infty} f (x) g (x) d x }[/math] jest zbieżna.
Zadanie E49
Korzystając z kryterium Dirichleta, pokazać, że całki
- [math]\displaystyle{ \int_{0}^{\infty} {\small\frac{\sin x}{x}} d x = {\small\frac{1}{2}} \pi }[/math]
- [math]\displaystyle{ \int_{2}^{\infty} {\small\frac{P_1 (x)}{\log x}} d x = - 0.117923474371 \ldots }[/math]
są zbieżne.
Punkt 1.
Zauważmy, że funkcja [math]\displaystyle{ {\small\frac{\sin x}{x}} }[/math] jest ciągła w punkcie [math]\displaystyle{ x = 0 }[/math]. Mamy też [math]\displaystyle{ \lim_{x \to 0} {\small\frac{\sin x}{x}} = 1 }[/math]. Oszacowanie całki jest natychmiastowe
- [math]\displaystyle{ \left| \int^b_0 \sin t d t \right| = \biggl| - \cos t \big\rvert_{0}^{b} \biggr| = | - \cos b + 1 | \leqslant 2 }[/math]
Zatem z kryterium Dirichleta wynika, że całka [math]\displaystyle{ \int_{0}^{\infty} {\small\frac{\sin x}{x}} d x }[/math] jest zbieżna.
Punkt 2.
Ponieważ [math]\displaystyle{ P_1 (x) }[/math] jest funkcją okresową o okresie równym [math]\displaystyle{ 1 }[/math], to całka oznaczona będzie równa sumie wielokrotności całek na odcinku [math]\displaystyle{ [0, 1] }[/math] i całce na odcinku [math]\displaystyle{ [0, x - \lfloor x \rfloor] }[/math]. Pamiętając o tym, że
- [math]\displaystyle{ \int^1_0 P_1 (t) d t = 0 }[/math]
- [math]\displaystyle{ \int B_n (x) = {\small\frac{1}{n + 1}} B_{n + 1} (x) }[/math]
otrzymujemy
- [math]\displaystyle{ \int^b_2 P_1 (t) d t = (\lfloor b \rfloor - 2) \cdot \int^1_0 P_1 (t) d t + \int_{0}^{b - \lfloor b \rfloor} P_1 (t) d t = }[/math]
- [math]\displaystyle{ \;\;\, = \int_{0}^{b - \lfloor b \rfloor} B_1 (t) d t }[/math]
- [math]\displaystyle{ \;\;\, = {\small\frac{1}{2}} B_2 (t) \biggr\rvert_{0}^{b - \lfloor b \rfloor} }[/math]
- [math]\displaystyle{ \;\;\, = {\small\frac{1}{2}} (B_2 (b - \lfloor b \rfloor) - B_2 (0)) }[/math]
Ponieważ [math]\displaystyle{ | B_{2 k} (x) | \leqslant | B_{2 k} | \, }[/math] dla [math]\displaystyle{ \, 0 \leqslant x \leqslant 1 \; }[/math] i [math]\displaystyle{ \; k \in \mathbb{N}_0 }[/math] (zobacz E15), zatem
- [math]\displaystyle{ \left| \int^b_2 P_1 (t) d t \right| = {\small\frac{1}{2}} | B_2 (b - \lfloor b \rfloor) - B_2 | \leqslant {\small\frac{1}{2}} (| B_2 (b - \lfloor b \rfloor) | + | B_2 |) \leqslant B_2 }[/math]
Z kryterium Dirichleta wynika natychmiast, że całka [math]\displaystyle{ \int_{2}^{\infty} P_1 (t) d t }[/math] jest zbieżna.
□
Przykłady
Przykład E50
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^n k^2 }[/math]
Ponieważ [math]\displaystyle{ f(t) = t^2 }[/math], to [math]\displaystyle{ f'(t) = 2 t }[/math], [math]\displaystyle{ f''(t) = 2 }[/math], a dla [math]\displaystyle{ i \geqslant 3 }[/math] mamy [math]\displaystyle{ f^{(i)}(t) = 0 }[/math]. Zatem dla [math]\displaystyle{ r = 3 }[/math] wyraz [math]\displaystyle{ {\small\frac{1}{6}} \int_1^n P_3(t) f^{(3)}(t) d t }[/math] jest równy zero i otrzymujemy
- [math]\displaystyle{ \sum_{k = 1}^n k^2 = {\small\frac{1}{6}} n (n + 1) (2 n + 1) }[/math]
Przykład E51
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k^2}} }[/math]
Wiemy, że przypadku szeregu nieskończonego jest
- [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k^2}} = {\small\frac{\pi^2}{6}} }[/math]
gdzie [math]\displaystyle{ {\small\frac{\pi^2}{6}} = 1.644934066848226436472415166646 \ldots }[/math]
Dla [math]\displaystyle{ r = 1 }[/math] mamy
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k^2}} = {\small\frac{3}{2}} - {\small\frac{1}{n}} + {\small\frac{1}{2 n^2}} - 2 \int_1^n {\small\frac{P_1 (t)}{t^3}} d t }[/math]
Przechodząc z [math]\displaystyle{ n }[/math] do nieskończoności, otrzymujemy
- [math]\displaystyle{ \sum_{k = 1}^{\infty} {\small\frac{1}{k^2}} = {\small\frac{3}{2}} - 2 \int_1^{\infty} {\small\frac{P_1 (t)}{t^3}} d t }[/math]
Rzeczywiście, całka po prawej stronie jest zbieżna i równa [math]\displaystyle{ \tfrac{1}{12} ( 9 - \pi^2 ) }[/math].
Jeżeli tak, to możemy sumę zapisać w postaci
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k^2}} = {\small\frac{3}{2}} - {\small\frac{1}{n}} + {\small\frac{1}{2 n^2}} - 2 \int_1^{\infty} {\small\frac{P_1 (t)}{t^3}} d t + 2 \int_n^{\infty} {\small\frac{P_1 (t)}{t^3}} d t }[/math]
- [math]\displaystyle{ \:\:\, = {\small\frac{\pi^2}{6}} - {\small\frac{1}{n}} + {\small\frac{1}{2 n^2}} + 2 \int_n^{\infty} {\small\frac{P_1 (t)}{t^3}} d t }[/math]
Ponieważ dla [math]\displaystyle{ P_1(t) = t - \lfloor t \rfloor - {\small\frac{1}{2}} }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ - {\small\frac{1}{2}} \leqslant P_1(t) \leqslant {\small\frac{1}{2}} }[/math], to korzystając z pokazanego w zadaniu E47 wzoru, dostajemy
- [math]\displaystyle{ - {\small\frac{1}{4 n^2}} \leqslant \int_n^{\infty} {\small\frac{P_1 (t)}{t^3}} d t \leqslant {\small\frac{1}{4 n^2}} }[/math]
Teraz już łatwo otrzymujemy oszacowania
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k^2}} \leqslant {\small\frac{\pi^2}{6}} - {\small\frac{1}{n}} + {\small\frac{1}{n^2}} }[/math]
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k^2}} \geqslant {\small\frac{\pi^2}{6}} - {\small\frac{1}{n}} }[/math]
Jeśli we wzorze Eulera-Maclaurina uwzględnimy więcej wyrazów, to otrzymamy dokładniejsze oszacowania.
Przykład E52
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} }[/math]
Rozwinięcie asymptotyczne tej sumy jest dobrze znane[12]
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} = \log n + \gamma + {\small\frac{1}{2 n}} - \sum_{k = 1}^{\infty} {\small\frac{B_{2 k}}{2k \cdot n^{2 k}}} }[/math]
- [math]\displaystyle{ = \log n + \gamma + {\small\frac{1}{2 n}} - {\small\frac{1}{12 n^2}} + {\small\frac{1}{120 n^4}} - {\small\frac{1}{252 n^6}} + {\small\frac{1}{240 n^8}} - {\small\frac{1}{132 n^{10}}} + \cdots }[/math]
gdzie [math]\displaystyle{ \gamma = 0.57721566490153286060651209 \ldots }[/math] jest stałą Eulera.
Stosując wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 1 }[/math], mamy
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} = \log n + {\small\frac{1}{2}} + {\small\frac{1}{2 n}} - \int_1^n {\small\frac{P_1 (t)}{t^2}} d t }[/math]
W granicy, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, dostajemy
- [math]\displaystyle{ \lim_{n \to \infty} \left( \sum_{k = 1}^{n} {\small\frac{1}{k}} - \log n \right) = {\small\frac{1}{2}} - \int_1^{\infty} {\small\frac{P_1 (t)}{t^2}} d t }[/math]
Rzeczywiście, całka po prawej stronie jest zbieżna i równa [math]\displaystyle{ \tfrac{1}{2} - \gamma }[/math].
Zastosujemy teraz wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 3 }[/math] i znajdziemy oszacowanie
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} = \log n + {\small\frac{7}{12}} + {\small\frac{1}{2 n}} - {\small\frac{1}{12 n^2}} - \int_1^n {\small\frac{P_3 (t)}{t^4}} d t }[/math]
- [math]\displaystyle{ \: = \log n + {\small\frac{7}{12}} + {\small\frac{1}{2 n}} - {\small\frac{1}{12 n^2}} - \int_1^{\infty} {\small\frac{P_3 (t)}{t^4}} d t + \int_n^{\infty} {\small\frac{P_3 (t)}{t^4}} d t }[/math]
Oczywiście
- [math]\displaystyle{ {\small\frac{7}{12}} - \int_1^{\infty} {\small\frac{P_3 (t)}{t^4}} d t = \gamma }[/math]
Dostajemy
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} = \log n + \gamma + {\small\frac{1}{2 n}} - {\small\frac{1}{12 n^2}} + \int_n^{\infty} {\small\frac{P_3 (t)}{t^4}} d t }[/math]
Ponieważ prawdziwe są oszacowania (zobacz przykłady E16 i E17)
- [math]\displaystyle{ - {\small\frac{\sqrt{3}}{36}} \leqslant P_3 (t) \leqslant {\small\frac{\sqrt{3}}{36}} }[/math]
to korzystając z pokazanego w zadaniu E47 wzoru, dostajemy
- [math]\displaystyle{ - {\small\frac{\sqrt{3}}{108 n^3}} \leqslant \int_n^{\infty} {\small\frac{P_3 (t)}{t^4}} d t \leqslant {\small\frac{\sqrt{3}}{108 n^3}} }[/math]
Zatem
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} \leqslant \log n + \gamma + {\small\frac{1}{2 n}} - {\small\frac{1}{12 n^2}} + {\small\frac{\sqrt{3}}{108 n^3}} }[/math]
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} \geqslant \log n + \gamma + {\small\frac{1}{2 n}} - {\small\frac{1}{12 n^2}} - {\small\frac{\sqrt{3}}{108 n^3}} }[/math]
Powyższe nierówności mogą nam posłużyć do wyznaczenia stałej [math]\displaystyle{ \gamma }[/math]. Przykładowo dla [math]\displaystyle{ n = 10^6 }[/math], otrzymujemy
- [math]\displaystyle{ 0.5772156649015328605 \leqslant \gamma \leqslant 0.5772156649015328607 }[/math]
Przykład E53
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^{n} \log k }[/math]
Rozwinięcie asymptotyczne tej sumy jest dobrze znane[13]
- [math]\displaystyle{ \log n! = n \log n - n + {\small\frac{1}{2}} \log n + \tfrac{1}{2} \log \left( 2 \pi \right) + \sum_{k = 1}^{\infty} {\small\frac{B_{2 k}}{2 k (2 k - 1) \cdot n^{2 k - 1}}} }[/math]
- [math]\displaystyle{ \quad \; = n \log n - n + {\small\frac{1}{2}} \log n + \tfrac{1}{2} \log \left( 2 \pi \right) + {\small\frac{1}{12 n}} - {\small\frac{1}{360 n^3}} + {\small\frac{1}{1260 n^5}} - {\small\frac{1}{1680 n^7}} + {\small\frac{1}{1188 n^9}} - \cdots }[/math]
gdzie [math]\displaystyle{ \tfrac{1}{2} \log \left( 2 \pi \right) = 0.91893853320467274178 \ldots }[/math]
Stosując wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 1 }[/math], mamy
- [math]\displaystyle{ \sum_{k = 1}^{n} \log k = n \log n - n + {\small\frac{1}{2}} \log n + 1 + \int_1^n {\small\frac{P_1 (t)}{t}} d t }[/math]
W granicy, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, dostajemy
- [math]\displaystyle{ \lim_{n \to \infty} \left[ \sum_{k = 1}^{n} \log k - \left( n \log n - n + {\small\frac{1}{2}} \log n \right) \right] = 1 + \int_{1}^{\infty} {\small\frac{P_1(t)}{t}} d t }[/math]
Z twierdzenia E44 wiemy, że całka [math]\displaystyle{ \int_{1}^{\infty} {\small\frac{P_1 (t)}{t}} d t }[/math] jest zbieżna, a z rozwinięcia asymptotycznego wiemy, że granica po lewej stronie jest równa [math]\displaystyle{ \tfrac{1}{2} \log \left( 2 \pi \right) }[/math], zatem otrzymujemy
- [math]\displaystyle{ \int_{1}^{\infty} {\small\frac{P_1 (t)}{t}} d t = \tfrac{1}{2} \log (2 \pi) - 1 }[/math]
Stosując wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 4 }[/math], otrzymujemy
- [math]\displaystyle{ \sum_{k = 1}^{n} \log k = n \log n - n + {\small\frac{1}{2}} \log n + {\small\frac{331}{360}} + {\small\frac{1}{12 n}} - {\small\frac{1}{360 n^3}} + {\small\frac{1}{4}} \int_1^n {\small\frac{P_4 (t)}{t^4}} d t }[/math]
W granicy, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, dostajemy
- [math]\displaystyle{ \lim_{n \to \infty} \left[ \sum_{k = 1}^{n} \log k - \left( n \log n - n + {\small\frac{1}{2}} \log n \right) \right] = {\small\frac{331}{360}} + {\small\frac{1}{4}} \int_1^{\infty} {\small\frac{P_4 (t)}{t^4}} d t }[/math]
Ponieważ całka po prawej stronie jest zbieżna, to granica wypisana po lewej stronie istnieje i jest równa stałej – w tym przypadku [math]\displaystyle{ \tfrac{1}{2} \log \left( 2 \pi \right) }[/math]. Możemy teraz wzór Eulera-Maclaurina zapisać w postaci
- [math]\displaystyle{ \sum_{k = 1}^{n} \log k = n \log n - n + {\small\frac{1}{2}} \log n + {\small\frac{331}{360}} + {\small\frac{1}{12 n}} - {\small\frac{1}{360 n^3}} + {\small\frac{1}{4}} \int_1^{\infty} {\small\frac{P_4(t)}{t^4}} d t - {\small\frac{1}{4}} \int_n^{\infty} {\small\frac{P_4 (t)}{t^4}} d t }[/math]
Czyli
- [math]\displaystyle{ \sum_{k = 1}^{n} \log k = n \log n - n + {\small\frac{1}{2}} \log n + \tfrac{1}{2} \log \left( 2 \pi \right) + {\small\frac{1}{12 n}} - {\small\frac{1}{360 n^3}} - {\small\frac{1}{4}} \int_n^{\infty} {\small\frac{P_4 (t)}{t^4}} d t }[/math]
Z przykładów E16 i E17 wiemy, że prawdziwe są oszacowania
- [math]\displaystyle{ - {\small\frac{1}{30}} \leqslant P_4 (x) \leqslant {\small\frac{7}{240}} }[/math]
Zatem korzystając z pokazanego w zadaniu E47 wzoru, dostajemy
- [math]\displaystyle{ - {\small\frac{1}{90 n^3}} \leqslant \int_n^{\infty} {\small\frac{P_4 (t)}{t^4}} (t) d t \leqslant {\small\frac{7}{720 n^3}} }[/math]
Czyli
- [math]\displaystyle{ - {\small\frac{7}{2880 n^3}} \leqslant - {\small\frac{1}{4}} \int_n^{\infty} {\small\frac{P_4(t)}{t^4}} (t) d t \leqslant {\small\frac{1}{360 n^3}} }[/math]
Skąd natychmiast otrzymujemy oszacowania
- [math]\displaystyle{ \sum_{k = 1}^{n} \log k \leqslant n \log n - n + {\small\frac{1}{2}} \log n + \tfrac{1}{2} \log \left( 2 \pi \right) + {\small\frac{1}{12 n}} }[/math]
- [math]\displaystyle{ \sum_{k = 1}^{n} \log k \geqslant n \log n - n + {\small\frac{1}{2}} \log n + \tfrac{1}{2} \log \left( 2 \pi \right) + {\small\frac{1}{12 n}} - {\small\frac{1}{192 n^3}} }[/math]
Oczywiście, podobnie jak w poprzednim przykładzie, powyższe nierówności mogą służyć do wyznaczenia wartości stałej.
Przykład E54
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^{n} \sqrt{k} }[/math]
Stosując wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 4 }[/math], mamy
- [math]\displaystyle{ \sum_{k = 1}^{n} \sqrt{k} = {\small\frac{2}{3}} n^{3 / 2} + {\small\frac{1}{2}} n^{1 / 2} - {\small\frac{133}{640}} + {\small\frac{1}{24}} n^{- 1 / 2} - {\small\frac{1}{1920}} n^{- 5 / 2} + {\small\frac{5}{128}} \int_1^n {\small\frac{P_4 (t)}{t^{7 / 2}}} (t) d t }[/math]
W granicy, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, dostajemy
- [math]\displaystyle{ \lim_{n \to \infty} \left[ \sum_{k = 1}^{n} \sqrt{k} - \left( {\small\frac{2}{3}} n^{3 / 2} + {\small\frac{1}{2}} n^{1 / 2} \right) \right] = - {\small\frac{133}{640}} + {\small\frac{5}{128}} \int_1^{\infty} {\small\frac{P_4 (t)}{t^{7 / 2}}} (t) d t }[/math]
Ponieważ całka po prawej stronie jest zbieżna, to granica wypisana po lewej stronie istnieje i jest równa pewnej stałej [math]\displaystyle{ C }[/math]. Możemy teraz wzór Eulera-Maclaurina zapisać w postaci
- [math]\displaystyle{ \sum_{k = 1}^{n} \sqrt{k} = {\small\frac{2}{3}} n^{3 / 2} + {\small\frac{1}{2}} n^{1 / 2} - {\small\frac{133}{640}} + {\small\frac{1}{24}} n^{- 1 / 2} - {\small\frac{1}{1920}} n^{- 5 / 2} + {\small\frac{5}{128}} \int_1^{\infty} {\small\frac{P_4 (t)}{t^{7 / 2}}} (t) d t - {\small\frac{5}{128}} \int_n^{\infty} {\small\frac{P_4 (t)}{t^{7 / 2}}} (t) d t }[/math]
Zatem
- [math]\displaystyle{ \sum_{k = 1}^{n} \sqrt{k} = {\small\frac{2}{3}} n^{3 / 2} + {\small\frac{1}{2}} n^{1 / 2} + C + {\small\frac{1}{24}} n^{- 1 / 2} - {\small\frac{1}{1920}} n^{- 5 / 2} - {\small\frac{5}{128}} \int_n^{\infty} {\small\frac{P_4 (t)}{t^{7 / 2}}} (t) d t }[/math]
Z przykładów E16 i E17 wiemy, że prawdziwe są oszacowania
- [math]\displaystyle{ - {\small\frac{1}{30}} \leqslant P_4 (x) \leqslant {\small\frac{7}{240}} }[/math]
Zatem korzystając z pokazanego w zadaniu E47 wzoru, dostajemy
- [math]\displaystyle{ - {\small\frac{1}{75}} n^{- 5 / 2} \leqslant \int_n^{\infty} {\small\frac{P_4 (t)}{t^{7 / 2}}} (t) d t \leqslant {\small\frac{7}{600}} n^{- 5 / 2} }[/math]
Czyli
- [math]\displaystyle{ - {\small\frac{7}{15360}} n^{- 5 / 2} \leqslant - {\small\frac{5}{128}} \int_n^{\infty} {\small\frac{P_4 (t)}{t^{7 / 2}}} (t) d t \leqslant {\small\frac{1}{1920}} n^{- 5 / 2} }[/math]
I otrzymujemy oszacowania
- [math]\displaystyle{ \sum_{k = 1}^{n} \sqrt{k} \leqslant {\small\frac{2}{3}} n^{3 / 2} + {\small\frac{1}{2}} n^{1 / 2} + C + {\small\frac{1}{24}} n^{- 1 / 2} }[/math]
- [math]\displaystyle{ \sum_{k = 1}^{n} \sqrt{k} \geqslant {\small\frac{2}{3}} n^{3 / 2} + {\small\frac{1}{2}} n^{1 / 2} + C + {\small\frac{1}{24}} n^{- 1 / 2} - {\small\frac{1}{1024}} n^{- 5 / 2} }[/math]
Powyższe nierówności mogą nam posłużyć do wyznaczenia stałej [math]\displaystyle{ C }[/math]. Przykładowo dla [math]\displaystyle{ n = 10^6 }[/math], otrzymujemy
- [math]\displaystyle{ - 0.207886224977354567 \leqslant C \leqslant - 0.207886224977354565 }[/math]
Przykład E55
Pokażemy, dlaczego lepiej wybrać wartość [math]\displaystyle{ r }[/math] za dużą niż za małą i dlaczego należy sprawdzać zbieżność całki
- [math]\displaystyle{ \int_a^b P_r(t) f^{(r)}(t) d t }[/math]
korzystając z kryterium Dirichleta (twierdzenie E48) lub z twierdzenia E44. Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^{n} k^{3 / 2} }[/math]
Stosując wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 1 }[/math], mamy
- [math]\displaystyle{ \sum_{k = 1}^{n} k^{3 / 2} = {\small\frac{2}{5}} n^{5 / 2} + {\small\frac{1}{2}} n^{3 / 2} + {\small\frac{1}{10}} + {\small\frac{3}{2}} \int_1^n \sqrt{t} \cdot P_1 (t) d t }[/math]
W granicy, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, dostajemy
- [math]\displaystyle{ \lim_{n \to \infty} \left[ \sum_{k = 1}^{n} k^{3 / 2} - \left( {\small\frac{2}{5}} n^{5 / 2} + {\small\frac{1}{2}} n^{3 / 2} \right) \right] = {\small\frac{1}{10}} + {\small\frac{3}{2}} \int_1^{\infty} \sqrt{t} \cdot P_1(t) d t }[/math]
Jeszcze nie wszystkie wyrazy rozbieżne, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, zostały wyodrębnione – lewa strona jest rozbieżna. Podobnie rozbieżna jest całka po prawej stronie – rozbieżność tej całki informuje nas, że wybraliśmy za małą wartość [math]\displaystyle{ r }[/math].
Stosując wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 2 }[/math], mamy
- [math]\displaystyle{ \sum_{k = 1}^{n} k^{3 / 2} = {\small\frac{2}{5}} n^{5 / 2} + {\small\frac{1}{2}} n^{3 / 2} + {\small\frac{1}{8}} n^{1 / 2} - {\small\frac{1}{40}} - {\small\frac{3}{8}} \int_1^n {\small\frac{P_2(t)}{\sqrt{t}}} d t }[/math]
W granicy, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, otrzymujemy
- [math]\displaystyle{ \lim_{n \to \infty} \left[ \sum_{k = 1}^{n} k^{3 / 2} - \left( {\small\frac{2}{5}} n^{5 / 2} + {\small\frac{1}{2}} n^{3 / 2} + {\small\frac{1}{8}} n^{1 / 2} \right) \right] = - {\small\frac{1}{40}} - {\small\frac{3}{8}} \int_1^{\infty} {\small\frac{P_2(t)}{\sqrt{t}}} d t }[/math]
Całka po prawej stronie jest zbieżna, co wynika z kryterium Dirichleta. Zatem i lewa strona jest zbieżna, czyli wszystkie wyrazy rozbieżne, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, zostały wyodrębnione. Możemy to łatwo sprawdzić, obierając większą wartość [math]\displaystyle{ r }[/math].
Stosując wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 4 }[/math], mamy
- [math]\displaystyle{ \sum_{k = 1}^{n} k^{3 / 2} = {\small\frac{2}{5}} n^{5 / 2} + {\small\frac{1}{2}} n^{3 / 2} + {\small\frac{1}{8}} n^{1 / 2} - {\small\frac{49}{1920}} + {\small\frac{1}{1920}} n^{- 3 / 2} - {\small\frac{3}{128}} \int_1^n {\small\frac{P_4 (t)}{t^{5 / 2}}} d t }[/math]
W granicy, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, dostajemy
- [math]\displaystyle{ \lim_{n \to \infty} \left[ \sum_{k = 1}^{n} k^{3 / 2} - \left( {\small\frac{2}{5}} n^{5 / 2} + {\small\frac{1}{2}} n^{3 / 2} + {\small\frac{1}{8}} n^{1 / 2} \right) \right] = - {\small\frac{49}{1920}} - {\small\frac{3}{128}} \int_1^{\infty} {\small\frac{P_4(t)}{t^{5 / 2}}} d t }[/math]
Uwaga E56
Rozwiązując przykłady znaleźliśmy wartości następujących całek oznaczonych
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_1 (t)}{t}} d t = {\small\frac{1}{2}} \log (2 \pi) - 1 }[/math]
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_1 (t)}{t^2}} d t = {\small\frac{1}{2}} - \gamma }[/math]
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_1 (t)}{t^3}} d t = {\small\frac{9 - \pi^2}{12}} }[/math]
Jeżeli funkcja rzeczywista [math]\displaystyle{ f(t) }[/math] ma ciągłą pochodną w [math]\displaystyle{ [a, b] \subset \mathbb{R} }[/math] oraz [math]\displaystyle{ \lim_{t \to \infty} f (t) = 0 }[/math], to dla [math]\displaystyle{ n \geqslant 1 }[/math] mamy
- [math]\displaystyle{ \int_a^{\infty} P_{n + 1} (t) f'(t) d t = - B_{n + 1} f(a) - (n + 1) \int_a^{\infty} P_n(t) f(t) d t }[/math]
(Jest to prosty wniosek z twierdzenia E32).
Powyższy rezultat możemy wykorzystać do wyliczenia kolejnych całek zawierających funkcje okresowe Bernoulliego. Przykładowo mamy
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_2 (t)}{t^2}} d t = \log (2 \pi) - {\small\frac{11}{6}} }[/math]
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_2 (t)}{t^3}} d t = {\small\frac{7}{12}} - \gamma }[/math]
- [math]\displaystyle{ \int_1^{\infty} {\small\frac{P_2 (t)}{t^4}} d t = {\small\frac{10 - \pi^2}{18}} }[/math]
Metody wyliczania stałej we wzorze Eulera-Maclaurina
Uwaga E57
W przedstawionych wyżej przykładach wyliczyliśmy wartość stałej we wzorze Eulera-Maclaurina (przykład E52 i E54) oraz pokazaliśmy, że wartość całki [math]\displaystyle{ \int_a^{\infty} P_r (t) f^{(r)} (t) d t }[/math] jest związana z wartością stałej (przykład E51, E52 i E53). Obecnie dokładnie omówimy ten problem.
Twierdzenie E58
Jeżeli założymy, że
● całka nieoznaczona [math]\displaystyle{ F(x) = \int f(x) d x }[/math] nie zawiera wyrazów, które nie zależą od [math]\displaystyle{ x }[/math] (takie wyrazy ulegają redukcji przy wyliczaniu całki [math]\displaystyle{ \int_a^b f(t) d t = F(b) - F(a) }[/math] i nie występują we wzorze Eulera-Maclaurina) ● dla pewnego [math]\displaystyle{ r \geqslant 1 }[/math] całka [math]\displaystyle{ \int_a^{\infty} P_r (t) f^{(r)} (t) d t }[/math] jest zbieżna
to wzór Eulera-Maclaurina może być zapisany w postaci
- [math]\displaystyle{ \sum_{k = a}^b f (k) = C (a) + E (b) }[/math]
gdzie
- [math]\displaystyle{ C(a) = - F (a) + {\small\frac{1}{2}} f (a) - \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)} (a) - {\small\frac{(- 1)^r}{r!}} \int_a^{\infty} P_r (t) f^{(r)} (t) d t }[/math]
- [math]\displaystyle{ E(b) = F (b) + {\small\frac{1}{2}} f (b) + \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)}(b) + {\small\frac{(- 1)^r}{r!}} \int_b^{\infty} P_r (t) f^{(r)} (t) d t }[/math]
Jeżeli całka [math]\displaystyle{ \int_a^{\infty} P_r (t) f^{(r)} (t) d t }[/math] jest zbieżna, to możemy napisać
- [math]\displaystyle{ \sum_{k = a}^b f(k) = \int_a^b f(t) d t + {\small\frac{1}{2}} [f(b) + f(a)] + \sum_{k = 2}^r {\small\frac{B_k}{k!}} [f^{(k - 1)}(b) - f^{(k - 1)}(a)] - {\small\frac{(- 1)^r}{r!}} \int_a^b P_r(t) f^{(r)}(t) d t }[/math]
- [math]\displaystyle{ \;\;\,\, = F(b) - F(a) + {\small\frac{1}{2}} [f(b) + f(a)] + \sum_{k = 2}^r {\small\frac{B_k}{k!}} [f^{(k - 1)}(b) - f^{(k - 1)}(a)] - {\small\frac{(- 1)^r}{r!}} \int_a^{\infty} P_r(t) f^{(r)}(t) d t + {\small\frac{(- 1)^r}{r!}} \int_b^{\infty} P_r(t) f^{(r)}(t) d t }[/math]
- [math]\displaystyle{ \;\;\,\, = \left[ - F (a) + {\small\frac{1}{2}} f (a) - \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)} (a) - {\small\frac{(- 1)^r}{r!}} \int_a^{\infty} P_r (t) f^{(r)} (t) d t \right] + \left[ F (b) + {\small\frac{1}{2}} f (b) + \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)} (b) + {\small\frac{(- 1)^r}{r!}} \int_b^{\infty} P_r (t) f^{(r)} (t) d t \right] }[/math]
- [math]\displaystyle{ \;\;\,\, = C (a) + E (b) }[/math]
gdzie
- [math]\displaystyle{ C(a) = - F (a) + {\small\frac{1}{2}} f (a) - \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)}(a) - {\small\frac{(- 1)^r}{r!}} \int_a^{\infty} P_r (t) f^{(r)}(t) d t }[/math]
- [math]\displaystyle{ E(b) = F (b) + {\small\frac{1}{2}} f (b) + \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)}(b) + {\small\frac{(- 1)^r}{r!}} \int_b^{\infty} P_r (t) f^{(r)} (t) d t }[/math]
Co należało pokazać.
□
Uwaga E59
We wzorze
- [math]\displaystyle{ \sum_{k = a}^b f (k) = C (a) + E (b) }[/math]
składnik [math]\displaystyle{ C(a) }[/math] jest wartością stałej [math]\displaystyle{ C }[/math] we wzorze Eulera-Maclaurina, a [math]\displaystyle{ E(b) }[/math] zwraca kolejne wyrazy rozwinięcia. Pokażemy, że wartość tej stałej możemy wyliczyć bezpośrednio ze wzoru
- [math]\displaystyle{ C = C (a) }[/math]
lub metodą pośrednią, wykorzystując związek
- [math]\displaystyle{ C(a) = \sum_{k = a}^b f (k) - E (b) }[/math]
W obydwu przypadkach obliczenia wykonamy dla znanej już Czytelnikowi sumy [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} }[/math] (przykład E48).
Przykład E60
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} }[/math]
Ponieważ
- [math]\displaystyle{ f(x) = {\small\frac{1}{x}} }[/math]
- [math]\displaystyle{ F(x) = \int {\small\frac{d x}{x}} = \log x }[/math]
- [math]\displaystyle{ f^{(r)} (x) = {\small\frac{d^r}{d x^r}} {\small\frac{1}{x}} = {\small\frac{(- 1)^r r!}{x^{r + 1}}} }[/math]
to wzór na wartość stałej z twierdzenia E57
- [math]\displaystyle{ C(a) = - F(a) + {\small\frac{1}{2}} f(a) - \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)}(a) - {\small\frac{(- 1)^r}{r!}} \int_a^{\infty} P_r(t) f^{(r)}(t) d t }[/math]
przyjmuje postać
- [math]\displaystyle{ C(1) = - \log (1) + {\small\frac{1}{2}} - \sum_{k = 2}^r {\small\frac{B_k}{k!}} \cdot {\small\frac{(- 1)^{k - 1} (k - 1) !}{x^k}} - {\small\frac{(- 1)^r}{r!}} \int_a^{\infty} P_r (t) \cdot {\small\frac{(- 1)^r r!}{x^{r + 1}}} d t }[/math]
- [math]\displaystyle{ C(1) = {\small\frac{1}{2}} + \sum_{k = 2}^r {\small\frac{B_k}{k}} - \int_1^{\infty} {\small\frac{P_r(t)}{t^{r + 1}}} d t }[/math]
Oznaczmy
- [math]\displaystyle{ C_r = {\small\frac{1}{2}} + \sum_{k = 2}^r {\small\frac{B_k}{k}} }[/math]
- [math]\displaystyle{ I_r = - \int_1^{\infty} {\small\frac{P_r (t)}{t^{r + 1}}} d t }[/math]
Wartość [math]\displaystyle{ I_r }[/math] obliczymy numerycznie w programie PARI/GP poleceniem
Int(r) = - intnum(t = 1,+oo, P(r, t)/t^(r+1), 12 )
gdzie
P(r, t) = B(r, t - floor(t))
jest funkcją okresową Bernoulliego [math]\displaystyle{ P_r (t) }[/math].
Ponieważ wyliczenie wartości [math]\displaystyle{ C_r }[/math] jest bardzo łatwe, to w tabeli przedstawiamy jedynie wartość całki [math]\displaystyle{ I_r }[/math] oraz wielkość błędu, z jakim wyliczyliśmy wartość stałej we wzorze Eulera-Maclaurina. Przy precyzji obliczeń w PARI/GP równej [math]\displaystyle{ 77 }[/math] cyfr znaczących (wyświetlanych jest tylko [math]\displaystyle{ 60 }[/math]) otrzymujemy
[math]\displaystyle{ \quad r \quad }[/math] [math]\displaystyle{ I_r }[/math] [math]\displaystyle{ C_r + I_r - \gamma }[/math] [math]\displaystyle{ \quad 2 \quad }[/math] [math]\displaystyle{ - 0.00611766843643217216316093584671186131649649607150165105785840 }[/math] [math]\displaystyle{ - 4.7 \cdot 10^{- 12} }[/math] [math]\displaystyle{ \quad 4 \quad }[/math] [math]\displaystyle{ 0.00221566490153286060651266099862945942063253146614696094725279 }[/math] [math]\displaystyle{ 5.8 \cdot 10^{- 25} }[/math] [math]\displaystyle{ \quad 6 \quad }[/math] [math]\displaystyle{ - 0.00175258906672110764745616388586252127113304104807585093607060 }[/math] [math]\displaystyle{ - 1.1 \cdot 10^{- 32} }[/math] [math]\displaystyle{ \quad 8 \quad }[/math] [math]\displaystyle{ 0.00241407759994555901921050278081512945505072420777227470125753 }[/math] [math]\displaystyle{ 2.0 \cdot 10^{- 40} }[/math] [math]\displaystyle{ \quad 10 \quad }[/math] [math]\displaystyle{ - 0.00516167997581201673836525479494244630271800893829613819256332 }[/math] [math]\displaystyle{ - 8.8 \cdot 10^{- 49} }[/math] [math]\displaystyle{ \quad 12 \quad }[/math] [math]\displaystyle{ 0.0159311161169840760577275412978536464933747871553748142613412 }[/math] [math]\displaystyle{ 4.4 \cdot 10^{- 57} }[/math] [math]\displaystyle{ \quad 14 \quad }[/math] [math]\displaystyle{ - 0.0674022172163492572756057920354796868399585461779585190763506 }[/math] [math]\displaystyle{ - 2.7 \cdot 10^{- 65} }[/math] [math]\displaystyle{ \quad 16 \quad }[/math] [math]\displaystyle{ 0.375857586705219370175374600121383058258080669508315990727571 }[/math] [math]\displaystyle{ 2.1 \cdot 10^{- 73} }[/math] [math]\displaystyle{ \quad 18 \quad }[/math] [math]\displaystyle{ - 2.67809674356490037362857973014873668554587366076180375307638 }[/math] [math]\displaystyle{ - 1.8 \cdot 10^{- 77} }[/math] [math]\displaystyle{ \quad 20 \quad }[/math] [math]\displaystyle{ 23.7781153776472208384926323910633845265753384604503174590448 }[/math] [math]\displaystyle{ - 2.6 \cdot 10^{- 76} }[/math] [math]\displaystyle{ \quad 22 \quad }[/math] [math]\displaystyle{ - 257.682029549889011045565338623429369096613067336651131816317 }[/math] [math]\displaystyle{ 3.6 \cdot 10^{- 74} }[/math] [math]\displaystyle{ \quad 24 \quad }[/math] [math]\displaystyle{ 3349.82851684815738700083270777461702894978497906139526623008 }[/math] [math]\displaystyle{ - 2.5 \cdot 10^{- 73} }[/math]
Zwróćmy uwagę, jak bardzo [math]\displaystyle{ C_r \approx \gamma - I_r }[/math] odbiega od wartości stałej [math]\displaystyle{ \gamma }[/math] dla dużych wartości [math]\displaystyle{ r }[/math] – dopiero suma [math]\displaystyle{ C_r + I_r }[/math] daje prawidłowy rezultat. Tylko po to, aby uwidocznić ten fakt, przedstawiliśmy dane dla tak wielu wartości [math]\displaystyle{ r }[/math].
Uwaga E61
W przykładzie E60 uzyskaliśmy zaskakująco dokładny wynik, ale wiemy o tym tylko dlatego, że znaliśmy wynik prawidłowy. Gdybyśmy nie znali wartości stałej [math]\displaystyle{ \gamma }[/math], to nie bylibyśmy w stanie określić, ile cyfr sumy [math]\displaystyle{ C_r + I_r }[/math] jest prawidłowych.
Nim przejdziemy do przedstawienia drugiego sposobu wyliczania stałej we wzorze Eulera-Maclaurina, udowodnimy twierdzenie, które pozwoli nam działać bardziej efektywnie.
Twierdzenie E62
Jeżeli założymy, że
● całka nieoznaczona [math]\displaystyle{ F(x) = \int f (x) d x }[/math] nie zawiera wyrazów, które nie zależą od [math]\displaystyle{ x }[/math] (takie wyrazy ulegają redukcji przy wyliczaniu całki [math]\displaystyle{ \int_a^b f (t) d t = F (b) - F (a) }[/math] i nie występują we wzorze Eulera-Maclaurina) ● funkcja [math]\displaystyle{ f^{(2 s)} (t) }[/math] jest funkcją ciągłą i ma stały znak w przedziale [math]\displaystyle{ [b, \infty) }[/math] ● [math]\displaystyle{ \lim_{t \to \infty} f^{(2 s - 1)} (t) = 0 }[/math]
to dla stałej [math]\displaystyle{ C(a) }[/math] we wzorze Eulera-Maclaurina prawdziwe jest oszacowanie
- [math]\displaystyle{ W - \Delta \leqslant C(a) \leqslant W + \Delta }[/math]
gdzie
- [math]\displaystyle{ W = W (s, a, b) = \sum_{k = a}^b f(k) - \left[ F (b) + {\small\frac{1}{2}} f(b) + \sum_{k = 1}^s {\small\frac{B_{2 k}}{(2 k) !}} f^{(2 k - 1)}(b) \right] }[/math]
- [math]\displaystyle{ \Delta = \Delta (s, b) = {\small\frac{| B_{2 s} |}{(2 s) !}} | f^{(2 s - 1)} (b) | }[/math]
Czyli błąd, jakim obarczony jest wynik [math]\displaystyle{ W }[/math], jest nie większy od wartości bezwzględnej ostatniego składnika sumy.
Z twierdzenia E57 wiemy, że przy poczynionych założeniach wzór Eulera-Maclaurina może być zapisany w postaci
- [math]\displaystyle{ \sum_{k = a}^b f (k) = C (a) + E (b) }[/math]
gdzie
- [math]\displaystyle{ C(a) = - F(a) + {\small\frac{1}{2}} f(a) - \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)}(a) - {\small\frac{(- 1)^r}{r!}} \int_a^{\infty} P_r(t) f^{(r)}(t) d t }[/math]
- [math]\displaystyle{ E(b) = F(b) + {\small\frac{1}{2}} f(b) + \sum_{k = 2}^r {\small\frac{B_k}{k!}} f^{(k - 1)}(b) + {\small\frac{(- 1)^r}{r!}} \int_b^{\infty} P_r(t) f^{(r)}(t) d t }[/math]
Zatem
- [math]\displaystyle{ C(a) = \sum_{k = a}^b f(k) - E(b) }[/math]
W przypadku, gdy [math]\displaystyle{ r = 2 s }[/math] jest liczbą parzystą, możemy położyć [math]\displaystyle{ k = 2 j }[/math] i otrzymujemy
- [math]\displaystyle{ E(b) = F(b) + {\small\frac{1}{2}} f(b) + \sum_{j = 1}^s {\small\frac{B_{2 j}}{(2 j) !}} f^{(2 j - 1)}(b) + {\small\frac{1}{(2 s) !}} \int_b^{\infty} P_{2 s}(t) f^{(2 s)}(t) d t }[/math]
Ponieważ [math]\displaystyle{ f^{(2 s - 1)} (t) }[/math] jest funkcją pierwotną funkcji [math]\displaystyle{ f^{(2 s)}(t) }[/math], a z założenia jest [math]\displaystyle{ \lim_{t \to \infty} f^{(2 s - 1)}(t) = 0 }[/math], to na podstawie twierdzenia E41 całka [math]\displaystyle{ \int_b^{\infty} f^{(2 s)}(t) d t }[/math] jest zbieżna.
Ponieważ [math]\displaystyle{ | B_{2 s} (x) | \leqslant | B_{2 s} | \, }[/math] dla [math]\displaystyle{ \, 0 \leqslant x \leqslant 1 \; }[/math] i [math]\displaystyle{ \; s \in \mathbb{N}_0 }[/math] (zobacz E15), zatem dla funkcji okresowych Bernoulliego o indeksie parzystym prawdziwe jest oszacowanie [math]\displaystyle{ | P_{2 s}(x) | \leqslant | B_{2 s} | }[/math]. Z twierdzenia E42 i założenia, że [math]\displaystyle{ \lim_{t \to \infty} f^{(2 s - 1)}(t) = 0 }[/math] dostajemy oszacowanie całki
- [math]\displaystyle{ {\small\frac{1}{(2 s) !}} \left| \int_b^{\infty} P_{2 s} (t) f^{(2 s)}(t) d t \right| \leqslant {\small\frac{1}{(2 s) !}} \int_b^{\infty} | P_{2 s}(t) f^{(2 s)}(t) | d t }[/math]
- [math]\displaystyle{ \,\, \leqslant {\small\frac{1}{(2 s) !}} | B_{2 s} | \cdot \left| \int_b^{\infty} f^{(2 s)}(t) d t \right| }[/math]
- [math]\displaystyle{ \,\, = {\small\frac{1}{(2 s) !}} | B_{2 s} | \cdot \biggl| f^{(2 s - 1)}(t) \big\rvert_{b}^{\infty} \biggr| }[/math]
- [math]\displaystyle{ \,\, = {\small\frac{1}{(2 s) !}} | B_{2 s} | \cdot | - f^{(2 s - 1)}(b) | }[/math]
- [math]\displaystyle{ \,\, = {\small\frac{| B_{2 s} |}{(2 s) !}} | f^{(2 s - 1)}(b) | }[/math]
Łącząc powyższe rezultaty, otrzymujemy oszacowanie stałej [math]\displaystyle{ C(a) }[/math]
- [math]\displaystyle{ C(a) = \sum_{k = a}^b f (k) - \left[ F (b) + {\small\frac{1}{2}} f (b) + \sum_{j = 1}^s {\small\frac{B_{2 j}}{(2 j) !}} f^{(2 j - 1)} (b) \right] - {\small\frac{1}{(2 s) !}} \int_b^{\infty} P_{2 s} (t) f^{(2 s)} (t) d t }[/math]
- [math]\displaystyle{ \;\:\:\: \leqslant \sum_{k = a}^b f (k) - \left[ F (b) + {\small\frac{1}{2}} f (b) + \sum_{j = 1}^s {\small\frac{B_{2 j}}{(2 j) !}} f^{(2 j - 1)} (b) \right] + \Delta }[/math]
- [math]\displaystyle{ C(a) = \sum_{k = a}^b f (k) - \left[ F (b) + {\small\frac{1}{2}} f (b) + \sum_{j = 1}^s {\small\frac{B_{2 j}}{(2 j) !}} f^{(2 j - 1)} (b) \right] - {\small\frac{1}{(2 s) !}} \int_b^{\infty} P_{2 s} (t) f^{(2 s)} (t) d t }[/math]
- [math]\displaystyle{ \;\:\:\: \geqslant \sum_{k = a}^b f (k) - \left[ F (b) + {\small\frac{1}{2}} f (b) + \sum_{j = 1}^s {\small\frac{B_{2 j}}{(2 j) !}} f^{(2 j - 1)} (b) \right] - \Delta }[/math]
gdzie oznaczyliśmy
- [math]\displaystyle{ \Delta = {\small\frac{| B_{2 s} |}{(2 s) !}} | f^{(2 s - 1)} (b) | }[/math]
Jeśli dodatkowo oznaczymy
- [math]\displaystyle{ W = \sum_{k = a}^b f (k) - \left[ F (b) + {\small\frac{1}{2}} f (b) + \sum_{j = 1}^s {\small\frac{B_{2 j}}{(2 j) !}} f^{(2 j - 1)} (b) \right] }[/math]
to dostaniemy oszacowanie
- [math]\displaystyle{ W - \Delta \leqslant C(a) \leqslant W + \Delta }[/math]
Co należało pokazać.
□
Przykład E63
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 1}^{n} {\small\frac{1}{k}} }[/math]
Ponieważ
- [math]\displaystyle{ f(x) = {\small\frac{1}{x}} }[/math]
- [math]\displaystyle{ F(x) = \int {\small\frac{d x}{x}} = \log x }[/math]
- [math]\displaystyle{ f^{(r)} (x) = {\small\frac{d^r}{d x^r}} {\small\frac{1}{x}} = {\small\frac{(- 1)^r r!}{x^{r + 1}}} }[/math]
to z twierdzenia E61 dostajemy
- [math]\displaystyle{ W = \sum_{k = 1}^n {\small\frac{1}{k}} - \left[ \log n + {\small\frac{1}{2 n}} - \sum_{k = 1}^s {\small\frac{B_{2 k}}{2 k \cdot n^{2 k}}} \right] }[/math]
- [math]\displaystyle{ \Delta = {\small\frac{| B_{2 s} |}{2 s \cdot n^{2 s}}} }[/math]
Dla [math]\displaystyle{ s = 4 }[/math] i [math]\displaystyle{ n = 10^8 }[/math] mamy
- [math]\displaystyle{ \Delta = 4.17 \cdot 10^{- 67} }[/math]
Uznając, że dokładność rzędu [math]\displaystyle{ 10^{- 65} }[/math] nas zadowala, otrzymujemy dla [math]\displaystyle{ s = 4 }[/math]
- [math]\displaystyle{ W = \sum_{k = 1}^n {\small\frac{1}{k}} - \left[ \log n + {\small\frac{1}{2 n}} - {\small\frac{1}{12 n^2}} + {\small\frac{1}{120 n^4}} - {\small\frac{1}{252 n^6}} + {\small\frac{1}{240 n^8}} \right] }[/math]
Wyliczając wartość prawej strony dla [math]\displaystyle{ n = 10^8 }[/math], dostajemy
- [math]\displaystyle{ W = 0.57721566490153286060651209008240243104215933593992359880576723488486772677766467 \ldots }[/math]
Ponieważ [math]\displaystyle{ \Delta = 4.17 \cdot 10^{- 67} }[/math], to ostatecznie możemy napisać
- [math]\displaystyle{ \gamma = 0.57721566490153286060651209008240243104215933593992359880576723488 \ldots }[/math]
Wyznaczyliśmy stałą [math]\displaystyle{ \gamma }[/math] z dokładnością [math]\displaystyle{ 65 }[/math] cyfr po przecinku. W rzeczywistości błąd jest mniejszy od [math]\displaystyle{ 10^{- 81} }[/math].
Uwaga E64
Zauważmy, że wyliczając wartość [math]\displaystyle{ \Delta }[/math], znamy wartość błędu jeszcze przed wykonaniem całości obliczeń. Dobierając odpowiednie wartości liczb [math]\displaystyle{ s }[/math] i [math]\displaystyle{ n }[/math] możemy sprawić, że błąd będzie odpowiednio mały. Unikamy numerycznego całkowania, które w przypadku bardziej skomplikowanych funkcji może być długie i obarczone znacznym i nieznanym błędem.
Przykład E65
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 2}^n \mathop{\text{li}}(k) }[/math]
W PARI/GP funkcję specjalną [math]\displaystyle{ \mathop{\text{li}}(x) = \int^x_0 {\small\frac{d t}{\log t}} }[/math] (logarytm całkowy[14][15]) możemy uzyskać następująco
li(x) = real( -eint1( -log(x) ) )
W powyższym wzorze wykorzystaliśmy zaimplementowaną pod nazwą [math]\displaystyle{ \text{eint1} (x) }[/math] inną funkcję specjalną [math]\displaystyle{ E_1 (x) = \int_{x}^{\infty} {\small\frac{e^{- t}}{t}} d t }[/math][16][17].
Mamy:
- [math]\displaystyle{ f(x) = \mathop{\text{li}}(x) }[/math]
- [math]\displaystyle{ F(x) = \int \mathop{\text{li}}(x) d x = x \mathop{\text{li}}(x) - \mathop{\text{li}}(x^2) }[/math]
- [math]\displaystyle{ f^{(1)} (x) = {\small\frac{1}{\log x}} }[/math]
dla [math]\displaystyle{ k \geqslant 2 }[/math] jest
- [math]\displaystyle{ f^{(k)} (x) = {\small\frac{d^{k - 1}}{d x^{k - 1}}} {\small\frac{1}{\log x}} = (- 1)^{k - 1} \sum_{j = 1}^{k - 1} {\small\frac{A^{k - 1}_j}{x^{k - 1} \log^{j + 1} x}} = \mathop{\text{DLog}}(k - 1, x) }[/math]
Oznaczenie [math]\displaystyle{ k }[/math]-tej pochodnej funkcji [math]\displaystyle{ {\small\frac{1}{\log x}} }[/math] jako [math]\displaystyle{ \mathop{\text{DLog}}(k, x) }[/math] znacząco ułatwi nam zapisywanie wzorów. Liczby naturalne [math]\displaystyle{ A^k_j }[/math] spełniają następujące równania rekurencyjne
- [math]\displaystyle{ A^k_1 = (k - 1) A^{k - 1}_1 }[/math]
- [math]\displaystyle{ A_j^k = j A^{k - 1}_{j - 1} + (k - 1) A^{k - 1}_j \qquad }[/math] dla [math]\displaystyle{ \quad j = 2, \ldots, k - 1 }[/math]
- [math]\displaystyle{ A^k_k = k A^{k - 1}_{k - 1} }[/math]
gdzie [math]\displaystyle{ A^1_1 = 1 }[/math] (zobacz twierdzenia E68 i E69).
Zauważmy, że dla [math]\displaystyle{ k \geqslant 2 }[/math] funkcje [math]\displaystyle{ f^{(k)} (x) = {\small\frac{d^{k - 1}}{d x^{k - 1}}} {\small\frac{1}{\log x}} }[/math] są funkcjami ciągłymi i mają stały znak dla [math]\displaystyle{ x \gt 1 }[/math] oraz [math]\displaystyle{ \lim_{x \to \infty} f^{(k - 1)} (x) = 0 }[/math]. Zatem dla dowolnego [math]\displaystyle{ k \geqslant 2 }[/math] spełnione są założenia twierdzenia E62. W przypadku rozpatrywanej przez nas sumy z twierdzenia E62 otrzymujemy
- [math]\displaystyle{ \Delta = \Delta (s, n) = {\small\frac{| B_{2 s} |}{(2 s) !}} | \mathop{\text{DLog}}(2 s - 2, n) | }[/math]
- [math]\displaystyle{ W = W (s, 2, n) = \sum_{k = 2}^n \mathop{\text{li}}(k) - \left[ n \mathop{\text{li}}(n) - \mathop{\text{li}}(n^2) + {\small\frac{1}{2}} \mathop{\text{li}}(n) + {\small\frac{B_2}{2 \log n}} + \sum_{k = 2}^s {\small\frac{B_{2 k}}{(2 k) !}} \mathop{\text{DLog}}(2 k - 2, n) \right] }[/math]
Obliczenia przeprowadziliśmy w programie PARI/GP. Wymagają one zwiększenia precyzji obliczeń do [math]\displaystyle{ 80 }[/math] miejsc znaczących i wcześniejszego przygotowania kilku funkcji omówionych szerzej w uwadze E70. Mamy
B(n, x) = sum(k = 0, n, 1/(k+1)*sum(j = 0, k, (-1)^j*binomial(k,j)*(x+j)^n)) A(n, k) = if( k == 1 || k == n, k*(n-1)!, k*A(n-1, k-1) + (n-1)*A(n-1, k) ) DLog(n, x) = (-1)^n * sum(k = 1, n, A(n,k)/( x^n * log(x)^(k+1) )) li(x) = real( -eint1( -log(x) ) ) delta(s, n) = B(2*s, 0)/(2*s)! * DLog(2*s-2, n) W(s, n) = sum(k = 2, n, li(k)) - n*li(n) + li(n^2) - 1/2*li(n) - B(2,0)/2! * 1/log(n) - sum(k = 2, s, B(2*k,0)/(2*k)! * DLog(2*k-2, n))
Dla [math]\displaystyle{ s = 5 }[/math] i [math]\displaystyle{ n = 10^7 }[/math] otrzymujemy (porównaj WolframAlpha)
[math]\displaystyle{ \Delta = {\small\frac{B_{10}}{10!}} \cdot | \mathop{\text{DLog}}(8, 10^7) | = 5.632 \cdot 10^{- 63} }[/math]
[math]\displaystyle{ W = 1.28191595049146577908068521816208913078488987854947239276268700691879666704021184913771562 }[/math]
Po uwzględnieniu możliwego błędu znajdujemy wartość stałej z dokładnością [math]\displaystyle{ 61 }[/math] miejsc po przecinku.
[math]\displaystyle{ C = 1.2819159504914657790806852181620891307848898785494723927626870 \ldots }[/math]
Przykład E66
Rozważmy jeszcze raz sumę
- [math]\displaystyle{ \sum_{k = 2}^n \mathop{\text{li}}(k) }[/math]
Wypiszmy dla tej sumy wzór Eulera-Maclaurina dla [math]\displaystyle{ r = 1 }[/math].
- [math]\displaystyle{ \sum_{k = 2}^n \mathop{\text{li}}(k) = \int_2^n \mathop{\text{li}}(t) d t + {\small\frac{1}{2}} \mathop{\text{li}}(n) + {\small\frac{1}{2}} \mathop{\text{li}}(2) + \int_2^n {\small\frac{P_1(t)}{\log t}} d t }[/math]
- [math]\displaystyle{ \;\;\;\: = (x \mathop{\text{li}}(x) - \mathop{\text{li}}(x^2)) \biggr\rvert_{2}^{n} + {\small\frac{1}{2}} \mathop{\text{li}}(n) + {\small\frac{1}{2}} \mathop{\text{li}}(2) + \int_2^n {\small\frac{P_1 (t)}{\log t}} d t }[/math]
- [math]\displaystyle{ \;\;\;\: = n \mathop{\text{li}}(n) - \mathop{\text{li}}(n^2) - 2 \mathop{\text{li}}(2) + \mathop{\text{li}}(4) + {\small\frac{1}{2}} \mathop{\text{li}}(n) + {\small\frac{1}{2}} \mathop{\text{li}}(2) + \int_2^{\infty} {\small\frac{P_1 (t)}{\log t}} d t - \int_n^{\infty} {\small\frac{P_1 (t)}{\log t}} d t }[/math]
- [math]\displaystyle{ \;\;\;\: = \left[ - {\small\frac{3}{2}} \mathop{\text{li}}(2) + \mathop{\text{li}}(4) + \int_2^{\infty} {\small\frac{P_1 (t)}{\log t}} d t \right] + n \mathop{\text{li}}(n) - \mathop{\text{li}}(n^2) + {\small\frac{1}{2}} \mathop{\text{li}}(n) - \int_n^{\infty} {\small\frac{P_1 (t)}{\log t}} d t }[/math]
Wyrażenie w nawiasie kwadratowym jest stałą wstępującą we wzorze Eulera-Maclaurina, zatem
- [math]\displaystyle{ C = - {\small\frac{3}{2}} \mathop{\text{li}}(2) + \mathop{\text{li}}(4) + \int_2^{\infty} {\small\frac{P_1(t)}{\log t}} d t }[/math]
- [math]\displaystyle{ \int_2^{\infty} {\small\frac{P_1 (t)}{\log t}} d t = C + {\small\frac{3}{2}} \mathop{\text{li}}(2) - \mathop{\text{li}}(4) }[/math]
W poprzednim przykładzie wyliczyliśmy wartość stałej [math]\displaystyle{ C }[/math]
- [math]\displaystyle{ C = 1.2819159504914657790806852181620891307848898785494723927626870 \ldots }[/math]
Wynika stąd natychmiast, że
- [math]\displaystyle{ \int_2^{\infty} {\small\frac{P_1 (t)}{\log t}} d t = -0.117923474371345921663180326620119770994144590988603907635106 \ldots }[/math]
Właśnie w taki sposób została obliczona wartość całki niewłaściwej, która występuje w zadaniu E49.
Przykład E67
Rozważmy sumę
- [math]\displaystyle{ \sum_{k = 0}^{n} e^k }[/math]
Mamy
- [math]\displaystyle{ f(x) = e^x }[/math]
- [math]\displaystyle{ F(x) = \int e^x d x = e^x }[/math]
- [math]\displaystyle{ f^{(r)} (x) = {\small\frac{d^r}{d x^r}} e^x = e^x }[/math]
Zatem ze wzoru Eulera-Maclaurina otrzymujemy
- [math]\displaystyle{ \sum_{k = 0}^{n} e^k = e^n - 1 + {\small\frac{1}{2}} (e^n + 1) + \sum_{k = 1}^s {\small\frac{B_{2 k}}{(2 k) !}} (e^n - 1) - {\small\frac{1}{(2 s) !}} \int_0^n P_{2 s} (t) e^t d t }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} e^k = 1 + (e^n - 1) + {\small\frac{1}{2}} (e^n - 1) + \sum_{k = 1}^s {\small\frac{B_{2 k}}{(2 k) !}} (e^n - 1) - {\small\frac{1}{(2 s) !}} \int_0^n P_{2 s} (t) e^t d t }[/math]
- [math]\displaystyle{ \sum_{k = 0}^{n} e^k = 1 + (e^n - 1) \left( 1 + {\small\frac{1}{2}} + \sum_{k = 1}^s {\small\frac{B_{2 k}}{(2 k) !}} \right) - {\small\frac{1}{(2 s) !}} \int_0^n P_{2 s} (t) e^t d t }[/math]
Ponieważ dla [math]\displaystyle{ | x | \lt 2 \pi }[/math] prawdziwy jest wzór[18]
- [math]\displaystyle{ {\small\frac{x}{e^x - 1}} = \sum_{k = 0}^{\infty} {\small\frac{B_k \cdot x^k}{k!}} }[/math]
to dla [math]\displaystyle{ x = 1 }[/math] dostajemy
- [math]\displaystyle{ {\small\frac{1}{e - 1}} = \sum_{k = 0}^{\infty} {\small\frac{B_k}{k!}} = 1 - {\small\frac{1}{2}} + \sum_{k = 1}^{\infty} {\small\frac{B_{2 k}}{(2 k) !}} = {\small\frac{1}{2}} + \sum_{k = 1}^{\infty} {\small\frac{B_{2 k}}{(2 k) !}} }[/math]
W granicy, gdy [math]\displaystyle{ s }[/math] dąży do nieskończoności, mamy
- [math]\displaystyle{ \lim_{s \to \infty} \left[ 1 + (e^n - 1) \left( {\small\frac{3}{2}} + \sum_{k = 1}^s {\small\frac{B_{2 k}}{(2 k) !}} \right) \right] = 1 + (e^n - 1) \left( {\small\frac{3}{2}} + {\small\frac{1}{e - 1}} - {\small\frac{1}{2}} \right) = 1 + (e^n - 1) \left( 1 + {\small\frac{1}{e - 1}} \right) = {\small\frac{e^{n + 1} - 1}{e - 1}} }[/math]
W obliczeniu granicy całki dla [math]\displaystyle{ s }[/math] dążącego do nieskończoności pomocne będzie oszacowanie (zobacz E23)
- [math]\displaystyle{ {\small\frac{| B_{2 k} |}{(2 k) !}} \lt {\small\frac{2}{(2 \pi)^{2 k}}} \cdot {\small\frac{1}{1 - 2^{1 - 2 k}}} \leqslant {\small\frac{4}{(2 \pi)^{2 k}}} }[/math]
prawdziwe dla [math]\displaystyle{ k \geqslant 1 }[/math].
Teraz już łatwo znajdujemy
- [math]\displaystyle{ 0 \leqslant {\small\frac{1}{(2 s) !}} \left| \int_0^n P_{2 s} (t) e^t d t \right| \leqslant {\small\frac{1}{(2 s) !}} \int_0^n | P_{2 s} (t) | e^t d t \leqslant {\small\frac{| B_{2 s} |}{(2 s) !}} \int_0^n e^t d t = {\small\frac{| B_{2 s} |}{(2 s) !}} (e^n - 1) \lt {\small\frac{4}{(2 \pi)^{2 s}}} (e^n - 1) }[/math]
Dla dowolnego, ale ustalonego [math]\displaystyle{ n }[/math], jest
- [math]\displaystyle{ \lim_{s \to \infty} {\small\frac{4}{(2 \pi)^{2 s}}} (e^n - 1) = 0 }[/math]
Zatem z twierdzenia o trzech ciągach (zobacz twierdzenia C10 i C8) dostajemy natychmiast
- [math]\displaystyle{ \lim_{s \to \infty} {\small\frac{1}{(2 s) !}} \left| \int_0^n P_{2 s} (t) e^t d t \right| = \lim_{s \to \infty} {\small\frac{1}{(2 s) !}} \int_0^n P_{2 s} (t) e^t d t = 0 }[/math]
Ostatecznie otrzymujemy wzór
- [math]\displaystyle{ \sum_{k = 0}^{n} e^k = {\small\frac{e^{n + 1} - 1}{e - 1}} }[/math]
Znalezienie wzoru na sumę częściową szeregu geometrycznego nie jest odkrywcze, ale z pewnością było pouczające.
Uzupełnienie
Twierdzenie E68
Ogólny wzór na [math]\displaystyle{ n }[/math]-tą pochodną funkcji [math]\displaystyle{ {\small\frac{1}{\log x}} }[/math] ma postać
- [math]\displaystyle{ {\small\frac{d^n}{d x^n}} {\small\frac{1}{\log x}} = (- 1)^n \sum_{k = 1}^{n} {\small\frac{A^n_k}{x^n \log^{k + 1} x}} }[/math]
Liczby naturalne [math]\displaystyle{ A^n_k }[/math] spełniają następujące równania rekurencyjne
- [math]\displaystyle{ A^n_1 = (n - 1) A^{n - 1}_1 }[/math]
- [math]\displaystyle{ A_k^n = k A^{n - 1}_{k - 1} + (n - 1) A^{n - 1}_k \qquad }[/math] dla [math]\displaystyle{ \quad k = 2, \ldots, n - 1 }[/math]
- [math]\displaystyle{ A^n_n = n A^{n - 1}_{n - 1} }[/math]
gdzie [math]\displaystyle{ A^1_1 = 1 }[/math].
Indukcja matematyczna. Łatwo sprawdzamy, że dowodzony wzór jest prawdziwy dla [math]\displaystyle{ n = 1 }[/math]. Ponieważ
- [math]\displaystyle{ \left( {\small\frac{1}{x^n \log^{k + 1} x}} \right)' = \frac{- (k + 1)}{x^{n + 1} \log^{k + 2} x} + \frac{- n}{x^{n + 1} \log^{k + 1} x} }[/math]
to zakładając, że wzór
- [math]\displaystyle{ {\small\frac{d^n}{d x^n}} {\small\frac{1}{\log x}} = (- 1)^n \sum_{k = 1}^{n} {\normalsize\frac{A^n_k}{x^n \log^{k + 1} x}} }[/math]
jest prawdziwy dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]
- [math]\displaystyle{ {\small\frac{d^{n + 1}}{d x^{n + 1}}} {\small\frac{1}{\log x}} = (- 1)^n \sum_{k = 1}^{n} \left( {\normalsize\frac{A^n_k}{x^n \log^{k + 1} x}} \right)' = }[/math]
- [math]\displaystyle{ \;\,\, = (- 1)^n \sum_{k = 1}^{n} \left( \frac{- (k + 1) A^n_k}{x^{n + 1} \log^{k + 2} x} + \frac{- n A^n_k}{x^{n + 1} \log^{k + 1} x} \right) }[/math]
Mnożąc obie strony przez [math]\displaystyle{ (- 1)^{n + 1} }[/math] ułatwimy sobie przekształcanie prawej strony
- [math]\displaystyle{ (- 1)^{n + 1} {\small\frac{d^{n + 1}}{d x^{n + 1}}} {\small\frac{1}{\log x}} = \sum_{k = 1}^{n} \left( \frac{(k + 1) A^n_k}{x^{n + 1} \log^{k + 2} x} + \frac{n A^n_k}{x^{n + 1} \log^{k + 1} x} \right) = }[/math]
- [math]\displaystyle{ \! = \sum_{k = 1}^{n} \frac{(k + 1) A^n_k}{x^{n + 1} \log^{k + 2} x} + \sum_{k = 1}^{n} \frac{n A^n_k}{x^{n + 1} \log^{k + 1} x} = }[/math]
- [math]\displaystyle{ \! = \frac{(n + 1) A^n_n}{x^{n + 1} \log^{n + 2} x} + \sum_{k = 1}^{n - 1} \frac{(k + 1) A^n_k}{x^{n + 1} \log^{k + 2} x} + \sum_{k = 2}^{n} \frac{n A^n_k}{x^{n + 1} \log^{k + 1} x} + {\normalsize\frac{n A^n_1}{x^{n + 1} \log^2 x}} }[/math]
Zmieniając w pierwszej sumie wskaźnik sumowania na [math]\displaystyle{ j = k + 1 }[/math], dostajemy
- [math]\displaystyle{ (- 1)^{n + 1} {\small\frac{d^{n + 1}}{d x^{n + 1}}} {\small\frac{1}{\log x}} = \frac{(n + 1) A^n_n}{x^{n + 1} \log^{n + 2} x} + \sum_{j = 2}^{n} \frac{j A^n_{j - 1}}{x^{n + 1} \log^{j + 1} x} + \sum_{k = 2}^{n} \frac{n A^n_k}{x^{n + 1} \log^{k + 1} x} + {\normalsize\frac{n A^n_1}{x^{n + 1} \log^2 x}} = }[/math]
- [math]\displaystyle{ \! = {\normalsize\frac{n A^n_1}{x^{n + 1} \log^2 x}} + \sum_{k = 2}^{n} \left( \frac{k A^n_{k - 1} + n A^n_k}{x^{n + 1} \log^{k + 1} x} \right) + \frac{(n + 1) A^n_n}{x^{n + 1} \log^{n + 2} x} }[/math]
Oznaczając
- [math]\displaystyle{ A^{n + 1}_1 = n A^n_1 }[/math]
- [math]\displaystyle{ A_k^{n + 1} = k A^n_{k - 1} + n A^n_k \qquad }[/math] dla [math]\displaystyle{ \quad k = 2, \ldots, n }[/math]
- [math]\displaystyle{ A^{n + 1}_{n + 1} = (n + 1) A^n_n }[/math]
Otrzymujemy wzór
- [math]\displaystyle{ {\small\frac{d^{n+1}}{d x^{n+1}}} {\small\frac{1}{\log x}} = (- 1)^{n + 1} \sum_{k = 1}^{n + 1} {\small\frac{A^{n + 1}_k}{x^n \log^{k + 1} x}} }[/math]
Co kończy dowód indukcyjny. Aby uzyskać podane w twierdzeniu równania rekurencyjne, wystarczy we wprowadzonych oznaczeniach zamienić [math]\displaystyle{ n }[/math] na [math]\displaystyle{ n - 1 }[/math].
□
Twierdzenie E69
Z równań rekurencyjnych
- [math]\displaystyle{ A^n_1 = (n - 1) A^{n - 1}_1 }[/math]
- [math]\displaystyle{ A_k^n = k A^{n - 1}_{k - 1} + (n - 1) A^{n - 1}_k \qquad }[/math] dla [math]\displaystyle{ \quad k = 2, \ldots, n - 1 }[/math]
- [math]\displaystyle{ A^n_n = n A^{n - 1}_{n - 1} }[/math]
gdzie [math]\displaystyle{ A^1_1 = 1 }[/math], wynikają następujące wzory ogólne
- [math]\displaystyle{ A^n_1 = (n - 1) ! }[/math]
- [math]\displaystyle{ A^n_n = n! }[/math]
oraz
- [math]\displaystyle{ A^n_{n - 1} = {\small\frac{1}{2}} (n - 1) \cdot n! }[/math]
- [math]\displaystyle{ A^n_{n - 2} = {\small\frac{1}{24}} (n - 2) (3 n - 1) \cdot n! }[/math]
- [math]\displaystyle{ A^n_{n - 3} = {\small\frac{1}{48}} n (n - 1) (n - 3) \cdot n! }[/math]
- [math]\displaystyle{ A^n_{n - 4} = {\small\frac{1}{5760}} (n - 4) (15 n^3 - 30 n^2 + 5 n + 2) \cdot n! }[/math]
- [math]\displaystyle{ A^n_2 = 2 (n - 1) ! \cdot \sum_{k = 1}^{n - 1} {\small\frac{1}{k}} }[/math]
Rozwiązania pierwszego i trzeciego równania rekurencyjnego łatwo sprawdzamy. Drugie równanie jest znacznie trudniejsze. Rozważmy je dla [math]\displaystyle{ k = n - 1 }[/math], mamy
- [math]\displaystyle{ A_{n - 1}^n = (n - 1) A^{n - 1}_{n - 2} + (n - 1) A^{n - 1}_{n - 1} }[/math]
Uwzględniając, że [math]\displaystyle{ A^{n - 1}_{n - 1} = (n - 1) ! }[/math], dostajemy
- [math]\displaystyle{ A_{n - 1}^n = (n - 1) A^{n - 1}_{n - 2} + (n - 1) (n - 1) ! }[/math]
Połóżmy
- [math]\displaystyle{ A_{n - 1}^n = (n - 1) ! \cdot U^n_{n - 1} }[/math]
Zauważmy, że [math]\displaystyle{ A_1^2 = U^2_1 = 1 }[/math]. Podstawiając, mamy
- [math]\displaystyle{ (n - 1) ! \cdot U^n_{n - 1} = (n - 1) \cdot (n - 2) ! \cdot U^{n - 1}_{n - 2} + (n - 1) (n - 1) ! }[/math]
Zatem
- [math]\displaystyle{ U^n_{n - 1} = U^{n - 1}_{n - 2} + (n - 1) }[/math]
Czyli
- [math]\displaystyle{ U^n_{n - 1} - U^{n - 1}_{n - 2} = n - 1 }[/math]
Łatwo znajdujemy ogólną postać [math]\displaystyle{ U^n_{n - 1} }[/math]
- [math]\displaystyle{ U^n_{n - 1} = U^2_1 + \sum_{k = 3}^{n} (U^k_{k - 1} - U^{k - 1}_{k - 2}) = 1 + \sum_{k = 3}^{n} (k - 1) = 1 + {\small\frac{1}{2}} (n - 2) (n + 1) = {\small\frac{1}{2}} n (n - 1) }[/math]
Skąd natychmiast otrzymujemy
- [math]\displaystyle{ A_{n - 1}^n = (n - 1) ! \cdot U^n_{n - 1} = (n - 1) ! \cdot {\small\frac{1}{2}} n (n - 1) = {\small\frac{1}{2}} (n - 1) \cdot n! }[/math]
Zbadajmy drugie równanie rekurencyjne dla [math]\displaystyle{ k = n - 2 }[/math], mamy
- [math]\displaystyle{ A_{n - 2}^n = (n - 2) A^{n - 1}_{n - 3} + (n - 1) A^{n - 1}_{n - 2} }[/math]
Uwzględniając, że [math]\displaystyle{ A^{n - 1}_{n - 2} = {\small\frac{1}{2}} (n - 2) \cdot (n - 1)! }[/math], dostajemy
- [math]\displaystyle{ A_{n - 2}^n = (n - 2) A^{n - 1}_{n - 3} + {\small\frac{1}{2}} (n - 1) (n - 2) \cdot (n - 1) ! }[/math]
Połóżmy
- [math]\displaystyle{ A_{n - 2}^n = (n - 2) ! \cdot U^n_{n - 2} }[/math]
Zauważmy, że [math]\displaystyle{ A_1^3 = U^3_1 = 2 }[/math]. Podstawiając, mamy
- [math]\displaystyle{ (n - 2) ! \cdot U^n_{n - 2} = (n - 2) \cdot (n - 3) ! \cdot U^{n - 1}_{n - 3} + {\small\frac{1}{2}} (n - 1) (n - 2) \cdot (n - 1) ! }[/math]
Zatem
- [math]\displaystyle{ U^n_{n - 2} = U^{n - 1}_{n - 3} + {\small\frac{1}{2}} (n - 1)^2 (n - 2) }[/math]
Czyli
- [math]\displaystyle{ U^n_{n - 2} - U^{n - 1}_{n - 3} = {\small\frac{1}{2}} (n - 1)^2 (n - 2) }[/math]
Łatwo znajdujemy ogólną postać [math]\displaystyle{ U^n_{n - 2} }[/math]
- [math]\displaystyle{ U^n_{n - 2} = U^3_1 + \sum_{k = 4}^{n} (U^k_{k - 2} - U^{k - 1}_{k - 3}) = 2 + {\small\frac{1}{2}} \sum_{k = 4}^{n} (k - 1)^2 (k - 2) = {\small\frac{1}{24}} n (n - 1) (n - 2) (3 n - 1) }[/math]
Skąd natychmiast otrzymujemy
- [math]\displaystyle{ A_{n - 2}^n = (n - 2) ! \cdot U^n_{n - 2} = {\small\frac{1}{24}} (n - 2) (3 n - 1) \cdot n! }[/math]
Podobnie znajdujemy rozwiązania [math]\displaystyle{ k = n - 3 }[/math] i [math]\displaystyle{ k = n - 4 }[/math]. Przypadek [math]\displaystyle{ k = 2 }[/math] jest podobny do poprzednich, ale w tym przypadku wyliczona suma nie może być przedstawiona w zwartej formie. Dlatego omówimy go dodatkowo.
- [math]\displaystyle{ A_2^n = 2 A^{n - 1}_1 + (n - 1) A^{n - 1}_2 }[/math]
Uwzględniając, że [math]\displaystyle{ A^{n - 1}_1 = (n - 2) ! }[/math], dostajemy
- [math]\displaystyle{ A_2^n = 2 (n - 2) ! + (n - 1) A^{n - 1}_2 }[/math]
Połóżmy
- [math]\displaystyle{ A_2^n = (n - 1) ! \cdot U^n_2 }[/math]
Zauważmy, że [math]\displaystyle{ A_2^2 = U^2_2 = 2 }[/math]. Podstawiając, mamy
- [math]\displaystyle{ (n - 1) ! \cdot U^n_2 = (n - 1) \cdot (n - 2) ! \cdot U^{n - 1}_2 + 2 (n - 2)! }[/math]
Zatem
- [math]\displaystyle{ U^n_2 = U^{n - 1}_2 + {\small\frac{2}{n - 1}} }[/math]
Czyli
- [math]\displaystyle{ U^n_2 - U^{n - 1}_2 = {\small\frac{2}{n - 1}} }[/math]
Łatwo znajdujemy ogólną postać [math]\displaystyle{ U^n_2 }[/math]
- [math]\displaystyle{ U^n_2 = U^2_2 + \sum_{k = 3}^{n} (U^k_2 - U^{k - 1}_2) = 2 + 2 \sum_{k = 3}^{n} {\small\frac{1}{k - 1}} = 2 \sum_{k = 2}^{n} {\small\frac{1}{k - 1}} }[/math]
Skąd natychmiast otrzymujemy
- [math]\displaystyle{ A_2^n = (n - 1) ! \cdot U^n_2 = 2 (n - 1) ! \cdot \sum_{k = 2}^{n} {\small\frac{1}{k - 1}} = 2 (n - 1) ! \cdot \sum_{k = 1}^{n - 1} {\small\frac{1}{k}} }[/math]
- [math]\displaystyle{ A_2^n = (n - 1) ! \cdot U^n_2 = 2 (n - 1) ! \cdot \sum_{k = 2}^{n} {\small\frac{1}{k - 1}} = 2 (n - 1) ! \cdot \sum_{k = 1}^{n - 1} {\small\frac{1}{k}} }[/math]
□
Uwaga E70
Z twierdzeń E68 i E69 wynika, że ogólną postać [math]\displaystyle{ n }[/math]-tej pochodnej funkcji [math]\displaystyle{ {\small\frac{1}{\log x}} }[/math] możemy łatwo wypisać
- [math]\displaystyle{ {\small\frac{d^n}{d x^n}} {\small\frac{1}{\log x}} = (- 1)^n \sum_{k = 1}^{n} {\small\frac{A^n_k}{x^n \log^{k + 1} x}} }[/math]
ale nie istnieje wzór ogólny, który pozwoliłby łatwo wyliczać wartości współczynników [math]\displaystyle{ A_k^n }[/math]. W tej sytuacji jedynym wyjściem jest wykorzystanie równania rekurencyjnego
- [math]\displaystyle{ A_k^n = k A^{n - 1}_{k - 1} + (n - 1) A^{n - 1}_k \qquad }[/math] dla [math]\displaystyle{ \quad k = 2, \ldots, n - 1 }[/math]
oraz wzorów
- [math]\displaystyle{ A^n_1 = (n - 1) ! }[/math]
- [math]\displaystyle{ A^n_n = n! }[/math]
Programy odwołujące się do wzorów rekurencyjnych są zazwyczaj niezwykle proste, ale należy ich unikać, bo działają wolno i zużywają duże ilości pamięci. Niżej podajemy przykłady prostych funkcji rekurencyjnych wyliczających silnię i liczby Fibonacciego napisanych w PARI/GP
silnia(n) = if( n == 0, 1, n*silnia(n-1) )
Fibonacci(n) = if( n <= 1, n, Fibonacci(n-1) + Fibonacci(n-2) )
W naszym przypadku rekurencji ominąć nie można, ale rozwiązaniem problemu jest równie prosta funkcja
A(n, k) = if( k == 1 || k == n, k*(n-1)!, k*A(n-1, k-1) + (n-1)*A(n-1, k) )
Dysponując funkcją wyliczającą współczynniki A(n, k), możemy łatwo zapisać wzór na [math]\displaystyle{ n }[/math]-tą pochodną funkcji [math]\displaystyle{ {\small\frac{1}{\log x}} }[/math]
DLog(n, x) = (-1)^n * sum(k = 1, n, A(n, k)/( x^n * log(x)^(k+1) ))
Powyższy wzór jest bardzo przydatny przy wyliczaniu wartości [math]\displaystyle{ {\small\frac{d^n}{d x^n}} {\small\frac{1}{\log x}} }[/math] dla większych liczb [math]\displaystyle{ n }[/math]. Jednak [math]\displaystyle{ n }[/math] nie może być zbyt duże – ceną, jaką musimy zapłacić za użycie funkcji rekurencyjnych, jest wydłużenie czasu obliczeń. Przykładowo obliczenie
DLog(26, 10^8) = 7.1305293508389973644228947613613744962 10^(-186)
trwało ponad pół minuty. Zobacz też WolframAlpha
Przypisy
- ↑ Wikipedia, Bernoulli polynomials, (Wiki-en)
- ↑ WolframAlpha, Bernoulli Polynomial, (WolframAlpha)
- ↑ Wolfram MathWorld, Bernoulli Polynomial, (Wolfram)
- ↑ NIST Digital Library of Mathematical Functions, Bernoulli and Euler Polynomials, (LINK)
- ↑ 5,0 5,1 Wikipedia, Twierdzenie Rolle’a, (Wiki-pl), (Wiki-en)
- ↑ D. H. Lehmer, On the Maxima and Minima of Bernoulli Polynomials, The American Mathematical Monthly, Vol. 47, No. 8 (Oct., 1940), pp. 533-538
- ↑ M. Abramowitz and I. A. Stegun (Eds), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series 55, 10th printing, Washington, 1972, (LINK)
- ↑ Wikipedia, Abramowitz and Stegun, (Wiki-en)
- ↑ C. D'Aniello, On some inequalities for the Bernoulli numbers, Rendiconti del Circolo Matematico di Palermo Series II, Volume 43 (1994), pp. 329-332
- ↑ Feng Qi, A double inequality for the ratio of two non-zero neighbouring Bernoulli numbers, Journal of Computational and Applied Mathematics, Volume 351 (2019), pp. 1-5, (LINK)
- ↑ Twierdzenie Weierstrassa: Jeżeli funkcja [math]\displaystyle{ f(x) }[/math] określona w przedziale domkniętym jest ciągła, to jest w nim ograniczona. (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Euler–Maclaurin formula, (Wiki-en)
- ↑ Wikipedia, Wzór Stirlinga, (Wiki-pl), (Wiki-en)
- ↑ Wikipedia, Logarytm całkowy, (Wiki-pl), (Wiki-en)
- ↑ Wolfram MathWorld, Logarithmic Integral, (Wolfram)
- ↑ Wikipedia, Funkcja całkowo-wykładnicza, (Wiki-pl), (Wiki-en)
- ↑ Wolfram MathWorld, Exponential Integral, (Wolfram)
- ↑ Wikipedia, Liczby Bernoulliego, (Wiki-pl)