Dynamika rozprzestrzeniania się koronawirusa SARS-CoV-2 w Polsce
Podejrzewasz zakażenie koronawirusem SARS-CoV-2? Sprawdź co robić!
Zakażenie koronawirusem może spowodować pojawienie się u chorego następujących objawów:
- gorączka większa od 38°C
- kaszel
- duszność
- problemy z oddychaniem
Jeżeli wystąpił u Ciebie co najmniej jeden z wyżej wymienionych objawów, to powinieneś zgłosić się do szpitalnego oddziału chorób zakaźnych, najbliższego Twojego miejsca pobytu. (LINK)
Możesz też zadzwonić na całodobową infolinię Narodowego Funduszu Zdrowia 800 190 590, aby uzyskać więcej informacji o tym, jak postępować w przypadku podejrzenia zakażenia koronawirusem.
Listę szpitalnych oddziałów chorób zakaźnych (plik DOCX do pobrania) znajdziesz na stronie Ministerstwa Zdrowia: Byłeś w Chinach i źle się czujesz? Sprawdź co robić! (LINK).
Nie zgłaszaj się na SOR lub do przychodni POZ, bo możesz jedynie zarazić przebywające tam osoby.
Pamiętaj! Nie czekaj, aż objawy wystąpią u Ciebie lub u bliskich Ci osób. Pobierz plik już dziś! Już teraz musisz wiedzieć, co będziesz musiał zrobić. Twoja wiedza może okazać się przydatna, gdy choroba dotknie Ciebie lub inne osoby.
Poczyniwszy odpowiednie przygotowania, możemy teraz spokojnie przejść do zasadniczego tematu tego artykułu, jakim jest szybkość rozprzestrzeniania się koronawirusa w Polsce.
Dynamika rozprzestrzeniania się koronawirusa SARS-CoV-2 w Polsce
Na wstępie zauważmy, że tekst artykułu zmieniał się w czasie. Początkowo miał tylko pokazać, że liczba zakażeń nie wzrasta wykładniczo, a taką wersję przedstawiały wszystkie media. W rzeczywistości wzrost liczby zakażeń mieścił się między krzywymi wielomianowymi drugiego i trzeciego stopnia. Te rozważania, obecnie już całkowicie nieaktualne, przesunęliśmy na koniec tekstu.
Minęło już ponad 170 dni od początku epidemii w Polsce, czyli prawie 25 tygodni. Wygląda na to, że koronawirus zostanie z nami na dłużej i będzie problemem, dopóki większość osób nie przejdzie zakażenia (lub nie pojawi się szczepionka). Na zamieszczonym niżej wykresie prezentujemy wartości tygodniowej średniej kroczącej[1], czyli średniej liczby zakażeń obliczanej dla ostatnich siedmiu dni. Wybór tygodnia do obliczania średniej kroczącej wydaje się najbardziej właściwy. Wynika to z faktu, że intensywność pracy służb może spadać w weekendy, co skutkuje dziwnymi skokami średniej kroczącej obliczanej dla ostatnich pięciu dni (wcześniej wybraliśmy właśnie taką średnią kroczącą). Poza tym oczekiwany długi okres trwania epidemii zmienia podejście do prezentowania liczby zakażeń. Już nie oczekujemy, że koniec zachorowań jest bliski, a spadek liczby zakażeń zauważymy tym lepiej, im średnia krocząca będzie obliczana dla mniejszej liczby dni. Przeciwnie, uważamy, że wygaszanie epidemii będzie długotrwałe i posługiwanie się tygodniową średnią kroczącą nie spowoduje utraty informacji, a sprawi, że nie będą pojawiały się przypadkowe odchylenia na prezentowanym wykresie.

Po upływie ponad 380 dni widzimy, że możemy wydzielić trzy podstawowe etapy przebiegu epidemii:
- etap pierwszy w okresie od 4 marca 2020 roku (1 dzień epidemii) do 18 września 2020 roku (199 dzień epidemii)
- etap drugi w okresie od 19 września 2020 roku (200 dzień epidemii) do 9 lutego 2021 roku (343 dzień epidemii)
- etap trzeci w okresie od 10 lutego 2021 roku (344 dzień epidemii) do chwili obecnej
W pierwszym etapie dzienna liczba zakażeń nigdy nie przekroczyła tysiąca, w drugim etapie przekroczyła tysiąc i rozpoczął się szybki, a następnie bardzo szybki wzrost dziennej liczby zakażeń. Zauważmy też, że tygodniowa średnia krocząca po raz ostatni osiągnęła lokalne minimum 11.09.2020 (192) – 461 zakażeń i od tego czasu nieprzerwanie rosła przez 61 dni do 11.11.2020 (253) – 25615 zakażeń. Etap drugi zakończył się 09.02.2021 (343), kiedy to tygodniowa średnia krocząca osiągnęła najmniejszą wartość – 5215 zakażeń. Tak niskiej wartości tygodniowej średniej kroczącej nie notowano od dnia 14.10.2020 (225), kiedy to średnia ta była równa 4926. Konsekwentnie sporządzimy osobne wykresy dla każdego z etapów, bo pozwala to lepiej prezentować uzyskiwane dane.
Pierwszy etap epidemii: od 04.03.2020 (1) do 18.09.2020 (199)
Dynamika rozprzestrzeniania się koronawirusa SARS-CoV-2 w Polsce w pierwszym okresie epidemii wyglądała następująco:
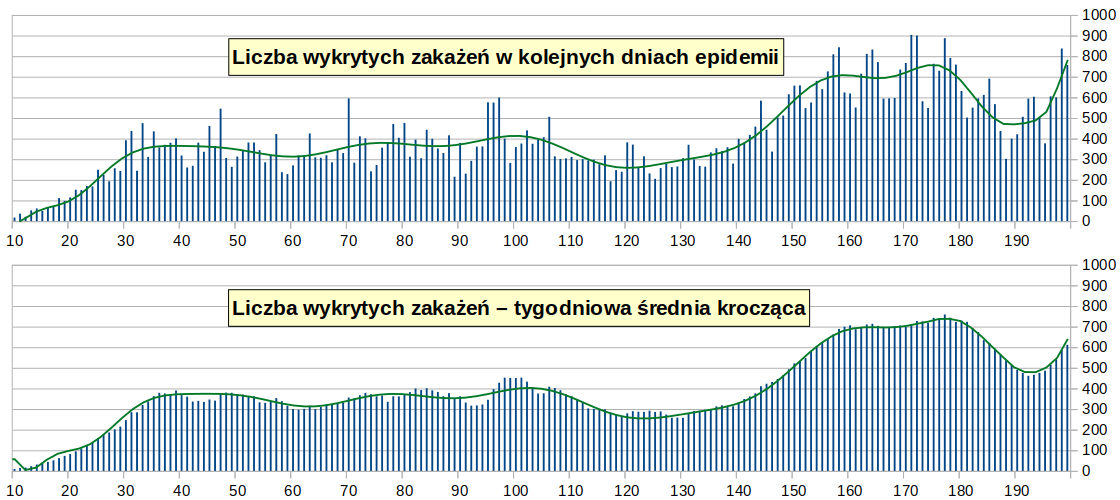
Drugi etap epidemii: od 19.09.2020 (200) do 09.02.2021 (343)
Dynamika rozprzestrzeniania się koronawirusa SARS-CoV-2 w Polsce w drugim okresie epidemii ma zupełnie inny przebieg i możemy powiedzieć, że dzienna liczba zakażeń wyrwała się spod kontroli. Czytelnik powinien mieć świadomość, że wzrost dziennej liczby przypadków jest na poniższym wykresie ponad dziesięciokrotnie szybszy niż na wykresie sporządzonym dla pierwszego etapu.
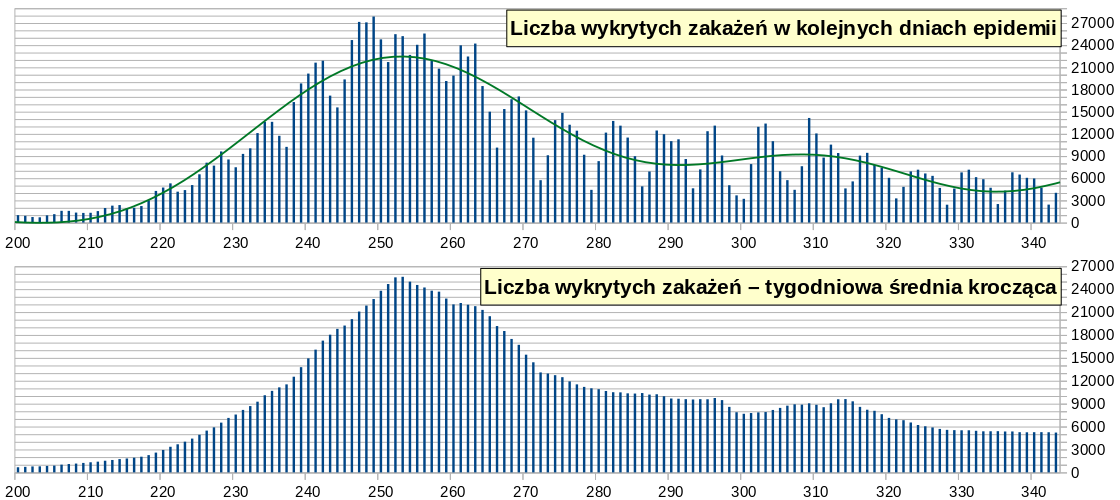
Trzeci etap epidemii: od 10.02.2021 (344) do chwili obecnej
Dynamika rozprzestrzeniania się koronawirusa SARS-CoV-2 w Polsce w trzecim okresie epidemii przedstawia się następująco:
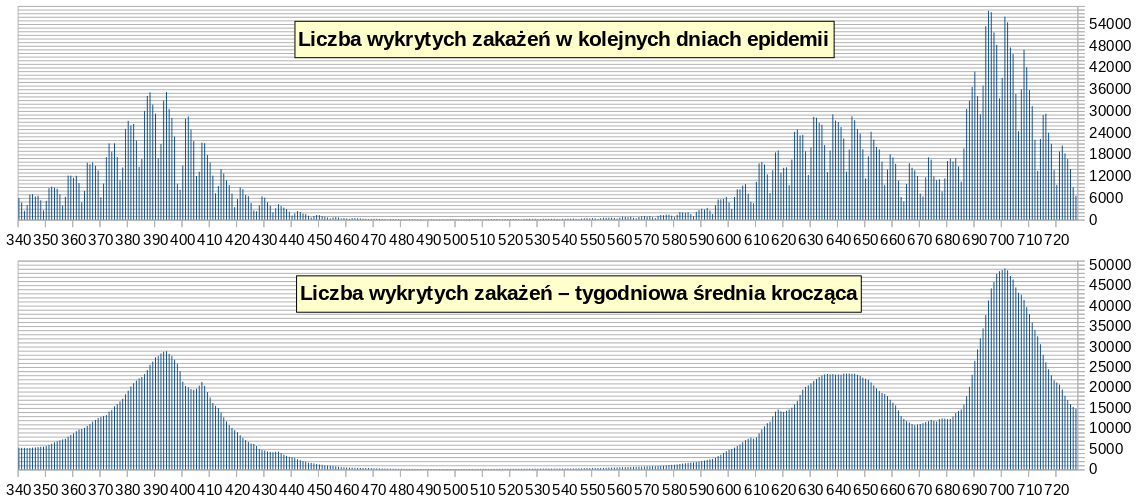
Liczba wykrytych zakażeń w kolejnych dniach
Poniższe tabele przedstawiają liczbę N stwierdzonych zakażeń w kolejnych dniach oraz sumę ∑ wszystkich zakażeń od początku epidemii. Liczby w nawiasie określają liczbę dni, które upłynęły od początku epidemii.
Pierwsze półrocze epidemii: od 04.03.2020 (1) do 31.08.2020 (181)
| MAR | N | ∑ | KWI | N | ∑ | MAJ | N | ∑ | CZE | N | ∑ | LIP | N | ∑ | SIE | N | ∑ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 ( ) | 01 ( 29) | 243 | 2554 | 01 ( 59) | 228 | 13105 | 01 ( 90) | 379 | 24165 | 01 (120) | 382 | 34775 | 01 (151) | 658 | 46346 | ||
| 02 ( ) | 02 ( 30) | 392 | 2946 | 02 ( 60) | 270 | 13375 | 02 ( 91) | 230 | 24395 | 02 (121) | 371 | 35146 | 02 (152) | 548 | 46894 | ||
| 03 ( ) | 03 ( 31) | 437 | 3383 | 03 ( 61) | 318 | 13693 | 03 ( 92) | 292 | 24687 | 03 (122) | 259 | 35405 | 03 (153) | 575 | 47469 | ||
| 04 ( 1) | 1 | 1 | 04 ( 32) | 244 | 3627 | 04 ( 62) | 313 | 14006 | 04 ( 93) | 361 | 25048 | 04 (123) | 314 | 35719 | 04 (154) | 680 | 48149 |
| 05 ( 2) | 0 | 1 | 05 ( 33) | 475 | 4102 | 05 ( 63) | 425 | 14431 | 05 ( 94) | 362 | 25410 | 05 (124) | 231 | 35950 | 05 (155) | 640 | 48789 |
| 06 ( 3) | 4 | 5 | 06 ( 34) | 311 | 4413 | 06 ( 64) | 309 | 14740 | 06 ( 95) | 576 | 25986 | 06 (125) | 205 | 36155 | 06 (156) | 726 | 49515 |
| 07 ( 4) | 1 | 6 | 07 ( 35) | 435 | 4848 | 07 ( 65) | 307 | 15047 | 07 ( 96) | 575 | 26561 | 07 (126) | 257 | 36412 | 07 (157) | 809 | 50324 |
| 08 ( 5) | 5 | 11 | 08 ( 36) | 357 | 5205 | 08 ( 66) | 319 | 15366 | 08 ( 97) | 599 | 27160 | 08 (127) | 277 | 36689 | 08 (158) | 843 | 51167 |
| 09 ( 6) | 6 | 17 | 09 ( 37) | 370 | 5575 | 09 ( 67) | 285 | 15651 | 09 ( 98) | 400 | 27560 | 09 (128) | 262 | 36951 | 09 (159) | 624 | 51791 |
| 10 ( 7) | 5 | 22 | 10 ( 38) | 380 | 5955 | 10 ( 68) | 345 | 15996 | 10 ( 99) | 282 | 27842 | 10 (129) | 265 | 37216 | 10 (160) | 619 | 52410 |
| 11 ( 8) | 9 | 31 | 11 ( 39) | 401 | 6356 | 11 ( 69) | 330 | 16326 | 11 (100)[2] | 359 | 28201 | 11 (130) | 305 | 37521 | 11 (161) | 551 | 52961 |
| 12 ( 9) | 20 | 51 | 12 ( 40) | 318 | 6674 | 12 ( 70) | 595 | 16921 | 12 (101) | 376 | 28577 | 12 (131) | 370 | 37891 | 12 (162) | 715 | 53676 |
| 13 ( 10) | 17 | 68 | 13 ( 41) | 260 | 6934 | 13 ( 71) | 283 | 17204 | 13 (102) | 440 | 29017 | 13 (132) | 299 | 38190 | 13 (163) | 811 | 54487 |
| 14 ( 11) | 36 | 104 | 14 ( 42) | 268 | 7202 | 14 ( 72) | 411 | 17615 | 14 (103) | 375 | 29392 | 14 (133) | 267 | 38457 | 14 (164) | 832 | 55319 |
| 15 ( 12) | 21 | 125 | 15 ( 43) | 380 | 7582 | 15 ( 73) | 401 | 18016 | 15 (104) | 396 | 29788 | 15 (134) | 264 | 38721 | 15 (165) | 771 | 56090 |
| 16 ( 13) | 52 | 177 | 16 ( 44) | 336 | 7918 | 16 ( 74) | 241 | 18257 | 16 (105) | 407 | 30195 | 16 (135) | 333 | 39054 | 16 (166) | 594 | 56684 |
| 17 ( 14) | 61 | 238 | 17 ( 45) | 461 | 8379 | 17 ( 75) | 272 | 18529 | 17 (106) | 506 | 30701 | 17 (136) | 353 | 39407 | 17 (167) | 595 | 57279 |
| 18 ( 15) | 49 | 287 | 18 ( 46) | 363 | 8742 | 18 ( 76) | 356 | 18885 | 18 (107) | 314 | 31015 | 18 (137) | 339 | 39746 | 18 (168) | 597 | 57876 |
| 19 ( 16) | 68 | 355 | 19 ( 47) | 545 | 9287 | 19 ( 77) | 383 | 19268 | 19 (108) | 301 | 31316 | 19 (138) | 358 | 40104 | 19 (169) | 735 | 58611 |
| 20 ( 17) | 70 | 425 | 20 ( 48) | 306 | 9593 | 20 ( 78) | 471 | 19739 | 20 (109) | 304 | 31620 | 20 (139) | 279 | 40383 | 20 (170) | 767 | 59378 |
| 21 ( 18) | 111 | 536 | 21 ( 49) | 263 | 9856 | 21 ( 79) | 404 | 20143 | 21 (110) | 311 | 31931 | 21 (140) | 399 | 40782 | 21 (171) | 903 | 60281 |
| 22 ( 19) | 98 | 634 | 22 ( 50) | 313 | 10169 | 22 ( 80) | 476 | 20619 | 22 (111) | 296 | 32227 | 22 (141) | 380 | 41162 | 22 (172) | 900 | 61181 |
| 23 ( 20) | 115 | 749 | 23 ( 51) | 342 | 10511 | 23 ( 81) | 312 | 20931 | 23 (112) | 300 | 32527 | 23 (142) | 418 | 41580 | 23 (173) | 581 | 61762 |
| 24 ( 21) | 152 | 901 | 24 ( 52) | 381 | 10892 | 24 ( 82) | 395 | 21326 | 24 (113) | 294 | 32821 | 24 (143) | 458 | 42038 | 24 (174) | 548 | 62310 |
| 25 ( 22) | 150 | 1051 | 25 ( 53) | 381 | 11273 | 25 ( 83) | 305 | 21631 | 25 (114) | 298 | 33119 | 25 (144) | 584 | 42622 | 25 (175) | 763 | 63073 |
| 26 ( 23) | 170 | 1221 | 26 ( 54) | 344 | 11617 | 26 ( 84) | 443 | 22074 | 26 (115) | 276 | 33395 | 26 (145) | 443 | 43065 | 26 (176) | 729 | 63802 |
| 27 ( 24) | 168 | 1389 | 27 ( 55) | 285 | 11902 | 27 ( 85) | 399 | 22473 | 27 (116) | 319 | 33714 | 27 (146) | 337 | 43402 | 27 (177) | 887 | 64689 |
| 28 ( 25) | 249 | 1638 | 28 ( 56) | 316 | 12218 | 28 ( 86) | 352 | 22825 | 28 (117) | 193 | 33907 | 28 (147) | 502 | 43904 | 28 (178) | 791 | 65480 |
| 29 ( 26) | 224 | 1862 | 29 ( 57) | 422 | 12640 | 29 ( 87) | 330 | 23155 | 29 (118) | 247 | 34154 | 29 (148) | 512 | 44416 | 29 (179) | 759 | 66239 |
| 30 ( 27) | 193 | 2055 | 30 ( 58) | 300 | 12877 | 30 ( 88) | 416 | 23571 | 30 (119) | 239 | 34393 | 30 (149) | 615 | 45031 | 30 (180) | 631 | 66870 |
| 31 ( 28) | 256 | 2311 | 31 ( 89) | 215 | 23786 | 31 (150) | 657 | 45688 | 31 (181) | 502 | 67372 |
Drugie półrocze epidemii: od 01.09.2020 (182) do 28.02.2021 (362)
| WRZ | N | ∑ | PAŹ | N | ∑ | LIS | N | ∑ | GRU | N | ∑ | STY | N | ∑ | LUT | N | ∑ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 (182) | 550 | 67922 | 01 (212) | 1967 | 93481 | 01 (243) | 17171 | 379902 | 01 (273) | 9105 | 999924 | 01 (304) | 11008 | 1305774 | 01 (335) | 2503 | 1515889 |
| 02 (183) | 595 | 68517 | 02 (213) | 2292 | 95773 | 02 (244) | 15578 | 395480 | 02 (274) | 13855 | 1013747 | 02 (305) | 6945 | 1312780 | 02 (336) | 4326 | 1520215 |
| 03 (184) | 612 | 69129 | 03 (214) | 2367 | 98140 | 03 (245) | 19364 | 414844 | 03 (275) | 14838 | 1028610 | 03 (306) | 5739 | 1318562 | 03 (337) | 6802 | 1527016 |
| 04 (185) | 691 | 69820 | 04 (215) | 1934 | 100074 | 04 (246) | 24692 | 439536 | 04 (276) | 13239 | 1041846 | 04 (307) | 4432 | 1322947 | 04 (338) | 6496 | 1533511 |
| 05 (186) | 567 | 70387 | 05 (216) | 2006 | 102080 | 05 (247) | 27143 | 466679 | 05 (277) | 12430 | 1054273 | 05 (308) | 7624 | 1330543 | 05 (339) | 6053 | 1539564 |
| 06 (187) | 437 | 70824 | 06 (217) | 2236 | 104316 | 06 (248) | 27086 | 493765 | 06 (278) | 9176 | 1063449 | 06 (309) | 14151 | 1344763 | 06 (340) | 5965 | 1545530 |
| 07 (188) | 302 | 71126 | 07 (218) | 3003 | 107319 | 07 (249) | 27875 | 521640 | 07 (279) | 4423 | 1067870 | 07 (310) | 12054 | 1356882 | 07 (341) | 4728 | 1550255 |
| 08 (189) | 400 | 71526 | 08 (219) | 4280 | 111599 | 08 (250) | 24785 | 546425 | 08 (280) | 8312 | 1076180 | 08 (311) | 8790 | 1365645 | 08 (342) | 2431 | 1552686 |
| 09 (190) | 421 | 71947 | 09 (220) | 4739 | 116338 | 09 (251) | 21713 | 568138 | 09 (281) | 12168 | 1088346 | 09 (312) | 10548 | 1376389 | 09 (343) | 4029 | 1556685 |
| 10 (191) | 506 | 72453 | 10 (221) | 5300 | 121638 | 10 (252) | 25484 | 593592 | 10 (282) | 13749 | 1102096 | 10 (313) | 9410 | 1385522 | 10 (344) | 6930 | 1563645 |
| 11 (192) | 594 | 73047 | 11 (222) | 4178 | 125816 | 11 (253) | 25221 | 618813 | 11 (283) | 13110 | 1115201 | 11 (314) | 4622 | 1390385 | 11 (345) | 7008 | 1570658 |
| 12 (193) | 603 | 73650 | 12 (223) | 4394 | 130210 | 12 (254) | 22683 | 641496 | 12 (284) | 11497 | 1126700 | 12 (315) | 5569 | 1395779 | 12 (346) | 6379 | 1577036 |
| 13 (194) | 502 | 74152 | 13 (224) | 5068 | 135278 | 13 (255) | 24051 | 665547 | 13 (285) | 8977 | 1135676 | 13 (316) | 9053 | 1404905 | 13 (347) | 6586 | 1583621 |
| 14 (195) | 377 | 74529 | 14 (225) | 6526 | 141804 | 14 (256) | 25571 | 691118 | 14 (286) | 4896 | 1140572 | 14 (317) | 9436 | 1414362 | 14 (348) | 5334 | 1588955 |
| 15 (196) | 605 | 75134 | 15 (226) | 8099 | 149903 | 15 (257) | 21854 | 712972 | 15 (287) | 6907 | 1147446 | 15 (318) | 7795 | 1422320 | 15 (349) | 2543 | 1591497 |
| 16 (197) | 600 | 75734 | 16 (227) | 7705 | 157608 | 16 (258) | 20816 | 733788 | 16 (288) | 12454 | 1159901 | 16 (319) | 7412 | 1429612 | 16 (350) | 5178 | 1596673 |
| 17 (198) | 837 | 76571 | 17 (228) | 9622 | 167230 | 17 (259) | 19152 | 752940 | 17 (289) | 11953 | 1171854 | 17 (320) | 6055 | 1435582 | 17 (351) | 8694 | 1605372 |
| 18 (199) | 757 | 77328 | 18 (229) | 8536 | 175766 | 18 (260) | 19883 | 772823 | 18 (290) | 11013 | 1182864 | 18 (321) | 3271 | 1438914 | 18 (352) | 9073 | 1614446 |
| 19 (200) | 1002 | 78330 | 19 (230) | 7482 | 183248 | 19 (261) | 23975 | 796798 | 19 (291) | 11267 | 1194110 | 19 (322) | 4835 | 1443804 | 19 (353) | 8777 | 1623218 |
| 20 (201) | 910 | 79240 | 20 (231) | 9291 | 192539 | 20 (262) | 22464 | 819262 | 20 (292) | 8594 | 1202700 | 20 (323) | 6919 | 1450747 | 20 (354) | 8510 | 1631727 |
| 21 (202) | 748 | 79988 | 21 (232) | 10040 | 202579 | 21 (263) | 24213 | 843475 | 21 (293) | 4633 | 1207333 | 21 (324) | 7152 | 1457755 | 21 (355) | 7038 | 1638767 |
| 22 (203) | 711 | 80699 | 22 (233) | 12107 | 214686 | 22 (264) | 18467 | 861331 | 22 (294) | 7192 | 1214525 | 22 (325) | 6640 | 1464448 | 22 (356) | 3890 | 1642658 |
| 23 (204) | 974 | 81673 | 23 (234) | 13632 | 228318 | 23 (265) | 15002 | 876333 | 23 (295) | 12361 | 1226883 | 23 (326) | 6322 | 1470879 | 23 (357) | 6310 | 1648962 |
| 24 (205) | 1136 | 82809 | 24 (235) | 13628 | 241946 | 24 (266) | 10139 | 909066 | 24 (296) | 13115 | 1239998 | 24 (327) | 4683 | 1475445 | 24 (358) | 12146 | 1661109 |
| 25 (206) | 1587 | 84396 | 25 (236) | 11742 | 253688 | 25 (267) | 15362 | 924422 | 25 (297) | 9077 | 1249079 | 25 (328) | 2419 | 1478119 | 25 (359) | 12142 | 1673252 |
| 26 (207) | 1584 | 85980 | 26 (237) | 10241 | 263929 | 26 (268) | 16687 | 941112 | 26 (298) | 5048 | 1253957 | 26 (329) | 4604 | 1482722 | 26 (360) | 11539 | 1684788 |
| 27 (208) | 1350 | 87330 | 27 (238) | 16300 | 280229 | 27 (269) | 17060 | 958416 | 27 (299) | 3678 | 1257799 | 27 (330) | 6789 | 1489512 | 27 (361) | 12100 | 1696885 |
| 28 (209) | 1306 | 88636 | 28 (239) | 18820 | 299049 | 28 (270) | 15178 | 973593 | 28 (300) | 3211 | 1261010 | 28 (331) | 7156 | 1496665 | 28 (362) | 10099 | 1706986 |
| 29 (210) | 1326 | 89962 | 29 (240) | 20156 | 319205 | 29 (271) | 11483 | 985075 | 29 (301) | 7914 | 1268634 | 29 (332) | 6144 | 1502810 | |||
| 30 (211) | 1552 | 91514 | 30 (241) | 21629 | 340834 | 30 (272) | 5733 | 990811 | 30 (302) | 12955 | 1281414 | 30 (333) | 5864 | 1508674 | |||
| 31 (242) | 21897 | 362731 | 31 (303) | 13397 | 1294878 | 31 (334) | 4706 | 1513385 |
Trzecie półrocze epidemii: od 01.03.2021 (363) do 31.08.2021 (546)
| MAR | N | ∑ | KWI | N | ∑ | MAJ | N | ∑ | CZE | N | ∑ | LIP | N | ∑ | SIE | N | ∑ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 (363) | 4786 | 1711772 | 01 (394) | 35251 | 2356970 | 01 (424) | 6469 | 2798617 | 01 (455) | 588 | 2872868 | 01 (485) | 98 | 2880010 | 01 (516) | 91 | 2883029 |
| 02 (364) | 7937 | 1719708 | 02 (395) | 30546 | 2387511 | 02 (425) | 4612 | 2803233 | 02 (456) | 664 | 2873527 | 02 (486) | 96 | 2880107 | 02 (517) | 91 | 2883120 |
| 03 (365) | 15698 | 1735406 | 03 (396) | 28073 | 2415584 | 03 (426) | 2525 | 2805756 | 03 (457) | 572 | 2874092 | 03 (487) | 107 | 2880215 | 03 (518) | 164 | 2883284 |
| 04 (366) | 15250 | 1750659 | 04 (397) | 22947 | 2438542 | 04 (427) | 2296 | 2808052 | 04 (458) | 319 | 2874411 | 04 (488) | 54 | 2880270 | 04 (519) | 164 | 2883448 |
| 05 (367) | 15829 | 1766490 | 05 (398) | 9902 | 2448463 | 05 (428) | 3896 | 2811951 | 05 (459) | 415 | 2874824 | 05 (489) | 38 | 2880308 | 05 (520) | 176 | 2883624 |
| 06 (368) | 14857 | 1781345 | 06 (399) | 8245 | 2456709 | 06 (429) | 6431 | 2818378 | 06 (460) | 312 | 2875136 | 06 (490) | 96 | 2880403 | 06 (521) | 172 | 2883796 |
| 07 (369) | 13574 | 1794914 | 07 (400) | 14910 | 2471617 | 07 (430) | 6047 | 2824425 | 07 (461) | 194 | 2875328 | 07 (491) | 103 | 2880503 | 07 (522) | 181 | 2883976 |
| 08 (370) | 6170 | 1801083 | 08 (401) | 27887 | 2499507 | 08 (431) | 4765 | 2829196 | 08 (462) | 400 | 2875729 | 08 (492) | 93 | 2880596 | 08 (523) | 122 | 2884098 |
| 09 (371) | 9954 | 1811036 | 09 (402) | 28487 | 2528006 | 09 (432) | 3852 | 2833052 | 09 (463) | 428 | 2876289 | 09 (493) | 76 | 2880670 | 09 (524) | 64 | 2884162 |
| 10 (372) | 17260 | 1828313 | 10 (403) | 24856 | 2552898 | 10 (433) | 2032 | 2835083 | 10 (464) | 382 | 2876667 | 10 (494) | 86 | 2880755 | 10 (525) | 200 | 2884361 |
| 11 (373) | 21045 | 1849424 | 11 (404) | 21703 | 2574631 | 11 (434) | 3098 | 2838180 | 11 (465) | 341 | 2877007 | 11 (495) | 66 | 2880821 | 11 (526) | 198 | 2884557 |
| 12 (374) | 18775 | 1868297 | 12 (405) | 12013 | 2586647 | 12 (435) | 4255 | 2842339 | 12 (466) | 239 | 2877243 | 12 (496) | 44 | 2880865 | 12 (527) | 223 | 2884780 |
| 13 (375) | 21049 | 1889360 | 13 (406) | 13227 | 2599850 | 13 (436) | 3730 | 2845762 | 13 (467) | 227 | 2877469 | 13 (497) | 96 | 2880959 | 13 (528) | 196 | 2884974 |
| 14 (376) | 17259 | 1906632 | 14 (407) | 21283 | 2621116 | 14 (437) | 3288 | 2849014 | 14 (468) | 140 | 2877608 | 14 (498) | 86 | 2881046 | 14 (529) | 211 | 2885185 |
| 15 (377) | 10896 | 1917527 | 15 (408) | 21130 | 2642242 | 15 (438) | 2896 | 2851911 | 15 (469) | 215 | 2877819 | 15 (499) | 105 | 2881151 | 15 (530) | 148 | 2885333 |
| 16 (378) | 14396 | 1931921 | 16 (409) | 17847 | 2660088 | 16 (439) | 2167 | 2854079 | 16 (470) | 241 | 2878061 | 16 (500) | 93 | 2881241 | 16 (531) | 128 | 2885461 |
| 17 (379) | 25052 | 1956974 | 17 (410) | 15763 | 2675874 | 17 (440) | 1109 | 2855190 | 17 (471) | 218 | 2878276 | 17 (501) | 114 | 2881355 | 17 (532) | 221 | 2885676 |
| 18 (380) | 27278 | 1984248 | 18 (411) | 12153 | 2688025 | 18 (441) | 1734 | 2856924 | 18 (472) | 190 | 2878466 | 18 (502) | 69 | 2881424 | 18 (533) | 208 | 2885883 |
| 19 (381) | 25998 | 2010244 | 19 (412) | 7283 | 2695327 | 19 (442) | 2344 | 2859261 | 19 (473) | 168 | 2878634 | 19 (503) | 67 | 2881491 | 19 (534) | 197 | 2886079 |
| 20 (382) | 26405 | 2036700 | 20 (413) | 9246 | 2704571 | 20 (443) | 2086 | 2861351 | 20 (474) | 133 | 2878767 | 20 (504) | 104 | 2881594 | 20 (535) | 212 | 2886291 |
| 21 (383) | 21849 | 2058550 | 21 (414) | 13926 | 2718493 | 21 (444) | 1679 | 2863031 | 21 (475) | 73 | 2878840 | 21 (505) | 124 | 2881718 | 21 (536) | 222 | 2886513 |
| 22 (384) | 14578 | 2073129 | 22 (415) | 12762 | 2731256 | 22 (445) | 1516 | 2864546 | 22 (476) | 188 | 2879030 | 22 (506) | 126 | 2881840 | 22 (537) | 185 | 2886698 |
| 23 (385) | 16741 | 2089869 | 23 (416) | 10858 | 2742122 | 23 (446) | 1075 | 2865622 | 23 (477) | 165 | 2879192 | 23 (507) | 108 | 2881948 | 23 (538) | 107 | 2886805 |
| 24 (386) | 29978 | 2120671 | 24 (417) | 9505 | 2751632 | 24 (447) | 559 | 2866181 | 24 (478) | 147 | 2879336 | 24 (508) | 122 | 2882066 | 24 (539) | 233 | 2887037 |
| 25 (387) | 34151 | 2154821 | 25 (418) | 7219 | 2758856 | 25 (448) | 1000 | 2867187 | 25 (479) | 133 | 2879470 | 25 (509) | 82 | 2882146 | 25 (540) | 234 | 2887270 |
| 26 (388) | 35143 | 2189966 | 26 (419) | 3451 | 2762323 | 26 (449) | 1267 | 2868450 | 26 (480) | 100 | 2879569 | 26 (510) | 74 | 2882220 | 26 (541) | 251 | 2887485 |
| 27 (389) | 31757 | 2221723 | 27 (420) | 5709 | 2768034 | 27 (450) | 1230 | 2869652 | 27 (481) | 71 | 2879638 | 27 (511) | 106 | 2882327 | 27 (542) | 258 | 2887739 |
| 28 (390) | 29253 | 2250991 | 28 (421) | 8895 | 2776927 | 28 (451) | 946 | 2870595 | 28 (482) | 52 | 2879689 | 28 (512) | 138 | 2882465 | 28 (543) | 290 | 2888028 |
| 29 (391) | 16965 | 2267964 | 29 (422) | 8427 | 2785353 | 29 (452) | 775 | 2871371 | 29 (483) | 123 | 2879811 | 29 (513) | 167 | 2882630 | 29 (544) | 204 | 2888231 |
| 30 (392) | 20870 | 2288826 | 30 (423) | 6796 | 2792142 | 30 (453) | 579 | 2871950 | 30 (484) | 104 | 2879912 | 30 (514) | 153 | 2882786 | 30 (545) | 151 | 2888385 |
| 31 (393) | 32874 | 2321717 | 31 (454) | 333 | 2872283 | 31 (515) | 153 | 2882939 | 31 (546) | 285 | 2888670 |
Czwarte półrocze epidemii: od 01.09.2021 (547) do chwili obecnej
| WRZ | N | ∑ | PAŹ | N | ∑ | LIS | N | ∑ | GRU | N | ∑ | STY | N | ∑ | LUT | N | ∑ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 (547) | 366 | 2889036 | 01 (577) | 1362 | 2908432 | 01 (608) | 4894 | 3030151 | 01 (638) | 29064 | 3569137 | 01 (669) | 12032 | 4120248 | 01 (700) | 39114 | 4925270 |
| 02 (548) | 390 | 2889412 | 02 (578) | 1344 | 2909776 | 02 (609) | 4514 | 3034668 | 02 (639) | 27356 | 3596491 | 02 (670) | 7179 | 4127428 | 02 (701) | 56051 | 4981321 |
| 03 (549) | 349 | 2889773 | 03 (579) | 1090 | 2910866 | 03 (610) | 10429 | 3045102 | 03 (640) | 26965 | 3623452 | 03 (671) | 6422 | 4133851 | 03 (702) | 54477 | 5035796 |
| 04 (550) | 389 | 2890161 | 04 (580) | 684 | 2911549 | 04 (611) | 15515 | 3060613 | 04 (641) | 25576 | 3649027 | 04 (672) | 11670 | 4145518 | 04 (703) | 47534 | 5083332 |
| 05 (551) | 324 | 2890484 | 05 (581) | 1325 | 2912876 | 05 (612) | 15904 | 3076518 | 05 (642) | 22389 | 3671421 | 05 (673) | 17196 | 4162715 | 05 (704) | 45749 | 5129080 |
| 06 (552) | 183 | 2890666 | 06 (582) | 2085 | 2914962 | 06 (613) | 15190 | 3091713 | 06 (643) | 13250 | 3684671 | 06 (674) | 16576 | 4179292 | 06 (705) | 34703 | 5163780 |
| 07 (553) | 406 | 2891071 | 07 (583) | 2007 | 2916969 | 07 (614) | 12493 | 3104220 | 07 (644) | 19366 | 3704040 | 07 (675) | 11902 | 4191193 | 07 (706) | 24404 | 5188184 |
| 08 (554) | 533 | 2891602 | 08 (584) | 1895 | 2918863 | 08 (615) | 7316 | 3111534 | 08 (645) | 28542 | 3732589 | 08 (676) | 10900 | 4202090 | 08 (707) | 35960 | 5224144 |
| 09 (555) | 510 | 2892113 | 09 (585) | 2012 | 2920874 | 09 (616) | 13644 | 3125179 | 09 (646) | 27458 | 3760048 | 09 (677) | 11106 | 4213197 | 09 (708) | 46872 | 5271016 |
| 10 (556) | 528 | 2892642 | 10 (586) | 1527 | 2922401 | 10 (617) | 18550 | 3143725 | 10 (647) | 24991 | 3785036 | 10 (678) | 7785 | 4220984 | 10 (709) | 42095 | 5313111 |
| 11 (557) | 530 | 2893173 | 11 (587) | 903 | 2923304 | 11 (618) | 19074 | 3162804 | 11 (648) | 23764 | 3808798 | 11 (679) | 11406 | 4232386 | 11 (710) | 35777 | 5348888 |
| 12 (558) | 476 | 2893649 | 12 (588) | 2118 | 2925425 | 12 (619) | 12965 | 3175769 | 12 (649) | 19452 | 3828248 | 12 (680) | 16173 | 4248559 | 12 (711) | 31331 | 5380219 |
| 13 (559) | 269 | 2893919 | 13 (589) | 2640 | 2928065 | 13 (620) | 14292 | 3190067 | 13 (650) | 11379 | 3839625 | 13 (681) | 16878 | 4265433 | 13 (712) | 22070 | 5402289 |
| 14 (560) | 537 | 2894455 | 14 (590) | 3000 | 2931064 | 14 (621) | 14442 | 3204515 | 14 (651) | 17460 | 3857085 | 14 (682) | 16047 | 4281482 | 14 (713) | 13473 | 5415762 |
| 15 (561) | 767 | 2895223 | 15 (591) | 2771 | 2933834 | 15 (622) | 9512 | 3214023 | 15 (652) | 24266 | 3881349 | 15 (683) | 16896 | 4298375 | 15 (714) | 22267 | 5438029 |
| 16 (562) | 722 | 2895947 | 16 (592) | 3236 | 2937069 | 16 (623) | 16590 | 3230634 | 16 (653) | 22097 | 3903445 | 16 (684) | 14667 | 4313036 | 16 (715) | 28859 | 5466491 |
| 17 (563) | 652 | 2896599 | 17 (593) | 2523 | 2939590 | 17 (624) | 24239 | 3254875 | 17 (654) | 20027 | 3923472 | 17 (685) | 10445 | 4323482 | 17 (716) | 29229 | 5495615 |
| 18 (564) | 797 | 2897395 | 18 (594) | 1537 | 2941126 | 18 (625) | 24882 | 3279787 | 18 (655) | 19397 | 3942864 | 18 (686) | 19652 | 4343130 | 18 (717) | 23990 | 5519282 |
| 19 (565) | 540 | 2897935 | 19 (595) | 3931 | 2945056 | 19 (626) | 23242 | 3303046 | 19 (656) | 15976 | 3958840 | 19 (687) | 30586 | 4373718 | 19 (718) | 20902 | 5540162 |
| 20 (566) | 363 | 2898299 | 20 (596) | 5559 | 2950616 | 20 (627) | 23414 | 3326464 | 20 (657) | 9609 | 3968450 | 20 (688) | 32835 | 4406553 | 20 (719) | 13687 | 5553841 |
| 21 (567) | 711 | 2899008 | 21 (597) | 5592 | 2956207 | 21 (628) | 18883 | 3345388 | 21 (658) | 13806 | 3982257 | 21 (689) | 36665 | 4443217 | 21 (720) | 9589 | 5563446 |
| 22 (568) | 882 | 2899888 | 22 (598) | 5706 | 2961923 | 22 (629) | 12334 | 3357763 | 22 (659) | 18021 | 4000270 | 22 (690) | 40876 | 4484095 | 22 (721) | 18792 | 5582217 |
| 23 (569) | 974 | 2900862 | 23 (599) | 6274 | 2968200 | 23 (630) | 19936 | 3377698 | 23 (660) | 17156 | 4017420 | 23 (691) | 34088 | 4518218 | 23 (722) | 20456 | 5602680 |
| 24 (570) | 813 | 2901674 | 24 (600) | 4728 | 2972927 | 24 (631) | 28380 | 3406129 | 24 (661) | 15392 | 4032796 | 24 (692) | 29100 | 4547315 | 24 (723) | 18282 | 5620946 |
| 25 (571) | 917 | 2902591 | 25 (601) | 2950 | 2975880 | 25 (632) | 28128 | 3434272 | 25 (662) | 10788 | 4043585 | 25 (693) | 36995 | 4584360 | 25 (724) | 16724 | 5637646 |
| 26 (572) | 643 | 2903234 | 26 (602) | 6265 | 2982143 | 26 (633) | 26735 | 3461066 | 26 (663) | 6252 | 4049838 | 26 (694) | 53420 | 4637776 | 26 (725) | 13960 | 5651596 |
| 27 (573) | 421 | 2903655 | 27 (603) | 8361 | 2990509 | 27 (634) | 26182 | 3487254 | 27 (664) | 5029 | 4054865 | 27 (695) | 57659 | 4695435 | 27 (726) | 8902 | 5660493 |
| 28 (574) | 975 | 2904631 | 28 (604) | 8378 | 2998891 | 28 (635) | 20576 | 3507828 | 28 (665) | 9843 | 4064715 | 28 (696) | 57262 | 4752700 | 28 (727) | 6564 | 5667054 |
| 29 (575) | 1234 | 2905866 | 29 (605) | 9387 | 3008294 | 29 (636) | 13115 | 3520961 | 29 (666) | 15571 | 4080282 | 29 (697) | 51695 | 4804390 | |||
| 30 (576) | 1208 | 2907071 | 30 (606) | 9798 | 3018100 | 30 (637) | 19074 | 3540061 | 30 (667) | 14325 | 4094608 | 30 (698) | 48251 | 4852677 | |||
| 31 (607) | 7145 | 3025247 | 31 (668) | 13601 | 4108215 | 31 (699) | 33480 | 4886154 |
Jak rozprzestrzeniają się zakażenia
Najgorszy przypadek rozprzestrzeniania się choroby opisuje krzywa wykładnicza. Typowy przykład: każda chora osoba w ciągu okresu T dni zaraża N zdrowych osób. Po upływie k takich okresów T zarażonych jest Nk osób. To wzrost wykładniczy – najgorszy z możliwych. Rozstrzygnięcie, z jakim rodzajem wzrostu mamy do czynienia w Polsce, jest kluczowe dla nas wszystkich. Najpierw przyjrzyjmy się rodzajom funkcji, które mogą opisywać wzrost liczby osób zakażonych i oczekiwaną liczbę przypadków w kolejnych dniach epidemii.
| Liczba chorych po n dniach epidemii | Przyrost liczby chorych w kolejnych dniach | Uwagi |
|---|---|---|
| y(n) = ea·n + b | y(n+1) - y(n) = ea·n + b + c | wzrost wykładniczy, c = log(ea - 1) podwojenie co T = log(2)/a dni |
| y(n) = a·n + b | y(n+1) - y(n) = a | wzrost liniowy |
| y(n) = a·n2 + b·n + c | y(n+1) - y(n) = 2a·n + b1 | wzrost kwadratowy, b1 = a + b |
| y(n) = a·n3 + b·n2 + c·n + d | y(n+1) - y(n) = 3a·n2 + b2·n + c2 | wzrost sześcienny, b2 = 3a + 2b, c2 = a + b + c |
Widzimy, że jeżeli wzrost ogólnej liczby przypadków jest opisywany funkcją wykładniczą, to dzienne przyrosty liczby chorych również są opisywane funkcją wykładniczą. W przypadku, gdy wzrost ogólnej liczby chorych opisywany jest wielomianem, to dzienne przyrosty liczby chorych są opisywane wielomianem o jeden stopień niższym.
Wykresy z kwietnia 2020 roku
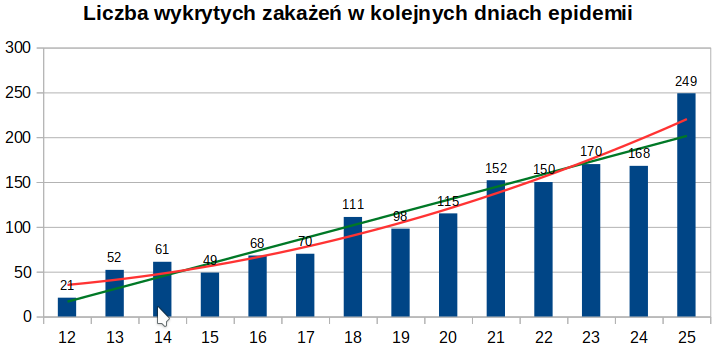

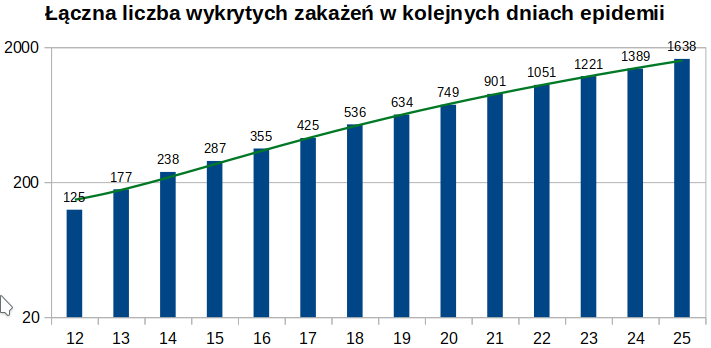
Zastosowany sposób analizy całkowitej liczby zakażeń
Do badania statystycznego wybieramy okres 14 dni. Ostatni dzień tego okresu to dzień nadejścia najnowszych danych. Omówimy jak znajdować wykładniczą i wielomianową funkcję regresji. Jeśli Czytelnik nie jest zainteresowany zapoznaniem się z zastosowaną metodą obliczeń, to bez najmniejszej straty może pominąć tę sekcję.
Wykładnicza krzywa regresji
Przypuśćmy, że wzrost całkowitej liczby zakażeń jest opisywany funkcją wykładniczą y(n) = exp(a·n + b) i wyznaczmy parametry tej funkcji. Łatwo zauważamy, że problem ten sprowadza się do problemu liniowego, bo logarytmując obie strony wypisanego równania mamy log( y(n) ) = a·n + b. Dlatego w kolejnych kolumnach arkusza kalkulacyjnego umieszczamy:
- logarytm naturalny całkowitej liczby zakażeń w kolejnych dniach wybranego przedziału (to są dane Y)
- numer kolejnego dnia epidemii odpowiadający datom z wybranego okresu (to są dane X)
Korzystając z funkcji arkusza REGLINP()[3][4], otrzymujemy wartości współczynników. Przykładowo dla dnia 25 marca 2020 r. (22 dzień epidemii) znajdujemy wartości:
- a = 0,229 (z błędem 0,018)
- b = 2,08 (z błędem 0,28)
Jako wartość błędu przyjęliśmy podwojoną wartość odchylenia standardowego σ dla każdego ze współczynników. Zatem szukana funkcja ma postać: y(n) = exp( 0,229·n + 2,08 ), gdzie n przyjmuje wartości z przedziału [9, 22].
Zwraca uwagę wysoka korelacja równa 0,992. Zauważmy, że znalezionej wartości współczynnika a odpowiada okres podwojenia całkowitej liczby zakażeń T2 = log(2)/a równy 3 dni. Wartość ta tak znacznie odbiega od rzeczywistości, że wykładniczej funkcji regresji w ogóle nie będziemy brali pod uwagę.
Już teraz zauważmy, że jeśli epidemia potrwa dłużej, to numery kolejnych dni epidemii osiągną duże wartości. Przykładowo będziemy mieli n = 101, 102, …, 114. Gdy argument funkcji przyjmuje tak duże wartości, to w funkcji opisującej znalezioną krzywą regresji pojawiają się ogromne współczynniki. Przewidując ten problem, warto dokonać podstawienia x = n – n0 + 1, gdzie n0 oznacza numer dnia epidemii dla pierwszego dnia wybranego przedziału danych. W naszym przypadku tak zdefiniowana zmienna x będzie zawsze przyjmowała wartości od 1 do 14.
Powtarzając obliczenia dla zmiennej x, otrzymujemy:
- a = 0,229 (z błędem 0,018)
- b = 3,92 (z błędem 0,15)
Czyli szukana funkcja wykładnicza ma postać: y(x) = exp( 0,229·x + 3,92 ), gdzie x przymuje wartości z przedziału [1, 14].
Zauważmy, że wartości współczynnika a oraz współczynnika korelacji nie zmieniły się, ale współczynnik b oraz jego błąd uległy zmianie. Czego należało się spodziewać.
Zawsze możemy przejść od zmiennej x do zmiennej n. W naszym przypadku wystarczy wykonać podstawienie: x = n – 8. Czytelnik może wykonać to podstawienie i porównać uzyskany wzór ze wzorem obliczonym wcześniej.
Dokładnie taka postać funkcji jest znajdowana, gdy tworzymy krzywą regresji przy pomocy Kreatora wykresów dostępnego w pakiecie LibreOffice Calc. W rzeczywistości jest to ogromne ułatwienie: nie musimy wzoru opisującego krzywą regresji znajdować sami, a zostaje on automatycznie wygenerowany w czasie tworzenia wykresu. Oczywiście nie uzyskamy w ten sposób innych informacji statystycznych (na przykład odchylenia standardowego dla wyliczonych współczynników), ale w pewnych przypadkach uzyskanie postaci funkcji może nas w zupełności zadowolić.
Kwadratowa funkcja regresji
Zauważmy, że wzrost całkowitej liczby zakażeń z pewnością nie jest opisywany funkcją liniową, bo liczba rejestrowanych każdego dnia przypadków nie jest stała, ale zdecydowanie rośnie. Przypuśćmy zatem, że wzrost ten jest opisywany funkcją kwadratową i wyznaczmy parametry tej funkcji. Sytuacja jest bardziej skomplikowana, bo odpowiednie wzory opisujące regresję liniową są łatwo dostępne, ale na regresję nieliniową już nie. Jednak niektóre problemy nieliniowe dają się łatwo zlinearyzować. Tak uczyniliśmy przed chwilą w przypadku funkcji wykładniczej: logarytmy wartości tej funkcji są opisywane funkcją liniową, dlatego przygotowaliśmy w kolumnie logarytmy ogólnej liczby przypadków. Podobnie w przypadku zjawiska opisywanego funkcją kwadratową postaci y = ax2 + b, podstawienie u = x2 linearyzuje problem, a w kolumnie wystarczy wpisać wartości kwadratów zmiennej niezależnej x.
W naszym przypadku uczynimy tak samo, choć problem będzie bardziej skomplikowany. Podstawiając u = x2 sprowadzamy problem badania funkcji y = ax2 + bx + c do badania funkcji y = au + bx + c, czyli do problemu dwukrotnej regresji liniowej[5], gdzie są już odpowiednie wzory, a funkcja REGLINP() ponownie okaże się przydatna.
Pamiętając o potrzebie przejścia do zmiennej x = n – n0 + 1, gdzie n0 oznacza numer dnia epidemii dla pierwszego dnia wybranego przedziału danych, w kolejnych kolumnach arkusza kalkulacyjnego umieszczamy:
- całkowitą liczbę zakażeń w kolejnych dniach wybranego przedziału (to są dane Y)
- liczby od 1 do 14 (numerują one dni epidemii w wybranym przedziale danych) (to są dane X)
- kwadraty liczb od 1 do 14 (to też są dane X)
Ponownie korzystając z funkcji arkusza REGLINP(), otrzymujemy wartości współczynników:
- a = 5,46 (z błędem 0,49)
- b = -7,3 (z błędem 7,5)
- c = 66 (z błędem 25)
Zwraca uwagę niezwykle wyskoki współczynnik korelacji równy 0,999.
Czyli szukany wielomian drugiego stopnia ma postać: z(x) = 5,46·x2 - 7,3·x + 66, gdzie x przyjmuje wartości z przedziału [1, 14].
Wzrost całkowitej liczby zakażeń opisywany funkcją kwadratową jest znacznie bardziej zbliżony do rzeczywistości. Funkcja kwadratowa jest znacznie lepiej dopasowana do rzeczywistych danych – pokazuje to efekt działań podjętych przez rząd: początkowo wykładniczy wzrost liczby chorych przeszedł we wzrost opisywany funkcją kwadratową i miejmy nadzieję, że za kilka tygodni zacznie wygasać.
Sześcienna funkcja regresji
Oczywiście (wbrew doniesieniom mediów) całkowita liczba zakażeń nie nie rośnie wykładniczo, a rośnie (od 20 dnia epidemii) wielomianowo i biegnie między krzywymi opisywanymi wielomianem 2 i 3 stopnia.
Sposób postępowania jest analogiczny jak dla wielomianu stopnia drugiego, dlatego jedynie go naszkicujemy. Podstawiając u = x2 i t = x3, sprowadzamy problem do badania funkcji postaci y = at + bu + cx + d, czyli sprowadzamy problem do trzykrotnej regresji liniowej[5] i ponownie funkcja REGLINP() okaże się niezwykle pomocna.
Dokonujemy przejścia do zmiennej x = n – n0 + 1, gdzie n0 oznacza numer dnia epidemii dla pierwszego dnia wybranego przedziału danych i w kolejnych kolumnach arkusza kalkulacyjnego umieszczamy:
- całkowitą liczbę zakażeń w kolejnych dniach wybranego przedziału (to są dane Y)
- liczby od 1 do 14 (numerują one dni epidemii w wybranym przedziale danych) (to są dane X)
- kwadraty liczb od 1 do 14 (to też są dane X)
- sześciany liczb od 1 do 14 (to również są dane X)
Korzystając z funkcji arkusza REGLINP(), otrzymujemy wartości współczynników (dla danych z dnia 26 marca 2020 r.):
- a = 0,206 (z błędem 0,077)
- b = 1,3 (z błędem 1,8)
- c = 26 (z błędem 12)
- d = 41 (z błędem 21)
Zwraca uwagę niezwykle wysoki współczynnik korelacji równy 0,9999.
Czyli szukany wielomian trzeciego stopnia ma postać: w(x) = 0,206·x3 + 1,3·x2 + 26·x + 41, gdzie x przyjmuje wartości z przedziału [1, 14].
Zestawienie wyników dla kolejnych dni
W tabeli przedstawiamy rezultaty otrzymane dla danych obejmujących 14 dni (do daty podanej w kolumnie Data). W kolumnach zamieszczamy:
- kolejne daty (w nawiasie dzień epidemii), dla których wykonane zostały obliczenia
- otrzymaną postać wielomianu drugiego stopnia
- liczbę dni T2 po jakiej (dla znalezionego wielomianu drugiego stopnia) nastąpi podwojenie łącznej liczby stwierdzonych zakażeń (dla wielomianu w(x), gdzie x przyjmuje wartości z przedziału [1, 14], wartość T2 wynika z rozwiązania równania w(T2 + 14) = 2·w(14)[6])
- otrzymaną postać wielomianu trzeciego stopnia
- liczbę dni T2 po jakiej (dla znalezionego wielomianu trzeciego stopnia) nastąpi podwojenie łącznej liczby stwierdzonych zakażeń (dla wielomianu w(x), gdzie x przyjmuje wartości z przedziału [1, 14], wartość T2 wynika z rozwiązania równania w(T2 + 14) = 2·w(14)[6])
- związek między zmienną x przyjmującą wartości z przedziału [1, 14], a zmienną n oznaczającą kolejne dni epidemii
Zauważmy, że kierunek zmian wartości T2 obserwowany w dłuższym okresie będzie bardzo dobrym wskaźnikiem przebiegu epidemii.
| Data | Wielomian 2 stopnia | T2 | Wielomian 3 stopnia | T2 | Uwagi |
|---|---|---|---|---|---|
| 23.03.2020 ( 20) | 4,37·x2 - 11,2·x + 39 | 4,80 | 0.127·x3 + 1.5·x2 + 7·x + 13 | 4.32 | x = n - 6 |
| 24.03.2020 ( 21) | 4,92·x2 - 9,7·x + 50 | 4,96 | 0.185·x3 + 0.8·x2 + 16·x + 12 | 4.35 | x = n - 7 |
| 25.03.2020 ( 22) | 5,46·x2 - 7,3·x + 66 | 5,13 | 0.196·x3 + 1.0·x2 + 20·x + 26 | 4.53 | x = n - 8 |
| 26.03.2020 ( 23) | 5,96·x2 - 3,3·x + 83 | 5,32 | 0,206·x3 + 1,3·x2 + 26·x + 41 | 4,73 | x = n - 9 |
| 27.03.2020 ( 24) | 6,33·x2 + 2,9·x + 104 | 5,55 | 0,136·x3 + 3,3·x2 + 22·x + 77 | 5,15 | x = n - 10 |
| 28.03.2020 ( 25) | 7,05·x2 + 6,3·x + 136 | 5,69 | 0,240·x3 + 1,6·x2 + 40·x + 87 | 5,08 | x = n - 11 |
| 29.03.2020 ( 26) | 7,79·x2 + 9,9·x + 180 | 5,84 | 0,207·x3 + 3,1·x2 + 39·x + 138 | 5,33 | x = n - 12 |
| 30.03.2020 ( 27) | 7,85·x2 + 23,1·x + 211 | 6,15 | 0,023·x3 + 7,3·x2 + 26·x + 206 | 6,09 | x = n - 13 |
| 31.03.2020 ( 28) | 7,79·x2 + 39,1·x + 242 | 6,50 | -0,028·x3 + 8,4·x2 + 35·x + 248 | 6,58 | x = n - 14 |
| 01.04.2020 ( 29) | 7,57·x2 + 57,2·x + 285 | 6,89 | -0,114·x3 + 10,1·x2 + 41·x + 308 | 7,25 | x = n - 15 |
| 02.04.2020 ( 30) | 8,39·x2 + 63,0·x + 367 | 7,01 | 0,161·x3 + 4,8·x2 + 85·x + 334 | 6,61 | x = n - 16 |
| 03.04.2020 ( 31) | 10,21·x2 + 57,3·x + 489 | 6,91 | 0,530·x3 -1,7·x2 + 131·x + 381 | 5,92 | x = n - 17 |
| 04.04.2020 ( 32) | 10,3·x2 + 74,8·x + 571 | 7,21 | 0,363·x3 + 2,2·x2 + 125·x + 497 | 6,49 | x = n - 18 |
| 05.04.2020 ( 33) | 11,4·x2 + 81,0·x + 694 | 7,30 | 0,447·x3 + 1,3·x2 + 144·x + 602 | 6,50 | x = n - 19 |
| 06.04.2020 ( 34) | 11,4·x2 + 101·x + 805 | 7,64 | 0,082·x3 + 9,5·x2 + 113·x + 788 | 7,46 | x = n - 20 |
| 07.04.2020 ( 35) | 11,3·x2 + 124·x + 925 | 7,97 | -0,101·x3 + 13,6·x2 + 110·x + 946 | 8,20 | x = n - 21 |
| 08.04.2020 ( 36) | 10,4·x2 + 156·x + 1043 | 8,50 | -0,437·x3 + 20,2·x2 + 95·x + 1132 | 9,74 | x = n - 22 |
| 09.04.2020 ( 37) | 8,9·x2 + 195·x + 1168 | 9,19 | -0,734·x3 + 25,4·x2 + 93·x + 1318 | 12,09 | x = n - 23 |
| 10.04.2020 ( 38) | 7,4·x2 + 233·x + 1327 | 9,98 | -0,999·x3 + 29,8·x2 + 93·x + 1531 | 16,35 | x = n - 24 |
| 11.04.2020 ( 39) | 5,3·x2 + 277·x + 1480 | 10,99 | -0,870·x3 + 24,9·x2 + 155·x + 1658 | 17,49 | x = n - 25 |
| 12.04.2020 ( 40) | 2,6·x2 + 328·x + 1642 | 12,50 | -0,676·x3 + 17,8·x2 + 233·x + 1780 | 18,81 | x = n - 26 |
| 13.04.2020 ( 41) | -0,40·x2 + 374·x + 1857 | 14,00[7] | -0,687·x3 + 15,1·x2 + 278·x + 1997 | 19,47[7] | x = n - 27 |
| 14.04.2020 ( 42) | -3,1·x2 + 411·x + 2122 | 16,54 | -0,661·x3 + 11,8·x2 + 319·x + 2257 | 25,91 | x = n - 28 |
| 15.04.2020 ( 43) | -3,6·x2 + 413·x + 2507 | 18,01 | -0,566·x3 + 9,2·x2 + 334·x + 2622 | 27,01 | x = n - 29 |
| 16.04.2020 ( 44) | -3,8·x2 + 410·x + 2894 | 19,35 | -0,332·x3 + 3,7·x2 + 364·x + 2962 | 23,86 | x = n - 30 |
| 17.04.2020 ( 45) | -3,3·x2 + 404·x + 3267 | 19,77 | 0,585·x3 - 16,5·x2 + 485·x + 3148 | 15,60 | x = n - 31 |
| 18.04.2020 ( 46) | -1,3·x2 + 370·x + 3738 | 18,96 | 0,751·x3 - 18,2·x2 + 475·x + 3585 | 14,56 | x = n - 32 |
| 19.04.2020 ( 47) | 1,3·x2 + 336·x + 4173 | 17,57 | 1,427·x3 - 30,8·x2 + 535·x + 3882 | 11,98 | x = n - 33 |
| 20.04.2020 ( 48) | 3,4·x2 + 308·x + 4611 | 16,96 | 1,049·x3 - 20,2·x2 + 454·x + 4397 | 12,84 | x = n - 34 |
| 21.04.2020 ( 49) | 3,3·x2 + 310·x + 4959 | 17,62 | 0,318·x3 - 3,9·x2 + 354·x + 4894 | 15,95 | x = n - 35 |
| 22.04.2020 ( 50) | 2,7·x2 + 318·x + 5293 | 18,64 | -0,489·x3 + 13,7·x2 + 250·x + 5393 | 23,06 | x = n - 36 |
| 23.04.2020 ( 51) | 1,8·x2 + 330·x + 5615 | 19,88 | -1,097·x3 + 26,5·x2 + 177·x + 5839 | ---- | x = n - 37 |
Rzeczywista dzienna liczba zakażonych a wartości oczekiwane
W zamieszczonej niżej tabeli zebraliśmy rzeczywiste liczby osób zakażonych koronawirusem, tak aby można było łatwo je porównać z przewidywanymi wartościami.
| Data | Rzeczywista liczba zakażeń | Przewidywana liczba - wielomian 2 stopnia | Przewidywana liczba - wielomian 3 stopnia |
|---|---|---|---|
| 24.03.2020 (21) | 152 | 105 | 131+ |
| 25.03.2020 (22) | 150 | 111 | 149+ |
| 26.03.2020 (23) | 170 | 134 | 174- |
| 27.03.2020 (24) | 168 | 154+ | 196 |
| 28.03.2020 (25) | 249 | 183 | 211+ |
| 29.03.2020 (26) | 224 | 179 | 228- |
| 30.03.2020 (27) | 193 | 218- | 260 |
| 31.03.2020 (28) | 256 | 268- | 273 |
| 01.04.2020 (29) | 243 | 272 | 266- |
| 02.04.2020 (30) | 392 | 292+ | 269 |
| 03.04.2020 (31) | 437 | 254 | 287+ |
| 04.04.2020 (32) | 244 | 263- | 371 |
| 05.04.2020 (33) | 475 | 388 | 462+ |
| 06.04.2020 (34) | 311 | 372- | 463 |
| 07.04.2020 (35) | 435 | 470- | 487 |
| 08.04.2020 (36) | 357 | 472 | 452- |
| 09.04.2020 (37) | 370 | 518 | 429- |
| 10.04.2020 (38) | 380 | 527 | 377+ |
| 11.04.2020 (39) | 401 | 518 | 314+ |
| 12.04.2020 (40) | 318 | 476 | 298+ |
| 13.04.2020 (41) | 260 | 461 | 323- |
| 14.04.2020 (42) | 268 | 448 | 308- |
| 15.04.2020 (43) | 380 | 397- | 262 |
| 16.04.2020 (44) | 336 | 313+ | 198 |
| 17.04.2020 (45) | 461 | 283+ | 215 |
| 18.04.2020 (46) | 363 | 199 | 318+ |
| 19.04.2020 (47) | 545 | 258 | 411+ |
| 20.04.2020 (48) | 306 | 229+ | 520 |
| 21.04.2020 (49) | 263 | 387- | 601 |
| 22.04.2020 (50) | 313 | 483- | 548 |
| 23.04.2020 (51) | 342 | 497 | 397- |
| 24.04.2020 (52) | 381 | 471- | 247 |
W ostatnim wierszu tabeli podajemy oczekiwaną liczbę nowych zakażeń koronawirusem w następnym dniu epidemii dla wielomianowych krzywych regresji. Najlepiej dopasowaną przewidywaną wartość do danych rzeczywistych zapisaliśmy pogrubioną czcionką. Znak + informuje nas, że wartość tę należy powiększyć, aby uzyskać wartość rzeczywistą, a znak - informuje nas, że wartość tę należy pomniejszyć. Tabela ta pokazuje w bardzo przejrzysty sposób sytuację epidemiczną. Rzeczywisty sukces w walce z epidemią zostanie natychmiast zauważony: najlepiej dopasowane będą wartości w trzeciej kolumnie i zostaną opatrzone znakiem minus.
28 marca 2020 r.: Duży wzrost liczby zakażonych, znacznie odbiegający od wartości oczekiwanych. W komunikacie z 20:02 Ministerstwo Zdrowia poinformowało o 157 nowych przypadkach, z których ponad połowę (103) stanowiły osoby z województwa mazowieckiego. Następnego dnia wyjaśniono, że wzrost ten spowodowany został wykryciem ogniska koronawirusa w Domu Pomocy Społecznej w Niedabylu – stwierdzono zakażenie koronawirusem u 60 osób[8].
31 marca 2020 r.: Po raz pierwszy współczynnik przy x3 zmienił znak i stał się liczbą ujemną. Oznacza to, że wielomian 3 stopnia dla pewnej wartości x osiągnie maksimum i przestanie rosnąć.
2 kwietnia 2020 r.: Duży wzrost liczby zakażonych, znacznie odbiegający od wartości oczekiwanych. W komunikacie z 21:14 Ministerstwo Zdrowia poinformowało o 254 nowych przypadkach, z których ponad połowę (142) stanowiły osoby z województwa mazowieckiego. Nie wyjaśniono powodów tak dużej liczby zakażeń. Może ma to związek ze znacznym zwiększeniem liczby wykonywanych testów[9], a może czeka nas gwałtowny wzrost liczby zakażeń.
3 kwietnia 2020 r.: W komunikacie z godziny 10:00 Ministerstwo poinformowało o 203 nowych przypadkach. Ponad połowa, bo 125 osób, były to przypadki z województwa śląskiego. Nie wyjaśniono przyczyn tak wielkiej liczby zakażeń w tym województwie.
7 kwietnia 2020 r.: Po raz drugi współczynnik przy x3 zmienił znak i stał się liczbą ujemną.
9 kwietnia 2020 r.: Wygląda na to, że współczynnik przy x3 w wielomianie trzeciego stopnia pozostanie liczbą ujemną. Bez trudu możemy policzyć, że wypisany wielomian osiągnie maksimum 48 dnia epidemii, czyli 20 kwietnia. Daje to pierwsze oszacowanie dnia, od którego liczba osób zakażonych w kolejnych dniach powinna zdecydowanie zmaleć.
11 kwietnia 2020 r.: Wielomian trzeciego stopnia osiąga maksimum 46 dnia epidemii, czyli 18 kwietnia. Zgodność tego wyniku i wyniku uzyskanego 9 kwietnia zwiększa zaufanie do uzyskanych rezultatów.
13 kwietnia 2020 r.: Po raz pierwszy współczynnik przy x2 w wielomianie drugiego stopnia zmienił znak i stał się liczbą ujemną. Wielomian trzeciego stopnia osiąga maksimum 48 dnia epidemii, czyli 20 kwietnia, co oznacza bardzo dobrą zgodność z poprzednimi wynikami. Od pięciu dni jest odnotowywana praktycznie stała liczba zakażeń (na poziomie ok. 350 osób dziennie), a dzisiaj nastąpił znaczący spadek (260 przypadków). Ze względu na brak rozwiązań odpowiedniego równania w przypadku wielomianu trzeciego stopnia nastąpiła zmiana sposobu obliczania okresu podwojenia T2[7]. Ta wymuszona zmiana jest również korzystnym sygnałem.
15 kwietnia 2020 r.: Od 9 kwietnia funkcja regresji kwadratowej dla liczby wykrytych zakażeń (w ciągu doby) osiąga maksimum w rozpatrywanym przedziale danych i przechodzi w funkcję malejącą. Podobnie od 14 kwietnia krzywa regresji liniowej jest krzywą malejącą. Mimo dzisiejszego wzrostu zakażeń (380 przypadków) obie krzywe regresji dla łącznej liczby przypadków utrzymały ujemne współczynniki przy wyrazach w najwyższej potędze. Wielomian trzeciego stopnia niezmiennie osiąga maksimum około 20 kwietnia. Najbliższe dni rozstrzygną, czy obserwujemy trwałe spowolnienie epidemii.
19 kwietnia 2020 r.: Wzrost liczby zakażeń koronawirusem wiąże się z wykryciem trzech nowych ognisk; dotyczą one ośrodków opieki długoterminowej w Kaliszu (woj. wielkopolskie) i Czernichowie (woj. śląskie) oraz szpitala w Jastrzębiu-Zdroju (woj. śląskie)[10].
23 kwietnia 2020 r.: Ponownie wystąpił brak rozwiązań odpowiedniego równania w przypadku wielomianu trzeciego stopnia, dlatego nie podajemy okresu podwojenia (nie będzie kolejnej modyfikacji formuły, według której obliczany jest okres podwojenia T2). Fakt ten utwierdza nas w przekonaniu, że epidemia zdecydowanie spowolniła.
Na podstawie następujących faktów:
- wzrost całkowitej liczby zakażeń nie ma charakteru wykładniczego, a wielomianowy o stopniu nie wyższym od trzeciego
- przewidywany okres podwojenia T2 systematycznie wydłuża się
- oczekiwane wartości liczby zakażeń w ciągu kolejnych dni dobrze odpowiadają odnotowanym danym rzeczywistym
łatwo stwierdzamy, że sytuacja w Polsce powoli się poprawia dzięki zdecydowanym działaniom rządu i wysiłkowi całego społeczeństwa, a sugestie, że w Polsce powtórzy się scenariusz włoski, są całkowicie nieprawdziwe.
Przedstawiony obraz był prawdziwy i przewidywalny do 2 kwietnia. Co takiego się stało, że epidemia przyspieszyła mimo nakładania kolejnych ograniczeń przez rząd? Trudno wskazać jakiekolwiek sensowne wyjaśnienie poza (być może) wykrytymi ogniskami zakażeń lub zwiększoną liczbą wykonywanych testów. Po gwałtownym skoku liczby zakażonych 2, 3 i 5 kwietnia obecnie sytuacja wydaje się stabilizować. Okres podwojenia całkowitej liczby osób zakażonych T2 wyraźnie rośnie, a przewidywana liczba osób zakażonych jest większa niż w rzeczywistości (od 6 kwietnia). Daje to ponownie nadzieję na zdecydowane spowolnienie epidemii w ciągu najbliższych 10 dni.
Przypisy
- ↑ Stosujemy prostą średnią kroczącą (ruchomą) dla n = 7. (LINK1), (LINK2)
- ↑ Od 11 czerwca 2020 r. Ministerstwo Zdrowia zmieniło sposób raportowania danych. Dane w tabeli do dnia 10 czerwca są danymi z godziny 17:30. Od 11 czerwca (100 dzień epidemii) dane są raportowane tylko raz na dobę i podawane ok. godziny 10:30.
- ↑ LibreOffice Calc, Funkcje macierzowe, (LINK)
- ↑ LibreOffice 6.4 Help, REGLINP, (LINK)
- ↑ 5,0 5,1 Wyznaczenie współczynników wielokrotnej regresji liniowej oraz ich odchyleń standardowych przy pomocy metody najmniejszych kwadratów, (Opracowanie własne - LINK)
- ↑ 6,0 6,1 W rzeczywistości okres podwojenia T2 wyliczamy w bardziej skomplikowany sposób. Najpierw wyliczamy, jaka liczba dni D musi upłynąć od ostatniego (czyli 14) dnia badanego okresu, aby całkowita liczba zakażeń wzrosła o 18,9207%. Gdyby taka tendencja wzrostu liczby zakażeń była trwała, to podwojenie całkowitej liczby zakażonych nastąpiłoby po 4·D dniach. Jest tak dlatego, że (1.189207)^4 = 2. Wnioskowanie o okresie podwojenia na podstawie rozwiązania równania w(T2 + 14) = 2·w(14) jest nieuprawnioną ekstrapolacją wielomianu w(x). Nieuprawnioną dlatego, że na podstawie danych z 14 dni sięgamy od 5 do 7 dni w przyszłość (takie wartości T2 wynikały z rozwiązania tego równania). Zbierając: rozwiązujemy równanie w(D + 14) = 2^(1/4)·w(14) i otrzymaną liczbę D mnożymy przez 4.
- ↑ 7,0 7,1 7,2 Od 13 kwietnia 2020 r. nastąpiła (wymuszona) zmiana sposobu wyliczania okres podwojenia T2. Zmiana została spowodowana brakiem rozwiązań równania w(D + 14) = 2^(1/4)·w(14) w przypadku wielomianu trzeciego stopnia. Dlatego od 13 kwietnia rozwiązujemy równanie w(D + 14) = 2^(1/8)·w(14) i otrzymaną liczbę D mnożymy przez 8.
- ↑ Polska Agencja Prasowa SA, Kraska: Żaden polityk nie podejmie decyzji o wyborach narażając ludzi na niebezpieczeństwo utraty życia i zdrowia, (LINK)
- ↑ Ministerstwo Zdrowia informowało o następujących liczbach testów przeprowadzonych w ciągu doby:
15 marca – 1 tys. (LINK)
17 marca – 1,2 tys. (LINK)
18 marca – 1,6 tys. (LINK)
19 marca – 1,6 tys. (LINK)
20 marca – 1,8 tys. (LINK)
21 marca – 2 tys. (LINK)
22 marca – 2,5 tys. (LINK)
23 marca – 2,5 tys. (LINK)
24 marca – 2,8 tys. (LINK)
25 marca – 3,3 tys. (LINK)
26 marca – 3,3 tys. (LINK)
27 marca – 4,5 tys. (LINK)
28 marca – 4,6 tys. (LINK)
29 marca – 4,1 tys. (LINK)
30 marca – 3,8 tys. (LINK)
31 marca – 4,8 tys. (LINK)
1 kwietnia – 4,3 tys. (LINK)
2 kwietnia – 5,3 tys. (LINK)
3 kwietnia – 5,7 tys. (LINK)
- ↑ Polska Agencja Prasowa SA, Rzecznik MZ: wzrost zakażeń koronawirusem wiąże się z wykryciem trzech nowych ognisk, (LINK)