Liczby zespolone i ciągi liczb zespolonych

06.04.2025

Liczby zespolone

Definicja ZA1
Liczbą zespoloną nazywamy liczbę [math]\displaystyle{ z = a + i b }[/math], gdzie [math]\displaystyle{ a, b \in \mathbb{R} }[/math] oraz [math]\displaystyle{ i^2 = - 1 }[/math]. Liczbę [math]\displaystyle{ a }[/math] (odpowiednio [math]\displaystyle{ b }[/math]) nazywamy częścią rzeczywistą (odpowiednio urojoną) liczby zespolonej [math]\displaystyle{ z }[/math]. Fakt ten zapisujemy następująco: [math]\displaystyle{ \operatorname{Re}(z) = a }[/math] oraz [math]\displaystyle{ \operatorname{Im}(z) = b }[/math]. Liczbę [math]\displaystyle{ \bar{z} = a - i b }[/math] nazywamy liczbą zespoloną sprzężoną z liczbą [math]\displaystyle{ z }[/math]. Przez [math]\displaystyle{ \mathbb{C} }[/math] oznaczamy zbiór wszystkich liczb zespolonych, czyli [math]\displaystyle{ \mathbb{C}= \{ z = x + i y \; : \; x, y \in \mathbb{R} \} }[/math].

Uwaga ZA2

Niech [math]\displaystyle{ z_1 = a + i b }[/math], [math]\displaystyle{ z_2 = c + i d }[/math]. Czytelnik łatwo pokaże, że

1.      [math]\displaystyle{ z_1 + z_2 = (a + i b) + (c + i d) = (a + c) + i (b + d) }[/math]

2.      [math]\displaystyle{ z_1 \cdot z_2 = (a + i b) \cdot (c + i d) = (a c - b d) + i (a d + b c) }[/math]

3.      [math]\displaystyle{ {\small\frac{z_1}{z_2}} = {\small\frac{a + i b}{c + i d}} = {\small\frac{a c + b d}{c^2 + d^2}} + i \cdot {\small\frac{b c - a d}{c^2 + d^2}} \qquad \qquad \text{ o ile } \; z_2 \neq 0 }[/math]

4.      [math]\displaystyle{ \overline{(\bar{z})} = z }[/math]

5.      [math]\displaystyle{ \overline{z_1 + z_2} = \overline{z_1} + \overline{z_2} }[/math]

6.      [math]\displaystyle{ \overline{z_1 \cdot z_2} = \overline{z_1} \cdot \overline{z_2} }[/math]

7.      [math]\displaystyle{ \overline{\left( {\small\frac{1}{z}} \right)} = {\small\frac{1}{\bar{z}}} }[/math]

8.      [math]\displaystyle{ \operatorname{Re}(z) = {\small\frac{z + \bar{z}}{2}} \qquad \qquad \operatorname{Im}(z) = {\small\frac{z - \bar{z}}{2 i}} }[/math]

Definicja ZA3
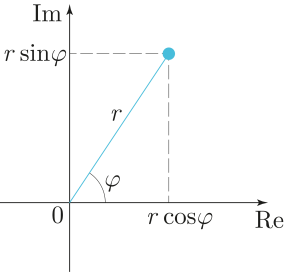
Niech [math]\displaystyle{ z = x + i y }[/math]. Liczbę [math]\displaystyle{ r = \sqrt{x^2 + y^2} = | z | }[/math] nazywamy modułem liczby zespolonej [math]\displaystyle{ z }[/math]. Jeżeli [math]\displaystyle{ z \neq 0 }[/math], to liczbę [math]\displaystyle{ \varphi }[/math] spełniającą układ równań

[math]\displaystyle{ \begin{cases} x = r \cos \varphi \\ y = r \sin \varphi \\ \end{cases} }[/math]

nazywamy argumentem liczby zespolonej [math]\displaystyle{ z }[/math], co zapisujemy jako [math]\displaystyle{ \varphi = \arg(z) }[/math]. Wynika stąd wzór [math]\displaystyle{ z = r (\cos \varphi + i \sin \varphi) }[/math]. Jeżeli [math]\displaystyle{ \varphi \in [0, 2 \pi) }[/math], to powiemy, że [math]\displaystyle{ \varphi }[/math] jest argumentem głównym liczby zespolonej [math]\displaystyle{ z }[/math] i oznaczamy [math]\displaystyle{ \varphi = \operatorname{Arg}(z) }[/math].

Punkt na płaszczyźnie zespolonej

Twierdzenie ZA4
Niech [math]\displaystyle{ z, z_1, z_2 \in \mathbb{C} \; }[/math] i [math]\displaystyle{ \; z = a + i b }[/math], [math]\displaystyle{ \; z_1 = r_1 (\cos \varphi_1 + i \sin \varphi_1) \; }[/math] oraz [math]\displaystyle{ \; z_2 = r_2 (\cos \varphi_2 + i \sin \varphi_2) }[/math], gdzie [math]\displaystyle{ r_1, r_2, \varphi_1, \varphi_2 \in \mathbb{R} }[/math]. Mamy

  1.      [math]\displaystyle{ | \bar{z} | = | z | }[/math]

  2.      [math]\displaystyle{ | \operatorname{Re}(z) | \leqslant | z | \qquad \qquad | \operatorname{Im}(z) | \leqslant | z | }[/math]

  3.      [math]\displaystyle{ | z |^2 = z \bar{z} }[/math]

  4.      [math]\displaystyle{ | z_1 z_2 | = | z_1 | \cdot | z_2 | }[/math]

  5.      [math]\displaystyle{ \left| {\small\frac{1}{z}} \right| = {\small\frac{1}{| z |}} }[/math]

  6.      [math]\displaystyle{ | z_1 + z_2 | \leqslant | z_1 | + | z_2 | }[/math]

  7.      [math]\displaystyle{ \left| \sum_{k = 1}^{n} z_k \right| \leqslant \sum_{k = 1}^{n} | z_k | }[/math]

  8.      [math]\displaystyle{ | | z_1 | - | z_2 | | \leqslant | z_1 - z_2 | }[/math]

  9.      [math]\displaystyle{ z_1 z_2 = r_1 r_2 (\cos (\varphi_1 + \varphi_2) + i \sin (\varphi_1 + \varphi_2)) }[/math]

10.      [math]\displaystyle{ {\small\frac{z_1}{z_2}} = {\small\frac{r_1}{r_2}} (\cos (\varphi_1 - \varphi_2) + i \sin (\varphi_1 - \varphi_2)) \qquad \qquad \text{ o ile } \; z_2 \neq 0 }[/math]

Dowód

Punkt 2.

[math]\displaystyle{ | z | = \sqrt{a^2 + b^2} \geqslant \sqrt{a^2} = | a | = | \operatorname{Re}(z) | }[/math]

Punkt 4.

[math]\displaystyle{ | z_1 z_2 | = | (a_1 + i b_1) (a_2 + i b_2) | }[/math]

[math]\displaystyle{ \;\;\;\:\, = | a_1 a_2 - b_1 b_2 + i (a_1 b_2 + a_2 b_1) | }[/math]

[math]\displaystyle{ \;\;\;\:\, = \sqrt{(a_1 a_2 - b_1 b_2)^2 + (a_1 b_2 + a_2 b_1)^2} }[/math]

[math]\displaystyle{ \;\;\;\:\, = \sqrt{(a_1)^2 (a_2)^2 - 2 a_1 a_2 b_1 b_2 + (b_1)^2 (b_2)^2 + (a_1)^2 (b_2)^2 + 2 a_1 b_2 a_2 b_1 + (b_1)^2 (a_2)^2} }[/math]

[math]\displaystyle{ \;\;\;\:\, = \sqrt{(a_1)^2 (a_2)^2 + (b_1)^2 (b_2)^2 + (a_1)^2 (b_2)^2 + (b_1)^2 (a_2)^2} }[/math]

[math]\displaystyle{ \;\;\;\:\, = \sqrt{[(a_1)^2 + (b_1)^2] \cdot [(a_2)^2 + (b_2)^2]} }[/math]

[math]\displaystyle{ \;\;\;\:\, = \sqrt{(a_1)^2 + (b_1)^2} \cdot \sqrt{(a_2)^2 + (b_2)^2} }[/math]

[math]\displaystyle{ \;\;\;\:\, = | z_1 | \cdot | z_2 | }[/math]

Punkt 6.

Wzór jest prawdziwy w przypadku, gdy [math]\displaystyle{ z_1 = z_2 = 0 }[/math]. Możemy zatem założyć, że przynajmniej jedna z liczb [math]\displaystyle{ z_1, z_2 }[/math] jest różna od zera.

[math]\displaystyle{ | z_1 + z_2 |^2 = (z_1 + z_2) \overline{(z_1 + z_2)} }[/math]

[math]\displaystyle{ \;\;\;\;\,\, = (z_1 + z_2) (\overline{z_1} + \overline{z_2}) }[/math]

[math]\displaystyle{ \;\;\;\;\,\, = z_1 \overline{z_1} + z_1 \overline{z_2} + z_2 \overline{z_1} + z_2 \overline{z_2} }[/math]

Zauważmy, że

[math]\displaystyle{ z_1 \overline{z_2} + z_2 \overline{z_1} = z_1 \overline{z_2} + \overline{z_1 \overline{z_2}} = 2 \operatorname{Re}(z_1 \overline{z_2}) }[/math]

Zatem

[math]\displaystyle{ | z_1 + z_2 |^2 = | z_1 |^2 + 2 \operatorname{Re}(z_1 \overline{z_2}) + | z_2 |^2 }[/math]

[math]\displaystyle{ \leqslant | z_1 |^2 + 2 | z_1 \overline{z_2} | + | z_2 |^2 }[/math]

[math]\displaystyle{ \leqslant | z_1 |^2 + 2 | z_1 | | z_2 | + | z_2 |^2 }[/math]

[math]\displaystyle{ \leqslant (| z_1 | + | z_2 |)^2 }[/math]

Wynika stąd, że

[math]\displaystyle{ [| z_1 + z_2 | - (| z_1 | + | z_2 |)] \cdot [| z_1 + z_2 | + (| z_1 | + | z_2 |)] \leqslant 0 }[/math]

Czyli

[math]\displaystyle{ | z_1 + z_2 | \leqslant | z_1 | + | z_2 | }[/math]

Co należało pokazać.

Punkt 7.

Indukcja matematyczna. Wzór jest prawdziwy dla [math]\displaystyle{ n = 1, 2 }[/math]. Zakładając prawdziwość wzoru dla [math]\displaystyle{ n }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ \left| \sum_{k = 1}^{n + 1} z_k \right| = \left| \left( \sum_{k = 1}^{n} z_k \right) + z_{n + 1} \right| }[/math]

[math]\displaystyle{ \;\:\, \leqslant \left| \sum_{k = 1}^{n} z_k \right| + | z_{n + 1} | }[/math]

[math]\displaystyle{ \;\:\, \leqslant \sum_{k = 1}^{n} | z_k | + | z_{n + 1} | }[/math]

[math]\displaystyle{ \;\:\, \leqslant \sum_{k = 1}^{n + 1} | z_k | }[/math]

Co należało pokazać.

Punkt 8.

Z punktu 6. otrzymujemy

[math]\displaystyle{ | z_1 | = | z_1 - z_2 + z_2 | \leqslant | z_1 - z_2 | + | z_2 | }[/math]

[math]\displaystyle{ | z_2 | = | z_2 - z_1 + z_1 | \leqslant | z_2 - z_1 | + | z_1 | = | z_1 - z_2 | + | z_1 | }[/math]

Zatem

[math]\displaystyle{ | z_1 - z_2 | \geqslant | z_1 | - | z_2 | }[/math]

[math]\displaystyle{ | z_1 - z_2 | \geqslant | z_2 | - | z_1 | = - (| z_1 | - | z_2 |) }[/math]

Zbierając

[math]\displaystyle{ | z_1 - z_2 | \geqslant \pm (| z_1 | - | z_2 |) }[/math]

Czyli

[math]\displaystyle{ | z_1 - z_2 | \geqslant | | z_1 | - | z_2 | | }[/math]

Co należało pokazać.

Punkt 9.

[math]\displaystyle{ z_1 z_2 = r_1 (\cos \varphi_1 + i \sin \varphi_1) \cdot r_2 (\cos \varphi_2 + i \sin \varphi_2) }[/math]

[math]\displaystyle{ \;\:\, = r_1 r_2 (\cos \varphi_1 \cdot \cos \varphi_2 - \sin \varphi_1 \cdot \sin \varphi_2 + i (\sin \varphi_1 \cdot \cos \varphi_2 + \cos \varphi_1 \cdot \sin \varphi_2)) }[/math]

[math]\displaystyle{ \;\:\, = r_1 r_2 (\cos (\varphi_1 + \varphi_2) + i \sin (\varphi_1 + \varphi_2)) }[/math]

Punkt 10.

[math]\displaystyle{ {\small\frac{z_1}{z_2}} = {\small\frac{r_1 (\cos \varphi_1 + i \sin \varphi_1)}{r_2 (\cos \varphi_2 + i \sin \varphi_2)}} }[/math]

[math]\displaystyle{ \: = {\small\frac{r_1}{r_2}} \cdot {\small\frac{(\cos \varphi_1 + i \sin \varphi_1) (\cos \varphi_2 - i \sin \varphi_2)}{(\cos \varphi_2 + i \sin \varphi_2) (\cos \varphi_2 - i \sin \varphi_2)}} }[/math]

[math]\displaystyle{ \: = {\small\frac{r_1}{r_2}} \cdot {\small\frac{\cos \varphi_1 \cdot \cos \varphi_2 + \sin \varphi_1 \cdot \sin \varphi_2 + i (\sin \varphi_1 \cdot \cos \varphi_2 - \cos \varphi_1 \cdot \sin \varphi_2)}{\cos^2 \varphi_2 + \sin^2 \varphi_2}} }[/math]

[math]\displaystyle{ \: = {\small\frac{r_1}{r_2}} \cdot (\cos (\varphi_1 - \varphi_2) + i \sin (\varphi_1 - \varphi_2)) }[/math]

Co należało pokazać.
□

Twierdzenie ZA5 (Abraham de Moivre, 1707)
Niech [math]\displaystyle{ z \in \mathbb{C} }[/math] i [math]\displaystyle{ \varphi = \arg z }[/math]. Mamy

[math]\displaystyle{ z^n = | z |^n (\cos n \varphi + i \sin n \varphi) }[/math]

Dowód

Wzór de Moivre'a jest uogólnieniem wzoru na iloczyn liczb zespolonych (zobacz ZA4 p. 9)

[math]\displaystyle{ z_1 z_2 = r_1 r_2 (\cos (\varphi_1 + \varphi_2) + i \sin (\varphi_1 + \varphi_2)) }[/math]

Indukcja matematyczna. Wzór de Moivre'a jest prawdziwy dla [math]\displaystyle{ n = 1 }[/math]. Zakładając prawdziwość wzoru dla [math]\displaystyle{ n \geqslant 1 }[/math], otrzymujemy dla [math]\displaystyle{ n + 1 }[/math]

[math]\displaystyle{ z^{n + 1} = z^n z }[/math]

[math]\displaystyle{ \;\;\, = | z |^n (\cos n \varphi + i \sin n \varphi) \cdot | z | (\cos \varphi + i \sin \varphi) }[/math]

[math]\displaystyle{ \;\;\, = | z |^{n + 1} (\cos (n + 1) \varphi + i \sin (n + 1) \varphi) }[/math]

Co kończy dowód.
□

Definicja ZA6
Niech [math]\displaystyle{ c, z \in \mathbb{C} }[/math]. Jeżeli [math]\displaystyle{ z^n = c }[/math], to powiemy, że [math]\displaystyle{ z }[/math] jest pierwiastkiem [math]\displaystyle{ n }[/math]-tego stopnia z liczby zespolonej [math]\displaystyle{ c }[/math]. Ten z pierwiastków, który ma najmniejszy nieujemny argument, będziemy nazywali pierwiastkiem głównym.

Zadanie ZA7
Pokazać, że ze wzoru de Moivre'a wynika następujący wzór na pierwiastki [math]\displaystyle{ n }[/math]-tego stopnia z liczby [math]\displaystyle{ z }[/math]

[math]\displaystyle{ z^{1 / n} = | z |^{1 / n} \left( \cos {\small\frac{\varphi + 2 k \pi}{n}} + i \sin {\small\frac{\varphi + 2 k \pi}{n}} \right) }[/math]

gdzie [math]\displaystyle{ \varphi = \arg z }[/math]. Zauważmy, że dla [math]\displaystyle{ k = 0, 1, \ldots, n - 1 }[/math] otrzymujemy [math]\displaystyle{ n }[/math] różnych pierwiastków [math]\displaystyle{ n }[/math]-tego stopnia z liczby [math]\displaystyle{ z }[/math].

Rozwiązanie

Niech [math]\displaystyle{ w }[/math] będzie pierwiastkiem [math]\displaystyle{ n }[/math]-tego stopnia z liczby zespolonej [math]\displaystyle{ z }[/math]. Z definicji [math]\displaystyle{ w^n = z }[/math]. Jeżeli zapiszemy liczby [math]\displaystyle{ z }[/math] i [math]\displaystyle{ w }[/math] jako

[math]\displaystyle{ z = R (\cos \varphi + i \sin \varphi) }[/math]

[math]\displaystyle{ w = r (\cos \theta + i \sin \theta) }[/math]

to równanie [math]\displaystyle{ w^n = z }[/math] możemy zapisać w postaci

[math]\displaystyle{ r^n (\cos n \theta + i \sin n \theta) = R (\cos \varphi + i \sin \varphi) }[/math]

Porównując część rzeczywistą i część urojoną, dostajemy

[math]\displaystyle{ r^n \cos n \theta = R \cos \varphi }[/math]

[math]\displaystyle{ r^n \sin n \theta = R \sin \varphi }[/math]

Mnożąc strony przez siebie, mamy

[math]\displaystyle{ r^n R \sin n \theta \cos \varphi = r^n R \cos n \theta \sin \varphi }[/math]

Skąd dostajemy

[math]\displaystyle{ \sin n \theta \cos \varphi - \cos n \theta \sin \varphi = \sin (n \theta - \varphi) = 0 }[/math]

Zatem

[math]\displaystyle{ n \theta = \varphi + 2 k \pi }[/math]

i oczywiście

[math]\displaystyle{ r = \sqrt[n]{R} }[/math]

Wszystkie wartości [math]\displaystyle{ \theta }[/math] wynikają z równania

[math]\displaystyle{ \theta = {\small\frac{\varphi}{n}} + {\small\frac{2 k \pi}{n}} }[/math]

gdzie [math]\displaystyle{ k = 0, 1, \ldots, n - 1 }[/math]. Pozostałym wartościom [math]\displaystyle{ k }[/math] odpowiadają kąty [math]\displaystyle{ \theta }[/math], które różnią się o [math]\displaystyle{ 2 \pi }[/math] od pewnego wypisanego wyżej kąta [math]\displaystyle{ \theta }[/math].
□

Zadanie ZA8
Obliczyć

[math]\displaystyle{ \text{a)} \;\; (1 - i)^{100} \qquad \qquad \text{b)} \;\; \sqrt{z} \qquad \qquad \text{c)} \;\; \sqrt[6]{2} \qquad \qquad \text{d)} \;\; \sqrt[4]{1 + i} }[/math]

Rozwiązanie

a) Liczbę [math]\displaystyle{ 1 - i }[/math] możemy zapisać w postaci

[math]\displaystyle{ 1 - i = \sqrt{2} \left( \cos \left( - {\small\frac{\pi}{4}} \right) + i \sin \left( - {\small\frac{\pi}{4}} \right) \right) }[/math]

Zatem ze wzoru de Moivre'a otrzymujemy

[math]\displaystyle{ (1 - i)^{100} = \left( \sqrt{2} \right)^{100} (\cos (- 25 \pi) + i \sin (- 25 \pi)) = - 2^{50} }[/math]

b) Z zadania ZA7 wynika natychmiast, że wszystkie pierwiastki drugiego stopnia z liczby [math]\displaystyle{ z }[/math] otrzymujemy ze wzoru

[math]\displaystyle{ \sqrt{z} = \sqrt{| z |} \left( \cos {\small\frac{\varphi + 2 k \pi}{2}} + i \sin {\small\frac{\varphi + 2 k \pi}{2}} \right) }[/math]

gdzie [math]\displaystyle{ \varphi = \arg (z) }[/math] i [math]\displaystyle{ k = 0, 1 }[/math]. Zatem są to liczby

[math]\displaystyle{ w_1 = \sqrt{| z |} \left( \cos {\small\frac{\varphi}{2}} + i \sin {\small\frac{\varphi}{2}} \right) }[/math]

[math]\displaystyle{ w_2 = \sqrt{| z |} \left( \cos \left( {\small\frac{\varphi}{2}} + \pi \right) + i \sin \left( {\small\frac{\varphi}{2}} + \pi \right) \right) = \sqrt{| z |} \left( - \cos {\small\frac{\varphi}{2}} - i \sin {\small\frac{\varphi}{2}} \right) = - \sqrt{| z |} \left( \cos {\small\frac{\varphi}{2}} + i \sin {\small\frac{\varphi}{2}} \right) = - w_1 }[/math]

I takiego wyniku należało oczekiwać.

c) Wszystkie pierwiastki [math]\displaystyle{ 6 }[/math]-tego stopnia z liczby [math]\displaystyle{ 2 }[/math] otrzymujemy ze wzoru

[math]\displaystyle{ \sqrt[6]{2} \left( \cos {\small\frac{k \pi}{3}} + i \sin {\small\frac{k \pi}{3}} \right) }[/math]

gdzie [math]\displaystyle{ k = 0, 1, 2, 3, 4, 5 }[/math]. Łatwo znajdujemy, że poszukiwanymi pierwiastkami są liczby

[math]\displaystyle{ \sqrt[6]{2} \qquad \sqrt[6]{2} \left( {\small\frac{1}{2}} + {\small\frac{i \sqrt{3}}{2}} \right) \qquad \sqrt[6]{2} \left( - {\small\frac{1}{2}} + {\small\frac{i \sqrt{3}}{2}} \right) \qquad - \sqrt[6]{2} \qquad \sqrt[6]{2} \left( - {\small\frac{1}{2}} - {\small\frac{i \sqrt{3}}{2}} \right) \qquad \sqrt[6]{2} \left( {\small\frac{1}{2}} - {\small\frac{i \sqrt{3}}{2}} \right) }[/math]

d) Ponieważ [math]\displaystyle{ \operatorname{Arg}(1 + i) = {\small\frac{\pi}{4}} }[/math], to liczbę [math]\displaystyle{ 1 + i }[/math] możemy zapisać w postaci

[math]\displaystyle{ 1 + i = \sqrt{2} \left( \cos {\small\frac{\pi}{4}} + i \sin {\small\frac{\pi}{4}} \right) }[/math]

Wszystkie pierwiastki [math]\displaystyle{ 4 }[/math]-tego stopnia z liczby [math]\displaystyle{ 1 + i }[/math] otrzymujemy ze wzoru

[math]\displaystyle{ \sqrt[8]{2} \left( \cos \left( {\small\frac{(8 k + 1) \pi}{16}} \right) + i \sin \left( {\small\frac{(8 k + 1) \pi}{16}} \right) \right) }[/math]

gdzie [math]\displaystyle{ k = 0, 1, 2, 3 }[/math].
□

Przykład ZA9
W przypadku liczb zespolonych łatwo jest napisać nierówności, które mają być spełnione, ale trudniej wyobrazić sobie ich rozwiązanie na płaszczyźnie zespolonej. Ogromnym ułatwieniem jest oprogramowanie WolframAlpha dostępne online. Podamy kilka przykładów.

•     [math]\displaystyle{ 1 \lt | z |^2 \lt 4 }[/math], czyli [math]\displaystyle{ \; 1 \lt x^2 + y^2 \lt 4 }[/math]     (WolframAlpha)

•     [math]\displaystyle{ | z |^2 \lt 1 \; }[/math] i [math]\displaystyle{ \; \operatorname{Im}(z) \gt 0 }[/math], czyli [math]\displaystyle{ \; x^2 + y^2 \lt 1 \; }[/math] i [math]\displaystyle{ \; y \gt 0 }[/math]     (WolframAlpha)

•     [math]\displaystyle{ | z |^2 \lt 1 \; }[/math] i [math]\displaystyle{ \; \operatorname{Im}(z) \gt \operatorname{Re}(z) }[/math], czyli [math]\displaystyle{ \; x^2 + y^2 \lt 1 \; }[/math] i [math]\displaystyle{ \; y \gt x }[/math]     (WolframAlpha)

•     [math]\displaystyle{ | z | = \arg (z) }[/math], czyli [math]\displaystyle{ \; r = \varphi }[/math]     (WolframAlpha)

•     [math]\displaystyle{ | z | = 1 + \cos (\operatorname{Arg}(z)) }[/math], czyli [math]\displaystyle{ \; r = 1 + \cos \varphi }[/math]     (WolframAlpha)

Ciągi nieskończone liczb zespolonych

Definicja ZA10
Niech [math]\displaystyle{ n \in \mathbb{N}_0 }[/math]. Jeżeli każdej liczbie [math]\displaystyle{ n }[/math] przypiszemy pewną liczbę zespoloną [math]\displaystyle{ c_n }[/math], to powiemy, że liczby [math]\displaystyle{ c_0, c_1, \ldots, c_n, \ldots }[/math] tworzą ciąg nieskończony o wyrazach zespolonych.

Definicja ZA11
Ciąg nieskończony [math]\displaystyle{ c_0, c_1, \ldots, c_n, \ldots }[/math] będziemy oznaczać symbolem [math]\displaystyle{ (c_n) }[/math]. Często, o ile nie będzie to prowadziło do nieporozumień, ciąg nieskończony będziemy nazywali po prostu ciągiem.

Definicja ZA12
Jeżeli dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka liczba naturalna [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest [math]\displaystyle{ | c_n - c | \lt \varepsilon }[/math], to powiemy, że [math]\displaystyle{ c }[/math] jest granicą ciągu [math]\displaystyle{ (c_n) }[/math] i w takim przypadku będziemy pisali [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = c }[/math]. Ciąg mający skończoną granicę będziemy nazywali zbieżnym.

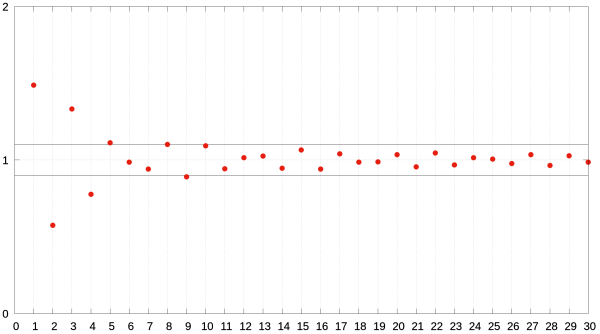
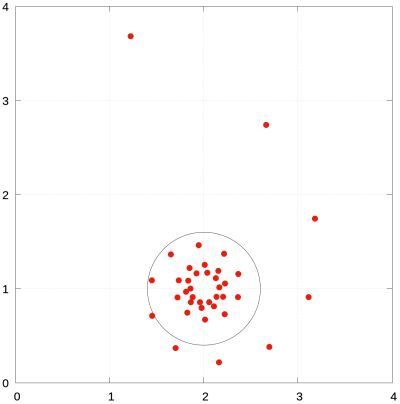
Uwaga ZA13
Porównajmy. W przypadku nieskończonego ciągu liczb rzeczywistych [math]\displaystyle{ (a_n) }[/math] mieliśmy taki obrazek granicy

Pomimo formalnego podobieństwa definicji, w przypadku liczb zespolonych obrazek wygląda tak

Definicja ZA14
Niech [math]\displaystyle{ a_n, b_n \in \mathbb{R}\; }[/math] i [math]\displaystyle{ \; c_n \in \mathbb{C} }[/math]. Ciągi [math]\displaystyle{ (a_n) }[/math], [math]\displaystyle{ (b_n) }[/math], [math]\displaystyle{ (c_n) }[/math] mają granice niewłaściwe, jeżeli dla dowolnego [math]\displaystyle{ M \gt 0 }[/math] istnieje taka liczba naturalna [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest

●      [math]\displaystyle{ a_n \gt M \qquad \;\;\, }[/math] (ciąg [math]\displaystyle{ (a_n) }[/math] ma granicę niewłaściwą równą [math]\displaystyle{ + \infty }[/math])

●      [math]\displaystyle{ b_n \lt - M \qquad }[/math] (ciąg [math]\displaystyle{ (b_n) }[/math] ma granicę niewłaściwą równą [math]\displaystyle{ - \infty }[/math])

●      [math]\displaystyle{ | c_n | \gt M \qquad \: }[/math] (ciąg [math]\displaystyle{ (c_n) }[/math] ma granicę niewłaściwą równą [math]\displaystyle{ \infty }[/math])

Powiemy wtedy, że

●      ciąg [math]\displaystyle{ (a_n) }[/math] jest rozbieżny do plus nieskończoności, co zapisujemy jako [math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = + \infty }[/math]

●      ciąg [math]\displaystyle{ (b_n) }[/math] jest rozbieżny do minus nieskończoności, co zapisujemy jako [math]\displaystyle{ \lim_{n \rightarrow \infty} b_n = - \infty }[/math]

●      ciąg [math]\displaystyle{ (c_n) }[/math] jest rozbieżny do nieskończoności, co zapisujemy jako [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = \infty }[/math]

Przykład ZA15
Ciąg [math]\displaystyle{ a_n = 1 + {\small\frac{1}{n}} }[/math] jest zbieżny do liczby [math]\displaystyle{ 1 }[/math]. Istotnie, dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 \; }[/math] i [math]\displaystyle{ \; N_0 = \left\lfloor {\small\frac{1}{\varepsilon}} \right\rfloor + 1 }[/math] dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest [math]\displaystyle{ | a_n - 1 | \lt \varepsilon }[/math]. Co łatwo sprawdzamy

[math]\displaystyle{ | a_n - 1 | = \left| {\small\frac{1}{n}} \right| = {\small\frac{1}{n}} \lt {\small\frac{1}{N_0}} = \frac{1}{\left\lfloor {\small\frac{1}{\varepsilon}} \right\rfloor + 1} \lt \frac{1}{{\small\frac{1}{\varepsilon}}} = \varepsilon }[/math]

Ciąg [math]\displaystyle{ a_n = n^2 }[/math] jest rozbieżny do plus nieskończoności. Istotnie, dla dowolnego [math]\displaystyle{ M \gt 0 \; }[/math] i [math]\displaystyle{ \; N_0 = \left\lfloor \sqrt{M} \right\rfloor + 1 }[/math] dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest [math]\displaystyle{ a_n \gt M }[/math]. Co łatwo sprawdzamy

[math]\displaystyle{ a_n = n^2 \gt N^2_0 = \left( \left\lfloor \sqrt{M} \right\rfloor + 1 \right)^2 \gt \left( \sqrt{M} \right)^2 = M }[/math]

Twierdzenie ZA16
Niech [math]\displaystyle{ c_n = a_n + i b_n }[/math] oraz [math]\displaystyle{ c = a + i b }[/math]. Ciąg [math]\displaystyle{ (c_n) }[/math] ma granicę [math]\displaystyle{ c }[/math] wtedy i tylko wtedy, gdy ciągi [math]\displaystyle{ (a_n) \; }[/math] i [math]\displaystyle{ \; (b_n) }[/math] mają granice [math]\displaystyle{ a }[/math] i [math]\displaystyle{ b }[/math].

Dowód

[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Z założenia ciąg [math]\displaystyle{ (c_n) }[/math] ma granicę równą [math]\displaystyle{ c }[/math], zatem z definicji granicy ciągu dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest [math]\displaystyle{ | c_n - c | \lt \varepsilon }[/math]. Korzystając z definicji modułu, otrzymujemy kolejno nierówności prawdziwe dla [math]\displaystyle{ n \gt N_0 }[/math]

[math]\displaystyle{ \sqrt{(a_n - a)^2 + (b_n - b)^2} \lt \varepsilon }[/math]

Tym bardziej

[math]\displaystyle{ \sqrt{(a_n - a)^2} \lt \varepsilon \qquad \qquad \text{oraz} \qquad \qquad \sqrt{(b_n - b)^2} \lt \varepsilon }[/math]

Czyli

[math]\displaystyle{ | a_n - a | \lt \varepsilon \qquad \qquad \text{oraz} \qquad \qquad | b_n - b | \lt \varepsilon }[/math]

Z definicji granicy otrzymujemy natychmiast, że

[math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = a \qquad \qquad \text{oraz} \qquad \qquad \lim_{n \rightarrow \infty} b_n = b }[/math].

[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Z założenia [math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = a }[/math] oraz [math]\displaystyle{ \lim_{n \rightarrow \infty} b_n = b }[/math]. Z definicji granicy ciągów [math]\displaystyle{ (a_n) }[/math] i [math]\displaystyle{ (b_n) }[/math] dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest [math]\displaystyle{ | a_n - a | \lt {\small\frac{\varepsilon}{2}} }[/math] oraz [math]\displaystyle{ | b_n - b | \lt \frac{\varepsilon}{2} }[/math]. Zatem dostajemy dla [math]\displaystyle{ n \gt N_0 }[/math]

[math]\displaystyle{ | c_n - c | = | (a_n - a) + i (b_n - b) | }[/math]

[math]\displaystyle{ \;\; \leqslant | a_n - a | + | i (b_n - b) | }[/math]

[math]\displaystyle{ \;\; \leqslant | a_n - a | + | b_n - b | }[/math]

[math]\displaystyle{ \;\; \lt {\small\frac{\varepsilon}{2}} + {\small\frac{\varepsilon}{2}} }[/math]

[math]\displaystyle{ \;\; = \varepsilon }[/math]

Z definicji granicy otrzymujemy natychmiast, że [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = c }[/math]. Co należało pokazać.
□

Definicja ZA17
Niech [math]\displaystyle{ n \in \mathbb{N}_0 }[/math]. Ciąg [math]\displaystyle{ (a_n) }[/math] liczb rzeczywistych będziemy nazywali

•      ciągiem rosnącym, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} \geqslant a_n }[/math]
•      ciągiem malejącym, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} \leqslant a_n }[/math]

Ciągi rosnące dzielimy na

•      ciągi silnie rosnące, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} \gt a_n }[/math]
•      ciągi słabo rosnące, jeżeli istnieją takie [math]\displaystyle{ n }[/math], że [math]\displaystyle{ a_{n + 1} = a_n }[/math]

Ciągi malejące dzielimy na

•      ciągi silnie malejące, jeżeli dla każdego [math]\displaystyle{ n }[/math] jest [math]\displaystyle{ a_{n + 1} \lt a_n }[/math]
•      ciągi słabo malejące, jeżeli istnieją takie [math]\displaystyle{ n }[/math], że [math]\displaystyle{ a_{n + 1} = a_n }[/math]

Zadanie ZA18
Jeżeli [math]\displaystyle{ (a_k) }[/math] jest malejącym ciągiem liczb rzeczywistych i [math]\displaystyle{ \lim_{k \rightarrow \infty} a_k = g }[/math], to [math]\displaystyle{ a_k \geqslant g }[/math] dla wszystkich wyrazów ciągu [math]\displaystyle{ (a_k) }[/math].

Jeżeli [math]\displaystyle{ (a_k) }[/math] jest silnie malejącym ciągiem liczb rzeczywistych i [math]\displaystyle{ \lim_{k \rightarrow \infty} a_k = g }[/math], to [math]\displaystyle{ a_k \gt g }[/math] dla wszystkich wyrazów ciągu [math]\displaystyle{ (a_k) }[/math].

Rozwiązanie

Punkt 1.

Przypuśćmy, że istnieje taki wyraz [math]\displaystyle{ a_m }[/math], że [math]\displaystyle{ a_m \lt g }[/math]. Wybierzmy liczby [math]\displaystyle{ r \; }[/math] i [math]\displaystyle{ \; \varepsilon }[/math] tak, aby [math]\displaystyle{ a_m \lt r \lt g \; }[/math] i [math]\displaystyle{ \; \varepsilon = g - r \gt 0 }[/math]. Zatem istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest

[math]\displaystyle{ | a_n - g | \lt \varepsilon }[/math]

Czyli

[math]\displaystyle{ - \varepsilon \lt a_n - g \lt \varepsilon }[/math]

[math]\displaystyle{ g - \varepsilon \lt a_n \lt \varepsilon + g }[/math]

Z lewej nierówności wynika, że

[math]\displaystyle{ a_n \gt g - \varepsilon = r \gt a_m }[/math]

Ponieważ wskaźnik [math]\displaystyle{ m }[/math] był liczbą ustaloną, a [math]\displaystyle{ n \gt N_0 }[/math] może być dowolnie duże, to istnieje takie [math]\displaystyle{ n \gt m }[/math], że [math]\displaystyle{ a_n \gt a_m }[/math], wbrew założeniu, że ciąg [math]\displaystyle{ (a_k) }[/math] jest ciągiem malejącym.

Punkt 2.

Przypuśćmy, że istnieje taki wyraz [math]\displaystyle{ a_m }[/math], że [math]\displaystyle{ a_m \leqslant g }[/math]. Jeżeli [math]\displaystyle{ a_m \lt g }[/math], to postępujemy tak jak wyżej i otrzymujemy, że istnieje takie [math]\displaystyle{ n \gt m }[/math], że [math]\displaystyle{ a_n \gt a_m }[/math], wbrew założeniu, że ciąg [math]\displaystyle{ (a_k) }[/math] jest ciągiem silnie malejącym.

Rozważmy przypadek, gdy [math]\displaystyle{ a_m = g }[/math]. Ponieważ ciąg [math]\displaystyle{ (a_k) }[/math] jest z założenia ciągiem silnie malejącym, to [math]\displaystyle{ a_{m + 1} \lt a_m = g }[/math]. Powtarzając rozumowanie z punktu 1. dla wyrazu [math]\displaystyle{ a_{m + 1} }[/math], otrzymujemy, że istnieje takie [math]\displaystyle{ n \gt m + 1 }[/math], że [math]\displaystyle{ a_n \gt a_{m + 1} }[/math], wbrew założeniu, że ciąg [math]\displaystyle{ (a_k) }[/math] jest ciągiem silnie malejącym.
□

Zadanie ZA19
Niech [math]\displaystyle{ c_n \in \mathbb{C} }[/math]. Pokazać, że

●      [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = c \qquad \qquad \Longleftrightarrow \qquad \qquad \lim_{n \rightarrow \infty} (c_n - c) = 0 \qquad \qquad \Longleftrightarrow \qquad \qquad \lim_{n \rightarrow \infty} | c_n - c | = 0 }[/math]

●      [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = 0 \qquad \qquad \Longleftrightarrow \qquad \qquad \lim_{n \rightarrow \infty} | c_n | = 0 }[/math]

●      [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = c \qquad \qquad \: \Longrightarrow \qquad \qquad \lim_{n \rightarrow \infty} | c_n | = | c | }[/math]

Rozwiązanie

Punkt 1.

Z definicji granicy ciąg [math]\displaystyle{ (c_n) }[/math] jest zbieżny do [math]\displaystyle{ c }[/math], jeżeli dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] wyrazy ciągu [math]\displaystyle{ (c_n) }[/math] spełniają warunek [math]\displaystyle{ | c_n - c | \lt \varepsilon }[/math]. Warunek ten możemy w sposób równoważny zapisać w postaci [math]\displaystyle{ | (c_n - c) - 0 | \lt \varepsilon \; }[/math] lub [math]\displaystyle{ \; | | c_n - c | - 0 | \lt \varepsilon }[/math]. Skąd natychmiast wynika wypisany ciąg równoważności.

Punkt 2.

Jest to jedynie szczególny przypadek punktu 1. dla [math]\displaystyle{ c = 0 }[/math].

Punkt 3.

Z założenia ciąg [math]\displaystyle{ (c_n) }[/math] jest zbieżny do [math]\displaystyle{ c }[/math], czyli dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] wyrazy ciągu [math]\displaystyle{ (c_n) }[/math] spełniają warunek [math]\displaystyle{ | c_n - c | \lt \varepsilon }[/math].

Wiemy, że dla dowolnych liczb zespolonych [math]\displaystyle{ z_1 \, }[/math] i [math]\displaystyle{ \, z_2 }[/math] prawdziwa jest nierówność (zobacz ZA4 p. 8)

[math]\displaystyle{ | | z_1 | - | z_2 | | \leqslant | z_1 - z_2 | }[/math]

Zatem dla [math]\displaystyle{ n \gt N_0 }[/math] wyrazy ciągu [math]\displaystyle{ (c_n) }[/math] spełniają warunek [math]\displaystyle{ | | c_n | - | c | | \lt \varepsilon }[/math]. Wynika stąd, że [math]\displaystyle{ \lim_{n \rightarrow \infty} | c_n | = | c | }[/math].
□

Definicja ZA20
Powiemy, że ciąg [math]\displaystyle{ (c_n) }[/math] liczb zespolonych jest ograniczony, jeżeli istnieje taka liczba rzeczywista [math]\displaystyle{ M }[/math], że [math]\displaystyle{ | c_n | \leqslant M }[/math] dla wszystkich [math]\displaystyle{ n \geqslant 0 }[/math].

Twierdzenie ZA21
Jeżeli ciąg [math]\displaystyle{ (c_n) }[/math] liczb zespolonych jest zbieżny, to jest ograniczony.

Dowód

Z założenia ciąg [math]\displaystyle{ (c_n) }[/math] jest zbieżny. Z definicji granicy dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] wyrazy ciągu [math]\displaystyle{ (c_n) }[/math] spełniają warunek [math]\displaystyle{ | c_n - c | \lt \varepsilon }[/math]. Zatem dla [math]\displaystyle{ n \gt N_0 }[/math] jest

[math]\displaystyle{ | | c_n | - | c | | \leqslant | c_n - c | \lt \varepsilon }[/math]

Czyli

[math]\displaystyle{ - \varepsilon \lt | c_n | - | c | \lt \varepsilon }[/math]

[math]\displaystyle{ | c_n | \lt | c | + \varepsilon }[/math]

Wynika stąd, że dla [math]\displaystyle{ n \geqslant 1 }[/math] jest

[math]\displaystyle{ | c_n | \lt M }[/math]

gdzie [math]\displaystyle{ M = \max (| c_1 |, \ldots, | c_{N_0} |, | c | + \varepsilon) }[/math]. Co należało pokazać.
□

Twierdzenie ZA22 (twierdzenie o trzech ciągach)
Niech [math]\displaystyle{ (x_n) }[/math] będzie ciągiem liczb rzeczywistych. Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] jest spełniony warunek

[math]\displaystyle{ a_n \leqslant x_n \leqslant b_n }[/math]

oraz

[math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = \lim_{n \rightarrow \infty} b_n = g }[/math]

to [math]\displaystyle{ \lim_{n \rightarrow \infty} x_n = g }[/math].

Dowód

Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Z definicji zbieżności ciągów [math]\displaystyle{ (a_n) \, }[/math] i [math]\displaystyle{ \, (b_n) }[/math] wynika, że dla ustalonego [math]\displaystyle{ \varepsilon }[/math] istnieją takie liczby [math]\displaystyle{ N_a \, }[/math] i [math]\displaystyle{ \, N_b }[/math], że

[math]\displaystyle{ | a_n - g | \lt \varepsilon \qquad \qquad \text{dla} \;\; n \gt N_a }[/math]

[math]\displaystyle{ | b_n - g | \lt \varepsilon \qquad \qquad \text{dla} \;\; n \gt N_b }[/math]

Czyli

[math]\displaystyle{ g - \varepsilon \lt a_n \lt g + \varepsilon \qquad \qquad \text{dla} \;\; n \gt N_a }[/math]

[math]\displaystyle{ g - \varepsilon \lt b_n \lt g + \varepsilon \qquad \qquad \text{dla} \;\; n \gt N_b }[/math]

Z założenia nierówność [math]\displaystyle{ a_n \leqslant x_n \leqslant b_n }[/math] jest spełniona dla [math]\displaystyle{ n \gt N_0 }[/math]. Niech [math]\displaystyle{ N_1 = \max (N_0, N_a, N_b) }[/math]. Zatem dla [math]\displaystyle{ n \gt N_1 }[/math] spełnione są jednocześnie nierówności

•     [math]\displaystyle{ g - \varepsilon \lt a_n \lt g + \varepsilon }[/math]

•     [math]\displaystyle{ g - \varepsilon \lt b_n \lt g + \varepsilon }[/math]

•     [math]\displaystyle{ a_n \leqslant x_n \leqslant b_n }[/math]

Z powyższych nierówności wynika natychmiast następujący ciąg nierówności

[math]\displaystyle{ g - \varepsilon \lt a_n \leqslant x_n \leqslant b_n \lt g + \varepsilon }[/math]

Co oznacza, że dla [math]\displaystyle{ n \gt N_1 }[/math] zachodzi

[math]\displaystyle{ g - \varepsilon \lt x_n \lt g + \varepsilon }[/math]

Czyli [math]\displaystyle{ | x_n - g | \lt \varepsilon }[/math], co oznacza, że ciąg [math]\displaystyle{ (x_n) }[/math] jest zbieżny i [math]\displaystyle{ \lim_{n \rightarrow \infty} x_n = g }[/math]. Co należało pokazać.
□

Twierdzenie ZA23
Niech [math]\displaystyle{ c \in \mathbb{C} }[/math] będzie pewną stałą zespoloną. Jeżeli ciągi [math]\displaystyle{ (w_n) \, }[/math] i [math]\displaystyle{ \, (z_n) }[/math] liczb zespolonych są zbieżne oraz [math]\displaystyle{ \lim_{n \rightarrow + \infty} w_n = w \; }[/math] i [math]\displaystyle{ \; \lim_{n \rightarrow \infty} z_n = z }[/math], to

●      [math]\displaystyle{ \lim_{n \rightarrow \infty} (c w_n) = c w }[/math]

●      [math]\displaystyle{ \lim_{n \rightarrow \infty} (w_n \pm z_n) = w \pm z }[/math]

●      [math]\displaystyle{ \lim_{n \rightarrow \infty} (w_n \cdot z_n) = w \cdot z }[/math]

Jeżeli dodatkowo [math]\displaystyle{ z_n \neq 0 }[/math] dla wszystkich [math]\displaystyle{ n \geqslant 1 \; }[/math] i [math]\displaystyle{ \; z \neq 0 }[/math], to

●      [math]\displaystyle{ \lim_{n \rightarrow \infty} {\small\frac{w_n}{z_n}} = {\small\frac{w}{z}} }[/math]

Dowód

Punkt 1.

Jeżeli [math]\displaystyle{ c = 0 }[/math], to ciąg [math]\displaystyle{ (c w_n) }[/math] składa się z samych zer i ma granicę równą zero – twierdzenie jest prawdziwe. Możemy zatem założyć, że [math]\displaystyle{ c \neq 0 }[/math]. Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Z definicji granicy ciągu [math]\displaystyle{ (w_n) }[/math] wynika, że istnieje liczba [math]\displaystyle{ N_0 }[/math] taka, że dla [math]\displaystyle{ n \gt N_0 }[/math]

[math]\displaystyle{ | w_n - w | \lt {\small\frac{\varepsilon}{| c |}} }[/math]

Zatem dla [math]\displaystyle{ n \gt N_0 }[/math] mamy

[math]\displaystyle{ | (c w_n) - (c w) | = | c | | w_n - w | \lt \varepsilon }[/math]

Co należało pokazać.

Punkt 2.

Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Z definicji granic ciągów [math]\displaystyle{ (w_n) \, }[/math] i [math]\displaystyle{ \, (z_n) }[/math] wynika, że istnieją liczby [math]\displaystyle{ N_1 \, }[/math] i [math]\displaystyle{ \, N_2 }[/math] takie, że

[math]\displaystyle{ | w_n - w | \lt {\small\frac{\varepsilon}{2}} \qquad \qquad \text{dla} \;\; n \gt N_1 }[/math]

[math]\displaystyle{ | z_n - z | \lt {\small\frac{\varepsilon}{2}} \qquad \qquad \text{dla} \;\; n \gt N_2 }[/math]

Niech [math]\displaystyle{ N_0 = \max (N_1, N_2) }[/math]. Zatem dla [math]\displaystyle{ n \gt N_0 }[/math] jest

[math]\displaystyle{ | (w_n + z_n) - (w + z) | = | (w_n - w) + (z_n - z) | \leqslant | w_n - w | + | z_n - z | = {\small\frac{\varepsilon}{2}} + {\small\frac{\varepsilon}{2}} = \varepsilon }[/math]

Wynika stąd, że ciąg [math]\displaystyle{ (w_n + z_n) }[/math] jest zbieżny do granicy [math]\displaystyle{ w + z }[/math]. Z punktu 1. wynika natychmiast, że ciąg [math]\displaystyle{ (- z_n) }[/math] jest zbieżny do granicy [math]\displaystyle{ - z }[/math]. Zatem ciąg [math]\displaystyle{ (w_n - z_n) }[/math] jest zbieżny do granicy [math]\displaystyle{ w - z }[/math].

Punkt 3.

Rozpoczniemy od dowodu prostszego przypadku i pokażemy, że iloczyn ciągów [math]\displaystyle{ (a_n) \, }[/math] i [math]\displaystyle{ \, (b_n) }[/math] zbieżnych do zera jest zbieżny do zera. Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Z definicji granic ciągów [math]\displaystyle{ (a_n) \, }[/math] i [math]\displaystyle{ \, (b_n) }[/math] wynika, że dla ustalonego [math]\displaystyle{ \varepsilon }[/math] istnieją liczby [math]\displaystyle{ N_1 \, }[/math] i [math]\displaystyle{ \, N_2 }[/math] takie, że

[math]\displaystyle{ | a_n | \lt \sqrt{\varepsilon} \qquad \qquad \text{dla} \;\; n \gt N_1 }[/math]

[math]\displaystyle{ | b_n | \lt \sqrt{\varepsilon} \qquad \qquad \text{dla} \;\; n \gt N_2 }[/math]

Niech [math]\displaystyle{ N_0 = \max (N_1, N_2) }[/math]. Zatem dla [math]\displaystyle{ n \gt N_0 }[/math] jest

[math]\displaystyle{ | a_n b_n | = | a_n | \cdot | b_n | \lt \varepsilon }[/math]

Wynika stąd, że [math]\displaystyle{ \lim_{n \rightarrow \infty} (w_n \cdot z_n) = w \cdot z \; }[/math] w przypadku, gdy obydwa ciągi są zbieżne do zera.

Dowodząc przypadek ogólny, wykorzystamy fakt, że [math]\displaystyle{ \lim_{n \rightarrow \infty} (w_n - w) = 0 \; }[/math] i [math]\displaystyle{ \; \lim_{n \rightarrow \infty} (z_n - z) = 0 }[/math]. Zatem

[math]\displaystyle{ 0 = \lim_{n \rightarrow \infty} ((w_n - w) (z_n - z)) }[/math]

[math]\displaystyle{ \;\:\: = \lim_{n \rightarrow \infty} (w_n z_n - w_n z - w z_n + w z) }[/math]

[math]\displaystyle{ \;\:\: = \lim_{n \rightarrow \infty} (w_n z_n) - \lim_{n \rightarrow \infty} (w_n z) - \lim_{n \rightarrow \infty} (w z_n) + \lim_{n \rightarrow \infty} (w z) }[/math]

[math]\displaystyle{ \;\:\: = \lim_{n \rightarrow \infty} (w_n z_n) - z \lim_{n \rightarrow \infty} (w_n) - w \lim_{n \rightarrow \infty} (z_n) + w z }[/math]

[math]\displaystyle{ \;\:\: = \lim_{n \rightarrow \infty} (w_n z_n) - w z }[/math]

Co kończy dowód.

Punkt 4.

Dla dowodu wystarczy pokazać, że [math]\displaystyle{ \lim_{n \rightarrow \infty} {\small\frac{1}{z_n}} = {\small\frac{1}{z}} }[/math]. Z definicji granicy ciągu [math]\displaystyle{ (z_n) }[/math] wiemy, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math], zatem w szczególności dla [math]\displaystyle{ \varepsilon = {\small\frac{1}{2}} | z | }[/math], istnieje takie [math]\displaystyle{ N_1 }[/math], że dla każdego [math]\displaystyle{ n \gt N_1 }[/math] jest

[math]\displaystyle{ | z_n - z | \lt {\small\frac{1}{2}} | z | }[/math]

Ponieważ [math]\displaystyle{ | z_n - z | \geqslant | | z_n | - | z | | }[/math], to

[math]\displaystyle{ | | z_n | - | z | | \lt {\small\frac{1}{2}} | z | }[/math]

Czyli

[math]\displaystyle{ - {\small\frac{1}{2}} | z | \lt | z_n | - | z | \lt {\small\frac{1}{2}} | z | }[/math]

[math]\displaystyle{ \;\;\: {\small\frac{1}{2}} | z | \lt | z_n | \lt {\small\frac{3}{2}} | z | }[/math]

Z lewej nierówności wynika, że dla każdego [math]\displaystyle{ n \gt N_1 }[/math] mamy

[math]\displaystyle{ {\small\frac{1}{| z_n |}} \lt {\small\frac{2}{| z |}} }[/math]

Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Z definicji granicy ciągu [math]\displaystyle{ (z_n) }[/math] wynika, że istnieje liczba [math]\displaystyle{ N_2 }[/math] taka, że dla każdego [math]\displaystyle{ n \gt N_2 }[/math] jest

[math]\displaystyle{ | z_n - z | \lt {\small\frac{1}{2}} | z |^2 \cdot \varepsilon }[/math]

Niech [math]\displaystyle{ N_0 = \max (N_1, N_2) }[/math]. Zatem dla [math]\displaystyle{ n \gt N_0 }[/math] jest

[math]\displaystyle{ \left| {\small\frac{1}{z_n}} - {\small\frac{1}{z}} \right| = \left| {\small\frac{z - z_n}{z_n z}} \right| = {\small\frac{| z_n - z |}{| z_n | | z |}} \lt {\small\frac{1}{2}} | z |^2 \cdot \varepsilon \cdot {\small\frac{2}{| z |}} \cdot {\small\frac{1}{| z |}} = \varepsilon }[/math]

Co kończy dowód.
□

Twierdzenie ZA24
Jeżeli [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = 0 }[/math], zaś ciąg [math]\displaystyle{ (z_n) }[/math] jest ograniczony, to [math]\displaystyle{ \lim_{n \rightarrow \infty} (z_n \cdot c_n) = 0 }[/math].

Dowód

Wystarczy pokazać, że (zobacz ZA19 p. 2)

[math]\displaystyle{ \lim_{n \rightarrow \infty} | z_n \cdot c_n | = 0 }[/math]

Z założenia ciąg [math]\displaystyle{ (z_n) }[/math] jest ograniczony, czyli istnieje taka liczba [math]\displaystyle{ M \gt 0 }[/math], że [math]\displaystyle{ | z_n | \leqslant M }[/math]. Zatem prawdziwe jest oszacowanie

[math]\displaystyle{ 0 \leqslant | z_n \cdot c_n | \leqslant | c_n | \cdot M }[/math]

Z twierdzenia o trzech ciągach otrzymujemy natychmiast, że

[math]\displaystyle{ \lim_{n \rightarrow \infty} | z_n \cdot c_n | = 0 }[/math]

Co kończy dowód.
□

Zadanie ZA25
Niech [math]\displaystyle{ x \in \mathbb{R} }[/math]. Pokazać, że [math]\displaystyle{ \lim_{n \rightarrow \infty} x^n = 0 }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ | x | \lt 1 }[/math].

Rozwiązanie

Zauważmy, że [math]\displaystyle{ \lim_{n \rightarrow \infty} 0^n = 0 \; }[/math] i [math]\displaystyle{ \; \lim_{n \rightarrow \infty} 1^n = 1 }[/math]. Mamy [math]\displaystyle{ (- 1)^{2 k} = + 1 \; }[/math] i [math]\displaystyle{ \; (- 1)^{2 k + 1} = - 1 }[/math], zatem granica [math]\displaystyle{ \lim_{n \rightarrow \infty} (- 1)^n }[/math] nie istnieje.

1. Przypadek, gdy [math]\displaystyle{ \boldsymbol{x \gt 1} }[/math]

[math]\displaystyle{ x^n = [1 + (x - 1)]^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} (x - 1)^k \gt n (x - 1) }[/math]

Ponieważ [math]\displaystyle{ x^n \gt n (x - 1) }[/math], to [math]\displaystyle{ \lim_{n \rightarrow \infty} x^n = + \infty }[/math].

2. Przypadek, gdy [math]\displaystyle{ \boldsymbol{0 \lt x \lt 1} }[/math]

Ponieważ [math]\displaystyle{ {\small\frac{1}{x}} \gt 1 }[/math], to możemy ponownie zastosować wzór z punktu 1.

[math]\displaystyle{ \left( {\small\frac{1}{x}} \right)^n = {\small\frac{1}{x^n}} \gt n \left( {\small\frac{1}{x}} - 1 \right) }[/math]

Czyli

[math]\displaystyle{ 0 \lt x^n \lt {\small\frac{1}{n}} \cdot {\small\frac{x}{1 - x}} }[/math]

Zatem z twierdzenia o trzech ciągach [math]\displaystyle{ \lim_{n \rightarrow \infty} x^n = 0 }[/math].

3. Przypadek, gdy [math]\displaystyle{ \boldsymbol{- 1 \lt x \lt 0} }[/math]

Mamy

[math]\displaystyle{ \lim_{n \rightarrow \infty} x^n = \lim_{n \rightarrow \infty} (- | x |)^n = \lim_{n \rightarrow \infty} ((- 1)^n | x |^n) = 0 }[/math]

Bo [math]\displaystyle{ \lim_{n \rightarrow \infty} | x |^n = 0 }[/math], a ciąg [math]\displaystyle{ (- 1)^n }[/math] jest ciągiem ograniczonym (zobacz ZA24).

4. Przypadek, gdy [math]\displaystyle{ \boldsymbol{x \lt - 1} }[/math]

Ponieważ [math]\displaystyle{ x = - | x | \; }[/math] i [math]\displaystyle{ \; \lim_{n \rightarrow \infty} | x |^n = + \infty }[/math], to ciąg [math]\displaystyle{ (x^n) }[/math] jest w tym przypadku rozbieżny. Dla parzystych [math]\displaystyle{ n }[/math] dąży do plus nieskończoności, a dla nieparzystych [math]\displaystyle{ n }[/math] dąży do minus nieskończoności.
□

Twierdzenie ZA26
Niech [math]\displaystyle{ z \in \mathbb{C} }[/math]. Granica [math]\displaystyle{ \lim_{n \rightarrow \infty} z^n = 0 }[/math] wtedy i tylko wtedy, gdy [math]\displaystyle{ | z | \lt 1 }[/math].

Dowód

Niech [math]\displaystyle{ \varphi = \operatorname{Arg}(z) }[/math]. Mamy [math]\displaystyle{ z = | z | (\cos \varphi + i \sin \varphi) }[/math], zatem

[math]\displaystyle{ z^n = | z |^n (\cos n \varphi + i \sin n \varphi) }[/math]

Ponieważ [math]\displaystyle{ \cos n \varphi }[/math] oraz [math]\displaystyle{ \sin n \varphi }[/math] nie mogą być jednocześnie równe zero (bo mielibyśmy wtedy [math]\displaystyle{ \cos^2 \! n \varphi + \sin^2 \! n \varphi = 0 }[/math]), to [math]\displaystyle{ | z |^n (\cos n \varphi + i \sin n \varphi) }[/math] dąży do zera wtedy i tylko wtedy, gdy [math]\displaystyle{ | z |^n }[/math] dąży do zera, czyli wtedy i tylko wtedy, gdy [math]\displaystyle{ | z | \lt 1 }[/math]. Co należało pokazać.
□

Zadanie ZA27
Niech [math]\displaystyle{ a \in \mathbb{R}_+ }[/math]. Pokazać, że [math]\displaystyle{ \lim_{n \rightarrow \infty} a^{1 / n} = 1 }[/math].

Rozwiązanie

1. Przypadek, gdy [math]\displaystyle{ \boldsymbol{a \gt 1} }[/math]

Niech [math]\displaystyle{ a^{1 / n} = 1 + d_n }[/math]. Ze wzoru dwumianowego dostajemy

[math]\displaystyle{ a = (1 + d_n)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} (d_n)^k \gt n d_n }[/math]

Zatem

[math]\displaystyle{ 0 \lt d_n \lt {\small\frac{a}{n}} }[/math]

Z twierdzenia o trzech ciągach otrzymujemy natychmiast [math]\displaystyle{ \lim_{n \rightarrow \infty} d_n = 0 }[/math], czyli [math]\displaystyle{ \lim_{n \rightarrow \infty} a^{1 / n} = 1 }[/math].

2. Przypadek, gdy [math]\displaystyle{ \boldsymbol{0 \lt a \lt 1} }[/math]

Ponieważ [math]\displaystyle{ {\small\frac{1}{a}} \gt 1 }[/math], to na podstawie punktu 1. dostajemy

[math]\displaystyle{ 1 = \lim_{n \rightarrow \infty} \left( {\small\frac{1}{a}} \right)^{1 / n} = \lim_{n \rightarrow \infty} {\small\frac{1}{a^{1 / n}}} = \frac{1}{\underset{n \rightarrow \infty}{\lim} a^{1 / n}} }[/math]

Czyli [math]\displaystyle{ \lim_{n \rightarrow \infty} a^{1 / n} = 1 }[/math]. Co należało pokazać.
□

Zadanie ZA28
Niech [math]\displaystyle{ z \in \mathbb{C} }[/math]. Pokazać, że [math]\displaystyle{ \lim_{n \rightarrow \infty} z^{1 / n} = 1 }[/math] pod warunkiem, że [math]\displaystyle{ z^{1 / n} }[/math] jest pierwiastkiem głównym [math]\displaystyle{ n }[/math]-tego stopnia z liczby [math]\displaystyle{ z }[/math].

Rozwiązanie

Wszystkie pierwiastki, których nieujemny argument główny jest najmniejszy, są określone wzorem (zobacz ZA7)

[math]\displaystyle{ z^{1 / n} = | z |^{1 / n} \left( \cos {\small\frac{\varphi + 2 k \pi}{n}} + i \sin {\small\frac{\varphi + 2 k \pi}{n}} \right) }[/math]

gdzie [math]\displaystyle{ \varphi = \operatorname{Arg}(z) \; }[/math] i [math]\displaystyle{ \; k = 0, 1, \ldots, n - 1 }[/math]. Pierwiastek główny otrzymujemy dla [math]\displaystyle{ k = 0 }[/math], czyli

[math]\displaystyle{ z^{1 / n} = | z |^{1 / n} \left( \cos {\small\frac{\varphi}{n}} + i \sin {\small\frac{\varphi}{n}} \right) }[/math]

I łatwo zauważamy, że

[math]\displaystyle{ \lim_{n \rightarrow \infty} z^{1 / n} = \lim_{n \rightarrow \infty} \left[ | z |^{1 / n} \left( \cos {\small\frac{\varphi}{n}} + i \sin {\small\frac{\varphi}{n}} \right) \right] = \left( \lim_{n \rightarrow \infty} | z |^{1 / n} \right) \cdot \left[ \left( \lim_{n \rightarrow \infty} \cos {\small\frac{\varphi}{n}} \right) + i \cdot \left( \lim_{n \rightarrow \infty} \sin {\small\frac{\varphi}{n}} \right) \right] = 1 }[/math]

□

Zadanie ZA29
Pokazać, że [math]\displaystyle{ \lim_{n \rightarrow \infty} n^{1 / n} = 1 }[/math].

Rozwiązanie

Niech [math]\displaystyle{ n^{1 / n} = 1 + d_n }[/math]. Ze wzoru dwumianowego dostajemy

[math]\displaystyle{ n = (1 + d_n)^n = \sum_{k = 0}^{n} {\small\binom{n}{k}} (d_n)^k \gt {\small\frac{n (n - 1)}{2}} \cdot (d_n)^2 }[/math]

Zatem

[math]\displaystyle{ 0 \lt d_n \lt \sqrt{{\small\frac{2}{n - 1}}} }[/math]

Z twierdzenia o trzech ciągach otrzymujemy natychmiast, że [math]\displaystyle{ \lim_{n \rightarrow \infty} d_n = 0 }[/math], skąd wynika, że [math]\displaystyle{ \lim_{n \rightarrow \infty} n^{1 / n} = 1 }[/math].
□

Zadanie ZA30
Pokazać, że [math]\displaystyle{ \lim_{n \rightarrow \infty} (n!)^{1 / n} = + \infty }[/math].

Rozwiązanie

Zauważmy, że

[math]\displaystyle{ (n!)^2 = [1 \cdot 2 \cdot 3 \cdot \ldots (n - 1) \cdot n] \cdot [1 \cdot 2 \cdot 3 \cdot \ldots (n - 1) \cdot n] }[/math]

[math]\displaystyle{ \;\;\:\, = [1 \cdot n] \cdot [2 \cdot (n - 1)] \cdot [3 \cdot (n - 2)] \cdot \ldots \cdot [(n - 1) \cdot 2] \cdot [n \cdot 1] }[/math]

[math]\displaystyle{ \;\;\:\, = \prod^n_{k = 1} k \cdot (n - k + 1) }[/math]

Łatwo widzimy, że dla [math]\displaystyle{ k = 1, 2, 3, \ldots, n - 1, n }[/math] prawdziwa jest nierówność [math]\displaystyle{ k \cdot (n - k + 1) \geqslant n }[/math], bo w równoważnej nierówności [math]\displaystyle{ (k - 1) (n - k) \geqslant 0 }[/math] obydwa czynniki są nieujemne. Zatem [math]\displaystyle{ (n!)^2 \geqslant n^n }[/math], czyli [math]\displaystyle{ n! \geqslant \sqrt{n^n} \; }[/math] i [math]\displaystyle{ \; (n!)^{1 / n} \geqslant \sqrt{n} }[/math]. Wynika stąd, że [math]\displaystyle{ \lim_{n \rightarrow \infty} \sqrt[n]{n!} = + \infty }[/math].
□

Podciągi, punkty skupienia, granica dolna i górna

Definicja ZA31
Jeżeli [math]\displaystyle{ (c_k) }[/math] jest ciągiem nieskończonym liczb zespolonych i [math]\displaystyle{ \left( {k_j} \right) }[/math] jest silnie rosnącym ciągiem nieskończonym liczb naturalnych, to powiemy, że ciąg [math]\displaystyle{ (c_{k_j}) }[/math] jest nieskończonym podciągiem ciągu [math]\displaystyle{ (c_k) }[/math].

Przykład ZA32
Ciąg [math]\displaystyle{ (c_{2 k}) }[/math], czyli ciąg postaci [math]\displaystyle{ c_2, c_4, c_6 \ldots }[/math] i ciąg [math]\displaystyle{ (c_{2^k}) }[/math], czyli ciąg postaci [math]\displaystyle{ c_2, c_4, c_8 \ldots }[/math] są podciągami ciągu [math]\displaystyle{ (c_k) }[/math]. Ciąg [math]\displaystyle{ c_2, c_8, c_4, c_{32}, c_{16}, \ldots }[/math] nie jest podciągiem, bo kolejne wskaźniki nie tworzą ciągu silnie rosnącego.

Pociągami ciągu [math]\displaystyle{ c_n = (- 1)^n }[/math] są ciągi [math]\displaystyle{ (1, 1, 1, \ldots) \; }[/math] i [math]\displaystyle{ \; (- 1, - 1, - 1, \ldots) }[/math]. Widzimy, że ciąg, który nie jest zbieżny, ma zbieżne podciągi. Oczywiście każdy podciąg ciągu zbieżnego jest ciągiem zbieżnym.

Definicja ZA33
Powiemy, że liczba [math]\displaystyle{ c }[/math] jest punktem skupienia ciągu liczb zespolonych [math]\displaystyle{ (c_k) }[/math], gdy istnieje podciąg ciągu [math]\displaystyle{ (c_k) }[/math] zbieżny do [math]\displaystyle{ c }[/math].
Powiemy, że [math]\displaystyle{ + \infty }[/math] jest punktem skupienia ciągu liczb rzeczywistych [math]\displaystyle{ (a_k) }[/math], gdy istnieje podciąg ciągu [math]\displaystyle{ (a_k) }[/math] rozbieżny do [math]\displaystyle{ + \infty }[/math].
Powiemy, że [math]\displaystyle{ - \infty }[/math] jest punktem skupienia ciągu liczb rzeczywistych [math]\displaystyle{ (a_k) }[/math], gdy istnieje podciąg ciągu [math]\displaystyle{ (a_k) }[/math] rozbieżny do [math]\displaystyle{ - \infty }[/math].

Przykład ZA34
Punktami skupienia ciągu [math]\displaystyle{ a_k = (- 1)^k }[/math] są liczby [math]\displaystyle{ - 1 }[/math] i [math]\displaystyle{ 1 }[/math]. Punktami skupienia ciągu [math]\displaystyle{ c_k = i^k }[/math] są liczby [math]\displaystyle{ 1, - 1, i, - i }[/math]. Punktami skupienia ciągu [math]\displaystyle{ a_k = k \cdot (- 1)^k }[/math] są [math]\displaystyle{ - \infty }[/math] i [math]\displaystyle{ + \infty }[/math].

W ogólności: jeżeli ciąg [math]\displaystyle{ (c_k) }[/math] zawiera nieskończenie wiele jednakowych wyrazów [math]\displaystyle{ c }[/math], to oczywiście liczba [math]\displaystyle{ c }[/math] jest punktem skupienia tego ciągu, bo łatwo możemy wybrać podciąg ciągu [math]\displaystyle{ (c_k) }[/math] zbieżny do [math]\displaystyle{ c }[/math].

Twierdzenie ZA35
Niech [math]\displaystyle{ c \in \mathbb{C} }[/math]. Jeżeli dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] otoczenie [math]\displaystyle{ | z - c | \lt \varepsilon }[/math] zawiera przynajmniej jeden wyraz ciągu [math]\displaystyle{ (c_k) }[/math] różny od [math]\displaystyle{ c }[/math], to punkt [math]\displaystyle{ c }[/math] jest punktem skupienia ciągu [math]\displaystyle{ (c_k) }[/math].

Dowód

Z założenia otoczenie [math]\displaystyle{ | z - c | \lt \varepsilon }[/math] zawiera przynajmniej jeden wyraz ciągu [math]\displaystyle{ (c_k) }[/math] różny od [math]\displaystyle{ c }[/math]. Zauważmy, że w rzeczywistości otoczenie [math]\displaystyle{ | z - c | \lt \varepsilon }[/math] musi zawierać nieskończenie wiele wyrazów ciągu [math]\displaystyle{ (c_k) }[/math] różnych od [math]\displaystyle{ c }[/math]. Istotnie, gdyby w rozpatrywanym otoczeniu była tylko skończona liczba wyrazów ciągu [math]\displaystyle{ (c_k) }[/math] różnych od [math]\displaystyle{ c }[/math], to moglibyśmy wyznaczyć taką liczbę [math]\displaystyle{ \varepsilon' \gt 0 }[/math], że w otoczeniu [math]\displaystyle{ | z - c | \lt \varepsilon' }[/math] nie byłoby ani jednego wyrazu ciągu [math]\displaystyle{ (c_k) }[/math] różnego od [math]\displaystyle{ c }[/math] wbrew założeniu, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] otoczenie [math]\displaystyle{ | z - c | \lt \varepsilon }[/math] zawiera przynajmniej jeden wyraz ciągu [math]\displaystyle{ (c_k) }[/math] różny od [math]\displaystyle{ c }[/math].

Niech [math]\displaystyle{ j \in \mathbb{Z}_+ }[/math]. Z nieskończenie wielu wyrazów ciągu [math]\displaystyle{ (c_k) }[/math] różnych od [math]\displaystyle{ c }[/math] zawartych w otoczeniu [math]\displaystyle{ | z - c | \lt {\small\frac{1}{j}} }[/math] wybieramy dowolny wyraz następujący po już wybranych wyrazach [math]\displaystyle{ c_{k_1}, c_{k_2}, \ldots, c_{k_{j - 1}} }[/math]. Oznaczmy ten wyraz przez [math]\displaystyle{ c_{k_j} }[/math]. Postępując tak dla kolejnych liczb [math]\displaystyle{ j }[/math], otrzymujemy podciąg [math]\displaystyle{ (c_{k_j}) }[/math] zbieżny do [math]\displaystyle{ c }[/math]. Pokażemy zbieżność podciągu [math]\displaystyle{ (c_{k_j}) }[/math]. Dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] obierzmy [math]\displaystyle{ N_0 }[/math] tak, aby [math]\displaystyle{ {\small\frac{1}{N_0}} \lt \varepsilon }[/math]. Z konstrukcji ciągu [math]\displaystyle{ (c_{k_j}) }[/math] widzimy, że dla każdego [math]\displaystyle{ j \gt N_0 }[/math] jest [math]\displaystyle{ | c_{k_j} - c | \lt {\small\frac{1}{N_0}} \lt \varepsilon }[/math]. Co kończy dowód.

Zauważmy, że twierdzenie odwrotne nie jest prawdziwe. Punkt [math]\displaystyle{ 1 }[/math] jest punktem skupienia ciągu [math]\displaystyle{ a_n = (- 1)^n }[/math], ale nieprawdą jest, że dowolne otoczenie punktu [math]\displaystyle{ 1 }[/math] zawiera przynajmniej jeden wyraz ciągu [math]\displaystyle{ (a_k) }[/math] różny od [math]\displaystyle{ 1 }[/math].
□

Definicja ZA36 (granica dolna i górna)
Granicą górną ciągu liczb rzeczywistych [math]\displaystyle{ (a_k) }[/math], nazywamy największy z jego punktów skupienia i oznaczamy symbolem [math]\displaystyle{ \limsup_{k \rightarrow \infty} a_k }[/math].
Granicą dolną ciągu liczb rzeczywistych [math]\displaystyle{ (a_k) }[/math], nazywamy najmniejszy z jego punktów skupienia i oznaczamy symbolem [math]\displaystyle{ \liminf_{k \rightarrow \infty} a_k }[/math].

Twierdzenie ZA37
Ciąg liczb rzeczywistych [math]\displaystyle{ (a_k) }[/math] jest zbieżny wtedy i tylko wtedy, gdy granice górna i dolna są skończone i jednakowe.

Przykład ZA38
Granice dolna i górna ciągu [math]\displaystyle{ a_k = (- 1)^k }[/math] są odpowiednio równe [math]\displaystyle{ - 1 }[/math] i [math]\displaystyle{ 1 }[/math].

Twierdzenie Bolzana-Weierstrassa i ciągi Cauchy'ego w [math]\displaystyle{ \mathbb{R} }[/math]

Dwa ważne twierdzenia podamy bez dowodu.
Twierdzenie ZA39*
Niech [math]\displaystyle{ (a_k) }[/math] będzie ciągiem liczb rzeczywistych. Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ n }[/math] i rzeczywista [math]\displaystyle{ M }[/math], że dla każdego [math]\displaystyle{ k \gt n }[/math] jest

[math]\displaystyle{ a_{k + 1}\geqslant a_k \qquad }[/math] oraz [math]\displaystyle{ \qquad a_k \leqslant M }[/math]

to ciąg [math]\displaystyle{ (a_k) }[/math] jest zbieżny.
Inaczej mówiąc: ciąg liczb rzeczywistych rosnący i ograniczony od góry jest zbieżny.

Twierdzenie ZA40*
Niech [math]\displaystyle{ (a_k) }[/math] będzie ciągiem liczb rzeczywistych. Jeżeli istnieje taka liczba całkowita [math]\displaystyle{ n }[/math] i rzeczywista [math]\displaystyle{ M }[/math], że dla każdego [math]\displaystyle{ k \gt n }[/math] jest

[math]\displaystyle{ a_{k + 1} \leqslant a_k \qquad }[/math] oraz [math]\displaystyle{ \qquad a_k \geqslant M }[/math]

to ciąg [math]\displaystyle{ (a_k) }[/math] jest zbieżny.
Inaczej mówiąc: ciąg liczb rzeczywistych malejący i ograniczony od dołu jest zbieżny.

Twierdzenie ZA41 (o przedziałach zstępujących)
Niech będzie dany nieskończony ciąg przedziałów domkniętych [math]\displaystyle{ I_n = [a_n, b_n] \subset \mathbb{R} }[/math] takich, że [math]\displaystyle{ I_{n + 1} \subset I_n }[/math]. Jeżeli długości przedziałów [math]\displaystyle{ I_n }[/math] dążą do zera, gdy [math]\displaystyle{ n }[/math] dąży do nieskończoności, czyli

[math]\displaystyle{ \lim_{n \rightarrow \infty} | I_n | = \lim_{n \rightarrow \infty} (b_n - a_n) = 0 }[/math]

to

[math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = \lim_{n \rightarrow \infty} b_n = g }[/math]

Dowód

Zauważmy, że

•      ciąg [math]\displaystyle{ (a_n) }[/math] jest ciągiem ograniczonym od góry, bo [math]\displaystyle{ a_n \lt b_1 }[/math]

•      ciąg [math]\displaystyle{ (b_n) }[/math] jest ciągiem ograniczonym od dołu, bo [math]\displaystyle{ b_n \gt a_1 }[/math]

•      ponieważ [math]\displaystyle{ [a_{n + 1}, b_{n + 1}] \subset [a_n, b_n] }[/math], to ciąg [math]\displaystyle{ (a_n) }[/math] jest ciągiem rosnącym (zobacz ZA17)

•      ponieważ [math]\displaystyle{ [a_{n + 1}, b_{n + 1}] \subset [a_n, b_n] }[/math], to ciąg [math]\displaystyle{ (a_n) }[/math] jest ciągiem malejącym (zobacz ZA17)

Z twierdzeń ZA39 i ZA40 wynika natychmiast, że ciągi [math]\displaystyle{ (a_n) }[/math] i [math]\displaystyle{ (b_n) }[/math] są zbieżne. Niech

[math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = a \qquad \qquad \text{oraz} \qquad \qquad \lim_{n \rightarrow \infty} b_n = b }[/math]

Ponieważ ciągi [math]\displaystyle{ (a_n) \; }[/math] i [math]\displaystyle{ \; (b_n) }[/math] są zbieżne, to

[math]\displaystyle{ 0 = \lim_{n \rightarrow \infty} (b_n - a_n) = \lim_{n \rightarrow \infty} b_n - \lim_{n \rightarrow \infty} a_n = b - a }[/math]

Zatem [math]\displaystyle{ b = a }[/math]. Co należało pokazać.
□

Twierdzenie ZA42 (Bernard Bolzano, 1817; Karl Weierstrass)
Każdy ograniczony ciąg liczb rzeczywistych ma podciąg zbieżny.

Dowód

Niech [math]\displaystyle{ (u_k) }[/math] będzie rozpatrywanym ciągiem. Z założenia ciąg [math]\displaystyle{ (u_k) }[/math] jest ograniczony, zatem istnieją takie liczby rzeczywiste [math]\displaystyle{ a_0 }[/math] i [math]\displaystyle{ b_0 }[/math], że [math]\displaystyle{ a_0 \leqslant u_k \leqslant b_0 }[/math]. Zbudujemy ciąg przedziałów zstępujących [math]\displaystyle{ I_0 \supset I_1 \supset I_2 \supset I_3 \supset \ldots }[/math] i związany z nimi podciąg zbieżny ciągu [math]\displaystyle{ (u_k) }[/math] powtarzając następującą procedurę

1. przedział [math]\displaystyle{ I_n = [a_n, b_n] }[/math] dzielimy na połowy tworząc dwa podprzedziały [math]\displaystyle{ \left[ a_n, {\small\frac{a_n + b_n}{2}} \right] }[/math] oraz [math]\displaystyle{ \left[ {\small\frac{a_n + b_n}{2}}, b_n \right] }[/math]

2. z utworzonych podprzedziałów wybieramy ten, w którym jest nieskończenie wiele wyrazów ciągu [math]\displaystyle{ (u_k) }[/math]^[a]; wybór definiuje przedział [math]\displaystyle{ I_{n + 1} = [a_{n + 1}, b_{n + 1}] }[/math]

3. ze sposobu konstrukcji przedziału [math]\displaystyle{ I_{n + 1} }[/math] wynika natychmiast, że [math]\displaystyle{ | I_{n + 1} | = {\small\frac{| I_n |}{2}} }[/math]

4. dowolny wyraz ciągu [math]\displaystyle{ (u_k) }[/math] w przedziale [math]\displaystyle{ I_{n + 1} }[/math] (ale następujący po wcześniej wybranych wyrazach [math]\displaystyle{ u_{k_1}, u_{k_2}, \ldots, u_{k_n} }[/math]) będzie [math]\displaystyle{ n + 1 }[/math] wyrazem budowanego podciągu i oznaczymy go jako [math]\displaystyle{ u_{k_{n + 1}} }[/math]

Zauważmy, że

•     ciąg przedziałów [math]\displaystyle{ I_0, I_1, I_2, \ldots }[/math] jest ciągiem przedziałów zstępujących, bo z definicji [math]\displaystyle{ I_{n + 1} \subset I_n }[/math] oraz [math]\displaystyle{ | I_n | = {\small\frac{b_0 - a_0}{2^n}} }[/math], czyli długość przedziałów [math]\displaystyle{ I_n }[/math] dąży do zera

•     ciągi [math]\displaystyle{ (a_n) \, }[/math] i [math]\displaystyle{ \, (b_n) }[/math] są zbieżne do wspólnej granicy [math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = \lim_{n \rightarrow \infty} b_n = g \; }[/math] (zobacz ZA41)

•     ponieważ [math]\displaystyle{ a_n \leqslant u_{k_n} \leqslant b_n }[/math], to z twierdzenia o trzech ciągach (zobacz ZA22) wynika natychmiast, że [math]\displaystyle{ \lim_{n \rightarrow \infty} u_{k_n} = g }[/math]

---

[a] Gdyby w każdym z podprzedziałów było nieskończenie wiele wyrazów ciągu [math]\displaystyle{ (u_k) }[/math], to wybieramy dowolny z nich.
□

Definicja ZA43 (ciąg Cauchy'ego liczb rzeczywistych)
Powiemy, że ciąg [math]\displaystyle{ (a_n) }[/math] liczb rzeczywistych jest ciągiem Cauchy'ego, jeżeli dla dowolnej liczby rzeczywistej dodatniej [math]\displaystyle{ \varepsilon }[/math] istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że [math]\displaystyle{ | a_n - a_m | \lt \varepsilon }[/math] dla dowolnych liczb [math]\displaystyle{ m, n }[/math] spełniających warunek [math]\displaystyle{ n \gt N_0 }[/math] i [math]\displaystyle{ m \gt N_0 }[/math].

Twierdzenie ZA44
Każdy ciąg Cauchy'ego liczb rzeczywistych jest ograniczony.

Dowód

Niech [math]\displaystyle{ (a_k) }[/math] będzie ciągiem Cauchy'ego liczb rzeczywistych. Zatem dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka liczba [math]\displaystyle{ N_0 = N_0 ( \varepsilon ) }[/math], że dla wszystkich liczb [math]\displaystyle{ m, n \gt N_0 }[/math] jest

[math]\displaystyle{ | a_n - a_m | \lt \varepsilon }[/math]

Jeżeli położymy [math]\displaystyle{ m = N_0 + 1 \gt N_0 }[/math], to dla [math]\displaystyle{ n \gt N_0 }[/math] otrzymujemy oszacowanie

[math]\displaystyle{ | a_n - a_{N_0 + 1} | \lt \varepsilon }[/math]

[math]\displaystyle{ - \varepsilon \lt a_n - a_{N_0 + 1} \lt \varepsilon }[/math]

[math]\displaystyle{ a_{N_0 + 1} - \varepsilon \lt a_n \lt a_{N_0 + 1} + \varepsilon }[/math]

Wynika stąd, że dla każdego [math]\displaystyle{ n \geqslant 0 }[/math] jest

[math]\displaystyle{ m \leqslant a_n \leqslant M }[/math]

gdzie

[math]\displaystyle{ M = \max (a_0, a_1, a_2, \ldots, a_{N_0}, a_{N_0 + 1} + \varepsilon) }[/math]

[math]\displaystyle{ m = \min (a_0, a_1, a_2, \ldots, a_{N_0}, a_{N_0 + 1} - \varepsilon) }[/math]

Ponieważ [math]\displaystyle{ - | m | \leqslant m \; }[/math] i [math]\displaystyle{ \; M \leqslant | M | }[/math], to

[math]\displaystyle{ - | m | \leqslant a_n \leqslant | M | }[/math]

Jeżeli oznaczymy [math]\displaystyle{ U = \max (| m |, | M |) }[/math], to możemy napisać

[math]\displaystyle{ - U \leqslant a_n \leqslant U }[/math]

Czyli dla każdego [math]\displaystyle{ n \geqslant 0 }[/math] jest [math]\displaystyle{ | a_n | \leqslant U }[/math]. Co należało pokazać.
□

Twierdzenie ZA45
Ciąg [math]\displaystyle{ (a_k) }[/math] liczb rzeczywistych jest zbieżny wtedy i tylko wtedy, gdy jest ciągiem Cauchy'ego.

Dowód

[math]\displaystyle{ \Large{\Longrightarrow} }[/math]

Z założenia ciąg [math]\displaystyle{ (a_k) }[/math] jest zbieżny. Niech [math]\displaystyle{ \lim_{n \rightarrow \infty} a_n = a \; }[/math] i [math]\displaystyle{ \; \varepsilon \in \mathbb{R}_+ }[/math]. Istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że dla wszystkich liczb [math]\displaystyle{ m, n \gt N_0 }[/math] jest

[math]\displaystyle{ | a_m - a | \lt {\small\frac{\varepsilon}{2}} }[/math]

[math]\displaystyle{ | a_n - a | \lt {\small\frac{\varepsilon}{2}} }[/math]

Zatem

[math]\displaystyle{ | a_n - a_m | = | (a_n - a) - (a_m - a) | \leqslant | a_n - a | + | a_m - a | \lt {\small\frac{\varepsilon}{2}} + {\small\frac{\varepsilon}{2}} = \varepsilon }[/math]

Czyli [math]\displaystyle{ (a_k) }[/math] jest ciągiem Cauchy'ego.

[math]\displaystyle{ \Large{\Longleftarrow} }[/math]

Z założenia ciąg [math]\displaystyle{ (a_k) }[/math] jest ciągiem Cauchy'ego. Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Wiemy, że istnieje taka liczba [math]\displaystyle{ N_1 }[/math], ża dla wszystch liczb [math]\displaystyle{ m, n \gt N_1 }[/math] jest

[math]\displaystyle{ | a_n - a_m | \lt {\small\frac{\varepsilon}{2}} }[/math]

Ponieważ każdy ciąg Cauchy'ego jest ograniczony (zobacz ZA44), to na mocy twierdzenia Bolzana-Weierstrassa można z ciągu [math]\displaystyle{ (a_k) }[/math] wybrać podciąg zbieżny [math]\displaystyle{ (a_{k_j}) }[/math]. Niech [math]\displaystyle{ \lim_{j \rightarrow \infty} a_{k_j} = \alpha }[/math]. Zatem istnieje taka liczba [math]\displaystyle{ N_2 }[/math], że dla wszystkich [math]\displaystyle{ k_j \gt N_2 }[/math] jest

[math]\displaystyle{ | a_{k_j} - \alpha | \lt {\small\frac{\varepsilon}{2}} }[/math]

Niech [math]\displaystyle{ N_0 = \max (N_1, N_2) }[/math]. Zatem dla [math]\displaystyle{ n, k_j \gt N_0 }[/math] mamy

[math]\displaystyle{ | a_n - \alpha | = | (a_n - a_{k_j}) + (a_{k_j} - \alpha) | \leqslant | a_n - a_{k_j} | + | a_{k_j} - \alpha | \lt {\small\frac{\varepsilon}{2}} + {\small\frac{\varepsilon}{2}} = \varepsilon }[/math]

Wynika stąd, że ciąg [math]\displaystyle{ (a_k) }[/math] jest zbieżny i [math]\displaystyle{ \lim_{k \rightarrow \infty} a_k = \alpha }[/math]. Ponieważ ciąg zbieżny ma tylko jedną granicę, to oczywiście [math]\displaystyle{ \alpha = a }[/math].
□

Twierdzenie Bolzana-Weierstrassa i ciągi Cauchy'ego w [math]\displaystyle{ \mathbb{C} }[/math]

Twierdzenie ZA46 (Bolzana-Weierstrassa dla liczb zespolonych)
Każdy ograniczony ciąg liczb zespolonych ma podciąg zbieżny.

Dowód

Niech [math]\displaystyle{ (c_k) }[/math] będzie rozpatrywanym ciągiem i niech [math]\displaystyle{ c_k = a_k + i b_k }[/math]. Z założenia [math]\displaystyle{ (c_k) }[/math] jest ograniczony, zatem ograniczone są ciągi [math]\displaystyle{ (a_k) \; }[/math] i [math]\displaystyle{ \; (b_k) }[/math], bo [math]\displaystyle{ | a_k | \leqslant | c_k | \; }[/math] i [math]\displaystyle{ \; | b_k | \leqslant | c_k | }[/math]. Z twierdzenia Bolzana-Weierstrassa dla liczb rzeczywistych wynika natychmiast, że z każdego z ciągów [math]\displaystyle{ (a_k) \; }[/math] i [math]\displaystyle{ \; (b_k) }[/math] można wybrać podciąg zbieżny. Oznaczmy te podciągi odpowiednio jako [math]\displaystyle{ (a_{k_j}) \; }[/math] i [math]\displaystyle{ \; (b_{k_j}) }[/math]. Zatem ciąg [math]\displaystyle{ c_{k_j} = a_{k_j} + i b_{k_j} }[/math] jest zbieżny i jest podciągiem ciągu [math]\displaystyle{ (c_k) }[/math]. Co należało pokazać.
□

Definicja ZA47
Powiemy, że ciąg [math]\displaystyle{ (c_n) }[/math] liczb zespolonych jest ciągiem Cauchy'ego, jeżeli dla dowolnej liczby rzeczywistej dodatniej [math]\displaystyle{ \varepsilon }[/math] istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że [math]\displaystyle{ | c_n - c_m | \lt \varepsilon }[/math] dla dowolnych liczb [math]\displaystyle{ m, n }[/math] spełniających warunek [math]\displaystyle{ n \gt N_0 \; }[/math] i [math]\displaystyle{ \; m \gt N_0 }[/math].

Twierdzenie ZA48
Jeżeli ciąg [math]\displaystyle{ (c_n) }[/math] liczb zespolonych jest ciągiem Cauchy'ego i [math]\displaystyle{ \, c_n = a_n + i b_n }[/math], to ciągi [math]\displaystyle{ (a_n) \; }[/math] i [math]\displaystyle{ \; (b_n) }[/math] też są ciągami Cauchy'ego.

Dowód

Niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Z założenia dla dowolnego [math]\displaystyle{ \varepsilon }[/math] istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że dla dowolnych [math]\displaystyle{ m, n \gt N_0 }[/math] jest [math]\displaystyle{ | c_n - c_m | \lt \varepsilon }[/math]. Ponieważ

[math]\displaystyle{ | c_n - c_m | = | (a_n + i b_n) - (a_m + i b_m) | = | (a_n - a_m) + i (b_n - b_m) | = \sqrt{(a_n - a_m)^2 + (b_n - b_m)^2} \lt \varepsilon }[/math]

to tym bardziej [math]\displaystyle{ | a_n - a_m | \lt \varepsilon \; }[/math] i [math]\displaystyle{ \; | b_n - b_m | \lt \varepsilon }[/math]. Zatem ciągi [math]\displaystyle{ (a_n) \; }[/math] i [math]\displaystyle{ \; (b_n) }[/math] też są ciągami Cauchy'ego. Co należało pokazać.
□

Twierdzenie ZA49
Każdy ciąg Cauchy'ego liczb zespolonych jest ograniczony.

Dowód

Niech [math]\displaystyle{ (c_n) }[/math] będzie ciągiem Cauchy'ego liczb zespolonych i [math]\displaystyle{ c_n = a_n + i b_n }[/math]. Ponieważ ciągi [math]\displaystyle{ (a_n) \; }[/math] i [math]\displaystyle{ \; (b_n) }[/math] są ciągami Cauchy'ego liczb rzeczywistych, to są ograniczone (zobacz ZA44). Zatem istnieją takie liczby rzeczywiste [math]\displaystyle{ M_a \; }[/math] i [math]\displaystyle{ \; M_b }[/math], że dla wszystkich [math]\displaystyle{ n \in \mathbb{N}_0 }[/math] jest [math]\displaystyle{ | a_n | \leqslant M_a \; }[/math] i [math]\displaystyle{ \; | b_n | \leqslant M_b }[/math]. Wynika stąd natychmiast, że

[math]\displaystyle{ | c_n | = \sqrt{a^2_n + b^2_n} = \sqrt{| a_n |^2 + | b_n |^2} \leqslant \sqrt{M^2_a + M^2_b} }[/math]

Czyli istnieje taka liczba rzeczywista [math]\displaystyle{ M_c }[/math], że dla wszystkich [math]\displaystyle{ n \in \mathbb{N}_0 }[/math] jest [math]\displaystyle{ | c_n | \leqslant M_c }[/math] (wystarczy przyjąć [math]\displaystyle{ M_c \geqslant \sqrt{M^2_a + M^2_b} }[/math]). Co oznacza, że ciąg Cauchy'ego liczb zespolonych [math]\displaystyle{ (c_n) }[/math] jest ograniczony.
□

Twierdzenie ZA50
Ciąg [math]\displaystyle{ (c_k) }[/math] liczb zespolonych jest zbieżny wtedy i tylko wtedy, gdy jest ciągiem Cauchy'ego.

Dowód

[math]\displaystyle{ \Large{\Longrightarrow} }[/math]
Z założenia ciąg [math]\displaystyle{ (c_k) }[/math] jest zbieżny. Niech [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = c \, }[/math] i niech [math]\displaystyle{ \varepsilon \in \mathbb{R}_+ }[/math]. Z definicji zbieżności wiemy, że dla dowolnego [math]\displaystyle{ \varepsilon }[/math] istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że dla wszystkich [math]\displaystyle{ n \gt N_0 }[/math] jest

[math]\displaystyle{ | c_n - c | \lt {\small\frac{\varepsilon}{2}} }[/math]

Oczywiście jest tak również dla wszystkich [math]\displaystyle{ m \gt N_0 }[/math], czyli

[math]\displaystyle{ | c_m - c | \lt {\small\frac{\varepsilon}{2}} }[/math]

Wynika stąd, że

[math]\displaystyle{ | c_n - c_m | = | (c_n - c) - (c_m - c) | \leqslant | (c_n - c) | + | (c_m - c) | \lt {\small\frac{\varepsilon}{2}} + {\small\frac{\varepsilon}{2}} = \varepsilon }[/math]

Pokazaliśmy, że dla ustalonego [math]\displaystyle{ \varepsilon }[/math] istnieje taka liczba [math]\displaystyle{ N_0 }[/math], że dla wszystkich [math]\displaystyle{ m, n \gt N_0 }[/math] jest [math]\displaystyle{ | c_n - c_m | \lt \varepsilon }[/math], czyli ciąg [math]\displaystyle{ (c_k) }[/math] jest ciągiem Cauchy'ego.

[math]\displaystyle{ \Large{\Longleftarrow} }[/math]
Z założenia ciąg [math]\displaystyle{ (c_k) }[/math] jest ciągiem Cauchy'ego. Niech [math]\displaystyle{ c_k = a_k + i b_k }[/math]. Wiemy, że ciągi [math]\displaystyle{ (a_n) \; }[/math] i [math]\displaystyle{ \; (b_n) }[/math] są ciągami Cauchy'ego liczb rzeczywistych (zobacz ZA48). Zatem ciągi [math]\displaystyle{ (a_n) \; }[/math] i [math]\displaystyle{ \; (b_n) }[/math] są zbieżne (zobacz ZA45). Wynika stąd zbieżność ciągu [math]\displaystyle{ (c_k) }[/math] (zobacz ZA16). Co należało pokazać.
□

Zadanie ZA51
Niech ciąg [math]\displaystyle{ (c_n) }[/math] będzie ograniczonym ciągiem liczb zespolonych, który ma dokładnie dwa punkty skupienia [math]\displaystyle{ z_1 }[/math] i [math]\displaystyle{ z_2 }[/math]. Pokazać, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n \gt N_0 }[/math] wyrazy ciągu [math]\displaystyle{ (c_n) }[/math] spełniają jeden z warunków

[math]\displaystyle{ | c_n - z_1 | \lt \varepsilon \qquad \qquad \text{lub} \qquad \qquad | c_n - z_2 | \lt \varepsilon }[/math]

Rozwiązanie

Z założenia ciąg [math]\displaystyle{ (c_n) }[/math] jest ograniczony, zatem dla [math]\displaystyle{ M \gt 0 }[/math] prawdziwe jest oszacowanie [math]\displaystyle{ | c_n | \leqslant M }[/math]. Przypuśćmy, dla uzyskania sprzeczności, że stwierdzenie, które mamy pokazać, nie jest prawdziwe. Zatem prawdziwe jest jego zaprzeczenie, które brzmi: istnieje takie [math]\displaystyle{ \varepsilon \gt 0 }[/math], że dla każdego [math]\displaystyle{ N_0 }[/math] istnieją takie [math]\displaystyle{ n \gt N_0 }[/math], że wyrazy ciągu [math]\displaystyle{ (c_n) }[/math] nie spełniają żadnego z warunków

[math]\displaystyle{ | c_n - z_1 | \lt \varepsilon \qquad \qquad \text{lub} \qquad \qquad | c_n - z_2 | \lt \varepsilon }[/math]

Wynika stąd, że wyrazów, które nie spełniają powyższych warunków, jest nieskończenie wiele i tworzą one nieskończony i ograniczony podciąg ciągu [math]\displaystyle{ (c_n) }[/math]. Na mocy twierdzenia Bolzana-Weierstrassa z tego podciągu możemy wybrać podciąg zbieżny. Co oznacza, wbrew założeniu, że ciąg [math]\displaystyle{ (c_n) }[/math] ma co najmniej trzy punkty skupienia.
□

Uzupełnienie

Zadanie ZA52
Dla dowolnych [math]\displaystyle{ x, y \in \mathbb{R} }[/math] prawdziwe są nierówności

[math]\displaystyle{ | \sin x - \sin y | \leqslant | x - y | }[/math]

[math]\displaystyle{ | \cos x - \cos y | \leqslant | x - y | }[/math]

Rozwiązanie

Punkt 1.

W przypadku, gdy [math]\displaystyle{ x = y }[/math] nierówność jest prawdziwa. Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ y \gt x }[/math]. Zauważmy, że funkcja [math]\displaystyle{ \sin x }[/math] jest ciągła w przedziale [math]\displaystyle{ [x, y] }[/math] i różniczkowalna w przedziale [math]\displaystyle{ (x, y) }[/math]. Oznacza to, że spełnione są założenia twierdzenia Lagrange'a. Zatem istnieje taki punkt [math]\displaystyle{ a \in (x, y) }[/math], że

[math]\displaystyle{ {\small\frac{\sin y - \sin x}{y - x}} = \sin' (a) = \cos (a) }[/math]

Otrzymujemy

[math]\displaystyle{ \sin y - \sin x = (y - x) \cdot \cos (a) }[/math]

[math]\displaystyle{ | \sin y - \sin x | = | y - x | \cdot | \cos (a) | }[/math]

[math]\displaystyle{ | \sin x - \sin y | \leqslant | x - y | }[/math]

Co należało pokazać. Analogicznie dowodzimy punkt 2.
□

Twierdzenie ZA53
Niech [math]\displaystyle{ x, y \in \mathbb{R} }[/math], [math]\displaystyle{ \, k \in \mathbb{Z} \; }[/math] i [math]\displaystyle{ \; n \in N_0 }[/math]. Część ułamkową liczby rzeczywistej [math]\displaystyle{ x }[/math] definiujemy następująco: [math]\displaystyle{ \{ x \} = x - \lfloor x \rfloor }[/math]. Prawdziwe są następujące właściwości funkcji [math]\displaystyle{ \{ x \} }[/math].

1.      [math]\displaystyle{ \{ k + x \} = \{ x \} }[/math]

2.      [math]\displaystyle{ \{ \{ x \} \} = \{ x \} }[/math]

3.      [math]\displaystyle{ \{ x \} + \{ - x \} = \begin{cases} 0 & \text{gdy } \, x \in \mathbb{Z} \\ 1 & \text{gdy } \, x \notin \mathbb{Z} \\ \end{cases} }[/math]

4.      [math]\displaystyle{ \{ k \{ x \} \} = \{ k x \} }[/math]

5.      [math]\displaystyle{ n \{ x \} \lt 1 \qquad \qquad \, \Longrightarrow \qquad n \{ x \} = \{ n x \} }[/math]

6.      [math]\displaystyle{ \{ x \} \geqslant \{ y \} \qquad \quad \;\;\, \Longrightarrow \qquad \{ x \} - \{ y \} = \{ x - y \} }[/math]

7.      [math]\displaystyle{ \{ x \} + \{ y \} \lt 1 \qquad \Longrightarrow \qquad \{ x \} + \{ y \} = \{ x + y \} }[/math]

Dowód

Punkt 1.

Wynika z analogicznej własności funkcji [math]\displaystyle{ \lfloor x \rfloor }[/math]: [math]\displaystyle{ \lfloor k + x \rfloor = k + \lfloor x \rfloor }[/math], którą łatwo dowodzimy, zapisując [math]\displaystyle{ x }[/math] w postaci [math]\displaystyle{ x = j + \varepsilon }[/math], gdzie [math]\displaystyle{ j \in \mathbb{Z} \; }[/math] i [math]\displaystyle{ \; 0 \lt \varepsilon \lt 1 }[/math].

Punkt 2.

[math]\displaystyle{ \{ \{ x \} \} = \{ x - \lfloor x \rfloor \} = \{ x \} }[/math]

Punkt 3.

W przypadku, gdy [math]\displaystyle{ x \in \mathbb{Z} }[/math] wynik jest natychmiastowy, bo [math]\displaystyle{ \{ x \} + \{ - x \} = 0 + 0 }[/math]. Załóżmy, że [math]\displaystyle{ x \notin \mathbb{Z} }[/math], zatem możemy napisać [math]\displaystyle{ x = k + \varepsilon }[/math], gdzie [math]\displaystyle{ k \in \mathbb{Z} \; }[/math] i [math]\displaystyle{ \; 0 \lt \varepsilon \lt 1 }[/math]. Łatwo zauważamy, że [math]\displaystyle{ 0 \lt 1 - \varepsilon \lt 1 \, }[/math] i otrzymujemy

[math]\displaystyle{ \{ x \} + \{ - x \} = \{ k + \varepsilon \} + \{ - k - \varepsilon \} = \varepsilon + \{ - k - 1 + 1 - \varepsilon \} = \varepsilon + \{ 1 - \varepsilon \} = \varepsilon + 1 - \varepsilon = 1 }[/math]

Punkt 4.

[math]\displaystyle{ \{ k \{ x \} \} = \{ k (x - \lfloor x \rfloor) \} = \{ k x - k \lfloor x \rfloor \} = \{ k x \} }[/math]

Punkt 5.

Z założenia [math]\displaystyle{ 0 \leqslant n \{ x \} \lt 1 }[/math]. Zatem

[math]\displaystyle{ n \{ x \} = \{ n \{ x \} \} = \{ n x \} }[/math]

Gdzie skorzystaliśmy z punktu 4.

Punkt 6.

Z założenia [math]\displaystyle{ 0 \leqslant \{ x \} - \{ y \} \lt 1 }[/math]. Zatem

[math]\displaystyle{ \{ x \} - \{ y \} = \{ \{ x \} - \{ y \} \} = \{ x - \lfloor x \rfloor - y + \lfloor y \rfloor \} = \{ (x - y) + (\lfloor y \rfloor - \lfloor x \rfloor) \} = \{ x - y \} }[/math]

Punkt 7.

Z założenia [math]\displaystyle{ 0 \leqslant \{ x \} + \{ y \} \lt 1 }[/math]. Zatem

[math]\displaystyle{ \{ x \} + \{ y \} = \{ \{ x \} + \{ y \} \} = \{ x - \lfloor x \rfloor + y - \lfloor y \rfloor \} = \{ (x + y) - (\lfloor y \rfloor + \lfloor x \rfloor) \} = \{ x + y \} }[/math]

Co należało pokazać.
□

Twierdzenie ZA54 (zasada szufladkowa)
Jeżeli więcej niż [math]\displaystyle{ n }[/math] przedmiotów (przynajmniej [math]\displaystyle{ n + 1 }[/math]) zostało rozmieszczonych w [math]\displaystyle{ n }[/math] szufladach, to jedna z szuflad zawiera więcej niż jeden przedmiot.

Dowód

Pierwszy sposób
Przypuśćmy, dla uzyskania sprzeczności, że żadna z szuflad nie zawiera więcej niż jednego przedmiotu. Zatem każda z szuflad zawiera jeden lub mniej przedmiotów, czyli ogólna liczba przedmiotów w szufladach nie może być większa niż [math]\displaystyle{ n \cdot 1 = n }[/math], wbrew założeniu, że w szufladach rozmieszczono więcej niż [math]\displaystyle{ n }[/math] przedmiotów.

Drugi sposób
Indukcja matematyczna. Twierdzenie jest prawdziwe dla [math]\displaystyle{ n = 1 }[/math]. Zakładając prawdziwość twierdzenia dla [math]\displaystyle{ n }[/math], przeprowadzimy dla liczby [math]\displaystyle{ n + 1 }[/math] następujące rozumowanie.

Rozmieśćmy więcej niż [math]\displaystyle{ n + 1 }[/math] przedmiotów w [math]\displaystyle{ n + 1 }[/math] szufladach. Zaglądając do jednej z szuflad, możemy stwierdzić, że

a)      zawiera ona więcej niż jeden przedmiot – co kończy dowód

b)      nie zawiera ona żadnego przedmiotu, wynika stąd, że więcej niż [math]\displaystyle{ n + 1 }[/math] przedmiotów (czyli więcej niż [math]\displaystyle{ n }[/math] przedmiotów) zostało rozmieszczonych w pozostałych [math]\displaystyle{ n }[/math] szufladach, zatem z założenia indukcyjnego jedna z nich zawiera więcej niż jeden przedmiot

c)      zawiera ona dokładnie jeden przedmiot, zatem pozostałe więcej niż [math]\displaystyle{ n }[/math] przedmiotów zostało rozmieszczone w pozostałych [math]\displaystyle{ n }[/math] szufladach i ponownie z założenia indukcyjnego wynika, że jedna z pozostałych szuflad zawiera więcej niż jeden przedmiot.

□

Twierdzenie ZA55
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną i niech [math]\displaystyle{ \{ n \alpha \} }[/math] oznacza część ułamkową liczby [math]\displaystyle{ n \alpha }[/math]. Nie istnieją takie różne liczby całkowite [math]\displaystyle{ j, k }[/math], że [math]\displaystyle{ \{ k \alpha \} = \{ j \alpha \} }[/math]. W szczególności dla dowolnej liczby całkowitej [math]\displaystyle{ k \neq 0 }[/math] mamy [math]\displaystyle{ \{ k \alpha \} \neq {\small\frac{p}{q}} }[/math], gdzie [math]\displaystyle{ p, q \in \mathbb{Z} \; }[/math] i [math]\displaystyle{ \; q \neq 0 }[/math].

Dowód

Część ułamkową liczby [math]\displaystyle{ x }[/math] definiujemy następująco: [math]\displaystyle{ \{ x \} = x - \lfloor x \rfloor }[/math]. Przypuśćmy, dla uzyskania sprzeczności, że takie liczby [math]\displaystyle{ j, k }[/math] istnieją. Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ k \gt j }[/math]. Otrzymujemy

[math]\displaystyle{ \{ k \alpha \} = \{ j \alpha \} }[/math]

[math]\displaystyle{ k \alpha - \lfloor k \alpha \rfloor = j \alpha - \lfloor j \alpha \rfloor }[/math]

[math]\displaystyle{ (k - j) \alpha = \lfloor k \alpha \rfloor - \lfloor j \alpha \rfloor }[/math]

[math]\displaystyle{ \alpha = {\small\frac{\lfloor k \alpha \rfloor - \lfloor j \alpha \rfloor}{k - j}} }[/math]

Zatem [math]\displaystyle{ \alpha }[/math] byłaby liczbą wymierną wbrew założeniu. Otrzymana sprzeczność kończy dowód. Gdyby było [math]\displaystyle{ \{ k \alpha \} = {\small\frac{p}{q}} }[/math], to mielibyśmy

[math]\displaystyle{ k \alpha - \lfloor k \alpha \rfloor = {\small\frac{p}{q}} }[/math]

[math]\displaystyle{ k \alpha = {\small\frac{p}{q}} + \lfloor k \alpha \rfloor }[/math]

[math]\displaystyle{ \alpha = {\small\frac{p}{k q}} + {\small\frac{\lfloor k \alpha \rfloor}{k}} }[/math]

Co jest niemożliwe, bo [math]\displaystyle{ \alpha }[/math] jest liczbą niewymierną.
□

Twierdzenie ZA56 (twierdzenie Dirichleta o aproksymacji)
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną i niech [math]\displaystyle{ N \in \mathbb{Z}_+ }[/math]. Istnieją takie liczby całkowite [math]\displaystyle{ p \; }[/math] i [math]\displaystyle{ \; q }[/math], gdzie [math]\displaystyle{ 1 \leqslant q \leqslant N }[/math], że

[math]\displaystyle{ | q \alpha - p | \lt {\small\frac{1}{N}} }[/math]

oraz

[math]\displaystyle{ \left| \alpha - {\small\frac{p}{q}} \right| \lt {\small\frac{1}{q^2}} }[/math]

Dowód

Podzielmy przedział [math]\displaystyle{ [0, 1) }[/math] na [math]\displaystyle{ N }[/math] podprzedziałów, każdy o długości [math]\displaystyle{ {\small\frac{1}{N}} }[/math].

[math]\displaystyle{ [0, 1) = \left[ 0, {\small\frac{1}{N}} \right) \cup \left[ {\small\frac{1}{N}}, {\small\frac{2}{N}} \right) \cup \left[ {\small\frac{2}{N}}, {\small\frac{3}{N}} \right) \cup \ldots \cup \left[ {\small\frac{N - 1}{N}}, 1 \right) }[/math]

Dla [math]\displaystyle{ k = 1, 2, 3, \ldots, N, N + 1 }[/math] wypiszmy części ułamkowe liczb [math]\displaystyle{ k \alpha }[/math], czyli [math]\displaystyle{ \{ k \alpha \} = k \alpha - \lfloor k \alpha \rfloor }[/math]. Dostajemy ciąg liczb

[math]\displaystyle{ \{ 1 \alpha \}, \{ 2 \alpha \}, \{ 3 \alpha \}, \ldots, \{ N \alpha \}, \{ (N + 1) \alpha \} }[/math]

z których każda należy do przedziału [math]\displaystyle{ (0, 1) }[/math].

Mamy [math]\displaystyle{ N + 1 }[/math] różnych liczb [math]\displaystyle{ \{ 1 \alpha \}, \{ 2 \alpha \}, \{ 3 \alpha \}, \ldots, \{ N \alpha \}, \{ (N + 1) \alpha \} \, }[/math] i [math]\displaystyle{ \, N }[/math] przedziałów, zatem z zasady szufladkowej w jednym z przedziałów znajdują się co najmniej dwie z tych liczb. Powiedzmy, że są to liczby [math]\displaystyle{ \{ i \alpha \} }[/math] oraz [math]\displaystyle{ \{ j \alpha \} }[/math]. Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ j \gt i }[/math]. Mamy

[math]\displaystyle{ | \{ j \alpha \} - \{ i \alpha \} | \lt {\small\frac{1}{N}} }[/math]

[math]\displaystyle{ | j \alpha - \lfloor j \alpha \rfloor - i \alpha + \lfloor i \alpha \rfloor | \lt {\small\frac{1}{N}} }[/math]

[math]\displaystyle{ | (j - i) \alpha - \lfloor j \alpha \rfloor + \lfloor i \alpha \rfloor | \lt {\small\frac{1}{N}} }[/math]

[math]\displaystyle{ | (j - i) \alpha - (\lfloor j \alpha \rfloor - \lfloor i \alpha \rfloor) | \lt {\small\frac{1}{N}} }[/math]

Jeżeli położymy [math]\displaystyle{ p = \lfloor j \alpha \rfloor - \lfloor i \alpha \rfloor }[/math] oraz [math]\displaystyle{ q = j - i }[/math], to [math]\displaystyle{ q \geqslant 1 \; }[/math] (bo [math]\displaystyle{ j \neq i }[/math])   i [math]\displaystyle{ \; q \leqslant (N + 1) - 1 = N }[/math]. Zatem otrzymujemy

[math]\displaystyle{ | q \alpha - p | \lt {\small\frac{1}{N}} }[/math]

gdzie [math]\displaystyle{ 1 \leqslant q \leqslant N }[/math]. Stąd łatwo wynika, że

[math]\displaystyle{ \left| \alpha - {\small\frac{p}{q}} \right| \lt {\small\frac{1}{q N}} \leqslant {\small\frac{1}{q^2}} }[/math]

Co należało pokazać.
□

Uwaga ZA57
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną i niech [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math], gdzie [math]\displaystyle{ N \in \mathbb{Z}_+ }[/math], będzie ułamkiem, którego istnienie wynika z twierdzenia Dirichleta o aproksymacji. Zauważmy, że ułamki [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math] dla różnych liczb [math]\displaystyle{ N }[/math] nie muszą być różne. Przykładowo dla [math]\displaystyle{ \alpha = \pi \; }[/math] i [math]\displaystyle{ \; N = 8, \ldots, 105 }[/math] znajdujemy jeden ułamek [math]\displaystyle{ {\small\frac{p_N}{q_N}} = {\small\frac{22}{7}} }[/math]. Jednak wśród ułamków [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math] jest nieskończenie wiele różnych ułamków.

Przypuśćmy, dla uzyskania sprzeczności, że wśród ułamków [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math], jest jedynie skończona ilość różnych ułamków. Gdyby tak było, to dla pewnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] nie byłoby żadnego ułamka [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math] takiego, że

[math]\displaystyle{ \left| \alpha - {\small\frac{p_N}{q_N}} \right| \lt \varepsilon }[/math]

Ale wystarczy przyjąć [math]\displaystyle{ k \gt {\small\frac{1}{\varepsilon}} }[/math], aby pokazać, że taki ułamek istnieje

[math]\displaystyle{ \left| \alpha - {\small\frac{p_k}{q_k}} \right| \lt {\small\frac{1}{q_k \cdot k}} \leqslant {\small\frac{1}{k}} \lt \varepsilon }[/math]

Otrzymana sprzeczność dowodzi, że wśród ułamków [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math] jest nieskończenie wiele różnych ułamków.

Przykład ZA58
Z twierdzenia o aproksymacji Dirichleta wiemy, że [math]\displaystyle{ 1 \leqslant q \leqslant N }[/math]. Dla ustalonego [math]\displaystyle{ q }[/math] mamy

[math]\displaystyle{ q \alpha - {\small\frac{1}{N}} \lt p \lt q \alpha + {\small\frac{1}{N}} }[/math]

Łatwo sprawdzamy, że jedynymi możliwymi wartościami [math]\displaystyle{ p }[/math] są liczby [math]\displaystyle{ p = \lfloor q \alpha \rfloor \; }[/math] i [math]\displaystyle{ \; p = \lfloor q \alpha \rfloor + 1 }[/math].

Dla zadanej liczby niewymiernej [math]\displaystyle{ a }[/math] i liczby całkowitej dodatniej [math]\displaystyle{ N }[/math] wystarczy prosta instrukcja w PARI/GP, aby znaleźć odpowiadające im ułamki [math]\displaystyle{ {\small\frac{p}{q}} }[/math].

for(q = 1, N, m = floor(q*a); for(p = m, m + 1, if( abs(q*a - p) < 1/N, print(p, "   ", q, "   ", p/q, "   ", 1.0*p/q) )))

Okazuje się, że takich ułamków nie ma zbyt wiele. Przykłady ułamków (w postaci nieskracalnej) zebraliśmy w tabeli.

[math]\displaystyle{ \boldsymbol{N} }[/math]	[math]\displaystyle{ 10 }[/math]	[math]\displaystyle{ 10^2 }[/math]	[math]\displaystyle{ 10^3 }[/math]	[math]\displaystyle{ 10^4 }[/math]	[math]\displaystyle{ 10^5 }[/math]	[math]\displaystyle{ 10^6 }[/math]	[math]\displaystyle{ 10^7 }[/math]
[math]\displaystyle{ \boldsymbol{\pi} }[/math]	[math]\displaystyle{ {\small\frac{22}{7}} }[/math]	[math]\displaystyle{ {\small\frac{22}{7}} }[/math]	[math]\displaystyle{ {\small\frac{355}{113}} }[/math]	[math]\displaystyle{ {\small\frac{355}{113}} }[/math]	[math]\displaystyle{ {\small\frac{208341}{66317}} }[/math], [math]\displaystyle{ {\small\frac{312689}{99532}} }[/math]	[math]\displaystyle{ {\small\frac{1146408}{364913}} }[/math]	[math]\displaystyle{ {\small\frac{5419351}{1725033}} }[/math]
[math]\displaystyle{ \boldsymbol{e} }[/math]	[math]\displaystyle{ {\small\frac{19}{7}} }[/math]	[math]\displaystyle{ {\small\frac{193}{71}} }[/math]	[math]\displaystyle{ {\small\frac{1457}{536}} }[/math]	[math]\displaystyle{ {\small\frac{23225}{8544}} }[/math], [math]\displaystyle{ {\small\frac{25946}{9545}} }[/math]	[math]\displaystyle{ {\small\frac{49171}{18089}} }[/math]	[math]\displaystyle{ {\small\frac{1084483}{398959}} }[/math]	[math]\displaystyle{ {\small\frac{13580623}{4996032}} }[/math], [math]\displaystyle{ {\small\frac{14665106}{5394991}} }[/math]
[math]\displaystyle{ \boldsymbol{\sqrt{2}} }[/math]	[math]\displaystyle{ {\small\frac{7}{5}} }[/math]	[math]\displaystyle{ {\small\frac{99}{70}} }[/math], [math]\displaystyle{ {\small\frac{140}{99}} }[/math]	[math]\displaystyle{ {\small\frac{577}{408}} }[/math], [math]\displaystyle{ {\small\frac{1393}{985}} }[/math]	[math]\displaystyle{ {\small\frac{8119}{5741}} }[/math], [math]\displaystyle{ {\small\frac{11482}{8119}} }[/math]	[math]\displaystyle{ {\small\frac{114243}{80782}} }[/math]	[math]\displaystyle{ {\small\frac{665857}{470832}} }[/math]	[math]\displaystyle{ {\small\frac{9369319}{6625109}} }[/math], [math]\displaystyle{ {\small\frac{13250218}{9369319}} }[/math]

Warto też zobaczyć jak znalezione ułamki [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math] zmieniają się ze wzrostem liczby [math]\displaystyle{ N }[/math]. W tabeli mamy tylko takie liczby [math]\displaystyle{ N }[/math], dla których nastąpiła zmiana w znalezionych ułamkach.

[math]\displaystyle{ \boldsymbol{N} }[/math]	[math]\displaystyle{ 1 }[/math]	[math]\displaystyle{ 2 }[/math]	[math]\displaystyle{ 6 }[/math]	[math]\displaystyle{ 7 }[/math]	[math]\displaystyle{ 8 }[/math]	[math]\displaystyle{ 106 }[/math]	[math]\displaystyle{ 113 }[/math]	[math]\displaystyle{ 114 }[/math]	[math]\displaystyle{ 33102 }[/math]	[math]\displaystyle{ 33174 }[/math]	[math]\displaystyle{ 33215 }[/math]	[math]\displaystyle{ 52276 }[/math]	[math]\displaystyle{ 66317 }[/math]	[math]\displaystyle{ 90786 }[/math]	[math]\displaystyle{ 99532 }[/math]	[math]\displaystyle{ 123239 }[/math]	[math]\displaystyle{ 165849 }[/math]	[math]\displaystyle{ 191806 }[/math]	[math]\displaystyle{ 265381 }[/math]	[math]\displaystyle{ 344745 }[/math]	[math]\displaystyle{ 364913 }[/math]
[math]\displaystyle{ \boldsymbol{\pi} }[/math]	[math]\displaystyle{ {\small\frac{3}{1}} , {\small\frac{4}{1}} }[/math]	[math]\displaystyle{ {\small\frac{3}{1}} }[/math]	[math]\displaystyle{ {\small\frac{3}{1}} , {\small\frac{9}{16}} }[/math]	[math]\displaystyle{ {\small\frac{3}{1}} , {\small\frac{22}{7}} }[/math]	[math]\displaystyle{ {\small\frac{22}{7}} }[/math]	[math]\displaystyle{ {\small\frac{22}{7}} , {\small\frac{333}{106}} }[/math]	[math]\displaystyle{ {\small\frac{333}{106}} , {\small\frac{355}{113}} }[/math]	[math]\displaystyle{ {\small\frac{355}{113}} }[/math]	[math]\displaystyle{ {\small\frac{355}{113}} , {\small\frac{103993}{33102}} }[/math]	[math]\displaystyle{ {\small\frac{103993}{33102}} }[/math]	[math]\displaystyle{ {\small\frac{103993}{33102}} , {\small\frac{104348}{33215}} }[/math]	[math]\displaystyle{ {\small\frac{104348}{33215}} }[/math]	[math]\displaystyle{ {\small\frac{104348}{33215}} , {\small\frac{208341}{66317}} }[/math]	[math]\displaystyle{ {\small\frac{208341}{66317}} }[/math]	[math]\displaystyle{ {\small\frac{208341}{66317}} , {\small\frac{312689}{99532}} }[/math]	[math]\displaystyle{ {\small\frac{312689}{99532}} }[/math]	[math]\displaystyle{ {\small\frac{312689}{99532}} , {\small\frac{521030}{165849}} }[/math]	[math]\displaystyle{ {\small\frac{312689}{99532}} }[/math]	[math]\displaystyle{ {\small\frac{312689}{99532}} , {\small\frac{833719}{265381}} }[/math]	[math]\displaystyle{ {\small\frac{833719}{265381}} }[/math]	[math]\displaystyle{ {\small\frac{833719}{265381}} , {\small\frac{1146408}{364913}} }[/math]

Liczbę [math]\displaystyle{ \pi }[/math] możemy zapisać w postaci ułamka łańcuchowego. Mamy

[math]\displaystyle{ \pi = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15, 3, 13, 1, 4, 2, 6, 6, 99, \ldots] }[/math]

Kolejne redukty tego ułamka łańcuchowego tworzą następujący ciąg liczb

[math]\displaystyle{ {\small\frac{3}{1}} }[/math], [math]\displaystyle{ {\small\frac{22}{7}} }[/math], [math]\displaystyle{ {\small\frac{333}{106}} }[/math], [math]\displaystyle{ {\small\frac{355}{113}} }[/math], [math]\displaystyle{ {\small\frac{103993}{33102}} }[/math], [math]\displaystyle{ {\small\frac{104348}{33215}} }[/math], [math]\displaystyle{ {\small\frac{208341}{66317}} }[/math], [math]\displaystyle{ {\small\frac{312689}{99532}} }[/math], [math]\displaystyle{ {\small\frac{833719}{265381}} }[/math], [math]\displaystyle{ {\small\frac{1146408}{364913}} }[/math], [math]\displaystyle{ {\small\frac{4272943}{1360120}} }[/math], [math]\displaystyle{ {\small\frac{5419351}{1725033}} }[/math], [math]\displaystyle{ {\small\frac{80143857}{25510582}} }[/math], [math]\displaystyle{ {\small\frac{245850922}{78256779}} }[/math], ...

Zauważmy, że każdy redukt ułamka łańcuchowego reprezentującego liczbę [math]\displaystyle{ \pi }[/math] występuje wśród ułamków [math]\displaystyle{ {\small\frac{p_N}{q_N}} }[/math].

Twierdzenie ZA59
Między dowolnymi różnymi liczbami rzeczywistymi znajduje się liczba wymierna.

Dowód

Rozważmy dwie liczby rzeczywiste [math]\displaystyle{ x, y }[/math]. Niech [math]\displaystyle{ y \gt x }[/math], [math]\displaystyle{ a = {\small\frac{x + y}{2}} \; }[/math] i [math]\displaystyle{ \; d = y - a = a - x }[/math]. Jeżeli [math]\displaystyle{ a }[/math] jest liczbą wymierną, to twierdzenie jest udowodnione. Jeżeli [math]\displaystyle{ a }[/math] jest liczbą niewymierną, to niech [math]\displaystyle{ N \gt {\small\frac{1}{d}} }[/math].

Pierwszy sposób

Z twierdzenia Dirichleta o aproksymacji mamy

[math]\displaystyle{ \left| a - {\small\frac{p}{q}} \right| \lt {\small\frac{1}{q N}} \leqslant {\small\frac{1}{N}} \lt d }[/math]

Zatem liczba wymierna [math]\displaystyle{ {\small\frac{p}{q}} }[/math] leży między liczbami rzeczywistymi [math]\displaystyle{ x \, }[/math] i [math]\displaystyle{ \, y }[/math].

Drugi sposób

Łatwo zauważamy, że

[math]\displaystyle{ a - {\small\frac{\lfloor a \cdot N \rfloor}{N}} = {\small\frac{a \cdot N - \lfloor a \cdot N \rfloor}{N}} \lt {\small\frac{1}{N}} \lt d }[/math]

Zatem liczba wymierna [math]\displaystyle{ {\small\frac{\lfloor a \cdot N \rfloor}{N}} }[/math] leży między liczbami rzeczywistymi [math]\displaystyle{ x \, }[/math] i [math]\displaystyle{ \, y }[/math]. Co należało pokazać.
□

Twierdzenie ZA60
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną i niech [math]\displaystyle{ m \in \mathbb{Z}_+ }[/math]. Dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka liczba [math]\displaystyle{ m }[/math], że [math]\displaystyle{ \{ m \alpha \} \lt \varepsilon }[/math].

Dowód

Liczbę naturalną [math]\displaystyle{ N }[/math] wybieramy tak, aby [math]\displaystyle{ {\small\frac{1}{N}} \lt \varepsilon }[/math]. Podzielmy przedział [math]\displaystyle{ [0, 1) }[/math] na [math]\displaystyle{ N }[/math] podprzedziałów, każdy o długości [math]\displaystyle{ {\small\frac{1}{N}} }[/math].

[math]\displaystyle{ [0, 1) = \left[ 0, {\small\frac{1}{N}} \right) \cup \left[ {\small\frac{1}{N}}, {\small\frac{2}{N}} \right) \cup \left[ {\small\frac{2}{N}}, {\small\frac{3}{N}} \right) \cup \ldots \cup \left[ {\small\frac{N - 1}{N}}, 1 \right) }[/math]

Dla [math]\displaystyle{ k = 1, 2, 3, \ldots, N, N + 1 }[/math] wypiszmy części ułamkowe liczb [math]\displaystyle{ k \alpha }[/math], czyli [math]\displaystyle{ \{ k \alpha \} = k \alpha - \lfloor k \alpha \rfloor }[/math]. Dostajemy ciąg liczb

[math]\displaystyle{ \{ 1 \alpha \}, \{ 2 \alpha \}, \{ 3 \alpha \}, \ldots, \{ N \alpha \}, \{ (N + 1) \alpha \} }[/math]

z których każda należy do przedziału [math]\displaystyle{ (0, 1) }[/math].

Mamy [math]\displaystyle{ N + 1 }[/math] różnych liczb [math]\displaystyle{ \{ 1 \alpha \}, \{ 2 \alpha \}, \{ 3 \alpha \}, \ldots, \{ N \alpha \}, \{ (N + 1) \alpha \} \; }[/math] i [math]\displaystyle{ \; N }[/math] przedziałów, zatem z zasady szufladkowej wynika, że w jednym z przedziałów znajdują się co najmniej dwie z tych liczb. Powiedzmy, że są to liczby [math]\displaystyle{ \{ i \alpha \} }[/math] oraz [math]\displaystyle{ \{ j \alpha \} }[/math]. Dostajemy

[math]\displaystyle{ | \{ j \alpha \} - \{ i \alpha \} | \lt {\small\frac{1}{N}} }[/math]

Nie zmniejszając ogólności, możemy założyć, że [math]\displaystyle{ \{ j \alpha \} \gt \{ i \alpha \} }[/math]. Zatem (zobacz ZA53 p. 6)

[math]\displaystyle{ | \{ (j - i) \alpha \} | \lt {\small\frac{1}{N}} }[/math]

Połóżmy teraz [math]\displaystyle{ m = j - i }[/math]. Mamy

[math]\displaystyle{ 0 \lt \{ m \alpha \} \lt {\small\frac{1}{N}} }[/math]

Czyli

[math]\displaystyle{ 0 \lt \{ m \alpha \} \lt \varepsilon }[/math]

W przypadku, gdy [math]\displaystyle{ m \gt 0 }[/math] dowód jest zakończony.

Rozważmy przypadek, gdy [math]\displaystyle{ m \lt 0 }[/math]. Wybierzmy liczbę całkowitą dodatnią [math]\displaystyle{ b }[/math] tak, aby spełniony był układ nierówności

[math]\displaystyle{ b \lt {\small\frac{1}{\{ m \alpha \}}} \lt b + 1 }[/math]

Z lewej nierówności wynika, że [math]\displaystyle{ b \{ m \alpha \} \lt 1 }[/math], zatem [math]\displaystyle{ b \{ m \alpha \} = \{ b m \alpha \} }[/math] (zobacz ZA53 p. 5). Przekształcając, otrzymujemy

[math]\displaystyle{ 0 \lt {\small\frac{1}{\{ m \alpha \}}} - b \lt 1 }[/math]

[math]\displaystyle{ 0 \lt 1 - b \{ m \alpha \} \lt \{ m \alpha \} \lt \varepsilon }[/math]

[math]\displaystyle{ 0 \lt 1 - \{ b m \alpha \} \lt \varepsilon }[/math]

Ze wzoru [math]\displaystyle{ 1 - \{ x \} = \{ - x \} }[/math] (zobacz ZA53 p. 3) dostajemy

[math]\displaystyle{ 0 \lt \{ - b m \alpha \} \lt \varepsilon }[/math]

Gdzie [math]\displaystyle{ - b m \in \mathbb{Z}_+ }[/math]. Co kończy dowód.
□

Zadanie ZA61
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną. Pokazać, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje nieskończenie wiele liczb całkowitych dodatnich [math]\displaystyle{ m_j }[/math] takich, że [math]\displaystyle{ \{ m_j \alpha \} \lt \varepsilon }[/math].

Rozwiązanie

Niech [math]\displaystyle{ \varepsilon }[/math] będzie dowolną liczbą rzeczywistą dodatnią. Z twierdzenia ZA60 wiemy, że zbiór liczb całkowitych dodatnich [math]\displaystyle{ m_j }[/math] takich, że [math]\displaystyle{ \{ m_j \alpha \} \lt \varepsilon }[/math] nie jest zbiorem pustym. Przypuśćmy, dla uzyskania sprzeczności, że istnieje jedynie skończona ilość liczb [math]\displaystyle{ m_j }[/math] takich, że [math]\displaystyle{ \{ m_j \alpha \} \lt \varepsilon }[/math]. Niech [math]\displaystyle{ n }[/math] oznacza największą z nich.

Zauważmy, że liczba [math]\displaystyle{ \beta = n \alpha }[/math] jest liczbą niewymierną i dla dowolnego [math]\displaystyle{ \varepsilon' \gt 0 }[/math] istnieje taka liczba [math]\displaystyle{ k \in \mathbb{Z}_+ }[/math], że [math]\displaystyle{ \{ k \beta \} \lt \varepsilon' }[/math].

Niech [math]\displaystyle{ \varepsilon' \lt \min (\varepsilon, \{ \beta \}) }[/math]. Przy takim wyborze liczby [math]\displaystyle{ \varepsilon' }[/math] nie może być [math]\displaystyle{ k = 1 }[/math], bo mielibyśmy [math]\displaystyle{ \varepsilon' \lt \{ \beta \} \lt \varepsilon' }[/math]. Zatem [math]\displaystyle{ k \gt 1 \; }[/math] i [math]\displaystyle{ \; \{ k \beta \} \lt \varepsilon' }[/math], czyli [math]\displaystyle{ \{ k n \alpha \} \lt \varepsilon' \lt \varepsilon }[/math]. Wynika stąd, że [math]\displaystyle{ m_j = k n }[/math] jest kolejną i większą od [math]\displaystyle{ n }[/math] liczbą całkowitą dodatnią taką, że [math]\displaystyle{ \{ m_j \alpha \} \lt \varepsilon }[/math]. Otrzymana sprzeczność kończy dowód.
□

Twierdzenie ZA62
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną. Jeżeli [math]\displaystyle{ g \in [0, 1] }[/math], to [math]\displaystyle{ g }[/math] jest punktem skupienia ciągu [math]\displaystyle{ (\{ n \alpha \}) }[/math].

Dowód

1. Przypadek, gdy [math]\displaystyle{ \boldsymbol{g = 0} }[/math]

Dla ustalonego [math]\displaystyle{ \varepsilon \gt 0 }[/math] w otoczeniu [math]\displaystyle{ (- \varepsilon, \varepsilon) }[/math] znajduje się przynajmniej jeden wyraz ciągu [math]\displaystyle{ a_n = \{ n \alpha \} }[/math] różny od zera. Fakt ten wynika natychmiast z twierdzenia ZA60. Zatem punkt [math]\displaystyle{ g = 0 }[/math] jest punktem skupienia ciągu [math]\displaystyle{ (\{ n \alpha \}) }[/math] (zobacz ZA35).

2. Przypadek, gdy [math]\displaystyle{ \boldsymbol{g \in (0, 1]} }[/math]

Z twierdzenia ZA60 wiemy, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka liczba [math]\displaystyle{ m }[/math], że [math]\displaystyle{ \{ m \alpha \} \lt \varepsilon }[/math]. Nie zmniejszając ogólności, możemy [math]\displaystyle{ \varepsilon }[/math] wybrać tak, aby spełniony był warunek [math]\displaystyle{ \varepsilon \lt g }[/math]. Mamy wtedy [math]\displaystyle{ \{ m \alpha \} \lt \varepsilon \lt g }[/math], czyli [math]\displaystyle{ {\small\frac{g}{\{ m \alpha \}}} \gt 1 }[/math].

Liczbę [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] wybieramy tak, aby

[math]\displaystyle{ n \lt {\small\frac{g}{\{ m \alpha \}}} \leqslant n + 1 }[/math]

Zatem

[math]\displaystyle{ 0 \lt {\small\frac{g}{\{ m \alpha \}}} - n \leqslant 1 }[/math]

[math]\displaystyle{ 0 \lt g - n \{ m \alpha \} \leqslant \{ m \alpha \} \lt \varepsilon }[/math]

Z lewej nierówności otrzymujemy [math]\displaystyle{ n \{ m \alpha \} \lt g \leqslant 1 }[/math]. Z twierdzenia ZA53 p. 5 mamy [math]\displaystyle{ n \{ m \alpha \} = \{ n m \alpha \} }[/math] i ostatecznie dostajemy

[math]\displaystyle{ 0 \lt g - \{ n m \alpha \} \lt \varepsilon }[/math]

Pokazaliśmy, że w otoczeniu [math]\displaystyle{ (g - \varepsilon, g + \varepsilon) }[/math] znajduje się przynajmniej jeden wyraz ciągu [math]\displaystyle{ a_n = \{ n \alpha \} }[/math] różny od [math]\displaystyle{ g }[/math]. Zatem [math]\displaystyle{ g }[/math] jest punktem skupienia ciągu [math]\displaystyle{ (\{ n \alpha \}) }[/math] (zobacz ZA35). Co należało pokazać.
□

Zadanie ZA63
Pokazać, że [math]\displaystyle{ \limsup_{n \rightarrow \infty} \sin n = 1 }[/math].

Rozwiązanie

Niech [math]\displaystyle{ \alpha = {\small\frac{1}{2 \pi}} }[/math]. Ponieważ [math]\displaystyle{ {\small\frac{1}{4}} \in [0, 1] }[/math], to [math]\displaystyle{ {\small\frac{1}{4}} }[/math] jest punktem skupienia ciągu [math]\displaystyle{ a_n = \{ n \alpha \} }[/math] (zobacz ZA62). Zatem istnieje podciąg ciągu [math]\displaystyle{ (a_n) }[/math] zbieżny do [math]\displaystyle{ {\small\frac{1}{4}} }[/math], co oznacza, że istnieje taki silnie rosnący ciąg liczb naturalnych [math]\displaystyle{ k_j }[/math], że [math]\displaystyle{ \lim_{k_j \rightarrow \infty} a_{k_j} = {\small\frac{1}{4}} }[/math], czyli [math]\displaystyle{ \lim_{k_j \rightarrow \infty} \{ k_j \alpha \} = {\small\frac{1}{4}} }[/math]. Z definicji zbieżności wynika, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ k_j \gt N_0 }[/math] jest

[math]\displaystyle{ \left| \{ k_j \alpha \} - {\small\frac{1}{4}} \right| \lt \varepsilon }[/math]

Niech [math]\displaystyle{ k_j \gt N_0 }[/math], mamy

[math]\displaystyle{ | \sin (k_j) - 1 | = \left| \sin \left( 2 \pi \cdot {\small\frac{k_j}{2 \pi}} \right) - \sin \left( {\small\frac{\pi}{2}} \right) \right| }[/math]

[math]\displaystyle{ \quad \, = \left| \sin \left( 2 \pi \cdot \left( \left\lfloor {\small\frac{k_j}{2 \pi}} \right\rfloor + \left\{ {\small\frac{k_j}{2 \pi}} \right\} \right) \right) - \sin \left( {\small\frac{\pi}{2}} \right) \right| }[/math]

[math]\displaystyle{ \quad \, = \left| \sin \left( 2 \pi \cdot \left\lfloor {\small\frac{k_j}{2 \pi}} \right\rfloor + 2 \pi \left\{ {\small\frac{k_j}{2 \pi}} \right\} \right) - \sin \left( {\small\frac{\pi}{2}} \right) \right| }[/math]

[math]\displaystyle{ \quad \, = \left| \sin \left( 2 \pi \left\{ {\small\frac{k_j}{2 \pi}} \right\} \right) - \sin \left( {\small\frac{\pi}{2}} \right) \right| }[/math]

[math]\displaystyle{ \quad \, \leqslant \left| 2 \pi \left\{ {\small\frac{k_j}{2 \pi}} \right\} - {\small\frac{\pi}{2}} \right| }[/math]

[math]\displaystyle{ \quad \, = 2 \pi \left| \left\{ {\small\frac{k_j}{2 \pi}} \right\} - {\small\frac{1}{4}} \right| }[/math]

[math]\displaystyle{ \quad \, \lt 2 \pi \varepsilon }[/math]

Gdzie skorzystaliśmy z nierówności podanej w zadaniu ZA52. Zatem [math]\displaystyle{ \lim_{k_j \rightarrow \infty} \sin (k_j) = 1 }[/math], czyli [math]\displaystyle{ 1 }[/math] jest punktem skupienia ciągu [math]\displaystyle{ (\sin n) }[/math]. Ponieważ [math]\displaystyle{ \sin x \leqslant 1 }[/math], to [math]\displaystyle{ 1 }[/math] największym puntem skupienia, zatem [math]\displaystyle{ \limsup_{n \rightarrow \infty} \sin n = 1 }[/math].
□

Twierdzenie ZA64
Jeżeli [math]\displaystyle{ g \in [- 1, 1] }[/math], to [math]\displaystyle{ g }[/math] jest punktem skupienia ciągu [math]\displaystyle{ s_n = \sin n }[/math].

Dowód

Niech [math]\displaystyle{ \alpha = {\small\frac{1}{2 \pi}} }[/math] i niech liczba rzeczywista [math]\displaystyle{ t \in [0, 2 \pi] }[/math] będzie wybrana tak, aby [math]\displaystyle{ \sin t = g }[/math]. Ponieważ [math]\displaystyle{ {\small\frac{t}{2 \pi}} \in [0, 1] }[/math], to [math]\displaystyle{ {\small\frac{t}{2 \pi}} }[/math] jest punktem skupienia ciągu [math]\displaystyle{ a_n = \{ n \alpha \} }[/math]. Zatem istnieje podciąg ciągu [math]\displaystyle{ (a_n) }[/math] zbieżny do [math]\displaystyle{ {\small\frac{t}{2 \pi}} }[/math], co oznacza, że istnieje taki silnie rosnący ciąg liczb naturalnych [math]\displaystyle{ k_j }[/math], że [math]\displaystyle{ \lim_{k_j \rightarrow \infty} a_{k_j} = {\small\frac{t}{2 \pi}} }[/math], czyli [math]\displaystyle{ \lim_{k_j \rightarrow \infty} \{ k_j \alpha \} = {\small\frac{t}{2 \pi}} }[/math]. Z definicji zbieżności wynika, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ k_j \gt N_0 }[/math] jest

[math]\displaystyle{ \left| \{ k_j \alpha \} - {\small\frac{t}{2 \pi}} \right| \lt \varepsilon }[/math]

Niech [math]\displaystyle{ k_j \gt N_0 }[/math], mamy

[math]\displaystyle{ | \sin (k_j) - g | = | \sin (k_j) - \sin (t) | }[/math]

[math]\displaystyle{ \quad \, = \left| \sin \left( 2 \pi \cdot {\small\frac{k_j}{2 \pi}} \right) - \sin (t) \right| }[/math]

[math]\displaystyle{ \quad \, = \left| \sin \left( 2 \pi \cdot \left( \left\lfloor {\small\frac{k_j}{2 \pi}} \right\rfloor + \left\{ {\small\frac{k_j}{2 \pi}} \right\} \right) \right) - \sin (t) \right| }[/math]

[math]\displaystyle{ \quad \, = \left| \sin \left( 2 \pi \cdot \left\lfloor {\small\frac{k_j}{2 \pi}} \right\rfloor + 2 \pi \cdot \left\{ {\small\frac{k_j}{2 \pi}} \right\} \right) - \sin (t) \right| }[/math]

[math]\displaystyle{ \quad \, = \left| \sin \left( 2 \pi \left\{ {\small\frac{k_j}{2 \pi}} \right\} \right) - \sin (t) \right| }[/math]

[math]\displaystyle{ \quad \, \leqslant \left| 2 \pi \left\{ {\small\frac{k_j}{2 \pi}} \right\} - t \right| }[/math]

[math]\displaystyle{ \quad \, = 2 \pi \left| \left\{ {\small\frac{k_j}{2 \pi}} \right\} - {\small\frac{t}{2 \pi}} \right| }[/math]

[math]\displaystyle{ \quad \, \lt 2 \pi \varepsilon }[/math]

Gdzie skorzystaliśmy z nierówności podanej w zadaniu ZA52. Zatem [math]\displaystyle{ \lim_{k_j \rightarrow \infty} \sin (k_j) = g }[/math], czyli [math]\displaystyle{ g }[/math] jest punktem skupienia ciągu [math]\displaystyle{ s_n = \sin n }[/math]. Co należało pokazać.
□

Twierdzenie ZA65
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną. Dla dowolnego [math]\displaystyle{ x \in \mathbb{R} \, }[/math] i dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka para liczb [math]\displaystyle{ m \in \mathbb{Z}_+ \, }[/math] i [math]\displaystyle{ \; k \in \mathbb{Z} , \, }[/math] że [math]\displaystyle{ \; | m \alpha + k - x | \lt \varepsilon }[/math].

Dowód

Pierwszy sposób

Ponieważ [math]\displaystyle{ \{ x \} \in [0, 1) }[/math], to [math]\displaystyle{ \{ x \} }[/math] jest punktem skupienia ciągu [math]\displaystyle{ (\{ n \alpha \}) }[/math] (zobacz ZA62). Zatem istnieje podciąg [math]\displaystyle{ (\{ n_j \alpha \}) }[/math] ciągu [math]\displaystyle{ (\{ n \alpha \}) }[/math] zbieżny do [math]\displaystyle{ \{ x \} }[/math].

Zauważmy, że dodając [math]\displaystyle{ \lfloor x \rfloor }[/math] do wyrazów podciągu [math]\displaystyle{ (\{ n_j \alpha \}) }[/math], otrzymujemy ciąg zbieżny do [math]\displaystyle{ x }[/math]. Wyrazy tak zmodyfikowanego podciągu możemy zapisać w postaci

[math]\displaystyle{ \lfloor x \rfloor + \{ n_j \alpha \} = \lfloor x \rfloor + n_j \alpha - \lfloor n_j \alpha \rfloor = n_j \alpha + \lfloor x \rfloor - \lfloor n_j \alpha \rfloor }[/math]

Z definicji zbieżności tego podciągu wynika, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje takie [math]\displaystyle{ N_0 }[/math], że dla każdego [math]\displaystyle{ n_j \gt N_0 }[/math] jest

[math]\displaystyle{ | n_j \alpha + \lfloor x \rfloor - \lfloor n_j \alpha \rfloor - x | \lt \varepsilon }[/math]

Liczby [math]\displaystyle{ m = n_j \gt N_0 \; }[/math] i [math]\displaystyle{ \; k = \lfloor x \rfloor - \lfloor n_j \alpha \rfloor }[/math] tworzą parę liczb [math]\displaystyle{ (m, k) }[/math] taką, że [math]\displaystyle{ \; | m \alpha + k - x | \lt \varepsilon }[/math].

Drugi sposób

Z twierdzenia ZA60 wiemy, że dla dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka liczba [math]\displaystyle{ r \in \mathbb{Z}_+ }[/math], że [math]\displaystyle{ \{ r \alpha \} \lt \varepsilon }[/math]. Wybierzmy [math]\displaystyle{ j \in \mathbb{Z} }[/math] tak, aby [math]\displaystyle{ x + j \gt \{ r \alpha \} }[/math] i wybierzmy [math]\displaystyle{ n \in \mathbb{Z}_+ }[/math] tak, aby

[math]\displaystyle{ n \lt {\small\frac{x + j}{\{ r \alpha \}}} \leqslant n + 1 }[/math]

[math]\displaystyle{ 0 \lt {\small\frac{x + j}{\{ r \alpha \}}} - n \leqslant 1 }[/math]

[math]\displaystyle{ 0 \lt x + j - n \{ r \alpha \} \leqslant \{ r \alpha \} \lt \varepsilon }[/math]

Czyli

[math]\displaystyle{ 0 \lt | n \{ r \alpha \} - j - x | \lt \varepsilon }[/math]

Ponieważ [math]\displaystyle{ n \{ r \alpha \} = n r \alpha - n \lfloor r \alpha \rfloor }[/math], to

[math]\displaystyle{ 0 \lt | n r \alpha - n \lfloor r \alpha \rfloor - j - x | \lt \varepsilon }[/math]

Co pokazuje, że poszukiwana para liczb istnieje i jest równa [math]\displaystyle{ (m, k) = (n r, - n \lfloor r \alpha \rfloor - j) }[/math].
□

Zadanie ZA66
Niech [math]\displaystyle{ \alpha }[/math] będzie liczbą niewymierną. Dla dowolnego [math]\displaystyle{ x \in \mathbb{R} \, }[/math] i dowolnego [math]\displaystyle{ \varepsilon \gt 0 }[/math] istnieje taka para liczb całkowitych [math]\displaystyle{ m, n }[/math], że [math]\displaystyle{ | m \alpha + n - x | \lt \varepsilon }[/math].

Rozwiązanie

Niech [math]\displaystyle{ N \in \mathbb{Z}_+ \; }[/math] i [math]\displaystyle{ \; {\small\frac{1}{N}} \lt \varepsilon }[/math]. Z twierdzenia Dirichleta o aproksymacji (ZA56) wiemy, że dla dowolnej liczby [math]\displaystyle{ N }[/math] istnieje taka para liczb [math]\displaystyle{ p, q }[/math], że

[math]\displaystyle{ | q \alpha - p | \lt {\small\frac{1}{N}} \lt \varepsilon }[/math]

Liczbę całkowitą [math]\displaystyle{ j }[/math] wybieramy tak, aby [math]\displaystyle{ x + j \gt | q \alpha - p | }[/math], a liczbę [math]\displaystyle{ k \in \mathbb{Z}_+ }[/math] wybieramy tak, aby

[math]\displaystyle{ k \lt {\small\frac{x + j}{| q \alpha - p |}} \leqslant k + 1 }[/math]

Otrzymujemy

[math]\displaystyle{ 0 \lt {\small\frac{x + j}{| q \alpha - p |}} - k \leqslant 1 }[/math]

[math]\displaystyle{ 0 \lt x + j - k | q \alpha - p | \leqslant | q \alpha - p | \lt \varepsilon }[/math]

[math]\displaystyle{ 0 \lt x + j - k | q \alpha - p | \lt \varepsilon }[/math]

Niech [math]\displaystyle{ s = \operatorname{sgn}(q \alpha - p) }[/math], oczywiście [math]\displaystyle{ s = \pm 1 }[/math]. Mamy [math]\displaystyle{ | q \alpha - p | = s (q \alpha - p) }[/math], zatem

[math]\displaystyle{ 0 \lt x + j - s k q \alpha + s k p \lt \varepsilon }[/math]

Czyli

[math]\displaystyle{ 0 \lt | s k q \alpha - s k p - j - x | \lt \varepsilon }[/math]

Wystarczy położyć: [math]\displaystyle{ m = s k q \; }[/math] i [math]\displaystyle{ \; n = - s k p - j }[/math], gdzie [math]\displaystyle{ k = \left\lceil {\small\frac{x + j}{| q \alpha - p |}} \right\rceil - 1 \; }[/math] i [math]\displaystyle{ \; s = \operatorname{sgn}(q \alpha - p) }[/math].
□